|
Operation
|
Formula
|
Example
|
|
Multiplication: add exponents
|
||
|
Dividing: subtract exponents
|
||
|
Power to a power: multiply exponents
|
||
|
Power of a product: distribute power
|
||
|
power of a quotient: distribute power
|
||
|
Negative exponents: make positive, shift across quotient line
|
or
|
|
|
Zero exponents: always equal to 1
|
<!DOCTYPE html>
<html>
<head>
<meta charset="utf-8" />
<meta name="generator" content="pandoc" />
<meta http-equiv="X-UA-Compatible" content="IE=EDGE" />
<title>03-mathematics.knit</title>
<script src="data:application/javascript;base64,Ly8gUGFuZG9jIDIuOSBhZGRzIGF0dHJpYnV0ZXMgb24gYm90aCBoZWFkZXIgYW5kIGRpdi4gV2UgcmVtb3ZlIHRoZSBmb3JtZXIgKHRvCi8vIGJlIGNvbXBhdGlibGUgd2l0aCB0aGUgYmVoYXZpb3Igb2YgUGFuZG9jIDwgMi44KS4KZG9jdW1lbnQuYWRkRXZlbnRMaXN0ZW5lcignRE9NQ29udGVudExvYWRlZCcsIGZ1bmN0aW9uKGUpIHsKICB2YXIgaHMgPSBkb2N1bWVudC5xdWVyeVNlbGVjdG9yQWxsKCJkaXYuc2VjdGlvbltjbGFzcyo9J2xldmVsJ10gPiA6Zmlyc3QtY2hpbGQiKTsKICB2YXIgaSwgaCwgYTsKICBmb3IgKGkgPSAwOyBpIDwgaHMubGVuZ3RoOyBpKyspIHsKICAgIGggPSBoc1tpXTsKICAgIGlmICghL15oWzEtNl0kL2kudGVzdChoLnRhZ05hbWUpKSBjb250aW51ZTsgIC8vIGl0IHNob3VsZCBiZSBhIGhlYWRlciBoMS1oNgogICAgYSA9IGguYXR0cmlidXRlczsKICAgIHdoaWxlIChhLmxlbmd0aCA+IDApIGgucmVtb3ZlQXR0cmlidXRlKGFbMF0ubmFtZSk7CiAgfQp9KTsK"></script>
<script src="data:application/javascript;base64,LyohIGpRdWVyeSB2MS4xMS4zIHwgKGMpIDIwMDUsIDIwMTUgalF1ZXJ5IEZvdW5kYXRpb24sIEluYy4gfCBqcXVlcnkub3JnL2xpY2Vuc2UgKi8KIWZ1bmN0aW9uKGEsYil7Im9iamVjdCI9PXR5cGVvZiBtb2R1bGUmJiJvYmplY3QiPT10eXBlb2YgbW9kdWxlLmV4cG9ydHM/bW9kdWxlLmV4cG9ydHM9YS5kb2N1bWVudD9iKGEsITApOmZ1bmN0aW9uKGEpe2lmKCFhLmRvY3VtZW50KXRocm93IG5ldyBFcnJvcigialF1ZXJ5IHJlcXVpcmVzIGEgd2luZG93IHdpdGggYSBkb2N1bWVudCIpO3JldHVybiBiKGEpfTpiKGEpfSgidW5kZWZpbmVkIiE9dHlwZW9mIHdpbmRvdz93aW5kb3c6dGhpcyxmdW5jdGlvbihhLGIpe3ZhciBjPVtdLGQ9Yy5zbGljZSxlPWMuY29uY2F0LGY9Yy5wdXNoLGc9Yy5pbmRleE9mLGg9e30saT1oLnRvU3RyaW5nLGo9aC5oYXNPd25Qcm9wZXJ0eSxrPXt9LGw9IjEuMTEuMyIsbT1mdW5jdGlvbihhLGIpe3JldHVybiBuZXcgbS5mbi5pbml0KGEsYil9LG49L15bXHNcdUZFRkZceEEwXSt8W1xzXHVGRUZGXHhBMF0rJC9nLG89L14tbXMtLyxwPS8tKFtcZGEtel0pL2dpLHE9ZnVuY3Rpb24oYSxiKXtyZXR1cm4gYi50b1VwcGVyQ2FzZSgpfTttLmZuPW0ucHJvdG90eXBlPXtqcXVlcnk6bCxjb25zdHJ1Y3RvcjptLHNlbGVjdG9yOiIiLGxlbmd0aDowLHRvQXJyYXk6ZnVuY3Rpb24oKXtyZXR1cm4gZC5jYWxsKHRoaXMpfSxnZXQ6ZnVuY3Rpb24oYSl7cmV0dXJuIG51bGwhPWE/MD5hP3RoaXNbYSt0aGlzLmxlbmd0aF06dGhpc1thXTpkLmNhbGwodGhpcyl9LHB1c2hTdGFjazpmdW5jdGlvbihhKXt2YXIgYj1tLm1lcmdlKHRoaXMuY29uc3RydWN0b3IoKSxhKTtyZXR1cm4gYi5wcmV2T2JqZWN0PXRoaXMsYi5jb250ZXh0PXRoaXMuY29udGV4dCxifSxlYWNoOmZ1bmN0aW9uKGEsYil7cmV0dXJuIG0uZWFjaCh0aGlzLGEsYil9LG1hcDpmdW5jdGlvbihhKXtyZXR1cm4gdGhpcy5wdXNoU3RhY2sobS5tYXAodGhpcyxmdW5jdGlvbihiLGMpe3JldHVybiBhLmNhbGwoYixjLGIpfSkpfSxzbGljZTpmdW5jdGlvbigpe3JldHVybiB0aGlzLnB1c2hTdGFjayhkLmFwcGx5KHRoaXMsYXJndW1lbnRzKSl9LGZpcnN0OmZ1bmN0aW9uKCl7cmV0dXJuIHRoaXMuZXEoMCl9LGxhc3Q6ZnVuY3Rpb24oKXtyZXR1cm4gdGhpcy5lcSgtMSl9LGVxOmZ1bmN0aW9uKGEpe3ZhciBiPXRoaXMubGVuZ3RoLGM9K2ErKDA+YT9iOjApO3JldHVybiB0aGlzLnB1c2hTdGFjayhjPj0wJiZiPmM/W3RoaXNbY11dOltdKX0sZW5kOmZ1bmN0aW9uKCl7cmV0dXJuIHRoaXMucHJldk9iamVjdHx8dGhpcy5jb25zdHJ1Y3RvcihudWxsKX0scHVzaDpmLHNvcnQ6Yy5zb3J0LHNwbGljZTpjLnNwbGljZX0sbS5leHRlbmQ9bS5mbi5leHRlbmQ9ZnVuY3Rpb24oKXt2YXIgYSxiLGMsZCxlLGYsZz1hcmd1bWVudHNbMF18fHt9LGg9MSxpPWFyZ3VtZW50cy5sZW5ndGgsaj0hMTtmb3IoImJvb2xlYW4iPT10eXBlb2YgZyYmKGo9ZyxnPWFyZ3VtZW50c1toXXx8e30saCsrKSwib2JqZWN0Ij09dHlwZW9mIGd8fG0uaXNGdW5jdGlvbihnKXx8KGc9e30pLGg9PT1pJiYoZz10aGlzLGgtLSk7aT5oO2grKylpZihudWxsIT0oZT1hcmd1bWVudHNbaF0pKWZvcihkIGluIGUpYT1nW2RdLGM9ZVtkXSxnIT09YyYmKGomJmMmJihtLmlzUGxhaW5PYmplY3QoYyl8fChiPW0uaXNBcnJheShjKSkpPyhiPyhiPSExLGY9YSYmbS5pc0FycmF5KGEpP2E6W10pOmY9YSYmbS5pc1BsYWluT2JqZWN0KGEpP2E6e30sZ1tkXT1tLmV4dGVuZChqLGYsYykpOnZvaWQgMCE9PWMmJihnW2RdPWMpKTtyZXR1cm4gZ30sbS5leHRlbmQoe2V4cGFuZG86ImpRdWVyeSIrKGwrTWF0aC5yYW5kb20oKSkucmVwbGFjZSgvXEQvZywiIiksaXNSZWFkeTohMCxlcnJvcjpmdW5jdGlvbihhKXt0aHJvdyBuZXcgRXJyb3IoYSl9LG5vb3A6ZnVuY3Rpb24oKXt9LGlzRnVuY3Rpb246ZnVuY3Rpb24oYSl7cmV0dXJuImZ1bmN0aW9uIj09PW0udHlwZShhKX0saXNBcnJheTpBcnJheS5pc0FycmF5fHxmdW5jdGlvbihhKXtyZXR1cm4iYXJyYXkiPT09bS50eXBlKGEpfSxpc1dpbmRvdzpmdW5jdGlvbihhKXtyZXR1cm4gbnVsbCE9YSYmYT09YS53aW5kb3d9LGlzTnVtZXJpYzpmdW5jdGlvbihhKXtyZXR1cm4hbS5pc0FycmF5KGEpJiZhLXBhcnNlRmxvYXQoYSkrMT49MH0saXNFbXB0eU9iamVjdDpmdW5jdGlvbihhKXt2YXIgYjtmb3IoYiBpbiBhKXJldHVybiExO3JldHVybiEwfSxpc1BsYWluT2JqZWN0OmZ1bmN0aW9uKGEpe3ZhciBiO2lmKCFhfHwib2JqZWN0IiE9PW0udHlwZShhKXx8YS5ub2RlVHlwZXx8bS5pc1dpbmRvdyhhKSlyZXR1cm4hMTt0cnl7aWYoYS5jb25zdHJ1Y3RvciYmIWouY2FsbChhLCJjb25zdHJ1Y3RvciIpJiYhai5jYWxsKGEuY29uc3RydWN0b3IucHJvdG90eXBlLCJpc1Byb3RvdHlwZU9mIikpcmV0dXJuITF9Y2F0Y2goYyl7cmV0dXJuITF9aWYoay5vd25MYXN0KWZvcihiIGluIGEpcmV0dXJuIGouY2FsbChhLGIpO2ZvcihiIGluIGEpO3JldHVybiB2b2lkIDA9PT1ifHxqLmNhbGwoYSxiKX0sdHlwZTpmdW5jdGlvbihhKXtyZXR1cm4gbnVsbD09YT9hKyIiOiJvYmplY3QiPT10eXBlb2YgYXx8ImZ1bmN0aW9uIj09dHlwZW9mIGE/aFtpLmNhbGwoYSldfHwib2JqZWN0Ijp0eXBlb2YgYX0sZ2xvYmFsRXZhbDpmdW5jdGlvbihiKXtiJiZtLnRyaW0oYikmJihhLmV4ZWNTY3JpcHR8fGZ1bmN0aW9uKGIpe2EuZXZhbC5jYWxsKGEsYil9KShiKX0sY2FtZWxDYXNlOmZ1bmN0aW9uKGEpe3JldHVybiBhLnJlcGxhY2UobywibXMtIikucmVwbGFjZShwLHEpfSxub2RlTmFtZTpmdW5jdGlvbihhLGIpe3JldHVybiBhLm5vZGVOYW1lJiZhLm5vZGVOYW1lLnRvTG93ZXJDYXNlKCk9PT1iLnRvTG93ZXJDYXNlKCl9LGVhY2g6ZnVuY3Rpb24oYSxiLGMpe3ZhciBkLGU9MCxmPWEubGVuZ3RoLGc9cihhKTtpZihjKXtpZihnKXtmb3IoO2Y+ZTtlKyspaWYoZD1iLmFwcGx5KGFbZV0sYyksZD09PSExKWJyZWFrfWVsc2UgZm9yKGUgaW4gYSlpZihkPWIuYXBwbHkoYVtlXSxjKSxkPT09ITEpYnJlYWt9ZWxzZSBpZihnKXtmb3IoO2Y+ZTtlKyspaWYoZD1iLmNhbGwoYVtlXSxlLGFbZV0pLGQ9PT0hMSlicmVha31lbHNlIGZvcihlIGluIGEpaWYoZD1iLmNhbGwoYVtlXSxlLGFbZV0pLGQ9PT0hMSlicmVhaztyZXR1cm4gYX0sdHJpbTpmdW5jdGlvbihhKXtyZXR1cm4gbnVsbD09YT8iIjooYSsiIikucmVwbGFjZShuLCIiKX0sbWFrZUFycmF5OmZ1bmN0aW9uKGEsYil7dmFyIGM9Ynx8W107cmV0dXJuIG51bGwhPWEmJihyKE9iamVjdChhKSk/bS5tZXJnZShjLCJzdHJpbmciPT10eXBlb2YgYT9bYV06YSk6Zi5jYWxsKGMsYSkpLGN9LGluQXJyYXk6ZnVuY3Rpb24oYSxiLGMpe3ZhciBkO2lmKGIpe2lmKGcpcmV0dXJuIGcuY2FsbChiLGEsYyk7Zm9yKGQ9Yi5sZW5ndGgsYz1jPzA+Yz9NYXRoLm1heCgwLGQrYyk6YzowO2Q+YztjKyspaWYoYyBpbiBiJiZiW2NdPT09YSlyZXR1cm4gY31yZXR1cm4tMX0sbWVyZ2U6ZnVuY3Rpb24oYSxiKXt2YXIgYz0rYi5sZW5ndGgsZD0wLGU9YS5sZW5ndGg7d2hpbGUoYz5kKWFbZSsrXT1iW2QrK107aWYoYyE9PWMpd2hpbGUodm9pZCAwIT09YltkXSlhW2UrK109YltkKytdO3JldHVybiBhLmxlbmd0aD1lLGF9LGdyZXA6ZnVuY3Rpb24oYSxiLGMpe2Zvcih2YXIgZCxlPVtdLGY9MCxnPWEubGVuZ3RoLGg9IWM7Zz5mO2YrKylkPSFiKGFbZl0sZiksZCE9PWgmJmUucHVzaChhW2ZdKTtyZXR1cm4gZX0sbWFwOmZ1bmN0aW9uKGEsYixjKXt2YXIgZCxmPTAsZz1hLmxlbmd0aCxoPXIoYSksaT1bXTtpZihoKWZvcig7Zz5mO2YrKylkPWIoYVtmXSxmLGMpLG51bGwhPWQmJmkucHVzaChkKTtlbHNlIGZvcihmIGluIGEpZD1iKGFbZl0sZixjKSxudWxsIT1kJiZpLnB1c2goZCk7cmV0dXJuIGUuYXBwbHkoW10saSl9LGd1aWQ6MSxwcm94eTpmdW5jdGlvbihhLGIpe3ZhciBjLGUsZjtyZXR1cm4ic3RyaW5nIj09dHlwZW9mIGImJihmPWFbYl0sYj1hLGE9ZiksbS5pc0Z1bmN0aW9uKGEpPyhjPWQuY2FsbChhcmd1bWVudHMsMiksZT1mdW5jdGlvbigpe3JldHVybiBhLmFwcGx5KGJ8fHRoaXMsYy5jb25jYXQoZC5jYWxsKGFyZ3VtZW50cykpKX0sZS5ndWlkPWEuZ3VpZD1hLmd1aWR8fG0uZ3VpZCsrLGUpOnZvaWQgMH0sbm93OmZ1bmN0aW9uKCl7cmV0dXJuK25ldyBEYXRlfSxzdXBwb3J0Omt9KSxtLmVhY2goIkJvb2xlYW4gTnVtYmVyIFN0cmluZyBGdW5jdGlvbiBBcnJheSBEYXRlIFJlZ0V4cCBPYmplY3QgRXJyb3IiLnNwbGl0KCIgIiksZnVuY3Rpb24oYSxiKXtoWyJbb2JqZWN0ICIrYisiXSJdPWIudG9Mb3dlckNhc2UoKX0pO2Z1bmN0aW9uIHIoYSl7dmFyIGI9Imxlbmd0aCJpbiBhJiZhLmxlbmd0aCxjPW0udHlwZShhKTtyZXR1cm4iZnVuY3Rpb24iPT09Y3x8bS5pc1dpbmRvdyhhKT8hMToxPT09YS5ub2RlVHlwZSYmYj8hMDoiYXJyYXkiPT09Y3x8MD09PWJ8fCJudW1iZXIiPT10eXBlb2YgYiYmYj4wJiZiLTEgaW4gYX12YXIgcz1mdW5jdGlvbihhKXt2YXIgYixjLGQsZSxmLGcsaCxpLGosayxsLG0sbixvLHAscSxyLHMsdCx1PSJzaXp6bGUiKzEqbmV3IERhdGUsdj1hLmRvY3VtZW50LHc9MCx4PTAseT1oYSgpLHo9aGEoKSxBPWhhKCksQj1mdW5jdGlvbihhLGIpe3JldHVybiBhPT09YiYmKGw9ITApLDB9LEM9MTw8MzEsRD17fS5oYXNPd25Qcm9wZXJ0eSxFPVtdLEY9RS5wb3AsRz1FLnB1c2gsSD1FLnB1c2gsST1FLnNsaWNlLEo9ZnVuY3Rpb24oYSxiKXtmb3IodmFyIGM9MCxkPWEubGVuZ3RoO2Q+YztjKyspaWYoYVtjXT09PWIpcmV0dXJuIGM7cmV0dXJuLTF9LEs9ImNoZWNrZWR8c2VsZWN0ZWR8YXN5bmN8YXV0b2ZvY3VzfGF1dG9wbGF5fGNvbnRyb2xzfGRlZmVyfGRpc2FibGVkfGhpZGRlbnxpc21hcHxsb29wfG11bHRpcGxlfG9wZW58cmVhZG9ubHl8cmVxdWlyZWR8c2NvcGVkIixMPSJbXFx4MjBcXHRcXHJcXG5cXGZdIixNPSIoPzpcXFxcLnxbXFx3LV18W15cXHgwMC1cXHhhMF0pKyIsTj1NLnJlcGxhY2UoInciLCJ3IyIpLE89IlxcWyIrTCsiKigiK00rIikoPzoiK0wrIiooWypeJHwhfl0/PSkiK0wrIiooPzonKCg/OlxcXFwufFteXFxcXCddKSopJ3xcIigoPzpcXFxcLnxbXlxcXFxcIl0pKilcInwoIitOKyIpKXwpIitMKyIqXFxdIixQPSI6KCIrTSsiKSg/OlxcKCgoJygoPzpcXFxcLnxbXlxcXFwnXSkqKSd8XCIoKD86XFxcXC58W15cXFxcXCJdKSopXCIpfCgoPzpcXFxcLnxbXlxcXFwoKVtcXF1dfCIrTysiKSopfC4qKVxcKXwpIixRPW5ldyBSZWdFeHAoTCsiKyIsImciKSxSPW5ldyBSZWdFeHAoIl4iK0wrIit8KCg/Ol58W15cXFxcXSkoPzpcXFxcLikqKSIrTCsiKyQiLCJnIiksUz1uZXcgUmVnRXhwKCJeIitMKyIqLCIrTCsiKiIpLFQ9bmV3IFJlZ0V4cCgiXiIrTCsiKihbPit+XXwiK0wrIikiK0wrIioiKSxVPW5ldyBSZWdFeHAoIj0iK0wrIiooW15cXF0nXCJdKj8pIitMKyIqXFxdIiwiZyIpLFY9bmV3IFJlZ0V4cChQKSxXPW5ldyBSZWdFeHAoIl4iK04rIiQiKSxYPXtJRDpuZXcgUmVnRXhwKCJeIygiK00rIikiKSxDTEFTUzpuZXcgUmVnRXhwKCJeXFwuKCIrTSsiKSIpLFRBRzpuZXcgUmVnRXhwKCJeKCIrTS5yZXBsYWNlKCJ3IiwidyoiKSsiKSIpLEFUVFI6bmV3IFJlZ0V4cCgiXiIrTyksUFNFVURPOm5ldyBSZWdFeHAoIl4iK1ApLENISUxEOm5ldyBSZWdFeHAoIl46KG9ubHl8Zmlyc3R8bGFzdHxudGh8bnRoLWxhc3QpLShjaGlsZHxvZi10eXBlKSg/OlxcKCIrTCsiKihldmVufG9kZHwoKFsrLV18KShcXGQqKW58KSIrTCsiKig/OihbKy1dfCkiK0wrIiooXFxkKyl8KSkiK0wrIipcXCl8KSIsImkiKSxib29sOm5ldyBSZWdFeHAoIl4oPzoiK0srIikkIiwiaSIpLG5lZWRzQ29udGV4dDpuZXcgUmVnRXhwKCJeIitMKyIqWz4rfl18OihldmVufG9kZHxlcXxndHxsdHxudGh8Zmlyc3R8bGFzdCkoPzpcXCgiK0wrIiooKD86LVxcZCk/XFxkKikiK0wrIipcXCl8KSg/PVteLV18JCkiLCJpIil9LFk9L14oPzppbnB1dHxzZWxlY3R8dGV4dGFyZWF8YnV0dG9uKSQvaSxaPS9eaFxkJC9pLCQ9L15bXntdK1x7XHMqXFtuYXRpdmUgXHcvLF89L14oPzojKFtcdy1dKyl8KFx3Kyl8XC4oW1x3LV0rKSkkLyxhYT0vWyt+XS8sYmE9Lyd8XFwvZyxjYT1uZXcgUmVnRXhwKCJcXFxcKFtcXGRhLWZdezEsNn0iK0wrIj98KCIrTCsiKXwuKSIsImlnIiksZGE9ZnVuY3Rpb24oYSxiLGMpe3ZhciBkPSIweCIrYi02NTUzNjtyZXR1cm4gZCE9PWR8fGM/YjowPmQ/U3RyaW5nLmZyb21DaGFyQ29kZShkKzY1NTM2KTpTdHJpbmcuZnJvbUNoYXJDb2RlKGQ+PjEwfDU1Mjk2LDEwMjMmZHw1NjMyMCl9LGVhPWZ1bmN0aW9uKCl7bSgpfTt0cnl7SC5hcHBseShFPUkuY2FsbCh2LmNoaWxkTm9kZXMpLHYuY2hpbGROb2RlcyksRVt2LmNoaWxkTm9kZXMubGVuZ3RoXS5ub2RlVHlwZX1jYXRjaChmYSl7SD17YXBwbHk6RS5sZW5ndGg/ZnVuY3Rpb24oYSxiKXtHLmFwcGx5KGEsSS5jYWxsKGIpKX06ZnVuY3Rpb24oYSxiKXt2YXIgYz1hLmxlbmd0aCxkPTA7d2hpbGUoYVtjKytdPWJbZCsrXSk7YS5sZW5ndGg9Yy0xfX19ZnVuY3Rpb24gZ2EoYSxiLGQsZSl7dmFyIGYsaCxqLGssbCxvLHIscyx3LHg7aWYoKGI/Yi5vd25lckRvY3VtZW50fHxiOnYpIT09biYmbShiKSxiPWJ8fG4sZD1kfHxbXSxrPWIubm9kZVR5cGUsInN0cmluZyIhPXR5cGVvZiBhfHwhYXx8MSE9PWsmJjkhPT1rJiYxMSE9PWspcmV0dXJuIGQ7aWYoIWUmJnApe2lmKDExIT09ayYmKGY9Xy5leGVjKGEpKSlpZihqPWZbMV0pe2lmKDk9PT1rKXtpZihoPWIuZ2V0RWxlbWVudEJ5SWQoaiksIWh8fCFoLnBhcmVudE5vZGUpcmV0dXJuIGQ7aWYoaC5pZD09PWopcmV0dXJuIGQucHVzaChoKSxkfWVsc2UgaWYoYi5vd25lckRvY3VtZW50JiYoaD1iLm93bmVyRG9jdW1lbnQuZ2V0RWxlbWVudEJ5SWQoaikpJiZ0KGIsaCkmJmguaWQ9PT1qKXJldHVybiBkLnB1c2goaCksZH1lbHNle2lmKGZbMl0pcmV0dXJuIEguYXBwbHkoZCxiLmdldEVsZW1lbnRzQnlUYWdOYW1lKGEpKSxkO2lmKChqPWZbM10pJiZjLmdldEVsZW1lbnRzQnlDbGFzc05hbWUpcmV0dXJuIEguYXBwbHkoZCxiLmdldEVsZW1lbnRzQnlDbGFzc05hbWUoaikpLGR9aWYoYy5xc2EmJighcXx8IXEudGVzdChhKSkpe2lmKHM9cj11LHc9Yix4PTEhPT1rJiZhLDE9PT1rJiYib2JqZWN0IiE9PWIubm9kZU5hbWUudG9Mb3dlckNhc2UoKSl7bz1nKGEpLChyPWIuZ2V0QXR0cmlidXRlKCJpZCIpKT9zPXIucmVwbGFjZShiYSwiXFwkJiIpOmIuc2V0QXR0cmlidXRlKCJpZCIscykscz0iW2lkPSciK3MrIiddICIsbD1vLmxlbmd0aDt3aGlsZShsLS0pb1tsXT1zK3JhKG9bbF0pO3c9YWEudGVzdChhKSYmcGEoYi5wYXJlbnROb2RlKXx8Yix4PW8uam9pbigiLCIpfWlmKHgpdHJ5e3JldHVybiBILmFwcGx5KGQsdy5xdWVyeVNlbGVjdG9yQWxsKHgpKSxkfWNhdGNoKHkpe31maW5hbGx5e3J8fGIucmVtb3ZlQXR0cmlidXRlKCJpZCIpfX19cmV0dXJuIGkoYS5yZXBsYWNlKFIsIiQxIiksYixkLGUpfWZ1bmN0aW9uIGhhKCl7dmFyIGE9W107ZnVuY3Rpb24gYihjLGUpe3JldHVybiBhLnB1c2goYysiICIpPmQuY2FjaGVMZW5ndGgmJmRlbGV0ZSBiW2Euc2hpZnQoKV0sYltjKyIgIl09ZX1yZXR1cm4gYn1mdW5jdGlvbiBpYShhKXtyZXR1cm4gYVt1XT0hMCxhfWZ1bmN0aW9uIGphKGEpe3ZhciBiPW4uY3JlYXRlRWxlbWVudCgiZGl2Iik7dHJ5e3JldHVybiEhYShiKX1jYXRjaChjKXtyZXR1cm4hMX1maW5hbGx5e2IucGFyZW50Tm9kZSYmYi5wYXJlbnROb2RlLnJlbW92ZUNoaWxkKGIpLGI9bnVsbH19ZnVuY3Rpb24ga2EoYSxiKXt2YXIgYz1hLnNwbGl0KCJ8IiksZT1hLmxlbmd0aDt3aGlsZShlLS0pZC5hdHRySGFuZGxlW2NbZV1dPWJ9ZnVuY3Rpb24gbGEoYSxiKXt2YXIgYz1iJiZhLGQ9YyYmMT09PWEubm9kZVR5cGUmJjE9PT1iLm5vZGVUeXBlJiYofmIuc291cmNlSW5kZXh8fEMpLSh+YS5zb3VyY2VJbmRleHx8Qyk7aWYoZClyZXR1cm4gZDtpZihjKXdoaWxlKGM9Yy5uZXh0U2libGluZylpZihjPT09YilyZXR1cm4tMTtyZXR1cm4gYT8xOi0xfWZ1bmN0aW9uIG1hKGEpe3JldHVybiBmdW5jdGlvbihiKXt2YXIgYz1iLm5vZGVOYW1lLnRvTG93ZXJDYXNlKCk7cmV0dXJuImlucHV0Ij09PWMmJmIudHlwZT09PWF9fWZ1bmN0aW9uIG5hKGEpe3JldHVybiBmdW5jdGlvbihiKXt2YXIgYz1iLm5vZGVOYW1lLnRvTG93ZXJDYXNlKCk7cmV0dXJuKCJpbnB1dCI9PT1jfHwiYnV0dG9uIj09PWMpJiZiLnR5cGU9PT1hfX1mdW5jdGlvbiBvYShhKXtyZXR1cm4gaWEoZnVuY3Rpb24oYil7cmV0dXJuIGI9K2IsaWEoZnVuY3Rpb24oYyxkKXt2YXIgZSxmPWEoW10sYy5sZW5ndGgsYiksZz1mLmxlbmd0aDt3aGlsZShnLS0pY1tlPWZbZ11dJiYoY1tlXT0hKGRbZV09Y1tlXSkpfSl9KX1mdW5jdGlvbiBwYShhKXtyZXR1cm4gYSYmInVuZGVmaW5lZCIhPXR5cGVvZiBhLmdldEVsZW1lbnRzQnlUYWdOYW1lJiZhfWM9Z2Euc3VwcG9ydD17fSxmPWdhLmlzWE1MPWZ1bmN0aW9uKGEpe3ZhciBiPWEmJihhLm93bmVyRG9jdW1lbnR8fGEpLmRvY3VtZW50RWxlbWVudDtyZXR1cm4gYj8iSFRNTCIhPT1iLm5vZGVOYW1lOiExfSxtPWdhLnNldERvY3VtZW50PWZ1bmN0aW9uKGEpe3ZhciBiLGUsZz1hP2Eub3duZXJEb2N1bWVudHx8YTp2O3JldHVybiBnIT09biYmOT09PWcubm9kZVR5cGUmJmcuZG9jdW1lbnRFbGVtZW50PyhuPWcsbz1nLmRvY3VtZW50RWxlbWVudCxlPWcuZGVmYXVsdFZpZXcsZSYmZSE9PWUudG9wJiYoZS5hZGRFdmVudExpc3RlbmVyP2UuYWRkRXZlbnRMaXN0ZW5lcigidW5sb2FkIixlYSwhMSk6ZS5hdHRhY2hFdmVudCYmZS5hdHRhY2hFdmVudCgib251bmxvYWQiLGVhKSkscD0hZihnKSxjLmF0dHJpYnV0ZXM9amEoZnVuY3Rpb24oYSl7cmV0dXJuIGEuY2xhc3NOYW1lPSJpIiwhYS5nZXRBdHRyaWJ1dGUoImNsYXNzTmFtZSIpfSksYy5nZXRFbGVtZW50c0J5VGFnTmFtZT1qYShmdW5jdGlvbihhKXtyZXR1cm4gYS5hcHBlbmRDaGlsZChnLmNyZWF0ZUNvbW1lbnQoIiIpKSwhYS5nZXRFbGVtZW50c0J5VGFnTmFtZSgiKiIpLmxlbmd0aH0pLGMuZ2V0RWxlbWVudHNCeUNsYXNzTmFtZT0kLnRlc3QoZy5nZXRFbGVtZW50c0J5Q2xhc3NOYW1lKSxjLmdldEJ5SWQ9amEoZnVuY3Rpb24oYSl7cmV0dXJuIG8uYXBwZW5kQ2hpbGQoYSkuaWQ9dSwhZy5nZXRFbGVtZW50c0J5TmFtZXx8IWcuZ2V0RWxlbWVudHNCeU5hbWUodSkubGVuZ3RofSksYy5nZXRCeUlkPyhkLmZpbmQuSUQ9ZnVuY3Rpb24oYSxiKXtpZigidW5kZWZpbmVkIiE9dHlwZW9mIGIuZ2V0RWxlbWVudEJ5SWQmJnApe3ZhciBjPWIuZ2V0RWxlbWVudEJ5SWQoYSk7cmV0dXJuIGMmJmMucGFyZW50Tm9kZT9bY106W119fSxkLmZpbHRlci5JRD1mdW5jdGlvbihhKXt2YXIgYj1hLnJlcGxhY2UoY2EsZGEpO3JldHVybiBmdW5jdGlvbihhKXtyZXR1cm4gYS5nZXRBdHRyaWJ1dGUoImlkIik9PT1ifX0pOihkZWxldGUgZC5maW5kLklELGQuZmlsdGVyLklEPWZ1bmN0aW9uKGEpe3ZhciBiPWEucmVwbGFjZShjYSxkYSk7cmV0dXJuIGZ1bmN0aW9uKGEpe3ZhciBjPSJ1bmRlZmluZWQiIT10eXBlb2YgYS5nZXRBdHRyaWJ1dGVOb2RlJiZhLmdldEF0dHJpYnV0ZU5vZGUoImlkIik7cmV0dXJuIGMmJmMudmFsdWU9PT1ifX0pLGQuZmluZC5UQUc9Yy5nZXRFbGVtZW50c0J5VGFnTmFtZT9mdW5jdGlvbihhLGIpe3JldHVybiJ1bmRlZmluZWQiIT10eXBlb2YgYi5nZXRFbGVtZW50c0J5VGFnTmFtZT9iLmdldEVsZW1lbnRzQnlUYWdOYW1lKGEpOmMucXNhP2IucXVlcnlTZWxlY3RvckFsbChhKTp2b2lkIDB9OmZ1bmN0aW9uKGEsYil7dmFyIGMsZD1bXSxlPTAsZj1iLmdldEVsZW1lbnRzQnlUYWdOYW1lKGEpO2lmKCIqIj09PWEpe3doaWxlKGM9ZltlKytdKTE9PT1jLm5vZGVUeXBlJiZkLnB1c2goYyk7cmV0dXJuIGR9cmV0dXJuIGZ9LGQuZmluZC5DTEFTUz1jLmdldEVsZW1lbnRzQnlDbGFzc05hbWUmJmZ1bmN0aW9uKGEsYil7cmV0dXJuIHA/Yi5nZXRFbGVtZW50c0J5Q2xhc3NOYW1lKGEpOnZvaWQgMH0scj1bXSxxPVtdLChjLnFzYT0kLnRlc3QoZy5xdWVyeVNlbGVjdG9yQWxsKSkmJihqYShmdW5jdGlvbihhKXtvLmFwcGVuZENoaWxkKGEpLmlubmVySFRNTD0iPGEgaWQ9JyIrdSsiJz48L2E+PHNlbGVjdCBpZD0nIit1KyItXGZdJyBtc2FsbG93Y2FwdHVyZT0nJz48b3B0aW9uIHNlbGVjdGVkPScnPjwvb3B0aW9uPjwvc2VsZWN0PiIsYS5xdWVyeVNlbGVjdG9yQWxsKCJbbXNhbGxvd2NhcHR1cmVePScnXSIpLmxlbmd0aCYmcS5wdXNoKCJbKl4kXT0iK0wrIiooPzonJ3xcIlwiKSIpLGEucXVlcnlTZWxlY3RvckFsbCgiW3NlbGVjdGVkXSIpLmxlbmd0aHx8cS5wdXNoKCJcXFsiK0wrIiooPzp2YWx1ZXwiK0srIikiKSxhLnF1ZXJ5U2VsZWN0b3JBbGwoIltpZH49Iit1KyItXSIpLmxlbmd0aHx8cS5wdXNoKCJ+PSIpLGEucXVlcnlTZWxlY3RvckFsbCgiOmNoZWNrZWQiKS5sZW5ndGh8fHEucHVzaCgiOmNoZWNrZWQiKSxhLnF1ZXJ5U2VsZWN0b3JBbGwoImEjIit1KyIrKiIpLmxlbmd0aHx8cS5wdXNoKCIuIy4rWyt+XSIpfSksamEoZnVuY3Rpb24oYSl7dmFyIGI9Zy5jcmVhdGVFbGVtZW50KCJpbnB1dCIpO2Iuc2V0QXR0cmlidXRlKCJ0eXBlIiwiaGlkZGVuIiksYS5hcHBlbmRDaGlsZChiKS5zZXRBdHRyaWJ1dGUoIm5hbWUiLCJEIiksYS5xdWVyeVNlbGVjdG9yQWxsKCJbbmFtZT1kXSIpLmxlbmd0aCYmcS5wdXNoKCJuYW1lIitMKyIqWypeJHwhfl0/PSIpLGEucXVlcnlTZWxlY3RvckFsbCgiOmVuYWJsZWQiKS5sZW5ndGh8fHEucHVzaCgiOmVuYWJsZWQiLCI6ZGlzYWJsZWQiKSxhLnF1ZXJ5U2VsZWN0b3JBbGwoIiosOngiKSxxLnB1c2goIiwuKjoiKX0pKSwoYy5tYXRjaGVzU2VsZWN0b3I9JC50ZXN0KHM9by5tYXRjaGVzfHxvLndlYmtpdE1hdGNoZXNTZWxlY3Rvcnx8by5tb3pNYXRjaGVzU2VsZWN0b3J8fG8ub01hdGNoZXNTZWxlY3Rvcnx8by5tc01hdGNoZXNTZWxlY3RvcikpJiZqYShmdW5jdGlvbihhKXtjLmRpc2Nvbm5lY3RlZE1hdGNoPXMuY2FsbChhLCJkaXYiKSxzLmNhbGwoYSwiW3MhPScnXTp4Iiksci5wdXNoKCIhPSIsUCl9KSxxPXEubGVuZ3RoJiZuZXcgUmVnRXhwKHEuam9pbigifCIpKSxyPXIubGVuZ3RoJiZuZXcgUmVnRXhwKHIuam9pbigifCIpKSxiPSQudGVzdChvLmNvbXBhcmVEb2N1bWVudFBvc2l0aW9uKSx0PWJ8fCQudGVzdChvLmNvbnRhaW5zKT9mdW5jdGlvbihhLGIpe3ZhciBjPTk9PT1hLm5vZGVUeXBlP2EuZG9jdW1lbnRFbGVtZW50OmEsZD1iJiZiLnBhcmVudE5vZGU7cmV0dXJuIGE9PT1kfHwhKCFkfHwxIT09ZC5ub2RlVHlwZXx8IShjLmNvbnRhaW5zP2MuY29udGFpbnMoZCk6YS5jb21wYXJlRG9jdW1lbnRQb3NpdGlvbiYmMTYmYS5jb21wYXJlRG9jdW1lbnRQb3NpdGlvbihkKSkpfTpmdW5jdGlvbihhLGIpe2lmKGIpd2hpbGUoYj1iLnBhcmVudE5vZGUpaWYoYj09PWEpcmV0dXJuITA7cmV0dXJuITF9LEI9Yj9mdW5jdGlvbihhLGIpe2lmKGE9PT1iKXJldHVybiBsPSEwLDA7dmFyIGQ9IWEuY29tcGFyZURvY3VtZW50UG9zaXRpb24tIWIuY29tcGFyZURvY3VtZW50UG9zaXRpb247cmV0dXJuIGQ/ZDooZD0oYS5vd25lckRvY3VtZW50fHxhKT09PShiLm93bmVyRG9jdW1lbnR8fGIpP2EuY29tcGFyZURvY3VtZW50UG9zaXRpb24oYik6MSwxJmR8fCFjLnNvcnREZXRhY2hlZCYmYi5jb21wYXJlRG9jdW1lbnRQb3NpdGlvbihhKT09PWQ/YT09PWd8fGEub3duZXJEb2N1bWVudD09PXYmJnQodixhKT8tMTpiPT09Z3x8Yi5vd25lckRvY3VtZW50PT09diYmdCh2LGIpPzE6az9KKGssYSktSihrLGIpOjA6NCZkPy0xOjEpfTpmdW5jdGlvbihhLGIpe2lmKGE9PT1iKXJldHVybiBsPSEwLDA7dmFyIGMsZD0wLGU9YS5wYXJlbnROb2RlLGY9Yi5wYXJlbnROb2RlLGg9W2FdLGk9W2JdO2lmKCFlfHwhZilyZXR1cm4gYT09PWc/LTE6Yj09PWc/MTplPy0xOmY/MTprP0ooayxhKS1KKGssYik6MDtpZihlPT09ZilyZXR1cm4gbGEoYSxiKTtjPWE7d2hpbGUoYz1jLnBhcmVudE5vZGUpaC51bnNoaWZ0KGMpO2M9Yjt3aGlsZShjPWMucGFyZW50Tm9kZSlpLnVuc2hpZnQoYyk7d2hpbGUoaFtkXT09PWlbZF0pZCsrO3JldHVybiBkP2xhKGhbZF0saVtkXSk6aFtkXT09PXY/LTE6aVtkXT09PXY/MTowfSxnKTpufSxnYS5tYXRjaGVzPWZ1bmN0aW9uKGEsYil7cmV0dXJuIGdhKGEsbnVsbCxudWxsLGIpfSxnYS5tYXRjaGVzU2VsZWN0b3I9ZnVuY3Rpb24oYSxiKXtpZigoYS5vd25lckRvY3VtZW50fHxhKSE9PW4mJm0oYSksYj1iLnJlcGxhY2UoVSwiPSckMSddIiksISghYy5tYXRjaGVzU2VsZWN0b3J8fCFwfHxyJiZyLnRlc3QoYil8fHEmJnEudGVzdChiKSkpdHJ5e3ZhciBkPXMuY2FsbChhLGIpO2lmKGR8fGMuZGlzY29ubmVjdGVkTWF0Y2h8fGEuZG9jdW1lbnQmJjExIT09YS5kb2N1bWVudC5ub2RlVHlwZSlyZXR1cm4gZH1jYXRjaChlKXt9cmV0dXJuIGdhKGIsbixudWxsLFthXSkubGVuZ3RoPjB9LGdhLmNvbnRhaW5zPWZ1bmN0aW9uKGEsYil7cmV0dXJuKGEub3duZXJEb2N1bWVudHx8YSkhPT1uJiZtKGEpLHQoYSxiKX0sZ2EuYXR0cj1mdW5jdGlvbihhLGIpeyhhLm93bmVyRG9jdW1lbnR8fGEpIT09biYmbShhKTt2YXIgZT1kLmF0dHJIYW5kbGVbYi50b0xvd2VyQ2FzZSgpXSxmPWUmJkQuY2FsbChkLmF0dHJIYW5kbGUsYi50b0xvd2VyQ2FzZSgpKT9lKGEsYiwhcCk6dm9pZCAwO3JldHVybiB2b2lkIDAhPT1mP2Y6Yy5hdHRyaWJ1dGVzfHwhcD9hLmdldEF0dHJpYnV0ZShiKTooZj1hLmdldEF0dHJpYnV0ZU5vZGUoYikpJiZmLnNwZWNpZmllZD9mLnZhbHVlOm51bGx9LGdhLmVycm9yPWZ1bmN0aW9uKGEpe3Rocm93IG5ldyBFcnJvcigiU3ludGF4IGVycm9yLCB1bnJlY29nbml6ZWQgZXhwcmVzc2lvbjogIithKX0sZ2EudW5pcXVlU29ydD1mdW5jdGlvbihhKXt2YXIgYixkPVtdLGU9MCxmPTA7aWYobD0hYy5kZXRlY3REdXBsaWNhdGVzLGs9IWMuc29ydFN0YWJsZSYmYS5zbGljZSgwKSxhLnNvcnQoQiksbCl7d2hpbGUoYj1hW2YrK10pYj09PWFbZl0mJihlPWQucHVzaChmKSk7d2hpbGUoZS0tKWEuc3BsaWNlKGRbZV0sMSl9cmV0dXJuIGs9bnVsbCxhfSxlPWdhLmdldFRleHQ9ZnVuY3Rpb24oYSl7dmFyIGIsYz0iIixkPTAsZj1hLm5vZGVUeXBlO2lmKGYpe2lmKDE9PT1mfHw5PT09Znx8MTE9PT1mKXtpZigic3RyaW5nIj09dHlwZW9mIGEudGV4dENvbnRlbnQpcmV0dXJuIGEudGV4dENvbnRlbnQ7Zm9yKGE9YS5maXJzdENoaWxkO2E7YT1hLm5leHRTaWJsaW5nKWMrPWUoYSl9ZWxzZSBpZigzPT09Znx8ND09PWYpcmV0dXJuIGEubm9kZVZhbHVlfWVsc2Ugd2hpbGUoYj1hW2QrK10pYys9ZShiKTtyZXR1cm4gY30sZD1nYS5zZWxlY3RvcnM9e2NhY2hlTGVuZ3RoOjUwLGNyZWF0ZVBzZXVkbzppYSxtYXRjaDpYLGF0dHJIYW5kbGU6e30sZmluZDp7fSxyZWxhdGl2ZTp7Ij4iOntkaXI6InBhcmVudE5vZGUiLGZpcnN0OiEwfSwiICI6e2RpcjoicGFyZW50Tm9kZSJ9LCIrIjp7ZGlyOiJwcmV2aW91c1NpYmxpbmciLGZpcnN0OiEwfSwifiI6e2RpcjoicHJldmlvdXNTaWJsaW5nIn19LHByZUZpbHRlcjp7QVRUUjpmdW5jdGlvbihhKXtyZXR1cm4gYVsxXT1hWzFdLnJlcGxhY2UoY2EsZGEpLGFbM109KGFbM118fGFbNF18fGFbNV18fCIiKS5yZXBsYWNlKGNhLGRhKSwifj0iPT09YVsyXSYmKGFbM109IiAiK2FbM10rIiAiKSxhLnNsaWNlKDAsNCl9LENISUxEOmZ1bmN0aW9uKGEpe3JldHVybiBhWzFdPWFbMV0udG9Mb3dlckNhc2UoKSwibnRoIj09PWFbMV0uc2xpY2UoMCwzKT8oYVszXXx8Z2EuZXJyb3IoYVswXSksYVs0XT0rKGFbNF0/YVs1XSsoYVs2XXx8MSk6MiooImV2ZW4iPT09YVszXXx8Im9kZCI9PT1hWzNdKSksYVs1XT0rKGFbN10rYVs4XXx8Im9kZCI9PT1hWzNdKSk6YVszXSYmZ2EuZXJyb3IoYVswXSksYX0sUFNFVURPOmZ1bmN0aW9uKGEpe3ZhciBiLGM9IWFbNl0mJmFbMl07cmV0dXJuIFguQ0hJTEQudGVzdChhWzBdKT9udWxsOihhWzNdP2FbMl09YVs0XXx8YVs1XXx8IiI6YyYmVi50ZXN0KGMpJiYoYj1nKGMsITApKSYmKGI9Yy5pbmRleE9mKCIpIixjLmxlbmd0aC1iKS1jLmxlbmd0aCkmJihhWzBdPWFbMF0uc2xpY2UoMCxiKSxhWzJdPWMuc2xpY2UoMCxiKSksYS5zbGljZSgwLDMpKX19LGZpbHRlcjp7VEFHOmZ1bmN0aW9uKGEpe3ZhciBiPWEucmVwbGFjZShjYSxkYSkudG9Mb3dlckNhc2UoKTtyZXR1cm4iKiI9PT1hP2Z1bmN0aW9uKCl7cmV0dXJuITB9OmZ1bmN0aW9uKGEpe3JldHVybiBhLm5vZGVOYW1lJiZhLm5vZGVOYW1lLnRvTG93ZXJDYXNlKCk9PT1ifX0sQ0xBU1M6ZnVuY3Rpb24oYSl7dmFyIGI9eVthKyIgIl07cmV0dXJuIGJ8fChiPW5ldyBSZWdFeHAoIihefCIrTCsiKSIrYSsiKCIrTCsifCQpIikpJiZ5KGEsZnVuY3Rpb24oYSl7cmV0dXJuIGIudGVzdCgic3RyaW5nIj09dHlwZW9mIGEuY2xhc3NOYW1lJiZhLmNsYXNzTmFtZXx8InVuZGVmaW5lZCIhPXR5cGVvZiBhLmdldEF0dHJpYnV0ZSYmYS5nZXRBdHRyaWJ1dGUoImNsYXNzIil8fCIiKX0pfSxBVFRSOmZ1bmN0aW9uKGEsYixjKXtyZXR1cm4gZnVuY3Rpb24oZCl7dmFyIGU9Z2EuYXR0cihkLGEpO3JldHVybiBudWxsPT1lPyIhPSI9PT1iOmI/KGUrPSIiLCI9Ij09PWI/ZT09PWM6IiE9Ij09PWI/ZSE9PWM6Il49Ij09PWI/YyYmMD09PWUuaW5kZXhPZihjKToiKj0iPT09Yj9jJiZlLmluZGV4T2YoYyk+LTE6IiQ9Ij09PWI/YyYmZS5zbGljZSgtYy5sZW5ndGgpPT09Yzoifj0iPT09Yj8oIiAiK2UucmVwbGFjZShRLCIgIikrIiAiKS5pbmRleE9mKGMpPi0xOiJ8PSI9PT1iP2U9PT1jfHxlLnNsaWNlKDAsYy5sZW5ndGgrMSk9PT1jKyItIjohMSk6ITB9fSxDSElMRDpmdW5jdGlvbihhLGIsYyxkLGUpe3ZhciBmPSJudGgiIT09YS5zbGljZSgwLDMpLGc9Imxhc3QiIT09YS5zbGljZSgtNCksaD0ib2YtdHlwZSI9PT1iO3JldHVybiAxPT09ZCYmMD09PWU/ZnVuY3Rpb24oYSl7cmV0dXJuISFhLnBhcmVudE5vZGV9OmZ1bmN0aW9uKGIsYyxpKXt2YXIgaixrLGwsbSxuLG8scD1mIT09Zz8ibmV4dFNpYmxpbmciOiJwcmV2aW91c1NpYmxpbmciLHE9Yi5wYXJlbnROb2RlLHI9aCYmYi5ub2RlTmFtZS50b0xvd2VyQ2FzZSgpLHM9IWkmJiFoO2lmKHEpe2lmKGYpe3doaWxlKHApe2w9Yjt3aGlsZShsPWxbcF0paWYoaD9sLm5vZGVOYW1lLnRvTG93ZXJDYXNlKCk9PT1yOjE9PT1sLm5vZGVUeXBlKXJldHVybiExO289cD0ib25seSI9PT1hJiYhbyYmIm5leHRTaWJsaW5nIn1yZXR1cm4hMH1pZihvPVtnP3EuZmlyc3RDaGlsZDpxLmxhc3RDaGlsZF0sZyYmcyl7az1xW3VdfHwocVt1XT17fSksaj1rW2FdfHxbXSxuPWpbMF09PT13JiZqWzFdLG09alswXT09PXcmJmpbMl0sbD1uJiZxLmNoaWxkTm9kZXNbbl07d2hpbGUobD0rK24mJmwmJmxbcF18fChtPW49MCl8fG8ucG9wKCkpaWYoMT09PWwubm9kZVR5cGUmJisrbSYmbD09PWIpe2tbYV09W3csbixtXTticmVha319ZWxzZSBpZihzJiYoaj0oYlt1XXx8KGJbdV09e30pKVthXSkmJmpbMF09PT13KW09alsxXTtlbHNlIHdoaWxlKGw9KytuJiZsJiZsW3BdfHwobT1uPTApfHxvLnBvcCgpKWlmKChoP2wubm9kZU5hbWUudG9Mb3dlckNhc2UoKT09PXI6MT09PWwubm9kZVR5cGUpJiYrK20mJihzJiYoKGxbdV18fChsW3VdPXt9KSlbYV09W3csbV0pLGw9PT1iKSlicmVhaztyZXR1cm4gbS09ZSxtPT09ZHx8bSVkPT09MCYmbS9kPj0wfX19LFBTRVVETzpmdW5jdGlvbihhLGIpe3ZhciBjLGU9ZC5wc2V1ZG9zW2FdfHxkLnNldEZpbHRlcnNbYS50b0xvd2VyQ2FzZSgpXXx8Z2EuZXJyb3IoInVuc3VwcG9ydGVkIHBzZXVkbzogIithKTtyZXR1cm4gZVt1XT9lKGIpOmUubGVuZ3RoPjE/KGM9W2EsYSwiIixiXSxkLnNldEZpbHRlcnMuaGFzT3duUHJvcGVydHkoYS50b0xvd2VyQ2FzZSgpKT9pYShmdW5jdGlvbihhLGMpe3ZhciBkLGY9ZShhLGIpLGc9Zi5sZW5ndGg7d2hpbGUoZy0tKWQ9SihhLGZbZ10pLGFbZF09IShjW2RdPWZbZ10pfSk6ZnVuY3Rpb24oYSl7cmV0dXJuIGUoYSwwLGMpfSk6ZX19LHBzZXVkb3M6e25vdDppYShmdW5jdGlvbihhKXt2YXIgYj1bXSxjPVtdLGQ9aChhLnJlcGxhY2UoUiwiJDEiKSk7cmV0dXJuIGRbdV0/aWEoZnVuY3Rpb24oYSxiLGMsZSl7dmFyIGYsZz1kKGEsbnVsbCxlLFtdKSxoPWEubGVuZ3RoO3doaWxlKGgtLSkoZj1nW2hdKSYmKGFbaF09IShiW2hdPWYpKX0pOmZ1bmN0aW9uKGEsZSxmKXtyZXR1cm4gYlswXT1hLGQoYixudWxsLGYsYyksYlswXT1udWxsLCFjLnBvcCgpfX0pLGhhczppYShmdW5jdGlvbihhKXtyZXR1cm4gZnVuY3Rpb24oYil7cmV0dXJuIGdhKGEsYikubGVuZ3RoPjB9fSksY29udGFpbnM6aWEoZnVuY3Rpb24oYSl7cmV0dXJuIGE9YS5yZXBsYWNlKGNhLGRhKSxmdW5jdGlvbihiKXtyZXR1cm4oYi50ZXh0Q29udGVudHx8Yi5pbm5lclRleHR8fGUoYikpLmluZGV4T2YoYSk+LTF9fSksbGFuZzppYShmdW5jdGlvbihhKXtyZXR1cm4gVy50ZXN0KGF8fCIiKXx8Z2EuZXJyb3IoInVuc3VwcG9ydGVkIGxhbmc6ICIrYSksYT1hLnJlcGxhY2UoY2EsZGEpLnRvTG93ZXJDYXNlKCksZnVuY3Rpb24oYil7dmFyIGM7ZG8gaWYoYz1wP2IubGFuZzpiLmdldEF0dHJpYnV0ZSgieG1sOmxhbmciKXx8Yi5nZXRBdHRyaWJ1dGUoImxhbmciKSlyZXR1cm4gYz1jLnRvTG93ZXJDYXNlKCksYz09PWF8fDA9PT1jLmluZGV4T2YoYSsiLSIpO3doaWxlKChiPWIucGFyZW50Tm9kZSkmJjE9PT1iLm5vZGVUeXBlKTtyZXR1cm4hMX19KSx0YXJnZXQ6ZnVuY3Rpb24oYil7dmFyIGM9YS5sb2NhdGlvbiYmYS5sb2NhdGlvbi5oYXNoO3JldHVybiBjJiZjLnNsaWNlKDEpPT09Yi5pZH0scm9vdDpmdW5jdGlvbihhKXtyZXR1cm4gYT09PW99LGZvY3VzOmZ1bmN0aW9uKGEpe3JldHVybiBhPT09bi5hY3RpdmVFbGVtZW50JiYoIW4uaGFzRm9jdXN8fG4uaGFzRm9jdXMoKSkmJiEhKGEudHlwZXx8YS5ocmVmfHx+YS50YWJJbmRleCl9LGVuYWJsZWQ6ZnVuY3Rpb24oYSl7cmV0dXJuIGEuZGlzYWJsZWQ9PT0hMX0sZGlzYWJsZWQ6ZnVuY3Rpb24oYSl7cmV0dXJuIGEuZGlzYWJsZWQ9PT0hMH0sY2hlY2tlZDpmdW5jdGlvbihhKXt2YXIgYj1hLm5vZGVOYW1lLnRvTG93ZXJDYXNlKCk7cmV0dXJuImlucHV0Ij09PWImJiEhYS5jaGVja2VkfHwib3B0aW9uIj09PWImJiEhYS5zZWxlY3RlZH0sc2VsZWN0ZWQ6ZnVuY3Rpb24oYSl7cmV0dXJuIGEucGFyZW50Tm9kZSYmYS5wYXJlbnROb2RlLnNlbGVjdGVkSW5kZXgsYS5zZWxlY3RlZD09PSEwfSxlbXB0eTpmdW5jdGlvbihhKXtmb3IoYT1hLmZpcnN0Q2hpbGQ7YTthPWEubmV4dFNpYmxpbmcpaWYoYS5ub2RlVHlwZTw2KXJldHVybiExO3JldHVybiEwfSxwYXJlbnQ6ZnVuY3Rpb24oYSl7cmV0dXJuIWQucHNldWRvcy5lbXB0eShhKX0saGVhZGVyOmZ1bmN0aW9uKGEpe3JldHVybiBaLnRlc3QoYS5ub2RlTmFtZSl9LGlucHV0OmZ1bmN0aW9uKGEpe3JldHVybiBZLnRlc3QoYS5ub2RlTmFtZSl9LGJ1dHRvbjpmdW5jdGlvbihhKXt2YXIgYj1hLm5vZGVOYW1lLnRvTG93ZXJDYXNlKCk7cmV0dXJuImlucHV0Ij09PWImJiJidXR0b24iPT09YS50eXBlfHwiYnV0dG9uIj09PWJ9LHRleHQ6ZnVuY3Rpb24oYSl7dmFyIGI7cmV0dXJuImlucHV0Ij09PWEubm9kZU5hbWUudG9Mb3dlckNhc2UoKSYmInRleHQiPT09YS50eXBlJiYobnVsbD09KGI9YS5nZXRBdHRyaWJ1dGUoInR5cGUiKSl8fCJ0ZXh0Ij09PWIudG9Mb3dlckNhc2UoKSl9LGZpcnN0Om9hKGZ1bmN0aW9uKCl7cmV0dXJuWzBdfSksbGFzdDpvYShmdW5jdGlvbihhLGIpe3JldHVybltiLTFdfSksZXE6b2EoZnVuY3Rpb24oYSxiLGMpe3JldHVyblswPmM/YytiOmNdfSksZXZlbjpvYShmdW5jdGlvbihhLGIpe2Zvcih2YXIgYz0wO2I+YztjKz0yKWEucHVzaChjKTtyZXR1cm4gYX0pLG9kZDpvYShmdW5jdGlvbihhLGIpe2Zvcih2YXIgYz0xO2I+YztjKz0yKWEucHVzaChjKTtyZXR1cm4gYX0pLGx0Om9hKGZ1bmN0aW9uKGEsYixjKXtmb3IodmFyIGQ9MD5jP2MrYjpjOy0tZD49MDspYS5wdXNoKGQpO3JldHVybiBhfSksZ3Q6b2EoZnVuY3Rpb24oYSxiLGMpe2Zvcih2YXIgZD0wPmM/YytiOmM7KytkPGI7KWEucHVzaChkKTtyZXR1cm4gYX0pfX0sZC5wc2V1ZG9zLm50aD1kLnBzZXVkb3MuZXE7Zm9yKGIgaW57cmFkaW86ITAsY2hlY2tib3g6ITAsZmlsZTohMCxwYXNzd29yZDohMCxpbWFnZTohMH0pZC5wc2V1ZG9zW2JdPW1hKGIpO2ZvcihiIGlue3N1Ym1pdDohMCxyZXNldDohMH0pZC5wc2V1ZG9zW2JdPW5hKGIpO2Z1bmN0aW9uIHFhKCl7fXFhLnByb3RvdHlwZT1kLmZpbHRlcnM9ZC5wc2V1ZG9zLGQuc2V0RmlsdGVycz1uZXcgcWEsZz1nYS50b2tlbml6ZT1mdW5jdGlvbihhLGIpe3ZhciBjLGUsZixnLGgsaSxqLGs9elthKyIgIl07aWYoaylyZXR1cm4gYj8wOmsuc2xpY2UoMCk7aD1hLGk9W10saj1kLnByZUZpbHRlcjt3aGlsZShoKXsoIWN8fChlPVMuZXhlYyhoKSkpJiYoZSYmKGg9aC5zbGljZShlWzBdLmxlbmd0aCl8fGgpLGkucHVzaChmPVtdKSksYz0hMSwoZT1ULmV4ZWMoaCkpJiYoYz1lLnNoaWZ0KCksZi5wdXNoKHt2YWx1ZTpjLHR5cGU6ZVswXS5yZXBsYWNlKFIsIiAiKX0pLGg9aC5zbGljZShjLmxlbmd0aCkpO2ZvcihnIGluIGQuZmlsdGVyKSEoZT1YW2ddLmV4ZWMoaCkpfHxqW2ddJiYhKGU9altnXShlKSl8fChjPWUuc2hpZnQoKSxmLnB1c2goe3ZhbHVlOmMsdHlwZTpnLG1hdGNoZXM6ZX0pLGg9aC5zbGljZShjLmxlbmd0aCkpO2lmKCFjKWJyZWFrfXJldHVybiBiP2gubGVuZ3RoOmg/Z2EuZXJyb3IoYSk6eihhLGkpLnNsaWNlKDApfTtmdW5jdGlvbiByYShhKXtmb3IodmFyIGI9MCxjPWEubGVuZ3RoLGQ9IiI7Yz5iO2IrKylkKz1hW2JdLnZhbHVlO3JldHVybiBkfWZ1bmN0aW9uIHNhKGEsYixjKXt2YXIgZD1iLmRpcixlPWMmJiJwYXJlbnROb2RlIj09PWQsZj14Kys7cmV0dXJuIGIuZmlyc3Q/ZnVuY3Rpb24oYixjLGYpe3doaWxlKGI9YltkXSlpZigxPT09Yi5ub2RlVHlwZXx8ZSlyZXR1cm4gYShiLGMsZil9OmZ1bmN0aW9uKGIsYyxnKXt2YXIgaCxpLGo9W3csZl07aWYoZyl7d2hpbGUoYj1iW2RdKWlmKCgxPT09Yi5ub2RlVHlwZXx8ZSkmJmEoYixjLGcpKXJldHVybiEwfWVsc2Ugd2hpbGUoYj1iW2RdKWlmKDE9PT1iLm5vZGVUeXBlfHxlKXtpZihpPWJbdV18fChiW3VdPXt9KSwoaD1pW2RdKSYmaFswXT09PXcmJmhbMV09PT1mKXJldHVybiBqWzJdPWhbMl07aWYoaVtkXT1qLGpbMl09YShiLGMsZykpcmV0dXJuITB9fX1mdW5jdGlvbiB0YShhKXtyZXR1cm4gYS5sZW5ndGg+MT9mdW5jdGlvbihiLGMsZCl7dmFyIGU9YS5sZW5ndGg7d2hpbGUoZS0tKWlmKCFhW2VdKGIsYyxkKSlyZXR1cm4hMTtyZXR1cm4hMH06YVswXX1mdW5jdGlvbiB1YShhLGIsYyl7Zm9yKHZhciBkPTAsZT1iLmxlbmd0aDtlPmQ7ZCsrKWdhKGEsYltkXSxjKTtyZXR1cm4gY31mdW5jdGlvbiB2YShhLGIsYyxkLGUpe2Zvcih2YXIgZixnPVtdLGg9MCxpPWEubGVuZ3RoLGo9bnVsbCE9YjtpPmg7aCsrKShmPWFbaF0pJiYoIWN8fGMoZixkLGUpKSYmKGcucHVzaChmKSxqJiZiLnB1c2goaCkpO3JldHVybiBnfWZ1bmN0aW9uIHdhKGEsYixjLGQsZSxmKXtyZXR1cm4gZCYmIWRbdV0mJihkPXdhKGQpKSxlJiYhZVt1XSYmKGU9d2EoZSxmKSksaWEoZnVuY3Rpb24oZixnLGgsaSl7dmFyIGosayxsLG09W10sbj1bXSxvPWcubGVuZ3RoLHA9Znx8dWEoYnx8IioiLGgubm9kZVR5cGU/W2hdOmgsW10pLHE9IWF8fCFmJiZiP3A6dmEocCxtLGEsaCxpKSxyPWM/ZXx8KGY/YTpvfHxkKT9bXTpnOnE7aWYoYyYmYyhxLHIsaCxpKSxkKXtqPXZhKHIsbiksZChqLFtdLGgsaSksaz1qLmxlbmd0aDt3aGlsZShrLS0pKGw9altrXSkmJihyW25ba11dPSEocVtuW2tdXT1sKSl9aWYoZil7aWYoZXx8YSl7aWYoZSl7aj1bXSxrPXIubGVuZ3RoO3doaWxlKGstLSkobD1yW2tdKSYmai5wdXNoKHFba109bCk7ZShudWxsLHI9W10saixpKX1rPXIubGVuZ3RoO3doaWxlKGstLSkobD1yW2tdKSYmKGo9ZT9KKGYsbCk6bVtrXSk+LTEmJihmW2pdPSEoZ1tqXT1sKSl9fWVsc2Ugcj12YShyPT09Zz9yLnNwbGljZShvLHIubGVuZ3RoKTpyKSxlP2UobnVsbCxnLHIsaSk6SC5hcHBseShnLHIpfSl9ZnVuY3Rpb24geGEoYSl7Zm9yKHZhciBiLGMsZSxmPWEubGVuZ3RoLGc9ZC5yZWxhdGl2ZVthWzBdLnR5cGVdLGg9Z3x8ZC5yZWxhdGl2ZVsiICJdLGk9Zz8xOjAsaz1zYShmdW5jdGlvbihhKXtyZXR1cm4gYT09PWJ9LGgsITApLGw9c2EoZnVuY3Rpb24oYSl7cmV0dXJuIEooYixhKT4tMX0saCwhMCksbT1bZnVuY3Rpb24oYSxjLGQpe3ZhciBlPSFnJiYoZHx8YyE9PWopfHwoKGI9Yykubm9kZVR5cGU/ayhhLGMsZCk6bChhLGMsZCkpO3JldHVybiBiPW51bGwsZX1dO2Y+aTtpKyspaWYoYz1kLnJlbGF0aXZlW2FbaV0udHlwZV0pbT1bc2EodGEobSksYyldO2Vsc2V7aWYoYz1kLmZpbHRlclthW2ldLnR5cGVdLmFwcGx5KG51bGwsYVtpXS5tYXRjaGVzKSxjW3VdKXtmb3IoZT0rK2k7Zj5lO2UrKylpZihkLnJlbGF0aXZlW2FbZV0udHlwZV0pYnJlYWs7cmV0dXJuIHdhKGk+MSYmdGEobSksaT4xJiZyYShhLnNsaWNlKDAsaS0xKS5jb25jYXQoe3ZhbHVlOiIgIj09PWFbaS0yXS50eXBlPyIqIjoiIn0pKS5yZXBsYWNlKFIsIiQxIiksYyxlPmkmJnhhKGEuc2xpY2UoaSxlKSksZj5lJiZ4YShhPWEuc2xpY2UoZSkpLGY+ZSYmcmEoYSkpfW0ucHVzaChjKX1yZXR1cm4gdGEobSl9ZnVuY3Rpb24geWEoYSxiKXt2YXIgYz1iLmxlbmd0aD4wLGU9YS5sZW5ndGg+MCxmPWZ1bmN0aW9uKGYsZyxoLGksayl7dmFyIGwsbSxvLHA9MCxxPSIwIixyPWYmJltdLHM9W10sdD1qLHU9Znx8ZSYmZC5maW5kLlRBRygiKiIsayksdj13Kz1udWxsPT10PzE6TWF0aC5yYW5kb20oKXx8LjEseD11Lmxlbmd0aDtmb3IoayYmKGo9ZyE9PW4mJmcpO3EhPT14JiZudWxsIT0obD11W3FdKTtxKyspe2lmKGUmJmwpe209MDt3aGlsZShvPWFbbSsrXSlpZihvKGwsZyxoKSl7aS5wdXNoKGwpO2JyZWFrfWsmJih3PXYpfWMmJigobD0hbyYmbCkmJnAtLSxmJiZyLnB1c2gobCkpfWlmKHArPXEsYyYmcSE9PXApe209MDt3aGlsZShvPWJbbSsrXSlvKHIscyxnLGgpO2lmKGYpe2lmKHA+MCl3aGlsZShxLS0pcltxXXx8c1txXXx8KHNbcV09Ri5jYWxsKGkpKTtzPXZhKHMpfUguYXBwbHkoaSxzKSxrJiYhZiYmcy5sZW5ndGg+MCYmcCtiLmxlbmd0aD4xJiZnYS51bmlxdWVTb3J0KGkpfXJldHVybiBrJiYodz12LGo9dCkscn07cmV0dXJuIGM/aWEoZik6Zn1yZXR1cm4gaD1nYS5jb21waWxlPWZ1bmN0aW9uKGEsYil7dmFyIGMsZD1bXSxlPVtdLGY9QVthKyIgIl07aWYoIWYpe2J8fChiPWcoYSkpLGM9Yi5sZW5ndGg7d2hpbGUoYy0tKWY9eGEoYltjXSksZlt1XT9kLnB1c2goZik6ZS5wdXNoKGYpO2Y9QShhLHlhKGUsZCkpLGYuc2VsZWN0b3I9YX1yZXR1cm4gZn0saT1nYS5zZWxlY3Q9ZnVuY3Rpb24oYSxiLGUsZil7dmFyIGksaixrLGwsbSxuPSJmdW5jdGlvbiI9PXR5cGVvZiBhJiZhLG89IWYmJmcoYT1uLnNlbGVjdG9yfHxhKTtpZihlPWV8fFtdLDE9PT1vLmxlbmd0aCl7aWYoaj1vWzBdPW9bMF0uc2xpY2UoMCksai5sZW5ndGg+MiYmIklEIj09PShrPWpbMF0pLnR5cGUmJmMuZ2V0QnlJZCYmOT09PWIubm9kZVR5cGUmJnAmJmQucmVsYXRpdmVbalsxXS50eXBlXSl7aWYoYj0oZC5maW5kLklEKGsubWF0Y2hlc1swXS5yZXBsYWNlKGNhLGRhKSxiKXx8W10pWzBdLCFiKXJldHVybiBlO24mJihiPWIucGFyZW50Tm9kZSksYT1hLnNsaWNlKGouc2hpZnQoKS52YWx1ZS5sZW5ndGgpfWk9WC5uZWVkc0NvbnRleHQudGVzdChhKT8wOmoubGVuZ3RoO3doaWxlKGktLSl7aWYoaz1qW2ldLGQucmVsYXRpdmVbbD1rLnR5cGVdKWJyZWFrO2lmKChtPWQuZmluZFtsXSkmJihmPW0oay5tYXRjaGVzWzBdLnJlcGxhY2UoY2EsZGEpLGFhLnRlc3QoalswXS50eXBlKSYmcGEoYi5wYXJlbnROb2RlKXx8YikpKXtpZihqLnNwbGljZShpLDEpLGE9Zi5sZW5ndGgmJnJhKGopLCFhKXJldHVybiBILmFwcGx5KGUsZiksZTticmVha319fXJldHVybihufHxoKGEsbykpKGYsYiwhcCxlLGFhLnRlc3QoYSkmJnBhKGIucGFyZW50Tm9kZSl8fGIpLGV9LGMuc29ydFN0YWJsZT11LnNwbGl0KCIiKS5zb3J0KEIpLmpvaW4oIiIpPT09dSxjLmRldGVjdER1cGxpY2F0ZXM9ISFsLG0oKSxjLnNvcnREZXRhY2hlZD1qYShmdW5jdGlvbihhKXtyZXR1cm4gMSZhLmNvbXBhcmVEb2N1bWVudFBvc2l0aW9uKG4uY3JlYXRlRWxlbWVudCgiZGl2IikpfSksamEoZnVuY3Rpb24oYSl7cmV0dXJuIGEuaW5uZXJIVE1MPSI8YSBocmVmPScjJz48L2E+IiwiIyI9PT1hLmZpcnN0Q2hpbGQuZ2V0QXR0cmlidXRlKCJocmVmIil9KXx8a2EoInR5cGV8aHJlZnxoZWlnaHR8d2lkdGgiLGZ1bmN0aW9uKGEsYixjKXtyZXR1cm4gYz92b2lkIDA6YS5nZXRBdHRyaWJ1dGUoYiwidHlwZSI9PT1iLnRvTG93ZXJDYXNlKCk/MToyKX0pLGMuYXR0cmlidXRlcyYmamEoZnVuY3Rpb24oYSl7cmV0dXJuIGEuaW5uZXJIVE1MPSI8aW5wdXQvPiIsYS5maXJzdENoaWxkLnNldEF0dHJpYnV0ZSgidmFsdWUiLCIiKSwiIj09PWEuZmlyc3RDaGlsZC5nZXRBdHRyaWJ1dGUoInZhbHVlIil9KXx8a2EoInZhbHVlIixmdW5jdGlvbihhLGIsYyl7cmV0dXJuIGN8fCJpbnB1dCIhPT1hLm5vZGVOYW1lLnRvTG93ZXJDYXNlKCk/dm9pZCAwOmEuZGVmYXVsdFZhbHVlfSksamEoZnVuY3Rpb24oYSl7cmV0dXJuIG51bGw9PWEuZ2V0QXR0cmlidXRlKCJkaXNhYmxlZCIpfSl8fGthKEssZnVuY3Rpb24oYSxiLGMpe3ZhciBkO3JldHVybiBjP3ZvaWQgMDphW2JdPT09ITA/Yi50b0xvd2VyQ2FzZSgpOihkPWEuZ2V0QXR0cmlidXRlTm9kZShiKSkmJmQuc3BlY2lmaWVkP2QudmFsdWU6bnVsbH0pLGdhfShhKTttLmZpbmQ9cyxtLmV4cHI9cy5zZWxlY3RvcnMsbS5leHByWyI6Il09bS5leHByLnBzZXVkb3MsbS51bmlxdWU9cy51bmlxdWVTb3J0LG0udGV4dD1zLmdldFRleHQsbS5pc1hNTERvYz1zLmlzWE1MLG0uY29udGFpbnM9cy5jb250YWluczt2YXIgdD1tLmV4cHIubWF0Y2gubmVlZHNDb250ZXh0LHU9L148KFx3KylccypcLz8+KD86PFwvXDE+fCkkLyx2PS9eLlteOiNcW1wuLF0qJC87ZnVuY3Rpb24gdyhhLGIsYyl7aWYobS5pc0Z1bmN0aW9uKGIpKXJldHVybiBtLmdyZXAoYSxmdW5jdGlvbihhLGQpe3JldHVybiEhYi5jYWxsKGEsZCxhKSE9PWN9KTtpZihiLm5vZGVUeXBlKXJldHVybiBtLmdyZXAoYSxmdW5jdGlvbihhKXtyZXR1cm4gYT09PWIhPT1jfSk7aWYoInN0cmluZyI9PXR5cGVvZiBiKXtpZih2LnRlc3QoYikpcmV0dXJuIG0uZmlsdGVyKGIsYSxjKTtiPW0uZmlsdGVyKGIsYSl9cmV0dXJuIG0uZ3JlcChhLGZ1bmN0aW9uKGEpe3JldHVybiBtLmluQXJyYXkoYSxiKT49MCE9PWN9KX1tLmZpbHRlcj1mdW5jdGlvbihhLGIsYyl7dmFyIGQ9YlswXTtyZXR1cm4gYyYmKGE9Ijpub3QoIithKyIpIiksMT09PWIubGVuZ3RoJiYxPT09ZC5ub2RlVHlwZT9tLmZpbmQubWF0Y2hlc1NlbGVjdG9yKGQsYSk/W2RdOltdOm0uZmluZC5tYXRjaGVzKGEsbS5ncmVwKGIsZnVuY3Rpb24oYSl7cmV0dXJuIDE9PT1hLm5vZGVUeXBlfSkpfSxtLmZuLmV4dGVuZCh7ZmluZDpmdW5jdGlvbihhKXt2YXIgYixjPVtdLGQ9dGhpcyxlPWQubGVuZ3RoO2lmKCJzdHJpbmciIT10eXBlb2YgYSlyZXR1cm4gdGhpcy5wdXNoU3RhY2sobShhKS5maWx0ZXIoZnVuY3Rpb24oKXtmb3IoYj0wO2U+YjtiKyspaWYobS5jb250YWlucyhkW2JdLHRoaXMpKXJldHVybiEwfSkpO2ZvcihiPTA7ZT5iO2IrKyltLmZpbmQoYSxkW2JdLGMpO3JldHVybiBjPXRoaXMucHVzaFN0YWNrKGU+MT9tLnVuaXF1ZShjKTpjKSxjLnNlbGVjdG9yPXRoaXMuc2VsZWN0b3I/dGhpcy5zZWxlY3RvcisiICIrYTphLGN9LGZpbHRlcjpmdW5jdGlvbihhKXtyZXR1cm4gdGhpcy5wdXNoU3RhY2sodyh0aGlzLGF8fFtdLCExKSl9LG5vdDpmdW5jdGlvbihhKXtyZXR1cm4gdGhpcy5wdXNoU3RhY2sodyh0aGlzLGF8fFtdLCEwKSl9LGlzOmZ1bmN0aW9uKGEpe3JldHVybiEhdyh0aGlzLCJzdHJpbmciPT10eXBlb2YgYSYmdC50ZXN0KGEpP20oYSk6YXx8W10sITEpLmxlbmd0aH19KTt2YXIgeCx5PWEuZG9jdW1lbnQsej0vXig/OlxzKig8W1x3XFddKz4pW14+XSp8IyhbXHctXSopKSQvLEE9bS5mbi5pbml0PWZ1bmN0aW9uKGEsYil7dmFyIGMsZDtpZighYSlyZXR1cm4gdGhpcztpZigic3RyaW5nIj09dHlwZW9mIGEpe2lmKGM9IjwiPT09YS5jaGFyQXQoMCkmJiI+Ij09PWEuY2hhckF0KGEubGVuZ3RoLTEpJiZhLmxlbmd0aD49Mz9bbnVsbCxhLG51bGxdOnouZXhlYyhhKSwhY3x8IWNbMV0mJmIpcmV0dXJuIWJ8fGIuanF1ZXJ5PyhifHx4KS5maW5kKGEpOnRoaXMuY29uc3RydWN0b3IoYikuZmluZChhKTtpZihjWzFdKXtpZihiPWIgaW5zdGFuY2VvZiBtP2JbMF06YixtLm1lcmdlKHRoaXMsbS5wYXJzZUhUTUwoY1sxXSxiJiZiLm5vZGVUeXBlP2Iub3duZXJEb2N1bWVudHx8Yjp5LCEwKSksdS50ZXN0KGNbMV0pJiZtLmlzUGxhaW5PYmplY3QoYikpZm9yKGMgaW4gYiltLmlzRnVuY3Rpb24odGhpc1tjXSk/dGhpc1tjXShiW2NdKTp0aGlzLmF0dHIoYyxiW2NdKTtyZXR1cm4gdGhpc31pZihkPXkuZ2V0RWxlbWVudEJ5SWQoY1syXSksZCYmZC5wYXJlbnROb2RlKXtpZihkLmlkIT09Y1syXSlyZXR1cm4geC5maW5kKGEpO3RoaXMubGVuZ3RoPTEsdGhpc1swXT1kfXJldHVybiB0aGlzLmNvbnRleHQ9eSx0aGlzLnNlbGVjdG9yPWEsdGhpc31yZXR1cm4gYS5ub2RlVHlwZT8odGhpcy5jb250ZXh0PXRoaXNbMF09YSx0aGlzLmxlbmd0aD0xLHRoaXMpOm0uaXNGdW5jdGlvbihhKT8idW5kZWZpbmVkIiE9dHlwZW9mIHgucmVhZHk/eC5yZWFkeShhKTphKG0pOih2b2lkIDAhPT1hLnNlbGVjdG9yJiYodGhpcy5zZWxlY3Rvcj1hLnNlbGVjdG9yLHRoaXMuY29udGV4dD1hLmNvbnRleHQpLG0ubWFrZUFycmF5KGEsdGhpcykpfTtBLnByb3RvdHlwZT1tLmZuLHg9bSh5KTt2YXIgQj0vXig/OnBhcmVudHN8cHJldig/OlVudGlsfEFsbCkpLyxDPXtjaGlsZHJlbjohMCxjb250ZW50czohMCxuZXh0OiEwLHByZXY6ITB9O20uZXh0ZW5kKHtkaXI6ZnVuY3Rpb24oYSxiLGMpe3ZhciBkPVtdLGU9YVtiXTt3aGlsZShlJiY5IT09ZS5ub2RlVHlwZSYmKHZvaWQgMD09PWN8fDEhPT1lLm5vZGVUeXBlfHwhbShlKS5pcyhjKSkpMT09PWUubm9kZVR5cGUmJmQucHVzaChlKSxlPWVbYl07cmV0dXJuIGR9LHNpYmxpbmc6ZnVuY3Rpb24oYSxiKXtmb3IodmFyIGM9W107YTthPWEubmV4dFNpYmxpbmcpMT09PWEubm9kZVR5cGUmJmEhPT1iJiZjLnB1c2goYSk7cmV0dXJuIGN9fSksbS5mbi5leHRlbmQoe2hhczpmdW5jdGlvbihhKXt2YXIgYixjPW0oYSx0aGlzKSxkPWMubGVuZ3RoO3JldHVybiB0aGlzLmZpbHRlcihmdW5jdGlvbigpe2ZvcihiPTA7ZD5iO2IrKylpZihtLmNvbnRhaW5zKHRoaXMsY1tiXSkpcmV0dXJuITB9KX0sY2xvc2VzdDpmdW5jdGlvbihhLGIpe2Zvcih2YXIgYyxkPTAsZT10aGlzLmxlbmd0aCxmPVtdLGc9dC50ZXN0KGEpfHwic3RyaW5nIiE9dHlwZW9mIGE/bShhLGJ8fHRoaXMuY29udGV4dCk6MDtlPmQ7ZCsrKWZvcihjPXRoaXNbZF07YyYmYyE9PWI7Yz1jLnBhcmVudE5vZGUpaWYoYy5ub2RlVHlwZTwxMSYmKGc/Zy5pbmRleChjKT4tMToxPT09Yy5ub2RlVHlwZSYmbS5maW5kLm1hdGNoZXNTZWxlY3RvcihjLGEpKSl7Zi5wdXNoKGMpO2JyZWFrfXJldHVybiB0aGlzLnB1c2hTdGFjayhmLmxlbmd0aD4xP20udW5pcXVlKGYpOmYpfSxpbmRleDpmdW5jdGlvbihhKXtyZXR1cm4gYT8ic3RyaW5nIj09dHlwZW9mIGE/bS5pbkFycmF5KHRoaXNbMF0sbShhKSk6bS5pbkFycmF5KGEuanF1ZXJ5P2FbMF06YSx0aGlzKTp0aGlzWzBdJiZ0aGlzWzBdLnBhcmVudE5vZGU/dGhpcy5maXJzdCgpLnByZXZBbGwoKS5sZW5ndGg6LTF9LGFkZDpmdW5jdGlvbihhLGIpe3JldHVybiB0aGlzLnB1c2hTdGFjayhtLnVuaXF1ZShtLm1lcmdlKHRoaXMuZ2V0KCksbShhLGIpKSkpfSxhZGRCYWNrOmZ1bmN0aW9uKGEpe3JldHVybiB0aGlzLmFkZChudWxsPT1hP3RoaXMucHJldk9iamVjdDp0aGlzLnByZXZPYmplY3QuZmlsdGVyKGEpKX19KTtmdW5jdGlvbiBEKGEsYil7ZG8gYT1hW2JdO3doaWxlKGEmJjEhPT1hLm5vZGVUeXBlKTtyZXR1cm4gYX1tLmVhY2goe3BhcmVudDpmdW5jdGlvbihhKXt2YXIgYj1hLnBhcmVudE5vZGU7cmV0dXJuIGImJjExIT09Yi5ub2RlVHlwZT9iOm51bGx9LHBhcmVudHM6ZnVuY3Rpb24oYSl7cmV0dXJuIG0uZGlyKGEsInBhcmVudE5vZGUiKX0scGFyZW50c1VudGlsOmZ1bmN0aW9uKGEsYixjKXtyZXR1cm4gbS5kaXIoYSwicGFyZW50Tm9kZSIsYyl9LG5leHQ6ZnVuY3Rpb24oYSl7cmV0dXJuIEQoYSwibmV4dFNpYmxpbmciKX0scHJldjpmdW5jdGlvbihhKXtyZXR1cm4gRChhLCJwcmV2aW91c1NpYmxpbmciKX0sbmV4dEFsbDpmdW5jdGlvbihhKXtyZXR1cm4gbS5kaXIoYSwibmV4dFNpYmxpbmciKX0scHJldkFsbDpmdW5jdGlvbihhKXtyZXR1cm4gbS5kaXIoYSwicHJldmlvdXNTaWJsaW5nIil9LG5leHRVbnRpbDpmdW5jdGlvbihhLGIsYyl7cmV0dXJuIG0uZGlyKGEsIm5leHRTaWJsaW5nIixjKX0scHJldlVudGlsOmZ1bmN0aW9uKGEsYixjKXtyZXR1cm4gbS5kaXIoYSwicHJldmlvdXNTaWJsaW5nIixjKX0sc2libGluZ3M6ZnVuY3Rpb24oYSl7cmV0dXJuIG0uc2libGluZygoYS5wYXJlbnROb2RlfHx7fSkuZmlyc3RDaGlsZCxhKX0sY2hpbGRyZW46ZnVuY3Rpb24oYSl7cmV0dXJuIG0uc2libGluZyhhLmZpcnN0Q2hpbGQpfSxjb250ZW50czpmdW5jdGlvbihhKXtyZXR1cm4gbS5ub2RlTmFtZShhLCJpZnJhbWUiKT9hLmNvbnRlbnREb2N1bWVudHx8YS5jb250ZW50V2luZG93LmRvY3VtZW50Om0ubWVyZ2UoW10sYS5jaGlsZE5vZGVzKX19LGZ1bmN0aW9uKGEsYil7bS5mblthXT1mdW5jdGlvbihjLGQpe3ZhciBlPW0ubWFwKHRoaXMsYixjKTtyZXR1cm4iVW50aWwiIT09YS5zbGljZSgtNSkmJihkPWMpLGQmJiJzdHJpbmciPT10eXBlb2YgZCYmKGU9bS5maWx0ZXIoZCxlKSksdGhpcy5sZW5ndGg+MSYmKENbYV18fChlPW0udW5pcXVlKGUpKSxCLnRlc3QoYSkmJihlPWUucmV2ZXJzZSgpKSksdGhpcy5wdXNoU3RhY2soZSl9fSk7dmFyIEU9L1xTKy9nLEY9e307ZnVuY3Rpb24gRyhhKXt2YXIgYj1GW2FdPXt9O3JldHVybiBtLmVhY2goYS5tYXRjaChFKXx8W10sZnVuY3Rpb24oYSxjKXtiW2NdPSEwfSksYn1tLkNhbGxiYWNrcz1mdW5jdGlvbihhKXthPSJzdHJpbmciPT10eXBlb2YgYT9GW2FdfHxHKGEpOm0uZXh0ZW5kKHt9LGEpO3ZhciBiLGMsZCxlLGYsZyxoPVtdLGk9IWEub25jZSYmW10saj1mdW5jdGlvbihsKXtmb3IoYz1hLm1lbW9yeSYmbCxkPSEwLGY9Z3x8MCxnPTAsZT1oLmxlbmd0aCxiPSEwO2gmJmU+ZjtmKyspaWYoaFtmXS5hcHBseShsWzBdLGxbMV0pPT09ITEmJmEuc3RvcE9uRmFsc2Upe2M9ITE7YnJlYWt9Yj0hMSxoJiYoaT9pLmxlbmd0aCYmaihpLnNoaWZ0KCkpOmM/aD1bXTprLmRpc2FibGUoKSl9LGs9e2FkZDpmdW5jdGlvbigpe2lmKGgpe3ZhciBkPWgubGVuZ3RoOyFmdW5jdGlvbiBmKGIpe20uZWFjaChiLGZ1bmN0aW9uKGIsYyl7dmFyIGQ9bS50eXBlKGMpOyJmdW5jdGlvbiI9PT1kP2EudW5pcXVlJiZrLmhhcyhjKXx8aC5wdXNoKGMpOmMmJmMubGVuZ3RoJiYic3RyaW5nIiE9PWQmJmYoYyl9KX0oYXJndW1lbnRzKSxiP2U9aC5sZW5ndGg6YyYmKGc9ZCxqKGMpKX1yZXR1cm4gdGhpc30scmVtb3ZlOmZ1bmN0aW9uKCl7cmV0dXJuIGgmJm0uZWFjaChhcmd1bWVudHMsZnVuY3Rpb24oYSxjKXt2YXIgZDt3aGlsZSgoZD1tLmluQXJyYXkoYyxoLGQpKT4tMSloLnNwbGljZShkLDEpLGImJihlPj1kJiZlLS0sZj49ZCYmZi0tKX0pLHRoaXN9LGhhczpmdW5jdGlvbihhKXtyZXR1cm4gYT9tLmluQXJyYXkoYSxoKT4tMTohKCFofHwhaC5sZW5ndGgpfSxlbXB0eTpmdW5jdGlvbigpe3JldHVybiBoPVtdLGU9MCx0aGlzfSxkaXNhYmxlOmZ1bmN0aW9uKCl7cmV0dXJuIGg9aT1jPXZvaWQgMCx0aGlzfSxkaXNhYmxlZDpmdW5jdGlvbigpe3JldHVybiFofSxsb2NrOmZ1bmN0aW9uKCl7cmV0dXJuIGk9dm9pZCAwLGN8fGsuZGlzYWJsZSgpLHRoaXN9LGxvY2tlZDpmdW5jdGlvbigpe3JldHVybiFpfSxmaXJlV2l0aDpmdW5jdGlvbihhLGMpe3JldHVybiFofHxkJiYhaXx8KGM9Y3x8W10sYz1bYSxjLnNsaWNlP2Muc2xpY2UoKTpjXSxiP2kucHVzaChjKTpqKGMpKSx0aGlzfSxmaXJlOmZ1bmN0aW9uKCl7cmV0dXJuIGsuZmlyZVdpdGgodGhpcyxhcmd1bWVudHMpLHRoaXN9LGZpcmVkOmZ1bmN0aW9uKCl7cmV0dXJuISFkfX07cmV0dXJuIGt9LG0uZXh0ZW5kKHtEZWZlcnJlZDpmdW5jdGlvbihhKXt2YXIgYj1bWyJyZXNvbHZlIiwiZG9uZSIsbS5DYWxsYmFja3MoIm9uY2UgbWVtb3J5IiksInJlc29sdmVkIl0sWyJyZWplY3QiLCJmYWlsIixtLkNhbGxiYWNrcygib25jZSBtZW1vcnkiKSwicmVqZWN0ZWQiXSxbIm5vdGlmeSIsInByb2dyZXNzIixtLkNhbGxiYWNrcygibWVtb3J5IildXSxjPSJwZW5kaW5nIixkPXtzdGF0ZTpmdW5jdGlvbigpe3JldHVybiBjfSxhbHdheXM6ZnVuY3Rpb24oKXtyZXR1cm4gZS5kb25lKGFyZ3VtZW50cykuZmFpbChhcmd1bWVudHMpLHRoaXN9LHRoZW46ZnVuY3Rpb24oKXt2YXIgYT1hcmd1bWVudHM7cmV0dXJuIG0uRGVmZXJyZWQoZnVuY3Rpb24oYyl7bS5lYWNoKGIsZnVuY3Rpb24oYixmKXt2YXIgZz1tLmlzRnVuY3Rpb24oYVtiXSkmJmFbYl07ZVtmWzFdXShmdW5jdGlvbigpe3ZhciBhPWcmJmcuYXBwbHkodGhpcyxhcmd1bWVudHMpO2EmJm0uaXNGdW5jdGlvbihhLnByb21pc2UpP2EucHJvbWlzZSgpLmRvbmUoYy5yZXNvbHZlKS5mYWlsKGMucmVqZWN0KS5wcm9ncmVzcyhjLm5vdGlmeSk6Y1tmWzBdKyJXaXRoIl0odGhpcz09PWQ/Yy5wcm9taXNlKCk6dGhpcyxnP1thXTphcmd1bWVudHMpfSl9KSxhPW51bGx9KS5wcm9taXNlKCl9LHByb21pc2U6ZnVuY3Rpb24oYSl7cmV0dXJuIG51bGwhPWE/bS5leHRlbmQoYSxkKTpkfX0sZT17fTtyZXR1cm4gZC5waXBlPWQudGhlbixtLmVhY2goYixmdW5jdGlvbihhLGYpe3ZhciBnPWZbMl0saD1mWzNdO2RbZlsxXV09Zy5hZGQsaCYmZy5hZGQoZnVuY3Rpb24oKXtjPWh9LGJbMV5hXVsyXS5kaXNhYmxlLGJbMl1bMl0ubG9jayksZVtmWzBdXT1mdW5jdGlvbigpe3JldHVybiBlW2ZbMF0rIldpdGgiXSh0aGlzPT09ZT9kOnRoaXMsYXJndW1lbnRzKSx0aGlzfSxlW2ZbMF0rIldpdGgiXT1nLmZpcmVXaXRofSksZC5wcm9taXNlKGUpLGEmJmEuY2FsbChlLGUpLGV9LHdoZW46ZnVuY3Rpb24oYSl7dmFyIGI9MCxjPWQuY2FsbChhcmd1bWVudHMpLGU9Yy5sZW5ndGgsZj0xIT09ZXx8YSYmbS5pc0Z1bmN0aW9uKGEucHJvbWlzZSk/ZTowLGc9MT09PWY/YTptLkRlZmVycmVkKCksaD1mdW5jdGlvbihhLGIsYyl7cmV0dXJuIGZ1bmN0aW9uKGUpe2JbYV09dGhpcyxjW2FdPWFyZ3VtZW50cy5sZW5ndGg+MT9kLmNhbGwoYXJndW1lbnRzKTplLGM9PT1pP2cubm90aWZ5V2l0aChiLGMpOi0tZnx8Zy5yZXNvbHZlV2l0aChiLGMpfX0saSxqLGs7aWYoZT4xKWZvcihpPW5ldyBBcnJheShlKSxqPW5ldyBBcnJheShlKSxrPW5ldyBBcnJheShlKTtlPmI7YisrKWNbYl0mJm0uaXNGdW5jdGlvbihjW2JdLnByb21pc2UpP2NbYl0ucHJvbWlzZSgpLmRvbmUoaChiLGssYykpLmZhaWwoZy5yZWplY3QpLnByb2dyZXNzKGgoYixqLGkpKTotLWY7cmV0dXJuIGZ8fGcucmVzb2x2ZVdpdGgoayxjKSxnLnByb21pc2UoKX19KTt2YXIgSDttLmZuLnJlYWR5PWZ1bmN0aW9uKGEpe3JldHVybiBtLnJlYWR5LnByb21pc2UoKS5kb25lKGEpLHRoaXN9LG0uZXh0ZW5kKHtpc1JlYWR5OiExLHJlYWR5V2FpdDoxLGhvbGRSZWFkeTpmdW5jdGlvbihhKXthP20ucmVhZHlXYWl0Kys6bS5yZWFkeSghMCl9LHJlYWR5OmZ1bmN0aW9uKGEpe2lmKGE9PT0hMD8hLS1tLnJlYWR5V2FpdDohbS5pc1JlYWR5KXtpZigheS5ib2R5KXJldHVybiBzZXRUaW1lb3V0KG0ucmVhZHkpO20uaXNSZWFkeT0hMCxhIT09ITAmJi0tbS5yZWFkeVdhaXQ+MHx8KEgucmVzb2x2ZVdpdGgoeSxbbV0pLG0uZm4udHJpZ2dlckhhbmRsZXImJihtKHkpLnRyaWdnZXJIYW5kbGVyKCJyZWFkeSIpLG0oeSkub2ZmKCJyZWFkeSIpKSl9fX0pO2Z1bmN0aW9uIEkoKXt5LmFkZEV2ZW50TGlzdGVuZXI/KHkucmVtb3ZlRXZlbnRMaXN0ZW5lcigiRE9NQ29udGVudExvYWRlZCIsSiwhMSksYS5yZW1vdmVFdmVudExpc3RlbmVyKCJsb2FkIixKLCExKSk6KHkuZGV0YWNoRXZlbnQoIm9ucmVhZHlzdGF0ZWNoYW5nZSIsSiksYS5kZXRhY2hFdmVudCgib25sb2FkIixKKSl9ZnVuY3Rpb24gSigpeyh5LmFkZEV2ZW50TGlzdGVuZXJ8fCJsb2FkIj09PWV2ZW50LnR5cGV8fCJjb21wbGV0ZSI9PT15LnJlYWR5U3RhdGUpJiYoSSgpLG0ucmVhZHkoKSl9bS5yZWFkeS5wcm9taXNlPWZ1bmN0aW9uKGIpe2lmKCFIKWlmKEg9bS5EZWZlcnJlZCgpLCJjb21wbGV0ZSI9PT15LnJlYWR5U3RhdGUpc2V0VGltZW91dChtLnJlYWR5KTtlbHNlIGlmKHkuYWRkRXZlbnRMaXN0ZW5lcil5LmFkZEV2ZW50TGlzdGVuZXIoIkRPTUNvbnRlbnRMb2FkZWQiLEosITEpLGEuYWRkRXZlbnRMaXN0ZW5lcigibG9hZCIsSiwhMSk7ZWxzZXt5LmF0dGFjaEV2ZW50KCJvbnJlYWR5c3RhdGVjaGFuZ2UiLEopLGEuYXR0YWNoRXZlbnQoIm9ubG9hZCIsSik7dmFyIGM9ITE7dHJ5e2M9bnVsbD09YS5mcmFtZUVsZW1lbnQmJnkuZG9jdW1lbnRFbGVtZW50fWNhdGNoKGQpe31jJiZjLmRvU2Nyb2xsJiYhZnVuY3Rpb24gZSgpe2lmKCFtLmlzUmVhZHkpe3RyeXtjLmRvU2Nyb2xsKCJsZWZ0Iil9Y2F0Y2goYSl7cmV0dXJuIHNldFRpbWVvdXQoZSw1MCl9SSgpLG0ucmVhZHkoKX19KCl9cmV0dXJuIEgucHJvbWlzZShiKX07dmFyIEs9InVuZGVmaW5lZCIsTDtmb3IoTCBpbiBtKGspKWJyZWFrO2sub3duTGFzdD0iMCIhPT1MLGsuaW5saW5lQmxvY2tOZWVkc0xheW91dD0hMSxtKGZ1bmN0aW9uKCl7dmFyIGEsYixjLGQ7Yz15LmdldEVsZW1lbnRzQnlUYWdOYW1lKCJib2R5IilbMF0sYyYmYy5zdHlsZSYmKGI9eS5jcmVhdGVFbGVtZW50KCJkaXYiKSxkPXkuY3JlYXRlRWxlbWVudCgiZGl2IiksZC5zdHlsZS5jc3NUZXh0PSJwb3NpdGlvbjphYnNvbHV0ZTtib3JkZXI6MDt3aWR0aDowO2hlaWdodDowO3RvcDowO2xlZnQ6LTk5OTlweCIsYy5hcHBlbmRDaGlsZChkKS5hcHBlbmRDaGlsZChiKSx0eXBlb2YgYi5zdHlsZS56b29tIT09SyYmKGIuc3R5bGUuY3NzVGV4dD0iZGlzcGxheTppbmxpbmU7bWFyZ2luOjA7Ym9yZGVyOjA7cGFkZGluZzoxcHg7d2lkdGg6MXB4O3pvb206MSIsay5pbmxpbmVCbG9ja05lZWRzTGF5b3V0PWE9Mz09PWIub2Zmc2V0V2lkdGgsYSYmKGMuc3R5bGUuem9vbT0xKSksYy5yZW1vdmVDaGlsZChkKSl9KSxmdW5jdGlvbigpe3ZhciBhPXkuY3JlYXRlRWxlbWVudCgiZGl2Iik7aWYobnVsbD09ay5kZWxldGVFeHBhbmRvKXtrLmRlbGV0ZUV4cGFuZG89ITA7dHJ5e2RlbGV0ZSBhLnRlc3R9Y2F0Y2goYil7ay5kZWxldGVFeHBhbmRvPSExfX1hPW51bGx9KCksbS5hY2NlcHREYXRhPWZ1bmN0aW9uKGEpe3ZhciBiPW0ubm9EYXRhWyhhLm5vZGVOYW1lKyIgIikudG9Mb3dlckNhc2UoKV0sYz0rYS5ub2RlVHlwZXx8MTtyZXR1cm4gMSE9PWMmJjkhPT1jPyExOiFifHxiIT09ITAmJmEuZ2V0QXR0cmlidXRlKCJjbGFzc2lkIik9PT1ifTt2YXIgTT0vXig/Olx7W1x3XFddKlx9fFxbW1x3XFddKlxdKSQvLE49LyhbQS1aXSkvZztmdW5jdGlvbiBPKGEsYixjKXtpZih2b2lkIDA9PT1jJiYxPT09YS5ub2RlVHlwZSl7dmFyIGQ9ImRhdGEtIitiLnJlcGxhY2UoTiwiLSQxIikudG9Mb3dlckNhc2UoKTtpZihjPWEuZ2V0QXR0cmlidXRlKGQpLCJzdHJpbmciPT10eXBlb2YgYyl7dHJ5e2M9InRydWUiPT09Yz8hMDoiZmFsc2UiPT09Yz8hMToibnVsbCI9PT1jP251bGw6K2MrIiI9PT1jPytjOk0udGVzdChjKT9tLnBhcnNlSlNPTihjKTpjfWNhdGNoKGUpe31tLmRhdGEoYSxiLGMpfWVsc2UgYz12b2lkIDB9cmV0dXJuIGN9ZnVuY3Rpb24gUChhKXt2YXIgYjtmb3IoYiBpbiBhKWlmKCgiZGF0YSIhPT1ifHwhbS5pc0VtcHR5T2JqZWN0KGFbYl0pKSYmInRvSlNPTiIhPT1iKXJldHVybiExOwoKcmV0dXJuITB9ZnVuY3Rpb24gUShhLGIsZCxlKXtpZihtLmFjY2VwdERhdGEoYSkpe3ZhciBmLGcsaD1tLmV4cGFuZG8saT1hLm5vZGVUeXBlLGo9aT9tLmNhY2hlOmEsaz1pP2FbaF06YVtoXSYmaDtpZihrJiZqW2tdJiYoZXx8altrXS5kYXRhKXx8dm9pZCAwIT09ZHx8InN0cmluZyIhPXR5cGVvZiBiKXJldHVybiBrfHwoaz1pP2FbaF09Yy5wb3AoKXx8bS5ndWlkKys6aCksaltrXXx8KGpba109aT97fTp7dG9KU09OOm0ubm9vcH0pLCgib2JqZWN0Ij09dHlwZW9mIGJ8fCJmdW5jdGlvbiI9PXR5cGVvZiBiKSYmKGU/altrXT1tLmV4dGVuZChqW2tdLGIpOmpba10uZGF0YT1tLmV4dGVuZChqW2tdLmRhdGEsYikpLGc9altrXSxlfHwoZy5kYXRhfHwoZy5kYXRhPXt9KSxnPWcuZGF0YSksdm9pZCAwIT09ZCYmKGdbbS5jYW1lbENhc2UoYildPWQpLCJzdHJpbmciPT10eXBlb2YgYj8oZj1nW2JdLG51bGw9PWYmJihmPWdbbS5jYW1lbENhc2UoYildKSk6Zj1nLGZ9fWZ1bmN0aW9uIFIoYSxiLGMpe2lmKG0uYWNjZXB0RGF0YShhKSl7dmFyIGQsZSxmPWEubm9kZVR5cGUsZz1mP20uY2FjaGU6YSxoPWY/YVttLmV4cGFuZG9dOm0uZXhwYW5kbztpZihnW2hdKXtpZihiJiYoZD1jP2dbaF06Z1toXS5kYXRhKSl7bS5pc0FycmF5KGIpP2I9Yi5jb25jYXQobS5tYXAoYixtLmNhbWVsQ2FzZSkpOmIgaW4gZD9iPVtiXTooYj1tLmNhbWVsQ2FzZShiKSxiPWIgaW4gZD9bYl06Yi5zcGxpdCgiICIpKSxlPWIubGVuZ3RoO3doaWxlKGUtLSlkZWxldGUgZFtiW2VdXTtpZihjPyFQKGQpOiFtLmlzRW1wdHlPYmplY3QoZCkpcmV0dXJufShjfHwoZGVsZXRlIGdbaF0uZGF0YSxQKGdbaF0pKSkmJihmP20uY2xlYW5EYXRhKFthXSwhMCk6ay5kZWxldGVFeHBhbmRvfHxnIT1nLndpbmRvdz9kZWxldGUgZ1toXTpnW2hdPW51bGwpfX19bS5leHRlbmQoe2NhY2hlOnt9LG5vRGF0YTp7ImFwcGxldCAiOiEwLCJlbWJlZCAiOiEwLCJvYmplY3QgIjoiY2xzaWQ6RDI3Q0RCNkUtQUU2RC0xMWNmLTk2QjgtNDQ0NTUzNTQwMDAwIn0saGFzRGF0YTpmdW5jdGlvbihhKXtyZXR1cm4gYT1hLm5vZGVUeXBlP20uY2FjaGVbYVttLmV4cGFuZG9dXTphW20uZXhwYW5kb10sISFhJiYhUChhKX0sZGF0YTpmdW5jdGlvbihhLGIsYyl7cmV0dXJuIFEoYSxiLGMpfSxyZW1vdmVEYXRhOmZ1bmN0aW9uKGEsYil7cmV0dXJuIFIoYSxiKX0sX2RhdGE6ZnVuY3Rpb24oYSxiLGMpe3JldHVybiBRKGEsYixjLCEwKX0sX3JlbW92ZURhdGE6ZnVuY3Rpb24oYSxiKXtyZXR1cm4gUihhLGIsITApfX0pLG0uZm4uZXh0ZW5kKHtkYXRhOmZ1bmN0aW9uKGEsYil7dmFyIGMsZCxlLGY9dGhpc1swXSxnPWYmJmYuYXR0cmlidXRlcztpZih2b2lkIDA9PT1hKXtpZih0aGlzLmxlbmd0aCYmKGU9bS5kYXRhKGYpLDE9PT1mLm5vZGVUeXBlJiYhbS5fZGF0YShmLCJwYXJzZWRBdHRycyIpKSl7Yz1nLmxlbmd0aDt3aGlsZShjLS0pZ1tjXSYmKGQ9Z1tjXS5uYW1lLDA9PT1kLmluZGV4T2YoImRhdGEtIikmJihkPW0uY2FtZWxDYXNlKGQuc2xpY2UoNSkpLE8oZixkLGVbZF0pKSk7bS5fZGF0YShmLCJwYXJzZWRBdHRycyIsITApfXJldHVybiBlfXJldHVybiJvYmplY3QiPT10eXBlb2YgYT90aGlzLmVhY2goZnVuY3Rpb24oKXttLmRhdGEodGhpcyxhKX0pOmFyZ3VtZW50cy5sZW5ndGg+MT90aGlzLmVhY2goZnVuY3Rpb24oKXttLmRhdGEodGhpcyxhLGIpfSk6Zj9PKGYsYSxtLmRhdGEoZixhKSk6dm9pZCAwfSxyZW1vdmVEYXRhOmZ1bmN0aW9uKGEpe3JldHVybiB0aGlzLmVhY2goZnVuY3Rpb24oKXttLnJlbW92ZURhdGEodGhpcyxhKX0pfX0pLG0uZXh0ZW5kKHtxdWV1ZTpmdW5jdGlvbihhLGIsYyl7dmFyIGQ7cmV0dXJuIGE/KGI9KGJ8fCJmeCIpKyJxdWV1ZSIsZD1tLl9kYXRhKGEsYiksYyYmKCFkfHxtLmlzQXJyYXkoYyk/ZD1tLl9kYXRhKGEsYixtLm1ha2VBcnJheShjKSk6ZC5wdXNoKGMpKSxkfHxbXSk6dm9pZCAwfSxkZXF1ZXVlOmZ1bmN0aW9uKGEsYil7Yj1ifHwiZngiO3ZhciBjPW0ucXVldWUoYSxiKSxkPWMubGVuZ3RoLGU9Yy5zaGlmdCgpLGY9bS5fcXVldWVIb29rcyhhLGIpLGc9ZnVuY3Rpb24oKXttLmRlcXVldWUoYSxiKX07ImlucHJvZ3Jlc3MiPT09ZSYmKGU9Yy5zaGlmdCgpLGQtLSksZSYmKCJmeCI9PT1iJiZjLnVuc2hpZnQoImlucHJvZ3Jlc3MiKSxkZWxldGUgZi5zdG9wLGUuY2FsbChhLGcsZikpLCFkJiZmJiZmLmVtcHR5LmZpcmUoKX0sX3F1ZXVlSG9va3M6ZnVuY3Rpb24oYSxiKXt2YXIgYz1iKyJxdWV1ZUhvb2tzIjtyZXR1cm4gbS5fZGF0YShhLGMpfHxtLl9kYXRhKGEsYyx7ZW1wdHk6bS5DYWxsYmFja3MoIm9uY2UgbWVtb3J5IikuYWRkKGZ1bmN0aW9uKCl7bS5fcmVtb3ZlRGF0YShhLGIrInF1ZXVlIiksbS5fcmVtb3ZlRGF0YShhLGMpfSl9KX19KSxtLmZuLmV4dGVuZCh7cXVldWU6ZnVuY3Rpb24oYSxiKXt2YXIgYz0yO3JldHVybiJzdHJpbmciIT10eXBlb2YgYSYmKGI9YSxhPSJmeCIsYy0tKSxhcmd1bWVudHMubGVuZ3RoPGM/bS5xdWV1ZSh0aGlzWzBdLGEpOnZvaWQgMD09PWI/dGhpczp0aGlzLmVhY2goZnVuY3Rpb24oKXt2YXIgYz1tLnF1ZXVlKHRoaXMsYSxiKTttLl9xdWV1ZUhvb2tzKHRoaXMsYSksImZ4Ij09PWEmJiJpbnByb2dyZXNzIiE9PWNbMF0mJm0uZGVxdWV1ZSh0aGlzLGEpfSl9LGRlcXVldWU6ZnVuY3Rpb24oYSl7cmV0dXJuIHRoaXMuZWFjaChmdW5jdGlvbigpe20uZGVxdWV1ZSh0aGlzLGEpfSl9LGNsZWFyUXVldWU6ZnVuY3Rpb24oYSl7cmV0dXJuIHRoaXMucXVldWUoYXx8ImZ4IixbXSl9LHByb21pc2U6ZnVuY3Rpb24oYSxiKXt2YXIgYyxkPTEsZT1tLkRlZmVycmVkKCksZj10aGlzLGc9dGhpcy5sZW5ndGgsaD1mdW5jdGlvbigpey0tZHx8ZS5yZXNvbHZlV2l0aChmLFtmXSl9OyJzdHJpbmciIT10eXBlb2YgYSYmKGI9YSxhPXZvaWQgMCksYT1hfHwiZngiO3doaWxlKGctLSljPW0uX2RhdGEoZltnXSxhKyJxdWV1ZUhvb2tzIiksYyYmYy5lbXB0eSYmKGQrKyxjLmVtcHR5LmFkZChoKSk7cmV0dXJuIGgoKSxlLnByb21pc2UoYil9fSk7dmFyIFM9L1srLV0/KD86XGQqXC58KVxkKyg/OltlRV1bKy1dP1xkK3wpLy5zb3VyY2UsVD1bIlRvcCIsIlJpZ2h0IiwiQm90dG9tIiwiTGVmdCJdLFU9ZnVuY3Rpb24oYSxiKXtyZXR1cm4gYT1ifHxhLCJub25lIj09PW0uY3NzKGEsImRpc3BsYXkiKXx8IW0uY29udGFpbnMoYS5vd25lckRvY3VtZW50LGEpfSxWPW0uYWNjZXNzPWZ1bmN0aW9uKGEsYixjLGQsZSxmLGcpe3ZhciBoPTAsaT1hLmxlbmd0aCxqPW51bGw9PWM7aWYoIm9iamVjdCI9PT1tLnR5cGUoYykpe2U9ITA7Zm9yKGggaW4gYyltLmFjY2VzcyhhLGIsaCxjW2hdLCEwLGYsZyl9ZWxzZSBpZih2b2lkIDAhPT1kJiYoZT0hMCxtLmlzRnVuY3Rpb24oZCl8fChnPSEwKSxqJiYoZz8oYi5jYWxsKGEsZCksYj1udWxsKTooaj1iLGI9ZnVuY3Rpb24oYSxiLGMpe3JldHVybiBqLmNhbGwobShhKSxjKX0pKSxiKSlmb3IoO2k+aDtoKyspYihhW2hdLGMsZz9kOmQuY2FsbChhW2hdLGgsYihhW2hdLGMpKSk7cmV0dXJuIGU/YTpqP2IuY2FsbChhKTppP2IoYVswXSxjKTpmfSxXPS9eKD86Y2hlY2tib3h8cmFkaW8pJC9pOyFmdW5jdGlvbigpe3ZhciBhPXkuY3JlYXRlRWxlbWVudCgiaW5wdXQiKSxiPXkuY3JlYXRlRWxlbWVudCgiZGl2IiksYz15LmNyZWF0ZURvY3VtZW50RnJhZ21lbnQoKTtpZihiLmlubmVySFRNTD0iICA8bGluay8+PHRhYmxlPjwvdGFibGU+PGEgaHJlZj0nL2EnPmE8L2E+PGlucHV0IHR5cGU9J2NoZWNrYm94Jy8+IixrLmxlYWRpbmdXaGl0ZXNwYWNlPTM9PT1iLmZpcnN0Q2hpbGQubm9kZVR5cGUsay50Ym9keT0hYi5nZXRFbGVtZW50c0J5VGFnTmFtZSgidGJvZHkiKS5sZW5ndGgsay5odG1sU2VyaWFsaXplPSEhYi5nZXRFbGVtZW50c0J5VGFnTmFtZSgibGluayIpLmxlbmd0aCxrLmh0bWw1Q2xvbmU9Ijw6bmF2PjwvOm5hdj4iIT09eS5jcmVhdGVFbGVtZW50KCJuYXYiKS5jbG9uZU5vZGUoITApLm91dGVySFRNTCxhLnR5cGU9ImNoZWNrYm94IixhLmNoZWNrZWQ9ITAsYy5hcHBlbmRDaGlsZChhKSxrLmFwcGVuZENoZWNrZWQ9YS5jaGVja2VkLGIuaW5uZXJIVE1MPSI8dGV4dGFyZWE+eDwvdGV4dGFyZWE+IixrLm5vQ2xvbmVDaGVja2VkPSEhYi5jbG9uZU5vZGUoITApLmxhc3RDaGlsZC5kZWZhdWx0VmFsdWUsYy5hcHBlbmRDaGlsZChiKSxiLmlubmVySFRNTD0iPGlucHV0IHR5cGU9J3JhZGlvJyBjaGVja2VkPSdjaGVja2VkJyBuYW1lPSd0Jy8+IixrLmNoZWNrQ2xvbmU9Yi5jbG9uZU5vZGUoITApLmNsb25lTm9kZSghMCkubGFzdENoaWxkLmNoZWNrZWQsay5ub0Nsb25lRXZlbnQ9ITAsYi5hdHRhY2hFdmVudCYmKGIuYXR0YWNoRXZlbnQoIm9uY2xpY2siLGZ1bmN0aW9uKCl7ay5ub0Nsb25lRXZlbnQ9ITF9KSxiLmNsb25lTm9kZSghMCkuY2xpY2soKSksbnVsbD09ay5kZWxldGVFeHBhbmRvKXtrLmRlbGV0ZUV4cGFuZG89ITA7dHJ5e2RlbGV0ZSBiLnRlc3R9Y2F0Y2goZCl7ay5kZWxldGVFeHBhbmRvPSExfX19KCksZnVuY3Rpb24oKXt2YXIgYixjLGQ9eS5jcmVhdGVFbGVtZW50KCJkaXYiKTtmb3IoYiBpbntzdWJtaXQ6ITAsY2hhbmdlOiEwLGZvY3VzaW46ITB9KWM9Im9uIitiLChrW2IrIkJ1YmJsZXMiXT1jIGluIGEpfHwoZC5zZXRBdHRyaWJ1dGUoYywidCIpLGtbYisiQnViYmxlcyJdPWQuYXR0cmlidXRlc1tjXS5leHBhbmRvPT09ITEpO2Q9bnVsbH0oKTt2YXIgWD0vXig/OmlucHV0fHNlbGVjdHx0ZXh0YXJlYSkkL2ksWT0vXmtleS8sWj0vXig/Om1vdXNlfHBvaW50ZXJ8Y29udGV4dG1lbnUpfGNsaWNrLywkPS9eKD86Zm9jdXNpbmZvY3VzfGZvY3Vzb3V0Ymx1cikkLyxfPS9eKFteLl0qKSg/OlwuKC4rKXwpJC87ZnVuY3Rpb24gYWEoKXtyZXR1cm4hMH1mdW5jdGlvbiBiYSgpe3JldHVybiExfWZ1bmN0aW9uIGNhKCl7dHJ5e3JldHVybiB5LmFjdGl2ZUVsZW1lbnR9Y2F0Y2goYSl7fX1tLmV2ZW50PXtnbG9iYWw6e30sYWRkOmZ1bmN0aW9uKGEsYixjLGQsZSl7dmFyIGYsZyxoLGksaixrLGwsbixvLHAscSxyPW0uX2RhdGEoYSk7aWYocil7Yy5oYW5kbGVyJiYoaT1jLGM9aS5oYW5kbGVyLGU9aS5zZWxlY3RvciksYy5ndWlkfHwoYy5ndWlkPW0uZ3VpZCsrKSwoZz1yLmV2ZW50cyl8fChnPXIuZXZlbnRzPXt9KSwoaz1yLmhhbmRsZSl8fChrPXIuaGFuZGxlPWZ1bmN0aW9uKGEpe3JldHVybiB0eXBlb2YgbT09PUt8fGEmJm0uZXZlbnQudHJpZ2dlcmVkPT09YS50eXBlP3ZvaWQgMDptLmV2ZW50LmRpc3BhdGNoLmFwcGx5KGsuZWxlbSxhcmd1bWVudHMpfSxrLmVsZW09YSksYj0oYnx8IiIpLm1hdGNoKEUpfHxbIiJdLGg9Yi5sZW5ndGg7d2hpbGUoaC0tKWY9Xy5leGVjKGJbaF0pfHxbXSxvPXE9ZlsxXSxwPShmWzJdfHwiIikuc3BsaXQoIi4iKS5zb3J0KCksbyYmKGo9bS5ldmVudC5zcGVjaWFsW29dfHx7fSxvPShlP2ouZGVsZWdhdGVUeXBlOmouYmluZFR5cGUpfHxvLGo9bS5ldmVudC5zcGVjaWFsW29dfHx7fSxsPW0uZXh0ZW5kKHt0eXBlOm8sb3JpZ1R5cGU6cSxkYXRhOmQsaGFuZGxlcjpjLGd1aWQ6Yy5ndWlkLHNlbGVjdG9yOmUsbmVlZHNDb250ZXh0OmUmJm0uZXhwci5tYXRjaC5uZWVkc0NvbnRleHQudGVzdChlKSxuYW1lc3BhY2U6cC5qb2luKCIuIil9LGkpLChuPWdbb10pfHwobj1nW29dPVtdLG4uZGVsZWdhdGVDb3VudD0wLGouc2V0dXAmJmouc2V0dXAuY2FsbChhLGQscCxrKSE9PSExfHwoYS5hZGRFdmVudExpc3RlbmVyP2EuYWRkRXZlbnRMaXN0ZW5lcihvLGssITEpOmEuYXR0YWNoRXZlbnQmJmEuYXR0YWNoRXZlbnQoIm9uIitvLGspKSksai5hZGQmJihqLmFkZC5jYWxsKGEsbCksbC5oYW5kbGVyLmd1aWR8fChsLmhhbmRsZXIuZ3VpZD1jLmd1aWQpKSxlP24uc3BsaWNlKG4uZGVsZWdhdGVDb3VudCsrLDAsbCk6bi5wdXNoKGwpLG0uZXZlbnQuZ2xvYmFsW29dPSEwKTthPW51bGx9fSxyZW1vdmU6ZnVuY3Rpb24oYSxiLGMsZCxlKXt2YXIgZixnLGgsaSxqLGssbCxuLG8scCxxLHI9bS5oYXNEYXRhKGEpJiZtLl9kYXRhKGEpO2lmKHImJihrPXIuZXZlbnRzKSl7Yj0oYnx8IiIpLm1hdGNoKEUpfHxbIiJdLGo9Yi5sZW5ndGg7d2hpbGUoai0tKWlmKGg9Xy5leGVjKGJbal0pfHxbXSxvPXE9aFsxXSxwPShoWzJdfHwiIikuc3BsaXQoIi4iKS5zb3J0KCksbyl7bD1tLmV2ZW50LnNwZWNpYWxbb118fHt9LG89KGQ/bC5kZWxlZ2F0ZVR5cGU6bC5iaW5kVHlwZSl8fG8sbj1rW29dfHxbXSxoPWhbMl0mJm5ldyBSZWdFeHAoIihefFxcLikiK3Auam9pbigiXFwuKD86LipcXC58KSIpKyIoXFwufCQpIiksaT1mPW4ubGVuZ3RoO3doaWxlKGYtLSlnPW5bZl0sIWUmJnEhPT1nLm9yaWdUeXBlfHxjJiZjLmd1aWQhPT1nLmd1aWR8fGgmJiFoLnRlc3QoZy5uYW1lc3BhY2UpfHxkJiZkIT09Zy5zZWxlY3RvciYmKCIqKiIhPT1kfHwhZy5zZWxlY3Rvcil8fChuLnNwbGljZShmLDEpLGcuc2VsZWN0b3ImJm4uZGVsZWdhdGVDb3VudC0tLGwucmVtb3ZlJiZsLnJlbW92ZS5jYWxsKGEsZykpO2kmJiFuLmxlbmd0aCYmKGwudGVhcmRvd24mJmwudGVhcmRvd24uY2FsbChhLHAsci5oYW5kbGUpIT09ITF8fG0ucmVtb3ZlRXZlbnQoYSxvLHIuaGFuZGxlKSxkZWxldGUga1tvXSl9ZWxzZSBmb3IobyBpbiBrKW0uZXZlbnQucmVtb3ZlKGEsbytiW2pdLGMsZCwhMCk7bS5pc0VtcHR5T2JqZWN0KGspJiYoZGVsZXRlIHIuaGFuZGxlLG0uX3JlbW92ZURhdGEoYSwiZXZlbnRzIikpfX0sdHJpZ2dlcjpmdW5jdGlvbihiLGMsZCxlKXt2YXIgZixnLGgsaSxrLGwsbixvPVtkfHx5XSxwPWouY2FsbChiLCJ0eXBlIik/Yi50eXBlOmIscT1qLmNhbGwoYiwibmFtZXNwYWNlIik/Yi5uYW1lc3BhY2Uuc3BsaXQoIi4iKTpbXTtpZihoPWw9ZD1kfHx5LDMhPT1kLm5vZGVUeXBlJiY4IT09ZC5ub2RlVHlwZSYmISQudGVzdChwK20uZXZlbnQudHJpZ2dlcmVkKSYmKHAuaW5kZXhPZigiLiIpPj0wJiYocT1wLnNwbGl0KCIuIikscD1xLnNoaWZ0KCkscS5zb3J0KCkpLGc9cC5pbmRleE9mKCI6Iik8MCYmIm9uIitwLGI9YlttLmV4cGFuZG9dP2I6bmV3IG0uRXZlbnQocCwib2JqZWN0Ij09dHlwZW9mIGImJmIpLGIuaXNUcmlnZ2VyPWU/MjozLGIubmFtZXNwYWNlPXEuam9pbigiLiIpLGIubmFtZXNwYWNlX3JlPWIubmFtZXNwYWNlP25ldyBSZWdFeHAoIihefFxcLikiK3Euam9pbigiXFwuKD86LipcXC58KSIpKyIoXFwufCQpIik6bnVsbCxiLnJlc3VsdD12b2lkIDAsYi50YXJnZXR8fChiLnRhcmdldD1kKSxjPW51bGw9PWM/W2JdOm0ubWFrZUFycmF5KGMsW2JdKSxrPW0uZXZlbnQuc3BlY2lhbFtwXXx8e30sZXx8IWsudHJpZ2dlcnx8ay50cmlnZ2VyLmFwcGx5KGQsYykhPT0hMSkpe2lmKCFlJiYhay5ub0J1YmJsZSYmIW0uaXNXaW5kb3coZCkpe2ZvcihpPWsuZGVsZWdhdGVUeXBlfHxwLCQudGVzdChpK3ApfHwoaD1oLnBhcmVudE5vZGUpO2g7aD1oLnBhcmVudE5vZGUpby5wdXNoKGgpLGw9aDtsPT09KGQub3duZXJEb2N1bWVudHx8eSkmJm8ucHVzaChsLmRlZmF1bHRWaWV3fHxsLnBhcmVudFdpbmRvd3x8YSl9bj0wO3doaWxlKChoPW9bbisrXSkmJiFiLmlzUHJvcGFnYXRpb25TdG9wcGVkKCkpYi50eXBlPW4+MT9pOmsuYmluZFR5cGV8fHAsZj0obS5fZGF0YShoLCJldmVudHMiKXx8e30pW2IudHlwZV0mJm0uX2RhdGEoaCwiaGFuZGxlIiksZiYmZi5hcHBseShoLGMpLGY9ZyYmaFtnXSxmJiZmLmFwcGx5JiZtLmFjY2VwdERhdGEoaCkmJihiLnJlc3VsdD1mLmFwcGx5KGgsYyksYi5yZXN1bHQ9PT0hMSYmYi5wcmV2ZW50RGVmYXVsdCgpKTtpZihiLnR5cGU9cCwhZSYmIWIuaXNEZWZhdWx0UHJldmVudGVkKCkmJighay5fZGVmYXVsdHx8ay5fZGVmYXVsdC5hcHBseShvLnBvcCgpLGMpPT09ITEpJiZtLmFjY2VwdERhdGEoZCkmJmcmJmRbcF0mJiFtLmlzV2luZG93KGQpKXtsPWRbZ10sbCYmKGRbZ109bnVsbCksbS5ldmVudC50cmlnZ2VyZWQ9cDt0cnl7ZFtwXSgpfWNhdGNoKHIpe31tLmV2ZW50LnRyaWdnZXJlZD12b2lkIDAsbCYmKGRbZ109bCl9cmV0dXJuIGIucmVzdWx0fX0sZGlzcGF0Y2g6ZnVuY3Rpb24oYSl7YT1tLmV2ZW50LmZpeChhKTt2YXIgYixjLGUsZixnLGg9W10saT1kLmNhbGwoYXJndW1lbnRzKSxqPShtLl9kYXRhKHRoaXMsImV2ZW50cyIpfHx7fSlbYS50eXBlXXx8W10saz1tLmV2ZW50LnNwZWNpYWxbYS50eXBlXXx8e307aWYoaVswXT1hLGEuZGVsZWdhdGVUYXJnZXQ9dGhpcywhay5wcmVEaXNwYXRjaHx8ay5wcmVEaXNwYXRjaC5jYWxsKHRoaXMsYSkhPT0hMSl7aD1tLmV2ZW50LmhhbmRsZXJzLmNhbGwodGhpcyxhLGopLGI9MDt3aGlsZSgoZj1oW2IrK10pJiYhYS5pc1Byb3BhZ2F0aW9uU3RvcHBlZCgpKXthLmN1cnJlbnRUYXJnZXQ9Zi5lbGVtLGc9MDt3aGlsZSgoZT1mLmhhbmRsZXJzW2crK10pJiYhYS5pc0ltbWVkaWF0ZVByb3BhZ2F0aW9uU3RvcHBlZCgpKSghYS5uYW1lc3BhY2VfcmV8fGEubmFtZXNwYWNlX3JlLnRlc3QoZS5uYW1lc3BhY2UpKSYmKGEuaGFuZGxlT2JqPWUsYS5kYXRhPWUuZGF0YSxjPSgobS5ldmVudC5zcGVjaWFsW2Uub3JpZ1R5cGVdfHx7fSkuaGFuZGxlfHxlLmhhbmRsZXIpLmFwcGx5KGYuZWxlbSxpKSx2b2lkIDAhPT1jJiYoYS5yZXN1bHQ9Yyk9PT0hMSYmKGEucHJldmVudERlZmF1bHQoKSxhLnN0b3BQcm9wYWdhdGlvbigpKSl9cmV0dXJuIGsucG9zdERpc3BhdGNoJiZrLnBvc3REaXNwYXRjaC5jYWxsKHRoaXMsYSksYS5yZXN1bHR9fSxoYW5kbGVyczpmdW5jdGlvbihhLGIpe3ZhciBjLGQsZSxmLGc9W10saD1iLmRlbGVnYXRlQ291bnQsaT1hLnRhcmdldDtpZihoJiZpLm5vZGVUeXBlJiYoIWEuYnV0dG9ufHwiY2xpY2siIT09YS50eXBlKSlmb3IoO2khPXRoaXM7aT1pLnBhcmVudE5vZGV8fHRoaXMpaWYoMT09PWkubm9kZVR5cGUmJihpLmRpc2FibGVkIT09ITB8fCJjbGljayIhPT1hLnR5cGUpKXtmb3IoZT1bXSxmPTA7aD5mO2YrKylkPWJbZl0sYz1kLnNlbGVjdG9yKyIgIix2b2lkIDA9PT1lW2NdJiYoZVtjXT1kLm5lZWRzQ29udGV4dD9tKGMsdGhpcykuaW5kZXgoaSk+PTA6bS5maW5kKGMsdGhpcyxudWxsLFtpXSkubGVuZ3RoKSxlW2NdJiZlLnB1c2goZCk7ZS5sZW5ndGgmJmcucHVzaCh7ZWxlbTppLGhhbmRsZXJzOmV9KX1yZXR1cm4gaDxiLmxlbmd0aCYmZy5wdXNoKHtlbGVtOnRoaXMsaGFuZGxlcnM6Yi5zbGljZShoKX0pLGd9LGZpeDpmdW5jdGlvbihhKXtpZihhW20uZXhwYW5kb10pcmV0dXJuIGE7dmFyIGIsYyxkLGU9YS50eXBlLGY9YSxnPXRoaXMuZml4SG9va3NbZV07Z3x8KHRoaXMuZml4SG9va3NbZV09Zz1aLnRlc3QoZSk/dGhpcy5tb3VzZUhvb2tzOlkudGVzdChlKT90aGlzLmtleUhvb2tzOnt9KSxkPWcucHJvcHM/dGhpcy5wcm9wcy5jb25jYXQoZy5wcm9wcyk6dGhpcy5wcm9wcyxhPW5ldyBtLkV2ZW50KGYpLGI9ZC5sZW5ndGg7d2hpbGUoYi0tKWM9ZFtiXSxhW2NdPWZbY107cmV0dXJuIGEudGFyZ2V0fHwoYS50YXJnZXQ9Zi5zcmNFbGVtZW50fHx5KSwzPT09YS50YXJnZXQubm9kZVR5cGUmJihhLnRhcmdldD1hLnRhcmdldC5wYXJlbnROb2RlKSxhLm1ldGFLZXk9ISFhLm1ldGFLZXksZy5maWx0ZXI/Zy5maWx0ZXIoYSxmKTphfSxwcm9wczoiYWx0S2V5IGJ1YmJsZXMgY2FuY2VsYWJsZSBjdHJsS2V5IGN1cnJlbnRUYXJnZXQgZXZlbnRQaGFzZSBtZXRhS2V5IHJlbGF0ZWRUYXJnZXQgc2hpZnRLZXkgdGFyZ2V0IHRpbWVTdGFtcCB2aWV3IHdoaWNoIi5zcGxpdCgiICIpLGZpeEhvb2tzOnt9LGtleUhvb2tzOntwcm9wczoiY2hhciBjaGFyQ29kZSBrZXkga2V5Q29kZSIuc3BsaXQoIiAiKSxmaWx0ZXI6ZnVuY3Rpb24oYSxiKXtyZXR1cm4gbnVsbD09YS53aGljaCYmKGEud2hpY2g9bnVsbCE9Yi5jaGFyQ29kZT9iLmNoYXJDb2RlOmIua2V5Q29kZSksYX19LG1vdXNlSG9va3M6e3Byb3BzOiJidXR0b24gYnV0dG9ucyBjbGllbnRYIGNsaWVudFkgZnJvbUVsZW1lbnQgb2Zmc2V0WCBvZmZzZXRZIHBhZ2VYIHBhZ2VZIHNjcmVlblggc2NyZWVuWSB0b0VsZW1lbnQiLnNwbGl0KCIgIiksZmlsdGVyOmZ1bmN0aW9uKGEsYil7dmFyIGMsZCxlLGY9Yi5idXR0b24sZz1iLmZyb21FbGVtZW50O3JldHVybiBudWxsPT1hLnBhZ2VYJiZudWxsIT1iLmNsaWVudFgmJihkPWEudGFyZ2V0Lm93bmVyRG9jdW1lbnR8fHksZT1kLmRvY3VtZW50RWxlbWVudCxjPWQuYm9keSxhLnBhZ2VYPWIuY2xpZW50WCsoZSYmZS5zY3JvbGxMZWZ0fHxjJiZjLnNjcm9sbExlZnR8fDApLShlJiZlLmNsaWVudExlZnR8fGMmJmMuY2xpZW50TGVmdHx8MCksYS5wYWdlWT1iLmNsaWVudFkrKGUmJmUuc2Nyb2xsVG9wfHxjJiZjLnNjcm9sbFRvcHx8MCktKGUmJmUuY2xpZW50VG9wfHxjJiZjLmNsaWVudFRvcHx8MCkpLCFhLnJlbGF0ZWRUYXJnZXQmJmcmJihhLnJlbGF0ZWRUYXJnZXQ9Zz09PWEudGFyZ2V0P2IudG9FbGVtZW50OmcpLGEud2hpY2h8fHZvaWQgMD09PWZ8fChhLndoaWNoPTEmZj8xOjImZj8zOjQmZj8yOjApLGF9fSxzcGVjaWFsOntsb2FkOntub0J1YmJsZTohMH0sZm9jdXM6e3RyaWdnZXI6ZnVuY3Rpb24oKXtpZih0aGlzIT09Y2EoKSYmdGhpcy5mb2N1cyl0cnl7cmV0dXJuIHRoaXMuZm9jdXMoKSwhMX1jYXRjaChhKXt9fSxkZWxlZ2F0ZVR5cGU6ImZvY3VzaW4ifSxibHVyOnt0cmlnZ2VyOmZ1bmN0aW9uKCl7cmV0dXJuIHRoaXM9PT1jYSgpJiZ0aGlzLmJsdXI/KHRoaXMuYmx1cigpLCExKTp2b2lkIDB9LGRlbGVnYXRlVHlwZToiZm9jdXNvdXQifSxjbGljazp7dHJpZ2dlcjpmdW5jdGlvbigpe3JldHVybiBtLm5vZGVOYW1lKHRoaXMsImlucHV0IikmJiJjaGVja2JveCI9PT10aGlzLnR5cGUmJnRoaXMuY2xpY2s/KHRoaXMuY2xpY2soKSwhMSk6dm9pZCAwfSxfZGVmYXVsdDpmdW5jdGlvbihhKXtyZXR1cm4gbS5ub2RlTmFtZShhLnRhcmdldCwiYSIpfX0sYmVmb3JldW5sb2FkOntwb3N0RGlzcGF0Y2g6ZnVuY3Rpb24oYSl7dm9pZCAwIT09YS5yZXN1bHQmJmEub3JpZ2luYWxFdmVudCYmKGEub3JpZ2luYWxFdmVudC5yZXR1cm5WYWx1ZT1hLnJlc3VsdCl9fX0sc2ltdWxhdGU6ZnVuY3Rpb24oYSxiLGMsZCl7dmFyIGU9bS5leHRlbmQobmV3IG0uRXZlbnQsYyx7dHlwZTphLGlzU2ltdWxhdGVkOiEwLG9yaWdpbmFsRXZlbnQ6e319KTtkP20uZXZlbnQudHJpZ2dlcihlLG51bGwsYik6bS5ldmVudC5kaXNwYXRjaC5jYWxsKGIsZSksZS5pc0RlZmF1bHRQcmV2ZW50ZWQoKSYmYy5wcmV2ZW50RGVmYXVsdCgpfX0sbS5yZW1vdmVFdmVudD15LnJlbW92ZUV2ZW50TGlzdGVuZXI/ZnVuY3Rpb24oYSxiLGMpe2EucmVtb3ZlRXZlbnRMaXN0ZW5lciYmYS5yZW1vdmVFdmVudExpc3RlbmVyKGIsYywhMSl9OmZ1bmN0aW9uKGEsYixjKXt2YXIgZD0ib24iK2I7YS5kZXRhY2hFdmVudCYmKHR5cGVvZiBhW2RdPT09SyYmKGFbZF09bnVsbCksYS5kZXRhY2hFdmVudChkLGMpKX0sbS5FdmVudD1mdW5jdGlvbihhLGIpe3JldHVybiB0aGlzIGluc3RhbmNlb2YgbS5FdmVudD8oYSYmYS50eXBlPyh0aGlzLm9yaWdpbmFsRXZlbnQ9YSx0aGlzLnR5cGU9YS50eXBlLHRoaXMuaXNEZWZhdWx0UHJldmVudGVkPWEuZGVmYXVsdFByZXZlbnRlZHx8dm9pZCAwPT09YS5kZWZhdWx0UHJldmVudGVkJiZhLnJldHVyblZhbHVlPT09ITE/YWE6YmEpOnRoaXMudHlwZT1hLGImJm0uZXh0ZW5kKHRoaXMsYiksdGhpcy50aW1lU3RhbXA9YSYmYS50aW1lU3RhbXB8fG0ubm93KCksdm9pZCh0aGlzW20uZXhwYW5kb109ITApKTpuZXcgbS5FdmVudChhLGIpfSxtLkV2ZW50LnByb3RvdHlwZT17aXNEZWZhdWx0UHJldmVudGVkOmJhLGlzUHJvcGFnYXRpb25TdG9wcGVkOmJhLGlzSW1tZWRpYXRlUHJvcGFnYXRpb25TdG9wcGVkOmJhLHByZXZlbnREZWZhdWx0OmZ1bmN0aW9uKCl7dmFyIGE9dGhpcy5vcmlnaW5hbEV2ZW50O3RoaXMuaXNEZWZhdWx0UHJldmVudGVkPWFhLGEmJihhLnByZXZlbnREZWZhdWx0P2EucHJldmVudERlZmF1bHQoKTphLnJldHVyblZhbHVlPSExKX0sc3RvcFByb3BhZ2F0aW9uOmZ1bmN0aW9uKCl7dmFyIGE9dGhpcy5vcmlnaW5hbEV2ZW50O3RoaXMuaXNQcm9wYWdhdGlvblN0b3BwZWQ9YWEsYSYmKGEuc3RvcFByb3BhZ2F0aW9uJiZhLnN0b3BQcm9wYWdhdGlvbigpLGEuY2FuY2VsQnViYmxlPSEwKX0sc3RvcEltbWVkaWF0ZVByb3BhZ2F0aW9uOmZ1bmN0aW9uKCl7dmFyIGE9dGhpcy5vcmlnaW5hbEV2ZW50O3RoaXMuaXNJbW1lZGlhdGVQcm9wYWdhdGlvblN0b3BwZWQ9YWEsYSYmYS5zdG9wSW1tZWRpYXRlUHJvcGFnYXRpb24mJmEuc3RvcEltbWVkaWF0ZVByb3BhZ2F0aW9uKCksdGhpcy5zdG9wUHJvcGFnYXRpb24oKX19LG0uZWFjaCh7bW91c2VlbnRlcjoibW91c2VvdmVyIixtb3VzZWxlYXZlOiJtb3VzZW91dCIscG9pbnRlcmVudGVyOiJwb2ludGVyb3ZlciIscG9pbnRlcmxlYXZlOiJwb2ludGVyb3V0In0sZnVuY3Rpb24oYSxiKXttLmV2ZW50LnNwZWNpYWxbYV09e2RlbGVnYXRlVHlwZTpiLGJpbmRUeXBlOmIsaGFuZGxlOmZ1bmN0aW9uKGEpe3ZhciBjLGQ9dGhpcyxlPWEucmVsYXRlZFRhcmdldCxmPWEuaGFuZGxlT2JqO3JldHVybighZXx8ZSE9PWQmJiFtLmNvbnRhaW5zKGQsZSkpJiYoYS50eXBlPWYub3JpZ1R5cGUsYz1mLmhhbmRsZXIuYXBwbHkodGhpcyxhcmd1bWVudHMpLGEudHlwZT1iKSxjfX19KSxrLnN1Ym1pdEJ1YmJsZXN8fChtLmV2ZW50LnNwZWNpYWwuc3VibWl0PXtzZXR1cDpmdW5jdGlvbigpe3JldHVybiBtLm5vZGVOYW1lKHRoaXMsImZvcm0iKT8hMTp2b2lkIG0uZXZlbnQuYWRkKHRoaXMsImNsaWNrLl9zdWJtaXQga2V5cHJlc3MuX3N1Ym1pdCIsZnVuY3Rpb24oYSl7dmFyIGI9YS50YXJnZXQsYz1tLm5vZGVOYW1lKGIsImlucHV0Iil8fG0ubm9kZU5hbWUoYiwiYnV0dG9uIik/Yi5mb3JtOnZvaWQgMDtjJiYhbS5fZGF0YShjLCJzdWJtaXRCdWJibGVzIikmJihtLmV2ZW50LmFkZChjLCJzdWJtaXQuX3N1Ym1pdCIsZnVuY3Rpb24oYSl7YS5fc3VibWl0X2J1YmJsZT0hMH0pLG0uX2RhdGEoYywic3VibWl0QnViYmxlcyIsITApKX0pfSxwb3N0RGlzcGF0Y2g6ZnVuY3Rpb24oYSl7YS5fc3VibWl0X2J1YmJsZSYmKGRlbGV0ZSBhLl9zdWJtaXRfYnViYmxlLHRoaXMucGFyZW50Tm9kZSYmIWEuaXNUcmlnZ2VyJiZtLmV2ZW50LnNpbXVsYXRlKCJzdWJtaXQiLHRoaXMucGFyZW50Tm9kZSxhLCEwKSl9LHRlYXJkb3duOmZ1bmN0aW9uKCl7cmV0dXJuIG0ubm9kZU5hbWUodGhpcywiZm9ybSIpPyExOnZvaWQgbS5ldmVudC5yZW1vdmUodGhpcywiLl9zdWJtaXQiKX19KSxrLmNoYW5nZUJ1YmJsZXN8fChtLmV2ZW50LnNwZWNpYWwuY2hhbmdlPXtzZXR1cDpmdW5jdGlvbigpe3JldHVybiBYLnRlc3QodGhpcy5ub2RlTmFtZSk/KCgiY2hlY2tib3giPT09dGhpcy50eXBlfHwicmFkaW8iPT09dGhpcy50eXBlKSYmKG0uZXZlbnQuYWRkKHRoaXMsInByb3BlcnR5Y2hhbmdlLl9jaGFuZ2UiLGZ1bmN0aW9uKGEpeyJjaGVja2VkIj09PWEub3JpZ2luYWxFdmVudC5wcm9wZXJ0eU5hbWUmJih0aGlzLl9qdXN0X2NoYW5nZWQ9ITApfSksbS5ldmVudC5hZGQodGhpcywiY2xpY2suX2NoYW5nZSIsZnVuY3Rpb24oYSl7dGhpcy5fanVzdF9jaGFuZ2VkJiYhYS5pc1RyaWdnZXImJih0aGlzLl9qdXN0X2NoYW5nZWQ9ITEpLG0uZXZlbnQuc2ltdWxhdGUoImNoYW5nZSIsdGhpcyxhLCEwKX0pKSwhMSk6dm9pZCBtLmV2ZW50LmFkZCh0aGlzLCJiZWZvcmVhY3RpdmF0ZS5fY2hhbmdlIixmdW5jdGlvbihhKXt2YXIgYj1hLnRhcmdldDtYLnRlc3QoYi5ub2RlTmFtZSkmJiFtLl9kYXRhKGIsImNoYW5nZUJ1YmJsZXMiKSYmKG0uZXZlbnQuYWRkKGIsImNoYW5nZS5fY2hhbmdlIixmdW5jdGlvbihhKXshdGhpcy5wYXJlbnROb2RlfHxhLmlzU2ltdWxhdGVkfHxhLmlzVHJpZ2dlcnx8bS5ldmVudC5zaW11bGF0ZSgiY2hhbmdlIix0aGlzLnBhcmVudE5vZGUsYSwhMCl9KSxtLl9kYXRhKGIsImNoYW5nZUJ1YmJsZXMiLCEwKSl9KX0saGFuZGxlOmZ1bmN0aW9uKGEpe3ZhciBiPWEudGFyZ2V0O3JldHVybiB0aGlzIT09Ynx8YS5pc1NpbXVsYXRlZHx8YS5pc1RyaWdnZXJ8fCJyYWRpbyIhPT1iLnR5cGUmJiJjaGVja2JveCIhPT1iLnR5cGU/YS5oYW5kbGVPYmouaGFuZGxlci5hcHBseSh0aGlzLGFyZ3VtZW50cyk6dm9pZCAwfSx0ZWFyZG93bjpmdW5jdGlvbigpe3JldHVybiBtLmV2ZW50LnJlbW92ZSh0aGlzLCIuX2NoYW5nZSIpLCFYLnRlc3QodGhpcy5ub2RlTmFtZSl9fSksay5mb2N1c2luQnViYmxlc3x8bS5lYWNoKHtmb2N1czoiZm9jdXNpbiIsYmx1cjoiZm9jdXNvdXQifSxmdW5jdGlvbihhLGIpe3ZhciBjPWZ1bmN0aW9uKGEpe20uZXZlbnQuc2ltdWxhdGUoYixhLnRhcmdldCxtLmV2ZW50LmZpeChhKSwhMCl9O20uZXZlbnQuc3BlY2lhbFtiXT17c2V0dXA6ZnVuY3Rpb24oKXt2YXIgZD10aGlzLm93bmVyRG9jdW1lbnR8fHRoaXMsZT1tLl9kYXRhKGQsYik7ZXx8ZC5hZGRFdmVudExpc3RlbmVyKGEsYywhMCksbS5fZGF0YShkLGIsKGV8fDApKzEpfSx0ZWFyZG93bjpmdW5jdGlvbigpe3ZhciBkPXRoaXMub3duZXJEb2N1bWVudHx8dGhpcyxlPW0uX2RhdGEoZCxiKS0xO2U/bS5fZGF0YShkLGIsZSk6KGQucmVtb3ZlRXZlbnRMaXN0ZW5lcihhLGMsITApLG0uX3JlbW92ZURhdGEoZCxiKSl9fX0pLG0uZm4uZXh0ZW5kKHtvbjpmdW5jdGlvbihhLGIsYyxkLGUpe3ZhciBmLGc7aWYoIm9iamVjdCI9PXR5cGVvZiBhKXsic3RyaW5nIiE9dHlwZW9mIGImJihjPWN8fGIsYj12b2lkIDApO2ZvcihmIGluIGEpdGhpcy5vbihmLGIsYyxhW2ZdLGUpO3JldHVybiB0aGlzfWlmKG51bGw9PWMmJm51bGw9PWQ/KGQ9YixjPWI9dm9pZCAwKTpudWxsPT1kJiYoInN0cmluZyI9PXR5cGVvZiBiPyhkPWMsYz12b2lkIDApOihkPWMsYz1iLGI9dm9pZCAwKSksZD09PSExKWQ9YmE7ZWxzZSBpZighZClyZXR1cm4gdGhpcztyZXR1cm4gMT09PWUmJihnPWQsZD1mdW5jdGlvbihhKXtyZXR1cm4gbSgpLm9mZihhKSxnLmFwcGx5KHRoaXMsYXJndW1lbnRzKX0sZC5ndWlkPWcuZ3VpZHx8KGcuZ3VpZD1tLmd1aWQrKykpLHRoaXMuZWFjaChmdW5jdGlvbigpe20uZXZlbnQuYWRkKHRoaXMsYSxkLGMsYil9KX0sb25lOmZ1bmN0aW9uKGEsYixjLGQpe3JldHVybiB0aGlzLm9uKGEsYixjLGQsMSl9LG9mZjpmdW5jdGlvbihhLGIsYyl7dmFyIGQsZTtpZihhJiZhLnByZXZlbnREZWZhdWx0JiZhLmhhbmRsZU9iailyZXR1cm4gZD1hLmhhbmRsZU9iaixtKGEuZGVsZWdhdGVUYXJnZXQpLm9mZihkLm5hbWVzcGFjZT9kLm9yaWdUeXBlKyIuIitkLm5hbWVzcGFjZTpkLm9yaWdUeXBlLGQuc2VsZWN0b3IsZC5oYW5kbGVyKSx0aGlzO2lmKCJvYmplY3QiPT10eXBlb2YgYSl7Zm9yKGUgaW4gYSl0aGlzLm9mZihlLGIsYVtlXSk7cmV0dXJuIHRoaXN9cmV0dXJuKGI9PT0hMXx8ImZ1bmN0aW9uIj09dHlwZW9mIGIpJiYoYz1iLGI9dm9pZCAwKSxjPT09ITEmJihjPWJhKSx0aGlzLmVhY2goZnVuY3Rpb24oKXttLmV2ZW50LnJlbW92ZSh0aGlzLGEsYyxiKX0pfSx0cmlnZ2VyOmZ1bmN0aW9uKGEsYil7cmV0dXJuIHRoaXMuZWFjaChmdW5jdGlvbigpe20uZXZlbnQudHJpZ2dlcihhLGIsdGhpcyl9KX0sdHJpZ2dlckhhbmRsZXI6ZnVuY3Rpb24oYSxiKXt2YXIgYz10aGlzWzBdO3JldHVybiBjP20uZXZlbnQudHJpZ2dlcihhLGIsYywhMCk6dm9pZCAwfX0pO2Z1bmN0aW9uIGRhKGEpe3ZhciBiPWVhLnNwbGl0KCJ8IiksYz1hLmNyZWF0ZURvY3VtZW50RnJhZ21lbnQoKTtpZihjLmNyZWF0ZUVsZW1lbnQpd2hpbGUoYi5sZW5ndGgpYy5jcmVhdGVFbGVtZW50KGIucG9wKCkpO3JldHVybiBjfXZhciBlYT0iYWJicnxhcnRpY2xlfGFzaWRlfGF1ZGlvfGJkaXxjYW52YXN8ZGF0YXxkYXRhbGlzdHxkZXRhaWxzfGZpZ2NhcHRpb258ZmlndXJlfGZvb3RlcnxoZWFkZXJ8aGdyb3VwfG1hcmt8bWV0ZXJ8bmF2fG91dHB1dHxwcm9ncmVzc3xzZWN0aW9ufHN1bW1hcnl8dGltZXx2aWRlbyIsZmE9LyBqUXVlcnlcZCs9Iig/Om51bGx8XGQrKSIvZyxnYT1uZXcgUmVnRXhwKCI8KD86IitlYSsiKVtcXHMvPl0iLCJpIiksaGE9L15ccysvLGlhPS88KD8hYXJlYXxicnxjb2x8ZW1iZWR8aHJ8aW1nfGlucHV0fGxpbmt8bWV0YXxwYXJhbSkoKFtcdzpdKylbXj5dKilcLz4vZ2ksamE9LzwoW1x3Ol0rKS8sa2E9Lzx0Ym9keS9pLGxhPS88fCYjP1x3KzsvLG1hPS88KD86c2NyaXB0fHN0eWxlfGxpbmspL2ksbmE9L2NoZWNrZWRccyooPzpbXj1dfD1ccyouY2hlY2tlZC4pL2ksb2E9L14kfFwvKD86amF2YXxlY21hKXNjcmlwdC9pLHBhPS9edHJ1ZVwvKC4qKS8scWE9L15ccyo8ISg/OlxbQ0RBVEFcW3wtLSl8KD86XF1cXXwtLSk+XHMqJC9nLHJhPXtvcHRpb246WzEsIjxzZWxlY3QgbXVsdGlwbGU9J211bHRpcGxlJz4iLCI8L3NlbGVjdD4iXSxsZWdlbmQ6WzEsIjxmaWVsZHNldD4iLCI8L2ZpZWxkc2V0PiJdLGFyZWE6WzEsIjxtYXA+IiwiPC9tYXA+Il0scGFyYW06WzEsIjxvYmplY3Q+IiwiPC9vYmplY3Q+Il0sdGhlYWQ6WzEsIjx0YWJsZT4iLCI8L3RhYmxlPiJdLHRyOlsyLCI8dGFibGU+PHRib2R5PiIsIjwvdGJvZHk+PC90YWJsZT4iXSxjb2w6WzIsIjx0YWJsZT48dGJvZHk+PC90Ym9keT48Y29sZ3JvdXA+IiwiPC9jb2xncm91cD48L3RhYmxlPiJdLHRkOlszLCI8dGFibGU+PHRib2R5Pjx0cj4iLCI8L3RyPjwvdGJvZHk+PC90YWJsZT4iXSxfZGVmYXVsdDprLmh0bWxTZXJpYWxpemU/WzAsIiIsIiJdOlsxLCJYPGRpdj4iLCI8L2Rpdj4iXX0sc2E9ZGEoeSksdGE9c2EuYXBwZW5kQ2hpbGQoeS5jcmVhdGVFbGVtZW50KCJkaXYiKSk7cmEub3B0Z3JvdXA9cmEub3B0aW9uLHJhLnRib2R5PXJhLnRmb290PXJhLmNvbGdyb3VwPXJhLmNhcHRpb249cmEudGhlYWQscmEudGg9cmEudGQ7ZnVuY3Rpb24gdWEoYSxiKXt2YXIgYyxkLGU9MCxmPXR5cGVvZiBhLmdldEVsZW1lbnRzQnlUYWdOYW1lIT09Sz9hLmdldEVsZW1lbnRzQnlUYWdOYW1lKGJ8fCIqIik6dHlwZW9mIGEucXVlcnlTZWxlY3RvckFsbCE9PUs/YS5xdWVyeVNlbGVjdG9yQWxsKGJ8fCIqIik6dm9pZCAwO2lmKCFmKWZvcihmPVtdLGM9YS5jaGlsZE5vZGVzfHxhO251bGwhPShkPWNbZV0pO2UrKykhYnx8bS5ub2RlTmFtZShkLGIpP2YucHVzaChkKTptLm1lcmdlKGYsdWEoZCxiKSk7cmV0dXJuIHZvaWQgMD09PWJ8fGImJm0ubm9kZU5hbWUoYSxiKT9tLm1lcmdlKFthXSxmKTpmfWZ1bmN0aW9uIHZhKGEpe1cudGVzdChhLnR5cGUpJiYoYS5kZWZhdWx0Q2hlY2tlZD1hLmNoZWNrZWQpfWZ1bmN0aW9uIHdhKGEsYil7cmV0dXJuIG0ubm9kZU5hbWUoYSwidGFibGUiKSYmbS5ub2RlTmFtZSgxMSE9PWIubm9kZVR5cGU/YjpiLmZpcnN0Q2hpbGQsInRyIik/YS5nZXRFbGVtZW50c0J5VGFnTmFtZSgidGJvZHkiKVswXXx8YS5hcHBlbmRDaGlsZChhLm93bmVyRG9jdW1lbnQuY3JlYXRlRWxlbWVudCgidGJvZHkiKSk6YX1mdW5jdGlvbiB4YShhKXtyZXR1cm4gYS50eXBlPShudWxsIT09bS5maW5kLmF0dHIoYSwidHlwZSIpKSsiLyIrYS50eXBlLGF9ZnVuY3Rpb24geWEoYSl7dmFyIGI9cGEuZXhlYyhhLnR5cGUpO3JldHVybiBiP2EudHlwZT1iWzFdOmEucmVtb3ZlQXR0cmlidXRlKCJ0eXBlIiksYX1mdW5jdGlvbiB6YShhLGIpe2Zvcih2YXIgYyxkPTA7bnVsbCE9KGM9YVtkXSk7ZCsrKW0uX2RhdGEoYywiZ2xvYmFsRXZhbCIsIWJ8fG0uX2RhdGEoYltkXSwiZ2xvYmFsRXZhbCIpKX1mdW5jdGlvbiBBYShhLGIpe2lmKDE9PT1iLm5vZGVUeXBlJiZtLmhhc0RhdGEoYSkpe3ZhciBjLGQsZSxmPW0uX2RhdGEoYSksZz1tLl9kYXRhKGIsZiksaD1mLmV2ZW50cztpZihoKXtkZWxldGUgZy5oYW5kbGUsZy5ldmVudHM9e307Zm9yKGMgaW4gaClmb3IoZD0wLGU9aFtjXS5sZW5ndGg7ZT5kO2QrKyltLmV2ZW50LmFkZChiLGMsaFtjXVtkXSl9Zy5kYXRhJiYoZy5kYXRhPW0uZXh0ZW5kKHt9LGcuZGF0YSkpfX1mdW5jdGlvbiBCYShhLGIpe3ZhciBjLGQsZTtpZigxPT09Yi5ub2RlVHlwZSl7aWYoYz1iLm5vZGVOYW1lLnRvTG93ZXJDYXNlKCksIWsubm9DbG9uZUV2ZW50JiZiW20uZXhwYW5kb10pe2U9bS5fZGF0YShiKTtmb3IoZCBpbiBlLmV2ZW50cyltLnJlbW92ZUV2ZW50KGIsZCxlLmhhbmRsZSk7Yi5yZW1vdmVBdHRyaWJ1dGUobS5leHBhbmRvKX0ic2NyaXB0Ij09PWMmJmIudGV4dCE9PWEudGV4dD8oeGEoYikudGV4dD1hLnRleHQseWEoYikpOiJvYmplY3QiPT09Yz8oYi5wYXJlbnROb2RlJiYoYi5vdXRlckhUTUw9YS5vdXRlckhUTUwpLGsuaHRtbDVDbG9uZSYmYS5pbm5lckhUTUwmJiFtLnRyaW0oYi5pbm5lckhUTUwpJiYoYi5pbm5lckhUTUw9YS5pbm5lckhUTUwpKToiaW5wdXQiPT09YyYmVy50ZXN0KGEudHlwZSk/KGIuZGVmYXVsdENoZWNrZWQ9Yi5jaGVja2VkPWEuY2hlY2tlZCxiLnZhbHVlIT09YS52YWx1ZSYmKGIudmFsdWU9YS52YWx1ZSkpOiJvcHRpb24iPT09Yz9iLmRlZmF1bHRTZWxlY3RlZD1iLnNlbGVjdGVkPWEuZGVmYXVsdFNlbGVjdGVkOigiaW5wdXQiPT09Y3x8InRleHRhcmVhIj09PWMpJiYoYi5kZWZhdWx0VmFsdWU9YS5kZWZhdWx0VmFsdWUpfX1tLmV4dGVuZCh7Y2xvbmU6ZnVuY3Rpb24oYSxiLGMpe3ZhciBkLGUsZixnLGgsaT1tLmNvbnRhaW5zKGEub3duZXJEb2N1bWVudCxhKTtpZihrLmh0bWw1Q2xvbmV8fG0uaXNYTUxEb2MoYSl8fCFnYS50ZXN0KCI8IithLm5vZGVOYW1lKyI+Iik/Zj1hLmNsb25lTm9kZSghMCk6KHRhLmlubmVySFRNTD1hLm91dGVySFRNTCx0YS5yZW1vdmVDaGlsZChmPXRhLmZpcnN0Q2hpbGQpKSwhKGsubm9DbG9uZUV2ZW50JiZrLm5vQ2xvbmVDaGVja2VkfHwxIT09YS5ub2RlVHlwZSYmMTEhPT1hLm5vZGVUeXBlfHxtLmlzWE1MRG9jKGEpKSlmb3IoZD11YShmKSxoPXVhKGEpLGc9MDtudWxsIT0oZT1oW2ddKTsrK2cpZFtnXSYmQmEoZSxkW2ddKTtpZihiKWlmKGMpZm9yKGg9aHx8dWEoYSksZD1kfHx1YShmKSxnPTA7bnVsbCE9KGU9aFtnXSk7ZysrKUFhKGUsZFtnXSk7ZWxzZSBBYShhLGYpO3JldHVybiBkPXVhKGYsInNjcmlwdCIpLGQubGVuZ3RoPjAmJnphKGQsIWkmJnVhKGEsInNjcmlwdCIpKSxkPWg9ZT1udWxsLGZ9LGJ1aWxkRnJhZ21lbnQ6ZnVuY3Rpb24oYSxiLGMsZCl7Zm9yKHZhciBlLGYsZyxoLGksaixsLG49YS5sZW5ndGgsbz1kYShiKSxwPVtdLHE9MDtuPnE7cSsrKWlmKGY9YVtxXSxmfHwwPT09ZilpZigib2JqZWN0Ij09PW0udHlwZShmKSltLm1lcmdlKHAsZi5ub2RlVHlwZT9bZl06Zik7ZWxzZSBpZihsYS50ZXN0KGYpKXtoPWh8fG8uYXBwZW5kQ2hpbGQoYi5jcmVhdGVFbGVtZW50KCJkaXYiKSksaT0oamEuZXhlYyhmKXx8WyIiLCIiXSlbMV0udG9Mb3dlckNhc2UoKSxsPXJhW2ldfHxyYS5fZGVmYXVsdCxoLmlubmVySFRNTD1sWzFdK2YucmVwbGFjZShpYSwiPCQxPjwvJDI+IikrbFsyXSxlPWxbMF07d2hpbGUoZS0tKWg9aC5sYXN0Q2hpbGQ7aWYoIWsubGVhZGluZ1doaXRlc3BhY2UmJmhhLnRlc3QoZikmJnAucHVzaChiLmNyZWF0ZVRleHROb2RlKGhhLmV4ZWMoZilbMF0pKSwhay50Ym9keSl7Zj0idGFibGUiIT09aXx8a2EudGVzdChmKT8iPHRhYmxlPiIhPT1sWzFdfHxrYS50ZXN0KGYpPzA6aDpoLmZpcnN0Q2hpbGQsZT1mJiZmLmNoaWxkTm9kZXMubGVuZ3RoO3doaWxlKGUtLSltLm5vZGVOYW1lKGo9Zi5jaGlsZE5vZGVzW2VdLCJ0Ym9keSIpJiYhai5jaGlsZE5vZGVzLmxlbmd0aCYmZi5yZW1vdmVDaGlsZChqKX1tLm1lcmdlKHAsaC5jaGlsZE5vZGVzKSxoLnRleHRDb250ZW50PSIiO3doaWxlKGguZmlyc3RDaGlsZCloLnJlbW92ZUNoaWxkKGguZmlyc3RDaGlsZCk7aD1vLmxhc3RDaGlsZH1lbHNlIHAucHVzaChiLmNyZWF0ZVRleHROb2RlKGYpKTtoJiZvLnJlbW92ZUNoaWxkKGgpLGsuYXBwZW5kQ2hlY2tlZHx8bS5ncmVwKHVhKHAsImlucHV0IiksdmEpLHE9MDt3aGlsZShmPXBbcSsrXSlpZigoIWR8fC0xPT09bS5pbkFycmF5KGYsZCkpJiYoZz1tLmNvbnRhaW5zKGYub3duZXJEb2N1bWVudCxmKSxoPXVhKG8uYXBwZW5kQ2hpbGQoZiksInNjcmlwdCIpLGcmJnphKGgpLGMpKXtlPTA7d2hpbGUoZj1oW2UrK10pb2EudGVzdChmLnR5cGV8fCIiKSYmYy5wdXNoKGYpfXJldHVybiBoPW51bGwsb30sY2xlYW5EYXRhOmZ1bmN0aW9uKGEsYil7Zm9yKHZhciBkLGUsZixnLGg9MCxpPW0uZXhwYW5kbyxqPW0uY2FjaGUsbD1rLmRlbGV0ZUV4cGFuZG8sbj1tLmV2ZW50LnNwZWNpYWw7bnVsbCE9KGQ9YVtoXSk7aCsrKWlmKChifHxtLmFjY2VwdERhdGEoZCkpJiYoZj1kW2ldLGc9ZiYmaltmXSkpe2lmKGcuZXZlbnRzKWZvcihlIGluIGcuZXZlbnRzKW5bZV0/bS5ldmVudC5yZW1vdmUoZCxlKTptLnJlbW92ZUV2ZW50KGQsZSxnLmhhbmRsZSk7altmXSYmKGRlbGV0ZSBqW2ZdLGw/ZGVsZXRlIGRbaV06dHlwZW9mIGQucmVtb3ZlQXR0cmlidXRlIT09Sz9kLnJlbW92ZUF0dHJpYnV0ZShpKTpkW2ldPW51bGwsYy5wdXNoKGYpKX19fSksbS5mbi5leHRlbmQoe3RleHQ6ZnVuY3Rpb24oYSl7cmV0dXJuIFYodGhpcyxmdW5jdGlvbihhKXtyZXR1cm4gdm9pZCAwPT09YT9tLnRleHQodGhpcyk6dGhpcy5lbXB0eSgpLmFwcGVuZCgodGhpc1swXSYmdGhpc1swXS5vd25lckRvY3VtZW50fHx5KS5jcmVhdGVUZXh0Tm9kZShhKSl9LG51bGwsYSxhcmd1bWVudHMubGVuZ3RoKX0sYXBwZW5kOmZ1bmN0aW9uKCl7cmV0dXJuIHRoaXMuZG9tTWFuaXAoYXJndW1lbnRzLGZ1bmN0aW9uKGEpe2lmKDE9PT10aGlzLm5vZGVUeXBlfHwxMT09PXRoaXMubm9kZVR5cGV8fDk9PT10aGlzLm5vZGVUeXBlKXt2YXIgYj13YSh0aGlzLGEpO2IuYXBwZW5kQ2hpbGQoYSl9fSl9LHByZXBlbmQ6ZnVuY3Rpb24oKXtyZXR1cm4gdGhpcy5kb21NYW5pcChhcmd1bWVudHMsZnVuY3Rpb24oYSl7aWYoMT09PXRoaXMubm9kZVR5cGV8fDExPT09dGhpcy5ub2RlVHlwZXx8OT09PXRoaXMubm9kZVR5cGUpe3ZhciBiPXdhKHRoaXMsYSk7Yi5pbnNlcnRCZWZvcmUoYSxiLmZpcnN0Q2hpbGQpfX0pfSxiZWZvcmU6ZnVuY3Rpb24oKXtyZXR1cm4gdGhpcy5kb21NYW5pcChhcmd1bWVudHMsZnVuY3Rpb24oYSl7dGhpcy5wYXJlbnROb2RlJiZ0aGlzLnBhcmVudE5vZGUuaW5zZXJ0QmVmb3JlKGEsdGhpcyl9KX0sYWZ0ZXI6ZnVuY3Rpb24oKXtyZXR1cm4gdGhpcy5kb21NYW5pcChhcmd1bWVudHMsZnVuY3Rpb24oYSl7dGhpcy5wYXJlbnROb2RlJiZ0aGlzLnBhcmVudE5vZGUuaW5zZXJ0QmVmb3JlKGEsdGhpcy5uZXh0U2libGluZyl9KX0scmVtb3ZlOmZ1bmN0aW9uKGEsYil7Zm9yKHZhciBjLGQ9YT9tLmZpbHRlcihhLHRoaXMpOnRoaXMsZT0wO251bGwhPShjPWRbZV0pO2UrKylifHwxIT09Yy5ub2RlVHlwZXx8bS5jbGVhbkRhdGEodWEoYykpLGMucGFyZW50Tm9kZSYmKGImJm0uY29udGFpbnMoYy5vd25lckRvY3VtZW50LGMpJiZ6YSh1YShjLCJzY3JpcHQiKSksYy5wYXJlbnROb2RlLnJlbW92ZUNoaWxkKGMpKTtyZXR1cm4gdGhpc30sZW1wdHk6ZnVuY3Rpb24oKXtmb3IodmFyIGEsYj0wO251bGwhPShhPXRoaXNbYl0pO2IrKyl7MT09PWEubm9kZVR5cGUmJm0uY2xlYW5EYXRhKHVhKGEsITEpKTt3aGlsZShhLmZpcnN0Q2hpbGQpYS5yZW1vdmVDaGlsZChhLmZpcnN0Q2hpbGQpO2Eub3B0aW9ucyYmbS5ub2RlTmFtZShhLCJzZWxlY3QiKSYmKGEub3B0aW9ucy5sZW5ndGg9MCl9cmV0dXJuIHRoaXN9LGNsb25lOmZ1bmN0aW9uKGEsYil7cmV0dXJuIGE9bnVsbD09YT8hMTphLGI9bnVsbD09Yj9hOmIsdGhpcy5tYXAoZnVuY3Rpb24oKXtyZXR1cm4gbS5jbG9uZSh0aGlzLGEsYil9KX0saHRtbDpmdW5jdGlvbihhKXtyZXR1cm4gVih0aGlzLGZ1bmN0aW9uKGEpe3ZhciBiPXRoaXNbMF18fHt9LGM9MCxkPXRoaXMubGVuZ3RoO2lmKHZvaWQgMD09PWEpcmV0dXJuIDE9PT1iLm5vZGVUeXBlP2IuaW5uZXJIVE1MLnJlcGxhY2UoZmEsIiIpOnZvaWQgMDtpZighKCJzdHJpbmciIT10eXBlb2YgYXx8bWEudGVzdChhKXx8IWsuaHRtbFNlcmlhbGl6ZSYmZ2EudGVzdChhKXx8IWsubGVhZGluZ1doaXRlc3BhY2UmJmhhLnRlc3QoYSl8fHJhWyhqYS5leGVjKGEpfHxbIiIsIiJdKVsxXS50b0xvd2VyQ2FzZSgpXSkpe2E9YS5yZXBsYWNlKGlhLCI8JDE+PC8kMj4iKTt0cnl7Zm9yKDtkPmM7YysrKWI9dGhpc1tjXXx8e30sMT09PWIubm9kZVR5cGUmJihtLmNsZWFuRGF0YSh1YShiLCExKSksYi5pbm5lckhUTUw9YSk7Yj0wfWNhdGNoKGUpe319YiYmdGhpcy5lbXB0eSgpLmFwcGVuZChhKX0sbnVsbCxhLGFyZ3VtZW50cy5sZW5ndGgpfSxyZXBsYWNlV2l0aDpmdW5jdGlvbigpe3ZhciBhPWFyZ3VtZW50c1swXTtyZXR1cm4gdGhpcy5kb21NYW5pcChhcmd1bWVudHMsZnVuY3Rpb24oYil7YT10aGlzLnBhcmVudE5vZGUsbS5jbGVhbkRhdGEodWEodGhpcykpLGEmJmEucmVwbGFjZUNoaWxkKGIsdGhpcyl9KSxhJiYoYS5sZW5ndGh8fGEubm9kZVR5cGUpP3RoaXM6dGhpcy5yZW1vdmUoKX0sZGV0YWNoOmZ1bmN0aW9uKGEpe3JldHVybiB0aGlzLnJlbW92ZShhLCEwKX0sZG9tTWFuaXA6ZnVuY3Rpb24oYSxiKXthPWUuYXBwbHkoW10sYSk7dmFyIGMsZCxmLGcsaCxpLGo9MCxsPXRoaXMubGVuZ3RoLG49dGhpcyxvPWwtMSxwPWFbMF0scT1tLmlzRnVuY3Rpb24ocCk7aWYocXx8bD4xJiYic3RyaW5nIj09dHlwZW9mIHAmJiFrLmNoZWNrQ2xvbmUmJm5hLnRlc3QocCkpcmV0dXJuIHRoaXMuZWFjaChmdW5jdGlvbihjKXt2YXIgZD1uLmVxKGMpO3EmJihhWzBdPXAuY2FsbCh0aGlzLGMsZC5odG1sKCkpKSxkLmRvbU1hbmlwKGEsYil9KTtpZihsJiYoaT1tLmJ1aWxkRnJhZ21lbnQoYSx0aGlzWzBdLm93bmVyRG9jdW1lbnQsITEsdGhpcyksYz1pLmZpcnN0Q2hpbGQsMT09PWkuY2hpbGROb2Rlcy5sZW5ndGgmJihpPWMpLGMpKXtmb3IoZz1tLm1hcCh1YShpLCJzY3JpcHQiKSx4YSksZj1nLmxlbmd0aDtsPmo7aisrKWQ9aSxqIT09byYmKGQ9bS5jbG9uZShkLCEwLCEwKSxmJiZtLm1lcmdlKGcsdWEoZCwic2NyaXB0IikpKSxiLmNhbGwodGhpc1tqXSxkLGopO2lmKGYpZm9yKGg9Z1tnLmxlbmd0aC0xXS5vd25lckRvY3VtZW50LG0ubWFwKGcseWEpLGo9MDtmPmo7aisrKWQ9Z1tqXSxvYS50ZXN0KGQudHlwZXx8IiIpJiYhbS5fZGF0YShkLCJnbG9iYWxFdmFsIikmJm0uY29udGFpbnMoaCxkKSYmKGQuc3JjP20uX2V2YWxVcmwmJm0uX2V2YWxVcmwoZC5zcmMpOm0uZ2xvYmFsRXZhbCgoZC50ZXh0fHxkLnRleHRDb250ZW50fHxkLmlubmVySFRNTHx8IiIpLnJlcGxhY2UocWEsIiIpKSk7aT1jPW51bGx9cmV0dXJuIHRoaXN9fSksbS5lYWNoKHthcHBlbmRUbzoiYXBwZW5kIixwcmVwZW5kVG86InByZXBlbmQiLGluc2VydEJlZm9yZToiYmVmb3JlIixpbnNlcnRBZnRlcjoiYWZ0ZXIiLHJlcGxhY2VBbGw6InJlcGxhY2VXaXRoIn0sZnVuY3Rpb24oYSxiKXttLmZuW2FdPWZ1bmN0aW9uKGEpe2Zvcih2YXIgYyxkPTAsZT1bXSxnPW0oYSksaD1nLmxlbmd0aC0xO2g+PWQ7ZCsrKWM9ZD09PWg/dGhpczp0aGlzLmNsb25lKCEwKSxtKGdbZF0pW2JdKGMpLGYuYXBwbHkoZSxjLmdldCgpKTtyZXR1cm4gdGhpcy5wdXNoU3RhY2soZSl9fSk7dmFyIENhLERhPXt9O2Z1bmN0aW9uIEVhKGIsYyl7dmFyIGQsZT1tKGMuY3JlYXRlRWxlbWVudChiKSkuYXBwZW5kVG8oYy5ib2R5KSxmPWEuZ2V0RGVmYXVsdENvbXB1dGVkU3R5bGUmJihkPWEuZ2V0RGVmYXVsdENvbXB1dGVkU3R5bGUoZVswXSkpP2QuZGlzcGxheTptLmNzcyhlWzBdLCJkaXNwbGF5Iik7cmV0dXJuIGUuZGV0YWNoKCksZn1mdW5jdGlvbiBGYShhKXt2YXIgYj15LGM9RGFbYV07cmV0dXJuIGN8fChjPUVhKGEsYiksIm5vbmUiIT09YyYmY3x8KENhPShDYXx8bSgiPGlmcmFtZSBmcmFtZWJvcmRlcj0nMCcgd2lkdGg9JzAnIGhlaWdodD0nMCcvPiIpKS5hcHBlbmRUbyhiLmRvY3VtZW50RWxlbWVudCksYj0oQ2FbMF0uY29udGVudFdpbmRvd3x8Q2FbMF0uY29udGVudERvY3VtZW50KS5kb2N1bWVudCxiLndyaXRlKCksYi5jbG9zZSgpLGM9RWEoYSxiKSxDYS5kZXRhY2goKSksRGFbYV09YyksY30hZnVuY3Rpb24oKXt2YXIgYTtrLnNocmlua1dyYXBCbG9ja3M9ZnVuY3Rpb24oKXtpZihudWxsIT1hKXJldHVybiBhO2E9ITE7dmFyIGIsYyxkO3JldHVybiBjPXkuZ2V0RWxlbWVudHNCeVRhZ05hbWUoImJvZHkiKVswXSxjJiZjLnN0eWxlPyhiPXkuY3JlYXRlRWxlbWVudCgiZGl2IiksZD15LmNyZWF0ZUVsZW1lbnQoImRpdiIpLGQuc3R5bGUuY3NzVGV4dD0icG9zaXRpb246YWJzb2x1dGU7Ym9yZGVyOjA7d2lkdGg6MDtoZWlnaHQ6MDt0b3A6MDtsZWZ0Oi05OTk5cHgiLGMuYXBwZW5kQ2hpbGQoZCkuYXBwZW5kQ2hpbGQoYiksdHlwZW9mIGIuc3R5bGUuem9vbSE9PUsmJihiLnN0eWxlLmNzc1RleHQ9Ii13ZWJraXQtYm94LXNpemluZzpjb250ZW50LWJveDstbW96LWJveC1zaXppbmc6Y29udGVudC1ib3g7Ym94LXNpemluZzpjb250ZW50LWJveDtkaXNwbGF5OmJsb2NrO21hcmdpbjowO2JvcmRlcjowO3BhZGRpbmc6MXB4O3dpZHRoOjFweDt6b29tOjEiLGIuYXBwZW5kQ2hpbGQoeS5jcmVhdGVFbGVtZW50KCJkaXYiKSkuc3R5bGUud2lkdGg9IjVweCIsYT0zIT09Yi5vZmZzZXRXaWR0aCksYy5yZW1vdmVDaGlsZChkKSxhKTp2b2lkIDB9fSgpO3ZhciBHYT0vXm1hcmdpbi8sSGE9bmV3IFJlZ0V4cCgiXigiK1MrIikoPyFweClbYS16JV0rJCIsImkiKSxJYSxKYSxLYT0vXih0b3B8cmlnaHR8Ym90dG9tfGxlZnQpJC87YS5nZXRDb21wdXRlZFN0eWxlPyhJYT1mdW5jdGlvbihiKXtyZXR1cm4gYi5vd25lckRvY3VtZW50LmRlZmF1bHRWaWV3Lm9wZW5lcj9iLm93bmVyRG9jdW1lbnQuZGVmYXVsdFZpZXcuZ2V0Q29tcHV0ZWRTdHlsZShiLG51bGwpOmEuZ2V0Q29tcHV0ZWRTdHlsZShiLG51bGwpfSxKYT1mdW5jdGlvbihhLGIsYyl7dmFyIGQsZSxmLGcsaD1hLnN0eWxlO3JldHVybiBjPWN8fElhKGEpLGc9Yz9jLmdldFByb3BlcnR5VmFsdWUoYil8fGNbYl06dm9pZCAwLGMmJigiIiE9PWd8fG0uY29udGFpbnMoYS5vd25lckRvY3VtZW50LGEpfHwoZz1tLnN0eWxlKGEsYikpLEhhLnRlc3QoZykmJkdhLnRlc3QoYikmJihkPWgud2lkdGgsZT1oLm1pbldpZHRoLGY9aC5tYXhXaWR0aCxoLm1pbldpZHRoPWgubWF4V2lkdGg9aC53aWR0aD1nLGc9Yy53aWR0aCxoLndpZHRoPWQsaC5taW5XaWR0aD1lLGgubWF4V2lkdGg9ZikpLHZvaWQgMD09PWc/ZzpnKyIifSk6eS5kb2N1bWVudEVsZW1lbnQuY3VycmVudFN0eWxlJiYoSWE9ZnVuY3Rpb24oYSl7cmV0dXJuIGEuY3VycmVudFN0eWxlfSxKYT1mdW5jdGlvbihhLGIsYyl7dmFyIGQsZSxmLGcsaD1hLnN0eWxlO3JldHVybiBjPWN8fElhKGEpLGc9Yz9jW2JdOnZvaWQgMCxudWxsPT1nJiZoJiZoW2JdJiYoZz1oW2JdKSxIYS50ZXN0KGcpJiYhS2EudGVzdChiKSYmKGQ9aC5sZWZ0LGU9YS5ydW50aW1lU3R5bGUsZj1lJiZlLmxlZnQsZiYmKGUubGVmdD1hLmN1cnJlbnRTdHlsZS5sZWZ0KSxoLmxlZnQ9ImZvbnRTaXplIj09PWI/IjFlbSI6ZyxnPWgucGl4ZWxMZWZ0KyJweCIsaC5sZWZ0PWQsZiYmKGUubGVmdD1mKSksdm9pZCAwPT09Zz9nOmcrIiJ8fCJhdXRvIn0pO2Z1bmN0aW9uIExhKGEsYil7cmV0dXJue2dldDpmdW5jdGlvbigpe3ZhciBjPWEoKTtpZihudWxsIT1jKXJldHVybiBjP3ZvaWQgZGVsZXRlIHRoaXMuZ2V0Oih0aGlzLmdldD1iKS5hcHBseSh0aGlzLGFyZ3VtZW50cyl9fX0hZnVuY3Rpb24oKXt2YXIgYixjLGQsZSxmLGcsaDtpZihiPXkuY3JlYXRlRWxlbWVudCgiZGl2IiksYi5pbm5lckhUTUw9IiAgPGxpbmsvPjx0YWJsZT48L3RhYmxlPjxhIGhyZWY9Jy9hJz5hPC9hPjxpbnB1dCB0eXBlPSdjaGVja2JveCcvPiIsZD1iLmdldEVsZW1lbnRzQnlUYWdOYW1lKCJhIilbMF0sYz1kJiZkLnN0eWxlKXtjLmNzc1RleHQ9ImZsb2F0OmxlZnQ7b3BhY2l0eTouNSIsay5vcGFjaXR5PSIwLjUiPT09Yy5vcGFjaXR5LGsuY3NzRmxvYXQ9ISFjLmNzc0Zsb2F0LGIuc3R5bGUuYmFja2dyb3VuZENsaXA9ImNvbnRlbnQtYm94IixiLmNsb25lTm9kZSghMCkuc3R5bGUuYmFja2dyb3VuZENsaXA9IiIsay5jbGVhckNsb25lU3R5bGU9ImNvbnRlbnQtYm94Ij09PWIuc3R5bGUuYmFja2dyb3VuZENsaXAsay5ib3hTaXppbmc9IiI9PT1jLmJveFNpemluZ3x8IiI9PT1jLk1vekJveFNpemluZ3x8IiI9PT1jLldlYmtpdEJveFNpemluZyxtLmV4dGVuZChrLHtyZWxpYWJsZUhpZGRlbk9mZnNldHM6ZnVuY3Rpb24oKXtyZXR1cm4gbnVsbD09ZyYmaSgpLGd9LGJveFNpemluZ1JlbGlhYmxlOmZ1bmN0aW9uKCl7cmV0dXJuIG51bGw9PWYmJmkoKSxmfSxwaXhlbFBvc2l0aW9uOmZ1bmN0aW9uKCl7cmV0dXJuIG51bGw9PWUmJmkoKSxlfSxyZWxpYWJsZU1hcmdpblJpZ2h0OmZ1bmN0aW9uKCl7cmV0dXJuIG51bGw9PWgmJmkoKSxofX0pO2Z1bmN0aW9uIGkoKXt2YXIgYixjLGQsaTtjPXkuZ2V0RWxlbWVudHNCeVRhZ05hbWUoImJvZHkiKVswXSxjJiZjLnN0eWxlJiYoYj15LmNyZWF0ZUVsZW1lbnQoImRpdiIpLGQ9eS5jcmVhdGVFbGVtZW50KCJkaXYiKSxkLnN0eWxlLmNzc1RleHQ9InBvc2l0aW9uOmFic29sdXRlO2JvcmRlcjowO3dpZHRoOjA7aGVpZ2h0OjA7dG9wOjA7bGVmdDotOTk5OXB4IixjLmFwcGVuZENoaWxkKGQpLmFwcGVuZENoaWxkKGIpLGIuc3R5bGUuY3NzVGV4dD0iLXdlYmtpdC1ib3gtc2l6aW5nOmJvcmRlci1ib3g7LW1vei1ib3gtc2l6aW5nOmJvcmRlci1ib3g7Ym94LXNpemluZzpib3JkZXItYm94O2Rpc3BsYXk6YmxvY2s7bWFyZ2luLXRvcDoxJTt0b3A6MSU7Ym9yZGVyOjFweDtwYWRkaW5nOjFweDt3aWR0aDo0cHg7cG9zaXRpb246YWJzb2x1dGUiLGU9Zj0hMSxoPSEwLGEuZ2V0Q29tcHV0ZWRTdHlsZSYmKGU9IjElIiE9PShhLmdldENvbXB1dGVkU3R5bGUoYixudWxsKXx8e30pLnRvcCxmPSI0cHgiPT09KGEuZ2V0Q29tcHV0ZWRTdHlsZShiLG51bGwpfHx7d2lkdGg6IjRweCJ9KS53aWR0aCxpPWIuYXBwZW5kQ2hpbGQoeS5jcmVhdGVFbGVtZW50KCJkaXYiKSksaS5zdHlsZS5jc3NUZXh0PWIuc3R5bGUuY3NzVGV4dD0iLXdlYmtpdC1ib3gtc2l6aW5nOmNvbnRlbnQtYm94Oy1tb3otYm94LXNpemluZzpjb250ZW50LWJveDtib3gtc2l6aW5nOmNvbnRlbnQtYm94O2Rpc3BsYXk6YmxvY2s7bWFyZ2luOjA7Ym9yZGVyOjA7cGFkZGluZzowIixpLnN0eWxlLm1hcmdpblJpZ2h0PWkuc3R5bGUud2lkdGg9IjAiLGIuc3R5bGUud2lkdGg9IjFweCIsaD0hcGFyc2VGbG9hdCgoYS5nZXRDb21wdXRlZFN0eWxlKGksbnVsbCl8fHt9KS5tYXJnaW5SaWdodCksYi5yZW1vdmVDaGlsZChpKSksYi5pbm5lckhUTUw9Ijx0YWJsZT48dHI+PHRkPjwvdGQ+PHRkPnQ8L3RkPjwvdHI+PC90YWJsZT4iLGk9Yi5nZXRFbGVtZW50c0J5VGFnTmFtZSgidGQiKSxpWzBdLnN0eWxlLmNzc1RleHQ9Im1hcmdpbjowO2JvcmRlcjowO3BhZGRpbmc6MDtkaXNwbGF5Om5vbmUiLGc9MD09PWlbMF0ub2Zmc2V0SGVpZ2h0LGcmJihpWzBdLnN0eWxlLmRpc3BsYXk9IiIsaVsxXS5zdHlsZS5kaXNwbGF5PSJub25lIixnPTA9PT1pWzBdLm9mZnNldEhlaWdodCksYy5yZW1vdmVDaGlsZChkKSl9fX0oKSxtLnN3YXA9ZnVuY3Rpb24oYSxiLGMsZCl7dmFyIGUsZixnPXt9O2ZvcihmIGluIGIpZ1tmXT1hLnN0eWxlW2ZdLGEuc3R5bGVbZl09YltmXTtlPWMuYXBwbHkoYSxkfHxbXSk7Zm9yKGYgaW4gYilhLnN0eWxlW2ZdPWdbZl07cmV0dXJuIGV9O3ZhciBNYT0vYWxwaGFcKFteKV0qXCkvaSxOYT0vb3BhY2l0eVxzKj1ccyooW14pXSopLyxPYT0vXihub25lfHRhYmxlKD8hLWNbZWFdKS4rKS8sUGE9bmV3IFJlZ0V4cCgiXigiK1MrIikoLiopJCIsImkiKSxRYT1uZXcgUmVnRXhwKCJeKFsrLV0pPSgiK1MrIikiLCJpIiksUmE9e3Bvc2l0aW9uOiJhYnNvbHV0ZSIsdmlzaWJpbGl0eToiaGlkZGVuIixkaXNwbGF5OiJibG9jayJ9LFNhPXtsZXR0ZXJTcGFjaW5nOiIwIixmb250V2VpZ2h0OiI0MDAifSxUYT1bIldlYmtpdCIsIk8iLCJNb3oiLCJtcyJdO2Z1bmN0aW9uIFVhKGEsYil7aWYoYiBpbiBhKXJldHVybiBiO3ZhciBjPWIuY2hhckF0KDApLnRvVXBwZXJDYXNlKCkrYi5zbGljZSgxKSxkPWIsZT1UYS5sZW5ndGg7d2hpbGUoZS0tKWlmKGI9VGFbZV0rYyxiIGluIGEpcmV0dXJuIGI7cmV0dXJuIGR9ZnVuY3Rpb24gVmEoYSxiKXtmb3IodmFyIGMsZCxlLGY9W10sZz0wLGg9YS5sZW5ndGg7aD5nO2crKylkPWFbZ10sZC5zdHlsZSYmKGZbZ109bS5fZGF0YShkLCJvbGRkaXNwbGF5IiksYz1kLnN0eWxlLmRpc3BsYXksYj8oZltnXXx8Im5vbmUiIT09Y3x8KGQuc3R5bGUuZGlzcGxheT0iIiksIiI9PT1kLnN0eWxlLmRpc3BsYXkmJlUoZCkmJihmW2ddPW0uX2RhdGEoZCwib2xkZGlzcGxheSIsRmEoZC5ub2RlTmFtZSkpKSk6KGU9VShkKSwoYyYmIm5vbmUiIT09Y3x8IWUpJiZtLl9kYXRhKGQsIm9sZGRpc3BsYXkiLGU/YzptLmNzcyhkLCJkaXNwbGF5IikpKSk7Zm9yKGc9MDtoPmc7ZysrKWQ9YVtnXSxkLnN0eWxlJiYoYiYmIm5vbmUiIT09ZC5zdHlsZS5kaXNwbGF5JiYiIiE9PWQuc3R5bGUuZGlzcGxheXx8KGQuc3R5bGUuZGlzcGxheT1iP2ZbZ118fCIiOiJub25lIikpO3JldHVybiBhfWZ1bmN0aW9uIFdhKGEsYixjKXt2YXIgZD1QYS5leGVjKGIpO3JldHVybiBkP01hdGgubWF4KDAsZFsxXS0oY3x8MCkpKyhkWzJdfHwicHgiKTpifWZ1bmN0aW9uIFhhKGEsYixjLGQsZSl7Zm9yKHZhciBmPWM9PT0oZD8iYm9yZGVyIjoiY29udGVudCIpPzQ6IndpZHRoIj09PWI/MTowLGc9MDs0PmY7Zis9MikibWFyZ2luIj09PWMmJihnKz1tLmNzcyhhLGMrVFtmXSwhMCxlKSksZD8oImNvbnRlbnQiPT09YyYmKGctPW0uY3NzKGEsInBhZGRpbmciK1RbZl0sITAsZSkpLCJtYXJnaW4iIT09YyYmKGctPW0uY3NzKGEsImJvcmRlciIrVFtmXSsiV2lkdGgiLCEwLGUpKSk6KGcrPW0uY3NzKGEsInBhZGRpbmciK1RbZl0sITAsZSksInBhZGRpbmciIT09YyYmKGcrPW0uY3NzKGEsImJvcmRlciIrVFtmXSsiV2lkdGgiLCEwLGUpKSk7cmV0dXJuIGd9ZnVuY3Rpb24gWWEoYSxiLGMpe3ZhciBkPSEwLGU9IndpZHRoIj09PWI/YS5vZmZzZXRXaWR0aDphLm9mZnNldEhlaWdodCxmPUlhKGEpLGc9ay5ib3hTaXppbmcmJiJib3JkZXItYm94Ij09PW0uY3NzKGEsImJveFNpemluZyIsITEsZik7aWYoMD49ZXx8bnVsbD09ZSl7aWYoZT1KYShhLGIsZiksKDA+ZXx8bnVsbD09ZSkmJihlPWEuc3R5bGVbYl0pLEhhLnRlc3QoZSkpcmV0dXJuIGU7ZD1nJiYoay5ib3hTaXppbmdSZWxpYWJsZSgpfHxlPT09YS5zdHlsZVtiXSksZT1wYXJzZUZsb2F0KGUpfHwwfXJldHVybiBlK1hhKGEsYixjfHwoZz8iYm9yZGVyIjoiY29udGVudCIpLGQsZikrInB4In1tLmV4dGVuZCh7Y3NzSG9va3M6e29wYWNpdHk6e2dldDpmdW5jdGlvbihhLGIpe2lmKGIpe3ZhciBjPUphKGEsIm9wYWNpdHkiKTtyZXR1cm4iIj09PWM/IjEiOmN9fX19LGNzc051bWJlcjp7Y29sdW1uQ291bnQ6ITAsZmlsbE9wYWNpdHk6ITAsZmxleEdyb3c6ITAsZmxleFNocmluazohMCxmb250V2VpZ2h0OiEwLGxpbmVIZWlnaHQ6ITAsb3BhY2l0eTohMCxvcmRlcjohMCxvcnBoYW5zOiEwLHdpZG93czohMCx6SW5kZXg6ITAsem9vbTohMH0sY3NzUHJvcHM6eyJmbG9hdCI6ay5jc3NGbG9hdD8iY3NzRmxvYXQiOiJzdHlsZUZsb2F0In0sc3R5bGU6ZnVuY3Rpb24oYSxiLGMsZCl7aWYoYSYmMyE9PWEubm9kZVR5cGUmJjghPT1hLm5vZGVUeXBlJiZhLnN0eWxlKXt2YXIgZSxmLGcsaD1tLmNhbWVsQ2FzZShiKSxpPWEuc3R5bGU7aWYoYj1tLmNzc1Byb3BzW2hdfHwobS5jc3NQcm9wc1toXT1VYShpLGgpKSxnPW0uY3NzSG9va3NbYl18fG0uY3NzSG9va3NbaF0sdm9pZCAwPT09YylyZXR1cm4gZyYmImdldCJpbiBnJiZ2b2lkIDAhPT0oZT1nLmdldChhLCExLGQpKT9lOmlbYl07aWYoZj10eXBlb2YgYywic3RyaW5nIj09PWYmJihlPVFhLmV4ZWMoYykpJiYoYz0oZVsxXSsxKSplWzJdK3BhcnNlRmxvYXQobS5jc3MoYSxiKSksZj0ibnVtYmVyIiksbnVsbCE9YyYmYz09PWMmJigibnVtYmVyIiE9PWZ8fG0uY3NzTnVtYmVyW2hdfHwoYys9InB4Iiksay5jbGVhckNsb25lU3R5bGV8fCIiIT09Y3x8MCE9PWIuaW5kZXhPZigiYmFja2dyb3VuZCIpfHwoaVtiXT0iaW5oZXJpdCIpLCEoZyYmInNldCJpbiBnJiZ2b2lkIDA9PT0oYz1nLnNldChhLGMsZCkpKSkpdHJ5e2lbYl09Y31jYXRjaChqKXt9fX0sY3NzOmZ1bmN0aW9uKGEsYixjLGQpe3ZhciBlLGYsZyxoPW0uY2FtZWxDYXNlKGIpO3JldHVybiBiPW0uY3NzUHJvcHNbaF18fChtLmNzc1Byb3BzW2hdPVVhKGEuc3R5bGUsaCkpLGc9bS5jc3NIb29rc1tiXXx8bS5jc3NIb29rc1toXSxnJiYiZ2V0ImluIGcmJihmPWcuZ2V0KGEsITAsYykpLHZvaWQgMD09PWYmJihmPUphKGEsYixkKSksIm5vcm1hbCI9PT1mJiZiIGluIFNhJiYoZj1TYVtiXSksIiI9PT1jfHxjPyhlPXBhcnNlRmxvYXQoZiksYz09PSEwfHxtLmlzTnVtZXJpYyhlKT9lfHwwOmYpOmZ9fSksbS5lYWNoKFsiaGVpZ2h0Iiwid2lkdGgiXSxmdW5jdGlvbihhLGIpe20uY3NzSG9va3NbYl09e2dldDpmdW5jdGlvbihhLGMsZCl7cmV0dXJuIGM/T2EudGVzdChtLmNzcyhhLCJkaXNwbGF5IikpJiYwPT09YS5vZmZzZXRXaWR0aD9tLnN3YXAoYSxSYSxmdW5jdGlvbigpe3JldHVybiBZYShhLGIsZCl9KTpZYShhLGIsZCk6dm9pZCAwfSxzZXQ6ZnVuY3Rpb24oYSxjLGQpe3ZhciBlPWQmJklhKGEpO3JldHVybiBXYShhLGMsZD9YYShhLGIsZCxrLmJveFNpemluZyYmImJvcmRlci1ib3giPT09bS5jc3MoYSwiYm94U2l6aW5nIiwhMSxlKSxlKTowKX19fSksay5vcGFjaXR5fHwobS5jc3NIb29rcy5vcGFjaXR5PXtnZXQ6ZnVuY3Rpb24oYSxiKXtyZXR1cm4gTmEudGVzdCgoYiYmYS5jdXJyZW50U3R5bGU/YS5jdXJyZW50U3R5bGUuZmlsdGVyOmEuc3R5bGUuZmlsdGVyKXx8IiIpPy4wMSpwYXJzZUZsb2F0KFJlZ0V4cC4kMSkrIiI6Yj8iMSI6IiJ9LHNldDpmdW5jdGlvbihhLGIpe3ZhciBjPWEuc3R5bGUsZD1hLmN1cnJlbnRTdHlsZSxlPW0uaXNOdW1lcmljKGIpPyJhbHBoYShvcGFjaXR5PSIrMTAwKmIrIikiOiIiLGY9ZCYmZC5maWx0ZXJ8fGMuZmlsdGVyfHwiIjtjLnpvb209MSwoYj49MXx8IiI9PT1iKSYmIiI9PT1tLnRyaW0oZi5yZXBsYWNlKE1hLCIiKSkmJmMucmVtb3ZlQXR0cmlidXRlJiYoYy5yZW1vdmVBdHRyaWJ1dGUoImZpbHRlciIpLCIiPT09Ynx8ZCYmIWQuZmlsdGVyKXx8KGMuZmlsdGVyPU1hLnRlc3QoZik/Zi5yZXBsYWNlKE1hLGUpOmYrIiAiK2UpfX0pLG0uY3NzSG9va3MubWFyZ2luUmlnaHQ9TGEoay5yZWxpYWJsZU1hcmdpblJpZ2h0LGZ1bmN0aW9uKGEsYil7cmV0dXJuIGI/bS5zd2FwKGEse2Rpc3BsYXk6ImlubGluZS1ibG9jayJ9LEphLFthLCJtYXJnaW5SaWdodCJdKTp2b2lkIDB9KSxtLmVhY2goe21hcmdpbjoiIixwYWRkaW5nOiIiLGJvcmRlcjoiV2lkdGgifSxmdW5jdGlvbihhLGIpe20uY3NzSG9va3NbYStiXT17ZXhwYW5kOmZ1bmN0aW9uKGMpe2Zvcih2YXIgZD0wLGU9e30sZj0ic3RyaW5nIj09dHlwZW9mIGM/Yy5zcGxpdCgiICIpOltjXTs0PmQ7ZCsrKWVbYStUW2RdK2JdPWZbZF18fGZbZC0yXXx8ZlswXTtyZXR1cm4gZX19LEdhLnRlc3QoYSl8fChtLmNzc0hvb2tzW2ErYl0uc2V0PVdhKX0pLG0uZm4uZXh0ZW5kKHtjc3M6ZnVuY3Rpb24oYSxiKXtyZXR1cm4gVih0aGlzLGZ1bmN0aW9uKGEsYixjKXt2YXIgZCxlLGY9e30sZz0wO2lmKG0uaXNBcnJheShiKSl7Zm9yKGQ9SWEoYSksZT1iLmxlbmd0aDtlPmc7ZysrKWZbYltnXV09bS5jc3MoYSxiW2ddLCExLGQpO3JldHVybiBmfXJldHVybiB2b2lkIDAhPT1jP20uc3R5bGUoYSxiLGMpOm0uY3NzKGEsYil9LGEsYixhcmd1bWVudHMubGVuZ3RoPjEpfSxzaG93OmZ1bmN0aW9uKCl7cmV0dXJuIFZhKHRoaXMsITApfSxoaWRlOmZ1bmN0aW9uKCl7cmV0dXJuIFZhKHRoaXMpfSx0b2dnbGU6ZnVuY3Rpb24oYSl7cmV0dXJuImJvb2xlYW4iPT10eXBlb2YgYT9hP3RoaXMuc2hvdygpOnRoaXMuaGlkZSgpOnRoaXMuZWFjaChmdW5jdGlvbigpe1UodGhpcyk/bSh0aGlzKS5zaG93KCk6bSh0aGlzKS5oaWRlKCl9KX19KTtmdW5jdGlvbiBaYShhLGIsYyxkLGUpewpyZXR1cm4gbmV3IFphLnByb3RvdHlwZS5pbml0KGEsYixjLGQsZSl9bS5Ud2Vlbj1aYSxaYS5wcm90b3R5cGU9e2NvbnN0cnVjdG9yOlphLGluaXQ6ZnVuY3Rpb24oYSxiLGMsZCxlLGYpe3RoaXMuZWxlbT1hLHRoaXMucHJvcD1jLHRoaXMuZWFzaW5nPWV8fCJzd2luZyIsdGhpcy5vcHRpb25zPWIsdGhpcy5zdGFydD10aGlzLm5vdz10aGlzLmN1cigpLHRoaXMuZW5kPWQsdGhpcy51bml0PWZ8fChtLmNzc051bWJlcltjXT8iIjoicHgiKX0sY3VyOmZ1bmN0aW9uKCl7dmFyIGE9WmEucHJvcEhvb2tzW3RoaXMucHJvcF07cmV0dXJuIGEmJmEuZ2V0P2EuZ2V0KHRoaXMpOlphLnByb3BIb29rcy5fZGVmYXVsdC5nZXQodGhpcyl9LHJ1bjpmdW5jdGlvbihhKXt2YXIgYixjPVphLnByb3BIb29rc1t0aGlzLnByb3BdO3JldHVybiB0aGlzLm9wdGlvbnMuZHVyYXRpb24/dGhpcy5wb3M9Yj1tLmVhc2luZ1t0aGlzLmVhc2luZ10oYSx0aGlzLm9wdGlvbnMuZHVyYXRpb24qYSwwLDEsdGhpcy5vcHRpb25zLmR1cmF0aW9uKTp0aGlzLnBvcz1iPWEsdGhpcy5ub3c9KHRoaXMuZW5kLXRoaXMuc3RhcnQpKmIrdGhpcy5zdGFydCx0aGlzLm9wdGlvbnMuc3RlcCYmdGhpcy5vcHRpb25zLnN0ZXAuY2FsbCh0aGlzLmVsZW0sdGhpcy5ub3csdGhpcyksYyYmYy5zZXQ/Yy5zZXQodGhpcyk6WmEucHJvcEhvb2tzLl9kZWZhdWx0LnNldCh0aGlzKSx0aGlzfX0sWmEucHJvdG90eXBlLmluaXQucHJvdG90eXBlPVphLnByb3RvdHlwZSxaYS5wcm9wSG9va3M9e19kZWZhdWx0OntnZXQ6ZnVuY3Rpb24oYSl7dmFyIGI7cmV0dXJuIG51bGw9PWEuZWxlbVthLnByb3BdfHxhLmVsZW0uc3R5bGUmJm51bGwhPWEuZWxlbS5zdHlsZVthLnByb3BdPyhiPW0uY3NzKGEuZWxlbSxhLnByb3AsIiIpLGImJiJhdXRvIiE9PWI/YjowKTphLmVsZW1bYS5wcm9wXX0sc2V0OmZ1bmN0aW9uKGEpe20uZnguc3RlcFthLnByb3BdP20uZnguc3RlcFthLnByb3BdKGEpOmEuZWxlbS5zdHlsZSYmKG51bGwhPWEuZWxlbS5zdHlsZVttLmNzc1Byb3BzW2EucHJvcF1dfHxtLmNzc0hvb2tzW2EucHJvcF0pP20uc3R5bGUoYS5lbGVtLGEucHJvcCxhLm5vdythLnVuaXQpOmEuZWxlbVthLnByb3BdPWEubm93fX19LFphLnByb3BIb29rcy5zY3JvbGxUb3A9WmEucHJvcEhvb2tzLnNjcm9sbExlZnQ9e3NldDpmdW5jdGlvbihhKXthLmVsZW0ubm9kZVR5cGUmJmEuZWxlbS5wYXJlbnROb2RlJiYoYS5lbGVtW2EucHJvcF09YS5ub3cpfX0sbS5lYXNpbmc9e2xpbmVhcjpmdW5jdGlvbihhKXtyZXR1cm4gYX0sc3dpbmc6ZnVuY3Rpb24oYSl7cmV0dXJuLjUtTWF0aC5jb3MoYSpNYXRoLlBJKS8yfX0sbS5meD1aYS5wcm90b3R5cGUuaW5pdCxtLmZ4LnN0ZXA9e307dmFyICRhLF9hLGFiPS9eKD86dG9nZ2xlfHNob3d8aGlkZSkkLyxiYj1uZXcgUmVnRXhwKCJeKD86KFsrLV0pPXwpKCIrUysiKShbYS16JV0qKSQiLCJpIiksY2I9L3F1ZXVlSG9va3MkLyxkYj1baWJdLGViPXsiKiI6W2Z1bmN0aW9uKGEsYil7dmFyIGM9dGhpcy5jcmVhdGVUd2VlbihhLGIpLGQ9Yy5jdXIoKSxlPWJiLmV4ZWMoYiksZj1lJiZlWzNdfHwobS5jc3NOdW1iZXJbYV0/IiI6InB4IiksZz0obS5jc3NOdW1iZXJbYV18fCJweCIhPT1mJiYrZCkmJmJiLmV4ZWMobS5jc3MoYy5lbGVtLGEpKSxoPTEsaT0yMDtpZihnJiZnWzNdIT09Zil7Zj1mfHxnWzNdLGU9ZXx8W10sZz0rZHx8MTtkbyBoPWh8fCIuNSIsZy89aCxtLnN0eWxlKGMuZWxlbSxhLGcrZik7d2hpbGUoaCE9PShoPWMuY3VyKCkvZCkmJjEhPT1oJiYtLWkpfXJldHVybiBlJiYoZz1jLnN0YXJ0PStnfHwrZHx8MCxjLnVuaXQ9ZixjLmVuZD1lWzFdP2crKGVbMV0rMSkqZVsyXTorZVsyXSksY31dfTtmdW5jdGlvbiBmYigpe3JldHVybiBzZXRUaW1lb3V0KGZ1bmN0aW9uKCl7JGE9dm9pZCAwfSksJGE9bS5ub3coKX1mdW5jdGlvbiBnYihhLGIpe3ZhciBjLGQ9e2hlaWdodDphfSxlPTA7Zm9yKGI9Yj8xOjA7ND5lO2UrPTItYiljPVRbZV0sZFsibWFyZ2luIitjXT1kWyJwYWRkaW5nIitjXT1hO3JldHVybiBiJiYoZC5vcGFjaXR5PWQud2lkdGg9YSksZH1mdW5jdGlvbiBoYihhLGIsYyl7Zm9yKHZhciBkLGU9KGViW2JdfHxbXSkuY29uY2F0KGViWyIqIl0pLGY9MCxnPWUubGVuZ3RoO2c+ZjtmKyspaWYoZD1lW2ZdLmNhbGwoYyxiLGEpKXJldHVybiBkfWZ1bmN0aW9uIGliKGEsYixjKXt2YXIgZCxlLGYsZyxoLGksaixsLG49dGhpcyxvPXt9LHA9YS5zdHlsZSxxPWEubm9kZVR5cGUmJlUoYSkscj1tLl9kYXRhKGEsImZ4c2hvdyIpO2MucXVldWV8fChoPW0uX3F1ZXVlSG9va3MoYSwiZngiKSxudWxsPT1oLnVucXVldWVkJiYoaC51bnF1ZXVlZD0wLGk9aC5lbXB0eS5maXJlLGguZW1wdHkuZmlyZT1mdW5jdGlvbigpe2gudW5xdWV1ZWR8fGkoKX0pLGgudW5xdWV1ZWQrKyxuLmFsd2F5cyhmdW5jdGlvbigpe24uYWx3YXlzKGZ1bmN0aW9uKCl7aC51bnF1ZXVlZC0tLG0ucXVldWUoYSwiZngiKS5sZW5ndGh8fGguZW1wdHkuZmlyZSgpfSl9KSksMT09PWEubm9kZVR5cGUmJigiaGVpZ2h0ImluIGJ8fCJ3aWR0aCJpbiBiKSYmKGMub3ZlcmZsb3c9W3Aub3ZlcmZsb3cscC5vdmVyZmxvd1gscC5vdmVyZmxvd1ldLGo9bS5jc3MoYSwiZGlzcGxheSIpLGw9Im5vbmUiPT09aj9tLl9kYXRhKGEsIm9sZGRpc3BsYXkiKXx8RmEoYS5ub2RlTmFtZSk6aiwiaW5saW5lIj09PWwmJiJub25lIj09PW0uY3NzKGEsImZsb2F0IikmJihrLmlubGluZUJsb2NrTmVlZHNMYXlvdXQmJiJpbmxpbmUiIT09RmEoYS5ub2RlTmFtZSk/cC56b29tPTE6cC5kaXNwbGF5PSJpbmxpbmUtYmxvY2siKSksYy5vdmVyZmxvdyYmKHAub3ZlcmZsb3c9ImhpZGRlbiIsay5zaHJpbmtXcmFwQmxvY2tzKCl8fG4uYWx3YXlzKGZ1bmN0aW9uKCl7cC5vdmVyZmxvdz1jLm92ZXJmbG93WzBdLHAub3ZlcmZsb3dYPWMub3ZlcmZsb3dbMV0scC5vdmVyZmxvd1k9Yy5vdmVyZmxvd1syXX0pKTtmb3IoZCBpbiBiKWlmKGU9YltkXSxhYi5leGVjKGUpKXtpZihkZWxldGUgYltkXSxmPWZ8fCJ0b2dnbGUiPT09ZSxlPT09KHE/ImhpZGUiOiJzaG93Iikpe2lmKCJzaG93IiE9PWV8fCFyfHx2b2lkIDA9PT1yW2RdKWNvbnRpbnVlO3E9ITB9b1tkXT1yJiZyW2RdfHxtLnN0eWxlKGEsZCl9ZWxzZSBqPXZvaWQgMDtpZihtLmlzRW1wdHlPYmplY3QobykpImlubGluZSI9PT0oIm5vbmUiPT09aj9GYShhLm5vZGVOYW1lKTpqKSYmKHAuZGlzcGxheT1qKTtlbHNle3I/ImhpZGRlbiJpbiByJiYocT1yLmhpZGRlbik6cj1tLl9kYXRhKGEsImZ4c2hvdyIse30pLGYmJihyLmhpZGRlbj0hcSkscT9tKGEpLnNob3coKTpuLmRvbmUoZnVuY3Rpb24oKXttKGEpLmhpZGUoKX0pLG4uZG9uZShmdW5jdGlvbigpe3ZhciBiO20uX3JlbW92ZURhdGEoYSwiZnhzaG93Iik7Zm9yKGIgaW4gbyltLnN0eWxlKGEsYixvW2JdKX0pO2ZvcihkIGluIG8pZz1oYihxP3JbZF06MCxkLG4pLGQgaW4gcnx8KHJbZF09Zy5zdGFydCxxJiYoZy5lbmQ9Zy5zdGFydCxnLnN0YXJ0PSJ3aWR0aCI9PT1kfHwiaGVpZ2h0Ij09PWQ/MTowKSl9fWZ1bmN0aW9uIGpiKGEsYil7dmFyIGMsZCxlLGYsZztmb3IoYyBpbiBhKWlmKGQ9bS5jYW1lbENhc2UoYyksZT1iW2RdLGY9YVtjXSxtLmlzQXJyYXkoZikmJihlPWZbMV0sZj1hW2NdPWZbMF0pLGMhPT1kJiYoYVtkXT1mLGRlbGV0ZSBhW2NdKSxnPW0uY3NzSG9va3NbZF0sZyYmImV4cGFuZCJpbiBnKXtmPWcuZXhwYW5kKGYpLGRlbGV0ZSBhW2RdO2ZvcihjIGluIGYpYyBpbiBhfHwoYVtjXT1mW2NdLGJbY109ZSl9ZWxzZSBiW2RdPWV9ZnVuY3Rpb24ga2IoYSxiLGMpe3ZhciBkLGUsZj0wLGc9ZGIubGVuZ3RoLGg9bS5EZWZlcnJlZCgpLmFsd2F5cyhmdW5jdGlvbigpe2RlbGV0ZSBpLmVsZW19KSxpPWZ1bmN0aW9uKCl7aWYoZSlyZXR1cm4hMTtmb3IodmFyIGI9JGF8fGZiKCksYz1NYXRoLm1heCgwLGouc3RhcnRUaW1lK2ouZHVyYXRpb24tYiksZD1jL2ouZHVyYXRpb258fDAsZj0xLWQsZz0wLGk9ai50d2VlbnMubGVuZ3RoO2k+ZztnKyspai50d2VlbnNbZ10ucnVuKGYpO3JldHVybiBoLm5vdGlmeVdpdGgoYSxbaixmLGNdKSwxPmYmJmk/YzooaC5yZXNvbHZlV2l0aChhLFtqXSksITEpfSxqPWgucHJvbWlzZSh7ZWxlbTphLHByb3BzOm0uZXh0ZW5kKHt9LGIpLG9wdHM6bS5leHRlbmQoITAse3NwZWNpYWxFYXNpbmc6e319LGMpLG9yaWdpbmFsUHJvcGVydGllczpiLG9yaWdpbmFsT3B0aW9uczpjLHN0YXJ0VGltZTokYXx8ZmIoKSxkdXJhdGlvbjpjLmR1cmF0aW9uLHR3ZWVuczpbXSxjcmVhdGVUd2VlbjpmdW5jdGlvbihiLGMpe3ZhciBkPW0uVHdlZW4oYSxqLm9wdHMsYixjLGoub3B0cy5zcGVjaWFsRWFzaW5nW2JdfHxqLm9wdHMuZWFzaW5nKTtyZXR1cm4gai50d2VlbnMucHVzaChkKSxkfSxzdG9wOmZ1bmN0aW9uKGIpe3ZhciBjPTAsZD1iP2oudHdlZW5zLmxlbmd0aDowO2lmKGUpcmV0dXJuIHRoaXM7Zm9yKGU9ITA7ZD5jO2MrKylqLnR3ZWVuc1tjXS5ydW4oMSk7cmV0dXJuIGI/aC5yZXNvbHZlV2l0aChhLFtqLGJdKTpoLnJlamVjdFdpdGgoYSxbaixiXSksdGhpc319KSxrPWoucHJvcHM7Zm9yKGpiKGssai5vcHRzLnNwZWNpYWxFYXNpbmcpO2c+ZjtmKyspaWYoZD1kYltmXS5jYWxsKGosYSxrLGoub3B0cykpcmV0dXJuIGQ7cmV0dXJuIG0ubWFwKGssaGIsaiksbS5pc0Z1bmN0aW9uKGoub3B0cy5zdGFydCkmJmoub3B0cy5zdGFydC5jYWxsKGEsaiksbS5meC50aW1lcihtLmV4dGVuZChpLHtlbGVtOmEsYW5pbTpqLHF1ZXVlOmoub3B0cy5xdWV1ZX0pKSxqLnByb2dyZXNzKGoub3B0cy5wcm9ncmVzcykuZG9uZShqLm9wdHMuZG9uZSxqLm9wdHMuY29tcGxldGUpLmZhaWwoai5vcHRzLmZhaWwpLmFsd2F5cyhqLm9wdHMuYWx3YXlzKX1tLkFuaW1hdGlvbj1tLmV4dGVuZChrYix7dHdlZW5lcjpmdW5jdGlvbihhLGIpe20uaXNGdW5jdGlvbihhKT8oYj1hLGE9WyIqIl0pOmE9YS5zcGxpdCgiICIpO2Zvcih2YXIgYyxkPTAsZT1hLmxlbmd0aDtlPmQ7ZCsrKWM9YVtkXSxlYltjXT1lYltjXXx8W10sZWJbY10udW5zaGlmdChiKX0scHJlZmlsdGVyOmZ1bmN0aW9uKGEsYil7Yj9kYi51bnNoaWZ0KGEpOmRiLnB1c2goYSl9fSksbS5zcGVlZD1mdW5jdGlvbihhLGIsYyl7dmFyIGQ9YSYmIm9iamVjdCI9PXR5cGVvZiBhP20uZXh0ZW5kKHt9LGEpOntjb21wbGV0ZTpjfHwhYyYmYnx8bS5pc0Z1bmN0aW9uKGEpJiZhLGR1cmF0aW9uOmEsZWFzaW5nOmMmJmJ8fGImJiFtLmlzRnVuY3Rpb24oYikmJmJ9O3JldHVybiBkLmR1cmF0aW9uPW0uZngub2ZmPzA6Im51bWJlciI9PXR5cGVvZiBkLmR1cmF0aW9uP2QuZHVyYXRpb246ZC5kdXJhdGlvbiBpbiBtLmZ4LnNwZWVkcz9tLmZ4LnNwZWVkc1tkLmR1cmF0aW9uXTptLmZ4LnNwZWVkcy5fZGVmYXVsdCwobnVsbD09ZC5xdWV1ZXx8ZC5xdWV1ZT09PSEwKSYmKGQucXVldWU9ImZ4IiksZC5vbGQ9ZC5jb21wbGV0ZSxkLmNvbXBsZXRlPWZ1bmN0aW9uKCl7bS5pc0Z1bmN0aW9uKGQub2xkKSYmZC5vbGQuY2FsbCh0aGlzKSxkLnF1ZXVlJiZtLmRlcXVldWUodGhpcyxkLnF1ZXVlKX0sZH0sbS5mbi5leHRlbmQoe2ZhZGVUbzpmdW5jdGlvbihhLGIsYyxkKXtyZXR1cm4gdGhpcy5maWx0ZXIoVSkuY3NzKCJvcGFjaXR5IiwwKS5zaG93KCkuZW5kKCkuYW5pbWF0ZSh7b3BhY2l0eTpifSxhLGMsZCl9LGFuaW1hdGU6ZnVuY3Rpb24oYSxiLGMsZCl7dmFyIGU9bS5pc0VtcHR5T2JqZWN0KGEpLGY9bS5zcGVlZChiLGMsZCksZz1mdW5jdGlvbigpe3ZhciBiPWtiKHRoaXMsbS5leHRlbmQoe30sYSksZik7KGV8fG0uX2RhdGEodGhpcywiZmluaXNoIikpJiZiLnN0b3AoITApfTtyZXR1cm4gZy5maW5pc2g9ZyxlfHxmLnF1ZXVlPT09ITE/dGhpcy5lYWNoKGcpOnRoaXMucXVldWUoZi5xdWV1ZSxnKX0sc3RvcDpmdW5jdGlvbihhLGIsYyl7dmFyIGQ9ZnVuY3Rpb24oYSl7dmFyIGI9YS5zdG9wO2RlbGV0ZSBhLnN0b3AsYihjKX07cmV0dXJuInN0cmluZyIhPXR5cGVvZiBhJiYoYz1iLGI9YSxhPXZvaWQgMCksYiYmYSE9PSExJiZ0aGlzLnF1ZXVlKGF8fCJmeCIsW10pLHRoaXMuZWFjaChmdW5jdGlvbigpe3ZhciBiPSEwLGU9bnVsbCE9YSYmYSsicXVldWVIb29rcyIsZj1tLnRpbWVycyxnPW0uX2RhdGEodGhpcyk7aWYoZSlnW2VdJiZnW2VdLnN0b3AmJmQoZ1tlXSk7ZWxzZSBmb3IoZSBpbiBnKWdbZV0mJmdbZV0uc3RvcCYmY2IudGVzdChlKSYmZChnW2VdKTtmb3IoZT1mLmxlbmd0aDtlLS07KWZbZV0uZWxlbSE9PXRoaXN8fG51bGwhPWEmJmZbZV0ucXVldWUhPT1hfHwoZltlXS5hbmltLnN0b3AoYyksYj0hMSxmLnNwbGljZShlLDEpKTsoYnx8IWMpJiZtLmRlcXVldWUodGhpcyxhKX0pfSxmaW5pc2g6ZnVuY3Rpb24oYSl7cmV0dXJuIGEhPT0hMSYmKGE9YXx8ImZ4IiksdGhpcy5lYWNoKGZ1bmN0aW9uKCl7dmFyIGIsYz1tLl9kYXRhKHRoaXMpLGQ9Y1thKyJxdWV1ZSJdLGU9Y1thKyJxdWV1ZUhvb2tzIl0sZj1tLnRpbWVycyxnPWQ/ZC5sZW5ndGg6MDtmb3IoYy5maW5pc2g9ITAsbS5xdWV1ZSh0aGlzLGEsW10pLGUmJmUuc3RvcCYmZS5zdG9wLmNhbGwodGhpcywhMCksYj1mLmxlbmd0aDtiLS07KWZbYl0uZWxlbT09PXRoaXMmJmZbYl0ucXVldWU9PT1hJiYoZltiXS5hbmltLnN0b3AoITApLGYuc3BsaWNlKGIsMSkpO2ZvcihiPTA7Zz5iO2IrKylkW2JdJiZkW2JdLmZpbmlzaCYmZFtiXS5maW5pc2guY2FsbCh0aGlzKTtkZWxldGUgYy5maW5pc2h9KX19KSxtLmVhY2goWyJ0b2dnbGUiLCJzaG93IiwiaGlkZSJdLGZ1bmN0aW9uKGEsYil7dmFyIGM9bS5mbltiXTttLmZuW2JdPWZ1bmN0aW9uKGEsZCxlKXtyZXR1cm4gbnVsbD09YXx8ImJvb2xlYW4iPT10eXBlb2YgYT9jLmFwcGx5KHRoaXMsYXJndW1lbnRzKTp0aGlzLmFuaW1hdGUoZ2IoYiwhMCksYSxkLGUpfX0pLG0uZWFjaCh7c2xpZGVEb3duOmdiKCJzaG93Iiksc2xpZGVVcDpnYigiaGlkZSIpLHNsaWRlVG9nZ2xlOmdiKCJ0b2dnbGUiKSxmYWRlSW46e29wYWNpdHk6InNob3cifSxmYWRlT3V0OntvcGFjaXR5OiJoaWRlIn0sZmFkZVRvZ2dsZTp7b3BhY2l0eToidG9nZ2xlIn19LGZ1bmN0aW9uKGEsYil7bS5mblthXT1mdW5jdGlvbihhLGMsZCl7cmV0dXJuIHRoaXMuYW5pbWF0ZShiLGEsYyxkKX19KSxtLnRpbWVycz1bXSxtLmZ4LnRpY2s9ZnVuY3Rpb24oKXt2YXIgYSxiPW0udGltZXJzLGM9MDtmb3IoJGE9bS5ub3coKTtjPGIubGVuZ3RoO2MrKylhPWJbY10sYSgpfHxiW2NdIT09YXx8Yi5zcGxpY2UoYy0tLDEpO2IubGVuZ3RofHxtLmZ4LnN0b3AoKSwkYT12b2lkIDB9LG0uZngudGltZXI9ZnVuY3Rpb24oYSl7bS50aW1lcnMucHVzaChhKSxhKCk/bS5meC5zdGFydCgpOm0udGltZXJzLnBvcCgpfSxtLmZ4LmludGVydmFsPTEzLG0uZnguc3RhcnQ9ZnVuY3Rpb24oKXtfYXx8KF9hPXNldEludGVydmFsKG0uZngudGljayxtLmZ4LmludGVydmFsKSl9LG0uZnguc3RvcD1mdW5jdGlvbigpe2NsZWFySW50ZXJ2YWwoX2EpLF9hPW51bGx9LG0uZnguc3BlZWRzPXtzbG93OjYwMCxmYXN0OjIwMCxfZGVmYXVsdDo0MDB9LG0uZm4uZGVsYXk9ZnVuY3Rpb24oYSxiKXtyZXR1cm4gYT1tLmZ4P20uZnguc3BlZWRzW2FdfHxhOmEsYj1ifHwiZngiLHRoaXMucXVldWUoYixmdW5jdGlvbihiLGMpe3ZhciBkPXNldFRpbWVvdXQoYixhKTtjLnN0b3A9ZnVuY3Rpb24oKXtjbGVhclRpbWVvdXQoZCl9fSl9LGZ1bmN0aW9uKCl7dmFyIGEsYixjLGQsZTtiPXkuY3JlYXRlRWxlbWVudCgiZGl2IiksYi5zZXRBdHRyaWJ1dGUoImNsYXNzTmFtZSIsInQiKSxiLmlubmVySFRNTD0iICA8bGluay8+PHRhYmxlPjwvdGFibGU+PGEgaHJlZj0nL2EnPmE8L2E+PGlucHV0IHR5cGU9J2NoZWNrYm94Jy8+IixkPWIuZ2V0RWxlbWVudHNCeVRhZ05hbWUoImEiKVswXSxjPXkuY3JlYXRlRWxlbWVudCgic2VsZWN0IiksZT1jLmFwcGVuZENoaWxkKHkuY3JlYXRlRWxlbWVudCgib3B0aW9uIikpLGE9Yi5nZXRFbGVtZW50c0J5VGFnTmFtZSgiaW5wdXQiKVswXSxkLnN0eWxlLmNzc1RleHQ9InRvcDoxcHgiLGsuZ2V0U2V0QXR0cmlidXRlPSJ0IiE9PWIuY2xhc3NOYW1lLGsuc3R5bGU9L3RvcC8udGVzdChkLmdldEF0dHJpYnV0ZSgic3R5bGUiKSksay5ocmVmTm9ybWFsaXplZD0iL2EiPT09ZC5nZXRBdHRyaWJ1dGUoImhyZWYiKSxrLmNoZWNrT249ISFhLnZhbHVlLGsub3B0U2VsZWN0ZWQ9ZS5zZWxlY3RlZCxrLmVuY3R5cGU9ISF5LmNyZWF0ZUVsZW1lbnQoImZvcm0iKS5lbmN0eXBlLGMuZGlzYWJsZWQ9ITAsay5vcHREaXNhYmxlZD0hZS5kaXNhYmxlZCxhPXkuY3JlYXRlRWxlbWVudCgiaW5wdXQiKSxhLnNldEF0dHJpYnV0ZSgidmFsdWUiLCIiKSxrLmlucHV0PSIiPT09YS5nZXRBdHRyaWJ1dGUoInZhbHVlIiksYS52YWx1ZT0idCIsYS5zZXRBdHRyaWJ1dGUoInR5cGUiLCJyYWRpbyIpLGsucmFkaW9WYWx1ZT0idCI9PT1hLnZhbHVlfSgpO3ZhciBsYj0vXHIvZzttLmZuLmV4dGVuZCh7dmFsOmZ1bmN0aW9uKGEpe3ZhciBiLGMsZCxlPXRoaXNbMF07e2lmKGFyZ3VtZW50cy5sZW5ndGgpcmV0dXJuIGQ9bS5pc0Z1bmN0aW9uKGEpLHRoaXMuZWFjaChmdW5jdGlvbihjKXt2YXIgZTsxPT09dGhpcy5ub2RlVHlwZSYmKGU9ZD9hLmNhbGwodGhpcyxjLG0odGhpcykudmFsKCkpOmEsbnVsbD09ZT9lPSIiOiJudW1iZXIiPT10eXBlb2YgZT9lKz0iIjptLmlzQXJyYXkoZSkmJihlPW0ubWFwKGUsZnVuY3Rpb24oYSl7cmV0dXJuIG51bGw9PWE/IiI6YSsiIn0pKSxiPW0udmFsSG9va3NbdGhpcy50eXBlXXx8bS52YWxIb29rc1t0aGlzLm5vZGVOYW1lLnRvTG93ZXJDYXNlKCldLGImJiJzZXQiaW4gYiYmdm9pZCAwIT09Yi5zZXQodGhpcyxlLCJ2YWx1ZSIpfHwodGhpcy52YWx1ZT1lKSl9KTtpZihlKXJldHVybiBiPW0udmFsSG9va3NbZS50eXBlXXx8bS52YWxIb29rc1tlLm5vZGVOYW1lLnRvTG93ZXJDYXNlKCldLGImJiJnZXQiaW4gYiYmdm9pZCAwIT09KGM9Yi5nZXQoZSwidmFsdWUiKSk/YzooYz1lLnZhbHVlLCJzdHJpbmciPT10eXBlb2YgYz9jLnJlcGxhY2UobGIsIiIpOm51bGw9PWM/IiI6Yyl9fX0pLG0uZXh0ZW5kKHt2YWxIb29rczp7b3B0aW9uOntnZXQ6ZnVuY3Rpb24oYSl7dmFyIGI9bS5maW5kLmF0dHIoYSwidmFsdWUiKTtyZXR1cm4gbnVsbCE9Yj9iOm0udHJpbShtLnRleHQoYSkpfX0sc2VsZWN0OntnZXQ6ZnVuY3Rpb24oYSl7Zm9yKHZhciBiLGMsZD1hLm9wdGlvbnMsZT1hLnNlbGVjdGVkSW5kZXgsZj0ic2VsZWN0LW9uZSI9PT1hLnR5cGV8fDA+ZSxnPWY/bnVsbDpbXSxoPWY/ZSsxOmQubGVuZ3RoLGk9MD5lP2g6Zj9lOjA7aD5pO2krKylpZihjPWRbaV0sISghYy5zZWxlY3RlZCYmaSE9PWV8fChrLm9wdERpc2FibGVkP2MuZGlzYWJsZWQ6bnVsbCE9PWMuZ2V0QXR0cmlidXRlKCJkaXNhYmxlZCIpKXx8Yy5wYXJlbnROb2RlLmRpc2FibGVkJiZtLm5vZGVOYW1lKGMucGFyZW50Tm9kZSwib3B0Z3JvdXAiKSkpe2lmKGI9bShjKS52YWwoKSxmKXJldHVybiBiO2cucHVzaChiKX1yZXR1cm4gZ30sc2V0OmZ1bmN0aW9uKGEsYil7dmFyIGMsZCxlPWEub3B0aW9ucyxmPW0ubWFrZUFycmF5KGIpLGc9ZS5sZW5ndGg7d2hpbGUoZy0tKWlmKGQ9ZVtnXSxtLmluQXJyYXkobS52YWxIb29rcy5vcHRpb24uZ2V0KGQpLGYpPj0wKXRyeXtkLnNlbGVjdGVkPWM9ITB9Y2F0Y2goaCl7ZC5zY3JvbGxIZWlnaHR9ZWxzZSBkLnNlbGVjdGVkPSExO3JldHVybiBjfHwoYS5zZWxlY3RlZEluZGV4PS0xKSxlfX19fSksbS5lYWNoKFsicmFkaW8iLCJjaGVja2JveCJdLGZ1bmN0aW9uKCl7bS52YWxIb29rc1t0aGlzXT17c2V0OmZ1bmN0aW9uKGEsYil7cmV0dXJuIG0uaXNBcnJheShiKT9hLmNoZWNrZWQ9bS5pbkFycmF5KG0oYSkudmFsKCksYik+PTA6dm9pZCAwfX0say5jaGVja09ufHwobS52YWxIb29rc1t0aGlzXS5nZXQ9ZnVuY3Rpb24oYSl7cmV0dXJuIG51bGw9PT1hLmdldEF0dHJpYnV0ZSgidmFsdWUiKT8ib24iOmEudmFsdWV9KX0pO3ZhciBtYixuYixvYj1tLmV4cHIuYXR0ckhhbmRsZSxwYj0vXig/OmNoZWNrZWR8c2VsZWN0ZWQpJC9pLHFiPWsuZ2V0U2V0QXR0cmlidXRlLHJiPWsuaW5wdXQ7bS5mbi5leHRlbmQoe2F0dHI6ZnVuY3Rpb24oYSxiKXtyZXR1cm4gVih0aGlzLG0uYXR0cixhLGIsYXJndW1lbnRzLmxlbmd0aD4xKX0scmVtb3ZlQXR0cjpmdW5jdGlvbihhKXtyZXR1cm4gdGhpcy5lYWNoKGZ1bmN0aW9uKCl7bS5yZW1vdmVBdHRyKHRoaXMsYSl9KX19KSxtLmV4dGVuZCh7YXR0cjpmdW5jdGlvbihhLGIsYyl7dmFyIGQsZSxmPWEubm9kZVR5cGU7aWYoYSYmMyE9PWYmJjghPT1mJiYyIT09ZilyZXR1cm4gdHlwZW9mIGEuZ2V0QXR0cmlidXRlPT09Sz9tLnByb3AoYSxiLGMpOigxPT09ZiYmbS5pc1hNTERvYyhhKXx8KGI9Yi50b0xvd2VyQ2FzZSgpLGQ9bS5hdHRySG9va3NbYl18fChtLmV4cHIubWF0Y2guYm9vbC50ZXN0KGIpP25iOm1iKSksdm9pZCAwPT09Yz9kJiYiZ2V0ImluIGQmJm51bGwhPT0oZT1kLmdldChhLGIpKT9lOihlPW0uZmluZC5hdHRyKGEsYiksbnVsbD09ZT92b2lkIDA6ZSk6bnVsbCE9PWM/ZCYmInNldCJpbiBkJiZ2b2lkIDAhPT0oZT1kLnNldChhLGMsYikpP2U6KGEuc2V0QXR0cmlidXRlKGIsYysiIiksYyk6dm9pZCBtLnJlbW92ZUF0dHIoYSxiKSl9LHJlbW92ZUF0dHI6ZnVuY3Rpb24oYSxiKXt2YXIgYyxkLGU9MCxmPWImJmIubWF0Y2goRSk7aWYoZiYmMT09PWEubm9kZVR5cGUpd2hpbGUoYz1mW2UrK10pZD1tLnByb3BGaXhbY118fGMsbS5leHByLm1hdGNoLmJvb2wudGVzdChjKT9yYiYmcWJ8fCFwYi50ZXN0KGMpP2FbZF09ITE6YVttLmNhbWVsQ2FzZSgiZGVmYXVsdC0iK2MpXT1hW2RdPSExOm0uYXR0cihhLGMsIiIpLGEucmVtb3ZlQXR0cmlidXRlKHFiP2M6ZCl9LGF0dHJIb29rczp7dHlwZTp7c2V0OmZ1bmN0aW9uKGEsYil7aWYoIWsucmFkaW9WYWx1ZSYmInJhZGlvIj09PWImJm0ubm9kZU5hbWUoYSwiaW5wdXQiKSl7dmFyIGM9YS52YWx1ZTtyZXR1cm4gYS5zZXRBdHRyaWJ1dGUoInR5cGUiLGIpLGMmJihhLnZhbHVlPWMpLGJ9fX19fSksbmI9e3NldDpmdW5jdGlvbihhLGIsYyl7cmV0dXJuIGI9PT0hMT9tLnJlbW92ZUF0dHIoYSxjKTpyYiYmcWJ8fCFwYi50ZXN0KGMpP2Euc2V0QXR0cmlidXRlKCFxYiYmbS5wcm9wRml4W2NdfHxjLGMpOmFbbS5jYW1lbENhc2UoImRlZmF1bHQtIitjKV09YVtjXT0hMCxjfX0sbS5lYWNoKG0uZXhwci5tYXRjaC5ib29sLnNvdXJjZS5tYXRjaCgvXHcrL2cpLGZ1bmN0aW9uKGEsYil7dmFyIGM9b2JbYl18fG0uZmluZC5hdHRyO29iW2JdPXJiJiZxYnx8IXBiLnRlc3QoYik/ZnVuY3Rpb24oYSxiLGQpe3ZhciBlLGY7cmV0dXJuIGR8fChmPW9iW2JdLG9iW2JdPWUsZT1udWxsIT1jKGEsYixkKT9iLnRvTG93ZXJDYXNlKCk6bnVsbCxvYltiXT1mKSxlfTpmdW5jdGlvbihhLGIsYyl7cmV0dXJuIGM/dm9pZCAwOmFbbS5jYW1lbENhc2UoImRlZmF1bHQtIitiKV0/Yi50b0xvd2VyQ2FzZSgpOm51bGx9fSkscmImJnFifHwobS5hdHRySG9va3MudmFsdWU9e3NldDpmdW5jdGlvbihhLGIsYyl7cmV0dXJuIG0ubm9kZU5hbWUoYSwiaW5wdXQiKT92b2lkKGEuZGVmYXVsdFZhbHVlPWIpOm1iJiZtYi5zZXQoYSxiLGMpfX0pLHFifHwobWI9e3NldDpmdW5jdGlvbihhLGIsYyl7dmFyIGQ9YS5nZXRBdHRyaWJ1dGVOb2RlKGMpO3JldHVybiBkfHxhLnNldEF0dHJpYnV0ZU5vZGUoZD1hLm93bmVyRG9jdW1lbnQuY3JlYXRlQXR0cmlidXRlKGMpKSxkLnZhbHVlPWIrPSIiLCJ2YWx1ZSI9PT1jfHxiPT09YS5nZXRBdHRyaWJ1dGUoYyk/Yjp2b2lkIDB9fSxvYi5pZD1vYi5uYW1lPW9iLmNvb3Jkcz1mdW5jdGlvbihhLGIsYyl7dmFyIGQ7cmV0dXJuIGM/dm9pZCAwOihkPWEuZ2V0QXR0cmlidXRlTm9kZShiKSkmJiIiIT09ZC52YWx1ZT9kLnZhbHVlOm51bGx9LG0udmFsSG9va3MuYnV0dG9uPXtnZXQ6ZnVuY3Rpb24oYSxiKXt2YXIgYz1hLmdldEF0dHJpYnV0ZU5vZGUoYik7cmV0dXJuIGMmJmMuc3BlY2lmaWVkP2MudmFsdWU6dm9pZCAwfSxzZXQ6bWIuc2V0fSxtLmF0dHJIb29rcy5jb250ZW50ZWRpdGFibGU9e3NldDpmdW5jdGlvbihhLGIsYyl7bWIuc2V0KGEsIiI9PT1iPyExOmIsYyl9fSxtLmVhY2goWyJ3aWR0aCIsImhlaWdodCJdLGZ1bmN0aW9uKGEsYil7bS5hdHRySG9va3NbYl09e3NldDpmdW5jdGlvbihhLGMpe3JldHVybiIiPT09Yz8oYS5zZXRBdHRyaWJ1dGUoYiwiYXV0byIpLGMpOnZvaWQgMH19fSkpLGsuc3R5bGV8fChtLmF0dHJIb29rcy5zdHlsZT17Z2V0OmZ1bmN0aW9uKGEpe3JldHVybiBhLnN0eWxlLmNzc1RleHR8fHZvaWQgMH0sc2V0OmZ1bmN0aW9uKGEsYil7cmV0dXJuIGEuc3R5bGUuY3NzVGV4dD1iKyIifX0pO3ZhciBzYj0vXig/OmlucHV0fHNlbGVjdHx0ZXh0YXJlYXxidXR0b258b2JqZWN0KSQvaSx0Yj0vXig/OmF8YXJlYSkkL2k7bS5mbi5leHRlbmQoe3Byb3A6ZnVuY3Rpb24oYSxiKXtyZXR1cm4gVih0aGlzLG0ucHJvcCxhLGIsYXJndW1lbnRzLmxlbmd0aD4xKX0scmVtb3ZlUHJvcDpmdW5jdGlvbihhKXtyZXR1cm4gYT1tLnByb3BGaXhbYV18fGEsdGhpcy5lYWNoKGZ1bmN0aW9uKCl7dHJ5e3RoaXNbYV09dm9pZCAwLGRlbGV0ZSB0aGlzW2FdfWNhdGNoKGIpe319KX19KSxtLmV4dGVuZCh7cHJvcEZpeDp7ImZvciI6Imh0bWxGb3IiLCJjbGFzcyI6ImNsYXNzTmFtZSJ9LHByb3A6ZnVuY3Rpb24oYSxiLGMpe3ZhciBkLGUsZixnPWEubm9kZVR5cGU7aWYoYSYmMyE9PWcmJjghPT1nJiYyIT09ZylyZXR1cm4gZj0xIT09Z3x8IW0uaXNYTUxEb2MoYSksZiYmKGI9bS5wcm9wRml4W2JdfHxiLGU9bS5wcm9wSG9va3NbYl0pLHZvaWQgMCE9PWM/ZSYmInNldCJpbiBlJiZ2b2lkIDAhPT0oZD1lLnNldChhLGMsYikpP2Q6YVtiXT1jOmUmJiJnZXQiaW4gZSYmbnVsbCE9PShkPWUuZ2V0KGEsYikpP2Q6YVtiXX0scHJvcEhvb2tzOnt0YWJJbmRleDp7Z2V0OmZ1bmN0aW9uKGEpe3ZhciBiPW0uZmluZC5hdHRyKGEsInRhYmluZGV4Iik7cmV0dXJuIGI/cGFyc2VJbnQoYiwxMCk6c2IudGVzdChhLm5vZGVOYW1lKXx8dGIudGVzdChhLm5vZGVOYW1lKSYmYS5ocmVmPzA6LTF9fX19KSxrLmhyZWZOb3JtYWxpemVkfHxtLmVhY2goWyJocmVmIiwic3JjIl0sZnVuY3Rpb24oYSxiKXttLnByb3BIb29rc1tiXT17Z2V0OmZ1bmN0aW9uKGEpe3JldHVybiBhLmdldEF0dHJpYnV0ZShiLDQpfX19KSxrLm9wdFNlbGVjdGVkfHwobS5wcm9wSG9va3Muc2VsZWN0ZWQ9e2dldDpmdW5jdGlvbihhKXt2YXIgYj1hLnBhcmVudE5vZGU7cmV0dXJuIGImJihiLnNlbGVjdGVkSW5kZXgsYi5wYXJlbnROb2RlJiZiLnBhcmVudE5vZGUuc2VsZWN0ZWRJbmRleCksbnVsbH19KSxtLmVhY2goWyJ0YWJJbmRleCIsInJlYWRPbmx5IiwibWF4TGVuZ3RoIiwiY2VsbFNwYWNpbmciLCJjZWxsUGFkZGluZyIsInJvd1NwYW4iLCJjb2xTcGFuIiwidXNlTWFwIiwiZnJhbWVCb3JkZXIiLCJjb250ZW50RWRpdGFibGUiXSxmdW5jdGlvbigpe20ucHJvcEZpeFt0aGlzLnRvTG93ZXJDYXNlKCldPXRoaXN9KSxrLmVuY3R5cGV8fChtLnByb3BGaXguZW5jdHlwZT0iZW5jb2RpbmciKTt2YXIgdWI9L1tcdFxyXG5cZl0vZzttLmZuLmV4dGVuZCh7YWRkQ2xhc3M6ZnVuY3Rpb24oYSl7dmFyIGIsYyxkLGUsZixnLGg9MCxpPXRoaXMubGVuZ3RoLGo9InN0cmluZyI9PXR5cGVvZiBhJiZhO2lmKG0uaXNGdW5jdGlvbihhKSlyZXR1cm4gdGhpcy5lYWNoKGZ1bmN0aW9uKGIpe20odGhpcykuYWRkQ2xhc3MoYS5jYWxsKHRoaXMsYix0aGlzLmNsYXNzTmFtZSkpfSk7aWYoailmb3IoYj0oYXx8IiIpLm1hdGNoKEUpfHxbXTtpPmg7aCsrKWlmKGM9dGhpc1toXSxkPTE9PT1jLm5vZGVUeXBlJiYoYy5jbGFzc05hbWU/KCIgIitjLmNsYXNzTmFtZSsiICIpLnJlcGxhY2UodWIsIiAiKToiICIpKXtmPTA7d2hpbGUoZT1iW2YrK10pZC5pbmRleE9mKCIgIitlKyIgIik8MCYmKGQrPWUrIiAiKTtnPW0udHJpbShkKSxjLmNsYXNzTmFtZSE9PWcmJihjLmNsYXNzTmFtZT1nKX1yZXR1cm4gdGhpc30scmVtb3ZlQ2xhc3M6ZnVuY3Rpb24oYSl7dmFyIGIsYyxkLGUsZixnLGg9MCxpPXRoaXMubGVuZ3RoLGo9MD09PWFyZ3VtZW50cy5sZW5ndGh8fCJzdHJpbmciPT10eXBlb2YgYSYmYTtpZihtLmlzRnVuY3Rpb24oYSkpcmV0dXJuIHRoaXMuZWFjaChmdW5jdGlvbihiKXttKHRoaXMpLnJlbW92ZUNsYXNzKGEuY2FsbCh0aGlzLGIsdGhpcy5jbGFzc05hbWUpKX0pO2lmKGopZm9yKGI9KGF8fCIiKS5tYXRjaChFKXx8W107aT5oO2grKylpZihjPXRoaXNbaF0sZD0xPT09Yy5ub2RlVHlwZSYmKGMuY2xhc3NOYW1lPygiICIrYy5jbGFzc05hbWUrIiAiKS5yZXBsYWNlKHViLCIgIik6IiIpKXtmPTA7d2hpbGUoZT1iW2YrK10pd2hpbGUoZC5pbmRleE9mKCIgIitlKyIgIik+PTApZD1kLnJlcGxhY2UoIiAiK2UrIiAiLCIgIik7Zz1hP20udHJpbShkKToiIixjLmNsYXNzTmFtZSE9PWcmJihjLmNsYXNzTmFtZT1nKX1yZXR1cm4gdGhpc30sdG9nZ2xlQ2xhc3M6ZnVuY3Rpb24oYSxiKXt2YXIgYz10eXBlb2YgYTtyZXR1cm4iYm9vbGVhbiI9PXR5cGVvZiBiJiYic3RyaW5nIj09PWM/Yj90aGlzLmFkZENsYXNzKGEpOnRoaXMucmVtb3ZlQ2xhc3MoYSk6dGhpcy5lYWNoKG0uaXNGdW5jdGlvbihhKT9mdW5jdGlvbihjKXttKHRoaXMpLnRvZ2dsZUNsYXNzKGEuY2FsbCh0aGlzLGMsdGhpcy5jbGFzc05hbWUsYiksYil9OmZ1bmN0aW9uKCl7aWYoInN0cmluZyI9PT1jKXt2YXIgYixkPTAsZT1tKHRoaXMpLGY9YS5tYXRjaChFKXx8W107d2hpbGUoYj1mW2QrK10pZS5oYXNDbGFzcyhiKT9lLnJlbW92ZUNsYXNzKGIpOmUuYWRkQ2xhc3MoYil9ZWxzZShjPT09S3x8ImJvb2xlYW4iPT09YykmJih0aGlzLmNsYXNzTmFtZSYmbS5fZGF0YSh0aGlzLCJfX2NsYXNzTmFtZV9fIix0aGlzLmNsYXNzTmFtZSksdGhpcy5jbGFzc05hbWU9dGhpcy5jbGFzc05hbWV8fGE9PT0hMT8iIjptLl9kYXRhKHRoaXMsIl9fY2xhc3NOYW1lX18iKXx8IiIpfSl9LGhhc0NsYXNzOmZ1bmN0aW9uKGEpe2Zvcih2YXIgYj0iICIrYSsiICIsYz0wLGQ9dGhpcy5sZW5ndGg7ZD5jO2MrKylpZigxPT09dGhpc1tjXS5ub2RlVHlwZSYmKCIgIit0aGlzW2NdLmNsYXNzTmFtZSsiICIpLnJlcGxhY2UodWIsIiAiKS5pbmRleE9mKGIpPj0wKXJldHVybiEwO3JldHVybiExfX0pLG0uZWFjaCgiYmx1ciBmb2N1cyBmb2N1c2luIGZvY3Vzb3V0IGxvYWQgcmVzaXplIHNjcm9sbCB1bmxvYWQgY2xpY2sgZGJsY2xpY2sgbW91c2Vkb3duIG1vdXNldXAgbW91c2Vtb3ZlIG1vdXNlb3ZlciBtb3VzZW91dCBtb3VzZWVudGVyIG1vdXNlbGVhdmUgY2hhbmdlIHNlbGVjdCBzdWJtaXQga2V5ZG93biBrZXlwcmVzcyBrZXl1cCBlcnJvciBjb250ZXh0bWVudSIuc3BsaXQoIiAiKSxmdW5jdGlvbihhLGIpe20uZm5bYl09ZnVuY3Rpb24oYSxjKXtyZXR1cm4gYXJndW1lbnRzLmxlbmd0aD4wP3RoaXMub24oYixudWxsLGEsYyk6dGhpcy50cmlnZ2VyKGIpfX0pLG0uZm4uZXh0ZW5kKHtob3ZlcjpmdW5jdGlvbihhLGIpe3JldHVybiB0aGlzLm1vdXNlZW50ZXIoYSkubW91c2VsZWF2ZShifHxhKX0sYmluZDpmdW5jdGlvbihhLGIsYyl7cmV0dXJuIHRoaXMub24oYSxudWxsLGIsYyl9LHVuYmluZDpmdW5jdGlvbihhLGIpe3JldHVybiB0aGlzLm9mZihhLG51bGwsYil9LGRlbGVnYXRlOmZ1bmN0aW9uKGEsYixjLGQpe3JldHVybiB0aGlzLm9uKGIsYSxjLGQpfSx1bmRlbGVnYXRlOmZ1bmN0aW9uKGEsYixjKXtyZXR1cm4gMT09PWFyZ3VtZW50cy5sZW5ndGg/dGhpcy5vZmYoYSwiKioiKTp0aGlzLm9mZihiLGF8fCIqKiIsYyl9fSk7dmFyIHZiPW0ubm93KCksd2I9L1w/Lyx4Yj0vKCwpfChcW3x7KXwofXxdKXwiKD86W14iXFxcclxuXXxcXFsiXFxcL2JmbnJ0XXxcXHVbXGRhLWZBLUZdezR9KSoiXHMqOj98dHJ1ZXxmYWxzZXxudWxsfC0/KD8hMFxkKVxkKyg/OlwuXGQrfCkoPzpbZUVdWystXT9cZCt8KS9nO20ucGFyc2VKU09OPWZ1bmN0aW9uKGIpe2lmKGEuSlNPTiYmYS5KU09OLnBhcnNlKXJldHVybiBhLkpTT04ucGFyc2UoYisiIik7dmFyIGMsZD1udWxsLGU9bS50cmltKGIrIiIpO3JldHVybiBlJiYhbS50cmltKGUucmVwbGFjZSh4YixmdW5jdGlvbihhLGIsZSxmKXtyZXR1cm4gYyYmYiYmKGQ9MCksMD09PWQ/YTooYz1lfHxiLGQrPSFmLSFlLCIiKX0pKT9GdW5jdGlvbigicmV0dXJuICIrZSkoKTptLmVycm9yKCJJbnZhbGlkIEpTT046ICIrYil9LG0ucGFyc2VYTUw9ZnVuY3Rpb24oYil7dmFyIGMsZDtpZighYnx8InN0cmluZyIhPXR5cGVvZiBiKXJldHVybiBudWxsO3RyeXthLkRPTVBhcnNlcj8oZD1uZXcgRE9NUGFyc2VyLGM9ZC5wYXJzZUZyb21TdHJpbmcoYiwidGV4dC94bWwiKSk6KGM9bmV3IEFjdGl2ZVhPYmplY3QoIk1pY3Jvc29mdC5YTUxET00iKSxjLmFzeW5jPSJmYWxzZSIsYy5sb2FkWE1MKGIpKX1jYXRjaChlKXtjPXZvaWQgMH1yZXR1cm4gYyYmYy5kb2N1bWVudEVsZW1lbnQmJiFjLmdldEVsZW1lbnRzQnlUYWdOYW1lKCJwYXJzZXJlcnJvciIpLmxlbmd0aHx8bS5lcnJvcigiSW52YWxpZCBYTUw6ICIrYiksY307dmFyIHliLHpiLEFiPS8jLiokLyxCYj0vKFs/Jl0pXz1bXiZdKi8sQ2I9L14oLio/KTpbIFx0XSooW15cclxuXSopXHI/JC9nbSxEYj0vXig/OmFib3V0fGFwcHxhcHAtc3RvcmFnZXwuKy1leHRlbnNpb258ZmlsZXxyZXN8d2lkZ2V0KTokLyxFYj0vXig/OkdFVHxIRUFEKSQvLEZiPS9eXC9cLy8sR2I9L14oW1x3ListXSs6KSg/OlwvXC8oPzpbXlwvPyNdKkB8KShbXlwvPyM6XSopKD86OihcZCspfCl8KS8sSGI9e30sSWI9e30sSmI9IiovIi5jb25jYXQoIioiKTt0cnl7emI9bG9jYXRpb24uaHJlZn1jYXRjaChLYil7emI9eS5jcmVhdGVFbGVtZW50KCJhIiksemIuaHJlZj0iIix6Yj16Yi5ocmVmfXliPUdiLmV4ZWMoemIudG9Mb3dlckNhc2UoKSl8fFtdO2Z1bmN0aW9uIExiKGEpe3JldHVybiBmdW5jdGlvbihiLGMpeyJzdHJpbmciIT10eXBlb2YgYiYmKGM9YixiPSIqIik7dmFyIGQsZT0wLGY9Yi50b0xvd2VyQ2FzZSgpLm1hdGNoKEUpfHxbXTtpZihtLmlzRnVuY3Rpb24oYykpd2hpbGUoZD1mW2UrK10pIisiPT09ZC5jaGFyQXQoMCk/KGQ9ZC5zbGljZSgxKXx8IioiLChhW2RdPWFbZF18fFtdKS51bnNoaWZ0KGMpKTooYVtkXT1hW2RdfHxbXSkucHVzaChjKX19ZnVuY3Rpb24gTWIoYSxiLGMsZCl7dmFyIGU9e30sZj1hPT09SWI7ZnVuY3Rpb24gZyhoKXt2YXIgaTtyZXR1cm4gZVtoXT0hMCxtLmVhY2goYVtoXXx8W10sZnVuY3Rpb24oYSxoKXt2YXIgaj1oKGIsYyxkKTtyZXR1cm4ic3RyaW5nIiE9dHlwZW9mIGp8fGZ8fGVbal0/Zj8hKGk9aik6dm9pZCAwOihiLmRhdGFUeXBlcy51bnNoaWZ0KGopLGcoaiksITEpfSksaX1yZXR1cm4gZyhiLmRhdGFUeXBlc1swXSl8fCFlWyIqIl0mJmcoIioiKX1mdW5jdGlvbiBOYihhLGIpe3ZhciBjLGQsZT1tLmFqYXhTZXR0aW5ncy5mbGF0T3B0aW9uc3x8e307Zm9yKGQgaW4gYil2b2lkIDAhPT1iW2RdJiYoKGVbZF0/YTpjfHwoYz17fSkpW2RdPWJbZF0pO3JldHVybiBjJiZtLmV4dGVuZCghMCxhLGMpLGF9ZnVuY3Rpb24gT2IoYSxiLGMpe3ZhciBkLGUsZixnLGg9YS5jb250ZW50cyxpPWEuZGF0YVR5cGVzO3doaWxlKCIqIj09PWlbMF0paS5zaGlmdCgpLHZvaWQgMD09PWUmJihlPWEubWltZVR5cGV8fGIuZ2V0UmVzcG9uc2VIZWFkZXIoIkNvbnRlbnQtVHlwZSIpKTtpZihlKWZvcihnIGluIGgpaWYoaFtnXSYmaFtnXS50ZXN0KGUpKXtpLnVuc2hpZnQoZyk7YnJlYWt9aWYoaVswXWluIGMpZj1pWzBdO2Vsc2V7Zm9yKGcgaW4gYyl7aWYoIWlbMF18fGEuY29udmVydGVyc1tnKyIgIitpWzBdXSl7Zj1nO2JyZWFrfWR8fChkPWcpfWY9Znx8ZH1yZXR1cm4gZj8oZiE9PWlbMF0mJmkudW5zaGlmdChmKSxjW2ZdKTp2b2lkIDB9ZnVuY3Rpb24gUGIoYSxiLGMsZCl7dmFyIGUsZixnLGgsaSxqPXt9LGs9YS5kYXRhVHlwZXMuc2xpY2UoKTtpZihrWzFdKWZvcihnIGluIGEuY29udmVydGVycylqW2cudG9Mb3dlckNhc2UoKV09YS5jb252ZXJ0ZXJzW2ddO2Y9ay5zaGlmdCgpO3doaWxlKGYpaWYoYS5yZXNwb25zZUZpZWxkc1tmXSYmKGNbYS5yZXNwb25zZUZpZWxkc1tmXV09YiksIWkmJmQmJmEuZGF0YUZpbHRlciYmKGI9YS5kYXRhRmlsdGVyKGIsYS5kYXRhVHlwZSkpLGk9ZixmPWsuc2hpZnQoKSlpZigiKiI9PT1mKWY9aTtlbHNlIGlmKCIqIiE9PWkmJmkhPT1mKXtpZihnPWpbaSsiICIrZl18fGpbIiogIitmXSwhZylmb3IoZSBpbiBqKWlmKGg9ZS5zcGxpdCgiICIpLGhbMV09PT1mJiYoZz1qW2krIiAiK2hbMF1dfHxqWyIqICIraFswXV0pKXtnPT09ITA/Zz1qW2VdOmpbZV0hPT0hMCYmKGY9aFswXSxrLnVuc2hpZnQoaFsxXSkpO2JyZWFrfWlmKGchPT0hMClpZihnJiZhWyJ0aHJvd3MiXSliPWcoYik7ZWxzZSB0cnl7Yj1nKGIpfWNhdGNoKGwpe3JldHVybntzdGF0ZToicGFyc2VyZXJyb3IiLGVycm9yOmc/bDoiTm8gY29udmVyc2lvbiBmcm9tICIraSsiIHRvICIrZn19fXJldHVybntzdGF0ZToic3VjY2VzcyIsZGF0YTpifX1tLmV4dGVuZCh7YWN0aXZlOjAsbGFzdE1vZGlmaWVkOnt9LGV0YWc6e30sYWpheFNldHRpbmdzOnt1cmw6emIsdHlwZToiR0VUIixpc0xvY2FsOkRiLnRlc3QoeWJbMV0pLGdsb2JhbDohMCxwcm9jZXNzRGF0YTohMCxhc3luYzohMCxjb250ZW50VHlwZToiYXBwbGljYXRpb24veC13d3ctZm9ybS11cmxlbmNvZGVkOyBjaGFyc2V0PVVURi04IixhY2NlcHRzOnsiKiI6SmIsdGV4dDoidGV4dC9wbGFpbiIsaHRtbDoidGV4dC9odG1sIix4bWw6ImFwcGxpY2F0aW9uL3htbCwgdGV4dC94bWwiLGpzb246ImFwcGxpY2F0aW9uL2pzb24sIHRleHQvamF2YXNjcmlwdCJ9LGNvbnRlbnRzOnt4bWw6L3htbC8saHRtbDovaHRtbC8sanNvbjovanNvbi99LHJlc3BvbnNlRmllbGRzOnt4bWw6InJlc3BvbnNlWE1MIix0ZXh0OiJyZXNwb25zZVRleHQiLGpzb246InJlc3BvbnNlSlNPTiJ9LGNvbnZlcnRlcnM6eyIqIHRleHQiOlN0cmluZywidGV4dCBodG1sIjohMCwidGV4dCBqc29uIjptLnBhcnNlSlNPTiwidGV4dCB4bWwiOm0ucGFyc2VYTUx9LGZsYXRPcHRpb25zOnt1cmw6ITAsY29udGV4dDohMH19LGFqYXhTZXR1cDpmdW5jdGlvbihhLGIpe3JldHVybiBiP05iKE5iKGEsbS5hamF4U2V0dGluZ3MpLGIpOk5iKG0uYWpheFNldHRpbmdzLGEpfSxhamF4UHJlZmlsdGVyOkxiKEhiKSxhamF4VHJhbnNwb3J0OkxiKEliKSxhamF4OmZ1bmN0aW9uKGEsYil7Im9iamVjdCI9PXR5cGVvZiBhJiYoYj1hLGE9dm9pZCAwKSxiPWJ8fHt9O3ZhciBjLGQsZSxmLGcsaCxpLGosaz1tLmFqYXhTZXR1cCh7fSxiKSxsPWsuY29udGV4dHx8ayxuPWsuY29udGV4dCYmKGwubm9kZVR5cGV8fGwuanF1ZXJ5KT9tKGwpOm0uZXZlbnQsbz1tLkRlZmVycmVkKCkscD1tLkNhbGxiYWNrcygib25jZSBtZW1vcnkiKSxxPWsuc3RhdHVzQ29kZXx8e30scj17fSxzPXt9LHQ9MCx1PSJjYW5jZWxlZCIsdj17cmVhZHlTdGF0ZTowLGdldFJlc3BvbnNlSGVhZGVyOmZ1bmN0aW9uKGEpe3ZhciBiO2lmKDI9PT10KXtpZighail7aj17fTt3aGlsZShiPUNiLmV4ZWMoZikpaltiWzFdLnRvTG93ZXJDYXNlKCldPWJbMl19Yj1qW2EudG9Mb3dlckNhc2UoKV19cmV0dXJuIG51bGw9PWI/bnVsbDpifSxnZXRBbGxSZXNwb25zZUhlYWRlcnM6ZnVuY3Rpb24oKXtyZXR1cm4gMj09PXQ/ZjpudWxsfSxzZXRSZXF1ZXN0SGVhZGVyOmZ1bmN0aW9uKGEsYil7dmFyIGM9YS50b0xvd2VyQ2FzZSgpO3JldHVybiB0fHwoYT1zW2NdPXNbY118fGEsclthXT1iKSx0aGlzfSxvdmVycmlkZU1pbWVUeXBlOmZ1bmN0aW9uKGEpe3JldHVybiB0fHwoay5taW1lVHlwZT1hKSx0aGlzfSxzdGF0dXNDb2RlOmZ1bmN0aW9uKGEpe3ZhciBiO2lmKGEpaWYoMj50KWZvcihiIGluIGEpcVtiXT1bcVtiXSxhW2JdXTtlbHNlIHYuYWx3YXlzKGFbdi5zdGF0dXNdKTtyZXR1cm4gdGhpc30sYWJvcnQ6ZnVuY3Rpb24oYSl7dmFyIGI9YXx8dTtyZXR1cm4gaSYmaS5hYm9ydChiKSx4KDAsYiksdGhpc319O2lmKG8ucHJvbWlzZSh2KS5jb21wbGV0ZT1wLmFkZCx2LnN1Y2Nlc3M9di5kb25lLHYuZXJyb3I9di5mYWlsLGsudXJsPSgoYXx8ay51cmx8fHpiKSsiIikucmVwbGFjZShBYiwiIikucmVwbGFjZShGYix5YlsxXSsiLy8iKSxrLnR5cGU9Yi5tZXRob2R8fGIudHlwZXx8ay5tZXRob2R8fGsudHlwZSxrLmRhdGFUeXBlcz1tLnRyaW0oay5kYXRhVHlwZXx8IioiKS50b0xvd2VyQ2FzZSgpLm1hdGNoKEUpfHxbIiJdLG51bGw9PWsuY3Jvc3NEb21haW4mJihjPUdiLmV4ZWMoay51cmwudG9Mb3dlckNhc2UoKSksay5jcm9zc0RvbWFpbj0hKCFjfHxjWzFdPT09eWJbMV0mJmNbMl09PT15YlsyXSYmKGNbM118fCgiaHR0cDoiPT09Y1sxXT8iODAiOiI0NDMiKSk9PT0oeWJbM118fCgiaHR0cDoiPT09eWJbMV0/IjgwIjoiNDQzIikpKSksay5kYXRhJiZrLnByb2Nlc3NEYXRhJiYic3RyaW5nIiE9dHlwZW9mIGsuZGF0YSYmKGsuZGF0YT1tLnBhcmFtKGsuZGF0YSxrLnRyYWRpdGlvbmFsKSksTWIoSGIsayxiLHYpLDI9PT10KXJldHVybiB2O2g9bS5ldmVudCYmay5nbG9iYWwsaCYmMD09PW0uYWN0aXZlKysmJm0uZXZlbnQudHJpZ2dlcigiYWpheFN0YXJ0Iiksay50eXBlPWsudHlwZS50b1VwcGVyQ2FzZSgpLGsuaGFzQ29udGVudD0hRWIudGVzdChrLnR5cGUpLGU9ay51cmwsay5oYXNDb250ZW50fHwoay5kYXRhJiYoZT1rLnVybCs9KHdiLnRlc3QoZSk/IiYiOiI/Iikray5kYXRhLGRlbGV0ZSBrLmRhdGEpLGsuY2FjaGU9PT0hMSYmKGsudXJsPUJiLnRlc3QoZSk/ZS5yZXBsYWNlKEJiLCIkMV89Iit2YisrKTplKyh3Yi50ZXN0KGUpPyImIjoiPyIpKyJfPSIrdmIrKykpLGsuaWZNb2RpZmllZCYmKG0ubGFzdE1vZGlmaWVkW2VdJiZ2LnNldFJlcXVlc3RIZWFkZXIoIklmLU1vZGlmaWVkLVNpbmNlIixtLmxhc3RNb2RpZmllZFtlXSksbS5ldGFnW2VdJiZ2LnNldFJlcXVlc3RIZWFkZXIoIklmLU5vbmUtTWF0Y2giLG0uZXRhZ1tlXSkpLChrLmRhdGEmJmsuaGFzQ29udGVudCYmay5jb250ZW50VHlwZSE9PSExfHxiLmNvbnRlbnRUeXBlKSYmdi5zZXRSZXF1ZXN0SGVhZGVyKCJDb250ZW50LVR5cGUiLGsuY29udGVudFR5cGUpLHYuc2V0UmVxdWVzdEhlYWRlcigiQWNjZXB0IixrLmRhdGFUeXBlc1swXSYmay5hY2NlcHRzW2suZGF0YVR5cGVzWzBdXT9rLmFjY2VwdHNbay5kYXRhVHlwZXNbMF1dKygiKiIhPT1rLmRhdGFUeXBlc1swXT8iLCAiK0piKyI7IHE9MC4wMSI6IiIpOmsuYWNjZXB0c1siKiJdKTtmb3IoZCBpbiBrLmhlYWRlcnMpdi5zZXRSZXF1ZXN0SGVhZGVyKGQsay5oZWFkZXJzW2RdKTtpZihrLmJlZm9yZVNlbmQmJihrLmJlZm9yZVNlbmQuY2FsbChsLHYsayk9PT0hMXx8Mj09PXQpKXJldHVybiB2LmFib3J0KCk7dT0iYWJvcnQiO2ZvcihkIGlue3N1Y2Nlc3M6MSxlcnJvcjoxLGNvbXBsZXRlOjF9KXZbZF0oa1tkXSk7aWYoaT1NYihJYixrLGIsdikpe3YucmVhZHlTdGF0ZT0xLGgmJm4udHJpZ2dlcigiYWpheFNlbmQiLFt2LGtdKSxrLmFzeW5jJiZrLnRpbWVvdXQ+MCYmKGc9c2V0VGltZW91dChmdW5jdGlvbigpe3YuYWJvcnQoInRpbWVvdXQiKX0say50aW1lb3V0KSk7dHJ5e3Q9MSxpLnNlbmQocix4KX1jYXRjaCh3KXtpZighKDI+dCkpdGhyb3cgdzt4KC0xLHcpfX1lbHNlIHgoLTEsIk5vIFRyYW5zcG9ydCIpO2Z1bmN0aW9uIHgoYSxiLGMsZCl7dmFyIGoscixzLHUsdyx4PWI7MiE9PXQmJih0PTIsZyYmY2xlYXJUaW1lb3V0KGcpLGk9dm9pZCAwLGY9ZHx8IiIsdi5yZWFkeVN0YXRlPWE+MD80OjAsaj1hPj0yMDAmJjMwMD5hfHwzMDQ9PT1hLGMmJih1PU9iKGssdixjKSksdT1QYihrLHUsdixqKSxqPyhrLmlmTW9kaWZpZWQmJih3PXYuZ2V0UmVzcG9uc2VIZWFkZXIoIkxhc3QtTW9kaWZpZWQiKSx3JiYobS5sYXN0TW9kaWZpZWRbZV09dyksdz12LmdldFJlc3BvbnNlSGVhZGVyKCJldGFnIiksdyYmKG0uZXRhZ1tlXT13KSksMjA0PT09YXx8IkhFQUQiPT09ay50eXBlP3g9Im5vY29udGVudCI6MzA0PT09YT94PSJub3Rtb2RpZmllZCI6KHg9dS5zdGF0ZSxyPXUuZGF0YSxzPXUuZXJyb3Isaj0hcykpOihzPXgsKGF8fCF4KSYmKHg9ImVycm9yIiwwPmEmJihhPTApKSksdi5zdGF0dXM9YSx2LnN0YXR1c1RleHQ9KGJ8fHgpKyIiLGo/by5yZXNvbHZlV2l0aChsLFtyLHgsdl0pOm8ucmVqZWN0V2l0aChsLFt2LHgsc10pLHYuc3RhdHVzQ29kZShxKSxxPXZvaWQgMCxoJiZuLnRyaWdnZXIoaj8iYWpheFN1Y2Nlc3MiOiJhamF4RXJyb3IiLFt2LGssaj9yOnNdKSxwLmZpcmVXaXRoKGwsW3YseF0pLGgmJihuLnRyaWdnZXIoImFqYXhDb21wbGV0ZSIsW3Ysa10pLC0tbS5hY3RpdmV8fG0uZXZlbnQudHJpZ2dlcigiYWpheFN0b3AiKSkpfXJldHVybiB2fSxnZXRKU09OOmZ1bmN0aW9uKGEsYixjKXtyZXR1cm4gbS5nZXQoYSxiLGMsImpzb24iKX0sZ2V0U2NyaXB0OmZ1bmN0aW9uKGEsYil7cmV0dXJuIG0uZ2V0KGEsdm9pZCAwLGIsInNjcmlwdCIpfX0pLG0uZWFjaChbImdldCIsInBvc3QiXSxmdW5jdGlvbihhLGIpe21bYl09ZnVuY3Rpb24oYSxjLGQsZSl7cmV0dXJuIG0uaXNGdW5jdGlvbihjKSYmKGU9ZXx8ZCxkPWMsYz12b2lkIDApLG0uYWpheCh7dXJsOmEsdHlwZTpiLGRhdGFUeXBlOmUsZGF0YTpjLHN1Y2Nlc3M6ZH0pfX0pLG0uX2V2YWxVcmw9ZnVuY3Rpb24oYSl7cmV0dXJuIG0uYWpheCh7dXJsOmEsdHlwZToiR0VUIixkYXRhVHlwZToic2NyaXB0Iixhc3luYzohMSxnbG9iYWw6ITEsInRocm93cyI6ITB9KX0sbS5mbi5leHRlbmQoe3dyYXBBbGw6ZnVuY3Rpb24oYSl7aWYobS5pc0Z1bmN0aW9uKGEpKXJldHVybiB0aGlzLmVhY2goZnVuY3Rpb24oYil7bSh0aGlzKS53cmFwQWxsKGEuY2FsbCh0aGlzLGIpKX0pO2lmKHRoaXNbMF0pe3ZhciBiPW0oYSx0aGlzWzBdLm93bmVyRG9jdW1lbnQpLmVxKDApLmNsb25lKCEwKTt0aGlzWzBdLnBhcmVudE5vZGUmJmIuaW5zZXJ0QmVmb3JlKHRoaXNbMF0pLGIubWFwKGZ1bmN0aW9uKCl7dmFyIGE9dGhpczt3aGlsZShhLmZpcnN0Q2hpbGQmJjE9PT1hLmZpcnN0Q2hpbGQubm9kZVR5cGUpYT1hLmZpcnN0Q2hpbGQ7cmV0dXJuIGF9KS5hcHBlbmQodGhpcyl9cmV0dXJuIHRoaXN9LHdyYXBJbm5lcjpmdW5jdGlvbihhKXtyZXR1cm4gdGhpcy5lYWNoKG0uaXNGdW5jdGlvbihhKT9mdW5jdGlvbihiKXttKHRoaXMpLndyYXBJbm5lcihhLmNhbGwodGhpcyxiKSl9OmZ1bmN0aW9uKCl7dmFyIGI9bSh0aGlzKSxjPWIuY29udGVudHMoKTtjLmxlbmd0aD9jLndyYXBBbGwoYSk6Yi5hcHBlbmQoYSl9KX0sd3JhcDpmdW5jdGlvbihhKXt2YXIgYj1tLmlzRnVuY3Rpb24oYSk7cmV0dXJuIHRoaXMuZWFjaChmdW5jdGlvbihjKXttKHRoaXMpLndyYXBBbGwoYj9hLmNhbGwodGhpcyxjKTphKX0pfSx1bndyYXA6ZnVuY3Rpb24oKXtyZXR1cm4gdGhpcy5wYXJlbnQoKS5lYWNoKGZ1bmN0aW9uKCl7bS5ub2RlTmFtZSh0aGlzLCJib2R5Iil8fG0odGhpcykucmVwbGFjZVdpdGgodGhpcy5jaGlsZE5vZGVzKX0pLmVuZCgpfX0pLG0uZXhwci5maWx0ZXJzLmhpZGRlbj1mdW5jdGlvbihhKXtyZXR1cm4gYS5vZmZzZXRXaWR0aDw9MCYmYS5vZmZzZXRIZWlnaHQ8PTB8fCFrLnJlbGlhYmxlSGlkZGVuT2Zmc2V0cygpJiYibm9uZSI9PT0oYS5zdHlsZSYmYS5zdHlsZS5kaXNwbGF5fHxtLmNzcyhhLCJkaXNwbGF5IikpfSxtLmV4cHIuZmlsdGVycy52aXNpYmxlPWZ1bmN0aW9uKGEpe3JldHVybiFtLmV4cHIuZmlsdGVycy5oaWRkZW4oYSl9O3ZhciBRYj0vJTIwL2csUmI9L1xbXF0kLyxTYj0vXHI/XG4vZyxUYj0vXig/OnN1Ym1pdHxidXR0b258aW1hZ2V8cmVzZXR8ZmlsZSkkL2ksVWI9L14oPzppbnB1dHxzZWxlY3R8dGV4dGFyZWF8a2V5Z2VuKS9pO2Z1bmN0aW9uIFZiKGEsYixjLGQpe3ZhciBlO2lmKG0uaXNBcnJheShiKSltLmVhY2goYixmdW5jdGlvbihiLGUpe2N8fFJiLnRlc3QoYSk/ZChhLGUpOlZiKGErIlsiKygib2JqZWN0Ij09dHlwZW9mIGU/YjoiIikrIl0iLGUsYyxkKX0pO2Vsc2UgaWYoY3x8Im9iamVjdCIhPT1tLnR5cGUoYikpZChhLGIpO2Vsc2UgZm9yKGUgaW4gYilWYihhKyJbIitlKyJdIixiW2VdLGMsZCl9bS5wYXJhbT1mdW5jdGlvbihhLGIpe3ZhciBjLGQ9W10sZT1mdW5jdGlvbihhLGIpe2I9bS5pc0Z1bmN0aW9uKGIpP2IoKTpudWxsPT1iPyIiOmIsZFtkLmxlbmd0aF09ZW5jb2RlVVJJQ29tcG9uZW50KGEpKyI9IitlbmNvZGVVUklDb21wb25lbnQoYil9O2lmKHZvaWQgMD09PWImJihiPW0uYWpheFNldHRpbmdzJiZtLmFqYXhTZXR0aW5ncy50cmFkaXRpb25hbCksbS5pc0FycmF5KGEpfHxhLmpxdWVyeSYmIW0uaXNQbGFpbk9iamVjdChhKSltLmVhY2goYSxmdW5jdGlvbigpe2UodGhpcy5uYW1lLHRoaXMudmFsdWUpfSk7ZWxzZSBmb3IoYyBpbiBhKVZiKGMsYVtjXSxiLGUpO3JldHVybiBkLmpvaW4oIiYiKS5yZXBsYWNlKFFiLCIrIil9LG0uZm4uZXh0ZW5kKHtzZXJpYWxpemU6ZnVuY3Rpb24oKXtyZXR1cm4gbS5wYXJhbSh0aGlzLnNlcmlhbGl6ZUFycmF5KCkpfSxzZXJpYWxpemVBcnJheTpmdW5jdGlvbigpe3JldHVybiB0aGlzLm1hcChmdW5jdGlvbigpe3ZhciBhPW0ucHJvcCh0aGlzLCJlbGVtZW50cyIpO3JldHVybiBhP20ubWFrZUFycmF5KGEpOnRoaXN9KS5maWx0ZXIoZnVuY3Rpb24oKXt2YXIgYT10aGlzLnR5cGU7cmV0dXJuIHRoaXMubmFtZSYmIW0odGhpcykuaXMoIjpkaXNhYmxlZCIpJiZVYi50ZXN0KHRoaXMubm9kZU5hbWUpJiYhVGIudGVzdChhKSYmKHRoaXMuY2hlY2tlZHx8IVcudGVzdChhKSl9KS5tYXAoZnVuY3Rpb24oYSxiKXt2YXIgYz1tKHRoaXMpLnZhbCgpO3JldHVybiBudWxsPT1jP251bGw6bS5pc0FycmF5KGMpP20ubWFwKGMsZnVuY3Rpb24oYSl7cmV0dXJue25hbWU6Yi5uYW1lLHZhbHVlOmEucmVwbGFjZShTYiwiXHJcbiIpfX0pOntuYW1lOmIubmFtZSx2YWx1ZTpjLnJlcGxhY2UoU2IsIlxyXG4iKX19KS5nZXQoKX19KSxtLmFqYXhTZXR0aW5ncy54aHI9dm9pZCAwIT09YS5BY3RpdmVYT2JqZWN0P2Z1bmN0aW9uKCl7cmV0dXJuIXRoaXMuaXNMb2NhbCYmL14oZ2V0fHBvc3R8aGVhZHxwdXR8ZGVsZXRlfG9wdGlvbnMpJC9pLnRlc3QodGhpcy50eXBlKSYmWmIoKXx8JGIoKX06WmI7dmFyIFdiPTAsWGI9e30sWWI9bS5hamF4U2V0dGluZ3MueGhyKCk7YS5hdHRhY2hFdmVudCYmYS5hdHRhY2hFdmVudCgib251bmxvYWQiLGZ1bmN0aW9uKCl7Zm9yKHZhciBhIGluIFhiKVhiW2FdKHZvaWQgMCwhMCl9KSxrLmNvcnM9ISFZYiYmIndpdGhDcmVkZW50aWFscyJpbiBZYixZYj1rLmFqYXg9ISFZYixZYiYmbS5hamF4VHJhbnNwb3J0KGZ1bmN0aW9uKGEpe2lmKCFhLmNyb3NzRG9tYWlufHxrLmNvcnMpe3ZhciBiO3JldHVybntzZW5kOmZ1bmN0aW9uKGMsZCl7dmFyIGUsZj1hLnhocigpLGc9KytXYjtpZihmLm9wZW4oYS50eXBlLGEudXJsLGEuYXN5bmMsYS51c2VybmFtZSxhLnBhc3N3b3JkKSxhLnhockZpZWxkcylmb3IoZSBpbiBhLnhockZpZWxkcylmW2VdPWEueGhyRmllbGRzW2VdO2EubWltZVR5cGUmJmYub3ZlcnJpZGVNaW1lVHlwZSYmZi5vdmVycmlkZU1pbWVUeXBlKGEubWltZVR5cGUpLGEuY3Jvc3NEb21haW58fGNbIlgtUmVxdWVzdGVkLVdpdGgiXXx8KGNbIlgtUmVxdWVzdGVkLVdpdGgiXT0iWE1MSHR0cFJlcXVlc3QiKTtmb3IoZSBpbiBjKXZvaWQgMCE9PWNbZV0mJmYuc2V0UmVxdWVzdEhlYWRlcihlLGNbZV0rIiIpO2Yuc2VuZChhLmhhc0NvbnRlbnQmJmEuZGF0YXx8bnVsbCksYj1mdW5jdGlvbihjLGUpe3ZhciBoLGksajtpZihiJiYoZXx8ND09PWYucmVhZHlTdGF0ZSkpaWYoZGVsZXRlIFhiW2ddLGI9dm9pZCAwLGYub25yZWFkeXN0YXRlY2hhbmdlPW0ubm9vcCxlKTQhPT1mLnJlYWR5U3RhdGUmJmYuYWJvcnQoKTtlbHNle2o9e30saD1mLnN0YXR1cywic3RyaW5nIj09dHlwZW9mIGYucmVzcG9uc2VUZXh0JiYoai50ZXh0PWYucmVzcG9uc2VUZXh0KTt0cnl7aT1mLnN0YXR1c1RleHR9Y2F0Y2goayl7aT0iIn1ofHwhYS5pc0xvY2FsfHxhLmNyb3NzRG9tYWluPzEyMjM9PT1oJiYoaD0yMDQpOmg9ai50ZXh0PzIwMDo0MDR9aiYmZChoLGksaixmLmdldEFsbFJlc3BvbnNlSGVhZGVycygpKX0sYS5hc3luYz80PT09Zi5yZWFkeVN0YXRlP3NldFRpbWVvdXQoYik6Zi5vbnJlYWR5c3RhdGVjaGFuZ2U9WGJbZ109YjpiKCl9LGFib3J0OmZ1bmN0aW9uKCl7YiYmYih2b2lkIDAsITApfX19fSk7ZnVuY3Rpb24gWmIoKXt0cnl7cmV0dXJuIG5ldyBhLlhNTEh0dHBSZXF1ZXN0fWNhdGNoKGIpe319ZnVuY3Rpb24gJGIoKXt0cnl7cmV0dXJuIG5ldyBhLkFjdGl2ZVhPYmplY3QoIk1pY3Jvc29mdC5YTUxIVFRQIil9Y2F0Y2goYil7fX1tLmFqYXhTZXR1cCh7YWNjZXB0czp7c2NyaXB0OiJ0ZXh0L2phdmFzY3JpcHQsIGFwcGxpY2F0aW9uL2phdmFzY3JpcHQsIGFwcGxpY2F0aW9uL2VjbWFzY3JpcHQsIGFwcGxpY2F0aW9uL3gtZWNtYXNjcmlwdCJ9LGNvbnRlbnRzOntzY3JpcHQ6Lyg/OmphdmF8ZWNtYSlzY3JpcHQvfSxjb252ZXJ0ZXJzOnsidGV4dCBzY3JpcHQiOmZ1bmN0aW9uKGEpe3JldHVybiBtLmdsb2JhbEV2YWwoYSksYX19fSksbS5hamF4UHJlZmlsdGVyKCJzY3JpcHQiLGZ1bmN0aW9uKGEpe3ZvaWQgMD09PWEuY2FjaGUmJihhLmNhY2hlPSExKSxhLmNyb3NzRG9tYWluJiYoYS50eXBlPSJHRVQiLGEuZ2xvYmFsPSExKX0pLG0uYWpheFRyYW5zcG9ydCgic2NyaXB0IixmdW5jdGlvbihhKXtpZihhLmNyb3NzRG9tYWluKXt2YXIgYixjPXkuaGVhZHx8bSgiaGVhZCIpWzBdfHx5LmRvY3VtZW50RWxlbWVudDtyZXR1cm57c2VuZDpmdW5jdGlvbihkLGUpe2I9eS5jcmVhdGVFbGVtZW50KCJzY3JpcHQiKSxiLmFzeW5jPSEwLGEuc2NyaXB0Q2hhcnNldCYmKGIuY2hhcnNldD1hLnNjcmlwdENoYXJzZXQpLGIuc3JjPWEudXJsLGIub25sb2FkPWIub25yZWFkeXN0YXRlY2hhbmdlPWZ1bmN0aW9uKGEsYyl7KGN8fCFiLnJlYWR5U3RhdGV8fC9sb2FkZWR8Y29tcGxldGUvLnRlc3QoYi5yZWFkeVN0YXRlKSkmJihiLm9ubG9hZD1iLm9ucmVhZHlzdGF0ZWNoYW5nZT1udWxsLGIucGFyZW50Tm9kZSYmYi5wYXJlbnROb2RlLnJlbW92ZUNoaWxkKGIpLGI9bnVsbCxjfHxlKDIwMCwic3VjY2VzcyIpKX0sYy5pbnNlcnRCZWZvcmUoYixjLmZpcnN0Q2hpbGQpfSxhYm9ydDpmdW5jdGlvbigpe2ImJmIub25sb2FkKHZvaWQgMCwhMCl9fX19KTt2YXIgX2I9W10sYWM9Lyg9KVw/KD89JnwkKXxcP1w/LzttLmFqYXhTZXR1cCh7anNvbnA6ImNhbGxiYWNrIixqc29ucENhbGxiYWNrOmZ1bmN0aW9uKCl7dmFyIGE9X2IucG9wKCl8fG0uZXhwYW5kbysiXyIrdmIrKztyZXR1cm4gdGhpc1thXT0hMCxhfX0pLG0uYWpheFByZWZpbHRlcigianNvbiBqc29ucCIsZnVuY3Rpb24oYixjLGQpe3ZhciBlLGYsZyxoPWIuanNvbnAhPT0hMSYmKGFjLnRlc3QoYi51cmwpPyJ1cmwiOiJzdHJpbmciPT10eXBlb2YgYi5kYXRhJiYhKGIuY29udGVudFR5cGV8fCIiKS5pbmRleE9mKCJhcHBsaWNhdGlvbi94LXd3dy1mb3JtLXVybGVuY29kZWQiKSYmYWMudGVzdChiLmRhdGEpJiYiZGF0YSIpO3JldHVybiBofHwianNvbnAiPT09Yi5kYXRhVHlwZXNbMF0/KGU9Yi5qc29ucENhbGxiYWNrPW0uaXNGdW5jdGlvbihiLmpzb25wQ2FsbGJhY2spP2IuanNvbnBDYWxsYmFjaygpOmIuanNvbnBDYWxsYmFjayxoP2JbaF09YltoXS5yZXBsYWNlKGFjLCIkMSIrZSk6Yi5qc29ucCE9PSExJiYoYi51cmwrPSh3Yi50ZXN0KGIudXJsKT8iJiI6Ij8iKStiLmpzb25wKyI9IitlKSxiLmNvbnZlcnRlcnNbInNjcmlwdCBqc29uIl09ZnVuY3Rpb24oKXtyZXR1cm4gZ3x8bS5lcnJvcihlKyIgd2FzIG5vdCBjYWxsZWQiKSxnWzBdfSxiLmRhdGFUeXBlc1swXT0ianNvbiIsZj1hW2VdLGFbZV09ZnVuY3Rpb24oKXtnPWFyZ3VtZW50c30sZC5hbHdheXMoZnVuY3Rpb24oKXthW2VdPWYsYltlXSYmKGIuanNvbnBDYWxsYmFjaz1jLmpzb25wQ2FsbGJhY2ssX2IucHVzaChlKSksZyYmbS5pc0Z1bmN0aW9uKGYpJiZmKGdbMF0pLGc9Zj12b2lkIDB9KSwic2NyaXB0Iik6dm9pZCAwfSksbS5wYXJzZUhUTUw9ZnVuY3Rpb24oYSxiLGMpe2lmKCFhfHwic3RyaW5nIiE9dHlwZW9mIGEpcmV0dXJuIG51bGw7ImJvb2xlYW4iPT10eXBlb2YgYiYmKGM9YixiPSExKSxiPWJ8fHk7dmFyIGQ9dS5leGVjKGEpLGU9IWMmJltdO3JldHVybiBkP1tiLmNyZWF0ZUVsZW1lbnQoZFsxXSldOihkPW0uYnVpbGRGcmFnbWVudChbYV0sYixlKSxlJiZlLmxlbmd0aCYmbShlKS5yZW1vdmUoKSxtLm1lcmdlKFtdLGQuY2hpbGROb2RlcykpfTt2YXIgYmM9bS5mbi5sb2FkO20uZm4ubG9hZD1mdW5jdGlvbihhLGIsYyl7aWYoInN0cmluZyIhPXR5cGVvZiBhJiZiYylyZXR1cm4gYmMuYXBwbHkodGhpcyxhcmd1bWVudHMpO3ZhciBkLGUsZixnPXRoaXMsaD1hLmluZGV4T2YoIiAiKTtyZXR1cm4gaD49MCYmKGQ9bS50cmltKGEuc2xpY2UoaCxhLmxlbmd0aCkpLGE9YS5zbGljZSgwLGgpKSxtLmlzRnVuY3Rpb24oYik/KGM9YixiPXZvaWQgMCk6YiYmIm9iamVjdCI9PXR5cGVvZiBiJiYoZj0iUE9TVCIpLGcubGVuZ3RoPjAmJm0uYWpheCh7dXJsOmEsdHlwZTpmLGRhdGFUeXBlOiJodG1sIixkYXRhOmJ9KS5kb25lKGZ1bmN0aW9uKGEpe2U9YXJndW1lbnRzLGcuaHRtbChkP20oIjxkaXY+IikuYXBwZW5kKG0ucGFyc2VIVE1MKGEpKS5maW5kKGQpOmEpfSkuY29tcGxldGUoYyYmZnVuY3Rpb24oYSxiKXtnLmVhY2goYyxlfHxbYS5yZXNwb25zZVRleHQsYixhXSl9KSx0aGlzfSxtLmVhY2goWyJhamF4U3RhcnQiLCJhamF4U3RvcCIsImFqYXhDb21wbGV0ZSIsImFqYXhFcnJvciIsImFqYXhTdWNjZXNzIiwiYWpheFNlbmQiXSxmdW5jdGlvbihhLGIpe20uZm5bYl09ZnVuY3Rpb24oYSl7cmV0dXJuIHRoaXMub24oYixhKX19KSxtLmV4cHIuZmlsdGVycy5hbmltYXRlZD1mdW5jdGlvbihhKXtyZXR1cm4gbS5ncmVwKG0udGltZXJzLGZ1bmN0aW9uKGIpe3JldHVybiBhPT09Yi5lbGVtfSkubGVuZ3RofTt2YXIgY2M9YS5kb2N1bWVudC5kb2N1bWVudEVsZW1lbnQ7ZnVuY3Rpb24gZGMoYSl7cmV0dXJuIG0uaXNXaW5kb3coYSk/YTo5PT09YS5ub2RlVHlwZT9hLmRlZmF1bHRWaWV3fHxhLnBhcmVudFdpbmRvdzohMX1tLm9mZnNldD17c2V0T2Zmc2V0OmZ1bmN0aW9uKGEsYixjKXt2YXIgZCxlLGYsZyxoLGksaixrPW0uY3NzKGEsInBvc2l0aW9uIiksbD1tKGEpLG49e307InN0YXRpYyI9PT1rJiYoYS5zdHlsZS5wb3NpdGlvbj0icmVsYXRpdmUiKSxoPWwub2Zmc2V0KCksZj1tLmNzcyhhLCJ0b3AiKSxpPW0uY3NzKGEsImxlZnQiKSxqPSgiYWJzb2x1dGUiPT09a3x8ImZpeGVkIj09PWspJiZtLmluQXJyYXkoImF1dG8iLFtmLGldKT4tMSxqPyhkPWwucG9zaXRpb24oKSxnPWQudG9wLGU9ZC5sZWZ0KTooZz1wYXJzZUZsb2F0KGYpfHwwLGU9cGFyc2VGbG9hdChpKXx8MCksbS5pc0Z1bmN0aW9uKGIpJiYoYj1iLmNhbGwoYSxjLGgpKSxudWxsIT1iLnRvcCYmKG4udG9wPWIudG9wLWgudG9wK2cpLG51bGwhPWIubGVmdCYmKG4ubGVmdD1iLmxlZnQtaC5sZWZ0K2UpLCJ1c2luZyJpbiBiP2IudXNpbmcuY2FsbChhLG4pOmwuY3NzKG4pfX0sbS5mbi5leHRlbmQoe29mZnNldDpmdW5jdGlvbihhKXtpZihhcmd1bWVudHMubGVuZ3RoKXJldHVybiB2b2lkIDA9PT1hP3RoaXM6dGhpcy5lYWNoKGZ1bmN0aW9uKGIpe20ub2Zmc2V0LnNldE9mZnNldCh0aGlzLGEsYil9KTt2YXIgYixjLGQ9e3RvcDowLGxlZnQ6MH0sZT10aGlzWzBdLGY9ZSYmZS5vd25lckRvY3VtZW50O2lmKGYpcmV0dXJuIGI9Zi5kb2N1bWVudEVsZW1lbnQsbS5jb250YWlucyhiLGUpPyh0eXBlb2YgZS5nZXRCb3VuZGluZ0NsaWVudFJlY3QhPT1LJiYoZD1lLmdldEJvdW5kaW5nQ2xpZW50UmVjdCgpKSxjPWRjKGYpLHt0b3A6ZC50b3ArKGMucGFnZVlPZmZzZXR8fGIuc2Nyb2xsVG9wKS0oYi5jbGllbnRUb3B8fDApLGxlZnQ6ZC5sZWZ0KyhjLnBhZ2VYT2Zmc2V0fHxiLnNjcm9sbExlZnQpLShiLmNsaWVudExlZnR8fDApfSk6ZH0scG9zaXRpb246ZnVuY3Rpb24oKXtpZih0aGlzWzBdKXt2YXIgYSxiLGM9e3RvcDowLGxlZnQ6MH0sZD10aGlzWzBdO3JldHVybiJmaXhlZCI9PT1tLmNzcyhkLCJwb3NpdGlvbiIpP2I9ZC5nZXRCb3VuZGluZ0NsaWVudFJlY3QoKTooYT10aGlzLm9mZnNldFBhcmVudCgpLGI9dGhpcy5vZmZzZXQoKSxtLm5vZGVOYW1lKGFbMF0sImh0bWwiKXx8KGM9YS5vZmZzZXQoKSksYy50b3ArPW0uY3NzKGFbMF0sImJvcmRlclRvcFdpZHRoIiwhMCksYy5sZWZ0Kz1tLmNzcyhhWzBdLCJib3JkZXJMZWZ0V2lkdGgiLCEwKSkse3RvcDpiLnRvcC1jLnRvcC1tLmNzcyhkLCJtYXJnaW5Ub3AiLCEwKSxsZWZ0OmIubGVmdC1jLmxlZnQtbS5jc3MoZCwibWFyZ2luTGVmdCIsITApfX19LG9mZnNldFBhcmVudDpmdW5jdGlvbigpe3JldHVybiB0aGlzLm1hcChmdW5jdGlvbigpe3ZhciBhPXRoaXMub2Zmc2V0UGFyZW50fHxjYzt3aGlsZShhJiYhbS5ub2RlTmFtZShhLCJodG1sIikmJiJzdGF0aWMiPT09bS5jc3MoYSwicG9zaXRpb24iKSlhPWEub2Zmc2V0UGFyZW50O3JldHVybiBhfHxjY30pfX0pLG0uZWFjaCh7c2Nyb2xsTGVmdDoicGFnZVhPZmZzZXQiLHNjcm9sbFRvcDoicGFnZVlPZmZzZXQifSxmdW5jdGlvbihhLGIpe3ZhciBjPS9ZLy50ZXN0KGIpO20uZm5bYV09ZnVuY3Rpb24oZCl7cmV0dXJuIFYodGhpcyxmdW5jdGlvbihhLGQsZSl7dmFyIGY9ZGMoYSk7cmV0dXJuIHZvaWQgMD09PWU/Zj9iIGluIGY/ZltiXTpmLmRvY3VtZW50LmRvY3VtZW50RWxlbWVudFtkXTphW2RdOnZvaWQoZj9mLnNjcm9sbFRvKGM/bShmKS5zY3JvbGxMZWZ0KCk6ZSxjP2U6bShmKS5zY3JvbGxUb3AoKSk6YVtkXT1lKX0sYSxkLGFyZ3VtZW50cy5sZW5ndGgsbnVsbCl9fSksbS5lYWNoKFsidG9wIiwibGVmdCJdLGZ1bmN0aW9uKGEsYil7bS5jc3NIb29rc1tiXT1MYShrLnBpeGVsUG9zaXRpb24sZnVuY3Rpb24oYSxjKXtyZXR1cm4gYz8oYz1KYShhLGIpLEhhLnRlc3QoYyk/bShhKS5wb3NpdGlvbigpW2JdKyJweCI6Yyk6dm9pZCAwfSl9KSxtLmVhY2goe0hlaWdodDoiaGVpZ2h0IixXaWR0aDoid2lkdGgifSxmdW5jdGlvbihhLGIpe20uZWFjaCh7cGFkZGluZzoiaW5uZXIiK2EsY29udGVudDpiLCIiOiJvdXRlciIrYX0sZnVuY3Rpb24oYyxkKXttLmZuW2RdPWZ1bmN0aW9uKGQsZSl7dmFyIGY9YXJndW1lbnRzLmxlbmd0aCYmKGN8fCJib29sZWFuIiE9dHlwZW9mIGQpLGc9Y3x8KGQ9PT0hMHx8ZT09PSEwPyJtYXJnaW4iOiJib3JkZXIiKTtyZXR1cm4gVih0aGlzLGZ1bmN0aW9uKGIsYyxkKXt2YXIgZTtyZXR1cm4gbS5pc1dpbmRvdyhiKT9iLmRvY3VtZW50LmRvY3VtZW50RWxlbWVudFsiY2xpZW50IithXTo5PT09Yi5ub2RlVHlwZT8oZT1iLmRvY3VtZW50RWxlbWVudCxNYXRoLm1heChiLmJvZHlbInNjcm9sbCIrYV0sZVsic2Nyb2xsIithXSxiLmJvZHlbIm9mZnNldCIrYV0sZVsib2Zmc2V0IithXSxlWyJjbGllbnQiK2FdKSk6dm9pZCAwPT09ZD9tLmNzcyhiLGMsZyk6bS5zdHlsZShiLGMsZCxnKX0sYixmP2Q6dm9pZCAwLGYsbnVsbCl9fSl9KSxtLmZuLnNpemU9ZnVuY3Rpb24oKXtyZXR1cm4gdGhpcy5sZW5ndGh9LG0uZm4uYW5kU2VsZj1tLmZuLmFkZEJhY2ssImZ1bmN0aW9uIj09dHlwZW9mIGRlZmluZSYmZGVmaW5lLmFtZCYmZGVmaW5lKCJqcXVlcnkiLFtdLGZ1bmN0aW9uKCl7cmV0dXJuIG19KTt2YXIgZWM9YS5qUXVlcnksZmM9YS4kO3JldHVybiBtLm5vQ29uZmxpY3Q9ZnVuY3Rpb24oYil7cmV0dXJuIGEuJD09PW0mJihhLiQ9ZmMpLGImJmEualF1ZXJ5PT09bSYmKGEualF1ZXJ5PWVjKSxtfSx0eXBlb2YgYj09PUsmJihhLmpRdWVyeT1hLiQ9bSksbX0pOwo="></script>
<meta name="viewport" content="width=device-width, initial-scale=1" />
<link href="data:text/css,html%7Bfont%2Dfamily%3Asans%2Dserif%3B%2Dwebkit%2Dtext%2Dsize%2Dadjust%3A100%25%3B%2Dms%2Dtext%2Dsize%2Dadjust%3A100%25%7Dbody%7Bmargin%3A0%7Darticle%2Caside%2Cdetails%2Cfigcaption%2Cfigure%2Cfooter%2Cheader%2Chgroup%2Cmain%2Cmenu%2Cnav%2Csection%2Csummary%7Bdisplay%3Ablock%7Daudio%2Ccanvas%2Cprogress%2Cvideo%7Bdisplay%3Ainline%2Dblock%3Bvertical%2Dalign%3Abaseline%7Daudio%3Anot%28%5Bcontrols%5D%29%7Bdisplay%3Anone%3Bheight%3A0%7D%5Bhidden%5D%2Ctemplate%7Bdisplay%3Anone%7Da%7Bbackground%2Dcolor%3Atransparent%7Da%3Aactive%2Ca%3Ahover%7Boutline%3A0%7Dabbr%5Btitle%5D%7Bborder%2Dbottom%3A1px%20dotted%7Db%2Cstrong%7Bfont%2Dweight%3A700%7Ddfn%7Bfont%2Dstyle%3Aitalic%7Dh1%7Bmargin%3A%2E67em%200%3Bfont%2Dsize%3A2em%7Dmark%7Bcolor%3A%23000%3Bbackground%3A%23ff0%7Dsmall%7Bfont%2Dsize%3A80%25%7Dsub%2Csup%7Bposition%3Arelative%3Bfont%2Dsize%3A75%25%3Bline%2Dheight%3A0%3Bvertical%2Dalign%3Abaseline%7Dsup%7Btop%3A%2D%2E5em%7Dsub%7Bbottom%3A%2D%2E25em%7Dimg%7Bborder%3A0%7Dsvg%3Anot%28%3Aroot%29%7Boverflow%3Ahidden%7Dfigure%7Bmargin%3A1em%2040px%7Dhr%7Bheight%3A0%3B%2Dwebkit%2Dbox%2Dsizing%3Acontent%2Dbox%3B%2Dmoz%2Dbox%2Dsizing%3Acontent%2Dbox%3Bbox%2Dsizing%3Acontent%2Dbox%7Dpre%7Boverflow%3Aauto%7Dcode%2Ckbd%2Cpre%2Csamp%7Bfont%2Dfamily%3Amonospace%2Cmonospace%3Bfont%2Dsize%3A1em%7Dbutton%2Cinput%2Coptgroup%2Cselect%2Ctextarea%7Bmargin%3A0%3Bfont%3Ainherit%3Bcolor%3Ainherit%7Dbutton%7Boverflow%3Avisible%7Dbutton%2Cselect%7Btext%2Dtransform%3Anone%7Dbutton%2Chtml%20input%5Btype%3Dbutton%5D%2Cinput%5Btype%3Dreset%5D%2Cinput%5Btype%3Dsubmit%5D%7B%2Dwebkit%2Dappearance%3Abutton%3Bcursor%3Apointer%7Dbutton%5Bdisabled%5D%2Chtml%20input%5Bdisabled%5D%7Bcursor%3Adefault%7Dbutton%3A%3A%2Dmoz%2Dfocus%2Dinner%2Cinput%3A%3A%2Dmoz%2Dfocus%2Dinner%7Bpadding%3A0%3Bborder%3A0%7Dinput%7Bline%2Dheight%3Anormal%7Dinput%5Btype%3Dcheckbox%5D%2Cinput%5Btype%3Dradio%5D%7B%2Dwebkit%2Dbox%2Dsizing%3Aborder%2Dbox%3B%2Dmoz%2Dbox%2Dsizing%3Aborder%2Dbox%3Bbox%2Dsizing%3Aborder%2Dbox%3Bpadding%3A0%7Dinput%5Btype%3Dnumber%5D%3A%3A%2Dwebkit%2Dinner%2Dspin%2Dbutton%2Cinput%5Btype%3Dnumber%5D%3A%3A%2Dwebkit%2Douter%2Dspin%2Dbutton%7Bheight%3Aauto%7Dinput%5Btype%3Dsearch%5D%7B%2Dwebkit%2Dbox%2Dsizing%3Acontent%2Dbox%3B%2Dmoz%2Dbox%2Dsizing%3Acontent%2Dbox%3Bbox%2Dsizing%3Acontent%2Dbox%3B%2Dwebkit%2Dappearance%3Atextfield%7Dinput%5Btype%3Dsearch%5D%3A%3A%2Dwebkit%2Dsearch%2Dcancel%2Dbutton%2Cinput%5Btype%3Dsearch%5D%3A%3A%2Dwebkit%2Dsearch%2Ddecoration%7B%2Dwebkit%2Dappearance%3Anone%7Dfieldset%7Bpadding%3A%2E35em%20%2E625em%20%2E75em%3Bmargin%3A0%202px%3Bborder%3A1px%20solid%20silver%7Dlegend%7Bpadding%3A0%3Bborder%3A0%7Dtextarea%7Boverflow%3Aauto%7Doptgroup%7Bfont%2Dweight%3A700%7Dtable%7Bborder%2Dspacing%3A0%3Bborder%2Dcollapse%3Acollapse%7Dtd%2Cth%7Bpadding%3A0%7D%40media%20print%7B%2A%2C%3Aafter%2C%3Abefore%7Bcolor%3A%23000%21important%3Btext%2Dshadow%3Anone%21important%3Bbackground%3A0%200%21important%3B%2Dwebkit%2Dbox%2Dshadow%3Anone%21important%3Bbox%2Dshadow%3Anone%21important%7Da%2Ca%3Avisited%7Btext%2Ddecoration%3Aunderline%7Da%5Bhref%5D%3Aafter%7Bcontent%3A%22%20%28%22%20attr%28href%29%20%22%29%22%7Dabbr%5Btitle%5D%3Aafter%7Bcontent%3A%22%20%28%22%20attr%28title%29%20%22%29%22%7Da%5Bhref%5E%3D%22javascript%3A%22%5D%3Aafter%2Ca%5Bhref%5E%3D%22%23%22%5D%3Aafter%7Bcontent%3A%22%22%7Dblockquote%2Cpre%7Bborder%3A1px%20solid%20%23999%3Bpage%2Dbreak%2Dinside%3Aavoid%7Dthead%7Bdisplay%3Atable%2Dheader%2Dgroup%7Dimg%2Ctr%7Bpage%2Dbreak%2Dinside%3Aavoid%7Dimg%7Bmax%2Dwidth%3A100%25%21important%7Dh2%2Ch3%2Cp%7Borphans%3A3%3Bwidows%3A3%7Dh2%2Ch3%7Bpage%2Dbreak%2Dafter%3Aavoid%7D%2Enavbar%7Bdisplay%3Anone%7D%2Ebtn%3E%2Ecaret%2C%2Edropup%3E%2Ebtn%3E%2Ecaret%7Bborder%2Dtop%2Dcolor%3A%23000%21important%7D%2Elabel%7Bborder%3A1px%20solid%20%23000%7D%2Etable%7Bborder%2Dcollapse%3Acollapse%21important%7D%2Etable%20td%2C%2Etable%20th%7Bbackground%2Dcolor%3A%23fff%21important%7D%2Etable%2Dbordered%20td%2C%2Etable%2Dbordered%20th%7Bborder%3A1px%20solid%20%23ddd%21important%7D%7D%40font%2Dface%7Bfont%2Dfamily%3A%27Glyphicons%20Halflings%27%3Bsrc%3Aurl%28data%3Aapplication%2Fvnd%2Ems%2Dfontobject%3Bbase64%2Cn04AAEFNAAACAAIABAAAAAAABQAAAAAAAAABAJABAAAEAExQAAAAAAAAAAIAAAAAAAAAAAEAAAAAAAAAJxJ%2FLAAAAAAAAAAAAAAAAAAAAAAAACgARwBMAFkAUABIAEkAQwBPAE4AUwAgAEgAYQBsAGYAbABpAG4AZwBzAAAADgBSAGUAZwB1AGwAYQByAAAAeABWAGUAcgBzAGkAbwBuACAAMQAuADAAMAA5ADsAUABTACAAMAAwADEALgAwADAAOQA7AGgAbwB0AGMAbwBuAHYAIAAxAC4AMAAuADcAMAA7AG0AYQBrAGUAbwB0AGYALgBsAGkAYgAyAC4ANQAuADUAOAAzADIAOQAAADgARwBMAFkAUABIAEkAQwBPAE4AUwAgAEgAYQBsAGYAbABpAG4AZwBzACAAUgBlAGcAdQBsAGEAcgAAAAAAQlNHUAAAAAAAAAAAAAAAAAAAAAADAKncAE0TAE0ZAEbuFM3pjM%2FSEdmjKHUbyow8ATBE40IvWA3vTu8LiABDQ%2BpexwUMcm1SMnNryctQSiI1K5ZnbOlXKmnVV5YvRe6RnNMFNCOs1KNVpn6yZhCJkRtVRNzEufeIq7HgSrcx4S8h%2Fv4vnrrKc6oCNxmSk2uKlZQHBii6iKFoH0746ThvkO1kJHlxjrkxs%2BLWORaDQBEtiYJIR5IB9Bi1UyL4Rmr0BNigNkMzlKQmnofBHviqVzUxwdMb3NdCn69hy%2BpRYVKGVS%2F1tnsqv4LL7wCCPZZAZPT4aCShHjHJVNuXbmMrY5LeQaGnvAkXlVrJgKRAUdFjrWEah9XebPeQMj7KS7DIBAFt8ycgC5PLGUOHSE3ErGZCiViNLL5ZARfywnCoZaKQCu6NuFX42AEeKtKUGnr%2FCm2Cy8tpFhBPMW5Fxi4Qm4TkDWh4IWFDClhU2hRWosUWqcKLlgyXB%2BlSHaWaHiWlBAR8SeSgSPCQxdVQgzUixWKSTrIQEbU94viDctkvX%2BVSjJuUmV8L4CXShI11esnp0pjWNZIyxKHS4wVQ2ime1P4RnhvGw0aDN1OLAXGERsB7buFpFGGBAre4QEQR0HOIO5oYH305G%2BKspT%2FFupEGGafCCwxSe6ZUa%2B073rXHnNdVXE6eWvibUS27XtRzkH838mYLMBmYysZTM0EM3A1fbpCBYFccN1B%2FEnCYu%2FTgCGmr7bMh8GfYL%2BBfcLvB0gRagC09w9elfldaIy%2FhNCBLRgBgtCC7jAF63wLSMAfbfAlEggYU0bUA7ACCJmTDpEmJtI78w4%2FBO7dN7JR7J7ZvbYaUbaILSQsRBiF3HGk5fEg6p9unwLvn98r%2BvnsV%2B372uf1xBLq4qU%2F45fTuqaAP%2BpssmCCCTF0mhEow8ZXZOS8D7Q85JsxZ%2BAzok7B7O%2Ff6J8AzYBySZQB%2FQHYUSA%2BEeQhEWiS6AIQzgcsDiER4MjgMBAWDV4AgQ3g1eBgIdweCQmCjJEMkJ%2BPKRWyFHHmg1Wi%2F6xzUgA0LREoKJChwnQa9B%2B5RQZRB3IlBlkAnxyQNaANwHMowzlYSMCBgnbpzvqpl0iTJNCQidDI9ZrSYNIRBhHtUa5YHMHxyGEik9hDE0AKj72AbTCaxtHPUaKZdAZSnQTyjGqGLsmBStCejApUhg4uBMU6mATujEl%2BKdDPbI6Ag4vLr%2BhjY6lbjBeoLKnZl0UZgRX8gTySOeynZVz1wOq7e1hFGYIq%2BMhrGxDLak0PrwYzSXtcuyhXEhwOYofiW%2BEcI%2Fjw8P6IY6ed%2BetAbuqKp5QIapT77LnAe505lMuqL79a0ut4rWexzFttsOsLDy7zvtQzcq3U1qabe7tB0wHWVXji%2BzDbo8x8HyIRUbXnwUcklFv51fvTymiV%2BMXLSmGH9d9%2BaXpD5X6lao41anWGig7IwIdnoBY2ht%2FpO9mClLo4NdXHAsefqWUKlXJkbqPOFhMoR4aiA1BXqhRNbB2Xwi%2B7u%2FjpAoOpKJ0UX24EsrzMfHXViakCNcKjBxuQX8BO0ZqjJ3xXzf%2B61t2VXOSgJ8xu65QKgtN6FibPmPYsXbJRHHqbgATcSZxBqGiDiU4NNNsYBsKD0MIP%2FOfKnlk%2FLkaid%2FO2NbKeuQrwOB2Gq3YHyr6ALgzym5wIBnsdC1ZkoBFZSQXChZvlesPqvK2c5oHHT3Q65jYpNxnQcGF0EHbvYqoFw60WNlXIHQF2HQB7zD6lWjZ9rVqUKBXUT6hrkZOle0RFYII0V5ZYGl1JAP0Ud1fZZMvSomBzJ710j4Me8mjQDwEre5Uv2wQfk1ifDwb5ksuJQQ3xt423lbuQjvoIQByQrNDh1JxGFkOdlJvu%2FgFtuW0wR4cgd%2BZKesSV7QkNE2kw6AV4hoIuC02LGmTomyf8PiO6CZzOTLTPQ%2BHW06H%2Btx%2BbQ8LmDYg1pTFrp2oJXgkZTyeRJZM0C8aE2LpFrNVDuhARsN543%2FFV6klQ6Tv1OoZGXLv0igKrl%2FCmJxRmX7JJbJ998VSIPQRyDBICzl4JJlYHbdql30NvYcOuZ7a10uWRrgoieOdgIm4rlq6vNOQBuqESLbXG5lzdJGHw2m0sDYmODXbYGTfSTGRKpssTO95fothJCjUGQgEL4yKoGAF%2F0SrpUDNn8CBgBcSDQByAeNkCXp4S4Ro2Xh4OeaGRgR66PVOsU8bc6TR5%2FxTcn4IVMLOkXSWiXxkZQCbvKfmoAvQaKjO3EDKwkwqHChCDEM5loQRPd5ACBki1TjF772oaQhQbQ5C0lcWXPFOzrfsDGUXGrpxasbG4iab6eByaQkQfm0VFlP0ZsDkvvqCL6QXMUwCjdMx1ZOyKhTJ7a1GWAdOUcJ8RSejxNVyGs31OKMyRyBVoZFjqIkmKlLQ5eHMeEL4MkUf23cQ%2F1SgRCJ1dk4UdBT7OoyuNgLs0oCd8RnrEIb6QdMxT2QjD4zMrJkfgx5aDMcA4orsTtKCqWb%2FVeyceqa5OGSmB28YwH4rFbkQaLoUN8OQQYnD3w2eXpI4ScQfbCUZiJ4yMOIKLyyTc7BQ4uXUw6Ee6%2FxM%2B4Y67ngNBknxIPwuppgIhFcwJyr6EIj%2BLzNj%2FmfR2vhhRlx0BILZoAYruF0caWQ7YxO66UmeguDREAFHYuC7HJviRgVO6ruJH59h%2FC%2FPkgSle8xNzZJULLWq9JMDTE2fjGE146a1Us6PZDGYle6ldWRqn%2FpdpgHKNGrGIdkRK%2BKPETT9nKT6kLyDI8xd9A1FgWmXWRAIHwZ37WyZHOVyCadJEmMVz0MadMjDrPho%2BEIochkVC2xgGiwwsQ6DMv2P7UXqT4x7CdcYGId2BJQQa85EQKmCmwcRejQ9Bm4oATENFPkxPXILHpMPUyWTI5rjNOsIlmEeMbcOCEqInpXACYQ9DDxmFo9vcmsDblcMtg4tqBerNngkIKaFJmrQAPnq1dEzsMXcwjcHdfdCibcAxxA%2Bq%2Fj9m3LM%2FO7WJka4tSidVCjsvo2lQ%2F2ewyoYyXwAYyr2PlRoR5MpgVmSUIrM3PQxXPbgjBOaDQFIyFMJvx3Pc5RSYj12ySVF9fwFPQu2e2KWVoL9q3Ayv3IzpGHUdvdPdrNUdicjsTQ2ISy7QU3DrEytIjvbzJnAkmANXjAFERA0MUoPF3%2F5KFmW14bBNOhwircYgMqoDpUMcDtCmBE82QM2YtdjVLB4kBuKho%2FbcwQdeboqfQartuU3CsCf%2BcXkgYAqp%2F0Ee3RorAZt0AvvOCSI4JICIlGlsV0bsSid%2FNIEALAAzb6HAgyWHBps6xAOwkJIGcB82CxRQq4sJf3FzA70A%2BTRqcqjEMETCoez3mkPcpnoALs0ugJY8kQwrC%2BJE5ik3w9rzrvDRjAQnqgEVvdGrNwlanR0SOKWzxOJOvLJhcd8Cl4AshACUkv9czdMkJCVQSQhp6kp7StAlpVRpK0t0SW6LHeBJnE2QchB5Ccu8kxRghZXGIgZIiSj7gEKMJDClcnX6hgoqJMwiQDigIXg3ioFLCgDgjPtYHYpsF5EiA4kcnN18MZtOrY866dEQAb0FB34OGKHGZQjwW%2FWDHA60cYFaI%2FPjpzquUqdaYGcIq%2BmLez3WLFFCtNBN2QJcrlcoELgiPku5R5dSlJFaCEqEZle1AQzAKC%2B1SotMcBNyQUFuRHRF6OlimSBgjZeTBCwLyc6A%2BP%2FoFRchXTz5ADknYJHxzrJ5pGuIKRQISU6WyKTBBjD8WozmVYWIsto1AS5rxzKlvJu4E%2FvwOiKxRtCWsDM%2BeTHUrmwrCK5BIfMzGkD%2B0Fk5LzBs0jMYXktNDblB06LMNJ09U8pzSLmo14MS0OMjcdrZ31pyQqxJJpRImlSvfYAK8inkYU52QY2FPEVsjoWewpwhRp5yAuNpkqhdb7ku9Seefl2D0B8SMTFD90xi4CSOwwZy9IKkpMtI3FmFUg3%2FkFutpQGNc3pCR7gvC4sgwbupDu3DyEN%2BW6YGLNM21jpB49irxy9BSlHrVDlnihGKHwPrbVFtc%2Bh1rVQKZduxIyojccZIIcOCmhEnC7UkY68WXKQgLi2JCDQkQWJRQuk60hZp0D3rtCTINSeY9Ej2kIKYfGxwOs4j9qMM7fYZiipzgcf7TamnehqdhsiMiCawXnz4xAbyCkLAx5EGbo3Ax1u3dUIKnTxIaxwQTHehPl3V491H0%2BbC5zgpGz7Io%2BmjdhKlPJ01EeMpM7UsRJMi1nGjmJg35i6bQBAAxjO%2FENJubU2mg3ONySEoWklCwdABETcs7ck3jgiuU9pcKKpbgn%2B3YlzV1FzIkB6pmEDOSSyDfPPlQskznctFji0kpgZjW5RZe6x9kYT4KJcXg0bNiCyif%2BpZACCyRMmYsfiKmN9tSO65F0R2OO6ytlEhY5Sj6uRKfFxw0ijJaAx%2Fk3QgnAFSq27%2F2i4GEBA%2BUvTJKK%2F9eISNvG46Em5RZfjTYLdeD8kdXHyrwId%2FDQZUaMCY4gGbke2C8vfjgV%2FY9kkRQOJIn%2FxM9INZSpiBnqX0Q9GlQPpPKAyO5y%2BW5NMPSRdBCUlmuxl40ZfMCnf2Cp044uI9WLFtCi4YVxKjuRCOBWIb4XbIsGdbo4qtMQnNOQz4XDSui7W%2FN6l54qOynCqD3DpWQ%2BmpD7C40D8BZEWGJX3tlAaZBMj1yjvDYKwCJBa201u6nBKE5UE%2B7QSEhCwrXfbRZylAaAkplhBWX50dumrElePyNMRYUrC99UmcSSNgImhFhDI4BXjMtiqkgizUGCrZ8iwFxU6fQ8GEHCFdLewwxYWxgScAYMdMLmcZR6b7rZl95eQVDGVoUKcRMM1ixXQtXNkBETZkVVPg8LoSrdetHzkuM7DjZRHP02tCxA1fmkXKF3VzfN1pc1cv%2F8lbTIkkYpqKM9VOhp65ktYk%2BQ46myFWBapDfyWUCnsnI00QTBQmuFjMZTcd0V2NQ768Fhpby04k2IzNR1wKabuGJqYWwSly6ocMFGTeeI%2BejsWDYgEvr66QgqdcIbFYDNgsm0x9UHY6SCd5%2B7tpsLpKdvhahIDyYmEJQCqMqtCF6UlrE5GXRmbu%2Bvtm3BFSxI6ND6UxIE7GsGMgWqghXxSnaRJuGFveTcK5ZVSPJyjUxe1dKgI6kNF7EZhIZs8y8FVqwEfbM0Xk2ltORVDKZZM40SD3qQoQe0orJEKwPfZwm3YPqwixhUMOndis6MhbmfvLBKjC8sKKIZKbJk8L11oNkCQzCgvjhyyEiQSuJcgCQSG4Mocfgc0Hkwcjal1UNgP0CBPikYqBIk9tONv4kLtBswH07vUCjEaHiFGlLf8MgXKzSgjp2HolRRccAOh0ILHz9qlGgIFkwAnzHJRjWFhlA7ROwINyB5HFj59PRZHFor6voq7l23EPNRwdWhgawqbivLSjRA4htEYUFkjESu67icTg5S0aW1sOkCiIysfJ9UnIWevOOLGpepcBxy1wEhd2WI3AZg7sr9WBmHWyasxMcvY%2FiOmsLtHSWNUWEGk9hScMPShasUA1AcHOtRZlqMeQ0OzYS9vQvYUjOLrzP07BUAFikcJNMi7gIxEw4pL1G54TcmmmoAQ5s7TGWErJZ2Io4yQ0ljRYhL8H5e62oDtLF8aDpnIvZ5R3GWJyAugdiiJW9hQAVTsnCBHhwu7rkBlBX6r3b7ejEY0k5GGeyKv66v%2B6dg7mcJTrWHbtMywbedYqCQ0FPwoytmSWsL8WTtChZCKKzEF7vP6De4x2BJkkniMgSdWhbeBSLtJZR9CTHetK1xb34AYIJ37OegYIoPVbXgJ%2FqDQK%2BbfCtxQRVKQu77WzOoM6SGL7MaZwCGJVk46aImai9fmam%2BWpHG%2B0BtQPWUgZ7RIAlPq6lkECUhZQ2gqWkMYKcYMYaIc4gYCDFHYa2d1nzp3%2BJ1eCBay8IYZ0wQRKGAqvCuZ%2FUgbQPyllosq%2BXtfKIZOzmeJqRazpmmoP%2F76YfkjzV2NlXTDSBYB04SVlNQsFTbGPk1t%2FI4Jktu0XSgifO2ozFOiwd%2F0SssJDn0dn4xqk4GDTTKX73%2FwQyBLdqgJ%2BWx6AQaba3BA9CKEzjtQYIfAsiYamapq80LAamYjinlKXUkxdpIDk0puXUEYzSalfRibAeDAKpNiqQ0FTwoxuGYzRnisyTotdVTclis1LHRQCy%2FqqL8oUaQzWRxilq5Mi0IJGtMY02cGLD69vGjkj3p6pGePKI8bkBv5evq8SjjyU04vJR2cQXQwSJyoinDsUJHCQ50jrFTT7yRdbdYQMB3MYCb6uBzJ9ewhXYPAIZSXfeEQBZZ3GPN3Nbhh%2FwkvAJLXnQMdi5NYYZ5GHE400GS5rXkOZSQsdZgIbzRnF9ueLnsfQ47wHAsirITnTlkCcuWWIUhJSbpM3wWhXNHvt2xUsKKMpdBSbJnBMcihkoDqAd1Zml%2FR4yrzow1Q2A5G%2Bkzo%2FRhRxQS2lCSDRV8LlYLBOOoo1bF4jwJAwKMK1tWLHlu9i0j4Ig8qVm6wE1DxXwAwQwsaBWUg2pOOol2dHxyt6npwJEdLDDVYyRc2D0HbcbLUJQj8gPevQBUBOUHXPrsAPBERICpnYESeu2OHotpXQxRGlCCtLdIsu23MhZVEoJg8Qumj%2FUMMc34IBqTKLDTp76WzL%2FdMjCxK7MjhiGjeYAC%2Fkj%2FjY%2FRde7hpSM1xChrog6yZ7OWTuD56xBJnGFE%2BpT2ElSyCnJcwVzCjkqeNLfMEJqKW0G7OFIp0G%2B9mh50I9o8k1tpCY0xYqFNIALgIfc2me4n1bmJnRZ89oepgLPT0NTMLNZsvSCZAc3TXaNB07vail36%2FdBySis4m9%2FDR8izaLJW6bWCkVgm5T%2Bius3ZXq4xI%2BGnbveLbdRwF2mNtsrE0JjYc1AXknCOrLSu7Te%2Fr4dPYMCl5qtiHNTn%2BTPbh1jCBHH%2BdMJNhwNgs3nT%2BOhQoQ0vYif56BMG6WowAcHR3DjQolxLzyVekHj00PBAaW7IIAF1EF%2BuRIWyXjQMAs2chdpaKPNaB%2BkSezYt0%2BCA04sOg5vx8Fr7Ofa9sUv87h7SLAUFSzbetCCZ9pmyLt6l6%2FTzoA1%2FZBG9bIUVHLAbi%2FkdBFgYGyGwRQGBpkqCEg2ah9UD6EedEcEL3j4y0BQQCiExEnocA3SZboh%2Bepgd3YsOkHskZwPuQ5OoyA0fTA5AXrHcUOQF%2BzkJHIA7PwCDk1gGVmGUZSSoPhNf%2BTklauz98QofOlCIQ%2FtCD4dosHYPqtPCXB3agggQQIqQJsSkB%2Bqn0rkQ1toJjON%2FOtCIB9RYv3PqRA4C4U68ZMlZn6BdgEvi2ziU%2BTQ6NIw3ej%2BAtDwMGEZk7e2IjxUWKdAxyaw9OCwSmeADTPPleyk6UhGDNXQb%2B%2BW6Uk4q6F7%2Frg6WVTo82IoCxSIsFDrav4EPHphD3u4hR53WKVvYZUwNCCeM4PMBWzK%2BEfIthZOkuAwPo5C5jgoZgn6dUdvx5rIDmd58cXXdKNfw3l%2BwM2UjgrDJeQHhbD7HW2QDoZMCujgIUkk5Fg8VCsdyjOtnGRx8wgKRPZN5dR0zPUyfGZFVihbFRniXZFOZGKPnEQzU3AnD1KfR6weHW2XS6KbPJxUkOTZsAB9vTVp3Le1F8q5l%2BDMcLiIq78jxAImD2pGFw0VHfRatScGlK6SMu8leTmhUSMy8Uhdd6xBiH3Gdman4tjQGLboJfqz6fL2WKHTmrfsKZRYX6BTDjDldKMosaSTLdQS7oDisJNqAUhw1PfTlnacCO8vl8706Km1FROgLDmudzxg%2BEWTiArtHgLsRrAXYWdB0NmToNCJdKm0KWycZQqb%2BMw76Qy29iQ5up%2FX7oyw8QZ75kP5F6iJAJz6KCmqxz8fEa%2FxnsMYcIO%2FvEkGRuMckhr4rIeLrKaXnmIzlNLxbFspOphkcnJdnz%2FChp%2FVlpj2P7jJQmQRwGnltkTV5dbF9fE3%2FfxoSqTROgq9wFUlbuYzYcasE0ouzBo%2BdDCDzxKAfhbAZYxQiHrLzV2iVexnDX%2FQnT1fsT%2Fxuhu1ui5qIytgbGmRoQkeQooO8eJNNZsf0iALur8QxZFH0nCMnjerYQqG1pIfjyVZWxhVRznmmfLG00BcBWJE6hzQWRyFknuJnXuk8A5FRDCulwrWASSNoBtR%2BCtGdkPwYN2o7DOw%2FVGlCZPusRBFXODQdUM5zeHDIVuAJBLqbO%2Ff9Qua%2BpDqEPk230Sob9lEZ8BHiCorjVghuI0lI4JDgHGRDD%2FprQ84B1pVGkIpVUAHCG%2Biz3Bn3qm2AVrYcYWhock4jso5%2BJ7HfHVj4WMIQdGctq3psBCVVzupQOEioBGA2Bk%2BUILT7%2BVoX5mdxxA5fS42gISQVi%2FHTzrgMxu0fY6hE1ocUwwbsbWcezrY2n6S8%2F6cxXkOH4prpmPuFoikTzY7T85C4T2XYlbxLglSv2uLCgFv8Quk%2FwdesUdWPeHYIH0R729JIisN9Apdd4eB10aqwXrPt%2BSu9mA8k8n1sjMwnfsfF2j3jMUzXepSHmZ%2FBfqXvzgUNQQWOXO8YEuFBh4QTYCkOAPxywpYu1VxiDyJmKVcmJPGWk%2Fgc3Pov02StyYDahwmzw3E1gYC9wkupyWfDqDSUMpCTH5e5N8B%2F%2FlHiMuIkTNw4USHrJU67bjXGqNav6PBuQSoqTxc8avHoGmvqNtXzIaoyMIQIiiUHIM64cXieouplhNYln7qgc4wBVAYR104kO%2BCvKqsg4yIUlFNThVUAKZxZt1XA34h3TCUUiXVkZ0w8Hh2R0Z5L0b4LZvPd%2Fp1gi%2F07h8qfwHrByuSxglc9cI4QIg2oqvC%2Fqm0i7tjPLTgDhoWTAKDO2ONW5oe%2B%2FeKB9vZB8K6C25yCZ9RFVMnb6NRdRjyVK57CHHSkJBfnM2%2Fj4ODUwRkqrtBBCrDsDpt8jhZdXoy%2F1BCqw3sSGhgGGy0a5Jw6BP%2FTExoCmNFYjZl248A0osgPyGEmRA%2BfAsqPVaNAfytu0vuQJ7rk3J4kTDTR2AlCHJ5cls26opZM4w3jMULh2YXKpcqGBtuleAlOZnaZGbD6DHzMd6i2oFeJ8z9XYmalg1Szd%2FocZDc1C7Y6vcALJz2lYnTXiWEr2wawtoR4g3jvWUU2Ngjd1cewtFzEvM1NiHZPeLlIXFbBPawxNgMwwAlyNSuGF3zizVeOoC9bag1qRAQKQE%2FEZBWC2J8mnXAN2aTBboZ7HewnObE8CwROudZHmUM5oZ%2FUgd%2FJZQK8lvAm43uDRAbyW8gZ%2BZGq0EVerVGUKUSm%2FIdn8AQHdR4m7bue88WBwft9mSCeMOt1ncBwziOmJYI2ZR7ewNMPiCugmSsE4EyQ%2BQATJG6qORMGd4snEzc6B4shPIo4G1T7PgSm8PY5eUkPdF8JZ0VBtadbHXoJgnEhZQaODPj2gpODKJY5Yp4DOsLBFxWbvXN755KWylJm%2BoOd4zEL9Hpubuy2gyyfxh8oEfFutnYWdfB8PdESLWYvSqbElP9qo3u6KTmkhoacDauMNNjj0oy40DFV7Ql0aZj77xfGl7TJNHnIwgqOkenruYYNo6h724%2BzUQ7%2BvkCpZB%2BpGA562hYQiDxHVWOq0oDQl%2FQsoiY%2BcuI7iWq%2FZIBtHcXJ7kks%2Bh2fCNUPA82BzjnqktNts%2BRLdk1VSu%2BtqEn7QZCCsvEqk6FkfiOYkrsw092J8jsfIuEKypNjLxrKA9kiA19mxBD2suxQKCzwXGws7kEJvlhUiV9tArLIdZW0IORcxEzdzKmjtFhsjKy%2F44XYXdI5noQoRcvjZ1RMPACRqYg2V1%2BOwOepcOknRLLFdYgTkT5UApt%2FJhLM3jeFYprZV%2BZow2g8fP%2BU68hkKFWJj2yBbKqsrp25xkZX1DAjUw52IMYWaOhab8Kp05VrdNftqwRrymWF4OQSjbdfzmRZirK8FMJELEgER2PHjEAN9pGfLhCUiTJFbd5LBkOBMaxLr%2FA1SY9dXFz4RjzoU9ExfJCmx%2FI9FKEGT3n2cmzl2X42L3Jh%2BAbQq6sA%2BSs1kitoa4TAYgKHaoybHUDJ51oETdeI%2F9ThSmjWGkyLi5QAGWhL0BG1UsTyRGRJOldKBrYJeB8ljLJHfATWTEQBXBDnQexOHTB%2BUn44zExFE4vLytcu5NwpWrUxO%2F0ZICUGM7hGABXym0V6ZvDST0E370St9MIWQOTWngeoQHUTdCJUP04spMBMS8LSker9cReVQkULFDIZDFPrhTzBl6sed9wcZQTbL%2BBDqMyaN3RJPh%2Fanbx%2BIv%2BqgQdAa3M9Z5JmvYlh4qop%2BHo1F1W5gbOE9YKLgAnWytXElU4G8GtW47lhgFE6gaSs%2Bgs37sFvi0PPVvA5dnCBgILTwoKd%2F%2BDoL9F6inlM7H4rOTzD79KJgKlZO%2FZgt22UsKhrAaXU5ZcLrAglTVKJEmNJvORGN1vqrcfSMizfpsgbIe9zno%2BgBoKVXgIL%2FVI8dB1O5o%2FR3Suez%2FgD7M781ShjKpIIORM%2FnxG%2BjjhhgPwsn2IoXsPGPqYHXA63zJ07M2GPEykQwJBYLK808qYxuIew4frk52nhCsnCYmXiR6CuapvE1IwRB4%2FQftDbEn%2BAucIr1oxrLabRj9q4ae0%2BfXkHnteAJwXRbVkR0mctVSwEbqhJiMSZUp9DNbEDMmjX22m3ABpkrPQQTP3S1sib5pD2VRKRd%2BeNAjLYyT0hGrdjWJZy24OYXRoWQAIhGBZRxuBFMjjZQhpgrWo8SiFYbojcHO8V5DyscJpLTHyx9Fimassyo5U6WNtquUMYgccaHY5amgR3PQzq3ToNM5ABnoB9kuxsebqmYZm0R9qxJbFXCQ1UPyFIbxoUraTJFDpCk0Wk9GaYJKz%2F6oHwEP0Q14lMtlddQsOAU9zlYdMVHiT7RQP3XCmWYDcHCGbVRHGnHuwzScA0BaSBOGkz3lM8CArjrBsyEoV6Ys4qgDK3ykQQPZ3hCRGNXQTNNXbEb6tDiTDLKOyMzRhCFT%2BmAUmiYbV3YQVqFVp9dorv%2BTsLeCykS2b5yyu8AV7IS9cxcL8z4Kfwp%2BxJyYLv1OsxQCZwTB4a8BZ%2F5EdxTBJthApqyfd9u3ifr%2FWILTqq5VqgwMT9SOxbSGWLQJUUWCVi4k9tho9nEsbUh7U6NUsLmkYFXOhZ0kmamaJLRNJzSj%2Fqn4Mso6zb6iLLBXoaZ6AqeWCjHQm2lztnejYYM2eubnpBdKVLORZhudH3JF1waBJKA9%2BW8EhMj3Kzf0L4vi4k6RoHh3Z5YgmSZmk6ns4fjScjAoL8GoOECgqgYEBYUGFVO4FUv4%2FYtowhEmTs0vrvlD%2FCrisnoBNDAcUi%2FteY7OctFlmARQzjOItrrlKuPO6E2Ox93L4O%2F4DcgV%2FdZ7qR3VBwVQxP1GCieA4RIpweYJ5FoYrHxqRBdJjnqbsikA2Ictbb8vE1GYIo9dacK0REgDX4smy6GAkxlH1yCGGsk%2BtgiDhNKuKu3yNrMdxafmKTF632F8Vx4BNK57GvlFisrkjN9WDAtjsWA0ENT2e2nETUb%2Fn7qwhvGnrHuf5bX6Vh%2Fn3xffU3PeHdR%2BFA92i6ufT3AlyAREoNDh6chiMWTvjKjHDeRhOa9YkOQRq1vQXEMppAQVwHCuIcV2g5rBn6GmZZpTR7vnSD6ZmhdSl176gqKTXu5E%2BYbfL0adwNtHP7dT7t7b46DVZIkzaRJOM%2BS6KcrzYVg%2BT3wSRFRQashjfU18NutrKa%2F7PXbtuJvpIjbgPeqd%2BpjmRw6YKpnANFSQcpzTZgpSNJ6J7uiagAbir%2F8tNXJ%2FOsOnRh6iuIexxrmkIneAgz8QoLmiaJ8sLQrELVK2yn3wOHp57BAZJhDZjTBzyoRAuuZ4eoxHruY1pSb7qq79cIeAdOwin4GdgMeIMHeG%2BFZWYaiUQQyC5b50zKjYw97dFjAeY2I4Bnl105Iku1y0lMA1ZHolLx19uZnRdILcXKlZGQx%2FGdEqSsMRU1BIrFqRcV1qQOOHyxOLXEGcbRtAEsuAC2V4K3p5mFJ22IDWaEkk9ttf5Izb2LkD1MnrSwztXmmD%2FQi%2FEmVEFBfiKGmftsPwVaIoZanlKndMZsIBOskFYpDOq3QUs9aSbAAtL5Dbokus2G4%2FasthNMK5UQKCOhU97oaOYNGsTah%2BjfCKsZnTRn5TbhFX8ghg8CBYt%2FBjeYYYUrtUZ5jVij%2Fop7V5SsbA4mYTOwZ46hqdpbB6Qvq3AS2HHNkC15pTDIcDNGsMPXaBidXYPHc6PJAkRh29Vx8KcgX46LoUQBhRM%2B3SW6Opll%2FwgxxsPgKJKzr5QCmwkUxNbeg6Wj34SUnEzOemSuvS2OetRCO8Tyy%2BQbSKVJcqkia%2BGvDefFwMOmgnD7h81TUtMn%2BmRpyJJ349HhAnoWFTejhpYTL9G8N2nVg1qkXBeoS9Nw2fB27t7trm7d%2FQK7Cr4uoCeOQ7%2F8JfKT77KiDzLImESHw%2F0wf73QeHu74hxv7uihi4fTX%2BXEwAyQG3264dwv17aJ5N335Vt9sdrAXhPOAv8JFvzqyYXwfx8WYJaef1gMl98JRFyl5Mv5Uo%2FoVH5ww5OzLFsiTPDns7fS6EURSSWd%2F92BxMYQ8sBaH%2Bj%2BwthQPdVgDGpTfi%2BJQIWMD8xKqULliRH01rTeyF8x8q%2FGBEEEBrAJMPf25UQwi0b8tmqRXY7kIvNkzrkvRWLnxoGYEJsz8u4oOyMp8cHyaybb1HdMCaLApUE%2B%2F7xLIZGP6H9xuSEXp1zLIdjk5nBaMuV%2FyTDRRP8Y2ww5RO6d2D94o%2B6ucWIqUAvgHIHXhZsmDhjVLczmZ3ca0Cb3PpKwt2UtHVQ0BgFJsqqTsnzZPlKahRUkEu4qmkJt%2Bkqdae76ViWe3STan69yaF9%2BfESD2lcQshLHWVu4ovItXxO69bqC5p1nZLvI8NdQB9s9UNaJGlQ5mG947ipdDA0eTIw%2FA1zEdjWquIsQXXGIVEH0thC5M%2BW9pZe7IhAVnPJkYCCXN5a32HjN6nsvokEqRS44tGIs7s2LVTvcrHAF%2BRVmI8L4HUYk4x%2B67AxSMJKqCg8zrGOgvK9kNMdDrNiUtSWuHFpC8%2Fp5qIQrEo%2FH%2B1l%2F0cAwQ2nKmpWxKcMIuHY44Y6DlkpO48tRuUGBWT0FyHwSKO72Ud%2BtJUfdaZ4CWNijzZtlRa8%2BCkmO%2FEwHYfPZFU%2FhzjFWH7vnzHRMo%2BaF9u8qHSAiEkA2HjoNQPEwHsDKOt6hOoK3Ce%2F%2B%2F9boMWDa44I6FrQhdgS7OnNaSzwxWKZMcyHi6LN4WC6sSj0qm2PSOGBTvDs%2FGWJS6SwEN%2FULwpb4LQo9fYjUfSXRwZkynUazlSpvX9e%2BG2zor8l%2BYaMxSEomDdLHGcD6YVQPegTaA74H8%2BV4WvJkFUrjMLGLlvSZQWvi8%2FQA7yzQ8GPno%2F%2F5SJHRP%2FOqKObPCo81s%2F%2B6WgLqykYpGAgQZhVDEBPXWgU%2FWzFZjKUhSFInufPRiMAUULC6T11yL45ZrRoB4DzOyJShKXaAJIBS9wzLYIoCEcJKQW8GVCx4fihqJ6mshBUXSw3wWVj3grrHQlGNGhIDNNzsxQ3M%2BGWn6ASobIWC%2BLbYOC6UpahVO13Zs2zOzZC8z7FmA05JhUGyBsF4tsG0drcggIFzgg%2Fkpf3%2BCnAXKiMgIE8Jk%2FMhpkc8DUJEUzDSnWlQFme3d0sHZDrg7LavtsEX3cHwjCYA17pMTfx8Ajw9hHscN67hyo%2BRJQ4458RmPywXykkVcW688oVUrQhahpPRvTWPnuI0B%2BSkQu7dCyvLRyFYlC1LG1gRCIvn3rwQeINzZQC2KXq31FaR9UmVV2QeGVqBHjmE%2BVMd3b1fhCynD0pQNhCG6%2FWCDbKPyE7NRQzL3BzQAJ0g09aUzcQA6mUp9iZFK6Sbp%2FYbHjo%2B%2B7%2FWj8S4YNa%2BZdqAw1hDrKWFXv9%2BzaXpf8ZTDSbiqsxnwN%2FCzK5tPkOr4tRh2kY3Bn9JtalbIOI4b3F7F1vPQMfoDcdxMS8CW9m%2FNCW%2FHILTUVWQIPiD0j1A6bo8vsv6P1hCESl2abrSJWDrq5sSzUpwoxaCU9FtJyYH4QFMxDBpkkBR6kn0LMPO%2B5EJ7Z6bCiRoPedRZ%2FP0SSdii7ZnPAtVwwHUidcdyspwncz5uq6vvm4IEDbJVLUFCn%2FLvIHfooUBTkFO130FC7CmmcrKdgDJcid9mvVzsDSibOoXtIf9k6ABle3PmIxejodc4aob0QKS432srrCMndbfD454q52V01G4q913mC5HOsTzWF4h2No1av1VbcUgWAqyoZl%2B11PoFYnNv2HwAODeNRkHj%2B8SF1fcvVBu6MrehHAZK1Gm69ICcTKizykHgGFx7QdowTVAsYEF2tVc0Z6wLryz2FI1sc5By2znJAAmINndoJiB4sfPdPrTC8RnkW7KRCwxC6YvXg5ahMlQuMpoCSXjOlBy0Kij%2BbsCYPbGp8BdCBiLmLSAkEQRaieWo1SYvZIKJGj9Ur%2FeWHjiB7SOVdqMAVmpBvfRiebsFjger7DC%2B8kRFGtNrTrnnGD2GAJb8rQCWkUPYHhwXsjNBSkE6lGWUj5QNhK0DMNM2l%2BkXRZ0KLZaGsFSIdQz%2FHXDxf3%2FTE30%2BDgBKWGWdxElyLccJfEpjsnszECNoDGZpdwdRgCixeg9L4EPhH%2BRptvRMVRaahu4cySjS3P5wxAUCPkmn%2BrhyASpmiTaiDeggaIxYBmtLZDDhiWIJaBgzfCsAGUF1Q1SFZYyXDt9skCaxJsxK2Ms65dmdp5WAZyxik%2FzbrTQk5KmgxCg%2Ff45L0jywebOWUYFJQAJia7XzCV0x89rpp%2Ff3AVWhSPyTanqmik2SkD8A3Ml4NhIGLAjBXtPShwKYfi2eXtrDuKLk4QlSyTw1ftXgwqA2jUuopDl%2B5tfUWZNwBpEPXghzbBggYCw%2Fdhy0ntds2yeHCDKkF%2FYxQjNIL%2FF%2F37jLPHCKBO9ibwYCmuxImIo0ijV2Wbg3kSN2psoe8IsABv3RNFaF9uMyCtCYtqcD%2BqNOhwMlfARQUdJ2tUX%2BMNJqOwIciWalZsmEjt07tfa8ma4cji9sqz%2BQ9hWfmMoKEbIHPOQORbhQRHIsrTYlnVTNvcq1imqmmPDdVDkJgRcTgB8Sb6epCQVmFZe%2BjGDiNJQLWnfx%2BdrTKYjm0G8yH0ZAGMWzEJhUEQ4Maimgf%2Fbkvo8PLVBsZl152y5S8%2BHRDfZIMCbYZ1WDp4yrdchOJw8k6R%2B%2F2pHmydK4NIK2PHdFPHtoLmHxRDwLFb7eB%2BM4zNZcB9NrAgjVyzLM7xyYSY13ykWfIEEd2n5%2FiYp3ZdrCf7fL%2Ben%2BsIJu2W7E30MrAgZBD1rAAbZHPgeAMtKCg3NpSpYQUDWJu9bT3V7tOKv%2BNRiJc8JAKqqgCA%2FPNRBR7ChpiEulyQApMK1AyqcWnpSOmYh6yLiWkGJ2mklCSPIqN7UypWj3dGi5MvsHQ87MrB4VFgypJaFriaHivwcHIpmyi5LhNqtem4q0n8awM19Qk8BOS0EsqGscuuydYsIGsbT5GHnERUiMpKJl4ON7qjB4fEqlGN%2FhCky89232UQCiaeWpDYCJINXjT6xl4Gc7DxRCtgV0i1ma4RgWLsNtnEBRQFqZggCLiuyEydmFd7WlogpkCw5G1x4ft2psm3KAREwVwr1Gzl6RT7FDAqpVal34ewVm3VH4qn5mjGj%2BbYL1NgfLNeXDwtmYSpwzbruDKpTjOdgiIHDVQSb5%2FzBgSMbHLkxWWgghIh9QTFSDILixVwg0Eg1puooBiHAt7DzwJ7m8i8%2Fi%2BjHvKf0QDnnHVkVTIqMvIQImOrzCJwhSR7qYB5gSwL6aWL9hERHCZc4G2%2BJrpgHNB8eCCmcIWIQ6rSdyPCyftXkDlErUkHafHRlkOIjxGbAktz75bnh50dU7YHk%2BMz7wwstg6RFZb%2BTZuSOx1qqP5C66c0mptQmzIC2dlpte7vZrauAMm%2F7RfBYkGtXWGiaWTtwvAQiq2oD4YixPLXE2khB2FRaNRDTk%2B9sZ6K74Ia9VntCpN4BhJGJMT4Z5c5FhSepRCRWmBXqx%2BwhVZC4me4saDs2iNqXMuCl6iAZflH8fscC1sTsy4PHeC%2BXYuqMBMUun5YezKbRKmEPwuK%2BCLzijPEQgfhahQswBBLfg%2FGBgBiI4QwAqzJkkyYAWtjzSg2ILgMAgqxYfwERRo3zruBL9WOryUArSD8sQOcD7fvIODJxKFS615KFPsb68USBEPPj1orNzFY2xoTtNBVTyzBhPbhFH0PI5AtlJBl2aSgNPYzxYLw7XTDBDinmVoENwiGzmngrMo8OmnRP0Z0i0Zrln9DDFcnmOoBZjABaQIbPOJYZGqX%2BRCMlDDbElcjaROLDoualmUIQ88Kekk3iM4OQrADcxi3rJguS4MOIBIgKgXrjd1WkbCdqxJk%2F4efRIFsavZA7KvvJQqp3Iid5Z0NFc5aiMRzGN3vrpBzaMy4JYde3wr96PjN90AYOIbyp6T4zj8LoE66OGcX1Ef4Z3KoWLAUF4BTg7ug%2FAbkG5UNQXAMkQezujSHeir2uTThgd3gpyzDrbnEdDRH2W7U6PeRvBX1ZFMP5RM%2BZu6UUZZD8hDPHldVWntTCNk7To8IeOW9yn2wx0gmurwqC60AOde4r3ETi5pVMSDK8wxhoGAoEX9NLWHIR33VbrbMveii2jAJlrxwytTHbWNu8Y4N8vCCyZjAX%2FpcsfwXbLze2%2BD%2Bu33OGBoJyAAL3jn3RuEcdp5If8O%2Ba4NKWvxOTyDltG0IWoHhwVGe7dKkCWFT%2B%2Btm%2BhaBCikRUUMrMhYKZJKYoVuv%2FbsJzO8DwfVIInQq3g3BYypiz8baogH3r3GwqCwFtZnz4xMjAVOYnyOi5HWbFA8n0qz1OjSpHWFzpQOpvkNETZBGpxN8ybhtqV%2FDMUxd9uFZmBfKXMCn%2FSqkWJyKPnT6lq%2B4zBZni6fYRByJn6OK%2BOgPBGRAJluwGSk4wxjOOzyce%2FPKODwRlsgrVkdcsEiYrqYdXo0Er2GXi2GQZd0tNJT6c9pK1EEJG1zgDJBoTVuCXGAU8BKTvCO%2FcEQ1Wjk3Zzuy90JX4m3O5IlxVFhYkSUwuQB2up7jhvkm%2BbddRQu5F9s0XftGEJ9JSuSk%2BZachCbdU45fEqbugzTIUokwoAKvpUQF%2FCvLbWW5BNQFqFkJg2f30E%2F48StNe5QwBg8zz3YAJ82FZoXBxXSv4QDooDo79NixyglO9AembuBcx5Re3CwOKTHebOPhkmFC7wNaWtoBhFuV4AkEuJ0J%2B1pT0tLkvFVZaNzfhs%2FKd3%2BA9YsImlO4XK4vpCo%2FelHQi%2F9gkFg07xxnuXLt21unCIpDV%2BbbRxb7FC6nWYTsMFF8%2B1LUg4JFjVt3vqbuhHmDKbgQ4e%2BRGizRiO8ky05LQGMdL2IKLSNar0kNG7lHJMaXr5mLdG3nykgj6vB%2FKVijd1ARWkFEf3yiUw1v%2FWaQivVUpIDdSNrrKbjO5NPnxz6qTTGgYg03HgPhDrCFyYZTi3XQw3HXCva39mpLNFtz8AiEhxAJHpWX13gCTAwgm9YTvMeiqetdNQv6IU0hH0G%2BZManTqDLPjyrOse7WiiwOJCG%2BJ0pZYULhN8NILulmYYvmVcV2MjAfA39sGKqGdjpiPo86fecg65UPyXDIAOyOkCx5NQsLeD4gGVjTVDwOHWkbbBW0GeNjDkcSOn2Nq4cEssP54t9D749A7M1AIOBl0Fi0sSO5v3P7LCBrM6ZwFY6kp2FX6AcbGUdybnfChHPyu6WlRZ2Fwv9YM0RMI7kISRgR8HpQSJJOyTfXj%2F6gQKuihPtiUtlCQVPohUgzfezTg8o1b3n9pNZeco1QucaoXe40Fa5JYhqdTspFmxGtW9h5ezLFZs3j%2FN46f%2BS2rjYNC2JySXrnSAFhvAkz9a5L3pza8eYKHNoPrvBRESpxYPJdKVUxBE39nJ1chrAFpy4MMkf0qKgYALctGg1DQI1kIymyeS2AJNT4X240d3IFQb%2F0jQbaHJ2YRK8A%2Bls6WMhWmpCXYG5jqapGs5%2FeOJErxi2%2F2KWVHiPellTgh%2FfNl%2F2KYPKb7DUcAg%2BmCOPQFCiU9Mq%2FWLcU1xxC8aLePFZZlE%2BPCLzf7ey46INWRw2kcXySR9FDgByXzfxiNKwDFbUSMMhALPFSedyjEVM5442GZ4hTrsAEvZxIieSHGSgkwFh%2FnFNdrrFD4tBH4Il7fW6ur4J8Xaz7RW9jgtuPEXQsYk7gcMs2neu3zJwTyUerHKSh1iTBkj2YJh1SSOZL5pLuQbFFAvyO4k1Hxg2h99MTC6cTUkbONQIAnEfGsGkNFWRbuRyyaEZInM5pij73EA9rPIUfU4XoqQpHT9THZkW%2BoKFLvpyvTBMM69tN1Ydwv1LIEhHsC%2BueVG%2Bw%2BkyCPsvV3erRikcscHjZCkccx6VrBkBRusTDDd8847GA7p2Ucy0y0HdSRN6YIBciYa4vuXcAZbQAuSEmzw%2BH%2FAuOx%2BaH%2BtBL88H57D0MsqyiZxhOEQkF%2F8DR1d2hSPMj%2FsNOa5rxcUnBgH8ictv2J%2Bcb4BA4v3MCShdZ2vtK30vAwkobnEWh7rsSyhmos3WC93Gn9C4nnAd%2FPjMMtQfyDNZsOPd6XcAsnBE%2FmRHtHEyJMzJfZFLE9OvQa0i9kUmToJ0ZxknTgdl%2FXPV8xoh0K7wNHHsnBdvFH3sv52lU7UFteseLG%2FVanIvcwycVA7%2BBE1Ulyb20BvwUWZcMTKhaCcmY3ROpvonVMV4N7yBXTL7IDtHzQ4CCcqF66LjF3xUqgErKzolLyCG6Kb7irP%2FMVTCCwGRxfrPGpMMGvPLgJ881PHMNMIO09T5ig7AzZTX%2F5PLlwnJLDAPfuHynSGhV4tPqR3gJ4kg4c06c%2FF1AcjGytKm2Yb5jwMotF7vro4YDLWlnMIpmPg36NgAZsGA0W1spfLSue4xxat0Gdwd0lqDBOgIaMANykwwDKejt5YaNtJYIkrSgu0KjIg0pznY0SCd1qlC6R19g97UrWDoYJGlrvCE05J%2F5wkjpkre727p5PTRX5FGrSBIfJqhJE%2FIS876PaHFkx9pGTH3oaY3jJRvLX9Iy3Edoar7cFvJqyUlOhAEiOSAyYgVEGkzHdug%2BoRHIEOXAExMiTSKU9A6nmRC8mp8iYhwWdP2U%2F5EkFAdPrZw03YA3gSyNUtMZeh7dDCu8pF5x0VORCTgKp07ehy7NZqKTpIC4UJJ89lnboyAfy5OyXzXtuDRbtAFjZRSyGFTpFrXwkpjSLIQIG3N0Vj4BtzK3wdlkBJrO18MNsgseR4BysJilI0wI6ZahLhBFA0XBmV8d4LUzEcNVb0xbLjLTETYN8OEVqNxkt10W614dd1FlFFVTIgB7%2FBQQp1sWlNolpIu4ekxUTBV7NmxOFKEBmmN%2BnA7pvF78%2FRII5ZHA09OAiE%2F66MF6HQ%2BqVEJCHxwymukkNvzqHEh52dULPbVasfQMgTDyBZzx4007YiKdBuUauQOt27Gmy8ISclPmEUCIcuLbkb1mzQSqIa3iE0PJh7UMYQbkpe%2BhXjTJKdldyt2mVPwywoODGJtBV1lJTgMsuSQBlDMwhEKIfrvsxGQjHPCEfNfMAY2oxvyKcKPUbQySkKG6tj9AQyEW3Q5rpaDJ5Sns9ScLKeizPRbvWYAw4bXkrZdmB7CQopCH8NAmqbuciZChHN8lVGaDbCnmddnqO1PQ4ieMYfcSiBE5zzMz%2BJV%2F4eyzrzTEShvqSGzgWimkNxLvUj86iAwcZuIkqdB0VaIB7wncLRmzHkiUQpPBIXbDDLHBlq7vp9xwuC9AiNkIptAYlG7Biyuk8ILdynuUM1cHWJgeB%2BK3wBP%2FineogxkvBNNQ4AkW0hvpBOQGFfeptF2YTR75MexYDUy7Q%2F9uocGsx41O4IZhViw%2F2FvAEuGO5g2kyXBUijAggWM08bRhXg5ijgMwDJy40QeY%2FcQpUDZiIzmvskQpO5G1zyGZA8WByjIQU4jRoFJt56behxtHUUE%2Fom7Rj2psYXGmq3llVOCgGYKNMo4pzwntITtapDqjvQtqpjaJwjHmDzSVGLxMt12gEXAdLi%2FcaHSM3FPRGRf7dB7YC%2BcD2ho6oL2zGDCkjlf%2FDFoQVl8GS%2F56wur3rdV6ggtzZW60MRB3g%2BU1W8o8cvqIpMkctiGVMzXUFI7FacFLrgtdz4mTEr4aRAaQ2AFQaNeG7GX0yOJgMRYFziXdJf24kg%2FgBQIZMG%2FYcPEllRTVNoDYR6oSJ8wQNLuihfw81UpiKPm714bZX1KYjcXJdfclCUOOpvTxr9AAJevTY4HK%2FG7F3mUc3GOAKqh60zM0v34v%2BELyhJZqhkaMA8UMMOU90f8RKEJFj7EqepBVwsRiLbwMo1J2zrE2UYJnsgIAscDmjPjnzI8a719Wxp757wqmSJBjXowhc46QN4RwKIxqEE6E5218OeK7RfcpGjWG1jD7qND%2B%2FGTk6M56Ig4yMsU6LUW1EWE%2BfIYycVV1thldSlbP6ltdC01y3KUfkobkt2q01YYMmxpKRvh1Z48uNKzP%2FIoRIZ%2FF6buOymSnW8gICitpJjKWBscSb9JJKaWkvEkqinAJ2kowKoqkqZftRqfRQlLtKoqvTRDi2vg%2FRrPD%2Fd3a09J8JhGZlEkOM6znTsoMCsuvTmywxTCDhw5dd0GJOHCMPbsj3QLkTE3MInsZsimDQ3HkvthT7U9VA4s6G07sID0FW4SHJmRGwCl%2BMu4xf0ezqeXD2PtPDnwMPo86sbwDV%2B9PWcgFcARUVYm3hrFQrHcgMElFGbSM2A1zUYA3baWfheJp2AINmTJLuoyYD%2FOwA4a6V0ChBN97E8YtDBerUECv0u0TlxR5yhJCXvJxgyM73Bb6pyq0jTFJDZ4p1Am1SA6sh8nADd1hAcGBMfq4d%2FUfwnmBqe0Jun1n1LzrgKuZMAnxA3NtCN7Klf4BH%2B14B7ibBmgt0TGUafVzI4uKlpF7v8NmgNjg90D6QE3tbx8AjSAC%2BOA1YJvclyPKgT27QpIEgVYpbPYGBsnyCNrGz9XUsCHkW1QAHgL2STZk12QGqmvAB0NFteERkvBIH7INDsNW9KKaAYyDMdBEMzJiWaJHZALqDxQDWRntumSDPcplyFiI1oDpT8wbwe01AHhW6%2BvAUUBoGhY3CT2tgwehdPqU%2F4Q7ZLYvhRl%2FogOvR9O2%2BwkkPKW5vCTjD2fHRYXONCoIl4Jh1bZY0ZE1O94mMGn%2FdFSWBWzQ%2FVYk%2BGezi46RgiDv3EshoTmMSlioUK6MQEN8qeyK6FRninyX8ZPeUWjjbMJChn0n%2FyJvrq5bh5UcCAcBYSafTFg7p0jDgrXo2QWLb3WpSOET%2FHh4oSadBTvyDo10IufLzxiMLAnbZ1vcUmj3w7BQuIXjEZXifwukVxrGa9j%2BDXfpi12m1RbzYLg9J2wFergEwOxFyD0%2FJstNK06ZN2XdZSGWxcJODpQHOq4iKqjqkJUmPu1VczL5xTGUfCgLEYyNBCCbMBFT%2FcUP6pE%2FmujnHsSDeWxMbhrNilS5MyYR0nJyzanWXBeVcEQrRIhQeJA6Xt4f2eQESNeLwmC10WJVHqwx8SSyrtAAjpGjidcj1E2FYN0LObUcFQhafUKTiGmHWRHGsFCB%2BHEXgrzJEB5bp0QiF8ZHh11nFX8AboTD0PS4O1LqF8XBks2MpjsQnwKHF6HgaKCVLJtcr0XjqFMRGfKv8tmmykhLRzu%2BvqQ02%2BKpJBjaLt9ye1Ab%2BBbEBhy4EVdIJDrL2naV0o4wU8YZ2Lq04FG1mWCKC%2BUwkXOoAjneU%2FxHplMQo2cXUlrVNqJYczgYlaOEczVCs%2FOCgkyvLmTmdaBJc1iBLuKwmr6qtRnhowngsDxhzKFAi02tf8bmET8BO27ovJKF1plJwm3b0JpMh38%2BxsrXXg7U74QUM8ZCIMOpXujHntKdaRtsgyEZl5MClMVMMMZkZLNxH9%2Bb8fH6%2Bb8Lev30A9TuEVj9CqAdmwAAHBPbfOBFEATAPZ2CS0OH1Pj%2F0Q7PFUcC8hDrxESWdfgFRm%2B7vvWbkEppHB4T%2F1ApWnlTIqQwjcPl0VgS1yHSmD0OdsCVST8CQVwuiew1Y%2Bg3QGFjNMzwRB2DSsAk26cmA8lp2wIU4p93AUBiUHFGOxOajAqD7Gm6NezNDjYzwLOaSXRBYcWipTSONHjUDXCY4mMI8XoVCR%2FRrs%2FJLKXgEx%2BqkmeDlFOD1%2FyTQNDClRuiUyKYCllfMiQiyFkmuTz2vLsBNyRW%2Bxz%2B5FElFxWB28VjYIGZ0Yd%2B5wIjkcoMaggxswbT0pCmckRAErbRlIlcOGdBo4djTNO8FAgQ%2BlT6vPS60BwTRSUAM3ddkEAZiwtEyArrkiDRnS7LJ%2B2hwbzd2YDQagSgACpsovmjil5wfPuXq3GuH0CyE7FK3M4FgRaFoIkaodORrPx1%2BJpI9psyNYIFuJogZa0%2F1AhOWdlHQxdAgbwacsHqPZo8u%2FngAH2GmaTdhYnBfSDbBfh8CHq6Bx5bttP2%2BRdM%2BMAaYaZ0Y%2FADkbNCZuAyAVQa2OcXOeICmDn9Q%2FeFkDeFQg5MgHEDXq%2FtVjj%2Bjtd26nhaaolWxs1ixSUgOBwrDhRIGOLyOVk2%2FBc0UxvseQCO2pQ2i%2BKrfhu%2FWeBovNb5dJxQtJRUDv2mCwYVpNl2efQM9xQHnK0JwLYt%2FU0Wf%2BphiA4uw8G91slC832pmOTCAoZXohg1fewCZqLBhkOUBofBWpMPsqg7XEXgPfAlDo2U5WXjtFdS87PIqClCK5nW6adCeXPkUiTGx0emOIDQqw1yFYGHEVx20xKjJVYe0O8iLmnQr3FA9nSIQilUKtJ4ZAdcTm7%2BExseJauyqo30hs%2B1qSW211A1SFAOUgDlCGq7eTIcMAeyZkV1SQJ4j%2Fe1Smbq4HcjqgFbLAGLyKxlMDMgZavK5NAYH19Olz3la%2FQCTiVelFnU6O%2FGCvykqS%2FwZJDhKN9gBtSOp%2F1SP5VRgJcoVj%2Bkmf2wBgv4gjrgARBWiURYx8xENV3bEVUAAWWD3dYDKAIWk5opaCFCMR5ZjJExiCAw7gYiSZ2rkyTce4eNMY3lfGn%2B8p6%2BvBckGlKEXnA6Eota69OxDO9oOsJoy28BXOR0UoXNRaJD5ceKdlWMJlOFzDdZNpc05tkMGQtqeNF2lttZqNco1VtwXgRstLSQ6tSPChgqtGV5h2DcDReIQadaNRR6AsAYKL5gSFsCJMgfsaZ7DpKh8mg8Wz8V7H%2BgDnLuMxaWEIUPevIbClgap4dqmVWSrPgVYCzAoZHIa5z2Ocx1D%2FGvDOEqMOKLrMefWIbSWHZ6jbgA8qVBhYNHpx0P%2BjAgN5TB3haSifDcApp6yymEi6Ij%2FGsEpDYUgcHATJUYDUAmC1SCkJ4cuZXSAP2DEpQsGUjQmKJfJOvlC2x%2FpChkOyLW7KEoMYc5FDC4v2FGqSoRWiLsbPCiyg1U5yiHZVm1XLkHMMZL11%2Fyxyw0UnGig3MFdZklN5FI%2FqiT65T%2BjOXOdO7XbgWurOAZR6Cv9uu1cm5LjkXX4xi6mWn5r5NjBS0gTliHhMZI2WNqSiSphEtiCAwnafS11JhseDGHYQ5%2BbqWiAYiAv6Jsf79%2FVUs4cIl%2Bn6%2BWOjcgB%2F2l5TreoAV2717JzZbQIR0W1cl%2FdEqCy5kJ3ZSIHuU0vBoHooEpiHeQWVkkkOqRX27eD1FWw4BfO9CJDdKoSogQi3hAAwsPRFrN5RbX7bqLdBJ9JYMohWrgJKHSjVl1sy2xAG0E3sNyO0oCbSGOxCNBRRXTXenYKuwAoDLfnDcQaCwehUOIDiHAu5m5hMpKeKM4sIo3vxACakIxKoH2YWF2QM84e6F5C5hJU4g8uxuFOlAYnqtwxmHyNEawLW%2FPhoawJDrGAP0JYWHgAVUByo%2FbGdiv2T2EMg8gsS14%2FrAdzlOYazFE7w4OzxeKiWdm3nSOnQRRKXSlVo8HEAbBfyJMKqoq%2BSCcTSx5NDtbFwNlh8VhjGGDu7JG5%2FTAGAvniQSSUog0pNzTim8Owc6QTuSKSTXlQqwV3eiEnklS3LeSXYPXGK2VgeZBqNcHG6tZHvA3vTINhV0ELuQdp3t1y9%2BogD8Kk%2FW7QoRN1UWPqM4%2BxdygkFDPLoTaumKReKiLWoPHOfY54m3qPx4c%2B4pgY3MRKKbljG8w4wvz8pxk3AqKsy4GMAkAtmRjRMsCxbb4Q2Ds0Ia9ci8cMT6DmsJG00XaHCIS%2Bo3F8YVVeikw13w%2BOEDaCYYhC0ZE54kA4jpjruBr5STWeqQG6M74HHL6TZ3lXrd99ZX%2B%2B7LhNatQaZosuxEf5yRA15S9gPeHskBIq3Gcw81AGb9%2FO53DYi%2F5CsQ51EmEh8Rkg4vOciClpy4d04eYsfr6fyQkBmtD%2BP8sNh6e%2BXYHJXT%2FlkXxT4KXU5F2sGxYyzfniMMQkb9OjDN2C8tRRgTyL7GwozH14PrEUZc6oz05Emne3Ts5EG7WolDmU8OB1LDG3VrpQxp%2BpT0KYV5dGtknU64JhabdqcVQbGZiAxQAnvN1u70y1AnmvOSPgLI6uB4AuDGhmAu3ATkJSw7OtS%2F2ToPjqkaq62%2F7WFG8advGlRRqxB9diP07JrXowKR9tpRa%2BjGJ91zxNTT1h8I2PcSfoUPtd7NejVoH03EUcqSBuFZPkMZhegHyo2ZAITovmm3zAIdGFWxoNNORiMRShgwdYwFzkPw5PA4a5MIIQpmq%2Bnsp3YMuXt%2FGkXxLx%2FP6%2BZJS0lFyz4MunC3eWSGE8xlCQrKvhKUPXr0hjpAN9ZK4PfEDrPMfMbGNWcHDzjA7ngMxTPnT7GMHar%2BgMQQ3NwHCv4zH4BIMYvzsdiERi6gebRmerTsVwZJTRsL8dkZgxgRxmpbgRcud%2BYlCIRpPwHShlUSwuipZnx9QCsEWziVazdDeKSYU5CF7UVPAhLer3CgJOQXl%2Fzh575R5rsrmRnKAzq4POFdgbYBuEviM4%2BLVC15ssLNFghbTtHWerS1hDt5s4qkLUha%2FqpZXhWh1C6lTQAqCNQnaDjS7UGFBC6wTu8yFnKJnExCnAs3Ok9yj5KpfZESQ4lTy5pTGTnkAUpxI%2ByjEldJfSo4y0QhG4i4IwkRFGcjWY8%2BEzgYYJUK7BXQksLxAww%2FYYWBMhJILB9e8ePEJ4OP7z%2B4%2FwOQDl64iOYDp26DaONPxpKtBxq%2FaTzRGarm3VkPYTLJKx6Z%2FMw2YbBGseJhPMwhhNswrIkyvV2BYzrvZbxLpKwcWJhYmFtVZ%2BlPEq91FzVp1HlQY1bZVLqeNR9SAUn6n0E28k%2FUuGkNpP1DBI5ch%2FEehZfjUQ9aE41NhETExoPT2gGQz0IhWJbEOvTQ4wgcXCHHFBhewYUiFHuhRSAUVmEHeCRQHQkXGFwkAgyzREJCVN7TRnTon36Zw3tPhx4EALwNdwDv%2BJ41YSP4B2CQqz0EFgARZ4ESgBHQgROwAVn9GTI%2BHYexTUevLUeta4%2FDqKrbMVS%2BYqb8hUwYCrlgKtmAq1YCrFgKrd4qpXiqZcKn1oqdWipjYKpWwVPVYqW6xUpVipKqFR3QKjagVEtAqHpxUMTitsnFaJOKx2cVhswq35RVpyiq9lFVNIKnOQVMkgqtYxVNxiqQjFS7GKlSIVIsQqPIhUWwioigFQ%2B%2BKkN8VHr49HDw9Ebo9EDo9DTo9Crg9BDg9%2FWx7gWx7YWwlobYrOGxWPNisAaAHEyALpkAVDIAeWAArsABVXACYuAD5cAF6wAKFQAQqgAbVAAsoAAlQAUaYAfkwAvogBWQACOgAD9AAHSAAKT4GUdMiOvFngBTwCn2AZ7Dv6B6k%2F90B8%2ByRnkV144AIBoAMTQATGgAjNAA4YABgwABZgB%2FmQCwyAVlwCguASlwCEuAQFwB4uAMlwBYuAJlQAUVAAhUD2KgdpUDaJgaRMDFJgX5MC1JgWJEAokQCWRAHxEAWkQBMRADpEAMkQAYROAEecC484DRpwBDTnwNOdw05tjTmiNOYwtswhYFwLA7BYG4LA2BYGOLAwRYFuLAsxYFQJAohIEyJAMwkAwiQC0JAJgkAeiQBkJAFokAPCQA0JABwcD4Dgc4cDdDgaYcDIDgYgUC6CgWgUClCgUYUAVBQBOFAEYMALgwAgDA9QYAdIn8AZzeBB2L5EcWrenUT1KXienEsuJJ7x5U8XlTjc1NVzUyXFTGb1LlpUtWlTDIjqwE4LsagowoCi2gJLKAkpoBgJQNpAIhNqaEoneI6kiiqQ6Go%2Fn6j0cS%2Ba2gEU8gIHJ%2BBwfgZX4GL%2BBd%2FgW34FZ%2BBS%2FgUH4FN6BTegTvoEv6BJegRnYEF2A79gOvYDl2BdEjCkqkGtwXp0LNToIskOTXzh%2FF062yJ7AAAAEDAWAAABWhJ%2BKPEIJgBFxMVP7w2QJBGHASQnOBKXKFIdUK4igKA9IEaYJg%29%3Bsrc%3Aurl%28data%3Aapplication%2Fvnd%2Ems%2Dfontobject%3Bbase64%2Cn04AAEFNAAACAAIABAAAAAAABQAAAAAAAAABAJABAAAEAExQAAAAAAAAAAIAAAAAAAAAAAEAAAAAAAAAJxJ%2FLAAAAAAAAAAAAAAAAAAAAAAAACgARwBMAFkAUABIAEkAQwBPAE4AUwAgAEgAYQBsAGYAbABpAG4AZwBzAAAADgBSAGUAZwB1AGwAYQByAAAAeABWAGUAcgBzAGkAbwBuACAAMQAuADAAMAA5ADsAUABTACAAMAAwADEALgAwADAAOQA7AGgAbwB0AGMAbwBuAHYAIAAxAC4AMAAuADcAMAA7AG0AYQBrAGUAbwB0AGYALgBsAGkAYgAyAC4ANQAuADUAOAAzADIAOQAAADgARwBMAFkAUABIAEkAQwBPAE4AUwAgAEgAYQBsAGYAbABpAG4AZwBzACAAUgBlAGcAdQBsAGEAcgAAAAAAQlNHUAAAAAAAAAAAAAAAAAAAAAADAKncAE0TAE0ZAEbuFM3pjM%2FSEdmjKHUbyow8ATBE40IvWA3vTu8LiABDQ%2BpexwUMcm1SMnNryctQSiI1K5ZnbOlXKmnVV5YvRe6RnNMFNCOs1KNVpn6yZhCJkRtVRNzEufeIq7HgSrcx4S8h%2Fv4vnrrKc6oCNxmSk2uKlZQHBii6iKFoH0746ThvkO1kJHlxjrkxs%2BLWORaDQBEtiYJIR5IB9Bi1UyL4Rmr0BNigNkMzlKQmnofBHviqVzUxwdMb3NdCn69hy%2BpRYVKGVS%2F1tnsqv4LL7wCCPZZAZPT4aCShHjHJVNuXbmMrY5LeQaGnvAkXlVrJgKRAUdFjrWEah9XebPeQMj7KS7DIBAFt8ycgC5PLGUOHSE3ErGZCiViNLL5ZARfywnCoZaKQCu6NuFX42AEeKtKUGnr%2FCm2Cy8tpFhBPMW5Fxi4Qm4TkDWh4IWFDClhU2hRWosUWqcKLlgyXB%2BlSHaWaHiWlBAR8SeSgSPCQxdVQgzUixWKSTrIQEbU94viDctkvX%2BVSjJuUmV8L4CXShI11esnp0pjWNZIyxKHS4wVQ2ime1P4RnhvGw0aDN1OLAXGERsB7buFpFGGBAre4QEQR0HOIO5oYH305G%2BKspT%2FFupEGGafCCwxSe6ZUa%2B073rXHnNdVXE6eWvibUS27XtRzkH838mYLMBmYysZTM0EM3A1fbpCBYFccN1B%2FEnCYu%2FTgCGmr7bMh8GfYL%2BBfcLvB0gRagC09w9elfldaIy%2FhNCBLRgBgtCC7jAF63wLSMAfbfAlEggYU0bUA7ACCJmTDpEmJtI78w4%2FBO7dN7JR7J7ZvbYaUbaILSQsRBiF3HGk5fEg6p9unwLvn98r%2BvnsV%2B372uf1xBLq4qU%2F45fTuqaAP%2BpssmCCCTF0mhEow8ZXZOS8D7Q85JsxZ%2BAzok7B7O%2Ff6J8AzYBySZQB%2FQHYUSA%2BEeQhEWiS6AIQzgcsDiER4MjgMBAWDV4AgQ3g1eBgIdweCQmCjJEMkJ%2BPKRWyFHHmg1Wi%2F6xzUgA0LREoKJChwnQa9B%2B5RQZRB3IlBlkAnxyQNaANwHMowzlYSMCBgnbpzvqpl0iTJNCQidDI9ZrSYNIRBhHtUa5YHMHxyGEik9hDE0AKj72AbTCaxtHPUaKZdAZSnQTyjGqGLsmBStCejApUhg4uBMU6mATujEl%2BKdDPbI6Ag4vLr%2BhjY6lbjBeoLKnZl0UZgRX8gTySOeynZVz1wOq7e1hFGYIq%2BMhrGxDLak0PrwYzSXtcuyhXEhwOYofiW%2BEcI%2Fjw8P6IY6ed%2BetAbuqKp5QIapT77LnAe505lMuqL79a0ut4rWexzFttsOsLDy7zvtQzcq3U1qabe7tB0wHWVXji%2BzDbo8x8HyIRUbXnwUcklFv51fvTymiV%2BMXLSmGH9d9%2BaXpD5X6lao41anWGig7IwIdnoBY2ht%2FpO9mClLo4NdXHAsefqWUKlXJkbqPOFhMoR4aiA1BXqhRNbB2Xwi%2B7u%2FjpAoOpKJ0UX24EsrzMfHXViakCNcKjBxuQX8BO0ZqjJ3xXzf%2B61t2VXOSgJ8xu65QKgtN6FibPmPYsXbJRHHqbgATcSZxBqGiDiU4NNNsYBsKD0MIP%2FOfKnlk%2FLkaid%2FO2NbKeuQrwOB2Gq3YHyr6ALgzym5wIBnsdC1ZkoBFZSQXChZvlesPqvK2c5oHHT3Q65jYpNxnQcGF0EHbvYqoFw60WNlXIHQF2HQB7zD6lWjZ9rVqUKBXUT6hrkZOle0RFYII0V5ZYGl1JAP0Ud1fZZMvSomBzJ710j4Me8mjQDwEre5Uv2wQfk1ifDwb5ksuJQQ3xt423lbuQjvoIQByQrNDh1JxGFkOdlJvu%2FgFtuW0wR4cgd%2BZKesSV7QkNE2kw6AV4hoIuC02LGmTomyf8PiO6CZzOTLTPQ%2BHW06H%2Btx%2BbQ8LmDYg1pTFrp2oJXgkZTyeRJZM0C8aE2LpFrNVDuhARsN543%2FFV6klQ6Tv1OoZGXLv0igKrl%2FCmJxRmX7JJbJ998VSIPQRyDBICzl4JJlYHbdql30NvYcOuZ7a10uWRrgoieOdgIm4rlq6vNOQBuqESLbXG5lzdJGHw2m0sDYmODXbYGTfSTGRKpssTO95fothJCjUGQgEL4yKoGAF%2F0SrpUDNn8CBgBcSDQByAeNkCXp4S4Ro2Xh4OeaGRgR66PVOsU8bc6TR5%2FxTcn4IVMLOkXSWiXxkZQCbvKfmoAvQaKjO3EDKwkwqHChCDEM5loQRPd5ACBki1TjF772oaQhQbQ5C0lcWXPFOzrfsDGUXGrpxasbG4iab6eByaQkQfm0VFlP0ZsDkvvqCL6QXMUwCjdMx1ZOyKhTJ7a1GWAdOUcJ8RSejxNVyGs31OKMyRyBVoZFjqIkmKlLQ5eHMeEL4MkUf23cQ%2F1SgRCJ1dk4UdBT7OoyuNgLs0oCd8RnrEIb6QdMxT2QjD4zMrJkfgx5aDMcA4orsTtKCqWb%2FVeyceqa5OGSmB28YwH4rFbkQaLoUN8OQQYnD3w2eXpI4ScQfbCUZiJ4yMOIKLyyTc7BQ4uXUw6Ee6%2FxM%2B4Y67ngNBknxIPwuppgIhFcwJyr6EIj%2BLzNj%2FmfR2vhhRlx0BILZoAYruF0caWQ7YxO66UmeguDREAFHYuC7HJviRgVO6ruJH59h%2FC%2FPkgSle8xNzZJULLWq9JMDTE2fjGE146a1Us6PZDGYle6ldWRqn%2FpdpgHKNGrGIdkRK%2BKPETT9nKT6kLyDI8xd9A1FgWmXWRAIHwZ37WyZHOVyCadJEmMVz0MadMjDrPho%2BEIochkVC2xgGiwwsQ6DMv2P7UXqT4x7CdcYGId2BJQQa85EQKmCmwcRejQ9Bm4oATENFPkxPXILHpMPUyWTI5rjNOsIlmEeMbcOCEqInpXACYQ9DDxmFo9vcmsDblcMtg4tqBerNngkIKaFJmrQAPnq1dEzsMXcwjcHdfdCibcAxxA%2Bq%2Fj9m3LM%2FO7WJka4tSidVCjsvo2lQ%2F2ewyoYyXwAYyr2PlRoR5MpgVmSUIrM3PQxXPbgjBOaDQFIyFMJvx3Pc5RSYj12ySVF9fwFPQu2e2KWVoL9q3Ayv3IzpGHUdvdPdrNUdicjsTQ2ISy7QU3DrEytIjvbzJnAkmANXjAFERA0MUoPF3%2F5KFmW14bBNOhwircYgMqoDpUMcDtCmBE82QM2YtdjVLB4kBuKho%2FbcwQdeboqfQartuU3CsCf%2BcXkgYAqp%2F0Ee3RorAZt0AvvOCSI4JICIlGlsV0bsSid%2FNIEALAAzb6HAgyWHBps6xAOwkJIGcB82CxRQq4sJf3FzA70A%2BTRqcqjEMETCoez3mkPcpnoALs0ugJY8kQwrC%2BJE5ik3w9rzrvDRjAQnqgEVvdGrNwlanR0SOKWzxOJOvLJhcd8Cl4AshACUkv9czdMkJCVQSQhp6kp7StAlpVRpK0t0SW6LHeBJnE2QchB5Ccu8kxRghZXGIgZIiSj7gEKMJDClcnX6hgoqJMwiQDigIXg3ioFLCgDgjPtYHYpsF5EiA4kcnN18MZtOrY866dEQAb0FB34OGKHGZQjwW%2FWDHA60cYFaI%2FPjpzquUqdaYGcIq%2BmLez3WLFFCtNBN2QJcrlcoELgiPku5R5dSlJFaCEqEZle1AQzAKC%2B1SotMcBNyQUFuRHRF6OlimSBgjZeTBCwLyc6A%2BP%2FoFRchXTz5ADknYJHxzrJ5pGuIKRQISU6WyKTBBjD8WozmVYWIsto1AS5rxzKlvJu4E%2FvwOiKxRtCWsDM%2BeTHUrmwrCK5BIfMzGkD%2B0Fk5LzBs0jMYXktNDblB06LMNJ09U8pzSLmo14MS0OMjcdrZ31pyQqxJJpRImlSvfYAK8inkYU52QY2FPEVsjoWewpwhRp5yAuNpkqhdb7ku9Seefl2D0B8SMTFD90xi4CSOwwZy9IKkpMtI3FmFUg3%2FkFutpQGNc3pCR7gvC4sgwbupDu3DyEN%2BW6YGLNM21jpB49irxy9BSlHrVDlnihGKHwPrbVFtc%2Bh1rVQKZduxIyojccZIIcOCmhEnC7UkY68WXKQgLi2JCDQkQWJRQuk60hZp0D3rtCTINSeY9Ej2kIKYfGxwOs4j9qMM7fYZiipzgcf7TamnehqdhsiMiCawXnz4xAbyCkLAx5EGbo3Ax1u3dUIKnTxIaxwQTHehPl3V491H0%2BbC5zgpGz7Io%2BmjdhKlPJ01EeMpM7UsRJMi1nGjmJg35i6bQBAAxjO%2FENJubU2mg3ONySEoWklCwdABETcs7ck3jgiuU9pcKKpbgn%2B3YlzV1FzIkB6pmEDOSSyDfPPlQskznctFji0kpgZjW5RZe6x9kYT4KJcXg0bNiCyif%2BpZACCyRMmYsfiKmN9tSO65F0R2OO6ytlEhY5Sj6uRKfFxw0ijJaAx%2Fk3QgnAFSq27%2F2i4GEBA%2BUvTJKK%2F9eISNvG46Em5RZfjTYLdeD8kdXHyrwId%2FDQZUaMCY4gGbke2C8vfjgV%2FY9kkRQOJIn%2FxM9INZSpiBnqX0Q9GlQPpPKAyO5y%2BW5NMPSRdBCUlmuxl40ZfMCnf2Cp044uI9WLFtCi4YVxKjuRCOBWIb4XbIsGdbo4qtMQnNOQz4XDSui7W%2FN6l54qOynCqD3DpWQ%2BmpD7C40D8BZEWGJX3tlAaZBMj1yjvDYKwCJBa201u6nBKE5UE%2B7QSEhCwrXfbRZylAaAkplhBWX50dumrElePyNMRYUrC99UmcSSNgImhFhDI4BXjMtiqkgizUGCrZ8iwFxU6fQ8GEHCFdLewwxYWxgScAYMdMLmcZR6b7rZl95eQVDGVoUKcRMM1ixXQtXNkBETZkVVPg8LoSrdetHzkuM7DjZRHP02tCxA1fmkXKF3VzfN1pc1cv%2F8lbTIkkYpqKM9VOhp65ktYk%2BQ46myFWBapDfyWUCnsnI00QTBQmuFjMZTcd0V2NQ768Fhpby04k2IzNR1wKabuGJqYWwSly6ocMFGTeeI%2BejsWDYgEvr66QgqdcIbFYDNgsm0x9UHY6SCd5%2B7tpsLpKdvhahIDyYmEJQCqMqtCF6UlrE5GXRmbu%2Bvtm3BFSxI6ND6UxIE7GsGMgWqghXxSnaRJuGFveTcK5ZVSPJyjUxe1dKgI6kNF7EZhIZs8y8FVqwEfbM0Xk2ltORVDKZZM40SD3qQoQe0orJEKwPfZwm3YPqwixhUMOndis6MhbmfvLBKjC8sKKIZKbJk8L11oNkCQzCgvjhyyEiQSuJcgCQSG4Mocfgc0Hkwcjal1UNgP0CBPikYqBIk9tONv4kLtBswH07vUCjEaHiFGlLf8MgXKzSgjp2HolRRccAOh0ILHz9qlGgIFkwAnzHJRjWFhlA7ROwINyB5HFj59PRZHFor6voq7l23EPNRwdWhgawqbivLSjRA4htEYUFkjESu67icTg5S0aW1sOkCiIysfJ9UnIWevOOLGpepcBxy1wEhd2WI3AZg7sr9WBmHWyasxMcvY%2FiOmsLtHSWNUWEGk9hScMPShasUA1AcHOtRZlqMeQ0OzYS9vQvYUjOLrzP07BUAFikcJNMi7gIxEw4pL1G54TcmmmoAQ5s7TGWErJZ2Io4yQ0ljRYhL8H5e62oDtLF8aDpnIvZ5R3GWJyAugdiiJW9hQAVTsnCBHhwu7rkBlBX6r3b7ejEY0k5GGeyKv66v%2B6dg7mcJTrWHbtMywbedYqCQ0FPwoytmSWsL8WTtChZCKKzEF7vP6De4x2BJkkniMgSdWhbeBSLtJZR9CTHetK1xb34AYIJ37OegYIoPVbXgJ%2FqDQK%2BbfCtxQRVKQu77WzOoM6SGL7MaZwCGJVk46aImai9fmam%2BWpHG%2B0BtQPWUgZ7RIAlPq6lkECUhZQ2gqWkMYKcYMYaIc4gYCDFHYa2d1nzp3%2BJ1eCBay8IYZ0wQRKGAqvCuZ%2FUgbQPyllosq%2BXtfKIZOzmeJqRazpmmoP%2F76YfkjzV2NlXTDSBYB04SVlNQsFTbGPk1t%2FI4Jktu0XSgifO2ozFOiwd%2F0SssJDn0dn4xqk4GDTTKX73%2FwQyBLdqgJ%2BWx6AQaba3BA9CKEzjtQYIfAsiYamapq80LAamYjinlKXUkxdpIDk0puXUEYzSalfRibAeDAKpNiqQ0FTwoxuGYzRnisyTotdVTclis1LHRQCy%2FqqL8oUaQzWRxilq5Mi0IJGtMY02cGLD69vGjkj3p6pGePKI8bkBv5evq8SjjyU04vJR2cQXQwSJyoinDsUJHCQ50jrFTT7yRdbdYQMB3MYCb6uBzJ9ewhXYPAIZSXfeEQBZZ3GPN3Nbhh%2FwkvAJLXnQMdi5NYYZ5GHE400GS5rXkOZSQsdZgIbzRnF9ueLnsfQ47wHAsirITnTlkCcuWWIUhJSbpM3wWhXNHvt2xUsKKMpdBSbJnBMcihkoDqAd1Zml%2FR4yrzow1Q2A5G%2Bkzo%2FRhRxQS2lCSDRV8LlYLBOOoo1bF4jwJAwKMK1tWLHlu9i0j4Ig8qVm6wE1DxXwAwQwsaBWUg2pOOol2dHxyt6npwJEdLDDVYyRc2D0HbcbLUJQj8gPevQBUBOUHXPrsAPBERICpnYESeu2OHotpXQxRGlCCtLdIsu23MhZVEoJg8Qumj%2FUMMc34IBqTKLDTp76WzL%2FdMjCxK7MjhiGjeYAC%2Fkj%2FjY%2FRde7hpSM1xChrog6yZ7OWTuD56xBJnGFE%2BpT2ElSyCnJcwVzCjkqeNLfMEJqKW0G7OFIp0G%2B9mh50I9o8k1tpCY0xYqFNIALgIfc2me4n1bmJnRZ89oepgLPT0NTMLNZsvSCZAc3TXaNB07vail36%2FdBySis4m9%2FDR8izaLJW6bWCkVgm5T%2Bius3ZXq4xI%2BGnbveLbdRwF2mNtsrE0JjYc1AXknCOrLSu7Te%2Fr4dPYMCl5qtiHNTn%2BTPbh1jCBHH%2BdMJNhwNgs3nT%2BOhQoQ0vYif56BMG6WowAcHR3DjQolxLzyVekHj00PBAaW7IIAF1EF%2BuRIWyXjQMAs2chdpaKPNaB%2BkSezYt0%2BCA04sOg5vx8Fr7Ofa9sUv87h7SLAUFSzbetCCZ9pmyLt6l6%2FTzoA1%2FZBG9bIUVHLAbi%2FkdBFgYGyGwRQGBpkqCEg2ah9UD6EedEcEL3j4y0BQQCiExEnocA3SZboh%2Bepgd3YsOkHskZwPuQ5OoyA0fTA5AXrHcUOQF%2BzkJHIA7PwCDk1gGVmGUZSSoPhNf%2BTklauz98QofOlCIQ%2FtCD4dosHYPqtPCXB3agggQQIqQJsSkB%2Bqn0rkQ1toJjON%2FOtCIB9RYv3PqRA4C4U68ZMlZn6BdgEvi2ziU%2BTQ6NIw3ej%2BAtDwMGEZk7e2IjxUWKdAxyaw9OCwSmeADTPPleyk6UhGDNXQb%2B%2BW6Uk4q6F7%2Frg6WVTo82IoCxSIsFDrav4EPHphD3u4hR53WKVvYZUwNCCeM4PMBWzK%2BEfIthZOkuAwPo5C5jgoZgn6dUdvx5rIDmd58cXXdKNfw3l%2BwM2UjgrDJeQHhbD7HW2QDoZMCujgIUkk5Fg8VCsdyjOtnGRx8wgKRPZN5dR0zPUyfGZFVihbFRniXZFOZGKPnEQzU3AnD1KfR6weHW2XS6KbPJxUkOTZsAB9vTVp3Le1F8q5l%2BDMcLiIq78jxAImD2pGFw0VHfRatScGlK6SMu8leTmhUSMy8Uhdd6xBiH3Gdman4tjQGLboJfqz6fL2WKHTmrfsKZRYX6BTDjDldKMosaSTLdQS7oDisJNqAUhw1PfTlnacCO8vl8706Km1FROgLDmudzxg%2BEWTiArtHgLsRrAXYWdB0NmToNCJdKm0KWycZQqb%2BMw76Qy29iQ5up%2FX7oyw8QZ75kP5F6iJAJz6KCmqxz8fEa%2FxnsMYcIO%2FvEkGRuMckhr4rIeLrKaXnmIzlNLxbFspOphkcnJdnz%2FChp%2FVlpj2P7jJQmQRwGnltkTV5dbF9fE3%2FfxoSqTROgq9wFUlbuYzYcasE0ouzBo%2BdDCDzxKAfhbAZYxQiHrLzV2iVexnDX%2FQnT1fsT%2Fxuhu1ui5qIytgbGmRoQkeQooO8eJNNZsf0iALur8QxZFH0nCMnjerYQqG1pIfjyVZWxhVRznmmfLG00BcBWJE6hzQWRyFknuJnXuk8A5FRDCulwrWASSNoBtR%2BCtGdkPwYN2o7DOw%2FVGlCZPusRBFXODQdUM5zeHDIVuAJBLqbO%2Ff9Qua%2BpDqEPk230Sob9lEZ8BHiCorjVghuI0lI4JDgHGRDD%2FprQ84B1pVGkIpVUAHCG%2Biz3Bn3qm2AVrYcYWhock4jso5%2BJ7HfHVj4WMIQdGctq3psBCVVzupQOEioBGA2Bk%2BUILT7%2BVoX5mdxxA5fS42gISQVi%2FHTzrgMxu0fY6hE1ocUwwbsbWcezrY2n6S8%2F6cxXkOH4prpmPuFoikTzY7T85C4T2XYlbxLglSv2uLCgFv8Quk%2FwdesUdWPeHYIH0R729JIisN9Apdd4eB10aqwXrPt%2BSu9mA8k8n1sjMwnfsfF2j3jMUzXepSHmZ%2FBfqXvzgUNQQWOXO8YEuFBh4QTYCkOAPxywpYu1VxiDyJmKVcmJPGWk%2Fgc3Pov02StyYDahwmzw3E1gYC9wkupyWfDqDSUMpCTH5e5N8B%2F%2FlHiMuIkTNw4USHrJU67bjXGqNav6PBuQSoqTxc8avHoGmvqNtXzIaoyMIQIiiUHIM64cXieouplhNYln7qgc4wBVAYR104kO%2BCvKqsg4yIUlFNThVUAKZxZt1XA34h3TCUUiXVkZ0w8Hh2R0Z5L0b4LZvPd%2Fp1gi%2F07h8qfwHrByuSxglc9cI4QIg2oqvC%2Fqm0i7tjPLTgDhoWTAKDO2ONW5oe%2B%2FeKB9vZB8K6C25yCZ9RFVMnb6NRdRjyVK57CHHSkJBfnM2%2Fj4ODUwRkqrtBBCrDsDpt8jhZdXoy%2F1BCqw3sSGhgGGy0a5Jw6BP%2FTExoCmNFYjZl248A0osgPyGEmRA%2BfAsqPVaNAfytu0vuQJ7rk3J4kTDTR2AlCHJ5cls26opZM4w3jMULh2YXKpcqGBtuleAlOZnaZGbD6DHzMd6i2oFeJ8z9XYmalg1Szd%2FocZDc1C7Y6vcALJz2lYnTXiWEr2wawtoR4g3jvWUU2Ngjd1cewtFzEvM1NiHZPeLlIXFbBPawxNgMwwAlyNSuGF3zizVeOoC9bag1qRAQKQE%2FEZBWC2J8mnXAN2aTBboZ7HewnObE8CwROudZHmUM5oZ%2FUgd%2FJZQK8lvAm43uDRAbyW8gZ%2BZGq0EVerVGUKUSm%2FIdn8AQHdR4m7bue88WBwft9mSCeMOt1ncBwziOmJYI2ZR7ewNMPiCugmSsE4EyQ%2BQATJG6qORMGd4snEzc6B4shPIo4G1T7PgSm8PY5eUkPdF8JZ0VBtadbHXoJgnEhZQaODPj2gpODKJY5Yp4DOsLBFxWbvXN755KWylJm%2BoOd4zEL9Hpubuy2gyyfxh8oEfFutnYWdfB8PdESLWYvSqbElP9qo3u6KTmkhoacDauMNNjj0oy40DFV7Ql0aZj77xfGl7TJNHnIwgqOkenruYYNo6h724%2BzUQ7%2BvkCpZB%2BpGA562hYQiDxHVWOq0oDQl%2FQsoiY%2BcuI7iWq%2FZIBtHcXJ7kks%2Bh2fCNUPA82BzjnqktNts%2BRLdk1VSu%2BtqEn7QZCCsvEqk6FkfiOYkrsw092J8jsfIuEKypNjLxrKA9kiA19mxBD2suxQKCzwXGws7kEJvlhUiV9tArLIdZW0IORcxEzdzKmjtFhsjKy%2F44XYXdI5noQoRcvjZ1RMPACRqYg2V1%2BOwOepcOknRLLFdYgTkT5UApt%2FJhLM3jeFYprZV%2BZow2g8fP%2BU68hkKFWJj2yBbKqsrp25xkZX1DAjUw52IMYWaOhab8Kp05VrdNftqwRrymWF4OQSjbdfzmRZirK8FMJELEgER2PHjEAN9pGfLhCUiTJFbd5LBkOBMaxLr%2FA1SY9dXFz4RjzoU9ExfJCmx%2FI9FKEGT3n2cmzl2X42L3Jh%2BAbQq6sA%2BSs1kitoa4TAYgKHaoybHUDJ51oETdeI%2F9ThSmjWGkyLi5QAGWhL0BG1UsTyRGRJOldKBrYJeB8ljLJHfATWTEQBXBDnQexOHTB%2BUn44zExFE4vLytcu5NwpWrUxO%2F0ZICUGM7hGABXym0V6ZvDST0E370St9MIWQOTWngeoQHUTdCJUP04spMBMS8LSker9cReVQkULFDIZDFPrhTzBl6sed9wcZQTbL%2BBDqMyaN3RJPh%2Fanbx%2BIv%2BqgQdAa3M9Z5JmvYlh4qop%2BHo1F1W5gbOE9YKLgAnWytXElU4G8GtW47lhgFE6gaSs%2Bgs37sFvi0PPVvA5dnCBgILTwoKd%2F%2BDoL9F6inlM7H4rOTzD79KJgKlZO%2FZgt22UsKhrAaXU5ZcLrAglTVKJEmNJvORGN1vqrcfSMizfpsgbIe9zno%2BgBoKVXgIL%2FVI8dB1O5o%2FR3Suez%2FgD7M781ShjKpIIORM%2FnxG%2BjjhhgPwsn2IoXsPGPqYHXA63zJ07M2GPEykQwJBYLK808qYxuIew4frk52nhCsnCYmXiR6CuapvE1IwRB4%2FQftDbEn%2BAucIr1oxrLabRj9q4ae0%2BfXkHnteAJwXRbVkR0mctVSwEbqhJiMSZUp9DNbEDMmjX22m3ABpkrPQQTP3S1sib5pD2VRKRd%2BeNAjLYyT0hGrdjWJZy24OYXRoWQAIhGBZRxuBFMjjZQhpgrWo8SiFYbojcHO8V5DyscJpLTHyx9Fimassyo5U6WNtquUMYgccaHY5amgR3PQzq3ToNM5ABnoB9kuxsebqmYZm0R9qxJbFXCQ1UPyFIbxoUraTJFDpCk0Wk9GaYJKz%2F6oHwEP0Q14lMtlddQsOAU9zlYdMVHiT7RQP3XCmWYDcHCGbVRHGnHuwzScA0BaSBOGkz3lM8CArjrBsyEoV6Ys4qgDK3ykQQPZ3hCRGNXQTNNXbEb6tDiTDLKOyMzRhCFT%2BmAUmiYbV3YQVqFVp9dorv%2BTsLeCykS2b5yyu8AV7IS9cxcL8z4Kfwp%2BxJyYLv1OsxQCZwTB4a8BZ%2F5EdxTBJthApqyfd9u3ifr%2FWILTqq5VqgwMT9SOxbSGWLQJUUWCVi4k9tho9nEsbUh7U6NUsLmkYFXOhZ0kmamaJLRNJzSj%2Fqn4Mso6zb6iLLBXoaZ6AqeWCjHQm2lztnejYYM2eubnpBdKVLORZhudH3JF1waBJKA9%2BW8EhMj3Kzf0L4vi4k6RoHh3Z5YgmSZmk6ns4fjScjAoL8GoOECgqgYEBYUGFVO4FUv4%2FYtowhEmTs0vrvlD%2FCrisnoBNDAcUi%2FteY7OctFlmARQzjOItrrlKuPO6E2Ox93L4O%2F4DcgV%2FdZ7qR3VBwVQxP1GCieA4RIpweYJ5FoYrHxqRBdJjnqbsikA2Ictbb8vE1GYIo9dacK0REgDX4smy6GAkxlH1yCGGsk%2BtgiDhNKuKu3yNrMdxafmKTF632F8Vx4BNK57GvlFisrkjN9WDAtjsWA0ENT2e2nETUb%2Fn7qwhvGnrHuf5bX6Vh%2Fn3xffU3PeHdR%2BFA92i6ufT3AlyAREoNDh6chiMWTvjKjHDeRhOa9YkOQRq1vQXEMppAQVwHCuIcV2g5rBn6GmZZpTR7vnSD6ZmhdSl176gqKTXu5E%2BYbfL0adwNtHP7dT7t7b46DVZIkzaRJOM%2BS6KcrzYVg%2BT3wSRFRQashjfU18NutrKa%2F7PXbtuJvpIjbgPeqd%2BpjmRw6YKpnANFSQcpzTZgpSNJ6J7uiagAbir%2F8tNXJ%2FOsOnRh6iuIexxrmkIneAgz8QoLmiaJ8sLQrELVK2yn3wOHp57BAZJhDZjTBzyoRAuuZ4eoxHruY1pSb7qq79cIeAdOwin4GdgMeIMHeG%2BFZWYaiUQQyC5b50zKjYw97dFjAeY2I4Bnl105Iku1y0lMA1ZHolLx19uZnRdILcXKlZGQx%2FGdEqSsMRU1BIrFqRcV1qQOOHyxOLXEGcbRtAEsuAC2V4K3p5mFJ22IDWaEkk9ttf5Izb2LkD1MnrSwztXmmD%2FQi%2FEmVEFBfiKGmftsPwVaIoZanlKndMZsIBOskFYpDOq3QUs9aSbAAtL5Dbokus2G4%2FasthNMK5UQKCOhU97oaOYNGsTah%2BjfCKsZnTRn5TbhFX8ghg8CBYt%2FBjeYYYUrtUZ5jVij%2Fop7V5SsbA4mYTOwZ46hqdpbB6Qvq3AS2HHNkC15pTDIcDNGsMPXaBidXYPHc6PJAkRh29Vx8KcgX46LoUQBhRM%2B3SW6Opll%2FwgxxsPgKJKzr5QCmwkUxNbeg6Wj34SUnEzOemSuvS2OetRCO8Tyy%2BQbSKVJcqkia%2BGvDefFwMOmgnD7h81TUtMn%2BmRpyJJ349HhAnoWFTejhpYTL9G8N2nVg1qkXBeoS9Nw2fB27t7trm7d%2FQK7Cr4uoCeOQ7%2F8JfKT77KiDzLImESHw%2F0wf73QeHu74hxv7uihi4fTX%2BXEwAyQG3264dwv17aJ5N335Vt9sdrAXhPOAv8JFvzqyYXwfx8WYJaef1gMl98JRFyl5Mv5Uo%2FoVH5ww5OzLFsiTPDns7fS6EURSSWd%2F92BxMYQ8sBaH%2Bj%2BwthQPdVgDGpTfi%2BJQIWMD8xKqULliRH01rTeyF8x8q%2FGBEEEBrAJMPf25UQwi0b8tmqRXY7kIvNkzrkvRWLnxoGYEJsz8u4oOyMp8cHyaybb1HdMCaLApUE%2B%2F7xLIZGP6H9xuSEXp1zLIdjk5nBaMuV%2FyTDRRP8Y2ww5RO6d2D94o%2B6ucWIqUAvgHIHXhZsmDhjVLczmZ3ca0Cb3PpKwt2UtHVQ0BgFJsqqTsnzZPlKahRUkEu4qmkJt%2Bkqdae76ViWe3STan69yaF9%2BfESD2lcQshLHWVu4ovItXxO69bqC5p1nZLvI8NdQB9s9UNaJGlQ5mG947ipdDA0eTIw%2FA1zEdjWquIsQXXGIVEH0thC5M%2BW9pZe7IhAVnPJkYCCXN5a32HjN6nsvokEqRS44tGIs7s2LVTvcrHAF%2BRVmI8L4HUYk4x%2B67AxSMJKqCg8zrGOgvK9kNMdDrNiUtSWuHFpC8%2Fp5qIQrEo%2FH%2B1l%2F0cAwQ2nKmpWxKcMIuHY44Y6DlkpO48tRuUGBWT0FyHwSKO72Ud%2BtJUfdaZ4CWNijzZtlRa8%2BCkmO%2FEwHYfPZFU%2FhzjFWH7vnzHRMo%2BaF9u8qHSAiEkA2HjoNQPEwHsDKOt6hOoK3Ce%2F%2B%2F9boMWDa44I6FrQhdgS7OnNaSzwxWKZMcyHi6LN4WC6sSj0qm2PSOGBTvDs%2FGWJS6SwEN%2FULwpb4LQo9fYjUfSXRwZkynUazlSpvX9e%2BG2zor8l%2BYaMxSEomDdLHGcD6YVQPegTaA74H8%2BV4WvJkFUrjMLGLlvSZQWvi8%2FQA7yzQ8GPno%2F%2F5SJHRP%2FOqKObPCo81s%2F%2B6WgLqykYpGAgQZhVDEBPXWgU%2FWzFZjKUhSFInufPRiMAUULC6T11yL45ZrRoB4DzOyJShKXaAJIBS9wzLYIoCEcJKQW8GVCx4fihqJ6mshBUXSw3wWVj3grrHQlGNGhIDNNzsxQ3M%2BGWn6ASobIWC%2BLbYOC6UpahVO13Zs2zOzZC8z7FmA05JhUGyBsF4tsG0drcggIFzgg%2Fkpf3%2BCnAXKiMgIE8Jk%2FMhpkc8DUJEUzDSnWlQFme3d0sHZDrg7LavtsEX3cHwjCYA17pMTfx8Ajw9hHscN67hyo%2BRJQ4458RmPywXykkVcW688oVUrQhahpPRvTWPnuI0B%2BSkQu7dCyvLRyFYlC1LG1gRCIvn3rwQeINzZQC2KXq31FaR9UmVV2QeGVqBHjmE%2BVMd3b1fhCynD0pQNhCG6%2FWCDbKPyE7NRQzL3BzQAJ0g09aUzcQA6mUp9iZFK6Sbp%2FYbHjo%2B%2B7%2FWj8S4YNa%2BZdqAw1hDrKWFXv9%2BzaXpf8ZTDSbiqsxnwN%2FCzK5tPkOr4tRh2kY3Bn9JtalbIOI4b3F7F1vPQMfoDcdxMS8CW9m%2FNCW%2FHILTUVWQIPiD0j1A6bo8vsv6P1hCESl2abrSJWDrq5sSzUpwoxaCU9FtJyYH4QFMxDBpkkBR6kn0LMPO%2B5EJ7Z6bCiRoPedRZ%2FP0SSdii7ZnPAtVwwHUidcdyspwncz5uq6vvm4IEDbJVLUFCn%2FLvIHfooUBTkFO130FC7CmmcrKdgDJcid9mvVzsDSibOoXtIf9k6ABle3PmIxejodc4aob0QKS432srrCMndbfD454q52V01G4q913mC5HOsTzWF4h2No1av1VbcUgWAqyoZl%2B11PoFYnNv2HwAODeNRkHj%2B8SF1fcvVBu6MrehHAZK1Gm69ICcTKizykHgGFx7QdowTVAsYEF2tVc0Z6wLryz2FI1sc5By2znJAAmINndoJiB4sfPdPrTC8RnkW7KRCwxC6YvXg5ahMlQuMpoCSXjOlBy0Kij%2BbsCYPbGp8BdCBiLmLSAkEQRaieWo1SYvZIKJGj9Ur%2FeWHjiB7SOVdqMAVmpBvfRiebsFjger7DC%2B8kRFGtNrTrnnGD2GAJb8rQCWkUPYHhwXsjNBSkE6lGWUj5QNhK0DMNM2l%2BkXRZ0KLZaGsFSIdQz%2FHXDxf3%2FTE30%2BDgBKWGWdxElyLccJfEpjsnszECNoDGZpdwdRgCixeg9L4EPhH%2BRptvRMVRaahu4cySjS3P5wxAUCPkmn%2BrhyASpmiTaiDeggaIxYBmtLZDDhiWIJaBgzfCsAGUF1Q1SFZYyXDt9skCaxJsxK2Ms65dmdp5WAZyxik%2FzbrTQk5KmgxCg%2Ff45L0jywebOWUYFJQAJia7XzCV0x89rpp%2Ff3AVWhSPyTanqmik2SkD8A3Ml4NhIGLAjBXtPShwKYfi2eXtrDuKLk4QlSyTw1ftXgwqA2jUuopDl%2B5tfUWZNwBpEPXghzbBggYCw%2Fdhy0ntds2yeHCDKkF%2FYxQjNIL%2FF%2F37jLPHCKBO9ibwYCmuxImIo0ijV2Wbg3kSN2psoe8IsABv3RNFaF9uMyCtCYtqcD%2BqNOhwMlfARQUdJ2tUX%2BMNJqOwIciWalZsmEjt07tfa8ma4cji9sqz%2BQ9hWfmMoKEbIHPOQORbhQRHIsrTYlnVTNvcq1imqmmPDdVDkJgRcTgB8Sb6epCQVmFZe%2BjGDiNJQLWnfx%2BdrTKYjm0G8yH0ZAGMWzEJhUEQ4Maimgf%2Fbkvo8PLVBsZl152y5S8%2BHRDfZIMCbYZ1WDp4yrdchOJw8k6R%2B%2F2pHmydK4NIK2PHdFPHtoLmHxRDwLFb7eB%2BM4zNZcB9NrAgjVyzLM7xyYSY13ykWfIEEd2n5%2FiYp3ZdrCf7fL%2Ben%2BsIJu2W7E30MrAgZBD1rAAbZHPgeAMtKCg3NpSpYQUDWJu9bT3V7tOKv%2BNRiJc8JAKqqgCA%2FPNRBR7ChpiEulyQApMK1AyqcWnpSOmYh6yLiWkGJ2mklCSPIqN7UypWj3dGi5MvsHQ87MrB4VFgypJaFriaHivwcHIpmyi5LhNqtem4q0n8awM19Qk8BOS0EsqGscuuydYsIGsbT5GHnERUiMpKJl4ON7qjB4fEqlGN%2FhCky89232UQCiaeWpDYCJINXjT6xl4Gc7DxRCtgV0i1ma4RgWLsNtnEBRQFqZggCLiuyEydmFd7WlogpkCw5G1x4ft2psm3KAREwVwr1Gzl6RT7FDAqpVal34ewVm3VH4qn5mjGj%2BbYL1NgfLNeXDwtmYSpwzbruDKpTjOdgiIHDVQSb5%2FzBgSMbHLkxWWgghIh9QTFSDILixVwg0Eg1puooBiHAt7DzwJ7m8i8%2Fi%2BjHvKf0QDnnHVkVTIqMvIQImOrzCJwhSR7qYB5gSwL6aWL9hERHCZc4G2%2BJrpgHNB8eCCmcIWIQ6rSdyPCyftXkDlErUkHafHRlkOIjxGbAktz75bnh50dU7YHk%2BMz7wwstg6RFZb%2BTZuSOx1qqP5C66c0mptQmzIC2dlpte7vZrauAMm%2F7RfBYkGtXWGiaWTtwvAQiq2oD4YixPLXE2khB2FRaNRDTk%2B9sZ6K74Ia9VntCpN4BhJGJMT4Z5c5FhSepRCRWmBXqx%2BwhVZC4me4saDs2iNqXMuCl6iAZflH8fscC1sTsy4PHeC%2BXYuqMBMUun5YezKbRKmEPwuK%2BCLzijPEQgfhahQswBBLfg%2FGBgBiI4QwAqzJkkyYAWtjzSg2ILgMAgqxYfwERRo3zruBL9WOryUArSD8sQOcD7fvIODJxKFS615KFPsb68USBEPPj1orNzFY2xoTtNBVTyzBhPbhFH0PI5AtlJBl2aSgNPYzxYLw7XTDBDinmVoENwiGzmngrMo8OmnRP0Z0i0Zrln9DDFcnmOoBZjABaQIbPOJYZGqX%2BRCMlDDbElcjaROLDoualmUIQ88Kekk3iM4OQrADcxi3rJguS4MOIBIgKgXrjd1WkbCdqxJk%2F4efRIFsavZA7KvvJQqp3Iid5Z0NFc5aiMRzGN3vrpBzaMy4JYde3wr96PjN90AYOIbyp6T4zj8LoE66OGcX1Ef4Z3KoWLAUF4BTg7ug%2FAbkG5UNQXAMkQezujSHeir2uTThgd3gpyzDrbnEdDRH2W7U6PeRvBX1ZFMP5RM%2BZu6UUZZD8hDPHldVWntTCNk7To8IeOW9yn2wx0gmurwqC60AOde4r3ETi5pVMSDK8wxhoGAoEX9NLWHIR33VbrbMveii2jAJlrxwytTHbWNu8Y4N8vCCyZjAX%2FpcsfwXbLze2%2BD%2Bu33OGBoJyAAL3jn3RuEcdp5If8O%2Ba4NKWvxOTyDltG0IWoHhwVGe7dKkCWFT%2B%2Btm%2BhaBCikRUUMrMhYKZJKYoVuv%2FbsJzO8DwfVIInQq3g3BYypiz8baogH3r3GwqCwFtZnz4xMjAVOYnyOi5HWbFA8n0qz1OjSpHWFzpQOpvkNETZBGpxN8ybhtqV%2FDMUxd9uFZmBfKXMCn%2FSqkWJyKPnT6lq%2B4zBZni6fYRByJn6OK%2BOgPBGRAJluwGSk4wxjOOzyce%2FPKODwRlsgrVkdcsEiYrqYdXo0Er2GXi2GQZd0tNJT6c9pK1EEJG1zgDJBoTVuCXGAU8BKTvCO%2FcEQ1Wjk3Zzuy90JX4m3O5IlxVFhYkSUwuQB2up7jhvkm%2BbddRQu5F9s0XftGEJ9JSuSk%2BZachCbdU45fEqbugzTIUokwoAKvpUQF%2FCvLbWW5BNQFqFkJg2f30E%2F48StNe5QwBg8zz3YAJ82FZoXBxXSv4QDooDo79NixyglO9AembuBcx5Re3CwOKTHebOPhkmFC7wNaWtoBhFuV4AkEuJ0J%2B1pT0tLkvFVZaNzfhs%2FKd3%2BA9YsImlO4XK4vpCo%2FelHQi%2F9gkFg07xxnuXLt21unCIpDV%2BbbRxb7FC6nWYTsMFF8%2B1LUg4JFjVt3vqbuhHmDKbgQ4e%2BRGizRiO8ky05LQGMdL2IKLSNar0kNG7lHJMaXr5mLdG3nykgj6vB%2FKVijd1ARWkFEf3yiUw1v%2FWaQivVUpIDdSNrrKbjO5NPnxz6qTTGgYg03HgPhDrCFyYZTi3XQw3HXCva39mpLNFtz8AiEhxAJHpWX13gCTAwgm9YTvMeiqetdNQv6IU0hH0G%2BZManTqDLPjyrOse7WiiwOJCG%2BJ0pZYULhN8NILulmYYvmVcV2MjAfA39sGKqGdjpiPo86fecg65UPyXDIAOyOkCx5NQsLeD4gGVjTVDwOHWkbbBW0GeNjDkcSOn2Nq4cEssP54t9D749A7M1AIOBl0Fi0sSO5v3P7LCBrM6ZwFY6kp2FX6AcbGUdybnfChHPyu6WlRZ2Fwv9YM0RMI7kISRgR8HpQSJJOyTfXj%2F6gQKuihPtiUtlCQVPohUgzfezTg8o1b3n9pNZeco1QucaoXe40Fa5JYhqdTspFmxGtW9h5ezLFZs3j%2FN46f%2BS2rjYNC2JySXrnSAFhvAkz9a5L3pza8eYKHNoPrvBRESpxYPJdKVUxBE39nJ1chrAFpy4MMkf0qKgYALctGg1DQI1kIymyeS2AJNT4X240d3IFQb%2F0jQbaHJ2YRK8A%2Bls6WMhWmpCXYG5jqapGs5%2FeOJErxi2%2F2KWVHiPellTgh%2FfNl%2F2KYPKb7DUcAg%2BmCOPQFCiU9Mq%2FWLcU1xxC8aLePFZZlE%2BPCLzf7ey46INWRw2kcXySR9FDgByXzfxiNKwDFbUSMMhALPFSedyjEVM5442GZ4hTrsAEvZxIieSHGSgkwFh%2FnFNdrrFD4tBH4Il7fW6ur4J8Xaz7RW9jgtuPEXQsYk7gcMs2neu3zJwTyUerHKSh1iTBkj2YJh1SSOZL5pLuQbFFAvyO4k1Hxg2h99MTC6cTUkbONQIAnEfGsGkNFWRbuRyyaEZInM5pij73EA9rPIUfU4XoqQpHT9THZkW%2BoKFLvpyvTBMM69tN1Ydwv1LIEhHsC%2BueVG%2Bw%2BkyCPsvV3erRikcscHjZCkccx6VrBkBRusTDDd8847GA7p2Ucy0y0HdSRN6YIBciYa4vuXcAZbQAuSEmzw%2BH%2FAuOx%2BaH%2BtBL88H57D0MsqyiZxhOEQkF%2F8DR1d2hSPMj%2FsNOa5rxcUnBgH8ictv2J%2Bcb4BA4v3MCShdZ2vtK30vAwkobnEWh7rsSyhmos3WC93Gn9C4nnAd%2FPjMMtQfyDNZsOPd6XcAsnBE%2FmRHtHEyJMzJfZFLE9OvQa0i9kUmToJ0ZxknTgdl%2FXPV8xoh0K7wNHHsnBdvFH3sv52lU7UFteseLG%2FVanIvcwycVA7%2BBE1Ulyb20BvwUWZcMTKhaCcmY3ROpvonVMV4N7yBXTL7IDtHzQ4CCcqF66LjF3xUqgErKzolLyCG6Kb7irP%2FMVTCCwGRxfrPGpMMGvPLgJ881PHMNMIO09T5ig7AzZTX%2F5PLlwnJLDAPfuHynSGhV4tPqR3gJ4kg4c06c%2FF1AcjGytKm2Yb5jwMotF7vro4YDLWlnMIpmPg36NgAZsGA0W1spfLSue4xxat0Gdwd0lqDBOgIaMANykwwDKejt5YaNtJYIkrSgu0KjIg0pznY0SCd1qlC6R19g97UrWDoYJGlrvCE05J%2F5wkjpkre727p5PTRX5FGrSBIfJqhJE%2FIS876PaHFkx9pGTH3oaY3jJRvLX9Iy3Edoar7cFvJqyUlOhAEiOSAyYgVEGkzHdug%2BoRHIEOXAExMiTSKU9A6nmRC8mp8iYhwWdP2U%2F5EkFAdPrZw03YA3gSyNUtMZeh7dDCu8pF5x0VORCTgKp07ehy7NZqKTpIC4UJJ89lnboyAfy5OyXzXtuDRbtAFjZRSyGFTpFrXwkpjSLIQIG3N0Vj4BtzK3wdlkBJrO18MNsgseR4BysJilI0wI6ZahLhBFA0XBmV8d4LUzEcNVb0xbLjLTETYN8OEVqNxkt10W614dd1FlFFVTIgB7%2FBQQp1sWlNolpIu4ekxUTBV7NmxOFKEBmmN%2BnA7pvF78%2FRII5ZHA09OAiE%2F66MF6HQ%2BqVEJCHxwymukkNvzqHEh52dULPbVasfQMgTDyBZzx4007YiKdBuUauQOt27Gmy8ISclPmEUCIcuLbkb1mzQSqIa3iE0PJh7UMYQbkpe%2BhXjTJKdldyt2mVPwywoODGJtBV1lJTgMsuSQBlDMwhEKIfrvsxGQjHPCEfNfMAY2oxvyKcKPUbQySkKG6tj9AQyEW3Q5rpaDJ5Sns9ScLKeizPRbvWYAw4bXkrZdmB7CQopCH8NAmqbuciZChHN8lVGaDbCnmddnqO1PQ4ieMYfcSiBE5zzMz%2BJV%2F4eyzrzTEShvqSGzgWimkNxLvUj86iAwcZuIkqdB0VaIB7wncLRmzHkiUQpPBIXbDDLHBlq7vp9xwuC9AiNkIptAYlG7Biyuk8ILdynuUM1cHWJgeB%2BK3wBP%2FineogxkvBNNQ4AkW0hvpBOQGFfeptF2YTR75MexYDUy7Q%2F9uocGsx41O4IZhViw%2F2FvAEuGO5g2kyXBUijAggWM08bRhXg5ijgMwDJy40QeY%2FcQpUDZiIzmvskQpO5G1zyGZA8WByjIQU4jRoFJt56behxtHUUE%2Fom7Rj2psYXGmq3llVOCgGYKNMo4pzwntITtapDqjvQtqpjaJwjHmDzSVGLxMt12gEXAdLi%2FcaHSM3FPRGRf7dB7YC%2BcD2ho6oL2zGDCkjlf%2FDFoQVl8GS%2F56wur3rdV6ggtzZW60MRB3g%2BU1W8o8cvqIpMkctiGVMzXUFI7FacFLrgtdz4mTEr4aRAaQ2AFQaNeG7GX0yOJgMRYFziXdJf24kg%2FgBQIZMG%2FYcPEllRTVNoDYR6oSJ8wQNLuihfw81UpiKPm714bZX1KYjcXJdfclCUOOpvTxr9AAJevTY4HK%2FG7F3mUc3GOAKqh60zM0v34v%2BELyhJZqhkaMA8UMMOU90f8RKEJFj7EqepBVwsRiLbwMo1J2zrE2UYJnsgIAscDmjPjnzI8a719Wxp757wqmSJBjXowhc46QN4RwKIxqEE6E5218OeK7RfcpGjWG1jD7qND%2B%2FGTk6M56Ig4yMsU6LUW1EWE%2BfIYycVV1thldSlbP6ltdC01y3KUfkobkt2q01YYMmxpKRvh1Z48uNKzP%2FIoRIZ%2FF6buOymSnW8gICitpJjKWBscSb9JJKaWkvEkqinAJ2kowKoqkqZftRqfRQlLtKoqvTRDi2vg%2FRrPD%2Fd3a09J8JhGZlEkOM6znTsoMCsuvTmywxTCDhw5dd0GJOHCMPbsj3QLkTE3MInsZsimDQ3HkvthT7U9VA4s6G07sID0FW4SHJmRGwCl%2BMu4xf0ezqeXD2PtPDnwMPo86sbwDV%2B9PWcgFcARUVYm3hrFQrHcgMElFGbSM2A1zUYA3baWfheJp2AINmTJLuoyYD%2FOwA4a6V0ChBN97E8YtDBerUECv0u0TlxR5yhJCXvJxgyM73Bb6pyq0jTFJDZ4p1Am1SA6sh8nADd1hAcGBMfq4d%2FUfwnmBqe0Jun1n1LzrgKuZMAnxA3NtCN7Klf4BH%2B14B7ibBmgt0TGUafVzI4uKlpF7v8NmgNjg90D6QE3tbx8AjSAC%2BOA1YJvclyPKgT27QpIEgVYpbPYGBsnyCNrGz9XUsCHkW1QAHgL2STZk12QGqmvAB0NFteERkvBIH7INDsNW9KKaAYyDMdBEMzJiWaJHZALqDxQDWRntumSDPcplyFiI1oDpT8wbwe01AHhW6%2BvAUUBoGhY3CT2tgwehdPqU%2F4Q7ZLYvhRl%2FogOvR9O2%2BwkkPKW5vCTjD2fHRYXONCoIl4Jh1bZY0ZE1O94mMGn%2FdFSWBWzQ%2FVYk%2BGezi46RgiDv3EshoTmMSlioUK6MQEN8qeyK6FRninyX8ZPeUWjjbMJChn0n%2FyJvrq5bh5UcCAcBYSafTFg7p0jDgrXo2QWLb3WpSOET%2FHh4oSadBTvyDo10IufLzxiMLAnbZ1vcUmj3w7BQuIXjEZXifwukVxrGa9j%2BDXfpi12m1RbzYLg9J2wFergEwOxFyD0%2FJstNK06ZN2XdZSGWxcJODpQHOq4iKqjqkJUmPu1VczL5xTGUfCgLEYyNBCCbMBFT%2FcUP6pE%2FmujnHsSDeWxMbhrNilS5MyYR0nJyzanWXBeVcEQrRIhQeJA6Xt4f2eQESNeLwmC10WJVHqwx8SSyrtAAjpGjidcj1E2FYN0LObUcFQhafUKTiGmHWRHGsFCB%2BHEXgrzJEB5bp0QiF8ZHh11nFX8AboTD0PS4O1LqF8XBks2MpjsQnwKHF6HgaKCVLJtcr0XjqFMRGfKv8tmmykhLRzu%2BvqQ02%2BKpJBjaLt9ye1Ab%2BBbEBhy4EVdIJDrL2naV0o4wU8YZ2Lq04FG1mWCKC%2BUwkXOoAjneU%2FxHplMQo2cXUlrVNqJYczgYlaOEczVCs%2FOCgkyvLmTmdaBJc1iBLuKwmr6qtRnhowngsDxhzKFAi02tf8bmET8BO27ovJKF1plJwm3b0JpMh38%2BxsrXXg7U74QUM8ZCIMOpXujHntKdaRtsgyEZl5MClMVMMMZkZLNxH9%2Bb8fH6%2Bb8Lev30A9TuEVj9CqAdmwAAHBPbfOBFEATAPZ2CS0OH1Pj%2F0Q7PFUcC8hDrxESWdfgFRm%2B7vvWbkEppHB4T%2F1ApWnlTIqQwjcPl0VgS1yHSmD0OdsCVST8CQVwuiew1Y%2Bg3QGFjNMzwRB2DSsAk26cmA8lp2wIU4p93AUBiUHFGOxOajAqD7Gm6NezNDjYzwLOaSXRBYcWipTSONHjUDXCY4mMI8XoVCR%2FRrs%2FJLKXgEx%2BqkmeDlFOD1%2FyTQNDClRuiUyKYCllfMiQiyFkmuTz2vLsBNyRW%2Bxz%2B5FElFxWB28VjYIGZ0Yd%2B5wIjkcoMaggxswbT0pCmckRAErbRlIlcOGdBo4djTNO8FAgQ%2BlT6vPS60BwTRSUAM3ddkEAZiwtEyArrkiDRnS7LJ%2B2hwbzd2YDQagSgACpsovmjil5wfPuXq3GuH0CyE7FK3M4FgRaFoIkaodORrPx1%2BJpI9psyNYIFuJogZa0%2F1AhOWdlHQxdAgbwacsHqPZo8u%2FngAH2GmaTdhYnBfSDbBfh8CHq6Bx5bttP2%2BRdM%2BMAaYaZ0Y%2FADkbNCZuAyAVQa2OcXOeICmDn9Q%2FeFkDeFQg5MgHEDXq%2FtVjj%2Bjtd26nhaaolWxs1ixSUgOBwrDhRIGOLyOVk2%2FBc0UxvseQCO2pQ2i%2BKrfhu%2FWeBovNb5dJxQtJRUDv2mCwYVpNl2efQM9xQHnK0JwLYt%2FU0Wf%2BphiA4uw8G91slC832pmOTCAoZXohg1fewCZqLBhkOUBofBWpMPsqg7XEXgPfAlDo2U5WXjtFdS87PIqClCK5nW6adCeXPkUiTGx0emOIDQqw1yFYGHEVx20xKjJVYe0O8iLmnQr3FA9nSIQilUKtJ4ZAdcTm7%2BExseJauyqo30hs%2B1qSW211A1SFAOUgDlCGq7eTIcMAeyZkV1SQJ4j%2Fe1Smbq4HcjqgFbLAGLyKxlMDMgZavK5NAYH19Olz3la%2FQCTiVelFnU6O%2FGCvykqS%2FwZJDhKN9gBtSOp%2F1SP5VRgJcoVj%2Bkmf2wBgv4gjrgARBWiURYx8xENV3bEVUAAWWD3dYDKAIWk5opaCFCMR5ZjJExiCAw7gYiSZ2rkyTce4eNMY3lfGn%2B8p6%2BvBckGlKEXnA6Eota69OxDO9oOsJoy28BXOR0UoXNRaJD5ceKdlWMJlOFzDdZNpc05tkMGQtqeNF2lttZqNco1VtwXgRstLSQ6tSPChgqtGV5h2DcDReIQadaNRR6AsAYKL5gSFsCJMgfsaZ7DpKh8mg8Wz8V7H%2BgDnLuMxaWEIUPevIbClgap4dqmVWSrPgVYCzAoZHIa5z2Ocx1D%2FGvDOEqMOKLrMefWIbSWHZ6jbgA8qVBhYNHpx0P%2BjAgN5TB3haSifDcApp6yymEi6Ij%2FGsEpDYUgcHATJUYDUAmC1SCkJ4cuZXSAP2DEpQsGUjQmKJfJOvlC2x%2FpChkOyLW7KEoMYc5FDC4v2FGqSoRWiLsbPCiyg1U5yiHZVm1XLkHMMZL11%2Fyxyw0UnGig3MFdZklN5FI%2FqiT65T%2BjOXOdO7XbgWurOAZR6Cv9uu1cm5LjkXX4xi6mWn5r5NjBS0gTliHhMZI2WNqSiSphEtiCAwnafS11JhseDGHYQ5%2BbqWiAYiAv6Jsf79%2FVUs4cIl%2Bn6%2BWOjcgB%2F2l5TreoAV2717JzZbQIR0W1cl%2FdEqCy5kJ3ZSIHuU0vBoHooEpiHeQWVkkkOqRX27eD1FWw4BfO9CJDdKoSogQi3hAAwsPRFrN5RbX7bqLdBJ9JYMohWrgJKHSjVl1sy2xAG0E3sNyO0oCbSGOxCNBRRXTXenYKuwAoDLfnDcQaCwehUOIDiHAu5m5hMpKeKM4sIo3vxACakIxKoH2YWF2QM84e6F5C5hJU4g8uxuFOlAYnqtwxmHyNEawLW%2FPhoawJDrGAP0JYWHgAVUByo%2FbGdiv2T2EMg8gsS14%2FrAdzlOYazFE7w4OzxeKiWdm3nSOnQRRKXSlVo8HEAbBfyJMKqoq%2BSCcTSx5NDtbFwNlh8VhjGGDu7JG5%2FTAGAvniQSSUog0pNzTim8Owc6QTuSKSTXlQqwV3eiEnklS3LeSXYPXGK2VgeZBqNcHG6tZHvA3vTINhV0ELuQdp3t1y9%2BogD8Kk%2FW7QoRN1UWPqM4%2BxdygkFDPLoTaumKReKiLWoPHOfY54m3qPx4c%2B4pgY3MRKKbljG8w4wvz8pxk3AqKsy4GMAkAtmRjRMsCxbb4Q2Ds0Ia9ci8cMT6DmsJG00XaHCIS%2Bo3F8YVVeikw13w%2BOEDaCYYhC0ZE54kA4jpjruBr5STWeqQG6M74HHL6TZ3lXrd99ZX%2B%2B7LhNatQaZosuxEf5yRA15S9gPeHskBIq3Gcw81AGb9%2FO53DYi%2F5CsQ51EmEh8Rkg4vOciClpy4d04eYsfr6fyQkBmtD%2BP8sNh6e%2BXYHJXT%2FlkXxT4KXU5F2sGxYyzfniMMQkb9OjDN2C8tRRgTyL7GwozH14PrEUZc6oz05Emne3Ts5EG7WolDmU8OB1LDG3VrpQxp%2BpT0KYV5dGtknU64JhabdqcVQbGZiAxQAnvN1u70y1AnmvOSPgLI6uB4AuDGhmAu3ATkJSw7OtS%2F2ToPjqkaq62%2F7WFG8advGlRRqxB9diP07JrXowKR9tpRa%2BjGJ91zxNTT1h8I2PcSfoUPtd7NejVoH03EUcqSBuFZPkMZhegHyo2ZAITovmm3zAIdGFWxoNNORiMRShgwdYwFzkPw5PA4a5MIIQpmq%2Bnsp3YMuXt%2FGkXxLx%2FP6%2BZJS0lFyz4MunC3eWSGE8xlCQrKvhKUPXr0hjpAN9ZK4PfEDrPMfMbGNWcHDzjA7ngMxTPnT7GMHar%2BgMQQ3NwHCv4zH4BIMYvzsdiERi6gebRmerTsVwZJTRsL8dkZgxgRxmpbgRcud%2BYlCIRpPwHShlUSwuipZnx9QCsEWziVazdDeKSYU5CF7UVPAhLer3CgJOQXl%2Fzh575R5rsrmRnKAzq4POFdgbYBuEviM4%2BLVC15ssLNFghbTtHWerS1hDt5s4qkLUha%2FqpZXhWh1C6lTQAqCNQnaDjS7UGFBC6wTu8yFnKJnExCnAs3Ok9yj5KpfZESQ4lTy5pTGTnkAUpxI%2ByjEldJfSo4y0QhG4i4IwkRFGcjWY8%2BEzgYYJUK7BXQksLxAww%2FYYWBMhJILB9e8ePEJ4OP7z%2B4%2FwOQDl64iOYDp26DaONPxpKtBxq%2FaTzRGarm3VkPYTLJKx6Z%2FMw2YbBGseJhPMwhhNswrIkyvV2BYzrvZbxLpKwcWJhYmFtVZ%2BlPEq91FzVp1HlQY1bZVLqeNR9SAUn6n0E28k%2FUuGkNpP1DBI5ch%2FEehZfjUQ9aE41NhETExoPT2gGQz0IhWJbEOvTQ4wgcXCHHFBhewYUiFHuhRSAUVmEHeCRQHQkXGFwkAgyzREJCVN7TRnTon36Zw3tPhx4EALwNdwDv%2BJ41YSP4B2CQqz0EFgARZ4ESgBHQgROwAVn9GTI%2BHYexTUevLUeta4%2FDqKrbMVS%2BYqb8hUwYCrlgKtmAq1YCrFgKrd4qpXiqZcKn1oqdWipjYKpWwVPVYqW6xUpVipKqFR3QKjagVEtAqHpxUMTitsnFaJOKx2cVhswq35RVpyiq9lFVNIKnOQVMkgqtYxVNxiqQjFS7GKlSIVIsQqPIhUWwioigFQ%2B%2BKkN8VHr49HDw9Ebo9EDo9DTo9Crg9BDg9%2FWx7gWx7YWwlobYrOGxWPNisAaAHEyALpkAVDIAeWAArsABVXACYuAD5cAF6wAKFQAQqgAbVAAsoAAlQAUaYAfkwAvogBWQACOgAD9AAHSAAKT4GUdMiOvFngBTwCn2AZ7Dv6B6k%2F90B8%2ByRnkV144AIBoAMTQATGgAjNAA4YABgwABZgB%2FmQCwyAVlwCguASlwCEuAQFwB4uAMlwBYuAJlQAUVAAhUD2KgdpUDaJgaRMDFJgX5MC1JgWJEAokQCWRAHxEAWkQBMRADpEAMkQAYROAEecC484DRpwBDTnwNOdw05tjTmiNOYwtswhYFwLA7BYG4LA2BYGOLAwRYFuLAsxYFQJAohIEyJAMwkAwiQC0JAJgkAeiQBkJAFokAPCQA0JABwcD4Dgc4cDdDgaYcDIDgYgUC6CgWgUClCgUYUAVBQBOFAEYMALgwAgDA9QYAdIn8AZzeBB2L5EcWrenUT1KXienEsuJJ7x5U8XlTjc1NVzUyXFTGb1LlpUtWlTDIjqwE4LsagowoCi2gJLKAkpoBgJQNpAIhNqaEoneI6kiiqQ6Go%2Fn6j0cS%2Ba2gEU8gIHJ%2BBwfgZX4GL%2BBd%2FgW34FZ%2BBS%2FgUH4FN6BTegTvoEv6BJegRnYEF2A79gOvYDl2BdEjCkqkGtwXp0LNToIskOTXzh%2FF062yJ7AAAAEDAWAAABWhJ%2BKPEIJgBFxMVP7w2QJBGHASQnOBKXKFIdUK4igKA9IEaYJg%29%20format%28%27embedded%2Dopentype%27%29%2Curl%28data%3Aapplication%2Ffont%2Dwoff%3Bbase64%2Cd09GRgABAAAAAFuAAA8AAAAAsVwAAQAAAAAAAAAAAAAAAAAAAAAAAAAAAABGRlRNAAABWAAAABwAAAAcbSqX3EdERUYAAAF0AAAAHwAAACABRAAET1MvMgAAAZQAAABFAAAAYGe5a4ljbWFwAAAB3AAAAsAAAAZy2q3jgWN2dCAAAAScAAAABAAAAAQAKAL4Z2FzcAAABKAAAAAIAAAACP%2F%2FAANnbHlmAAAEqAAATRcAAJSkfV3Cb2hlYWQAAFHAAAAANAAAADYFTS%2FYaGhlYQAAUfQAAAAcAAAAJApEBBFobXR4AABSEAAAAU8AAAN00scgYGxvY2EAAFNgAAACJwAAAjBv%2B5XObWF4cAAAVYgAAAAgAAAAIAFqANhuYW1lAABVqAAAAZ4AAAOisyygm3Bvc3QAAFdIAAAELQAACtG6o%2BU1d2ViZgAAW3gAAAAGAAAABsMYVFAAAAABAAAAAMw9os8AAAAA0HaBdQAAAADQdnOXeNpjYGRgYOADYgkGEGBiYGRgZBQDkixgHgMABUgASgB42mNgZulmnMDAysDCzMN0gYGBIQpCMy5hMGLaAeQDpRCACYkd6h3ux%2BDAoPD%2FP%2FOB%2FwJAdSIM1UBhRiQlCgyMADGWCwwAAAB42u2UP2hTQRzHf5ekaVPExv6JjW3fvTQ0sa3QLA5xylBLgyBx0gzSWEUaXbIoBBQyCQGHLqXUqYNdtIIgIg5FHJxEtwqtpbnfaV1E1KFaSvX5vVwGEbW6OPngk8%2FvvXfv7pt3v4SImojIDw6BViKxRgIVBaZwVdSv%2BxvXA%2BIuzqcog2cOkkvDNE8Lbqs74k64i%2B5Sf3u8Z2AnIRLbyVCyTflVSEXVoEqrrMqrgiqqsqqqWQ5xlAc5zWOc5TwXucxVnuE5HdQhHdFRHdNJndZZndeFLc%2FzsKJLQ%2FWV6BcrCdWkwspVKZVROaw0qUqqoqZZcJhdTnGGxznHBS5xhad5VhNWCuturBTXKZ3RObuS98pb9c57k6ql9rp2v1as5deb1r6s9q1GV2IrHSt73T631424YXzjgPwqt%2BRn%2BVG%2BlRvyirwsS%2FKCPCfPytPypDwhj8mjctRZd9acF86y89x55jxxHjkPnXstXfbt%2FpNjj%2FnwXW%2BcHa6%2FSYvZ7yEwbDYazDcIgoUGzY3h2HtqgUcs1AFPWKgTXrRQF7xkoQhRf7uF9hPFeyzUTTSwY6EoUUJY6AC8bSGMS4Ys1Au3WaiPSGGsMtkdGH2rzJgYHAaYjxIwQqtB1CnYkEZ9BM6ALOpROAfyqI%2FDBQudgidBETXuqRIooz4DV0AV9UV4GsyivkTEyMMmw1UYGdhkuAYjA5sMGMvIwCbDDRgZeAz1TXgcmDy3YeRhk%2BcOjCxsMjyAkYFNhscwMrDJ8BQ2886gXoaRhedQvyTSkDZ7uA6HLLQBI5vGntAbGHugTc53cMxC7%2BE4SKL%2BACOzNpk3YWTWJid%2BiRo5NXIKM3fBItAPW55FdJLY3FeHBDr90606JCIU9Jk%2BMs3%2FY%2F8L8jUq3y79bJ%2F0%2F%2BROoP4v9v%2F4%2Fmj%2Bi7HBXUd0%2FelU6IHfHt8Aj9EPGAAoAvgAAAAB%2F%2F8AAnjaxb0JfBvVtTA%2BdxaN1hltI1m2ZVuSJVneLVlSHCdy9oTEWchqtrBEJRAgCYEsQNhC2EsbWmpI2dqkQBoSYgKlpaQthVL0yusrpW77aEubfq%2Fly%2BujvJampSTW5Dvnzmi1E%2Bjr%2F%2F3%2BXmbu3Llz77nnbuece865DMu0MAy5jGtiOEZkOp8lTNeUwyLP%2FDH%2BrEH41ZTDHAtB5lkOowWMPiwayNiUwwTjE46AI5xwhFrINPXYn%2F7ENY0dbWHfZAiTZbL8ID%2FInAd5xz2NpIH4STpDGonHIJNE3OP1KG4ISaSNeBuITAyRLgIxoiEUhFAnmUpEiXSRSGqAQEw0kuyFUIb0k2gnGSApyBFi0il2SI5YLGb5MdFjXCey4mNHzQ7WwLGEdZiPPgYR64we8THZHAt%2BwnT84D%2Fx8YTpGPgheKH4CMEDVF9xBOIeP3EbQgGH29BGgpGkIxCMTCW9qUTA0Zsir%2BQUP1mt%2BP2KusevwIO6Bx%2FIaj8%2FOD5O0VNrZW2EsqZBWbO1skRiEKE0DdlKKaSVO5VAuRpqk8VQJAqY7ydxaK44YJvrO2EWjOoDBoFYzQbDNkON%2BUbiKoRkywMWWf1j4bEY2iIY1AeMgvmEz%2FkVo9v4FSc%2FaMZMrFbjl4zWLL0%2BY5FlyzNlEVYDudJohg8gPUP7kcB%2Fmn%2BG6cd%2B5PV4Q72dXCgocWJADBgUuDTwiXiGSyZo14HOEQ2lE6k0XDIEusexDzZOMXwt1Dutz%2BtqmxTvlskNWXXUQIbhaurum9GrePqm9Yaeabjkiqf%2BbUvzDOvb2Y1E%2BEX2DnemcTP%2FzLcuu7xjQXdAtjR0Lo5n4%2FHs%2FGtntMlysHt%2B29NXbH6se%2F%2FWbFcyu%2Br28H0MwzI30DYeYTLMXIA2EG8QlHpAsyS0EfEToR0a3utIxFPJ3kiIHCCrZ66b0e2xEmL1dM9YN%2FMwS5p01N5jMX%2FBLKt%2F1R83l0LyC29M6%2BiYxo%2FUNg%2FEF7c2WyyW5tYl8WnhWg2%2FhyySbD5UhnDyS7OcU0dnrFw%2BDfGdI7v4QfYIIzOMq9hFtY55gmvC7jZ2FK7sEdrn6IXBuucYhjsGdQ8z0yEbWkkczjjsE5hNAIZrPx2zOLZDmKNXcXtg7EMqidAEEWg%2BSJCBBNwxvxJfc%2FbZa%2BKKf%2BxoKZybnq5vaqpPTye7CiF%2BZFjxZ8%2F7Qij0hfOG%2FcowPA1rT1l4ymWnrKmxxqfErTVrpgwPlz1kC%2BOy8NMDz6c%2BIO38K%2Fx0xkPnLW8Kx6qGAoQdL%2BTD9V9rb%2B%2Fctn%2F%2Ftrxz8dUrZrD%2Fzk%2FferF0cNt1BzctmX2FZPXt%2FjnFCQNz4Ah%2FiKllGiCMs1w5Lkg0kiEwj6VTXCDKsX9rMpnvIj9pcDecXAIXMnqn2dTUbN6w0XQ9ue6FV%2FnnXCH7S3lPWGltVcLsH75ub3ab7A8M28caNrIeOr3o5Q0yFsYL80xaa0EY%2FUEczV7icUMY5pnelAkmUAXmHYjvFWFGxuqlSaow3OM%2B%2FiYY7%2Fl%2FhVELF4EjRqNR%2FbvRbOY%2BDUGzGR%2FOh3EqmE%2FugIQQguGt%2FeMYz%2F%2BL0cimjeZfQDI3phXMbMQsqH%2BCjwVz%2Fhf4idHovgVmB8gLvjbicDcC%2FNypP536E%2F9N%2FpuMibExdohBmNwyiaZdJGoigos7GpF222xrfnZhML%2F7Z%2BylaqP63Hr%2Bm7bdUkQ6%2F2cXqdfmvwixY%2Bs2ksXFeXcE%2BiX0Z%2BIow76DBNgjJ7TOdUK18iPsPflfQD%2BDPsZG2Aj9VmKMMJ4fYRrhIaxhTDR0Elh2vA6h%2FAE6xUb29mj3sjmL72petXjejPy%2Boel60M99tFduCI59N3221xe7apOvxs6aHs7vab1IqY2tv7q2xsHeHGml%2FcV06u%2F8S%2FxTjJ%2BJYc0bWEX0ukW6YmIbGkJRMdjJ9mYIH5QIdJF4hvRGyK7cC7ctImQRcUET99fGXOoft35GYLMQu%2Bg2smnkgZUrH8AL%2F9Si217IssJ916nv14ZrJrvdxLkQvrvtBcjgPC0NXOicO8Qf4mcxPqh3hgUw3DDfdvLJXngg7N3dN2zbPJSaed3OfZnMU7dvmznp3C3bruO%2BNmue0LFsy7S%2B6265%2BfCKFYdvvuW6vmlblnUI8xCXp37CrOZv4B9gauDBlYp7adcUXB5DNCwYImlXOJJKkAdvExXxVvKEYnCo%2B3eIskP9qrrfIYs71CccBjfXRC52udTHHdaP1A1ui%2FVvH1otbrLrpNXBsGX5B89QghDyimlvNB2KfkxZ5C9%2Fem3%2Bd1%2Bd%2F%2FIfFp2%2B2Oxn%2Fs%2B9n%2F79p39S3s8idN6g0yZObwJOgKUpNB3GyU0Ls0PbRzIRq4lcarLKOJBkLRzJQD4j2090XrbA7DW8K3jNF5hlGS5e4V2D17zgss4T20egOJte5iD0bReM9yjTxnQxCRj3c5kFzGJmGbNKmwGw39IJDJcXJZGMkaAB4jyJAKw0jt5IAuIE%2BA%2BU3cVAZZrq9zhDyBrU8oosuxcGNTzCKJfla7JjNVmuSb%2F%2BtuzN2H%2BX4vlB%2BPpdfMXXmuVsNiub1T34SFbjYw5itEvVi0K0Nt9pNJUMI7SLGRhf2xipfCYf8z5OdlGKayOucFeVPeS%2Fdbo3lBrbSMmwUiQN5%2Fed7g0Ds1s17IuZC5kNzM3MZ6EWCa0DtekdJfAxz%2BR%2FOX28sND7yRMTBcf%2B%2Bs8mQCQWHya4qBv%2FufeMoWyslPA9DtMxUknxkH%2FyfTnm2CMYzs%2BCq3r7PxY%2FMXomrvTEsRpfEGHa%2BWN8E1AHjElb7d06ddA7oK%2F%2B5Mdsv9EtPms0jv0Z5kf1FqPxWdFtfFr0kHfgDX0Y%2B5PRSG7RUj0tQr7rmfX8DH4G5W28kKeJLtmQsQkuwMP1pk16EV4sl7vrMJATfyUWo%2FGwEco4rh4XFQgaiUX9qxZHrMQqKnz%2Fc2d8b9TysYrAuXpP%2FRf%2FGr8b1qwwc5a%2BeuLa6S6sneNXToG2XrEJi4R5SGs8Sq2S3d97bsfCRaTdaLwKClRHt37mkudvXbjwVrLhuYeGhh56bvfQkHpk2CwvwClqgWwuBfndC3c8dwmstj81KkagcUgbfPY8Zje0W%2F82VPWJHmSq6pP8hPWpotc%2FEexDOK3qU%2BwngPhOCiO9MJRm8TJefjelrzoKnG2Bn%2B1NCUmPE4gHFmBN9jrTigRIpsACrc9Gstg58ULkp9467%2BGf%2FeFnD5%2F31lNrt2967dhrm7bzI%2BVT5m%2BfzKhvf2MzpICEm79Bopkn07lt1762adNr127LwVqQLdJ5%2BlpQDcvHPQtVY5knhYrK6q8%2FJsiP6EuhGZdFdaNszjvpqvc%2BPI0CdjN0AXsFOC3ZfALDJwr4q2Xq%2BGF%2BGNbsxUg5NLLIEXi8otcDQcUts0D8eQ1iVDRAMBTsYiNdRIxE09EIBJO9A2xqgERTaW86BUFn0OD2xFO97FAgFhF6OoQ7prYt4XwSeUgQHiJyDbeke9IdQntciLQ1FlJMaYcUNvZBg%2BFB1ubjlnRNvl3o6IEU2w7fdNPhm%2Fhh%2BFLysUu6%2B%2BDLHkOkrSHYEjH0tEPe7WdD3uyDgvAgK%2Fm4szFFR7ch0toUgBTdWHr7EpaWru6%2B6dmbbnqWEbV2EtxAsXiZAPTtGPSbHsotI2leoM8TePEqgSQprs7AGFf8kuOkPdZPXGb55POAW1d%2FjLST9v5YflasP6v%2FCO7%2BGNAPC2BMZWmsOjp2NNbfHwMCJD%2BLPVL%2BD%2FOYlWEEI%2F9jpPddOFkB5d1GSuKZYggmCCd7JUxD7EXAzxyirYnNDLdDZoFdx14kivkvGc3579Jm36reTTvDgBnaO6vzyQ6chQmlsMoIkIQ2%2BbBDWBud1Va4pcCn8CPqxlh%2FfgtG8IPaPH8C5wk6%2FnZDv69jurV5QhtwE0x2iqOsj9Mx8B9%2F0EaUdiPfOYYDCi%2Fq9jhWRuupMDEU0%2BCtX0sDFxv07T%2FK5niBPqN9%2BtQjgEc31NGCXFeMcCEuQBIc%2FBK4CO78u7EPYvl3yaEfK3vcb6qP1R2tI7vUjVDDUdKubsSrNjYKY1qBEa2P50SJoaXiksIoLiCwnxS6EBuBde87botNfdEWwYvF%2FR0%2Fu5yCqhGeEOR2ynSeyXjt6ka7neyye8kryBSWE52y%2BRBgogrXPZ8E1yIHoHIFUM%2BAbJhE7lbMtt8ApL%2BxmZW7PwbjAO0fAVoXQOuiSP%2FksIVdFZ0aulsamKUzwPZ%2FNYDMJRBPCxsBqLzqHyneXF6Ej9HlIFo7%2Bpg%2BjUb3unRmGpstGkm6etOuDBGA5wCMefp1gTHcdZlvPBXlOslvYTp1cd8UjYLVd%2FJ5awNrIOKLnIt9MD9qdrKrWCvA6ALm3QV9VrsPm60Q7%2BRHJHP%2B2hqfugo%2FMvI2H%2Fmqr4b9tFnKSRY1Y5Ek80Nm%2FWIhr1ikKnxGz9TWXrokf9xwujfvcOTtNTWnxd0F37Y2W79tteBqZ4G5qLCuomw%2BnSr28QESCRVLTyYKILGJOPfcnaIFOsewhRdvv%2BrWa%2FWih0vlbX6Zb75T5C0qNKVFvH1QL%2FvazSWgC2s6oWXXIuUxQelKiJbowuJDQViatLmLijg9CQBMg8WiPgiw3LEeYRmm5f%2BXdnvkDnxLLjMLxtvX74C3OlwPQqx4xwIdpPx38LrlDphiyWUWHWKAzzxurS%2FxTo%2BP5wGFak62ap1PVFFN4v%2Fy%2BxuR39WnIO7lsWfwgVsK17wxrs9K8ltIKuhkw7f%2F6dhK6gQokFKhWX3urrjk%2FrnI0pgfpGMeuQIUaEM7%2BGF5q2iMkCaMQwxxOzcvU0eXbsnS9XknXvP7Gtw5dwPXlFu2ecvSHEZgNDsU6x%2FGdXBYXyOQjzZReSedeEPY6nEv9gJR4oBQJtFO6Kd0fwC6BO4LNHDeBujB6dSNcUQC9zIv2LnAzGk99bUDrdFY%2B9yGFQtEo0GQPNv6vS2drj4%2B1jHbv3aJSMUWP%2BQTZrmbNTjU8wyG%2FiXNNpskybLcJ3CiTF5Ir%2BJYzmJwE0mSVhlxbtbmvweB3ulB6Til5UuUZydpgiFVeobhU0WaBqpJ198d%2B%2FXeNRTZ9%2F1OPfG7%2B2hwzd5W3D%2BhmyjsRcUg%2F%2BCavb%2B%2BVh2ls3L7zT%2FetOnHNxeerv313vzLVqPai4nJv%2BK1FC6040%2F4udw7sAb3laSg0XCkAAs0npBO6VJabS4Elk%2FU%2BD4gTXW%2Bj0wnrMlqNamq4tMIYB87tE10i0FR3LZNhJsb7%2FR561btmes8YBCRkhYNByRtKd55mqTas9FYhJnbRGHuOh3M4QTdgQSqmgRxuzGdSvZGcbMxNQGk5C3ebLjoXIOFM4l%2BWKHmLTJwRv9E8GWJ6dYvf%2FFmEyEGr%2Bgyrr1p5zrgkz0Cw2j94Hv8Jdx7dIVegBSNtgsqGsRQEYiIBoXwD0LNvQ5d7s5Z00QzwNhqZA0b%2BtMG1tQq5nd84uq8R0zPvX35G8uRaze4jcOHzz0w1%2BQ2BIRvf6J6Kgatnrbiem%2BCFvAxfkrndzD9MFPP1GWTUHclpASUkCNAQkpCCcCgDSUDAhDZ%2BCuEkgn8J7i9nMA7pA4lISappxILKfAeSAbIcSDuN2bJcfZILqeO5rLs0MnngSHYRdrHjmaz7JEsEPw51ZqDJDmUIOZIe34WaQeegNsJn1qz8AIpT3yCjyEih%2FxELkuJ0lEMYTLVCiWpo5oYMleMH6USyYJcD%2BuOe%2BkWKpn1Qns34iyYDjkSLvgnZXcgVQNeqINXr48m3iS7cjm8tedyY0f1QvTnHHdsrKby%2F%2BSSbPY8%2FNH6vpl%2FEsq3Ae4ZU1HC44KFiI9o7CEgab%2FRqHbj7s5KAg06s39ZP%2FzxI%2FmVuF%2FTbTSy%2B3Fb8If9%2Fcv7%2Bwt91yy8RfP1QXtW5RzQn7qIiZyuFM5QfJ5E9uVnqT85TanFx0lkP3ukBAMprvsRyi%2FC8NAJL1xbIIirSvnSj4O5netb4JxmNANHPssHAcHMHsFRgEug816gDBeMbdfiuRcghqYcm0%2BXxx%2F5IAEtN3fqFF3LzAXqwoT0PN0OVTNqxo8sxMkd5Ig6k79Zk7VxxX6gMLOZFQgvpW2RrMW1D0BDihaXQ9wVRoBxPLfpknmkeMtoB%2FqM9cRc9IqmMD2XUmdZ7GSRKPUZvChf8BoykriM2MnKYbOHX8R7cLdNCxSFFVQqoYswnlWtlFS2mNkhswVpZiQW1J%2FUKFfipHGlUkM6UKBhMz1istELIHJLMSctu3ugzfaVSOjKvUgc%2FTHK4Sdg2Wscz69leKIkkrwuuWiOe9yGYKQXRumkC3qbRcMwrvhjNXgdZk3RxAUEhuSPvn3nnd%2B%2BU%2F3vlVOmrJzCD8JLxV1OHRjrZifbcFDOuRNTGqdgQm1tSNJ2OcQ04YiEXuxtII1ECSQRoQGYioEsgCfchB4ghAtw7FfJre4WZ9hkVi9MtjuWqtdNDlpMrfEG9fOT6q21okg%2Be4As38MfGquNt7oUws6Ysarj1%2FefE%2Byst86YUVNvDdts3Pv5c8m%2FaP0C%2Bf8%2FQb%2BIMnGq09BgwN01oIOAnAdagI8mBSrqk1gxTDUBOtk2ousEtBH2z4Ir2d3f6k8PXXVlt2qN9RODxRuoJT%2Fv27wm09jRYVc%2Fe%2B%2Biyx2tyzJb%2Fn3J0htXP87eSsQaf2Ly0s6Zmxela88REy1cf4273mI3iXNJ7KxrZibOm9xm6rl4fqy%2Ft27smU8tOfdW2ucBzg2UfmOIVyLIl3kpYlwphDISTXJXsctmiDtN7fNV6zelgxwnWxsVr83Aj%2FS5ki1jL%2Fa0GC6%2B2L6Um%2BaoddlNFuj%2BbJ8mH%2FiaLh8I0%2FU51NspIEfq0dohwyFXKgm4NggwQ4rRhCOUFtxxo8XnitT4cnGfT93IS8FaT85XE3H5LMY4zIEPL1hw443wz%2B1UmhTJyJGxZzw%2BwsKkKZgUiVtKOKMEb2AKHTv61FNc01PQFwKnvsZ%2F9pPA4RKTASWahmh%2B8MxwzHxKy74IRn5LGRjsPUUwTu64UYNY38caqd7HKucZ%2FtHnODtENw%2F2UfHRMaq1UUPDJQ0OKkWCeet5fYOhII1VRz8%2B%2FElg5j4Gxur3J8o2PJ4rg%2B2d08T%2FfwEzSVbyZ9XPro95T477lRKqUSRXQnauHNsISAl27oWi6Fv9z48JMv8r%2FaMMj8onCP%2FDuDZOuN%2BGPPr%2F%2Bp7bx%2B7JlbYdppcNhzKU%2F1Px5aiaGDn%2Fs1iGMaBcleKUo%2Fv9rcxkZj7DBEKOfrayytXNLYiUdBY%2BpleQXdnscKlQcpzuWluxsieeyuXIK6SdxozitWyGOV3vOHHjguyCQ6fpIYy2JwvrQEF%2FQa9Pdf%2FQqOSqCiE%2FEE1%2FXIVKTc2tzWbHnimrEd%2BVyz311Ml3P0GVTj7PD5aDnsvCvH36alEaPMePcMegXs7x8igTu4B9v7G9vTHvhCu%2FkzIdx%2BBxC0ay9zRSvoS0F2lIxI%2BX7klU63I40gLQ3w5ep5na%2BSFnba3z5D64zv%2BQtM4n4ffG3tq4aNHGRfxgrXPMim%2B5487abL7xhdseIRn1KDl%2B7aINixdv0OD%2BJSPwKf5%2BxoP6aiTeQIDVlIhMcL1H5R9PYXvprs3fv2bO7MOplCmweuiq2JRZ1zz%2B9a%2Fv2PH1Hfz9236w%2BZrPXvWfAxlj4NLLHpq3c%2FPQ3uvmvbrjG7fe%2Bo2y%2FcLdtE6VUlXi0ASb1VLUBVSUWSU4HdvAraTyS8xzM8NxvxFkXV6pUVRiJwcgC5zEeht4rwcp7ki0k41G0qlQhG1Vzlq8alEmnFi58caB5Q9vn988MLhqyVlHvLEWjtQFeupdiocF%2FtkkOGPW2ibWaBTkeZ%2FdvPWazXfOnnvL6jkRXpi85sFzZt%2B55ZptW3bl1cCCHZPD06MhySha7UFzjcjbp8fOecFCirzAG%2FyVjBX6OFIaadSjQq1nNhyIe8tVbaaSdHlXIWKacMeuZA1uxS95zILhyrxAdsXTL6m7kNQlx2P9uZf2qhufePFFbpI6%2FOU0WcP99RrCsrwseVot5mtytpf6Y0gm9sdeyKnPQ7onyK4nXlR%2Frg7H95M1upzu89DH6pgUcikoiihJ6NJKmRxV1x%2BMJiOA3YwhDRQrWU0u%2F0rvq0VYXnyCwsLeTJYBq3dAtJDavuzyoVpzZ99Z0%2Ba0uoiFH%2FxcqgDR7rUFeOrUn6Cywb8ZeNMbhLV5ugP9l0zv9UN5b5mFkjzxUcpPJCn3V402pRxtJd2GrnLdhtVk9ZSZh9W91fCSH5B7ofxPiWL%2Bj3D%2FuwhBRdyAyozeZwvQzs79soi%2BBKSnafLviZCcfrpBpLyimfLfTyJtbyruIQKD01tUwJyKEo%2FybaxkSNFUMdMkhQoJyRBQFhnUkDQSXhTM%2B3NmY0EDM7ffLIjqWEGt8lCO6mLia3PukFnghosJD5p5SIho%2FVDkzQfLE%2BIrYoJXkD19pdP7OwG%2FvoIUtagiWiZ4PAFTHHlTVhRZ7dYmPar%2BNJ%2B8JhmR6DFK5DV1foHoLNO%2FpHrvZfmWZ15RQlwvoVDKhCWNK3CCch9lfFBuAqUgpFSShmNaPj%2Bi5%2B%2BWZfKeViJfW5HnUakVL4UCNVkA4%2BETfIqx4B5xSaP2L1yn0zn2ltPn4%2BOqZGmwwEVCaCSqG53ldtL1oLGAhdMLd09MpCCF6tD6ZnAZBY9hDaYsP0jzZ0j5ZjKsF4i1UmLuhbJMCnYJPt5VwFNvmZawXjEvLJqIH8STonZjq7BZ8gKgR20C9MDFqJAX1H64QW2NEup6qgzLP8cvppL%2FNNTOBTCJABOHeWoXzLhw4Wuy7gaBtjKr9kgKq8ZlRYBS32Lpxc8vIhpNDTfyNXWybMJbn2RyQ5EmWc2QF9wmSZ0KYCE%2BcPuYO6b15Uotj2Kd4MItLS7gtFbkTdrFND6pvEZqv5Yv7jXAus7Pg7avo7KDot50NX3CPkP%2BKps8J9%2F3mGQIteY%2FLGPC%2BL7872SPR2br5fy8MtKBMHedGuM28%2FMZmPJMrGgi3Gb1S%2BSi1%2FL%2FzrZwO9XH1ce%2Fz7ZQ1WSoY%2F%2BpMb5FT4ua0Wm%2BJf%2F298nFmChEQ%2BTi71est4mq9VYI6RsymoRJKYidElT2FGnDTZvqtfhGAFTbeqEw68GqtfmbVa%2F1IFO1%2FjdWr%2F8BDRRtQh9XNjubEm4aWVpVonpTGR7PVGc%2BKJNoBIWF7kYi4gUV3r1U6723i6TxUl3n3%2FtM27aZfKb7THiHW9VzFSwHJ05VfK6Ar7kaB0XgPPE0BSkSFKsBUpaLihEWoA9wBt8qirh2VSOkZwXEwyrxZ5jyt2rJmSo9gX7cg6jsEUGJU9z9xJPOEM3uQQxKgkh35DNATnVyrmJ3mbCNyIB%2Fyox4wH1bg2DwN7q9kov4pFqny8oSm3RQbGgJ1QQTs6ZMLilOVYJ9v6Wha3HcJ9jddsXp9YhGUXLXt%2FqMDnvLpPNTXfNa60z5%2FyjXQOMq%2BlNmwh5egpYrdfZQZV9rI47xlRkuyTjpzsmCBSWNkAXVoK8sgYWqQJWbo1RLo6QH0YW6pxqfCnRgkd%2BRiFjUQUQ7poIaYoakgXxwFd9BuuI38H1xBxXSFb%2FpBDIKQFn7YB3dB36l7sG1FLaKiBdp1KxLvfswap%2F30lnVESgNnvjbUoT6w9N%2BXoio0qcYOIM%2Bheg940YimsucQVvli9NEcft2UZwGQwLuilj1fFr1i3NP94X%2BPE7Hpvtj6lBJfJ4R6NvWiaL6MgzWHxiN66DExa%2BdAdAbMYX6HVF8A%2B7rjEZIXAVbDe7PVI9rmN69JOLV1DOSvRPxWNPZBZf%2FNf%2BNy65BhYxxxV%2B77XJ2wfQ389%2FIQPgajXbwMsuAz%2F0IaQcXJavKbRqR2IqyZruXjVC2%2Bhdee%2F5vdnYOedpmVtR3NGXldxSzDSIiBVpkGb9by89UpEPKrSLZmyFDzMab%2FwXl2CNe7s%2FqCtTvWgG5kpBmCBlSzDS%2Fr8N4uwBwohRW63JTS1y32f0TQsPfXVGEHQrV8%2FNCfiOUVirYcBbIeA2%2BiF68rQIo3B%2FS628vYESr79ehzS7Q9LEL9UXmik9XVHb1yBO3Ngvt5935%2Bk1efkV51mzzrM0LL3%2F20avnwMeKuWyOUZg2TasSqZ%2BKcZQiOn1Iu2Vh497ALUVZiCKt%2Fgh6IvTIj1ZLRjWAkpHKOKovNwp00eqPROiAbiNEKieXwMLcXhVJ1%2FuzmLP4tfxaHR59cBdJVG1kTAgl9ze9QKUEQ946Hkb%2BokJ5JRDyf54Axur1D%2BWS49cLr0tTPEu7UmXrxcSr3XNvumv4yXzInXKH4F7Tc7p17Zt%2Bt%2FqW2%2B93k063X7VW6lALxTY7i1nBXMxcxmzQbabxz%2BtJo%2BwijYaIGMNS8AoSMgAPt84DdHOoMPfjXhF%2BkuH1tZvuFQrRCN07xGcXRX9MYxYchDe5BcHj%2BZ4i%2B42WyPc8Xofi7bbZJN5nJLJ5qr6IqRtzqNlM17SpFsnkEyTWoABEjz4JXOQvzWYuwdnV5LNGOwTM5v9r4RpQ8ZXsYodks3o31JBlzbYtNotisnm22MxiwGFXam5oN1n0TA%2FhRvshvTSDwHff4nNzRo9Dum6PaJbMXzDz%2Bx%2BFkj4L4bFNBb1asqsgH7Dyh4DvbkPtf5yMDKzEwyoaESMSNS9P9gJVA3%2FRTlwoMwZvxECFWxIPNw9gi01nOHjP32esZTtmXHnxvZd8ZtakqQ7ekajbXetpNa6ocTVxJtY%2BuSe69OLz77zh5bDR3xjZMzUz6fxrz1nqrZGcHQHfPVefN%2BfiK86LeXj%2BSc5lPKy%2Bk%2FvCUI%2FDaLFYCWHr6nbXuILTIsb5imNKY%2FrCm28fSMxPhkN1XbNMNZGuqwOBhtTSxWuTk6bw0ZaG86b1hKddePOKuBvmiguYBn4T%2FyOqOyGRBt7bKUI1GjioBC8aUKwF7Q319UgcmtFGIzCJGBqwQij0ynDsfdFGc3TS3BlNfJ25xmzniMkpXXTPvCaD3ZaZvyzjmZdudBostmhb0ORZNN2sJBeed1HXkrUsywueQH%2BL0eCPxmsa5ZpgRJSDZ11yDv%2Bjmbd86vxZfc1WcZJ3UkMq1BOOOVtvu%2F%2BpB%2Ben186d3GTwWAw2jheaJs09%2F%2BLNfZft37DALyrNj1wABMuUKbODyTVnT%2FKYbJ3Tpq8IrNh92dkxOj5P%2FYpZx4%2FycyiVcDYdn4JbEoKdQi9054iBKsygLW46FRGxAb0NPNCm8BSNCPjoKcj6EAus4SuP3rB%2BcV99%2FeTF6294dA8%2BTK6v74MHVpYNRt%2FI30e8QGTOOdfGWzzxcy%2B87a7bLjw37rHw1nPzp0KyyRSeZO%2BQQhInt3dYgvycjrPOv%2BT8s1rptaP84VeywdWX2T4ysr0%2F7TLIs6%2Bx9zib56ye1dM9e%2FXsZmePY3NDs9zlnNVt4%2BWgHJbbz3Livg4P9WWgviOMm4kCRT6I8vw0NbUUEnFvOuFKoxQW1gTsvFirsF5pb7qTUCx4i7VmtToveaDxvK9uOaedVvPRpVOnNz0Q6bry7uiSdQ8t7Vy4JQKVS%2BXPplV2ts4bvCwZu%2BKzgITtxepaPRzWdpv74muvv6RO0SorX6cu%2FdqKn%2FXWnrtp%2FZragz13DUCl5myiFW2Ycvb0PtsXnU%2Btx8pvLFbUspLX68mdegwmOif%2FNPDONajTGoUh6tU56HBJCTBASVvNUB5VIiKpc9kd7kludodSFz7xQbiOmMk5dOYk56gzL6uaf7N8a6MQOHm0ae6snZpFDfuT3%2FjdYzjzwkXXIVHoXNuCfQslQZqBZjTsoHMqrkE4jaYdgkGz2ATOgB3cPkSukD01DnV3ttb1wx%2B6arPqbkcNAHoFPzKUUQ%2BqL0k97pjbZv1I%2FegC9zTFbrrlFpNdmea%2BgIgfWW3wqkcis8ky5FAcRd1If5nNZrl2FFpungc8wpoCl1BpQV%2FScS%2BzjlASyUTVv%2FAJ46gkJI4bHX4lTnloctxPZE1ckS3%2BjG2fKIjkQFyzuo8jvYQG1OrGvJPSTu%2FnSp9PHNTl4z5hK%2F8gtXVKF6gEKiglgcKiRlCESsQCV5QIlKWKpr34lt%2FwkSx%2FJCmP5%2FcBKQfl%2F5gd%2BrOS%2F%2Bp91%2F%2BYCg5CXK2W4M9fu%2B%2F6xxX%2BvnelVuldIDCG0VQTpU9Dw4pRfei%2B6zWx0MLie0gPbyrkmRU7OwT16JGeyXLHqOLqAfVN1GPlBzWtFNzj0TRTCjogtP1NjIvu5habN5Aoa1k66wGpqriVetJgiGdwDZtKhnN0y4n9sXYnsqGmZfDSR15%2B5NLBlhoDaedEm7sxmpqRija6ZEEg2EAnTiAC8IrmFbGz1q08P9PSkjl%2F5bqzYqT9hMmptEXDgTqP3Wiye%2BsD4Wir4jCeoHbbp5hRfpB7BakUIppIlPCD30dR1GtslDz8OsqbXmejFC%2Fv8wu5X2myq7SJ8Avzv9DFUJySf5uNvq4%2BTi7W9D%2FOZrLChdwxmPNiBRqVjnpK%2FaGxRCDspVYKAW9AN1JANoo8wP4BJUlGqdgw6m1qPQ2QW3%2BOfU5%2FieLS%2FNuKpDU3uf8bcAXyBal5jMR2NEAbPAZt0K3hvxHBEDlUxfIGcD%2BN2gNSNx36nfqlAYow0puatNpRz0e4W2oahKzQHsjf2c16ad%2F3t2KTtPobnX6D8C8pd0MDP%2BKx7wnXqGGlLQcvikMErm6TmfsuxJXbSAxqNjOogJLQBLiKEHAE%2BJGTS3JoEhTrz8%2FCB%2B5YlupJ58aOat8Kv4JvregxwcU5Cp8GFAFm1FyOfto6GS2m1NGTS6CPNKkbsTdCBlnN9onMho55BX8IJZtEQ35lk%2BhtwN5A0V3RCPoD%2FyXAcv6pAtbZczRUA64JmcUf4q7Q89ZHLeJVZ5D1Ps%2Ft%2B0iCT3AHVtZC7JDCXfR7OSb%2FXja5H3zQbZL1B%2BULX1BMTEk3AseSpmnKEK4T9ekMIidUCRQFfcbj7z8gNLvzF7mbhQN8h6ZbRset%2BnQWdS%2FZX3k7WpS8P9sfo0iGS64wV516pOhjI6TZ2dApgI5%2BLhxywYoWxKUrykKJsIoDsR4mSrCTg0egMPnLW%2F3Q5Nn8BZEuzqEI7HK3n0%2BzFmuO3TtWQ5WJoG9YqCD6Gc32SxnbnVPfsxvrFXK2dILl7bLthDp6glhcsfp4bYvbSmj%2FmQ94uBTw0E73x2jbNRCvC6VL6GCFDwU7eWQDcC5FY5s0slieRDwtAbRsbLXbaXAuu14e2OJw1dc6jQ3ZdY8v7rv2%2FBWZLqvFWVvvcmwZkK9f5jS4muO9yR5res4kfkRxhV03L1RfPOiPtYi8pd7jNEsOpyTwxpaY%2FyCZu%2FAmd5Or9uS3DYaeqVOhH7gZN%2F8I%2Fwi1fEuLXvyNivibjuKvN%2B1Nc01HF%2F3h%2Bef%2FsOhox8MPd5SFucPjorQwXT%2BytA8EmA5mamHNFDVhBI5pjZbQpugBNkO8MvRub8KVDKST1Wag7D3xlin1ZF7LFP%2F79nbvCXFOY%2BPUjrT7%2FotsPXXZ4exdPzuhZuL5LUXVAn7k7PbhG89uz3b41X01gbjP1xwlu5rrvvf9%2Bpbs6E%2FVu7Nk642%2FPYRaAiUBdrmO6CDTBLPQFA1ur0uXoBR1INDMkypKpoTqnSMx5GiEdTEaSHLs0Alvu%2F19%2F5QW9Rv1U1ridT22i%2B53pzumbs%2BXFFXYC%2B%2BCGsTj5JUT%2FGCgRt3n78i2n71FHG4%2Fu6X%2B%2B9%2Braya7os3ZbDmgWfXun44e%2Bu2NZKuGZ0HiF8M4TlMPR%2BEU6rPKRJ8wOU2RFUFLex3egEsz3YqEAq0cqhAAW19dBZIlVzR61tuIdTnpXH7l%2BuXrbjPUyep%2B8cl6aXKWhPHpDcXl9KiTWDNr4mBQc8Tq%2BNzK%2FOKSbsfl79o9G20R%2BbrBXYvUg0rLHhtrc4TN81TTOWSZ0gL1ZVlOYH2ery%2F7XVUjFMbzYpg7UswcqJPQwBd0LKLabJ8IaCr2otcjSkIrGwootKECaUd4XH1%2BSdazRrfddkBU98t1htvWrbjqSqjaCguxrffM%2F5zDCpBALUycmajhd%2BR6ww4SWafuZ5eU%2BtPid4lgd3gt%2Bb%2FY9rQoZNmiXYPXyRHbRs8zX%2Ff4WIFjWZJtUdSD55AP3xtXH%2BZipC0EqdBGDA4CoYEU6gRLGPU11QhkLTBiEYPiqOeQgwTCl9aok1Qr5pFf71qEeNxjy%2F8F0GoqYPv75Yh9j3x4DuJ%2BuEzHRpAq2lMqb%2BqfTdiq6kGtzfOWsv0c7lSeMXDHBDe1MT%2BLUgx0Pg%2Fp87u2UicdIvqQi8DkxhcUwUXCedMpb4NQjwY3npTmgsURJavLwCRyEcN2HfWsDVGfv%2Fu9ZUWUx%2BPYFueUKwaNvbtu%2BXps3eVWbN1GcgVrdMnWJ7WmJz9SD66EBidag0NF1Ukep0t5A7sFCWdhzvYwHv6L%2FBehXuHqfaBwBEU7hfVLcXvS4VQv%2BT%2FvaSIl7cbeMc7ekv9i8S3e1L5xxpvMGcu1EYPbKyCiijjGXcDKckm43PqU2qNWlXusZMiqF82cuVzolUHN9NNR0HZPxFPV9V0wLtvq%2Bk4DqOwVWDlzuQLVdqFiP08cRX7aRlBVfR8cb55bWe5LExnlcsDp1vAP8Q9BucPMk1Ulh4GnN0SAdxcNHv3q9ohx1Ati4S%2FtkWjIDe3hQdkUGrGRaFBiUdiTSkI41UkMuuQHP%2BEaSQYlPQTFWJF03BNPpTu5KFAdkWgDukzsZKMG0Q1TAQQglScOaP%2FdsZ8%2BfP75D%2F9Uu5Gs3FY%2F2SxPld0DHOciXI9gqjcEidXjE%2B3BLosy0OcX3T7O5g65ROGyzQ2BZs7WbZVnO5ydLe32hMwTQ4wnnKXW6XW5LAa7oaXOIHoUl0FgLQLH2by8wSTWeAx2Y5PDazK3BqZbeJZwXGPaYhX87ZNszoDdaRxotXO1nNlpdvAPFWHDm8PqEE0sZxDEqGzxisFNnuCWetPcGrObN0p23tTZwMuRVodSV8%2BLTrOV3eRvzjQZiSjaLYS1WEJe0kNsJlZu9LFun7%2B%2BwW4gRDRbaxw2nrOGm%2BxOj9cmtbp9ZqeTM1m8UXfQQCSTVSQox6pvtjot%2FFpHvIUjJovFEoYvHYV9C5Y%2FxN9OfcalvII37UEhTbTg%2FAQIaPb4Vz6j5u8%2FaViycMod%2FfkDcpu8QZbZoeBi%2FvbzP3XPsZvOubMtaPHkD9jt6%2BU2O7vqU%2F9C9SMvgrXpQNG%2FE0oJxun%2BCiElUa0IKQSUwERxOntKSV7ekcuh9VBZBBo3VUcB58ofKBHCwLyf9qFosz9Ibf8dGqwaBMjRig4SGOZ2UkWI7UiO9OfUPdxOYFApUZyfpY7mgEc5rtNGGk2H1lPhAk1Hp%2FVAMqQEHEUfEYkkUQq1JMdzsX7kklRrTrUi1wMcDjmu1YYfATj7Y%2BpGpPEBXuoQIj8rR9mgCl4C9yqmF7xnVWxGVniNqtpVmXBvQ6iwni5YQ8a1jYrXtc2J13HvgkvqWxuva1sbr%2BP2S5ceKGyBwDv2DbrToe1u6BkAJV7xnVLUaq0sJB8pFqcUIPi3yuwxi4JuLr%2BP30f3OkPQ72aO0xYo3%2FEsmO3QO5qEF8S0qQH0UsKXv0brnl9%2B8M7jF174%2BDsfvPOl1au%2FRL5%2F9DsbNnwHL2pHR1NTRxMZhJtHktOOxLxErPF6YlLvpC9YP73x%2B4ofw%2B3xVdrHcDE0dQQCmCRgvt9b35xINDf1CDcRSfJ%2BpYl%2BSf8YcurfmXP5F%2Fkj6J82jNsrkWiEuhVlgFfyNkB3S5MUzLhoNiwSCYcxQ7Ui4J0Xh7fmqRbaPa1tzujxkBRlsEHy0%2FOM4pYLPb7g9O6BQJN6l9zQ0OGyCaZz0vMTbHOzXfQ7a2tsterTcqxeInODoemdktw%2B1SbVhKwtW9ffe8VKadK0OVuC3bWzyKm5LeddsWTeorWyY9IMtUFutdu5g%2BRn533qkocdvLs2HmhU75br%2FMmWtD8zA3OP2t1ea636jEzqYxJZGAwFiDEd61oTsrRuW3%2F3pYNi3bS%2BRd%2BGjOfVpAPNd6y64Gsz1GaZleWIPoYL%2Fv9mTeQBENVEguiF1aC4YeXxFETw6QyPfn0m9g8IrMFAvKM1EI11DARnbqibHk%2FIojy5rSdgCyZi06y8sS024PeuO4MfwQ5Y9yKRZCqyYaF30vzeHlmUprR21tR0t0yz8KZY66zWuGvxVQB%2F36kP%2BK38t2Hu6NQ9SFJfw0AdpqPEK2qTMpf2VCqJwqPoJezTL824b8akoL%2Bx03nhh%2BoNo5e77psxg9Q5LzebIKD%2BfsY34f2MtB9fk9v5b8PT6tYrgv4kRPwd0q9z3gdJSJ0653KjCYPwCaR5aUY63eW48O%2Fkdo33yxX9wCiMv2QTrk8eGSI6Ag6moG9t2P%2FF7GRNlDjl0gw7pJ5aOXXqyqn8SENnXBmbSwUYLyqJjv3UmY1nKr4t80no0faXsaIEiF%2FBRaIBnItSce4OUif7W6Vm9T9H1X9Vj71BEm%2BRdmIJQST%2FZfVdudUvh9S%2FqqNvqT98g9SQ3lHibZY0mRVHooyDN%2FFHmTgzjdozKw28NwQ0hwN6BCoPKaEk3YtKwNhwRLXuk076CGoZNXDQcRwZvreTZY9EZi%2Bd0s4%2Bztv8iei04JQl6ZbDD2eHV7X4uHuFVfPrOmcs6m6Kr7hssr%2B1VZFcEZ%2FPdJkn1hOs8SXS%2FNFFgqt94PIZzZ3tdaL6Q5vo6piSzdy737pwsX1VyxUrF15iJ4uNkq%2Brbyg1Z%2BO8VsNC1UmcvORPRfxtPrfRwL2p%2FoA1eZp6Z%2FaGffoewaXcA%2FxBlKlQLfhQL%2FoPgBGP3qsA7IQS8qDVNswHKRSheDUvA3Q7MZoRcJMxlEygujn1QdyzfPfq3dEp%2FbXh5e5YXW2Ngfvza0ZF6UgFL%2FE0fTq4LBlvTE2qb%2FKuuzYSXVnjTfM1osvqMHVbm9950quIZlbqaL6YP7jk3kUtA0GnX2nvq53f3WoSsvEdDRnULgo2fN7lNZJgI8%2FVWi33c3bBZnGY05%2Bdm%2B3qc7fNmj4YGKLj2nfqFP%2Bg7jdDlxEV5XsJQZP6hYrS1l0VQr4c69Xueixp90gnZPmE5OF22j%2BSYEWHlZ0K%2FHgsh%2FZtsbh6h2DNRlvv6jJh9XaJaHCZDiUDKNTMkvb8vsqCyf3ZNdSmO0fa0Y4baJTtpbKzuVzeeSI7fCKr2Z0WypapnXJ4gnoWy3PoUIlIQ1TXdqhQJIXp9Wx5fYdpeWh2TY5D%2BYVyKd0jw3iumwi%2FBC3cEy4o83QlZnW79MrCgCjbhWXBlRZVVZZv4rIKpXC01HFlHdHLoeWVl6UVc%2FJ5uGm6CViW5mulYMk%2BHqNYr0AyUPivLg2oMs2MPqtuhHyRyiwvNJej1Br%2BfcLyoAyu8D9B7bgmzUqfFobF5nKnK4%2Bt8MPJkI%2FxHUNWk117jugWF%2BxazTAALQn6%2BUE9lhoI5ApGA%2FiuJOsrlNP28SVVuBVajXmircLel46w2bJS1Q0Ft0KDuikDFL%2F3pYrid1Q4FvofwRIo4R9h2ftSwc6jHAMqLcCql8YPHtlzGoByNXYN6v8hXnRaOhUvx0sVLCexwupGDR4NOYC7PePa5keIPACnuAdD7dEadRuTIiS6Lb7uskb381My5yjzF8lGCjBRqdwrWJCagfB3yCy7XT1i92hbcZ5Ci1FJkgYMDf6n%2BjspIsHFjJrTOdzSMuOa9DbDcj%2FnH9N9bIoGVgzHPWIQuFuYtaMRaq8eCKI0gEF6lPOZjBz3EEvaaxwSUT9U%2F8JbJZPJJLBLolH1La%2FRbF9AbC8JJjv%2FmMnssKjLRBJyqj9QXxNko0Ux%2FX79epfiXkm6fmKwF%2Fen1HLc6LxloXWKvGa5rVCVL83VuiPcDEX%2FK5pTXOxHfx6HHB0t2FI0qI2rCZFTrvPWU67zVuS%2FkTsLnc7IKhFg30e4FOkqNSfH5PtkmUy6Cpiv%2F36k2sbqCeCFNa%2BURpoY0sZoYmCgCr3qgZz6s8I0gP1bYiR%2BD79H56NOz0EVWCTy2%2FfffvSCCx59W7uRV9995eqrX8GLesOXNm360iZ%2BT%2FEl3uZqL%2BFyzSZ8XxpTiI%2FG0nkT4zznFZ0t4ipMz5v4q9ssqbdKUZt6u82knPCrt6PZwsnn0XySVnyPR1ZXAn72yx48bWJsu7apnI3Hy8bygUK5Js32qcytapqgmn95uexccj205vGgJ%2BeuOeG2SORmKZr%2FqKzcx9SFctMJdwMUFZDJITs7dnOp1EKZCxg304Cevyfya%2BvlKqv6aXK1qIj3imL%2BL6hL%2ByvUlFfE0VKZ7E8gBY3M%2F8VoJCFgizH1W6VyC76nH6b7jiibYVxUmVIEspry%2FLgZIlCeP11Z4zs%2FAwvVwtGFEut5S1JY4lfyT0N%2FevOLo%2BrUEgjcqc9IkGpQbv3iW7Co5b%2BKgjvpzYdH85PLcc4X21ouwEGl%2FS4qnUAvoSlXUUhR1eKr2VWFTB%2BGMl6FsiQsVD1R3urlAAIoSn7JQkmiVVCHSpCwDH%2FqPepXQ0Db77CJOAImohB%2BRPWr31ev5g%2FkE%2BzTa4lbvZo8xdWPffQu9yJTPCNB66s%2BzXoJt%2F0L6hSoCuBIoK8fnBGG87OoRckJpLqyWe4YbpGi50g0%2B3I3UD85Oa0fzubfoXxPLbW3FDWzigmyJeM0tQkax7PqTy80%2BUxfUHPlBZIRVNQ%2Bv0xRm8REKPoLmNr0%2BUo48v9GFbXPKylqQ2IKm00QddgyWGMROCTxdLB9nCY8P7j2DjlsV%2F%2Bmfr0C0r%2FNkeXbbpPlOTBBwT0mVz1zx9S%2FwJecBF9Wgv3p032iP2v4VSgfgW2G%2BHUEdEXU6iq4CtpLJfIN9XQG8dwa1VoO8XC2SrPDDyCOQptXgbcPvlAgBfxBoGwftQKeKFrNTASPt3pGGqDt%2FQRasn2kri%2BH6L80MJRsmVYJrAKyDItpJUy3%2F15WYIJqcJ9Q5N%2FLFJ4c3dc1URpWl9hW6mu50MUIelg4ucTPf15zs5DFo1c0VSp1tKB9jkwIyuM45kb%2BIP8gHed%2B6jO3v0KbIknzLy636E8KPTdCuUpB0wLo9JKnAO6pv0vS31EtBha%2FfJemkgLVVnd8KCk4qBTpQ5m7FbifBKrPJcq0pZAFVG%2FXbOFz%2BTcq2MLrcmV28Nmi%2FOHskh82bau0k8eWCaPijQPWQ5lUvslwVCfHkXBMIehqUgtDNLeauH1huvZTbYmw%2BluPjyWoNGEuxRLR7LK5fSyXFUyK7PURQv2v8D3XOt2NJ6liBbmPGOsakw1kbeOs%2B31Wm5qpH%2BiJWSzqdPr2O7zc2TmtnrzCig6bBd%2FvgQmzOlz0STWIlmZEQfupogOZFHUZ7EkUnMn0RrpIMqAgHRJAOjIJ3yGw1I%2FMAp9q9S3Q%2FclADNm1wEeO%2Bxbwg5OIYHZLY3ehG5lJk2xhco%2B6JWybpEVz2wrR6hZyD0QXZbeDVB%2BonmlimpkWprdAs4WEZDSQppsDlcdCBJJESIYFuAtUnC4GIF2C3Uu2Kv7L1bdz6FxtqxpG4TqQOqOUNAJ2HLvPWA2GgDy4O4vaDrtyl6P%2B1fAll%2BSyFcQ28GHqh7fvvf37udylf0fNwhzgz87Y%2Bcf5x9GnF6ygHu18sAbipWeF0YPBgp2GaKeQduxxdEr3SgbH1kvH7tvqSLhedomOvZyts2dw8acu3dY%2Ff%2BucuMtCuP%2Fe4zC4XnH3OLZ8ZuxTWxy8dJfU5dhDeKPSlJy5pn%2F%2B7u3XrJhmr9C5CuleGflGQocKnlAUaRKp0BAHV0ZwUt9VCqk6zYOgRIuMfePJzdmBdpPJ7%2F6B23%2Bf%2Bsp9NMDZevovvfYHG5dGPISQq1DojqNckchVrCcCYz%2FQ0hI0m3NKDRfkgsrnamo%2Bp0CAq1FyvC3a3Nak%2Fs5VX282x9Ufy3E39VAx6o7LpCvO2wK%2Bch9jNqpJCutcIOooKnYWtDK8gTRVYygRQfwgzKM5%2BjP2jOZdx3r32Py7rQUPOzAnoRs95NvRAR0qLGU11Taqu1bUYSzMcWjMEir067JQQHfIrLBHsrgv00%2FWavd8HRLMEEYFSW3HCSNQehnrHztKqHcDyo4VfZ6gPKCR%2BgufwA8GegxUEo4A%2Bgd0BASHiH6jYMLIsUdQJTs%2FC641KN4oCHWolCMLlMfIdtWKScjx7SM5LD9HnfmhrGI0S139UWfUnxgOXdJFW%2BAMcGjKr6eHAttHF5sUoeArYKDcxMSYcKA%2FxUDhPiEOEAPafSIUFArN0r24ynI91EPARDXvIDYyvqZaWeroBOUABQA%2FE%2BDXC7PWafDLQY2oiwpUEyj4RQtVlUp1GrM7In2p2A7VuiOW6otMiGOo5Mrp05ejVuTy6dNX%2Fk%2F7mybZQ0nUmfrbx3U4KueDnlHm5wdh8FFeKnoaKKh%2FTK18StOPhwG9Xo5mqXAxvw%2F79YQwwDR%2BnAKQQ4izVXioB84qcppWB7IqjU45z4CE17OvF1Dw%2BoTFqxtz8dxwtogBnF9MjIl%2Fin%2BK8s3hM9laIn0TiCbTAXL0T798bPXqx36p3chrv0O%2BGC9Xaj48Ecv8U8UEeBvUEsDlTepiU5OvlpeNGvpnKF0RvUooWhIjnx6GeBapXCQYTw9DNg6%2FOC3gZjp76oNTj9Kz6Jqobxb9NDqc08vcKReOpcsQV2K8InXFaXW3aI6Ofr1k48rp7CX7rx%2Bv1UKPsfvzQU0Kc83i2VdILmd2%2FyX55zT9luN2%2BCu4nKfwPcK%2FCvDVU%2BpHh8%2BLaldIf1fA5h3ndT6Fln9%2FW%2F9Ce1vndfvJtnPVO2xhm3qbafHVCN1X363UXHq9xuVD8OSD29Z8pZ5cZrern9cAdGW%2Fuib%2Fud%2BVK0L9a42r6C90kL8KzxwLQw9NkIQJL0ASU8M%2BVG0KsUdgdvpgP%2F6NqqP0%2FgHZFUfGEijZLHpiIgvV5%2FBltrj8Qd7XQd5p4P%2B7tJo30NMO6VGBwahSPMYiaaBYoLY6uEnciyhhh1Z%2FvvacG%2Frjpsvnpzs0B1Id6fmX8119l88XnOxe%2FuGrzzHcdu7UtY3%2B2vmXN5zUyj3ZcPl8p1sZSs6%2FnGXtwrV7Ka0XZdz83fwjjINpZWYw85lL8BRK4nGyIir2RiOsEyipuEcIakpGjWgBjLiHWOgj0Yi34gW1kKPxHt2Na5q%2Blwg1RdRSpFDNzosb44YJXnAfoEOpZW%2F%2F6u1lhYA6leevezbI26zNHO811M2dc5HFxpk4i1jPC0s21%2FBWW5DnPQbn2X1WK43%2FaM2n18DfSoybbNHijFpamzXI31eRibGUOxSu%2FlT96YZlq1Yt20DaSBuG6knw2eusHs5EPBfNmVvHKdaQzcDfz9ZsXmLDWGXy2U5OsYSsIn8CS12jQIyD12KKqZrLPy7mSPdICmd6WGHG8NDZkkHuE4h9TU8FpmUO%2FVjC%2FEinToFyoNDz2p9XD6g78WgQdPG7Z3R0T%2FZ5dTM9lsL8Ktek7szl2L%2BgQwGgwkZHc2g5Su7NvVqwGy2Ua4KSXUwt1X4PaM5paaEu6jQ5zVFyNabxvUksVt2T%2F4VeamYPlLtffdQsk%2B2sUTY%2FzDXl%2F05W53%2FBz9UK3p7LjapZ2ZxOm%2BUlZXrL3HHGqO8%2BwVroDaCTTnTxitMxmiAAYQzVJQH%2Bnj3oIHnPaN6Zq6sNSLjBl8tKgVr2mj%2F9CWi9dnKca8rBQBsd5R1tzVlgrl5pbnPw6kZclCr2CHxMnHohLz%2B3KRQokzALyeIKFU1TNCiayJdoHvDYe7K6mZLm8S3uJ9dojuaJ62%2FqN%2FtjQxnSnhnKPw%2BLNrLi8ZKyJ3x1YhiI1aNAtP6NzCGzYv3DmaGh%2FLvQZnt0evgIhTFV0kE%2FPYxAnOHhCQUZdCWY5JWJwMzlAGl1mpNbDU7yyGnhRMILsYhH3VRAijrPcBU8%2FCj1Y9NY6cnGVW0CjTLaz7E3epvaT%2FLtTV72Rs%2B0WVVmd0dz%2FMGTI5F0OsIviaqDlbbO5X6xT3PeXbXHRtf%2Fz%2Bfdka%2BeKPr8KF7IF4vBsT9MFPuPJMBTBMq9hQxXelQ%2Bbewnf18ap4Ib%2BmSMrtDU5zqlD8QANa5MBGh%2FOwOvSDfcV2d66mfEWsbGWmIz6nsyZDWQSmqmxDneYyvjHPmRXHZxeueyRGLZzvRioKnGto9nIPkibAJA16adcOZRQr1iAP3bUyBR7T4RgAWTKxhkCYFwshq%2B7iV9r0whk50cmRcTg4fy5x4OmmNkHndIA2%2BYuMbmE9dwGYB4KFTsvnDE6Ah47r%2FfE3AYI%2BoXADpkdlENcZ8OZEEf8FFGZNxMs6ZLpG3SUFLL7Q2kcFU%2FA%2FJsw%2BvWDa%2F7emewLaoeibaF1B9qUNnuqWK3%2BUfXYVL1v%2FomD15xxeDkPnXTOKSVcCbDGtOu0YQNpGAP7U1HU58UrqGu8xIbHtkQ3LVhb7Dx46ET3Ffcm1q0YcOizNmf3bC3VjWfAcpSv3MyTlgJ23FHQgmgvk%2Bgk8pL0mcCDOn08MDAQlf%2B%2FSlTZ1z12fnqntOhbOTL9%2FZdevbAPN%2Byby1f%2FuUtC%2Fixm8ZBo59LTXEW060hGrTDplNprWd58fwB%2Fb%2FE27BdS%2Fs7U%2BrGVCeQ46nzaw9QccnmZerGZZs3Yw9aVHt%2BKh6HN4ti6lxIhT%2FwahnZtWwzlY9QHQ2c79C%2BdxzvVDKy8GqKWQERO9YAKbpsDUTLdWV5dE8PVPjvj9pqw7ah%2FPFVtkit7aj6G5xY9mfJrCz1j1e0BcnPol4UjtrCdbahIVtd2HaURujnFJR8CuOuUUfhrGhgKKgjCYNSvCc1WKlEp8wHUaAYynFNyzZn%2B2MnYv36dbMDBTonl%2FT%2Fma5IKAyEGz%2B4eRnVtaX6tss2o34u8mWorFtuFgm4A6qK%2Fyp%2FgLEBVat5WnPDdKA574ubuFJ%2FIUfZ%2FY2Nt6mN%2BZNNTSTaeI56gKwkXerTe9DDHUw8%2FH35FY3nNN7GGuBKWhrV9ep%2B0k1WjNWVaHkW1yA%2BQHWNu8rtBw2a5YXuE40rs7%2FGA%2Bj09V3hA98yRnFPOGr8ltGlsFdD%2F7tRce3LH6Trcneuiy7K7J3khKu%2B3qUaXPWaX7T6%2FKfj9BX2eZq2XAcZT79u1ClJzUtHUqfqSMWBcZS43Ena0cUGLgpkKxB1QM%2B0Fxz10wgg6r5rltnFpH05pepUq3Y2HfYqeKRntmUFNz%2BXmcOs1H31U6cC6RTVLfCg7RNBF1UF2%2FwBgu0fFQtPEU1sSg3VcNsR7dWq3af87tUFn1l3ltXpaJxpNvtcZkH2WmMst3JqRpxUH%2BWC0E1qOGtP66s1MYv%2BVLu8%2FXFXvV%2FZbunYYBeVN64ls0ur6NzpV9xzlmQwB5qC4Tq70WC0tk8dWJXeHvkD0h9zJOM0vD86%2F1NJMaIAolctvlByferCsqOKDKceOfUu1PsmoFCamV5mCrMUOCi6V6FJosMF22AcrKJgQDVhfYh6tepp%2FlYgvnCEAbJQ1L0rOpajEmRcasMiPfxhgGoVo4rwreQpV6fUJHH2e8fa1s2c13Apl1b89a58ozdoap2sjgLN9uISl7P1DrulyeIkt0zr6JjWocoPOZsaXPb6jtqBblsgsaRre2xHi4nELm0MhG1%2Bx1SXwLpFi53b%2BaHRYo%2FIrbZtuWAKu5cSEXfybnnmUCaXGTpQr0xK2O2WWY76f%2BnAjNVf7nCZHU5XqIkTnpt6VtvsFlPXg1031g%2FVRdpkkyVpD7jnmax88QwDvg%2F66NnMRdRXTcGTmQc3cuINwN5IQqi0yzb%2BYFVHuVqI5s4ADfg5oE4ybDLd28mFSFmYvRoomsWXEdLU2Wl3GJy93ZNb%2Fd5gqmNaqJZSO1l6PVRy0nZIj%2F45EetjLguh1rLqR%2BSK0hO6NrsqcNX8zoUdjQYDJ7tb4os6%2Bi%2BY0qpY2AWlnLRDWdGFTfGY1gV0zNAtJ7pdo24se0D88AwLY%2FgZmE9iuP4V5v7CSR%2FRThaHLh%2BUeBkXwU6BC7lGOevK65udTv%2BtS%2FPfW7qj3ljTcj3b9OkbV85t8xsMj7Ddj7DGpthZKwKPvso%2Fc%2F1K9aLE12fMWLV1y1D9ua8lyJdWXr%2FbG%2BnoCFutf%2FmLILe39ITUV4igr3876fpX5g2zeB52sWnIL4fXHlgeUzOx5QfIvJQyrKQE9wHUqVq%2BPEaOrz0wVvNbJZVSfsuMzxN4l9PkedFzw9V5Dj%2BnzpgoT4ZxCxJfC5RWLc74YVHxKlExCYt0JAOMatREhHBSCAtSfod6x6Ls8HCWECLwXZ9nd5Dz1T24JUdWs6fU3%2B%2BfcnT49Qe%2BkBs%2BwdsMZgPXMp3U5S958snPP%2FEE7bvkOPCuTUDTUQ%2FUzirLhML9yPahoe1D5Fj5jWsaoveyP00PehdUAHk%2FseDVWsvDWXXXsyn%2F4wfpXc2V3%2FQxli3jl%2F5hj%2F83avSCfpTNxOEKLmTjxOEKuxgNlsQn0xgct724mhynupNW1Ph6o3RYS3%2F%2B2TJrzLlkFz%2Bip3qCHKf6eqW02QJLjBYuuj4sobhCWqa%2FYHGEHpcnumuWSOhxeaL7sOakNR6vvmo%2BYcfFA8UFXEPZf9UjyudIOyNwx%2Fi90DdsujS%2FFX2UAwvWSVK4NxaMhAGw3oowp%2Fuc8CTi7D2rBgZWwb%2F60faR7SPsEbjkXy4G0XaqhXPwe2cePjxjxuHD6ssQuR1fq6PF0E%2Bo2t1nePTn8TUmxz%2FA3crMoCc7egESuoTHYc7mYdg6etORoOhR7BBGD%2BqJopELrl4S6cJNRtEAsLP%2FOdvnJq0Wo0GolY2Et9VFB2Kf%2B4bZvVyxfOMz3WdFfSIryj6DwWghre7aQbdiDrkTL3A3vNDuDpk93HqXwam%2BbWmUJZfNn5ozKV5Pmmq8PF%2FjVY%2B2Tlk2M2RzSXKjmbQ4RZcQavEYrN%2F9rlXwtIQqzxQNMzPPfHYLvuPoO9TbT8bpGw5CQPGd%2BSyX%2FCyf0Vxjd2R9NmsunnXYa8xGHzn%2BsSfM5J0y0DZEXWWxkXjcR75KBLNLHi7XvX2G8VOrf4Ykg0AMdBESIpo7MgAfyakA6rkqpI6UjNs0px7cMV%2BD5BF49Tez1VGnYmq0WIijp985m4Sn2gJR9b07riPPFo97OYbUZbxJCpot7H%2FlpZBicglCPN7WOfJkcHqc3ElWqvvz%2F1E6bIQrG%2Btz6WkM1SM9FBTR7FSs8KyBBytSmNEoquJNFN5EQyTiCrnKDx1h58yxCepPHU5nxGoxEQeeOZi2m80DxNxncVhr6BmEfUarxejw%2BWSiHhWk19bSY7aKR5MsteblJpfTLtjimBouXsm3d3djjYM%2BwEW0El9dM%2FueVRWIsXwe43R7SgbVZqrnqoJ1X%2FkuF7pcgf8duv4q6vayV5U9zMV91GxO59UUjW8rHV6u799WzKMT7umRCXbYUKM%2BfoaCcwgaoqZUtmodV3p%2BX7akb4dnU9B9La38RPFUG2SCC90tVA4XwEFhyOpZZrUCsgWYHsczLFBBVGNtstoN1bw0Z%2BO4fYIbvZVt4EUcJEKOhHeincWqONw%2Bq6w5Go%2BWGOSR7LhKV%2BKBqbBPpfUvOf9QqkpDyVhBeyyZQGMsdA5FBUqvFMtUyGq9vjnsAJU4UcrxldP1CCaofyDkSAifoP5QwWx%2BSyUGxp75BzGAvtG7uQ38LehlyEQMeh0TeE6Bm7tYdXqdkt0uOb3kfYlNwmOdDyacOq%2FqlFo1v%2BPTmTi3E%2FglC9W11b34A22zmLzvb231Q0L2Bgg60OTW4YdstO%2BYOJnO38TtpH7zy9ymokWyA79qlVSn38HtpFlImFnhu3b4boNWXklOXV0Iwo7lQ1hrZyPFcwtjwFP7iEKSHSSJw509kh8kj6pr%2BH1jR7km9vcvqN9657vffefkv%2BfKxge1X%2B7RdjYUPIESN7gTvRkB%2FRMYtEkaVkdHApmdBPpnKmz0n1xSWFOyVIuLrinZwpoCRe6kyiVZoHX088F%2BUX4%2BWKS4iBTP0IWxGtZgOdMaV4KTayqHQF%2FVihBwTbgDXTCmKoOBJeNhwJMzEVjtjIFLuU38fPR7hqNG1JS7g%2FqRCuy3vmQ3W9Vu8qbVbP%2BSzazGRJH83MzP90Ck2m31mMjP8TiLn5uwD2Ugr2PFvPQjB5BnSJvQxGQZZEB%2BLopqzGzDbMmbkAPkZVJjeO5FzOSBKCgJze2ZS4Gemc9twrwY6u9H61iUQTcRvtdT9RW3tRxAWwFs2tcuJRnI6xjmBdWjbgFNRHMHiF1uHYBfUR%2Fut5Ug2jXAaT96%2B9RH%2FFToRwIzGbKmVJ1AZQnoabSB1yyIg7ByAridHApPMjyw0OiV6RjSbCuzwLAvFizBliWJua1tsuAgvNPbmljYbpt8lkWam7b3XZiOiKJskMOtmfScnsbPW208knwjuXrXK4Q1iKIgNyYXXDVT9C2Ye%2F78GQ5BEEXfFdde2RwauOysdJNL5AzCy84ard%2FnGAVN8alecnFdgu5Gbd5DJTL%2BhHZK0vApVy3OfU8XTSJg1TlssivsPYUlIqvn66PzrVTymCc4wgF6SDNR0pDf%2B9Gp%2BVnsUH5WtpHYsuhOaey8zdwLN47V8MTbm78g687%2BP3cx6tcAeNpjYGRgYGBk8s0%2FzBIfz2%2FzlUGeZQNQhOFCWfF0GP0%2F8P8c1jusIkAuBwMTSBQAYwQM6HjaY2BkYGAV%2Bd8KJgP%2FXWG9wwAUQQGLAYqPBl942n1TvUoDQRCe1VM8kWARjNrZGIurBAsRBIuA2vkAFsJiKTYW4guIjT5ARMgTxCLoA1hcb5OgDyGHrY7f7M65e8fpLF%2B%2B2W%2FnZ2eTmGfaIJi5I0qGDlZZcD51QzTTJirZPAI9JIwVA%2BwT8L5nOdMaV0AuMJ%2BicRHq8of6LSD18fzq8ds7xjpwBnQiSI9V5QVl6NwPvgM15NXn%2FAtWZyj3W0HjEXitOc%2FdIdbetPdFTZ%2BP6t%2BX7xU0%2Fk6GJtOe1%2FB3arN0%2Fpmz1J4UZc%2BD6ExwjD7vioeGd5HvhvU%2BR%2BDZcGZ6YBPNfAi0G97iBPwFXqph2cW8%2BD7kjMfwtinHb6kLb6Wygk3cZytSEoptGrlScdHtLPeri1JKueACMZfU1ViJG1Sq5E43dIt7SZZFl1zuRhb%2FGOs44xFVDbrJzB5tYs35OmaXTrEmkv0DajnMWQB42mNgYNCCwk0MLxheMPrhgUuY2JiUmOqY2pjWMD1hdmPOY%2B5hPsLCwWLEksSyiOUOawzrLrYiti%2FsCuxJ7Kc45DiSOPZxmnG2cG7jvMelweXDNYXrEbcBdxf3KR4OngheLd443g18fHwZfFv4NfiX8T8TEBIIEZggsEpQS7BMcJsQl5CFUI3QAWEp4RLhCyJaIldEbURXiJ4RYxEzE0sQ2yD2TzxIfJkEk4SeRJbENIkNEg8k%2FklqSGZITpE8InlL8p2UmVSG1A6pb9Jx0ltkjGSmyDySlZF1kc2RnSK7R%2FaZnJ5cmdwB%2BST5SwpuCvsUjRTLFHcoOShNU9qhzKespGyhXKV8SPmBCpOKgUqcyjSVR6omqgmqe9RE1OrUnqkHqO9R%2F6FholGgsUZzgeYZLTUtL60WbS7tKh0OnQydXTpvdGV0O3S%2F6Gnopekt0ruhz6fvpl%2Bnv0n%2Fh4GdQYvBJUMhwwTDdYYvjFSM4oxmGd0zVjK2M84w3mYiYZJgssLkkqmO6TzTF2Z2ZjVmd8ylzP3MJ5lfsRCwcLJoszhhyWXpZdlhecZKxirHapbVPesF1ndsJGwCbBbZ%2FLA1sn1jZ2XXY3fFXsM%2Bz36V%2FS8HD4cGh2OOTI51ThJOK5zeOUs4OzmXOS9wPuUi4JLgss7lm2uU6zY3NrcSty1u39zN3Mvct7l%2F8xDzMPLw88jyaPM44ynkaeEZ59niucqLyUvPKwgAn3OqOQAAAQAAARcApwARAAAAAAACAAAAAQABAAAAQAAuAAAAAHjarZK9TgJBEMf%2Fd6CRaAyRhMLqCgsbL4ciglTGRPEjSiSKlnLycXJ86CEniU%2FhM9jYWPgIFkYfwd6nsDD%2Bd1mBIIUx3mZnfzs3MzszuwDCeIYG8UUwQxmAFgxxPeeuyxrmcaNYxzTuFAewi0fFQSTxqXgM11pC8TgS2oPiCUS1d8Uh8ofiSczpYcVT5LjiCPlY8Qui%2BncOr7D02y6%2FBTCrP%2Fm%2Bb5bdTrPi2I26Z9qNGtbRQBMdXMJBGRW0YOCecxEWYoiTCvxrYBunqHPdoX2bLOyrMKlZg8thDETw5K7Itci1TXlGy0124QRZZLDFU%2FexhxztMozlosTpMH6ZPge0L%2BOKGnFKjJ4WRwppHPL0PP3SI2P9jLQwFOu3GRhDfkeyDo%2F%2FG7IHgzllZQxLdquvrdCyBVvat3seJlYo06gxapUxhU2JWnFygR03sSxnEkvcpf5Y5eibGq315TDp7fKWm8zbUVl71Aqq%2FZtNnlkWmLnQtno9ycvXYbA6W2pF3aKfCayyC0Ja7Fr%2FPW70%2FHO4YM0OKxFvzf0C1MyPjwAAeNpt1VWUU2cYRuHsgxenQt1d8%2F3JOUnqAyR1d%2FcCLQVKO22pu7tQd3d3d3d3d3cXmGzumrWy3pWLs%2FNdPDMpZaWu1783l1Lpf14MnfzO6FbqVupfGkD30iR60JNe9KYP09CXfvRnAAMZxGCGMG3pW6ZjemZgKDMyEzMzC7MyG7MzB3MyF3MzD%2FMyH%2FOzAAuyEAuzCIuyGIuzBGWCRIUqOQU16jRYkqVYmmVYluVYng6GMZwRNGmxAiuyEiuzCquyGquzBmuyFmuzDuuyHuuzARuyERuzCZuyGZuzBVuyFVuzDduyHdszklGMZgd2ZAw7MZZxjGdnJrALu9LJbuzOHkxkT%2FZib%2FZhX%2FZjfw7gQA7iYA7hUA7jcI7gSI7iaI7hWI7jeE7gRE7iZE5hEqdyGqdzBmdyFmdzDudyHudzARdyERdzCZdyGZdzBVdyFVdzDddyHddzAzdyEzdzC7dyG7dzB3dyF3dzD%2FdyH%2FfzAA%2FyEA%2FzCI%2FyGI%2FzBE%2FyFE%2FzDM%2FyHM%2FzAi%2FyEi%2FzCq%2FyGq%2FzBm%2FyFm%2FzDu%2FyHu%2FzAR%2FyER%2FzCZ%2FyGZ%2FzBV%2FyFV%2FzDd%2FyHd%2FzAz%2FyEz%2FzC7%2FyG7%2FzB3%2FyF3%2FzD%2F9mpYwsy7pl3bMeWc%2BsV9Y765NNk%2FXN%2BmX9swHZwGxQNjgb0nPkmInjR0V7Uq%2FOsaPL5Y7ylE3l8tQNN7kVt%2BrmbuHW3LrbcDvam1rtzVvdm50TxrU%2FDBvRtZUY1rV5a3jXFn550Wo%2FXDNWK3dFmh7X9LimxzU9qulRTY9qelTTo5rlKLt2wk7YiaprL%2ByFvbAX9pK9ZC%2FZS%2FaSvWQv2Uv2kr1kr2KvYq9ir2KvYq9ir2KvYq9ir2Kvaq9qr2qvaq9qr2qvaq9qr2qvai%2B3l9vL7eX2cnu5vdxebi%2B3l9sr7BV2CjuFncJOYaewU9gp7NTs1LyrZq9mr2avZq9mr2avZq9mr26vbq9ur26vbq9ur26vbq9ur26vYa9hr2GvYa9hr2GvYa%2FR7oXuQ%2Feh%2B2j%2FUU7e3C3cqc%2FV3fYdof%2FQf%2Bg%2F9B%2F6D%2F2H%2FkP%2Fof%2FQf%2Bg%2F9B%2F6D%2F2H%2FkP%2Fof%2FQf%2Bg%2F9B%2F6D%2F2H%2FkP%2Fof%2FQf%2Bg%2F9B%2F6D%2F2H%2FkP%2Fof%2FQf%2Bg%2F9B%2F6D92H7kP3ofvQfeg%2BdB%2B6D92H7kP3ofvQfRT29B%2F6D%2F2H%2FkP%2Fof%2FQf%2Bg%2F9B%2F6D%2F2H%2FkP%2Fof%2FQf%2Bg%2F9B%2F6D%2F2H%2FkP%2Fof%2FQf%2Bg%2F9B%2F6D%2F2H%2FkP%2Fof%2FQf%2Bg%2F9B%2F6j6nuG3Ya7U5q%2F0hN3nCTW3Grbu4Wrs%2FrP%2Bk%2F6T%2FpP%2Bk%2F6T%2FpP%2Bk%2B6T7pPek86TzpPOk86TzpOuk66TrpOuk66TrpOlWmPu%2F36zrpOuk66TrpOuk66TrpOvl%2FPek76TvpO%2Bk76TvpO%2Bk76TvpO%2Bk76TvpO7V9t%2BqtVs%2FOaOURU6bo6PgPt6rZbwAAAAABVFDDFwAA%29%20format%28%27woff%27%29%2Curl%28data%3Aapplication%2Ffont%2Dsfnt%3Bbase64%2CAAEAAAAPAIAAAwBwRkZUTW0ql9wAAAD8AAAAHEdERUYBRAAEAAABGAAAACBPUy8yZ7lriQAAATgAAABgY21hcNqt44EAAAGYAAAGcmN2dCAAKAL4AAAIDAAAAARnYXNw%2F%2F8AAwAACBAAAAAIZ2x5Zn1dwm8AAAgYAACUpGhlYWQFTS%2FYAACcvAAAADZoaGVhCkQEEQAAnPQAAAAkaG10eNLHIGAAAJ0YAAADdGxvY2Fv%2B5XOAACgjAAAAjBtYXhwAWoA2AAAorwAAAAgbmFtZbMsoJsAAKLcAAADonBvc3S6o%2BU1AACmgAAACtF3ZWJmwxhUUAAAsVQAAAAGAAAAAQAAAADMPaLPAAAAANB2gXUAAAAA0HZzlwABAAAADgAAABgAAAAAAAIAAQABARYAAQAEAAAAAgAAAAMEiwGQAAUABAMMAtAAAABaAwwC0AAAAaQAMgK4AAAAAAUAAAAAAAAAAAAAAAIAAAAAAAAAAAAAAFVLV04AQAAg%2F%2F8DwP8QAAAFFAB7AAAAAQAAAAAAAAAAAAAAIAABAAAABQAAAAMAAAAsAAAACgAAAdwAAQAAAAAEaAADAAEAAAAsAAMACgAAAdwABAGwAAAAaABAAAUAKAAgACsAoAClIAogLyBfIKwgvSISIxsl%2FCYBJvonCScP4APgCeAZ4CngOeBJ4FngYOBp4HngieCX4QnhGeEp4TnhRuFJ4VnhaeF54YnhleGZ4gbiCeIW4hniIeIn4jniSeJZ4mD4%2F%2F%2F%2FAAAAIAAqAKAApSAAIC8gXyCsIL0iEiMbJfwmASb6JwknD%2BAB4AXgEOAg4DDgQOBQ4GDgYuBw4IDgkOEB4RDhIOEw4UDhSOFQ4WDhcOGA4ZDhl%2BIA4gniEOIY4iHiI%2BIw4kDiUOJg%2BP%2F%2F%2F%2F%2Fj%2F9r%2FZv9i4Ajf5N%2B132nfWd4F3P3aHdoZ2SHZE9kOIB0gHCAWIBAgCiAEH%2F4f%2BB%2F3H%2FEf6x%2FlH3wfdh9wH2ofZB9jH10fVx9RH0sfRR9EHt4e3B7WHtUezh7NHsUevx65HrMIFQABAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADAAAAAACjAAAAAAAAAA1AAAAIAAAACAAAAADAAAAKgAAACsAAAAEAAAAoAAAAKAAAAAGAAAApQAAAKUAAAAHAAAgAAAAIAoAAAAIAAAgLwAAIC8AAAATAAAgXwAAIF8AAAAUAAAgrAAAIKwAAAAVAAAgvQAAIL0AAAAWAAAiEgAAIhIAAAAXAAAjGwAAIxsAAAAYAAAl%2FAAAJfwAAAAZAAAmAQAAJgEAAAAaAAAm%2BgAAJvoAAAAbAAAnCQAAJwkAAAAcAAAnDwAAJw8AAAAdAADgAQAA4AMAAAAeAADgBQAA4AkAAAAhAADgEAAA4BkAAAAmAADgIAAA4CkAAAAwAADgMAAA4DkAAAA6AADgQAAA4EkAAABEAADgUAAA4FkAAABOAADgYAAA4GAAAABYAADgYgAA4GkAAABZAADgcAAA4HkAAABhAADggAAA4IkAAABrAADgkAAA4JcAAAB1AADhAQAA4QkAAAB9AADhEAAA4RkAAACGAADhIAAA4SkAAACQAADhMAAA4TkAAACaAADhQAAA4UYAAACkAADhSAAA4UkAAACrAADhUAAA4VkAAACtAADhYAAA4WkAAAC3AADhcAAA4XkAAADBAADhgAAA4YkAAADLAADhkAAA4ZUAAADVAADhlwAA4ZkAAADbAADiAAAA4gYAAADeAADiCQAA4gkAAADlAADiEAAA4hYAAADmAADiGAAA4hkAAADtAADiIQAA4iEAAADvAADiIwAA4icAAADwAADiMAAA4jkAAAD1AADiQAAA4kkAAAD%2FAADiUAAA4lkAAAEJAADiYAAA4mAAAAETAAD4%2FwAA%2BP8AAAEUAAH1EQAB9REAAAEVAAH2qgAB9qoAAAEWAAYCCgAAAAABAAABAAAAAAAAAAAAAAAAAAAAAQACAAAAAAAAAAIAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAQAAAAAAAwAAAAAAAAAAAAAAAAAAAAAAAAAEAAUAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAHAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAYAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAVAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAEUAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAKAL4AAAAAf%2F%2FAAIAAgAoAAABaAMgAAMABwAusQEALzyyBwQA7TKxBgXcPLIDAgDtMgCxAwAvPLIFBADtMrIHBgH8PLIBAgDtMjMRIRElMxEjKAFA%2Fujw8AMg%2FOAoAtAAAQBkAGQETARMAFsAAAEyFh8BHgEdATc%2BAR8BFgYPATMyFhcWFRQGDwEOASsBFx4BDwEGJi8BFRQGBwYjIiYvAS4BPQEHDgEvASY2PwEjIiYnJjU0Nj8BPgE7AScuAT8BNhYfATU0Njc2AlgPJgsLCg%2BeBxYIagcCB57gChECBgMCAQIRCuCeBwIHaggWB54PCikiDyYLCwoPngcWCGoHAgee4AoRAgYDAgECEQrgngcCB2oIFgeeDwopBEwDAgECEQrgngcCB2oIFgeeDwopIg8mCwsKD54HFghqBwIHnuAKEQIGAwIBAhEK4J4HAgdqCBYHng8KKSIPJgsLCg%2BeBxYIagcCB57gChECBgAAAAABAAAAAARMBEwAIwAAATMyFhURITIWHQEUBiMhERQGKwEiJjURISImPQE0NjMhETQ2AcLIFR0BXhUdHRX%2Boh0VyBUd%2FqIVHR0VAV4dBEwdFf6iHRXIFR3%2BohUdHRUBXh0VyBUdAV4VHQAAAAABAHAAAARABEwARQAAATMyFgcBBgchMhYPAQ4BKwEVITIWDwEOASsBFRQGKwEiJj0BISImPwE%2BATsBNSEiJj8BPgE7ASYnASY2OwEyHwEWMj8BNgM5%2BgoFCP6UBgUBDAoGBngGGAp9ARMKBgZ4BhgKfQ8LlAsP%2Fu0KBgZ4BhgKff7tCgYGeAYYCnYFBv6UCAUK%2BhkSpAgUCKQSBEwKCP6UBgwMCKAIDGQMCKAIDK4LDw8LrgwIoAgMZAwIoAgMDAYBbAgKEqQICKQSAAABAGQABQSMBK4AOwAAATIXFhcjNC4DIyIOAwchByEGFSEHIR4EMzI%2BAzUzBgcGIyInLgEnIzczNjcjNzM%2BATc2AujycDwGtSM0QDkXEys4MjAPAXtk%2FtQGAZZk%2FtQJMDlCNBUWOUA0I64eYmunznYkQgzZZHABBdpkhhQ%2BH3UErr1oaS1LMCEPCx4uTzJkMjJkSnRCKw8PIjBKK6trdZ4wqndkLzVkV4UljQAAAgB7AAAETASwAD4ARwAAASEyHgUVHAEVFA4FKwEHITIWDwEOASsBFRQGKwEiJj0BISImPwE%2BATsBNSEiJj8BPgE7ARE0NhcRMzI2NTQmIwGsAV5DakIwFgwBAQwWMEJqQ7ICASAKBgZ4BhgKigsKlQoP%2FvUKBgZ4BhgKdf71CgYGeAYYCnUPtstALS1ABLAaJD8yTyokCwsLJCpQMkAlGmQMCKAIDK8LDg8KrwwIoAgMZAwIoAgMAdsKD8j%2B1EJWVEAAAAEAyAGQBEwCvAAPAAATITIWHQEUBiMhIiY9ATQ2%2BgMgFR0dFfzgFR0dArwdFcgVHR0VyBUdAAAAAgDIAAAD6ASwACUAQQAAARUUBisBFRQGBx4BHQEzMhYdASE1NDY7ATU0NjcuAT0BIyImPQEXFRQWFx4BFAYHDgEdASE1NCYnLgE0Njc%2BAT0BA%2BgdFTJjUVFjMhUd%2FOAdFTJjUVFjMhUdyEE3HCAgHDdBAZBBNxwgIBw3QQSwlhUdZFuVIyOVW5YdFZaWFR2WW5UjI5VbZB0VlshkPGMYDDI8MgwYYzyWljxjGAwyPDIMGGM8ZAAAAAEAAAAAAAAAAAAAAAAxAAAB%2F%2FIBLATCBEEAFgAAATIWFzYzMhYVFAYjISImNTQ2NyY1NDYB9261LCwueKqqeP0ST3FVQgLYBEF3YQ6teHmtclBFaw4MGZnXAAAAAgAAAGQEsASvABoAHgAAAB4BDwEBMzIWHQEhNTQ2OwEBJyY%2BARYfATc2AyEnAwL2IAkKiAHTHhQe%2B1AeFB4B1IcKCSAkCm9wCXoBebbDBLMTIxC7%2FRYlFSoqFSUC6rcQJBQJEJSWEPwecAIWAAAAAAQAAABkBLAETAALABcAIwA3AAATITIWBwEGIicBJjYXARYUBwEGJjURNDYJATYWFREUBicBJjQHARYGIyEiJjcBNjIfARYyPwE2MhkEfgoFCP3MCBQI%2FcwIBQMBCAgI%2FvgICgoDjAEICAoKCP74CFwBbAgFCvuCCgUIAWwIFAikCBQIpAgUBEwKCP3JCAgCNwgK2v74CBQI%2FvgIBQoCJgoF%2FvABCAgFCv3aCgUIAQgIFID%2BlAgKCggBbAgIpAgIpAgAAAAD%2F%2FD%2F8AS6BLoACQANABAAAAAyHwEWFA8BJzcTAScJAQUTA%2BAmDpkNDWPWXyL9mdYCZv4f%2FrNuBLoNmQ4mDlzWYP50%2FZrWAmb8anABTwAAAAEAAAAABLAEsAAPAAABETMyFh0BITU0NjsBEQEhArz6FR384B0V%2Bv4MBLACiv3aHRUyMhUdAiYCJgAAAAEADgAIBEwEnAAfAAABJTYWFREUBgcGLgE2NzYXEQURFAYHBi4BNjc2FxE0NgFwAoUnMFNGT4gkV09IQv2oWEFPiCRXT0hCHQP5ow8eIvzBN1EXGSltchkYEAIJm%2F2iKmAVGilucRoYEQJ%2FJioAAAACAAn%2F%2BAS7BKcAHQApAAAAMh4CFQcXFAcBFgYPAQYiJwEGIycHIi4CND4BBCIOARQeATI%2BATQmAZDItoNOAQFOARMXARY7GikT%2Fu13jgUCZLaDTk6DAXKwlFZWlLCUVlYEp06DtmQCBY15%2Fu4aJRg6FBQBEk0BAU6Dtsi2g1tWlLCUVlaUsJQAAQBkAFgErwREABkAAAE%2BAh4CFRQOAwcuBDU0PgIeAQKJMHt4dVg2Q3mEqD4%2Bp4V4Qzhadnh5A7VESAUtU3ZAOXmAf7JVVbJ%2FgHk5QHZTLQVIAAAAAf%2FTAF4EewSUABgAAAETNjIXEyEyFgcFExYGJyUFBiY3EyUmNjMBl4MHFQeBAaUVBhH%2BqoIHDxH%2Bqf6qEQ8Hgv6lEQYUAyABYRMT%2Fp8RDPn%2BbxQLDPb3DAsUAZD7DBEAAv%2FTAF4EewSUABgAIgAAARM2MhcTITIWBwUTFgYnJQUGJjcTJSY2MwUjFwc3Fyc3IycBl4MHFQeBAaUVBhH%2BqoIHDxH%2Bqf6qEQ8Hgv6lEQYUAfPwxUrBw0rA6k4DIAFhExP%2BnxEM%2Bf5vFAsM9vcMCxQBkPsMEWSO4ouM5YzTAAABAAAAAASwBLAAJgAAATIWHQEUBiMVFBYXBR4BHQEUBiMhIiY9ATQ2NyU%2BAT0BIiY9ATQ2Alh8sD4mDAkBZgkMDwr7ggoPDAkBZgkMJj6wBLCwfPouaEsKFwbmBRcKXQoPDwpdChcF5gYXCktoLvp8sAAAAA0AAAAABLAETAAPABMAIwAnACsALwAzADcARwBLAE8AUwBXAAATITIWFREUBiMhIiY1ETQ2FxUzNSkBIgYVERQWMyEyNjURNCYzFTM1BRUzNSEVMzUFFTM1IRUzNQchIgYVERQWMyEyNjURNCYFFTM1IRUzNQUVMzUhFTM1GQR%2BCg8PCvuCCg8PVWQCo%2F3aCg8PCgImCg8Pc2T8GGQDIGT8GGQDIGTh%2FdoKDw8KAiYKDw%2F872QDIGT8GGQDIGQETA8K%2B%2BYKDw8KBBoKD2RkZA8K%2FqIKDw8KAV4KD2RkyGRkZGTIZGRkZGQPCv6iCg8PCgFeCg9kZGRkZMhkZGRkAAAEAAAAAARMBEwADwAfAC8APwAAEyEyFhURFAYjISImNRE0NikBMhYVERQGIyEiJjURNDYBITIWFREUBiMhIiY1ETQ2KQEyFhURFAYjISImNRE0NjIBkBUdHRX%2BcBUdHQJtAZAVHR0V%2FnAVHR39vQGQFR0dFf5wFR0dAm0BkBUdHRX%2BcBUdHQRMHRX%2BcBUdHRUBkBUdHRX%2BcBUdHRUBkBUd%2FagdFf5wFR0dFQGQFR0dFf5wFR0dFQGQFR0AAAkAAAAABEwETAAPAB8ALwA%2FAE8AXwBvAH8AjwAAEzMyFh0BFAYrASImPQE0NiEzMhYdARQGKwEiJj0BNDYhMzIWHQEUBisBIiY9ATQ2ATMyFh0BFAYrASImPQE0NiEzMhYdARQGKwEiJj0BNDYhMzIWHQEUBisBIiY9ATQ2ATMyFh0BFAYrASImPQE0NiEzMhYdARQGKwEiJj0BNDYhMzIWHQEUBisBIiY9ATQ2MsgVHR0VyBUdHQGlyBUdHRXIFR0dAaXIFR0dFcgVHR389cgVHR0VyBUdHQGlyBUdHRXIFR0dAaXIFR0dFcgVHR389cgVHR0VyBUdHQGlyBUdHRXIFR0dAaXIFR0dFcgVHR0ETB0VyBUdHRXIFR0dFcgVHR0VyBUdHRXIFR0dFcgVHf5wHRXIFR0dFcgVHR0VyBUdHRXIFR0dFcgVHR0VyBUd%2FnAdFcgVHR0VyBUdHRXIFR0dFcgVHR0VyBUdHRXIFR0ABgAAAAAEsARMAA8AHwAvAD8ATwBfAAATMzIWHQEUBisBIiY9ATQ2KQEyFh0BFAYjISImPQE0NgEzMhYdARQGKwEiJj0BNDYpATIWHQEUBiMhIiY9ATQ2ATMyFh0BFAYrASImPQE0NikBMhYdARQGIyEiJj0BNDYyyBUdHRXIFR0dAaUCvBUdHRX9RBUdHf6FyBUdHRXIFR0dAaUCvBUdHRX9RBUdHf6FyBUdHRXIFR0dAaUCvBUdHRX9RBUdHQRMHRXIFR0dFcgVHR0VyBUdHRXIFR3%2BcB0VyBUdHRXIFR0dFcgVHR0VyBUd%2FnAdFcgVHR0VyBUdHRXIFR0dFcgVHQAAAAABACYALAToBCAAFwAACQE2Mh8BFhQHAQYiJwEmND8BNjIfARYyAdECOwgUB7EICPzxBxUH%2FoAICLEHFAirBxYB3QI7CAixBxQI%2FPAICAGACBQHsQgIqwcAAQBuAG4EQgRCACMAAAEXFhQHCQEWFA8BBiInCQEGIi8BJjQ3CQEmND8BNjIXCQE2MgOIsggI%2FvUBCwgIsggVB%2F70%2FvQHFQiyCAgBC%2F71CAiyCBUHAQwBDAcVBDuzCBUH%2FvT%2B9AcVCLIICAEL%2FvUICLIIFQcBDAEMBxUIsggI%2FvUBDAcAAwAX%2F%2BsExQSZABkAJQBJAAAAMh4CFRQHARYUDwEGIicBBiMiLgI0PgEEIg4BFB4BMj4BNCYFMzIWHQEzMhYdARQGKwEVFAYrASImPQEjIiY9ATQ2OwE1NDYBmcSzgk1OASwICG0HFQj%2B1HeOYrSBTU2BAW%2BzmFhYmLOZWFj%2BvJYKD0sKDw8KSw8KlgoPSwoPDwpLDwSZTYKzYo15%2FtUIFQhsCAgBK01NgbTEs4JNWJmzmFhYmLOZIw8KSw8KlgoPSwoPDwpLDwqWCg9LCg8AAAMAF%2F%2FrBMUEmQAZACUANQAAADIeAhUUBwEWFA8BBiInAQYjIi4CND4BBCIOARQeATI%2BATQmBSEyFh0BFAYjISImPQE0NgGZxLOCTU4BLAgIbQcVCP7Ud45itIFNTYEBb7OYWFiYs5lYWP5YAV4KDw8K%2FqIKDw8EmU2Cs2KNef7VCBUIbAgIAStNTYG0xLOCTViZs5hYWJizmYcPCpYKDw8KlgoPAAAAAAIAFwAXBJkEsAAPAC0AAAEzMhYVERQGKwEiJjURNDYFNRYSFRQOAiIuAjU0EjcVDgEVFB4BMj4BNTQmAiZkFR0dFWQVHR0BD6fSW5vW6tabW9KnZ3xyxejFcnwEsB0V%2FnAVHR0VAZAVHeGmPv7ZuHXWm1tbm9Z1uAEnPqY3yHh0xXJyxXR4yAAEAGQAAASwBLAADwAfAC8APwAAATMyFhURFAYrASImNRE0NgEzMhYVERQGKwEiJjURNDYBMzIWFREUBisBIiY1ETQ2BTMyFh0BFAYrASImPQE0NgQBlgoPDwqWCg8P%2Ft6WCg8PCpYKDw%2F%2B3pYKDw8KlgoPD%2F7elgoPDwqWCg8PBLAPCvuCCg8PCgR%2BCg%2F%2BcA8K%2FRIKDw8KAu4KD%2F7UDwr%2BPgoPDwoBwgoPyA8K%2BgoPDwr6Cg8AAAAAAgAaABsElgSWAEcATwAAATIfAhYfATcWFwcXFh8CFhUUDwIGDwEXBgcnBwYPAgYjIi8CJi8BByYnNycmLwImNTQ%2FAjY%2FASc2Nxc3Nj8CNhIiBhQWMjY0AlghKSYFMS0Fhj0rUAMZDgGYBQWYAQ8YA1AwOIYFLDIFJisfISkmBTEtBYY8LFADGQ0ClwYGlwINGQNQLzqFBS0xBSYreLJ%2BfrJ%2BBJYFmAEOGQJQMDmGBSwxBiYrHiIoJgYxLAWGPSxRAxkOApcFBZcCDhkDUTA5hgUtMAYmKiAhKCYGMC0Fhj0sUAIZDgGYBf6ZfrF%2BfrEABwBkAAAEsAUUABMAFwAhACUAKQAtADEAAAEhMhYdASEyFh0BITU0NjMhNTQ2FxUhNQERFAYjISImNREXETMRMxEzETMRMxEzETMRAfQBLCk7ARMKD%2Fu0DwoBEzspASwBLDsp%2FUQpO2RkZGRkZGRkBRQ7KWQPCktLCg9kKTtkZGT%2B1PzgKTs7KQMgZP1EArz9RAK8%2FUQCvP1EArwAAQAMAAAFCATRAB8AABMBNjIXARYGKwERFAYrASImNREhERQGKwEiJjURIyImEgJsCBUHAmAIBQqvDwr6Cg%2F%2B1A8K%2BgoPrwoFAmoCYAcH%2FaAICv3BCg8PCgF3%2FokKDw8KAj8KAAIAZAAAA%2BgEsAARABcAAAERFBYzIREUBiMhIiY1ETQ2MwEjIiY9AQJYOykBLB0V%2FOAVHR0VA1L6FR0EsP5wKTv9dhUdHRUETBUd%2FnAdFfoAAwAXABcEmQSZAA8AGwAwAAAAMh4CFA4CIi4CND4BBCIOARQeATI%2BATQmBTMyFhURMzIWHQEUBisBIiY1ETQ2AePq1ptbW5vW6tabW1ubAb%2FoxXJyxejFcnL%2BfDIKD68KDw8K%2BgoPDwSZW5vW6tabW1ub1urWmztyxejFcnLF6MUNDwr%2B7Q8KMgoPDwoBXgoPAAAAAAL%2FnAAABRQEsAALAA8AACkBAyMDIQEzAzMDMwEDMwMFFP3mKfIp%2FeYBr9EVohTQ%2Fp4b4BsBkP5wBLD%2B1AEs%2FnD%2B1AEsAAAAAAIAZAAABLAEsAAVAC8AAAEzMhYVETMyFgcBBiInASY2OwERNDYBMzIWFREUBiMhIiY1ETQ2OwEyFh0BITU0NgImyBUdvxQLDf65DSYN%2FrkNCxS%2FHQJUMgoPDwr75goPDwoyCg8DhA8EsB0V%2Fj4XEP5wEBABkBAXAcIVHfzgDwr%2BogoPDwoBXgoPDwqvrwoPAAMAFwAXBJkEmQAPABsAMQAAADIeAhQOAiIuAjQ%2BAQQiDgEUHgEyPgE0JgUzMhYVETMyFgcDBiInAyY2OwERNDYB4%2BrWm1tbm9bq1ptbW5sBv%2BjFcnLF6MVycv58lgoPiRUKDd8NJg3fDQoViQ8EmVub1urWm1tbm9bq1ps7csXoxXJyxejFDQ8K%2Fu0XEP7tEBABExAXARMKDwAAAAMAFwAXBJkEmQAPABsAMQAAADIeAhQOAiIuAjQ%2BAQQiDgEUHgEyPgE0JiUTFgYrAREUBisBIiY1ESMiJjcTNjIB4%2BrWm1tbm9bq1ptbW5sBv%2BjFcnLF6MVycv7n3w0KFYkPCpYKD4kVCg3fDSYEmVub1urWm1tbm9bq1ps7csXoxXJyxejFAf7tEBf%2B7QoPDwoBExcQARMQAAAAAAIAAAAABLAEsAAZADkAABMhMhYXExYVERQGBwYjISImJyY1EzQ3Ez4BBSEiBgcDBhY7ATIWHwEeATsBMjY%2FAT4BOwEyNicDLgHhAu4KEwO6BwgFDBn7tAweAgYBB7kDEwKX%2FdQKEgJXAgwKlgoTAiYCEwr6ChMCJgITCpYKDAJXAhIEsA4K%2FXQYGf5XDB4CBggEDRkBqRkYAowKDsgOC%2F4%2BCw4OCpgKDg4KmAoODgsBwgsOAAMAFwAXBJkEmQAPABsAJwAAADIeAhQOAiIuAjQ%2BAQQiDgEUHgEyPgE0JgUXFhQPAQYmNRE0NgHj6tabW1ub1urWm1tbmwG%2F6MVycsXoxXJy%2Fov9ERH9EBgYBJlbm9bq1ptbW5vW6tabO3LF6MVycsXoxV2%2BDCQMvgwLFQGQFQsAAQAXABcEmQSwACgAAAE3NhYVERQGIyEiJj8BJiMiDgEUHgEyPgE1MxQOAiIuAjQ%2BAjMyA7OHBwsPCv6WCwQHhW2BdMVycsXoxXKWW5vW6tabW1ub1nXABCSHBwQL%2FpYKDwsHhUxyxejFcnLFdHXWm1tbm9bq1ptbAAAAAAIAFwABBJkEsAAaADUAAAE3NhYVERQGIyEiJj8BJiMiDgEVIzQ%2BAjMyEzMUDgIjIicHBiY1ETQ2MyEyFg8BFjMyPgEDs4cHCw8L%2FpcLBAeGboF0xXKWW5vWdcDrllub1nXAnIYHCw8LAWgKBQiFboJ0xXIEJIcHBAv%2BlwsPCweGS3LFdHXWm1v9v3XWm1t2hggFCgFoCw8LB4VMcsUAAAAKAGQAAASwBLAADwAfAC8APwBPAF8AbwB%2FAI8AnwAAEyEyFhURFAYjISImNRE0NgUhIgYVERQWMyEyNjURNCYFMzIWHQEUBisBIiY9ATQ2MyEyFh0BFAYjISImPQE0NgczMhYdARQGKwEiJj0BNDYzITIWHQEUBiMhIiY9ATQ2BzMyFh0BFAYrASImPQE0NjMhMhYdARQGIyEiJj0BNDYHMzIWHQEUBisBIiY9ATQ2MyEyFh0BFAYjISImPQE0Nn0EGgoPDwr75goPDwPA%2FK4KDw8KA1IKDw%2F9CDIKDw8KMgoPD9IBwgoPDwr%2BPgoPD74yCg8PCjIKDw%2FSAcIKDw8K%2Fj4KDw%2B%2BMgoPDwoyCg8P0gHCCg8PCv4%2BCg8PvjIKDw8KMgoPD9IBwgoPDwr%2BPgoPDwSwDwr7ggoPDwoEfgoPyA8K%2FK4KDw8KA1IKD2QPCjIKDw8KMgoPDwoyCg8PCjIKD8gPCjIKDw8KMgoPDwoyCg8PCjIKD8gPCjIKDw8KMgoPDwoyCg8PCjIKD8gPCjIKDw8KMgoPDwoyCg8PCjIKDwAAAAACAAAAAARMBLAAGQAjAAABNTQmIyEiBh0BIyIGFREUFjMhMjY1ETQmIyE1NDY7ATIWHQEDhHVT%2FtRSdmQpOzspA4QpOzsp%2FageFMgUHgMgyFN1dlLIOyn9qCk7OykCWCk7lhUdHRWWAAIAZAAABEwETAAJADcAABMzMhYVESMRNDYFMhcWFREUBw4DIyIuAScuAiMiBwYjIicmNRE%2BATc2HgMXHgIzMjc2fTIKD2QPA8AEBRADIUNAMRwaPyonKSxHHlVLBwgGBQ4WeDsXKC4TOQQpLUUdZ1AHBEwPCvvNBDMKDzACBhH%2BWwYGO1AkDQ0ODg8PDzkFAwcPAbY3VwMCAwsGFAEODg5XCAAAAwAAAAAEsASXACEAMQBBAAAAMh4CFREUBisBIiY1ETQuASAOARURFAYrASImNRE0PgEDMzIWFREUBisBIiY1ETQ2ITMyFhURFAYrASImNRE0NgHk6N6jYw8KMgoPjeT%2B%2BuSNDwoyCg9joyqgCAwMCKAIDAwCYKAIDAwIoAgMDASXY6PedP7UCg8PCgEsf9FyctF%2F%2FtQKDw8KASx03qP9wAwI%2FjQIDAwIAcwIDAwI%2FjQIDAwIAcwIDAAAAAACAAAA0wRHA90AFQA5AAABJTYWFREUBiclJisBIiY1ETQ2OwEyBTc2Mh8BFhQPARcWFA8BBiIvAQcGIi8BJjQ%2FAScmND8BNjIXAUEBAgkMDAn%2B%2FhUZ%2BgoPDwr6GQJYeAcUByIHB3h4BwciBxQHeHgHFAciBwd3dwcHIgcUBwMurAYHCv0SCgcGrA4PCgFeCg%2BEeAcHIgcUB3h4BxQHIgcHd3cHByIHFAd4eAcUByIICAAAAAACAAAA0wNyA90AFQAvAAABJTYWFREUBiclJisBIiY1ETQ2OwEyJTMWFxYVFAcGDwEiLwEuATc2NTQnJjY%2FATYBQQECCQwMCf7%2BFRn6Cg8PCvoZAdIECgZgWgYLAwkHHQcDBkhOBgMIHQcDLqwGBwr9EgoHBqwODwoBXgoPZAEJgaGafwkBAQYXBxMIZ36EaggUBxYFAAAAAAMAAADEBGID7AAbADEASwAAATMWFxYVFAYHBgcjIi8BLgE3NjU0JicmNj8BNgUlNhYVERQGJyUmKwEiJjURNDY7ATIlMxYXFhUUBwYPASIvAS4BNzY1NCcmNj8BNgPHAwsGh0RABwoDCQcqCAIGbzs3BgIJKgf9ggECCQwMCf7%2BFRn6Cg8PCvoZAdIECgZgWgYLAwkHHQcDBkhOBgMIHQcD7AEJs9lpy1QJAQYiBhQIlrJarEcJFAYhBb6sBgcK%2FRIKBwasDg8KAV4KD2QBCYGhmn8JAQEGFwcTCGd%2BhGoIFQYWBQAAAAANAAAAAASwBLAACQAVABkAHQAhACUALQA7AD8AQwBHAEsATwAAATMVIxUhFSMRIQEjFTMVIREjESM1IQURIREhESERBSM1MwUjNTMBMxEhETM1MwEzFSMVIzUjNTM1IzUhBREhEQcjNTMFIzUzASM1MwUhNSEB9GRk%2FnBkAfQCvMjI%2FtTIZAJY%2B7QBLAGQASz84GRkArxkZP1EyP4MyGQB9MhkyGRkyAEs%2FUQBLGRkZAOEZGT%2BDGRkAfT%2B1AEsA4RkZGQCWP4MZMgBLAEsyGT%2B1AEs%2FtQBLMhkZGT%2BDP4MAfRk%2FtRkZGRkyGTI%2FtQBLMhkZGT%2B1GRkZAAAAAAJAAAAAASwBLAAAwAHAAsADwATABcAGwAfACMAADcjETMTIxEzASMRMxMjETMBIxEzASE1IRcjNTMXIzUzBSM1M2RkZMhkZAGQyMjIZGQBLMjI%2FOD%2B1AEsyGRkyGRkASzIyMgD6PwYA%2Bj8GAPo%2FBgD6PwYA%2Bj7UGRkW1tbW1sAAAIAAAAKBKYEsAANABUAAAkBFhQHAQYiJwETNDYzBCYiBhQWMjYB9AKqCAj%2BMAgUCP1WAQ8KAUM7Uzs7UzsEsP1WCBQI%2FjAICAKqAdsKD807O1Q7OwAAAAADAAAACgXSBLAADQAZACEAAAkBFhQHAQYiJwETNDYzIQEWFAcBBiIvAQkBBCYiBhQWMjYB9AKqCAj%2BMAgUCP1WAQ8KAwYCqggI%2FjAIFAg4Aaj9RP7TO1M7O1M7BLD9VggUCP4wCAgCqgHbCg%2F9VggUCP4wCAg4AaoCvM07O1Q7OwAAAAABAGQAAASwBLAAJgAAASEyFREUDwEGJjURNCYjISIPAQYWMyEyFhURFAYjISImNRE0PwE2ASwDOUsSQAgKDwr9RBkSQAgFCgK8Cg8PCvyuCg8SixIEsEv8fBkSQAgFCgO2Cg8SQAgKDwr8SgoPDwoDzxkSixIAAAABAMj%2F%2FwRMBLAACgAAEyEyFhURCQERNDb6AyAVHf4%2B%2Fj4dBLAdFfuCAbz%2BQwR%2FFR0AAAAAAwAAAAAEsASwABUARQBVAAABISIGBwMGHwEeATMhMjY%2FATYnAy4BASMiBg8BDgEjISImLwEuASsBIgYVERQWOwEyNj0BNDYzITIWHQEUFjsBMjY1ETQmASEiBg8BBhYzITI2LwEuAQM2%2FkQLEAFOBw45BhcKAcIKFwY%2BDgdTARABVpYKFgROBBYK%2FdoKFgROBBYKlgoPDwqWCg8PCgLuCg8PCpYKDw%2F%2Bsf4MChMCJgILCgJYCgsCJgITBLAPCv7TGBVsCQwMCWwVGAEtCg%2F%2BcA0JnAkNDQmcCQ0PCv12Cg8PCpYKDw8KlgoPDwoCigoP%2FagOCpgKDg4KmAoOAAAAAAQAAABkBLAETAAdACEAKQAxAAABMzIeAh8BMzIWFREUBiMhIiY1ETQ2OwE%2BBAEVMzUEIgYUFjI2NCQyFhQGIiY0AfTIOF00JAcGlik7Oyn8GCk7OymWAgknM10ByGT%2Bz76Hh76H%2Fu9WPDxWPARMKTs7FRQ7Kf2oKTs7KQJYKTsIG0U1K%2F7UZGRGh76Hh74IPFY8PFYAAAAAAgA1AAAEsASvACAAIwAACQEWFx4BHwEVITUyNi8BIQYHBh4CMxUhNTY3PgE%2FAQEDIQMCqQGBFCgSJQkK%2Fl81LBFS%2Fnk6IgsJKjIe%2FpM4HAwaBwcBj6wBVKIEr%2FwaMioTFQECQkJXLd6RWSIuHAxCQhgcDCUNDQPu%2FVoByQAAAAADAGQAAAPwBLAAJwAyADsAAAEeBhUUDgMjITU%2BATURNC4EJzUFMh4CFRQOAgclMzI2NTQuAisBETMyNjU0JisBAvEFEzUwOyodN1htbDD%2BDCk7AQYLFyEaAdc5dWM%2BHy0tEP6Pi05pESpTPnbYUFJ9Xp8CgQEHGB0zOlIuQ3VONxpZBzMoAzsYFBwLEAkHRwEpSXNDM1s6KwkxYUopOzQb%2FK5lUFqBAAABAMgAAANvBLAAGQAAARcOAQcDBhYXFSE1NjcTNjQuBCcmJzUDbQJTQgeECSxK%2Fgy6Dq0DAw8MHxUXDQYEsDkTNSj8uTEoBmFhEFIDQBEaExAJCwYHAwI5AAAAAAL%2FtQAABRQEsAAlAC8AAAEjNC4FKwERFBYfARUhNTI%2BAzURIyIOBRUjESEFIxEzByczESM3BRQyCAsZEyYYGcgyGRn%2BcAQOIhoWyBkYJhMZCwgyA%2Bj7m0tLfX1LS30DhBUgFQ4IAwH8rhYZAQJkZAEFCRUOA1IBAwgOFSAVASzI%2FOCnpwMgpwACACH%2FtQSPBLAAJQAvAAABIzQuBSsBERQWHwEVITUyPgM1ESMiDgUVIxEhEwc1IRUnNxUhNQRMMggLGRMmGBnIMhkZ%2FnAEDiIaFsgZGCYTGQsIMgPoQ6f84KenAyADhBUgFQ4IAwH9dhYZAQJkZAEFCRUOAooBAwgOFSAVASz7gn1LS319S0sABAAAAAAEsARMAA8AHwAvAD8AABMhMhYdARQGIyEiJj0BNDYTITIWHQEUBiMhIiY9ATQ2EyEyFh0BFAYjISImPQE0NhMhMhYdARQGIyEiJj0BNDYyAlgVHR0V%2FagVHR0VA%2BgVHR0V%2FBgVHR0VAyAVHR0V%2FOAVHR0VBEwVHR0V%2B7QVHR0ETB0VZBUdHRVkFR3%2B1B0VZBUdHRVkFR3%2B1B0VZBUdHRVkFR3%2B1B0VZBUdHRVkFR0ABAAAAAAEsARMAA8AHwAvAD8AABMhMhYdARQGIyEiJj0BNDYDITIWHQEUBiMhIiY9ATQ2EyEyFh0BFAYjISImPQE0NgMhMhYdARQGIyEiJj0BNDb6ArwVHR0V%2FUQVHR2zBEwVHR0V%2B7QVHR3dArwVHR0V%2FUQVHR2zBEwVHR0V%2B7QVHR0ETB0VZBUdHRVkFR3%2B1B0VZBUdHRVkFR3%2B1B0VZBUdHRVkFR3%2B1B0VZBUdHRVkFR0ABAAAAAAEsARMAA8AHwAvAD8AAAE1NDYzITIWHQEUBiMhIiYBNTQ2MyEyFh0BFAYjISImEzU0NjMhMhYdARQGIyEiJgE1NDYzITIWHQEUBiMhIiYB9B0VAlgVHR0V%2FagVHf5wHRUD6BUdHRX8GBUdyB0VAyAVHR0V%2FOAVHf7UHRUETBUdHRX7tBUdA7ZkFR0dFWQVHR3%2B6WQVHR0VZBUdHf7pZBUdHRVkFR0d%2FulkFR0dFWQVHR0AAAQAAAAABLAETAAPAB8ALwA%2FAAATITIWHQEUBiMhIiY9ATQ2EyEyFh0BFAYjISImPQE0NhMhMhYdARQGIyEiJj0BNDYTITIWHQEUBiMhIiY9ATQ2MgRMFR0dFfu0FR0dFQRMFR0dFfu0FR0dFQRMFR0dFfu0FR0dFQRMFR0dFfu0FR0dBEwdFWQVHR0VZBUd%2FtQdFWQVHR0VZBUd%2FtQdFWQVHR0VZBUd%2FtQdFWQVHR0VZBUdAAgAAAAABLAETAAPAB8ALwA%2FAE8AXwBvAH8AABMzMhYdARQGKwEiJj0BNDYpATIWHQEUBiMhIiY9ATQ2ATMyFh0BFAYrASImPQE0NikBMhYdARQGIyEiJj0BNDYBMzIWHQEUBisBIiY9ATQ2KQEyFh0BFAYjISImPQE0NgEzMhYdARQGKwEiJj0BNDYpATIWHQEUBiMhIiY9ATQ2MmQVHR0VZBUdHQFBAyAVHR0V%2FOAVHR3%2B6WQVHR0VZBUdHQFBAyAVHR0V%2FOAVHR3%2B6WQVHR0VZBUdHQFBAyAVHR0V%2FOAVHR3%2B6WQVHR0VZBUdHQFBAyAVHR0V%2FOAVHR0ETB0VZBUdHRVkFR0dFWQVHR0VZBUd%2FtQdFWQVHR0VZBUdHRVkFR0dFWQVHf7UHRVkFR0dFWQVHR0VZBUdHRVkFR3%2B1B0VZBUdHRVkFR0dFWQVHR0VZBUdAAAG%2F5wAAASwBEwAAwATACMAKgA6AEoAACEjETsCMhYdARQGKwEiJj0BNDYTITIWHQEUBiMhIiY9ATQ2BQc1IzUzNQUhMhYdARQGIyEiJj0BNDYTITIWHQEUBiMhIiY9ATQ2AZBkZJZkFR0dFWQVHR0VAfQVHR0V%2FgwVHR3%2B%2BqfIyAHCASwVHR0V%2FtQVHR0VAlgVHR0V%2FagVHR0ETB0VZBUdHRVkFR3%2B1B0VZBUdHRVkFR36fUtkS68dFWQVHR0VZBUd%2FtQdFWQVHR0VZBUdAAAABgAAAAAFFARMAA8AEwAjACoAOgBKAAATMzIWHQEUBisBIiY9ATQ2ASMRMwEhMhYdARQGIyEiJj0BNDYFMxUjFSc3BSEyFh0BFAYjISImPQE0NhMhMhYdARQGIyEiJj0BNDYyZBUdHRVkFR0dA2dkZPyuAfQVHR0V%2FgwVHR0EL8jIp6f75gEsFR0dFf7UFR0dFQJYFR0dFf2oFR0dBEwdFWQVHR0VZBUd%2B7QETP7UHRVkFR0dFWQVHchkS319rx0VZBUdHRVkFR3%2B1B0VZBUdHRVkFR0AAAAAAgAAAMgEsAPoAA8AEgAAEyEyFhURFAYjISImNRE0NgkCSwLuHywsH%2F0SHywsBIT%2B1AEsA%2BgsH%2F12HywsHwKKHyz9RAEsASwAAwAAAAAEsARMAA8AFwAfAAATITIWFREUBiMhIiY1ETQ2FxE3BScBExEEMhYUBiImNCwEWBIaGhL7qBIaGkr3ASpKASXs%2FNJwTk5wTgRMGhL8DBIaGhID9BIaZP0ftoOcAT7%2B4AH0dE5vT09vAAAAAAIA2wAFBDYEkQAWAB4AAAEyHgEVFAcOAQ8BLgQnJjU0PgIWIgYUFjI2NAKIdcZzRkWyNjYJIV5YbSk8RHOft7eCgreCBJF4ynVzj23pPz4IIWZomEiEdVijeUjDgriBgbgAAAACABcAFwSZBJkADwAXAAAAMh4CFA4CIi4CND4BAREiDgEUHgEB4%2BrWm1tbm9bq1ptbW5sBS3TFcnLFBJlbm9bq1ptbW5vW6tab%2FG8DVnLF6MVyAAACAHUAAwPfBQ8AGgA1AAABHgYVFA4DBy4DNTQ%2BBQMOAhceBBcWNj8BNiYnLgInJjc2IyYCKhVJT1dOPiUzVnB9P1SbfEokP0xXUEm8FykoAwEbITEcExUWAgYCCQkFEikMGiACCAgFD0iPdXdzdYdFR4BeRiYEBTpjl1lFh3ZzeHaQ%2Ff4hS4I6JUEnIw4IBwwQIgoYBwQQQSlZtgsBAAAAAwAAAAAEywRsAAwAKgAvAAABNz4CHgEXHgEPAiUhMhcHISIGFREUFjMhMjY9ATcRFAYjISImNRE0NgkBBzcBA%2BhsAgYUFR0OFgoFBmz9BQGQMje7%2FpApOzspAfQpO8i7o%2F5wpbm5Azj%2BlqE3AWMD9XMBAgIEDw4WKgsKc8gNuzsp%2FgwpOzsptsj%2BtKW5uaUBkKW5%2Ftf%2BljKqAWMAAgAAAAAEkwRMABsANgAAASEGByMiBhURFBYzITI2NTcVFAYjISImNRE0NgUBFhQHAQYmJzUmDgMHPgY3NT4BAV4BaaQ0wyk7OykB9Ck7yLml%2FnClubkCfwFTCAj%2BrAcLARo5ZFRYGgouOUlARioTAQsETJI2Oyn%2BDCk7OymZZ6W5uaUBkKW5G%2F7TBxUH%2Fs4GBAnLAQINFjAhO2JBNB0UBwHSCgUAAAAAAgAAAAAEnQRMAB0ANQAAASEyFwchIgYVERQWMyEyNj0BNxUUBiMhIiY1ETQ2CQE2Mh8BFhQHAQYiLwEmND8BNjIfARYyAV4BXjxDsv6jKTs7KQH0KTvIuaX%2BcKW5uQHKAYsHFQdlBwf97QcVB%2FgHB2UHFQdvCBQETBexOyn%2BDCk7OylFyNulubmlAZCluf4zAYsHB2UHFQf97AcH%2BAcVB2UHB28HAAAAAQAKAAoEpgSmADsAAAkBNjIXARYGKwEVMzU0NhcBFhQHAQYmPQEjFTMyFgcBBiInASY2OwE1IxUUBicBJjQ3ATYWHQEzNSMiJgE%2BAQgIFAgBBAcFCqrICggBCAgI%2FvgICsiqCgUH%2FvwIFAj%2B%2BAgFCq%2FICgj%2B%2BAgIAQgICsivCgUDlgEICAj%2B%2BAgKyK0KBAf%2B%2FAcVB%2F73BwQKrcgKCP74CAgBCAgKyK0KBAcBCQcVBwEEBwQKrcgKAAEAyAAAA4QETAAZAAATMzIWFREBNhYVERQGJwERFAYrASImNRE0NvpkFR0B0A8VFQ%2F%2BMB0VZBUdHQRMHRX%2BSgHFDggV%2FBgVCA4Bxf5KFR0dFQPoFR0AAAABAAAAAASwBEwAIwAAEzMyFhURATYWFREBNhYVERQGJwERFAYnAREUBisBIiY1ETQ2MmQVHQHQDxUB0A8VFQ%2F%2BMBUP%2FjAdFWQVHR0ETB0V%2FkoBxQ4IFf5KAcUOCBX8GBUIDgHF%2FkoVCA4Bxf5KFR0dFQPoFR0AAAABAJ0AGQSwBDMAFQAAAREUBicBERQGJwEmNDcBNhYVEQE2FgSwFQ%2F%2BMBUP%2FhQPDwHsDxUB0A8VBBr8GBUIDgHF%2FkoVCA4B4A4qDgHgDggV%2FkoBxQ4IAAAAAQDIABYEMwQ2AAsAABMBFhQHAQYmNRE0NvMDLhIS%2FNISGRkEMv4OCx4L%2Fg4LDhUD6BUOAAIAyABkA4QD6AAPAB8AABMzMhYVERQGKwEiJjURNDYhMzIWFREUBisBIiY1ETQ2%2BsgVHR0VyBUdHQGlyBUdHRXIFR0dA%2BgdFfzgFR0dFQMgFR0dFfzgFR0dFQMgFR0AAAEAyABkBEwD6AAPAAABERQGIyEiJjURNDYzITIWBEwdFfzgFR0dFQMgFR0DtvzgFR0dFQMgFR0dAAAAAAEAAAAZBBMEMwAVAAABETQ2FwEWFAcBBiY1EQEGJjURNDYXAfQVDwHsDw%2F%2BFA8V%2FjAPFRUPAmQBthUIDv4gDioO%2FiAOCBUBtv47DggVA%2BgVCA4AAAH%2F%2FgACBLMETwAjAAABNzIWFRMUBiMHIiY1AwEGJjUDAQYmNQM0NhcBAzQ2FwEDNDYEGGQUHgUdFWQVHQL%2BMQ4VAv4yDxUFFQ8B0gIVDwHSAh0ETgEdFfwYFR0BHRUBtf46DwkVAbX%2BOQ4JFAPoFQkP%2Fj4BthQJDv49AbYVHQAAAQEsAAAD6ARMABkAAAEzMhYVERQGKwEiJjURAQYmNRE0NhcBETQ2A1JkFR0dFWQVHf4wDxUVDwHQHQRMHRX8GBUdHRUBtv47DggVA%2BgVCA7%2BOwG2FR0AAAIAZADIBLAESAALABsAAAkBFgYjISImNwE2MgEhMhYdARQGIyEiJj0BNDYCrgH1DwkW%2B%2B4WCQ8B9Q8q%2FfcD6BUdHRX8GBUdHQQ5%2FeQPFhYPAhwP%2FUgdFWQVHR0VZBUdAAEAiP%2F8A3UESgAFAAAJAgcJAQN1%2FqABYMX92AIoA4T%2Bn%2F6fxgIoAiYAAAAAAQE7%2F%2FwEKARKAAUAAAkBJwkBNwQo%2FdnGAWH%2Bn8YCI%2F3ZxgFhAWHGAAIAFwAXBJkEmQAPADMAAAAyHgIUDgIiLgI0PgEFIyIGHQEjIgYdARQWOwEVFBY7ATI2PQEzMjY9ATQmKwE1NCYB4%2BrWm1tbm9bq1ptbW5sBfWQVHZYVHR0Vlh0VZBUdlhUdHRWWHQSZW5vW6tabW1ub1urWm7odFZYdFWQVHZYVHR0Vlh0VZBUdlhUdAAAAAAIAFwAXBJkEmQAPAB8AAAAyHgIUDgIiLgI0PgEBISIGHQEUFjMhMjY9ATQmAePq1ptbW5vW6tabW1ubAkX%2BDBUdHRUB9BUdHQSZW5vW6tabW1ub1urWm%2F5%2BHRVkFR0dFWQVHQACABcAFwSZBJkADwAzAAAAMh4CFA4CIi4CND4BBCIPAScmIg8BBhQfAQcGFB8BFjI%2FARcWMj8BNjQvATc2NC8BAePq1ptbW5vW6tabW1ubAeUZCXh4CRkJjQkJeHgJCY0JGQl4eAkZCY0JCXh4CQmNBJlbm9bq1ptbW5vW6tabrQl4eAkJjQkZCXh4CRkJjQkJeHgJCY0JGQl4eAkZCY0AAgAXABcEmQSZAA8AJAAAADIeAhQOAiIuAjQ%2BAQEnJiIPAQYUHwEWMjcBNjQvASYiBwHj6tabW1ub1urWm1tbmwEVVAcVCIsHB%2FIHFQcBdwcHiwcVBwSZW5vW6tabW1ub1urWm%2F4xVQcHiwgUCPEICAF3BxUIiwcHAAAAAAMAFwAXBJkEmQAPADsASwAAADIeAhQOAiIuAjQ%2BAQUiDgMVFDsBFjc%2BATMyFhUUBgciDgUHBhY7ATI%2BAzU0LgMTIyIGHQEUFjsBMjY9ATQmAePq1ptbW5vW6tabW1ubAT8dPEIyIRSDHgUGHR8UFw4TARkOGhITDAIBDQ6tBx4oIxgiM0Q8OpYKDw8KlgoPDwSZW5vW6tabW1ub1urWm5ELHi9PMhkFEBQQFRIXFgcIBw4UHCoZCBEQKDhcNi9IKhsJ%2FeMPCpYKDw8KlgoPAAADABcAFwSZBJkADwAfAD4AAAAyHgIUDgIiLgI0PgEFIyIGHQEUFjsBMjY9ATQmAyMiBh0BFBY7ARUjIgYdARQWMyEyNj0BNCYrARE0JgHj6tabW1ub1urWm1tbmwGWlgoPDwqWCg8PCvoKDw8KS0sKDw8KAV4KDw8KSw8EmVub1urWm1tbm9bq1ptWDwqWCg8PCpYKD%2F7UDwoyCg%2FIDwoyCg8PCjIKDwETCg8AAgAAAAAEsASwAC8AXwAAATMyFh0BHgEXMzIWHQEUBisBDgEHFRQGKwEiJj0BLgEnIyImPQE0NjsBPgE3NTQ2ExUUBisBIiY9AQ4BBzMyFh0BFAYrAR4BFzU0NjsBMhYdAT4BNyMiJj0BNDY7AS4BAg2WCg9nlxvCCg8PCsIbl2cPCpYKD2eXG8IKDw8KwhuXZw%2B5DwqWCg9EZheoCg8PCqgXZkQPCpYKD0RmF6gKDw8KqBdmBLAPCsIbl2cPCpYKD2eXG8IKDw8KwhuXZw8KlgoPZ5cbwgoP%2Fs2oCg8PCqgXZkQPCpYKD0RmF6gKDw8KqBdmRA8KlgoPRGYAAwAXABcEmQSZAA8AGwA%2FAAAAMh4CFA4CIi4CND4BBCIOARQeATI%2BATQmBxcWFA8BFxYUDwEGIi8BBwYiLwEmND8BJyY0PwE2Mh8BNzYyAePq1ptbW5vW6tabW1ubAb%2FoxXJyxejFcnKaQAcHfHwHB0AHFQd8fAcVB0AHB3x8BwdABxUHfHwHFQSZW5vW6tabW1ub1urWmztyxejFcnLF6MVaQAcVB3x8BxUHQAcHfHwHB0AHFQd8fAcVB0AHB3x8BwAAAAMAFwAXBJkEmQAPABsAMAAAADIeAhQOAiIuAjQ%2BAQQiDgEUHgEyPgE0JgcXFhQHAQYiLwEmND8BNjIfATc2MgHj6tabW1ub1urWm1tbmwG%2F6MVycsXoxXJyg2oHB%2F7ACBQIyggIagcVB0%2FFBxUEmVub1urWm1tbm9bq1ps7csXoxXJyxejFfWoHFQf%2BvwcHywcVB2oICE%2FFBwAAAAMAFwAXBJkEmQAPABgAIQAAADIeAhQOAiIuAjQ%2BAQUiDgEVFBcBJhcBFjMyPgE1NAHj6tabW1ub1urWm1tbmwFLdMVyQQJLafX9uGhzdMVyBJlbm9bq1ptbW5vW6tabO3LFdHhpAktB0P24PnLFdHMAAAAAAQAXAFMEsAP5ABUAABMBNhYVESEyFh0BFAYjIREUBicBJjQnAgoQFwImFR0dFf3aFxD99hACRgGrDQoV%2Ft0dFcgVHf7dFQoNAasNJgAAAAABAAAAUwSZA%2FkAFQAACQEWFAcBBiY1ESEiJj0BNDYzIRE0NgJ%2FAgoQEP32EBf92hUdHRUCJhcD8f5VDSYN%2FlUNChUBIx0VyBUdASMVCgAAAAEAtwAABF0EmQAVAAAJARYGIyERFAYrASImNREhIiY3ATYyAqoBqw0KFf7dHRXIFR3%2B3RUKDQGrDSYEif32EBf92hUdHRUCJhcQAgoQAAAAAQC3ABcEXQSwABUAAAEzMhYVESEyFgcBBiInASY2MyERNDYCJsgVHQEjFQoN%2FlUNJg3%2BVQ0KFQEjHQSwHRX92hcQ%2FfYQEAIKEBcCJhUdAAABAAAAtwSZBF0AFwAACQEWFAcBBiY1EQ4DBz4ENxE0NgJ%2FAgoQEP32EBdesKWBJAUsW4fHfhcEVf5VDSYN%2FlUNChUBIwIkRHVNabGdcUYHAQYVCgACAAAAAASwBLAAFQArAAABITIWFREUBi8BBwYiLwEmND8BJyY2ASEiJjURNDYfATc2Mh8BFhQPARcWBgNSASwVHRUOXvkIFAhqBwf5Xg4I%2FiH%2B1BUdFQ5e%2BQgUCGoHB%2FleDggEsB0V%2FtQVCA5e%2BQcHaggUCPleDhX7UB0VASwVCA5e%2BQcHaggUCPleDhUAAAACAEkASQRnBGcAFQArAAABFxYUDwEXFgYjISImNRE0Nh8BNzYyASEyFhURFAYvAQcGIi8BJjQ%2FAScmNgP2agcH%2BV4OCBX%2B1BUdFQ5e%2BQgU%2FQwBLBUdFQ5e%2BQgUCGoHB%2FleDggEYGoIFAj5Xg4VHRUBLBUIDl75B%2F3xHRX%2B1BUIDl75BwdqCBQI%2BV4OFQAAAAADABcAFwSZBJkADwAfAC8AAAAyHgIUDgIiLgI0PgEFIyIGFxMeATsBMjY3EzYmAyMiBh0BFBY7ATI2PQE0JgHj6tabW1ub1urWm1tbmwGz0BQYBDoEIxQ2FCMEOgQYMZYKDw8KlgoPDwSZW5vW6tabW1ub1urWm7odFP7SFB0dFAEuFB3%2BDA8KlgoPDwqWCg8AAAAABQAAAAAEsASwAEkAVQBhAGgAbwAAATIWHwEWHwEWFxY3Nj8BNjc2MzIWHwEWHwIeATsBMhYdARQGKwEiBh0BIREjESE1NCYrASImPQE0NjsBMjY1ND8BNjc%2BBAUHBhY7ATI2LwEuAQUnJgYPAQYWOwEyNhMhIiY1ESkBERQGIyERAQQJFAUFFhbEFQ8dCAsmxBYXERUXMA0NDgQZCAEPCj0KDw8KMgoP%2FnDI%2FnAPCjIKDw8KPQsOCRkFDgIGFRYfAp2mBwQK2woKAzMDEP41sQgQAzMDCgrnCwMe%2FokKDwGQAlgPCv6JBLAEAgIKDXYNCxUJDRZ2DQoHIREQFRh7LAkLDwoyCg8PCq8BLP7UrwoPDwoyCg8GBQQwgBkUAwgWEQ55ogcKDgqVCgSqnQcECo8KDgr8cg8KAXf%2BiQoPAZAAAAAAAgAAAAwErwSmACsASQAAATYWFQYCDgQuAScmByYOAQ8BBiY1NDc%2BATc%2BAScuAT4BNz4GFyYGBw4BDwEOBAcOARY2Nz4CNz4DNz4BBI0IGgItQmxhi2KORDg9EQQRMxuZGhYqCFUYEyADCQIQOjEnUmFch3vAJQgdHyaiPT44XHRZUhcYDhItIRmKcVtGYWtbKRYEBKYDEwiy%2Ft3IlVgxEQgLCwwBAQIbG5kYEyJAJghKFRE8Hzdff4U%2FM0o1JSMbL0QJGCYvcSEhHjZST2c1ODwEJygeW0AxJUBff1UyFAABAF0AHgRyBM8ATwAAAQ4BHgQXLgc%2BATceAwYHDgQHBicmNzY3PgQuAScWDgMmJy4BJyY%2BBDcGHgM3PgEuAicmPgMCjScfCic4R0IgBBsKGAoQAwEJEg5gikggBhANPkpTPhZINx8SBgsNJysiCRZOQQoVNU1bYC9QZwICBAUWITsoCAYdJzIYHw8YIiYHDyJJYlkEz0OAZVxEOSQMBzgXOB42IzElKRIqg5Gnl0o3Z0c6IAYWCwYNAwQFIDhHXGF1OWiqb0sdBxUknF0XNTQ8PEUiNWNROBYJDS5AQVUhVZloUSkAAAAAA%2F%2FcAGoE1ARGABsAPwBRAAAAMh4FFA4FIi4FND4EBSYGFxYVFAYiJjU0NzYmBwYHDgEXHgQyPgM3NiYnJgUHDgEXFhcWNj8BNiYnJicuAQIGpJ17bk85HBw6T257naKde25POhwcOU9uewIPDwYIGbD4sBcIBw5GWg0ECxYyWl%2BDiINfWjIWCwQMWv3%2FIw8JCSU4EC0OIw4DDywtCyIERi1JXGJcSSpJXGJcSS0tSVxiXEkqSVxiXEncDwYTOT58sLB8OzcTBg9FcxAxEiRGXkQxMEVeRSQSMRF1HiQPLxJEMA0EDyIPJQ8sSRIEAAAABP%2FcAAAE1ASwABQAJwA7AEwAACEjNy4ENTQ%2BBTMyFzczEzceARUUDgMHNz4BNzYmJyYlBgcOARceBBc3LgE1NDc2JhcHDgEXFhcWNj8CJyYnLgECUJQfW6l2WSwcOU9ue51SPUEglCYvbIknUGqYUi5NdiYLBAw2%2FVFGWg0ECxIqSExoNSlrjxcIB3wjDwkJJTgQLQ4MFgMsLQsieBRhdHpiGxVJXGJcSS0Pef5StVXWNBpacm5jGq0xiD8SMRFGckVzEDESHjxRQTkNmhKnbjs3EwZwJA8vEkQwDQQPC1YELEkSBAAAAAP%2FngAABRIEqwALABgAKAAAJwE2FhcBFgYjISImJSE1NDY7ATIWHQEhAQczMhYPAQ4BKwEiJi8BJjZaAoIUOBQCghUbJfryJRsBCgFZDwqWCg8BWf5DaNAUGAQ6BCMUNhQjBDoEGGQEKh8FIfvgIEdEhEsKDw8KSwLT3x0U%2FBQdHRT8FB0AAAABAGQAFQSwBLAAKAAAADIWFREBHgEdARQGJyURFh0BFAYvAQcGJj0BNDcRBQYmPQE0NjcBETQCTHxYAWsPFhgR%2FplkGhPNzRMaZP6ZERgWDwFrBLBYPv6t%2FrsOMRQpFA0M%2Bf75XRRAFRAJgIAJEBVAFF0BB%2FkMDRQpFDEOAUUBUz4AAAARAAAAAARMBLAAHQAnACsALwAzADcAOwA%2FAEMARwBLAE8AUwBXAFsAXwBjAAABMzIWHQEzMhYdASE1NDY7ATU0NjsBMhYdASE1NDYBERQGIyEiJjURFxUzNTMVMzUzFTM1MxUzNTMVMzUFFTM1MxUzNTMVMzUzFTM1MxUzNQUVMzUzFTM1MxUzNTMVMzUzFTM1A1JkFR0yFR37tB0VMh0VZBUdAfQdAQ8dFfwYFR1kZGRkZGRkZGRk%2FHxkZGRkZGRkZGT8fGRkZGRkZGRkZASwHRUyHRWWlhUdMhUdHRUyMhUd%2FnD9EhUdHRUC7shkZGRkZGRkZGRkyGRkZGRkZGRkZGTIZGRkZGRkZGRkZAAAAAMAAAAZBXcElwAZACUANwAAARcWFA8BBiY9ASMBISImPQE0NjsBATM1NDYBBycjIiY9ATQ2MyEBFxYUDwEGJj0BIyc3FzM1NDYEb%2FkPD%2FkOFZ%2F9qP7dFR0dFdECWPEV%2FamNetEVHR0VASMDGvkPD%2FkOFfG1jXqfFQSN5g4qDuYOCBWW%2FagdFWQVHQJYlhUI%2FpiNeh0VZBUd%2Fk3mDioO5g4IFZa1jXqWFQgAAAABAAAAAASwBEwAEgAAEyEyFhURFAYjIQERIyImNRE0NmQD6Ck7Oyn9rP7QZCk7OwRMOyn9qCk7%2FtQBLDspAlgpOwAAAAMAZAAABEwEsAAJABMAPwAAEzMyFh0BITU0NiEzMhYdASE1NDYBERQOBSIuBTURIRUUFRwBHgYyPgYmNTQ9AZbIFR3%2B1B0C0cgVHf7UHQEPBhgoTGacwJxmTCgYBgEsAwcNFB8nNkI2Jx8TDwUFAQSwHRX6%2BhUdHRX6%2BhUd%2FnD%2B1ClJalZcPigoPlxWakkpASz6CRIVKyclIRsWEAgJEBccISUnKhURCPoAAAAB%2F%2F8A1ARMA8IABQAAAQcJAScBBEzG%2Fp%2F%2Bn8UCJwGbxwFh%2Fp%2FHAicAAQAAAO4ETQPcAAUAAAkCNwkBBE392v3ZxgFhAWEDFf3ZAifH%2Fp8BYQAAAAAC%2F1EAZAVfA%2BgAFAApAAABITIWFREzMhYPAQYiLwEmNjsBESElFxYGKwERIRchIiY1ESMiJj8BNjIBlALqFR2WFQgO5g4qDuYOCBWW%2FoP%2BHOYOCBWWAYHX%2FRIVHZYVCA7mDioD6B0V%2FdkVDvkPD%2FkOFQGRuPkOFf5wyB0VAiYVDvkPAAABAAYAAASeBLAAMAAAEzMyFh8BITIWBwMOASMhFyEyFhQGKwEVFAYiJj0BIRUUBiImPQEjIiYvAQMjIiY0NjheERwEJgOAGB4FZAUsIf2HMAIXFR0dFTIdKh3%2B1B0qHR8SHQYFyTYUHh4EsBYQoiUY%2FiUVK8gdKh0yFR0dFTIyFR0dFTIUCQoDwR0qHQAAAAACAAAAAASwBEwACwAPAAABFSE1MzQ2MyEyFhUFIREhBLD7UMg7KQEsKTv9RASw%2B1AD6GRkKTs7Kcj84AACAAAAAAXcBEwADAAQAAATAxEzNDYzITIWFSEVBQEhAcjIyDspASwqOgH0ASz%2B1PtQASwDIP5wAlgpOzspyGT9RAK8AAEBRQAAA2sErwAbAAABFxYGKwERMzIWDwEGIi8BJjY7AREjIiY%2FATYyAnvmDggVlpYVCA7mDioO5g4IFZaWFQgO5g4qBKD5DhX9pxUO%2BQ8P%2BQ4VAlkVDvkPAAAAAQABAUQErwNrABsAAAEXFhQPAQYmPQEhFRQGLwEmND8BNhYdASE1NDYDqPkODvkPFf2oFQ%2F5Dg75DxUCWBUDYOUPKQ%2FlDwkUl5cUCQ%2FlDykP5Q8JFZWVFQkAAAAEAAAAAASwBLAACQAZAB0AIQAAAQMuASMhIgYHAwUhIgYdARQWMyEyNj0BNCYFNTMVMzUzFQSRrAUkFP1gFCQFrAQt%2FBgpOzspA%2BgpOzv%2Bq2RkZAGQAtwXLSgV%2FR1kOylkKTs7KWQpO8hkZGRkAAAAA%2F%2BcAGQEsARMAAsAIwAxAAAAMhYVERQGIiY1ETQDJSMTFgYjIisBIiYnAj0BNDU0PgE7ASUBFSIuAz0BND4CNwRpKh0dKh1k%2FV0mLwMRFQUCVBQdBDcCCwzIAqP8GAQOIhoWFR0dCwRMHRX8rhUdHRUDUhX8mcj%2B7BAIHBUBUQ76AgQQDw36%2FtT6AQsTKRwyGigUDAEAAAACAEoAAARmBLAALAA1AAABMzIWDwEeARcTFzMyFhQGBw4EIyIuBC8BLgE0NjsBNxM%2BATcnJjYDFjMyNw4BIiYCKV4UEgYSU3oPP3YRExwaEggeZGqfTzl0XFU%2BLwwLEhocExF2Pw96UxIGEyQyNDUxDDdGOASwFRMlE39N%2FrmtHSkoBwQLHBYSCg4REg4FBAgoKR2tAUdNfhQgExr7vgYGMT09AAEAFAAUBJwEnAAXAAABNwcXBxcHFycHJwcnBzcnNyc3Jxc3FzcDIOBO6rS06k7gLZubLeBO6rS06k7gLZubA7JO4C2bmy3gTuq0tOpO4C2bmy3gTuq0tAADAAAAZASwBLAAIQAtAD0AAAEzMhYdAQchMhYdARQHAw4BKwEiJi8BIyImNRE0PwI%2BARcPAREzFzMTNSE3NQEzMhYVERQGKwEiJjURNDYCijIoPBwBSCg8He4QLBf6B0YfHz0tNxSRYA0xG2SWZIjW%2Bv4%2BMv12ZBUdHRVkFR0dBLBRLJZ9USxkLR3%2BqBghMhkZJCcBkCQbxMYcKGTU1f6JZAF3feGv%2FtQdFf4MFR0dFQH0FR0AAAAAAwAAAAAEsARMACAAMAA8AAABMzIWFxMWHQEUBiMhFh0BFAYrASImLwImNRE0NjsBNgUzMhYVERQGKwEiJjURNDYhByMRHwEzNSchNQMCWPoXLBDuHTwo%2FrgcPCgyGzENYJEUNy09fP3pZBUdHRVkFR0dAl%2BIZJZkMjIBwvoETCEY%2FqgdLWQsUXYHlixRKBzGxBskAZAnJGRkHRX%2BDBUdHRUB9BUdZP6J1dSv4X0BdwADAAAAZAUOBE8AGwA3AEcAAAElNh8BHgEPASEyFhQGKwEDDgEjISImNRE0NjcXERchEz4BOwEyNiYjISoDLgQnJj8BJwUzMhYVERQGKwEiJjURNDYBZAFrHxZuDQEMVAEuVGxuVGqDBhsP%2FqoHphwOOmQBJYMGGw%2FLFRMSFv44AgoCCQMHAwUDAQwRklb9T2QVHR0VZBUdHQNp5hAWcA0mD3lMkE7%2BrRUoog0CDRElCkj%2BCVkBUxUoMjIBAgIDBQIZFrdT5B0V%2FgwVHR0VAfQVHQAAAAP%2FnABkBLAETwAdADYARgAAAQUeBBURFAYjISImJwMjIiY0NjMhJyY2PwE2BxcWBw4FKgIjIRUzMhYXEyE3ESUFMzIWFREUBisBIiY1ETQ2AdsBbgIIFBANrAf%2Bqg8bBoNqVW1sVAEuVQsBDW4WSpIRDAIDBQMHAwkDCgH%2BJd0PHAaCASZq%2FqoCUGQVHR0VZBUdHQRP5gEFEBEXC%2F3zDaIoFQFTTpBMeQ8mDXAWrrcWGQIFAwICAWQoFf6tWQH37OQdFf4MFR0dFQH0FR0AAAADAGEAAARMBQ4AGwA3AEcAAAAyFh0BBR4BFREUBiMhIiYvAQMmPwE%2BAR8BETQXNTQmBhURHAMOBAcGLwEHEyE3ESUuAQMhMhYdARQGIyEiJj0BNDYB3pBOAVMVKKIN%2FfMRJQoJ5hAWcA0mD3nGMjIBAgIDBQIZFrdT7AH3Wf6tFSiWAfQVHR0V%2FgwVHR0FDm5UaoMGGw%2F%2BqgemHA4OAWsfFm4NAQxUAS5U1ssVExIW%2FjgCCgIJAwcDBQMBDBGSVv6tZAElgwYb%2FQsdFWQVHR0VZBUdAAP%2F%2FQAGA%2BgFFAAPAC0ASQAAASEyNj0BNCYjISIGHQEUFgEVFAYiJjURBwYmLwEmNxM%2BBDMhMhYVERQGBwEDFzc2Fx4FHAIVERQWNj0BNDY3JREnAV4B9BUdHRX%2BDBUdHQEPTpBMeQ8mDXAWEOYBBRARFwsCDQ2iKBX9iexTtxYZAgUDAgIBMjIoFQFTWQRMHRVkFR0dFWQVHfzmalRubFQBLlQMAQ1uFh8BawIIEw8Mpgf%2Bqg8bBgHP%2Fq1WkhEMAQMFAwcDCQIKAv44FhITFcsPGwaDASVkAAIAFgAWBJoEmgAPACUAAAAyHgIUDgIiLgI0PgEBJSYGHQEhIgYdARQWMyEVFBY3JTY0AeLs1ptbW5vW7NabW1ubAob%2B7RAX%2Fu0KDw8KARMXEAETEASaW5vW7NabW1ub1uzWm%2F453w0KFYkPCpYKD4kVCg3fDSYAAAIAFgAWBJoEmgAPACUAAAAyHgIUDgIiLgI0PgENAQYUFwUWNj0BITI2PQE0JiMhNTQmAeLs1ptbW5vW7NabW1ubASX%2B7RAQARMQFwETCg8PCv7tFwSaW5vW7NabW1ub1uzWm%2BjfDSYN3w0KFYkPCpYKD4kVCgAAAAIAFgAWBJoEmgAPACUAAAAyHgIUDgIiLgI0PgEBAyYiBwMGFjsBERQWOwEyNjURMzI2AeLs1ptbW5vW7NabW1ubAkvfDSYN3w0KFYkPCpYKD4kVCgSaW5vW7NabW1ub1uzWm%2F5AARMQEP7tEBf%2B7QoPDwoBExcAAAIAFgAWBJoEmgAPACUAAAAyHgIUDgIiLgI0PgEFIyIGFREjIgYXExYyNxM2JisBETQmAeLs1ptbW5vW7NabW1ubAZeWCg%2BJFQoN3w0mDd8NChWJDwSaW5vW7NabW1ub1uzWm7sPCv7tFxD%2B7RAQARMQFwETCg8AAAMAGAAYBJgEmAAPAJYApgAAADIeAhQOAiIuAjQ%2BASUOAwcGJgcOAQcGFgcOAQcGFgcUFgcyHgEXHgIXHgI3Fg4BFx4CFxQGFBcWNz4CNy4BJy4BJyIOAgcGJyY2NS4BJzYuAQYHBicmNzY3HgIXHgMfAT4CJyY%2BATc%2BAzcmNzIWMjY3LgMnND4CJiceAT8BNi4CJwYHFB4BFS4CJz4BNxYyPgEB5OjVm1xcm9Xo1ZtcXJsBZA8rHDoKDz0PFD8DAxMBAzEFCRwGIgEMFhkHECIvCxU%2FOR0HFBkDDRQjEwcFaHUeISQDDTAMD0UREi4oLBAzDwQBBikEAQMLGhIXExMLBhAGKBsGBxYVEwYFAgsFAwMNFwQGCQcYFgYQCCARFwkKKiFBCwQCAQMDHzcLDAUdLDgNEiEQEgg%2FKhADGgMKEgoRBJhcm9Xo1ZtcXJvV6NWbEQwRBwkCAwYFBycPCxcHInIWInYcCUcYChQECA4QBAkuHgQPJioRFRscBAcSCgwCch0kPiAIAQcHEAsBAgsLIxcBMQENCQIPHxkCFBkdHB4QBgEBBwoMGBENBAMMJSAQEhYXDQ4qFBkKEhIDCQsXJxQiBgEOCQwHAQ0DBAUcJAwSCwRnETIoAwEJCwsLJQcKDBEAAAAAAQAAAAIErwSFABYAAAE2FwUXNxYGBw4BJwEGIi8BJjQ3ASY2AvSkjv79kfsGUE08hjv9rA8rD28PDwJYIk8EhVxliuh%2BWYcrIgsW%2FawQEG4PKxACV2XJAAYAAABgBLAErAAPABMAIwAnADcAOwAAEyEyFh0BFAYjISImPQE0NgUjFTMFITIWHQEUBiMhIiY9ATQ2BSEVIQUhMhYdARQGIyEiJj0BNDYFIRUhZAPoKTs7KfwYKTs7BBHIyPwYA%2BgpOzsp%2FBgpOzsEEf4MAfT8GAPoKTs7KfwYKTs7BBH%2B1AEsBKw7KWQpOzspZCk7ZGTIOylkKTs7KWQpO2RkyDspZCk7OylkKTtkZAAAAAIAZAAABEwEsAALABEAABMhMhYUBiMhIiY0NgERBxEBIZYDhBUdHRX8fBUdHQI7yP6iA4QEsB0qHR0qHf1E%2FtTIAfQB9AAAAAMAAABkBLAEsAAXABsAJQAAATMyFh0BITIWFREhNSMVIRE0NjMhNTQ2FxUzNQEVFAYjISImPQEB9MgpOwEsKTv%2BDMj%2BDDspASw7KcgB9Dsp%2FBgpOwSwOylkOyn%2BcGRkAZApO2QpO2RkZP1EyCk7OynIAAAABAAAAAAEsASwABUAKwBBAFcAABMhMhYPARcWFA8BBiIvAQcGJjURNDYpATIWFREUBi8BBwYiLwEmND8BJyY2ARcWFA8BFxYGIyEiJjURNDYfATc2MgU3NhYVERQGIyEiJj8BJyY0PwE2MhcyASwVCA5exwcHaggUCMdeDhUdAzUBLBUdFQ5exwgUCGoHB8deDgj%2BL2oHB8deDggV%2FtQVHRUOXscIFALLXg4VHRX%2B1BUIDl7HBwdqCBQIBLAVDl7HCBQIagcHx14OCBUBLBUdHRX%2B1BUIDl7HBwdqCBQIx14OFf0maggUCMdeDhUdFQEsFQgOXscHzl4OCBX%2B1BUdFQ5exwgUCGoHBwAAAAYAAAAABKgEqAAPABsAIwA7AEMASwAAADIeAhQOAiIuAjQ%2BAQQiDgEUHgEyPgE0JiQyFhQGIiY0JDIWFAYjIicHFhUUBiImNTQ2PwImNTQEMhYUBiImNCQyFhQGIiY0Advy3Z9fX5%2Fd8t2gXl6gAcbgv29vv%2BC%2Fb2%2F%2BLS0gIC0gAUwtICAWDg83ETNIMykfegEJ%2FoctICAtIAIdLSAgLSAEqF%2Bf3fLdoF5eoN3y3Z9Xb7%2Fgv29vv%2BC%2FBiAtISEtICAtIQqRFxwkMzMkIDEFfgEODhekIC0gIC0gIC0gIC0AAf%2FYAFoEuQS8AFsAACUBNjc2JicmIyIOAwcABw4EFx4BMzI3ATYnLgEjIgcGBwEOASY0NwA3PgEzMhceARcWBgcOBgcGIyImJyY2NwE2NzYzMhceARcWBgcBDgEnLgECIgHVWwgHdl8WGSJBMD8hIP6IDx4eLRMNBQlZN0ozAiQkEAcdEhoYDRr%2Bqw8pHA4BRyIjQS4ODyw9DQ4YIwwod26La1YOOEBGdiIwGkQB%2F0coW2tQSE5nDxE4Qv4eDyoQEAOtAdZbZWKbEQQUGjIhH%2F6JDxsdNSg3HT5CMwIkJCcQFBcMGv6uDwEcKQ4BTSIjIQEINykvYyMLKnhuiWZMBxtAOU6%2BRAH%2FSBg3ISSGV121Qv4kDwIPDyYAAAACAGQAWASvBEQAGQBEAAABPgIeAhUUDgMHLgQ1ND4CHgEFIg4DIi4DIyIGFRQeAhcWFx4EMj4DNzY3PgQ1NCYCiTB7eHVYNkN5hKg%2BPqeFeEM4WnZ4eQEjIT8yLSohJyktPyJDbxtBMjMPBw86KzEhDSIzKUAMBAgrKT8dF2oDtURIBS1TdkA5eYB%2FslVVsn%2BAeTlAdlMtBUgtJjY1JiY1NiZvTRc4SjQxDwcOPCouGBgwKEALBAkpKkQqMhNPbQACADn%2F8gR3BL4AFwAuAAAAMh8BFhUUBg8BJi8BNycBFwcvASY0NwEDNxYfARYUBwEGIi8BJjQ%2FARYfAQcXAQKru0KNQjgiHR8uEl%2F3%2FnvUaRONQkIBGxJpCgmNQkL%2B5UK6Qo1CQjcdLhJf9wGFBL5CjUJeKmsiHTUuEl%2F4%2FnvUahKNQrpCARv%2BRmkICY1CukL%2B5UJCjUK7Qjc3LxFf%2BAGFAAAAAAMAyAAAA%2BgEsAARABUAHQAAADIeAhURFAYjISImNRE0PgEHESERACIGFBYyNjQCBqqaZDo7Kf2oKTs8Zj4CWP7%2FVj09Vj0EsB4uMhX8Ryk7OykDuRUzLar9RAK8%2FRY9Vj09VgABAAAAAASwBLAAFgAACQEWFAYiLwEBEScBBRMBJyEBJyY0NjIDhgEbDx0qDiT%2B6dT%2BzP7oywEz0gEsAQsjDx0qBKH%2B5g8qHQ8j%2FvX%2B1NL%2BzcsBGAE01AEXJA4qHQAAAAADAScAEQQJBOAAMgBAAEsAAAEVHgQXIy4DJxEXHgQVFAYHFSM1JicuASczHgEXEScuBDU0PgI3NRkBDgMVFB4DFxYXET4ENC4CArwmRVI8LAKfBA0dMydAIjxQNyiym2SWVygZA4sFV0obLkJOMCAyVWg6HSoqFQ4TJhkZCWgWKTEiGBkzNwTgTgUTLD9pQiQuLBsH%2Fs0NBxMtPGQ%2Bi6oMTU8QVyhrVk1iEAFPCA4ZLzlYNkZwSCoGTf4SARIEDh02Jh0rGRQIBgPQ%2FsoCCRYgNEM0JRkAAAABAGQAZgOUBK0ASgAAATIeARUjNC4CIyIGBwYVFB4BFxYXMxUjFgYHBgc%2BATM2FjMyNxcOAyMiLgEHDgEPASc%2BBTc%2BAScjNTMmJy4CPgE3NgIxVJlemSc8OxolVBQpGxoYBgPxxQgVFS02ImIWIIwiUzUyHzY4HCAXanQmJ1YYFzcEGAcTDBEJMAwk3aYXFQcKAg4tJGEErVCLTig%2FIhIdFSw5GkowKgkFZDKCHj4yCg8BIh6TExcIASIfBAMaDAuRAxAFDQsRCjePR2QvORQrREFMIVgAAAACABn%2F%2FwSXBLAADwAfAAABMzIWDwEGIi8BJjY7AREzBRcWBisBESMRIyImPwE2MgGQlhUIDuYOKg7mDggVlsgCF%2BYOCBWWyJYVCA7mDioBLBYO%2Bg8P%2Bg4WA4QQ%2BQ4V%2FHwDhBUO%2BQ8AAAQAGf%2F%2FA%2BgEsAAHABcAGwAlAAABIzUjFSMRIQEzMhYPAQYiLwEmNjsBETMFFTM1EwczFSE1NyM1IQPoZGRkASz9qJYVCA7mDioO5g4IFZbIAZFkY8jI%2FtTIyAEsArxkZAH0%2FHwWDvoPD%2FoOFgOEZMjI%2FRL6ZJb6ZAAAAAAEABn%2F%2FwPoBLAADwAZACEAJQAAATMyFg8BBiIvASY2OwERMwUHMxUhNTcjNSERIzUjFSMRIQcVMzUBkJYVCA7mDioO5g4IFZbIAljIyP7UyMgBLGRkZAEsx2QBLBYO%2Bg8P%2Bg4WA4SW%2BmSW%2BmT7UGRkAfRkyMgAAAAEABn%2F%2FwRMBLAADwAVABsAHwAAATMyFg8BBiIvASY2OwERMwEjESM1MxMjNSMRIQcVMzUBkJYVCA7mDioO5g4IFZbIAlhkZMhkZMgBLMdkASwWDvoPD%2FoOFgOE%2FgwBkGT7UGQBkGTIyAAAAAAEABn%2F%2FwRMBLAADwAVABkAHwAAATMyFg8BBiIvASY2OwERMwEjNSMRIQcVMzUDIxEjNTMBkJYVCA7mDioO5g4IFZbIArxkyAEsx2QBZGTIASwWDvoPD%2FoOFgOE%2FgxkAZBkyMj7tAGQZAAAAAAFABn%2F%2FwSwBLAADwATABcAGwAfAAABMzIWDwEGIi8BJjY7AREzBSM1MxMhNSETITUhEyE1IQGQlhUIDuYOKg7mDggVlsgB9MjIZP7UASxk%2FnABkGT%2BDAH0ASwWDvoPD%2FoOFgOEyMj%2BDMj%2BDMj%2BDMgABQAZ%2F%2F8EsASwAA8AEwAXABsAHwAAATMyFg8BBiIvASY2OwERMwUhNSEDITUhAyE1IQMjNTMBkJYVCA7mDioO5g4IFZbIAyD%2BDAH0ZP5wAZBk%2FtQBLGTIyAEsFg76Dw%2F6DhYDhMjI%2FgzI%2FgzI%2FgzIAAIAAAAABEwETAAPAB8AAAEhMhYVERQGIyEiJjURNDYFISIGFREUFjMhMjY1ETQmAV4BkKK8u6P%2BcKW5uQJn%2FgwpOzspAfQpOzsETLuj%2FnClubmlAZClucg7Kf4MKTs7KQH0KTsAAAAAAwAAAAAETARMAA8AHwArAAABITIWFREUBiMhIiY1ETQ2BSEiBhURFBYzITI2NRE0JgUXFhQPAQYmNRE0NgFeAZClubml%2FnCju7wCZP4MKTs7KQH0KTs7%2Fm%2F9ERH9EBgYBEy5pf5wpbm5pQGQo7vIOyn%2BDCk7OykB9Ck7gr4MJAy%2BDAsVAZAVCwAAAAADAAAAAARMBEwADwAfACsAAAEhMhYVERQGIyEiJjURNDYFISIGFREUFjMhMjY1ETQmBSEyFg8BBiIvASY2AV4BkKO7uaX%2BcKW5uQJn%2FgwpOzspAfQpOzv%2BFQGQFQsMvgwkDL4MCwRMvKL%2BcKW5uaUBkKO7yDsp%2FgwpOzspAfQpO8gYEP0REf0QGAAAAAMAAAAABEwETAAPAB8AKwAAASEyFhURFAYjISImNRE0NgUhIgYVERQWMyEyNjURNCYFFxYGIyEiJj8BNjIBXgGQpbm5pf5wo7u5Amf%2BDCk7OykB9Ck7O%2F77vgwLFf5wFQsMvgwkBEy5pf5wo7u8ogGQpbnIOyn%2BDCk7OykB9Ck7z%2F0QGBgQ%2FREAAAAAAgAAAAAFFARMAB8ANQAAASEyFhURFAYjISImPQE0NjMhMjY1ETQmIyEiJj0BNDYHARYUBwEGJj0BIyImPQE0NjsBNTQ2AiYBkKW5uaX%2BcBUdHRUBwik7Oyn%2BPhUdHb8BRBAQ%2FrwQFvoVHR0V%2BhYETLml%2FnCluR0VZBUdOykB9Ck7HRVkFR3p%2FuQOJg7%2B5A4KFZYdFcgVHZYVCgAAAQDZAAID1wSeACMAAAEXFgcGAgclMhYHIggBBwYrAScmNz4BPwEhIicmNzYANjc2MwMZCQgDA5gCASwYEQ4B%2Fvf%2B8wQMDgkJCQUCUCcn%2FtIXCAoQSwENuwUJEASeCQoRC%2F5TBwEjEv7K%2FsUFDwgLFQnlbm4TFRRWAS%2FTBhAAAAACAAAAAAT%2BBEwAHwA1AAABITIWHQEUBiMhIgYVERQWMyEyFh0BFAYjISImNRE0NgUBFhQHAQYmPQEjIiY9ATQ2OwE1NDYBXgGQFR0dFf4%2BKTs7KQHCFR0dFf5wpbm5AvEBRBAQ%2FrwQFvoVHR0V%2BhYETB0VZBUdOyn%2BDCk7HRVkFR25pQGQpbnp%2FuQOJg7%2B5A4KFZYdFcgVHZYVCgACAAAAAASwBLAAFQAxAAABITIWFREUBi8BAQYiLwEmNDcBJyY2ASMiBhURFBYzITI2PQE3ERQGIyEiJjURNDYzIQLuAZAVHRUObf7IDykPjQ8PAThtDgj%2B75wpOzspAfQpO8i7o%2F5wpbm5pQEsBLAdFf5wFQgObf7IDw%2BNDykPAThtDhX%2B1Dsp%2FgwpOzsplMj%2B1qW5uaUBkKW5AAADAA4ADgSiBKIADwAbACMAAAAyHgIUDgIiLgI0PgEEIg4BFB4BMj4BNCYEMhYUBiImNAHh7tmdXV2d2e7ZnV1dnQHD5sJxccLmwnFx%2FnugcnKgcgSiXZ3Z7tmdXV2d2e7ZnUdxwubCcXHC5sJzcqBycqAAAAMAAAAABEwEsAAVAB8AIwAAATMyFhURMzIWBwEGIicBJjY7ARE0NgEhMhYdASE1NDYFFTM1AcLIFR31FAoO%2FoEOJw3%2BhQ0JFfod%2FoUD6BUd%2B7QdA2dkBLAdFf6iFg%2F%2BVg8PAaoPFgFeFR38fB0V%2BvoVHWQyMgAAAAMAAAAABEwErAAVAB8AIwAACQEWBisBFRQGKwEiJj0BIyImNwE%2BAQEhMhYdASE1NDYFFTM1AkcBeg4KFfQiFsgUGPoUCw4Bfw4n%2FfkD6BUd%2B7QdA2dkBJ7%2BTQ8g%2BhQeHRX6IQ8BrxAC%2FH8dFfr6FR1kMjIAAwAAAAAETARLABQAHgAiAAAJATYyHwEWFAcBBiInASY0PwE2MhcDITIWHQEhNTQ2BRUzNQGMAXEHFQeLBwf98wcVB%2F7cBweLCBUH1APoFR37tB0DZ2QC0wFxBweLCBUH%2FfMICAEjCBQIiwcH%2FdIdFfr6FR1kMjIABAAAAAAETASbAAkAGQAjACcAABM3NjIfAQcnJjQFNzYWFQMOASMFIiY%2FASc3ASEyFh0BITU0NgUVMzWHjg4qDk3UTQ4CFtIOFQIBHRX9qxUIDtCa1P49A%2BgVHfu0HQNnZAP%2Fjg4OTdRMDyqa0g4IFf2pFB4BFQ7Qm9T9Oh0V%2BvoVHWQyMgAAAAQAAAAABEwEsAAPABkAIwAnAAABBR4BFRMUBi8BByc3JyY2EwcGIi8BJjQ%2FAQEhMhYdASE1NDYFFTM1AV4CVxQeARUO0JvUm9IOCMNMDyoOjg4OTf76A%2BgVHfu0HQNnZASwAgEdFf2rFQgO0JrUmtIOFf1QTQ4Ojg4qDk3%2BWB0V%2BvoVHWQyMgACAAT%2F7ASwBK8ABQAIAAAlCQERIQkBFQEEsP4d%2Fsb%2BcQSs%2FTMCq2cBFP5xAacDHPz55gO5AAAAAAIAAABkBEwEsAAVABkAAAERFAYrAREhESMiJjURNDY7AREhETMHIzUzBEwdFZb9RJYVHR0V%2BgH0ZMhkZAPo%2FK4VHQGQ%2FnAdFQPoFB7%2B1AEsyMgAAAMAAABFBN0EsAAWABoALwAAAQcBJyYiDwEhESMiJjURNDY7AREhETMHIzUzARcWFAcBBiIvASY0PwE2Mh8BATYyBEwC%2FtVfCRkJlf7IlhUdHRX6AfRkyGRkAbBqBwf%2BXAgUCMoICGoHFQdPASkHFQPolf7VXwkJk%2F5wHRUD6BQe%2FtQBLMjI%2Fc5qBxUH%2FlsHB8sHFQdqCAhPASkHAAMAAAANBQcEsAAWABoAPgAAAREHJy4BBwEhESMiJjURNDY7AREhETMHIzUzARcWFA8BFxYUDwEGIi8BBwYiLwEmND8BJyY0PwE2Mh8BNzYyBExnhg8lEP72%2FreWFR0dFfoB9GTIZGQB9kYPD4ODDw9GDykPg4MPKQ9GDw%2BDgw8PRg8pD4ODDykD6P7zZ4YPAw7%2B9v5wHRUD6BQe%2FtQBLMjI%2FYxGDykPg4MPKQ9GDw%2BDgw8PRg8pD4ODDykPRg8Pg4MPAAADAAAAFQSXBLAAFQAZAC8AAAERISIGHQEhESMiJjURNDY7AREhETMHIzUzEzMyFh0BMzIWDwEGIi8BJjY7ATU0NgRM%2FqIVHf4MlhUdHRX6AfRkyGRklmQVHZYVCA7mDioO5g4IFZYdA%2Bj%2B1B0Vlv5wHRUD6BQe%2FtQBLMjI%2FagdFfoVDuYODuYOFfoVHQAAAAADAAAAAASXBLAAFQAZAC8AAAERJyYiBwEhESMiJjURNDY7AREhETMHIzUzExcWBisBFRQGKwEiJj0BIyImPwE2MgRMpQ4qDv75%2Fm6WFR0dFfoB9GTIZGTr5g4IFZYdFWQVHZYVCA7mDioD6P5wpQ8P%2Fvf%2BcB0VA%2BgUHv7UASzIyP2F5Q8V%2BhQeHhT6FQ%2FlDwADAAAAyASwBEwACQATABcAABMhMhYdASE1NDYBERQGIyEiJjURExUhNTIETBUd%2B1AdBJMdFfu0FR1kAZAETB0VlpYVHf7U%2FdoVHR0VAib%2B1MjIAAAGAAMAfQStBJcADwAZAB0ALQAxADsAAAEXFhQPAQYmPQEhNSE1NDYBIyImPQE0NjsBFyM1MwE3NhYdASEVIRUUBi8BJjQFIzU7AjIWHQEUBisBA6f4Dg74DhX%2BcAGQFf0vMhUdHRUyyGRk%2FoL3DhUBkP5wFQ73DwOBZGRkMxQdHRQzBI3mDioO5g4IFZbIlhUI%2FoUdFWQVHcjI%2FcvmDggVlsiWFQgO5g4qecgdFWQVHQAAAAACAGQAAASwBLAAFgBRAAABJTYWFREUBisBIiY1ES4ENRE0NiUyFh8BERQOAg8BERQGKwEiJjURLgQ1ETQ%2BAzMyFh8BETMRPAE%2BAjMyFh8BETMRND4DA14BFBklHRXIFR0EDiIaFiX%2B4RYZAgEVHR0LCh0VyBUdBA4iGhYBBwoTDRQZAgNkBQkVDxcZAQFkAQUJFQQxdBIUH%2FuuFR0dFQGNAQgbHzUeAWcfRJEZDA3%2BPhw%2FMSkLC%2F5BFR0dFQG%2FBA8uLkAcAcICBxENCxkMDf6iAV4CBxENCxkMDf6iAV4CBxENCwABAGQAAASwBEwAMwAAARUiDgMVERQWHwEVITUyNjURIREUFjMVITUyPgM1ETQmLwE1IRUiBhURIRE0JiM1BLAEDiIaFjIZGf5wSxn%2BDBlL%2FnAEDiIaFjIZGQGQSxkB9BlLBEw4AQUKFA78iBYZAQI4OA0lAYr%2BdiUNODgBBQoUDgN4FhkBAjg4DSX%2BdgGKJQ04AAAABgAAAAAETARMAAwAHAAgACQAKAA0AAABITIWHQEjBTUnITchBSEyFhURFAYjISImNRE0NhcVITUBBTUlBRUhNQUVFAYjIQchJyE3MwKjAXcVHWn%2B2cj%2BcGQBd%2F4lASwpOzsp%2FtQpOzspASwCvP5wAZD8GAEsArwdFf6JZP6JZAGQyGkD6B0VlmJiyGTIOyn%2BDCk7OykB9Ck7ZMjI%2FveFo4XGyMhm%2BBUdZGTIAAEAEAAQBJ8EnwAmAAATNzYWHwEWBg8BHgEXNz4BHwEeAQ8BBiIuBicuBTcRohEuDosOBhF3ZvyNdxEzE8ATBxGjAw0uMUxPZWZ4O0p3RjITCwED76IRBhPCFDERdo78ZXYRBA6IDi8RogEECBUgNUNjO0qZfHNVQBAAAAACAAAAAASwBEwAIwBBAAAAMh4EHwEVFAYvAS4BPQEmIAcVFAYPAQYmPQE%2BBRIyHgIfARUBHgEdARQGIyEiJj0BNDY3ATU0PgIB%2FLimdWQ%2FLAkJHRTKFB2N%2FsKNHRTKFB0DDTE7ZnTKcFImFgEBAW0OFR0V%2B7QVHRUOAW0CFiYETBUhKCgiCgrIFRgDIgMiFZIYGJIVIgMiAxgVyAQNJyQrIP7kExwcCgoy%2FtEPMhTUFR0dFdQUMg8BLzIEDSEZAAADAAAAAASwBLAADQAdACcAAAEHIScRMxUzNTMVMzUzASEyFhQGKwEXITcjIiY0NgMhMhYdASE1NDYETMj9qMjIyMjIyPyuArwVHR0VDIn8SokMFR0dswRMFR37UB0CvMjIAfTIyMjI%2FOAdKh1kZB0qHf7UHRUyMhUdAAAAAwBkAAAEsARMAAkAEwAdAAABIyIGFREhETQmASMiBhURIRE0JgEhETQ2OwEyFhUCvGQpOwEsOwFnZCk7ASw7%2FRv%2B1DspZCk7BEw7KfwYA%2BgpO%2F7UOyn9RAK8KTv84AGQKTs7KQAAAAAF%2F5wAAASwBEwADwATAB8AJQApAAATITIWFREUBiMhIiY1ETQ2FxEhEQUjFTMRITUzNSMRIQURByMRMwcRMxHIArx8sLB8%2FUR8sLAYA4T%2BDMjI%2FtTIyAEsAZBkyMhkZARMsHz%2BDHywsHwB9HywyP1EArzIZP7UZGQBLGT%2B1GQB9GT%2B1AEsAAAABf%2BcAAAEsARMAA8AEwAfACUAKQAAEyEyFhURFAYjISImNRE0NhcRIREBIzUjFSMRMxUzNTMFEQcjETMHETMRyAK8fLCwfP1EfLCwGAOE%2FgxkZGRkZGQBkGTIyGRkBEywfP4MfLCwfAH0fLDI%2FUQCvP2oyMgB9MjIZP7UZAH0ZP7UASwABP%2BcAAAEsARMAA8AEwAbACMAABMhMhYVERQGIyEiJjURNDYXESERBSMRMxUhESEFIxEzFSERIcgCvHywsHz9RHywsBgDhP4MyMj%2B1AEsAZDIyP7UASwETLB8%2Fgx8sLB8AfR8sMj9RAK8yP7UZAH0ZP7UZAH0AAAABP%2BcAAAEsARMAA8AEwAWABkAABMhMhYVERQGIyEiJjURNDYXESERAS0BDQERyAK8fLCwfP1EfLCwGAOE%2Fgz%2B1AEsAZD%2B1ARMsHz%2BDHywsHwB9HywyP1EArz%2BDJaWlpYBLAAAAAX%2FnAAABLAETAAPABMAFwAgACkAABMhMhYVERQGIyEiJjURNDYXESERAyERIQcjIgYVFBY7AQERMzI2NTQmI8gCvHywsHz9RHywsBgDhGT9RAK8ZIImOTYpgv4Mgik2OSYETLB8%2Fgx8sLB8AfR8sMj9RAK8%2FagB9GRWQUFUASz%2B1FRBQVYAAAAF%2F5wAAASwBEwADwATAB8AJQApAAATITIWFREUBiMhIiY1ETQ2FxEhEQUjFTMRITUzNSMRIQEjESM1MwMjNTPIArx8sLB8%2FUR8sLAYA4T%2BDMjI%2FtTIyAEsAZBkZMjIZGQETLB8%2Fgx8sLB8AfR8sMj9RAK8yGT%2B1GRkASz%2BDAGQZP4MZAAG%2F5wAAASwBEwADwATABkAHwAjACcAABMhMhYVERQGIyEiJjURNDYXESERBTMRIREzASMRIzUzBRUzNQEjNTPIArx8sLB8%2FUR8sLAYA4T9RMj%2B1GQCWGRkyP2oZAEsZGQETLB8%2Fgx8sLB8AfR8sMj9RAK8yP5wAfT%2BDAGQZMjIyP7UZAAF%2F5wAAASwBEwADwATABwAIgAmAAATITIWFREUBiMhIiY1ETQ2FxEhEQEHIzU3NSM1IQEjESM1MwMjNTPIArx8sLB8%2FUR8sLAYA4T%2BDMdkx8gBLAGQZGTIx2RkBEywfP4MfLCwfAH0fLDI%2FUQCvP5wyDLIlmT%2BDAGQZP4MZAAAAAMACQAJBKcEpwAPABsAJQAAADIeAhQOAiIuAjQ%2BAQQiDgEUHgEyPgE0JgchFSEVISc1NyEB4PDbnl5entvw255eXp4BxeTCcXHC5MJxcWz%2B1AEs%2FtRkZAEsBKdentvw255eXp7b8NueTHHC5MJxccLkwtDIZGTIZAAAAAAEAAkACQSnBKcADwAbACcAKwAAADIeAhQOAiIuAjQ%2BAQQiDgEUHgEyPgE0JgcVBxcVIycjFSMRIQcVMzUB4PDbnl5entvw255eXp4BxeTCcXHC5MJxcWwyZGRklmQBLMjIBKdentvw255eXp7b8NueTHHC5MJxccLkwtBkMmQyZGQBkGRkZAAAAv%2Fy%2F50EwgRBACAANgAAATIWFzYzMhYUBisBNTQmIyEiBh0BIyImNTQ2NyY1ND4BEzMyFhURMzIWDwEGIi8BJjY7ARE0NgH3brUsLC54qqp4gB0V%2FtQVHd5QcFZBAmKqepYKD4kVCg3fDSYN3w0KFYkPBEF3YQ6t8a36FR0dFfpzT0VrDhMSZKpi%2FbMPCv7tFxD0EBD0EBcBEwoPAAAAAAL%2F8v%2BcBMMEQQAcADMAAAEyFhc2MzIWFxQGBwEmIgcBIyImNTQ2NyY1ND4BExcWBisBERQGKwEiJjURIyImNzY3NjIB9m62LCsueaoBeFr%2Bhg0lDf6DCU9xVkECYqnm3w0KFYkPCpYKD4kVCg3HGBMZBEF3YQ%2BteGOkHAFoEBD%2Bk3NPRWsOExNkqWP9kuQQF%2F7tCg8PCgETFxDMGBMAAAABAGQAAARMBG0AGAAAJTUhATMBMwkBMwEzASEVIyIGHQEhNTQmIwK8AZD%2B8qr%2B8qr%2B1P7Uqv7yqv7yAZAyFR0BkB0VZGQBLAEsAU3%2Bs%2F7U%2FtRkHRUyMhUdAAAAAAEAeQAABDcEmwAvAAABMhYXHgEVFAYHFhUUBiMiJxUyFh0BITU0NjM1BiMiJjU0Ny4BNTQ2MzIXNCY1NDYCWF6TGll7OzIJaUo3LRUd%2FtQdFS03SmkELzlpSgUSAqMEm3FZBoNaPWcfHRpKaR77HRUyMhUd%2Bx5pShIUFVg1SmkCAhAFdKMAAAAGACcAFASJBJwAEQAqAEIASgBiAHsAAAEWEgIHDgEiJicmAhI3PgEyFgUiBw4BBwYWHwEWMzI3Njc2Nz4BLwEmJyYXIgcOAQcGFh8BFjMyNz4BNz4BLwEmJyYWJiIGFBYyNjciBw4BBw4BHwEWFxYzMjc%2BATc2Ji8BJhciBwYHBgcOAR8BFhcWMzI3PgE3NiYvASYD8m9PT29T2dzZU29PT29T2dzZ%2Fj0EBHmxIgQNDCQDBBcGG0dGYAsNAwkDCwccBAVQdRgEDA0iBAQWBhJROQwMAwkDCwf5Y4xjY4xjVhYGElE6CwwDCQMLBwgEBVB1GAQNDCIEjRcGG0dGYAsNAwkDCwcIBAR5sSIEDQwkAwPyb%2F7V%2FtVvU1dXU28BKwErb1NXVxwBIrF5DBYDCQEWYEZHGwMVDCMNBgSRAhh1UA0WAwkBFTpREgMVCyMMBwT6Y2OMY2MVFTpREQQVCyMMBwQCGHVQDRYDCQEkFmBGRxsDFQwjDQYEASKxeQwWAwkBAAAABQBkAAAD6ASwAAwADwAWABwAIgAAASERIzUhFSERNDYzIQEjNQMzByczNTMDISImNREFFRQGKwECvAEstP6s%2FoQPCgI%2FASzIZKLU1KJktP51Cg8DhA8KwwMg%2FoTIyALzCg%2F%2B1Mj84NTUyP4MDwoBi8jDCg8AAAAABQBkAAAD6ASwAAkADAATABoAIQAAASERCQERNDYzIQEjNRMjFSM1IzcDISImPQEpARUUBisBNQK8ASz%2Bov3aDwoCPwEsyD6iZKLUqv6dCg8BfAIIDwqbAyD9%2BAFe%2FdoERwoP%2FtTI%2FHzIyNT%2BZA8KNzcKD1AAAAAAAwAAAAAEsAP0AAgAGQAfAAABIxUzFyERIzcFMzIeAhUhFSEDETM0PgIBMwMhASEEiqJkZP7UotT9EsgbGiEOASz9qMhkDiEaAnPw8PzgASwB9AMgyGQBLNTUBBErJGT%2BogHCJCsRBP5w%2FnAB9AAAAAMAAAAABEwETAAZADIAOQAAATMyFh0BMzIWHQEUBiMhIiY9ATQ2OwE1NDYFNTIWFREUBiMhIic3ARE0NjMVFBYzITI2AQc1IzUzNQKKZBUdMhUdHRX%2B1BUdHRUyHQFzKTs7Kf2oARP2%2Fro7KVg%2BASw%2BWP201MjIBEwdFTIdFWQVHR0VZBUdMhUd%2BpY7KfzgKTsE9gFGAUQpO5Y%2BWFj95tSiZKIAAwBkAAAEvARMABkANgA9AAABMzIWHQEzMhYdARQGIyEiJj0BNDY7ATU0NgU1MhYVESMRMxQOAiMhIiY1ETQ2MxUUFjMhMjYBBzUjNTM1AcJkFR0yFR0dFf7UFR0dFTIdAXMpO8jIDiEaG%2F2oKTs7KVg%2BASw%2BWAGc1MjIBEwdFTIdFWQVHR0VZBUdMhUd%2BpY7Kf4M%2FtQkKxEEOykDICk7lj5YWP3m1KJkogAAAAP%2FogAABRYE1AALABsAHwAACQEWBiMhIiY3ATYyEyMiBhcTHgE7ATI2NxM2JgMVMzUCkgJ9FyAs%2BwQsIBcCfRZARNAUGAQ6BCMUNhQjBDoEGODIBK37sCY3NyYEUCf%2BTB0U%2FtIUHR0UAS4UHf4MZGQAAAAACQAAAAAETARMAA8AHwAvAD8ATwBfAG8AfwCPAAABMzIWHQEUBisBIiY9ATQ2EzMyFh0BFAYrASImPQE0NiEzMhYdARQGKwEiJj0BNDYBMzIWHQEUBisBIiY9ATQ2ITMyFh0BFAYrASImPQE0NiEzMhYdARQGKwEiJj0BNDYBMzIWHQEUBisBIiY9ATQ2ITMyFh0BFAYrASImPQE0NiEzMhYdARQGKwEiJj0BNDYBqfoKDw8K%2BgoPDwr6Cg8PCvoKDw8BmvoKDw8K%2BgoPD%2Fzq%2BgoPDwr6Cg8PAZr6Cg8PCvoKDw8BmvoKDw8K%2BgoPD%2Fzq%2BgoPDwr6Cg8PAZr6Cg8PCvoKDw8BmvoKDw8K%2BgoPDwRMDwqWCg8PCpYKD%2F7UDwqWCg8PCpYKDw8KlgoPDwqWCg%2F%2B1A8KlgoPDwqWCg8PCpYKDw8KlgoPDwqWCg8PCpYKD%2F7UDwqWCg8PCpYKDw8KlgoPDwqWCg8PCpYKDw8KlgoPAAAAAwAAAAAEsAUUABkAKQAzAAABMxUjFSEyFg8BBgchJi8BJjYzITUjNTM1MwEhMhYUBisBFyE3IyImNDYDITIWHQEhNTQ2ArxkZAFePjEcQiko%2FPwoKUIcMT4BXmRkyP4%2BArwVHR0VDIn8SooNFR0dswRMFR37UB0EsMhkTzeEUzMzU4Q3T2TIZPx8HSodZGQdKh3%2B1B0VMjIVHQAABAAAAAAEsAUUAAUAGQArADUAAAAyFhUjNAchFhUUByEyFg8BIScmNjMhJjU0AyEyFhQGKwEVBSElNSMiJjQ2AyEyFh0BITU0NgIwUDnCPAE6EgMBSCkHIq%2F9WrIiCikBSAOvArwVHR0VlgET%2FEoBE5YVHR2zBEwVHftQHQUUOykpjSUmCBEhFpGRFiERCCb%2BlR0qHcjIyMgdKh39qB0VMjIVHQAEAAAAAASwBJ0ABwAUACQALgAAADIWFAYiJjQTMzIWFRQXITY1NDYzASEyFhQGKwEXITcjIiY0NgMhMhYdASE1NDYCDZZqapZqty4iKyf%2BvCcrI%2F7NArwVHR0VDYr8SokMFR0dswRMFR37UB0EnWqWamqW%2Fus5Okxra0w6Of5yHSodZGQdKh3%2B1B0VMjIVHQAEAAAAAASwBRQADwAcACwANgAAATIeARUUBiImNTQ3FzcnNhMzMhYVFBchNjU0NjMBITIWFAYrARchNyMiJjQ2AyEyFh0BITU0NgJYL1szb5xvIpBvoyIfLiIrJ%2F68Jysj%2Fs0CvBUdHRUNivxKiQwVHR2zBEwVHftQHQUUa4s2Tm9vTj5Rj2%2BjGv4KOTpMa2tMOjn%2Bch0qHWRkHSod%2FtQdFTIyFR0AAAADAAAAAASwBRIAEgAiACwAAAEFFSEUHgMXIS4BNTQ%2BAjcBITIWFAYrARchNyMiJjQ2AyEyFh0BITU0NgJYASz%2B1CU%2FP00T%2Fe48PUJtj0r%2BogK8FR0dFQ2K%2FEqJDBUdHbMETBUd%2B1AdBLChizlmUT9IGVO9VFShdksE%2FH4dKh1kZB0qHf7UHRUyMhUdAAIAyAAAA%2BgFFAAPACkAAAAyFh0BHgEdASE1NDY3NTQDITIWFyMVMxUjFTMVIxUzFAYjISImNRE0NgIvUjsuNv5wNi5kAZA2XBqsyMjIyMh1U%2F5wU3V1BRQ7KU4aXDYyMjZcGk4p%2Fkc2LmRkZGRkU3V1UwGQU3UAAAMAZP%2F%2FBEwETAAPAC8AMwAAEyEyFhURFAYjISImNRE0NgMhMhYdARQGIyEXFhQGIi8BIQcGIiY0PwEhIiY9ATQ2BQchJ5YDhBUdHRX8fBUdHQQDtgoPDwr%2B5eANGiUNWP30Vw0mGg3g%2Ft8KDw8BqmQBRGQETB0V%2FgwVHR0VAfQVHf1EDwoyCg%2FgDSUbDVhYDRslDeAPCjIKD2RkZAAAAAAEAAAAAASwBEwAGQAjAC0ANwAAEyEyFh0BIzQmKwEiBhUjNCYrASIGFSM1NDYDITIWFREhETQ2ExUUBisBIiY9ASEVFAYrASImPQHIAyBTdWQ7KfopO2Q7KfopO2R1EQPoKTv7UDvxHRVkFR0D6B0VZBUdBEx1U8gpOzspKTs7KchTdf4MOyn%2B1AEsKTv%2BDDIVHR0VMjIVHR0VMgADAAEAAASpBKwADQARABsAAAkBFhQPASEBJjQ3ATYyCQMDITIWHQEhNTQ2AeACqh8fg%2F4f%2FfsgIAEnH1n%2BrAFWAS%2F%2Bq6IDIBUd%2FHwdBI39VR9ZH4MCBh9ZHwEoH%2F5u%2FqoBMAFV%2FBsdFTIyFR0AAAAAAgCPAAAEIQSwABcALwAAAQMuASMhIgYHAwYWMyEVFBYyNj0BMzI2AyE1NDY7ATU0NjsBETMRMzIWHQEzMhYVBCG9CCcV%2FnAVJwi9CBMVAnEdKh19FROo%2Fa0dFTIdFTDILxUdMhUdAocB%2BhMcHBP%2BBhMclhUdHRWWHP2MMhUdMhUdASz%2B1B0VMh0VAAAEAAAAAASwBLAADQAQAB8AIgAAASERFAYjIREBNTQ2MyEBIzUBIREUBiMhIiY1ETQ2MyEBIzUDhAEsDwr%2Bif7UDwoBdwEsyP2oASwPCv12Cg8PCgF3ASzIAyD9wQoPAk8BLFQKD%2F7UyP4M%2FcEKDw8KA7YKD%2F7UyAAC%2F5wAZAUUBEcARgBWAAABMzIeAhcWFxY2NzYnJjc%2BARYXFgcOASsBDgEPAQ4BKwEiJj8BBisBIicHDgErASImPwEmLwEuAT0BNDY7ATY3JyY2OwE2BSMiBh0BFBY7ATI2PQE0JgHkw0uOakkMEhEfQwoKGRMKBQ8XDCkCA1Y9Pgc4HCcDIhVkFRgDDDEqwxgpCwMiFWQVGAMaVCyfExwdFXwLLW8QBxXLdAFF%2BgoPDwr6Cg8PBEdBa4pJDgYKISAiJRsQCAYIDCw9P1c3fCbqFB0dFEYOCEAUHR0UnUplNQcmFTIVHVdPXw4TZV8PCjIKDw8KMgoPAAb%2FnP%2FmBRQEfgAJACQANAA8AFIAYgAAASU2Fh8BFgYPASUzMhYfASEyFh0BFAYHBQYmJyYjISImPQE0NhcjIgYdARQ7ATI2NTQmJyYEIgYUFjI2NAE3PgEeARceAT8BFxYGDwEGJi8BJjYlBwYfAR4BPwE2Jy4BJy4BAoEBpxMuDiAOAxCL%2FCtqQ0geZgM3FR0cE%2F0fFyIJKjr%2B1D5YWLlQExIqhhALIAsSAYBALS1ALf4PmBIgHhMQHC0aPzANITNQL3wpgigJASlmHyElDR0RPRMFAhQHCxADhPcICxAmDyoNeMgiNtQdFTIVJgeEBBQPQ1g%2ByD5YrBwVODMQEAtEERzJLUAtLUD%2B24ITChESEyMgAwWzPUkrRSgJL5cvfRxYGyYrDwkLNRAhFEgJDAQAAAAAAwBkAAAEOQSwAFEAYABvAAABMzIWHQEeARcWDgIPATIeBRUUDgUjFRQGKwEiJj0BIxUUBisBIiY9ASMiJj0BNDY7AREjIiY9ATQ2OwE1NDY7ATIWHQEzNTQ2AxUhMj4CNTc0LgMjARUhMj4CNTc0LgMjAnGWCg9PaAEBIC4uEBEGEjQwOiodFyI2LUAjGg8KlgoPZA8KlgoPrwoPDwpLSwoPDwqvDwqWCg9kD9cBBxwpEwsBAQsTKRz%2B%2BQFrHCkTCwEBCxMpHASwDwptIW1KLk0tHwYGAw8UKDJOLTtdPCoVCwJLCg8PCktLCg8PCksPCpYKDwJYDwqWCg9LCg8PCktLCg%2F%2B1MgVHR0LCgQOIhoW%2FnDIFR0dCwoEDiIaFgAAAwAEAAIEsASuABcAKQAsAAATITIWFREUBg8BDgEjISImJy4CNRE0NgQiDgQPARchNy4FAyMT1AMMVnokEhIdgVL9xFKCHAgYKHoCIIx9VkcrHQYGnAIwnAIIIClJVSGdwwSuelb%2BYDO3QkJXd3ZYHFrFMwGgVnqZFyYtLSUMDPPzBQ8sKDEj%2FsIBBQACAMgAAAOEBRQADwAZAAABMzIWFREUBiMhIiY1ETQ2ARUUBisBIiY9AQHblmesVCn%2BPilUrAFINhWWFTYFFKxn%2FgwpVFQpAfRnrPwY4RU2NhXhAAACAMgAAAOEBRQADwAZAAABMxQWMxEUBiMhIiY1ETQ2ARUUBisBIiY9AQHbYLOWVCn%2BPilUrAFINhWWFTYFFJaz%2FkIpVFQpAfRnrPwY4RU2NhXhAAACAAAAFAUOBBoAFAAaAAAJASUHFRcVJwc1NzU0Jj4CPwEnCQEFJTUFJQUO%2FYL%2Bhk5klpZkAQEBBQQvkwKCAVz%2Bov6iAV4BXgL%2F%2FuWqPOCWx5SVyJb6BA0GCgYDKEEBG%2F1ipqaTpaUAAAMAZAH0BLADIAAHAA8AFwAAEjIWFAYiJjQkMhYUBiImNCQyFhQGIiY0vHxYWHxYAeh8WFh8WAHofFhYfFgDIFh8WFh8WFh8WFh8WFh8WFh8AAAAAAMBkAAAArwETAAHAA8AFwAAADIWFAYiJjQSMhYUBiImNBIyFhQGIiY0Aeh8WFh8WFh8WFh8WFh8WFh8WARMWHxYWHz%2ByFh8WFh8%2FshYfFhYfAAAAAMAZABkBEwETAAPAB8ALwAAEyEyFh0BFAYjISImPQE0NhMhMhYdARQGIyEiJj0BNDYTITIWHQEUBiMhIiY9ATQ2fQO2Cg8PCvxKCg8PCgO2Cg8PCvxKCg8PCgO2Cg8PCvxKCg8PBEwPCpYKDw8KlgoP%2FnAPCpYKDw8KlgoP%2FnAPCpYKDw8KlgoPAAAABAAAAAAEsASwAA8AHwAvADMAAAEhMhYVERQGIyEiJjURNDYFISIGFREUFjMhMjY1ETQmBSEyFhURFAYjISImNRE0NhcVITUBXgH0ory7o%2F4Mpbm5Asv9qCk7OykCWCk7O%2F2xAfQVHR0V%2FgwVHR1HAZAEsLuj%2FgylubmlAfSlucg7Kf2oKTs7KQJYKTtkHRX%2B1BUdHRUBLBUdZMjIAAAAAAEAZABkBLAETAA7AAATITIWFAYrARUzMhYUBisBFTMyFhQGKwEVMzIWFAYjISImNDY7ATUjIiY0NjsBNSMiJjQ2OwE1IyImNDaWA%2BgVHR0VMjIVHR0VMjIVHR0VMjIVHR0V%2FBgVHR0VMjIVHR0VMjIVHR0VMjIVHR0ETB0qHcgdKh3IHSodyB0qHR0qHcgdKh3IHSodyB0qHQAAAAYBLAAFA%2BgEowAHAA0AEwAZAB8AKgAAAR4BBgcuATYBMhYVIiYlFAYjNDYBMhYVIiYlFAYjNDYDFRQGIiY9ARYzMgKKVz8%2FV1c%2FP%2F75fLB8sAK8sHyw%2FcB8sHywArywfLCwHSodKAMRBKNDsrJCQrKy%2FsCwfLB8fLB8sP7UsHywfHywfLD%2B05AVHR0VjgQAAAH%2FtQDIBJQDgQBCAAABNzYXAR4BBw4BKwEyFRQOBCsBIhE0NyYiBxYVECsBIi4DNTQzIyImJyY2NwE2HwEeAQ4BLwEHIScHBi4BNgLpRRkUASoLCAYFGg8IAQQNGyc%2FKZK4ChRUFQu4jjBJJxkHAgcPGQYGCAsBKhQaTBQVCiMUM7YDe7YsFCMKFgNuEwYS%2FtkLHw8OEw0dNkY4MhwBIBgXBAQYF%2F7gKjxTQyMNEw4PHwoBKBIHEwUjKBYGDMHBDAUWKCMAAAAAAgAAAAAEsASwACUAQwAAASM0LgUrAREUFh8BFSE1Mj4DNREjIg4FFSMRIQEjNC4DKwERFBYXMxUjNTI1ESMiDgMVIzUhBLAyCAsZEyYYGcgyGRn%2BcAQOIhoWyBkYJhMZCwgyA%2Bj9RBkIChgQEWQZDQzIMmQREBgKCBkB9AOEFSAVDggDAfyuFhkBAmRkAQUJFQ4DUgEDCA4VIBUBLP0SDxMKBQH%2BVwsNATIyGQGpAQUKEw%2BWAAAAAAMAAAAABEwErgAdACAAMAAAATUiJy4BLwEBIwEGBw4BDwEVITUiJj8BIRcWBiMVARsBARUUBiMhIiY9ATQ2MyEyFgPoGR4OFgUE%2Ft9F%2FtQSFQkfCwsBETE7EkUBJT0NISf%2B7IZ5AbEdFfwYFR0dFQPoFR0BLDIgDiIKCwLr%2FQ4jFQkTBQUyMisusKYiQTIBhwFW%2Fqr942QVHR0VZBUdHQADAAAAAASwBLAADwBHAEoAABMhMhYVERQGIyEiJjURNDYFIyIHAQYHBgcGHQEUFjMhMjY9ATQmIyInJj8BIRcWBwYjIgYdARQWMyEyNj0BNCYnIicmJyMBJhMjEzIETBUdHRX7tBUdHQJGRg0F%2FtUREhImDAsJAREIDAwINxAKCj8BCjkLEQwYCAwMCAE5CAwLCBEZGQ8B%2FuAFDsVnBLAdFfu0FR0dFQRMFR1SDP0PIBMSEAUNMggMDAgyCAwXDhmjmR8YEQwIMggMDAgyBwwBGRskAuwM%2FgUBCAAABAAAAAAEsASwAAMAEwAjACcAAAEhNSEFITIWFREUBiMhIiY1ETQ2KQEyFhURFAYjISImNRE0NhcRIREEsPtQBLD7ggGQFR0dFf5wFR0dAm0BkBUdHRX%2BcBUdHUcBLARMZMgdFfx8FR0dFQOEFR0dFf5wFR0dFQGQFR1k%2FtQBLAAEAAAAAASwBLAADwAfACMAJwAAEyEyFhURFAYjISImNRE0NgEhMhYVERQGIyEiJjURNDYXESEREyE1ITIBkBUdHRX%2BcBUdHQJtAZAVHR0V%2FnAVHR1HASzI%2B1AEsASwHRX8fBUdHRUDhBUd%2FgwdFf5wFR0dFQGQFR1k%2FtQBLP2oZAAAAAACAAAAZASwA%2BgAJwArAAATITIWFREzNTQ2MyEyFh0BMxUjFRQGIyEiJj0BIxEUBiMhIiY1ETQ2AREhETIBkBUdZB0VAZAVHWRkHRX%2BcBUdZB0V%2FnAVHR0CnwEsA%2BgdFf6ilhUdHRWWZJYVHR0Vlv6iFR0dFQMgFR3%2B1P7UASwAAAQAAAAABLAEsAADABMAFwAnAAAzIxEzFyEyFhURFAYjISImNRE0NhcRIREBITIWFREUBiMhIiY1ETQ2ZGRklgGQFR0dFf5wFR0dRwEs%2FqIDhBUdHRX8fBUdHQSwZB0V%2FnAVHR0VAZAVHWT%2B1AEs%2FgwdFf5wFR0dFQGQFR0AAAAAAgBkAAAETASwACcAKwAAATMyFhURFAYrARUhMhYVERQGIyEiJjURNDYzITUjIiY1ETQ2OwE1MwcRIRECWJYVHR0VlgHCFR0dFfx8FR0dFQFelhUdHRWWZMgBLARMHRX%2BcBUdZB0V%2FnAVHR0VAZAVHWQdFQGQFR1kyP7UASwAAAAEAAAAAASwBLAAAwATABcAJwAAISMRMwUhMhYVERQGIyEiJjURNDYXESERASEyFhURFAYjISImNRE0NgSwZGT9dgGQFR0dFf5wFR0dRwEs%2FK4DhBUdHRX8fBUdHQSwZB0V%2FnAVHR0VAZAVHWT%2B1AEs%2FgwdFf5wFR0dFQGQFR0AAAEBLAAwA28EgAAPAAAJAQYjIiY1ETQ2MzIXARYUA2H%2BEhcSDhAQDhIXAe4OAjX%2BEhcbGQPoGRsX%2FhIOKgAAAAABAUEAMgOEBH4ACwAACQE2FhURFAYnASY0AU8B7h0qKh3%2BEg4CewHuHREp%2FBgpER0B7g4qAAAAAAEAMgFBBH4DhAALAAATITIWBwEGIicBJjZkA%2BgpER3%2BEg4qDv4SHREDhCod%2FhIODgHuHSoAAAAAAQAyASwEfgNvAAsAAAkBFgYjISImNwE2MgJ7Ae4dESn8GCkRHQHuDioDYf4SHSoqHQHuDgAAAAACAAgAAASwBCgABgAKAAABFQE1LQE1ASE1IQK8%2FUwBnf5jBKj84AMgAuW2%2Fr3dwcHd%2B9jIAAAAAAIAAABkBLAEsAALADEAAAEjFTMVIREzNSM1IQEzND4FOwERFAYPARUhNSIuAzURMzIeBRUzESEEsMjI%2FtTIyAEs%2B1AyCAsZEyYYGWQyGRkBkAQOIhoWZBkYJhMZCwgy%2FOADhGRkASxkZP4MFSAVDggDAf3aFhkBAmRkAQUJFQ4CJgEDCA4VIBUBLAAAAgAAAAAETAPoACUAMQAAASM0LgUrAREUFh8BFSE1Mj4DNREjIg4FFSMRIQEjFTMVIREzNSM1IQMgMggLGRMmGBlkMhkZ%2FnAEDiIaFmQZGCYTGQsIMgMgASzIyP7UyMgBLAK8FSAVDggDAf3aFhkCAWRkAQUJFQ4CJgEDCA4VIBUBLPzgZGQBLGRkAAABAMgAZgNyBEoAEgAAATMyFgcJARYGKwEiJwEmNDcBNgK9oBAKDP4wAdAMChCgDQr%2BKQcHAdcKBEoWDP4w%2FjAMFgkB1wgUCAHXCQAAAQE%2BAGYD6ARKABIAAAEzMhcBFhQHAQYrASImNwkBJjYBU6ANCgHXBwf%2BKQoNoBAKDAHQ%2FjAMCgRKCf4pCBQI%2FikJFgwB0AHQDBYAAAEAZgDIBEoDcgASAAAAFh0BFAcBBiInASY9ATQ2FwkBBDQWCf4pCBQI%2FikJFgwB0AHQA3cKEKANCv4pBwcB1woNoBAKDP4wAdAAAAABAGYBPgRKA%2BgAEgAACQEWHQEUBicJAQYmPQE0NwE2MgJqAdcJFgz%2BMP4wDBYJAdcIFAPh%2FikKDaAQCgwB0P4wDAoQoA0KAdcHAAAAAgDZ%2F%2FkEPQSwAAUAOgAAARQGIzQ2BTMyFh8BNjc%2BAh4EBgcOBgcGIiYjIgYiJy4DLwEuAT4EHgEXJyY2A%2BiwfLD%2BVmQVJgdPBQsiKFAzRyorDwURAQQSFyozTSwNOkkLDkc3EDlfNyYHBw8GDyUqPjdGMR%2BTDA0EsHywfLDIHBPCAQIGBwcFDx81S21DBxlLR1xKQhEFBQcHGWt0bCQjP2hJNyATBwMGBcASGAAAAAACAMgAFQOEBLAAFgAaAAATITIWFREUBisBEQcGJjURIyImNRE0NhcVITX6AlgVHR0Vlv8TGpYVHR2rASwEsB0V%2FnAVHf4MsgkQFQKKHRUBkBUdZGRkAAAAAgDIABkETASwAA4AEgAAEyEyFhURBRElIREjETQ2ARU3NfoC7ic9%2FUQCWP1EZB8BDWQEsFEs%2FFt1A7Z9%2FBgEARc0%2FV1kFGQAAQAAAAECTW%2FDBF9fDzz1AB8EsAAAAADQdnOXAAAAANB2c5f%2FUf%2BcBdwFFAAAAAgAAgAAAAAAAAABAAAFFP%2BFAAAFFP9R%2FtQF3AABAAAAAAAAAAAAAAAAAAAAowG4ACgAAAAAAZAAAASwAAAEsABkBLAAAASwAAAEsABwAooAAAUUAAACigAABRQAAAGxAAABRQAAANgAAADYAAAAogAAAQQAAABIAAABBAAAAUUAAASwAGQEsAB7BLAAyASwAMgB9AAABLD%2F8gSwAAAEsAAABLD%2F8ASwAAAEsAAOBLAACQSwAGQEsP%2FTBLD%2F0wSwAAAEsAAABLAAAASwAAAEsAAABLAAJgSwAG4EsAAXBLAAFwSwABcEsABkBLAAGgSwAGQEsAAMBLAAZASwABcEsP%2BcBLAAZASwABcEsAAXBLAAAASwABcEsAAXBLAAFwSwAGQEsAAABLAAZASwAAAEsAAABLAAAASwAAAEsAAABLAAAASwAAAEsAAABLAAZASwAMgEsAAABLAAAASwADUEsABkBLAAyASw%2F7UEsAAhBLAAAASwAAAEsAAABLAAAASwAAAEsP%2BcBLAAAASwAAAEsAAABLAA2wSwABcEsAB1BLAAAASwAAAEsAAABLAACgSwAMgEsAAABLAAnQSwAMgEsADIBLAAyASwAAAEsP%2F%2BBLABLASwAGQEsACIBLABOwSwABcEsAAXBLAAFwSwABcEsAAXBLAAFwSwAAAEsAAXBLAAFwSwABcEsAAXBLAAAASwALcEsAC3BLAAAASwAAAEsABJBLAAFwSwAAAEsAAABLAAXQSw%2F9wEsP%2FcBLD%2FnwSwAGQEsAAABLAAAASwAAAEsABkBLD%2F%2FwSwAAAEsP9RBLAABgSwAAAEsAAABLABRQSwAAEEsAAABLD%2FnASwAEoEsAAUBLAAAASwAAAEsAAABLD%2FnASwAGEEsP%2F9BLAAFgSwABYEsAAWBLAAFgSwABgEsAAABMQAAASwAGQAAAAAAAD%2F2ABkADkAyAAAAScAZAAZABkAGQAZABkAGQAZAAAAAAAAAAAAAADZAAAAAAAOAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAAAAMAZABkAAAAEAAAAAAAZP%2Bc%2F5z%2FnP%2Bc%2F5z%2FnP%2Bc%2F5wACQAJ%2F%2FL%2F8gBkAHkAJwBkAGQAAAAAAGT%2FogAAAAAAAAAAAAAAAADIAGQAAAABAI8AAP%2Bc%2F5wAZAAEAMgAyAAAAGQBkABkAAAAZAEs%2F7UAAAAAAAAAAAAAAAAAAABkAAABLAFBADIAMgAIAAAAAADIAT4AZgBmANkAyADIAAAAKgAqACoAKgCyAOgA6AFOAU4BTgFOAU4BTgFOAU4BTgFOAU4BTgFOAU4BpAIGAiICfgKGAqwC5ANGA24DjAPEBAgEMgRiBKIE3AVcBboGcgb0ByAHYgfKCB4IYgi%2BCTYJhAm2Cd4KKApMCpQK4gswC4oLygwIDFgNKg1eDbAODg5oDrQPKA%2BmD%2BYQEhBUEJAQqhEqEXYRthIKEjgSfBLAExoTdBPQFCoU1BU8FagVzBYEFjYWYBawFv4XUhemGAIYLhhqGJYYsBjgGP4ZKBloGZQZxBnaGe4aNhpoGrga9hteG7QcMhyUHOIdHB1EHWwdlB28HeYeLh52HsAfYh%2FSIEYgviEyIXYhuCJAIpYiuCMOIyIjOCN6I8Ij4CQCJDAkXiSWJOIlNCVgJbwmFCZ%2BJuYnUCe8J%2FgoNChwKKwpoCnMKiYqSiqEKworeiwILGgsuizsLRwtiC30LiguZi6iLtgvDi9GL34vsi%2F4MD4whDDSMRIxYDGuMegyJDJeMpoy3jMiMz4zaDO2NBg0YDSoNNI1LDWeNeg2PjZ8Ntw3GjdON5I31DgQOEI4hjjIOQo5SjmIOcw6HDpsOpo63jugO9w8GDxQPKI8%2BD0yPew%2BOj6MPtQ%2FKD9uP6o%2F%2BkBIQIBAxkECQX5CGEKoQu5DGENCQ3ZDoEPKRBBEYESuRPZFWkW2RgZGdEa0RvZHNkd2R7ZH9kgWSDJITkhqSIZIzEkSSThJXkmESapKAkouSlIAAQAAARcApwARAAAAAAACAAAAAQABAAAAQAAuAAAAAAAAABAAxgABAAAAAAATABIAAAADAAEECQAAAGoAEgADAAEECQABACgAfAADAAEECQACAA4ApAADAAEECQADAEwAsgADAAEECQAEADgA%2FgADAAEECQAFAHgBNgADAAEECQAGADYBrgADAAEECQAIABYB5AADAAEECQAJABYB%2BgADAAEECQALACQCEAADAAEECQAMACQCNAADAAEECQATACQCWAADAAEECQDIABYCfAADAAEECQDJADACkgADAAEECdkDABoCwnd3dy5nbHlwaGljb25zLmNvbQBDAG8AcAB5AHIAaQBnAGgAdAAgAKkAIAAyADAAMQA0ACAAYgB5ACAASgBhAG4AIABLAG8AdgBhAHIAaQBrAC4AIABBAGwAbAAgAHIAaQBnAGgAdABzACAAcgBlAHMAZQByAHYAZQBkAC4ARwBMAFkAUABIAEkAQwBPAE4AUwAgAEgAYQBsAGYAbABpAG4AZwBzAFIAZQBnAHUAbABhAHIAMQAuADAAMAA5ADsAVQBLAFcATgA7AEcATABZAFAASABJAEMATwBOAFMASABhAGwAZgBsAGkAbgBnAHMALQBSAGUAZwB1AGwAYQByAEcATABZAFAASABJAEMATwBOAFMAIABIAGEAbABmAGwAaQBuAGcAcwAgAFIAZQBnAHUAbABhAHIAVgBlAHIAcwBpAG8AbgAgADEALgAwADAAOQA7AFAAUwAgADAAMAAxAC4AMAAwADkAOwBoAG8AdABjAG8AbgB2ACAAMQAuADAALgA3ADAAOwBtAGEAawBlAG8AdABmAC4AbABpAGIAMgAuADUALgA1ADgAMwAyADkARwBMAFkAUABIAEkAQwBPAE4AUwBIAGEAbABmAGwAaQBuAGcAcwAtAFIAZQBnAHUAbABhAHIASgBhAG4AIABLAG8AdgBhAHIAaQBrAEoAYQBuACAASwBvAHYAYQByAGkAawB3AHcAdwAuAGcAbAB5AHAAaABpAGMAbwBuAHMALgBjAG8AbQB3AHcAdwAuAGcAbAB5AHAAaABpAGMAbwBuAHMALgBjAG8AbQB3AHcAdwAuAGcAbAB5AHAAaABpAGMAbwBuAHMALgBjAG8AbQBXAGUAYgBmAG8AbgB0ACAAMQAuADAAVwBlAGQAIABPAGMAdAAgADIAOQAgADAANgA6ADMANgA6ADAANwAgADIAMAAxADQARgBvAG4AdAAgAFMAcQB1AGkAcgByAGUAbAAAAAIAAAAAAAD%2FtQAyAAAAAAAAAAAAAAAAAAAAAAAAAAABFwAAAQIBAwADAA0ADgEEAJYBBQEGAQcBCAEJAQoBCwEMAQ0BDgEPARABEQESARMA7wEUARUBFgEXARgBGQEaARsBHAEdAR4BHwEgASEBIgEjASQBJQEmAScBKAEpASoBKwEsAS0BLgEvATABMQEyATMBNAE1ATYBNwE4ATkBOgE7ATwBPQE%2BAT8BQAFBAUIBQwFEAUUBRgFHAUgBSQFKAUsBTAFNAU4BTwFQAVEBUgFTAVQBVQFWAVcBWAFZAVoBWwFcAV0BXgFfAWABYQFiAWMBZAFlAWYBZwFoAWkBagFrAWwBbQFuAW8BcAFxAXIBcwF0AXUBdgF3AXgBeQF6AXsBfAF9AX4BfwGAAYEBggGDAYQBhQGGAYcBiAGJAYoBiwGMAY0BjgGPAZABkQGSAZMBlAGVAZYBlwGYAZkBmgGbAZwBnQGeAZ8BoAGhAaIBowGkAaUBpgGnAagBqQGqAasBrAGtAa4BrwGwAbEBsgGzAbQBtQG2AbcBuAG5AboBuwG8Ab0BvgG%2FAcABwQHCAcMBxAHFAcYBxwHIAckBygHLAcwBzQHOAc8B0AHRAdIB0wHUAdUB1gHXAdgB2QHaAdsB3AHdAd4B3wHgAeEB4gHjAeQB5QHmAecB6AHpAeoB6wHsAe0B7gHvAfAB8QHyAfMB9AH1AfYB9wH4AfkB%2BgH7AfwB%2FQH%2BAf8CAAIBAgICAwIEAgUCBgIHAggCCQIKAgsCDAINAg4CDwIQAhECEgZnbHlwaDEGZ2x5cGgyB3VuaTAwQTAHdW5pMjAwMAd1bmkyMDAxB3VuaTIwMDIHdW5pMjAwMwd1bmkyMDA0B3VuaTIwMDUHdW5pMjAwNgd1bmkyMDA3B3VuaTIwMDgHdW5pMjAwOQd1bmkyMDBBB3VuaTIwMkYHdW5pMjA1RgRFdXJvB3VuaTIwQkQHdW5pMjMxQgd1bmkyNUZDB3VuaTI2MDEHdW5pMjZGQQd1bmkyNzA5B3VuaTI3MEYHdW5pRTAwMQd1bmlFMDAyB3VuaUUwMDMHdW5pRTAwNQd1bmlFMDA2B3VuaUUwMDcHdW5pRTAwOAd1bmlFMDA5B3VuaUUwMTAHdW5pRTAxMQd1bmlFMDEyB3VuaUUwMTMHdW5pRTAxNAd1bmlFMDE1B3VuaUUwMTYHdW5pRTAxNwd1bmlFMDE4B3VuaUUwMTkHdW5pRTAyMAd1bmlFMDIxB3VuaUUwMjIHdW5pRTAyMwd1bmlFMDI0B3VuaUUwMjUHdW5pRTAyNgd1bmlFMDI3B3VuaUUwMjgHdW5pRTAyOQd1bmlFMDMwB3VuaUUwMzEHdW5pRTAzMgd1bmlFMDMzB3VuaUUwMzQHdW5pRTAzNQd1bmlFMDM2B3VuaUUwMzcHdW5pRTAzOAd1bmlFMDM5B3VuaUUwNDAHdW5pRTA0MQd1bmlFMDQyB3VuaUUwNDMHdW5pRTA0NAd1bmlFMDQ1B3VuaUUwNDYHdW5pRTA0Nwd1bmlFMDQ4B3VuaUUwNDkHdW5pRTA1MAd1bmlFMDUxB3VuaUUwNTIHdW5pRTA1Mwd1bmlFMDU0B3VuaUUwNTUHdW5pRTA1Ngd1bmlFMDU3B3VuaUUwNTgHdW5pRTA1OQd1bmlFMDYwB3VuaUUwNjIHdW5pRTA2Mwd1bmlFMDY0B3VuaUUwNjUHdW5pRTA2Ngd1bmlFMDY3B3VuaUUwNjgHdW5pRTA2OQd1bmlFMDcwB3VuaUUwNzEHdW5pRTA3Mgd1bmlFMDczB3VuaUUwNzQHdW5pRTA3NQd1bmlFMDc2B3VuaUUwNzcHdW5pRTA3OAd1bmlFMDc5B3VuaUUwODAHdW5pRTA4MQd1bmlFMDgyB3VuaUUwODMHdW5pRTA4NAd1bmlFMDg1B3VuaUUwODYHdW5pRTA4Nwd1bmlFMDg4B3VuaUUwODkHdW5pRTA5MAd1bmlFMDkxB3VuaUUwOTIHdW5pRTA5Mwd1bmlFMDk0B3VuaUUwOTUHdW5pRTA5Ngd1bmlFMDk3B3VuaUUxMDEHdW5pRTEwMgd1bmlFMTAzB3VuaUUxMDQHdW5pRTEwNQd1bmlFMTA2B3VuaUUxMDcHdW5pRTEwOAd1bmlFMTA5B3VuaUUxMTAHdW5pRTExMQd1bmlFMTEyB3VuaUUxMTMHdW5pRTExNAd1bmlFMTE1B3VuaUUxMTYHdW5pRTExNwd1bmlFMTE4B3VuaUUxMTkHdW5pRTEyMAd1bmlFMTIxB3VuaUUxMjIHdW5pRTEyMwd1bmlFMTI0B3VuaUUxMjUHdW5pRTEyNgd1bmlFMTI3B3VuaUUxMjgHdW5pRTEyOQd1bmlFMTMwB3VuaUUxMzEHdW5pRTEzMgd1bmlFMTMzB3VuaUUxMzQHdW5pRTEzNQd1bmlFMTM2B3VuaUUxMzcHdW5pRTEzOAd1bmlFMTM5B3VuaUUxNDAHdW5pRTE0MQd1bmlFMTQyB3VuaUUxNDMHdW5pRTE0NAd1bmlFMTQ1B3VuaUUxNDYHdW5pRTE0OAd1bmlFMTQ5B3VuaUUxNTAHdW5pRTE1MQd1bmlFMTUyB3VuaUUxNTMHdW5pRTE1NAd1bmlFMTU1B3VuaUUxNTYHdW5pRTE1Nwd1bmlFMTU4B3VuaUUxNTkHdW5pRTE2MAd1bmlFMTYxB3VuaUUxNjIHdW5pRTE2Mwd1bmlFMTY0B3VuaUUxNjUHdW5pRTE2Ngd1bmlFMTY3B3VuaUUxNjgHdW5pRTE2OQd1bmlFMTcwB3VuaUUxNzEHdW5pRTE3Mgd1bmlFMTczB3VuaUUxNzQHdW5pRTE3NQd1bmlFMTc2B3VuaUUxNzcHdW5pRTE3OAd1bmlFMTc5B3VuaUUxODAHdW5pRTE4MQd1bmlFMTgyB3VuaUUxODMHdW5pRTE4NAd1bmlFMTg1B3VuaUUxODYHdW5pRTE4Nwd1bmlFMTg4B3VuaUUxODkHdW5pRTE5MAd1bmlFMTkxB3VuaUUxOTIHdW5pRTE5Mwd1bmlFMTk0B3VuaUUxOTUHdW5pRTE5Nwd1bmlFMTk4B3VuaUUxOTkHdW5pRTIwMAd1bmlFMjAxB3VuaUUyMDIHdW5pRTIwMwd1bmlFMjA0B3VuaUUyMDUHdW5pRTIwNgd1bmlFMjA5B3VuaUUyMTAHdW5pRTIxMQd1bmlFMjEyB3VuaUUyMTMHdW5pRTIxNAd1bmlFMjE1B3VuaUUyMTYHdW5pRTIxOAd1bmlFMjE5B3VuaUUyMjEHdW5pRTIyMwd1bmlFMjI0B3VuaUUyMjUHdW5pRTIyNgd1bmlFMjI3B3VuaUUyMzAHdW5pRTIzMQd1bmlFMjMyB3VuaUUyMzMHdW5pRTIzNAd1bmlFMjM1B3VuaUUyMzYHdW5pRTIzNwd1bmlFMjM4B3VuaUUyMzkHdW5pRTI0MAd1bmlFMjQxB3VuaUUyNDIHdW5pRTI0Mwd1bmlFMjQ0B3VuaUUyNDUHdW5pRTI0Ngd1bmlFMjQ3B3VuaUUyNDgHdW5pRTI0OQd1bmlFMjUwB3VuaUUyNTEHdW5pRTI1Mgd1bmlFMjUzB3VuaUUyNTQHdW5pRTI1NQd1bmlFMjU2B3VuaUUyNTcHdW5pRTI1OAd1bmlFMjU5B3VuaUUyNjAHdW5pRjhGRgZ1MUY1MTEGdTFGNkFBAAAAAAFUUMMXAAA%3D%29%20format%28%27truetype%27%29%2Curl%28data%3Aimage%2Fsvg%2Bxml%3Bbase64%2CPD94bWwgdmVyc2lvbj0iMS4wIiBzdGFuZGFsb25lPSJubyI%2FPgo8IURPQ1RZUEUgc3ZnIFBVQkxJQyAiLS8vVzNDLy9EVEQgU1ZHIDEuMS8vRU4iICJodHRwOi8vd3d3LnczLm9yZy9HcmFwaGljcy9TVkcvMS4xL0RURC9zdmcxMS5kdGQiID4KPHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciPgo8bWV0YWRhdGE%2BPC9tZXRhZGF0YT4KPGRlZnM%2BCjxmb250IGlkPSJnbHlwaGljb25zX2hhbGZsaW5nc3JlZ3VsYXIiIGhvcml6LWFkdi14PSIxMjAwIiA%2BCjxmb250LWZhY2UgdW5pdHMtcGVyLWVtPSIxMjAwIiBhc2NlbnQ9Ijk2MCIgZGVzY2VudD0iLTI0MCIgLz4KPG1pc3NpbmctZ2x5cGggaG9yaXotYWR2LXg9IjUwMCIgLz4KPGdseXBoIGhvcml6LWFkdi14PSIwIiAvPgo8Z2x5cGggaG9yaXotYWR2LXg9IjQwMCIgLz4KPGdseXBoIHVuaWNvZGU9IiAiIC8%2BCjxnbHlwaCB1bmljb2RlPSIqIiBkPSJNNjAwIDExMDBxMTUgMCAzNCAtMS41dDMwIC0zLjVsMTEgLTFxMTAgLTIgMTcuNSAtMTAuNXQ3LjUgLTE4LjV2LTIyNGwxNTggMTU4cTcgNyAxOCA4dDE5IC02bDEwNiAtMTA2cTcgLTggNiAtMTl0LTggLTE4bC0xNTggLTE1OGgyMjRxMTAgMCAxOC41IC03LjV0MTAuNSAtMTcuNXE2IC00MSA2IC03NXEwIC0xNSAtMS41IC0zNHQtMy41IC0zMGwtMSAtMTFxLTIgLTEwIC0xMC41IC0xNy41dC0xOC41IC03LjVoLTIyNGwxNTggLTE1OCBxNyAtNyA4IC0xOHQtNiAtMTlsLTEwNiAtMTA2cS04IC03IC0xOSAtNnQtMTggOGwtMTU4IDE1OHYtMjI0cTAgLTEwIC03LjUgLTE4LjV0LTE3LjUgLTEwLjVxLTQxIC02IC03NSAtNnEtMTUgMCAtMzQgMS41dC0zMCAzLjVsLTExIDFxLTEwIDIgLTE3LjUgMTAuNXQtNy41IDE4LjV2MjI0bC0xNTggLTE1OHEtNyAtNyAtMTggLTh0LTE5IDZsLTEwNiAxMDZxLTcgOCAtNiAxOXQ4IDE4bDE1OCAxNThoLTIyNHEtMTAgMCAtMTguNSA3LjUgdC0xMC41IDE3LjVxLTYgNDEgLTYgNzVxMCAxNSAxLjUgMzR0My41IDMwbDEgMTFxMiAxMCAxMC41IDE3LjV0MTguNSA3LjVoMjI0bC0xNTggMTU4cS03IDcgLTggMTh0NiAxOWwxMDYgMTA2cTggNyAxOSA2dDE4IC04bDE1OCAtMTU4djIyNHEwIDEwIDcuNSAxOC41dDE3LjUgMTAuNXE0MSA2IDc1IDZ6IiAvPgo8Z2x5cGggdW5pY29kZT0iKyIgZD0iTTQ1MCAxMTAwaDIwMHEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXYtMzUwaDM1MHEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXYtMjAwcTAgLTIxIC0xNC41IC0zNS41dC0zNS41IC0xNC41aC0zNTB2LTM1MHEwIC0yMSAtMTQuNSAtMzUuNXQtMzUuNSAtMTQuNWgtMjAwcS0yMSAwIC0zNS41IDE0LjV0LTE0LjUgMzUuNXYzNTBoLTM1MHEtMjEgMCAtMzUuNSAxNC41dC0xNC41IDM1LjV2MjAwcTAgMjEgMTQuNSAzNS41dDM1LjUgMTQuNSBoMzUwdjM1MHEwIDIxIDE0LjUgMzUuNXQzNS41IDE0LjV6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4YTA7IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4YTU7IiBkPSJNODI1IDExMDBoMjUwcTEwIDAgMTIuNSAtNXQtNS41IC0xM2wtMzY0IC0zNjRxLTYgLTYgLTExIC0xOGgyNjhxMTAgMCAxMyAtNnQtMyAtMTRsLTEyMCAtMTYwcS02IC04IC0xOCAtMTR0LTIyIC02aC0xMjV2LTEwMGgyNzVxMTAgMCAxMyAtNnQtMyAtMTRsLTEyMCAtMTYwcS02IC04IC0xOCAtMTR0LTIyIC02aC0xMjV2LTE3NHEwIC0xMSAtNy41IC0xOC41dC0xOC41IC03LjVoLTE0OHEtMTEgMCAtMTguNSA3LjV0LTcuNSAxOC41djE3NCBoLTI3NXEtMTAgMCAtMTMgNnQzIDE0bDEyMCAxNjBxNiA4IDE4IDE0dDIyIDZoMTI1djEwMGgtMjc1cS0xMCAwIC0xMyA2dDMgMTRsMTIwIDE2MHE2IDggMTggMTR0MjIgNmgxMThxLTUgMTIgLTExIDE4bC0zNjQgMzY0cS04IDggLTUuNSAxM3QxMi41IDVoMjUwcTI1IDAgNDMgLTE4bDE2NCAtMTY0cTggLTggMTggLTh0MTggOGwxNjQgMTY0cTE4IDE4IDQzIDE4eiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeDIwMDA7IiBob3Jpei1hZHYteD0iNjUwIiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4MjAwMTsiIGhvcml6LWFkdi14PSIxMzAwIiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4MjAwMjsiIGhvcml6LWFkdi14PSI2NTAiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3gyMDAzOyIgaG9yaXotYWR2LXg9IjEzMDAiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3gyMDA0OyIgaG9yaXotYWR2LXg9IjQzMyIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeDIwMDU7IiBob3Jpei1hZHYteD0iMzI1IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4MjAwNjsiIGhvcml6LWFkdi14PSIyMTYiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3gyMDA3OyIgaG9yaXotYWR2LXg9IjIxNiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeDIwMDg7IiBob3Jpei1hZHYteD0iMTYyIiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4MjAwOTsiIGhvcml6LWFkdi14PSIyNjAiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3gyMDBhOyIgaG9yaXotYWR2LXg9IjcyIiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4MjAyZjsiIGhvcml6LWFkdi14PSIyNjAiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3gyMDVmOyIgaG9yaXotYWR2LXg9IjMyNSIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeDIwYWM7IiBkPSJNNzQ0IDExOThxMjQyIDAgMzU0IC0xODlxNjAgLTEwNCA2NiAtMjA5aC0xODFxMCA0NSAtMTcuNSA4Mi41dC00My41IDYxLjV0LTU4IDQwLjV0LTYwLjUgMjR0LTUxLjUgNy41cS0xOSAwIC00MC41IC01LjV0LTQ5LjUgLTIwLjV0LTUzIC0zOHQtNDkgLTYyLjV0LTM5IC04OS41aDM3OWwtMTAwIC0xMDBoLTMwMHEtNiAtNTAgLTYgLTEwMGg0MDZsLTEwMCAtMTAwaC0zMDBxOSAtNzQgMzMgLTEzMnQ1Mi41IC05MXQ2MS41IC01NC41dDU5IC0yOSB0NDcgLTcuNXEyMiAwIDUwLjUgNy41dDYwLjUgMjQuNXQ1OCA0MXQ0My41IDYxdDE3LjUgODBoMTc0cS0zMCAtMTcxIC0xMjggLTI3OHEtMTA3IC0xMTcgLTI3NCAtMTE3cS0yMDYgMCAtMzI0IDE1OHEtMzYgNDggLTY5IDEzM3QtNDUgMjA0aC0yMTdsMTAwIDEwMGgxMTJxMSA0NyA2IDEwMGgtMjE4bDEwMCAxMDBoMTM0cTIwIDg3IDUxIDE1My41dDYyIDEwMy41cTExNyAxNDEgMjk3IDE0MXoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3gyMGJkOyIgZD0iTTQyOCAxMjAwaDM1MHE2NyAwIDEyMCAtMTN0ODYgLTMxdDU3IC00OS41dDM1IC01Ni41dDE3IC02NC41dDYuNSAtNjAuNXQwLjUgLTU3di0xNi41di0xNi41cTAgLTM2IC0wLjUgLTU3dC02LjUgLTYxdC0xNyAtNjV0LTM1IC01N3QtNTcgLTUwLjV0LTg2IC0zMS41dC0xMjAgLTEzaC0xNzhsLTIgLTEwMGgyODhxMTAgMCAxMyAtNnQtMyAtMTRsLTEyMCAtMTYwcS02IC04IC0xOCAtMTR0LTIyIC02aC0xMzh2LTE3NXEwIC0xMSAtNS41IC0xOCB0LTE1LjUgLTdoLTE0OXEtMTAgMCAtMTcuNSA3LjV0LTcuNSAxNy41djE3NWgtMjY3cS0xMCAwIC0xMyA2dDMgMTRsMTIwIDE2MHE2IDggMTggMTR0MjIgNmgxMTd2MTAwaC0yNjdxLTEwIDAgLTEzIDZ0MyAxNGwxMjAgMTYwcTYgOCAxOCAxNHQyMiA2aDExN3Y0NzVxMCAxMCA3LjUgMTcuNXQxNy41IDcuNXpNNjAwIDEwMDB2LTMwMGgyMDNxNjQgMCA4Ni41IDMzdDIyLjUgMTE5cTAgODQgLTIyLjUgMTE2dC04Ni41IDMyaC0yMDN6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4MjIxMjsiIGQ9Ik0yNTAgNzAwaDgwMHEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXYtMjAwcTAgLTIxIC0xNC41IC0zNS41dC0zNS41IC0xNC41aC04MDBxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41djIwMHEwIDIxIDE0LjUgMzUuNXQzNS41IDE0LjV6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4MjMxYjsiIGQ9Ik0xMDAwIDEyMDB2LTE1MHEwIC0yMSAtMTQuNSAtMzUuNXQtMzUuNSAtMTQuNWgtNTB2LTEwMHEwIC05MSAtNDkuNSAtMTY1LjV0LTEzMC41IC0xMDkuNXE4MSAtMzUgMTMwLjUgLTEwOS41dDQ5LjUgLTE2NS41di0xNTBoNTBxMjEgMCAzNS41IC0xNC41dDE0LjUgLTM1LjV2LTE1MGgtODAwdjE1MHEwIDIxIDE0LjUgMzUuNXQzNS41IDE0LjVoNTB2MTUwcTAgOTEgNDkuNSAxNjUuNXQxMzAuNSAxMDkuNXEtODEgMzUgLTEzMC41IDEwOS41IHQtNDkuNSAxNjUuNXYxMDBoLTUwcS0yMSAwIC0zNS41IDE0LjV0LTE0LjUgMzUuNXYxNTBoODAwek00MDAgMTAwMHYtMTAwcTAgLTYwIDMyLjUgLTEwOS41dDg3LjUgLTczLjVxMjggLTEyIDQ0IC0zN3QxNiAtNTV0LTE2IC01NXQtNDQgLTM3cS01NSAtMjQgLTg3LjUgLTczLjV0LTMyLjUgLTEwOS41di0xNTBoNDAwdjE1MHEwIDYwIC0zMi41IDEwOS41dC04Ny41IDczLjVxLTI4IDEyIC00NCAzN3QtMTYgNTV0MTYgNTV0NDQgMzcgcTU1IDI0IDg3LjUgNzMuNXQzMi41IDEwOS41djEwMGgtNDAweiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeDI1ZmM7IiBob3Jpei1hZHYteD0iNTAwIiBkPSJNMCAweiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeDI2MDE7IiBkPSJNNTAzIDEwODlxMTEwIDAgMjAwLjUgLTU5LjV0MTM0LjUgLTE1Ni41cTQ0IDE0IDkwIDE0cTEyMCAwIDIwNSAtODYuNXQ4NSAtMjA2LjVxMCAtMTIxIC04NSAtMjA3LjV0LTIwNSAtODYuNWgtNzUwcS03OSAwIC0xMzUuNSA1N3QtNTYuNSAxMzdxMCA2OSA0Mi41IDEyMi41dDEwOC41IDY3LjVxLTIgMTIgLTIgMzdxMCAxNTMgMTA4IDI2MC41dDI2MCAxMDcuNXoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3gyNmZhOyIgZD0iTTc3NCAxMTkzLjVxMTYgLTkuNSAyMC41IC0yN3QtNS41IC0zMy41bC0xMzYgLTE4N2w0NjcgLTc0NmgzMHEyMCAwIDM1IC0xOC41dDE1IC0zOS41di00MmgtMTIwMHY0MnEwIDIxIDE1IDM5LjV0MzUgMTguNWgzMGw0NjggNzQ2bC0xMzUgMTgzcS0xMCAxNiAtNS41IDM0dDIwLjUgMjh0MzQgNS41dDI4IC0yMC41bDExMSAtMTQ4bDExMiAxNTBxOSAxNiAyNyAyMC41dDM0IC01ek02MDAgMjAwaDM3N2wtMTgyIDExMmwtMTk1IDUzNHYtNjQ2eiAiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3gyNzA5OyIgZD0iTTI1IDExMDBoMTE1MHExMCAwIDEyLjUgLTV0LTUuNSAtMTNsLTU2NCAtNTY3cS04IC04IC0xOCAtOHQtMTggOGwtNTY0IDU2N3EtOCA4IC01LjUgMTN0MTIuNSA1ek0xOCA4ODJsMjY0IC0yNjRxOCAtOCA4IC0xOHQtOCAtMThsLTI2NCAtMjY0cS04IC04IC0xMyAtNS41dC01IDEyLjV2NTUwcTAgMTAgNSAxMi41dDEzIC01LjV6TTkxOCA2MThsMjY0IDI2NHE4IDggMTMgNS41dDUgLTEyLjV2LTU1MHEwIC0xMCAtNSAtMTIuNXQtMTMgNS41IGwtMjY0IDI2NHEtOCA4IC04IDE4dDggMTh6TTgxOCA0ODJsMzY0IC0zNjRxOCAtOCA1LjUgLTEzdC0xMi41IC01aC0xMTUwcS0xMCAwIC0xMi41IDV0NS41IDEzbDM2NCAzNjRxOCA4IDE4IDh0MTggLThsMTY0IC0xNjRxOCAtOCAxOCAtOHQxOCA4bDE2NCAxNjRxOCA4IDE4IDh0MTggLTh6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4MjcwZjsiIGQ9Ik0xMDExIDEyMTBxMTkgMCAzMyAtMTNsMTUzIC0xNTNxMTMgLTE0IDEzIC0zM3QtMTMgLTMzbC05OSAtOTJsLTIxNCAyMTRsOTUgOTZxMTMgMTQgMzIgMTR6TTEwMTMgODAwbC02MTUgLTYxNGwtMjE0IDIxNGw2MTQgNjE0ek0zMTcgOTZsLTMzMyAtMTEybDExMCAzMzV6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTAwMTsiIGQ9Ik03MDAgNjUwdi01NTBoMjUwcTIxIDAgMzUuNSAtMTQuNXQxNC41IC0zNS41di01MGgtODAwdjUwcTAgMjEgMTQuNSAzNS41dDM1LjUgMTQuNWgyNTB2NTUwbC01MDAgNTUwaDEyMDB6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTAwMjsiIGQ9Ik0zNjggMTAxN2w2NDUgMTYzcTM5IDE1IDYzIDB0MjQgLTQ5di04MzFxMCAtNTUgLTQxLjUgLTk1LjV0LTExMS41IC02My41cS03OSAtMjUgLTE0NyAtNC41dC04NiA3NXQyNS41IDExMS41dDEyMi41IDgycTcyIDI0IDEzOCA4djUyMWwtNjAwIC0xNTV2LTYwNnEwIC00MiAtNDQgLTkwdC0xMDkgLTY5cS03OSAtMjYgLTE0NyAtNS41dC04NiA3NS41dDI1LjUgMTExLjV0MTIyLjUgODIuNXE3MiAyNCAxMzggN3Y2MzlxMCAzOCAxNC41IDU5IHQ1My41IDM0eiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUwMDM7IiBkPSJNNTAwIDExOTFxMTAwIDAgMTkxIC0zOXQxNTYuNSAtMTA0LjV0MTA0LjUgLTE1Ni41dDM5IC0xOTFsLTEgLTJsMSAtNXEwIC0xNDEgLTc4IC0yNjJsMjc1IC0yNzRxMjMgLTI2IDIyLjUgLTQ0LjV0LTIyLjUgLTQyLjVsLTU5IC01OHEtMjYgLTIwIC00Ni41IC0yMHQtMzkuNSAyMGwtMjc1IDI3NHEtMTE5IC03NyAtMjYxIC03N2wtNSAxbC0yIC0xcS0xMDAgMCAtMTkxIDM5dC0xNTYuNSAxMDQuNXQtMTA0LjUgMTU2LjV0LTM5IDE5MSB0MzkgMTkxdDEwNC41IDE1Ni41dDE1Ni41IDEwNC41dDE5MSAzOXpNNTAwIDEwMjJxLTg4IDAgLTE2MiAtNDN0LTExNyAtMTE3dC00MyAtMTYydDQzIC0xNjJ0MTE3IC0xMTd0MTYyIC00M3QxNjIgNDN0MTE3IDExN3Q0MyAxNjJ0LTQzIDE2MnQtMTE3IDExN3QtMTYyIDQzeiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUwMDU7IiBkPSJNNjQ5IDk0OXE0OCA2OCAxMDkuNSAxMDR0MTIxLjUgMzguNXQxMTguNSAtMjB0MTAyLjUgLTY0dDcxIC0xMDAuNXQyNyAtMTIzcTAgLTU3IC0zMy41IC0xMTcuNXQtOTQgLTEyNC41dC0xMjYuNSAtMTI3LjV0LTE1MCAtMTUyLjV0LTE0NiAtMTc0cS02MiA4NSAtMTQ1LjUgMTc0dC0xNTAgMTUyLjV0LTEyNi41IDEyNy41dC05My41IDEyNC41dC0zMy41IDExNy41cTAgNjQgMjggMTIzdDczIDEwMC41dDEwNCA2NHQxMTkgMjAgdDEyMC41IC0zOC41dDEwNC41IC0xMDR6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTAwNjsiIGQ9Ik00MDcgODAwbDEzMSAzNTNxNyAxOSAxNy41IDE5dDE3LjUgLTE5bDEyOSAtMzUzaDQyMXEyMSAwIDI0IC04LjV0LTE0IC0yMC41bC0zNDIgLTI0OWwxMzAgLTQwMXE3IC0yMCAtMC41IC0yNS41dC0yNC41IDYuNWwtMzQzIDI0NmwtMzQyIC0yNDdxLTE3IC0xMiAtMjQuNSAtNi41dC0wLjUgMjUuNWwxMzAgNDAwbC0zNDcgMjUxcS0xNyAxMiAtMTQgMjAuNXQyMyA4LjVoNDI5eiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUwMDc7IiBkPSJNNDA3IDgwMGwxMzEgMzUzcTcgMTkgMTcuNSAxOXQxNy41IC0xOWwxMjkgLTM1M2g0MjFxMjEgMCAyNCAtOC41dC0xNCAtMjAuNWwtMzQyIC0yNDlsMTMwIC00MDFxNyAtMjAgLTAuNSAtMjUuNXQtMjQuNSA2LjVsLTM0MyAyNDZsLTM0MiAtMjQ3cS0xNyAtMTIgLTI0LjUgLTYuNXQtMC41IDI1LjVsMTMwIDQwMGwtMzQ3IDI1MXEtMTcgMTIgLTE0IDIwLjV0MjMgOC41aDQyOXpNNDc3IDcwMGgtMjQwbDE5NyAtMTQybC03NCAtMjI2IGwxOTMgMTM5bDE5NSAtMTQwbC03NCAyMjlsMTkyIDE0MGgtMjM0bC03OCAyMTF6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTAwODsiIGQ9Ik02MDAgMTIwMHExMjQgMCAyMTIgLTg4dDg4IC0yMTJ2LTI1MHEwIC00NiAtMzEgLTk4dC02OSAtNTJ2LTc1cTAgLTEwIDYgLTIxLjV0MTUgLTE3LjVsMzU4IC0yMzBxOSAtNSAxNSAtMTYuNXQ2IC0yMS41di05M3EwIC0xMCAtNy41IC0xNy41dC0xNy41IC03LjVoLTExNTBxLTEwIDAgLTE3LjUgNy41dC03LjUgMTcuNXY5M3EwIDEwIDYgMjEuNXQxNSAxNi41bDM1OCAyMzBxOSA2IDE1IDE3LjV0NiAyMS41djc1cS0zOCAwIC02OSA1MiB0LTMxIDk4djI1MHEwIDEyNCA4OCAyMTJ0MjEyIDg4eiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUwMDk7IiBkPSJNMjUgMTEwMGgxMTUwcTEwIDAgMTcuNSAtNy41dDcuNSAtMTcuNXYtMTA1MHEwIC0xMCAtNy41IC0xNy41dC0xNy41IC03LjVoLTExNTBxLTEwIDAgLTE3LjUgNy41dC03LjUgMTcuNXYxMDUwcTAgMTAgNy41IDE3LjV0MTcuNSA3LjV6TTEwMCAxMDAwdi0xMDBoMTAwdjEwMGgtMTAwek04NzUgMTAwMGgtNTUwcS0xMCAwIC0xNy41IC03LjV0LTcuNSAtMTcuNXYtMzUwcTAgLTEwIDcuNSAtMTcuNXQxNy41IC03LjVoNTUwIHExMCAwIDE3LjUgNy41dDcuNSAxNy41djM1MHEwIDEwIC03LjUgMTcuNXQtMTcuNSA3LjV6TTEwMDAgMTAwMHYtMTAwaDEwMHYxMDBoLTEwMHpNMTAwIDgwMHYtMTAwaDEwMHYxMDBoLTEwMHpNMTAwMCA4MDB2LTEwMGgxMDB2MTAwaC0xMDB6TTEwMCA2MDB2LTEwMGgxMDB2MTAwaC0xMDB6TTEwMDAgNjAwdi0xMDBoMTAwdjEwMGgtMTAwek04NzUgNTAwaC01NTBxLTEwIDAgLTE3LjUgLTcuNXQtNy41IC0xNy41di0zNTBxMCAtMTAgNy41IC0xNy41IHQxNy41IC03LjVoNTUwcTEwIDAgMTcuNSA3LjV0Ny41IDE3LjV2MzUwcTAgMTAgLTcuNSAxNy41dC0xNy41IDcuNXpNMTAwIDQwMHYtMTAwaDEwMHYxMDBoLTEwMHpNMTAwMCA0MDB2LTEwMGgxMDB2MTAwaC0xMDB6TTEwMCAyMDB2LTEwMGgxMDB2MTAwaC0xMDB6TTEwMDAgMjAwdi0xMDBoMTAwdjEwMGgtMTAweiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUwMTA7IiBkPSJNNTAgMTEwMGg0MDBxMjEgMCAzNS41IC0xNC41dDE0LjUgLTM1LjV2LTQwMHEwIC0yMSAtMTQuNSAtMzUuNXQtMzUuNSAtMTQuNWgtNDAwcS0yMSAwIC0zNS41IDE0LjV0LTE0LjUgMzUuNXY0MDBxMCAyMSAxNC41IDM1LjV0MzUuNSAxNC41ek02NTAgMTEwMGg0MDBxMjEgMCAzNS41IC0xNC41dDE0LjUgLTM1LjV2LTQwMHEwIC0yMSAtMTQuNSAtMzUuNXQtMzUuNSAtMTQuNWgtNDAwcS0yMSAwIC0zNS41IDE0LjV0LTE0LjUgMzUuNXY0MDAgcTAgMjEgMTQuNSAzNS41dDM1LjUgMTQuNXpNNTAgNTAwaDQwMHEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXYtNDAwcTAgLTIxIC0xNC41IC0zNS41dC0zNS41IC0xNC41aC00MDBxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41djQwMHEwIDIxIDE0LjUgMzUuNXQzNS41IDE0LjV6TTY1MCA1MDBoNDAwcTIxIDAgMzUuNSAtMTQuNXQxNC41IC0zNS41di00MDBxMCAtMjEgLTE0LjUgLTM1LjV0LTM1LjUgLTE0LjVoLTQwMCBxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41djQwMHEwIDIxIDE0LjUgMzUuNXQzNS41IDE0LjV6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTAxMTsiIGQ9Ik01MCAxMTAwaDIwMHEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXYtMjAwcTAgLTIxIC0xNC41IC0zNS41dC0zNS41IC0xNC41aC0yMDBxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41djIwMHEwIDIxIDE0LjUgMzUuNXQzNS41IDE0LjV6TTQ1MCAxMTAwaDIwMHEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXYtMjAwcTAgLTIxIC0xNC41IC0zNS41dC0zNS41IC0xNC41aC0yMDBxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41djIwMCBxMCAyMSAxNC41IDM1LjV0MzUuNSAxNC41ek04NTAgMTEwMGgyMDBxMjEgMCAzNS41IC0xNC41dDE0LjUgLTM1LjV2LTIwMHEwIC0yMSAtMTQuNSAtMzUuNXQtMzUuNSAtMTQuNWgtMjAwcS0yMSAwIC0zNS41IDE0LjV0LTE0LjUgMzUuNXYyMDBxMCAyMSAxNC41IDM1LjV0MzUuNSAxNC41ek01MCA3MDBoMjAwcTIxIDAgMzUuNSAtMTQuNXQxNC41IC0zNS41di0yMDBxMCAtMjEgLTE0LjUgLTM1LjV0LTM1LjUgLTE0LjVoLTIwMCBxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41djIwMHEwIDIxIDE0LjUgMzUuNXQzNS41IDE0LjV6TTQ1MCA3MDBoMjAwcTIxIDAgMzUuNSAtMTQuNXQxNC41IC0zNS41di0yMDBxMCAtMjEgLTE0LjUgLTM1LjV0LTM1LjUgLTE0LjVoLTIwMHEtMjEgMCAtMzUuNSAxNC41dC0xNC41IDM1LjV2MjAwcTAgMjEgMTQuNSAzNS41dDM1LjUgMTQuNXpNODUwIDcwMGgyMDBxMjEgMCAzNS41IC0xNC41dDE0LjUgLTM1LjV2LTIwMCBxMCAtMjEgLTE0LjUgLTM1LjV0LTM1LjUgLTE0LjVoLTIwMHEtMjEgMCAtMzUuNSAxNC41dC0xNC41IDM1LjV2MjAwcTAgMjEgMTQuNSAzNS41dDM1LjUgMTQuNXpNNTAgMzAwaDIwMHEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXYtMjAwcTAgLTIxIC0xNC41IC0zNS41dC0zNS41IC0xNC41aC0yMDBxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41djIwMHEwIDIxIDE0LjUgMzUuNXQzNS41IDE0LjV6TTQ1MCAzMDBoMjAwIHEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXYtMjAwcTAgLTIxIC0xNC41IC0zNS41dC0zNS41IC0xNC41aC0yMDBxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41djIwMHEwIDIxIDE0LjUgMzUuNXQzNS41IDE0LjV6TTg1MCAzMDBoMjAwcTIxIDAgMzUuNSAtMTQuNXQxNC41IC0zNS41di0yMDBxMCAtMjEgLTE0LjUgLTM1LjV0LTM1LjUgLTE0LjVoLTIwMHEtMjEgMCAtMzUuNSAxNC41dC0xNC41IDM1LjV2MjAwcTAgMjEgMTQuNSAzNS41IHQzNS41IDE0LjV6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTAxMjsiIGQ9Ik01MCAxMTAwaDIwMHEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXYtMjAwcTAgLTIxIC0xNC41IC0zNS41dC0zNS41IC0xNC41aC0yMDBxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41djIwMHEwIDIxIDE0LjUgMzUuNXQzNS41IDE0LjV6TTQ1MCAxMTAwaDcwMHEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXYtMjAwcTAgLTIxIC0xNC41IC0zNS41dC0zNS41IC0xNC41aC03MDBxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41djIwMCBxMCAyMSAxNC41IDM1LjV0MzUuNSAxNC41ek01MCA3MDBoMjAwcTIxIDAgMzUuNSAtMTQuNXQxNC41IC0zNS41di0yMDBxMCAtMjEgLTE0LjUgLTM1LjV0LTM1LjUgLTE0LjVoLTIwMHEtMjEgMCAtMzUuNSAxNC41dC0xNC41IDM1LjV2MjAwcTAgMjEgMTQuNSAzNS41dDM1LjUgMTQuNXpNNDUwIDcwMGg3MDBxMjEgMCAzNS41IC0xNC41dDE0LjUgLTM1LjV2LTIwMHEwIC0yMSAtMTQuNSAtMzUuNXQtMzUuNSAtMTQuNWgtNzAwIHEtMjEgMCAtMzUuNSAxNC41dC0xNC41IDM1LjV2MjAwcTAgMjEgMTQuNSAzNS41dDM1LjUgMTQuNXpNNTAgMzAwaDIwMHEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXYtMjAwcTAgLTIxIC0xNC41IC0zNS41dC0zNS41IC0xNC41aC0yMDBxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41djIwMHEwIDIxIDE0LjUgMzUuNXQzNS41IDE0LjV6TTQ1MCAzMDBoNzAwcTIxIDAgMzUuNSAtMTQuNXQxNC41IC0zNS41di0yMDAgcTAgLTIxIC0xNC41IC0zNS41dC0zNS41IC0xNC41aC03MDBxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41djIwMHEwIDIxIDE0LjUgMzUuNXQzNS41IDE0LjV6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTAxMzsiIGQ9Ik00NjUgNDc3bDU3MSA1NzFxOCA4IDE4IDh0MTcgLThsMTc3IC0xNzdxOCAtNyA4IC0xN3QtOCAtMThsLTc4MyAtNzg0cS03IC04IC0xNy41IC04dC0xNy41IDhsLTM4NCAzODRxLTggOCAtOCAxOHQ4IDE3bDE3NyAxNzdxNyA4IDE3IDh0MTggLThsMTcxIC0xNzFxNyAtNyAxOCAtN3QxOCA3eiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUwMTQ7IiBkPSJNOTA0IDEwODNsMTc4IC0xNzlxOCAtOCA4IC0xOC41dC04IC0xNy41bC0yNjcgLTI2OGwyNjcgLTI2OHE4IC03IDggLTE3LjV0LTggLTE4LjVsLTE3OCAtMTc4cS04IC04IC0xOC41IC04dC0xNy41IDhsLTI2OCAyNjdsLTI2OCAtMjY3cS03IC04IC0xNy41IC04dC0xOC41IDhsLTE3OCAxNzhxLTggOCAtOCAxOC41dDggMTcuNWwyNjcgMjY4bC0yNjcgMjY4cS04IDcgLTggMTcuNXQ4IDE4LjVsMTc4IDE3OHE4IDggMTguNSA4dDE3LjUgLTggbDI2OCAtMjY3bDI2OCAyNjhxNyA3IDE3LjUgN3QxOC41IC03eiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUwMTU7IiBkPSJNNTA3IDExNzdxOTggMCAxODcuNSAtMzguNXQxNTQuNSAtMTAzLjV0MTAzLjUgLTE1NC41dDM4LjUgLTE4Ny41cTAgLTE0MSAtNzggLTI2MmwzMDAgLTI5OXE4IC04IDggLTE4LjV0LTggLTE4LjVsLTEwOSAtMTA4cS03IC04IC0xNy41IC04dC0xOC41IDhsLTMwMCAyOTlxLTExOSAtNzcgLTI2MSAtNzdxLTk4IDAgLTE4OCAzOC41dC0xNTQuNSAxMDN0LTEwMyAxNTQuNXQtMzguNSAxODh0MzguNSAxODcuNXQxMDMgMTU0LjUgdDE1NC41IDEwMy41dDE4OCAzOC41ek01MDYuNSAxMDIzcS04OS41IDAgLTE2NS41IC00NHQtMTIwIC0xMjAuNXQtNDQgLTE2NnQ0NCAtMTY1LjV0MTIwIC0xMjB0MTY1LjUgLTQ0dDE2NiA0NHQxMjAuNSAxMjB0NDQgMTY1LjV0LTQ0IDE2NnQtMTIwLjUgMTIwLjV0LTE2NiA0NHpNNDI1IDkwMGgxNTBxMTAgMCAxNy41IC03LjV0Ny41IC0xNy41di03NWg3NXExMCAwIDE3LjUgLTcuNXQ3LjUgLTE3LjV2LTE1MHEwIC0xMCAtNy41IC0xNy41IHQtMTcuNSAtNy41aC03NXYtNzVxMCAtMTAgLTcuNSAtMTcuNXQtMTcuNSAtNy41aC0xNTBxLTEwIDAgLTE3LjUgNy41dC03LjUgMTcuNXY3NWgtNzVxLTEwIDAgLTE3LjUgNy41dC03LjUgMTcuNXYxNTBxMCAxMCA3LjUgMTcuNXQxNy41IDcuNWg3NXY3NXEwIDEwIDcuNSAxNy41dDE3LjUgNy41eiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUwMTY7IiBkPSJNNTA3IDExNzdxOTggMCAxODcuNSAtMzguNXQxNTQuNSAtMTAzLjV0MTAzLjUgLTE1NC41dDM4LjUgLTE4Ny41cTAgLTE0MSAtNzggLTI2MmwzMDAgLTI5OXE4IC04IDggLTE4LjV0LTggLTE4LjVsLTEwOSAtMTA4cS03IC04IC0xNy41IC04dC0xOC41IDhsLTMwMCAyOTlxLTExOSAtNzcgLTI2MSAtNzdxLTk4IDAgLTE4OCAzOC41dC0xNTQuNSAxMDN0LTEwMyAxNTQuNXQtMzguNSAxODh0MzguNSAxODcuNXQxMDMgMTU0LjUgdDE1NC41IDEwMy41dDE4OCAzOC41ek01MDYuNSAxMDIzcS04OS41IDAgLTE2NS41IC00NHQtMTIwIC0xMjAuNXQtNDQgLTE2NnQ0NCAtMTY1LjV0MTIwIC0xMjB0MTY1LjUgLTQ0dDE2NiA0NHQxMjAuNSAxMjB0NDQgMTY1LjV0LTQ0IDE2NnQtMTIwLjUgMTIwLjV0LTE2NiA0NHpNMzI1IDgwMGgzNTBxMTAgMCAxNy41IC03LjV0Ny41IC0xNy41di0xNTBxMCAtMTAgLTcuNSAtMTcuNXQtMTcuNSAtNy41aC0zNTBxLTEwIDAgLTE3LjUgNy41IHQtNy41IDE3LjV2MTUwcTAgMTAgNy41IDE3LjV0MTcuNSA3LjV6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTAxNzsiIGQ9Ik01NTAgMTIwMGgxMDBxMjEgMCAzNS41IC0xNC41dDE0LjUgLTM1LjV2LTQwMHEwIC0yMSAtMTQuNSAtMzUuNXQtMzUuNSAtMTQuNWgtMTAwcS0yMSAwIC0zNS41IDE0LjV0LTE0LjUgMzUuNXY0MDBxMCAyMSAxNC41IDM1LjV0MzUuNSAxNC41ek04MDAgOTc1djE2NnExNjcgLTYyIDI3MiAtMjA5LjV0MTA1IC0zMzEuNXEwIC0xMTcgLTQ1LjUgLTIyNHQtMTIzIC0xODQuNXQtMTg0LjUgLTEyM3QtMjI0IC00NS41dC0yMjQgNDUuNSB0LTE4NC41IDEyM3QtMTIzIDE4NC41dC00NS41IDIyNHEwIDE4NCAxMDUgMzMxLjV0MjcyIDIwOS41di0xNjZxLTEwMyAtNTUgLTE2NSAtMTU1dC02MiAtMjIwcTAgLTExNiA1NyAtMjE0LjV0MTU1LjUgLTE1NS41dDIxNC41IC01N3QyMTQuNSA1N3QxNTUuNSAxNTUuNXQ1NyAyMTQuNXEwIDEyMCAtNjIgMjIwdC0xNjUgMTU1eiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUwMTg7IiBkPSJNMTAyNSAxMjAwaDE1MHExMCAwIDE3LjUgLTcuNXQ3LjUgLTE3LjV2LTExNTBxMCAtMTAgLTcuNSAtMTcuNXQtMTcuNSAtNy41aC0xNTBxLTEwIDAgLTE3LjUgNy41dC03LjUgMTcuNXYxMTUwcTAgMTAgNy41IDE3LjV0MTcuNSA3LjV6TTcyNSA4MDBoMTUwcTEwIDAgMTcuNSAtNy41dDcuNSAtMTcuNXYtNzUwcTAgLTEwIC03LjUgLTE3LjV0LTE3LjUgLTcuNWgtMTUwcS0xMCAwIC0xNy41IDcuNXQtNy41IDE3LjV2NzUwIHEwIDEwIDcuNSAxNy41dDE3LjUgNy41ek00MjUgNTAwaDE1MHExMCAwIDE3LjUgLTcuNXQ3LjUgLTE3LjV2LTQ1MHEwIC0xMCAtNy41IC0xNy41dC0xNy41IC03LjVoLTE1MHEtMTAgMCAtMTcuNSA3LjV0LTcuNSAxNy41djQ1MHEwIDEwIDcuNSAxNy41dDE3LjUgNy41ek0xMjUgMzAwaDE1MHExMCAwIDE3LjUgLTcuNXQ3LjUgLTE3LjV2LTI1MHEwIC0xMCAtNy41IC0xNy41dC0xNy41IC03LjVoLTE1MHEtMTAgMCAtMTcuNSA3LjV0LTcuNSAxNy41IHYyNTBxMCAxMCA3LjUgMTcuNXQxNy41IDcuNXoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMDE5OyIgZD0iTTYwMCAxMTc0cTMzIDAgNzQgLTVsMzggLTE1Mmw1IC0xcTQ5IC0xNCA5NCAtMzlsNSAtMmwxMzQgODBxNjEgLTQ4IDEwNCAtMTA1bC04MCAtMTM0bDMgLTVxMjUgLTQ0IDM5IC05M2wxIC02bDE1MiAtMzhxNSAtNDMgNSAtNzNxMCAtMzQgLTUgLTc0bC0xNTIgLTM4bC0xIC02cS0xNSAtNDkgLTM5IC05M2wtMyAtNWw4MCAtMTM0cS00OCAtNjEgLTEwNCAtMTA1bC0xMzQgODFsLTUgLTNxLTQ0IC0yNSAtOTQgLTM5bC01IC0ybC0zOCAtMTUxIHEtNDMgLTUgLTc0IC01cS0zMyAwIC03NCA1bC0zOCAxNTFsLTUgMnEtNDkgMTQgLTk0IDM5bC01IDNsLTEzNCAtODFxLTYwIDQ4IC0xMDQgMTA1bDgwIDEzNGwtMyA1cS0yNSA0NSAtMzggOTNsLTIgNmwtMTUxIDM4cS02IDQyIC02IDc0cTAgMzMgNiA3M2wxNTEgMzhsMiA2cTEzIDQ4IDM4IDkzbDMgNWwtODAgMTM0cTQ3IDYxIDEwNSAxMDVsMTMzIC04MGw1IDJxNDUgMjUgOTQgMzlsNSAxbDM4IDE1MnE0MyA1IDc0IDV6TTYwMCA4MTUgcS04OSAwIC0xNTIgLTYzdC02MyAtMTUxLjV0NjMgLTE1MS41dDE1MiAtNjN0MTUyIDYzdDYzIDE1MS41dC02MyAxNTEuNXQtMTUyIDYzeiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUwMjA7IiBkPSJNNTAwIDEzMDBoMzAwcTQxIDAgNzAuNSAtMjkuNXQyOS41IC03MC41di0xMDBoMjc1cTEwIDAgMTcuNSAtNy41dDcuNSAtMTcuNXYtNzVoLTExMDB2NzVxMCAxMCA3LjUgMTcuNXQxNy41IDcuNWgyNzV2MTAwcTAgNDEgMjkuNSA3MC41dDcwLjUgMjkuNXpNNTAwIDEyMDB2LTEwMGgzMDB2MTAwaC0zMDB6TTExMDAgOTAwdi04MDBxMCAtNDEgLTI5LjUgLTcwLjV0LTcwLjUgLTI5LjVoLTcwMHEtNDEgMCAtNzAuNSAyOS41dC0yOS41IDcwLjUgdjgwMGg5MDB6TTMwMCA4MDB2LTcwMGgxMDB2NzAwaC0xMDB6TTUwMCA4MDB2LTcwMGgxMDB2NzAwaC0xMDB6TTcwMCA4MDB2LTcwMGgxMDB2NzAwaC0xMDB6TTkwMCA4MDB2LTcwMGgxMDB2NzAwaC0xMDB6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTAyMTsiIGQ9Ik0xOCA2MThsNjIwIDYwOHE4IDcgMTguNSA3dDE3LjUgLTdsNjA4IC02MDhxOCAtOCA1LjUgLTEzdC0xMi41IC01aC0xNzV2LTU3NXEwIC0xMCAtNy41IC0xNy41dC0xNy41IC03LjVoLTI1MHEtMTAgMCAtMTcuNSA3LjV0LTcuNSAxNy41djM3NWgtMzAwdi0zNzVxMCAtMTAgLTcuNSAtMTcuNXQtMTcuNSAtNy41aC0yNTBxLTEwIDAgLTE3LjUgNy41dC03LjUgMTcuNXY1NzVoLTE3NXEtMTAgMCAtMTIuNSA1dDUuNSAxM3oiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMDIyOyIgZD0iTTYwMCAxMjAwdi00MDBxMCAtNDEgMjkuNSAtNzAuNXQ3MC41IC0yOS41aDMwMHYtNjUwcTAgLTIxIC0xNC41IC0zNS41dC0zNS41IC0xNC41aC04MDBxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41djExMDBxMCAyMSAxNC41IDM1LjV0MzUuNSAxNC41aDQ1MHpNMTAwMCA4MDBoLTI1MHEtMjEgMCAtMzUuNSAxNC41dC0xNC41IDM1LjV2MjUweiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUwMjM7IiBkPSJNNjAwIDExNzdxMTE3IDAgMjI0IC00NS41dDE4NC41IC0xMjN0MTIzIC0xODQuNXQ0NS41IC0yMjR0LTQ1LjUgLTIyNHQtMTIzIC0xODQuNXQtMTg0LjUgLTEyM3QtMjI0IC00NS41dC0yMjQgNDUuNXQtMTg0LjUgMTIzdC0xMjMgMTg0LjV0LTQ1LjUgMjI0dDQ1LjUgMjI0dDEyMyAxODQuNXQxODQuNSAxMjN0MjI0IDQ1LjV6TTYwMCAxMDI3cS0xMTYgMCAtMjE0LjUgLTU3dC0xNTUuNSAtMTU1LjV0LTU3IC0yMTQuNXQ1NyAtMjE0LjUgdDE1NS41IC0xNTUuNXQyMTQuNSAtNTd0MjE0LjUgNTd0MTU1LjUgMTU1LjV0NTcgMjE0LjV0LTU3IDIxNC41dC0xNTUuNSAxNTUuNXQtMjE0LjUgNTd6TTUyNSA5MDBoNTBxMTAgMCAxNy41IC03LjV0Ny41IC0xNy41di0yNzVoMTc1cTEwIDAgMTcuNSAtNy41dDcuNSAtMTcuNXYtNTBxMCAtMTAgLTcuNSAtMTcuNXQtMTcuNSAtNy41aC0yNTBxLTEwIDAgLTE3LjUgNy41dC03LjUgMTcuNXYzNTBxMCAxMCA3LjUgMTcuNXQxNy41IDcuNXoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMDI0OyIgZD0iTTEzMDAgMGgtNTM4bC00MSA0MDBoLTI0MmwtNDEgLTQwMGgtNTM4bDQzMSAxMjAwaDIwOWwtMjEgLTMwMGgxNjJsLTIwIDMwMGgyMDh6TTUxNSA4MDBsLTI3IC0zMDBoMjI0bC0yNyAzMDBoLTE3MHoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMDI1OyIgZD0iTTU1MCAxMjAwaDIwMHEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXYtNDUwaDE5MXEyMCAwIDI1LjUgLTExLjV0LTcuNSAtMjcuNWwtMzI3IC00MDBxLTEzIC0xNiAtMzIgLTE2dC0zMiAxNmwtMzI3IDQwMHEtMTMgMTYgLTcuNSAyNy41dDI1LjUgMTEuNWgxOTF2NDUwcTAgMjEgMTQuNSAzNS41dDM1LjUgMTQuNXpNMTEyNSA0MDBoNTBxMTAgMCAxNy41IC03LjV0Ny41IC0xNy41di0zNTBxMCAtMTAgLTcuNSAtMTcuNXQtMTcuNSAtNy41IGgtMTA1MHEtMTAgMCAtMTcuNSA3LjV0LTcuNSAxNy41djM1MHEwIDEwIDcuNSAxNy41dDE3LjUgNy41aDUwcTEwIDAgMTcuNSAtNy41dDcuNSAtMTcuNXYtMTc1aDkwMHYxNzVxMCAxMCA3LjUgMTcuNXQxNy41IDcuNXoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMDI2OyIgZD0iTTYwMCAxMTc3cTExNyAwIDIyNCAtNDUuNXQxODQuNSAtMTIzdDEyMyAtMTg0LjV0NDUuNSAtMjI0dC00NS41IC0yMjR0LTEyMyAtMTg0LjV0LTE4NC41IC0xMjN0LTIyNCAtNDUuNXQtMjI0IDQ1LjV0LTE4NC41IDEyM3QtMTIzIDE4NC41dC00NS41IDIyNHQ0NS41IDIyNHQxMjMgMTg0LjV0MTg0LjUgMTIzdDIyNCA0NS41ek02MDAgMTAyN3EtMTE2IDAgLTIxNC41IC01N3QtMTU1LjUgLTE1NS41dC01NyAtMjE0LjV0NTcgLTIxNC41IHQxNTUuNSAtMTU1LjV0MjE0LjUgLTU3dDIxNC41IDU3dDE1NS41IDE1NS41dDU3IDIxNC41dC01NyAyMTQuNXQtMTU1LjUgMTU1LjV0LTIxNC41IDU3ek01MjUgOTAwaDE1MHExMCAwIDE3LjUgLTcuNXQ3LjUgLTE3LjV2LTI3NWgxMzdxMjEgMCAyNiAtMTEuNXQtOCAtMjcuNWwtMjIzIC0yNzVxLTEzIC0xNiAtMzIgLTE2dC0zMiAxNmwtMjIzIDI3NXEtMTMgMTYgLTggMjcuNXQyNiAxMS41aDEzN3YyNzVxMCAxMCA3LjUgMTcuNXQxNy41IDcuNXogIiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTAyNzsiIGQ9Ik02MDAgMTE3N3ExMTcgMCAyMjQgLTQ1LjV0MTg0LjUgLTEyM3QxMjMgLTE4NC41dDQ1LjUgLTIyNHQtNDUuNSAtMjI0dC0xMjMgLTE4NC41dC0xODQuNSAtMTIzdC0yMjQgLTQ1LjV0LTIyNCA0NS41dC0xODQuNSAxMjN0LTEyMyAxODQuNXQtNDUuNSAyMjR0NDUuNSAyMjR0MTIzIDE4NC41dDE4NC41IDEyM3QyMjQgNDUuNXpNNjAwIDEwMjdxLTExNiAwIC0yMTQuNSAtNTd0LTE1NS41IC0xNTUuNXQtNTcgLTIxNC41dDU3IC0yMTQuNSB0MTU1LjUgLTE1NS41dDIxNC41IC01N3QyMTQuNSA1N3QxNTUuNSAxNTUuNXQ1NyAyMTQuNXQtNTcgMjE0LjV0LTE1NS41IDE1NS41dC0yMTQuNSA1N3pNNjMyIDkxNGwyMjMgLTI3NXExMyAtMTYgOCAtMjcuNXQtMjYgLTExLjVoLTEzN3YtMjc1cTAgLTEwIC03LjUgLTE3LjV0LTE3LjUgLTcuNWgtMTUwcS0xMCAwIC0xNy41IDcuNXQtNy41IDE3LjV2Mjc1aC0xMzdxLTIxIDAgLTI2IDExLjV0OCAyNy41bDIyMyAyNzVxMTMgMTYgMzIgMTYgdDMyIC0xNnoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMDI4OyIgZD0iTTIyNSAxMjAwaDc1MHExMCAwIDE5LjUgLTd0MTIuNSAtMTdsMTg2IC02NTJxNyAtMjQgNyAtNDl2LTQyNXEwIC0xMiAtNCAtMjd0LTkgLTE3cS0xMiAtNiAtMzcgLTZoLTExMDBxLTEyIDAgLTI3IDR0LTE3IDhxLTYgMTMgLTYgMzhsMSA0MjVxMCAyNSA3IDQ5bDE4NSA2NTJxMyAxMCAxMi41IDE3dDE5LjUgN3pNODc4IDEwMDBoLTU1NnEtMTAgMCAtMTkgLTd0LTExIC0xOGwtODcgLTQ1MHEtMiAtMTEgNCAtMTh0MTYgLTdoMTUwIHExMCAwIDE5LjUgLTd0MTEuNSAtMTdsMzggLTE1MnEyIC0xMCAxMS41IC0xN3QxOS41IC03aDI1MHExMCAwIDE5LjUgN3QxMS41IDE3bDM4IDE1MnEyIDEwIDExLjUgMTd0MTkuNSA3aDE1MHExMCAwIDE2IDd0NCAxOGwtODcgNDUwcS0yIDExIC0xMSAxOHQtMTkgN3oiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMDI5OyIgZD0iTTYwMCAxMTc3cTExNyAwIDIyNCAtNDUuNXQxODQuNSAtMTIzdDEyMyAtMTg0LjV0NDUuNSAtMjI0dC00NS41IC0yMjR0LTEyMyAtMTg0LjV0LTE4NC41IC0xMjN0LTIyNCAtNDUuNXQtMjI0IDQ1LjV0LTE4NC41IDEyM3QtMTIzIDE4NC41dC00NS41IDIyNHQ0NS41IDIyNHQxMjMgMTg0LjV0MTg0LjUgMTIzdDIyNCA0NS41ek02MDAgMTAyN3EtMTE2IDAgLTIxNC41IC01N3QtMTU1LjUgLTE1NS41dC01NyAtMjE0LjV0NTcgLTIxNC41IHQxNTUuNSAtMTU1LjV0MjE0LjUgLTU3dDIxNC41IDU3dDE1NS41IDE1NS41dDU3IDIxNC41dC01NyAyMTQuNXQtMTU1LjUgMTU1LjV0LTIxNC41IDU3ek01NDAgODIwbDI1MyAtMTkwcTE3IC0xMiAxNyAtMzB0LTE3IC0zMGwtMjUzIC0xOTBxLTE2IC0xMiAtMjggLTYuNXQtMTIgMjYuNXY0MDBxMCAyMSAxMiAyNi41dDI4IC02LjV6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTAzMDsiIGQ9Ik05NDcgMTA2MGwxMzUgMTM1cTcgNyAxMi41IDV0NS41IC0xM3YtMzYycTAgLTEwIC03LjUgLTE3LjV0LTE3LjUgLTcuNWgtMzYycS0xMSAwIC0xMyA1LjV0NSAxMi41bDEzMyAxMzNxLTEwOSA3NiAtMjM4IDc2cS0xMTYgMCAtMjE0LjUgLTU3dC0xNTUuNSAtMTU1LjV0LTU3IC0yMTQuNXQ1NyAtMjE0LjV0MTU1LjUgLTE1NS41dDIxNC41IC01N3QyMTQuNSA1N3QxNTUuNSAxNTUuNXQ1NyAyMTQuNWgxNTBxMCAtMTE3IC00NS41IC0yMjQgdC0xMjMgLTE4NC41dC0xODQuNSAtMTIzdC0yMjQgLTQ1LjV0LTIyNCA0NS41dC0xODQuNSAxMjN0LTEyMyAxODQuNXQtNDUuNSAyMjR0NDUuNSAyMjR0MTIzIDE4NC41dDE4NC41IDEyM3QyMjQgNDUuNXExOTIgMCAzNDcgLTExN3oiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMDMxOyIgZD0iTTk0NyAxMDYwbDEzNSAxMzVxNyA3IDEyLjUgNXQ1LjUgLTEzdi0zNjFxMCAtMTEgLTcuNSAtMTguNXQtMTguNSAtNy41aC0zNjFxLTExIDAgLTEzIDUuNXQ1IDEyLjVsMTM0IDEzNHEtMTEwIDc1IC0yMzkgNzVxLTExNiAwIC0yMTQuNSAtNTd0LTE1NS41IC0xNTUuNXQtNTcgLTIxNC41aC0xNTBxMCAxMTcgNDUuNSAyMjR0MTIzIDE4NC41dDE4NC41IDEyM3QyMjQgNDUuNXExOTIgMCAzNDcgLTExN3pNMTAyNyA2MDBoMTUwIHEwIC0xMTcgLTQ1LjUgLTIyNHQtMTIzIC0xODQuNXQtMTg0LjUgLTEyM3QtMjI0IC00NS41cS0xOTIgMCAtMzQ4IDExOGwtMTM0IC0xMzRxLTcgLTggLTEyLjUgLTUuNXQtNS41IDEyLjV2MzYwcTAgMTEgNy41IDE4LjV0MTguNSA3LjVoMzYwcTEwIDAgMTIuNSAtNS41dC01LjUgLTEyLjVsLTEzMyAtMTMzcTExMCAtNzYgMjQwIC03NnExMTYgMCAyMTQuNSA1N3QxNTUuNSAxNTUuNXQ1NyAyMTQuNXoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMDMyOyIgZD0iTTEyNSAxMjAwaDEwNTBxMTAgMCAxNy41IC03LjV0Ny41IC0xNy41di0xMTUwcTAgLTEwIC03LjUgLTE3LjV0LTE3LjUgLTcuNWgtMTA1MHEtMTAgMCAtMTcuNSA3LjV0LTcuNSAxNy41djExNTBxMCAxMCA3LjUgMTcuNXQxNy41IDcuNXpNMTA3NSAxMDAwaC04NTBxLTEwIDAgLTE3LjUgLTcuNXQtNy41IC0xNy41di04NTBxMCAtMTAgNy41IC0xNy41dDE3LjUgLTcuNWg4NTBxMTAgMCAxNy41IDcuNXQ3LjUgMTcuNXY4NTAgcTAgMTAgLTcuNSAxNy41dC0xNy41IDcuNXpNMzI1IDkwMGg1MHExMCAwIDE3LjUgLTcuNXQ3LjUgLTE3LjV2LTUwcTAgLTEwIC03LjUgLTE3LjV0LTE3LjUgLTcuNWgtNTBxLTEwIDAgLTE3LjUgNy41dC03LjUgMTcuNXY1MHEwIDEwIDcuNSAxNy41dDE3LjUgNy41ek01MjUgOTAwaDQ1MHExMCAwIDE3LjUgLTcuNXQ3LjUgLTE3LjV2LTUwcTAgLTEwIC03LjUgLTE3LjV0LTE3LjUgLTcuNWgtNDUwcS0xMCAwIC0xNy41IDcuNXQtNy41IDE3LjV2NTAgcTAgMTAgNy41IDE3LjV0MTcuNSA3LjV6TTMyNSA3MDBoNTBxMTAgMCAxNy41IC03LjV0Ny41IC0xNy41di01MHEwIC0xMCAtNy41IC0xNy41dC0xNy41IC03LjVoLTUwcS0xMCAwIC0xNy41IDcuNXQtNy41IDE3LjV2NTBxMCAxMCA3LjUgMTcuNXQxNy41IDcuNXpNNTI1IDcwMGg0NTBxMTAgMCAxNy41IC03LjV0Ny41IC0xNy41di01MHEwIC0xMCAtNy41IC0xNy41dC0xNy41IC03LjVoLTQ1MHEtMTAgMCAtMTcuNSA3LjV0LTcuNSAxNy41djUwIHEwIDEwIDcuNSAxNy41dDE3LjUgNy41ek0zMjUgNTAwaDUwcTEwIDAgMTcuNSAtNy41dDcuNSAtMTcuNXYtNTBxMCAtMTAgLTcuNSAtMTcuNXQtMTcuNSAtNy41aC01MHEtMTAgMCAtMTcuNSA3LjV0LTcuNSAxNy41djUwcTAgMTAgNy41IDE3LjV0MTcuNSA3LjV6TTUyNSA1MDBoNDUwcTEwIDAgMTcuNSAtNy41dDcuNSAtMTcuNXYtNTBxMCAtMTAgLTcuNSAtMTcuNXQtMTcuNSAtNy41aC00NTBxLTEwIDAgLTE3LjUgNy41dC03LjUgMTcuNXY1MCBxMCAxMCA3LjUgMTcuNXQxNy41IDcuNXpNMzI1IDMwMGg1MHExMCAwIDE3LjUgLTcuNXQ3LjUgLTE3LjV2LTUwcTAgLTEwIC03LjUgLTE3LjV0LTE3LjUgLTcuNWgtNTBxLTEwIDAgLTE3LjUgNy41dC03LjUgMTcuNXY1MHEwIDEwIDcuNSAxNy41dDE3LjUgNy41ek01MjUgMzAwaDQ1MHExMCAwIDE3LjUgLTcuNXQ3LjUgLTE3LjV2LTUwcTAgLTEwIC03LjUgLTE3LjV0LTE3LjUgLTcuNWgtNDUwcS0xMCAwIC0xNy41IDcuNXQtNy41IDE3LjV2NTAgcTAgMTAgNy41IDE3LjV0MTcuNSA3LjV6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTAzMzsiIGQ9Ik05MDAgODAwdjIwMHEwIDgzIC01OC41IDE0MS41dC0xNDEuNSA1OC41aC0zMDBxLTgyIDAgLTE0MSAtNTl0LTU5IC0xNDF2LTIwMGgtMTAwcS00MSAwIC03MC41IC0yOS41dC0yOS41IC03MC41di02MDBxMCAtNDEgMjkuNSAtNzAuNXQ3MC41IC0yOS41aDkwMHE0MSAwIDcwLjUgMjkuNXQyOS41IDcwLjV2NjAwcTAgNDEgLTI5LjUgNzAuNXQtNzAuNSAyOS41aC0xMDB6TTQwMCA4MDB2MTUwcTAgMjEgMTUgMzUuNXQzNSAxNC41aDIwMCBxMjAgMCAzNSAtMTQuNXQxNSAtMzUuNXYtMTUwaC0zMDB6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTAzNDsiIGQ9Ik0xMjUgMTEwMGg1MHExMCAwIDE3LjUgLTcuNXQ3LjUgLTE3LjV2LTEwNzVoLTEwMHYxMDc1cTAgMTAgNy41IDE3LjV0MTcuNSA3LjV6TTEwNzUgMTA1MnE0IDAgOSAtMnExNiAtNiAxNiAtMjN2LTQyMXEwIC02IC0zIC0xMnEtMzMgLTU5IC02Ni41IC05OXQtNjUuNSAtNTh0LTU2LjUgLTI0LjV0LTUyLjUgLTYuNXEtMjYgMCAtNTcuNSA2LjV0LTUyLjUgMTMuNXQtNjAgMjFxLTQxIDE1IC02MyAyMi41dC01Ny41IDE1dC02NS41IDcuNSBxLTg1IDAgLTE2MCAtNTdxLTcgLTUgLTE1IC01cS02IDAgLTExIDNxLTE0IDcgLTE0IDIydjQzOHEyMiA1NSA4MiA5OC41dDExOSA0Ni41cTIzIDIgNDMgMC41dDQzIC03dDMyLjUgLTguNXQzOCAtMTN0MzIuNSAtMTFxNDEgLTE0IDYzLjUgLTIxdDU3IC0xNHQ2My41IC03cTEwMyAwIDE4MyA4N3E3IDggMTggOHoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMDM1OyIgZD0iTTYwMCAxMTc1cTExNiAwIDIyNyAtNDkuNXQxOTIuNSAtMTMxdDEzMSAtMTkyLjV0NDkuNSAtMjI3di0zMDBxMCAtMTAgLTcuNSAtMTcuNXQtMTcuNSAtNy41aC01MHEtMTAgMCAtMTcuNSA3LjV0LTcuNSAxNy41djMwMHEwIDEyNyAtNzAuNSAyMzEuNXQtMTg0LjUgMTYxLjV0LTI0NSA1N3QtMjQ1IC01N3QtMTg0LjUgLTE2MS41dC03MC41IC0yMzEuNXYtMzAwcTAgLTEwIC03LjUgLTE3LjV0LTE3LjUgLTcuNWgtNTAgcS0xMCAwIC0xNy41IDcuNXQtNy41IDE3LjV2MzAwcTAgMTE2IDQ5LjUgMjI3dDEzMSAxOTIuNXQxOTIuNSAxMzF0MjI3IDQ5LjV6TTIyMCA1MDBoMTYwcTggMCAxNCAtNnQ2IC0xNHYtNDYwcTAgLTggLTYgLTE0dC0xNCAtNmgtMTYwcS04IDAgLTE0IDZ0LTYgMTR2NDYwcTAgOCA2IDE0dDE0IDZ6TTgyMCA1MDBoMTYwcTggMCAxNCAtNnQ2IC0xNHYtNDYwcTAgLTggLTYgLTE0dC0xNCAtNmgtMTYwcS04IDAgLTE0IDZ0LTYgMTR2NDYwIHEwIDggNiAxNHQxNCA2eiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUwMzY7IiBkPSJNMzIxIDgxNGwyNTggMTcycTkgNiAxNSAyLjV0NiAtMTMuNXYtNzUwcTAgLTEwIC02IC0xMy41dC0xNSAyLjVsLTI1OCAxNzJxLTIxIDE0IC00NiAxNGgtMjUwcS0xMCAwIC0xNy41IDcuNXQtNy41IDE3LjV2MzUwcTAgMTAgNy41IDE3LjV0MTcuNSA3LjVoMjUwcTI1IDAgNDYgMTR6TTkwMCA2NjhsMTIwIDEyMHE3IDcgMTcgN3QxNyAtN2wzNCAtMzRxNyAtNyA3IC0xN3QtNyAtMTdsLTEyMCAtMTIwbDEyMCAtMTIwcTcgLTcgNyAtMTcgdC03IC0xN2wtMzQgLTM0cS03IC03IC0xNyAtN3QtMTcgN2wtMTIwIDExOWwtMTIwIC0xMTlxLTcgLTcgLTE3IC03dC0xNyA3bC0zNCAzNHEtNyA3IC03IDE3dDcgMTdsMTE5IDEyMGwtMTE5IDEyMHEtNyA3IC03IDE3dDcgMTdsMzQgMzRxNyA4IDE3IDh0MTcgLTh6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTAzNzsiIGQ9Ik0zMjEgODE0bDI1OCAxNzJxOSA2IDE1IDIuNXQ2IC0xMy41di03NTBxMCAtMTAgLTYgLTEzLjV0LTE1IDIuNWwtMjU4IDE3MnEtMjEgMTQgLTQ2IDE0aC0yNTBxLTEwIDAgLTE3LjUgNy41dC03LjUgMTcuNXYzNTBxMCAxMCA3LjUgMTcuNXQxNy41IDcuNWgyNTBxMjUgMCA0NiAxNHpNNzY2IDkwMGg0cTEwIC0xIDE2IC0xMHE5NiAtMTI5IDk2IC0yOTBxMCAtMTU0IC05MCAtMjgxcS02IC05IC0xNyAtMTBsLTMgLTFxLTkgMCAtMTYgNiBsLTI5IDIzcS03IDcgLTguNSAxNi41dDQuNSAxNy41cTcyIDEwMyA3MiAyMjlxMCAxMzIgLTc4IDIzOHEtNiA4IC00LjUgMTh0OS41IDE3bDI5IDIycTcgNSAxNSA1eiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUwMzg7IiBkPSJNOTY3IDEwMDRoM3ExMSAtMSAxNyAtMTBxMTM1IC0xNzkgMTM1IC0zOTZxMCAtMTA1IC0zNCAtMjA2LjV0LTk4IC0xODUuNXEtNyAtOSAtMTcgLTEwaC0zcS05IDAgLTE2IDZsLTQyIDM0cS04IDYgLTkgMTZ0NSAxOHExMTEgMTUwIDExMSAzMjhxMCA5MCAtMjkuNSAxNzZ0LTg0LjUgMTU3cS02IDkgLTUgMTl0MTAgMTZsNDIgMzNxNyA1IDE1IDV6TTMyMSA4MTRsMjU4IDE3MnE5IDYgMTUgMi41dDYgLTEzLjV2LTc1MHEwIC0xMCAtNiAtMTMuNSB0LTE1IDIuNWwtMjU4IDE3MnEtMjEgMTQgLTQ2IDE0aC0yNTBxLTEwIDAgLTE3LjUgNy41dC03LjUgMTcuNXYzNTBxMCAxMCA3LjUgMTcuNXQxNy41IDcuNWgyNTBxMjUgMCA0NiAxNHpNNzY2IDkwMGg0cTEwIC0xIDE2IC0xMHE5NiAtMTI5IDk2IC0yOTBxMCAtMTU0IC05MCAtMjgxcS02IC05IC0xNyAtMTBsLTMgLTFxLTkgMCAtMTYgNmwtMjkgMjNxLTcgNyAtOC41IDE2LjV0NC41IDE3LjVxNzIgMTAzIDcyIDIyOXEwIDEzMiAtNzggMjM4IHEtNiA4IC00LjUgMTguNXQ5LjUgMTYuNWwyOSAyMnE3IDUgMTUgNXoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMDM5OyIgZD0iTTUwMCA5MDBoMTAwdi0xMDBoLTEwMHYtMTAwaC00MDB2LTEwMGgtMTAwdjYwMGg1MDB2LTMwMHpNMTIwMCA3MDBoLTIwMHYtMTAwaDIwMHYtMjAwaC0zMDB2MzAwaC0yMDB2MzAwaC0xMDB2MjAwaDYwMHYtNTAwek0xMDAgMTEwMHYtMzAwaDMwMHYzMDBoLTMwMHpNODAwIDExMDB2LTMwMGgzMDB2MzAwaC0zMDB6TTMwMCA5MDBoLTEwMHYxMDBoMTAwdi0xMDB6TTEwMDAgOTAwaC0xMDB2MTAwaDEwMHYtMTAwek0zMDAgNTAwaDIwMHYtNTAwIGgtNTAwdjUwMGgyMDB2MTAwaDEwMHYtMTAwek04MDAgMzAwaDIwMHYtMTAwaC0xMDB2LTEwMGgtMjAwdjEwMGgtMTAwdjEwMGgxMDB2MjAwaC0yMDB2MTAwaDMwMHYtMzAwek0xMDAgNDAwdi0zMDBoMzAwdjMwMGgtMzAwek0zMDAgMjAwaC0xMDB2MTAwaDEwMHYtMTAwek0xMjAwIDIwMGgtMTAwdjEwMGgxMDB2LTEwMHpNNzAwIDBoLTEwMHYxMDBoMTAwdi0xMDB6TTEyMDAgMGgtMzAwdjEwMGgzMDB2LTEwMHoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMDQwOyIgZD0iTTEwMCAyMDBoLTEwMHYxMDAwaDEwMHYtMTAwMHpNMzAwIDIwMGgtMTAwdjEwMDBoMTAwdi0xMDAwek03MDAgMjAwaC0yMDB2MTAwMGgyMDB2LTEwMDB6TTkwMCAyMDBoLTEwMHYxMDAwaDEwMHYtMTAwMHpNMTIwMCAyMDBoLTIwMHYxMDAwaDIwMHYtMTAwMHpNNDAwIDBoLTMwMHYxMDBoMzAwdi0xMDB6TTYwMCAwaC0xMDB2OTFoMTAwdi05MXpNODAwIDBoLTEwMHY5MWgxMDB2LTkxek0xMTAwIDBoLTIwMHY5MWgyMDB2LTkxeiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUwNDE7IiBkPSJNNTAwIDEyMDBsNjgyIC02ODJxOCAtOCA4IC0xOHQtOCAtMThsLTQ2NCAtNDY0cS04IC04IC0xOCAtOHQtMTggOGwtNjgyIDY4MmwxIDQ3NXEwIDEwIDcuNSAxNy41dDE3LjUgNy41aDQ3NHpNMzE5LjUgMTAyNC41cS0yOS41IDI5LjUgLTcxIDI5LjV0LTcxIC0yOS41dC0yOS41IC03MS41dDI5LjUgLTcxLjV0NzEgLTI5LjV0NzEgMjkuNXQyOS41IDcxLjV0LTI5LjUgNzEuNXoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMDQyOyIgZD0iTTUwMCAxMjAwbDY4MiAtNjgycTggLTggOCAtMTh0LTggLTE4bC00NjQgLTQ2NHEtOCAtOCAtMTggLTh0LTE4IDhsLTY4MiA2ODJsMSA0NzVxMCAxMCA3LjUgMTcuNXQxNy41IDcuNWg0NzR6TTgwMCAxMjAwbDY4MiAtNjgycTggLTggOCAtMTh0LTggLTE4bC00NjQgLTQ2NHEtOCAtOCAtMTggLTh0LTE4IDhsLTU2IDU2bDQyNCA0MjZsLTcwMCA3MDBoMTUwek0zMTkuNSAxMDI0LjVxLTI5LjUgMjkuNSAtNzEgMjkuNXQtNzEgLTI5LjUgdC0yOS41IC03MS41dDI5LjUgLTcxLjV0NzEgLTI5LjV0NzEgMjkuNXQyOS41IDcxLjV0LTI5LjUgNzEuNXoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMDQzOyIgZD0iTTMwMCAxMjAwaDgyNXE3NSAwIDc1IC03NXYtOTAwcTAgLTI1IC0xOCAtNDNsLTY0IC02NHEtOCAtOCAtMTMgLTUuNXQtNSAxMi41djk1MHEwIDEwIC03LjUgMTcuNXQtMTcuNSA3LjVoLTcwMHEtMjUgMCAtNDMgLTE4bC02NCAtNjRxLTggLTggLTUuNSAtMTN0MTIuNSAtNWg3MDBxMTAgMCAxNy41IC03LjV0Ny41IC0xNy41di05NTBxMCAtMTAgLTcuNSAtMTcuNXQtMTcuNSAtNy41aC04NTBxLTEwIDAgLTE3LjUgNy41dC03LjUgMTcuNXY5NzUgcTAgMjUgMTggNDNsMTM5IDEzOXExOCAxOCA0MyAxOHoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMDQ0OyIgZD0iTTI1MCAxMjAwaDgwMHEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXYtMTE1MGwtNDUwIDQ0NGwtNDUwIC00NDV2MTE1MXEwIDIxIDE0LjUgMzUuNXQzNS41IDE0LjV6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTA0NTsiIGQ9Ik04MjIgMTIwMGgtNDQ0cS0xMSAwIC0xOSAtNy41dC05IC0xNy41bC03OCAtMzAxcS03IC0yNCA3IC00NWw1NyAtMTA4cTYgLTkgMTcuNSAtMTV0MjEuNSAtNmg0NTBxMTAgMCAyMS41IDZ0MTcuNSAxNWw2MiAxMDhxMTQgMjEgNyA0NWwtODMgMzAxcS0xIDEwIC05IDE3LjV0LTE5IDcuNXpNMTE3NSA4MDBoLTE1MHEtMTAgMCAtMjEgLTYuNXQtMTUgLTE1LjVsLTc4IC0xNTZxLTQgLTkgLTE1IC0xNS41dC0yMSAtNi41aC01NTAgcS0xMCAwIC0yMSA2LjV0LTE1IDE1LjVsLTc4IDE1NnEtNCA5IC0xNSAxNS41dC0yMSA2LjVoLTE1MHEtMTAgMCAtMTcuNSAtNy41dC03LjUgLTE3LjV2LTY1MHEwIC0xMCA3LjUgLTE3LjV0MTcuNSAtNy41aDE1MHExMCAwIDE3LjUgNy41dDcuNSAxNy41djE1MHEwIDEwIDcuNSAxNy41dDE3LjUgNy41aDc1MHExMCAwIDE3LjUgLTcuNXQ3LjUgLTE3LjV2LTE1MHEwIC0xMCA3LjUgLTE3LjV0MTcuNSAtNy41aDE1MHExMCAwIDE3LjUgNy41IHQ3LjUgMTcuNXY2NTBxMCAxMCAtNy41IDE3LjV0LTE3LjUgNy41ek04NTAgMjAwaC01MDBxLTEwIDAgLTE5LjUgLTd0LTExLjUgLTE3bC0zOCAtMTUycS0yIC0xMCAzLjUgLTE3dDE1LjUgLTdoNjAwcTEwIDAgMTUuNSA3dDMuNSAxN2wtMzggMTUycS0yIDEwIC0xMS41IDE3dC0xOS41IDd6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTA0NjsiIGQ9Ik01MDAgMTEwMGgyMDBxNTYgMCAxMDIuNSAtMjAuNXQ3Mi41IC01MHQ0NCAtNTl0MjUgLTUwLjVsNiAtMjBoMTUwcTQxIDAgNzAuNSAtMjkuNXQyOS41IC03MC41di02MDBxMCAtNDEgLTI5LjUgLTcwLjV0LTcwLjUgLTI5LjVoLTEwMDBxLTQxIDAgLTcwLjUgMjkuNXQtMjkuNSA3MC41djYwMHEwIDQxIDI5LjUgNzAuNXQ3MC41IDI5LjVoMTUwcTIgOCA2LjUgMjEuNXQyNCA0OHQ0NSA2MXQ3MiA0OHQxMDIuNSAyMS41ek05MDAgODAwdi0xMDAgaDEwMHYxMDBoLTEwMHpNNjAwIDczMHEtOTUgMCAtMTYyLjUgLTY3LjV0LTY3LjUgLTE2Mi41dDY3LjUgLTE2Mi41dDE2Mi41IC02Ny41dDE2Mi41IDY3LjV0NjcuNSAxNjIuNXQtNjcuNSAxNjIuNXQtMTYyLjUgNjcuNXpNNjAwIDYwM3E0MyAwIDczIC0zMHQzMCAtNzN0LTMwIC03M3QtNzMgLTMwdC03MyAzMHQtMzAgNzN0MzAgNzN0NzMgMzB6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTA0NzsiIGQ9Ik02ODEgMTE5OWwzODUgLTk5OHEyMCAtNTAgNjAgLTkycTE4IC0xOSAzNi41IC0yOS41dDI3LjUgLTExLjVsMTAgLTJ2LTY2aC00MTd2NjZxNTMgMCA3NSA0My41dDUgODguNWwtODIgMjIyaC0zOTFxLTU4IC0xNDUgLTkyIC0yMzRxLTExIC0zNCAtNi41IC01N3QyNS41IC0zN3Q0NiAtMjB0NTUgLTZ2LTY2aC0zNjV2NjZxNTYgMjQgODQgNTJxMTIgMTIgMjUgMzAuNXQyMCAzMS41bDcgMTNsMzk5IDEwMDZoOTN6TTQxNiA1MjFoMzQwIGwtMTYyIDQ1N3oiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMDQ4OyIgZD0iTTc1MyA2NDFxNSAtMSAxNC41IC00LjV0MzYgLTE1LjV0NTAuNSAtMjYuNXQ1My41IC00MHQ1MC41IC01NC41dDM1LjUgLTcwdDE0LjUgLTg3cTAgLTY3IC0yNy41IC0xMjUuNXQtNzEuNSAtOTcuNXQtOTguNSAtNjYuNXQtMTA4LjUgLTQwLjV0LTEwMiAtMTNoLTUwMHY4OXE0MSA3IDcwLjUgMzIuNXQyOS41IDY1LjV2ODI3cTAgMjQgLTAuNSAzNHQtMy41IDI0dC04LjUgMTkuNXQtMTcgMTMuNXQtMjggMTIuNXQtNDIuNSAxMS41djcxIGw0NzEgLTFxNTcgMCAxMTUuNSAtMjAuNXQxMDggLTU3dDgwLjUgLTk0dDMxIC0xMjQuNXEwIC01MSAtMTUuNSAtOTYuNXQtMzggLTc0LjV0LTQ1IC01MC41dC0zOC41IC0zMC41ek00MDAgNzAwaDEzOXE3OCAwIDEzMC41IDQ4LjV0NTIuNSAxMjIuNXEwIDQxIC04LjUgNzAuNXQtMjkuNSA1NS41dC02Mi41IDM5LjV0LTEwMy41IDEzLjVoLTExOHYtMzUwek00MDAgMjAwaDIxNnE4MCAwIDEyMSA1MC41dDQxIDEzMC41cTAgOTAgLTYyLjUgMTU0LjUgdC0xNTYuNSA2NC41aC0xNTl2LTQwMHoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMDQ5OyIgZD0iTTg3NyAxMjAwbDIgLTU3cS04MyAtMTkgLTExNiAtNDUuNXQtNDAgLTY2LjVsLTEzMiAtODM5cS05IC00OSAxMyAtNjl0OTYgLTI2di05N2gtNTAwdjk3cTE4NiAxNiAyMDAgOThsMTczIDgzMnEzIDE3IDMgMzB0LTEuNSAyMi41dC05IDE3LjV0LTEzLjUgMTIuNXQtMjEuNSAxMHQtMjYgOC41dC0zMy41IDEwcS0xMyAzIC0xOSA1djU3aDQyNXoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMDUwOyIgZD0iTTEzMDAgOTAwaC01MHEwIDIxIC00IDM3dC05LjUgMjYuNXQtMTggMTcuNXQtMjIgMTF0LTI4LjUgNS41dC0zMSAydC0zNyAwLjVoLTIwMHYtODUwcTAgLTIyIDI1IC0zNC41dDUwIC0xMy41bDI1IC0ydi0xMDBoLTQwMHYxMDBxNCAwIDExIDAuNXQyNCAzdDMwIDd0MjQgMTV0MTEgMjQuNXY4NTBoLTIwMHEtMjUgMCAtMzcgLTAuNXQtMzEgLTJ0LTI4LjUgLTUuNXQtMjIgLTExdC0xOCAtMTcuNXQtOS41IC0yNi41dC00IC0zN2gtNTB2MzAwIGgxMDAwdi0zMDB6TTE3NSAxMDAwaC03NXYtODAwaDc1bC0xMjUgLTE2N2wtMTI1IDE2N2g3NXY4MDBoLTc1bDEyNSAxNjd6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTA1MTsiIGQ9Ik0xMTAwIDkwMGgtNTBxMCAyMSAtNCAzN3QtOS41IDI2LjV0LTE4IDE3LjV0LTIyIDExdC0yOC41IDUuNXQtMzEgMnQtMzcgMC41aC0yMDB2LTY1MHEwIC0yMiAyNSAtMzQuNXQ1MCAtMTMuNWwyNSAtMnYtMTAwaC00MDB2MTAwcTQgMCAxMSAwLjV0MjQgM3QzMCA3dDI0IDE1dDExIDI0LjV2NjUwaC0yMDBxLTI1IDAgLTM3IC0wLjV0LTMxIC0ydC0yOC41IC01LjV0LTIyIC0xMXQtMTggLTE3LjV0LTkuNSAtMjYuNXQtNCAtMzdoLTUwdjMwMCBoMTAwMHYtMzAwek0xMTY3IDUwbC0xNjcgLTEyNXY3NWgtODAwdi03NWwtMTY3IDEyNWwxNjcgMTI1di03NWg4MDB2NzV6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTA1MjsiIGQ9Ik01MCAxMTAwaDYwMHEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXYtMTAwcTAgLTIxIC0xNC41IC0zNS41dC0zNS41IC0xNC41aC02MDBxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41djEwMHEwIDIxIDE0LjUgMzUuNXQzNS41IDE0LjV6TTUwIDgwMGgxMDAwcTIxIDAgMzUuNSAtMTQuNXQxNC41IC0zNS41di0xMDBxMCAtMjEgLTE0LjUgLTM1LjV0LTM1LjUgLTE0LjVoLTEwMDBxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41djEwMCBxMCAyMSAxNC41IDM1LjV0MzUuNSAxNC41ek01MCA1MDBoODAwcTIxIDAgMzUuNSAtMTQuNXQxNC41IC0zNS41di0xMDBxMCAtMjEgLTE0LjUgLTM1LjV0LTM1LjUgLTE0LjVoLTgwMHEtMjEgMCAtMzUuNSAxNC41dC0xNC41IDM1LjV2MTAwcTAgMjEgMTQuNSAzNS41dDM1LjUgMTQuNXpNNTAgMjAwaDExMDBxMjEgMCAzNS41IC0xNC41dDE0LjUgLTM1LjV2LTEwMHEwIC0yMSAtMTQuNSAtMzUuNXQtMzUuNSAtMTQuNWgtMTEwMCBxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41djEwMHEwIDIxIDE0LjUgMzUuNXQzNS41IDE0LjV6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTA1MzsiIGQ9Ik0yNTAgMTEwMGg3MDBxMjEgMCAzNS41IC0xNC41dDE0LjUgLTM1LjV2LTEwMHEwIC0yMSAtMTQuNSAtMzUuNXQtMzUuNSAtMTQuNWgtNzAwcS0yMSAwIC0zNS41IDE0LjV0LTE0LjUgMzUuNXYxMDBxMCAyMSAxNC41IDM1LjV0MzUuNSAxNC41ek01MCA4MDBoMTEwMHEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXYtMTAwcTAgLTIxIC0xNC41IC0zNS41dC0zNS41IC0xNC41aC0xMTAwcS0yMSAwIC0zNS41IDE0LjV0LTE0LjUgMzUuNXYxMDAgcTAgMjEgMTQuNSAzNS41dDM1LjUgMTQuNXpNMjUwIDUwMGg3MDBxMjEgMCAzNS41IC0xNC41dDE0LjUgLTM1LjV2LTEwMHEwIC0yMSAtMTQuNSAtMzUuNXQtMzUuNSAtMTQuNWgtNzAwcS0yMSAwIC0zNS41IDE0LjV0LTE0LjUgMzUuNXYxMDBxMCAyMSAxNC41IDM1LjV0MzUuNSAxNC41ek01MCAyMDBoMTEwMHEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXYtMTAwcTAgLTIxIC0xNC41IC0zNS41dC0zNS41IC0xNC41aC0xMTAwIHEtMjEgMCAtMzUuNSAxNC41dC0xNC41IDM1LjV2MTAwcTAgMjEgMTQuNSAzNS41dDM1LjUgMTQuNXoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMDU0OyIgZD0iTTUwMCA5NTB2MTAwcTAgMjEgMTQuNSAzNS41dDM1LjUgMTQuNWg2MDBxMjEgMCAzNS41IC0xNC41dDE0LjUgLTM1LjV2LTEwMHEwIC0yMSAtMTQuNSAtMzUuNXQtMzUuNSAtMTQuNWgtNjAwcS0yMSAwIC0zNS41IDE0LjV0LTE0LjUgMzUuNXpNMTAwIDY1MHYxMDBxMCAyMSAxNC41IDM1LjV0MzUuNSAxNC41aDEwMDBxMjEgMCAzNS41IC0xNC41dDE0LjUgLTM1LjV2LTEwMHEwIC0yMSAtMTQuNSAtMzUuNXQtMzUuNSAtMTQuNWgtMTAwMCBxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41ek0zMDAgMzUwdjEwMHEwIDIxIDE0LjUgMzUuNXQzNS41IDE0LjVoODAwcTIxIDAgMzUuNSAtMTQuNXQxNC41IC0zNS41di0xMDBxMCAtMjEgLTE0LjUgLTM1LjV0LTM1LjUgLTE0LjVoLTgwMHEtMjEgMCAtMzUuNSAxNC41dC0xNC41IDM1LjV6TTAgNTB2MTAwcTAgMjEgMTQuNSAzNS41dDM1LjUgMTQuNWgxMTAwcTIxIDAgMzUuNSAtMTQuNXQxNC41IC0zNS41di0xMDAgcTAgLTIxIC0xNC41IC0zNS41dC0zNS41IC0xNC41aC0xMTAwcS0yMSAwIC0zNS41IDE0LjV0LTE0LjUgMzUuNXoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMDU1OyIgZD0iTTUwIDExMDBoMTEwMHEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXYtMTAwcTAgLTIxIC0xNC41IC0zNS41dC0zNS41IC0xNC41aC0xMTAwcS0yMSAwIC0zNS41IDE0LjV0LTE0LjUgMzUuNXYxMDBxMCAyMSAxNC41IDM1LjV0MzUuNSAxNC41ek01MCA4MDBoMTEwMHEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXYtMTAwcTAgLTIxIC0xNC41IC0zNS41dC0zNS41IC0xNC41aC0xMTAwcS0yMSAwIC0zNS41IDE0LjV0LTE0LjUgMzUuNXYxMDAgcTAgMjEgMTQuNSAzNS41dDM1LjUgMTQuNXpNNTAgNTAwaDExMDBxMjEgMCAzNS41IC0xNC41dDE0LjUgLTM1LjV2LTEwMHEwIC0yMSAtMTQuNSAtMzUuNXQtMzUuNSAtMTQuNWgtMTEwMHEtMjEgMCAtMzUuNSAxNC41dC0xNC41IDM1LjV2MTAwcTAgMjEgMTQuNSAzNS41dDM1LjUgMTQuNXpNNTAgMjAwaDExMDBxMjEgMCAzNS41IC0xNC41dDE0LjUgLTM1LjV2LTEwMHEwIC0yMSAtMTQuNSAtMzUuNXQtMzUuNSAtMTQuNWgtMTEwMCBxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41djEwMHEwIDIxIDE0LjUgMzUuNXQzNS41IDE0LjV6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTA1NjsiIGQ9Ik01MCAxMTAwaDEwMHEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXYtMTAwcTAgLTIxIC0xNC41IC0zNS41dC0zNS41IC0xNC41aC0xMDBxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41djEwMHEwIDIxIDE0LjUgMzUuNXQzNS41IDE0LjV6TTM1MCAxMTAwaDgwMHEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXYtMTAwcTAgLTIxIC0xNC41IC0zNS41dC0zNS41IC0xNC41aC04MDBxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41djEwMCBxMCAyMSAxNC41IDM1LjV0MzUuNSAxNC41ek01MCA4MDBoMTAwcTIxIDAgMzUuNSAtMTQuNXQxNC41IC0zNS41di0xMDBxMCAtMjEgLTE0LjUgLTM1LjV0LTM1LjUgLTE0LjVoLTEwMHEtMjEgMCAtMzUuNSAxNC41dC0xNC41IDM1LjV2MTAwcTAgMjEgMTQuNSAzNS41dDM1LjUgMTQuNXpNMzUwIDgwMGg4MDBxMjEgMCAzNS41IC0xNC41dDE0LjUgLTM1LjV2LTEwMHEwIC0yMSAtMTQuNSAtMzUuNXQtMzUuNSAtMTQuNWgtODAwIHEtMjEgMCAtMzUuNSAxNC41dC0xNC41IDM1LjV2MTAwcTAgMjEgMTQuNSAzNS41dDM1LjUgMTQuNXpNNTAgNTAwaDEwMHEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXYtMTAwcTAgLTIxIC0xNC41IC0zNS41dC0zNS41IC0xNC41aC0xMDBxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41djEwMHEwIDIxIDE0LjUgMzUuNXQzNS41IDE0LjV6TTM1MCA1MDBoODAwcTIxIDAgMzUuNSAtMTQuNXQxNC41IC0zNS41di0xMDAgcTAgLTIxIC0xNC41IC0zNS41dC0zNS41IC0xNC41aC04MDBxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41djEwMHEwIDIxIDE0LjUgMzUuNXQzNS41IDE0LjV6TTUwIDIwMGgxMDBxMjEgMCAzNS41IC0xNC41dDE0LjUgLTM1LjV2LTEwMHEwIC0yMSAtMTQuNSAtMzUuNXQtMzUuNSAtMTQuNWgtMTAwcS0yMSAwIC0zNS41IDE0LjV0LTE0LjUgMzUuNXYxMDBxMCAyMSAxNC41IDM1LjV0MzUuNSAxNC41ek0zNTAgMjAwaDgwMCBxMjEgMCAzNS41IC0xNC41dDE0LjUgLTM1LjV2LTEwMHEwIC0yMSAtMTQuNSAtMzUuNXQtMzUuNSAtMTQuNWgtODAwcS0yMSAwIC0zNS41IDE0LjV0LTE0LjUgMzUuNXYxMDBxMCAyMSAxNC41IDM1LjV0MzUuNSAxNC41eiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUwNTc7IiBkPSJNNDAwIDBoLTEwMHYxMTAwaDEwMHYtMTEwMHpNNTUwIDExMDBoMTAwcTIxIDAgMzUuNSAtMTQuNXQxNC41IC0zNS41di0xMDBxMCAtMjEgLTE0LjUgLTM1LjV0LTM1LjUgLTE0LjVoLTEwMHEtMjEgMCAtMzUuNSAxNC41dC0xNC41IDM1LjV2MTAwcTAgMjEgMTQuNSAzNS41dDM1LjUgMTQuNXpNNTUwIDgwMGg1MDBxMjEgMCAzNS41IC0xNC41dDE0LjUgLTM1LjV2LTEwMHEwIC0yMSAtMTQuNSAtMzUuNXQtMzUuNSAtMTQuNWgtNTAwIHEtMjEgMCAtMzUuNSAxNC41dC0xNC41IDM1LjV2MTAwcTAgMjEgMTQuNSAzNS41dDM1LjUgMTQuNXpNMjY3IDU1MGwtMTY3IC0xMjV2NzVoLTIwMHYxMDBoMjAwdjc1ek01NTAgNTAwaDMwMHEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXYtMTAwcTAgLTIxIC0xNC41IC0zNS41dC0zNS41IC0xNC41aC0zMDBxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41djEwMHEwIDIxIDE0LjUgMzUuNXQzNS41IDE0LjV6TTU1MCAyMDBoNjAwIHEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXYtMTAwcTAgLTIxIC0xNC41IC0zNS41dC0zNS41IC0xNC41aC02MDBxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41djEwMHEwIDIxIDE0LjUgMzUuNXQzNS41IDE0LjV6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTA1ODsiIGQ9Ik01MCAxMTAwaDEwMHEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXYtMTAwcTAgLTIxIC0xNC41IC0zNS41dC0zNS41IC0xNC41aC0xMDBxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41djEwMHEwIDIxIDE0LjUgMzUuNXQzNS41IDE0LjV6TTkwMCAwaC0xMDB2MTEwMGgxMDB2LTExMDB6TTUwIDgwMGg1MDBxMjEgMCAzNS41IC0xNC41dDE0LjUgLTM1LjV2LTEwMHEwIC0yMSAtMTQuNSAtMzUuNXQtMzUuNSAtMTQuNWgtNTAwIHEtMjEgMCAtMzUuNSAxNC41dC0xNC41IDM1LjV2MTAwcTAgMjEgMTQuNSAzNS41dDM1LjUgMTQuNXpNMTEwMCA2MDBoMjAwdi0xMDBoLTIwMHYtNzVsLTE2NyAxMjVsMTY3IDEyNXYtNzV6TTUwIDUwMGgzMDBxMjEgMCAzNS41IC0xNC41dDE0LjUgLTM1LjV2LTEwMHEwIC0yMSAtMTQuNSAtMzUuNXQtMzUuNSAtMTQuNWgtMzAwcS0yMSAwIC0zNS41IDE0LjV0LTE0LjUgMzUuNXYxMDBxMCAyMSAxNC41IDM1LjV0MzUuNSAxNC41ek01MCAyMDBoNjAwIHEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXYtMTAwcTAgLTIxIC0xNC41IC0zNS41dC0zNS41IC0xNC41aC02MDBxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41djEwMHEwIDIxIDE0LjUgMzUuNXQzNS41IDE0LjV6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTA1OTsiIGQ9Ik03NSAxMDAwaDc1MHEzMSAwIDUzIC0yMnQyMiAtNTN2LTY1MHEwIC0zMSAtMjIgLTUzdC01MyAtMjJoLTc1MHEtMzEgMCAtNTMgMjJ0LTIyIDUzdjY1MHEwIDMxIDIyIDUzdDUzIDIyek0xMjAwIDMwMGwtMzAwIDMwMGwzMDAgMzAwdi02MDB6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTA2MDsiIGQ9Ik00NCAxMTAwaDExMTJxMTggMCAzMSAtMTN0MTMgLTMxdi0xMDEycTAgLTE4IC0xMyAtMzF0LTMxIC0xM2gtMTExMnEtMTggMCAtMzEgMTN0LTEzIDMxdjEwMTJxMCAxOCAxMyAzMXQzMSAxM3pNMTAwIDEwMDB2LTczN2wyNDcgMTgybDI5OCAtMTMxbC03NCAxNTZsMjkzIDMxOGwyMzYgLTI4OHY1MDBoLTEwMDB6TTM0MiA4ODRxNTYgMCA5NSAtMzl0MzkgLTk0LjV0LTM5IC05NXQtOTUgLTM5LjV0LTk1IDM5LjV0LTM5IDk1dDM5IDk0LjUgdDk1IDM5eiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUwNjI7IiBkPSJNNjQ4IDExNjlxMTE3IDAgMjE2IC02MHQxNTYuNSAtMTYxdDU3LjUgLTIxOHEwIC0xMTUgLTcwIC0yNThxLTY5IC0xMDkgLTE1OCAtMjI1LjV0LTE0MyAtMTc5LjVsLTU0IC02MnEtOSA4IC0yNS41IDI0LjV0LTYzLjUgNjcuNXQtOTEgMTAzdC05OC41IDEyOHQtOTUuNSAxNDhxLTYwIDEzMiAtNjAgMjQ5cTAgODggMzQgMTY5LjV0OTEuNSAxNDJ0MTM3IDk2LjV0MTY2LjUgMzZ6TTY1Mi41IDk3NHEtOTEuNSAwIC0xNTYuNSAtNjUgdC02NSAtMTU3dDY1IC0xNTYuNXQxNTYuNSAtNjQuNXQxNTYuNSA2NC41dDY1IDE1Ni41dC02NSAxNTd0LTE1Ni41IDY1eiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUwNjM7IiBkPSJNNjAwIDExNzdxMTE3IDAgMjI0IC00NS41dDE4NC41IC0xMjN0MTIzIC0xODQuNXQ0NS41IC0yMjR0LTQ1LjUgLTIyNHQtMTIzIC0xODQuNXQtMTg0LjUgLTEyM3QtMjI0IC00NS41dC0yMjQgNDUuNXQtMTg0LjUgMTIzdC0xMjMgMTg0LjV0LTQ1LjUgMjI0dDQ1LjUgMjI0dDEyMyAxODQuNXQxODQuNSAxMjN0MjI0IDQ1LjV6TTYwMCAxNzN2ODU0cS0xMTYgMCAtMjE0LjUgLTU3dC0xNTUuNSAtMTU1LjV0LTU3IC0yMTQuNXQ1NyAtMjE0LjUgdDE1NS41IC0xNTUuNXQyMTQuNSAtNTd6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTA2NDsiIGQ9Ik01NTQgMTI5NXEyMSAtNzIgNTcuNSAtMTQzLjV0NzYgLTEzMHQ4MyAtMTE4dDgyLjUgLTExN3Q3MCAtMTE2dDQ5LjUgLTEyNnQxOC41IC0xMzYuNXEwIC03MSAtMjUuNSAtMTM1dC02OC41IC0xMTF0LTk5IC04MnQtMTE4LjUgLTU0dC0xMjUuNSAtMjNxLTg0IDUgLTE2MS41IDM0dC0xMzkuNSA3OC41dC05OSAxMjV0LTM3IDE2NC41cTAgNjkgMTggMTM2LjV0NDkuNSAxMjYuNXQ2OS41IDExNi41dDgxLjUgMTE3LjV0ODMuNSAxMTkgdDc2LjUgMTMxdDU4LjUgMTQzek0zNDQgNzEwcS0yMyAtMzMgLTQzLjUgLTcwLjV0LTQwLjUgLTEwMi41dC0xNyAtMTIzcTEgLTM3IDE0LjUgLTY5LjV0MzAgLTUydDQxIC0zN3QzOC41IC0yNC41dDMzIC0xNXEyMSAtNyAzMiAtMXQxMyAyMmw2IDM0cTIgMTAgLTIuNSAyMnQtMTMuNSAxOXEtNSA0IC0xNCAxMnQtMjkuNSA0MC41dC0zMi41IDczLjVxLTI2IDg5IDYgMjcxcTIgMTEgLTYgMTFxLTggMSAtMTUgLTEweiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUwNjU7IiBkPSJNMTAwMCAxMDEzbDEwOCAxMTVxMiAxIDUgMnQxMyAydDIwLjUgLTF0MjUgLTkuNXQyOC41IC0yMS41cTIyIC0yMiAyNyAtNDN0MCAtMzJsLTYgLTEwbC0xMDggLTExNXpNMzUwIDExMDBoNDAwcTUwIDAgMTA1IC0xM2wtMTg3IC0xODdoLTM2OHEtNDEgMCAtNzAuNSAtMjkuNXQtMjkuNSAtNzAuNXYtNTAwcTAgLTQxIDI5LjUgLTcwLjV0NzAuNSAtMjkuNWg1MDBxNDEgMCA3MC41IDI5LjV0MjkuNSA3MC41djE4MmwyMDAgMjAwdi0zMzIgcTAgLTE2NSAtOTMuNSAtMjU3LjV0LTI1Ni41IC05Mi41aC00MDBxLTE2NSAwIC0yNTcuNSA5Mi41dC05Mi41IDI1Ny41djQwMHEwIDE2NSA5Mi41IDI1Ny41dDI1Ny41IDkyLjV6TTEwMDkgODAzbC0zNjIgLTM2MmwtMTYxIC01MGw1NSAxNzBsMzU1IDM1NXoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMDY2OyIgZD0iTTM1MCAxMTAwaDM2MXEtMTY0IC0xNDYgLTIxNiAtMjAwaC0xOTVxLTQxIDAgLTcwLjUgLTI5LjV0LTI5LjUgLTcwLjV2LTUwMHEwIC00MSAyOS41IC03MC41dDcwLjUgLTI5LjVoNTAwcTQxIDAgNzAuNSAyOS41dDI5LjUgNzAuNWwyMDAgMTUzdi0xMDNxMCAtMTY1IC05Mi41IC0yNTcuNXQtMjU3LjUgLTkyLjVoLTQwMHEtMTY1IDAgLTI1Ny41IDkyLjV0LTkyLjUgMjU3LjV2NDAwcTAgMTY1IDkyLjUgMjU3LjV0MjU3LjUgOTIuNXogTTgyNCAxMDczbDMzOSAtMzAxcTggLTcgOCAtMTcuNXQtOCAtMTcuNWwtMzQwIC0zMDZxLTcgLTYgLTEyLjUgLTR0LTYuNSAxMXYyMDNxLTI2IDEgLTU0LjUgMHQtNzguNSAtNy41dC05MiAtMTcuNXQtODYgLTM1dC03MCAtNTdxMTAgNTkgMzMgMTA4dDUxLjUgODEuNXQ2NSA1OC41dDY4LjUgNDAuNXQ2NyAyNC41dDU2IDEzLjV0NDAgNC41djIxMHExIDEwIDYuNSAxMi41dDEzLjUgLTQuNXoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMDY3OyIgZD0iTTM1MCAxMTAwaDM1MHE2MCAwIDEyNyAtMjNsLTE3OCAtMTc3aC0zNDlxLTQxIDAgLTcwLjUgLTI5LjV0LTI5LjUgLTcwLjV2LTUwMHEwIC00MSAyOS41IC03MC41dDcwLjUgLTI5LjVoNTAwcTQxIDAgNzAuNSAyOS41dDI5LjUgNzAuNXY2OWwyMDAgMjAwdi0yMTlxMCAtMTY1IC05Mi41IC0yNTcuNXQtMjU3LjUgLTkyLjVoLTQwMHEtMTY1IDAgLTI1Ny41IDkyLjV0LTkyLjUgMjU3LjV2NDAwcTAgMTY1IDkyLjUgMjU3LjV0MjU3LjUgOTIuNXogTTY0MyA2MzlsMzk1IDM5NXE3IDcgMTcuNSA3dDE3LjUgLTdsMTAxIC0xMDFxNyAtNyA3IC0xNy41dC03IC0xNy41bC01MzEgLTUzMnEtNyAtNyAtMTcuNSAtN3QtMTcuNSA3bC0yNDggMjQ4cS03IDcgLTcgMTcuNXQ3IDE3LjVsMTAxIDEwMXE3IDcgMTcuNSA3dDE3LjUgLTdsMTExIC0xMTFxOCAtNyAxOCAtN3QxOCA3eiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUwNjg7IiBkPSJNMzE4IDkxOGwyNjQgMjY0cTggOCAxOCA4dDE4IC04bDI2MCAtMjY0cTcgLTggNC41IC0xM3QtMTIuNSAtNWgtMTcwdi0yMDBoMjAwdjE3M3EwIDEwIDUgMTJ0MTMgLTVsMjY0IC0yNjBxOCAtNyA4IC0xNy41dC04IC0xNy41bC0yNjQgLTI2NXEtOCAtNyAtMTMgLTV0LTUgMTJ2MTczaC0yMDB2LTIwMGgxNzBxMTAgMCAxMi41IC01dC00LjUgLTEzbC0yNjAgLTI2NHEtOCAtOCAtMTggLTh0LTE4IDhsLTI2NCAyNjRxLTggOCAtNS41IDEzIHQxMi41IDVoMTc1djIwMGgtMjAwdi0xNzNxMCAtMTAgLTUgLTEydC0xMyA1bC0yNjQgMjY1cS04IDcgLTggMTcuNXQ4IDE3LjVsMjY0IDI2MHE4IDcgMTMgNXQ1IC0xMnYtMTczaDIwMHYyMDBoLTE3NXEtMTAgMCAtMTIuNSA1dDUuNSAxM3oiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMDY5OyIgZD0iTTI1MCAxMTAwaDEwMHEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXYtNDM4bDQ2NCA0NTNxMTUgMTQgMjUuNSAxMHQxMC41IC0yNXYtMTAwMHEwIC0yMSAtMTAuNSAtMjV0LTI1LjUgMTBsLTQ2NCA0NTN2LTQzOHEwIC0yMSAtMTQuNSAtMzUuNXQtMzUuNSAtMTQuNWgtMTAwcS0yMSAwIC0zNS41IDE0LjV0LTE0LjUgMzUuNXYxMDAwcTAgMjEgMTQuNSAzNS41dDM1LjUgMTQuNXoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMDcwOyIgZD0iTTUwIDExMDBoMTAwcTIxIDAgMzUuNSAtMTQuNXQxNC41IC0zNS41di00MzhsNDY0IDQ1M3ExNSAxNCAyNS41IDEwdDEwLjUgLTI1di00MzhsNDY0IDQ1M3ExNSAxNCAyNS41IDEwdDEwLjUgLTI1di0xMDAwcTAgLTIxIC0xMC41IC0yNXQtMjUuNSAxMGwtNDY0IDQ1M3YtNDM4cTAgLTIxIC0xMC41IC0yNXQtMjUuNSAxMGwtNDY0IDQ1M3YtNDM4cTAgLTIxIC0xNC41IC0zNS41dC0zNS41IC0xNC41aC0xMDBxLTIxIDAgLTM1LjUgMTQuNSB0LTE0LjUgMzUuNXYxMDAwcTAgMjEgMTQuNSAzNS41dDM1LjUgMTQuNXoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMDcxOyIgZD0iTTEyMDAgMTA1MHYtMTAwMHEwIC0yMSAtMTAuNSAtMjV0LTI1LjUgMTBsLTQ2NCA0NTN2LTQzOHEwIC0yMSAtMTAuNSAtMjV0LTI1LjUgMTBsLTQ5MiA0ODBxLTE1IDE0IC0xNSAzNXQxNSAzNWw0OTIgNDgwcTE1IDE0IDI1LjUgMTB0MTAuNSAtMjV2LTQzOGw0NjQgNDUzcTE1IDE0IDI1LjUgMTB0MTAuNSAtMjV6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTA3MjsiIGQ9Ik0yNDMgMTA3NGw4MTQgLTQ5OHExOCAtMTEgMTggLTI2dC0xOCAtMjZsLTgxNCAtNDk4cS0xOCAtMTEgLTMwLjUgLTR0LTEyLjUgMjh2MTAwMHEwIDIxIDEyLjUgMjh0MzAuNSAtNHoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMDczOyIgZD0iTTI1MCAxMDAwaDIwMHEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXYtODAwcTAgLTIxIC0xNC41IC0zNS41dC0zNS41IC0xNC41aC0yMDBxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41djgwMHEwIDIxIDE0LjUgMzUuNXQzNS41IDE0LjV6TTY1MCAxMDAwaDIwMHEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXYtODAwcTAgLTIxIC0xNC41IC0zNS41dC0zNS41IC0xNC41aC0yMDBxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41djgwMCBxMCAyMSAxNC41IDM1LjV0MzUuNSAxNC41eiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUwNzQ7IiBkPSJNMTEwMCA5NTB2LTgwMHEwIC0yMSAtMTQuNSAtMzUuNXQtMzUuNSAtMTQuNWgtODAwcS0yMSAwIC0zNS41IDE0LjV0LTE0LjUgMzUuNXY4MDBxMCAyMSAxNC41IDM1LjV0MzUuNSAxNC41aDgwMHEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMDc1OyIgZD0iTTUwMCA2MTJ2NDM4cTAgMjEgMTAuNSAyNXQyNS41IC0xMGw0OTIgLTQ4MHExNSAtMTQgMTUgLTM1dC0xNSAtMzVsLTQ5MiAtNDgwcS0xNSAtMTQgLTI1LjUgLTEwdC0xMC41IDI1djQzOGwtNDY0IC00NTNxLTE1IC0xNCAtMjUuNSAtMTB0LTEwLjUgMjV2MTAwMHEwIDIxIDEwLjUgMjV0MjUuNSAtMTB6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTA3NjsiIGQ9Ik0xMDQ4IDExMDJsMTAwIDFxMjAgMCAzNSAtMTQuNXQxNSAtMzUuNWw1IC0xMDAwcTAgLTIxIC0xNC41IC0zNS41dC0zNS41IC0xNC41bC0xMDAgLTFxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41bC0yIDQzN2wtNDYzIC00NTRxLTE0IC0xNSAtMjQuNSAtMTAuNXQtMTAuNSAyNS41bC0yIDQzN2wtNDYyIC00NTVxLTE1IC0xNCAtMjUuNSAtOS41dC0xMC41IDI0LjVsLTUgMTAwMHEwIDIxIDEwLjUgMjUuNXQyNS41IC0xMC41bDQ2NiAtNDUwIGwtMiA0MzhxMCAyMCAxMC41IDI0LjV0MjUuNSAtOS41bDQ2NiAtNDUxbC0yIDQzOHEwIDIxIDE0LjUgMzUuNXQzNS41IDE0LjV6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTA3NzsiIGQ9Ik04NTAgMTEwMGgxMDBxMjEgMCAzNS41IC0xNC41dDE0LjUgLTM1LjV2LTEwMDBxMCAtMjEgLTE0LjUgLTM1LjV0LTM1LjUgLTE0LjVoLTEwMHEtMjEgMCAtMzUuNSAxNC41dC0xNC41IDM1LjV2NDM4bC00NjQgLTQ1M3EtMTUgLTE0IC0yNS41IC0xMHQtMTAuNSAyNXYxMDAwcTAgMjEgMTAuNSAyNXQyNS41IC0xMGw0NjQgLTQ1M3Y0MzhxMCAyMSAxNC41IDM1LjV0MzUuNSAxNC41eiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUwNzg7IiBkPSJNNjg2IDEwODFsNTAxIC01NDBxMTUgLTE1IDEwLjUgLTI2dC0yNi41IC0xMWgtMTA0MnEtMjIgMCAtMjYuNSAxMXQxMC41IDI2bDUwMSA1NDBxMTUgMTUgMzYgMTV0MzYgLTE1ek0xNTAgNDAwaDEwMDBxMjEgMCAzNS41IC0xNC41dDE0LjUgLTM1LjV2LTEwMHEwIC0yMSAtMTQuNSAtMzUuNXQtMzUuNSAtMTQuNWgtMTAwMHEtMjEgMCAtMzUuNSAxNC41dC0xNC41IDM1LjV2MTAwcTAgMjEgMTQuNSAzNS41dDM1LjUgMTQuNXoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMDc5OyIgZD0iTTg4NSA5MDBsLTM1MiAtMzUzbDM1MiAtMzUzbC0xOTcgLTE5OGwtNTUyIDU1Mmw1NTIgNTUweiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUwODA7IiBkPSJNMTA2NCA1NDdsLTU1MSAtNTUxbC0xOTggMTk4bDM1MyAzNTNsLTM1MyAzNTNsMTk4IDE5OHoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMDgxOyIgZD0iTTYwMCAxMTc3cTExNyAwIDIyNCAtNDUuNXQxODQuNSAtMTIzdDEyMyAtMTg0LjV0NDUuNSAtMjI0dC00NS41IC0yMjR0LTEyMyAtMTg0LjV0LTE4NC41IC0xMjN0LTIyNCAtNDUuNXQtMjI0IDQ1LjV0LTE4NC41IDEyM3QtMTIzIDE4NC41dC00NS41IDIyNHQ0NS41IDIyNHQxMjMgMTg0LjV0MTg0LjUgMTIzdDIyNCA0NS41ek02NTAgOTAwaC0xMDBxLTIxIDAgLTM1LjUgLTE0LjV0LTE0LjUgLTM1LjV2LTE1MGgtMTUwIHEtMjEgMCAtMzUuNSAtMTQuNXQtMTQuNSAtMzUuNXYtMTAwcTAgLTIxIDE0LjUgLTM1LjV0MzUuNSAtMTQuNWgxNTB2LTE1MHEwIC0yMSAxNC41IC0zNS41dDM1LjUgLTE0LjVoMTAwcTIxIDAgMzUuNSAxNC41dDE0LjUgMzUuNXYxNTBoMTUwcTIxIDAgMzUuNSAxNC41dDE0LjUgMzUuNXYxMDBxMCAyMSAtMTQuNSAzNS41dC0zNS41IDE0LjVoLTE1MHYxNTBxMCAyMSAtMTQuNSAzNS41dC0zNS41IDE0LjV6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTA4MjsiIGQ9Ik02MDAgMTE3N3ExMTcgMCAyMjQgLTQ1LjV0MTg0LjUgLTEyM3QxMjMgLTE4NC41dDQ1LjUgLTIyNHQtNDUuNSAtMjI0dC0xMjMgLTE4NC41dC0xODQuNSAtMTIzdC0yMjQgLTQ1LjV0LTIyNCA0NS41dC0xODQuNSAxMjN0LTEyMyAxODQuNXQtNDUuNSAyMjR0NDUuNSAyMjR0MTIzIDE4NC41dDE4NC41IDEyM3QyMjQgNDUuNXpNODUwIDcwMGgtNTAwcS0yMSAwIC0zNS41IC0xNC41dC0xNC41IC0zNS41di0xMDBxMCAtMjEgMTQuNSAtMzUuNSB0MzUuNSAtMTQuNWg1MDBxMjEgMCAzNS41IDE0LjV0MTQuNSAzNS41djEwMHEwIDIxIC0xNC41IDM1LjV0LTM1LjUgMTQuNXoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMDgzOyIgZD0iTTYwMCAxMTc3cTExNyAwIDIyNCAtNDUuNXQxODQuNSAtMTIzdDEyMyAtMTg0LjV0NDUuNSAtMjI0dC00NS41IC0yMjR0LTEyMyAtMTg0LjV0LTE4NC41IC0xMjN0LTIyNCAtNDUuNXQtMjI0IDQ1LjV0LTE4NC41IDEyM3QtMTIzIDE4NC41dC00NS41IDIyNHQ0NS41IDIyNHQxMjMgMTg0LjV0MTg0LjUgMTIzdDIyNCA0NS41ek03NDEuNSA5MTNxLTEyLjUgMCAtMjEuNSAtOWwtMTIwIC0xMjBsLTEyMCAxMjBxLTkgOSAtMjEuNSA5IHQtMjEuNSAtOWwtMTQxIC0xNDFxLTkgLTkgLTkgLTIxLjV0OSAtMjEuNWwxMjAgLTEyMGwtMTIwIC0xMjBxLTkgLTkgLTkgLTIxLjV0OSAtMjEuNWwxNDEgLTE0MXE5IC05IDIxLjUgLTl0MjEuNSA5bDEyMCAxMjBsMTIwIC0xMjBxOSAtOSAyMS41IC05dDIxLjUgOWwxNDEgMTQxcTkgOSA5IDIxLjV0LTkgMjEuNWwtMTIwIDEyMGwxMjAgMTIwcTkgOSA5IDIxLjV0LTkgMjEuNWwtMTQxIDE0MXEtOSA5IC0yMS41IDl6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTA4NDsiIGQ9Ik02MDAgMTE3N3ExMTcgMCAyMjQgLTQ1LjV0MTg0LjUgLTEyM3QxMjMgLTE4NC41dDQ1LjUgLTIyNHQtNDUuNSAtMjI0dC0xMjMgLTE4NC41dC0xODQuNSAtMTIzdC0yMjQgLTQ1LjV0LTIyNCA0NS41dC0xODQuNSAxMjN0LTEyMyAxODQuNXQtNDUuNSAyMjR0NDUuNSAyMjR0MTIzIDE4NC41dDE4NC41IDEyM3QyMjQgNDUuNXpNNTQ2IDYyM2wtODQgODVxLTcgNyAtMTcuNSA3dC0xOC41IC03bC0xMzkgLTEzOXEtNyAtOCAtNyAtMTh0NyAtMTggbDI0MiAtMjQxcTcgLTggMTcuNSAtOHQxNy41IDhsMzc1IDM3NXE3IDcgNyAxNy41dC03IDE4LjVsLTEzOSAxMzlxLTcgNyAtMTcuNSA3dC0xNy41IC03eiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUwODU7IiBkPSJNNjAwIDExNzdxMTE3IDAgMjI0IC00NS41dDE4NC41IC0xMjN0MTIzIC0xODQuNXQ0NS41IC0yMjR0LTQ1LjUgLTIyNHQtMTIzIC0xODQuNXQtMTg0LjUgLTEyM3QtMjI0IC00NS41dC0yMjQgNDUuNXQtMTg0LjUgMTIzdC0xMjMgMTg0LjV0LTQ1LjUgMjI0dDQ1LjUgMjI0dDEyMyAxODQuNXQxODQuNSAxMjN0MjI0IDQ1LjV6TTU4OCA5NDFxLTI5IDAgLTU5IC01LjV0LTYzIC0yMC41dC01OCAtMzguNXQtNDEuNSAtNjN0LTE2LjUgLTg5LjUgcTAgLTI1IDIwIC0yNWgxMzFxMzAgLTUgMzUgMTFxNiAyMCAyMC41IDI4dDQ1LjUgOHEyMCAwIDMxLjUgLTEwLjV0MTEuNSAtMjguNXEwIC0yMyAtNyAtMzR0LTI2IC0xOHEtMSAwIC0xMy41IC00dC0xOS41IC03LjV0LTIwIC0xMC41dC0yMiAtMTd0LTE4LjUgLTI0dC0xNS41IC0zNXQtOCAtNDZxLTEgLTggNS41IC0xNi41dDIwLjUgLTguNWgxNzNxNyAwIDIyIDh0MzUgMjh0MzcuNSA0OHQyOS41IDc0dDEyIDEwMHEwIDQ3IC0xNyA4MyB0LTQyLjUgNTd0LTU5LjUgMzQuNXQtNjQgMTh0LTU5IDQuNXpNNjc1IDQwMGgtMTUwcS0xMCAwIC0xNy41IC03LjV0LTcuNSAtMTcuNXYtMTUwcTAgLTEwIDcuNSAtMTcuNXQxNy41IC03LjVoMTUwcTEwIDAgMTcuNSA3LjV0Ny41IDE3LjV2MTUwcTAgMTAgLTcuNSAxNy41dC0xNy41IDcuNXoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMDg2OyIgZD0iTTYwMCAxMTc3cTExNyAwIDIyNCAtNDUuNXQxODQuNSAtMTIzdDEyMyAtMTg0LjV0NDUuNSAtMjI0dC00NS41IC0yMjR0LTEyMyAtMTg0LjV0LTE4NC41IC0xMjN0LTIyNCAtNDUuNXQtMjI0IDQ1LjV0LTE4NC41IDEyM3QtMTIzIDE4NC41dC00NS41IDIyNHQ0NS41IDIyNHQxMjMgMTg0LjV0MTg0LjUgMTIzdDIyNCA0NS41ek02NzUgMTAwMGgtMTUwcS0xMCAwIC0xNy41IC03LjV0LTcuNSAtMTcuNXYtMTUwcTAgLTEwIDcuNSAtMTcuNSB0MTcuNSAtNy41aDE1MHExMCAwIDE3LjUgNy41dDcuNSAxNy41djE1MHEwIDEwIC03LjUgMTcuNXQtMTcuNSA3LjV6TTY3NSA3MDBoLTI1MHEtMTAgMCAtMTcuNSAtNy41dC03LjUgLTE3LjV2LTUwcTAgLTEwIDcuNSAtMTcuNXQxNy41IC03LjVoNzV2LTIwMGgtNzVxLTEwIDAgLTE3LjUgLTcuNXQtNy41IC0xNy41di01MHEwIC0xMCA3LjUgLTE3LjV0MTcuNSAtNy41aDM1MHExMCAwIDE3LjUgNy41dDcuNSAxNy41djUwcTAgMTAgLTcuNSAxNy41IHQtMTcuNSA3LjVoLTc1djI3NXEwIDEwIC03LjUgMTcuNXQtMTcuNSA3LjV6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTA4NzsiIGQ9Ik01MjUgMTIwMGgxNTBxMTAgMCAxNy41IC03LjV0Ny41IC0xNy41di0xOTRxMTAzIC0yNyAxNzguNSAtMTAyLjV0MTAyLjUgLTE3OC41aDE5NHExMCAwIDE3LjUgLTcuNXQ3LjUgLTE3LjV2LTE1MHEwIC0xMCAtNy41IC0xNy41dC0xNy41IC03LjVoLTE5NHEtMjcgLTEwMyAtMTAyLjUgLTE3OC41dC0xNzguNSAtMTAyLjV2LTE5NHEwIC0xMCAtNy41IC0xNy41dC0xNy41IC03LjVoLTE1MHEtMTAgMCAtMTcuNSA3LjV0LTcuNSAxNy41djE5NCBxLTEwMyAyNyAtMTc4LjUgMTAyLjV0LTEwMi41IDE3OC41aC0xOTRxLTEwIDAgLTE3LjUgNy41dC03LjUgMTcuNXYxNTBxMCAxMCA3LjUgMTcuNXQxNy41IDcuNWgxOTRxMjcgMTAzIDEwMi41IDE3OC41dDE3OC41IDEwMi41djE5NHEwIDEwIDcuNSAxNy41dDE3LjUgNy41ek03MDAgODkzdi0xNjhxMCAtMTAgLTcuNSAtMTcuNXQtMTcuNSAtNy41aC0xNTBxLTEwIDAgLTE3LjUgNy41dC03LjUgMTcuNXYxNjhxLTY4IC0yMyAtMTE5IC03NCB0LTc0IC0xMTloMTY4cTEwIDAgMTcuNSAtNy41dDcuNSAtMTcuNXYtMTUwcTAgLTEwIC03LjUgLTE3LjV0LTE3LjUgLTcuNWgtMTY4cTIzIC02OCA3NCAtMTE5dDExOSAtNzR2MTY4cTAgMTAgNy41IDE3LjV0MTcuNSA3LjVoMTUwcTEwIDAgMTcuNSAtNy41dDcuNSAtMTcuNXYtMTY4cTY4IDIzIDExOSA3NHQ3NCAxMTloLTE2OHEtMTAgMCAtMTcuNSA3LjV0LTcuNSAxNy41djE1MHEwIDEwIDcuNSAxNy41dDE3LjUgNy41aDE2OCBxLTIzIDY4IC03NCAxMTl0LTExOSA3NHoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMDg4OyIgZD0iTTYwMCAxMTc3cTExNyAwIDIyNCAtNDUuNXQxODQuNSAtMTIzdDEyMyAtMTg0LjV0NDUuNSAtMjI0dC00NS41IC0yMjR0LTEyMyAtMTg0LjV0LTE4NC41IC0xMjN0LTIyNCAtNDUuNXQtMjI0IDQ1LjV0LTE4NC41IDEyM3QtMTIzIDE4NC41dC00NS41IDIyNHQ0NS41IDIyNHQxMjMgMTg0LjV0MTg0LjUgMTIzdDIyNCA0NS41ek02MDAgMTAyN3EtMTE2IDAgLTIxNC41IC01N3QtMTU1LjUgLTE1NS41dC01NyAtMjE0LjV0NTcgLTIxNC41IHQxNTUuNSAtMTU1LjV0MjE0LjUgLTU3dDIxNC41IDU3dDE1NS41IDE1NS41dDU3IDIxNC41dC01NyAyMTQuNXQtMTU1LjUgMTU1LjV0LTIxNC41IDU3ek03NTkgODIzbDY0IC02NHE3IC03IDcgLTE3LjV0LTcgLTE3LjVsLTEyNCAtMTI0bDEyNCAtMTI0cTcgLTcgNyAtMTcuNXQtNyAtMTcuNWwtNjQgLTY0cS03IC03IC0xNy41IC03dC0xNy41IDdsLTEyNCAxMjRsLTEyNCAtMTI0cS03IC03IC0xNy41IC03dC0xNy41IDdsLTY0IDY0IHEtNyA3IC03IDE3LjV0NyAxNy41bDEyNCAxMjRsLTEyNCAxMjRxLTcgNyAtNyAxNy41dDcgMTcuNWw2NCA2NHE3IDcgMTcuNSA3dDE3LjUgLTdsMTI0IC0xMjRsMTI0IDEyNHE3IDcgMTcuNSA3dDE3LjUgLTd6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTA4OTsiIGQ9Ik02MDAgMTE3N3ExMTcgMCAyMjQgLTQ1LjV0MTg0LjUgLTEyM3QxMjMgLTE4NC41dDQ1LjUgLTIyNHQtNDUuNSAtMjI0dC0xMjMgLTE4NC41dC0xODQuNSAtMTIzdC0yMjQgLTQ1LjV0LTIyNCA0NS41dC0xODQuNSAxMjN0LTEyMyAxODQuNXQtNDUuNSAyMjR0NDUuNSAyMjR0MTIzIDE4NC41dDE4NC41IDEyM3QyMjQgNDUuNXpNNjAwIDEwMjdxLTExNiAwIC0yMTQuNSAtNTd0LTE1NS41IC0xNTUuNXQtNTcgLTIxNC41dDU3IC0yMTQuNSB0MTU1LjUgLTE1NS41dDIxNC41IC01N3QyMTQuNSA1N3QxNTUuNSAxNTUuNXQ1NyAyMTQuNXQtNTcgMjE0LjV0LTE1NS41IDE1NS41dC0yMTQuNSA1N3pNNzgyIDc4OGwxMDYgLTEwNnE3IC03IDcgLTE3LjV0LTcgLTE3LjVsLTMyMCAtMzIxcS04IC03IC0xOCAtN3QtMTggN2wtMjAyIDIwM3EtOCA3IC04IDE3LjV0OCAxNy41bDEwNiAxMDZxNyA4IDE3LjUgOHQxNy41IC04bDc5IC03OWwxOTcgMTk3cTcgNyAxNy41IDd0MTcuNSAtN3oiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMDkwOyIgZD0iTTYwMCAxMTc3cTExNyAwIDIyNCAtNDUuNXQxODQuNSAtMTIzdDEyMyAtMTg0LjV0NDUuNSAtMjI0dC00NS41IC0yMjR0LTEyMyAtMTg0LjV0LTE4NC41IC0xMjN0LTIyNCAtNDUuNXQtMjI0IDQ1LjV0LTE4NC41IDEyM3QtMTIzIDE4NC41dC00NS41IDIyNHQ0NS41IDIyNHQxMjMgMTg0LjV0MTg0LjUgMTIzdDIyNCA0NS41ek02MDAgMTAyN3EtMTE2IDAgLTIxNC41IC01N3QtMTU1LjUgLTE1NS41dC01NyAtMjE0LjVxMCAtMTIwIDY1IC0yMjUgbDU4NyA1ODdxLTEwNSA2NSAtMjI1IDY1ek05NjUgODE5bC01ODQgLTU4NHExMDQgLTYyIDIxOSAtNjJxMTE2IDAgMjE0LjUgNTd0MTU1LjUgMTU1LjV0NTcgMjE0LjVxMCAxMTUgLTYyIDIxOXoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMDkxOyIgZD0iTTM5IDU4Mmw1MjIgNDI3cTE2IDEzIDI3LjUgOHQxMS41IC0yNnYtMjkxaDU1MHEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXYtMjAwcTAgLTIxIC0xNC41IC0zNS41dC0zNS41IC0xNC41aC01NTB2LTI5MXEwIC0yMSAtMTEuNSAtMjZ0LTI3LjUgOGwtNTIyIDQyN3EtMTYgMTMgLTE2IDMydDE2IDMyeiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUwOTI7IiBkPSJNNjM5IDEwMDlsNTIyIC00MjdxMTYgLTEzIDE2IC0zMnQtMTYgLTMybC01MjIgLTQyN3EtMTYgLTEzIC0yNy41IC04dC0xMS41IDI2djI5MWgtNTUwcS0yMSAwIC0zNS41IDE0LjV0LTE0LjUgMzUuNXYyMDBxMCAyMSAxNC41IDM1LjV0MzUuNSAxNC41aDU1MHYyOTFxMCAyMSAxMS41IDI2dDI3LjUgLTh6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTA5MzsiIGQ9Ik02ODIgMTE2MWw0MjcgLTUyMnExMyAtMTYgOCAtMjcuNXQtMjYgLTExLjVoLTI5MXYtNTUwcTAgLTIxIC0xNC41IC0zNS41dC0zNS41IC0xNC41aC0yMDBxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41djU1MGgtMjkxcS0yMSAwIC0yNiAxMS41dDggMjcuNWw0MjcgNTIycTEzIDE2IDMyIDE2dDMyIC0xNnoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMDk0OyIgZD0iTTU1MCAxMjAwaDIwMHEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXYtNTUwaDI5MXEyMSAwIDI2IC0xMS41dC04IC0yNy41bC00MjcgLTUyMnEtMTMgLTE2IC0zMiAtMTZ0LTMyIDE2bC00MjcgNTIycS0xMyAxNiAtOCAyNy41dDI2IDExLjVoMjkxdjU1MHEwIDIxIDE0LjUgMzUuNXQzNS41IDE0LjV6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTA5NTsiIGQ9Ik02MzkgMTEwOWw1MjIgLTQyN3ExNiAtMTMgMTYgLTMydC0xNiAtMzJsLTUyMiAtNDI3cS0xNiAtMTMgLTI3LjUgLTh0LTExLjUgMjZ2MjkxcS05NCAtMiAtMTgyIC0yMHQtMTcwLjUgLTUydC0xNDcgLTkyLjV0LTEwMC41IC0xMzUuNXE1IDEwNSAyNyAxOTMuNXQ2Ny41IDE2N3QxMTMgMTM1dDE2NyA5MS41dDIyNS41IDQydjI2MnEwIDIxIDExLjUgMjZ0MjcuNSAtOHoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMDk2OyIgZD0iTTg1MCAxMjAwaDMwMHEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXYtMzAwcTAgLTIxIC0xMC41IC0yNXQtMjQuNSAxMGwtOTQgOTRsLTI0OSAtMjQ5cS04IC03IC0xOCAtN3QtMTggN2wtMTA2IDEwNnEtNyA4IC03IDE4dDcgMThsMjQ5IDI0OWwtOTQgOTRxLTE0IDE0IC0xMCAyNC41dDI1IDEwLjV6TTM1MCAwaC0zMDBxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41djMwMHEwIDIxIDEwLjUgMjV0MjQuNSAtMTBsOTQgLTk0bDI0OSAyNDkgcTggNyAxOCA3dDE4IC03bDEwNiAtMTA2cTcgLTggNyAtMTh0LTcgLTE4bC0yNDkgLTI0OWw5NCAtOTRxMTQgLTE0IDEwIC0yNC41dC0yNSAtMTAuNXoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMDk3OyIgZD0iTTEwMTQgMTEyMGwxMDYgLTEwNnE3IC04IDcgLTE4dC03IC0xOGwtMjQ5IC0yNDlsOTQgLTk0cTE0IC0xNCAxMCAtMjQuNXQtMjUgLTEwLjVoLTMwMHEtMjEgMCAtMzUuNSAxNC41dC0xNC41IDM1LjV2MzAwcTAgMjEgMTAuNSAyNXQyNC41IC0xMGw5NCAtOTRsMjQ5IDI0OXE4IDcgMTggN3QxOCAtN3pNMjUwIDYwMGgzMDBxMjEgMCAzNS41IC0xNC41dDE0LjUgLTM1LjV2LTMwMHEwIC0yMSAtMTAuNSAtMjV0LTI0LjUgMTBsLTk0IDk0IGwtMjQ5IC0yNDlxLTggLTcgLTE4IC03dC0xOCA3bC0xMDYgMTA2cS03IDggLTcgMTh0NyAxOGwyNDkgMjQ5bC05NCA5NHEtMTQgMTQgLTEwIDI0LjV0MjUgMTAuNXoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMTAxOyIgZD0iTTYwMCAxMTc3cTExNyAwIDIyNCAtNDUuNXQxODQuNSAtMTIzdDEyMyAtMTg0LjV0NDUuNSAtMjI0dC00NS41IC0yMjR0LTEyMyAtMTg0LjV0LTE4NC41IC0xMjN0LTIyNCAtNDUuNXQtMjI0IDQ1LjV0LTE4NC41IDEyM3QtMTIzIDE4NC41dC00NS41IDIyNHQ0NS41IDIyNHQxMjMgMTg0LjV0MTg0LjUgMTIzdDIyNCA0NS41ek03MDQgOTAwaC0yMDhxLTIwIDAgLTMyIC0xNC41dC04IC0zNC41bDU4IC0zMDJxNCAtMjAgMjEuNSAtMzQuNSB0MzcuNSAtMTQuNWg1NHEyMCAwIDM3LjUgMTQuNXQyMS41IDM0LjVsNTggMzAycTQgMjAgLTggMzQuNXQtMzIgMTQuNXpNNjc1IDQwMGgtMTUwcS0xMCAwIC0xNy41IC03LjV0LTcuNSAtMTcuNXYtMTUwcTAgLTEwIDcuNSAtMTcuNXQxNy41IC03LjVoMTUwcTEwIDAgMTcuNSA3LjV0Ny41IDE3LjV2MTUwcTAgMTAgLTcuNSAxNy41dC0xNy41IDcuNXoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMTAyOyIgZD0iTTI2MCAxMjAwcTkgMCAxOSAtMnQxNSAtNGw1IC0ycTIyIC0xMCA0NCAtMjNsMTk2IC0xMThxMjEgLTEzIDM2IC0yNHEyOSAtMjEgMzcgLTEycTExIDEzIDQ5IDM1bDE5NiAxMThxMjIgMTMgNDUgMjNxMTcgNyAzOCA3cTIzIDAgNDcgLTE2LjV0MzcgLTMzLjVsMTMgLTE2cTE0IC0yMSAxOCAtNDVsMjUgLTEyM2w4IC00NHExIC05IDguNSAtMTQuNXQxNy41IC01LjVoNjFxMTAgMCAxNy41IC03LjV0Ny41IC0xNy41di01MCBxMCAtMTAgLTcuNSAtMTcuNXQtMTcuNSAtNy41aC01MHEtMTAgMCAtMTcuNSAtNy41dC03LjUgLTE3LjV2LTE3NWgtNDAwdjMwMGgtMjAwdi0zMDBoLTQwMHYxNzVxMCAxMCAtNy41IDE3LjV0LTE3LjUgNy41aC01MHEtMTAgMCAtMTcuNSA3LjV0LTcuNSAxNy41djUwcTAgMTAgNy41IDE3LjV0MTcuNSA3LjVoNjFxMTEgMCAxOCAzdDcgOHEwIDQgOSA1MmwyNSAxMjhxNSAyNSAxOSA0NXEyIDMgNSA3dDEzLjUgMTV0MjEuNSAxOS41dDI2LjUgMTUuNSB0MjkuNSA3ek05MTUgMTA3OWwtMTY2IC0xNjJxLTcgLTcgLTUgLTEydDEyIC01aDIxOXExMCAwIDE1IDd0MiAxN2wtNTEgMTQ5cS0zIDEwIC0xMSAxMnQtMTUgLTZ6TTQ2MyA5MTdsLTE3NyAxNTdxLTggNyAtMTYgNXQtMTEgLTEybC01MSAtMTQzcS0zIC0xMCAyIC0xN3QxNSAtN2gyMzFxMTEgMCAxMi41IDV0LTUuNSAxMnpNNTAwIDBoLTM3NXEtMTAgMCAtMTcuNSA3LjV0LTcuNSAxNy41djM3NWg0MDB2LTQwMHpNMTEwMCA0MDB2LTM3NSBxMCAtMTAgLTcuNSAtMTcuNXQtMTcuNSAtNy41aC0zNzV2NDAwaDQwMHoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMTAzOyIgZD0iTTExNjUgMTE5MHE4IDMgMjEgLTYuNXQxMyAtMTcuNXEtMiAtMTc4IC0yNC41IC0zMjMuNXQtNTUuNSAtMjQ1LjV0LTg3IC0xNzQuNXQtMTAyLjUgLTExOC41dC0xMTggLTY4LjV0LTExOC41IC0zM3QtMTIwIC00LjV0LTEwNSA5LjV0LTkwIDE2LjVxLTYxIDEyIC03OCAxMXEtNCAxIC0xMi41IDB0LTM0IC0xNC41dC01Mi41IC00MC41bC0xNTMgLTE1M3EtMjYgLTI0IC0zNyAtMTQuNXQtMTEgNDMuNXEwIDY0IDQyIDEwMnE4IDggNTAuNSA0NSB0NjYuNSA1OHExOSAxNyAzNSA0N3QxMyA2MXEtOSA1NSAtMTAgMTAyLjV0NyAxMTF0MzcgMTMwdDc4IDEyOS41cTM5IDUxIDgwIDg4dDg5LjUgNjMuNXQ5NC41IDQ1dDExMy41IDM2dDEyOSAzMXQxNTcuNSAzN3QxODIgNDcuNXpNMTExNiAxMDk4cS04IDkgLTIyLjUgLTN0LTQ1LjUgLTUwcS0zOCAtNDcgLTExOSAtMTAzLjV0LTE0MiAtODkuNWwtNjIgLTMzcS01NiAtMzAgLTEwMiAtNTd0LTEwNCAtNjh0LTEwMi41IC04MC41dC04NS41IC05MSB0LTY0IC0xMDQuNXEtMjQgLTU2IC0zMSAtODZ0MiAtMzJ0MzEuNSAxNy41dDU1LjUgNTkuNXEyNSAzMCA5NCA3NS41dDEyNS41IDc3LjV0MTQ3LjUgODFxNzAgMzcgMTE4LjUgNjl0MTAyIDc5LjV0OTkgMTExdDg2LjUgMTQ4LjVxMjIgNTAgMjQgNjB0LTYgMTl6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTEwNDsiIGQ9Ik02NTMgMTIzMXEtMzkgLTY3IC01NC41IC0xMzF0LTEwLjUgLTExNC41dDI0LjUgLTk2LjV0NDcuNSAtODB0NjMuNSAtNjIuNXQ2OC41IC00Ni41dDY1IC0zMHEtNCA3IC0xNy41IDM1dC0xOC41IDM5LjV0LTE3IDM5LjV0LTE3IDQzdC0xMyA0MnQtOS41IDQ0LjV0LTIgNDJ0NCA0M3QxMy41IDM5dDIzIDM4LjVxOTYgLTQyIDE2NSAtMTA3LjV0MTA1IC0xMzh0NTIgLTE1NnQxMyAtMTU5dC0xOSAtMTQ5LjVxLTEzIC01NSAtNDQgLTEwNi41IHQtNjggLTg3dC03OC41IC02NC41dC03Mi41IC00NXQtNTMgLTIycS03MiAtMjIgLTEyNyAtMTFxLTMxIDYgLTEzIDE5cTYgMyAxNyA3cTEzIDUgMzIuNSAyMXQ0MSA0NHQzOC41IDYzLjV0MjEuNSA4MS41dC02LjUgOTQuNXQtNTAgMTA3dC0xMDQgMTE1LjVxMTAgLTEwNCAtMC41IC0xODl0LTM3IC0xNDAuNXQtNjUgLTkzdC04NCAtNTJ0LTkzLjUgLTExdC05NSAyNC41cS04MCAzNiAtMTMxLjUgMTE0dC01My41IDE3MXEtMiAyMyAwIDQ5LjUgdDQuNSA1Mi41dDEzLjUgNTZ0MjcuNSA2MHQ0NiA2NC41dDY5LjUgNjguNXEtOCAtNTMgLTUgLTEwMi41dDE3LjUgLTkwdDM0IC02OC41dDQ0LjUgLTM5dDQ5IC0ycTMxIDEzIDM4LjUgMzZ0LTQuNSA1NXQtMjkgNjQuNXQtMzYgNzV0LTI2IDc1LjVxLTE1IDg1IDIgMTYxLjV0NTMuNSAxMjguNXQ4NS41IDkyLjV0OTMuNSA2MXQ4MS41IDI1LjV6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTEwNTsiIGQ9Ik02MDAgMTA5NHE4MiAwIDE2MC41IC0yMi41dDE0MCAtNTl0MTE2LjUgLTgyLjV0OTQuNSAtOTV0NjggLTk1dDQyLjUgLTgyLjV0MTQgLTU3LjV0LTE0IC01Ny41dC00MyAtODIuNXQtNjguNSAtOTV0LTk0LjUgLTk1dC0xMTYuNSAtODIuNXQtMTQwIC01OXQtMTU5LjUgLTIyLjV0LTE1OS41IDIyLjV0LTE0MCA1OXQtMTE2LjUgODIuNXQtOTQuNSA5NXQtNjguNSA5NXQtNDMgODIuNXQtMTQgNTcuNXQxNCA1Ny41dDQyLjUgODIuNXQ2OCA5NSB0OTQuNSA5NXQxMTYuNSA4Mi41dDE0MCA1OXQxNjAuNSAyMi41ek04ODggODI5cS0xNSAxNSAtMTggMTJ0NSAtMjJxMjUgLTU3IDI1IC0xMTlxMCAtMTI0IC04OCAtMjEydC0yMTIgLTg4dC0yMTIgODh0LTg4IDIxMnEwIDU5IDIzIDExNHE4IDE5IDQuNSAyMnQtMTcuNSAtMTJxLTcwIC02OSAtMTYwIC0xODRxLTEzIC0xNiAtMTUgLTQwLjV0OSAtNDIuNXEyMiAtMzYgNDcgLTcxdDcwIC04MnQ5Mi41IC04MXQxMTMgLTU4LjV0MTMzLjUgLTI0LjUgdDEzMy41IDI0dDExMyA1OC41dDkyLjUgODEuNXQ3MCA4MS41dDQ3IDcwLjVxMTEgMTggOSA0Mi41dC0xNCA0MS41cS05MCAxMTcgLTE2MyAxODl6TTQ0OCA3MjdsLTM1IC0zNnEtMTUgLTE1IC0xOS41IC0zOC41dDQuNSAtNDEuNXEzNyAtNjggOTMgLTExNnExNiAtMTMgMzguNSAtMTF0MzYuNSAxN2wzNSAzNHExNCAxNSAxMi41IDMzLjV0LTE2LjUgMzMuNXEtNDQgNDQgLTg5IDExN3EtMTEgMTggLTI4IDIwdC0zMiAtMTJ6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTEwNjsiIGQ9Ik01OTIgMGgtMTQ4bDMxIDEyMHEtOTEgMjAgLTE3NS41IDY4LjV0LTE0My41IDEwNi41dC0xMDMuNSAxMTl0LTY2LjUgMTEwdC0yMiA3NnEwIDIxIDE0IDU3LjV0NDIuNSA4Mi41dDY4IDk1dDk0LjUgOTV0MTE2LjUgODIuNXQxNDAgNTl0MTYwLjUgMjIuNXE2MSAwIDEyNiAtMTVsMzIgMTIxaDE0OHpNOTQ0IDc3MGw0NyAxODFxMTA4IC04NSAxNzYuNSAtMTkydDY4LjUgLTE1OXEwIC0yNiAtMTkuNSAtNzF0LTU5LjUgLTEwMnQtOTMgLTExMiB0LTEyOSAtMTA0LjV0LTE1OCAtNzUuNWw0NiAxNzNxNzcgNDkgMTM2IDExN3Q5NyAxMzFxMTEgMTggOSA0Mi41dC0xNCA0MS41cS01NCA3MCAtMTA3IDEzMHpNMzEwIDgyNHEtNzAgLTY5IC0xNjAgLTE4NHEtMTMgLTE2IC0xNSAtNDAuNXQ5IC00Mi41cTE4IC0zMCAzOSAtNjB0NTcgLTcwLjV0NzQgLTczdDkwIC02MXQxMDUgLTQxLjVsNDEgMTU0cS0xMDcgMTggLTE3OC41IDEwMS41dC03MS41IDE5My41cTAgNTkgMjMgMTE0cTggMTkgNC41IDIyIHQtMTcuNSAtMTJ6TTQ0OCA3MjdsLTM1IC0zNnEtMTUgLTE1IC0xOS41IC0zOC41dDQuNSAtNDEuNXEzNyAtNjggOTMgLTExNnExNiAtMTMgMzguNSAtMTF0MzYuNSAxN2wxMiAxMWwyMiA4NmwtMyA0cS00NCA0NCAtODkgMTE3cS0xMSAxOCAtMjggMjB0LTMyIC0xMnoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMTA3OyIgZD0iTS05MCAxMDBsNjQyIDEwNjZxMjAgMzEgNDggMjguNXQ0OCAtMzUuNWw2NDIgLTEwNTZxMjEgLTMyIDcuNSAtNjcuNXQtNTAuNSAtMzUuNWgtMTI5NHEtMzcgMCAtNTAuNSAzNHQ3LjUgNjZ6TTE1NSAyMDBoMzQ1djc1cTAgMTAgNy41IDE3LjV0MTcuNSA3LjVoMTUwcTEwIDAgMTcuNSAtNy41dDcuNSAtMTcuNXYtNzVoMzQ1bC00NDUgNzIzek00OTYgNzAwaDIwOHEyMCAwIDMyIC0xNC41dDggLTM0LjVsLTU4IC0yNTIgcS00IC0yMCAtMjEuNSAtMzQuNXQtMzcuNSAtMTQuNWgtNTRxLTIwIDAgLTM3LjUgMTQuNXQtMjEuNSAzNC41bC01OCAyNTJxLTQgMjAgOCAzNC41dDMyIDE0LjV6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTEwODsiIGQ9Ik02NTAgMTIwMHE2MiAwIDEwNiAtNDR0NDQgLTEwNnYtMzM5bDM2MyAtMzI1cTE1IC0xNCAyNiAtMzguNXQxMSAtNDQuNXYtNDFxMCAtMjAgLTEyIC0yNi41dC0yOSA1LjVsLTM1OSAyNDl2LTI2M3ExMDAgLTkzIDEwMCAtMTEzdi02NHEwIC0yMSAtMTMgLTI5dC0zMiAxbC0yMDUgMTI4bC0yMDUgLTEyOHEtMTkgLTkgLTMyIC0xdC0xMyAyOXY2NHEwIDIwIDEwMCAxMTN2MjYzbC0zNTkgLTI0OXEtMTcgLTEyIC0yOSAtNS41dC0xMiAyNi41djQxIHEwIDIwIDExIDQ0LjV0MjYgMzguNWwzNjMgMzI1djMzOXEwIDYyIDQ0IDEwNnQxMDYgNDR6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTEwOTsiIGQ9Ik04NTAgMTIwMGgxMDBxMjEgMCAzNS41IC0xNC41dDE0LjUgLTM1LjV2LTUwaDUwcTIxIDAgMzUuNSAtMTQuNXQxNC41IC0zNS41di0xNTBoLTExMDB2MTUwcTAgMjEgMTQuNSAzNS41dDM1LjUgMTQuNWg1MHY1MHEwIDIxIDE0LjUgMzUuNXQzNS41IDE0LjVoMTAwcTIxIDAgMzUuNSAtMTQuNXQxNC41IC0zNS41di01MGg1MDB2NTBxMCAyMSAxNC41IDM1LjV0MzUuNSAxNC41ek0xMTAwIDgwMHYtNzUwcTAgLTIxIC0xNC41IC0zNS41IHQtMzUuNSAtMTQuNWgtMTAwMHEtMjEgMCAtMzUuNSAxNC41dC0xNC41IDM1LjV2NzUwaDExMDB6TTEwMCA2MDB2LTEwMGgxMDB2MTAwaC0xMDB6TTMwMCA2MDB2LTEwMGgxMDB2MTAwaC0xMDB6TTUwMCA2MDB2LTEwMGgxMDB2MTAwaC0xMDB6TTcwMCA2MDB2LTEwMGgxMDB2MTAwaC0xMDB6TTkwMCA2MDB2LTEwMGgxMDB2MTAwaC0xMDB6TTEwMCA0MDB2LTEwMGgxMDB2MTAwaC0xMDB6TTMwMCA0MDB2LTEwMGgxMDB2MTAwaC0xMDB6TTUwMCA0MDAgdi0xMDBoMTAwdjEwMGgtMTAwek03MDAgNDAwdi0xMDBoMTAwdjEwMGgtMTAwek05MDAgNDAwdi0xMDBoMTAwdjEwMGgtMTAwek0xMDAgMjAwdi0xMDBoMTAwdjEwMGgtMTAwek0zMDAgMjAwdi0xMDBoMTAwdjEwMGgtMTAwek01MDAgMjAwdi0xMDBoMTAwdjEwMGgtMTAwek03MDAgMjAwdi0xMDBoMTAwdjEwMGgtMTAwek05MDAgMjAwdi0xMDBoMTAwdjEwMGgtMTAweiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUxMTA7IiBkPSJNMTEzNSAxMTY1bDI0OSAtMjMwcTE1IC0xNCAxNSAtMzV0LTE1IC0zNWwtMjQ5IC0yMzBxLTE0IC0xNCAtMjQuNSAtMTB0LTEwLjUgMjV2MTUwaC0xNTlsLTYwMCAtNjAwaC0yOTFxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41djEwMHEwIDIxIDE0LjUgMzUuNXQzNS41IDE0LjVoMjA5bDYwMCA2MDBoMjQxdjE1MHEwIDIxIDEwLjUgMjV0MjQuNSAtMTB6TTUyMiA4MTlsLTE0MSAtMTQxbC0xMjIgMTIyaC0yMDlxLTIxIDAgLTM1LjUgMTQuNSB0LTE0LjUgMzUuNXYxMDBxMCAyMSAxNC41IDM1LjV0MzUuNSAxNC41aDI5MXpNMTEzNSA1NjVsMjQ5IC0yMzBxMTUgLTE0IDE1IC0zNXQtMTUgLTM1bC0yNDkgLTIzMHEtMTQgLTE0IC0yNC41IC0xMHQtMTAuNSAyNXYxNTBoLTI0MWwtMTgxIDE4MWwxNDEgMTQxbDEyMiAtMTIyaDE1OXYxNTBxMCAyMSAxMC41IDI1dDI0LjUgLTEweiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUxMTE7IiBkPSJNMTAwIDExMDBoMTAwMHE0MSAwIDcwLjUgLTI5LjV0MjkuNSAtNzAuNXYtNjAwcTAgLTQxIC0yOS41IC03MC41dC03MC41IC0yOS41aC01OTZsLTMwNCAtMzAwdjMwMGgtMTAwcS00MSAwIC03MC41IDI5LjV0LTI5LjUgNzAuNXY2MDBxMCA0MSAyOS41IDcwLjV0NzAuNSAyOS41eiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUxMTI7IiBkPSJNMTUwIDEyMDBoMjAwcTIxIDAgMzUuNSAtMTQuNXQxNC41IC0zNS41di0yNTBoLTMwMHYyNTBxMCAyMSAxNC41IDM1LjV0MzUuNSAxNC41ek04NTAgMTIwMGgyMDBxMjEgMCAzNS41IC0xNC41dDE0LjUgLTM1LjV2LTI1MGgtMzAwdjI1MHEwIDIxIDE0LjUgMzUuNXQzNS41IDE0LjV6TTExMDAgODAwdi0zMDBxMCAtNDEgLTMgLTc3LjV0LTE1IC04OS41dC0zMiAtOTZ0LTU4IC04OXQtODkgLTc3dC0xMjkgLTUxdC0xNzQgLTIwdC0xNzQgMjAgdC0xMjkgNTF0LTg5IDc3dC01OCA4OXQtMzIgOTZ0LTE1IDg5LjV0LTMgNzcuNXYzMDBoMzAwdi0yNTB2LTI3di00Mi41dDEuNSAtNDF0NSAtMzh0MTAgLTM1dDE2LjUgLTMwdDI1LjUgLTI0LjV0MzUgLTE5dDQ2LjUgLTEydDYwIC00dDYwIDQuNXQ0Ni41IDEyLjV0MzUgMTkuNXQyNSAyNS41dDE3IDMwLjV0MTAgMzV0NSAzOHQyIDQwLjV0LTAuNSA0MnYyNXYyNTBoMzAweiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUxMTM7IiBkPSJNMTEwMCA0MTFsLTE5OCAtMTk5bC0zNTMgMzUzbC0zNTMgLTM1M2wtMTk3IDE5OWw1NTEgNTUxeiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUxMTQ7IiBkPSJNMTEwMSA3ODlsLTU1MCAtNTUxbC01NTEgNTUxbDE5OCAxOTlsMzUzIC0zNTNsMzUzIDM1M3oiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMTE1OyIgZD0iTTQwNCAxMDAwaDc0NnEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXYtNTUxaDE1MHEyMSAwIDI1IC0xMC41dC0xMCAtMjQuNWwtMjMwIC0yNDlxLTE0IC0xNSAtMzUgLTE1dC0zNSAxNWwtMjMwIDI0OXEtMTQgMTQgLTEwIDI0LjV0MjUgMTAuNWgxNTB2NDAxaC0zODF6TTEzNSA5ODRsMjMwIC0yNDlxMTQgLTE0IDEwIC0yNC41dC0yNSAtMTAuNWgtMTUwdi00MDBoMzg1bDIxNSAtMjAwaC03NTBxLTIxIDAgLTM1LjUgMTQuNSB0LTE0LjUgMzUuNXY1NTBoLTE1MHEtMjEgMCAtMjUgMTAuNXQxMCAyNC41bDIzMCAyNDlxMTQgMTUgMzUgMTV0MzUgLTE1eiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUxMTY7IiBkPSJNNTYgMTIwMGg5NHExNyAwIDMxIC0xMXQxOCAtMjdsMzggLTE2Mmg4OTZxMjQgMCAzOSAtMTguNXQxMCAtNDIuNWwtMTAwIC00NzVxLTUgLTIxIC0yNyAtNDIuNXQtNTUgLTIxLjVoLTYzM2w0OCAtMjAwaDUzNXEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXQtMTQuNSAtMzUuNXQtMzUuNSAtMTQuNWgtNTB2LTUwcTAgLTIxIC0xNC41IC0zNS41dC0zNS41IC0xNC41dC0zNS41IDE0LjV0LTE0LjUgMzUuNXY1MGgtMzAwdi01MCBxMCAtMjEgLTE0LjUgLTM1LjV0LTM1LjUgLTE0LjV0LTM1LjUgMTQuNXQtMTQuNSAzNS41djUwaC0zMXEtMTggMCAtMzIuNSAxMHQtMjAuNSAxOWwtNSAxMGwtMjAxIDk2MWgtNTRxLTIwIDAgLTM1IDE0LjV0LTE1IDM1LjV0MTUgMzUuNXQzNSAxNC41eiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUxMTc7IiBkPSJNMTIwMCAxMDAwdi0xMDBoLTEyMDB2MTAwaDIwMHEwIDQxIDI5LjUgNzAuNXQ3MC41IDI5LjVoMzAwcTQxIDAgNzAuNSAtMjkuNXQyOS41IC03MC41aDUwMHpNMCA4MDBoMTIwMHYtODAwaC0xMjAwdjgwMHoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMTE4OyIgZD0iTTIwMCA4MDBsLTIwMCAtNDAwdjYwMGgyMDBxMCA0MSAyOS41IDcwLjV0NzAuNSAyOS41aDMwMHE0MiAwIDcxIC0yOS41dDI5IC03MC41aDUwMHYtMjAwaC0xMDAwek0xNTAwIDcwMGwtMzAwIC03MDBoLTEyMDBsMzAwIDcwMGgxMjAweiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUxMTk7IiBkPSJNNjM1IDExODRsMjMwIC0yNDlxMTQgLTE0IDEwIC0yNC41dC0yNSAtMTAuNWgtMTUwdi02MDFoMTUwcTIxIDAgMjUgLTEwLjV0LTEwIC0yNC41bC0yMzAgLTI0OXEtMTQgLTE1IC0zNSAtMTV0LTM1IDE1bC0yMzAgMjQ5cS0xNCAxNCAtMTAgMjQuNXQyNSAxMC41aDE1MHY2MDFoLTE1MHEtMjEgMCAtMjUgMTAuNXQxMCAyNC41bDIzMCAyNDlxMTQgMTUgMzUgMTV0MzUgLTE1eiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUxMjA7IiBkPSJNOTM2IDg2NGwyNDkgLTIyOXExNCAtMTUgMTQgLTM1LjV0LTE0IC0zNS41bC0yNDkgLTIyOXEtMTUgLTE1IC0yNS41IC0xMC41dC0xMC41IDI0LjV2MTUxaC02MDB2LTE1MXEwIC0yMCAtMTAuNSAtMjQuNXQtMjUuNSAxMC41bC0yNDkgMjI5cS0xNCAxNSAtMTQgMzUuNXQxNCAzNS41bDI0OSAyMjlxMTUgMTUgMjUuNSAxMC41dDEwLjUgLTI1LjV2LTE0OWg2MDB2MTQ5cTAgMjEgMTAuNSAyNS41dDI1LjUgLTEwLjV6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTEyMTsiIGQ9Ik0xMTY5IDQwMGwtMTcyIDczMnEtNSAyMyAtMjMgNDUuNXQtMzggMjIuNWgtNjcycS0yMCAwIC0zOCAtMjB0LTIzIC00MWwtMTcyIC03MzloMTEzOHpNMTEwMCAzMDBoLTEwMDBxLTQxIDAgLTcwLjUgLTI5LjV0LTI5LjUgLTcwLjV2LTEwMHEwIC00MSAyOS41IC03MC41dDcwLjUgLTI5LjVoMTAwMHE0MSAwIDcwLjUgMjkuNXQyOS41IDcwLjV2MTAwcTAgNDEgLTI5LjUgNzAuNXQtNzAuNSAyOS41ek04MDAgMTAwdjEwMGgxMDB2LTEwMGgtMTAwIHpNMTAwMCAxMDB2MTAwaDEwMHYtMTAwaC0xMDB6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTEyMjsiIGQ9Ik0xMTUwIDExMDBxMjEgMCAzNS41IC0xNC41dDE0LjUgLTM1LjV2LTg1MHEwIC0yMSAtMTQuNSAtMzUuNXQtMzUuNSAtMTQuNXQtMzUuNSAxNC41dC0xNC41IDM1LjV2ODUwcTAgMjEgMTQuNSAzNS41dDM1LjUgMTQuNXpNMTAwMCAyMDBsLTY3NSAyMDBoLTM4bDQ3IC0yNzZxMyAtMTYgLTUuNSAtMjB0LTI5LjUgLTRoLTdoLTg0cS0yMCAwIC0zNC41IDE0dC0xOC41IDM1cS01NSAzMzcgLTU1IDM1MXYyNTB2NnEwIDE2IDEgMjMuNXQ2LjUgMTQgdDE3LjUgNi41aDIwMGw2NzUgMjUwdi04NTB6TTAgNzUwdi0yNTBxLTQgMCAtMTEgMC41dC0yNCA2dC0zMCAxNXQtMjQgMzB0LTExIDQ4LjV2NTBxMCAyNiAxMC41IDQ2dDI1IDMwdDI5IDE2dDI1LjUgN3oiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMTIzOyIgZD0iTTU1MyAxMjAwaDk0cTIwIDAgMjkgLTEwLjV0MyAtMjkuNWwtMTggLTM3cTgzIC0xOSAxNDQgLTgyLjV0NzYgLTE0MC41bDYzIC0zMjdsMTE4IC0xNzNoMTdxMTkgMCAzMyAtMTQuNXQxNCAtMzV0LTEzIC00MC41dC0zMSAtMjdxLTggLTQgLTIzIC05LjV0LTY1IC0xOS41dC0xMDMgLTI1dC0xMzIuNSAtMjB0LTE1OC41IC05cS01NyAwIC0xMTUgNXQtMTA0IDEydC04OC41IDE1LjV0LTczLjUgMTcuNXQtNTQuNSAxNnQtMzUuNSAxMmwtMTEgNCBxLTE4IDggLTMxIDI4dC0xMyA0MC41dDE0IDM1dDMzIDE0LjVoMTdsMTE4IDE3M2w2MyAzMjdxMTUgNzcgNzYgMTQwdDE0NCA4M2wtMTggMzJxLTYgMTkgMy41IDMydDI4LjUgMTN6TTQ5OCAxMTBxNTAgLTYgMTAyIC02cTUzIDAgMTAyIDZxLTEyIC00OSAtMzkuNSAtNzkuNXQtNjIuNSAtMzAuNXQtNjMgMzAuNXQtMzkgNzkuNXoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMTI0OyIgZD0iTTgwMCA5NDZsMjI0IDc4bC03OCAtMjI0bDIzNCAtNDVsLTE4MCAtMTU1bDE4MCAtMTU1bC0yMzQgLTQ1bDc4IC0yMjRsLTIyNCA3OGwtNDUgLTIzNGwtMTU1IDE4MGwtMTU1IC0xODBsLTQ1IDIzNGwtMjI0IC03OGw3OCAyMjRsLTIzNCA0NWwxODAgMTU1bC0xODAgMTU1bDIzNCA0NWwtNzggMjI0bDIyNCAtNzhsNDUgMjM0bDE1NSAtMTgwbDE1NSAxODB6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTEyNTsiIGQ9Ik02NTAgMTIwMGg1MHE0MCAwIDcwIC00MC41dDMwIC04NC41di0xNTBsLTI4IC0xMjVoMzI4cTQwIDAgNzAgLTQwLjV0MzAgLTg0LjV2LTEwMHEwIC00NSAtMjkgLTc0bC0yMzggLTM0NHEtMTYgLTI0IC0zOCAtNDAuNXQtNDUgLTE2LjVoLTI1MHEtNyAwIC00MiAyNXQtNjYgNTBsLTMxIDI1aC02MXEtNDUgMCAtNzIuNSAxOHQtMjcuNSA1N3Y0MDBxMCAzNiAyMCA2M2wxNDUgMTk2bDk2IDE5OHExMyAyOCAzNy41IDQ4dDUxLjUgMjB6IE02NTAgMTEwMGwtMTAwIC0yMTJsLTE1MCAtMjEzdi0zNzVoMTAwbDEzNiAtMTAwaDIxNGwyNTAgMzc1djEyNWgtNDUwbDUwIDIyNXYxNzVoLTUwek01MCA4MDBoMTAwcTIxIDAgMzUuNSAtMTQuNXQxNC41IC0zNS41di01MDBxMCAtMjEgLTE0LjUgLTM1LjV0LTM1LjUgLTE0LjVoLTEwMHEtMjEgMCAtMzUuNSAxNC41dC0xNC41IDM1LjV2NTAwcTAgMjEgMTQuNSAzNS41dDM1LjUgMTQuNXoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMTI2OyIgZD0iTTYwMCAxMTAwaDI1MHEyMyAwIDQ1IC0xNi41dDM4IC00MC41bDIzOCAtMzQ0cTI5IC0yOSAyOSAtNzR2LTEwMHEwIC00NCAtMzAgLTg0LjV0LTcwIC00MC41aC0zMjhxMjggLTExOCAyOCAtMTI1di0xNTBxMCAtNDQgLTMwIC04NC41dC03MCAtNDAuNWgtNTBxLTI3IDAgLTUxLjUgMjB0LTM3LjUgNDhsLTk2IDE5OGwtMTQ1IDE5NnEtMjAgMjcgLTIwIDYzdjQwMHEwIDM5IDI3LjUgNTd0NzIuNSAxOGg2MXExMjQgMTAwIDEzOSAxMDB6IE01MCAxMDAwaDEwMHEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXYtNTAwcTAgLTIxIC0xNC41IC0zNS41dC0zNS41IC0xNC41aC0xMDBxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41djUwMHEwIDIxIDE0LjUgMzUuNXQzNS41IDE0LjV6TTYzNiAxMDAwbC0xMzYgLTEwMGgtMTAwdi0zNzVsMTUwIC0yMTNsMTAwIC0yMTJoNTB2MTc1bC01MCAyMjVoNDUwdjEyNWwtMjUwIDM3NWgtMjE0eiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUxMjc7IiBkPSJNMzU2IDg3M2wzNjMgMjMwcTMxIDE2IDUzIC02bDExMCAtMTEycTEzIC0xMyAxMy41IC0zMnQtMTEuNSAtMzRsLTg0IC0xMjFoMzAycTg0IDAgMTM4IC0zOHQ1NCAtMTEwdC01NSAtMTExdC0xMzkgLTM5aC0xMDZsLTEzMSAtMzM5cS02IC0yMSAtMTkuNSAtNDF0LTI4LjUgLTIwaC0zNDJxLTcgMCAtOTAgODF0LTgzIDk0djUyNXEwIDE3IDE0IDM1LjV0MjggMjguNXpNNDAwIDc5MnYtNTAzbDEwMCAtODloMjkzbDEzMSAzMzkgcTYgMjEgMTkuNSA0MXQyOC41IDIwaDIwM3EyMSAwIDMwLjUgMjV0MC41IDUwdC0zMSAyNWgtNDU2aC03aC02aC01LjV0LTYgMC41dC01IDEuNXQtNSAydC00IDIuNXQtNCA0dC0yLjUgNC41cS0xMiAyNSA1IDQ3bDE0NiAxODNsLTg2IDgzek01MCA4MDBoMTAwcTIxIDAgMzUuNSAtMTQuNXQxNC41IC0zNS41di01MDBxMCAtMjEgLTE0LjUgLTM1LjV0LTM1LjUgLTE0LjVoLTEwMHEtMjEgMCAtMzUuNSAxNC41dC0xNC41IDM1LjV2NTAwIHEwIDIxIDE0LjUgMzUuNXQzNS41IDE0LjV6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTEyODsiIGQ9Ik00NzUgMTEwM2wzNjYgLTIzMHEyIC0xIDYgLTMuNXQxNCAtMTAuNXQxOCAtMTYuNXQxNC41IC0yMHQ2LjUgLTIyLjV2LTUyNXEwIC0xMyAtODYgLTk0dC05MyAtODFoLTM0MnEtMTUgMCAtMjguNSAyMHQtMTkuNSA0MWwtMTMxIDMzOWgtMTA2cS04NSAwIC0xMzkuNSAzOXQtNTQuNSAxMTF0NTQgMTEwdDEzOCAzOGgzMDJsLTg1IDEyMXEtMTEgMTUgLTEwLjUgMzR0MTMuNSAzMmwxMTAgMTEycTIyIDIyIDUzIDZ6TTM3MCA5NDVsMTQ2IC0xODMgcTE3IC0yMiA1IC00N3EtMiAtMiAtMy41IC00LjV0LTQgLTR0LTQgLTIuNXQtNSAtMnQtNSAtMS41dC02IC0wLjVoLTZoLTYuNWgtNmgtNDc1di0xMDBoMjIxcTE1IDAgMjkgLTIwdDIwIC00MWwxMzAgLTMzOWgyOTRsMTA2IDg5djUwM2wtMzQyIDIzNnpNMTA1MCA4MDBoMTAwcTIxIDAgMzUuNSAtMTQuNXQxNC41IC0zNS41di01MDBxMCAtMjEgLTE0LjUgLTM1LjV0LTM1LjUgLTE0LjVoLTEwMHEtMjEgMCAtMzUuNSAxNC41dC0xNC41IDM1LjUgdjUwMHEwIDIxIDE0LjUgMzUuNXQzNS41IDE0LjV6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTEyOTsiIGQ9Ik01NTAgMTI5NHE3MiAwIDExMSAtNTV0MzkgLTEzOXYtMTA2bDMzOSAtMTMxcTIxIC02IDQxIC0xOS41dDIwIC0yOC41di0zNDJxMCAtNyAtODEgLTkwdC05NCAtODNoLTUyNXEtMTcgMCAtMzUuNSAxNHQtMjguNSAyOGwtOSAxNGwtMjMwIDM2M3EtMTYgMzEgNiA1M2wxMTIgMTEwcTEzIDEzIDMyIDEzLjV0MzQgLTExLjVsMTIxIC04NHYzMDJxMCA4NCAzOCAxMzh0MTEwIDU0ek02MDAgOTcydjIwM3EwIDIxIC0yNSAzMC41dC01MCAwLjUgdC0yNSAtMzF2LTQ1NnYtN3YtNnYtNS41dC0wLjUgLTZ0LTEuNSAtNXQtMiAtNXQtMi41IC00dC00IC00dC00LjUgLTIuNXEtMjUgLTEyIC00NyA1bC0xODMgMTQ2bC04MyAtODZsMjM2IC0zMzloNTAzbDg5IDEwMHYyOTNsLTMzOSAxMzFxLTIxIDYgLTQxIDE5LjV0LTIwIDI4LjV6TTQ1MCAyMDBoNTAwcTIxIDAgMzUuNSAtMTQuNXQxNC41IC0zNS41di0xMDBxMCAtMjEgLTE0LjUgLTM1LjV0LTM1LjUgLTE0LjVoLTUwMCBxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41djEwMHEwIDIxIDE0LjUgMzUuNXQzNS41IDE0LjV6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTEzMDsiIGQ9Ik0zNTAgMTEwMGg1MDBxMjEgMCAzNS41IDE0LjV0MTQuNSAzNS41djEwMHEwIDIxIC0xNC41IDM1LjV0LTM1LjUgMTQuNWgtNTAwcS0yMSAwIC0zNS41IC0xNC41dC0xNC41IC0zNS41di0xMDBxMCAtMjEgMTQuNSAtMzUuNXQzNS41IC0xNC41ek02MDAgMzA2di0xMDZxMCAtODQgLTM5IC0xMzl0LTExMSAtNTV0LTExMCA1NHQtMzggMTM4djMwMmwtMTIxIC04NHEtMTUgLTEyIC0zNCAtMTEuNXQtMzIgMTMuNWwtMTEyIDExMCBxLTIyIDIyIC02IDUzbDIzMCAzNjNxMSAyIDMuNSA2dDEwLjUgMTMuNXQxNi41IDE3dDIwIDEzLjV0MjIuNSA2aDUyNXExMyAwIDk0IC04M3Q4MSAtOTB2LTM0MnEwIC0xNSAtMjAgLTI4LjV0LTQxIC0xOS41ek0zMDggOTAwbC0yMzYgLTMzOWw4MyAtODZsMTgzIDE0NnEyMiAxNyA0NyA1cTIgLTEgNC41IC0yLjV0NCAtNHQyLjUgLTR0MiAtNXQxLjUgLTV0MC41IC02di01LjV2LTZ2LTd2LTQ1NnEwIC0yMiAyNSAtMzF0NTAgMC41dDI1IDMwLjUgdjIwM3EwIDE1IDIwIDI4LjV0NDEgMTkuNWwzMzkgMTMxdjI5M2wtODkgMTAwaC01MDN6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTEzMTsiIGQ9Ik02MDAgMTE3OHExMTggMCAyMjUgLTQ1LjV0MTg0LjUgLTEyM3QxMjMgLTE4NC41dDQ1LjUgLTIyNXQtNDUuNSAtMjI1dC0xMjMgLTE4NC41dC0xODQuNSAtMTIzdC0yMjUgLTQ1LjV0LTIyNSA0NS41dC0xODQuNSAxMjN0LTEyMyAxODQuNXQtNDUuNSAyMjV0NDUuNSAyMjV0MTIzIDE4NC41dDE4NC41IDEyM3QyMjUgNDUuNXpNOTE0IDYzMmwtMjc1IDIyM3EtMTYgMTMgLTI3LjUgOHQtMTEuNSAtMjZ2LTEzN2gtMjc1IHEtMTAgMCAtMTcuNSAtNy41dC03LjUgLTE3LjV2LTE1MHEwIC0xMCA3LjUgLTE3LjV0MTcuNSAtNy41aDI3NXYtMTM3cTAgLTIxIDExLjUgLTI2dDI3LjUgOGwyNzUgMjIzcTE2IDEzIDE2IDMydC0xNiAzMnoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMTMyOyIgZD0iTTYwMCAxMTc4cTExOCAwIDIyNSAtNDUuNXQxODQuNSAtMTIzdDEyMyAtMTg0LjV0NDUuNSAtMjI1dC00NS41IC0yMjV0LTEyMyAtMTg0LjV0LTE4NC41IC0xMjN0LTIyNSAtNDUuNXQtMjI1IDQ1LjV0LTE4NC41IDEyM3QtMTIzIDE4NC41dC00NS41IDIyNXQ0NS41IDIyNXQxMjMgMTg0LjV0MTg0LjUgMTIzdDIyNSA0NS41ek01NjEgODU1bC0yNzUgLTIyM3EtMTYgLTEzIC0xNiAtMzJ0MTYgLTMybDI3NSAtMjIzcTE2IC0xMyAyNy41IC04IHQxMS41IDI2djEzN2gyNzVxMTAgMCAxNy41IDcuNXQ3LjUgMTcuNXYxNTBxMCAxMCAtNy41IDE3LjV0LTE3LjUgNy41aC0yNzV2MTM3cTAgMjEgLTExLjUgMjZ0LTI3LjUgLTh6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTEzMzsiIGQ9Ik02MDAgMTE3OHExMTggMCAyMjUgLTQ1LjV0MTg0LjUgLTEyM3QxMjMgLTE4NC41dDQ1LjUgLTIyNXQtNDUuNSAtMjI1dC0xMjMgLTE4NC41dC0xODQuNSAtMTIzdC0yMjUgLTQ1LjV0LTIyNSA0NS41dC0xODQuNSAxMjN0LTEyMyAxODQuNXQtNDUuNSAyMjV0NDUuNSAyMjV0MTIzIDE4NC41dDE4NC41IDEyM3QyMjUgNDUuNXpNODU1IDYzOWwtMjIzIDI3NXEtMTMgMTYgLTMyIDE2dC0zMiAtMTZsLTIyMyAtMjc1cS0xMyAtMTYgLTggLTI3LjUgdDI2IC0xMS41aDEzN3YtMjc1cTAgLTEwIDcuNSAtMTcuNXQxNy41IC03LjVoMTUwcTEwIDAgMTcuNSA3LjV0Ny41IDE3LjV2Mjc1aDEzN3EyMSAwIDI2IDExLjV0LTggMjcuNXoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMTM0OyIgZD0iTTYwMCAxMTc4cTExOCAwIDIyNSAtNDUuNXQxODQuNSAtMTIzdDEyMyAtMTg0LjV0NDUuNSAtMjI1dC00NS41IC0yMjV0LTEyMyAtMTg0LjV0LTE4NC41IC0xMjN0LTIyNSAtNDUuNXQtMjI1IDQ1LjV0LTE4NC41IDEyM3QtMTIzIDE4NC41dC00NS41IDIyNXQ0NS41IDIyNXQxMjMgMTg0LjV0MTg0LjUgMTIzdDIyNSA0NS41ek02NzUgOTAwaC0xNTBxLTEwIDAgLTE3LjUgLTcuNXQtNy41IC0xNy41di0yNzVoLTEzN3EtMjEgMCAtMjYgLTExLjUgdDggLTI3LjVsMjIzIC0yNzVxMTMgLTE2IDMyIC0xNnQzMiAxNmwyMjMgMjc1cTEzIDE2IDggMjcuNXQtMjYgMTEuNWgtMTM3djI3NXEwIDEwIC03LjUgMTcuNXQtMTcuNSA3LjV6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTEzNTsiIGQ9Ik02MDAgMTE3NnExMTYgMCAyMjIuNSAtNDZ0MTg0IC0xMjMuNXQxMjMuNSAtMTg0dDQ2IC0yMjIuNXQtNDYgLTIyMi41dC0xMjMuNSAtMTg0dC0xODQgLTEyMy41dC0yMjIuNSAtNDZ0LTIyMi41IDQ2dC0xODQgMTIzLjV0LTEyMy41IDE4NHQtNDYgMjIyLjV0NDYgMjIyLjV0MTIzLjUgMTg0dDE4NCAxMjMuNXQyMjIuNSA0NnpNNjI3IDExMDFxLTE1IC0xMiAtMzYuNSAtMjAuNXQtMzUuNSAtMTJ0LTQzIC04dC0zOSAtNi41IHEtMTUgLTMgLTQ1LjUgMHQtNDUuNSAtMnEtMjAgLTcgLTUxLjUgLTI2LjV0LTM0LjUgLTM0LjVxLTMgLTExIDYuNSAtMjIuNXQ4LjUgLTE4LjVxLTMgLTM0IC0yNy41IC05MXQtMjkuNSAtNzlxLTkgLTM0IDUgLTkzdDggLTg3cTAgLTkgMTcgLTQ0LjV0MTYgLTU5LjVxMTIgMCAyMyAtNXQyMy41IC0xNXQxOS41IC0xNHExNiAtOCAzMyAtMTV0NDAuNSAtMTV0MzQuNSAtMTJxMjEgLTkgNTIuNSAtMzJ0NjAgLTM4dDU3LjUgLTExIHE3IC0xNSAtMyAtMzR0LTIyLjUgLTQwdC05LjUgLTM4cTEzIC0yMSAyMyAtMzQuNXQyNy41IC0yNy41dDM2LjUgLTE4cTAgLTcgLTMuNSAtMTZ0LTMuNSAtMTR0NSAtMTdxMTA0IC0yIDIyMSAxMTJxMzAgMjkgNDYuNSA0N3QzNC41IDQ5dDIxIDYzcS0xMyA4IC0zNyA4LjV0LTM2IDcuNXEtMTUgNyAtNDkuNSAxNXQtNTEuNSAxOXEtMTggMCAtNDEgLTAuNXQtNDMgLTEuNXQtNDIgLTYuNXQtMzggLTE2LjVxLTUxIC0zNSAtNjYgLTEyIHEtNCAxIC0zLjUgMjUuNXQwLjUgMjUuNXEtNiAxMyAtMjYuNSAxNy41dC0yNC41IDYuNXExIDE1IC0wLjUgMzAuNXQtNyAyOHQtMTguNSAxMS41dC0zMSAtMjFxLTIzIC0yNSAtNDIgNHEtMTkgMjggLTggNThxNiAxNiAyMiAyMnE2IC0xIDI2IC0xLjV0MzMuNSAtNHQxOS41IC0xMy41cTcgLTEyIDE4IC0yNHQyMS41IC0yMC41dDIwIC0xNXQxNS41IC0xMC41bDUgLTNxMiAxMiA3LjUgMzAuNXQ4IDM0LjV0LTAuNSAzMnEtMyAxOCAzLjUgMjkgdDE4IDIyLjV0MTUuNSAyNC41cTYgMTQgMTAuNSAzNXQ4IDMxdDE1LjUgMjIuNXQzNCAyMi41cS02IDE4IDEwIDM2cTggMCAyNCAtMS41dDI0LjUgLTEuNXQyMCA0LjV0MjAuNSAxNS41cS0xMCAyMyAtMzEgNDIuNXQtMzcuNSAyOS41dC00OSAyN3QtNDMuNSAyM3EwIDEgMiA4dDMgMTEuNXQxLjUgMTAuNXQtMSA5LjV0LTQuNSA0LjVxMzEgLTEzIDU4LjUgLTE0LjV0MzguNSAyLjVsMTIgNXE1IDI4IC05LjUgNDZ0LTM2LjUgMjR0LTUwIDE1IHQtNDEgMjBxLTE4IC00IC0zNyAwek02MTMgOTk0cTAgLTE3IDggLTQydDE3IC00NXQ5IC0yM3EtOCAxIC0zOS41IDUuNXQtNTIuNSAxMHQtMzcgMTYuNXEzIDExIDE2IDI5LjV0MTYgMjUuNXExMCAtMTAgMTkgLTEwdDE0IDZ0MTMuNSAxNC41dDE2LjUgMTIuNXoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMTM2OyIgZD0iTTc1NiAxMTU3cTE2NCA5MiAzMDYgLTlsLTI1OSAtMTM4bDE0NSAtMjMybDI1MSAxMjZxNiAtODkgLTM0IC0xNTYuNXQtMTE3IC0xMTAuNXEtNjAgLTM0IC0xMjcgLTM5LjV0LTEyNiAxNi41bC01OTYgLTU5NnEtMTUgLTE2IC0zNi41IC0xNnQtMzYuNSAxNmwtMTExIDExMHEtMTUgMTUgLTE1IDM2LjV0MTUgMzcuNWw2MDAgNTk5cS0zNCAxMDEgNS41IDIwMS41dDEzNS41IDE1NC41eiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUxMzc7IiBob3Jpei1hZHYteD0iMTIyMCIgZD0iTTEwMCAxMTk2aDEwMDBxNDEgMCA3MC41IC0yOS41dDI5LjUgLTcwLjV2LTEwMHEwIC00MSAtMjkuNSAtNzAuNXQtNzAuNSAtMjkuNWgtMTAwMHEtNDEgMCAtNzAuNSAyOS41dC0yOS41IDcwLjV2MTAwcTAgNDEgMjkuNSA3MC41dDcwLjUgMjkuNXpNMTEwMCAxMDk2aC0yMDB2LTEwMGgyMDB2MTAwek0xMDAgNzk2aDEwMDBxNDEgMCA3MC41IC0yOS41dDI5LjUgLTcwLjV2LTEwMHEwIC00MSAtMjkuNSAtNzAuNXQtNzAuNSAtMjkuNWgtMTAwMCBxLTQxIDAgLTcwLjUgMjkuNXQtMjkuNSA3MC41djEwMHEwIDQxIDI5LjUgNzAuNXQ3MC41IDI5LjV6TTExMDAgNjk2aC01MDB2LTEwMGg1MDB2MTAwek0xMDAgMzk2aDEwMDBxNDEgMCA3MC41IC0yOS41dDI5LjUgLTcwLjV2LTEwMHEwIC00MSAtMjkuNSAtNzAuNXQtNzAuNSAtMjkuNWgtMTAwMHEtNDEgMCAtNzAuNSAyOS41dC0yOS41IDcwLjV2MTAwcTAgNDEgMjkuNSA3MC41dDcwLjUgMjkuNXpNMTEwMCAyOTZoLTMwMHYtMTAwaDMwMHYxMDB6ICIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUxMzg7IiBkPSJNMTUwIDEyMDBoOTAwcTIxIDAgMzUuNSAtMTQuNXQxNC41IC0zNS41dC0xNC41IC0zNS41dC0zNS41IC0xNC41aC05MDBxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41dDE0LjUgMzUuNXQzNS41IDE0LjV6TTcwMCA1MDB2LTMwMGwtMjAwIC0yMDB2NTAwbC0zNTAgNTAwaDkwMHoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMTM5OyIgZD0iTTUwMCAxMjAwaDIwMHE0MSAwIDcwLjUgLTI5LjV0MjkuNSAtNzAuNXYtMTAwaDMwMHE0MSAwIDcwLjUgLTI5LjV0MjkuNSAtNzAuNXYtNDAwaC01MDB2MTAwaC0yMDB2LTEwMGgtNTAwdjQwMHEwIDQxIDI5LjUgNzAuNXQ3MC41IDI5LjVoMzAwdjEwMHEwIDQxIDI5LjUgNzAuNXQ3MC41IDI5LjV6TTUwMCAxMTAwdi0xMDBoMjAwdjEwMGgtMjAwek0xMjAwIDQwMHYtMjAwcTAgLTQxIC0yOS41IC03MC41dC03MC41IC0yOS41aC0xMDAwIHEtNDEgMCAtNzAuNSAyOS41dC0yOS41IDcwLjV2MjAwaDEyMDB6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTE0MDsiIGQ9Ik01MCAxMjAwaDMwMHEyMSAwIDI1IC0xMC41dC0xMCAtMjQuNWwtOTQgLTk0bDE5OSAtMTk5cTcgLTggNyAtMTh0LTcgLTE4bC0xMDYgLTEwNnEtOCAtNyAtMTggLTd0LTE4IDdsLTE5OSAxOTlsLTk0IC05NHEtMTQgLTE0IC0yNC41IC0xMHQtMTAuNSAyNXYzMDBxMCAyMSAxNC41IDM1LjV0MzUuNSAxNC41ek04NTAgMTIwMGgzMDBxMjEgMCAzNS41IC0xNC41dDE0LjUgLTM1LjV2LTMwMHEwIC0yMSAtMTAuNSAtMjV0LTI0LjUgMTBsLTk0IDk0IGwtMTk5IC0xOTlxLTggLTcgLTE4IC03dC0xOCA3bC0xMDYgMTA2cS03IDggLTcgMTh0NyAxOGwxOTkgMTk5bC05NCA5NHEtMTQgMTQgLTEwIDI0LjV0MjUgMTAuNXpNMzY0IDQ3MGwxMDYgLTEwNnE3IC04IDcgLTE4dC03IC0xOGwtMTk5IC0xOTlsOTQgLTk0cTE0IC0xNCAxMCAtMjQuNXQtMjUgLTEwLjVoLTMwMHEtMjEgMCAtMzUuNSAxNC41dC0xNC41IDM1LjV2MzAwcTAgMjEgMTAuNSAyNXQyNC41IC0xMGw5NCAtOTRsMTk5IDE5OSBxOCA3IDE4IDd0MTggLTd6TTEwNzEgMjcxbDk0IDk0cTE0IDE0IDI0LjUgMTB0MTAuNSAtMjV2LTMwMHEwIC0yMSAtMTQuNSAtMzUuNXQtMzUuNSAtMTQuNWgtMzAwcS0yMSAwIC0yNSAxMC41dDEwIDI0LjVsOTQgOTRsLTE5OSAxOTlxLTcgOCAtNyAxOHQ3IDE4bDEwNiAxMDZxOCA3IDE4IDd0MTggLTd6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTE0MTsiIGQ9Ik01OTYgMTE5MnExMjEgMCAyMzEuNSAtNDcuNXQxOTAgLTEyN3QxMjcgLTE5MHQ0Ny41IC0yMzEuNXQtNDcuNSAtMjMxLjV0LTEyNyAtMTkwLjV0LTE5MCAtMTI3dC0yMzEuNSAtNDd0LTIzMS41IDQ3dC0xOTAuNSAxMjd0LTEyNyAxOTAuNXQtNDcgMjMxLjV0NDcgMjMxLjV0MTI3IDE5MHQxOTAuNSAxMjd0MjMxLjUgNDcuNXpNNTk2IDEwMTBxLTExMiAwIC0yMDcuNSAtNTUuNXQtMTUxIC0xNTF0LTU1LjUgLTIwNy41dDU1LjUgLTIwNy41IHQxNTEgLTE1MXQyMDcuNSAtNTUuNXQyMDcuNSA1NS41dDE1MSAxNTF0NTUuNSAyMDcuNXQtNTUuNSAyMDcuNXQtMTUxIDE1MXQtMjA3LjUgNTUuNXpNNDU0LjUgOTA1cTIyLjUgMCAzOC41IC0xNnQxNiAtMzguNXQtMTYgLTM5dC0zOC41IC0xNi41dC0zOC41IDE2LjV0LTE2IDM5dDE2IDM4LjV0MzguNSAxNnpNNzU0LjUgOTA1cTIyLjUgMCAzOC41IC0xNnQxNiAtMzguNXQtMTYgLTM5dC0zOCAtMTYuNXEtMTQgMCAtMjkgMTBsLTU1IC0xNDUgcTE3IC0yMyAxNyAtNTFxMCAtMzYgLTI1LjUgLTYxLjV0LTYxLjUgLTI1LjV0LTYxLjUgMjUuNXQtMjUuNSA2MS41cTAgMzIgMjAuNSA1Ni41dDUxLjUgMjkuNWwxMjIgMTI2bDEgMXEtOSAxNCAtOSAyOHEwIDIzIDE2IDM5dDM4LjUgMTZ6TTM0NS41IDcwOXEyMi41IDAgMzguNSAtMTZ0MTYgLTM4LjV0LTE2IC0zOC41dC0zOC41IC0xNnQtMzguNSAxNnQtMTYgMzguNXQxNiAzOC41dDM4LjUgMTZ6TTg1NC41IDcwOXEyMi41IDAgMzguNSAtMTYgdDE2IC0zOC41dC0xNiAtMzguNXQtMzguNSAtMTZ0LTM4LjUgMTZ0LTE2IDM4LjV0MTYgMzguNXQzOC41IDE2eiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUxNDI7IiBkPSJNNTQ2IDE3M2w0NjkgNDcwcTkxIDkxIDk5IDE5MnE3IDk4IC01MiAxNzUuNXQtMTU0IDk0LjVxLTIyIDQgLTQ3IDRxLTM0IDAgLTY2LjUgLTEwdC01Ni41IC0yM3QtNTUuNSAtMzh0LTQ4IC00MS41dC00OC41IC00Ny41cS0zNzYgLTM3NSAtMzkxIC0zOTBxLTMwIC0yNyAtNDUgLTQxLjV0LTM3LjUgLTQxdC0zMiAtNDYuNXQtMTYgLTQ3LjV0LTEuNSAtNTYuNXE5IC02MiA1My41IC05NXQ5OS41IC0zM3E3NCAwIDEyNSA1MWw1NDggNTQ4IHEzNiAzNiAyMCA3NXEtNyAxNiAtMjEuNSAyNnQtMzIuNSAxMHEtMjYgMCAtNTAgLTIzcS0xMyAtMTIgLTM5IC0zOGwtMzQxIC0zMzhxLTE1IC0xNSAtMzUuNSAtMTUuNXQtMzQuNSAxMy41dC0xNCAzNC41dDE0IDM0LjVxMzI3IDMzMyAzNjEgMzY3cTM1IDM1IDY3LjUgNTEuNXQ3OC41IDE2LjVxMTQgMCAyOSAtMXE0NCAtOCA3NC41IC0zNS41dDQzLjUgLTY4LjVxMTQgLTQ3IDIgLTk2LjV0LTQ3IC04NC41cS0xMiAtMTEgLTMyIC0zMiB0LTc5LjUgLTgxdC0xMTQuNSAtMTE1dC0xMjQuNSAtMTIzLjV0LTEyMyAtMTE5LjV0LTk2LjUgLTg5dC01NyAtNDVxLTU2IC0yNyAtMTIwIC0yN3EtNzAgMCAtMTI5IDMydC05MyA4OXEtNDggNzggLTM1IDE3M3Q4MSAxNjNsNTExIDUxMXE3MSA3MiAxMTEgOTZxOTEgNTUgMTk4IDU1cTgwIDAgMTUyIC0zM3E3OCAtMzYgMTI5LjUgLTEwM3Q2Ni41IC0xNTRxMTcgLTkzIC0xMSAtMTgzLjV0LTk0IC0xNTYuNWwtNDgyIC00NzYgcS0xNSAtMTUgLTM2IC0xNnQtMzcgMTR0LTE3LjUgMzR0MTQuNSAzNXoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMTQzOyIgZD0iTTY0OSA5NDlxNDggNjggMTA5LjUgMTA0dDEyMS41IDM4LjV0MTE4LjUgLTIwdDEwMi41IC02NHQ3MSAtMTAwLjV0MjcgLTEyM3EwIC01NyAtMzMuNSAtMTE3LjV0LTk0IC0xMjQuNXQtMTI2LjUgLTEyNy41dC0xNTAgLTE1Mi41dC0xNDYgLTE3NHEtNjIgODUgLTE0NS41IDE3NHQtMTUwIDE1Mi41dC0xMjYuNSAxMjcuNXQtOTMuNSAxMjQuNXQtMzMuNSAxMTcuNXEwIDY0IDI4IDEyM3Q3MyAxMDAuNXQxMDQgNjR0MTE5IDIwIHQxMjAuNSAtMzguNXQxMDQuNSAtMTA0ek04OTYgOTcycS0zMyAwIC02NC41IC0xOXQtNTYuNSAtNDZ0LTQ3LjUgLTUzLjV0LTQzLjUgLTQ1LjV0LTM3LjUgLTE5dC0zNiAxOXQtNDAgNDUuNXQtNDMgNTMuNXQtNTQgNDZ0LTY1LjUgMTlxLTY3IDAgLTEyMi41IC01NS41dC01NS41IC0xMzIuNXEwIC0yMyAxMy41IC01MXQ0NiAtNjV0NTcuNSAtNjN0NzYgLTc1bDIyIC0yMnExNSAtMTQgNDQgLTQ0dDUwLjUgLTUxdDQ2IC00NHQ0MSAtMzV0MjMgLTEyIHQyMy41IDEydDQyLjUgMzZ0NDYgNDR0NTIuNSA1MnQ0NCA0M3E0IDQgMTIgMTNxNDMgNDEgNjMuNSA2MnQ1MiA1NXQ0NiA1NXQyNiA0NnQxMS41IDQ0cTAgNzkgLTUzIDEzMy41dC0xMjAgNTQuNXoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMTQ0OyIgZD0iTTc3Ni41IDEyMTRxOTMuNSAwIDE1OS41IC02NmwxNDEgLTE0MXE2NiAtNjYgNjYgLTE2MHEwIC00MiAtMjggLTk1LjV0LTYyIC04Ny41bC0yOSAtMjlxLTMxIDUzIC03NyA5OWwtMTggMThsOTUgOTVsLTI0NyAyNDhsLTM4OSAtMzg5bDIxMiAtMjEybC0xMDUgLTEwNmwtMTkgMThsLTE0MSAxNDFxLTY2IDY2IC02NiAxNTl0NjYgMTU5bDI4MyAyODNxNjUgNjYgMTU4LjUgNjZ6TTYwMCA3MDZsMTA1IDEwNXExMCAtOCAxOSAtMTdsMTQxIC0xNDEgcTY2IC02NiA2NiAtMTU5dC02NiAtMTU5bC0yODMgLTI4M3EtNjYgLTY2IC0xNTkgLTY2dC0xNTkgNjZsLTE0MSAxNDFxLTY2IDY2IC02NiAxNTkuNXQ2NiAxNTkuNWw1NSA1NXEyOSAtNTUgNzUgLTEwMmwxOCAtMTdsLTk1IC05NWwyNDcgLTI0OGwzODkgMzg5eiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUxNDU7IiBkPSJNNjAzIDEyMDBxODUgMCAxNjIgLTE1dDEyNyAtMzh0NzkgLTQ4dDI5IC00NnYtOTUzcTAgLTQxIC0yOS41IC03MC41dC03MC41IC0yOS41aC02MDBxLTQxIDAgLTcwLjUgMjkuNXQtMjkuNSA3MC41djk1M3EwIDIxIDMwIDQ2LjV0ODEgNDh0MTI5IDM3LjV0MTYzIDE1ek0zMDAgMTAwMHYtNzAwaDYwMHY3MDBoLTYwMHpNNjAwIDI1NHEtNDMgMCAtNzMuNSAtMzAuNXQtMzAuNSAtNzMuNXQzMC41IC03My41dDczLjUgLTMwLjV0NzMuNSAzMC41IHQzMC41IDczLjV0LTMwLjUgNzMuNXQtNzMuNSAzMC41eiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUxNDY7IiBkPSJNOTAyIDExODVsMjgzIC0yODJxMTUgLTE1IDE1IC0zNnQtMTQuNSAtMzUuNXQtMzUuNSAtMTQuNXQtMzUgMTVsLTM2IDM1bC0yNzkgLTI2N3YtMzAwbC0yMTIgMjEwbC0zMDggLTMwN2wtMjgwIC0yMDNsMjAzIDI4MGwzMDcgMzA4bC0yMTAgMjEyaDMwMGwyNjcgMjc5bC0zNSAzNnEtMTUgMTQgLTE1IDM1dDE0LjUgMzUuNXQzNS41IDE0LjV0MzUgLTE1eiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUxNDg7IiBkPSJNNzAwIDEyNDh2LTc4cTM4IC01IDcyLjUgLTE0LjV0NzUuNSAtMzEuNXQ3MSAtNTMuNXQ1MiAtODR0MjQgLTExOC41aC0xNTlxLTQgMzYgLTEwLjUgNTl0LTIxIDQ1dC00MCAzNS41dC02NC41IDIwLjV2LTMwN2w2NCAtMTNxMzQgLTcgNjQgLTE2LjV0NzAgLTMydDY3LjUgLTUyLjV0NDcuNSAtODB0MjAgLTExMnEwIC0xMzkgLTg5IC0yMjR0LTI0NCAtOTd2LTc3aC0xMDB2NzlxLTE1MCAxNiAtMjM3IDEwM3EtNDAgNDAgLTUyLjUgOTMuNSB0LTE1LjUgMTM5LjVoMTM5cTUgLTc3IDQ4LjUgLTEyNnQxMTcuNSAtNjV2MzM1bC0yNyA4cS00NiAxNCAtNzkgMjYuNXQtNzIgMzZ0LTYzIDUydC00MCA3Mi41dC0xNiA5OHEwIDcwIDI1IDEyNnQ2Ny41IDkydDk0LjUgNTd0MTEwIDI3djc3aDEwMHpNNjAwIDc1NHYyNzRxLTI5IC00IC01MCAtMTF0LTQyIC0yMS41dC0zMS41IC00MS41dC0xMC41IC02NXEwIC0yOSA3IC01MC41dDE2LjUgLTM0dDI4LjUgLTIyLjV0MzEuNSAtMTR0MzcuNSAtMTAgcTkgLTMgMTMgLTR6TTcwMCA1NDd2LTMxMHEyMiAyIDQyLjUgNi41dDQ1IDE1LjV0NDEuNSAyN3QyOSA0MnQxMiA1OS41dC0xMi41IDU5LjV0LTM4IDQ0LjV0LTUzIDMxdC02Ni41IDI0LjV6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTE0OTsiIGQ9Ik01NjEgMTE5N3E4NCAwIDE2MC41IC00MHQxMjMuNSAtMTA5LjV0NDcgLTE0Ny41aC0xNTNxMCA0MCAtMTkuNSA3MS41dC00OS41IDQ4LjV0LTU5LjUgMjZ0LTU1LjUgOXEtMzcgMCAtNzkgLTE0LjV0LTYyIC0zNS41cS00MSAtNDQgLTQxIC0xMDFxMCAtMjYgMTMuNSAtNjN0MjYuNSAtNjF0MzcgLTY2cTYgLTkgOSAtMTRoMjQxdi0xMDBoLTE5N3E4IC01MCAtMi41IC0xMTV0LTMxLjUgLTk1cS00NSAtNjIgLTk5IC0xMTIgcTM0IDEwIDgzIDE3LjV0NzEgNy41cTMyIDEgMTAyIC0xNnQxMDQgLTE3cTgzIDAgMTM2IDMwbDUwIC0xNDdxLTMxIC0xOSAtNTggLTMwLjV0LTU1IC0xNS41dC00MiAtNC41dC00NiAtMC41cS0yMyAwIC03NiAxN3QtMTExIDMyLjV0LTk2IDExLjVxLTM5IC0zIC04MiAtMTZ0LTY3IC0yNWwtMjMgLTExbC01NSAxNDVxNCAzIDE2IDExdDE1LjUgMTAuNXQxMyA5dDE1LjUgMTJ0MTQuNSAxNHQxNy41IDE4LjVxNDggNTUgNTQgMTI2LjUgdC0zMCAxNDIuNWgtMjIxdjEwMGgxNjZxLTIzIDQ3IC00NCAxMDRxLTcgMjAgLTEyIDQxLjV0LTYgNTUuNXQ2IDY2LjV0MjkuNSA3MC41dDU4LjUgNzFxOTcgODggMjYzIDg4eiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUxNTA7IiBkPSJNNDAwIDMwMGgxNTBxMjEgMCAyNSAtMTF0LTEwIC0yNWwtMjMwIC0yNTBxLTE0IC0xNSAtMzUgLTE1dC0zNSAxNWwtMjMwIDI1MHEtMTQgMTQgLTEwIDI1dDI1IDExaDE1MHY5MDBoMjAwdi05MDB6TTkzNSAxMTg0bDIzMCAtMjQ5cTE0IC0xNCAxMCAtMjQuNXQtMjUgLTEwLjVoLTE1MHYtOTAwaC0yMDB2OTAwaC0xNTBxLTIxIDAgLTI1IDEwLjV0MTAgMjQuNWwyMzAgMjQ5cTE0IDE1IDM1IDE1dDM1IC0xNXoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMTUxOyIgZD0iTTEwMDAgNzAwaC0xMDB2MTAwaC0xMDB2LTEwMGgtMTAwdjUwMGgzMDB2LTUwMHpNNDAwIDMwMGgxNTBxMjEgMCAyNSAtMTF0LTEwIC0yNWwtMjMwIC0yNTBxLTE0IC0xNSAtMzUgLTE1dC0zNSAxNWwtMjMwIDI1MHEtMTQgMTQgLTEwIDI1dDI1IDExaDE1MHY5MDBoMjAwdi05MDB6TTgwMSAxMTAwdi0yMDBoMTAwdjIwMGgtMTAwek0xMDAwIDM1MGwtMjAwIC0yNTBoMjAwdi0xMDBoLTMwMHYxNTBsMjAwIDI1MGgtMjAwdjEwMGgzMDB2LTE1MHogIiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTE1MjsiIGQ9Ik00MDAgMzAwaDE1MHEyMSAwIDI1IC0xMXQtMTAgLTI1bC0yMzAgLTI1MHEtMTQgLTE1IC0zNSAtMTV0LTM1IDE1bC0yMzAgMjUwcS0xNCAxNCAtMTAgMjV0MjUgMTFoMTUwdjkwMGgyMDB2LTkwMHpNMTAwMCAxMDUwbC0yMDAgLTI1MGgyMDB2LTEwMGgtMzAwdjE1MGwyMDAgMjUwaC0yMDB2MTAwaDMwMHYtMTUwek0xMDAwIDBoLTEwMHYxMDBoLTEwMHYtMTAwaC0xMDB2NTAwaDMwMHYtNTAwek04MDEgNDAwdi0yMDBoMTAwdjIwMGgtMTAweiAiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMTUzOyIgZD0iTTQwMCAzMDBoMTUwcTIxIDAgMjUgLTExdC0xMCAtMjVsLTIzMCAtMjUwcS0xNCAtMTUgLTM1IC0xNXQtMzUgMTVsLTIzMCAyNTBxLTE0IDE0IC0xMCAyNXQyNSAxMWgxNTB2OTAwaDIwMHYtOTAwek0xMDAwIDcwMGgtMTAwdjQwMGgtMTAwdjEwMGgyMDB2LTUwMHpNMTEwMCAwaC0xMDB2MTAwaC0yMDB2NDAwaDMwMHYtNTAwek05MDEgNDAwdi0yMDBoMTAwdjIwMGgtMTAweiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUxNTQ7IiBkPSJNNDAwIDMwMGgxNTBxMjEgMCAyNSAtMTF0LTEwIC0yNWwtMjMwIC0yNTBxLTE0IC0xNSAtMzUgLTE1dC0zNSAxNWwtMjMwIDI1MHEtMTQgMTQgLTEwIDI1dDI1IDExaDE1MHY5MDBoMjAwdi05MDB6TTExMDAgNzAwaC0xMDB2MTAwaC0yMDB2NDAwaDMwMHYtNTAwek05MDEgMTEwMHYtMjAwaDEwMHYyMDBoLTEwMHpNMTAwMCAwaC0xMDB2NDAwaC0xMDB2MTAwaDIwMHYtNTAweiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUxNTU7IiBkPSJNNDAwIDMwMGgxNTBxMjEgMCAyNSAtMTF0LTEwIC0yNWwtMjMwIC0yNTBxLTE0IC0xNSAtMzUgLTE1dC0zNSAxNWwtMjMwIDI1MHEtMTQgMTQgLTEwIDI1dDI1IDExaDE1MHY5MDBoMjAwdi05MDB6TTkwMCAxMDAwaC0yMDB2MjAwaDIwMHYtMjAwek0xMDAwIDcwMGgtMzAwdjIwMGgzMDB2LTIwMHpNMTEwMCA0MDBoLTQwMHYyMDBoNDAwdi0yMDB6TTEyMDAgMTAwaC01MDB2MjAwaDUwMHYtMjAweiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUxNTY7IiBkPSJNNDAwIDMwMGgxNTBxMjEgMCAyNSAtMTF0LTEwIC0yNWwtMjMwIC0yNTBxLTE0IC0xNSAtMzUgLTE1dC0zNSAxNWwtMjMwIDI1MHEtMTQgMTQgLTEwIDI1dDI1IDExaDE1MHY5MDBoMjAwdi05MDB6TTEyMDAgMTAwMGgtNTAwdjIwMGg1MDB2LTIwMHpNMTEwMCA3MDBoLTQwMHYyMDBoNDAwdi0yMDB6TTEwMDAgNDAwaC0zMDB2MjAwaDMwMHYtMjAwek05MDAgMTAwaC0yMDB2MjAwaDIwMHYtMjAweiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUxNTc7IiBkPSJNMzUwIDExMDBoNDAwcTE2MiAwIDI1NiAtOTMuNXQ5NCAtMjU2LjV2LTQwMHEwIC0xNjUgLTkzLjUgLTI1Ny41dC0yNTYuNSAtOTIuNWgtNDAwcS0xNjUgMCAtMjU3LjUgOTIuNXQtOTIuNSAyNTcuNXY0MDBxMCAxNjUgOTIuNSAyNTcuNXQyNTcuNSA5Mi41ek04MDAgOTAwaC01MDBxLTQxIDAgLTcwLjUgLTI5LjV0LTI5LjUgLTcwLjV2LTUwMHEwIC00MSAyOS41IC03MC41dDcwLjUgLTI5LjVoNTAwcTQxIDAgNzAuNSAyOS41dDI5LjUgNzAuNSB2NTAwcTAgNDEgLTI5LjUgNzAuNXQtNzAuNSAyOS41eiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUxNTg7IiBkPSJNMzUwIDExMDBoNDAwcTE2NSAwIDI1Ny41IC05Mi41dDkyLjUgLTI1Ny41di00MDBxMCAtMTY1IC05Mi41IC0yNTcuNXQtMjU3LjUgLTkyLjVoLTQwMHEtMTYzIDAgLTI1Ni41IDkyLjV0LTkzLjUgMjU3LjV2NDAwcTAgMTYzIDk0IDI1Ni41dDI1NiA5My41ek04MDAgOTAwaC01MDBxLTQxIDAgLTcwLjUgLTI5LjV0LTI5LjUgLTcwLjV2LTUwMHEwIC00MSAyOS41IC03MC41dDcwLjUgLTI5LjVoNTAwcTQxIDAgNzAuNSAyOS41dDI5LjUgNzAuNSB2NTAwcTAgNDEgLTI5LjUgNzAuNXQtNzAuNSAyOS41ek00NDAgNzcwbDI1MyAtMTkwcTE3IC0xMiAxNyAtMzB0LTE3IC0zMGwtMjUzIC0xOTBxLTE2IC0xMiAtMjggLTYuNXQtMTIgMjYuNXY0MDBxMCAyMSAxMiAyNi41dDI4IC02LjV6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTE1OTsiIGQ9Ik0zNTAgMTEwMGg0MDBxMTYzIDAgMjU2LjUgLTk0dDkzLjUgLTI1NnYtNDAwcTAgLTE2NSAtOTIuNSAtMjU3LjV0LTI1Ny41IC05Mi41aC00MDBxLTE2NSAwIC0yNTcuNSA5Mi41dC05Mi41IDI1Ny41djQwMHEwIDE2MyA5Mi41IDI1Ni41dDI1Ny41IDkzLjV6TTgwMCA5MDBoLTUwMHEtNDEgMCAtNzAuNSAtMjkuNXQtMjkuNSAtNzAuNXYtNTAwcTAgLTQxIDI5LjUgLTcwLjV0NzAuNSAtMjkuNWg1MDBxNDEgMCA3MC41IDI5LjV0MjkuNSA3MC41IHY1MDBxMCA0MSAtMjkuNSA3MC41dC03MC41IDI5LjV6TTM1MCA3MDBoNDAwcTIxIDAgMjYuNSAtMTJ0LTYuNSAtMjhsLTE5MCAtMjUzcS0xMiAtMTcgLTMwIC0xN3QtMzAgMTdsLTE5MCAyNTNxLTEyIDE2IC02LjUgMjh0MjYuNSAxMnoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMTYwOyIgZD0iTTM1MCAxMTAwaDQwMHExNjUgMCAyNTcuNSAtOTIuNXQ5Mi41IC0yNTcuNXYtNDAwcTAgLTE2MyAtOTIuNSAtMjU2LjV0LTI1Ny41IC05My41aC00MDBxLTE2MyAwIC0yNTYuNSA5NHQtOTMuNSAyNTZ2NDAwcTAgMTY1IDkyLjUgMjU3LjV0MjU3LjUgOTIuNXpNODAwIDkwMGgtNTAwcS00MSAwIC03MC41IC0yOS41dC0yOS41IC03MC41di01MDBxMCAtNDEgMjkuNSAtNzAuNXQ3MC41IC0yOS41aDUwMHE0MSAwIDcwLjUgMjkuNXQyOS41IDcwLjUgdjUwMHEwIDQxIC0yOS41IDcwLjV0LTcwLjUgMjkuNXpNNTgwIDY5M2wxOTAgLTI1M3ExMiAtMTYgNi41IC0yOHQtMjYuNSAtMTJoLTQwMHEtMjEgMCAtMjYuNSAxMnQ2LjUgMjhsMTkwIDI1M3ExMiAxNyAzMCAxN3QzMCAtMTd6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTE2MTsiIGQ9Ik01NTAgMTEwMGg0MDBxMTY1IDAgMjU3LjUgLTkyLjV0OTIuNSAtMjU3LjV2LTQwMHEwIC0xNjUgLTkyLjUgLTI1Ny41dC0yNTcuNSAtOTIuNWgtNDAwcS0yMSAwIC0zNS41IDE0LjV0LTE0LjUgMzUuNXYxMDBxMCAyMSAxNC41IDM1LjV0MzUuNSAxNC41aDQ1MHE0MSAwIDcwLjUgMjkuNXQyOS41IDcwLjV2NTAwcTAgNDEgLTI5LjUgNzAuNXQtNzAuNSAyOS41aC00NTBxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41djEwMCBxMCAyMSAxNC41IDM1LjV0MzUuNSAxNC41ek0zMzggODY3bDMyNCAtMjg0cTE2IC0xNCAxNiAtMzN0LTE2IC0zM2wtMzI0IC0yODRxLTE2IC0xNCAtMjcgLTl0LTExIDI2djE1MGgtMjUwcS0yMSAwIC0zNS41IDE0LjV0LTE0LjUgMzUuNXYyMDBxMCAyMSAxNC41IDM1LjV0MzUuNSAxNC41aDI1MHYxNTBxMCAyMSAxMSAyNnQyNyAtOXoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMTYyOyIgZD0iTTc5MyAxMTgybDkgLTlxOCAtMTAgNSAtMjdxLTMgLTExIC03OSAtMjI1LjV0LTc4IC0yMjEuNWwzMDAgMXEyNCAwIDMyLjUgLTE3LjV0LTUuNSAtMzUuNXEtMSAwIC0xMzMuNSAtMTU1dC0yNjcgLTMxMi41dC0xMzguNSAtMTYyLjVxLTEyIC0xNSAtMjYgLTE1aC05bC05IDhxLTkgMTEgLTQgMzJxMiA5IDQyIDEyMy41dDc5IDIyNC41bDM5IDExMGgtMzAycS0yMyAwIC0zMSAxOXEtMTAgMjEgNiA0MXE3NSA4NiAyMDkuNSAyMzcuNSB0MjI4IDI1N3Q5OC41IDExMS41cTkgMTYgMjUgMTZoOXoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMTYzOyIgZD0iTTM1MCAxMTAwaDQwMHEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXYtMTAwcTAgLTIxIC0xNC41IC0zNS41dC0zNS41IC0xNC41aC00NTBxLTQxIDAgLTcwLjUgLTI5LjV0LTI5LjUgLTcwLjV2LTUwMHEwIC00MSAyOS41IC03MC41dDcwLjUgLTI5LjVoNDUwcTIxIDAgMzUuNSAtMTQuNXQxNC41IC0zNS41di0xMDBxMCAtMjEgLTE0LjUgLTM1LjV0LTM1LjUgLTE0LjVoLTQwMHEtMTY1IDAgLTI1Ny41IDkyLjV0LTkyLjUgMjU3LjV2NDAwIHEwIDE2NSA5Mi41IDI1Ny41dDI1Ny41IDkyLjV6TTkzOCA4NjdsMzI0IC0yODRxMTYgLTE0IDE2IC0zM3QtMTYgLTMzbC0zMjQgLTI4NHEtMTYgLTE0IC0yNyAtOXQtMTEgMjZ2MTUwaC0yNTBxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41djIwMHEwIDIxIDE0LjUgMzUuNXQzNS41IDE0LjVoMjUwdjE1MHEwIDIxIDExIDI2dDI3IC05eiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUxNjQ7IiBkPSJNNzUwIDEyMDBoNDAwcTIxIDAgMzUuNSAtMTQuNXQxNC41IC0zNS41di00MDBxMCAtMjEgLTEwLjUgLTI1dC0yNC41IDEwbC0xMDkgMTA5bC0zMTIgLTMxMnEtMTUgLTE1IC0zNS41IC0xNXQtMzUuNSAxNWwtMTQxIDE0MXEtMTUgMTUgLTE1IDM1LjV0MTUgMzUuNWwzMTIgMzEybC0xMDkgMTA5cS0xNCAxNCAtMTAgMjQuNXQyNSAxMC41ek00NTYgOTAwaC0xNTZxLTQxIDAgLTcwLjUgLTI5LjV0LTI5LjUgLTcwLjV2LTUwMCBxMCAtNDEgMjkuNSAtNzAuNXQ3MC41IC0yOS41aDUwMHE0MSAwIDcwLjUgMjkuNXQyOS41IDcwLjV2MTQ4bDIwMCAyMDB2LTI5OHEwIC0xNjUgLTkzLjUgLTI1Ny41dC0yNTYuNSAtOTIuNWgtNDAwcS0xNjUgMCAtMjU3LjUgOTIuNXQtOTIuNSAyNTcuNXY0MDBxMCAxNjUgOTIuNSAyNTcuNXQyNTcuNSA5Mi41aDMwMHoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMTY1OyIgZD0iTTYwMCAxMTg2cTExOSAwIDIyNy41IC00Ni41dDE4NyAtMTI1dDEyNSAtMTg3dDQ2LjUgLTIyNy41dC00Ni41IC0yMjcuNXQtMTI1IC0xODd0LTE4NyAtMTI1dC0yMjcuNSAtNDYuNXQtMjI3LjUgNDYuNXQtMTg3IDEyNXQtMTI1IDE4N3QtNDYuNSAyMjcuNXQ0Ni41IDIyNy41dDEyNSAxODd0MTg3IDEyNXQyMjcuNSA0Ni41ek02MDAgMTAyMnEtMTE1IDAgLTIxMiAtNTYuNXQtMTUzLjUgLTE1My41dC01Ni41IC0yMTJ0NTYuNSAtMjEyIHQxNTMuNSAtMTUzLjV0MjEyIC01Ni41dDIxMiA1Ni41dDE1My41IDE1My41dDU2LjUgMjEydC01Ni41IDIxMnQtMTUzLjUgMTUzLjV0LTIxMiA1Ni41ek02MDAgNzk0cTgwIDAgMTM3IC01N3Q1NyAtMTM3dC01NyAtMTM3dC0xMzcgLTU3dC0xMzcgNTd0LTU3IDEzN3Q1NyAxMzd0MTM3IDU3eiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUxNjY7IiBkPSJNNDUwIDEyMDBoMjAwcTIxIDAgMzUuNSAtMTQuNXQxNC41IC0zNS41di0zNTBoMjQ1cTIwIDAgMjUgLTExdC05IC0yNmwtMzgzIC00MjZxLTE0IC0xNSAtMzMuNSAtMTV0LTMyLjUgMTVsLTM3OSA0MjZxLTEzIDE1IC04LjUgMjZ0MjUuNSAxMWgyNTB2MzUwcTAgMjEgMTQuNSAzNS41dDM1LjUgMTQuNXpNNTAgMzAwaDEwMDBxMjEgMCAzNS41IC0xNC41dDE0LjUgLTM1LjV2LTI1MGgtMTEwMHYyNTBxMCAyMSAxNC41IDM1LjV0MzUuNSAxNC41eiBNOTAwIDIwMHYtNTBoMTAwdjUwaC0xMDB6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTE2NzsiIGQ9Ik01ODMgMTE4MmwzNzggLTQzNXExNCAtMTUgOSAtMzF0LTI2IC0xNmgtMjQ0di0yNTBxMCAtMjAgLTE3IC0zNXQtMzkgLTE1aC0yMDBxLTIwIDAgLTMyIDE0LjV0LTEyIDM1LjV2MjUwaC0yNTBxLTIwIDAgLTI1LjUgMTYuNXQ4LjUgMzEuNWwzODMgNDMxcTE0IDE2IDMzLjUgMTd0MzMuNSAtMTR6TTUwIDMwMGgxMDAwcTIxIDAgMzUuNSAtMTQuNXQxNC41IC0zNS41di0yNTBoLTExMDB2MjUwcTAgMjEgMTQuNSAzNS41dDM1LjUgMTQuNXogTTkwMCAyMDB2LTUwaDEwMHY1MGgtMTAweiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUxNjg7IiBkPSJNMzk2IDcyM2wzNjkgMzY5cTcgNyAxNy41IDd0MTcuNSAtN2wxMzkgLTEzOXE3IC04IDcgLTE4LjV0LTcgLTE3LjVsLTUyNSAtNTI1cS03IC04IC0xNy41IC04dC0xNy41IDhsLTI5MiAyOTFxLTcgOCAtNyAxOHQ3IDE4bDEzOSAxMzlxOCA3IDE4LjUgN3QxNy41IC03ek01MCAzMDBoMTAwMHEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXYtMjUwaC0xMTAwdjI1MHEwIDIxIDE0LjUgMzUuNXQzNS41IDE0LjV6TTkwMCAyMDB2LTUwaDEwMHY1MCBoLTEwMHoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMTY5OyIgZD0iTTEzNSAxMDIzbDE0MiAxNDJxMTQgMTQgMzUgMTR0MzUgLTE0bDc3IC03N2wtMjEyIC0yMTJsLTc3IDc2cS0xNCAxNSAtMTQgMzZ0MTQgMzV6TTY1NSA4NTVsMjEwIDIxMHExNCAxNCAyNC41IDEwdDEwLjUgLTI1bC0yIC01OTlxLTEgLTIwIC0xNS41IC0zNXQtMzUuNSAtMTVsLTU5NyAtMXEtMjEgMCAtMjUgMTAuNXQxMCAyNC41bDIwOCAyMDhsLTE1NCAxNTVsMjEyIDIxMnpNNTAgMzAwaDEwMDBxMjEgMCAzNS41IC0xNC41dDE0LjUgLTM1LjUgdi0yNTBoLTExMDB2MjUwcTAgMjEgMTQuNSAzNS41dDM1LjUgMTQuNXpNOTAwIDIwMHYtNTBoMTAwdjUwaC0xMDB6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTE3MDsiIGQ9Ik0zNTAgMTIwMGw1OTkgLTJxMjAgLTEgMzUgLTE1LjV0MTUgLTM1LjVsMSAtNTk3cTAgLTIxIC0xMC41IC0yNXQtMjQuNSAxMGwtMjA4IDIwOGwtMTU1IC0xNTRsLTIxMiAyMTJsMTU1IDE1NGwtMjEwIDIxMHEtMTQgMTQgLTEwIDI0LjV0MjUgMTAuNXpNNTI0IDUxMmwtNzYgLTc3cS0xNSAtMTQgLTM2IC0xNHQtMzUgMTRsLTE0MiAxNDJxLTE0IDE0IC0xNCAzNXQxNCAzNWw3NyA3N3pNNTAgMzAwaDEwMDBxMjEgMCAzNS41IC0xNC41IHQxNC41IC0zNS41di0yNTBoLTExMDB2MjUwcTAgMjEgMTQuNSAzNS41dDM1LjUgMTQuNXpNOTAwIDIwMHYtNTBoMTAwdjUwaC0xMDB6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTE3MTsiIGQ9Ik0xMjAwIDEwM2wtNDgzIDI3NmwtMzE0IC0zOTl2NDIzaC0zOTlsMTE5NiA3OTZ2LTEwOTZ6TTQ4MyA0MjR2LTIzMGw2ODMgOTUzeiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUxNzI7IiBkPSJNMTEwMCAxMDAwdi04NTBxMCAtMjEgLTE0LjUgLTM1LjV0LTM1LjUgLTE0LjVoLTE1MHY0MDBoLTcwMHYtNDAwaC0xNTBxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41djEwMDBxMCAyMCAxNC41IDM1dDM1LjUgMTVoMjUwdi0zMDBoNTAwdjMwMGgxMDB6TTcwMCAxMDAwaC0xMDB2MjAwaDEwMHYtMjAweiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUxNzM7IiBkPSJNMTEwMCAxMDAwbC0yIC0xNDlsLTI5OSAtMjk5bC05NSA5NXEtOSA5IC0yMS41IDl0LTIxLjUgLTlsLTE0OSAtMTQ3aC0zMTJ2LTQwMGgtMTUwcS0yMSAwIC0zNS41IDE0LjV0LTE0LjUgMzUuNXYxMDAwcTAgMjAgMTQuNSAzNXQzNS41IDE1aDI1MHYtMzAwaDUwMHYzMDBoMTAwek03MDAgMTAwMGgtMTAwdjIwMGgxMDB2LTIwMHpNMTEzMiA2MzhsMTA2IC0xMDZxNyAtNyA3IC0xNy41dC03IC0xNy41bC00MjAgLTQyMXEtOCAtNyAtMTggLTcgdC0xOCA3bC0yMDIgMjAzcS04IDcgLTggMTcuNXQ4IDE3LjVsMTA2IDEwNnE3IDggMTcuNSA4dDE3LjUgLThsNzkgLTc5bDI5NyAyOTdxNyA3IDE3LjUgN3QxNy41IC03eiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUxNzQ7IiBkPSJNMTEwMCAxMDAwdi0yNjlsLTEwMyAtMTAzbC0xMzQgMTM0cS0xNSAxNSAtMzMuNSAxNi41dC0zNC41IC0xMi41bC0yNjYgLTI2NmgtMzI5di00MDBoLTE1MHEtMjEgMCAtMzUuNSAxNC41dC0xNC41IDM1LjV2MTAwMHEwIDIwIDE0LjUgMzV0MzUuNSAxNWgyNTB2LTMwMGg1MDB2MzAwaDEwMHpNNzAwIDEwMDBoLTEwMHYyMDBoMTAwdi0yMDB6TTEyMDIgNTcybDcwIC03MHExNSAtMTUgMTUgLTM1LjV0LTE1IC0zNS41bC0xMzEgLTEzMSBsMTMxIC0xMzFxMTUgLTE1IDE1IC0zNS41dC0xNSAtMzUuNWwtNzAgLTcwcS0xNSAtMTUgLTM1LjUgLTE1dC0zNS41IDE1bC0xMzEgMTMxbC0xMzEgLTEzMXEtMTUgLTE1IC0zNS41IC0xNXQtMzUuNSAxNWwtNzAgNzBxLTE1IDE1IC0xNSAzNS41dDE1IDM1LjVsMTMxIDEzMWwtMTMxIDEzMXEtMTUgMTUgLTE1IDM1LjV0MTUgMzUuNWw3MCA3MHExNSAxNSAzNS41IDE1dDM1LjUgLTE1bDEzMSAtMTMxbDEzMSAxMzFxMTUgMTUgMzUuNSAxNSB0MzUuNSAtMTV6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTE3NTsiIGQ9Ik0xMTAwIDEwMDB2LTMwMGgtMzUwcS0yMSAwIC0zNS41IC0xNC41dC0xNC41IC0zNS41di0xNTBoLTUwMHYtNDAwaC0xNTBxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41djEwMDBxMCAyMCAxNC41IDM1dDM1LjUgMTVoMjUwdi0zMDBoNTAwdjMwMGgxMDB6TTcwMCAxMDAwaC0xMDB2MjAwaDEwMHYtMjAwek04NTAgNjAwaDEwMHEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXYtMjUwaDE1MHEyMSAwIDI1IC0xMC41dC0xMCAtMjQuNSBsLTIzMCAtMjMwcS0xNCAtMTQgLTM1IC0xNHQtMzUgMTRsLTIzMCAyMzBxLTE0IDE0IC0xMCAyNC41dDI1IDEwLjVoMTUwdjI1MHEwIDIxIDE0LjUgMzUuNXQzNS41IDE0LjV6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTE3NjsiIGQ9Ik0xMTAwIDEwMDB2LTQwMGwtMTY1IDE2NXEtMTQgMTUgLTM1IDE1dC0zNSAtMTVsLTI2MyAtMjY1aC00MDJ2LTQwMGgtMTUwcS0yMSAwIC0zNS41IDE0LjV0LTE0LjUgMzUuNXYxMDAwcTAgMjAgMTQuNSAzNXQzNS41IDE1aDI1MHYtMzAwaDUwMHYzMDBoMTAwek03MDAgMTAwMGgtMTAwdjIwMGgxMDB2LTIwMHpNOTM1IDU2NWwyMzAgLTIyOXExNCAtMTUgMTAgLTI1LjV0LTI1IC0xMC41aC0xNTB2LTI1MHEwIC0yMCAtMTQuNSAtMzUgdC0zNS41IC0xNWgtMTAwcS0yMSAwIC0zNS41IDE1dC0xNC41IDM1djI1MGgtMTUwcS0yMSAwIC0yNSAxMC41dDEwIDI1LjVsMjMwIDIyOXExNCAxNSAzNSAxNXQzNSAtMTV6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTE3NzsiIGQ9Ik01MCAxMTAwaDExMDBxMjEgMCAzNS41IC0xNC41dDE0LjUgLTM1LjV2LTE1MGgtMTIwMHYxNTBxMCAyMSAxNC41IDM1LjV0MzUuNSAxNC41ek0xMjAwIDgwMHYtNTUwcTAgLTIxIC0xNC41IC0zNS41dC0zNS41IC0xNC41aC0xMTAwcS0yMSAwIC0zNS41IDE0LjV0LTE0LjUgMzUuNXY1NTBoMTIwMHpNMTAwIDUwMHYtMjAwaDQwMHYyMDBoLTQwMHoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMTc4OyIgZD0iTTkzNSAxMTY1bDI0OCAtMjMwcTE0IC0xNCAxNCAtMzV0LTE0IC0zNWwtMjQ4IC0yMzBxLTE0IC0xNCAtMjQuNSAtMTB0LTEwLjUgMjV2MTUwaC00MDB2MjAwaDQwMHYxNTBxMCAyMSAxMC41IDI1dDI0LjUgLTEwek0yMDAgODAwaC01MHEtMjEgMCAtMzUuNSAxNC41dC0xNC41IDM1LjV2MTAwcTAgMjEgMTQuNSAzNS41dDM1LjUgMTQuNWg1MHYtMjAwek00MDAgODAwaC0xMDB2MjAwaDEwMHYtMjAwek0xOCA0MzVsMjQ3IDIzMCBxMTQgMTQgMjQuNSAxMHQxMC41IC0yNXYtMTUwaDQwMHYtMjAwaC00MDB2LTE1MHEwIC0yMSAtMTAuNSAtMjV0LTI0LjUgMTBsLTI0NyAyMzBxLTE1IDE0IC0xNSAzNXQxNSAzNXpNOTAwIDMwMGgtMTAwdjIwMGgxMDB2LTIwMHpNMTAwMCA1MDBoNTFxMjAgMCAzNC41IC0xNC41dDE0LjUgLTM1LjV2LTEwMHEwIC0yMSAtMTQuNSAtMzUuNXQtMzQuNSAtMTQuNWgtNTF2MjAweiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUxNzk7IiBkPSJNODYyIDEwNzNsMjc2IDExNnEyNSAxOCA0My41IDh0MTguNSAtNDF2LTExMDZxMCAtMjEgLTE0LjUgLTM1LjV0LTM1LjUgLTE0LjVoLTIwMHEtMjEgMCAtMzUuNSAxNC41dC0xNC41IDM1LjV2Mzk3cS00IDEgLTExIDV0LTI0IDE3LjV0LTMwIDI5dC0yNCA0MnQtMTEgNTYuNXYzNTlxMCAzMSAxOC41IDY1dDQzLjUgNTJ6TTU1MCAxMjAwcTIyIDAgMzQuNSAtMTIuNXQxNC41IC0yNC41bDEgLTEzdi00NTBxMCAtMjggLTEwLjUgLTU5LjUgdC0yNSAtNTZ0LTI5IC00NXQtMjUuNSAtMzEuNWwtMTAgLTExdi00NDdxMCAtMjEgLTE0LjUgLTM1LjV0LTM1LjUgLTE0LjVoLTIwMHEtMjEgMCAtMzUuNSAxNC41dC0xNC41IDM1LjV2NDQ3cS00IDQgLTExIDExLjV0LTI0IDMwLjV0LTMwIDQ2dC0yNCA1NXQtMTEgNjB2NDUwcTAgMiAwLjUgNS41dDQgMTJ0OC41IDE1dDE0LjUgMTJ0MjIuNSA1LjVxMjAgMCAzMi41IC0xMi41dDE0LjUgLTI0LjVsMyAtMTN2LTM1MGgxMDB2MzUwdjUuNXQyLjUgMTIgdDcgMTV0MTUgMTJ0MjUuNSA1LjVxMjMgMCAzNS41IC0xMi41dDEzLjUgLTI0LjVsMSAtMTN2LTM1MGgxMDB2MzUwcTAgMiAwLjUgNS41dDMgMTJ0NyAxNXQxNSAxMnQyNC41IDUuNXoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMTgwOyIgZD0iTTEyMDAgMTEwMHYtNTZxLTQgMCAtMTEgLTAuNXQtMjQgLTN0LTMwIC03LjV0LTI0IC0xNXQtMTEgLTI0di04ODhxMCAtMjIgMjUgLTM0LjV0NTAgLTEzLjVsMjUgLTJ2LTU2aC00MDB2NTZxNzUgMCA4Ny41IDYuNXQxMi41IDQzLjV2Mzk0aC01MDB2LTM5NHEwIC0zNyAxMi41IC00My41dDg3LjUgLTYuNXYtNTZoLTQwMHY1NnE0IDAgMTEgMC41dDI0IDN0MzAgNy41dDI0IDE1dDExIDI0djg4OHEwIDIyIC0yNSAzNC41dC01MCAxMy41IGwtMjUgMnY1Nmg0MDB2LTU2cS03NSAwIC04Ny41IC02LjV0LTEyLjUgLTQzLjV2LTM5NGg1MDB2Mzk0cTAgMzcgLTEyLjUgNDMuNXQtODcuNSA2LjV2NTZoNDAweiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUxODE7IiBkPSJNNjc1IDEwMDBoMzc1cTIxIDAgMzUuNSAtMTQuNXQxNC41IC0zNS41di0xNTBoLTEwNWwtMjk1IC05OHY5OGwtMjAwIDIwMGgtNDAwbDEwMCAxMDBoMzc1ek0xMDAgOTAwaDMwMHE0MSAwIDcwLjUgLTI5LjV0MjkuNSAtNzAuNXYtNTAwcTAgLTQxIC0yOS41IC03MC41dC03MC41IC0yOS41aC0zMDBxLTQxIDAgLTcwLjUgMjkuNXQtMjkuNSA3MC41djUwMHEwIDQxIDI5LjUgNzAuNXQ3MC41IDI5LjV6TTEwMCA4MDB2LTIwMGgzMDB2MjAwIGgtMzAwek0xMTAwIDUzNWwtNDAwIC0xMzN2MTYzbDQwMCAxMzN2LTE2M3pNMTAwIDUwMHYtMjAwaDMwMHYyMDBoLTMwMHpNMTEwMCAzOTh2LTI0OHEwIC0yMSAtMTQuNSAtMzUuNXQtMzUuNSAtMTQuNWgtMzc1bC0xMDAgLTEwMGgtMzc1bC0xMDAgMTAwaDQwMGwyMDAgMjAwaDEwNXoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMTgyOyIgZD0iTTE3IDEwMDdsMTYyIDE2MnExNyAxNyA0MCAxNHQzNyAtMjJsMTM5IC0xOTRxMTQgLTIwIDExIC00NC41dC0yMCAtNDEuNWwtMTE5IC0xMThxMTAyIC0xNDIgMjI4IC0yNjh0MjY3IC0yMjdsMTE5IDExOHExNyAxNyA0Mi41IDE5dDQ0LjUgLTEybDE5MiAtMTM2cTE5IC0xNCAyMi41IC0zNy41dC0xMy41IC00MC41bC0xNjMgLTE2MnEtMyAtMSAtOS41IC0xdC0yOS41IDJ0LTQ3LjUgNnQtNjIuNSAxNC41dC03Ny41IDI2LjV0LTkwIDQyLjUgdC0xMDEuNSA2MHQtMTExIDgzdC0xMTkgMTA4LjVxLTc0IDc0IC0xMzMuNSAxNTAuNXQtOTQuNSAxMzguNXQtNjAgMTE5LjV0LTM0LjUgMTAwdC0xNSA3NC41dC00LjUgNDh6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTE4MzsiIGQ9Ik02MDAgMTEwMHE5MiAwIDE3NSAtMTAuNXQxNDEuNSAtMjd0MTA4LjUgLTM2LjV0ODEuNSAtNDB0NTMuNSAtMzd0MzEgLTI3bDkgLTEwdi0yMDBxMCAtMjEgLTE0LjUgLTMzdC0zNC41IC05bC0yMDIgMzRxLTIwIDMgLTM0LjUgMjB0LTE0LjUgMzh2MTQ2cS0xNDEgMjQgLTMwMCAyNHQtMzAwIC0yNHYtMTQ2cTAgLTIxIC0xNC41IC0zOHQtMzQuNSAtMjBsLTIwMiAtMzRxLTIwIC0zIC0zNC41IDl0LTE0LjUgMzN2MjAwcTMgNCA5LjUgMTAuNSB0MzEgMjZ0NTQgMzcuNXQ4MC41IDM5LjV0MTA5IDM3LjV0MTQxIDI2LjV0MTc1IDEwLjV6TTYwMCA3OTVxNTYgMCA5NyAtOS41dDYwIC0yMy41dDMwIC0yOHQxMiAtMjRsMSAtMTB2LTUwbDM2NSAtMzAzcTE0IC0xNSAyNC41IC00MHQxMC41IC00NXYtMjEycTAgLTIxIC0xNC41IC0zNS41dC0zNS41IC0xNC41aC0xMTAwcS0yMSAwIC0zNS41IDE0LjV0LTE0LjUgMzUuNXYyMTJxMCAyMCAxMC41IDQ1dDI0LjUgNDBsMzY1IDMwM3Y1MCBxMCA0IDEgMTAuNXQxMiAyM3QzMCAyOXQ2MCAyMi41dDk3IDEweiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUxODQ7IiBkPSJNMTEwMCA3MDBsLTIwMCAtMjAwaC02MDBsLTIwMCAyMDB2NTAwaDIwMHYtMjAwaDIwMHYyMDBoMjAwdi0yMDBoMjAwdjIwMGgyMDB2LTUwMHpNMjUwIDQwMGg3MDBxMjEgMCAzNS41IC0xNC41dDE0LjUgLTM1LjV0LTE0LjUgLTM1LjV0LTM1LjUgLTE0LjVoLTEybDEzNyAtMTAwaC05NTBsMTM3IDEwMGgtMTJxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41dDE0LjUgMzUuNXQzNS41IDE0LjV6TTUwIDEwMGgxMTAwcTIxIDAgMzUuNSAtMTQuNSB0MTQuNSAtMzUuNXYtNTBoLTEyMDB2NTBxMCAyMSAxNC41IDM1LjV0MzUuNSAxNC41eiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUxODU7IiBkPSJNNzAwIDExMDBoLTEwMHEtNDEgMCAtNzAuNSAtMjkuNXQtMjkuNSAtNzAuNXYtMTAwMGgzMDB2MTAwMHEwIDQxIC0yOS41IDcwLjV0LTcwLjUgMjkuNXpNMTEwMCA4MDBoLTEwMHEtNDEgMCAtNzAuNSAtMjkuNXQtMjkuNSAtNzAuNXYtNzAwaDMwMHY3MDBxMCA0MSAtMjkuNSA3MC41dC03MC41IDI5LjV6TTQwMCAwaC0zMDB2NDAwcTAgNDEgMjkuNSA3MC41dDcwLjUgMjkuNWgxMDBxNDEgMCA3MC41IC0yOS41dDI5LjUgLTcwLjV2LTQwMHogIiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTE4NjsiIGQ9Ik0yMDAgMTEwMGg3MDBxMTI0IDAgMjEyIC04OHQ4OCAtMjEydi01MDBxMCAtMTI0IC04OCAtMjEydC0yMTIgLTg4aC03MDBxLTEyNCAwIC0yMTIgODh0LTg4IDIxMnY1MDBxMCAxMjQgODggMjEydDIxMiA4OHpNMTAwIDkwMHYtNzAwaDkwMHY3MDBoLTkwMHpNNTAwIDcwMGgtMjAwdi0xMDBoMjAwdi0zMDBoLTMwMHYxMDBoMjAwdjEwMGgtMjAwdjMwMGgzMDB2LTEwMHpNOTAwIDcwMHYtMzAwbC0xMDAgLTEwMGgtMjAwdjUwMGgyMDB6IE03MDAgNzAwdi0zMDBoMTAwdjMwMGgtMTAweiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUxODc7IiBkPSJNMjAwIDExMDBoNzAwcTEyNCAwIDIxMiAtODh0ODggLTIxMnYtNTAwcTAgLTEyNCAtODggLTIxMnQtMjEyIC04OGgtNzAwcS0xMjQgMCAtMjEyIDg4dC04OCAyMTJ2NTAwcTAgMTI0IDg4IDIxMnQyMTIgODh6TTEwMCA5MDB2LTcwMGg5MDB2NzAwaC05MDB6TTUwMCAzMDBoLTEwMHYyMDBoLTEwMHYtMjAwaC0xMDB2NTAwaDEwMHYtMjAwaDEwMHYyMDBoMTAwdi01MDB6TTkwMCA3MDB2LTMwMGwtMTAwIC0xMDBoLTIwMHY1MDBoMjAweiBNNzAwIDcwMHYtMzAwaDEwMHYzMDBoLTEwMHoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMTg4OyIgZD0iTTIwMCAxMTAwaDcwMHExMjQgMCAyMTIgLTg4dDg4IC0yMTJ2LTUwMHEwIC0xMjQgLTg4IC0yMTJ0LTIxMiAtODhoLTcwMHEtMTI0IDAgLTIxMiA4OHQtODggMjEydjUwMHEwIDEyNCA4OCAyMTJ0MjEyIDg4ek0xMDAgOTAwdi03MDBoOTAwdjcwMGgtOTAwek01MDAgNzAwaC0yMDB2LTMwMGgyMDB2LTEwMGgtMzAwdjUwMGgzMDB2LTEwMHpNOTAwIDcwMGgtMjAwdi0zMDBoMjAwdi0xMDBoLTMwMHY1MDBoMzAwdi0xMDB6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTE4OTsiIGQ9Ik0yMDAgMTEwMGg3MDBxMTI0IDAgMjEyIC04OHQ4OCAtMjEydi01MDBxMCAtMTI0IC04OCAtMjEydC0yMTIgLTg4aC03MDBxLTEyNCAwIC0yMTIgODh0LTg4IDIxMnY1MDBxMCAxMjQgODggMjEydDIxMiA4OHpNMTAwIDkwMHYtNzAwaDkwMHY3MDBoLTkwMHpNNTAwIDQwMGwtMzAwIDE1MGwzMDAgMTUwdi0zMDB6TTkwMCA1NTBsLTMwMCAtMTUwdjMwMHoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMTkwOyIgZD0iTTIwMCAxMTAwaDcwMHExMjQgMCAyMTIgLTg4dDg4IC0yMTJ2LTUwMHEwIC0xMjQgLTg4IC0yMTJ0LTIxMiAtODhoLTcwMHEtMTI0IDAgLTIxMiA4OHQtODggMjEydjUwMHEwIDEyNCA4OCAyMTJ0MjEyIDg4ek0xMDAgOTAwdi03MDBoOTAwdjcwMGgtOTAwek05MDAgMzAwaC03MDB2NTAwaDcwMHYtNTAwek04MDAgNzAwaC0xMzBxLTM4IDAgLTY2LjUgLTQzdC0yOC41IC0xMDh0MjcgLTEwN3Q2OCAtNDJoMTMwdjMwMHpNMzAwIDcwMHYtMzAwIGgxMzBxNDEgMCA2OCA0MnQyNyAxMDd0LTI4LjUgMTA4dC02Ni41IDQzaC0xMzB6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTE5MTsiIGQ9Ik0yMDAgMTEwMGg3MDBxMTI0IDAgMjEyIC04OHQ4OCAtMjEydi01MDBxMCAtMTI0IC04OCAtMjEydC0yMTIgLTg4aC03MDBxLTEyNCAwIC0yMTIgODh0LTg4IDIxMnY1MDBxMCAxMjQgODggMjEydDIxMiA4OHpNMTAwIDkwMHYtNzAwaDkwMHY3MDBoLTkwMHpNNTAwIDcwMGgtMjAwdi0xMDBoMjAwdi0zMDBoLTMwMHYxMDBoMjAwdjEwMGgtMjAwdjMwMGgzMDB2LTEwMHpNOTAwIDMwMGgtMTAwdjQwMGgtMTAwdjEwMGgyMDB2LTUwMHogTTcwMCAzMDBoLTEwMHYxMDBoMTAwdi0xMDB6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTE5MjsiIGQ9Ik0yMDAgMTEwMGg3MDBxMTI0IDAgMjEyIC04OHQ4OCAtMjEydi01MDBxMCAtMTI0IC04OCAtMjEydC0yMTIgLTg4aC03MDBxLTEyNCAwIC0yMTIgODh0LTg4IDIxMnY1MDBxMCAxMjQgODggMjEydDIxMiA4OHpNMTAwIDkwMHYtNzAwaDkwMHY3MDBoLTkwMHpNMzAwIDcwMGgyMDB2LTQwMGgtMzAwdjUwMGgxMDB2LTEwMHpNOTAwIDMwMGgtMTAwdjQwMGgtMTAwdjEwMGgyMDB2LTUwMHpNMzAwIDYwMHYtMjAwaDEwMHYyMDBoLTEwMHogTTcwMCAzMDBoLTEwMHYxMDBoMTAwdi0xMDB6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTE5MzsiIGQ9Ik0yMDAgMTEwMGg3MDBxMTI0IDAgMjEyIC04OHQ4OCAtMjEydi01MDBxMCAtMTI0IC04OCAtMjEydC0yMTIgLTg4aC03MDBxLTEyNCAwIC0yMTIgODh0LTg4IDIxMnY1MDBxMCAxMjQgODggMjEydDIxMiA4OHpNMTAwIDkwMHYtNzAwaDkwMHY3MDBoLTkwMHpNNTAwIDUwMGwtMTk5IC0yMDBoLTEwMHY1MGwxOTkgMjAwdjE1MGgtMjAwdjEwMGgzMDB2LTMwMHpNOTAwIDMwMGgtMTAwdjQwMGgtMTAwdjEwMGgyMDB2LTUwMHpNNzAxIDMwMGgtMTAwIHYxMDBoMTAwdi0xMDB6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTE5NDsiIGQ9Ik02MDAgMTE5MXExMjAgMCAyMjkuNSAtNDd0MTg4LjUgLTEyNnQxMjYgLTE4OC41dDQ3IC0yMjkuNXQtNDcgLTIyOS41dC0xMjYgLTE4OC41dC0xODguNSAtMTI2dC0yMjkuNSAtNDd0LTIyOS41IDQ3dC0xODguNSAxMjZ0LTEyNiAxODguNXQtNDcgMjI5LjV0NDcgMjI5LjV0MTI2IDE4OC41dDE4OC41IDEyNnQyMjkuNSA0N3pNNjAwIDEwMjFxLTExNCAwIC0yMTEgLTU2LjV0LTE1My41IC0xNTMuNXQtNTYuNSAtMjExdDU2LjUgLTIxMSB0MTUzLjUgLTE1My41dDIxMSAtNTYuNXQyMTEgNTYuNXQxNTMuNSAxNTMuNXQ1Ni41IDIxMXQtNTYuNSAyMTF0LTE1My41IDE1My41dC0yMTEgNTYuNXpNODAwIDcwMGgtMzAwdi0yMDBoMzAwdi0xMDBoLTMwMGwtMTAwIDEwMHYyMDBsMTAwIDEwMGgzMDB2LTEwMHoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMTk1OyIgZD0iTTYwMCAxMTkxcTEyMCAwIDIyOS41IC00N3QxODguNSAtMTI2dDEyNiAtMTg4LjV0NDcgLTIyOS41dC00NyAtMjI5LjV0LTEyNiAtMTg4LjV0LTE4OC41IC0xMjZ0LTIyOS41IC00N3QtMjI5LjUgNDd0LTE4OC41IDEyNnQtMTI2IDE4OC41dC00NyAyMjkuNXQ0NyAyMjkuNXQxMjYgMTg4LjV0MTg4LjUgMTI2dDIyOS41IDQ3ek02MDAgMTAyMXEtMTE0IDAgLTIxMSAtNTYuNXQtMTUzLjUgLTE1My41dC01Ni41IC0yMTF0NTYuNSAtMjExIHQxNTMuNSAtMTUzLjV0MjExIC01Ni41dDIxMSA1Ni41dDE1My41IDE1My41dDU2LjUgMjExdC01Ni41IDIxMXQtMTUzLjUgMTUzLjV0LTIxMSA1Ni41ek04MDAgNzAwdi0xMDBsLTUwIC01MGwxMDAgLTEwMHYtNTBoLTEwMGwtMTAwIDEwMGgtMTUwdi0xMDBoLTEwMHY0MDBoMzAwek01MDAgNzAwdi0xMDBoMjAwdjEwMGgtMjAweiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUxOTc7IiBkPSJNNTAzIDEwODlxMTEwIDAgMjAwLjUgLTU5LjV0MTM0LjUgLTE1Ni41cTQ0IDE0IDkwIDE0cTEyMCAwIDIwNSAtODYuNXQ4NSAtMjA3dC04NSAtMjA3dC0yMDUgLTg2LjVoLTEyOHYyNTBxMCAyMSAtMTQuNSAzNS41dC0zNS41IDE0LjVoLTMwMHEtMjEgMCAtMzUuNSAtMTQuNXQtMTQuNSAtMzUuNXYtMjUwaC0yMjJxLTgwIDAgLTEzNiA1Ny41dC01NiAxMzYuNXEwIDY5IDQzIDEyMi41dDEwOCA2Ny41cS0yIDE5IC0yIDM3cTAgMTAwIDQ5IDE4NSB0MTM0IDEzNHQxODUgNDl6TTUyNSA1MDBoMTUwcTEwIDAgMTcuNSAtNy41dDcuNSAtMTcuNXYtMjc1aDEzN3EyMSAwIDI2IC0xMS41dC04IC0yNy41bC0yMjMgLTI0NHEtMTMgLTE2IC0zMiAtMTZ0LTMyIDE2bC0yMjMgMjQ0cS0xMyAxNiAtOCAyNy41dDI2IDExLjVoMTM3djI3NXEwIDEwIDcuNSAxNy41dDE3LjUgNy41eiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUxOTg7IiBkPSJNNTAyIDEwODlxMTEwIDAgMjAxIC01OS41dDEzNSAtMTU2LjVxNDMgMTUgODkgMTVxMTIxIDAgMjA2IC04Ni41dDg2IC0yMDYuNXEwIC05OSAtNjAgLTE4MXQtMTUwIC0xMTBsLTM3OCAzNjBxLTEzIDE2IC0zMS41IDE2dC0zMS41IC0xNmwtMzgxIC0zNjVoLTlxLTc5IDAgLTEzNS41IDU3LjV0LTU2LjUgMTM2LjVxMCA2OSA0MyAxMjIuNXQxMDggNjcuNXEtMiAxOSAtMiAzOHEwIDEwMCA0OSAxODQuNXQxMzMuNSAxMzR0MTg0LjUgNDkuNXogTTYzMiA0NjdsMjIzIC0yMjhxMTMgLTE2IDggLTI3LjV0LTI2IC0xMS41aC0xMzd2LTI3NXEwIC0xMCAtNy41IC0xNy41dC0xNy41IC03LjVoLTE1MHEtMTAgMCAtMTcuNSA3LjV0LTcuNSAxNy41djI3NWgtMTM3cS0yMSAwIC0yNiAxMS41dDggMjcuNXExOTkgMjA0IDIyMyAyMjhxMTkgMTkgMzEuNSAxOXQzMi41IC0xOXoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMTk5OyIgZD0iTTcwMCAxMDB2MTAwaDQwMGwtMjcwIDMwMGgxNzBsLTI3MCAzMDBoMTcwbC0zMDAgMzMzbC0zMDAgLTMzM2gxNzBsLTI3MCAtMzAwaDE3MGwtMjcwIC0zMDBoNDAwdi0xMDBoLTUwcS0yMSAwIC0zNS41IC0xNC41dC0xNC41IC0zNS41di01MGg0MDB2NTBxMCAyMSAtMTQuNSAzNS41dC0zNS41IDE0LjVoLTUweiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUyMDA7IiBkPSJNNjAwIDExNzlxOTQgMCAxNjcuNSAtNTYuNXQ5OS41IC0xNDUuNXE4OSAtNiAxNTAuNSAtNzEuNXQ2MS41IC0xNTUuNXEwIC02MSAtMjkuNSAtMTEyLjV0LTc5LjUgLTgyLjVxOSAtMjkgOSAtNTVxMCAtNzQgLTUyLjUgLTEyNi41dC0xMjYuNSAtNTIuNXEtNTUgMCAtMTAwIDMwdi0yNTFxMjEgMCAzNS41IC0xNC41dDE0LjUgLTM1LjV2LTUwaC0zMDB2NTBxMCAyMSAxNC41IDM1LjV0MzUuNSAxNC41djI1MXEtNDUgLTMwIC0xMDAgLTMwIHEtNzQgMCAtMTI2LjUgNTIuNXQtNTIuNSAxMjYuNXEwIDE4IDQgMzhxLTQ3IDIxIC03NS41IDY1dC0yOC41IDk3cTAgNzQgNTIuNSAxMjYuNXQxMjYuNSA1Mi41cTUgMCAyMyAtMnEwIDIgLTEgMTB0LTEgMTNxMCAxMTYgODEuNSAxOTcuNXQxOTcuNSA4MS41eiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUyMDE7IiBkPSJNMTAxMCAxMDEwcTExMSAtMTExIDE1MC41IC0yNjAuNXQwIC0yOTl0LTE1MC41IC0yNjAuNXEtODMgLTgzIC0xOTEuNSAtMTI2LjV0LTIxOC41IC00My41dC0yMTguNSA0My41dC0xOTEuNSAxMjYuNXEtMTExIDExMSAtMTUwLjUgMjYwLjV0MCAyOTl0MTUwLjUgMjYwLjVxODMgODMgMTkxLjUgMTI2LjV0MjE4LjUgNDMuNXQyMTguNSAtNDMuNXQxOTEuNSAtMTI2LjV6TTQ3NiAxMDY1cS00IDAgLTggLTFxLTEyMSAtMzQgLTIwOS41IC0xMjIuNSB0LTEyMi41IC0yMDkuNXEtNCAtMTIgMi41IC0yM3QxOC41IC0xNGwzNiAtOXEzIC0xIDcgLTFxMjMgMCAyOSAyMnEyNyA5NiA5OCAxNjZxNzAgNzEgMTY2IDk4cTExIDMgMTcuNSAxMy41dDMuNSAyMi41bC05IDM1cS0zIDEzIC0xNCAxOXEtNyA0IC0xNSA0ek01MTIgOTIwcS00IDAgLTkgLTJxLTgwIC0yNCAtMTM4LjUgLTgyLjV0LTgyLjUgLTEzOC41cS00IC0xMyAyIC0yNHQxOSAtMTRsMzQgLTlxNCAtMSA4IC0xcTIyIDAgMjggMjEgcTE4IDU4IDU4LjUgOTguNXQ5Ny41IDU4LjVxMTIgMyAxOCAxMy41dDMgMjEuNWwtOSAzNXEtMyAxMiAtMTQgMTlxLTcgNCAtMTUgNHpNNzE5LjUgNzE5LjVxLTQ5LjUgNDkuNSAtMTE5LjUgNDkuNXQtMTE5LjUgLTQ5LjV0LTQ5LjUgLTExOS41dDQ5LjUgLTExOS41dDExOS41IC00OS41dDExOS41IDQ5LjV0NDkuNSAxMTkuNXQtNDkuNSAxMTkuNXpNODU1IDU1MXEtMjIgMCAtMjggLTIxcS0xOCAtNTggLTU4LjUgLTk4LjV0LTk4LjUgLTU3LjUgcS0xMSAtNCAtMTcgLTE0LjV0LTMgLTIxLjVsOSAtMzVxMyAtMTIgMTQgLTE5cTcgLTQgMTUgLTRxNCAwIDkgMnE4MCAyNCAxMzguNSA4Mi41dDgyLjUgMTM4LjVxNCAxMyAtMi41IDI0dC0xOC41IDE0bC0zNCA5cS00IDEgLTggMXpNMTAwMCA1MTVxLTIzIDAgLTI5IC0yMnEtMjcgLTk2IC05OCAtMTY2cS03MCAtNzEgLTE2NiAtOThxLTExIC0zIC0xNy41IC0xMy41dC0zLjUgLTIyLjVsOSAtMzVxMyAtMTMgMTQgLTE5cTcgLTQgMTUgLTQgcTQgMCA4IDFxMTIxIDM0IDIwOS41IDEyMi41dDEyMi41IDIwOS41cTQgMTIgLTIuNSAyM3QtMTguNSAxNGwtMzYgOXEtMyAxIC03IDF6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTIwMjsiIGQ9Ik03MDAgODAwaDMwMHYtMzgwaC0xODB2MjAwaC0zNDB2LTIwMGgtMzgwdjc1NXEwIDEwIDcuNSAxNy41dDE3LjUgNy41aDU3NXYtNDAwek0xMDAwIDkwMGgtMjAwdjIwMHpNNzAwIDMwMGgxNjJsLTIxMiAtMjEybC0yMTIgMjEyaDE2MnYyMDBoMTAwdi0yMDB6TTUyMCAwaC0zOTVxLTEwIDAgLTE3LjUgNy41dC03LjUgMTcuNXYzOTV6TTEwMDAgMjIwdi0xOTVxMCAtMTAgLTcuNSAtMTcuNXQtMTcuNSAtNy41aC0xOTV6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTIwMzsiIGQ9Ik03MDAgODAwaDMwMHYtNTIwbC0zNTAgMzUwbC01NTAgLTU1MHYxMDk1cTAgMTAgNy41IDE3LjV0MTcuNSA3LjVoNTc1di00MDB6TTEwMDAgOTAwaC0yMDB2MjAwek04NjIgMjAwaC0xNjJ2LTIwMGgtMTAwdjIwMGgtMTYybDIxMiAyMTJ6TTQ4MCAwaC0zNTVxLTEwIDAgLTE3LjUgNy41dC03LjUgMTcuNXY1NWgzODB2LTgwek0xMDAwIDgwdi01NXEwIC0xMCAtNy41IC0xNy41dC0xNy41IC03LjVoLTE1NXY4MGgxODB6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTIwNDsiIGQ9Ik0xMTYyIDgwMGgtMTYydi0yMDBoMTAwbDEwMCAtMTAwaC0zMDB2MzAwaC0xNjJsMjEyIDIxMnpNMjAwIDgwMGgyMDBxMjcgMCA0MCAtMnQyOS41IC0xMC41dDIzLjUgLTMwdDcgLTU3LjVoMzAwdi0xMDBoLTYwMGwtMjAwIC0zNTB2NDUwaDEwMHEwIDM2IDcgNTcuNXQyMy41IDMwdDI5LjUgMTAuNXQ0MCAyek04MDAgNDAwaDI0MGwtMjQwIC00MDBoLTgwMGwzMDAgNTAwaDUwMHYtMTAweiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUyMDU7IiBkPSJNNjUwIDExMDBoMTAwcTIxIDAgMzUuNSAtMTQuNXQxNC41IC0zNS41di01MGg1MHEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXYtMTAwcTAgLTIxIC0xNC41IC0zNS41dC0zNS41IC0xNC41aC0zMDBxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41djEwMHEwIDIxIDE0LjUgMzUuNXQzNS41IDE0LjVoNTB2NTBxMCAyMSAxNC41IDM1LjV0MzUuNSAxNC41ek0xMDAwIDg1MHYxNTBxNDEgMCA3MC41IC0yOS41dDI5LjUgLTcwLjV2LTgwMCBxMCAtNDEgLTI5LjUgLTcwLjV0LTcwLjUgLTI5LjVoLTYwMHEtMSAwIC0yMCA0bDI0NiAyNDZsLTMyNiAzMjZ2MzI0cTAgNDEgMjkuNSA3MC41dDcwLjUgMjkuNXYtMTUwcTAgLTYyIDQ0IC0xMDZ0MTA2IC00NGgzMDBxNjIgMCAxMDYgNDR0NDQgMTA2ek00MTIgMjUwbC0yMTIgLTIxMnYxNjJoLTIwMHYxMDBoMjAwdjE2MnoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMjA2OyIgZD0iTTQ1MCAxMTAwaDEwMHEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXYtNTBoNTBxMjEgMCAzNS41IC0xNC41dDE0LjUgLTM1LjV2LTEwMHEwIC0yMSAtMTQuNSAtMzUuNXQtMzUuNSAtMTQuNWgtMzAwcS0yMSAwIC0zNS41IDE0LjV0LTE0LjUgMzUuNXYxMDBxMCAyMSAxNC41IDM1LjV0MzUuNSAxNC41aDUwdjUwcTAgMjEgMTQuNSAzNS41dDM1LjUgMTQuNXpNODAwIDg1MHYxNTBxNDEgMCA3MC41IC0yOS41dDI5LjUgLTcwLjV2LTUwMCBoLTIwMHYtMzAwaDIwMHEwIC0zNiAtNyAtNTcuNXQtMjMuNSAtMzB0LTI5LjUgLTEwLjV0LTQwIC0yaC02MDBxLTQxIDAgLTcwLjUgMjkuNXQtMjkuNSA3MC41djgwMHEwIDQxIDI5LjUgNzAuNXQ3MC41IDI5LjV2LTE1MHEwIC02MiA0NCAtMTA2dDEwNiAtNDRoMzAwcTYyIDAgMTA2IDQ0dDQ0IDEwNnpNMTIxMiAyNTBsLTIxMiAtMjEydjE2MmgtMjAwdjEwMGgyMDB2MTYyeiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUyMDk7IiBkPSJNNjU4IDExOTdsNjM3IC0xMTA0cTIzIC0zOCA3IC02NS41dC02MCAtMjcuNWgtMTI3NnEtNDQgMCAtNjAgMjcuNXQ3IDY1LjVsNjM3IDExMDRxMjIgMzkgNTQgMzl0NTQgLTM5ek03MDQgODAwaC0yMDhxLTIwIDAgLTMyIC0xNC41dC04IC0zNC41bDU4IC0zMDJxNCAtMjAgMjEuNSAtMzQuNXQzNy41IC0xNC41aDU0cTIwIDAgMzcuNSAxNC41dDIxLjUgMzQuNWw1OCAzMDJxNCAyMCAtOCAzNC41dC0zMiAxNC41ek01MDAgMzAwdi0xMDBoMjAwIHYxMDBoLTIwMHoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMjEwOyIgZD0iTTQyNSAxMTAwaDI1MHExMCAwIDE3LjUgLTcuNXQ3LjUgLTE3LjV2LTE1MHEwIC0xMCAtNy41IC0xNy41dC0xNy41IC03LjVoLTI1MHEtMTAgMCAtMTcuNSA3LjV0LTcuNSAxNy41djE1MHEwIDEwIDcuNSAxNy41dDE3LjUgNy41ek00MjUgODAwaDI1MHExMCAwIDE3LjUgLTcuNXQ3LjUgLTE3LjV2LTE1MHEwIC0xMCAtNy41IC0xNy41dC0xNy41IC03LjVoLTI1MHEtMTAgMCAtMTcuNSA3LjV0LTcuNSAxNy41djE1MHEwIDEwIDcuNSAxNy41IHQxNy41IDcuNXpNODI1IDgwMGgyNTBxMTAgMCAxNy41IC03LjV0Ny41IC0xNy41di0xNTBxMCAtMTAgLTcuNSAtMTcuNXQtMTcuNSAtNy41aC0yNTBxLTEwIDAgLTE3LjUgNy41dC03LjUgMTcuNXYxNTBxMCAxMCA3LjUgMTcuNXQxNy41IDcuNXpNMjUgNTAwaDI1MHExMCAwIDE3LjUgLTcuNXQ3LjUgLTE3LjV2LTE1MHEwIC0xMCAtNy41IC0xNy41dC0xNy41IC03LjVoLTI1MHEtMTAgMCAtMTcuNSA3LjV0LTcuNSAxNy41djE1MCBxMCAxMCA3LjUgMTcuNXQxNy41IDcuNXpNNDI1IDUwMGgyNTBxMTAgMCAxNy41IC03LjV0Ny41IC0xNy41di0xNTBxMCAtMTAgLTcuNSAtMTcuNXQtMTcuNSAtNy41aC0yNTBxLTEwIDAgLTE3LjUgNy41dC03LjUgMTcuNXYxNTBxMCAxMCA3LjUgMTcuNXQxNy41IDcuNXpNODI1IDUwMGgyNTBxMTAgMCAxNy41IC03LjV0Ny41IC0xNy41di0xNTBxMCAtMTAgLTcuNSAtMTcuNXQtMTcuNSAtNy41aC0yNTBxLTEwIDAgLTE3LjUgNy41dC03LjUgMTcuNSB2MTUwcTAgMTAgNy41IDE3LjV0MTcuNSA3LjV6TTI1IDIwMGgyNTBxMTAgMCAxNy41IC03LjV0Ny41IC0xNy41di0xNTBxMCAtMTAgLTcuNSAtMTcuNXQtMTcuNSAtNy41aC0yNTBxLTEwIDAgLTE3LjUgNy41dC03LjUgMTcuNXYxNTBxMCAxMCA3LjUgMTcuNXQxNy41IDcuNXpNNDI1IDIwMGgyNTBxMTAgMCAxNy41IC03LjV0Ny41IC0xNy41di0xNTBxMCAtMTAgLTcuNSAtMTcuNXQtMTcuNSAtNy41aC0yNTBxLTEwIDAgLTE3LjUgNy41IHQtNy41IDE3LjV2MTUwcTAgMTAgNy41IDE3LjV0MTcuNSA3LjV6TTgyNSAyMDBoMjUwcTEwIDAgMTcuNSAtNy41dDcuNSAtMTcuNXYtMTUwcTAgLTEwIC03LjUgLTE3LjV0LTE3LjUgLTcuNWgtMjUwcS0xMCAwIC0xNy41IDcuNXQtNy41IDE3LjV2MTUwcTAgMTAgNy41IDE3LjV0MTcuNSA3LjV6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTIxMTsiIGQ9Ik03MDAgMTIwMGgxMDB2LTIwMGgtMTAwdi0xMDBoMzUwcTYyIDAgODYuNSAtMzkuNXQtMy41IC05NC41bC02NiAtMTMycS00MSAtODMgLTgxIC0xMzRoLTc3MnEtNDAgNTEgLTgxIDEzNGwtNjYgMTMycS0yOCA1NSAtMy41IDk0LjV0ODYuNSAzOS41aDM1MHYxMDBoLTEwMHYyMDBoMTAwdjEwMGgyMDB2LTEwMHpNMjUwIDQwMGg3MDBxMjEgMCAzNS41IC0xNC41dDE0LjUgLTM1LjV0LTE0LjUgLTM1LjV0LTM1LjUgLTE0LjVoLTEybDEzNyAtMTAwIGgtOTUwbDEzOCAxMDBoLTEzcS0yMSAwIC0zNS41IDE0LjV0LTE0LjUgMzUuNXQxNC41IDM1LjV0MzUuNSAxNC41ek01MCAxMDBoMTEwMHEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXYtNTBoLTEyMDB2NTBxMCAyMSAxNC41IDM1LjV0MzUuNSAxNC41eiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUyMTI7IiBkPSJNNjAwIDEzMDBxNDAgMCA2OC41IC0yOS41dDI4LjUgLTcwLjVoLTE5NHEwIDQxIDI4LjUgNzAuNXQ2OC41IDI5LjV6TTQ0MyAxMTAwaDMxNHExOCAtMzcgMTggLTc1cTAgLTggLTMgLTI1aDMyOHE0MSAwIDQ0LjUgLTE2LjV0LTMwLjUgLTM4LjVsLTE3NSAtMTQ1aC02NzhsLTE3OCAxNDVxLTM0IDIyIC0yOSAzOC41dDQ2IDE2LjVoMzI4cS0zIDE3IC0zIDI1cTAgMzggMTggNzV6TTI1MCA3MDBoNzAwcTIxIDAgMzUuNSAtMTQuNSB0MTQuNSAtMzUuNXQtMTQuNSAtMzUuNXQtMzUuNSAtMTQuNWgtMTUwdi0yMDBsMjc1IC0yMDBoLTk1MGwyNzUgMjAwdjIwMGgtMTUwcS0yMSAwIC0zNS41IDE0LjV0LTE0LjUgMzUuNXQxNC41IDM1LjV0MzUuNSAxNC41ek01MCAxMDBoMTEwMHEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXYtNTBoLTEyMDB2NTBxMCAyMSAxNC41IDM1LjV0MzUuNSAxNC41eiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUyMTM7IiBkPSJNNjAwIDExODFxNzUgMCAxMjggLTUzdDUzIC0xMjh0LTUzIC0xMjh0LTEyOCAtNTN0LTEyOCA1M3QtNTMgMTI4dDUzIDEyOHQxMjggNTN6TTYwMiA3OThoNDZxMzQgMCA1NS41IC0yOC41dDIxLjUgLTg2LjVxMCAtNzYgMzkgLTE4M2gtMzI0cTM5IDEwNyAzOSAxODNxMCA1OCAyMS41IDg2LjV0NTYuNSAyOC41aDQ1ek0yNTAgNDAwaDcwMHEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXQtMTQuNSAtMzUuNXQtMzUuNSAtMTQuNWgtMTMgbDEzOCAtMTAwaC05NTBsMTM3IDEwMGgtMTJxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41dDE0LjUgMzUuNXQzNS41IDE0LjV6TTUwIDEwMGgxMTAwcTIxIDAgMzUuNSAtMTQuNXQxNC41IC0zNS41di01MGgtMTIwMHY1MHEwIDIxIDE0LjUgMzUuNXQzNS41IDE0LjV6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTIxNDsiIGQ9Ik02MDAgMTMwMHE0NyAwIDkyLjUgLTUzLjV0NzEgLTEyM3QyNS41IC0xMjMuNXEwIC03OCAtNTUuNSAtMTMzLjV0LTEzMy41IC01NS41dC0xMzMuNSA1NS41dC01NS41IDEzMy41cTAgNjIgMzQgMTQzbDE0NCAtMTQzbDExMSAxMTFsLTE2MyAxNjNxMzQgMjYgNjMgMjZ6TTYwMiA3OThoNDZxMzQgMCA1NS41IC0yOC41dDIxLjUgLTg2LjVxMCAtNzYgMzkgLTE4M2gtMzI0cTM5IDEwNyAzOSAxODNxMCA1OCAyMS41IDg2LjV0NTYuNSAyOC41aDQ1IHpNMjUwIDQwMGg3MDBxMjEgMCAzNS41IC0xNC41dDE0LjUgLTM1LjV0LTE0LjUgLTM1LjV0LTM1LjUgLTE0LjVoLTEzbDEzOCAtMTAwaC05NTBsMTM3IDEwMGgtMTJxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41dDE0LjUgMzUuNXQzNS41IDE0LjV6TTUwIDEwMGgxMTAwcTIxIDAgMzUuNSAtMTQuNXQxNC41IC0zNS41di01MGgtMTIwMHY1MHEwIDIxIDE0LjUgMzUuNXQzNS41IDE0LjV6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTIxNTsiIGQ9Ik02MDAgMTIwMGwzMDAgLTE2MXYtMTM5aC0zMDBxMCAtNTcgMTguNSAtMTA4dDUwIC05MS41dDYzIC03MnQ3MCAtNjcuNXQ1Ny41IC02MWgtNTMwcS02MCA4MyAtOTAuNSAxNzcuNXQtMzAuNSAxNzguNXQzMyAxNjQuNXQ4Ny41IDEzOS41dDEyNiA5Ni41dDE0NS41IDQxLjV2LTk4ek0yNTAgNDAwaDcwMHEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXQtMTQuNSAtMzUuNXQtMzUuNSAtMTQuNWgtMTNsMTM4IC0xMDBoLTk1MGwxMzcgMTAwIGgtMTJxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41dDE0LjUgMzUuNXQzNS41IDE0LjV6TTUwIDEwMGgxMTAwcTIxIDAgMzUuNSAtMTQuNXQxNC41IC0zNS41di01MGgtMTIwMHY1MHEwIDIxIDE0LjUgMzUuNXQzNS41IDE0LjV6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTIxNjsiIGQ9Ik02MDAgMTMwMHE0MSAwIDcwLjUgLTI5LjV0MjkuNSAtNzAuNXYtNzhxNDYgLTI2IDczIC03MnQyNyAtMTAwdi01MGgtNDAwdjUwcTAgNTQgMjcgMTAwdDczIDcydjc4cTAgNDEgMjkuNSA3MC41dDcwLjUgMjkuNXpNNDAwIDgwMGg0MDBxNTQgMCAxMDAgLTI3dDcyIC03M2gtMTcydi0xMDBoMjAwdi0xMDBoLTIwMHYtMTAwaDIwMHYtMTAwaC0yMDB2LTEwMGgyMDBxMCAtODMgLTU4LjUgLTE0MS41dC0xNDEuNSAtNTguNWgtNDAwIHEtODMgMCAtMTQxLjUgNTguNXQtNTguNSAxNDEuNXY0MDBxMCA4MyA1OC41IDE0MS41dDE0MS41IDU4LjV6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTIxODsiIGQ9Ik0xNTAgMTEwMGg5MDBxMjEgMCAzNS41IC0xNC41dDE0LjUgLTM1LjV2LTUwMHEwIC0yMSAtMTQuNSAtMzUuNXQtMzUuNSAtMTQuNWgtOTAwcS0yMSAwIC0zNS41IDE0LjV0LTE0LjUgMzUuNXY1MDBxMCAyMSAxNC41IDM1LjV0MzUuNSAxNC41ek0xMjUgNDAwaDk1MHExMCAwIDE3LjUgLTcuNXQ3LjUgLTE3LjV2LTUwcTAgLTEwIC03LjUgLTE3LjV0LTE3LjUgLTcuNWgtMjgzbDIyNCAtMjI0cTEzIC0xMyAxMyAtMzEuNXQtMTMgLTMyIHQtMzEuNSAtMTMuNXQtMzEuNSAxM2wtODggODhoLTUyNGwtODcgLTg4cS0xMyAtMTMgLTMyIC0xM3QtMzIgMTMuNXQtMTMgMzJ0MTMgMzEuNWwyMjQgMjI0aC0yODlxLTEwIDAgLTE3LjUgNy41dC03LjUgMTcuNXY1MHEwIDEwIDcuNSAxNy41dDE3LjUgNy41ek01NDEgMzAwbC0xMDAgLTEwMGgzMjRsLTEwMCAxMDBoLTEyNHoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMjE5OyIgZD0iTTIwMCAxMTAwaDgwMHE4MyAwIDE0MS41IC01OC41dDU4LjUgLTE0MS41di0yMDBoLTEwMHEwIDQxIC0yOS41IDcwLjV0LTcwLjUgMjkuNWgtMjUwcS00MSAwIC03MC41IC0yOS41dC0yOS41IC03MC41aC0xMDBxMCA0MSAtMjkuNSA3MC41dC03MC41IDI5LjVoLTI1MHEtNDEgMCAtNzAuNSAtMjkuNXQtMjkuNSAtNzAuNWgtMTAwdjIwMHEwIDgzIDU4LjUgMTQxLjV0MTQxLjUgNTguNXpNMTAwIDYwMGgxMDAwcTQxIDAgNzAuNSAtMjkuNSB0MjkuNSAtNzAuNXYtMzAwaC0xMjAwdjMwMHEwIDQxIDI5LjUgNzAuNXQ3MC41IDI5LjV6TTMwMCAxMDB2LTUwcTAgLTIxIC0xNC41IC0zNS41dC0zNS41IC0xNC41aC0xMDBxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41djUwaDIwMHpNMTEwMCAxMDB2LTUwcTAgLTIxIC0xNC41IC0zNS41dC0zNS41IC0xNC41aC0xMDBxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41djUwaDIwMHoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMjIxOyIgZD0iTTQ4MCAxMTY1bDY4MiAtNjgzcTMxIC0zMSAzMSAtNzUuNXQtMzEgLTc1LjVsLTEzMSAtMTMxaC00ODFsLTUxNyA1MThxLTMyIDMxIC0zMiA3NS41dDMyIDc1LjVsMjk1IDI5NnEzMSAzMSA3NS41IDMxdDc2LjUgLTMxek0xMDggNzk0bDM0MiAtMzQybDMwMyAzMDRsLTM0MSAzNDF6TTI1MCAxMDBoODAwcTIxIDAgMzUuNSAtMTQuNXQxNC41IC0zNS41di01MGgtOTAwdjUwcTAgMjEgMTQuNSAzNS41dDM1LjUgMTQuNXoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMjIzOyIgZD0iTTEwNTcgNjQ3bC0xODkgNTA2cS04IDE5IC0yNy41IDMzdC00MC41IDE0aC00MDBxLTIxIDAgLTQwLjUgLTE0dC0yNy41IC0zM2wtMTg5IC01MDZxLTggLTE5IDEuNSAtMzN0MzAuNSAtMTRoNjI1di0xNTBxMCAtMjEgMTQuNSAtMzUuNXQzNS41IC0xNC41dDM1LjUgMTQuNXQxNC41IDM1LjV2MTUwaDEyNXEyMSAwIDMwLjUgMTR0MS41IDMzek04OTcgMGgtNTk1djUwcTAgMjEgMTQuNSAzNS41dDM1LjUgMTQuNWg1MHY1MCBxMCAyMSAxNC41IDM1LjV0MzUuNSAxNC41aDQ4djMwMGgyMDB2LTMwMGg0N3EyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXYtNTBoNTBxMjEgMCAzNS41IC0xNC41dDE0LjUgLTM1LjV2LTUweiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUyMjQ7IiBkPSJNOTAwIDgwMGgzMDB2LTU3NXEwIC0xMCAtNy41IC0xNy41dC0xNy41IC03LjVoLTM3NXY1OTFsLTMwMCAzMDB2ODRxMCAxMCA3LjUgMTcuNXQxNy41IDcuNWgzNzV2LTQwMHpNMTIwMCA5MDBoLTIwMHYyMDB6TTQwMCA2MDBoMzAwdi01NzVxMCAtMTAgLTcuNSAtMTcuNXQtMTcuNSAtNy41aC02NTBxLTEwIDAgLTE3LjUgNy41dC03LjUgMTcuNXY5NTBxMCAxMCA3LjUgMTcuNXQxNy41IDcuNWgzNzV2LTQwMHpNNzAwIDcwMGgtMjAwdjIwMHogIiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTIyNTsiIGQ9Ik00ODQgMTA5NWgxOTVxNzUgMCAxNDYgLTMyLjV0MTI0IC04NnQ4OS41IC0xMjIuNXQ0OC41IC0xNDJxMTggLTE0IDM1IC0yMHEzMSAtMTAgNjQuNSA2LjV0NDMuNSA0OC41cTEwIDM0IC0xNSA3MXEtMTkgMjcgLTkgNDNxNSA4IDEyLjUgMTF0MTkgLTF0MjMuNSAtMTZxNDEgLTQ0IDM5IC0xMDVxLTMgLTYzIC00NiAtMTA2LjV0LTEwNCAtNDMuNWgtNjJxLTcgLTU1IC0zNSAtMTE3dC01NiAtMTAwbC0zOSAtMjM0cS0zIC0yMCAtMjAgLTM0LjUgdC0zOCAtMTQuNWgtMTAwcS0yMSAwIC0zMyAxNC41dC05IDM0LjVsMTIgNzBxLTQ5IC0xNCAtOTEgLTE0aC0xOTVxLTI0IDAgLTY1IDhsLTExIC02NHEtMyAtMjAgLTIwIC0zNC41dC0zOCAtMTQuNWgtMTAwcS0yMSAwIC0zMyAxNC41dC05IDM0LjVsMjYgMTU3cS04NCA3NCAtMTI4IDE3NWwtMTU5IDUzcS0xOSA3IC0zMyAyNnQtMTQgNDB2NTBxMCAyMSAxNC41IDM1LjV0MzUuNSAxNC41aDEyNHExMSA4NyA1NiAxNjZsLTExMSA5NSBxLTE2IDE0IC0xMi41IDIzLjV0MjQuNSA5LjVoMjAzcTExNiAxMDEgMjUwIDEwMXpNNjc1IDEwMDBoLTI1MHEtMTAgMCAtMTcuNSAtNy41dC03LjUgLTE3LjV2LTUwcTAgLTEwIDcuNSAtMTcuNXQxNy41IC03LjVoMjUwcTEwIDAgMTcuNSA3LjV0Ny41IDE3LjV2NTBxMCAxMCAtNy41IDE3LjV0LTE3LjUgNy41eiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUyMjY7IiBkPSJNNjQxIDkwMGw0MjMgMjQ3cTE5IDggNDIgMi41dDM3IC0yMS41bDMyIC0zOHExNCAtMTUgMTIuNSAtMzZ0LTE3LjUgLTM0bC0xMzkgLTEyMGgtMzkwek01MCAxMTAwaDEwNnE2NyAwIDEwMyAtMTd0NjYgLTcxbDEwMiAtMjEyaDgyM3EyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXYtNTBxMCAtMjEgLTE0IC00MHQtMzMgLTI2bC03MzcgLTEzMnEtMjMgLTQgLTQwIDZ0LTI2IDI1cS00MiA2NyAtMTAwIDY3aC0zMDBxLTYyIDAgLTEwNiA0NCB0LTQ0IDEwNnYyMDBxMCA2MiA0NCAxMDZ0MTA2IDQ0ek0xNzMgOTI4aC04MHEtMTkgMCAtMjggLTE0dC05IC0zNXYtNTZxMCAtNTEgNDIgLTUxaDEzNHExNiAwIDIxLjUgOHQ1LjUgMjRxMCAxMSAtMTYgNDV0LTI3IDUxcS0xOCAyOCAtNDMgMjh6TTU1MCA3MjdxLTMyIDAgLTU0LjUgLTIyLjV0LTIyLjUgLTU0LjV0MjIuNSAtNTQuNXQ1NC41IC0yMi41dDU0LjUgMjIuNXQyMi41IDU0LjV0LTIyLjUgNTQuNXQtNTQuNSAyMi41ek0xMzAgMzg5IGwxNTIgMTMwcTE4IDE5IDM0IDI0dDMxIC0zLjV0MjQuNSAtMTcuNXQyNS41IC0yOHEyOCAtMzUgNTAuNSAtNTF0NDguNSAtMTNsNjMgNWw0OCAtMTc5cTEzIC02MSAtMy41IC05Ny41dC02Ny41IC03OS41bC04MCAtNjlxLTQ3IC00MCAtMTA5IC0zNS41dC0xMDMgNTEuNWwtMTMwIDE1MXEtNDAgNDcgLTM1LjUgMTA5LjV0NTEuNSAxMDIuNXpNMzgwIDM3N2wtMTAyIC04OHEtMzEgLTI3IDIgLTY1bDM3IC00M3ExMyAtMTUgMjcuNSAtMTkuNSB0MzEuNSA2LjVsNjEgNTNxMTkgMTYgMTQgNDlxLTIgMjAgLTEyIDU2dC0xNyA0NXEtMTEgMTIgLTE5IDE0dC0yMyAtOHoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMjI3OyIgZD0iTTYyNSAxMjAwaDE1MHExMCAwIDE3LjUgLTcuNXQ3LjUgLTE3LjV2LTEwOXE3OSAtMzMgMTMxIC04Ny41dDUzIC0xMjguNXExIC00NiAtMTUgLTg0LjV0LTM5IC02MXQtNDYgLTM4dC0zOSAtMjEuNWwtMTcgLTZxNiAwIDE1IC0xLjV0MzUgLTl0NTAgLTE3LjV0NTMgLTMwdDUwIC00NXQzNS41IC02NHQxNC41IC04NHEwIC01OSAtMTEuNSAtMTA1LjV0LTI4LjUgLTc2LjV0LTQ0IC01MXQtNDkuNSAtMzEuNXQtNTQuNSAtMTZ0LTQ5LjUgLTYuNSB0LTQzLjUgLTF2LTc1cTAgLTEwIC03LjUgLTE3LjV0LTE3LjUgLTcuNWgtMTUwcS0xMCAwIC0xNy41IDcuNXQtNy41IDE3LjV2NzVoLTEwMHYtNzVxMCAtMTAgLTcuNSAtMTcuNXQtMTcuNSAtNy41aC0xNTBxLTEwIDAgLTE3LjUgNy41dC03LjUgMTcuNXY3NWgtMTc1cS0xMCAwIC0xNy41IDcuNXQtNy41IDE3LjV2MTUwcTAgMTAgNy41IDE3LjV0MTcuNSA3LjVoNzV2NjAwaC03NXEtMTAgMCAtMTcuNSA3LjV0LTcuNSAxNy41djE1MCBxMCAxMCA3LjUgMTcuNXQxNy41IDcuNWgxNzV2NzVxMCAxMCA3LjUgMTcuNXQxNy41IDcuNWgxNTBxMTAgMCAxNy41IC03LjV0Ny41IC0xNy41di03NWgxMDB2NzVxMCAxMCA3LjUgMTcuNXQxNy41IDcuNXpNNDAwIDkwMHYtMjAwaDI2M3EyOCAwIDQ4LjUgMTAuNXQzMCAyNXQxNSAyOXQ1LjUgMjUuNWwxIDEwcTAgNCAtMC41IDExdC02IDI0dC0xNSAzMHQtMzAgMjR0LTQ4LjUgMTFoLTI2M3pNNDAwIDUwMHYtMjAwaDM2M3EyOCAwIDQ4LjUgMTAuNSB0MzAgMjV0MTUgMjl0NS41IDI1LjVsMSAxMHEwIDQgLTAuNSAxMXQtNiAyNHQtMTUgMzB0LTMwIDI0dC00OC41IDExaC0zNjN6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTIzMDsiIGQ9Ik0yMTIgMTE5OGg3ODBxODYgMCAxNDcgLTYxdDYxIC0xNDd2LTQxNnEwIC01MSAtMTggLTE0Mi41dC0zNiAtMTU3LjVsLTE4IC02NnEtMjkgLTg3IC05My41IC0xNDYuNXQtMTQ2LjUgLTU5LjVoLTU3MnEtODIgMCAtMTQ3IDU5dC05MyAxNDdxLTggMjggLTIwIDczdC0zMiAxNDMuNXQtMjAgMTQ5LjV2NDE2cTAgODYgNjEgMTQ3dDE0NyA2MXpNNjAwIDEwNDVxLTcwIDAgLTEzMi41IC0xMS41dC0xMDUuNSAtMzAuNXQtNzguNSAtNDEuNSB0LTU3IC00NXQtMzYgLTQxdC0yMC41IC0zMC41bC02IC0xMmwxNTYgLTI0M2g1NjBsMTU2IDI0M3EtMiA1IC02IDEyLjV0LTIwIDI5LjV0LTM2LjUgNDJ0LTU3IDQ0LjV0LTc5IDQydC0xMDUgMjkuNXQtMTMyLjUgMTJ6TTc2MiA3MDNoLTE1N2wxOTUgMjYxeiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUyMzE7IiBkPSJNNDc1IDEzMDBoMTUwcTEwMyAwIDE4OSAtODZ0ODYgLTE4OXYtNTAwcTAgLTQxIC00MiAtODN0LTgzIC00MmgtNDUwcS00MSAwIC04MyA0MnQtNDIgODN2NTAwcTAgMTAzIDg2IDE4OXQxODkgODZ6TTcwMCAzMDB2LTIyNXEwIC0yMSAtMjcgLTQ4dC00OCAtMjdoLTE1MHEtMjEgMCAtNDggMjd0LTI3IDQ4djIyNWgzMDB6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTIzMjsiIGQ9Ik00NzUgMTMwMGg5NnEwIC0xNTAgODkuNSAtMjM5LjV0MjM5LjUgLTg5LjV2LTQ0NnEwIC00MSAtNDIgLTgzdC04MyAtNDJoLTQ1MHEtNDEgMCAtODMgNDJ0LTQyIDgzdjUwMHEwIDEwMyA4NiAxODl0MTg5IDg2ek03MDAgMzAwdi0yMjVxMCAtMjEgLTI3IC00OHQtNDggLTI3aC0xNTBxLTIxIDAgLTQ4IDI3dC0yNyA0OHYyMjVoMzAweiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUyMzM7IiBkPSJNMTI5NCA3NjdsLTYzOCAtMjgzbC0zNzggMTcwbC03OCAtNjB2LTIyNGwxMDAgLTE1MHYtMTk5bC0xNTAgMTQ4bC0xNTAgLTE0OXYyMDBsMTAwIDE1MHYyNTBxMCA0IC0wLjUgMTAuNXQwIDkuNXQxIDh0MyA4dDYuNSA2bDQ3IDQwbC0xNDcgNjVsNjQyIDI4M3pNMTAwMCAzODBsLTM1MCAtMTY2bC0zNTAgMTY2djE0N2wzNTAgLTE2NWwzNTAgMTY1di0xNDd6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTIzNDsiIGQ9Ik0yNTAgODAwcTYyIDAgMTA2IC00NHQ0NCAtMTA2dC00NCAtMTA2dC0xMDYgLTQ0dC0xMDYgNDR0LTQ0IDEwNnQ0NCAxMDZ0MTA2IDQ0ek02NTAgODAwcTYyIDAgMTA2IC00NHQ0NCAtMTA2dC00NCAtMTA2dC0xMDYgLTQ0dC0xMDYgNDR0LTQ0IDEwNnQ0NCAxMDZ0MTA2IDQ0ek0xMDUwIDgwMHE2MiAwIDEwNiAtNDR0NDQgLTEwNnQtNDQgLTEwNnQtMTA2IC00NHQtMTA2IDQ0dC00NCAxMDZ0NDQgMTA2dDEwNiA0NHoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMjM1OyIgZD0iTTU1MCAxMTAwcTYyIDAgMTA2IC00NHQ0NCAtMTA2dC00NCAtMTA2dC0xMDYgLTQ0dC0xMDYgNDR0LTQ0IDEwNnQ0NCAxMDZ0MTA2IDQ0ek01NTAgNzAwcTYyIDAgMTA2IC00NHQ0NCAtMTA2dC00NCAtMTA2dC0xMDYgLTQ0dC0xMDYgNDR0LTQ0IDEwNnQ0NCAxMDZ0MTA2IDQ0ek01NTAgMzAwcTYyIDAgMTA2IC00NHQ0NCAtMTA2dC00NCAtMTA2dC0xMDYgLTQ0dC0xMDYgNDR0LTQ0IDEwNnQ0NCAxMDZ0MTA2IDQ0eiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUyMzY7IiBkPSJNMTI1IDExMDBoOTUwcTEwIDAgMTcuNSAtNy41dDcuNSAtMTcuNXYtMTUwcTAgLTEwIC03LjUgLTE3LjV0LTE3LjUgLTcuNWgtOTUwcS0xMCAwIC0xNy41IDcuNXQtNy41IDE3LjV2MTUwcTAgMTAgNy41IDE3LjV0MTcuNSA3LjV6TTEyNSA3MDBoOTUwcTEwIDAgMTcuNSAtNy41dDcuNSAtMTcuNXYtMTUwcTAgLTEwIC03LjUgLTE3LjV0LTE3LjUgLTcuNWgtOTUwcS0xMCAwIC0xNy41IDcuNXQtNy41IDE3LjV2MTUwcTAgMTAgNy41IDE3LjUgdDE3LjUgNy41ek0xMjUgMzAwaDk1MHExMCAwIDE3LjUgLTcuNXQ3LjUgLTE3LjV2LTE1MHEwIC0xMCAtNy41IC0xNy41dC0xNy41IC03LjVoLTk1MHEtMTAgMCAtMTcuNSA3LjV0LTcuNSAxNy41djE1MHEwIDEwIDcuNSAxNy41dDE3LjUgNy41eiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUyMzc7IiBkPSJNMzUwIDEyMDBoNTAwcTE2MiAwIDI1NiAtOTMuNXQ5NCAtMjU2LjV2LTUwMHEwIC0xNjUgLTkzLjUgLTI1Ny41dC0yNTYuNSAtOTIuNWgtNTAwcS0xNjUgMCAtMjU3LjUgOTIuNXQtOTIuNSAyNTcuNXY1MDBxMCAxNjUgOTIuNSAyNTcuNXQyNTcuNSA5Mi41ek05MDAgMTAwMGgtNjAwcS00MSAwIC03MC41IC0yOS41dC0yOS41IC03MC41di02MDBxMCAtNDEgMjkuNSAtNzAuNXQ3MC41IC0yOS41aDYwMHE0MSAwIDcwLjUgMjkuNSB0MjkuNSA3MC41djYwMHEwIDQxIC0yOS41IDcwLjV0LTcwLjUgMjkuNXpNMzUwIDkwMGg1MDBxMjEgMCAzNS41IC0xNC41dDE0LjUgLTM1LjV2LTMwMHEwIC0yMSAtMTQuNSAtMzUuNXQtMzUuNSAtMTQuNWgtNTAwcS0yMSAwIC0zNS41IDE0LjV0LTE0LjUgMzUuNXYzMDBxMCAyMSAxNC41IDM1LjV0MzUuNSAxNC41ek00MDAgODAwdi0yMDBoNDAwdjIwMGgtNDAweiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUyMzg7IiBkPSJNMTUwIDExMDBoMTAwMHEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXQtMTQuNSAtMzUuNXQtMzUuNSAtMTQuNWgtNTB2LTIwMGg1MHEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXQtMTQuNSAtMzUuNXQtMzUuNSAtMTQuNWgtNTB2LTIwMGg1MHEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXQtMTQuNSAtMzUuNXQtMzUuNSAtMTQuNWgtNTB2LTIwMGg1MHEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXQtMTQuNSAtMzUuNSB0LTM1LjUgLTE0LjVoLTEwMDBxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41dDE0LjUgMzUuNXQzNS41IDE0LjVoNTB2MjAwaC01MHEtMjEgMCAtMzUuNSAxNC41dC0xNC41IDM1LjV0MTQuNSAzNS41dDM1LjUgMTQuNWg1MHYyMDBoLTUwcS0yMSAwIC0zNS41IDE0LjV0LTE0LjUgMzUuNXQxNC41IDM1LjV0MzUuNSAxNC41aDUwdjIwMGgtNTBxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41dDE0LjUgMzUuNXQzNS41IDE0LjV6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTIzOTsiIGQ9Ik02NTAgMTE4N3E4NyAtNjcgMTE4LjUgLTE1NnQwIC0xNzh0LTExOC41IC0xNTVxLTg3IDY2IC0xMTguNSAxNTV0MCAxNzh0MTE4LjUgMTU2ek0zMDAgODAwcTEyNCAwIDIxMiAtODh0ODggLTIxMnEtMTI0IDAgLTIxMiA4OHQtODggMjEyek0xMDAwIDgwMHEwIC0xMjQgLTg4IC0yMTJ0LTIxMiAtODhxMCAxMjQgODggMjEydDIxMiA4OHpNMzAwIDUwMHExMjQgMCAyMTIgLTg4dDg4IC0yMTJxLTEyNCAwIC0yMTIgODh0LTg4IDIxMnogTTEwMDAgNTAwcTAgLTEyNCAtODggLTIxMnQtMjEyIC04OHEwIDEyNCA4OCAyMTJ0MjEyIDg4ek03MDAgMTk5di0xNDRxMCAtMjEgLTE0LjUgLTM1LjV0LTM1LjUgLTE0LjV0LTM1LjUgMTQuNXQtMTQuNSAzNS41djE0MnE0MCAtNCA0MyAtNHExNyAwIDU3IDZ6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTI0MDsiIGQ9Ik03NDUgODc4bDY5IDE5cTI1IDYgNDUgLTEybDI5OCAtMjk1cTExIC0xMSAxNSAtMjYuNXQtMiAtMzAuNXEtNSAtMTQgLTE4IC0yMy41dC0yOCAtOS41aC04cTEgMCAxIC0xM3EwIC0yOSAtMiAtNTZ0LTguNSAtNjJ0LTIwIC02M3QtMzMgLTUzdC01MSAtMzl0LTcyLjUgLTE0aC0xNDZxLTE4NCAwIC0xODQgMjg4cTAgMjQgMTAgNDdxLTIwIDQgLTYyIDR0LTYzIC00cTExIC0yNCAxMSAtNDdxMCAtMjg4IC0xODQgLTI4OGgtMTQyIHEtNDggMCAtODQuNSAyMXQtNTYgNTF0LTMyIDcxLjV0LTE2IDc1dC0zLjUgNjguNXEwIDEzIDIgMTNoLTdxLTE1IDAgLTI3LjUgOS41dC0xOC41IDIzLjVxLTYgMTUgLTIgMzAuNXQxNSAyNS41bDI5OCAyOTZxMjAgMTggNDYgMTFsNzYgLTE5cTIwIC01IDMwLjUgLTIyLjV0NS41IC0zNy41dC0yMi41IC0zMXQtMzcuNSAtNWwtNTEgMTJsLTE4MiAtMTkzaDg5MWwtMTgyIDE5M2wtNDQgLTEycS0yMCAtNSAtMzcuNSA2dC0yMi41IDMxdDYgMzcuNSB0MzEgMjIuNXoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMjQxOyIgZD0iTTEyMDAgOTAwaC01MHEwIDIxIC00IDM3dC05LjUgMjYuNXQtMTggMTcuNXQtMjIgMTF0LTI4LjUgNS41dC0zMSAydC0zNyAwLjVoLTIwMHYtODUwcTAgLTIyIDI1IC0zNC41dDUwIC0xMy41bDI1IC0ydi0xMDBoLTQwMHYxMDBxNCAwIDExIDAuNXQyNCAzdDMwIDd0MjQgMTV0MTEgMjQuNXY4NTBoLTIwMHEtMjUgMCAtMzcgLTAuNXQtMzEgLTJ0LTI4LjUgLTUuNXQtMjIgLTExdC0xOCAtMTcuNXQtOS41IC0yNi41dC00IC0zN2gtNTB2MzAwIGgxMDAwdi0zMDB6TTUwMCA0NTBoLTI1cTAgMTUgLTQgMjQuNXQtOSAxNC41dC0xNyA3LjV0LTIwIDN0LTI1IDAuNWgtMTAwdi00MjVxMCAtMTEgMTIuNSAtMTcuNXQyNS41IC03LjVoMTJ2LTUwaC0yMDB2NTBxNTAgMCA1MCAyNXY0MjVoLTEwMHEtMTcgMCAtMjUgLTAuNXQtMjAgLTN0LTE3IC03LjV0LTkgLTE0LjV0LTQgLTI0LjVoLTI1djE1MGg1MDB2LTE1MHoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMjQyOyIgZD0iTTEwMDAgMzAwdjUwcS0yNSAwIC01NSAzMnEtMTQgMTQgLTI1IDMxdC0xNiAyN2wtNCAxMWwtMjg5IDc0N2gtNjlsLTMwMCAtNzU0cS0xOCAtMzUgLTM5IC01NnEtOSAtOSAtMjQuNSAtMTguNXQtMjYuNSAtMTQuNWwtMTEgLTV2LTUwaDI3M3Y1MHEtNDkgMCAtNzguNSAyMS41dC0xMS41IDY3LjVsNjkgMTc2aDI5M2w2MSAtMTY2cTEzIC0zNCAtMy41IC02Ni41dC01NS41IC0zMi41di01MGgzMTJ6TTQxMiA2OTFsMTM0IDM0MmwxMjEgLTM0MiBoLTI1NXpNMTEwMCAxNTB2LTEwMHEwIC0yMSAtMTQuNSAtMzUuNXQtMzUuNSAtMTQuNWgtMTAwMHEtMjEgMCAtMzUuNSAxNC41dC0xNC41IDM1LjV2MTAwcTAgMjEgMTQuNSAzNS41dDM1LjUgMTQuNWgxMDAwcTIxIDAgMzUuNSAtMTQuNXQxNC41IC0zNS41eiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUyNDM7IiBkPSJNNTAgMTIwMGgxMTAwcTIxIDAgMzUuNSAtMTQuNXQxNC41IC0zNS41di0xMTAwcTAgLTIxIC0xNC41IC0zNS41dC0zNS41IC0xNC41aC0xMTAwcS0yMSAwIC0zNS41IDE0LjV0LTE0LjUgMzUuNXYxMTAwcTAgMjEgMTQuNSAzNS41dDM1LjUgMTQuNXpNNjExIDExMThoLTcwcS0xMyAwIC0xOCAtMTJsLTI5OSAtNzUzcS0xNyAtMzIgLTM1IC01MXEtMTggLTE4IC01NiAtMzRxLTEyIC01IC0xMiAtMTh2LTUwcTAgLTggNS41IC0xNHQxNC41IC02IGgyNzNxOCAwIDE0IDZ0NiAxNHY1MHEwIDggLTYgMTR0LTE0IDZxLTU1IDAgLTcxIDIzcS0xMCAxNCAwIDM5bDYzIDE2M2gyNjZsNTcgLTE1M3ExMSAtMzEgLTYgLTU1cS0xMiAtMTcgLTM2IC0xN3EtOCAwIC0xNCAtNnQtNiAtMTR2LTUwcTAgLTggNiAtMTR0MTQgLTZoMzEzcTggMCAxNCA2dDYgMTR2NTBxMCA3IC01LjUgMTN0LTEzLjUgN3EtMTcgMCAtNDIgMjVxLTI1IDI3IC00MCA2M2gtMWwtMjg4IDc0OHEtNSAxMiAtMTkgMTJ6TTYzOSA2MTEgaC0xOTdsMTAzIDI2NHoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMjQ0OyIgZD0iTTEyMDAgMTEwMGgtMTIwMHYxMDBoMTIwMHYtMTAwek01MCAxMDAwaDQwMHEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXYtOTAwcTAgLTIxIC0xNC41IC0zNS41dC0zNS41IC0xNC41aC00MDBxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41djkwMHEwIDIxIDE0LjUgMzUuNXQzNS41IDE0LjV6TTY1MCAxMDAwaDQwMHEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXYtNDAwcTAgLTIxIC0xNC41IC0zNS41dC0zNS41IC0xNC41aC00MDAgcS0yMSAwIC0zNS41IDE0LjV0LTE0LjUgMzUuNXY0MDBxMCAyMSAxNC41IDM1LjV0MzUuNSAxNC41ek03MDAgOTAwdi0zMDBoMzAwdjMwMGgtMzAweiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUyNDU7IiBkPSJNNTAgMTIwMGg0MDBxMjEgMCAzNS41IC0xNC41dDE0LjUgLTM1LjV2LTkwMHEwIC0yMSAtMTQuNSAtMzUuNXQtMzUuNSAtMTQuNWgtNDAwcS0yMSAwIC0zNS41IDE0LjV0LTE0LjUgMzUuNXY5MDBxMCAyMSAxNC41IDM1LjV0MzUuNSAxNC41ek02NTAgNzAwaDQwMHEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXYtNDAwcTAgLTIxIC0xNC41IC0zNS41dC0zNS41IC0xNC41aC00MDBxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41djQwMCBxMCAyMSAxNC41IDM1LjV0MzUuNSAxNC41ek03MDAgNjAwdi0zMDBoMzAwdjMwMGgtMzAwek0xMjAwIDBoLTEyMDB2MTAwaDEyMDB2LTEwMHoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMjQ2OyIgZD0iTTUwIDEwMDBoNDAwcTIxIDAgMzUuNSAtMTQuNXQxNC41IC0zNS41di0zNTBoMTAwdjE1MHEwIDIxIDE0LjUgMzUuNXQzNS41IDE0LjVoNDAwcTIxIDAgMzUuNSAtMTQuNXQxNC41IC0zNS41di0xNTBoMTAwdi0xMDBoLTEwMHYtMTUwcTAgLTIxIC0xNC41IC0zNS41dC0zNS41IC0xNC41aC00MDBxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41djE1MGgtMTAwdi0zNTBxMCAtMjEgLTE0LjUgLTM1LjV0LTM1LjUgLTE0LjVoLTQwMCBxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41djgwMHEwIDIxIDE0LjUgMzUuNXQzNS41IDE0LjV6TTcwMCA3MDB2LTMwMGgzMDB2MzAwaC0zMDB6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTI0NzsiIGQ9Ik0xMDAgMGgtMTAwdjEyMDBoMTAwdi0xMjAwek0yNTAgMTEwMGg0MDBxMjEgMCAzNS41IC0xNC41dDE0LjUgLTM1LjV2LTQwMHEwIC0yMSAtMTQuNSAtMzUuNXQtMzUuNSAtMTQuNWgtNDAwcS0yMSAwIC0zNS41IDE0LjV0LTE0LjUgMzUuNXY0MDBxMCAyMSAxNC41IDM1LjV0MzUuNSAxNC41ek0zMDAgMTAwMHYtMzAwaDMwMHYzMDBoLTMwMHpNMjUwIDUwMGg5MDBxMjEgMCAzNS41IC0xNC41dDE0LjUgLTM1LjV2LTQwMCBxMCAtMjEgLTE0LjUgLTM1LjV0LTM1LjUgLTE0LjVoLTkwMHEtMjEgMCAtMzUuNSAxNC41dC0xNC41IDM1LjV2NDAwcTAgMjEgMTQuNSAzNS41dDM1LjUgMTQuNXoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMjQ4OyIgZD0iTTYwMCAxMTAwaDE1MHEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXYtNDAwcTAgLTIxIC0xNC41IC0zNS41dC0zNS41IC0xNC41aC0xNTB2LTEwMGg0NTBxMjEgMCAzNS41IC0xNC41dDE0LjUgLTM1LjV2LTQwMHEwIC0yMSAtMTQuNSAtMzUuNXQtMzUuNSAtMTQuNWgtOTAwcS0yMSAwIC0zNS41IDE0LjV0LTE0LjUgMzUuNXY0MDBxMCAyMSAxNC41IDM1LjV0MzUuNSAxNC41aDM1MHYxMDBoLTE1MHEtMjEgMCAtMzUuNSAxNC41IHQtMTQuNSAzNS41djQwMHEwIDIxIDE0LjUgMzUuNXQzNS41IDE0LjVoMTUwdjEwMGgxMDB2LTEwMHpNNDAwIDEwMDB2LTMwMGgzMDB2MzAwaC0zMDB6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTI0OTsiIGQ9Ik0xMjAwIDBoLTEwMHYxMjAwaDEwMHYtMTIwMHpNNTUwIDExMDBoNDAwcTIxIDAgMzUuNSAtMTQuNXQxNC41IC0zNS41di00MDBxMCAtMjEgLTE0LjUgLTM1LjV0LTM1LjUgLTE0LjVoLTQwMHEtMjEgMCAtMzUuNSAxNC41dC0xNC41IDM1LjV2NDAwcTAgMjEgMTQuNSAzNS41dDM1LjUgMTQuNXpNNjAwIDEwMDB2LTMwMGgzMDB2MzAwaC0zMDB6TTUwIDUwMGg5MDBxMjEgMCAzNS41IC0xNC41dDE0LjUgLTM1LjV2LTQwMCBxMCAtMjEgLTE0LjUgLTM1LjV0LTM1LjUgLTE0LjVoLTkwMHEtMjEgMCAtMzUuNSAxNC41dC0xNC41IDM1LjV2NDAwcTAgMjEgMTQuNSAzNS41dDM1LjUgMTQuNXoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMjUwOyIgZD0iTTg2NSA1NjVsLTQ5NCAtNDk0cS0yMyAtMjMgLTQxIC0yM3EtMTQgMCAtMjIgMTMuNXQtOCAzOC41djEwMDBxMCAyNSA4IDM4LjV0MjIgMTMuNXExOCAwIDQxIC0yM2w0OTQgLTQ5NHExNCAtMTQgMTQgLTM1dC0xNCAtMzV6IiAvPgo8Z2x5cGggdW5pY29kZT0iJiN4ZTI1MTsiIGQ9Ik0zMzUgNjM1bDQ5NCA0OTRxMjkgMjkgNTAgMjAuNXQyMSAtNDkuNXYtMTAwMHEwIC00MSAtMjEgLTQ5LjV0LTUwIDIwLjVsLTQ5NCA0OTRxLTE0IDE0IC0xNCAzNXQxNCAzNXoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMjUyOyIgZD0iTTEwMCA5MDBoMTAwMHE0MSAwIDQ5LjUgLTIxdC0yMC41IC01MGwtNDk0IC00OTRxLTE0IC0xNCAtMzUgLTE0dC0zNSAxNGwtNDk0IDQ5NHEtMjkgMjkgLTIwLjUgNTB0NDkuNSAyMXoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMjUzOyIgZD0iTTYzNSA4NjVsNDk0IC00OTRxMjkgLTI5IDIwLjUgLTUwdC00OS41IC0yMWgtMTAwMHEtNDEgMCAtNDkuNSAyMXQyMC41IDUwbDQ5NCA0OTRxMTQgMTQgMzUgMTR0MzUgLTE0eiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUyNTQ7IiBkPSJNNzAwIDc0MXYtMTgybC02OTIgLTMyM3YyMjFsNDEzIDE5M2wtNDEzIDE5M3YyMjF6TTEyMDAgMGgtODAwdjIwMGg4MDB2LTIwMHoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMjU1OyIgZD0iTTEyMDAgOTAwaC0yMDB2LTEwMGgyMDB2LTEwMGgtMzAwdjMwMGgyMDB2MTAwaC0yMDB2MTAwaDMwMHYtMzAwek0wIDcwMGg1MHEwIDIxIDQgMzd0OS41IDI2LjV0MTggMTcuNXQyMiAxMXQyOC41IDUuNXQzMSAydDM3IDAuNWgxMDB2LTU1MHEwIC0yMiAtMjUgLTM0LjV0LTUwIC0xMy41bC0yNSAtMnYtMTAwaDQwMHYxMDBxLTQgMCAtMTEgMC41dC0yNCAzdC0zMCA3dC0yNCAxNXQtMTEgMjQuNXY1NTBoMTAwcTI1IDAgMzcgLTAuNXQzMSAtMiB0MjguNSAtNS41dDIyIC0xMXQxOCAtMTcuNXQ5LjUgLTI2LjV0NCAtMzdoNTB2MzAwaC04MDB2LTMwMHoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMjU2OyIgZD0iTTgwMCA3MDBoLTUwcTAgMjEgLTQgMzd0LTkuNSAyNi41dC0xOCAxNy41dC0yMiAxMXQtMjguNSA1LjV0LTMxIDJ0LTM3IDAuNWgtMTAwdi01NTBxMCAtMjIgMjUgLTM0LjV0NTAgLTE0LjVsMjUgLTF2LTEwMGgtNDAwdjEwMHE0IDAgMTEgMC41dDI0IDN0MzAgN3QyNCAxNXQxMSAyNC41djU1MGgtMTAwcS0yNSAwIC0zNyAtMC41dC0zMSAtMnQtMjguNSAtNS41dC0yMiAtMTF0LTE4IC0xNy41dC05LjUgLTI2LjV0LTQgLTM3aC01MHYzMDAgaDgwMHYtMzAwek0xMTAwIDIwMGgtMjAwdi0xMDBoMjAwdi0xMDBoLTMwMHYzMDBoMjAwdjEwMGgtMjAwdjEwMGgzMDB2LTMwMHoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMjU3OyIgZD0iTTcwMSAxMDk4aDE2MHExNiAwIDIxIC0xMXQtNyAtMjNsLTQ2NCAtNDY0bDQ2NCAtNDY0cTEyIC0xMiA3IC0yM3QtMjEgLTExaC0xNjBxLTEzIDAgLTIzIDlsLTQ3MSA0NzFxLTcgOCAtNyAxOHQ3IDE4bDQ3MSA0NzFxMTAgOSAyMyA5eiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGUyNTg7IiBkPSJNMzM5IDEwOThoMTYwcTEzIDAgMjMgLTlsNDcxIC00NzFxNyAtOCA3IC0xOHQtNyAtMThsLTQ3MSAtNDcxcS0xMCAtOSAtMjMgLTloLTE2MHEtMTYgMCAtMjEgMTF0NyAyM2w0NjQgNDY0bC00NjQgNDY0cS0xMiAxMiAtNyAyM3QyMSAxMXoiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMjU5OyIgZD0iTTEwODcgODgycTExIC01IDExIC0yMXYtMTYwcTAgLTEzIC05IC0yM2wtNDcxIC00NzFxLTggLTcgLTE4IC03dC0xOCA3bC00NzEgNDcxcS05IDEwIC05IDIzdjE2MHEwIDE2IDExIDIxdDIzIC03bDQ2NCAtNDY0bDQ2NCA0NjRxMTIgMTIgMjMgN3oiIC8%2BCjxnbHlwaCB1bmljb2RlPSImI3hlMjYwOyIgZD0iTTYxOCA5OTNsNDcxIC00NzFxOSAtMTAgOSAtMjN2LTE2MHEwIC0xNiAtMTEgLTIxdC0yMyA3bC00NjQgNDY0bC00NjQgLTQ2NHEtMTIgLTEyIC0yMyAtN3QtMTEgMjF2MTYwcTAgMTMgOSAyM2w0NzEgNDcxcTggNyAxOCA3dDE4IC03eiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeGY4ZmY7IiBkPSJNMTAwMCAxMjAwcTAgLTEyNCAtODggLTIxMnQtMjEyIC04OHEwIDEyNCA4OCAyMTJ0MjEyIDg4ek00NTAgMTAwMGgxMDBxMjEgMCA0MCAtMTR0MjYgLTMzbDc5IC0xOTRxNSAxIDE2IDNxMzQgNiA1NCA5LjV0NjAgN3Q2NS41IDF0NjEgLTEwdDU2LjUgLTIzdDQyLjUgLTQydDI5IC02NHQ1IC05MnQtMTkuNSAtMTIxLjVxLTEgLTcgLTMgLTE5LjV0LTExIC01MHQtMjAuNSAtNzN0LTMyLjUgLTgxLjV0LTQ2LjUgLTgzdC02NCAtNzAgdC04Mi41IC01MHEtMTMgLTUgLTQyIC01dC02NS41IDIuNXQtNDcuNSAyLjVxLTE0IDAgLTQ5LjUgLTMuNXQtNjMgLTMuNXQtNDMuNSA3cS01NyAyNSAtMTA0LjUgNzguNXQtNzUgMTExLjV0LTQ2LjUgMTEydC0yNiA5MGwtNyAzNXEtMTUgNjMgLTE4IDExNXQ0LjUgODguNXQyNiA2NHQzOS41IDQzLjV0NTIgMjUuNXQ1OC41IDEzdDYyLjUgMnQ1OS41IC00LjV0NTUuNSAtOGwtMTQ3IDE5MnEtMTIgMTggLTUuNSAzMHQyNy41IDEyeiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeDFmNTExOyIgZD0iTTI1MCAxMjAwaDYwMHEyMSAwIDM1LjUgLTE0LjV0MTQuNSAtMzUuNXYtNDAwcTAgLTIxIC0xNC41IC0zNS41dC0zNS41IC0xNC41aC0xNTB2LTUwMGwtMjU1IC0xNzhxLTE5IC05IC0zMiAtMXQtMTMgMjl2NjUwaC0xNTBxLTIxIDAgLTM1LjUgMTQuNXQtMTQuNSAzNS41djQwMHEwIDIxIDE0LjUgMzUuNXQzNS41IDE0LjV6TTQwMCAxMTAwdi0xMDBoMzAwdjEwMGgtMzAweiIgLz4KPGdseXBoIHVuaWNvZGU9IiYjeDFmNmFhOyIgZD0iTTI1MCAxMjAwaDc1MHEzOSAwIDY5LjUgLTQwLjV0MzAuNSAtODQuNXYtOTMzbC03MDAgLTExN3Y5NTBsNjAwIDEyNWgtNzAwdi0xMDAwaC0xMDB2MTAyNXEwIDIzIDE1LjUgNDl0MzQuNSAyNnpNNTAwIDUyNXYtMTAwbDEwMCAyMHYxMDB6IiAvPgo8L2ZvbnQ%2BCjwvZGVmcz48L3N2Zz4g%29%20format%28%27svg%27%29%7D%2Eglyphicon%7Bposition%3Arelative%3Btop%3A1px%3Bdisplay%3Ainline%2Dblock%3Bfont%2Dfamily%3A%27Glyphicons%20Halflings%27%3Bfont%2Dstyle%3Anormal%3Bfont%2Dweight%3A400%3Bline%2Dheight%3A1%3B%2Dwebkit%2Dfont%2Dsmoothing%3Aantialiased%3B%2Dmoz%2Dosx%2Dfont%2Dsmoothing%3Agrayscale%7D%2Eglyphicon%2Dasterisk%3Abefore%7Bcontent%3A%22%5C2a%22%7D%2Eglyphicon%2Dplus%3Abefore%7Bcontent%3A%22%5C2b%22%7D%2Eglyphicon%2Deur%3Abefore%2C%2Eglyphicon%2Deuro%3Abefore%7Bcontent%3A%22%5C20ac%22%7D%2Eglyphicon%2Dminus%3Abefore%7Bcontent%3A%22%5C2212%22%7D%2Eglyphicon%2Dcloud%3Abefore%7Bcontent%3A%22%5C2601%22%7D%2Eglyphicon%2Denvelope%3Abefore%7Bcontent%3A%22%5C2709%22%7D%2Eglyphicon%2Dpencil%3Abefore%7Bcontent%3A%22%5C270f%22%7D%2Eglyphicon%2Dglass%3Abefore%7Bcontent%3A%22%5Ce001%22%7D%2Eglyphicon%2Dmusic%3Abefore%7Bcontent%3A%22%5Ce002%22%7D%2Eglyphicon%2Dsearch%3Abefore%7Bcontent%3A%22%5Ce003%22%7D%2Eglyphicon%2Dheart%3Abefore%7Bcontent%3A%22%5Ce005%22%7D%2Eglyphicon%2Dstar%3Abefore%7Bcontent%3A%22%5Ce006%22%7D%2Eglyphicon%2Dstar%2Dempty%3Abefore%7Bcontent%3A%22%5Ce007%22%7D%2Eglyphicon%2Duser%3Abefore%7Bcontent%3A%22%5Ce008%22%7D%2Eglyphicon%2Dfilm%3Abefore%7Bcontent%3A%22%5Ce009%22%7D%2Eglyphicon%2Dth%2Dlarge%3Abefore%7Bcontent%3A%22%5Ce010%22%7D%2Eglyphicon%2Dth%3Abefore%7Bcontent%3A%22%5Ce011%22%7D%2Eglyphicon%2Dth%2Dlist%3Abefore%7Bcontent%3A%22%5Ce012%22%7D%2Eglyphicon%2Dok%3Abefore%7Bcontent%3A%22%5Ce013%22%7D%2Eglyphicon%2Dremove%3Abefore%7Bcontent%3A%22%5Ce014%22%7D%2Eglyphicon%2Dzoom%2Din%3Abefore%7Bcontent%3A%22%5Ce015%22%7D%2Eglyphicon%2Dzoom%2Dout%3Abefore%7Bcontent%3A%22%5Ce016%22%7D%2Eglyphicon%2Doff%3Abefore%7Bcontent%3A%22%5Ce017%22%7D%2Eglyphicon%2Dsignal%3Abefore%7Bcontent%3A%22%5Ce018%22%7D%2Eglyphicon%2Dcog%3Abefore%7Bcontent%3A%22%5Ce019%22%7D%2Eglyphicon%2Dtrash%3Abefore%7Bcontent%3A%22%5Ce020%22%7D%2Eglyphicon%2Dhome%3Abefore%7Bcontent%3A%22%5Ce021%22%7D%2Eglyphicon%2Dfile%3Abefore%7Bcontent%3A%22%5Ce022%22%7D%2Eglyphicon%2Dtime%3Abefore%7Bcontent%3A%22%5Ce023%22%7D%2Eglyphicon%2Droad%3Abefore%7Bcontent%3A%22%5Ce024%22%7D%2Eglyphicon%2Ddownload%2Dalt%3Abefore%7Bcontent%3A%22%5Ce025%22%7D%2Eglyphicon%2Ddownload%3Abefore%7Bcontent%3A%22%5Ce026%22%7D%2Eglyphicon%2Dupload%3Abefore%7Bcontent%3A%22%5Ce027%22%7D%2Eglyphicon%2Dinbox%3Abefore%7Bcontent%3A%22%5Ce028%22%7D%2Eglyphicon%2Dplay%2Dcircle%3Abefore%7Bcontent%3A%22%5Ce029%22%7D%2Eglyphicon%2Drepeat%3Abefore%7Bcontent%3A%22%5Ce030%22%7D%2Eglyphicon%2Drefresh%3Abefore%7Bcontent%3A%22%5Ce031%22%7D%2Eglyphicon%2Dlist%2Dalt%3Abefore%7Bcontent%3A%22%5Ce032%22%7D%2Eglyphicon%2Dlock%3Abefore%7Bcontent%3A%22%5Ce033%22%7D%2Eglyphicon%2Dflag%3Abefore%7Bcontent%3A%22%5Ce034%22%7D%2Eglyphicon%2Dheadphones%3Abefore%7Bcontent%3A%22%5Ce035%22%7D%2Eglyphicon%2Dvolume%2Doff%3Abefore%7Bcontent%3A%22%5Ce036%22%7D%2Eglyphicon%2Dvolume%2Ddown%3Abefore%7Bcontent%3A%22%5Ce037%22%7D%2Eglyphicon%2Dvolume%2Dup%3Abefore%7Bcontent%3A%22%5Ce038%22%7D%2Eglyphicon%2Dqrcode%3Abefore%7Bcontent%3A%22%5Ce039%22%7D%2Eglyphicon%2Dbarcode%3Abefore%7Bcontent%3A%22%5Ce040%22%7D%2Eglyphicon%2Dtag%3Abefore%7Bcontent%3A%22%5Ce041%22%7D%2Eglyphicon%2Dtags%3Abefore%7Bcontent%3A%22%5Ce042%22%7D%2Eglyphicon%2Dbook%3Abefore%7Bcontent%3A%22%5Ce043%22%7D%2Eglyphicon%2Dbookmark%3Abefore%7Bcontent%3A%22%5Ce044%22%7D%2Eglyphicon%2Dprint%3Abefore%7Bcontent%3A%22%5Ce045%22%7D%2Eglyphicon%2Dcamera%3Abefore%7Bcontent%3A%22%5Ce046%22%7D%2Eglyphicon%2Dfont%3Abefore%7Bcontent%3A%22%5Ce047%22%7D%2Eglyphicon%2Dbold%3Abefore%7Bcontent%3A%22%5Ce048%22%7D%2Eglyphicon%2Ditalic%3Abefore%7Bcontent%3A%22%5Ce049%22%7D%2Eglyphicon%2Dtext%2Dheight%3Abefore%7Bcontent%3A%22%5Ce050%22%7D%2Eglyphicon%2Dtext%2Dwidth%3Abefore%7Bcontent%3A%22%5Ce051%22%7D%2Eglyphicon%2Dalign%2Dleft%3Abefore%7Bcontent%3A%22%5Ce052%22%7D%2Eglyphicon%2Dalign%2Dcenter%3Abefore%7Bcontent%3A%22%5Ce053%22%7D%2Eglyphicon%2Dalign%2Dright%3Abefore%7Bcontent%3A%22%5Ce054%22%7D%2Eglyphicon%2Dalign%2Djustify%3Abefore%7Bcontent%3A%22%5Ce055%22%7D%2Eglyphicon%2Dlist%3Abefore%7Bcontent%3A%22%5Ce056%22%7D%2Eglyphicon%2Dindent%2Dleft%3Abefore%7Bcontent%3A%22%5Ce057%22%7D%2Eglyphicon%2Dindent%2Dright%3Abefore%7Bcontent%3A%22%5Ce058%22%7D%2Eglyphicon%2Dfacetime%2Dvideo%3Abefore%7Bcontent%3A%22%5Ce059%22%7D%2Eglyphicon%2Dpicture%3Abefore%7Bcontent%3A%22%5Ce060%22%7D%2Eglyphicon%2Dmap%2Dmarker%3Abefore%7Bcontent%3A%22%5Ce062%22%7D%2Eglyphicon%2Dadjust%3Abefore%7Bcontent%3A%22%5Ce063%22%7D%2Eglyphicon%2Dtint%3Abefore%7Bcontent%3A%22%5Ce064%22%7D%2Eglyphicon%2Dedit%3Abefore%7Bcontent%3A%22%5Ce065%22%7D%2Eglyphicon%2Dshare%3Abefore%7Bcontent%3A%22%5Ce066%22%7D%2Eglyphicon%2Dcheck%3Abefore%7Bcontent%3A%22%5Ce067%22%7D%2Eglyphicon%2Dmove%3Abefore%7Bcontent%3A%22%5Ce068%22%7D%2Eglyphicon%2Dstep%2Dbackward%3Abefore%7Bcontent%3A%22%5Ce069%22%7D%2Eglyphicon%2Dfast%2Dbackward%3Abefore%7Bcontent%3A%22%5Ce070%22%7D%2Eglyphicon%2Dbackward%3Abefore%7Bcontent%3A%22%5Ce071%22%7D%2Eglyphicon%2Dplay%3Abefore%7Bcontent%3A%22%5Ce072%22%7D%2Eglyphicon%2Dpause%3Abefore%7Bcontent%3A%22%5Ce073%22%7D%2Eglyphicon%2Dstop%3Abefore%7Bcontent%3A%22%5Ce074%22%7D%2Eglyphicon%2Dforward%3Abefore%7Bcontent%3A%22%5Ce075%22%7D%2Eglyphicon%2Dfast%2Dforward%3Abefore%7Bcontent%3A%22%5Ce076%22%7D%2Eglyphicon%2Dstep%2Dforward%3Abefore%7Bcontent%3A%22%5Ce077%22%7D%2Eglyphicon%2Deject%3Abefore%7Bcontent%3A%22%5Ce078%22%7D%2Eglyphicon%2Dchevron%2Dleft%3Abefore%7Bcontent%3A%22%5Ce079%22%7D%2Eglyphicon%2Dchevron%2Dright%3Abefore%7Bcontent%3A%22%5Ce080%22%7D%2Eglyphicon%2Dplus%2Dsign%3Abefore%7Bcontent%3A%22%5Ce081%22%7D%2Eglyphicon%2Dminus%2Dsign%3Abefore%7Bcontent%3A%22%5Ce082%22%7D%2Eglyphicon%2Dremove%2Dsign%3Abefore%7Bcontent%3A%22%5Ce083%22%7D%2Eglyphicon%2Dok%2Dsign%3Abefore%7Bcontent%3A%22%5Ce084%22%7D%2Eglyphicon%2Dquestion%2Dsign%3Abefore%7Bcontent%3A%22%5Ce085%22%7D%2Eglyphicon%2Dinfo%2Dsign%3Abefore%7Bcontent%3A%22%5Ce086%22%7D%2Eglyphicon%2Dscreenshot%3Abefore%7Bcontent%3A%22%5Ce087%22%7D%2Eglyphicon%2Dremove%2Dcircle%3Abefore%7Bcontent%3A%22%5Ce088%22%7D%2Eglyphicon%2Dok%2Dcircle%3Abefore%7Bcontent%3A%22%5Ce089%22%7D%2Eglyphicon%2Dban%2Dcircle%3Abefore%7Bcontent%3A%22%5Ce090%22%7D%2Eglyphicon%2Darrow%2Dleft%3Abefore%7Bcontent%3A%22%5Ce091%22%7D%2Eglyphicon%2Darrow%2Dright%3Abefore%7Bcontent%3A%22%5Ce092%22%7D%2Eglyphicon%2Darrow%2Dup%3Abefore%7Bcontent%3A%22%5Ce093%22%7D%2Eglyphicon%2Darrow%2Ddown%3Abefore%7Bcontent%3A%22%5Ce094%22%7D%2Eglyphicon%2Dshare%2Dalt%3Abefore%7Bcontent%3A%22%5Ce095%22%7D%2Eglyphicon%2Dresize%2Dfull%3Abefore%7Bcontent%3A%22%5Ce096%22%7D%2Eglyphicon%2Dresize%2Dsmall%3Abefore%7Bcontent%3A%22%5Ce097%22%7D%2Eglyphicon%2Dexclamation%2Dsign%3Abefore%7Bcontent%3A%22%5Ce101%22%7D%2Eglyphicon%2Dgift%3Abefore%7Bcontent%3A%22%5Ce102%22%7D%2Eglyphicon%2Dleaf%3Abefore%7Bcontent%3A%22%5Ce103%22%7D%2Eglyphicon%2Dfire%3Abefore%7Bcontent%3A%22%5Ce104%22%7D%2Eglyphicon%2Deye%2Dopen%3Abefore%7Bcontent%3A%22%5Ce105%22%7D%2Eglyphicon%2Deye%2Dclose%3Abefore%7Bcontent%3A%22%5Ce106%22%7D%2Eglyphicon%2Dwarning%2Dsign%3Abefore%7Bcontent%3A%22%5Ce107%22%7D%2Eglyphicon%2Dplane%3Abefore%7Bcontent%3A%22%5Ce108%22%7D%2Eglyphicon%2Dcalendar%3Abefore%7Bcontent%3A%22%5Ce109%22%7D%2Eglyphicon%2Drandom%3Abefore%7Bcontent%3A%22%5Ce110%22%7D%2Eglyphicon%2Dcomment%3Abefore%7Bcontent%3A%22%5Ce111%22%7D%2Eglyphicon%2Dmagnet%3Abefore%7Bcontent%3A%22%5Ce112%22%7D%2Eglyphicon%2Dchevron%2Dup%3Abefore%7Bcontent%3A%22%5Ce113%22%7D%2Eglyphicon%2Dchevron%2Ddown%3Abefore%7Bcontent%3A%22%5Ce114%22%7D%2Eglyphicon%2Dretweet%3Abefore%7Bcontent%3A%22%5Ce115%22%7D%2Eglyphicon%2Dshopping%2Dcart%3Abefore%7Bcontent%3A%22%5Ce116%22%7D%2Eglyphicon%2Dfolder%2Dclose%3Abefore%7Bcontent%3A%22%5Ce117%22%7D%2Eglyphicon%2Dfolder%2Dopen%3Abefore%7Bcontent%3A%22%5Ce118%22%7D%2Eglyphicon%2Dresize%2Dvertical%3Abefore%7Bcontent%3A%22%5Ce119%22%7D%2Eglyphicon%2Dresize%2Dhorizontal%3Abefore%7Bcontent%3A%22%5Ce120%22%7D%2Eglyphicon%2Dhdd%3Abefore%7Bcontent%3A%22%5Ce121%22%7D%2Eglyphicon%2Dbullhorn%3Abefore%7Bcontent%3A%22%5Ce122%22%7D%2Eglyphicon%2Dbell%3Abefore%7Bcontent%3A%22%5Ce123%22%7D%2Eglyphicon%2Dcertificate%3Abefore%7Bcontent%3A%22%5Ce124%22%7D%2Eglyphicon%2Dthumbs%2Dup%3Abefore%7Bcontent%3A%22%5Ce125%22%7D%2Eglyphicon%2Dthumbs%2Ddown%3Abefore%7Bcontent%3A%22%5Ce126%22%7D%2Eglyphicon%2Dhand%2Dright%3Abefore%7Bcontent%3A%22%5Ce127%22%7D%2Eglyphicon%2Dhand%2Dleft%3Abefore%7Bcontent%3A%22%5Ce128%22%7D%2Eglyphicon%2Dhand%2Dup%3Abefore%7Bcontent%3A%22%5Ce129%22%7D%2Eglyphicon%2Dhand%2Ddown%3Abefore%7Bcontent%3A%22%5Ce130%22%7D%2Eglyphicon%2Dcircle%2Darrow%2Dright%3Abefore%7Bcontent%3A%22%5Ce131%22%7D%2Eglyphicon%2Dcircle%2Darrow%2Dleft%3Abefore%7Bcontent%3A%22%5Ce132%22%7D%2Eglyphicon%2Dcircle%2Darrow%2Dup%3Abefore%7Bcontent%3A%22%5Ce133%22%7D%2Eglyphicon%2Dcircle%2Darrow%2Ddown%3Abefore%7Bcontent%3A%22%5Ce134%22%7D%2Eglyphicon%2Dglobe%3Abefore%7Bcontent%3A%22%5Ce135%22%7D%2Eglyphicon%2Dwrench%3Abefore%7Bcontent%3A%22%5Ce136%22%7D%2Eglyphicon%2Dtasks%3Abefore%7Bcontent%3A%22%5Ce137%22%7D%2Eglyphicon%2Dfilter%3Abefore%7Bcontent%3A%22%5Ce138%22%7D%2Eglyphicon%2Dbriefcase%3Abefore%7Bcontent%3A%22%5Ce139%22%7D%2Eglyphicon%2Dfullscreen%3Abefore%7Bcontent%3A%22%5Ce140%22%7D%2Eglyphicon%2Ddashboard%3Abefore%7Bcontent%3A%22%5Ce141%22%7D%2Eglyphicon%2Dpaperclip%3Abefore%7Bcontent%3A%22%5Ce142%22%7D%2Eglyphicon%2Dheart%2Dempty%3Abefore%7Bcontent%3A%22%5Ce143%22%7D%2Eglyphicon%2Dlink%3Abefore%7Bcontent%3A%22%5Ce144%22%7D%2Eglyphicon%2Dphone%3Abefore%7Bcontent%3A%22%5Ce145%22%7D%2Eglyphicon%2Dpushpin%3Abefore%7Bcontent%3A%22%5Ce146%22%7D%2Eglyphicon%2Dusd%3Abefore%7Bcontent%3A%22%5Ce148%22%7D%2Eglyphicon%2Dgbp%3Abefore%7Bcontent%3A%22%5Ce149%22%7D%2Eglyphicon%2Dsort%3Abefore%7Bcontent%3A%22%5Ce150%22%7D%2Eglyphicon%2Dsort%2Dby%2Dalphabet%3Abefore%7Bcontent%3A%22%5Ce151%22%7D%2Eglyphicon%2Dsort%2Dby%2Dalphabet%2Dalt%3Abefore%7Bcontent%3A%22%5Ce152%22%7D%2Eglyphicon%2Dsort%2Dby%2Dorder%3Abefore%7Bcontent%3A%22%5Ce153%22%7D%2Eglyphicon%2Dsort%2Dby%2Dorder%2Dalt%3Abefore%7Bcontent%3A%22%5Ce154%22%7D%2Eglyphicon%2Dsort%2Dby%2Dattributes%3Abefore%7Bcontent%3A%22%5Ce155%22%7D%2Eglyphicon%2Dsort%2Dby%2Dattributes%2Dalt%3Abefore%7Bcontent%3A%22%5Ce156%22%7D%2Eglyphicon%2Dunchecked%3Abefore%7Bcontent%3A%22%5Ce157%22%7D%2Eglyphicon%2Dexpand%3Abefore%7Bcontent%3A%22%5Ce158%22%7D%2Eglyphicon%2Dcollapse%2Ddown%3Abefore%7Bcontent%3A%22%5Ce159%22%7D%2Eglyphicon%2Dcollapse%2Dup%3Abefore%7Bcontent%3A%22%5Ce160%22%7D%2Eglyphicon%2Dlog%2Din%3Abefore%7Bcontent%3A%22%5Ce161%22%7D%2Eglyphicon%2Dflash%3Abefore%7Bcontent%3A%22%5Ce162%22%7D%2Eglyphicon%2Dlog%2Dout%3Abefore%7Bcontent%3A%22%5Ce163%22%7D%2Eglyphicon%2Dnew%2Dwindow%3Abefore%7Bcontent%3A%22%5Ce164%22%7D%2Eglyphicon%2Drecord%3Abefore%7Bcontent%3A%22%5Ce165%22%7D%2Eglyphicon%2Dsave%3Abefore%7Bcontent%3A%22%5Ce166%22%7D%2Eglyphicon%2Dopen%3Abefore%7Bcontent%3A%22%5Ce167%22%7D%2Eglyphicon%2Dsaved%3Abefore%7Bcontent%3A%22%5Ce168%22%7D%2Eglyphicon%2Dimport%3Abefore%7Bcontent%3A%22%5Ce169%22%7D%2Eglyphicon%2Dexport%3Abefore%7Bcontent%3A%22%5Ce170%22%7D%2Eglyphicon%2Dsend%3Abefore%7Bcontent%3A%22%5Ce171%22%7D%2Eglyphicon%2Dfloppy%2Ddisk%3Abefore%7Bcontent%3A%22%5Ce172%22%7D%2Eglyphicon%2Dfloppy%2Dsaved%3Abefore%7Bcontent%3A%22%5Ce173%22%7D%2Eglyphicon%2Dfloppy%2Dremove%3Abefore%7Bcontent%3A%22%5Ce174%22%7D%2Eglyphicon%2Dfloppy%2Dsave%3Abefore%7Bcontent%3A%22%5Ce175%22%7D%2Eglyphicon%2Dfloppy%2Dopen%3Abefore%7Bcontent%3A%22%5Ce176%22%7D%2Eglyphicon%2Dcredit%2Dcard%3Abefore%7Bcontent%3A%22%5Ce177%22%7D%2Eglyphicon%2Dtransfer%3Abefore%7Bcontent%3A%22%5Ce178%22%7D%2Eglyphicon%2Dcutlery%3Abefore%7Bcontent%3A%22%5Ce179%22%7D%2Eglyphicon%2Dheader%3Abefore%7Bcontent%3A%22%5Ce180%22%7D%2Eglyphicon%2Dcompressed%3Abefore%7Bcontent%3A%22%5Ce181%22%7D%2Eglyphicon%2Dearphone%3Abefore%7Bcontent%3A%22%5Ce182%22%7D%2Eglyphicon%2Dphone%2Dalt%3Abefore%7Bcontent%3A%22%5Ce183%22%7D%2Eglyphicon%2Dtower%3Abefore%7Bcontent%3A%22%5Ce184%22%7D%2Eglyphicon%2Dstats%3Abefore%7Bcontent%3A%22%5Ce185%22%7D%2Eglyphicon%2Dsd%2Dvideo%3Abefore%7Bcontent%3A%22%5Ce186%22%7D%2Eglyphicon%2Dhd%2Dvideo%3Abefore%7Bcontent%3A%22%5Ce187%22%7D%2Eglyphicon%2Dsubtitles%3Abefore%7Bcontent%3A%22%5Ce188%22%7D%2Eglyphicon%2Dsound%2Dstereo%3Abefore%7Bcontent%3A%22%5Ce189%22%7D%2Eglyphicon%2Dsound%2Ddolby%3Abefore%7Bcontent%3A%22%5Ce190%22%7D%2Eglyphicon%2Dsound%2D5%2D1%3Abefore%7Bcontent%3A%22%5Ce191%22%7D%2Eglyphicon%2Dsound%2D6%2D1%3Abefore%7Bcontent%3A%22%5Ce192%22%7D%2Eglyphicon%2Dsound%2D7%2D1%3Abefore%7Bcontent%3A%22%5Ce193%22%7D%2Eglyphicon%2Dcopyright%2Dmark%3Abefore%7Bcontent%3A%22%5Ce194%22%7D%2Eglyphicon%2Dregistration%2Dmark%3Abefore%7Bcontent%3A%22%5Ce195%22%7D%2Eglyphicon%2Dcloud%2Ddownload%3Abefore%7Bcontent%3A%22%5Ce197%22%7D%2Eglyphicon%2Dcloud%2Dupload%3Abefore%7Bcontent%3A%22%5Ce198%22%7D%2Eglyphicon%2Dtree%2Dconifer%3Abefore%7Bcontent%3A%22%5Ce199%22%7D%2Eglyphicon%2Dtree%2Ddeciduous%3Abefore%7Bcontent%3A%22%5Ce200%22%7D%2Eglyphicon%2Dcd%3Abefore%7Bcontent%3A%22%5Ce201%22%7D%2Eglyphicon%2Dsave%2Dfile%3Abefore%7Bcontent%3A%22%5Ce202%22%7D%2Eglyphicon%2Dopen%2Dfile%3Abefore%7Bcontent%3A%22%5Ce203%22%7D%2Eglyphicon%2Dlevel%2Dup%3Abefore%7Bcontent%3A%22%5Ce204%22%7D%2Eglyphicon%2Dcopy%3Abefore%7Bcontent%3A%22%5Ce205%22%7D%2Eglyphicon%2Dpaste%3Abefore%7Bcontent%3A%22%5Ce206%22%7D%2Eglyphicon%2Dalert%3Abefore%7Bcontent%3A%22%5Ce209%22%7D%2Eglyphicon%2Dequalizer%3Abefore%7Bcontent%3A%22%5Ce210%22%7D%2Eglyphicon%2Dking%3Abefore%7Bcontent%3A%22%5Ce211%22%7D%2Eglyphicon%2Dqueen%3Abefore%7Bcontent%3A%22%5Ce212%22%7D%2Eglyphicon%2Dpawn%3Abefore%7Bcontent%3A%22%5Ce213%22%7D%2Eglyphicon%2Dbishop%3Abefore%7Bcontent%3A%22%5Ce214%22%7D%2Eglyphicon%2Dknight%3Abefore%7Bcontent%3A%22%5Ce215%22%7D%2Eglyphicon%2Dbaby%2Dformula%3Abefore%7Bcontent%3A%22%5Ce216%22%7D%2Eglyphicon%2Dtent%3Abefore%7Bcontent%3A%22%5C26fa%22%7D%2Eglyphicon%2Dblackboard%3Abefore%7Bcontent%3A%22%5Ce218%22%7D%2Eglyphicon%2Dbed%3Abefore%7Bcontent%3A%22%5Ce219%22%7D%2Eglyphicon%2Dapple%3Abefore%7Bcontent%3A%22%5Cf8ff%22%7D%2Eglyphicon%2Derase%3Abefore%7Bcontent%3A%22%5Ce221%22%7D%2Eglyphicon%2Dhourglass%3Abefore%7Bcontent%3A%22%5C231b%22%7D%2Eglyphicon%2Dlamp%3Abefore%7Bcontent%3A%22%5Ce223%22%7D%2Eglyphicon%2Dduplicate%3Abefore%7Bcontent%3A%22%5Ce224%22%7D%2Eglyphicon%2Dpiggy%2Dbank%3Abefore%7Bcontent%3A%22%5Ce225%22%7D%2Eglyphicon%2Dscissors%3Abefore%7Bcontent%3A%22%5Ce226%22%7D%2Eglyphicon%2Dbitcoin%3Abefore%7Bcontent%3A%22%5Ce227%22%7D%2Eglyphicon%2Dbtc%3Abefore%7Bcontent%3A%22%5Ce227%22%7D%2Eglyphicon%2Dxbt%3Abefore%7Bcontent%3A%22%5Ce227%22%7D%2Eglyphicon%2Dyen%3Abefore%7Bcontent%3A%22%5C00a5%22%7D%2Eglyphicon%2Djpy%3Abefore%7Bcontent%3A%22%5C00a5%22%7D%2Eglyphicon%2Druble%3Abefore%7Bcontent%3A%22%5C20bd%22%7D%2Eglyphicon%2Drub%3Abefore%7Bcontent%3A%22%5C20bd%22%7D%2Eglyphicon%2Dscale%3Abefore%7Bcontent%3A%22%5Ce230%22%7D%2Eglyphicon%2Dice%2Dlolly%3Abefore%7Bcontent%3A%22%5Ce231%22%7D%2Eglyphicon%2Dice%2Dlolly%2Dtasted%3Abefore%7Bcontent%3A%22%5Ce232%22%7D%2Eglyphicon%2Deducation%3Abefore%7Bcontent%3A%22%5Ce233%22%7D%2Eglyphicon%2Doption%2Dhorizontal%3Abefore%7Bcontent%3A%22%5Ce234%22%7D%2Eglyphicon%2Doption%2Dvertical%3Abefore%7Bcontent%3A%22%5Ce235%22%7D%2Eglyphicon%2Dmenu%2Dhamburger%3Abefore%7Bcontent%3A%22%5Ce236%22%7D%2Eglyphicon%2Dmodal%2Dwindow%3Abefore%7Bcontent%3A%22%5Ce237%22%7D%2Eglyphicon%2Doil%3Abefore%7Bcontent%3A%22%5Ce238%22%7D%2Eglyphicon%2Dgrain%3Abefore%7Bcontent%3A%22%5Ce239%22%7D%2Eglyphicon%2Dsunglasses%3Abefore%7Bcontent%3A%22%5Ce240%22%7D%2Eglyphicon%2Dtext%2Dsize%3Abefore%7Bcontent%3A%22%5Ce241%22%7D%2Eglyphicon%2Dtext%2Dcolor%3Abefore%7Bcontent%3A%22%5Ce242%22%7D%2Eglyphicon%2Dtext%2Dbackground%3Abefore%7Bcontent%3A%22%5Ce243%22%7D%2Eglyphicon%2Dobject%2Dalign%2Dtop%3Abefore%7Bcontent%3A%22%5Ce244%22%7D%2Eglyphicon%2Dobject%2Dalign%2Dbottom%3Abefore%7Bcontent%3A%22%5Ce245%22%7D%2Eglyphicon%2Dobject%2Dalign%2Dhorizontal%3Abefore%7Bcontent%3A%22%5Ce246%22%7D%2Eglyphicon%2Dobject%2Dalign%2Dleft%3Abefore%7Bcontent%3A%22%5Ce247%22%7D%2Eglyphicon%2Dobject%2Dalign%2Dvertical%3Abefore%7Bcontent%3A%22%5Ce248%22%7D%2Eglyphicon%2Dobject%2Dalign%2Dright%3Abefore%7Bcontent%3A%22%5Ce249%22%7D%2Eglyphicon%2Dtriangle%2Dright%3Abefore%7Bcontent%3A%22%5Ce250%22%7D%2Eglyphicon%2Dtriangle%2Dleft%3Abefore%7Bcontent%3A%22%5Ce251%22%7D%2Eglyphicon%2Dtriangle%2Dbottom%3Abefore%7Bcontent%3A%22%5Ce252%22%7D%2Eglyphicon%2Dtriangle%2Dtop%3Abefore%7Bcontent%3A%22%5Ce253%22%7D%2Eglyphicon%2Dconsole%3Abefore%7Bcontent%3A%22%5Ce254%22%7D%2Eglyphicon%2Dsuperscript%3Abefore%7Bcontent%3A%22%5Ce255%22%7D%2Eglyphicon%2Dsubscript%3Abefore%7Bcontent%3A%22%5Ce256%22%7D%2Eglyphicon%2Dmenu%2Dleft%3Abefore%7Bcontent%3A%22%5Ce257%22%7D%2Eglyphicon%2Dmenu%2Dright%3Abefore%7Bcontent%3A%22%5Ce258%22%7D%2Eglyphicon%2Dmenu%2Ddown%3Abefore%7Bcontent%3A%22%5Ce259%22%7D%2Eglyphicon%2Dmenu%2Dup%3Abefore%7Bcontent%3A%22%5Ce260%22%7D%2A%7B%2Dwebkit%2Dbox%2Dsizing%3Aborder%2Dbox%3B%2Dmoz%2Dbox%2Dsizing%3Aborder%2Dbox%3Bbox%2Dsizing%3Aborder%2Dbox%7D%3Aafter%2C%3Abefore%7B%2Dwebkit%2Dbox%2Dsizing%3Aborder%2Dbox%3B%2Dmoz%2Dbox%2Dsizing%3Aborder%2Dbox%3Bbox%2Dsizing%3Aborder%2Dbox%7Dhtml%7Bfont%2Dsize%3A10px%3B%2Dwebkit%2Dtap%2Dhighlight%2Dcolor%3Argba%280%2C0%2C0%2C0%29%7Dbody%7Bfont%2Dfamily%3A%22Helvetica%20Neue%22%2CHelvetica%2CArial%2Csans%2Dserif%3Bfont%2Dsize%3A14px%3Bline%2Dheight%3A1%2E42857143%3Bcolor%3A%23333%3Bbackground%2Dcolor%3A%23fff%7Dbutton%2Cinput%2Cselect%2Ctextarea%7Bfont%2Dfamily%3Ainherit%3Bfont%2Dsize%3Ainherit%3Bline%2Dheight%3Ainherit%7Da%7Bcolor%3A%23337ab7%3Btext%2Ddecoration%3Anone%7Da%3Afocus%2Ca%3Ahover%7Bcolor%3A%2323527c%3Btext%2Ddecoration%3Aunderline%7Da%3Afocus%7Boutline%3Athin%20dotted%3Boutline%3A5px%20auto%20%2Dwebkit%2Dfocus%2Dring%2Dcolor%3Boutline%2Doffset%3A%2D2px%7Dfigure%7Bmargin%3A0%7Dimg%7Bvertical%2Dalign%3Amiddle%7D%2Ecarousel%2Dinner%3E%2Eitem%3Ea%3Eimg%2C%2Ecarousel%2Dinner%3E%2Eitem%3Eimg%2C%2Eimg%2Dresponsive%2C%2Ethumbnail%20a%3Eimg%2C%2Ethumbnail%3Eimg%7Bdisplay%3Ablock%3Bmax%2Dwidth%3A100%25%3Bheight%3Aauto%7D%2Eimg%2Drounded%7Bborder%2Dradius%3A6px%7D%2Eimg%2Dthumbnail%7Bdisplay%3Ainline%2Dblock%3Bmax%2Dwidth%3A100%25%3Bheight%3Aauto%3Bpadding%3A4px%3Bline%2Dheight%3A1%2E42857143%3Bbackground%2Dcolor%3A%23fff%3Bborder%3A1px%20solid%20%23ddd%3Bborder%2Dradius%3A4px%3B%2Dwebkit%2Dtransition%3Aall%20%2E2s%20ease%2Din%2Dout%3B%2Do%2Dtransition%3Aall%20%2E2s%20ease%2Din%2Dout%3Btransition%3Aall%20%2E2s%20ease%2Din%2Dout%7D%2Eimg%2Dcircle%7Bborder%2Dradius%3A50%25%7Dhr%7Bmargin%2Dtop%3A20px%3Bmargin%2Dbottom%3A20px%3Bborder%3A0%3Bborder%2Dtop%3A1px%20solid%20%23eee%7D%2Esr%2Donly%7Bposition%3Aabsolute%3Bwidth%3A1px%3Bheight%3A1px%3Bpadding%3A0%3Bmargin%3A%2D1px%3Boverflow%3Ahidden%3Bclip%3Arect%280%2C0%2C0%2C0%29%3Bborder%3A0%7D%2Esr%2Donly%2Dfocusable%3Aactive%2C%2Esr%2Donly%2Dfocusable%3Afocus%7Bposition%3Astatic%3Bwidth%3Aauto%3Bheight%3Aauto%3Bmargin%3A0%3Boverflow%3Avisible%3Bclip%3Aauto%7D%5Brole%3Dbutton%5D%7Bcursor%3Apointer%7D%2Eh1%2C%2Eh2%2C%2Eh3%2C%2Eh4%2C%2Eh5%2C%2Eh6%2Ch1%2Ch2%2Ch3%2Ch4%2Ch5%2Ch6%7Bfont%2Dfamily%3Ainherit%3Bfont%2Dweight%3A500%3Bline%2Dheight%3A1%2E1%3Bcolor%3Ainherit%7D%2Eh1%20%2Esmall%2C%2Eh1%20small%2C%2Eh2%20%2Esmall%2C%2Eh2%20small%2C%2Eh3%20%2Esmall%2C%2Eh3%20small%2C%2Eh4%20%2Esmall%2C%2Eh4%20small%2C%2Eh5%20%2Esmall%2C%2Eh5%20small%2C%2Eh6%20%2Esmall%2C%2Eh6%20small%2Ch1%20%2Esmall%2Ch1%20small%2Ch2%20%2Esmall%2Ch2%20small%2Ch3%20%2Esmall%2Ch3%20small%2Ch4%20%2Esmall%2Ch4%20small%2Ch5%20%2Esmall%2Ch5%20small%2Ch6%20%2Esmall%2Ch6%20small%7Bfont%2Dweight%3A400%3Bline%2Dheight%3A1%3Bcolor%3A%23777%7D%2Eh1%2C%2Eh2%2C%2Eh3%2Ch1%2Ch2%2Ch3%7Bmargin%2Dtop%3A20px%3Bmargin%2Dbottom%3A10px%7D%2Eh1%20%2Esmall%2C%2Eh1%20small%2C%2Eh2%20%2Esmall%2C%2Eh2%20small%2C%2Eh3%20%2Esmall%2C%2Eh3%20small%2Ch1%20%2Esmall%2Ch1%20small%2Ch2%20%2Esmall%2Ch2%20small%2Ch3%20%2Esmall%2Ch3%20small%7Bfont%2Dsize%3A65%25%7D%2Eh4%2C%2Eh5%2C%2Eh6%2Ch4%2Ch5%2Ch6%7Bmargin%2Dtop%3A10px%3Bmargin%2Dbottom%3A10px%7D%2Eh4%20%2Esmall%2C%2Eh4%20small%2C%2Eh5%20%2Esmall%2C%2Eh5%20small%2C%2Eh6%20%2Esmall%2C%2Eh6%20small%2Ch4%20%2Esmall%2Ch4%20small%2Ch5%20%2Esmall%2Ch5%20small%2Ch6%20%2Esmall%2Ch6%20small%7Bfont%2Dsize%3A75%25%7D%2Eh1%2Ch1%7Bfont%2Dsize%3A36px%7D%2Eh2%2Ch2%7Bfont%2Dsize%3A30px%7D%2Eh3%2Ch3%7Bfont%2Dsize%3A24px%7D%2Eh4%2Ch4%7Bfont%2Dsize%3A18px%7D%2Eh5%2Ch5%7Bfont%2Dsize%3A14px%7D%2Eh6%2Ch6%7Bfont%2Dsize%3A12px%7Dp%7Bmargin%3A0%200%2010px%7D%2Elead%7Bmargin%2Dbottom%3A20px%3Bfont%2Dsize%3A16px%3Bfont%2Dweight%3A300%3Bline%2Dheight%3A1%2E4%7D%40media%20%28min%2Dwidth%3A768px%29%7B%2Elead%7Bfont%2Dsize%3A21px%7D%7D%2Esmall%2Csmall%7Bfont%2Dsize%3A85%25%7D%2Emark%2Cmark%7Bpadding%3A%2E2em%3Bbackground%2Dcolor%3A%23fcf8e3%7D%2Etext%2Dleft%7Btext%2Dalign%3Aleft%7D%2Etext%2Dright%7Btext%2Dalign%3Aright%7D%2Etext%2Dcenter%7Btext%2Dalign%3Acenter%7D%2Etext%2Djustify%7Btext%2Dalign%3Ajustify%7D%2Etext%2Dnowrap%7Bwhite%2Dspace%3Anowrap%7D%2Etext%2Dlowercase%7Btext%2Dtransform%3Alowercase%7D%2Etext%2Duppercase%7Btext%2Dtransform%3Auppercase%7D%2Etext%2Dcapitalize%7Btext%2Dtransform%3Acapitalize%7D%2Etext%2Dmuted%7Bcolor%3A%23777%7D%2Etext%2Dprimary%7Bcolor%3A%23337ab7%7Da%2Etext%2Dprimary%3Afocus%2Ca%2Etext%2Dprimary%3Ahover%7Bcolor%3A%23286090%7D%2Etext%2Dsuccess%7Bcolor%3A%233c763d%7Da%2Etext%2Dsuccess%3Afocus%2Ca%2Etext%2Dsuccess%3Ahover%7Bcolor%3A%232b542c%7D%2Etext%2Dinfo%7Bcolor%3A%2331708f%7Da%2Etext%2Dinfo%3Afocus%2Ca%2Etext%2Dinfo%3Ahover%7Bcolor%3A%23245269%7D%2Etext%2Dwarning%7Bcolor%3A%238a6d3b%7Da%2Etext%2Dwarning%3Afocus%2Ca%2Etext%2Dwarning%3Ahover%7Bcolor%3A%2366512c%7D%2Etext%2Ddanger%7Bcolor%3A%23a94442%7Da%2Etext%2Ddanger%3Afocus%2Ca%2Etext%2Ddanger%3Ahover%7Bcolor%3A%23843534%7D%2Ebg%2Dprimary%7Bcolor%3A%23fff%3Bbackground%2Dcolor%3A%23337ab7%7Da%2Ebg%2Dprimary%3Afocus%2Ca%2Ebg%2Dprimary%3Ahover%7Bbackground%2Dcolor%3A%23286090%7D%2Ebg%2Dsuccess%7Bbackground%2Dcolor%3A%23dff0d8%7Da%2Ebg%2Dsuccess%3Afocus%2Ca%2Ebg%2Dsuccess%3Ahover%7Bbackground%2Dcolor%3A%23c1e2b3%7D%2Ebg%2Dinfo%7Bbackground%2Dcolor%3A%23d9edf7%7Da%2Ebg%2Dinfo%3Afocus%2Ca%2Ebg%2Dinfo%3Ahover%7Bbackground%2Dcolor%3A%23afd9ee%7D%2Ebg%2Dwarning%7Bbackground%2Dcolor%3A%23fcf8e3%7Da%2Ebg%2Dwarning%3Afocus%2Ca%2Ebg%2Dwarning%3Ahover%7Bbackground%2Dcolor%3A%23f7ecb5%7D%2Ebg%2Ddanger%7Bbackground%2Dcolor%3A%23f2dede%7Da%2Ebg%2Ddanger%3Afocus%2Ca%2Ebg%2Ddanger%3Ahover%7Bbackground%2Dcolor%3A%23e4b9b9%7D%2Epage%2Dheader%7Bpadding%2Dbottom%3A9px%3Bmargin%3A40px%200%2020px%3Bborder%2Dbottom%3A1px%20solid%20%23eee%7Dol%2Cul%7Bmargin%2Dtop%3A0%3Bmargin%2Dbottom%3A10px%7Dol%20ol%2Col%20ul%2Cul%20ol%2Cul%20ul%7Bmargin%2Dbottom%3A0%7D%2Elist%2Dunstyled%7Bpadding%2Dleft%3A0%3Blist%2Dstyle%3Anone%7D%2Elist%2Dinline%7Bpadding%2Dleft%3A0%3Bmargin%2Dleft%3A%2D5px%3Blist%2Dstyle%3Anone%7D%2Elist%2Dinline%3Eli%7Bdisplay%3Ainline%2Dblock%3Bpadding%2Dright%3A5px%3Bpadding%2Dleft%3A5px%7Ddl%7Bmargin%2Dtop%3A0%3Bmargin%2Dbottom%3A20px%7Ddd%2Cdt%7Bline%2Dheight%3A1%2E42857143%7Ddt%7Bfont%2Dweight%3A700%7Ddd%7Bmargin%2Dleft%3A0%7D%40media%20%28min%2Dwidth%3A768px%29%7B%2Edl%2Dhorizontal%20dt%7Bfloat%3Aleft%3Bwidth%3A160px%3Boverflow%3Ahidden%3Bclear%3Aleft%3Btext%2Dalign%3Aright%3Btext%2Doverflow%3Aellipsis%3Bwhite%2Dspace%3Anowrap%7D%2Edl%2Dhorizontal%20dd%7Bmargin%2Dleft%3A180px%7D%7Dabbr%5Bdata%2Doriginal%2Dtitle%5D%2Cabbr%5Btitle%5D%7Bcursor%3Ahelp%3Bborder%2Dbottom%3A1px%20dotted%20%23777%7D%2Einitialism%7Bfont%2Dsize%3A90%25%3Btext%2Dtransform%3Auppercase%7Dblockquote%7Bpadding%3A10px%2020px%3Bmargin%3A0%200%2020px%3Bfont%2Dsize%3A17%2E5px%3Bborder%2Dleft%3A5px%20solid%20%23eee%7Dblockquote%20ol%3Alast%2Dchild%2Cblockquote%20p%3Alast%2Dchild%2Cblockquote%20ul%3Alast%2Dchild%7Bmargin%2Dbottom%3A0%7Dblockquote%20%2Esmall%2Cblockquote%20footer%2Cblockquote%20small%7Bdisplay%3Ablock%3Bfont%2Dsize%3A80%25%3Bline%2Dheight%3A1%2E42857143%3Bcolor%3A%23777%7Dblockquote%20%2Esmall%3Abefore%2Cblockquote%20footer%3Abefore%2Cblockquote%20small%3Abefore%7Bcontent%3A%27%5C2014%20%5C00A0%27%7D%2Eblockquote%2Dreverse%2Cblockquote%2Epull%2Dright%7Bpadding%2Dright%3A15px%3Bpadding%2Dleft%3A0%3Btext%2Dalign%3Aright%3Bborder%2Dright%3A5px%20solid%20%23eee%3Bborder%2Dleft%3A0%7D%2Eblockquote%2Dreverse%20%2Esmall%3Abefore%2C%2Eblockquote%2Dreverse%20footer%3Abefore%2C%2Eblockquote%2Dreverse%20small%3Abefore%2Cblockquote%2Epull%2Dright%20%2Esmall%3Abefore%2Cblockquote%2Epull%2Dright%20footer%3Abefore%2Cblockquote%2Epull%2Dright%20small%3Abefore%7Bcontent%3A%27%27%7D%2Eblockquote%2Dreverse%20%2Esmall%3Aafter%2C%2Eblockquote%2Dreverse%20footer%3Aafter%2C%2Eblockquote%2Dreverse%20small%3Aafter%2Cblockquote%2Epull%2Dright%20%2Esmall%3Aafter%2Cblockquote%2Epull%2Dright%20footer%3Aafter%2Cblockquote%2Epull%2Dright%20small%3Aafter%7Bcontent%3A%27%5C00A0%20%5C2014%27%7Daddress%7Bmargin%2Dbottom%3A20px%3Bfont%2Dstyle%3Anormal%3Bline%2Dheight%3A1%2E42857143%7Dcode%2Ckbd%2Cpre%2Csamp%7Bfont%2Dfamily%3Amonospace%7Dcode%7Bpadding%3A2px%204px%3Bfont%2Dsize%3A90%25%3Bcolor%3A%23c7254e%3Bbackground%2Dcolor%3A%23f9f2f4%3Bborder%2Dradius%3A4px%7Dkbd%7Bpadding%3A2px%204px%3Bfont%2Dsize%3A90%25%3Bcolor%3A%23fff%3Bbackground%2Dcolor%3A%23333%3Bborder%2Dradius%3A3px%3B%2Dwebkit%2Dbox%2Dshadow%3Ainset%200%20%2D1px%200%20rgba%280%2C0%2C0%2C%2E25%29%3Bbox%2Dshadow%3Ainset%200%20%2D1px%200%20rgba%280%2C0%2C0%2C%2E25%29%7Dkbd%20kbd%7Bpadding%3A0%3Bfont%2Dsize%3A100%25%3Bfont%2Dweight%3A700%3B%2Dwebkit%2Dbox%2Dshadow%3Anone%3Bbox%2Dshadow%3Anone%7Dpre%7Bdisplay%3Ablock%3Bpadding%3A9%2E5px%3Bmargin%3A0%200%2010px%3Bfont%2Dsize%3A13px%3Bline%2Dheight%3A1%2E42857143%3Bcolor%3A%23333%3Bword%2Dbreak%3Abreak%2Dall%3Bword%2Dwrap%3Abreak%2Dword%3Bbackground%2Dcolor%3A%23f5f5f5%3Bborder%3A1px%20solid%20%23ccc%3Bborder%2Dradius%3A4px%7Dpre%20code%7Bpadding%3A0%3Bfont%2Dsize%3Ainherit%3Bcolor%3Ainherit%3Bwhite%2Dspace%3Apre%2Dwrap%3Bbackground%2Dcolor%3Atransparent%3Bborder%2Dradius%3A0%7D%2Epre%2Dscrollable%7Bmax%2Dheight%3A340px%3Boverflow%2Dy%3Ascroll%7D%2Econtainer%7Bpadding%2Dright%3A15px%3Bpadding%2Dleft%3A15px%3Bmargin%2Dright%3Aauto%3Bmargin%2Dleft%3Aauto%7D%40media%20%28min%2Dwidth%3A768px%29%7B%2Econtainer%7Bwidth%3A750px%7D%7D%40media%20%28min%2Dwidth%3A992px%29%7B%2Econtainer%7Bwidth%3A970px%7D%7D%40media%20%28min%2Dwidth%3A1200px%29%7B%2Econtainer%7Bwidth%3A1170px%7D%7D%2Econtainer%2Dfluid%7Bpadding%2Dright%3A15px%3Bpadding%2Dleft%3A15px%3Bmargin%2Dright%3Aauto%3Bmargin%2Dleft%3Aauto%7D%2Erow%7Bmargin%2Dright%3A%2D15px%3Bmargin%2Dleft%3A%2D15px%7D%2Ecol%2Dlg%2D1%2C%2Ecol%2Dlg%2D10%2C%2Ecol%2Dlg%2D11%2C%2Ecol%2Dlg%2D12%2C%2Ecol%2Dlg%2D2%2C%2Ecol%2Dlg%2D3%2C%2Ecol%2Dlg%2D4%2C%2Ecol%2Dlg%2D5%2C%2Ecol%2Dlg%2D6%2C%2Ecol%2Dlg%2D7%2C%2Ecol%2Dlg%2D8%2C%2Ecol%2Dlg%2D9%2C%2Ecol%2Dmd%2D1%2C%2Ecol%2Dmd%2D10%2C%2Ecol%2Dmd%2D11%2C%2Ecol%2Dmd%2D12%2C%2Ecol%2Dmd%2D2%2C%2Ecol%2Dmd%2D3%2C%2Ecol%2Dmd%2D4%2C%2Ecol%2Dmd%2D5%2C%2Ecol%2Dmd%2D6%2C%2Ecol%2Dmd%2D7%2C%2Ecol%2Dmd%2D8%2C%2Ecol%2Dmd%2D9%2C%2Ecol%2Dsm%2D1%2C%2Ecol%2Dsm%2D10%2C%2Ecol%2Dsm%2D11%2C%2Ecol%2Dsm%2D12%2C%2Ecol%2Dsm%2D2%2C%2Ecol%2Dsm%2D3%2C%2Ecol%2Dsm%2D4%2C%2Ecol%2Dsm%2D5%2C%2Ecol%2Dsm%2D6%2C%2Ecol%2Dsm%2D7%2C%2Ecol%2Dsm%2D8%2C%2Ecol%2Dsm%2D9%2C%2Ecol%2Dxs%2D1%2C%2Ecol%2Dxs%2D10%2C%2Ecol%2Dxs%2D11%2C%2Ecol%2Dxs%2D12%2C%2Ecol%2Dxs%2D2%2C%2Ecol%2Dxs%2D3%2C%2Ecol%2Dxs%2D4%2C%2Ecol%2Dxs%2D5%2C%2Ecol%2Dxs%2D6%2C%2Ecol%2Dxs%2D7%2C%2Ecol%2Dxs%2D8%2C%2Ecol%2Dxs%2D9%7Bposition%3Arelative%3Bmin%2Dheight%3A1px%3Bpadding%2Dright%3A15px%3Bpadding%2Dleft%3A15px%7D%2Ecol%2Dxs%2D1%2C%2Ecol%2Dxs%2D10%2C%2Ecol%2Dxs%2D11%2C%2Ecol%2Dxs%2D12%2C%2Ecol%2Dxs%2D2%2C%2Ecol%2Dxs%2D3%2C%2Ecol%2Dxs%2D4%2C%2Ecol%2Dxs%2D5%2C%2Ecol%2Dxs%2D6%2C%2Ecol%2Dxs%2D7%2C%2Ecol%2Dxs%2D8%2C%2Ecol%2Dxs%2D9%7Bfloat%3Aleft%7D%2Ecol%2Dxs%2D12%7Bwidth%3A100%25%7D%2Ecol%2Dxs%2D11%7Bwidth%3A91%2E66666667%25%7D%2Ecol%2Dxs%2D10%7Bwidth%3A83%2E33333333%25%7D%2Ecol%2Dxs%2D9%7Bwidth%3A75%25%7D%2Ecol%2Dxs%2D8%7Bwidth%3A66%2E66666667%25%7D%2Ecol%2Dxs%2D7%7Bwidth%3A58%2E33333333%25%7D%2Ecol%2Dxs%2D6%7Bwidth%3A50%25%7D%2Ecol%2Dxs%2D5%7Bwidth%3A41%2E66666667%25%7D%2Ecol%2Dxs%2D4%7Bwidth%3A33%2E33333333%25%7D%2Ecol%2Dxs%2D3%7Bwidth%3A25%25%7D%2Ecol%2Dxs%2D2%7Bwidth%3A16%2E66666667%25%7D%2Ecol%2Dxs%2D1%7Bwidth%3A8%2E33333333%25%7D%2Ecol%2Dxs%2Dpull%2D12%7Bright%3A100%25%7D%2Ecol%2Dxs%2Dpull%2D11%7Bright%3A91%2E66666667%25%7D%2Ecol%2Dxs%2Dpull%2D10%7Bright%3A83%2E33333333%25%7D%2Ecol%2Dxs%2Dpull%2D9%7Bright%3A75%25%7D%2Ecol%2Dxs%2Dpull%2D8%7Bright%3A66%2E66666667%25%7D%2Ecol%2Dxs%2Dpull%2D7%7Bright%3A58%2E33333333%25%7D%2Ecol%2Dxs%2Dpull%2D6%7Bright%3A50%25%7D%2Ecol%2Dxs%2Dpull%2D5%7Bright%3A41%2E66666667%25%7D%2Ecol%2Dxs%2Dpull%2D4%7Bright%3A33%2E33333333%25%7D%2Ecol%2Dxs%2Dpull%2D3%7Bright%3A25%25%7D%2Ecol%2Dxs%2Dpull%2D2%7Bright%3A16%2E66666667%25%7D%2Ecol%2Dxs%2Dpull%2D1%7Bright%3A8%2E33333333%25%7D%2Ecol%2Dxs%2Dpull%2D0%7Bright%3Aauto%7D%2Ecol%2Dxs%2Dpush%2D12%7Bleft%3A100%25%7D%2Ecol%2Dxs%2Dpush%2D11%7Bleft%3A91%2E66666667%25%7D%2Ecol%2Dxs%2Dpush%2D10%7Bleft%3A83%2E33333333%25%7D%2Ecol%2Dxs%2Dpush%2D9%7Bleft%3A75%25%7D%2Ecol%2Dxs%2Dpush%2D8%7Bleft%3A66%2E66666667%25%7D%2Ecol%2Dxs%2Dpush%2D7%7Bleft%3A58%2E33333333%25%7D%2Ecol%2Dxs%2Dpush%2D6%7Bleft%3A50%25%7D%2Ecol%2Dxs%2Dpush%2D5%7Bleft%3A41%2E66666667%25%7D%2Ecol%2Dxs%2Dpush%2D4%7Bleft%3A33%2E33333333%25%7D%2Ecol%2Dxs%2Dpush%2D3%7Bleft%3A25%25%7D%2Ecol%2Dxs%2Dpush%2D2%7Bleft%3A16%2E66666667%25%7D%2Ecol%2Dxs%2Dpush%2D1%7Bleft%3A8%2E33333333%25%7D%2Ecol%2Dxs%2Dpush%2D0%7Bleft%3Aauto%7D%2Ecol%2Dxs%2Doffset%2D12%7Bmargin%2Dleft%3A100%25%7D%2Ecol%2Dxs%2Doffset%2D11%7Bmargin%2Dleft%3A91%2E66666667%25%7D%2Ecol%2Dxs%2Doffset%2D10%7Bmargin%2Dleft%3A83%2E33333333%25%7D%2Ecol%2Dxs%2Doffset%2D9%7Bmargin%2Dleft%3A75%25%7D%2Ecol%2Dxs%2Doffset%2D8%7Bmargin%2Dleft%3A66%2E66666667%25%7D%2Ecol%2Dxs%2Doffset%2D7%7Bmargin%2Dleft%3A58%2E33333333%25%7D%2Ecol%2Dxs%2Doffset%2D6%7Bmargin%2Dleft%3A50%25%7D%2Ecol%2Dxs%2Doffset%2D5%7Bmargin%2Dleft%3A41%2E66666667%25%7D%2Ecol%2Dxs%2Doffset%2D4%7Bmargin%2Dleft%3A33%2E33333333%25%7D%2Ecol%2Dxs%2Doffset%2D3%7Bmargin%2Dleft%3A25%25%7D%2Ecol%2Dxs%2Doffset%2D2%7Bmargin%2Dleft%3A16%2E66666667%25%7D%2Ecol%2Dxs%2Doffset%2D1%7Bmargin%2Dleft%3A8%2E33333333%25%7D%2Ecol%2Dxs%2Doffset%2D0%7Bmargin%2Dleft%3A0%7D%40media%20%28min%2Dwidth%3A768px%29%7B%2Ecol%2Dsm%2D1%2C%2Ecol%2Dsm%2D10%2C%2Ecol%2Dsm%2D11%2C%2Ecol%2Dsm%2D12%2C%2Ecol%2Dsm%2D2%2C%2Ecol%2Dsm%2D3%2C%2Ecol%2Dsm%2D4%2C%2Ecol%2Dsm%2D5%2C%2Ecol%2Dsm%2D6%2C%2Ecol%2Dsm%2D7%2C%2Ecol%2Dsm%2D8%2C%2Ecol%2Dsm%2D9%7Bfloat%3Aleft%7D%2Ecol%2Dsm%2D12%7Bwidth%3A100%25%7D%2Ecol%2Dsm%2D11%7Bwidth%3A91%2E66666667%25%7D%2Ecol%2Dsm%2D10%7Bwidth%3A83%2E33333333%25%7D%2Ecol%2Dsm%2D9%7Bwidth%3A75%25%7D%2Ecol%2Dsm%2D8%7Bwidth%3A66%2E66666667%25%7D%2Ecol%2Dsm%2D7%7Bwidth%3A58%2E33333333%25%7D%2Ecol%2Dsm%2D6%7Bwidth%3A50%25%7D%2Ecol%2Dsm%2D5%7Bwidth%3A41%2E66666667%25%7D%2Ecol%2Dsm%2D4%7Bwidth%3A33%2E33333333%25%7D%2Ecol%2Dsm%2D3%7Bwidth%3A25%25%7D%2Ecol%2Dsm%2D2%7Bwidth%3A16%2E66666667%25%7D%2Ecol%2Dsm%2D1%7Bwidth%3A8%2E33333333%25%7D%2Ecol%2Dsm%2Dpull%2D12%7Bright%3A100%25%7D%2Ecol%2Dsm%2Dpull%2D11%7Bright%3A91%2E66666667%25%7D%2Ecol%2Dsm%2Dpull%2D10%7Bright%3A83%2E33333333%25%7D%2Ecol%2Dsm%2Dpull%2D9%7Bright%3A75%25%7D%2Ecol%2Dsm%2Dpull%2D8%7Bright%3A66%2E66666667%25%7D%2Ecol%2Dsm%2Dpull%2D7%7Bright%3A58%2E33333333%25%7D%2Ecol%2Dsm%2Dpull%2D6%7Bright%3A50%25%7D%2Ecol%2Dsm%2Dpull%2D5%7Bright%3A41%2E66666667%25%7D%2Ecol%2Dsm%2Dpull%2D4%7Bright%3A33%2E33333333%25%7D%2Ecol%2Dsm%2Dpull%2D3%7Bright%3A25%25%7D%2Ecol%2Dsm%2Dpull%2D2%7Bright%3A16%2E66666667%25%7D%2Ecol%2Dsm%2Dpull%2D1%7Bright%3A8%2E33333333%25%7D%2Ecol%2Dsm%2Dpull%2D0%7Bright%3Aauto%7D%2Ecol%2Dsm%2Dpush%2D12%7Bleft%3A100%25%7D%2Ecol%2Dsm%2Dpush%2D11%7Bleft%3A91%2E66666667%25%7D%2Ecol%2Dsm%2Dpush%2D10%7Bleft%3A83%2E33333333%25%7D%2Ecol%2Dsm%2Dpush%2D9%7Bleft%3A75%25%7D%2Ecol%2Dsm%2Dpush%2D8%7Bleft%3A66%2E66666667%25%7D%2Ecol%2Dsm%2Dpush%2D7%7Bleft%3A58%2E33333333%25%7D%2Ecol%2Dsm%2Dpush%2D6%7Bleft%3A50%25%7D%2Ecol%2Dsm%2Dpush%2D5%7Bleft%3A41%2E66666667%25%7D%2Ecol%2Dsm%2Dpush%2D4%7Bleft%3A33%2E33333333%25%7D%2Ecol%2Dsm%2Dpush%2D3%7Bleft%3A25%25%7D%2Ecol%2Dsm%2Dpush%2D2%7Bleft%3A16%2E66666667%25%7D%2Ecol%2Dsm%2Dpush%2D1%7Bleft%3A8%2E33333333%25%7D%2Ecol%2Dsm%2Dpush%2D0%7Bleft%3Aauto%7D%2Ecol%2Dsm%2Doffset%2D12%7Bmargin%2Dleft%3A100%25%7D%2Ecol%2Dsm%2Doffset%2D11%7Bmargin%2Dleft%3A91%2E66666667%25%7D%2Ecol%2Dsm%2Doffset%2D10%7Bmargin%2Dleft%3A83%2E33333333%25%7D%2Ecol%2Dsm%2Doffset%2D9%7Bmargin%2Dleft%3A75%25%7D%2Ecol%2Dsm%2Doffset%2D8%7Bmargin%2Dleft%3A66%2E66666667%25%7D%2Ecol%2Dsm%2Doffset%2D7%7Bmargin%2Dleft%3A58%2E33333333%25%7D%2Ecol%2Dsm%2Doffset%2D6%7Bmargin%2Dleft%3A50%25%7D%2Ecol%2Dsm%2Doffset%2D5%7Bmargin%2Dleft%3A41%2E66666667%25%7D%2Ecol%2Dsm%2Doffset%2D4%7Bmargin%2Dleft%3A33%2E33333333%25%7D%2Ecol%2Dsm%2Doffset%2D3%7Bmargin%2Dleft%3A25%25%7D%2Ecol%2Dsm%2Doffset%2D2%7Bmargin%2Dleft%3A16%2E66666667%25%7D%2Ecol%2Dsm%2Doffset%2D1%7Bmargin%2Dleft%3A8%2E33333333%25%7D%2Ecol%2Dsm%2Doffset%2D0%7Bmargin%2Dleft%3A0%7D%7D%40media%20%28min%2Dwidth%3A992px%29%7B%2Ecol%2Dmd%2D1%2C%2Ecol%2Dmd%2D10%2C%2Ecol%2Dmd%2D11%2C%2Ecol%2Dmd%2D12%2C%2Ecol%2Dmd%2D2%2C%2Ecol%2Dmd%2D3%2C%2Ecol%2Dmd%2D4%2C%2Ecol%2Dmd%2D5%2C%2Ecol%2Dmd%2D6%2C%2Ecol%2Dmd%2D7%2C%2Ecol%2Dmd%2D8%2C%2Ecol%2Dmd%2D9%7Bfloat%3Aleft%7D%2Ecol%2Dmd%2D12%7Bwidth%3A100%25%7D%2Ecol%2Dmd%2D11%7Bwidth%3A91%2E66666667%25%7D%2Ecol%2Dmd%2D10%7Bwidth%3A83%2E33333333%25%7D%2Ecol%2Dmd%2D9%7Bwidth%3A75%25%7D%2Ecol%2Dmd%2D8%7Bwidth%3A66%2E66666667%25%7D%2Ecol%2Dmd%2D7%7Bwidth%3A58%2E33333333%25%7D%2Ecol%2Dmd%2D6%7Bwidth%3A50%25%7D%2Ecol%2Dmd%2D5%7Bwidth%3A41%2E66666667%25%7D%2Ecol%2Dmd%2D4%7Bwidth%3A33%2E33333333%25%7D%2Ecol%2Dmd%2D3%7Bwidth%3A25%25%7D%2Ecol%2Dmd%2D2%7Bwidth%3A16%2E66666667%25%7D%2Ecol%2Dmd%2D1%7Bwidth%3A8%2E33333333%25%7D%2Ecol%2Dmd%2Dpull%2D12%7Bright%3A100%25%7D%2Ecol%2Dmd%2Dpull%2D11%7Bright%3A91%2E66666667%25%7D%2Ecol%2Dmd%2Dpull%2D10%7Bright%3A83%2E33333333%25%7D%2Ecol%2Dmd%2Dpull%2D9%7Bright%3A75%25%7D%2Ecol%2Dmd%2Dpull%2D8%7Bright%3A66%2E66666667%25%7D%2Ecol%2Dmd%2Dpull%2D7%7Bright%3A58%2E33333333%25%7D%2Ecol%2Dmd%2Dpull%2D6%7Bright%3A50%25%7D%2Ecol%2Dmd%2Dpull%2D5%7Bright%3A41%2E66666667%25%7D%2Ecol%2Dmd%2Dpull%2D4%7Bright%3A33%2E33333333%25%7D%2Ecol%2Dmd%2Dpull%2D3%7Bright%3A25%25%7D%2Ecol%2Dmd%2Dpull%2D2%7Bright%3A16%2E66666667%25%7D%2Ecol%2Dmd%2Dpull%2D1%7Bright%3A8%2E33333333%25%7D%2Ecol%2Dmd%2Dpull%2D0%7Bright%3Aauto%7D%2Ecol%2Dmd%2Dpush%2D12%7Bleft%3A100%25%7D%2Ecol%2Dmd%2Dpush%2D11%7Bleft%3A91%2E66666667%25%7D%2Ecol%2Dmd%2Dpush%2D10%7Bleft%3A83%2E33333333%25%7D%2Ecol%2Dmd%2Dpush%2D9%7Bleft%3A75%25%7D%2Ecol%2Dmd%2Dpush%2D8%7Bleft%3A66%2E66666667%25%7D%2Ecol%2Dmd%2Dpush%2D7%7Bleft%3A58%2E33333333%25%7D%2Ecol%2Dmd%2Dpush%2D6%7Bleft%3A50%25%7D%2Ecol%2Dmd%2Dpush%2D5%7Bleft%3A41%2E66666667%25%7D%2Ecol%2Dmd%2Dpush%2D4%7Bleft%3A33%2E33333333%25%7D%2Ecol%2Dmd%2Dpush%2D3%7Bleft%3A25%25%7D%2Ecol%2Dmd%2Dpush%2D2%7Bleft%3A16%2E66666667%25%7D%2Ecol%2Dmd%2Dpush%2D1%7Bleft%3A8%2E33333333%25%7D%2Ecol%2Dmd%2Dpush%2D0%7Bleft%3Aauto%7D%2Ecol%2Dmd%2Doffset%2D12%7Bmargin%2Dleft%3A100%25%7D%2Ecol%2Dmd%2Doffset%2D11%7Bmargin%2Dleft%3A91%2E66666667%25%7D%2Ecol%2Dmd%2Doffset%2D10%7Bmargin%2Dleft%3A83%2E33333333%25%7D%2Ecol%2Dmd%2Doffset%2D9%7Bmargin%2Dleft%3A75%25%7D%2Ecol%2Dmd%2Doffset%2D8%7Bmargin%2Dleft%3A66%2E66666667%25%7D%2Ecol%2Dmd%2Doffset%2D7%7Bmargin%2Dleft%3A58%2E33333333%25%7D%2Ecol%2Dmd%2Doffset%2D6%7Bmargin%2Dleft%3A50%25%7D%2Ecol%2Dmd%2Doffset%2D5%7Bmargin%2Dleft%3A41%2E66666667%25%7D%2Ecol%2Dmd%2Doffset%2D4%7Bmargin%2Dleft%3A33%2E33333333%25%7D%2Ecol%2Dmd%2Doffset%2D3%7Bmargin%2Dleft%3A25%25%7D%2Ecol%2Dmd%2Doffset%2D2%7Bmargin%2Dleft%3A16%2E66666667%25%7D%2Ecol%2Dmd%2Doffset%2D1%7Bmargin%2Dleft%3A8%2E33333333%25%7D%2Ecol%2Dmd%2Doffset%2D0%7Bmargin%2Dleft%3A0%7D%7D%40media%20%28min%2Dwidth%3A1200px%29%7B%2Ecol%2Dlg%2D1%2C%2Ecol%2Dlg%2D10%2C%2Ecol%2Dlg%2D11%2C%2Ecol%2Dlg%2D12%2C%2Ecol%2Dlg%2D2%2C%2Ecol%2Dlg%2D3%2C%2Ecol%2Dlg%2D4%2C%2Ecol%2Dlg%2D5%2C%2Ecol%2Dlg%2D6%2C%2Ecol%2Dlg%2D7%2C%2Ecol%2Dlg%2D8%2C%2Ecol%2Dlg%2D9%7Bfloat%3Aleft%7D%2Ecol%2Dlg%2D12%7Bwidth%3A100%25%7D%2Ecol%2Dlg%2D11%7Bwidth%3A91%2E66666667%25%7D%2Ecol%2Dlg%2D10%7Bwidth%3A83%2E33333333%25%7D%2Ecol%2Dlg%2D9%7Bwidth%3A75%25%7D%2Ecol%2Dlg%2D8%7Bwidth%3A66%2E66666667%25%7D%2Ecol%2Dlg%2D7%7Bwidth%3A58%2E33333333%25%7D%2Ecol%2Dlg%2D6%7Bwidth%3A50%25%7D%2Ecol%2Dlg%2D5%7Bwidth%3A41%2E66666667%25%7D%2Ecol%2Dlg%2D4%7Bwidth%3A33%2E33333333%25%7D%2Ecol%2Dlg%2D3%7Bwidth%3A25%25%7D%2Ecol%2Dlg%2D2%7Bwidth%3A16%2E66666667%25%7D%2Ecol%2Dlg%2D1%7Bwidth%3A8%2E33333333%25%7D%2Ecol%2Dlg%2Dpull%2D12%7Bright%3A100%25%7D%2Ecol%2Dlg%2Dpull%2D11%7Bright%3A91%2E66666667%25%7D%2Ecol%2Dlg%2Dpull%2D10%7Bright%3A83%2E33333333%25%7D%2Ecol%2Dlg%2Dpull%2D9%7Bright%3A75%25%7D%2Ecol%2Dlg%2Dpull%2D8%7Bright%3A66%2E66666667%25%7D%2Ecol%2Dlg%2Dpull%2D7%7Bright%3A58%2E33333333%25%7D%2Ecol%2Dlg%2Dpull%2D6%7Bright%3A50%25%7D%2Ecol%2Dlg%2Dpull%2D5%7Bright%3A41%2E66666667%25%7D%2Ecol%2Dlg%2Dpull%2D4%7Bright%3A33%2E33333333%25%7D%2Ecol%2Dlg%2Dpull%2D3%7Bright%3A25%25%7D%2Ecol%2Dlg%2Dpull%2D2%7Bright%3A16%2E66666667%25%7D%2Ecol%2Dlg%2Dpull%2D1%7Bright%3A8%2E33333333%25%7D%2Ecol%2Dlg%2Dpull%2D0%7Bright%3Aauto%7D%2Ecol%2Dlg%2Dpush%2D12%7Bleft%3A100%25%7D%2Ecol%2Dlg%2Dpush%2D11%7Bleft%3A91%2E66666667%25%7D%2Ecol%2Dlg%2Dpush%2D10%7Bleft%3A83%2E33333333%25%7D%2Ecol%2Dlg%2Dpush%2D9%7Bleft%3A75%25%7D%2Ecol%2Dlg%2Dpush%2D8%7Bleft%3A66%2E66666667%25%7D%2Ecol%2Dlg%2Dpush%2D7%7Bleft%3A58%2E33333333%25%7D%2Ecol%2Dlg%2Dpush%2D6%7Bleft%3A50%25%7D%2Ecol%2Dlg%2Dpush%2D5%7Bleft%3A41%2E66666667%25%7D%2Ecol%2Dlg%2Dpush%2D4%7Bleft%3A33%2E33333333%25%7D%2Ecol%2Dlg%2Dpush%2D3%7Bleft%3A25%25%7D%2Ecol%2Dlg%2Dpush%2D2%7Bleft%3A16%2E66666667%25%7D%2Ecol%2Dlg%2Dpush%2D1%7Bleft%3A8%2E33333333%25%7D%2Ecol%2Dlg%2Dpush%2D0%7Bleft%3Aauto%7D%2Ecol%2Dlg%2Doffset%2D12%7Bmargin%2Dleft%3A100%25%7D%2Ecol%2Dlg%2Doffset%2D11%7Bmargin%2Dleft%3A91%2E66666667%25%7D%2Ecol%2Dlg%2Doffset%2D10%7Bmargin%2Dleft%3A83%2E33333333%25%7D%2Ecol%2Dlg%2Doffset%2D9%7Bmargin%2Dleft%3A75%25%7D%2Ecol%2Dlg%2Doffset%2D8%7Bmargin%2Dleft%3A66%2E66666667%25%7D%2Ecol%2Dlg%2Doffset%2D7%7Bmargin%2Dleft%3A58%2E33333333%25%7D%2Ecol%2Dlg%2Doffset%2D6%7Bmargin%2Dleft%3A50%25%7D%2Ecol%2Dlg%2Doffset%2D5%7Bmargin%2Dleft%3A41%2E66666667%25%7D%2Ecol%2Dlg%2Doffset%2D4%7Bmargin%2Dleft%3A33%2E33333333%25%7D%2Ecol%2Dlg%2Doffset%2D3%7Bmargin%2Dleft%3A25%25%7D%2Ecol%2Dlg%2Doffset%2D2%7Bmargin%2Dleft%3A16%2E66666667%25%7D%2Ecol%2Dlg%2Doffset%2D1%7Bmargin%2Dleft%3A8%2E33333333%25%7D%2Ecol%2Dlg%2Doffset%2D0%7Bmargin%2Dleft%3A0%7D%7Dtable%7Bbackground%2Dcolor%3Atransparent%7Dcaption%7Bpadding%2Dtop%3A8px%3Bpadding%2Dbottom%3A8px%3Bcolor%3A%23777%3Btext%2Dalign%3Aleft%7Dth%7B%7D%2Etable%7Bwidth%3A100%25%3Bmax%2Dwidth%3A100%25%3Bmargin%2Dbottom%3A20px%7D%2Etable%3Etbody%3Etr%3Etd%2C%2Etable%3Etbody%3Etr%3Eth%2C%2Etable%3Etfoot%3Etr%3Etd%2C%2Etable%3Etfoot%3Etr%3Eth%2C%2Etable%3Ethead%3Etr%3Etd%2C%2Etable%3Ethead%3Etr%3Eth%7Bpadding%3A8px%3Bline%2Dheight%3A1%2E42857143%3Bvertical%2Dalign%3Atop%3Bborder%2Dtop%3A1px%20solid%20%23ddd%7D%2Etable%3Ethead%3Etr%3Eth%7Bvertical%2Dalign%3Abottom%3Bborder%2Dbottom%3A2px%20solid%20%23ddd%7D%2Etable%3Ecaption%2Bthead%3Etr%3Afirst%2Dchild%3Etd%2C%2Etable%3Ecaption%2Bthead%3Etr%3Afirst%2Dchild%3Eth%2C%2Etable%3Ecolgroup%2Bthead%3Etr%3Afirst%2Dchild%3Etd%2C%2Etable%3Ecolgroup%2Bthead%3Etr%3Afirst%2Dchild%3Eth%2C%2Etable%3Ethead%3Afirst%2Dchild%3Etr%3Afirst%2Dchild%3Etd%2C%2Etable%3Ethead%3Afirst%2Dchild%3Etr%3Afirst%2Dchild%3Eth%7Bborder%2Dtop%3A0%7D%2Etable%3Etbody%2Btbody%7Bborder%2Dtop%3A2px%20solid%20%23ddd%7D%2Etable%20%2Etable%7Bbackground%2Dcolor%3A%23fff%7D%2Etable%2Dcondensed%3Etbody%3Etr%3Etd%2C%2Etable%2Dcondensed%3Etbody%3Etr%3Eth%2C%2Etable%2Dcondensed%3Etfoot%3Etr%3Etd%2C%2Etable%2Dcondensed%3Etfoot%3Etr%3Eth%2C%2Etable%2Dcondensed%3Ethead%3Etr%3Etd%2C%2Etable%2Dcondensed%3Ethead%3Etr%3Eth%7Bpadding%3A5px%7D%2Etable%2Dbordered%7Bborder%3A1px%20solid%20%23ddd%7D%2Etable%2Dbordered%3Etbody%3Etr%3Etd%2C%2Etable%2Dbordered%3Etbody%3Etr%3Eth%2C%2Etable%2Dbordered%3Etfoot%3Etr%3Etd%2C%2Etable%2Dbordered%3Etfoot%3Etr%3Eth%2C%2Etable%2Dbordered%3Ethead%3Etr%3Etd%2C%2Etable%2Dbordered%3Ethead%3Etr%3Eth%7Bborder%3A1px%20solid%20%23ddd%7D%2Etable%2Dbordered%3Ethead%3Etr%3Etd%2C%2Etable%2Dbordered%3Ethead%3Etr%3Eth%7Bborder%2Dbottom%2Dwidth%3A2px%7D%2Etable%2Dstriped%3Etbody%3Etr%3Anth%2Dof%2Dtype%28odd%29%7Bbackground%2Dcolor%3A%23f9f9f9%7D%2Etable%2Dhover%3Etbody%3Etr%3Ahover%7Bbackground%2Dcolor%3A%23f5f5f5%7Dtable%20col%5Bclass%2A%3Dcol%2D%5D%7Bposition%3Astatic%3Bdisplay%3Atable%2Dcolumn%3Bfloat%3Anone%7Dtable%20td%5Bclass%2A%3Dcol%2D%5D%2Ctable%20th%5Bclass%2A%3Dcol%2D%5D%7Bposition%3Astatic%3Bdisplay%3Atable%2Dcell%3Bfloat%3Anone%7D%2Etable%3Etbody%3Etr%2Eactive%3Etd%2C%2Etable%3Etbody%3Etr%2Eactive%3Eth%2C%2Etable%3Etbody%3Etr%3Etd%2Eactive%2C%2Etable%3Etbody%3Etr%3Eth%2Eactive%2C%2Etable%3Etfoot%3Etr%2Eactive%3Etd%2C%2Etable%3Etfoot%3Etr%2Eactive%3Eth%2C%2Etable%3Etfoot%3Etr%3Etd%2Eactive%2C%2Etable%3Etfoot%3Etr%3Eth%2Eactive%2C%2Etable%3Ethead%3Etr%2Eactive%3Etd%2C%2Etable%3Ethead%3Etr%2Eactive%3Eth%2C%2Etable%3Ethead%3Etr%3Etd%2Eactive%2C%2Etable%3Ethead%3Etr%3Eth%2Eactive%7Bbackground%2Dcolor%3A%23f5f5f5%7D%2Etable%2Dhover%3Etbody%3Etr%2Eactive%3Ahover%3Etd%2C%2Etable%2Dhover%3Etbody%3Etr%2Eactive%3Ahover%3Eth%2C%2Etable%2Dhover%3Etbody%3Etr%3Ahover%3E%2Eactive%2C%2Etable%2Dhover%3Etbody%3Etr%3Etd%2Eactive%3Ahover%2C%2Etable%2Dhover%3Etbody%3Etr%3Eth%2Eactive%3Ahover%7Bbackground%2Dcolor%3A%23e8e8e8%7D%2Etable%3Etbody%3Etr%2Esuccess%3Etd%2C%2Etable%3Etbody%3Etr%2Esuccess%3Eth%2C%2Etable%3Etbody%3Etr%3Etd%2Esuccess%2C%2Etable%3Etbody%3Etr%3Eth%2Esuccess%2C%2Etable%3Etfoot%3Etr%2Esuccess%3Etd%2C%2Etable%3Etfoot%3Etr%2Esuccess%3Eth%2C%2Etable%3Etfoot%3Etr%3Etd%2Esuccess%2C%2Etable%3Etfoot%3Etr%3Eth%2Esuccess%2C%2Etable%3Ethead%3Etr%2Esuccess%3Etd%2C%2Etable%3Ethead%3Etr%2Esuccess%3Eth%2C%2Etable%3Ethead%3Etr%3Etd%2Esuccess%2C%2Etable%3Ethead%3Etr%3Eth%2Esuccess%7Bbackground%2Dcolor%3A%23dff0d8%7D%2Etable%2Dhover%3Etbody%3Etr%2Esuccess%3Ahover%3Etd%2C%2Etable%2Dhover%3Etbody%3Etr%2Esuccess%3Ahover%3Eth%2C%2Etable%2Dhover%3Etbody%3Etr%3Ahover%3E%2Esuccess%2C%2Etable%2Dhover%3Etbody%3Etr%3Etd%2Esuccess%3Ahover%2C%2Etable%2Dhover%3Etbody%3Etr%3Eth%2Esuccess%3Ahover%7Bbackground%2Dcolor%3A%23d0e9c6%7D%2Etable%3Etbody%3Etr%2Einfo%3Etd%2C%2Etable%3Etbody%3Etr%2Einfo%3Eth%2C%2Etable%3Etbody%3Etr%3Etd%2Einfo%2C%2Etable%3Etbody%3Etr%3Eth%2Einfo%2C%2Etable%3Etfoot%3Etr%2Einfo%3Etd%2C%2Etable%3Etfoot%3Etr%2Einfo%3Eth%2C%2Etable%3Etfoot%3Etr%3Etd%2Einfo%2C%2Etable%3Etfoot%3Etr%3Eth%2Einfo%2C%2Etable%3Ethead%3Etr%2Einfo%3Etd%2C%2Etable%3Ethead%3Etr%2Einfo%3Eth%2C%2Etable%3Ethead%3Etr%3Etd%2Einfo%2C%2Etable%3Ethead%3Etr%3Eth%2Einfo%7Bbackground%2Dcolor%3A%23d9edf7%7D%2Etable%2Dhover%3Etbody%3Etr%2Einfo%3Ahover%3Etd%2C%2Etable%2Dhover%3Etbody%3Etr%2Einfo%3Ahover%3Eth%2C%2Etable%2Dhover%3Etbody%3Etr%3Ahover%3E%2Einfo%2C%2Etable%2Dhover%3Etbody%3Etr%3Etd%2Einfo%3Ahover%2C%2Etable%2Dhover%3Etbody%3Etr%3Eth%2Einfo%3Ahover%7Bbackground%2Dcolor%3A%23c4e3f3%7D%2Etable%3Etbody%3Etr%2Ewarning%3Etd%2C%2Etable%3Etbody%3Etr%2Ewarning%3Eth%2C%2Etable%3Etbody%3Etr%3Etd%2Ewarning%2C%2Etable%3Etbody%3Etr%3Eth%2Ewarning%2C%2Etable%3Etfoot%3Etr%2Ewarning%3Etd%2C%2Etable%3Etfoot%3Etr%2Ewarning%3Eth%2C%2Etable%3Etfoot%3Etr%3Etd%2Ewarning%2C%2Etable%3Etfoot%3Etr%3Eth%2Ewarning%2C%2Etable%3Ethead%3Etr%2Ewarning%3Etd%2C%2Etable%3Ethead%3Etr%2Ewarning%3Eth%2C%2Etable%3Ethead%3Etr%3Etd%2Ewarning%2C%2Etable%3Ethead%3Etr%3Eth%2Ewarning%7Bbackground%2Dcolor%3A%23fcf8e3%7D%2Etable%2Dhover%3Etbody%3Etr%2Ewarning%3Ahover%3Etd%2C%2Etable%2Dhover%3Etbody%3Etr%2Ewarning%3Ahover%3Eth%2C%2Etable%2Dhover%3Etbody%3Etr%3Ahover%3E%2Ewarning%2C%2Etable%2Dhover%3Etbody%3Etr%3Etd%2Ewarning%3Ahover%2C%2Etable%2Dhover%3Etbody%3Etr%3Eth%2Ewarning%3Ahover%7Bbackground%2Dcolor%3A%23faf2cc%7D%2Etable%3Etbody%3Etr%2Edanger%3Etd%2C%2Etable%3Etbody%3Etr%2Edanger%3Eth%2C%2Etable%3Etbody%3Etr%3Etd%2Edanger%2C%2Etable%3Etbody%3Etr%3Eth%2Edanger%2C%2Etable%3Etfoot%3Etr%2Edanger%3Etd%2C%2Etable%3Etfoot%3Etr%2Edanger%3Eth%2C%2Etable%3Etfoot%3Etr%3Etd%2Edanger%2C%2Etable%3Etfoot%3Etr%3Eth%2Edanger%2C%2Etable%3Ethead%3Etr%2Edanger%3Etd%2C%2Etable%3Ethead%3Etr%2Edanger%3Eth%2C%2Etable%3Ethead%3Etr%3Etd%2Edanger%2C%2Etable%3Ethead%3Etr%3Eth%2Edanger%7Bbackground%2Dcolor%3A%23f2dede%7D%2Etable%2Dhover%3Etbody%3Etr%2Edanger%3Ahover%3Etd%2C%2Etable%2Dhover%3Etbody%3Etr%2Edanger%3Ahover%3Eth%2C%2Etable%2Dhover%3Etbody%3Etr%3Ahover%3E%2Edanger%2C%2Etable%2Dhover%3Etbody%3Etr%3Etd%2Edanger%3Ahover%2C%2Etable%2Dhover%3Etbody%3Etr%3Eth%2Edanger%3Ahover%7Bbackground%2Dcolor%3A%23ebcccc%7D%2Etable%2Dresponsive%7Bmin%2Dheight%3A%2E01%25%3Boverflow%2Dx%3Aauto%7D%40media%20screen%20and%20%28max%2Dwidth%3A767px%29%7B%2Etable%2Dresponsive%7Bwidth%3A100%25%3Bmargin%2Dbottom%3A15px%3Boverflow%2Dy%3Ahidden%3B%2Dms%2Doverflow%2Dstyle%3A%2Dms%2Dautohiding%2Dscrollbar%3Bborder%3A1px%20solid%20%23ddd%7D%2Etable%2Dresponsive%3E%2Etable%7Bmargin%2Dbottom%3A0%7D%2Etable%2Dresponsive%3E%2Etable%3Etbody%3Etr%3Etd%2C%2Etable%2Dresponsive%3E%2Etable%3Etbody%3Etr%3Eth%2C%2Etable%2Dresponsive%3E%2Etable%3Etfoot%3Etr%3Etd%2C%2Etable%2Dresponsive%3E%2Etable%3Etfoot%3Etr%3Eth%2C%2Etable%2Dresponsive%3E%2Etable%3Ethead%3Etr%3Etd%2C%2Etable%2Dresponsive%3E%2Etable%3Ethead%3Etr%3Eth%7Bwhite%2Dspace%3Anowrap%7D%2Etable%2Dresponsive%3E%2Etable%2Dbordered%7Bborder%3A0%7D%2Etable%2Dresponsive%3E%2Etable%2Dbordered%3Etbody%3Etr%3Etd%3Afirst%2Dchild%2C%2Etable%2Dresponsive%3E%2Etable%2Dbordered%3Etbody%3Etr%3Eth%3Afirst%2Dchild%2C%2Etable%2Dresponsive%3E%2Etable%2Dbordered%3Etfoot%3Etr%3Etd%3Afirst%2Dchild%2C%2Etable%2Dresponsive%3E%2Etable%2Dbordered%3Etfoot%3Etr%3Eth%3Afirst%2Dchild%2C%2Etable%2Dresponsive%3E%2Etable%2Dbordered%3Ethead%3Etr%3Etd%3Afirst%2Dchild%2C%2Etable%2Dresponsive%3E%2Etable%2Dbordered%3Ethead%3Etr%3Eth%3Afirst%2Dchild%7Bborder%2Dleft%3A0%7D%2Etable%2Dresponsive%3E%2Etable%2Dbordered%3Etbody%3Etr%3Etd%3Alast%2Dchild%2C%2Etable%2Dresponsive%3E%2Etable%2Dbordered%3Etbody%3Etr%3Eth%3Alast%2Dchild%2C%2Etable%2Dresponsive%3E%2Etable%2Dbordered%3Etfoot%3Etr%3Etd%3Alast%2Dchild%2C%2Etable%2Dresponsive%3E%2Etable%2Dbordered%3Etfoot%3Etr%3Eth%3Alast%2Dchild%2C%2Etable%2Dresponsive%3E%2Etable%2Dbordered%3Ethead%3Etr%3Etd%3Alast%2Dchild%2C%2Etable%2Dresponsive%3E%2Etable%2Dbordered%3Ethead%3Etr%3Eth%3Alast%2Dchild%7Bborder%2Dright%3A0%7D%2Etable%2Dresponsive%3E%2Etable%2Dbordered%3Etbody%3Etr%3Alast%2Dchild%3Etd%2C%2Etable%2Dresponsive%3E%2Etable%2Dbordered%3Etbody%3Etr%3Alast%2Dchild%3Eth%2C%2Etable%2Dresponsive%3E%2Etable%2Dbordered%3Etfoot%3Etr%3Alast%2Dchild%3Etd%2C%2Etable%2Dresponsive%3E%2Etable%2Dbordered%3Etfoot%3Etr%3Alast%2Dchild%3Eth%7Bborder%2Dbottom%3A0%7D%7Dfieldset%7Bmin%2Dwidth%3A0%3Bpadding%3A0%3Bmargin%3A0%3Bborder%3A0%7Dlegend%7Bdisplay%3Ablock%3Bwidth%3A100%25%3Bpadding%3A0%3Bmargin%2Dbottom%3A20px%3Bfont%2Dsize%3A21px%3Bline%2Dheight%3Ainherit%3Bcolor%3A%23333%3Bborder%3A0%3Bborder%2Dbottom%3A1px%20solid%20%23e5e5e5%7Dlabel%7Bdisplay%3Ainline%2Dblock%3Bmax%2Dwidth%3A100%25%3Bmargin%2Dbottom%3A5px%3Bfont%2Dweight%3A700%7Dinput%5Btype%3Dsearch%5D%7B%2Dwebkit%2Dbox%2Dsizing%3Aborder%2Dbox%3B%2Dmoz%2Dbox%2Dsizing%3Aborder%2Dbox%3Bbox%2Dsizing%3Aborder%2Dbox%7Dinput%5Btype%3Dcheckbox%5D%2Cinput%5Btype%3Dradio%5D%7Bmargin%3A4px%200%200%3Bmargin%2Dtop%3A1px%5C9%3Bline%2Dheight%3Anormal%7Dinput%5Btype%3Dfile%5D%7Bdisplay%3Ablock%7Dinput%5Btype%3Drange%5D%7Bdisplay%3Ablock%3Bwidth%3A100%25%7Dselect%5Bmultiple%5D%2Cselect%5Bsize%5D%7Bheight%3Aauto%7Dinput%5Btype%3Dfile%5D%3Afocus%2Cinput%5Btype%3Dcheckbox%5D%3Afocus%2Cinput%5Btype%3Dradio%5D%3Afocus%7Boutline%3Athin%20dotted%3Boutline%3A5px%20auto%20%2Dwebkit%2Dfocus%2Dring%2Dcolor%3Boutline%2Doffset%3A%2D2px%7Doutput%7Bdisplay%3Ablock%3Bpadding%2Dtop%3A7px%3Bfont%2Dsize%3A14px%3Bline%2Dheight%3A1%2E42857143%3Bcolor%3A%23555%7D%2Eform%2Dcontrol%7Bdisplay%3Ablock%3Bwidth%3A100%25%3Bheight%3A34px%3Bpadding%3A6px%2012px%3Bfont%2Dsize%3A14px%3Bline%2Dheight%3A1%2E42857143%3Bcolor%3A%23555%3Bbackground%2Dcolor%3A%23fff%3Bbackground%2Dimage%3Anone%3Bborder%3A1px%20solid%20%23ccc%3Bborder%2Dradius%3A4px%3B%2Dwebkit%2Dbox%2Dshadow%3Ainset%200%201px%201px%20rgba%280%2C0%2C0%2C%2E075%29%3Bbox%2Dshadow%3Ainset%200%201px%201px%20rgba%280%2C0%2C0%2C%2E075%29%3B%2Dwebkit%2Dtransition%3Aborder%2Dcolor%20ease%2Din%2Dout%20%2E15s%2C%2Dwebkit%2Dbox%2Dshadow%20ease%2Din%2Dout%20%2E15s%3B%2Do%2Dtransition%3Aborder%2Dcolor%20ease%2Din%2Dout%20%2E15s%2Cbox%2Dshadow%20ease%2Din%2Dout%20%2E15s%3Btransition%3Aborder%2Dcolor%20ease%2Din%2Dout%20%2E15s%2Cbox%2Dshadow%20ease%2Din%2Dout%20%2E15s%7D%2Eform%2Dcontrol%3Afocus%7Bborder%2Dcolor%3A%2366afe9%3Boutline%3A0%3B%2Dwebkit%2Dbox%2Dshadow%3Ainset%200%201px%201px%20rgba%280%2C0%2C0%2C%2E075%29%2C0%200%208px%20rgba%28102%2C175%2C233%2C%2E6%29%3Bbox%2Dshadow%3Ainset%200%201px%201px%20rgba%280%2C0%2C0%2C%2E075%29%2C0%200%208px%20rgba%28102%2C175%2C233%2C%2E6%29%7D%2Eform%2Dcontrol%3A%3A%2Dmoz%2Dplaceholder%7Bcolor%3A%23999%3Bopacity%3A1%7D%2Eform%2Dcontrol%3A%2Dms%2Dinput%2Dplaceholder%7Bcolor%3A%23999%7D%2Eform%2Dcontrol%3A%3A%2Dwebkit%2Dinput%2Dplaceholder%7Bcolor%3A%23999%7D%2Eform%2Dcontrol%5Bdisabled%5D%2C%2Eform%2Dcontrol%5Breadonly%5D%2Cfieldset%5Bdisabled%5D%20%2Eform%2Dcontrol%7Bbackground%2Dcolor%3A%23eee%3Bopacity%3A1%7D%2Eform%2Dcontrol%5Bdisabled%5D%2Cfieldset%5Bdisabled%5D%20%2Eform%2Dcontrol%7Bcursor%3Anot%2Dallowed%7Dtextarea%2Eform%2Dcontrol%7Bheight%3Aauto%7Dinput%5Btype%3Dsearch%5D%7B%2Dwebkit%2Dappearance%3Anone%7D%40media%20screen%20and%20%28%2Dwebkit%2Dmin%2Ddevice%2Dpixel%2Dratio%3A0%29%7Binput%5Btype%3Ddate%5D%2Eform%2Dcontrol%2Cinput%5Btype%3Dtime%5D%2Eform%2Dcontrol%2Cinput%5Btype%3Ddatetime%2Dlocal%5D%2Eform%2Dcontrol%2Cinput%5Btype%3Dmonth%5D%2Eform%2Dcontrol%7Bline%2Dheight%3A34px%7D%2Einput%2Dgroup%2Dsm%20input%5Btype%3Ddate%5D%2C%2Einput%2Dgroup%2Dsm%20input%5Btype%3Dtime%5D%2C%2Einput%2Dgroup%2Dsm%20input%5Btype%3Ddatetime%2Dlocal%5D%2C%2Einput%2Dgroup%2Dsm%20input%5Btype%3Dmonth%5D%2Cinput%5Btype%3Ddate%5D%2Einput%2Dsm%2Cinput%5Btype%3Dtime%5D%2Einput%2Dsm%2Cinput%5Btype%3Ddatetime%2Dlocal%5D%2Einput%2Dsm%2Cinput%5Btype%3Dmonth%5D%2Einput%2Dsm%7Bline%2Dheight%3A30px%7D%2Einput%2Dgroup%2Dlg%20input%5Btype%3Ddate%5D%2C%2Einput%2Dgroup%2Dlg%20input%5Btype%3Dtime%5D%2C%2Einput%2Dgroup%2Dlg%20input%5Btype%3Ddatetime%2Dlocal%5D%2C%2Einput%2Dgroup%2Dlg%20input%5Btype%3Dmonth%5D%2Cinput%5Btype%3Ddate%5D%2Einput%2Dlg%2Cinput%5Btype%3Dtime%5D%2Einput%2Dlg%2Cinput%5Btype%3Ddatetime%2Dlocal%5D%2Einput%2Dlg%2Cinput%5Btype%3Dmonth%5D%2Einput%2Dlg%7Bline%2Dheight%3A46px%7D%7D%2Eform%2Dgroup%7Bmargin%2Dbottom%3A15px%7D%2Echeckbox%2C%2Eradio%7Bposition%3Arelative%3Bdisplay%3Ablock%3Bmargin%2Dtop%3A10px%3Bmargin%2Dbottom%3A10px%7D%2Echeckbox%20label%2C%2Eradio%20label%7Bmin%2Dheight%3A20px%3Bpadding%2Dleft%3A20px%3Bmargin%2Dbottom%3A0%3Bfont%2Dweight%3A400%3Bcursor%3Apointer%7D%2Echeckbox%20input%5Btype%3Dcheckbox%5D%2C%2Echeckbox%2Dinline%20input%5Btype%3Dcheckbox%5D%2C%2Eradio%20input%5Btype%3Dradio%5D%2C%2Eradio%2Dinline%20input%5Btype%3Dradio%5D%7Bposition%3Aabsolute%3Bmargin%2Dtop%3A4px%5C9%3Bmargin%2Dleft%3A%2D20px%7D%2Echeckbox%2B%2Echeckbox%2C%2Eradio%2B%2Eradio%7Bmargin%2Dtop%3A%2D5px%7D%2Echeckbox%2Dinline%2C%2Eradio%2Dinline%7Bposition%3Arelative%3Bdisplay%3Ainline%2Dblock%3Bpadding%2Dleft%3A20px%3Bmargin%2Dbottom%3A0%3Bfont%2Dweight%3A400%3Bvertical%2Dalign%3Amiddle%3Bcursor%3Apointer%7D%2Echeckbox%2Dinline%2B%2Echeckbox%2Dinline%2C%2Eradio%2Dinline%2B%2Eradio%2Dinline%7Bmargin%2Dtop%3A0%3Bmargin%2Dleft%3A10px%7Dfieldset%5Bdisabled%5D%20input%5Btype%3Dcheckbox%5D%2Cfieldset%5Bdisabled%5D%20input%5Btype%3Dradio%5D%2Cinput%5Btype%3Dcheckbox%5D%2Edisabled%2Cinput%5Btype%3Dcheckbox%5D%5Bdisabled%5D%2Cinput%5Btype%3Dradio%5D%2Edisabled%2Cinput%5Btype%3Dradio%5D%5Bdisabled%5D%7Bcursor%3Anot%2Dallowed%7D%2Echeckbox%2Dinline%2Edisabled%2C%2Eradio%2Dinline%2Edisabled%2Cfieldset%5Bdisabled%5D%20%2Echeckbox%2Dinline%2Cfieldset%5Bdisabled%5D%20%2Eradio%2Dinline%7Bcursor%3Anot%2Dallowed%7D%2Echeckbox%2Edisabled%20label%2C%2Eradio%2Edisabled%20label%2Cfieldset%5Bdisabled%5D%20%2Echeckbox%20label%2Cfieldset%5Bdisabled%5D%20%2Eradio%20label%7Bcursor%3Anot%2Dallowed%7D%2Eform%2Dcontrol%2Dstatic%7Bmin%2Dheight%3A34px%3Bpadding%2Dtop%3A7px%3Bpadding%2Dbottom%3A7px%3Bmargin%2Dbottom%3A0%7D%2Eform%2Dcontrol%2Dstatic%2Einput%2Dlg%2C%2Eform%2Dcontrol%2Dstatic%2Einput%2Dsm%7Bpadding%2Dright%3A0%3Bpadding%2Dleft%3A0%7D%2Einput%2Dsm%7Bheight%3A30px%3Bpadding%3A5px%2010px%3Bfont%2Dsize%3A12px%3Bline%2Dheight%3A1%2E5%3Bborder%2Dradius%3A3px%7Dselect%2Einput%2Dsm%7Bheight%3A30px%3Bline%2Dheight%3A30px%7Dselect%5Bmultiple%5D%2Einput%2Dsm%2Ctextarea%2Einput%2Dsm%7Bheight%3Aauto%7D%2Eform%2Dgroup%2Dsm%20%2Eform%2Dcontrol%7Bheight%3A30px%3Bpadding%3A5px%2010px%3Bfont%2Dsize%3A12px%3Bline%2Dheight%3A1%2E5%3Bborder%2Dradius%3A3px%7D%2Eform%2Dgroup%2Dsm%20select%2Eform%2Dcontrol%7Bheight%3A30px%3Bline%2Dheight%3A30px%7D%2Eform%2Dgroup%2Dsm%20select%5Bmultiple%5D%2Eform%2Dcontrol%2C%2Eform%2Dgroup%2Dsm%20textarea%2Eform%2Dcontrol%7Bheight%3Aauto%7D%2Eform%2Dgroup%2Dsm%20%2Eform%2Dcontrol%2Dstatic%7Bheight%3A30px%3Bmin%2Dheight%3A32px%3Bpadding%3A6px%2010px%3Bfont%2Dsize%3A12px%3Bline%2Dheight%3A1%2E5%7D%2Einput%2Dlg%7Bheight%3A46px%3Bpadding%3A10px%2016px%3Bfont%2Dsize%3A18px%3Bline%2Dheight%3A1%2E3333333%3Bborder%2Dradius%3A6px%7Dselect%2Einput%2Dlg%7Bheight%3A46px%3Bline%2Dheight%3A46px%7Dselect%5Bmultiple%5D%2Einput%2Dlg%2Ctextarea%2Einput%2Dlg%7Bheight%3Aauto%7D%2Eform%2Dgroup%2Dlg%20%2Eform%2Dcontrol%7Bheight%3A46px%3Bpadding%3A10px%2016px%3Bfont%2Dsize%3A18px%3Bline%2Dheight%3A1%2E3333333%3Bborder%2Dradius%3A6px%7D%2Eform%2Dgroup%2Dlg%20select%2Eform%2Dcontrol%7Bheight%3A46px%3Bline%2Dheight%3A46px%7D%2Eform%2Dgroup%2Dlg%20select%5Bmultiple%5D%2Eform%2Dcontrol%2C%2Eform%2Dgroup%2Dlg%20textarea%2Eform%2Dcontrol%7Bheight%3Aauto%7D%2Eform%2Dgroup%2Dlg%20%2Eform%2Dcontrol%2Dstatic%7Bheight%3A46px%3Bmin%2Dheight%3A38px%3Bpadding%3A11px%2016px%3Bfont%2Dsize%3A18px%3Bline%2Dheight%3A1%2E3333333%7D%2Ehas%2Dfeedback%7Bposition%3Arelative%7D%2Ehas%2Dfeedback%20%2Eform%2Dcontrol%7Bpadding%2Dright%3A42%2E5px%7D%2Eform%2Dcontrol%2Dfeedback%7Bposition%3Aabsolute%3Btop%3A0%3Bright%3A0%3Bz%2Dindex%3A2%3Bdisplay%3Ablock%3Bwidth%3A34px%3Bheight%3A34px%3Bline%2Dheight%3A34px%3Btext%2Dalign%3Acenter%3Bpointer%2Devents%3Anone%7D%2Eform%2Dgroup%2Dlg%20%2Eform%2Dcontrol%2B%2Eform%2Dcontrol%2Dfeedback%2C%2Einput%2Dgroup%2Dlg%2B%2Eform%2Dcontrol%2Dfeedback%2C%2Einput%2Dlg%2B%2Eform%2Dcontrol%2Dfeedback%7Bwidth%3A46px%3Bheight%3A46px%3Bline%2Dheight%3A46px%7D%2Eform%2Dgroup%2Dsm%20%2Eform%2Dcontrol%2B%2Eform%2Dcontrol%2Dfeedback%2C%2Einput%2Dgroup%2Dsm%2B%2Eform%2Dcontrol%2Dfeedback%2C%2Einput%2Dsm%2B%2Eform%2Dcontrol%2Dfeedback%7Bwidth%3A30px%3Bheight%3A30px%3Bline%2Dheight%3A30px%7D%2Ehas%2Dsuccess%20%2Echeckbox%2C%2Ehas%2Dsuccess%20%2Echeckbox%2Dinline%2C%2Ehas%2Dsuccess%20%2Econtrol%2Dlabel%2C%2Ehas%2Dsuccess%20%2Ehelp%2Dblock%2C%2Ehas%2Dsuccess%20%2Eradio%2C%2Ehas%2Dsuccess%20%2Eradio%2Dinline%2C%2Ehas%2Dsuccess%2Echeckbox%20label%2C%2Ehas%2Dsuccess%2Echeckbox%2Dinline%20label%2C%2Ehas%2Dsuccess%2Eradio%20label%2C%2Ehas%2Dsuccess%2Eradio%2Dinline%20label%7Bcolor%3A%233c763d%7D%2Ehas%2Dsuccess%20%2Eform%2Dcontrol%7Bborder%2Dcolor%3A%233c763d%3B%2Dwebkit%2Dbox%2Dshadow%3Ainset%200%201px%201px%20rgba%280%2C0%2C0%2C%2E075%29%3Bbox%2Dshadow%3Ainset%200%201px%201px%20rgba%280%2C0%2C0%2C%2E075%29%7D%2Ehas%2Dsuccess%20%2Eform%2Dcontrol%3Afocus%7Bborder%2Dcolor%3A%232b542c%3B%2Dwebkit%2Dbox%2Dshadow%3Ainset%200%201px%201px%20rgba%280%2C0%2C0%2C%2E075%29%2C0%200%206px%20%2367b168%3Bbox%2Dshadow%3Ainset%200%201px%201px%20rgba%280%2C0%2C0%2C%2E075%29%2C0%200%206px%20%2367b168%7D%2Ehas%2Dsuccess%20%2Einput%2Dgroup%2Daddon%7Bcolor%3A%233c763d%3Bbackground%2Dcolor%3A%23dff0d8%3Bborder%2Dcolor%3A%233c763d%7D%2Ehas%2Dsuccess%20%2Eform%2Dcontrol%2Dfeedback%7Bcolor%3A%233c763d%7D%2Ehas%2Dwarning%20%2Echeckbox%2C%2Ehas%2Dwarning%20%2Echeckbox%2Dinline%2C%2Ehas%2Dwarning%20%2Econtrol%2Dlabel%2C%2Ehas%2Dwarning%20%2Ehelp%2Dblock%2C%2Ehas%2Dwarning%20%2Eradio%2C%2Ehas%2Dwarning%20%2Eradio%2Dinline%2C%2Ehas%2Dwarning%2Echeckbox%20label%2C%2Ehas%2Dwarning%2Echeckbox%2Dinline%20label%2C%2Ehas%2Dwarning%2Eradio%20label%2C%2Ehas%2Dwarning%2Eradio%2Dinline%20label%7Bcolor%3A%238a6d3b%7D%2Ehas%2Dwarning%20%2Eform%2Dcontrol%7Bborder%2Dcolor%3A%238a6d3b%3B%2Dwebkit%2Dbox%2Dshadow%3Ainset%200%201px%201px%20rgba%280%2C0%2C0%2C%2E075%29%3Bbox%2Dshadow%3Ainset%200%201px%201px%20rgba%280%2C0%2C0%2C%2E075%29%7D%2Ehas%2Dwarning%20%2Eform%2Dcontrol%3Afocus%7Bborder%2Dcolor%3A%2366512c%3B%2Dwebkit%2Dbox%2Dshadow%3Ainset%200%201px%201px%20rgba%280%2C0%2C0%2C%2E075%29%2C0%200%206px%20%23c0a16b%3Bbox%2Dshadow%3Ainset%200%201px%201px%20rgba%280%2C0%2C0%2C%2E075%29%2C0%200%206px%20%23c0a16b%7D%2Ehas%2Dwarning%20%2Einput%2Dgroup%2Daddon%7Bcolor%3A%238a6d3b%3Bbackground%2Dcolor%3A%23fcf8e3%3Bborder%2Dcolor%3A%238a6d3b%7D%2Ehas%2Dwarning%20%2Eform%2Dcontrol%2Dfeedback%7Bcolor%3A%238a6d3b%7D%2Ehas%2Derror%20%2Echeckbox%2C%2Ehas%2Derror%20%2Echeckbox%2Dinline%2C%2Ehas%2Derror%20%2Econtrol%2Dlabel%2C%2Ehas%2Derror%20%2Ehelp%2Dblock%2C%2Ehas%2Derror%20%2Eradio%2C%2Ehas%2Derror%20%2Eradio%2Dinline%2C%2Ehas%2Derror%2Echeckbox%20label%2C%2Ehas%2Derror%2Echeckbox%2Dinline%20label%2C%2Ehas%2Derror%2Eradio%20label%2C%2Ehas%2Derror%2Eradio%2Dinline%20label%7Bcolor%3A%23a94442%7D%2Ehas%2Derror%20%2Eform%2Dcontrol%7Bborder%2Dcolor%3A%23a94442%3B%2Dwebkit%2Dbox%2Dshadow%3Ainset%200%201px%201px%20rgba%280%2C0%2C0%2C%2E075%29%3Bbox%2Dshadow%3Ainset%200%201px%201px%20rgba%280%2C0%2C0%2C%2E075%29%7D%2Ehas%2Derror%20%2Eform%2Dcontrol%3Afocus%7Bborder%2Dcolor%3A%23843534%3B%2Dwebkit%2Dbox%2Dshadow%3Ainset%200%201px%201px%20rgba%280%2C0%2C0%2C%2E075%29%2C0%200%206px%20%23ce8483%3Bbox%2Dshadow%3Ainset%200%201px%201px%20rgba%280%2C0%2C0%2C%2E075%29%2C0%200%206px%20%23ce8483%7D%2Ehas%2Derror%20%2Einput%2Dgroup%2Daddon%7Bcolor%3A%23a94442%3Bbackground%2Dcolor%3A%23f2dede%3Bborder%2Dcolor%3A%23a94442%7D%2Ehas%2Derror%20%2Eform%2Dcontrol%2Dfeedback%7Bcolor%3A%23a94442%7D%2Ehas%2Dfeedback%20label%7E%2Eform%2Dcontrol%2Dfeedback%7Btop%3A25px%7D%2Ehas%2Dfeedback%20label%2Esr%2Donly%7E%2Eform%2Dcontrol%2Dfeedback%7Btop%3A0%7D%2Ehelp%2Dblock%7Bdisplay%3Ablock%3Bmargin%2Dtop%3A5px%3Bmargin%2Dbottom%3A10px%3Bcolor%3A%23737373%7D%40media%20%28min%2Dwidth%3A768px%29%7B%2Eform%2Dinline%20%2Eform%2Dgroup%7Bdisplay%3Ainline%2Dblock%3Bmargin%2Dbottom%3A0%3Bvertical%2Dalign%3Amiddle%7D%2Eform%2Dinline%20%2Eform%2Dcontrol%7Bdisplay%3Ainline%2Dblock%3Bwidth%3Aauto%3Bvertical%2Dalign%3Amiddle%7D%2Eform%2Dinline%20%2Eform%2Dcontrol%2Dstatic%7Bdisplay%3Ainline%2Dblock%7D%2Eform%2Dinline%20%2Einput%2Dgroup%7Bdisplay%3Ainline%2Dtable%3Bvertical%2Dalign%3Amiddle%7D%2Eform%2Dinline%20%2Einput%2Dgroup%20%2Eform%2Dcontrol%2C%2Eform%2Dinline%20%2Einput%2Dgroup%20%2Einput%2Dgroup%2Daddon%2C%2Eform%2Dinline%20%2Einput%2Dgroup%20%2Einput%2Dgroup%2Dbtn%7Bwidth%3Aauto%7D%2Eform%2Dinline%20%2Einput%2Dgroup%3E%2Eform%2Dcontrol%7Bwidth%3A100%25%7D%2Eform%2Dinline%20%2Econtrol%2Dlabel%7Bmargin%2Dbottom%3A0%3Bvertical%2Dalign%3Amiddle%7D%2Eform%2Dinline%20%2Echeckbox%2C%2Eform%2Dinline%20%2Eradio%7Bdisplay%3Ainline%2Dblock%3Bmargin%2Dtop%3A0%3Bmargin%2Dbottom%3A0%3Bvertical%2Dalign%3Amiddle%7D%2Eform%2Dinline%20%2Echeckbox%20label%2C%2Eform%2Dinline%20%2Eradio%20label%7Bpadding%2Dleft%3A0%7D%2Eform%2Dinline%20%2Echeckbox%20input%5Btype%3Dcheckbox%5D%2C%2Eform%2Dinline%20%2Eradio%20input%5Btype%3Dradio%5D%7Bposition%3Arelative%3Bmargin%2Dleft%3A0%7D%2Eform%2Dinline%20%2Ehas%2Dfeedback%20%2Eform%2Dcontrol%2Dfeedback%7Btop%3A0%7D%7D%2Eform%2Dhorizontal%20%2Echeckbox%2C%2Eform%2Dhorizontal%20%2Echeckbox%2Dinline%2C%2Eform%2Dhorizontal%20%2Eradio%2C%2Eform%2Dhorizontal%20%2Eradio%2Dinline%7Bpadding%2Dtop%3A7px%3Bmargin%2Dtop%3A0%3Bmargin%2Dbottom%3A0%7D%2Eform%2Dhorizontal%20%2Echeckbox%2C%2Eform%2Dhorizontal%20%2Eradio%7Bmin%2Dheight%3A27px%7D%2Eform%2Dhorizontal%20%2Eform%2Dgroup%7Bmargin%2Dright%3A%2D15px%3Bmargin%2Dleft%3A%2D15px%7D%40media%20%28min%2Dwidth%3A768px%29%7B%2Eform%2Dhorizontal%20%2Econtrol%2Dlabel%7Bpadding%2Dtop%3A7px%3Bmargin%2Dbottom%3A0%3Btext%2Dalign%3Aright%7D%7D%2Eform%2Dhorizontal%20%2Ehas%2Dfeedback%20%2Eform%2Dcontrol%2Dfeedback%7Bright%3A15px%7D%40media%20%28min%2Dwidth%3A768px%29%7B%2Eform%2Dhorizontal%20%2Eform%2Dgroup%2Dlg%20%2Econtrol%2Dlabel%7Bpadding%2Dtop%3A14%2E33px%3Bfont%2Dsize%3A18px%7D%7D%40media%20%28min%2Dwidth%3A768px%29%7B%2Eform%2Dhorizontal%20%2Eform%2Dgroup%2Dsm%20%2Econtrol%2Dlabel%7Bpadding%2Dtop%3A6px%3Bfont%2Dsize%3A12px%7D%7D%2Ebtn%7Bdisplay%3Ainline%2Dblock%3Bpadding%3A6px%2012px%3Bmargin%2Dbottom%3A0%3Bfont%2Dsize%3A14px%3Bfont%2Dweight%3A400%3Bline%2Dheight%3A1%2E42857143%3Btext%2Dalign%3Acenter%3Bwhite%2Dspace%3Anowrap%3Bvertical%2Dalign%3Amiddle%3B%2Dms%2Dtouch%2Daction%3Amanipulation%3Btouch%2Daction%3Amanipulation%3Bcursor%3Apointer%3B%2Dwebkit%2Duser%2Dselect%3Anone%3B%2Dmoz%2Duser%2Dselect%3Anone%3B%2Dms%2Duser%2Dselect%3Anone%3Buser%2Dselect%3Anone%3Bbackground%2Dimage%3Anone%3Bborder%3A1px%20solid%20transparent%3Bborder%2Dradius%3A4px%7D%2Ebtn%2Eactive%2Efocus%2C%2Ebtn%2Eactive%3Afocus%2C%2Ebtn%2Efocus%2C%2Ebtn%3Aactive%2Efocus%2C%2Ebtn%3Aactive%3Afocus%2C%2Ebtn%3Afocus%7Boutline%3Athin%20dotted%3Boutline%3A5px%20auto%20%2Dwebkit%2Dfocus%2Dring%2Dcolor%3Boutline%2Doffset%3A%2D2px%7D%2Ebtn%2Efocus%2C%2Ebtn%3Afocus%2C%2Ebtn%3Ahover%7Bcolor%3A%23333%3Btext%2Ddecoration%3Anone%7D%2Ebtn%2Eactive%2C%2Ebtn%3Aactive%7Bbackground%2Dimage%3Anone%3Boutline%3A0%3B%2Dwebkit%2Dbox%2Dshadow%3Ainset%200%203px%205px%20rgba%280%2C0%2C0%2C%2E125%29%3Bbox%2Dshadow%3Ainset%200%203px%205px%20rgba%280%2C0%2C0%2C%2E125%29%7D%2Ebtn%2Edisabled%2C%2Ebtn%5Bdisabled%5D%2Cfieldset%5Bdisabled%5D%20%2Ebtn%7Bcursor%3Anot%2Dallowed%3Bfilter%3Aalpha%28opacity%3D65%29%3B%2Dwebkit%2Dbox%2Dshadow%3Anone%3Bbox%2Dshadow%3Anone%3Bopacity%3A%2E65%7Da%2Ebtn%2Edisabled%2Cfieldset%5Bdisabled%5D%20a%2Ebtn%7Bpointer%2Devents%3Anone%7D%2Ebtn%2Ddefault%7Bcolor%3A%23333%3Bbackground%2Dcolor%3A%23fff%3Bborder%2Dcolor%3A%23ccc%7D%2Ebtn%2Ddefault%2Efocus%2C%2Ebtn%2Ddefault%3Afocus%7Bcolor%3A%23333%3Bbackground%2Dcolor%3A%23e6e6e6%3Bborder%2Dcolor%3A%238c8c8c%7D%2Ebtn%2Ddefault%3Ahover%7Bcolor%3A%23333%3Bbackground%2Dcolor%3A%23e6e6e6%3Bborder%2Dcolor%3A%23adadad%7D%2Ebtn%2Ddefault%2Eactive%2C%2Ebtn%2Ddefault%3Aactive%2C%2Eopen%3E%2Edropdown%2Dtoggle%2Ebtn%2Ddefault%7Bcolor%3A%23333%3Bbackground%2Dcolor%3A%23e6e6e6%3Bborder%2Dcolor%3A%23adadad%7D%2Ebtn%2Ddefault%2Eactive%2Efocus%2C%2Ebtn%2Ddefault%2Eactive%3Afocus%2C%2Ebtn%2Ddefault%2Eactive%3Ahover%2C%2Ebtn%2Ddefault%3Aactive%2Efocus%2C%2Ebtn%2Ddefault%3Aactive%3Afocus%2C%2Ebtn%2Ddefault%3Aactive%3Ahover%2C%2Eopen%3E%2Edropdown%2Dtoggle%2Ebtn%2Ddefault%2Efocus%2C%2Eopen%3E%2Edropdown%2Dtoggle%2Ebtn%2Ddefault%3Afocus%2C%2Eopen%3E%2Edropdown%2Dtoggle%2Ebtn%2Ddefault%3Ahover%7Bcolor%3A%23333%3Bbackground%2Dcolor%3A%23d4d4d4%3Bborder%2Dcolor%3A%238c8c8c%7D%2Ebtn%2Ddefault%2Eactive%2C%2Ebtn%2Ddefault%3Aactive%2C%2Eopen%3E%2Edropdown%2Dtoggle%2Ebtn%2Ddefault%7Bbackground%2Dimage%3Anone%7D%2Ebtn%2Ddefault%2Edisabled%2C%2Ebtn%2Ddefault%2Edisabled%2Eactive%2C%2Ebtn%2Ddefault%2Edisabled%2Efocus%2C%2Ebtn%2Ddefault%2Edisabled%3Aactive%2C%2Ebtn%2Ddefault%2Edisabled%3Afocus%2C%2Ebtn%2Ddefault%2Edisabled%3Ahover%2C%2Ebtn%2Ddefault%5Bdisabled%5D%2C%2Ebtn%2Ddefault%5Bdisabled%5D%2Eactive%2C%2Ebtn%2Ddefault%5Bdisabled%5D%2Efocus%2C%2Ebtn%2Ddefault%5Bdisabled%5D%3Aactive%2C%2Ebtn%2Ddefault%5Bdisabled%5D%3Afocus%2C%2Ebtn%2Ddefault%5Bdisabled%5D%3Ahover%2Cfieldset%5Bdisabled%5D%20%2Ebtn%2Ddefault%2Cfieldset%5Bdisabled%5D%20%2Ebtn%2Ddefault%2Eactive%2Cfieldset%5Bdisabled%5D%20%2Ebtn%2Ddefault%2Efocus%2Cfieldset%5Bdisabled%5D%20%2Ebtn%2Ddefault%3Aactive%2Cfieldset%5Bdisabled%5D%20%2Ebtn%2Ddefault%3Afocus%2Cfieldset%5Bdisabled%5D%20%2Ebtn%2Ddefault%3Ahover%7Bbackground%2Dcolor%3A%23fff%3Bborder%2Dcolor%3A%23ccc%7D%2Ebtn%2Ddefault%20%2Ebadge%7Bcolor%3A%23fff%3Bbackground%2Dcolor%3A%23333%7D%2Ebtn%2Dprimary%7Bcolor%3A%23fff%3Bbackground%2Dcolor%3A%23337ab7%3Bborder%2Dcolor%3A%232e6da4%7D%2Ebtn%2Dprimary%2Efocus%2C%2Ebtn%2Dprimary%3Afocus%7Bcolor%3A%23fff%3Bbackground%2Dcolor%3A%23286090%3Bborder%2Dcolor%3A%23122b40%7D%2Ebtn%2Dprimary%3Ahover%7Bcolor%3A%23fff%3Bbackground%2Dcolor%3A%23286090%3Bborder%2Dcolor%3A%23204d74%7D%2Ebtn%2Dprimary%2Eactive%2C%2Ebtn%2Dprimary%3Aactive%2C%2Eopen%3E%2Edropdown%2Dtoggle%2Ebtn%2Dprimary%7Bcolor%3A%23fff%3Bbackground%2Dcolor%3A%23286090%3Bborder%2Dcolor%3A%23204d74%7D%2Ebtn%2Dprimary%2Eactive%2Efocus%2C%2Ebtn%2Dprimary%2Eactive%3Afocus%2C%2Ebtn%2Dprimary%2Eactive%3Ahover%2C%2Ebtn%2Dprimary%3Aactive%2Efocus%2C%2Ebtn%2Dprimary%3Aactive%3Afocus%2C%2Ebtn%2Dprimary%3Aactive%3Ahover%2C%2Eopen%3E%2Edropdown%2Dtoggle%2Ebtn%2Dprimary%2Efocus%2C%2Eopen%3E%2Edropdown%2Dtoggle%2Ebtn%2Dprimary%3Afocus%2C%2Eopen%3E%2Edropdown%2Dtoggle%2Ebtn%2Dprimary%3Ahover%7Bcolor%3A%23fff%3Bbackground%2Dcolor%3A%23204d74%3Bborder%2Dcolor%3A%23122b40%7D%2Ebtn%2Dprimary%2Eactive%2C%2Ebtn%2Dprimary%3Aactive%2C%2Eopen%3E%2Edropdown%2Dtoggle%2Ebtn%2Dprimary%7Bbackground%2Dimage%3Anone%7D%2Ebtn%2Dprimary%2Edisabled%2C%2Ebtn%2Dprimary%2Edisabled%2Eactive%2C%2Ebtn%2Dprimary%2Edisabled%2Efocus%2C%2Ebtn%2Dprimary%2Edisabled%3Aactive%2C%2Ebtn%2Dprimary%2Edisabled%3Afocus%2C%2Ebtn%2Dprimary%2Edisabled%3Ahover%2C%2Ebtn%2Dprimary%5Bdisabled%5D%2C%2Ebtn%2Dprimary%5Bdisabled%5D%2Eactive%2C%2Ebtn%2Dprimary%5Bdisabled%5D%2Efocus%2C%2Ebtn%2Dprimary%5Bdisabled%5D%3Aactive%2C%2Ebtn%2Dprimary%5Bdisabled%5D%3Afocus%2C%2Ebtn%2Dprimary%5Bdisabled%5D%3Ahover%2Cfieldset%5Bdisabled%5D%20%2Ebtn%2Dprimary%2Cfieldset%5Bdisabled%5D%20%2Ebtn%2Dprimary%2Eactive%2Cfieldset%5Bdisabled%5D%20%2Ebtn%2Dprimary%2Efocus%2Cfieldset%5Bdisabled%5D%20%2Ebtn%2Dprimary%3Aactive%2Cfieldset%5Bdisabled%5D%20%2Ebtn%2Dprimary%3Afocus%2Cfieldset%5Bdisabled%5D%20%2Ebtn%2Dprimary%3Ahover%7Bbackground%2Dcolor%3A%23337ab7%3Bborder%2Dcolor%3A%232e6da4%7D%2Ebtn%2Dprimary%20%2Ebadge%7Bcolor%3A%23337ab7%3Bbackground%2Dcolor%3A%23fff%7D%2Ebtn%2Dsuccess%7Bcolor%3A%23fff%3Bbackground%2Dcolor%3A%235cb85c%3Bborder%2Dcolor%3A%234cae4c%7D%2Ebtn%2Dsuccess%2Efocus%2C%2Ebtn%2Dsuccess%3Afocus%7Bcolor%3A%23fff%3Bbackground%2Dcolor%3A%23449d44%3Bborder%2Dcolor%3A%23255625%7D%2Ebtn%2Dsuccess%3Ahover%7Bcolor%3A%23fff%3Bbackground%2Dcolor%3A%23449d44%3Bborder%2Dcolor%3A%23398439%7D%2Ebtn%2Dsuccess%2Eactive%2C%2Ebtn%2Dsuccess%3Aactive%2C%2Eopen%3E%2Edropdown%2Dtoggle%2Ebtn%2Dsuccess%7Bcolor%3A%23fff%3Bbackground%2Dcolor%3A%23449d44%3Bborder%2Dcolor%3A%23398439%7D%2Ebtn%2Dsuccess%2Eactive%2Efocus%2C%2Ebtn%2Dsuccess%2Eactive%3Afocus%2C%2Ebtn%2Dsuccess%2Eactive%3Ahover%2C%2Ebtn%2Dsuccess%3Aactive%2Efocus%2C%2Ebtn%2Dsuccess%3Aactive%3Afocus%2C%2Ebtn%2Dsuccess%3Aactive%3Ahover%2C%2Eopen%3E%2Edropdown%2Dtoggle%2Ebtn%2Dsuccess%2Efocus%2C%2Eopen%3E%2Edropdown%2Dtoggle%2Ebtn%2Dsuccess%3Afocus%2C%2Eopen%3E%2Edropdown%2Dtoggle%2Ebtn%2Dsuccess%3Ahover%7Bcolor%3A%23fff%3Bbackground%2Dcolor%3A%23398439%3Bborder%2Dcolor%3A%23255625%7D%2Ebtn%2Dsuccess%2Eactive%2C%2Ebtn%2Dsuccess%3Aactive%2C%2Eopen%3E%2Edropdown%2Dtoggle%2Ebtn%2Dsuccess%7Bbackground%2Dimage%3Anone%7D%2Ebtn%2Dsuccess%2Edisabled%2C%2Ebtn%2Dsuccess%2Edisabled%2Eactive%2C%2Ebtn%2Dsuccess%2Edisabled%2Efocus%2C%2Ebtn%2Dsuccess%2Edisabled%3Aactive%2C%2Ebtn%2Dsuccess%2Edisabled%3Afocus%2C%2Ebtn%2Dsuccess%2Edisabled%3Ahover%2C%2Ebtn%2Dsuccess%5Bdisabled%5D%2C%2Ebtn%2Dsuccess%5Bdisabled%5D%2Eactive%2C%2Ebtn%2Dsuccess%5Bdisabled%5D%2Efocus%2C%2Ebtn%2Dsuccess%5Bdisabled%5D%3Aactive%2C%2Ebtn%2Dsuccess%5Bdisabled%5D%3Afocus%2C%2Ebtn%2Dsuccess%5Bdisabled%5D%3Ahover%2Cfieldset%5Bdisabled%5D%20%2Ebtn%2Dsuccess%2Cfieldset%5Bdisabled%5D%20%2Ebtn%2Dsuccess%2Eactive%2Cfieldset%5Bdisabled%5D%20%2Ebtn%2Dsuccess%2Efocus%2Cfieldset%5Bdisabled%5D%20%2Ebtn%2Dsuccess%3Aactive%2Cfieldset%5Bdisabled%5D%20%2Ebtn%2Dsuccess%3Afocus%2Cfieldset%5Bdisabled%5D%20%2Ebtn%2Dsuccess%3Ahover%7Bbackground%2Dcolor%3A%235cb85c%3Bborder%2Dcolor%3A%234cae4c%7D%2Ebtn%2Dsuccess%20%2Ebadge%7Bcolor%3A%235cb85c%3Bbackground%2Dcolor%3A%23fff%7D%2Ebtn%2Dinfo%7Bcolor%3A%23fff%3Bbackground%2Dcolor%3A%235bc0de%3Bborder%2Dcolor%3A%2346b8da%7D%2Ebtn%2Dinfo%2Efocus%2C%2Ebtn%2Dinfo%3Afocus%7Bcolor%3A%23fff%3Bbackground%2Dcolor%3A%2331b0d5%3Bborder%2Dcolor%3A%231b6d85%7D%2Ebtn%2Dinfo%3Ahover%7Bcolor%3A%23fff%3Bbackground%2Dcolor%3A%2331b0d5%3Bborder%2Dcolor%3A%23269abc%7D%2Ebtn%2Dinfo%2Eactive%2C%2Ebtn%2Dinfo%3Aactive%2C%2Eopen%3E%2Edropdown%2Dtoggle%2Ebtn%2Dinfo%7Bcolor%3A%23fff%3Bbackground%2Dcolor%3A%2331b0d5%3Bborder%2Dcolor%3A%23269abc%7D%2Ebtn%2Dinfo%2Eactive%2Efocus%2C%2Ebtn%2Dinfo%2Eactive%3Afocus%2C%2Ebtn%2Dinfo%2Eactive%3Ahover%2C%2Ebtn%2Dinfo%3Aactive%2Efocus%2C%2Ebtn%2Dinfo%3Aactive%3Afocus%2C%2Ebtn%2Dinfo%3Aactive%3Ahover%2C%2Eopen%3E%2Edropdown%2Dtoggle%2Ebtn%2Dinfo%2Efocus%2C%2Eopen%3E%2Edropdown%2Dtoggle%2Ebtn%2Dinfo%3Afocus%2C%2Eopen%3E%2Edropdown%2Dtoggle%2Ebtn%2Dinfo%3Ahover%7Bcolor%3A%23fff%3Bbackground%2Dcolor%3A%23269abc%3Bborder%2Dcolor%3A%231b6d85%7D%2Ebtn%2Dinfo%2Eactive%2C%2Ebtn%2Dinfo%3Aactive%2C%2Eopen%3E%2Edropdown%2Dtoggle%2Ebtn%2Dinfo%7Bbackground%2Dimage%3Anone%7D%2Ebtn%2Dinfo%2Edisabled%2C%2Ebtn%2Dinfo%2Edisabled%2Eactive%2C%2Ebtn%2Dinfo%2Edisabled%2Efocus%2C%2Ebtn%2Dinfo%2Edisabled%3Aactive%2C%2Ebtn%2Dinfo%2Edisabled%3Afocus%2C%2Ebtn%2Dinfo%2Edisabled%3Ahover%2C%2Ebtn%2Dinfo%5Bdisabled%5D%2C%2Ebtn%2Dinfo%5Bdisabled%5D%2Eactive%2C%2Ebtn%2Dinfo%5Bdisabled%5D%2Efocus%2C%2Ebtn%2Dinfo%5Bdisabled%5D%3Aactive%2C%2Ebtn%2Dinfo%5Bdisabled%5D%3Afocus%2C%2Ebtn%2Dinfo%5Bdisabled%5D%3Ahover%2Cfieldset%5Bdisabled%5D%20%2Ebtn%2Dinfo%2Cfieldset%5Bdisabled%5D%20%2Ebtn%2Dinfo%2Eactive%2Cfieldset%5Bdisabled%5D%20%2Ebtn%2Dinfo%2Efocus%2Cfieldset%5Bdisabled%5D%20%2Ebtn%2Dinfo%3Aactive%2Cfieldset%5Bdisabled%5D%20%2Ebtn%2Dinfo%3Afocus%2Cfieldset%5Bdisabled%5D%20%2Ebtn%2Dinfo%3Ahover%7Bbackground%2Dcolor%3A%235bc0de%3Bborder%2Dcolor%3A%2346b8da%7D%2Ebtn%2Dinfo%20%2Ebadge%7Bcolor%3A%235bc0de%3Bbackground%2Dcolor%3A%23fff%7D%2Ebtn%2Dwarning%7Bcolor%3A%23fff%3Bbackground%2Dcolor%3A%23f0ad4e%3Bborder%2Dcolor%3A%23eea236%7D%2Ebtn%2Dwarning%2Efocus%2C%2Ebtn%2Dwarning%3Afocus%7Bcolor%3A%23fff%3Bbackground%2Dcolor%3A%23ec971f%3Bborder%2Dcolor%3A%23985f0d%7D%2Ebtn%2Dwarning%3Ahover%7Bcolor%3A%23fff%3Bbackground%2Dcolor%3A%23ec971f%3Bborder%2Dcolor%3A%23d58512%7D%2Ebtn%2Dwarning%2Eactive%2C%2Ebtn%2Dwarning%3Aactive%2C%2Eopen%3E%2Edropdown%2Dtoggle%2Ebtn%2Dwarning%7Bcolor%3A%23fff%3Bbackground%2Dcolor%3A%23ec971f%3Bborder%2Dcolor%3A%23d58512%7D%2Ebtn%2Dwarning%2Eactive%2Efocus%2C%2Ebtn%2Dwarning%2Eactive%3Afocus%2C%2Ebtn%2Dwarning%2Eactive%3Ahover%2C%2Ebtn%2Dwarning%3Aactive%2Efocus%2C%2Ebtn%2Dwarning%3Aactive%3Afocus%2C%2Ebtn%2Dwarning%3Aactive%3Ahover%2C%2Eopen%3E%2Edropdown%2Dtoggle%2Ebtn%2Dwarning%2Efocus%2C%2Eopen%3E%2Edropdown%2Dtoggle%2Ebtn%2Dwarning%3Afocus%2C%2Eopen%3E%2Edropdown%2Dtoggle%2Ebtn%2Dwarning%3Ahover%7Bcolor%3A%23fff%3Bbackground%2Dcolor%3A%23d58512%3Bborder%2Dcolor%3A%23985f0d%7D%2Ebtn%2Dwarning%2Eactive%2C%2Ebtn%2Dwarning%3Aactive%2C%2Eopen%3E%2Edropdown%2Dtoggle%2Ebtn%2Dwarning%7Bbackground%2Dimage%3Anone%7D%2Ebtn%2Dwarning%2Edisabled%2C%2Ebtn%2Dwarning%2Edisabled%2Eactive%2C%2Ebtn%2Dwarning%2Edisabled%2Efocus%2C%2Ebtn%2Dwarning%2Edisabled%3Aactive%2C%2Ebtn%2Dwarning%2Edisabled%3Afocus%2C%2Ebtn%2Dwarning%2Edisabled%3Ahover%2C%2Ebtn%2Dwarning%5Bdisabled%5D%2C%2Ebtn%2Dwarning%5Bdisabled%5D%2Eactive%2C%2Ebtn%2Dwarning%5Bdisabled%5D%2Efocus%2C%2Ebtn%2Dwarning%5Bdisabled%5D%3Aactive%2C%2Ebtn%2Dwarning%5Bdisabled%5D%3Afocus%2C%2Ebtn%2Dwarning%5Bdisabled%5D%3Ahover%2Cfieldset%5Bdisabled%5D%20%2Ebtn%2Dwarning%2Cfieldset%5Bdisabled%5D%20%2Ebtn%2Dwarning%2Eactive%2Cfieldset%5Bdisabled%5D%20%2Ebtn%2Dwarning%2Efocus%2Cfieldset%5Bdisabled%5D%20%2Ebtn%2Dwarning%3Aactive%2Cfieldset%5Bdisabled%5D%20%2Ebtn%2Dwarning%3Afocus%2Cfieldset%5Bdisabled%5D%20%2Ebtn%2Dwarning%3Ahover%7Bbackground%2Dcolor%3A%23f0ad4e%3Bborder%2Dcolor%3A%23eea236%7D%2Ebtn%2Dwarning%20%2Ebadge%7Bcolor%3A%23f0ad4e%3Bbackground%2Dcolor%3A%23fff%7D%2Ebtn%2Ddanger%7Bcolor%3A%23fff%3Bbackground%2Dcolor%3A%23d9534f%3Bborder%2Dcolor%3A%23d43f3a%7D%2Ebtn%2Ddanger%2Efocus%2C%2Ebtn%2Ddanger%3Afocus%7Bcolor%3A%23fff%3Bbackground%2Dcolor%3A%23c9302c%3Bborder%2Dcolor%3A%23761c19%7D%2Ebtn%2Ddanger%3Ahover%7Bcolor%3A%23fff%3Bbackground%2Dcolor%3A%23c9302c%3Bborder%2Dcolor%3A%23ac2925%7D%2Ebtn%2Ddanger%2Eactive%2C%2Ebtn%2Ddanger%3Aactive%2C%2Eopen%3E%2Edropdown%2Dtoggle%2Ebtn%2Ddanger%7Bcolor%3A%23fff%3Bbackground%2Dcolor%3A%23c9302c%3Bborder%2Dcolor%3A%23ac2925%7D%2Ebtn%2Ddanger%2Eactive%2Efocus%2C%2Ebtn%2Ddanger%2Eactive%3Afocus%2C%2Ebtn%2Ddanger%2Eactive%3Ahover%2C%2Ebtn%2Ddanger%3Aactive%2Efocus%2C%2Ebtn%2Ddanger%3Aactive%3Afocus%2C%2Ebtn%2Ddanger%3Aactive%3Ahover%2C%2Eopen%3E%2Edropdown%2Dtoggle%2Ebtn%2Ddanger%2Efocus%2C%2Eopen%3E%2Edropdown%2Dtoggle%2Ebtn%2Ddanger%3Afocus%2C%2Eopen%3E%2Edropdown%2Dtoggle%2Ebtn%2Ddanger%3Ahover%7Bcolor%3A%23fff%3Bbackground%2Dcolor%3A%23ac2925%3Bborder%2Dcolor%3A%23761c19%7D%2Ebtn%2Ddanger%2Eactive%2C%2Ebtn%2Ddanger%3Aactive%2C%2Eopen%3E%2Edropdown%2Dtoggle%2Ebtn%2Ddanger%7Bbackground%2Dimage%3Anone%7D%2Ebtn%2Ddanger%2Edisabled%2C%2Ebtn%2Ddanger%2Edisabled%2Eactive%2C%2Ebtn%2Ddanger%2Edisabled%2Efocus%2C%2Ebtn%2Ddanger%2Edisabled%3Aactive%2C%2Ebtn%2Ddanger%2Edisabled%3Afocus%2C%2Ebtn%2Ddanger%2Edisabled%3Ahover%2C%2Ebtn%2Ddanger%5Bdisabled%5D%2C%2Ebtn%2Ddanger%5Bdisabled%5D%2Eactive%2C%2Ebtn%2Ddanger%5Bdisabled%5D%2Efocus%2C%2Ebtn%2Ddanger%5Bdisabled%5D%3Aactive%2C%2Ebtn%2Ddanger%5Bdisabled%5D%3Afocus%2C%2Ebtn%2Ddanger%5Bdisabled%5D%3Ahover%2Cfieldset%5Bdisabled%5D%20%2Ebtn%2Ddanger%2Cfieldset%5Bdisabled%5D%20%2Ebtn%2Ddanger%2Eactive%2Cfieldset%5Bdisabled%5D%20%2Ebtn%2Ddanger%2Efocus%2Cfieldset%5Bdisabled%5D%20%2Ebtn%2Ddanger%3Aactive%2Cfieldset%5Bdisabled%5D%20%2Ebtn%2Ddanger%3Afocus%2Cfieldset%5Bdisabled%5D%20%2Ebtn%2Ddanger%3Ahover%7Bbackground%2Dcolor%3A%23d9534f%3Bborder%2Dcolor%3A%23d43f3a%7D%2Ebtn%2Ddanger%20%2Ebadge%7Bcolor%3A%23d9534f%3Bbackground%2Dcolor%3A%23fff%7D%2Ebtn%2Dlink%7Bfont%2Dweight%3A400%3Bcolor%3A%23337ab7%3Bborder%2Dradius%3A0%7D%2Ebtn%2Dlink%2C%2Ebtn%2Dlink%2Eactive%2C%2Ebtn%2Dlink%3Aactive%2C%2Ebtn%2Dlink%5Bdisabled%5D%2Cfieldset%5Bdisabled%5D%20%2Ebtn%2Dlink%7Bbackground%2Dcolor%3Atransparent%3B%2Dwebkit%2Dbox%2Dshadow%3Anone%3Bbox%2Dshadow%3Anone%7D%2Ebtn%2Dlink%2C%2Ebtn%2Dlink%3Aactive%2C%2Ebtn%2Dlink%3Afocus%2C%2Ebtn%2Dlink%3Ahover%7Bborder%2Dcolor%3Atransparent%7D%2Ebtn%2Dlink%3Afocus%2C%2Ebtn%2Dlink%3Ahover%7Bcolor%3A%2323527c%3Btext%2Ddecoration%3Aunderline%3Bbackground%2Dcolor%3Atransparent%7D%2Ebtn%2Dlink%5Bdisabled%5D%3Afocus%2C%2Ebtn%2Dlink%5Bdisabled%5D%3Ahover%2Cfieldset%5Bdisabled%5D%20%2Ebtn%2Dlink%3Afocus%2Cfieldset%5Bdisabled%5D%20%2Ebtn%2Dlink%3Ahover%7Bcolor%3A%23777%3Btext%2Ddecoration%3Anone%7D%2Ebtn%2Dgroup%2Dlg%3E%2Ebtn%2C%2Ebtn%2Dlg%7Bpadding%3A10px%2016px%3Bfont%2Dsize%3A18px%3Bline%2Dheight%3A1%2E3333333%3Bborder%2Dradius%3A6px%7D%2Ebtn%2Dgroup%2Dsm%3E%2Ebtn%2C%2Ebtn%2Dsm%7Bpadding%3A5px%2010px%3Bfont%2Dsize%3A12px%3Bline%2Dheight%3A1%2E5%3Bborder%2Dradius%3A3px%7D%2Ebtn%2Dgroup%2Dxs%3E%2Ebtn%2C%2Ebtn%2Dxs%7Bpadding%3A1px%205px%3Bfont%2Dsize%3A12px%3Bline%2Dheight%3A1%2E5%3Bborder%2Dradius%3A3px%7D%2Ebtn%2Dblock%7Bdisplay%3Ablock%3Bwidth%3A100%25%7D%2Ebtn%2Dblock%2B%2Ebtn%2Dblock%7Bmargin%2Dtop%3A5px%7Dinput%5Btype%3Dbutton%5D%2Ebtn%2Dblock%2Cinput%5Btype%3Dreset%5D%2Ebtn%2Dblock%2Cinput%5Btype%3Dsubmit%5D%2Ebtn%2Dblock%7Bwidth%3A100%25%7D%2Efade%7Bopacity%3A0%3B%2Dwebkit%2Dtransition%3Aopacity%20%2E15s%20linear%3B%2Do%2Dtransition%3Aopacity%20%2E15s%20linear%3Btransition%3Aopacity%20%2E15s%20linear%7D%2Efade%2Ein%7Bopacity%3A1%7D%2Ecollapse%7Bdisplay%3Anone%7D%2Ecollapse%2Ein%7Bdisplay%3Ablock%7Dtr%2Ecollapse%2Ein%7Bdisplay%3Atable%2Drow%7Dtbody%2Ecollapse%2Ein%7Bdisplay%3Atable%2Drow%2Dgroup%7D%2Ecollapsing%7Bposition%3Arelative%3Bheight%3A0%3Boverflow%3Ahidden%3B%2Dwebkit%2Dtransition%2Dtiming%2Dfunction%3Aease%3B%2Do%2Dtransition%2Dtiming%2Dfunction%3Aease%3Btransition%2Dtiming%2Dfunction%3Aease%3B%2Dwebkit%2Dtransition%2Dduration%3A%2E35s%3B%2Do%2Dtransition%2Dduration%3A%2E35s%3Btransition%2Dduration%3A%2E35s%3B%2Dwebkit%2Dtransition%2Dproperty%3Aheight%2Cvisibility%3B%2Do%2Dtransition%2Dproperty%3Aheight%2Cvisibility%3Btransition%2Dproperty%3Aheight%2Cvisibility%7D%2Ecaret%7Bdisplay%3Ainline%2Dblock%3Bwidth%3A0%3Bheight%3A0%3Bmargin%2Dleft%3A2px%3Bvertical%2Dalign%3Amiddle%3Bborder%2Dtop%3A4px%20dashed%3Bborder%2Dtop%3A4px%20solid%5C9%3Bborder%2Dright%3A4px%20solid%20transparent%3Bborder%2Dleft%3A4px%20solid%20transparent%7D%2Edropdown%2C%2Edropup%7Bposition%3Arelative%7D%2Edropdown%2Dtoggle%3Afocus%7Boutline%3A0%7D%2Edropdown%2Dmenu%7Bposition%3Aabsolute%3Btop%3A100%25%3Bleft%3A0%3Bz%2Dindex%3A1000%3Bdisplay%3Anone%3Bfloat%3Aleft%3Bmin%2Dwidth%3A160px%3Bpadding%3A5px%200%3Bmargin%3A2px%200%200%3Bfont%2Dsize%3A14px%3Btext%2Dalign%3Aleft%3Blist%2Dstyle%3Anone%3Bbackground%2Dcolor%3A%23fff%3B%2Dwebkit%2Dbackground%2Dclip%3Apadding%2Dbox%3Bbackground%2Dclip%3Apadding%2Dbox%3Bborder%3A1px%20solid%20%23ccc%3Bborder%3A1px%20solid%20rgba%280%2C0%2C0%2C%2E15%29%3Bborder%2Dradius%3A4px%3B%2Dwebkit%2Dbox%2Dshadow%3A0%206px%2012px%20rgba%280%2C0%2C0%2C%2E175%29%3Bbox%2Dshadow%3A0%206px%2012px%20rgba%280%2C0%2C0%2C%2E175%29%7D%2Edropdown%2Dmenu%2Epull%2Dright%7Bright%3A0%3Bleft%3Aauto%7D%2Edropdown%2Dmenu%20%2Edivider%7Bheight%3A1px%3Bmargin%3A9px%200%3Boverflow%3Ahidden%3Bbackground%2Dcolor%3A%23e5e5e5%7D%2Edropdown%2Dmenu%3Eli%3Ea%7Bdisplay%3Ablock%3Bpadding%3A3px%2020px%3Bclear%3Aboth%3Bfont%2Dweight%3A400%3Bline%2Dheight%3A1%2E42857143%3Bcolor%3A%23333%3Bwhite%2Dspace%3Anowrap%7D%2Edropdown%2Dmenu%3Eli%3Ea%3Afocus%2C%2Edropdown%2Dmenu%3Eli%3Ea%3Ahover%7Bcolor%3A%23262626%3Btext%2Ddecoration%3Anone%3Bbackground%2Dcolor%3A%23f5f5f5%7D%2Edropdown%2Dmenu%3E%2Eactive%3Ea%2C%2Edropdown%2Dmenu%3E%2Eactive%3Ea%3Afocus%2C%2Edropdown%2Dmenu%3E%2Eactive%3Ea%3Ahover%7Bcolor%3A%23fff%3Btext%2Ddecoration%3Anone%3Bbackground%2Dcolor%3A%23337ab7%3Boutline%3A0%7D%2Edropdown%2Dmenu%3E%2Edisabled%3Ea%2C%2Edropdown%2Dmenu%3E%2Edisabled%3Ea%3Afocus%2C%2Edropdown%2Dmenu%3E%2Edisabled%3Ea%3Ahover%7Bcolor%3A%23777%7D%2Edropdown%2Dmenu%3E%2Edisabled%3Ea%3Afocus%2C%2Edropdown%2Dmenu%3E%2Edisabled%3Ea%3Ahover%7Btext%2Ddecoration%3Anone%3Bcursor%3Anot%2Dallowed%3Bbackground%2Dcolor%3Atransparent%3Bbackground%2Dimage%3Anone%3Bfilter%3Aprogid%3ADXImageTransform%2EMicrosoft%2Egradient%28enabled%3Dfalse%29%7D%2Eopen%3E%2Edropdown%2Dmenu%7Bdisplay%3Ablock%7D%2Eopen%3Ea%7Boutline%3A0%7D%2Edropdown%2Dmenu%2Dright%7Bright%3A0%3Bleft%3Aauto%7D%2Edropdown%2Dmenu%2Dleft%7Bright%3Aauto%3Bleft%3A0%7D%2Edropdown%2Dheader%7Bdisplay%3Ablock%3Bpadding%3A3px%2020px%3Bfont%2Dsize%3A12px%3Bline%2Dheight%3A1%2E42857143%3Bcolor%3A%23777%3Bwhite%2Dspace%3Anowrap%7D%2Edropdown%2Dbackdrop%7Bposition%3Afixed%3Btop%3A0%3Bright%3A0%3Bbottom%3A0%3Bleft%3A0%3Bz%2Dindex%3A990%7D%2Epull%2Dright%3E%2Edropdown%2Dmenu%7Bright%3A0%3Bleft%3Aauto%7D%2Edropup%20%2Ecaret%2C%2Enavbar%2Dfixed%2Dbottom%20%2Edropdown%20%2Ecaret%7Bcontent%3A%22%22%3Bborder%2Dtop%3A0%3Bborder%2Dbottom%3A4px%20dashed%3Bborder%2Dbottom%3A4px%20solid%5C9%7D%2Edropup%20%2Edropdown%2Dmenu%2C%2Enavbar%2Dfixed%2Dbottom%20%2Edropdown%20%2Edropdown%2Dmenu%7Btop%3Aauto%3Bbottom%3A100%25%3Bmargin%2Dbottom%3A2px%7D%40media%20%28min%2Dwidth%3A768px%29%7B%2Enavbar%2Dright%20%2Edropdown%2Dmenu%7Bright%3A0%3Bleft%3Aauto%7D%2Enavbar%2Dright%20%2Edropdown%2Dmenu%2Dleft%7Bright%3Aauto%3Bleft%3A0%7D%7D%2Ebtn%2Dgroup%2C%2Ebtn%2Dgroup%2Dvertical%7Bposition%3Arelative%3Bdisplay%3Ainline%2Dblock%3Bvertical%2Dalign%3Amiddle%7D%2Ebtn%2Dgroup%2Dvertical%3E%2Ebtn%2C%2Ebtn%2Dgroup%3E%2Ebtn%7Bposition%3Arelative%3Bfloat%3Aleft%7D%2Ebtn%2Dgroup%2Dvertical%3E%2Ebtn%2Eactive%2C%2Ebtn%2Dgroup%2Dvertical%3E%2Ebtn%3Aactive%2C%2Ebtn%2Dgroup%2Dvertical%3E%2Ebtn%3Afocus%2C%2Ebtn%2Dgroup%2Dvertical%3E%2Ebtn%3Ahover%2C%2Ebtn%2Dgroup%3E%2Ebtn%2Eactive%2C%2Ebtn%2Dgroup%3E%2Ebtn%3Aactive%2C%2Ebtn%2Dgroup%3E%2Ebtn%3Afocus%2C%2Ebtn%2Dgroup%3E%2Ebtn%3Ahover%7Bz%2Dindex%3A2%7D%2Ebtn%2Dgroup%20%2Ebtn%2B%2Ebtn%2C%2Ebtn%2Dgroup%20%2Ebtn%2B%2Ebtn%2Dgroup%2C%2Ebtn%2Dgroup%20%2Ebtn%2Dgroup%2B%2Ebtn%2C%2Ebtn%2Dgroup%20%2Ebtn%2Dgroup%2B%2Ebtn%2Dgroup%7Bmargin%2Dleft%3A%2D1px%7D%2Ebtn%2Dtoolbar%7Bmargin%2Dleft%3A%2D5px%7D%2Ebtn%2Dtoolbar%20%2Ebtn%2C%2Ebtn%2Dtoolbar%20%2Ebtn%2Dgroup%2C%2Ebtn%2Dtoolbar%20%2Einput%2Dgroup%7Bfloat%3Aleft%7D%2Ebtn%2Dtoolbar%3E%2Ebtn%2C%2Ebtn%2Dtoolbar%3E%2Ebtn%2Dgroup%2C%2Ebtn%2Dtoolbar%3E%2Einput%2Dgroup%7Bmargin%2Dleft%3A5px%7D%2Ebtn%2Dgroup%3E%2Ebtn%3Anot%28%3Afirst%2Dchild%29%3Anot%28%3Alast%2Dchild%29%3Anot%28%2Edropdown%2Dtoggle%29%7Bborder%2Dradius%3A0%7D%2Ebtn%2Dgroup%3E%2Ebtn%3Afirst%2Dchild%7Bmargin%2Dleft%3A0%7D%2Ebtn%2Dgroup%3E%2Ebtn%3Afirst%2Dchild%3Anot%28%3Alast%2Dchild%29%3Anot%28%2Edropdown%2Dtoggle%29%7Bborder%2Dtop%2Dright%2Dradius%3A0%3Bborder%2Dbottom%2Dright%2Dradius%3A0%7D%2Ebtn%2Dgroup%3E%2Ebtn%3Alast%2Dchild%3Anot%28%3Afirst%2Dchild%29%2C%2Ebtn%2Dgroup%3E%2Edropdown%2Dtoggle%3Anot%28%3Afirst%2Dchild%29%7Bborder%2Dtop%2Dleft%2Dradius%3A0%3Bborder%2Dbottom%2Dleft%2Dradius%3A0%7D%2Ebtn%2Dgroup%3E%2Ebtn%2Dgroup%7Bfloat%3Aleft%7D%2Ebtn%2Dgroup%3E%2Ebtn%2Dgroup%3Anot%28%3Afirst%2Dchild%29%3Anot%28%3Alast%2Dchild%29%3E%2Ebtn%7Bborder%2Dradius%3A0%7D%2Ebtn%2Dgroup%3E%2Ebtn%2Dgroup%3Afirst%2Dchild%3Anot%28%3Alast%2Dchild%29%3E%2Ebtn%3Alast%2Dchild%2C%2Ebtn%2Dgroup%3E%2Ebtn%2Dgroup%3Afirst%2Dchild%3Anot%28%3Alast%2Dchild%29%3E%2Edropdown%2Dtoggle%7Bborder%2Dtop%2Dright%2Dradius%3A0%3Bborder%2Dbottom%2Dright%2Dradius%3A0%7D%2Ebtn%2Dgroup%3E%2Ebtn%2Dgroup%3Alast%2Dchild%3Anot%28%3Afirst%2Dchild%29%3E%2Ebtn%3Afirst%2Dchild%7Bborder%2Dtop%2Dleft%2Dradius%3A0%3Bborder%2Dbottom%2Dleft%2Dradius%3A0%7D%2Ebtn%2Dgroup%20%2Edropdown%2Dtoggle%3Aactive%2C%2Ebtn%2Dgroup%2Eopen%20%2Edropdown%2Dtoggle%7Boutline%3A0%7D%2Ebtn%2Dgroup%3E%2Ebtn%2B%2Edropdown%2Dtoggle%7Bpadding%2Dright%3A8px%3Bpadding%2Dleft%3A8px%7D%2Ebtn%2Dgroup%3E%2Ebtn%2Dlg%2B%2Edropdown%2Dtoggle%7Bpadding%2Dright%3A12px%3Bpadding%2Dleft%3A12px%7D%2Ebtn%2Dgroup%2Eopen%20%2Edropdown%2Dtoggle%7B%2Dwebkit%2Dbox%2Dshadow%3Ainset%200%203px%205px%20rgba%280%2C0%2C0%2C%2E125%29%3Bbox%2Dshadow%3Ainset%200%203px%205px%20rgba%280%2C0%2C0%2C%2E125%29%7D%2Ebtn%2Dgroup%2Eopen%20%2Edropdown%2Dtoggle%2Ebtn%2Dlink%7B%2Dwebkit%2Dbox%2Dshadow%3Anone%3Bbox%2Dshadow%3Anone%7D%2Ebtn%20%2Ecaret%7Bmargin%2Dleft%3A0%7D%2Ebtn%2Dlg%20%2Ecaret%7Bborder%2Dwidth%3A5px%205px%200%3Bborder%2Dbottom%2Dwidth%3A0%7D%2Edropup%20%2Ebtn%2Dlg%20%2Ecaret%7Bborder%2Dwidth%3A0%205px%205px%7D%2Ebtn%2Dgroup%2Dvertical%3E%2Ebtn%2C%2Ebtn%2Dgroup%2Dvertical%3E%2Ebtn%2Dgroup%2C%2Ebtn%2Dgroup%2Dvertical%3E%2Ebtn%2Dgroup%3E%2Ebtn%7Bdisplay%3Ablock%3Bfloat%3Anone%3Bwidth%3A100%25%3Bmax%2Dwidth%3A100%25%7D%2Ebtn%2Dgroup%2Dvertical%3E%2Ebtn%2Dgroup%3E%2Ebtn%7Bfloat%3Anone%7D%2Ebtn%2Dgroup%2Dvertical%3E%2Ebtn%2B%2Ebtn%2C%2Ebtn%2Dgroup%2Dvertical%3E%2Ebtn%2B%2Ebtn%2Dgroup%2C%2Ebtn%2Dgroup%2Dvertical%3E%2Ebtn%2Dgroup%2B%2Ebtn%2C%2Ebtn%2Dgroup%2Dvertical%3E%2Ebtn%2Dgroup%2B%2Ebtn%2Dgroup%7Bmargin%2Dtop%3A%2D1px%3Bmargin%2Dleft%3A0%7D%2Ebtn%2Dgroup%2Dvertical%3E%2Ebtn%3Anot%28%3Afirst%2Dchild%29%3Anot%28%3Alast%2Dchild%29%7Bborder%2Dradius%3A0%7D%2Ebtn%2Dgroup%2Dvertical%3E%2Ebtn%3Afirst%2Dchild%3Anot%28%3Alast%2Dchild%29%7Bborder%2Dtop%2Dright%2Dradius%3A4px%3Bborder%2Dbottom%2Dright%2Dradius%3A0%3Bborder%2Dbottom%2Dleft%2Dradius%3A0%7D%2Ebtn%2Dgroup%2Dvertical%3E%2Ebtn%3Alast%2Dchild%3Anot%28%3Afirst%2Dchild%29%7Bborder%2Dtop%2Dleft%2Dradius%3A0%3Bborder%2Dtop%2Dright%2Dradius%3A0%3Bborder%2Dbottom%2Dleft%2Dradius%3A4px%7D%2Ebtn%2Dgroup%2Dvertical%3E%2Ebtn%2Dgroup%3Anot%28%3Afirst%2Dchild%29%3Anot%28%3Alast%2Dchild%29%3E%2Ebtn%7Bborder%2Dradius%3A0%7D%2Ebtn%2Dgroup%2Dvertical%3E%2Ebtn%2Dgroup%3Afirst%2Dchild%3Anot%28%3Alast%2Dchild%29%3E%2Ebtn%3Alast%2Dchild%2C%2Ebtn%2Dgroup%2Dvertical%3E%2Ebtn%2Dgroup%3Afirst%2Dchild%3Anot%28%3Alast%2Dchild%29%3E%2Edropdown%2Dtoggle%7Bborder%2Dbottom%2Dright%2Dradius%3A0%3Bborder%2Dbottom%2Dleft%2Dradius%3A0%7D%2Ebtn%2Dgroup%2Dvertical%3E%2Ebtn%2Dgroup%3Alast%2Dchild%3Anot%28%3Afirst%2Dchild%29%3E%2Ebtn%3Afirst%2Dchild%7Bborder%2Dtop%2Dleft%2Dradius%3A0%3Bborder%2Dtop%2Dright%2Dradius%3A0%7D%2Ebtn%2Dgroup%2Djustified%7Bdisplay%3Atable%3Bwidth%3A100%25%3Btable%2Dlayout%3Afixed%3Bborder%2Dcollapse%3Aseparate%7D%2Ebtn%2Dgroup%2Djustified%3E%2Ebtn%2C%2Ebtn%2Dgroup%2Djustified%3E%2Ebtn%2Dgroup%7Bdisplay%3Atable%2Dcell%3Bfloat%3Anone%3Bwidth%3A1%25%7D%2Ebtn%2Dgroup%2Djustified%3E%2Ebtn%2Dgroup%20%2Ebtn%7Bwidth%3A100%25%7D%2Ebtn%2Dgroup%2Djustified%3E%2Ebtn%2Dgroup%20%2Edropdown%2Dmenu%7Bleft%3Aauto%7D%5Bdata%2Dtoggle%3Dbuttons%5D%3E%2Ebtn%20input%5Btype%3Dcheckbox%5D%2C%5Bdata%2Dtoggle%3Dbuttons%5D%3E%2Ebtn%20input%5Btype%3Dradio%5D%2C%5Bdata%2Dtoggle%3Dbuttons%5D%3E%2Ebtn%2Dgroup%3E%2Ebtn%20input%5Btype%3Dcheckbox%5D%2C%5Bdata%2Dtoggle%3Dbuttons%5D%3E%2Ebtn%2Dgroup%3E%2Ebtn%20input%5Btype%3Dradio%5D%7Bposition%3Aabsolute%3Bclip%3Arect%280%2C0%2C0%2C0%29%3Bpointer%2Devents%3Anone%7D%2Einput%2Dgroup%7Bposition%3Arelative%3Bdisplay%3Atable%3Bborder%2Dcollapse%3Aseparate%7D%2Einput%2Dgroup%5Bclass%2A%3Dcol%2D%5D%7Bfloat%3Anone%3Bpadding%2Dright%3A0%3Bpadding%2Dleft%3A0%7D%2Einput%2Dgroup%20%2Eform%2Dcontrol%7Bposition%3Arelative%3Bz%2Dindex%3A2%3Bfloat%3Aleft%3Bwidth%3A100%25%3Bmargin%2Dbottom%3A0%7D%2Einput%2Dgroup%2Dlg%3E%2Eform%2Dcontrol%2C%2Einput%2Dgroup%2Dlg%3E%2Einput%2Dgroup%2Daddon%2C%2Einput%2Dgroup%2Dlg%3E%2Einput%2Dgroup%2Dbtn%3E%2Ebtn%7Bheight%3A46px%3Bpadding%3A10px%2016px%3Bfont%2Dsize%3A18px%3Bline%2Dheight%3A1%2E3333333%3Bborder%2Dradius%3A6px%7Dselect%2Einput%2Dgroup%2Dlg%3E%2Eform%2Dcontrol%2Cselect%2Einput%2Dgroup%2Dlg%3E%2Einput%2Dgroup%2Daddon%2Cselect%2Einput%2Dgroup%2Dlg%3E%2Einput%2Dgroup%2Dbtn%3E%2Ebtn%7Bheight%3A46px%3Bline%2Dheight%3A46px%7Dselect%5Bmultiple%5D%2Einput%2Dgroup%2Dlg%3E%2Eform%2Dcontrol%2Cselect%5Bmultiple%5D%2Einput%2Dgroup%2Dlg%3E%2Einput%2Dgroup%2Daddon%2Cselect%5Bmultiple%5D%2Einput%2Dgroup%2Dlg%3E%2Einput%2Dgroup%2Dbtn%3E%2Ebtn%2Ctextarea%2Einput%2Dgroup%2Dlg%3E%2Eform%2Dcontrol%2Ctextarea%2Einput%2Dgroup%2Dlg%3E%2Einput%2Dgroup%2Daddon%2Ctextarea%2Einput%2Dgroup%2Dlg%3E%2Einput%2Dgroup%2Dbtn%3E%2Ebtn%7Bheight%3Aauto%7D%2Einput%2Dgroup%2Dsm%3E%2Eform%2Dcontrol%2C%2Einput%2Dgroup%2Dsm%3E%2Einput%2Dgroup%2Daddon%2C%2Einput%2Dgroup%2Dsm%3E%2Einput%2Dgroup%2Dbtn%3E%2Ebtn%7Bheight%3A30px%3Bpadding%3A5px%2010px%3Bfont%2Dsize%3A12px%3Bline%2Dheight%3A1%2E5%3Bborder%2Dradius%3A3px%7Dselect%2Einput%2Dgroup%2Dsm%3E%2Eform%2Dcontrol%2Cselect%2Einput%2Dgroup%2Dsm%3E%2Einput%2Dgroup%2Daddon%2Cselect%2Einput%2Dgroup%2Dsm%3E%2Einput%2Dgroup%2Dbtn%3E%2Ebtn%7Bheight%3A30px%3Bline%2Dheight%3A30px%7Dselect%5Bmultiple%5D%2Einput%2Dgroup%2Dsm%3E%2Eform%2Dcontrol%2Cselect%5Bmultiple%5D%2Einput%2Dgroup%2Dsm%3E%2Einput%2Dgroup%2Daddon%2Cselect%5Bmultiple%5D%2Einput%2Dgroup%2Dsm%3E%2Einput%2Dgroup%2Dbtn%3E%2Ebtn%2Ctextarea%2Einput%2Dgroup%2Dsm%3E%2Eform%2Dcontrol%2Ctextarea%2Einput%2Dgroup%2Dsm%3E%2Einput%2Dgroup%2Daddon%2Ctextarea%2Einput%2Dgroup%2Dsm%3E%2Einput%2Dgroup%2Dbtn%3E%2Ebtn%7Bheight%3Aauto%7D%2Einput%2Dgroup%20%2Eform%2Dcontrol%2C%2Einput%2Dgroup%2Daddon%2C%2Einput%2Dgroup%2Dbtn%7Bdisplay%3Atable%2Dcell%7D%2Einput%2Dgroup%20%2Eform%2Dcontrol%3Anot%28%3Afirst%2Dchild%29%3Anot%28%3Alast%2Dchild%29%2C%2Einput%2Dgroup%2Daddon%3Anot%28%3Afirst%2Dchild%29%3Anot%28%3Alast%2Dchild%29%2C%2Einput%2Dgroup%2Dbtn%3Anot%28%3Afirst%2Dchild%29%3Anot%28%3Alast%2Dchild%29%7Bborder%2Dradius%3A0%7D%2Einput%2Dgroup%2Daddon%2C%2Einput%2Dgroup%2Dbtn%7Bwidth%3A1%25%3Bwhite%2Dspace%3Anowrap%3Bvertical%2Dalign%3Amiddle%7D%2Einput%2Dgroup%2Daddon%7Bpadding%3A6px%2012px%3Bfont%2Dsize%3A14px%3Bfont%2Dweight%3A400%3Bline%2Dheight%3A1%3Bcolor%3A%23555%3Btext%2Dalign%3Acenter%3Bbackground%2Dcolor%3A%23eee%3Bborder%3A1px%20solid%20%23ccc%3Bborder%2Dradius%3A4px%7D%2Einput%2Dgroup%2Daddon%2Einput%2Dsm%7Bpadding%3A5px%2010px%3Bfont%2Dsize%3A12px%3Bborder%2Dradius%3A3px%7D%2Einput%2Dgroup%2Daddon%2Einput%2Dlg%7Bpadding%3A10px%2016px%3Bfont%2Dsize%3A18px%3Bborder%2Dradius%3A6px%7D%2Einput%2Dgroup%2Daddon%20input%5Btype%3Dcheckbox%5D%2C%2Einput%2Dgroup%2Daddon%20input%5Btype%3Dradio%5D%7Bmargin%2Dtop%3A0%7D%2Einput%2Dgroup%20%2Eform%2Dcontrol%3Afirst%2Dchild%2C%2Einput%2Dgroup%2Daddon%3Afirst%2Dchild%2C%2Einput%2Dgroup%2Dbtn%3Afirst%2Dchild%3E%2Ebtn%2C%2Einput%2Dgroup%2Dbtn%3Afirst%2Dchild%3E%2Ebtn%2Dgroup%3E%2Ebtn%2C%2Einput%2Dgroup%2Dbtn%3Afirst%2Dchild%3E%2Edropdown%2Dtoggle%2C%2Einput%2Dgroup%2Dbtn%3Alast%2Dchild%3E%2Ebtn%2Dgroup%3Anot%28%3Alast%2Dchild%29%3E%2Ebtn%2C%2Einput%2Dgroup%2Dbtn%3Alast%2Dchild%3E%2Ebtn%3Anot%28%3Alast%2Dchild%29%3Anot%28%2Edropdown%2Dtoggle%29%7Bborder%2Dtop%2Dright%2Dradius%3A0%3Bborder%2Dbottom%2Dright%2Dradius%3A0%7D%2Einput%2Dgroup%2Daddon%3Afirst%2Dchild%7Bborder%2Dright%3A0%7D%2Einput%2Dgroup%20%2Eform%2Dcontrol%3Alast%2Dchild%2C%2Einput%2Dgroup%2Daddon%3Alast%2Dchild%2C%2Einput%2Dgroup%2Dbtn%3Afirst%2Dchild%3E%2Ebtn%2Dgroup%3Anot%28%3Afirst%2Dchild%29%3E%2Ebtn%2C%2Einput%2Dgroup%2Dbtn%3Afirst%2Dchild%3E%2Ebtn%3Anot%28%3Afirst%2Dchild%29%2C%2Einput%2Dgroup%2Dbtn%3Alast%2Dchild%3E%2Ebtn%2C%2Einput%2Dgroup%2Dbtn%3Alast%2Dchild%3E%2Ebtn%2Dgroup%3E%2Ebtn%2C%2Einput%2Dgroup%2Dbtn%3Alast%2Dchild%3E%2Edropdown%2Dtoggle%7Bborder%2Dtop%2Dleft%2Dradius%3A0%3Bborder%2Dbottom%2Dleft%2Dradius%3A0%7D%2Einput%2Dgroup%2Daddon%3Alast%2Dchild%7Bborder%2Dleft%3A0%7D%2Einput%2Dgroup%2Dbtn%7Bposition%3Arelative%3Bfont%2Dsize%3A0%3Bwhite%2Dspace%3Anowrap%7D%2Einput%2Dgroup%2Dbtn%3E%2Ebtn%7Bposition%3Arelative%7D%2Einput%2Dgroup%2Dbtn%3E%2Ebtn%2B%2Ebtn%7Bmargin%2Dleft%3A%2D1px%7D%2Einput%2Dgroup%2Dbtn%3E%2Ebtn%3Aactive%2C%2Einput%2Dgroup%2Dbtn%3E%2Ebtn%3Afocus%2C%2Einput%2Dgroup%2Dbtn%3E%2Ebtn%3Ahover%7Bz%2Dindex%3A2%7D%2Einput%2Dgroup%2Dbtn%3Afirst%2Dchild%3E%2Ebtn%2C%2Einput%2Dgroup%2Dbtn%3Afirst%2Dchild%3E%2Ebtn%2Dgroup%7Bmargin%2Dright%3A%2D1px%7D%2Einput%2Dgroup%2Dbtn%3Alast%2Dchild%3E%2Ebtn%2C%2Einput%2Dgroup%2Dbtn%3Alast%2Dchild%3E%2Ebtn%2Dgroup%7Bz%2Dindex%3A2%3Bmargin%2Dleft%3A%2D1px%7D%2Enav%7Bpadding%2Dleft%3A0%3Bmargin%2Dbottom%3A0%3Blist%2Dstyle%3Anone%7D%2Enav%3Eli%7Bposition%3Arelative%3Bdisplay%3Ablock%7D%2Enav%3Eli%3Ea%7Bposition%3Arelative%3Bdisplay%3Ablock%3Bpadding%3A10px%2015px%7D%2Enav%3Eli%3Ea%3Afocus%2C%2Enav%3Eli%3Ea%3Ahover%7Btext%2Ddecoration%3Anone%3Bbackground%2Dcolor%3A%23eee%7D%2Enav%3Eli%2Edisabled%3Ea%7Bcolor%3A%23777%7D%2Enav%3Eli%2Edisabled%3Ea%3Afocus%2C%2Enav%3Eli%2Edisabled%3Ea%3Ahover%7Bcolor%3A%23777%3Btext%2Ddecoration%3Anone%3Bcursor%3Anot%2Dallowed%3Bbackground%2Dcolor%3Atransparent%7D%2Enav%20%2Eopen%3Ea%2C%2Enav%20%2Eopen%3Ea%3Afocus%2C%2Enav%20%2Eopen%3Ea%3Ahover%7Bbackground%2Dcolor%3A%23eee%3Bborder%2Dcolor%3A%23337ab7%7D%2Enav%20%2Enav%2Ddivider%7Bheight%3A1px%3Bmargin%3A9px%200%3Boverflow%3Ahidden%3Bbackground%2Dcolor%3A%23e5e5e5%7D%2Enav%3Eli%3Ea%3Eimg%7Bmax%2Dwidth%3Anone%7D%2Enav%2Dtabs%7Bborder%2Dbottom%3A1px%20solid%20%23ddd%7D%2Enav%2Dtabs%3Eli%7Bfloat%3Aleft%3Bmargin%2Dbottom%3A%2D1px%7D%2Enav%2Dtabs%3Eli%3Ea%7Bmargin%2Dright%3A2px%3Bline%2Dheight%3A1%2E42857143%3Bborder%3A1px%20solid%20transparent%3Bborder%2Dradius%3A4px%204px%200%200%7D%2Enav%2Dtabs%3Eli%3Ea%3Ahover%7Bborder%2Dcolor%3A%23eee%20%23eee%20%23ddd%7D%2Enav%2Dtabs%3Eli%2Eactive%3Ea%2C%2Enav%2Dtabs%3Eli%2Eactive%3Ea%3Afocus%2C%2Enav%2Dtabs%3Eli%2Eactive%3Ea%3Ahover%7Bcolor%3A%23555%3Bcursor%3Adefault%3Bbackground%2Dcolor%3A%23fff%3Bborder%3A1px%20solid%20%23ddd%3Bborder%2Dbottom%2Dcolor%3Atransparent%7D%2Enav%2Dtabs%2Enav%2Djustified%7Bwidth%3A100%25%3Bborder%2Dbottom%3A0%7D%2Enav%2Dtabs%2Enav%2Djustified%3Eli%7Bfloat%3Anone%7D%2Enav%2Dtabs%2Enav%2Djustified%3Eli%3Ea%7Bmargin%2Dbottom%3A5px%3Btext%2Dalign%3Acenter%7D%2Enav%2Dtabs%2Enav%2Djustified%3E%2Edropdown%20%2Edropdown%2Dmenu%7Btop%3Aauto%3Bleft%3Aauto%7D%40media%20%28min%2Dwidth%3A768px%29%7B%2Enav%2Dtabs%2Enav%2Djustified%3Eli%7Bdisplay%3Atable%2Dcell%3Bwidth%3A1%25%7D%2Enav%2Dtabs%2Enav%2Djustified%3Eli%3Ea%7Bmargin%2Dbottom%3A0%7D%7D%2Enav%2Dtabs%2Enav%2Djustified%3Eli%3Ea%7Bmargin%2Dright%3A0%3Bborder%2Dradius%3A4px%7D%2Enav%2Dtabs%2Enav%2Djustified%3E%2Eactive%3Ea%2C%2Enav%2Dtabs%2Enav%2Djustified%3E%2Eactive%3Ea%3Afocus%2C%2Enav%2Dtabs%2Enav%2Djustified%3E%2Eactive%3Ea%3Ahover%7Bborder%3A1px%20solid%20%23ddd%7D%40media%20%28min%2Dwidth%3A768px%29%7B%2Enav%2Dtabs%2Enav%2Djustified%3Eli%3Ea%7Bborder%2Dbottom%3A1px%20solid%20%23ddd%3Bborder%2Dradius%3A4px%204px%200%200%7D%2Enav%2Dtabs%2Enav%2Djustified%3E%2Eactive%3Ea%2C%2Enav%2Dtabs%2Enav%2Djustified%3E%2Eactive%3Ea%3Afocus%2C%2Enav%2Dtabs%2Enav%2Djustified%3E%2Eactive%3Ea%3Ahover%7Bborder%2Dbottom%2Dcolor%3A%23fff%7D%7D%2Enav%2Dpills%3Eli%7Bfloat%3Aleft%7D%2Enav%2Dpills%3Eli%3Ea%7Bborder%2Dradius%3A4px%7D%2Enav%2Dpills%3Eli%2Bli%7Bmargin%2Dleft%3A2px%7D%2Enav%2Dpills%3Eli%2Eactive%3Ea%2C%2Enav%2Dpills%3Eli%2Eactive%3Ea%3Afocus%2C%2Enav%2Dpills%3Eli%2Eactive%3Ea%3Ahover%7Bcolor%3A%23fff%3Bbackground%2Dcolor%3A%23337ab7%7D%2Enav%2Dstacked%3Eli%7Bfloat%3Anone%7D%2Enav%2Dstacked%3Eli%2Bli%7Bmargin%2Dtop%3A2px%3Bmargin%2Dleft%3A0%7D%2Enav%2Djustified%7Bwidth%3A100%25%7D%2Enav%2Djustified%3Eli%7Bfloat%3Anone%7D%2Enav%2Djustified%3Eli%3Ea%7Bmargin%2Dbottom%3A5px%3Btext%2Dalign%3Acenter%7D%2Enav%2Djustified%3E%2Edropdown%20%2Edropdown%2Dmenu%7Btop%3Aauto%3Bleft%3Aauto%7D%40media%20%28min%2Dwidth%3A768px%29%7B%2Enav%2Djustified%3Eli%7Bdisplay%3Atable%2Dcell%3Bwidth%3A1%25%7D%2Enav%2Djustified%3Eli%3Ea%7Bmargin%2Dbottom%3A0%7D%7D%2Enav%2Dtabs%2Djustified%7Bborder%2Dbottom%3A0%7D%2Enav%2Dtabs%2Djustified%3Eli%3Ea%7Bmargin%2Dright%3A0%3Bborder%2Dradius%3A4px%7D%2Enav%2Dtabs%2Djustified%3E%2Eactive%3Ea%2C%2Enav%2Dtabs%2Djustified%3E%2Eactive%3Ea%3Afocus%2C%2Enav%2Dtabs%2Djustified%3E%2Eactive%3Ea%3Ahover%7Bborder%3A1px%20solid%20%23ddd%7D%40media%20%28min%2Dwidth%3A768px%29%7B%2Enav%2Dtabs%2Djustified%3Eli%3Ea%7Bborder%2Dbottom%3A1px%20solid%20%23ddd%3Bborder%2Dradius%3A4px%204px%200%200%7D%2Enav%2Dtabs%2Djustified%3E%2Eactive%3Ea%2C%2Enav%2Dtabs%2Djustified%3E%2Eactive%3Ea%3Afocus%2C%2Enav%2Dtabs%2Djustified%3E%2Eactive%3Ea%3Ahover%7Bborder%2Dbottom%2Dcolor%3A%23fff%7D%7D%2Etab%2Dcontent%3E%2Etab%2Dpane%7Bdisplay%3Anone%7D%2Etab%2Dcontent%3E%2Eactive%7Bdisplay%3Ablock%7D%2Enav%2Dtabs%20%2Edropdown%2Dmenu%7Bmargin%2Dtop%3A%2D1px%3Bborder%2Dtop%2Dleft%2Dradius%3A0%3Bborder%2Dtop%2Dright%2Dradius%3A0%7D%2Enavbar%7Bposition%3Arelative%3Bmin%2Dheight%3A50px%3Bmargin%2Dbottom%3A20px%3Bborder%3A1px%20solid%20transparent%7D%40media%20%28min%2Dwidth%3A768px%29%7B%2Enavbar%7Bborder%2Dradius%3A4px%7D%7D%40media%20%28min%2Dwidth%3A768px%29%7B%2Enavbar%2Dheader%7Bfloat%3Aleft%7D%7D%2Enavbar%2Dcollapse%7Bpadding%2Dright%3A15px%3Bpadding%2Dleft%3A15px%3Boverflow%2Dx%3Avisible%3B%2Dwebkit%2Doverflow%2Dscrolling%3Atouch%3Bborder%2Dtop%3A1px%20solid%20transparent%3B%2Dwebkit%2Dbox%2Dshadow%3Ainset%200%201px%200%20rgba%28255%2C255%2C255%2C%2E1%29%3Bbox%2Dshadow%3Ainset%200%201px%200%20rgba%28255%2C255%2C255%2C%2E1%29%7D%2Enavbar%2Dcollapse%2Ein%7Boverflow%2Dy%3Aauto%7D%40media%20%28min%2Dwidth%3A768px%29%7B%2Enavbar%2Dcollapse%7Bwidth%3Aauto%3Bborder%2Dtop%3A0%3B%2Dwebkit%2Dbox%2Dshadow%3Anone%3Bbox%2Dshadow%3Anone%7D%2Enavbar%2Dcollapse%2Ecollapse%7Bdisplay%3Ablock%21important%3Bheight%3Aauto%21important%3Bpadding%2Dbottom%3A0%3Boverflow%3Avisible%21important%7D%2Enavbar%2Dcollapse%2Ein%7Boverflow%2Dy%3Avisible%7D%2Enavbar%2Dfixed%2Dbottom%20%2Enavbar%2Dcollapse%2C%2Enavbar%2Dfixed%2Dtop%20%2Enavbar%2Dcollapse%2C%2Enavbar%2Dstatic%2Dtop%20%2Enavbar%2Dcollapse%7Bpadding%2Dright%3A0%3Bpadding%2Dleft%3A0%7D%7D%2Enavbar%2Dfixed%2Dbottom%20%2Enavbar%2Dcollapse%2C%2Enavbar%2Dfixed%2Dtop%20%2Enavbar%2Dcollapse%7Bmax%2Dheight%3A340px%7D%40media%20%28max%2Ddevice%2Dwidth%3A480px%29%20and%20%28orientation%3Alandscape%29%7B%2Enavbar%2Dfixed%2Dbottom%20%2Enavbar%2Dcollapse%2C%2Enavbar%2Dfixed%2Dtop%20%2Enavbar%2Dcollapse%7Bmax%2Dheight%3A200px%7D%7D%2Econtainer%2Dfluid%3E%2Enavbar%2Dcollapse%2C%2Econtainer%2Dfluid%3E%2Enavbar%2Dheader%2C%2Econtainer%3E%2Enavbar%2Dcollapse%2C%2Econtainer%3E%2Enavbar%2Dheader%7Bmargin%2Dright%3A%2D15px%3Bmargin%2Dleft%3A%2D15px%7D%40media%20%28min%2Dwidth%3A768px%29%7B%2Econtainer%2Dfluid%3E%2Enavbar%2Dcollapse%2C%2Econtainer%2Dfluid%3E%2Enavbar%2Dheader%2C%2Econtainer%3E%2Enavbar%2Dcollapse%2C%2Econtainer%3E%2Enavbar%2Dheader%7Bmargin%2Dright%3A0%3Bmargin%2Dleft%3A0%7D%7D%2Enavbar%2Dstatic%2Dtop%7Bz%2Dindex%3A1000%3Bborder%2Dwidth%3A0%200%201px%7D%40media%20%28min%2Dwidth%3A768px%29%7B%2Enavbar%2Dstatic%2Dtop%7Bborder%2Dradius%3A0%7D%7D%2Enavbar%2Dfixed%2Dbottom%2C%2Enavbar%2Dfixed%2Dtop%7Bposition%3Afixed%3Bright%3A0%3Bleft%3A0%3Bz%2Dindex%3A1030%7D%40media%20%28min%2Dwidth%3A768px%29%7B%2Enavbar%2Dfixed%2Dbottom%2C%2Enavbar%2Dfixed%2Dtop%7Bborder%2Dradius%3A0%7D%7D%2Enavbar%2Dfixed%2Dtop%7Btop%3A0%3Bborder%2Dwidth%3A0%200%201px%7D%2Enavbar%2Dfixed%2Dbottom%7Bbottom%3A0%3Bmargin%2Dbottom%3A0%3Bborder%2Dwidth%3A1px%200%200%7D%2Enavbar%2Dbrand%7Bfloat%3Aleft%3Bheight%3A50px%3Bpadding%3A15px%2015px%3Bfont%2Dsize%3A18px%3Bline%2Dheight%3A20px%7D%2Enavbar%2Dbrand%3Afocus%2C%2Enavbar%2Dbrand%3Ahover%7Btext%2Ddecoration%3Anone%7D%2Enavbar%2Dbrand%3Eimg%7Bdisplay%3Ablock%7D%40media%20%28min%2Dwidth%3A768px%29%7B%2Enavbar%3E%2Econtainer%20%2Enavbar%2Dbrand%2C%2Enavbar%3E%2Econtainer%2Dfluid%20%2Enavbar%2Dbrand%7Bmargin%2Dleft%3A%2D15px%7D%7D%2Enavbar%2Dtoggle%7Bposition%3Arelative%3Bfloat%3Aright%3Bpadding%3A9px%2010px%3Bmargin%2Dtop%3A8px%3Bmargin%2Dright%3A15px%3Bmargin%2Dbottom%3A8px%3Bbackground%2Dcolor%3Atransparent%3Bbackground%2Dimage%3Anone%3Bborder%3A1px%20solid%20transparent%3Bborder%2Dradius%3A4px%7D%2Enavbar%2Dtoggle%3Afocus%7Boutline%3A0%7D%2Enavbar%2Dtoggle%20%2Eicon%2Dbar%7Bdisplay%3Ablock%3Bwidth%3A22px%3Bheight%3A2px%3Bborder%2Dradius%3A1px%7D%2Enavbar%2Dtoggle%20%2Eicon%2Dbar%2B%2Eicon%2Dbar%7Bmargin%2Dtop%3A4px%7D%40media%20%28min%2Dwidth%3A768px%29%7B%2Enavbar%2Dtoggle%7Bdisplay%3Anone%7D%7D%2Enavbar%2Dnav%7Bmargin%3A7%2E5px%20%2D15px%7D%2Enavbar%2Dnav%3Eli%3Ea%7Bpadding%2Dtop%3A10px%3Bpadding%2Dbottom%3A10px%3Bline%2Dheight%3A20px%7D%40media%20%28max%2Dwidth%3A767px%29%7B%2Enavbar%2Dnav%20%2Eopen%20%2Edropdown%2Dmenu%7Bposition%3Astatic%3Bfloat%3Anone%3Bwidth%3Aauto%3Bmargin%2Dtop%3A0%3Bbackground%2Dcolor%3Atransparent%3Bborder%3A0%3B%2Dwebkit%2Dbox%2Dshadow%3Anone%3Bbox%2Dshadow%3Anone%7D%2Enavbar%2Dnav%20%2Eopen%20%2Edropdown%2Dmenu%20%2Edropdown%2Dheader%2C%2Enavbar%2Dnav%20%2Eopen%20%2Edropdown%2Dmenu%3Eli%3Ea%7Bpadding%3A5px%2015px%205px%2025px%7D%2Enavbar%2Dnav%20%2Eopen%20%2Edropdown%2Dmenu%3Eli%3Ea%7Bline%2Dheight%3A20px%7D%2Enavbar%2Dnav%20%2Eopen%20%2Edropdown%2Dmenu%3Eli%3Ea%3Afocus%2C%2Enavbar%2Dnav%20%2Eopen%20%2Edropdown%2Dmenu%3Eli%3Ea%3Ahover%7Bbackground%2Dimage%3Anone%7D%7D%40media%20%28min%2Dwidth%3A768px%29%7B%2Enavbar%2Dnav%7Bfloat%3Aleft%3Bmargin%3A0%7D%2Enavbar%2Dnav%3Eli%7Bfloat%3Aleft%7D%2Enavbar%2Dnav%3Eli%3Ea%7Bpadding%2Dtop%3A15px%3Bpadding%2Dbottom%3A15px%7D%7D%2Enavbar%2Dform%7Bpadding%3A10px%2015px%3Bmargin%2Dtop%3A8px%3Bmargin%2Dright%3A%2D15px%3Bmargin%2Dbottom%3A8px%3Bmargin%2Dleft%3A%2D15px%3Bborder%2Dtop%3A1px%20solid%20transparent%3Bborder%2Dbottom%3A1px%20solid%20transparent%3B%2Dwebkit%2Dbox%2Dshadow%3Ainset%200%201px%200%20rgba%28255%2C255%2C255%2C%2E1%29%2C0%201px%200%20rgba%28255%2C255%2C255%2C%2E1%29%3Bbox%2Dshadow%3Ainset%200%201px%200%20rgba%28255%2C255%2C255%2C%2E1%29%2C0%201px%200%20rgba%28255%2C255%2C255%2C%2E1%29%7D%40media%20%28min%2Dwidth%3A768px%29%7B%2Enavbar%2Dform%20%2Eform%2Dgroup%7Bdisplay%3Ainline%2Dblock%3Bmargin%2Dbottom%3A0%3Bvertical%2Dalign%3Amiddle%7D%2Enavbar%2Dform%20%2Eform%2Dcontrol%7Bdisplay%3Ainline%2Dblock%3Bwidth%3Aauto%3Bvertical%2Dalign%3Amiddle%7D%2Enavbar%2Dform%20%2Eform%2Dcontrol%2Dstatic%7Bdisplay%3Ainline%2Dblock%7D%2Enavbar%2Dform%20%2Einput%2Dgroup%7Bdisplay%3Ainline%2Dtable%3Bvertical%2Dalign%3Amiddle%7D%2Enavbar%2Dform%20%2Einput%2Dgroup%20%2Eform%2Dcontrol%2C%2Enavbar%2Dform%20%2Einput%2Dgroup%20%2Einput%2Dgroup%2Daddon%2C%2Enavbar%2Dform%20%2Einput%2Dgroup%20%2Einput%2Dgroup%2Dbtn%7Bwidth%3Aauto%7D%2Enavbar%2Dform%20%2Einput%2Dgroup%3E%2Eform%2Dcontrol%7Bwidth%3A100%25%7D%2Enavbar%2Dform%20%2Econtrol%2Dlabel%7Bmargin%2Dbottom%3A0%3Bvertical%2Dalign%3Amiddle%7D%2Enavbar%2Dform%20%2Echeckbox%2C%2Enavbar%2Dform%20%2Eradio%7Bdisplay%3Ainline%2Dblock%3Bmargin%2Dtop%3A0%3Bmargin%2Dbottom%3A0%3Bvertical%2Dalign%3Amiddle%7D%2Enavbar%2Dform%20%2Echeckbox%20label%2C%2Enavbar%2Dform%20%2Eradio%20label%7Bpadding%2Dleft%3A0%7D%2Enavbar%2Dform%20%2Echeckbox%20input%5Btype%3Dcheckbox%5D%2C%2Enavbar%2Dform%20%2Eradio%20input%5Btype%3Dradio%5D%7Bposition%3Arelative%3Bmargin%2Dleft%3A0%7D%2Enavbar%2Dform%20%2Ehas%2Dfeedback%20%2Eform%2Dcontrol%2Dfeedback%7Btop%3A0%7D%7D%40media%20%28max%2Dwidth%3A767px%29%7B%2Enavbar%2Dform%20%2Eform%2Dgroup%7Bmargin%2Dbottom%3A5px%7D%2Enavbar%2Dform%20%2Eform%2Dgroup%3Alast%2Dchild%7Bmargin%2Dbottom%3A0%7D%7D%40media%20%28min%2Dwidth%3A768px%29%7B%2Enavbar%2Dform%7Bwidth%3Aauto%3Bpadding%2Dtop%3A0%3Bpadding%2Dbottom%3A0%3Bmargin%2Dright%3A0%3Bmargin%2Dleft%3A0%3Bborder%3A0%3B%2Dwebkit%2Dbox%2Dshadow%3Anone%3Bbox%2Dshadow%3Anone%7D%7D%2Enavbar%2Dnav%3Eli%3E%2Edropdown%2Dmenu%7Bmargin%2Dtop%3A0%3Bborder%2Dtop%2Dleft%2Dradius%3A0%3Bborder%2Dtop%2Dright%2Dradius%3A0%7D%2Enavbar%2Dfixed%2Dbottom%20%2Enavbar%2Dnav%3Eli%3E%2Edropdown%2Dmenu%7Bmargin%2Dbottom%3A0%3Bborder%2Dtop%2Dleft%2Dradius%3A4px%3Bborder%2Dtop%2Dright%2Dradius%3A4px%3Bborder%2Dbottom%2Dright%2Dradius%3A0%3Bborder%2Dbottom%2Dleft%2Dradius%3A0%7D%2Enavbar%2Dbtn%7Bmargin%2Dtop%3A8px%3Bmargin%2Dbottom%3A8px%7D%2Enavbar%2Dbtn%2Ebtn%2Dsm%7Bmargin%2Dtop%3A10px%3Bmargin%2Dbottom%3A10px%7D%2Enavbar%2Dbtn%2Ebtn%2Dxs%7Bmargin%2Dtop%3A14px%3Bmargin%2Dbottom%3A14px%7D%2Enavbar%2Dtext%7Bmargin%2Dtop%3A15px%3Bmargin%2Dbottom%3A15px%7D%40media%20%28min%2Dwidth%3A768px%29%7B%2Enavbar%2Dtext%7Bfloat%3Aleft%3Bmargin%2Dright%3A15px%3Bmargin%2Dleft%3A15px%7D%7D%40media%20%28min%2Dwidth%3A768px%29%7B%2Enavbar%2Dleft%7Bfloat%3Aleft%21important%7D%2Enavbar%2Dright%7Bfloat%3Aright%21important%3Bmargin%2Dright%3A%2D15px%7D%2Enavbar%2Dright%7E%2Enavbar%2Dright%7Bmargin%2Dright%3A0%7D%7D%2Enavbar%2Ddefault%7Bbackground%2Dcolor%3A%23f8f8f8%3Bborder%2Dcolor%3A%23e7e7e7%7D%2Enavbar%2Ddefault%20%2Enavbar%2Dbrand%7Bcolor%3A%23777%7D%2Enavbar%2Ddefault%20%2Enavbar%2Dbrand%3Afocus%2C%2Enavbar%2Ddefault%20%2Enavbar%2Dbrand%3Ahover%7Bcolor%3A%235e5e5e%3Bbackground%2Dcolor%3Atransparent%7D%2Enavbar%2Ddefault%20%2Enavbar%2Dtext%7Bcolor%3A%23777%7D%2Enavbar%2Ddefault%20%2Enavbar%2Dnav%3Eli%3Ea%7Bcolor%3A%23777%7D%2Enavbar%2Ddefault%20%2Enavbar%2Dnav%3Eli%3Ea%3Afocus%2C%2Enavbar%2Ddefault%20%2Enavbar%2Dnav%3Eli%3Ea%3Ahover%7Bcolor%3A%23333%3Bbackground%2Dcolor%3Atransparent%7D%2Enavbar%2Ddefault%20%2Enavbar%2Dnav%3E%2Eactive%3Ea%2C%2Enavbar%2Ddefault%20%2Enavbar%2Dnav%3E%2Eactive%3Ea%3Afocus%2C%2Enavbar%2Ddefault%20%2Enavbar%2Dnav%3E%2Eactive%3Ea%3Ahover%7Bcolor%3A%23555%3Bbackground%2Dcolor%3A%23e7e7e7%7D%2Enavbar%2Ddefault%20%2Enavbar%2Dnav%3E%2Edisabled%3Ea%2C%2Enavbar%2Ddefault%20%2Enavbar%2Dnav%3E%2Edisabled%3Ea%3Afocus%2C%2Enavbar%2Ddefault%20%2Enavbar%2Dnav%3E%2Edisabled%3Ea%3Ahover%7Bcolor%3A%23ccc%3Bbackground%2Dcolor%3Atransparent%7D%2Enavbar%2Ddefault%20%2Enavbar%2Dtoggle%7Bborder%2Dcolor%3A%23ddd%7D%2Enavbar%2Ddefault%20%2Enavbar%2Dtoggle%3Afocus%2C%2Enavbar%2Ddefault%20%2Enavbar%2Dtoggle%3Ahover%7Bbackground%2Dcolor%3A%23ddd%7D%2Enavbar%2Ddefault%20%2Enavbar%2Dtoggle%20%2Eicon%2Dbar%7Bbackground%2Dcolor%3A%23888%7D%2Enavbar%2Ddefault%20%2Enavbar%2Dcollapse%2C%2Enavbar%2Ddefault%20%2Enavbar%2Dform%7Bborder%2Dcolor%3A%23e7e7e7%7D%2Enavbar%2Ddefault%20%2Enavbar%2Dnav%3E%2Eopen%3Ea%2C%2Enavbar%2Ddefault%20%2Enavbar%2Dnav%3E%2Eopen%3Ea%3Afocus%2C%2Enavbar%2Ddefault%20%2Enavbar%2Dnav%3E%2Eopen%3Ea%3Ahover%7Bcolor%3A%23555%3Bbackground%2Dcolor%3A%23e7e7e7%7D%40media%20%28max%2Dwidth%3A767px%29%7B%2Enavbar%2Ddefault%20%2Enavbar%2Dnav%20%2Eopen%20%2Edropdown%2Dmenu%3Eli%3Ea%7Bcolor%3A%23777%7D%2Enavbar%2Ddefault%20%2Enavbar%2Dnav%20%2Eopen%20%2Edropdown%2Dmenu%3Eli%3Ea%3Afocus%2C%2Enavbar%2Ddefault%20%2Enavbar%2Dnav%20%2Eopen%20%2Edropdown%2Dmenu%3Eli%3Ea%3Ahover%7Bcolor%3A%23333%3Bbackground%2Dcolor%3Atransparent%7D%2Enavbar%2Ddefault%20%2Enavbar%2Dnav%20%2Eopen%20%2Edropdown%2Dmenu%3E%2Eactive%3Ea%2C%2Enavbar%2Ddefault%20%2Enavbar%2Dnav%20%2Eopen%20%2Edropdown%2Dmenu%3E%2Eactive%3Ea%3Afocus%2C%2Enavbar%2Ddefault%20%2Enavbar%2Dnav%20%2Eopen%20%2Edropdown%2Dmenu%3E%2Eactive%3Ea%3Ahover%7Bcolor%3A%23555%3Bbackground%2Dcolor%3A%23e7e7e7%7D%2Enavbar%2Ddefault%20%2Enavbar%2Dnav%20%2Eopen%20%2Edropdown%2Dmenu%3E%2Edisabled%3Ea%2C%2Enavbar%2Ddefault%20%2Enavbar%2Dnav%20%2Eopen%20%2Edropdown%2Dmenu%3E%2Edisabled%3Ea%3Afocus%2C%2Enavbar%2Ddefault%20%2Enavbar%2Dnav%20%2Eopen%20%2Edropdown%2Dmenu%3E%2Edisabled%3Ea%3Ahover%7Bcolor%3A%23ccc%3Bbackground%2Dcolor%3Atransparent%7D%7D%2Enavbar%2Ddefault%20%2Enavbar%2Dlink%7Bcolor%3A%23777%7D%2Enavbar%2Ddefault%20%2Enavbar%2Dlink%3Ahover%7Bcolor%3A%23333%7D%2Enavbar%2Ddefault%20%2Ebtn%2Dlink%7Bcolor%3A%23777%7D%2Enavbar%2Ddefault%20%2Ebtn%2Dlink%3Afocus%2C%2Enavbar%2Ddefault%20%2Ebtn%2Dlink%3Ahover%7Bcolor%3A%23333%7D%2Enavbar%2Ddefault%20%2Ebtn%2Dlink%5Bdisabled%5D%3Afocus%2C%2Enavbar%2Ddefault%20%2Ebtn%2Dlink%5Bdisabled%5D%3Ahover%2Cfieldset%5Bdisabled%5D%20%2Enavbar%2Ddefault%20%2Ebtn%2Dlink%3Afocus%2Cfieldset%5Bdisabled%5D%20%2Enavbar%2Ddefault%20%2Ebtn%2Dlink%3Ahover%7Bcolor%3A%23ccc%7D%2Enavbar%2Dinverse%7Bbackground%2Dcolor%3A%23222%3Bborder%2Dcolor%3A%23080808%7D%2Enavbar%2Dinverse%20%2Enavbar%2Dbrand%7Bcolor%3A%239d9d9d%7D%2Enavbar%2Dinverse%20%2Enavbar%2Dbrand%3Afocus%2C%2Enavbar%2Dinverse%20%2Enavbar%2Dbrand%3Ahover%7Bcolor%3A%23fff%3Bbackground%2Dcolor%3Atransparent%7D%2Enavbar%2Dinverse%20%2Enavbar%2Dtext%7Bcolor%3A%239d9d9d%7D%2Enavbar%2Dinverse%20%2Enavbar%2Dnav%3Eli%3Ea%7Bcolor%3A%239d9d9d%7D%2Enavbar%2Dinverse%20%2Enavbar%2Dnav%3Eli%3Ea%3Afocus%2C%2Enavbar%2Dinverse%20%2Enavbar%2Dnav%3Eli%3Ea%3Ahover%7Bcolor%3A%23fff%3Bbackground%2Dcolor%3Atransparent%7D%2Enavbar%2Dinverse%20%2Enavbar%2Dnav%3E%2Eactive%3Ea%2C%2Enavbar%2Dinverse%20%2Enavbar%2Dnav%3E%2Eactive%3Ea%3Afocus%2C%2Enavbar%2Dinverse%20%2Enavbar%2Dnav%3E%2Eactive%3Ea%3Ahover%7Bcolor%3A%23fff%3Bbackground%2Dcolor%3A%23080808%7D%2Enavbar%2Dinverse%20%2Enavbar%2Dnav%3E%2Edisabled%3Ea%2C%2Enavbar%2Dinverse%20%2Enavbar%2Dnav%3E%2Edisabled%3Ea%3Afocus%2C%2Enavbar%2Dinverse%20%2Enavbar%2Dnav%3E%2Edisabled%3Ea%3Ahover%7Bcolor%3A%23444%3Bbackground%2Dcolor%3Atransparent%7D%2Enavbar%2Dinverse%20%2Enavbar%2Dtoggle%7Bborder%2Dcolor%3A%23333%7D%2Enavbar%2Dinverse%20%2Enavbar%2Dtoggle%3Afocus%2C%2Enavbar%2Dinverse%20%2Enavbar%2Dtoggle%3Ahover%7Bbackground%2Dcolor%3A%23333%7D%2Enavbar%2Dinverse%20%2Enavbar%2Dtoggle%20%2Eicon%2Dbar%7Bbackground%2Dcolor%3A%23fff%7D%2Enavbar%2Dinverse%20%2Enavbar%2Dcollapse%2C%2Enavbar%2Dinverse%20%2Enavbar%2Dform%7Bborder%2Dcolor%3A%23101010%7D%2Enavbar%2Dinverse%20%2Enavbar%2Dnav%3E%2Eopen%3Ea%2C%2Enavbar%2Dinverse%20%2Enavbar%2Dnav%3E%2Eopen%3Ea%3Afocus%2C%2Enavbar%2Dinverse%20%2Enavbar%2Dnav%3E%2Eopen%3Ea%3Ahover%7Bcolor%3A%23fff%3Bbackground%2Dcolor%3A%23080808%7D%40media%20%28max%2Dwidth%3A767px%29%7B%2Enavbar%2Dinverse%20%2Enavbar%2Dnav%20%2Eopen%20%2Edropdown%2Dmenu%3E%2Edropdown%2Dheader%7Bborder%2Dcolor%3A%23080808%7D%2Enavbar%2Dinverse%20%2Enavbar%2Dnav%20%2Eopen%20%2Edropdown%2Dmenu%20%2Edivider%7Bbackground%2Dcolor%3A%23080808%7D%2Enavbar%2Dinverse%20%2Enavbar%2Dnav%20%2Eopen%20%2Edropdown%2Dmenu%3Eli%3Ea%7Bcolor%3A%239d9d9d%7D%2Enavbar%2Dinverse%20%2Enavbar%2Dnav%20%2Eopen%20%2Edropdown%2Dmenu%3Eli%3Ea%3Afocus%2C%2Enavbar%2Dinverse%20%2Enavbar%2Dnav%20%2Eopen%20%2Edropdown%2Dmenu%3Eli%3Ea%3Ahover%7Bcolor%3A%23fff%3Bbackground%2Dcolor%3Atransparent%7D%2Enavbar%2Dinverse%20%2Enavbar%2Dnav%20%2Eopen%20%2Edropdown%2Dmenu%3E%2Eactive%3Ea%2C%2Enavbar%2Dinverse%20%2Enavbar%2Dnav%20%2Eopen%20%2Edropdown%2Dmenu%3E%2Eactive%3Ea%3Afocus%2C%2Enavbar%2Dinverse%20%2Enavbar%2Dnav%20%2Eopen%20%2Edropdown%2Dmenu%3E%2Eactive%3Ea%3Ahover%7Bcolor%3A%23fff%3Bbackground%2Dcolor%3A%23080808%7D%2Enavbar%2Dinverse%20%2Enavbar%2Dnav%20%2Eopen%20%2Edropdown%2Dmenu%3E%2Edisabled%3Ea%2C%2Enavbar%2Dinverse%20%2Enavbar%2Dnav%20%2Eopen%20%2Edropdown%2Dmenu%3E%2Edisabled%3Ea%3Afocus%2C%2Enavbar%2Dinverse%20%2Enavbar%2Dnav%20%2Eopen%20%2Edropdown%2Dmenu%3E%2Edisabled%3Ea%3Ahover%7Bcolor%3A%23444%3Bbackground%2Dcolor%3Atransparent%7D%7D%2Enavbar%2Dinverse%20%2Enavbar%2Dlink%7Bcolor%3A%239d9d9d%7D%2Enavbar%2Dinverse%20%2Enavbar%2Dlink%3Ahover%7Bcolor%3A%23fff%7D%2Enavbar%2Dinverse%20%2Ebtn%2Dlink%7Bcolor%3A%239d9d9d%7D%2Enavbar%2Dinverse%20%2Ebtn%2Dlink%3Afocus%2C%2Enavbar%2Dinverse%20%2Ebtn%2Dlink%3Ahover%7Bcolor%3A%23fff%7D%2Enavbar%2Dinverse%20%2Ebtn%2Dlink%5Bdisabled%5D%3Afocus%2C%2Enavbar%2Dinverse%20%2Ebtn%2Dlink%5Bdisabled%5D%3Ahover%2Cfieldset%5Bdisabled%5D%20%2Enavbar%2Dinverse%20%2Ebtn%2Dlink%3Afocus%2Cfieldset%5Bdisabled%5D%20%2Enavbar%2Dinverse%20%2Ebtn%2Dlink%3Ahover%7Bcolor%3A%23444%7D%2Ebreadcrumb%7Bpadding%3A8px%2015px%3Bmargin%2Dbottom%3A20px%3Blist%2Dstyle%3Anone%3Bbackground%2Dcolor%3A%23f5f5f5%3Bborder%2Dradius%3A4px%7D%2Ebreadcrumb%3Eli%7Bdisplay%3Ainline%2Dblock%7D%2Ebreadcrumb%3Eli%2Bli%3Abefore%7Bpadding%3A0%205px%3Bcolor%3A%23ccc%3Bcontent%3A%22%2F%5C00a0%22%7D%2Ebreadcrumb%3E%2Eactive%7Bcolor%3A%23777%7D%2Epagination%7Bdisplay%3Ainline%2Dblock%3Bpadding%2Dleft%3A0%3Bmargin%3A20px%200%3Bborder%2Dradius%3A4px%7D%2Epagination%3Eli%7Bdisplay%3Ainline%7D%2Epagination%3Eli%3Ea%2C%2Epagination%3Eli%3Espan%7Bposition%3Arelative%3Bfloat%3Aleft%3Bpadding%3A6px%2012px%3Bmargin%2Dleft%3A%2D1px%3Bline%2Dheight%3A1%2E42857143%3Bcolor%3A%23337ab7%3Btext%2Ddecoration%3Anone%3Bbackground%2Dcolor%3A%23fff%3Bborder%3A1px%20solid%20%23ddd%7D%2Epagination%3Eli%3Afirst%2Dchild%3Ea%2C%2Epagination%3Eli%3Afirst%2Dchild%3Espan%7Bmargin%2Dleft%3A0%3Bborder%2Dtop%2Dleft%2Dradius%3A4px%3Bborder%2Dbottom%2Dleft%2Dradius%3A4px%7D%2Epagination%3Eli%3Alast%2Dchild%3Ea%2C%2Epagination%3Eli%3Alast%2Dchild%3Espan%7Bborder%2Dtop%2Dright%2Dradius%3A4px%3Bborder%2Dbottom%2Dright%2Dradius%3A4px%7D%2Epagination%3Eli%3Ea%3Afocus%2C%2Epagination%3Eli%3Ea%3Ahover%2C%2Epagination%3Eli%3Espan%3Afocus%2C%2Epagination%3Eli%3Espan%3Ahover%7Bz%2Dindex%3A3%3Bcolor%3A%2323527c%3Bbackground%2Dcolor%3A%23eee%3Bborder%2Dcolor%3A%23ddd%7D%2Epagination%3E%2Eactive%3Ea%2C%2Epagination%3E%2Eactive%3Ea%3Afocus%2C%2Epagination%3E%2Eactive%3Ea%3Ahover%2C%2Epagination%3E%2Eactive%3Espan%2C%2Epagination%3E%2Eactive%3Espan%3Afocus%2C%2Epagination%3E%2Eactive%3Espan%3Ahover%7Bz%2Dindex%3A2%3Bcolor%3A%23fff%3Bcursor%3Adefault%3Bbackground%2Dcolor%3A%23337ab7%3Bborder%2Dcolor%3A%23337ab7%7D%2Epagination%3E%2Edisabled%3Ea%2C%2Epagination%3E%2Edisabled%3Ea%3Afocus%2C%2Epagination%3E%2Edisabled%3Ea%3Ahover%2C%2Epagination%3E%2Edisabled%3Espan%2C%2Epagination%3E%2Edisabled%3Espan%3Afocus%2C%2Epagination%3E%2Edisabled%3Espan%3Ahover%7Bcolor%3A%23777%3Bcursor%3Anot%2Dallowed%3Bbackground%2Dcolor%3A%23fff%3Bborder%2Dcolor%3A%23ddd%7D%2Epagination%2Dlg%3Eli%3Ea%2C%2Epagination%2Dlg%3Eli%3Espan%7Bpadding%3A10px%2016px%3Bfont%2Dsize%3A18px%3Bline%2Dheight%3A1%2E3333333%7D%2Epagination%2Dlg%3Eli%3Afirst%2Dchild%3Ea%2C%2Epagination%2Dlg%3Eli%3Afirst%2Dchild%3Espan%7Bborder%2Dtop%2Dleft%2Dradius%3A6px%3Bborder%2Dbottom%2Dleft%2Dradius%3A6px%7D%2Epagination%2Dlg%3Eli%3Alast%2Dchild%3Ea%2C%2Epagination%2Dlg%3Eli%3Alast%2Dchild%3Espan%7Bborder%2Dtop%2Dright%2Dradius%3A6px%3Bborder%2Dbottom%2Dright%2Dradius%3A6px%7D%2Epagination%2Dsm%3Eli%3Ea%2C%2Epagination%2Dsm%3Eli%3Espan%7Bpadding%3A5px%2010px%3Bfont%2Dsize%3A12px%3Bline%2Dheight%3A1%2E5%7D%2Epagination%2Dsm%3Eli%3Afirst%2Dchild%3Ea%2C%2Epagination%2Dsm%3Eli%3Afirst%2Dchild%3Espan%7Bborder%2Dtop%2Dleft%2Dradius%3A3px%3Bborder%2Dbottom%2Dleft%2Dradius%3A3px%7D%2Epagination%2Dsm%3Eli%3Alast%2Dchild%3Ea%2C%2Epagination%2Dsm%3Eli%3Alast%2Dchild%3Espan%7Bborder%2Dtop%2Dright%2Dradius%3A3px%3Bborder%2Dbottom%2Dright%2Dradius%3A3px%7D%2Epager%7Bpadding%2Dleft%3A0%3Bmargin%3A20px%200%3Btext%2Dalign%3Acenter%3Blist%2Dstyle%3Anone%7D%2Epager%20li%7Bdisplay%3Ainline%7D%2Epager%20li%3Ea%2C%2Epager%20li%3Espan%7Bdisplay%3Ainline%2Dblock%3Bpadding%3A5px%2014px%3Bbackground%2Dcolor%3A%23fff%3Bborder%3A1px%20solid%20%23ddd%3Bborder%2Dradius%3A15px%7D%2Epager%20li%3Ea%3Afocus%2C%2Epager%20li%3Ea%3Ahover%7Btext%2Ddecoration%3Anone%3Bbackground%2Dcolor%3A%23eee%7D%2Epager%20%2Enext%3Ea%2C%2Epager%20%2Enext%3Espan%7Bfloat%3Aright%7D%2Epager%20%2Eprevious%3Ea%2C%2Epager%20%2Eprevious%3Espan%7Bfloat%3Aleft%7D%2Epager%20%2Edisabled%3Ea%2C%2Epager%20%2Edisabled%3Ea%3Afocus%2C%2Epager%20%2Edisabled%3Ea%3Ahover%2C%2Epager%20%2Edisabled%3Espan%7Bcolor%3A%23777%3Bcursor%3Anot%2Dallowed%3Bbackground%2Dcolor%3A%23fff%7D%2Elabel%7Bdisplay%3Ainline%3Bpadding%3A%2E2em%20%2E6em%20%2E3em%3Bfont%2Dsize%3A75%25%3Bfont%2Dweight%3A700%3Bline%2Dheight%3A1%3Bcolor%3A%23fff%3Btext%2Dalign%3Acenter%3Bwhite%2Dspace%3Anowrap%3Bvertical%2Dalign%3Abaseline%3Bborder%2Dradius%3A%2E25em%7Da%2Elabel%3Afocus%2Ca%2Elabel%3Ahover%7Bcolor%3A%23fff%3Btext%2Ddecoration%3Anone%3Bcursor%3Apointer%7D%2Elabel%3Aempty%7Bdisplay%3Anone%7D%2Ebtn%20%2Elabel%7Bposition%3Arelative%3Btop%3A%2D1px%7D%2Elabel%2Ddefault%7Bbackground%2Dcolor%3A%23777%7D%2Elabel%2Ddefault%5Bhref%5D%3Afocus%2C%2Elabel%2Ddefault%5Bhref%5D%3Ahover%7Bbackground%2Dcolor%3A%235e5e5e%7D%2Elabel%2Dprimary%7Bbackground%2Dcolor%3A%23337ab7%7D%2Elabel%2Dprimary%5Bhref%5D%3Afocus%2C%2Elabel%2Dprimary%5Bhref%5D%3Ahover%7Bbackground%2Dcolor%3A%23286090%7D%2Elabel%2Dsuccess%7Bbackground%2Dcolor%3A%235cb85c%7D%2Elabel%2Dsuccess%5Bhref%5D%3Afocus%2C%2Elabel%2Dsuccess%5Bhref%5D%3Ahover%7Bbackground%2Dcolor%3A%23449d44%7D%2Elabel%2Dinfo%7Bbackground%2Dcolor%3A%235bc0de%7D%2Elabel%2Dinfo%5Bhref%5D%3Afocus%2C%2Elabel%2Dinfo%5Bhref%5D%3Ahover%7Bbackground%2Dcolor%3A%2331b0d5%7D%2Elabel%2Dwarning%7Bbackground%2Dcolor%3A%23f0ad4e%7D%2Elabel%2Dwarning%5Bhref%5D%3Afocus%2C%2Elabel%2Dwarning%5Bhref%5D%3Ahover%7Bbackground%2Dcolor%3A%23ec971f%7D%2Elabel%2Ddanger%7Bbackground%2Dcolor%3A%23d9534f%7D%2Elabel%2Ddanger%5Bhref%5D%3Afocus%2C%2Elabel%2Ddanger%5Bhref%5D%3Ahover%7Bbackground%2Dcolor%3A%23c9302c%7D%2Ebadge%7Bdisplay%3Ainline%2Dblock%3Bmin%2Dwidth%3A10px%3Bpadding%3A3px%207px%3Bfont%2Dsize%3A12px%3Bfont%2Dweight%3A700%3Bline%2Dheight%3A1%3Bcolor%3A%23fff%3Btext%2Dalign%3Acenter%3Bwhite%2Dspace%3Anowrap%3Bvertical%2Dalign%3Amiddle%3Bbackground%2Dcolor%3A%23777%3Bborder%2Dradius%3A10px%7D%2Ebadge%3Aempty%7Bdisplay%3Anone%7D%2Ebtn%20%2Ebadge%7Bposition%3Arelative%3Btop%3A%2D1px%7D%2Ebtn%2Dgroup%2Dxs%3E%2Ebtn%20%2Ebadge%2C%2Ebtn%2Dxs%20%2Ebadge%7Btop%3A0%3Bpadding%3A1px%205px%7Da%2Ebadge%3Afocus%2Ca%2Ebadge%3Ahover%7Bcolor%3A%23fff%3Btext%2Ddecoration%3Anone%3Bcursor%3Apointer%7D%2Elist%2Dgroup%2Ditem%2Eactive%3E%2Ebadge%2C%2Enav%2Dpills%3E%2Eactive%3Ea%3E%2Ebadge%7Bcolor%3A%23337ab7%3Bbackground%2Dcolor%3A%23fff%7D%2Elist%2Dgroup%2Ditem%3E%2Ebadge%7Bfloat%3Aright%7D%2Elist%2Dgroup%2Ditem%3E%2Ebadge%2B%2Ebadge%7Bmargin%2Dright%3A5px%7D%2Enav%2Dpills%3Eli%3Ea%3E%2Ebadge%7Bmargin%2Dleft%3A3px%7D%2Ejumbotron%7Bpadding%2Dtop%3A30px%3Bpadding%2Dbottom%3A30px%3Bmargin%2Dbottom%3A30px%3Bcolor%3Ainherit%3Bbackground%2Dcolor%3A%23eee%7D%2Ejumbotron%20%2Eh1%2C%2Ejumbotron%20h1%7Bcolor%3Ainherit%7D%2Ejumbotron%20p%7Bmargin%2Dbottom%3A15px%3Bfont%2Dsize%3A21px%3Bfont%2Dweight%3A200%7D%2Ejumbotron%3Ehr%7Bborder%2Dtop%2Dcolor%3A%23d5d5d5%7D%2Econtainer%20%2Ejumbotron%2C%2Econtainer%2Dfluid%20%2Ejumbotron%7Bborder%2Dradius%3A6px%7D%2Ejumbotron%20%2Econtainer%7Bmax%2Dwidth%3A100%25%7D%40media%20screen%20and%20%28min%2Dwidth%3A768px%29%7B%2Ejumbotron%7Bpadding%2Dtop%3A48px%3Bpadding%2Dbottom%3A48px%7D%2Econtainer%20%2Ejumbotron%2C%2Econtainer%2Dfluid%20%2Ejumbotron%7Bpadding%2Dright%3A60px%3Bpadding%2Dleft%3A60px%7D%2Ejumbotron%20%2Eh1%2C%2Ejumbotron%20h1%7Bfont%2Dsize%3A63px%7D%7D%2Ethumbnail%7Bdisplay%3Ablock%3Bpadding%3A4px%3Bmargin%2Dbottom%3A20px%3Bline%2Dheight%3A1%2E42857143%3Bbackground%2Dcolor%3A%23fff%3Bborder%3A1px%20solid%20%23ddd%3Bborder%2Dradius%3A4px%3B%2Dwebkit%2Dtransition%3Aborder%20%2E2s%20ease%2Din%2Dout%3B%2Do%2Dtransition%3Aborder%20%2E2s%20ease%2Din%2Dout%3Btransition%3Aborder%20%2E2s%20ease%2Din%2Dout%7D%2Ethumbnail%20a%3Eimg%2C%2Ethumbnail%3Eimg%7Bmargin%2Dright%3Aauto%3Bmargin%2Dleft%3Aauto%7Da%2Ethumbnail%2Eactive%2Ca%2Ethumbnail%3Afocus%2Ca%2Ethumbnail%3Ahover%7Bborder%2Dcolor%3A%23337ab7%7D%2Ethumbnail%20%2Ecaption%7Bpadding%3A9px%3Bcolor%3A%23333%7D%2Ealert%7Bpadding%3A15px%3Bmargin%2Dbottom%3A20px%3Bborder%3A1px%20solid%20transparent%3Bborder%2Dradius%3A4px%7D%2Ealert%20h4%7Bmargin%2Dtop%3A0%3Bcolor%3Ainherit%7D%2Ealert%20%2Ealert%2Dlink%7Bfont%2Dweight%3A700%7D%2Ealert%3Ep%2C%2Ealert%3Eul%7Bmargin%2Dbottom%3A0%7D%2Ealert%3Ep%2Bp%7Bmargin%2Dtop%3A5px%7D%2Ealert%2Ddismissable%2C%2Ealert%2Ddismissible%7Bpadding%2Dright%3A35px%7D%2Ealert%2Ddismissable%20%2Eclose%2C%2Ealert%2Ddismissible%20%2Eclose%7Bposition%3Arelative%3Btop%3A%2D2px%3Bright%3A%2D21px%3Bcolor%3Ainherit%7D%2Ealert%2Dsuccess%7Bcolor%3A%233c763d%3Bbackground%2Dcolor%3A%23dff0d8%3Bborder%2Dcolor%3A%23d6e9c6%7D%2Ealert%2Dsuccess%20hr%7Bborder%2Dtop%2Dcolor%3A%23c9e2b3%7D%2Ealert%2Dsuccess%20%2Ealert%2Dlink%7Bcolor%3A%232b542c%7D%2Ealert%2Dinfo%7Bcolor%3A%2331708f%3Bbackground%2Dcolor%3A%23d9edf7%3Bborder%2Dcolor%3A%23bce8f1%7D%2Ealert%2Dinfo%20hr%7Bborder%2Dtop%2Dcolor%3A%23a6e1ec%7D%2Ealert%2Dinfo%20%2Ealert%2Dlink%7Bcolor%3A%23245269%7D%2Ealert%2Dwarning%7Bcolor%3A%238a6d3b%3Bbackground%2Dcolor%3A%23fcf8e3%3Bborder%2Dcolor%3A%23faebcc%7D%2Ealert%2Dwarning%20hr%7Bborder%2Dtop%2Dcolor%3A%23f7e1b5%7D%2Ealert%2Dwarning%20%2Ealert%2Dlink%7Bcolor%3A%2366512c%7D%2Ealert%2Ddanger%7Bcolor%3A%23a94442%3Bbackground%2Dcolor%3A%23f2dede%3Bborder%2Dcolor%3A%23ebccd1%7D%2Ealert%2Ddanger%20hr%7Bborder%2Dtop%2Dcolor%3A%23e4b9c0%7D%2Ealert%2Ddanger%20%2Ealert%2Dlink%7Bcolor%3A%23843534%7D%40%2Dwebkit%2Dkeyframes%20progress%2Dbar%2Dstripes%7Bfrom%7Bbackground%2Dposition%3A40px%200%7Dto%7Bbackground%2Dposition%3A0%200%7D%7D%40%2Do%2Dkeyframes%20progress%2Dbar%2Dstripes%7Bfrom%7Bbackground%2Dposition%3A40px%200%7Dto%7Bbackground%2Dposition%3A0%200%7D%7D%40keyframes%20progress%2Dbar%2Dstripes%7Bfrom%7Bbackground%2Dposition%3A40px%200%7Dto%7Bbackground%2Dposition%3A0%200%7D%7D%2Eprogress%7Bheight%3A20px%3Bmargin%2Dbottom%3A20px%3Boverflow%3Ahidden%3Bbackground%2Dcolor%3A%23f5f5f5%3Bborder%2Dradius%3A4px%3B%2Dwebkit%2Dbox%2Dshadow%3Ainset%200%201px%202px%20rgba%280%2C0%2C0%2C%2E1%29%3Bbox%2Dshadow%3Ainset%200%201px%202px%20rgba%280%2C0%2C0%2C%2E1%29%7D%2Eprogress%2Dbar%7Bfloat%3Aleft%3Bwidth%3A0%3Bheight%3A100%25%3Bfont%2Dsize%3A12px%3Bline%2Dheight%3A20px%3Bcolor%3A%23fff%3Btext%2Dalign%3Acenter%3Bbackground%2Dcolor%3A%23337ab7%3B%2Dwebkit%2Dbox%2Dshadow%3Ainset%200%20%2D1px%200%20rgba%280%2C0%2C0%2C%2E15%29%3Bbox%2Dshadow%3Ainset%200%20%2D1px%200%20rgba%280%2C0%2C0%2C%2E15%29%3B%2Dwebkit%2Dtransition%3Awidth%20%2E6s%20ease%3B%2Do%2Dtransition%3Awidth%20%2E6s%20ease%3Btransition%3Awidth%20%2E6s%20ease%7D%2Eprogress%2Dbar%2Dstriped%2C%2Eprogress%2Dstriped%20%2Eprogress%2Dbar%7Bbackground%2Dimage%3A%2Dwebkit%2Dlinear%2Dgradient%2845deg%2Crgba%28255%2C255%2C255%2C%2E15%29%2025%25%2Ctransparent%2025%25%2Ctransparent%2050%25%2Crgba%28255%2C255%2C255%2C%2E15%29%2050%25%2Crgba%28255%2C255%2C255%2C%2E15%29%2075%25%2Ctransparent%2075%25%2Ctransparent%29%3Bbackground%2Dimage%3A%2Do%2Dlinear%2Dgradient%2845deg%2Crgba%28255%2C255%2C255%2C%2E15%29%2025%25%2Ctransparent%2025%25%2Ctransparent%2050%25%2Crgba%28255%2C255%2C255%2C%2E15%29%2050%25%2Crgba%28255%2C255%2C255%2C%2E15%29%2075%25%2Ctransparent%2075%25%2Ctransparent%29%3Bbackground%2Dimage%3Alinear%2Dgradient%2845deg%2Crgba%28255%2C255%2C255%2C%2E15%29%2025%25%2Ctransparent%2025%25%2Ctransparent%2050%25%2Crgba%28255%2C255%2C255%2C%2E15%29%2050%25%2Crgba%28255%2C255%2C255%2C%2E15%29%2075%25%2Ctransparent%2075%25%2Ctransparent%29%3B%2Dwebkit%2Dbackground%2Dsize%3A40px%2040px%3Bbackground%2Dsize%3A40px%2040px%7D%2Eprogress%2Dbar%2Eactive%2C%2Eprogress%2Eactive%20%2Eprogress%2Dbar%7B%2Dwebkit%2Danimation%3Aprogress%2Dbar%2Dstripes%202s%20linear%20infinite%3B%2Do%2Danimation%3Aprogress%2Dbar%2Dstripes%202s%20linear%20infinite%3Banimation%3Aprogress%2Dbar%2Dstripes%202s%20linear%20infinite%7D%2Eprogress%2Dbar%2Dsuccess%7Bbackground%2Dcolor%3A%235cb85c%7D%2Eprogress%2Dstriped%20%2Eprogress%2Dbar%2Dsuccess%7Bbackground%2Dimage%3A%2Dwebkit%2Dlinear%2Dgradient%2845deg%2Crgba%28255%2C255%2C255%2C%2E15%29%2025%25%2Ctransparent%2025%25%2Ctransparent%2050%25%2Crgba%28255%2C255%2C255%2C%2E15%29%2050%25%2Crgba%28255%2C255%2C255%2C%2E15%29%2075%25%2Ctransparent%2075%25%2Ctransparent%29%3Bbackground%2Dimage%3A%2Do%2Dlinear%2Dgradient%2845deg%2Crgba%28255%2C255%2C255%2C%2E15%29%2025%25%2Ctransparent%2025%25%2Ctransparent%2050%25%2Crgba%28255%2C255%2C255%2C%2E15%29%2050%25%2Crgba%28255%2C255%2C255%2C%2E15%29%2075%25%2Ctransparent%2075%25%2Ctransparent%29%3Bbackground%2Dimage%3Alinear%2Dgradient%2845deg%2Crgba%28255%2C255%2C255%2C%2E15%29%2025%25%2Ctransparent%2025%25%2Ctransparent%2050%25%2Crgba%28255%2C255%2C255%2C%2E15%29%2050%25%2Crgba%28255%2C255%2C255%2C%2E15%29%2075%25%2Ctransparent%2075%25%2Ctransparent%29%7D%2Eprogress%2Dbar%2Dinfo%7Bbackground%2Dcolor%3A%235bc0de%7D%2Eprogress%2Dstriped%20%2Eprogress%2Dbar%2Dinfo%7Bbackground%2Dimage%3A%2Dwebkit%2Dlinear%2Dgradient%2845deg%2Crgba%28255%2C255%2C255%2C%2E15%29%2025%25%2Ctransparent%2025%25%2Ctransparent%2050%25%2Crgba%28255%2C255%2C255%2C%2E15%29%2050%25%2Crgba%28255%2C255%2C255%2C%2E15%29%2075%25%2Ctransparent%2075%25%2Ctransparent%29%3Bbackground%2Dimage%3A%2Do%2Dlinear%2Dgradient%2845deg%2Crgba%28255%2C255%2C255%2C%2E15%29%2025%25%2Ctransparent%2025%25%2Ctransparent%2050%25%2Crgba%28255%2C255%2C255%2C%2E15%29%2050%25%2Crgba%28255%2C255%2C255%2C%2E15%29%2075%25%2Ctransparent%2075%25%2Ctransparent%29%3Bbackground%2Dimage%3Alinear%2Dgradient%2845deg%2Crgba%28255%2C255%2C255%2C%2E15%29%2025%25%2Ctransparent%2025%25%2Ctransparent%2050%25%2Crgba%28255%2C255%2C255%2C%2E15%29%2050%25%2Crgba%28255%2C255%2C255%2C%2E15%29%2075%25%2Ctransparent%2075%25%2Ctransparent%29%7D%2Eprogress%2Dbar%2Dwarning%7Bbackground%2Dcolor%3A%23f0ad4e%7D%2Eprogress%2Dstriped%20%2Eprogress%2Dbar%2Dwarning%7Bbackground%2Dimage%3A%2Dwebkit%2Dlinear%2Dgradient%2845deg%2Crgba%28255%2C255%2C255%2C%2E15%29%2025%25%2Ctransparent%2025%25%2Ctransparent%2050%25%2Crgba%28255%2C255%2C255%2C%2E15%29%2050%25%2Crgba%28255%2C255%2C255%2C%2E15%29%2075%25%2Ctransparent%2075%25%2Ctransparent%29%3Bbackground%2Dimage%3A%2Do%2Dlinear%2Dgradient%2845deg%2Crgba%28255%2C255%2C255%2C%2E15%29%2025%25%2Ctransparent%2025%25%2Ctransparent%2050%25%2Crgba%28255%2C255%2C255%2C%2E15%29%2050%25%2Crgba%28255%2C255%2C255%2C%2E15%29%2075%25%2Ctransparent%2075%25%2Ctransparent%29%3Bbackground%2Dimage%3Alinear%2Dgradient%2845deg%2Crgba%28255%2C255%2C255%2C%2E15%29%2025%25%2Ctransparent%2025%25%2Ctransparent%2050%25%2Crgba%28255%2C255%2C255%2C%2E15%29%2050%25%2Crgba%28255%2C255%2C255%2C%2E15%29%2075%25%2Ctransparent%2075%25%2Ctransparent%29%7D%2Eprogress%2Dbar%2Ddanger%7Bbackground%2Dcolor%3A%23d9534f%7D%2Eprogress%2Dstriped%20%2Eprogress%2Dbar%2Ddanger%7Bbackground%2Dimage%3A%2Dwebkit%2Dlinear%2Dgradient%2845deg%2Crgba%28255%2C255%2C255%2C%2E15%29%2025%25%2Ctransparent%2025%25%2Ctransparent%2050%25%2Crgba%28255%2C255%2C255%2C%2E15%29%2050%25%2Crgba%28255%2C255%2C255%2C%2E15%29%2075%25%2Ctransparent%2075%25%2Ctransparent%29%3Bbackground%2Dimage%3A%2Do%2Dlinear%2Dgradient%2845deg%2Crgba%28255%2C255%2C255%2C%2E15%29%2025%25%2Ctransparent%2025%25%2Ctransparent%2050%25%2Crgba%28255%2C255%2C255%2C%2E15%29%2050%25%2Crgba%28255%2C255%2C255%2C%2E15%29%2075%25%2Ctransparent%2075%25%2Ctransparent%29%3Bbackground%2Dimage%3Alinear%2Dgradient%2845deg%2Crgba%28255%2C255%2C255%2C%2E15%29%2025%25%2Ctransparent%2025%25%2Ctransparent%2050%25%2Crgba%28255%2C255%2C255%2C%2E15%29%2050%25%2Crgba%28255%2C255%2C255%2C%2E15%29%2075%25%2Ctransparent%2075%25%2Ctransparent%29%7D%2Emedia%7Bmargin%2Dtop%3A15px%7D%2Emedia%3Afirst%2Dchild%7Bmargin%2Dtop%3A0%7D%2Emedia%2C%2Emedia%2Dbody%7Boverflow%3Ahidden%3Bzoom%3A1%7D%2Emedia%2Dbody%7Bwidth%3A10000px%7D%2Emedia%2Dobject%7Bdisplay%3Ablock%7D%2Emedia%2Dobject%2Eimg%2Dthumbnail%7Bmax%2Dwidth%3Anone%7D%2Emedia%2Dright%2C%2Emedia%3E%2Epull%2Dright%7Bpadding%2Dleft%3A10px%7D%2Emedia%2Dleft%2C%2Emedia%3E%2Epull%2Dleft%7Bpadding%2Dright%3A10px%7D%2Emedia%2Dbody%2C%2Emedia%2Dleft%2C%2Emedia%2Dright%7Bdisplay%3Atable%2Dcell%3Bvertical%2Dalign%3Atop%7D%2Emedia%2Dmiddle%7Bvertical%2Dalign%3Amiddle%7D%2Emedia%2Dbottom%7Bvertical%2Dalign%3Abottom%7D%2Emedia%2Dheading%7Bmargin%2Dtop%3A0%3Bmargin%2Dbottom%3A5px%7D%2Emedia%2Dlist%7Bpadding%2Dleft%3A0%3Blist%2Dstyle%3Anone%7D%2Elist%2Dgroup%7Bpadding%2Dleft%3A0%3Bmargin%2Dbottom%3A20px%7D%2Elist%2Dgroup%2Ditem%7Bposition%3Arelative%3Bdisplay%3Ablock%3Bpadding%3A10px%2015px%3Bmargin%2Dbottom%3A%2D1px%3Bbackground%2Dcolor%3A%23fff%3Bborder%3A1px%20solid%20%23ddd%7D%2Elist%2Dgroup%2Ditem%3Afirst%2Dchild%7Bborder%2Dtop%2Dleft%2Dradius%3A4px%3Bborder%2Dtop%2Dright%2Dradius%3A4px%7D%2Elist%2Dgroup%2Ditem%3Alast%2Dchild%7Bmargin%2Dbottom%3A0%3Bborder%2Dbottom%2Dright%2Dradius%3A4px%3Bborder%2Dbottom%2Dleft%2Dradius%3A4px%7Da%2Elist%2Dgroup%2Ditem%2Cbutton%2Elist%2Dgroup%2Ditem%7Bcolor%3A%23555%7Da%2Elist%2Dgroup%2Ditem%20%2Elist%2Dgroup%2Ditem%2Dheading%2Cbutton%2Elist%2Dgroup%2Ditem%20%2Elist%2Dgroup%2Ditem%2Dheading%7Bcolor%3A%23333%7Da%2Elist%2Dgroup%2Ditem%3Afocus%2Ca%2Elist%2Dgroup%2Ditem%3Ahover%2Cbutton%2Elist%2Dgroup%2Ditem%3Afocus%2Cbutton%2Elist%2Dgroup%2Ditem%3Ahover%7Bcolor%3A%23555%3Btext%2Ddecoration%3Anone%3Bbackground%2Dcolor%3A%23f5f5f5%7Dbutton%2Elist%2Dgroup%2Ditem%7Bwidth%3A100%25%3Btext%2Dalign%3Aleft%7D%2Elist%2Dgroup%2Ditem%2Edisabled%2C%2Elist%2Dgroup%2Ditem%2Edisabled%3Afocus%2C%2Elist%2Dgroup%2Ditem%2Edisabled%3Ahover%7Bcolor%3A%23777%3Bcursor%3Anot%2Dallowed%3Bbackground%2Dcolor%3A%23eee%7D%2Elist%2Dgroup%2Ditem%2Edisabled%20%2Elist%2Dgroup%2Ditem%2Dheading%2C%2Elist%2Dgroup%2Ditem%2Edisabled%3Afocus%20%2Elist%2Dgroup%2Ditem%2Dheading%2C%2Elist%2Dgroup%2Ditem%2Edisabled%3Ahover%20%2Elist%2Dgroup%2Ditem%2Dheading%7Bcolor%3Ainherit%7D%2Elist%2Dgroup%2Ditem%2Edisabled%20%2Elist%2Dgroup%2Ditem%2Dtext%2C%2Elist%2Dgroup%2Ditem%2Edisabled%3Afocus%20%2Elist%2Dgroup%2Ditem%2Dtext%2C%2Elist%2Dgroup%2Ditem%2Edisabled%3Ahover%20%2Elist%2Dgroup%2Ditem%2Dtext%7Bcolor%3A%23777%7D%2Elist%2Dgroup%2Ditem%2Eactive%2C%2Elist%2Dgroup%2Ditem%2Eactive%3Afocus%2C%2Elist%2Dgroup%2Ditem%2Eactive%3Ahover%7Bz%2Dindex%3A2%3Bcolor%3A%23fff%3Bbackground%2Dcolor%3A%23337ab7%3Bborder%2Dcolor%3A%23337ab7%7D%2Elist%2Dgroup%2Ditem%2Eactive%20%2Elist%2Dgroup%2Ditem%2Dheading%2C%2Elist%2Dgroup%2Ditem%2Eactive%20%2Elist%2Dgroup%2Ditem%2Dheading%3E%2Esmall%2C%2Elist%2Dgroup%2Ditem%2Eactive%20%2Elist%2Dgroup%2Ditem%2Dheading%3Esmall%2C%2Elist%2Dgroup%2Ditem%2Eactive%3Afocus%20%2Elist%2Dgroup%2Ditem%2Dheading%2C%2Elist%2Dgroup%2Ditem%2Eactive%3Afocus%20%2Elist%2Dgroup%2Ditem%2Dheading%3E%2Esmall%2C%2Elist%2Dgroup%2Ditem%2Eactive%3Afocus%20%2Elist%2Dgroup%2Ditem%2Dheading%3Esmall%2C%2Elist%2Dgroup%2Ditem%2Eactive%3Ahover%20%2Elist%2Dgroup%2Ditem%2Dheading%2C%2Elist%2Dgroup%2Ditem%2Eactive%3Ahover%20%2Elist%2Dgroup%2Ditem%2Dheading%3E%2Esmall%2C%2Elist%2Dgroup%2Ditem%2Eactive%3Ahover%20%2Elist%2Dgroup%2Ditem%2Dheading%3Esmall%7Bcolor%3Ainherit%7D%2Elist%2Dgroup%2Ditem%2Eactive%20%2Elist%2Dgroup%2Ditem%2Dtext%2C%2Elist%2Dgroup%2Ditem%2Eactive%3Afocus%20%2Elist%2Dgroup%2Ditem%2Dtext%2C%2Elist%2Dgroup%2Ditem%2Eactive%3Ahover%20%2Elist%2Dgroup%2Ditem%2Dtext%7Bcolor%3A%23c7ddef%7D%2Elist%2Dgroup%2Ditem%2Dsuccess%7Bcolor%3A%233c763d%3Bbackground%2Dcolor%3A%23dff0d8%7Da%2Elist%2Dgroup%2Ditem%2Dsuccess%2Cbutton%2Elist%2Dgroup%2Ditem%2Dsuccess%7Bcolor%3A%233c763d%7Da%2Elist%2Dgroup%2Ditem%2Dsuccess%20%2Elist%2Dgroup%2Ditem%2Dheading%2Cbutton%2Elist%2Dgroup%2Ditem%2Dsuccess%20%2Elist%2Dgroup%2Ditem%2Dheading%7Bcolor%3Ainherit%7Da%2Elist%2Dgroup%2Ditem%2Dsuccess%3Afocus%2Ca%2Elist%2Dgroup%2Ditem%2Dsuccess%3Ahover%2Cbutton%2Elist%2Dgroup%2Ditem%2Dsuccess%3Afocus%2Cbutton%2Elist%2Dgroup%2Ditem%2Dsuccess%3Ahover%7Bcolor%3A%233c763d%3Bbackground%2Dcolor%3A%23d0e9c6%7Da%2Elist%2Dgroup%2Ditem%2Dsuccess%2Eactive%2Ca%2Elist%2Dgroup%2Ditem%2Dsuccess%2Eactive%3Afocus%2Ca%2Elist%2Dgroup%2Ditem%2Dsuccess%2Eactive%3Ahover%2Cbutton%2Elist%2Dgroup%2Ditem%2Dsuccess%2Eactive%2Cbutton%2Elist%2Dgroup%2Ditem%2Dsuccess%2Eactive%3Afocus%2Cbutton%2Elist%2Dgroup%2Ditem%2Dsuccess%2Eactive%3Ahover%7Bcolor%3A%23fff%3Bbackground%2Dcolor%3A%233c763d%3Bborder%2Dcolor%3A%233c763d%7D%2Elist%2Dgroup%2Ditem%2Dinfo%7Bcolor%3A%2331708f%3Bbackground%2Dcolor%3A%23d9edf7%7Da%2Elist%2Dgroup%2Ditem%2Dinfo%2Cbutton%2Elist%2Dgroup%2Ditem%2Dinfo%7Bcolor%3A%2331708f%7Da%2Elist%2Dgroup%2Ditem%2Dinfo%20%2Elist%2Dgroup%2Ditem%2Dheading%2Cbutton%2Elist%2Dgroup%2Ditem%2Dinfo%20%2Elist%2Dgroup%2Ditem%2Dheading%7Bcolor%3Ainherit%7Da%2Elist%2Dgroup%2Ditem%2Dinfo%3Afocus%2Ca%2Elist%2Dgroup%2Ditem%2Dinfo%3Ahover%2Cbutton%2Elist%2Dgroup%2Ditem%2Dinfo%3Afocus%2Cbutton%2Elist%2Dgroup%2Ditem%2Dinfo%3Ahover%7Bcolor%3A%2331708f%3Bbackground%2Dcolor%3A%23c4e3f3%7Da%2Elist%2Dgroup%2Ditem%2Dinfo%2Eactive%2Ca%2Elist%2Dgroup%2Ditem%2Dinfo%2Eactive%3Afocus%2Ca%2Elist%2Dgroup%2Ditem%2Dinfo%2Eactive%3Ahover%2Cbutton%2Elist%2Dgroup%2Ditem%2Dinfo%2Eactive%2Cbutton%2Elist%2Dgroup%2Ditem%2Dinfo%2Eactive%3Afocus%2Cbutton%2Elist%2Dgroup%2Ditem%2Dinfo%2Eactive%3Ahover%7Bcolor%3A%23fff%3Bbackground%2Dcolor%3A%2331708f%3Bborder%2Dcolor%3A%2331708f%7D%2Elist%2Dgroup%2Ditem%2Dwarning%7Bcolor%3A%238a6d3b%3Bbackground%2Dcolor%3A%23fcf8e3%7Da%2Elist%2Dgroup%2Ditem%2Dwarning%2Cbutton%2Elist%2Dgroup%2Ditem%2Dwarning%7Bcolor%3A%238a6d3b%7Da%2Elist%2Dgroup%2Ditem%2Dwarning%20%2Elist%2Dgroup%2Ditem%2Dheading%2Cbutton%2Elist%2Dgroup%2Ditem%2Dwarning%20%2Elist%2Dgroup%2Ditem%2Dheading%7Bcolor%3Ainherit%7Da%2Elist%2Dgroup%2Ditem%2Dwarning%3Afocus%2Ca%2Elist%2Dgroup%2Ditem%2Dwarning%3Ahover%2Cbutton%2Elist%2Dgroup%2Ditem%2Dwarning%3Afocus%2Cbutton%2Elist%2Dgroup%2Ditem%2Dwarning%3Ahover%7Bcolor%3A%238a6d3b%3Bbackground%2Dcolor%3A%23faf2cc%7Da%2Elist%2Dgroup%2Ditem%2Dwarning%2Eactive%2Ca%2Elist%2Dgroup%2Ditem%2Dwarning%2Eactive%3Afocus%2Ca%2Elist%2Dgroup%2Ditem%2Dwarning%2Eactive%3Ahover%2Cbutton%2Elist%2Dgroup%2Ditem%2Dwarning%2Eactive%2Cbutton%2Elist%2Dgroup%2Ditem%2Dwarning%2Eactive%3Afocus%2Cbutton%2Elist%2Dgroup%2Ditem%2Dwarning%2Eactive%3Ahover%7Bcolor%3A%23fff%3Bbackground%2Dcolor%3A%238a6d3b%3Bborder%2Dcolor%3A%238a6d3b%7D%2Elist%2Dgroup%2Ditem%2Ddanger%7Bcolor%3A%23a94442%3Bbackground%2Dcolor%3A%23f2dede%7Da%2Elist%2Dgroup%2Ditem%2Ddanger%2Cbutton%2Elist%2Dgroup%2Ditem%2Ddanger%7Bcolor%3A%23a94442%7Da%2Elist%2Dgroup%2Ditem%2Ddanger%20%2Elist%2Dgroup%2Ditem%2Dheading%2Cbutton%2Elist%2Dgroup%2Ditem%2Ddanger%20%2Elist%2Dgroup%2Ditem%2Dheading%7Bcolor%3Ainherit%7Da%2Elist%2Dgroup%2Ditem%2Ddanger%3Afocus%2Ca%2Elist%2Dgroup%2Ditem%2Ddanger%3Ahover%2Cbutton%2Elist%2Dgroup%2Ditem%2Ddanger%3Afocus%2Cbutton%2Elist%2Dgroup%2Ditem%2Ddanger%3Ahover%7Bcolor%3A%23a94442%3Bbackground%2Dcolor%3A%23ebcccc%7Da%2Elist%2Dgroup%2Ditem%2Ddanger%2Eactive%2Ca%2Elist%2Dgroup%2Ditem%2Ddanger%2Eactive%3Afocus%2Ca%2Elist%2Dgroup%2Ditem%2Ddanger%2Eactive%3Ahover%2Cbutton%2Elist%2Dgroup%2Ditem%2Ddanger%2Eactive%2Cbutton%2Elist%2Dgroup%2Ditem%2Ddanger%2Eactive%3Afocus%2Cbutton%2Elist%2Dgroup%2Ditem%2Ddanger%2Eactive%3Ahover%7Bcolor%3A%23fff%3Bbackground%2Dcolor%3A%23a94442%3Bborder%2Dcolor%3A%23a94442%7D%2Elist%2Dgroup%2Ditem%2Dheading%7Bmargin%2Dtop%3A0%3Bmargin%2Dbottom%3A5px%7D%2Elist%2Dgroup%2Ditem%2Dtext%7Bmargin%2Dbottom%3A0%3Bline%2Dheight%3A1%2E3%7D%2Epanel%7Bmargin%2Dbottom%3A20px%3Bbackground%2Dcolor%3A%23fff%3Bborder%3A1px%20solid%20transparent%3Bborder%2Dradius%3A4px%3B%2Dwebkit%2Dbox%2Dshadow%3A0%201px%201px%20rgba%280%2C0%2C0%2C%2E05%29%3Bbox%2Dshadow%3A0%201px%201px%20rgba%280%2C0%2C0%2C%2E05%29%7D%2Epanel%2Dbody%7Bpadding%3A15px%7D%2Epanel%2Dheading%7Bpadding%3A10px%2015px%3Bborder%2Dbottom%3A1px%20solid%20transparent%3Bborder%2Dtop%2Dleft%2Dradius%3A3px%3Bborder%2Dtop%2Dright%2Dradius%3A3px%7D%2Epanel%2Dheading%3E%2Edropdown%20%2Edropdown%2Dtoggle%7Bcolor%3Ainherit%7D%2Epanel%2Dtitle%7Bmargin%2Dtop%3A0%3Bmargin%2Dbottom%3A0%3Bfont%2Dsize%3A16px%3Bcolor%3Ainherit%7D%2Epanel%2Dtitle%3E%2Esmall%2C%2Epanel%2Dtitle%3E%2Esmall%3Ea%2C%2Epanel%2Dtitle%3Ea%2C%2Epanel%2Dtitle%3Esmall%2C%2Epanel%2Dtitle%3Esmall%3Ea%7Bcolor%3Ainherit%7D%2Epanel%2Dfooter%7Bpadding%3A10px%2015px%3Bbackground%2Dcolor%3A%23f5f5f5%3Bborder%2Dtop%3A1px%20solid%20%23ddd%3Bborder%2Dbottom%2Dright%2Dradius%3A3px%3Bborder%2Dbottom%2Dleft%2Dradius%3A3px%7D%2Epanel%3E%2Elist%2Dgroup%2C%2Epanel%3E%2Epanel%2Dcollapse%3E%2Elist%2Dgroup%7Bmargin%2Dbottom%3A0%7D%2Epanel%3E%2Elist%2Dgroup%20%2Elist%2Dgroup%2Ditem%2C%2Epanel%3E%2Epanel%2Dcollapse%3E%2Elist%2Dgroup%20%2Elist%2Dgroup%2Ditem%7Bborder%2Dwidth%3A1px%200%3Bborder%2Dradius%3A0%7D%2Epanel%3E%2Elist%2Dgroup%3Afirst%2Dchild%20%2Elist%2Dgroup%2Ditem%3Afirst%2Dchild%2C%2Epanel%3E%2Epanel%2Dcollapse%3E%2Elist%2Dgroup%3Afirst%2Dchild%20%2Elist%2Dgroup%2Ditem%3Afirst%2Dchild%7Bborder%2Dtop%3A0%3Bborder%2Dtop%2Dleft%2Dradius%3A3px%3Bborder%2Dtop%2Dright%2Dradius%3A3px%7D%2Epanel%3E%2Elist%2Dgroup%3Alast%2Dchild%20%2Elist%2Dgroup%2Ditem%3Alast%2Dchild%2C%2Epanel%3E%2Epanel%2Dcollapse%3E%2Elist%2Dgroup%3Alast%2Dchild%20%2Elist%2Dgroup%2Ditem%3Alast%2Dchild%7Bborder%2Dbottom%3A0%3Bborder%2Dbottom%2Dright%2Dradius%3A3px%3Bborder%2Dbottom%2Dleft%2Dradius%3A3px%7D%2Epanel%3E%2Epanel%2Dheading%2B%2Epanel%2Dcollapse%3E%2Elist%2Dgroup%20%2Elist%2Dgroup%2Ditem%3Afirst%2Dchild%7Bborder%2Dtop%2Dleft%2Dradius%3A0%3Bborder%2Dtop%2Dright%2Dradius%3A0%7D%2Epanel%2Dheading%2B%2Elist%2Dgroup%20%2Elist%2Dgroup%2Ditem%3Afirst%2Dchild%7Bborder%2Dtop%2Dwidth%3A0%7D%2Elist%2Dgroup%2B%2Epanel%2Dfooter%7Bborder%2Dtop%2Dwidth%3A0%7D%2Epanel%3E%2Epanel%2Dcollapse%3E%2Etable%2C%2Epanel%3E%2Etable%2C%2Epanel%3E%2Etable%2Dresponsive%3E%2Etable%7Bmargin%2Dbottom%3A0%7D%2Epanel%3E%2Epanel%2Dcollapse%3E%2Etable%20caption%2C%2Epanel%3E%2Etable%20caption%2C%2Epanel%3E%2Etable%2Dresponsive%3E%2Etable%20caption%7Bpadding%2Dright%3A15px%3Bpadding%2Dleft%3A15px%7D%2Epanel%3E%2Etable%2Dresponsive%3Afirst%2Dchild%3E%2Etable%3Afirst%2Dchild%2C%2Epanel%3E%2Etable%3Afirst%2Dchild%7Bborder%2Dtop%2Dleft%2Dradius%3A3px%3Bborder%2Dtop%2Dright%2Dradius%3A3px%7D%2Epanel%3E%2Etable%2Dresponsive%3Afirst%2Dchild%3E%2Etable%3Afirst%2Dchild%3Etbody%3Afirst%2Dchild%3Etr%3Afirst%2Dchild%2C%2Epanel%3E%2Etable%2Dresponsive%3Afirst%2Dchild%3E%2Etable%3Afirst%2Dchild%3Ethead%3Afirst%2Dchild%3Etr%3Afirst%2Dchild%2C%2Epanel%3E%2Etable%3Afirst%2Dchild%3Etbody%3Afirst%2Dchild%3Etr%3Afirst%2Dchild%2C%2Epanel%3E%2Etable%3Afirst%2Dchild%3Ethead%3Afirst%2Dchild%3Etr%3Afirst%2Dchild%7Bborder%2Dtop%2Dleft%2Dradius%3A3px%3Bborder%2Dtop%2Dright%2Dradius%3A3px%7D%2Epanel%3E%2Etable%2Dresponsive%3Afirst%2Dchild%3E%2Etable%3Afirst%2Dchild%3Etbody%3Afirst%2Dchild%3Etr%3Afirst%2Dchild%20td%3Afirst%2Dchild%2C%2Epanel%3E%2Etable%2Dresponsive%3Afirst%2Dchild%3E%2Etable%3Afirst%2Dchild%3Etbody%3Afirst%2Dchild%3Etr%3Afirst%2Dchild%20th%3Afirst%2Dchild%2C%2Epanel%3E%2Etable%2Dresponsive%3Afirst%2Dchild%3E%2Etable%3Afirst%2Dchild%3Ethead%3Afirst%2Dchild%3Etr%3Afirst%2Dchild%20td%3Afirst%2Dchild%2C%2Epanel%3E%2Etable%2Dresponsive%3Afirst%2Dchild%3E%2Etable%3Afirst%2Dchild%3Ethead%3Afirst%2Dchild%3Etr%3Afirst%2Dchild%20th%3Afirst%2Dchild%2C%2Epanel%3E%2Etable%3Afirst%2Dchild%3Etbody%3Afirst%2Dchild%3Etr%3Afirst%2Dchild%20td%3Afirst%2Dchild%2C%2Epanel%3E%2Etable%3Afirst%2Dchild%3Etbody%3Afirst%2Dchild%3Etr%3Afirst%2Dchild%20th%3Afirst%2Dchild%2C%2Epanel%3E%2Etable%3Afirst%2Dchild%3Ethead%3Afirst%2Dchild%3Etr%3Afirst%2Dchild%20td%3Afirst%2Dchild%2C%2Epanel%3E%2Etable%3Afirst%2Dchild%3Ethead%3Afirst%2Dchild%3Etr%3Afirst%2Dchild%20th%3Afirst%2Dchild%7Bborder%2Dtop%2Dleft%2Dradius%3A3px%7D%2Epanel%3E%2Etable%2Dresponsive%3Afirst%2Dchild%3E%2Etable%3Afirst%2Dchild%3Etbody%3Afirst%2Dchild%3Etr%3Afirst%2Dchild%20td%3Alast%2Dchild%2C%2Epanel%3E%2Etable%2Dresponsive%3Afirst%2Dchild%3E%2Etable%3Afirst%2Dchild%3Etbody%3Afirst%2Dchild%3Etr%3Afirst%2Dchild%20th%3Alast%2Dchild%2C%2Epanel%3E%2Etable%2Dresponsive%3Afirst%2Dchild%3E%2Etable%3Afirst%2Dchild%3Ethead%3Afirst%2Dchild%3Etr%3Afirst%2Dchild%20td%3Alast%2Dchild%2C%2Epanel%3E%2Etable%2Dresponsive%3Afirst%2Dchild%3E%2Etable%3Afirst%2Dchild%3Ethead%3Afirst%2Dchild%3Etr%3Afirst%2Dchild%20th%3Alast%2Dchild%2C%2Epanel%3E%2Etable%3Afirst%2Dchild%3Etbody%3Afirst%2Dchild%3Etr%3Afirst%2Dchild%20td%3Alast%2Dchild%2C%2Epanel%3E%2Etable%3Afirst%2Dchild%3Etbody%3Afirst%2Dchild%3Etr%3Afirst%2Dchild%20th%3Alast%2Dchild%2C%2Epanel%3E%2Etable%3Afirst%2Dchild%3Ethead%3Afirst%2Dchild%3Etr%3Afirst%2Dchild%20td%3Alast%2Dchild%2C%2Epanel%3E%2Etable%3Afirst%2Dchild%3Ethead%3Afirst%2Dchild%3Etr%3Afirst%2Dchild%20th%3Alast%2Dchild%7Bborder%2Dtop%2Dright%2Dradius%3A3px%7D%2Epanel%3E%2Etable%2Dresponsive%3Alast%2Dchild%3E%2Etable%3Alast%2Dchild%2C%2Epanel%3E%2Etable%3Alast%2Dchild%7Bborder%2Dbottom%2Dright%2Dradius%3A3px%3Bborder%2Dbottom%2Dleft%2Dradius%3A3px%7D%2Epanel%3E%2Etable%2Dresponsive%3Alast%2Dchild%3E%2Etable%3Alast%2Dchild%3Etbody%3Alast%2Dchild%3Etr%3Alast%2Dchild%2C%2Epanel%3E%2Etable%2Dresponsive%3Alast%2Dchild%3E%2Etable%3Alast%2Dchild%3Etfoot%3Alast%2Dchild%3Etr%3Alast%2Dchild%2C%2Epanel%3E%2Etable%3Alast%2Dchild%3Etbody%3Alast%2Dchild%3Etr%3Alast%2Dchild%2C%2Epanel%3E%2Etable%3Alast%2Dchild%3Etfoot%3Alast%2Dchild%3Etr%3Alast%2Dchild%7Bborder%2Dbottom%2Dright%2Dradius%3A3px%3Bborder%2Dbottom%2Dleft%2Dradius%3A3px%7D%2Epanel%3E%2Etable%2Dresponsive%3Alast%2Dchild%3E%2Etable%3Alast%2Dchild%3Etbody%3Alast%2Dchild%3Etr%3Alast%2Dchild%20td%3Afirst%2Dchild%2C%2Epanel%3E%2Etable%2Dresponsive%3Alast%2Dchild%3E%2Etable%3Alast%2Dchild%3Etbody%3Alast%2Dchild%3Etr%3Alast%2Dchild%20th%3Afirst%2Dchild%2C%2Epanel%3E%2Etable%2Dresponsive%3Alast%2Dchild%3E%2Etable%3Alast%2Dchild%3Etfoot%3Alast%2Dchild%3Etr%3Alast%2Dchild%20td%3Afirst%2Dchild%2C%2Epanel%3E%2Etable%2Dresponsive%3Alast%2Dchild%3E%2Etable%3Alast%2Dchild%3Etfoot%3Alast%2Dchild%3Etr%3Alast%2Dchild%20th%3Afirst%2Dchild%2C%2Epanel%3E%2Etable%3Alast%2Dchild%3Etbody%3Alast%2Dchild%3Etr%3Alast%2Dchild%20td%3Afirst%2Dchild%2C%2Epanel%3E%2Etable%3Alast%2Dchild%3Etbody%3Alast%2Dchild%3Etr%3Alast%2Dchild%20th%3Afirst%2Dchild%2C%2Epanel%3E%2Etable%3Alast%2Dchild%3Etfoot%3Alast%2Dchild%3Etr%3Alast%2Dchild%20td%3Afirst%2Dchild%2C%2Epanel%3E%2Etable%3Alast%2Dchild%3Etfoot%3Alast%2Dchild%3Etr%3Alast%2Dchild%20th%3Afirst%2Dchild%7Bborder%2Dbottom%2Dleft%2Dradius%3A3px%7D%2Epanel%3E%2Etable%2Dresponsive%3Alast%2Dchild%3E%2Etable%3Alast%2Dchild%3Etbody%3Alast%2Dchild%3Etr%3Alast%2Dchild%20td%3Alast%2Dchild%2C%2Epanel%3E%2Etable%2Dresponsive%3Alast%2Dchild%3E%2Etable%3Alast%2Dchild%3Etbody%3Alast%2Dchild%3Etr%3Alast%2Dchild%20th%3Alast%2Dchild%2C%2Epanel%3E%2Etable%2Dresponsive%3Alast%2Dchild%3E%2Etable%3Alast%2Dchild%3Etfoot%3Alast%2Dchild%3Etr%3Alast%2Dchild%20td%3Alast%2Dchild%2C%2Epanel%3E%2Etable%2Dresponsive%3Alast%2Dchild%3E%2Etable%3Alast%2Dchild%3Etfoot%3Alast%2Dchild%3Etr%3Alast%2Dchild%20th%3Alast%2Dchild%2C%2Epanel%3E%2Etable%3Alast%2Dchild%3Etbody%3Alast%2Dchild%3Etr%3Alast%2Dchild%20td%3Alast%2Dchild%2C%2Epanel%3E%2Etable%3Alast%2Dchild%3Etbody%3Alast%2Dchild%3Etr%3Alast%2Dchild%20th%3Alast%2Dchild%2C%2Epanel%3E%2Etable%3Alast%2Dchild%3Etfoot%3Alast%2Dchild%3Etr%3Alast%2Dchild%20td%3Alast%2Dchild%2C%2Epanel%3E%2Etable%3Alast%2Dchild%3Etfoot%3Alast%2Dchild%3Etr%3Alast%2Dchild%20th%3Alast%2Dchild%7Bborder%2Dbottom%2Dright%2Dradius%3A3px%7D%2Epanel%3E%2Epanel%2Dbody%2B%2Etable%2C%2Epanel%3E%2Epanel%2Dbody%2B%2Etable%2Dresponsive%2C%2Epanel%3E%2Etable%2B%2Epanel%2Dbody%2C%2Epanel%3E%2Etable%2Dresponsive%2B%2Epanel%2Dbody%7Bborder%2Dtop%3A1px%20solid%20%23ddd%7D%2Epanel%3E%2Etable%3Etbody%3Afirst%2Dchild%3Etr%3Afirst%2Dchild%20td%2C%2Epanel%3E%2Etable%3Etbody%3Afirst%2Dchild%3Etr%3Afirst%2Dchild%20th%7Bborder%2Dtop%3A0%7D%2Epanel%3E%2Etable%2Dbordered%2C%2Epanel%3E%2Etable%2Dresponsive%3E%2Etable%2Dbordered%7Bborder%3A0%7D%2Epanel%3E%2Etable%2Dbordered%3Etbody%3Etr%3Etd%3Afirst%2Dchild%2C%2Epanel%3E%2Etable%2Dbordered%3Etbody%3Etr%3Eth%3Afirst%2Dchild%2C%2Epanel%3E%2Etable%2Dbordered%3Etfoot%3Etr%3Etd%3Afirst%2Dchild%2C%2Epanel%3E%2Etable%2Dbordered%3Etfoot%3Etr%3Eth%3Afirst%2Dchild%2C%2Epanel%3E%2Etable%2Dbordered%3Ethead%3Etr%3Etd%3Afirst%2Dchild%2C%2Epanel%3E%2Etable%2Dbordered%3Ethead%3Etr%3Eth%3Afirst%2Dchild%2C%2Epanel%3E%2Etable%2Dresponsive%3E%2Etable%2Dbordered%3Etbody%3Etr%3Etd%3Afirst%2Dchild%2C%2Epanel%3E%2Etable%2Dresponsive%3E%2Etable%2Dbordered%3Etbody%3Etr%3Eth%3Afirst%2Dchild%2C%2Epanel%3E%2Etable%2Dresponsive%3E%2Etable%2Dbordered%3Etfoot%3Etr%3Etd%3Afirst%2Dchild%2C%2Epanel%3E%2Etable%2Dresponsive%3E%2Etable%2Dbordered%3Etfoot%3Etr%3Eth%3Afirst%2Dchild%2C%2Epanel%3E%2Etable%2Dresponsive%3E%2Etable%2Dbordered%3Ethead%3Etr%3Etd%3Afirst%2Dchild%2C%2Epanel%3E%2Etable%2Dresponsive%3E%2Etable%2Dbordered%3Ethead%3Etr%3Eth%3Afirst%2Dchild%7Bborder%2Dleft%3A0%7D%2Epanel%3E%2Etable%2Dbordered%3Etbody%3Etr%3Etd%3Alast%2Dchild%2C%2Epanel%3E%2Etable%2Dbordered%3Etbody%3Etr%3Eth%3Alast%2Dchild%2C%2Epanel%3E%2Etable%2Dbordered%3Etfoot%3Etr%3Etd%3Alast%2Dchild%2C%2Epanel%3E%2Etable%2Dbordered%3Etfoot%3Etr%3Eth%3Alast%2Dchild%2C%2Epanel%3E%2Etable%2Dbordered%3Ethead%3Etr%3Etd%3Alast%2Dchild%2C%2Epanel%3E%2Etable%2Dbordered%3Ethead%3Etr%3Eth%3Alast%2Dchild%2C%2Epanel%3E%2Etable%2Dresponsive%3E%2Etable%2Dbordered%3Etbody%3Etr%3Etd%3Alast%2Dchild%2C%2Epanel%3E%2Etable%2Dresponsive%3E%2Etable%2Dbordered%3Etbody%3Etr%3Eth%3Alast%2Dchild%2C%2Epanel%3E%2Etable%2Dresponsive%3E%2Etable%2Dbordered%3Etfoot%3Etr%3Etd%3Alast%2Dchild%2C%2Epanel%3E%2Etable%2Dresponsive%3E%2Etable%2Dbordered%3Etfoot%3Etr%3Eth%3Alast%2Dchild%2C%2Epanel%3E%2Etable%2Dresponsive%3E%2Etable%2Dbordered%3Ethead%3Etr%3Etd%3Alast%2Dchild%2C%2Epanel%3E%2Etable%2Dresponsive%3E%2Etable%2Dbordered%3Ethead%3Etr%3Eth%3Alast%2Dchild%7Bborder%2Dright%3A0%7D%2Epanel%3E%2Etable%2Dbordered%3Etbody%3Etr%3Afirst%2Dchild%3Etd%2C%2Epanel%3E%2Etable%2Dbordered%3Etbody%3Etr%3Afirst%2Dchild%3Eth%2C%2Epanel%3E%2Etable%2Dbordered%3Ethead%3Etr%3Afirst%2Dchild%3Etd%2C%2Epanel%3E%2Etable%2Dbordered%3Ethead%3Etr%3Afirst%2Dchild%3Eth%2C%2Epanel%3E%2Etable%2Dresponsive%3E%2Etable%2Dbordered%3Etbody%3Etr%3Afirst%2Dchild%3Etd%2C%2Epanel%3E%2Etable%2Dresponsive%3E%2Etable%2Dbordered%3Etbody%3Etr%3Afirst%2Dchild%3Eth%2C%2Epanel%3E%2Etable%2Dresponsive%3E%2Etable%2Dbordered%3Ethead%3Etr%3Afirst%2Dchild%3Etd%2C%2Epanel%3E%2Etable%2Dresponsive%3E%2Etable%2Dbordered%3Ethead%3Etr%3Afirst%2Dchild%3Eth%7Bborder%2Dbottom%3A0%7D%2Epanel%3E%2Etable%2Dbordered%3Etbody%3Etr%3Alast%2Dchild%3Etd%2C%2Epanel%3E%2Etable%2Dbordered%3Etbody%3Etr%3Alast%2Dchild%3Eth%2C%2Epanel%3E%2Etable%2Dbordered%3Etfoot%3Etr%3Alast%2Dchild%3Etd%2C%2Epanel%3E%2Etable%2Dbordered%3Etfoot%3Etr%3Alast%2Dchild%3Eth%2C%2Epanel%3E%2Etable%2Dresponsive%3E%2Etable%2Dbordered%3Etbody%3Etr%3Alast%2Dchild%3Etd%2C%2Epanel%3E%2Etable%2Dresponsive%3E%2Etable%2Dbordered%3Etbody%3Etr%3Alast%2Dchild%3Eth%2C%2Epanel%3E%2Etable%2Dresponsive%3E%2Etable%2Dbordered%3Etfoot%3Etr%3Alast%2Dchild%3Etd%2C%2Epanel%3E%2Etable%2Dresponsive%3E%2Etable%2Dbordered%3Etfoot%3Etr%3Alast%2Dchild%3Eth%7Bborder%2Dbottom%3A0%7D%2Epanel%3E%2Etable%2Dresponsive%7Bmargin%2Dbottom%3A0%3Bborder%3A0%7D%2Epanel%2Dgroup%7Bmargin%2Dbottom%3A20px%7D%2Epanel%2Dgroup%20%2Epanel%7Bmargin%2Dbottom%3A0%3Bborder%2Dradius%3A4px%7D%2Epanel%2Dgroup%20%2Epanel%2B%2Epanel%7Bmargin%2Dtop%3A5px%7D%2Epanel%2Dgroup%20%2Epanel%2Dheading%7Bborder%2Dbottom%3A0%7D%2Epanel%2Dgroup%20%2Epanel%2Dheading%2B%2Epanel%2Dcollapse%3E%2Elist%2Dgroup%2C%2Epanel%2Dgroup%20%2Epanel%2Dheading%2B%2Epanel%2Dcollapse%3E%2Epanel%2Dbody%7Bborder%2Dtop%3A1px%20solid%20%23ddd%7D%2Epanel%2Dgroup%20%2Epanel%2Dfooter%7Bborder%2Dtop%3A0%7D%2Epanel%2Dgroup%20%2Epanel%2Dfooter%2B%2Epanel%2Dcollapse%20%2Epanel%2Dbody%7Bborder%2Dbottom%3A1px%20solid%20%23ddd%7D%2Epanel%2Ddefault%7Bborder%2Dcolor%3A%23ddd%7D%2Epanel%2Ddefault%3E%2Epanel%2Dheading%7Bcolor%3A%23333%3Bbackground%2Dcolor%3A%23f5f5f5%3Bborder%2Dcolor%3A%23ddd%7D%2Epanel%2Ddefault%3E%2Epanel%2Dheading%2B%2Epanel%2Dcollapse%3E%2Epanel%2Dbody%7Bborder%2Dtop%2Dcolor%3A%23ddd%7D%2Epanel%2Ddefault%3E%2Epanel%2Dheading%20%2Ebadge%7Bcolor%3A%23f5f5f5%3Bbackground%2Dcolor%3A%23333%7D%2Epanel%2Ddefault%3E%2Epanel%2Dfooter%2B%2Epanel%2Dcollapse%3E%2Epanel%2Dbody%7Bborder%2Dbottom%2Dcolor%3A%23ddd%7D%2Epanel%2Dprimary%7Bborder%2Dcolor%3A%23337ab7%7D%2Epanel%2Dprimary%3E%2Epanel%2Dheading%7Bcolor%3A%23fff%3Bbackground%2Dcolor%3A%23337ab7%3Bborder%2Dcolor%3A%23337ab7%7D%2Epanel%2Dprimary%3E%2Epanel%2Dheading%2B%2Epanel%2Dcollapse%3E%2Epanel%2Dbody%7Bborder%2Dtop%2Dcolor%3A%23337ab7%7D%2Epanel%2Dprimary%3E%2Epanel%2Dheading%20%2Ebadge%7Bcolor%3A%23337ab7%3Bbackground%2Dcolor%3A%23fff%7D%2Epanel%2Dprimary%3E%2Epanel%2Dfooter%2B%2Epanel%2Dcollapse%3E%2Epanel%2Dbody%7Bborder%2Dbottom%2Dcolor%3A%23337ab7%7D%2Epanel%2Dsuccess%7Bborder%2Dcolor%3A%23d6e9c6%7D%2Epanel%2Dsuccess%3E%2Epanel%2Dheading%7Bcolor%3A%233c763d%3Bbackground%2Dcolor%3A%23dff0d8%3Bborder%2Dcolor%3A%23d6e9c6%7D%2Epanel%2Dsuccess%3E%2Epanel%2Dheading%2B%2Epanel%2Dcollapse%3E%2Epanel%2Dbody%7Bborder%2Dtop%2Dcolor%3A%23d6e9c6%7D%2Epanel%2Dsuccess%3E%2Epanel%2Dheading%20%2Ebadge%7Bcolor%3A%23dff0d8%3Bbackground%2Dcolor%3A%233c763d%7D%2Epanel%2Dsuccess%3E%2Epanel%2Dfooter%2B%2Epanel%2Dcollapse%3E%2Epanel%2Dbody%7Bborder%2Dbottom%2Dcolor%3A%23d6e9c6%7D%2Epanel%2Dinfo%7Bborder%2Dcolor%3A%23bce8f1%7D%2Epanel%2Dinfo%3E%2Epanel%2Dheading%7Bcolor%3A%2331708f%3Bbackground%2Dcolor%3A%23d9edf7%3Bborder%2Dcolor%3A%23bce8f1%7D%2Epanel%2Dinfo%3E%2Epanel%2Dheading%2B%2Epanel%2Dcollapse%3E%2Epanel%2Dbody%7Bborder%2Dtop%2Dcolor%3A%23bce8f1%7D%2Epanel%2Dinfo%3E%2Epanel%2Dheading%20%2Ebadge%7Bcolor%3A%23d9edf7%3Bbackground%2Dcolor%3A%2331708f%7D%2Epanel%2Dinfo%3E%2Epanel%2Dfooter%2B%2Epanel%2Dcollapse%3E%2Epanel%2Dbody%7Bborder%2Dbottom%2Dcolor%3A%23bce8f1%7D%2Epanel%2Dwarning%7Bborder%2Dcolor%3A%23faebcc%7D%2Epanel%2Dwarning%3E%2Epanel%2Dheading%7Bcolor%3A%238a6d3b%3Bbackground%2Dcolor%3A%23fcf8e3%3Bborder%2Dcolor%3A%23faebcc%7D%2Epanel%2Dwarning%3E%2Epanel%2Dheading%2B%2Epanel%2Dcollapse%3E%2Epanel%2Dbody%7Bborder%2Dtop%2Dcolor%3A%23faebcc%7D%2Epanel%2Dwarning%3E%2Epanel%2Dheading%20%2Ebadge%7Bcolor%3A%23fcf8e3%3Bbackground%2Dcolor%3A%238a6d3b%7D%2Epanel%2Dwarning%3E%2Epanel%2Dfooter%2B%2Epanel%2Dcollapse%3E%2Epanel%2Dbody%7Bborder%2Dbottom%2Dcolor%3A%23faebcc%7D%2Epanel%2Ddanger%7Bborder%2Dcolor%3A%23ebccd1%7D%2Epanel%2Ddanger%3E%2Epanel%2Dheading%7Bcolor%3A%23a94442%3Bbackground%2Dcolor%3A%23f2dede%3Bborder%2Dcolor%3A%23ebccd1%7D%2Epanel%2Ddanger%3E%2Epanel%2Dheading%2B%2Epanel%2Dcollapse%3E%2Epanel%2Dbody%7Bborder%2Dtop%2Dcolor%3A%23ebccd1%7D%2Epanel%2Ddanger%3E%2Epanel%2Dheading%20%2Ebadge%7Bcolor%3A%23f2dede%3Bbackground%2Dcolor%3A%23a94442%7D%2Epanel%2Ddanger%3E%2Epanel%2Dfooter%2B%2Epanel%2Dcollapse%3E%2Epanel%2Dbody%7Bborder%2Dbottom%2Dcolor%3A%23ebccd1%7D%2Eembed%2Dresponsive%7Bposition%3Arelative%3Bdisplay%3Ablock%3Bheight%3A0%3Bpadding%3A0%3Boverflow%3Ahidden%7D%2Eembed%2Dresponsive%20%2Eembed%2Dresponsive%2Ditem%2C%2Eembed%2Dresponsive%20embed%2C%2Eembed%2Dresponsive%20iframe%2C%2Eembed%2Dresponsive%20object%2C%2Eembed%2Dresponsive%20video%7Bposition%3Aabsolute%3Btop%3A0%3Bbottom%3A0%3Bleft%3A0%3Bwidth%3A100%25%3Bheight%3A100%25%3Bborder%3A0%7D%2Eembed%2Dresponsive%2D16by9%7Bpadding%2Dbottom%3A56%2E25%25%7D%2Eembed%2Dresponsive%2D4by3%7Bpadding%2Dbottom%3A75%25%7D%2Ewell%7Bmin%2Dheight%3A20px%3Bpadding%3A19px%3Bmargin%2Dbottom%3A20px%3Bbackground%2Dcolor%3A%23f5f5f5%3Bborder%3A1px%20solid%20%23e3e3e3%3Bborder%2Dradius%3A4px%3B%2Dwebkit%2Dbox%2Dshadow%3Ainset%200%201px%201px%20rgba%280%2C0%2C0%2C%2E05%29%3Bbox%2Dshadow%3Ainset%200%201px%201px%20rgba%280%2C0%2C0%2C%2E05%29%7D%2Ewell%20blockquote%7Bborder%2Dcolor%3A%23ddd%3Bborder%2Dcolor%3Argba%280%2C0%2C0%2C%2E15%29%7D%2Ewell%2Dlg%7Bpadding%3A24px%3Bborder%2Dradius%3A6px%7D%2Ewell%2Dsm%7Bpadding%3A9px%3Bborder%2Dradius%3A3px%7D%2Eclose%7Bfloat%3Aright%3Bfont%2Dsize%3A21px%3Bfont%2Dweight%3A700%3Bline%2Dheight%3A1%3Bcolor%3A%23000%3Btext%2Dshadow%3A0%201px%200%20%23fff%3Bfilter%3Aalpha%28opacity%3D20%29%3Bopacity%3A%2E2%7D%2Eclose%3Afocus%2C%2Eclose%3Ahover%7Bcolor%3A%23000%3Btext%2Ddecoration%3Anone%3Bcursor%3Apointer%3Bfilter%3Aalpha%28opacity%3D50%29%3Bopacity%3A%2E5%7Dbutton%2Eclose%7B%2Dwebkit%2Dappearance%3Anone%3Bpadding%3A0%3Bcursor%3Apointer%3Bbackground%3A0%200%3Bborder%3A0%7D%2Emodal%2Dopen%7Boverflow%3Ahidden%7D%2Emodal%7Bposition%3Afixed%3Btop%3A0%3Bright%3A0%3Bbottom%3A0%3Bleft%3A0%3Bz%2Dindex%3A1050%3Bdisplay%3Anone%3Boverflow%3Ahidden%3B%2Dwebkit%2Doverflow%2Dscrolling%3Atouch%3Boutline%3A0%7D%2Emodal%2Efade%20%2Emodal%2Ddialog%7B%2Dwebkit%2Dtransition%3A%2Dwebkit%2Dtransform%20%2E3s%20ease%2Dout%3B%2Do%2Dtransition%3A%2Do%2Dtransform%20%2E3s%20ease%2Dout%3Btransition%3Atransform%20%2E3s%20ease%2Dout%3B%2Dwebkit%2Dtransform%3Atranslate%280%2C%2D25%25%29%3B%2Dms%2Dtransform%3Atranslate%280%2C%2D25%25%29%3B%2Do%2Dtransform%3Atranslate%280%2C%2D25%25%29%3Btransform%3Atranslate%280%2C%2D25%25%29%7D%2Emodal%2Ein%20%2Emodal%2Ddialog%7B%2Dwebkit%2Dtransform%3Atranslate%280%2C0%29%3B%2Dms%2Dtransform%3Atranslate%280%2C0%29%3B%2Do%2Dtransform%3Atranslate%280%2C0%29%3Btransform%3Atranslate%280%2C0%29%7D%2Emodal%2Dopen%20%2Emodal%7Boverflow%2Dx%3Ahidden%3Boverflow%2Dy%3Aauto%7D%2Emodal%2Ddialog%7Bposition%3Arelative%3Bwidth%3Aauto%3Bmargin%3A10px%7D%2Emodal%2Dcontent%7Bposition%3Arelative%3Bbackground%2Dcolor%3A%23fff%3B%2Dwebkit%2Dbackground%2Dclip%3Apadding%2Dbox%3Bbackground%2Dclip%3Apadding%2Dbox%3Bborder%3A1px%20solid%20%23999%3Bborder%3A1px%20solid%20rgba%280%2C0%2C0%2C%2E2%29%3Bborder%2Dradius%3A6px%3Boutline%3A0%3B%2Dwebkit%2Dbox%2Dshadow%3A0%203px%209px%20rgba%280%2C0%2C0%2C%2E5%29%3Bbox%2Dshadow%3A0%203px%209px%20rgba%280%2C0%2C0%2C%2E5%29%7D%2Emodal%2Dbackdrop%7Bposition%3Afixed%3Btop%3A0%3Bright%3A0%3Bbottom%3A0%3Bleft%3A0%3Bz%2Dindex%3A1040%3Bbackground%2Dcolor%3A%23000%7D%2Emodal%2Dbackdrop%2Efade%7Bfilter%3Aalpha%28opacity%3D0%29%3Bopacity%3A0%7D%2Emodal%2Dbackdrop%2Ein%7Bfilter%3Aalpha%28opacity%3D50%29%3Bopacity%3A%2E5%7D%2Emodal%2Dheader%7Bmin%2Dheight%3A16%2E43px%3Bpadding%3A15px%3Bborder%2Dbottom%3A1px%20solid%20%23e5e5e5%7D%2Emodal%2Dheader%20%2Eclose%7Bmargin%2Dtop%3A%2D2px%7D%2Emodal%2Dtitle%7Bmargin%3A0%3Bline%2Dheight%3A1%2E42857143%7D%2Emodal%2Dbody%7Bposition%3Arelative%3Bpadding%3A15px%7D%2Emodal%2Dfooter%7Bpadding%3A15px%3Btext%2Dalign%3Aright%3Bborder%2Dtop%3A1px%20solid%20%23e5e5e5%7D%2Emodal%2Dfooter%20%2Ebtn%2B%2Ebtn%7Bmargin%2Dbottom%3A0%3Bmargin%2Dleft%3A5px%7D%2Emodal%2Dfooter%20%2Ebtn%2Dgroup%20%2Ebtn%2B%2Ebtn%7Bmargin%2Dleft%3A%2D1px%7D%2Emodal%2Dfooter%20%2Ebtn%2Dblock%2B%2Ebtn%2Dblock%7Bmargin%2Dleft%3A0%7D%2Emodal%2Dscrollbar%2Dmeasure%7Bposition%3Aabsolute%3Btop%3A%2D9999px%3Bwidth%3A50px%3Bheight%3A50px%3Boverflow%3Ascroll%7D%40media%20%28min%2Dwidth%3A768px%29%7B%2Emodal%2Ddialog%7Bwidth%3A600px%3Bmargin%3A30px%20auto%7D%2Emodal%2Dcontent%7B%2Dwebkit%2Dbox%2Dshadow%3A0%205px%2015px%20rgba%280%2C0%2C0%2C%2E5%29%3Bbox%2Dshadow%3A0%205px%2015px%20rgba%280%2C0%2C0%2C%2E5%29%7D%2Emodal%2Dsm%7Bwidth%3A300px%7D%7D%40media%20%28min%2Dwidth%3A992px%29%7B%2Emodal%2Dlg%7Bwidth%3A900px%7D%7D%2Etooltip%7Bposition%3Aabsolute%3Bz%2Dindex%3A1070%3Bdisplay%3Ablock%3Bfont%2Dfamily%3A%22Helvetica%20Neue%22%2CHelvetica%2CArial%2Csans%2Dserif%3Bfont%2Dsize%3A12px%3Bfont%2Dstyle%3Anormal%3Bfont%2Dweight%3A400%3Bline%2Dheight%3A1%2E42857143%3Btext%2Dalign%3Aleft%3Btext%2Dalign%3Astart%3Btext%2Ddecoration%3Anone%3Btext%2Dshadow%3Anone%3Btext%2Dtransform%3Anone%3Bletter%2Dspacing%3Anormal%3Bword%2Dbreak%3Anormal%3Bword%2Dspacing%3Anormal%3Bword%2Dwrap%3Anormal%3Bwhite%2Dspace%3Anormal%3Bfilter%3Aalpha%28opacity%3D0%29%3Bopacity%3A0%3Bline%2Dbreak%3Aauto%7D%2Etooltip%2Ein%7Bfilter%3Aalpha%28opacity%3D90%29%3Bopacity%3A%2E9%7D%2Etooltip%2Etop%7Bpadding%3A5px%200%3Bmargin%2Dtop%3A%2D3px%7D%2Etooltip%2Eright%7Bpadding%3A0%205px%3Bmargin%2Dleft%3A3px%7D%2Etooltip%2Ebottom%7Bpadding%3A5px%200%3Bmargin%2Dtop%3A3px%7D%2Etooltip%2Eleft%7Bpadding%3A0%205px%3Bmargin%2Dleft%3A%2D3px%7D%2Etooltip%2Dinner%7Bmax%2Dwidth%3A200px%3Bpadding%3A3px%208px%3Bcolor%3A%23fff%3Btext%2Dalign%3Acenter%3Bbackground%2Dcolor%3A%23000%3Bborder%2Dradius%3A4px%7D%2Etooltip%2Darrow%7Bposition%3Aabsolute%3Bwidth%3A0%3Bheight%3A0%3Bborder%2Dcolor%3Atransparent%3Bborder%2Dstyle%3Asolid%7D%2Etooltip%2Etop%20%2Etooltip%2Darrow%7Bbottom%3A0%3Bleft%3A50%25%3Bmargin%2Dleft%3A%2D5px%3Bborder%2Dwidth%3A5px%205px%200%3Bborder%2Dtop%2Dcolor%3A%23000%7D%2Etooltip%2Etop%2Dleft%20%2Etooltip%2Darrow%7Bright%3A5px%3Bbottom%3A0%3Bmargin%2Dbottom%3A%2D5px%3Bborder%2Dwidth%3A5px%205px%200%3Bborder%2Dtop%2Dcolor%3A%23000%7D%2Etooltip%2Etop%2Dright%20%2Etooltip%2Darrow%7Bbottom%3A0%3Bleft%3A5px%3Bmargin%2Dbottom%3A%2D5px%3Bborder%2Dwidth%3A5px%205px%200%3Bborder%2Dtop%2Dcolor%3A%23000%7D%2Etooltip%2Eright%20%2Etooltip%2Darrow%7Btop%3A50%25%3Bleft%3A0%3Bmargin%2Dtop%3A%2D5px%3Bborder%2Dwidth%3A5px%205px%205px%200%3Bborder%2Dright%2Dcolor%3A%23000%7D%2Etooltip%2Eleft%20%2Etooltip%2Darrow%7Btop%3A50%25%3Bright%3A0%3Bmargin%2Dtop%3A%2D5px%3Bborder%2Dwidth%3A5px%200%205px%205px%3Bborder%2Dleft%2Dcolor%3A%23000%7D%2Etooltip%2Ebottom%20%2Etooltip%2Darrow%7Btop%3A0%3Bleft%3A50%25%3Bmargin%2Dleft%3A%2D5px%3Bborder%2Dwidth%3A0%205px%205px%3Bborder%2Dbottom%2Dcolor%3A%23000%7D%2Etooltip%2Ebottom%2Dleft%20%2Etooltip%2Darrow%7Btop%3A0%3Bright%3A5px%3Bmargin%2Dtop%3A%2D5px%3Bborder%2Dwidth%3A0%205px%205px%3Bborder%2Dbottom%2Dcolor%3A%23000%7D%2Etooltip%2Ebottom%2Dright%20%2Etooltip%2Darrow%7Btop%3A0%3Bleft%3A5px%3Bmargin%2Dtop%3A%2D5px%3Bborder%2Dwidth%3A0%205px%205px%3Bborder%2Dbottom%2Dcolor%3A%23000%7D%2Epopover%7Bposition%3Aabsolute%3Btop%3A0%3Bleft%3A0%3Bz%2Dindex%3A1060%3Bdisplay%3Anone%3Bmax%2Dwidth%3A276px%3Bpadding%3A1px%3Bfont%2Dfamily%3A%22Helvetica%20Neue%22%2CHelvetica%2CArial%2Csans%2Dserif%3Bfont%2Dsize%3A14px%3Bfont%2Dstyle%3Anormal%3Bfont%2Dweight%3A400%3Bline%2Dheight%3A1%2E42857143%3Btext%2Dalign%3Aleft%3Btext%2Dalign%3Astart%3Btext%2Ddecoration%3Anone%3Btext%2Dshadow%3Anone%3Btext%2Dtransform%3Anone%3Bletter%2Dspacing%3Anormal%3Bword%2Dbreak%3Anormal%3Bword%2Dspacing%3Anormal%3Bword%2Dwrap%3Anormal%3Bwhite%2Dspace%3Anormal%3Bbackground%2Dcolor%3A%23fff%3B%2Dwebkit%2Dbackground%2Dclip%3Apadding%2Dbox%3Bbackground%2Dclip%3Apadding%2Dbox%3Bborder%3A1px%20solid%20%23ccc%3Bborder%3A1px%20solid%20rgba%280%2C0%2C0%2C%2E2%29%3Bborder%2Dradius%3A6px%3B%2Dwebkit%2Dbox%2Dshadow%3A0%205px%2010px%20rgba%280%2C0%2C0%2C%2E2%29%3Bbox%2Dshadow%3A0%205px%2010px%20rgba%280%2C0%2C0%2C%2E2%29%3Bline%2Dbreak%3Aauto%7D%2Epopover%2Etop%7Bmargin%2Dtop%3A%2D10px%7D%2Epopover%2Eright%7Bmargin%2Dleft%3A10px%7D%2Epopover%2Ebottom%7Bmargin%2Dtop%3A10px%7D%2Epopover%2Eleft%7Bmargin%2Dleft%3A%2D10px%7D%2Epopover%2Dtitle%7Bpadding%3A8px%2014px%3Bmargin%3A0%3Bfont%2Dsize%3A14px%3Bbackground%2Dcolor%3A%23f7f7f7%3Bborder%2Dbottom%3A1px%20solid%20%23ebebeb%3Bborder%2Dradius%3A5px%205px%200%200%7D%2Epopover%2Dcontent%7Bpadding%3A9px%2014px%7D%2Epopover%3E%2Earrow%2C%2Epopover%3E%2Earrow%3Aafter%7Bposition%3Aabsolute%3Bdisplay%3Ablock%3Bwidth%3A0%3Bheight%3A0%3Bborder%2Dcolor%3Atransparent%3Bborder%2Dstyle%3Asolid%7D%2Epopover%3E%2Earrow%7Bborder%2Dwidth%3A11px%7D%2Epopover%3E%2Earrow%3Aafter%7Bcontent%3A%22%22%3Bborder%2Dwidth%3A10px%7D%2Epopover%2Etop%3E%2Earrow%7Bbottom%3A%2D11px%3Bleft%3A50%25%3Bmargin%2Dleft%3A%2D11px%3Bborder%2Dtop%2Dcolor%3A%23999%3Bborder%2Dtop%2Dcolor%3Argba%280%2C0%2C0%2C%2E25%29%3Bborder%2Dbottom%2Dwidth%3A0%7D%2Epopover%2Etop%3E%2Earrow%3Aafter%7Bbottom%3A1px%3Bmargin%2Dleft%3A%2D10px%3Bcontent%3A%22%20%22%3Bborder%2Dtop%2Dcolor%3A%23fff%3Bborder%2Dbottom%2Dwidth%3A0%7D%2Epopover%2Eright%3E%2Earrow%7Btop%3A50%25%3Bleft%3A%2D11px%3Bmargin%2Dtop%3A%2D11px%3Bborder%2Dright%2Dcolor%3A%23999%3Bborder%2Dright%2Dcolor%3Argba%280%2C0%2C0%2C%2E25%29%3Bborder%2Dleft%2Dwidth%3A0%7D%2Epopover%2Eright%3E%2Earrow%3Aafter%7Bbottom%3A%2D10px%3Bleft%3A1px%3Bcontent%3A%22%20%22%3Bborder%2Dright%2Dcolor%3A%23fff%3Bborder%2Dleft%2Dwidth%3A0%7D%2Epopover%2Ebottom%3E%2Earrow%7Btop%3A%2D11px%3Bleft%3A50%25%3Bmargin%2Dleft%3A%2D11px%3Bborder%2Dtop%2Dwidth%3A0%3Bborder%2Dbottom%2Dcolor%3A%23999%3Bborder%2Dbottom%2Dcolor%3Argba%280%2C0%2C0%2C%2E25%29%7D%2Epopover%2Ebottom%3E%2Earrow%3Aafter%7Btop%3A1px%3Bmargin%2Dleft%3A%2D10px%3Bcontent%3A%22%20%22%3Bborder%2Dtop%2Dwidth%3A0%3Bborder%2Dbottom%2Dcolor%3A%23fff%7D%2Epopover%2Eleft%3E%2Earrow%7Btop%3A50%25%3Bright%3A%2D11px%3Bmargin%2Dtop%3A%2D11px%3Bborder%2Dright%2Dwidth%3A0%3Bborder%2Dleft%2Dcolor%3A%23999%3Bborder%2Dleft%2Dcolor%3Argba%280%2C0%2C0%2C%2E25%29%7D%2Epopover%2Eleft%3E%2Earrow%3Aafter%7Bright%3A1px%3Bbottom%3A%2D10px%3Bcontent%3A%22%20%22%3Bborder%2Dright%2Dwidth%3A0%3Bborder%2Dleft%2Dcolor%3A%23fff%7D%2Ecarousel%7Bposition%3Arelative%7D%2Ecarousel%2Dinner%7Bposition%3Arelative%3Bwidth%3A100%25%3Boverflow%3Ahidden%7D%2Ecarousel%2Dinner%3E%2Eitem%7Bposition%3Arelative%3Bdisplay%3Anone%3B%2Dwebkit%2Dtransition%3A%2E6s%20ease%2Din%2Dout%20left%3B%2Do%2Dtransition%3A%2E6s%20ease%2Din%2Dout%20left%3Btransition%3A%2E6s%20ease%2Din%2Dout%20left%7D%2Ecarousel%2Dinner%3E%2Eitem%3Ea%3Eimg%2C%2Ecarousel%2Dinner%3E%2Eitem%3Eimg%7Bline%2Dheight%3A1%7D%40media%20all%20and%20%28transform%2D3d%29%2C%28%2Dwebkit%2Dtransform%2D3d%29%7B%2Ecarousel%2Dinner%3E%2Eitem%7B%2Dwebkit%2Dtransition%3A%2Dwebkit%2Dtransform%20%2E6s%20ease%2Din%2Dout%3B%2Do%2Dtransition%3A%2Do%2Dtransform%20%2E6s%20ease%2Din%2Dout%3Btransition%3Atransform%20%2E6s%20ease%2Din%2Dout%3B%2Dwebkit%2Dbackface%2Dvisibility%3Ahidden%3Bbackface%2Dvisibility%3Ahidden%3B%2Dwebkit%2Dperspective%3A1000px%3Bperspective%3A1000px%7D%2Ecarousel%2Dinner%3E%2Eitem%2Eactive%2Eright%2C%2Ecarousel%2Dinner%3E%2Eitem%2Enext%7Bleft%3A0%3B%2Dwebkit%2Dtransform%3Atranslate3d%28100%25%2C0%2C0%29%3Btransform%3Atranslate3d%28100%25%2C0%2C0%29%7D%2Ecarousel%2Dinner%3E%2Eitem%2Eactive%2Eleft%2C%2Ecarousel%2Dinner%3E%2Eitem%2Eprev%7Bleft%3A0%3B%2Dwebkit%2Dtransform%3Atranslate3d%28%2D100%25%2C0%2C0%29%3Btransform%3Atranslate3d%28%2D100%25%2C0%2C0%29%7D%2Ecarousel%2Dinner%3E%2Eitem%2Eactive%2C%2Ecarousel%2Dinner%3E%2Eitem%2Enext%2Eleft%2C%2Ecarousel%2Dinner%3E%2Eitem%2Eprev%2Eright%7Bleft%3A0%3B%2Dwebkit%2Dtransform%3Atranslate3d%280%2C0%2C0%29%3Btransform%3Atranslate3d%280%2C0%2C0%29%7D%7D%2Ecarousel%2Dinner%3E%2Eactive%2C%2Ecarousel%2Dinner%3E%2Enext%2C%2Ecarousel%2Dinner%3E%2Eprev%7Bdisplay%3Ablock%7D%2Ecarousel%2Dinner%3E%2Eactive%7Bleft%3A0%7D%2Ecarousel%2Dinner%3E%2Enext%2C%2Ecarousel%2Dinner%3E%2Eprev%7Bposition%3Aabsolute%3Btop%3A0%3Bwidth%3A100%25%7D%2Ecarousel%2Dinner%3E%2Enext%7Bleft%3A100%25%7D%2Ecarousel%2Dinner%3E%2Eprev%7Bleft%3A%2D100%25%7D%2Ecarousel%2Dinner%3E%2Enext%2Eleft%2C%2Ecarousel%2Dinner%3E%2Eprev%2Eright%7Bleft%3A0%7D%2Ecarousel%2Dinner%3E%2Eactive%2Eleft%7Bleft%3A%2D100%25%7D%2Ecarousel%2Dinner%3E%2Eactive%2Eright%7Bleft%3A100%25%7D%2Ecarousel%2Dcontrol%7Bposition%3Aabsolute%3Btop%3A0%3Bbottom%3A0%3Bleft%3A0%3Bwidth%3A15%25%3Bfont%2Dsize%3A20px%3Bcolor%3A%23fff%3Btext%2Dalign%3Acenter%3Btext%2Dshadow%3A0%201px%202px%20rgba%280%2C0%2C0%2C%2E6%29%3Bfilter%3Aalpha%28opacity%3D50%29%3Bopacity%3A%2E5%7D%2Ecarousel%2Dcontrol%2Eleft%7Bbackground%2Dimage%3A%2Dwebkit%2Dlinear%2Dgradient%28left%2Crgba%280%2C0%2C0%2C%2E5%29%200%2Crgba%280%2C0%2C0%2C%2E0001%29%20100%25%29%3Bbackground%2Dimage%3A%2Do%2Dlinear%2Dgradient%28left%2Crgba%280%2C0%2C0%2C%2E5%29%200%2Crgba%280%2C0%2C0%2C%2E0001%29%20100%25%29%3Bbackground%2Dimage%3A%2Dwebkit%2Dgradient%28linear%2Cleft%20top%2Cright%20top%2Cfrom%28rgba%280%2C0%2C0%2C%2E5%29%29%2Cto%28rgba%280%2C0%2C0%2C%2E0001%29%29%29%3Bbackground%2Dimage%3Alinear%2Dgradient%28to%20right%2Crgba%280%2C0%2C0%2C%2E5%29%200%2Crgba%280%2C0%2C0%2C%2E0001%29%20100%25%29%3Bfilter%3Aprogid%3ADXImageTransform%2EMicrosoft%2Egradient%28startColorstr%3D%27%2380000000%27%2C%20endColorstr%3D%27%2300000000%27%2C%20GradientType%3D1%29%3Bbackground%2Drepeat%3Arepeat%2Dx%7D%2Ecarousel%2Dcontrol%2Eright%7Bright%3A0%3Bleft%3Aauto%3Bbackground%2Dimage%3A%2Dwebkit%2Dlinear%2Dgradient%28left%2Crgba%280%2C0%2C0%2C%2E0001%29%200%2Crgba%280%2C0%2C0%2C%2E5%29%20100%25%29%3Bbackground%2Dimage%3A%2Do%2Dlinear%2Dgradient%28left%2Crgba%280%2C0%2C0%2C%2E0001%29%200%2Crgba%280%2C0%2C0%2C%2E5%29%20100%25%29%3Bbackground%2Dimage%3A%2Dwebkit%2Dgradient%28linear%2Cleft%20top%2Cright%20top%2Cfrom%28rgba%280%2C0%2C0%2C%2E0001%29%29%2Cto%28rgba%280%2C0%2C0%2C%2E5%29%29%29%3Bbackground%2Dimage%3Alinear%2Dgradient%28to%20right%2Crgba%280%2C0%2C0%2C%2E0001%29%200%2Crgba%280%2C0%2C0%2C%2E5%29%20100%25%29%3Bfilter%3Aprogid%3ADXImageTransform%2EMicrosoft%2Egradient%28startColorstr%3D%27%2300000000%27%2C%20endColorstr%3D%27%2380000000%27%2C%20GradientType%3D1%29%3Bbackground%2Drepeat%3Arepeat%2Dx%7D%2Ecarousel%2Dcontrol%3Afocus%2C%2Ecarousel%2Dcontrol%3Ahover%7Bcolor%3A%23fff%3Btext%2Ddecoration%3Anone%3Bfilter%3Aalpha%28opacity%3D90%29%3Boutline%3A0%3Bopacity%3A%2E9%7D%2Ecarousel%2Dcontrol%20%2Eglyphicon%2Dchevron%2Dleft%2C%2Ecarousel%2Dcontrol%20%2Eglyphicon%2Dchevron%2Dright%2C%2Ecarousel%2Dcontrol%20%2Eicon%2Dnext%2C%2Ecarousel%2Dcontrol%20%2Eicon%2Dprev%7Bposition%3Aabsolute%3Btop%3A50%25%3Bz%2Dindex%3A5%3Bdisplay%3Ainline%2Dblock%3Bmargin%2Dtop%3A%2D10px%7D%2Ecarousel%2Dcontrol%20%2Eglyphicon%2Dchevron%2Dleft%2C%2Ecarousel%2Dcontrol%20%2Eicon%2Dprev%7Bleft%3A50%25%3Bmargin%2Dleft%3A%2D10px%7D%2Ecarousel%2Dcontrol%20%2Eglyphicon%2Dchevron%2Dright%2C%2Ecarousel%2Dcontrol%20%2Eicon%2Dnext%7Bright%3A50%25%3Bmargin%2Dright%3A%2D10px%7D%2Ecarousel%2Dcontrol%20%2Eicon%2Dnext%2C%2Ecarousel%2Dcontrol%20%2Eicon%2Dprev%7Bwidth%3A20px%3Bheight%3A20px%3Bfont%2Dfamily%3Aserif%3Bline%2Dheight%3A1%7D%2Ecarousel%2Dcontrol%20%2Eicon%2Dprev%3Abefore%7Bcontent%3A%27%5C2039%27%7D%2Ecarousel%2Dcontrol%20%2Eicon%2Dnext%3Abefore%7Bcontent%3A%27%5C203a%27%7D%2Ecarousel%2Dindicators%7Bposition%3Aabsolute%3Bbottom%3A10px%3Bleft%3A50%25%3Bz%2Dindex%3A15%3Bwidth%3A60%25%3Bpadding%2Dleft%3A0%3Bmargin%2Dleft%3A%2D30%25%3Btext%2Dalign%3Acenter%3Blist%2Dstyle%3Anone%7D%2Ecarousel%2Dindicators%20li%7Bdisplay%3Ainline%2Dblock%3Bwidth%3A10px%3Bheight%3A10px%3Bmargin%3A1px%3Btext%2Dindent%3A%2D999px%3Bcursor%3Apointer%3Bbackground%2Dcolor%3A%23000%5C9%3Bbackground%2Dcolor%3Argba%280%2C0%2C0%2C0%29%3Bborder%3A1px%20solid%20%23fff%3Bborder%2Dradius%3A10px%7D%2Ecarousel%2Dindicators%20%2Eactive%7Bwidth%3A12px%3Bheight%3A12px%3Bmargin%3A0%3Bbackground%2Dcolor%3A%23fff%7D%2Ecarousel%2Dcaption%7Bposition%3Aabsolute%3Bright%3A15%25%3Bbottom%3A20px%3Bleft%3A15%25%3Bz%2Dindex%3A10%3Bpadding%2Dtop%3A20px%3Bpadding%2Dbottom%3A20px%3Bcolor%3A%23fff%3Btext%2Dalign%3Acenter%3Btext%2Dshadow%3A0%201px%202px%20rgba%280%2C0%2C0%2C%2E6%29%7D%2Ecarousel%2Dcaption%20%2Ebtn%7Btext%2Dshadow%3Anone%7D%40media%20screen%20and%20%28min%2Dwidth%3A768px%29%7B%2Ecarousel%2Dcontrol%20%2Eglyphicon%2Dchevron%2Dleft%2C%2Ecarousel%2Dcontrol%20%2Eglyphicon%2Dchevron%2Dright%2C%2Ecarousel%2Dcontrol%20%2Eicon%2Dnext%2C%2Ecarousel%2Dcontrol%20%2Eicon%2Dprev%7Bwidth%3A30px%3Bheight%3A30px%3Bmargin%2Dtop%3A%2D15px%3Bfont%2Dsize%3A30px%7D%2Ecarousel%2Dcontrol%20%2Eglyphicon%2Dchevron%2Dleft%2C%2Ecarousel%2Dcontrol%20%2Eicon%2Dprev%7Bmargin%2Dleft%3A%2D15px%7D%2Ecarousel%2Dcontrol%20%2Eglyphicon%2Dchevron%2Dright%2C%2Ecarousel%2Dcontrol%20%2Eicon%2Dnext%7Bmargin%2Dright%3A%2D15px%7D%2Ecarousel%2Dcaption%7Bright%3A20%25%3Bleft%3A20%25%3Bpadding%2Dbottom%3A30px%7D%2Ecarousel%2Dindicators%7Bbottom%3A20px%7D%7D%2Ebtn%2Dgroup%2Dvertical%3E%2Ebtn%2Dgroup%3Aafter%2C%2Ebtn%2Dgroup%2Dvertical%3E%2Ebtn%2Dgroup%3Abefore%2C%2Ebtn%2Dtoolbar%3Aafter%2C%2Ebtn%2Dtoolbar%3Abefore%2C%2Eclearfix%3Aafter%2C%2Eclearfix%3Abefore%2C%2Econtainer%2Dfluid%3Aafter%2C%2Econtainer%2Dfluid%3Abefore%2C%2Econtainer%3Aafter%2C%2Econtainer%3Abefore%2C%2Edl%2Dhorizontal%20dd%3Aafter%2C%2Edl%2Dhorizontal%20dd%3Abefore%2C%2Eform%2Dhorizontal%20%2Eform%2Dgroup%3Aafter%2C%2Eform%2Dhorizontal%20%2Eform%2Dgroup%3Abefore%2C%2Emodal%2Dfooter%3Aafter%2C%2Emodal%2Dfooter%3Abefore%2C%2Enav%3Aafter%2C%2Enav%3Abefore%2C%2Enavbar%2Dcollapse%3Aafter%2C%2Enavbar%2Dcollapse%3Abefore%2C%2Enavbar%2Dheader%3Aafter%2C%2Enavbar%2Dheader%3Abefore%2C%2Enavbar%3Aafter%2C%2Enavbar%3Abefore%2C%2Epager%3Aafter%2C%2Epager%3Abefore%2C%2Epanel%2Dbody%3Aafter%2C%2Epanel%2Dbody%3Abefore%2C%2Erow%3Aafter%2C%2Erow%3Abefore%7Bdisplay%3Atable%3Bcontent%3A%22%20%22%7D%2Ebtn%2Dgroup%2Dvertical%3E%2Ebtn%2Dgroup%3Aafter%2C%2Ebtn%2Dtoolbar%3Aafter%2C%2Eclearfix%3Aafter%2C%2Econtainer%2Dfluid%3Aafter%2C%2Econtainer%3Aafter%2C%2Edl%2Dhorizontal%20dd%3Aafter%2C%2Eform%2Dhorizontal%20%2Eform%2Dgroup%3Aafter%2C%2Emodal%2Dfooter%3Aafter%2C%2Enav%3Aafter%2C%2Enavbar%2Dcollapse%3Aafter%2C%2Enavbar%2Dheader%3Aafter%2C%2Enavbar%3Aafter%2C%2Epager%3Aafter%2C%2Epanel%2Dbody%3Aafter%2C%2Erow%3Aafter%7Bclear%3Aboth%7D%2Ecenter%2Dblock%7Bdisplay%3Ablock%3Bmargin%2Dright%3Aauto%3Bmargin%2Dleft%3Aauto%7D%2Epull%2Dright%7Bfloat%3Aright%21important%7D%2Epull%2Dleft%7Bfloat%3Aleft%21important%7D%2Ehide%7Bdisplay%3Anone%21important%7D%2Eshow%7Bdisplay%3Ablock%21important%7D%2Einvisible%7Bvisibility%3Ahidden%7D%2Etext%2Dhide%7Bfont%3A0%2F0%20a%3Bcolor%3Atransparent%3Btext%2Dshadow%3Anone%3Bbackground%2Dcolor%3Atransparent%3Bborder%3A0%7D%2Ehidden%7Bdisplay%3Anone%21important%7D%2Eaffix%7Bposition%3Afixed%7D%40%2Dms%2Dviewport%7Bwidth%3Adevice%2Dwidth%7D%2Evisible%2Dlg%2C%2Evisible%2Dmd%2C%2Evisible%2Dsm%2C%2Evisible%2Dxs%7Bdisplay%3Anone%21important%7D%2Evisible%2Dlg%2Dblock%2C%2Evisible%2Dlg%2Dinline%2C%2Evisible%2Dlg%2Dinline%2Dblock%2C%2Evisible%2Dmd%2Dblock%2C%2Evisible%2Dmd%2Dinline%2C%2Evisible%2Dmd%2Dinline%2Dblock%2C%2Evisible%2Dsm%2Dblock%2C%2Evisible%2Dsm%2Dinline%2C%2Evisible%2Dsm%2Dinline%2Dblock%2C%2Evisible%2Dxs%2Dblock%2C%2Evisible%2Dxs%2Dinline%2C%2Evisible%2Dxs%2Dinline%2Dblock%7Bdisplay%3Anone%21important%7D%40media%20%28max%2Dwidth%3A767px%29%7B%2Evisible%2Dxs%7Bdisplay%3Ablock%21important%7Dtable%2Evisible%2Dxs%7Bdisplay%3Atable%21important%7Dtr%2Evisible%2Dxs%7Bdisplay%3Atable%2Drow%21important%7Dtd%2Evisible%2Dxs%2Cth%2Evisible%2Dxs%7Bdisplay%3Atable%2Dcell%21important%7D%7D%40media%20%28max%2Dwidth%3A767px%29%7B%2Evisible%2Dxs%2Dblock%7Bdisplay%3Ablock%21important%7D%7D%40media%20%28max%2Dwidth%3A767px%29%7B%2Evisible%2Dxs%2Dinline%7Bdisplay%3Ainline%21important%7D%7D%40media%20%28max%2Dwidth%3A767px%29%7B%2Evisible%2Dxs%2Dinline%2Dblock%7Bdisplay%3Ainline%2Dblock%21important%7D%7D%40media%20%28min%2Dwidth%3A768px%29%20and%20%28max%2Dwidth%3A991px%29%7B%2Evisible%2Dsm%7Bdisplay%3Ablock%21important%7Dtable%2Evisible%2Dsm%7Bdisplay%3Atable%21important%7Dtr%2Evisible%2Dsm%7Bdisplay%3Atable%2Drow%21important%7Dtd%2Evisible%2Dsm%2Cth%2Evisible%2Dsm%7Bdisplay%3Atable%2Dcell%21important%7D%7D%40media%20%28min%2Dwidth%3A768px%29%20and%20%28max%2Dwidth%3A991px%29%7B%2Evisible%2Dsm%2Dblock%7Bdisplay%3Ablock%21important%7D%7D%40media%20%28min%2Dwidth%3A768px%29%20and%20%28max%2Dwidth%3A991px%29%7B%2Evisible%2Dsm%2Dinline%7Bdisplay%3Ainline%21important%7D%7D%40media%20%28min%2Dwidth%3A768px%29%20and%20%28max%2Dwidth%3A991px%29%7B%2Evisible%2Dsm%2Dinline%2Dblock%7Bdisplay%3Ainline%2Dblock%21important%7D%7D%40media%20%28min%2Dwidth%3A992px%29%20and%20%28max%2Dwidth%3A1199px%29%7B%2Evisible%2Dmd%7Bdisplay%3Ablock%21important%7Dtable%2Evisible%2Dmd%7Bdisplay%3Atable%21important%7Dtr%2Evisible%2Dmd%7Bdisplay%3Atable%2Drow%21important%7Dtd%2Evisible%2Dmd%2Cth%2Evisible%2Dmd%7Bdisplay%3Atable%2Dcell%21important%7D%7D%40media%20%28min%2Dwidth%3A992px%29%20and%20%28max%2Dwidth%3A1199px%29%7B%2Evisible%2Dmd%2Dblock%7Bdisplay%3Ablock%21important%7D%7D%40media%20%28min%2Dwidth%3A992px%29%20and%20%28max%2Dwidth%3A1199px%29%7B%2Evisible%2Dmd%2Dinline%7Bdisplay%3Ainline%21important%7D%7D%40media%20%28min%2Dwidth%3A992px%29%20and%20%28max%2Dwidth%3A1199px%29%7B%2Evisible%2Dmd%2Dinline%2Dblock%7Bdisplay%3Ainline%2Dblock%21important%7D%7D%40media%20%28min%2Dwidth%3A1200px%29%7B%2Evisible%2Dlg%7Bdisplay%3Ablock%21important%7Dtable%2Evisible%2Dlg%7Bdisplay%3Atable%21important%7Dtr%2Evisible%2Dlg%7Bdisplay%3Atable%2Drow%21important%7Dtd%2Evisible%2Dlg%2Cth%2Evisible%2Dlg%7Bdisplay%3Atable%2Dcell%21important%7D%7D%40media%20%28min%2Dwidth%3A1200px%29%7B%2Evisible%2Dlg%2Dblock%7Bdisplay%3Ablock%21important%7D%7D%40media%20%28min%2Dwidth%3A1200px%29%7B%2Evisible%2Dlg%2Dinline%7Bdisplay%3Ainline%21important%7D%7D%40media%20%28min%2Dwidth%3A1200px%29%7B%2Evisible%2Dlg%2Dinline%2Dblock%7Bdisplay%3Ainline%2Dblock%21important%7D%7D%40media%20%28max%2Dwidth%3A767px%29%7B%2Ehidden%2Dxs%7Bdisplay%3Anone%21important%7D%7D%40media%20%28min%2Dwidth%3A768px%29%20and%20%28max%2Dwidth%3A991px%29%7B%2Ehidden%2Dsm%7Bdisplay%3Anone%21important%7D%7D%40media%20%28min%2Dwidth%3A992px%29%20and%20%28max%2Dwidth%3A1199px%29%7B%2Ehidden%2Dmd%7Bdisplay%3Anone%21important%7D%7D%40media%20%28min%2Dwidth%3A1200px%29%7B%2Ehidden%2Dlg%7Bdisplay%3Anone%21important%7D%7D%2Evisible%2Dprint%7Bdisplay%3Anone%21important%7D%40media%20print%7B%2Evisible%2Dprint%7Bdisplay%3Ablock%21important%7Dtable%2Evisible%2Dprint%7Bdisplay%3Atable%21important%7Dtr%2Evisible%2Dprint%7Bdisplay%3Atable%2Drow%21important%7Dtd%2Evisible%2Dprint%2Cth%2Evisible%2Dprint%7Bdisplay%3Atable%2Dcell%21important%7D%7D%2Evisible%2Dprint%2Dblock%7Bdisplay%3Anone%21important%7D%40media%20print%7B%2Evisible%2Dprint%2Dblock%7Bdisplay%3Ablock%21important%7D%7D%2Evisible%2Dprint%2Dinline%7Bdisplay%3Anone%21important%7D%40media%20print%7B%2Evisible%2Dprint%2Dinline%7Bdisplay%3Ainline%21important%7D%7D%2Evisible%2Dprint%2Dinline%2Dblock%7Bdisplay%3Anone%21important%7D%40media%20print%7B%2Evisible%2Dprint%2Dinline%2Dblock%7Bdisplay%3Ainline%2Dblock%21important%7D%7D%40media%20print%7B%2Ehidden%2Dprint%7Bdisplay%3Anone%21important%7D%7D%0A" rel="stylesheet" />
<script src="data:application/javascript;base64,LyohCiAqIEJvb3RzdHJhcCB2My4zLjUgKGh0dHA6Ly9nZXRib290c3RyYXAuY29tKQogKiBDb3B5cmlnaHQgMjAxMS0yMDE1IFR3aXR0ZXIsIEluYy4KICogTGljZW5zZWQgdW5kZXIgdGhlIE1JVCBsaWNlbnNlCiAqLwppZigidW5kZWZpbmVkIj09dHlwZW9mIGpRdWVyeSl0aHJvdyBuZXcgRXJyb3IoIkJvb3RzdHJhcCdzIEphdmFTY3JpcHQgcmVxdWlyZXMgalF1ZXJ5Iik7K2Z1bmN0aW9uKGEpeyJ1c2Ugc3RyaWN0Ijt2YXIgYj1hLmZuLmpxdWVyeS5zcGxpdCgiICIpWzBdLnNwbGl0KCIuIik7aWYoYlswXTwyJiZiWzFdPDl8fDE9PWJbMF0mJjk9PWJbMV0mJmJbMl08MSl0aHJvdyBuZXcgRXJyb3IoIkJvb3RzdHJhcCdzIEphdmFTY3JpcHQgcmVxdWlyZXMgalF1ZXJ5IHZlcnNpb24gMS45LjEgb3IgaGlnaGVyIil9KGpRdWVyeSksK2Z1bmN0aW9uKGEpeyJ1c2Ugc3RyaWN0IjtmdW5jdGlvbiBiKCl7dmFyIGE9ZG9jdW1lbnQuY3JlYXRlRWxlbWVudCgiYm9vdHN0cmFwIiksYj17V2Via2l0VHJhbnNpdGlvbjoid2Via2l0VHJhbnNpdGlvbkVuZCIsTW96VHJhbnNpdGlvbjoidHJhbnNpdGlvbmVuZCIsT1RyYW5zaXRpb246Im9UcmFuc2l0aW9uRW5kIG90cmFuc2l0aW9uZW5kIix0cmFuc2l0aW9uOiJ0cmFuc2l0aW9uZW5kIn07Zm9yKHZhciBjIGluIGIpaWYodm9pZCAwIT09YS5zdHlsZVtjXSlyZXR1cm57ZW5kOmJbY119O3JldHVybiExfWEuZm4uZW11bGF0ZVRyYW5zaXRpb25FbmQ9ZnVuY3Rpb24oYil7dmFyIGM9ITEsZD10aGlzO2EodGhpcykub25lKCJic1RyYW5zaXRpb25FbmQiLGZ1bmN0aW9uKCl7Yz0hMH0pO3ZhciBlPWZ1bmN0aW9uKCl7Y3x8YShkKS50cmlnZ2VyKGEuc3VwcG9ydC50cmFuc2l0aW9uLmVuZCl9O3JldHVybiBzZXRUaW1lb3V0KGUsYiksdGhpc30sYShmdW5jdGlvbigpe2Euc3VwcG9ydC50cmFuc2l0aW9uPWIoKSxhLnN1cHBvcnQudHJhbnNpdGlvbiYmKGEuZXZlbnQuc3BlY2lhbC5ic1RyYW5zaXRpb25FbmQ9e2JpbmRUeXBlOmEuc3VwcG9ydC50cmFuc2l0aW9uLmVuZCxkZWxlZ2F0ZVR5cGU6YS5zdXBwb3J0LnRyYW5zaXRpb24uZW5kLGhhbmRsZTpmdW5jdGlvbihiKXtyZXR1cm4gYShiLnRhcmdldCkuaXModGhpcyk/Yi5oYW5kbGVPYmouaGFuZGxlci5hcHBseSh0aGlzLGFyZ3VtZW50cyk6dm9pZCAwfX0pfSl9KGpRdWVyeSksK2Z1bmN0aW9uKGEpeyJ1c2Ugc3RyaWN0IjtmdW5jdGlvbiBiKGIpe3JldHVybiB0aGlzLmVhY2goZnVuY3Rpb24oKXt2YXIgYz1hKHRoaXMpLGU9Yy5kYXRhKCJicy5hbGVydCIpO2V8fGMuZGF0YSgiYnMuYWxlcnQiLGU9bmV3IGQodGhpcykpLCJzdHJpbmciPT10eXBlb2YgYiYmZVtiXS5jYWxsKGMpfSl9dmFyIGM9J1tkYXRhLWRpc21pc3M9ImFsZXJ0Il0nLGQ9ZnVuY3Rpb24oYil7YShiKS5vbigiY2xpY2siLGMsdGhpcy5jbG9zZSl9O2QuVkVSU0lPTj0iMy4zLjUiLGQuVFJBTlNJVElPTl9EVVJBVElPTj0xNTAsZC5wcm90b3R5cGUuY2xvc2U9ZnVuY3Rpb24oYil7ZnVuY3Rpb24gYygpe2cuZGV0YWNoKCkudHJpZ2dlcigiY2xvc2VkLmJzLmFsZXJ0IikucmVtb3ZlKCl9dmFyIGU9YSh0aGlzKSxmPWUuYXR0cigiZGF0YS10YXJnZXQiKTtmfHwoZj1lLmF0dHIoImhyZWYiKSxmPWYmJmYucmVwbGFjZSgvLiooPz0jW15cc10qJCkvLCIiKSk7dmFyIGc9YShmKTtiJiZiLnByZXZlbnREZWZhdWx0KCksZy5sZW5ndGh8fChnPWUuY2xvc2VzdCgiLmFsZXJ0IikpLGcudHJpZ2dlcihiPWEuRXZlbnQoImNsb3NlLmJzLmFsZXJ0IikpLGIuaXNEZWZhdWx0UHJldmVudGVkKCl8fChnLnJlbW92ZUNsYXNzKCJpbiIpLGEuc3VwcG9ydC50cmFuc2l0aW9uJiZnLmhhc0NsYXNzKCJmYWRlIik/Zy5vbmUoImJzVHJhbnNpdGlvbkVuZCIsYykuZW11bGF0ZVRyYW5zaXRpb25FbmQoZC5UUkFOU0lUSU9OX0RVUkFUSU9OKTpjKCkpfTt2YXIgZT1hLmZuLmFsZXJ0O2EuZm4uYWxlcnQ9YixhLmZuLmFsZXJ0LkNvbnN0cnVjdG9yPWQsYS5mbi5hbGVydC5ub0NvbmZsaWN0PWZ1bmN0aW9uKCl7cmV0dXJuIGEuZm4uYWxlcnQ9ZSx0aGlzfSxhKGRvY3VtZW50KS5vbigiY2xpY2suYnMuYWxlcnQuZGF0YS1hcGkiLGMsZC5wcm90b3R5cGUuY2xvc2UpfShqUXVlcnkpLCtmdW5jdGlvbihhKXsidXNlIHN0cmljdCI7ZnVuY3Rpb24gYihiKXtyZXR1cm4gdGhpcy5lYWNoKGZ1bmN0aW9uKCl7dmFyIGQ9YSh0aGlzKSxlPWQuZGF0YSgiYnMuYnV0dG9uIiksZj0ib2JqZWN0Ij09dHlwZW9mIGImJmI7ZXx8ZC5kYXRhKCJicy5idXR0b24iLGU9bmV3IGModGhpcyxmKSksInRvZ2dsZSI9PWI/ZS50b2dnbGUoKTpiJiZlLnNldFN0YXRlKGIpfSl9dmFyIGM9ZnVuY3Rpb24oYixkKXt0aGlzLiRlbGVtZW50PWEoYiksdGhpcy5vcHRpb25zPWEuZXh0ZW5kKHt9LGMuREVGQVVMVFMsZCksdGhpcy5pc0xvYWRpbmc9ITF9O2MuVkVSU0lPTj0iMy4zLjUiLGMuREVGQVVMVFM9e2xvYWRpbmdUZXh0OiJsb2FkaW5nLi4uIn0sYy5wcm90b3R5cGUuc2V0U3RhdGU9ZnVuY3Rpb24oYil7dmFyIGM9ImRpc2FibGVkIixkPXRoaXMuJGVsZW1lbnQsZT1kLmlzKCJpbnB1dCIpPyJ2YWwiOiJodG1sIixmPWQuZGF0YSgpO2IrPSJUZXh0IixudWxsPT1mLnJlc2V0VGV4dCYmZC5kYXRhKCJyZXNldFRleHQiLGRbZV0oKSksc2V0VGltZW91dChhLnByb3h5KGZ1bmN0aW9uKCl7ZFtlXShudWxsPT1mW2JdP3RoaXMub3B0aW9uc1tiXTpmW2JdKSwibG9hZGluZ1RleHQiPT1iPyh0aGlzLmlzTG9hZGluZz0hMCxkLmFkZENsYXNzKGMpLmF0dHIoYyxjKSk6dGhpcy5pc0xvYWRpbmcmJih0aGlzLmlzTG9hZGluZz0hMSxkLnJlbW92ZUNsYXNzKGMpLnJlbW92ZUF0dHIoYykpfSx0aGlzKSwwKX0sYy5wcm90b3R5cGUudG9nZ2xlPWZ1bmN0aW9uKCl7dmFyIGE9ITAsYj10aGlzLiRlbGVtZW50LmNsb3Nlc3QoJ1tkYXRhLXRvZ2dsZT0iYnV0dG9ucyJdJyk7aWYoYi5sZW5ndGgpe3ZhciBjPXRoaXMuJGVsZW1lbnQuZmluZCgiaW5wdXQiKTsicmFkaW8iPT1jLnByb3AoInR5cGUiKT8oYy5wcm9wKCJjaGVja2VkIikmJihhPSExKSxiLmZpbmQoIi5hY3RpdmUiKS5yZW1vdmVDbGFzcygiYWN0aXZlIiksdGhpcy4kZWxlbWVudC5hZGRDbGFzcygiYWN0aXZlIikpOiJjaGVja2JveCI9PWMucHJvcCgidHlwZSIpJiYoYy5wcm9wKCJjaGVja2VkIikhPT10aGlzLiRlbGVtZW50Lmhhc0NsYXNzKCJhY3RpdmUiKSYmKGE9ITEpLHRoaXMuJGVsZW1lbnQudG9nZ2xlQ2xhc3MoImFjdGl2ZSIpKSxjLnByb3AoImNoZWNrZWQiLHRoaXMuJGVsZW1lbnQuaGFzQ2xhc3MoImFjdGl2ZSIpKSxhJiZjLnRyaWdnZXIoImNoYW5nZSIpfWVsc2UgdGhpcy4kZWxlbWVudC5hdHRyKCJhcmlhLXByZXNzZWQiLCF0aGlzLiRlbGVtZW50Lmhhc0NsYXNzKCJhY3RpdmUiKSksdGhpcy4kZWxlbWVudC50b2dnbGVDbGFzcygiYWN0aXZlIil9O3ZhciBkPWEuZm4uYnV0dG9uO2EuZm4uYnV0dG9uPWIsYS5mbi5idXR0b24uQ29uc3RydWN0b3I9YyxhLmZuLmJ1dHRvbi5ub0NvbmZsaWN0PWZ1bmN0aW9uKCl7cmV0dXJuIGEuZm4uYnV0dG9uPWQsdGhpc30sYShkb2N1bWVudCkub24oImNsaWNrLmJzLmJ1dHRvbi5kYXRhLWFwaSIsJ1tkYXRhLXRvZ2dsZV49ImJ1dHRvbiJdJyxmdW5jdGlvbihjKXt2YXIgZD1hKGMudGFyZ2V0KTtkLmhhc0NsYXNzKCJidG4iKXx8KGQ9ZC5jbG9zZXN0KCIuYnRuIikpLGIuY2FsbChkLCJ0b2dnbGUiKSxhKGMudGFyZ2V0KS5pcygnaW5wdXRbdHlwZT0icmFkaW8iXScpfHxhKGMudGFyZ2V0KS5pcygnaW5wdXRbdHlwZT0iY2hlY2tib3giXScpfHxjLnByZXZlbnREZWZhdWx0KCl9KS5vbigiZm9jdXMuYnMuYnV0dG9uLmRhdGEtYXBpIGJsdXIuYnMuYnV0dG9uLmRhdGEtYXBpIiwnW2RhdGEtdG9nZ2xlXj0iYnV0dG9uIl0nLGZ1bmN0aW9uKGIpe2EoYi50YXJnZXQpLmNsb3Nlc3QoIi5idG4iKS50b2dnbGVDbGFzcygiZm9jdXMiLC9eZm9jdXMoaW4pPyQvLnRlc3QoYi50eXBlKSl9KX0oalF1ZXJ5KSwrZnVuY3Rpb24oYSl7InVzZSBzdHJpY3QiO2Z1bmN0aW9uIGIoYil7cmV0dXJuIHRoaXMuZWFjaChmdW5jdGlvbigpe3ZhciBkPWEodGhpcyksZT1kLmRhdGEoImJzLmNhcm91c2VsIiksZj1hLmV4dGVuZCh7fSxjLkRFRkFVTFRTLGQuZGF0YSgpLCJvYmplY3QiPT10eXBlb2YgYiYmYiksZz0ic3RyaW5nIj09dHlwZW9mIGI/YjpmLnNsaWRlO2V8fGQuZGF0YSgiYnMuY2Fyb3VzZWwiLGU9bmV3IGModGhpcyxmKSksIm51bWJlciI9PXR5cGVvZiBiP2UudG8oYik6Zz9lW2ddKCk6Zi5pbnRlcnZhbCYmZS5wYXVzZSgpLmN5Y2xlKCl9KX12YXIgYz1mdW5jdGlvbihiLGMpe3RoaXMuJGVsZW1lbnQ9YShiKSx0aGlzLiRpbmRpY2F0b3JzPXRoaXMuJGVsZW1lbnQuZmluZCgiLmNhcm91c2VsLWluZGljYXRvcnMiKSx0aGlzLm9wdGlvbnM9Yyx0aGlzLnBhdXNlZD1udWxsLHRoaXMuc2xpZGluZz1udWxsLHRoaXMuaW50ZXJ2YWw9bnVsbCx0aGlzLiRhY3RpdmU9bnVsbCx0aGlzLiRpdGVtcz1udWxsLHRoaXMub3B0aW9ucy5rZXlib2FyZCYmdGhpcy4kZWxlbWVudC5vbigia2V5ZG93bi5icy5jYXJvdXNlbCIsYS5wcm94eSh0aGlzLmtleWRvd24sdGhpcykpLCJob3ZlciI9PXRoaXMub3B0aW9ucy5wYXVzZSYmISgib250b3VjaHN0YXJ0ImluIGRvY3VtZW50LmRvY3VtZW50RWxlbWVudCkmJnRoaXMuJGVsZW1lbnQub24oIm1vdXNlZW50ZXIuYnMuY2Fyb3VzZWwiLGEucHJveHkodGhpcy5wYXVzZSx0aGlzKSkub24oIm1vdXNlbGVhdmUuYnMuY2Fyb3VzZWwiLGEucHJveHkodGhpcy5jeWNsZSx0aGlzKSl9O2MuVkVSU0lPTj0iMy4zLjUiLGMuVFJBTlNJVElPTl9EVVJBVElPTj02MDAsYy5ERUZBVUxUUz17aW50ZXJ2YWw6NWUzLHBhdXNlOiJob3ZlciIsd3JhcDohMCxrZXlib2FyZDohMH0sYy5wcm90b3R5cGUua2V5ZG93bj1mdW5jdGlvbihhKXtpZighL2lucHV0fHRleHRhcmVhL2kudGVzdChhLnRhcmdldC50YWdOYW1lKSl7c3dpdGNoKGEud2hpY2gpe2Nhc2UgMzc6dGhpcy5wcmV2KCk7YnJlYWs7Y2FzZSAzOTp0aGlzLm5leHQoKTticmVhaztkZWZhdWx0OnJldHVybn1hLnByZXZlbnREZWZhdWx0KCl9fSxjLnByb3RvdHlwZS5jeWNsZT1mdW5jdGlvbihiKXtyZXR1cm4gYnx8KHRoaXMucGF1c2VkPSExKSx0aGlzLmludGVydmFsJiZjbGVhckludGVydmFsKHRoaXMuaW50ZXJ2YWwpLHRoaXMub3B0aW9ucy5pbnRlcnZhbCYmIXRoaXMucGF1c2VkJiYodGhpcy5pbnRlcnZhbD1zZXRJbnRlcnZhbChhLnByb3h5KHRoaXMubmV4dCx0aGlzKSx0aGlzLm9wdGlvbnMuaW50ZXJ2YWwpKSx0aGlzfSxjLnByb3RvdHlwZS5nZXRJdGVtSW5kZXg9ZnVuY3Rpb24oYSl7cmV0dXJuIHRoaXMuJGl0ZW1zPWEucGFyZW50KCkuY2hpbGRyZW4oIi5pdGVtIiksdGhpcy4kaXRlbXMuaW5kZXgoYXx8dGhpcy4kYWN0aXZlKX0sYy5wcm90b3R5cGUuZ2V0SXRlbUZvckRpcmVjdGlvbj1mdW5jdGlvbihhLGIpe3ZhciBjPXRoaXMuZ2V0SXRlbUluZGV4KGIpLGQ9InByZXYiPT1hJiYwPT09Y3x8Im5leHQiPT1hJiZjPT10aGlzLiRpdGVtcy5sZW5ndGgtMTtpZihkJiYhdGhpcy5vcHRpb25zLndyYXApcmV0dXJuIGI7dmFyIGU9InByZXYiPT1hPy0xOjEsZj0oYytlKSV0aGlzLiRpdGVtcy5sZW5ndGg7cmV0dXJuIHRoaXMuJGl0ZW1zLmVxKGYpfSxjLnByb3RvdHlwZS50bz1mdW5jdGlvbihhKXt2YXIgYj10aGlzLGM9dGhpcy5nZXRJdGVtSW5kZXgodGhpcy4kYWN0aXZlPXRoaXMuJGVsZW1lbnQuZmluZCgiLml0ZW0uYWN0aXZlIikpO3JldHVybiBhPnRoaXMuJGl0ZW1zLmxlbmd0aC0xfHwwPmE/dm9pZCAwOnRoaXMuc2xpZGluZz90aGlzLiRlbGVtZW50Lm9uZSgic2xpZC5icy5jYXJvdXNlbCIsZnVuY3Rpb24oKXtiLnRvKGEpfSk6Yz09YT90aGlzLnBhdXNlKCkuY3ljbGUoKTp0aGlzLnNsaWRlKGE+Yz8ibmV4dCI6InByZXYiLHRoaXMuJGl0ZW1zLmVxKGEpKX0sYy5wcm90b3R5cGUucGF1c2U9ZnVuY3Rpb24oYil7cmV0dXJuIGJ8fCh0aGlzLnBhdXNlZD0hMCksdGhpcy4kZWxlbWVudC5maW5kKCIubmV4dCwgLnByZXYiKS5sZW5ndGgmJmEuc3VwcG9ydC50cmFuc2l0aW9uJiYodGhpcy4kZWxlbWVudC50cmlnZ2VyKGEuc3VwcG9ydC50cmFuc2l0aW9uLmVuZCksdGhpcy5jeWNsZSghMCkpLHRoaXMuaW50ZXJ2YWw9Y2xlYXJJbnRlcnZhbCh0aGlzLmludGVydmFsKSx0aGlzfSxjLnByb3RvdHlwZS5uZXh0PWZ1bmN0aW9uKCl7cmV0dXJuIHRoaXMuc2xpZGluZz92b2lkIDA6dGhpcy5zbGlkZSgibmV4dCIpfSxjLnByb3RvdHlwZS5wcmV2PWZ1bmN0aW9uKCl7cmV0dXJuIHRoaXMuc2xpZGluZz92b2lkIDA6dGhpcy5zbGlkZSgicHJldiIpfSxjLnByb3RvdHlwZS5zbGlkZT1mdW5jdGlvbihiLGQpe3ZhciBlPXRoaXMuJGVsZW1lbnQuZmluZCgiLml0ZW0uYWN0aXZlIiksZj1kfHx0aGlzLmdldEl0ZW1Gb3JEaXJlY3Rpb24oYixlKSxnPXRoaXMuaW50ZXJ2YWwsaD0ibmV4dCI9PWI/ImxlZnQiOiJyaWdodCIsaT10aGlzO2lmKGYuaGFzQ2xhc3MoImFjdGl2ZSIpKXJldHVybiB0aGlzLnNsaWRpbmc9ITE7dmFyIGo9ZlswXSxrPWEuRXZlbnQoInNsaWRlLmJzLmNhcm91c2VsIix7cmVsYXRlZFRhcmdldDpqLGRpcmVjdGlvbjpofSk7aWYodGhpcy4kZWxlbWVudC50cmlnZ2VyKGspLCFrLmlzRGVmYXVsdFByZXZlbnRlZCgpKXtpZih0aGlzLnNsaWRpbmc9ITAsZyYmdGhpcy5wYXVzZSgpLHRoaXMuJGluZGljYXRvcnMubGVuZ3RoKXt0aGlzLiRpbmRpY2F0b3JzLmZpbmQoIi5hY3RpdmUiKS5yZW1vdmVDbGFzcygiYWN0aXZlIik7dmFyIGw9YSh0aGlzLiRpbmRpY2F0b3JzLmNoaWxkcmVuKClbdGhpcy5nZXRJdGVtSW5kZXgoZildKTtsJiZsLmFkZENsYXNzKCJhY3RpdmUiKX12YXIgbT1hLkV2ZW50KCJzbGlkLmJzLmNhcm91c2VsIix7cmVsYXRlZFRhcmdldDpqLGRpcmVjdGlvbjpofSk7cmV0dXJuIGEuc3VwcG9ydC50cmFuc2l0aW9uJiZ0aGlzLiRlbGVtZW50Lmhhc0NsYXNzKCJzbGlkZSIpPyhmLmFkZENsYXNzKGIpLGZbMF0ub2Zmc2V0V2lkdGgsZS5hZGRDbGFzcyhoKSxmLmFkZENsYXNzKGgpLGUub25lKCJic1RyYW5zaXRpb25FbmQiLGZ1bmN0aW9uKCl7Zi5yZW1vdmVDbGFzcyhbYixoXS5qb2luKCIgIikpLmFkZENsYXNzKCJhY3RpdmUiKSxlLnJlbW92ZUNsYXNzKFsiYWN0aXZlIixoXS5qb2luKCIgIikpLGkuc2xpZGluZz0hMSxzZXRUaW1lb3V0KGZ1bmN0aW9uKCl7aS4kZWxlbWVudC50cmlnZ2VyKG0pfSwwKX0pLmVtdWxhdGVUcmFuc2l0aW9uRW5kKGMuVFJBTlNJVElPTl9EVVJBVElPTikpOihlLnJlbW92ZUNsYXNzKCJhY3RpdmUiKSxmLmFkZENsYXNzKCJhY3RpdmUiKSx0aGlzLnNsaWRpbmc9ITEsdGhpcy4kZWxlbWVudC50cmlnZ2VyKG0pKSxnJiZ0aGlzLmN5Y2xlKCksdGhpc319O3ZhciBkPWEuZm4uY2Fyb3VzZWw7YS5mbi5jYXJvdXNlbD1iLGEuZm4uY2Fyb3VzZWwuQ29uc3RydWN0b3I9YyxhLmZuLmNhcm91c2VsLm5vQ29uZmxpY3Q9ZnVuY3Rpb24oKXtyZXR1cm4gYS5mbi5jYXJvdXNlbD1kLHRoaXN9O3ZhciBlPWZ1bmN0aW9uKGMpe3ZhciBkLGU9YSh0aGlzKSxmPWEoZS5hdHRyKCJkYXRhLXRhcmdldCIpfHwoZD1lLmF0dHIoImhyZWYiKSkmJmQucmVwbGFjZSgvLiooPz0jW15cc10rJCkvLCIiKSk7aWYoZi5oYXNDbGFzcygiY2Fyb3VzZWwiKSl7dmFyIGc9YS5leHRlbmQoe30sZi5kYXRhKCksZS5kYXRhKCkpLGg9ZS5hdHRyKCJkYXRhLXNsaWRlLXRvIik7aCYmKGcuaW50ZXJ2YWw9ITEpLGIuY2FsbChmLGcpLGgmJmYuZGF0YSgiYnMuY2Fyb3VzZWwiKS50byhoKSxjLnByZXZlbnREZWZhdWx0KCl9fTthKGRvY3VtZW50KS5vbigiY2xpY2suYnMuY2Fyb3VzZWwuZGF0YS1hcGkiLCJbZGF0YS1zbGlkZV0iLGUpLm9uKCJjbGljay5icy5jYXJvdXNlbC5kYXRhLWFwaSIsIltkYXRhLXNsaWRlLXRvXSIsZSksYSh3aW5kb3cpLm9uKCJsb2FkIixmdW5jdGlvbigpe2EoJ1tkYXRhLXJpZGU9ImNhcm91c2VsIl0nKS5lYWNoKGZ1bmN0aW9uKCl7dmFyIGM9YSh0aGlzKTtiLmNhbGwoYyxjLmRhdGEoKSl9KX0pfShqUXVlcnkpLCtmdW5jdGlvbihhKXsidXNlIHN0cmljdCI7ZnVuY3Rpb24gYihiKXt2YXIgYyxkPWIuYXR0cigiZGF0YS10YXJnZXQiKXx8KGM9Yi5hdHRyKCJocmVmIikpJiZjLnJlcGxhY2UoLy4qKD89I1teXHNdKyQpLywiIik7cmV0dXJuIGEoZCl9ZnVuY3Rpb24gYyhiKXtyZXR1cm4gdGhpcy5lYWNoKGZ1bmN0aW9uKCl7dmFyIGM9YSh0aGlzKSxlPWMuZGF0YSgiYnMuY29sbGFwc2UiKSxmPWEuZXh0ZW5kKHt9LGQuREVGQVVMVFMsYy5kYXRhKCksIm9iamVjdCI9PXR5cGVvZiBiJiZiKTshZSYmZi50b2dnbGUmJi9zaG93fGhpZGUvLnRlc3QoYikmJihmLnRvZ2dsZT0hMSksZXx8Yy5kYXRhKCJicy5jb2xsYXBzZSIsZT1uZXcgZCh0aGlzLGYpKSwic3RyaW5nIj09dHlwZW9mIGImJmVbYl0oKX0pfXZhciBkPWZ1bmN0aW9uKGIsYyl7dGhpcy4kZWxlbWVudD1hKGIpLHRoaXMub3B0aW9ucz1hLmV4dGVuZCh7fSxkLkRFRkFVTFRTLGMpLHRoaXMuJHRyaWdnZXI9YSgnW2RhdGEtdG9nZ2xlPSJjb2xsYXBzZSJdW2hyZWY9IiMnK2IuaWQrJyJdLFtkYXRhLXRvZ2dsZT0iY29sbGFwc2UiXVtkYXRhLXRhcmdldD0iIycrYi5pZCsnIl0nKSx0aGlzLnRyYW5zaXRpb25pbmc9bnVsbCx0aGlzLm9wdGlvbnMucGFyZW50P3RoaXMuJHBhcmVudD10aGlzLmdldFBhcmVudCgpOnRoaXMuYWRkQXJpYUFuZENvbGxhcHNlZENsYXNzKHRoaXMuJGVsZW1lbnQsdGhpcy4kdHJpZ2dlciksdGhpcy5vcHRpb25zLnRvZ2dsZSYmdGhpcy50b2dnbGUoKX07ZC5WRVJTSU9OPSIzLjMuNSIsZC5UUkFOU0lUSU9OX0RVUkFUSU9OPTM1MCxkLkRFRkFVTFRTPXt0b2dnbGU6ITB9LGQucHJvdG90eXBlLmRpbWVuc2lvbj1mdW5jdGlvbigpe3ZhciBhPXRoaXMuJGVsZW1lbnQuaGFzQ2xhc3MoIndpZHRoIik7cmV0dXJuIGE/IndpZHRoIjoiaGVpZ2h0In0sZC5wcm90b3R5cGUuc2hvdz1mdW5jdGlvbigpe2lmKCF0aGlzLnRyYW5zaXRpb25pbmcmJiF0aGlzLiRlbGVtZW50Lmhhc0NsYXNzKCJpbiIpKXt2YXIgYixlPXRoaXMuJHBhcmVudCYmdGhpcy4kcGFyZW50LmNoaWxkcmVuKCIucGFuZWwiKS5jaGlsZHJlbigiLmluLCAuY29sbGFwc2luZyIpO2lmKCEoZSYmZS5sZW5ndGgmJihiPWUuZGF0YSgiYnMuY29sbGFwc2UiKSxiJiZiLnRyYW5zaXRpb25pbmcpKSl7dmFyIGY9YS5FdmVudCgic2hvdy5icy5jb2xsYXBzZSIpO2lmKHRoaXMuJGVsZW1lbnQudHJpZ2dlcihmKSwhZi5pc0RlZmF1bHRQcmV2ZW50ZWQoKSl7ZSYmZS5sZW5ndGgmJihjLmNhbGwoZSwiaGlkZSIpLGJ8fGUuZGF0YSgiYnMuY29sbGFwc2UiLG51bGwpKTt2YXIgZz10aGlzLmRpbWVuc2lvbigpO3RoaXMuJGVsZW1lbnQucmVtb3ZlQ2xhc3MoImNvbGxhcHNlIikuYWRkQ2xhc3MoImNvbGxhcHNpbmciKVtnXSgwKS5hdHRyKCJhcmlhLWV4cGFuZGVkIiwhMCksdGhpcy4kdHJpZ2dlci5yZW1vdmVDbGFzcygiY29sbGFwc2VkIikuYXR0cigiYXJpYS1leHBhbmRlZCIsITApLHRoaXMudHJhbnNpdGlvbmluZz0xO3ZhciBoPWZ1bmN0aW9uKCl7dGhpcy4kZWxlbWVudC5yZW1vdmVDbGFzcygiY29sbGFwc2luZyIpLmFkZENsYXNzKCJjb2xsYXBzZSBpbiIpW2ddKCIiKSx0aGlzLnRyYW5zaXRpb25pbmc9MCx0aGlzLiRlbGVtZW50LnRyaWdnZXIoInNob3duLmJzLmNvbGxhcHNlIil9O2lmKCFhLnN1cHBvcnQudHJhbnNpdGlvbilyZXR1cm4gaC5jYWxsKHRoaXMpO3ZhciBpPWEuY2FtZWxDYXNlKFsic2Nyb2xsIixnXS5qb2luKCItIikpO3RoaXMuJGVsZW1lbnQub25lKCJic1RyYW5zaXRpb25FbmQiLGEucHJveHkoaCx0aGlzKSkuZW11bGF0ZVRyYW5zaXRpb25FbmQoZC5UUkFOU0lUSU9OX0RVUkFUSU9OKVtnXSh0aGlzLiRlbGVtZW50WzBdW2ldKX19fX0sZC5wcm90b3R5cGUuaGlkZT1mdW5jdGlvbigpe2lmKCF0aGlzLnRyYW5zaXRpb25pbmcmJnRoaXMuJGVsZW1lbnQuaGFzQ2xhc3MoImluIikpe3ZhciBiPWEuRXZlbnQoImhpZGUuYnMuY29sbGFwc2UiKTtpZih0aGlzLiRlbGVtZW50LnRyaWdnZXIoYiksIWIuaXNEZWZhdWx0UHJldmVudGVkKCkpe3ZhciBjPXRoaXMuZGltZW5zaW9uKCk7dGhpcy4kZWxlbWVudFtjXSh0aGlzLiRlbGVtZW50W2NdKCkpWzBdLm9mZnNldEhlaWdodCx0aGlzLiRlbGVtZW50LmFkZENsYXNzKCJjb2xsYXBzaW5nIikucmVtb3ZlQ2xhc3MoImNvbGxhcHNlIGluIikuYXR0cigiYXJpYS1leHBhbmRlZCIsITEpLHRoaXMuJHRyaWdnZXIuYWRkQ2xhc3MoImNvbGxhcHNlZCIpLmF0dHIoImFyaWEtZXhwYW5kZWQiLCExKSx0aGlzLnRyYW5zaXRpb25pbmc9MTt2YXIgZT1mdW5jdGlvbigpe3RoaXMudHJhbnNpdGlvbmluZz0wLHRoaXMuJGVsZW1lbnQucmVtb3ZlQ2xhc3MoImNvbGxhcHNpbmciKS5hZGRDbGFzcygiY29sbGFwc2UiKS50cmlnZ2VyKCJoaWRkZW4uYnMuY29sbGFwc2UiKX07cmV0dXJuIGEuc3VwcG9ydC50cmFuc2l0aW9uP3ZvaWQgdGhpcy4kZWxlbWVudFtjXSgwKS5vbmUoImJzVHJhbnNpdGlvbkVuZCIsYS5wcm94eShlLHRoaXMpKS5lbXVsYXRlVHJhbnNpdGlvbkVuZChkLlRSQU5TSVRJT05fRFVSQVRJT04pOmUuY2FsbCh0aGlzKX19fSxkLnByb3RvdHlwZS50b2dnbGU9ZnVuY3Rpb24oKXt0aGlzW3RoaXMuJGVsZW1lbnQuaGFzQ2xhc3MoImluIik/ImhpZGUiOiJzaG93Il0oKX0sZC5wcm90b3R5cGUuZ2V0UGFyZW50PWZ1bmN0aW9uKCl7cmV0dXJuIGEodGhpcy5vcHRpb25zLnBhcmVudCkuZmluZCgnW2RhdGEtdG9nZ2xlPSJjb2xsYXBzZSJdW2RhdGEtcGFyZW50PSInK3RoaXMub3B0aW9ucy5wYXJlbnQrJyJdJykuZWFjaChhLnByb3h5KGZ1bmN0aW9uKGMsZCl7dmFyIGU9YShkKTt0aGlzLmFkZEFyaWFBbmRDb2xsYXBzZWRDbGFzcyhiKGUpLGUpfSx0aGlzKSkuZW5kKCl9LGQucHJvdG90eXBlLmFkZEFyaWFBbmRDb2xsYXBzZWRDbGFzcz1mdW5jdGlvbihhLGIpe3ZhciBjPWEuaGFzQ2xhc3MoImluIik7YS5hdHRyKCJhcmlhLWV4cGFuZGVkIixjKSxiLnRvZ2dsZUNsYXNzKCJjb2xsYXBzZWQiLCFjKS5hdHRyKCJhcmlhLWV4cGFuZGVkIixjKX07dmFyIGU9YS5mbi5jb2xsYXBzZTthLmZuLmNvbGxhcHNlPWMsYS5mbi5jb2xsYXBzZS5Db25zdHJ1Y3Rvcj1kLGEuZm4uY29sbGFwc2Uubm9Db25mbGljdD1mdW5jdGlvbigpe3JldHVybiBhLmZuLmNvbGxhcHNlPWUsdGhpc30sYShkb2N1bWVudCkub24oImNsaWNrLmJzLmNvbGxhcHNlLmRhdGEtYXBpIiwnW2RhdGEtdG9nZ2xlPSJjb2xsYXBzZSJdJyxmdW5jdGlvbihkKXt2YXIgZT1hKHRoaXMpO2UuYXR0cigiZGF0YS10YXJnZXQiKXx8ZC5wcmV2ZW50RGVmYXVsdCgpO3ZhciBmPWIoZSksZz1mLmRhdGEoImJzLmNvbGxhcHNlIiksaD1nPyJ0b2dnbGUiOmUuZGF0YSgpO2MuY2FsbChmLGgpfSl9KGpRdWVyeSksK2Z1bmN0aW9uKGEpeyJ1c2Ugc3RyaWN0IjtmdW5jdGlvbiBiKGIpe3ZhciBjPWIuYXR0cigiZGF0YS10YXJnZXQiKTtjfHwoYz1iLmF0dHIoImhyZWYiKSxjPWMmJi8jW0EtWmEtel0vLnRlc3QoYykmJmMucmVwbGFjZSgvLiooPz0jW15cc10qJCkvLCIiKSk7dmFyIGQ9YyYmYShjKTtyZXR1cm4gZCYmZC5sZW5ndGg/ZDpiLnBhcmVudCgpfWZ1bmN0aW9uIGMoYyl7YyYmMz09PWMud2hpY2h8fChhKGUpLnJlbW92ZSgpLGEoZikuZWFjaChmdW5jdGlvbigpe3ZhciBkPWEodGhpcyksZT1iKGQpLGY9e3JlbGF0ZWRUYXJnZXQ6dGhpc307ZS5oYXNDbGFzcygib3BlbiIpJiYoYyYmImNsaWNrIj09Yy50eXBlJiYvaW5wdXR8dGV4dGFyZWEvaS50ZXN0KGMudGFyZ2V0LnRhZ05hbWUpJiZhLmNvbnRhaW5zKGVbMF0sYy50YXJnZXQpfHwoZS50cmlnZ2VyKGM9YS5FdmVudCgiaGlkZS5icy5kcm9wZG93biIsZikpLGMuaXNEZWZhdWx0UHJldmVudGVkKCl8fChkLmF0dHIoImFyaWEtZXhwYW5kZWQiLCJmYWxzZSIpLGUucmVtb3ZlQ2xhc3MoIm9wZW4iKS50cmlnZ2VyKCJoaWRkZW4uYnMuZHJvcGRvd24iLGYpKSkpfSkpfWZ1bmN0aW9uIGQoYil7cmV0dXJuIHRoaXMuZWFjaChmdW5jdGlvbigpe3ZhciBjPWEodGhpcyksZD1jLmRhdGEoImJzLmRyb3Bkb3duIik7ZHx8Yy5kYXRhKCJicy5kcm9wZG93biIsZD1uZXcgZyh0aGlzKSksInN0cmluZyI9PXR5cGVvZiBiJiZkW2JdLmNhbGwoYyl9KX12YXIgZT0iLmRyb3Bkb3duLWJhY2tkcm9wIixmPSdbZGF0YS10b2dnbGU9ImRyb3Bkb3duIl0nLGc9ZnVuY3Rpb24oYil7YShiKS5vbigiY2xpY2suYnMuZHJvcGRvd24iLHRoaXMudG9nZ2xlKX07Zy5WRVJTSU9OPSIzLjMuNSIsZy5wcm90b3R5cGUudG9nZ2xlPWZ1bmN0aW9uKGQpe3ZhciBlPWEodGhpcyk7aWYoIWUuaXMoIi5kaXNhYmxlZCwgOmRpc2FibGVkIikpe3ZhciBmPWIoZSksZz1mLmhhc0NsYXNzKCJvcGVuIik7aWYoYygpLCFnKXsib250b3VjaHN0YXJ0ImluIGRvY3VtZW50LmRvY3VtZW50RWxlbWVudCYmIWYuY2xvc2VzdCgiLm5hdmJhci1uYXYiKS5sZW5ndGgmJmEoZG9jdW1lbnQuY3JlYXRlRWxlbWVudCgiZGl2IikpLmFkZENsYXNzKCJkcm9wZG93bi1iYWNrZHJvcCIpLmluc2VydEFmdGVyKGEodGhpcykpLm9uKCJjbGljayIsYyk7dmFyIGg9e3JlbGF0ZWRUYXJnZXQ6dGhpc307aWYoZi50cmlnZ2VyKGQ9YS5FdmVudCgic2hvdy5icy5kcm9wZG93biIsaCkpLGQuaXNEZWZhdWx0UHJldmVudGVkKCkpcmV0dXJuO2UudHJpZ2dlcigiZm9jdXMiKS5hdHRyKCJhcmlhLWV4cGFuZGVkIiwidHJ1ZSIpLGYudG9nZ2xlQ2xhc3MoIm9wZW4iKS50cmlnZ2VyKCJzaG93bi5icy5kcm9wZG93biIsaCl9cmV0dXJuITF9fSxnLnByb3RvdHlwZS5rZXlkb3duPWZ1bmN0aW9uKGMpe2lmKC8oMzh8NDB8Mjd8MzIpLy50ZXN0KGMud2hpY2gpJiYhL2lucHV0fHRleHRhcmVhL2kudGVzdChjLnRhcmdldC50YWdOYW1lKSl7dmFyIGQ9YSh0aGlzKTtpZihjLnByZXZlbnREZWZhdWx0KCksYy5zdG9wUHJvcGFnYXRpb24oKSwhZC5pcygiLmRpc2FibGVkLCA6ZGlzYWJsZWQiKSl7dmFyIGU9YihkKSxnPWUuaGFzQ2xhc3MoIm9wZW4iKTtpZighZyYmMjchPWMud2hpY2h8fGcmJjI3PT1jLndoaWNoKXJldHVybiAyNz09Yy53aGljaCYmZS5maW5kKGYpLnRyaWdnZXIoImZvY3VzIiksZC50cmlnZ2VyKCJjbGljayIpO3ZhciBoPSIgbGk6bm90KC5kaXNhYmxlZCk6dmlzaWJsZSBhIixpPWUuZmluZCgiLmRyb3Bkb3duLW1lbnUiK2gpO2lmKGkubGVuZ3RoKXt2YXIgaj1pLmluZGV4KGMudGFyZ2V0KTszOD09Yy53aGljaCYmaj4wJiZqLS0sNDA9PWMud2hpY2gmJmo8aS5sZW5ndGgtMSYmaisrLH5qfHwoaj0wKSxpLmVxKGopLnRyaWdnZXIoImZvY3VzIil9fX19O3ZhciBoPWEuZm4uZHJvcGRvd247YS5mbi5kcm9wZG93bj1kLGEuZm4uZHJvcGRvd24uQ29uc3RydWN0b3I9ZyxhLmZuLmRyb3Bkb3duLm5vQ29uZmxpY3Q9ZnVuY3Rpb24oKXtyZXR1cm4gYS5mbi5kcm9wZG93bj1oLHRoaXN9LGEoZG9jdW1lbnQpLm9uKCJjbGljay5icy5kcm9wZG93bi5kYXRhLWFwaSIsYykub24oImNsaWNrLmJzLmRyb3Bkb3duLmRhdGEtYXBpIiwiLmRyb3Bkb3duIGZvcm0iLGZ1bmN0aW9uKGEpe2Euc3RvcFByb3BhZ2F0aW9uKCl9KS5vbigiY2xpY2suYnMuZHJvcGRvd24uZGF0YS1hcGkiLGYsZy5wcm90b3R5cGUudG9nZ2xlKS5vbigia2V5ZG93bi5icy5kcm9wZG93bi5kYXRhLWFwaSIsZixnLnByb3RvdHlwZS5rZXlkb3duKS5vbigia2V5ZG93bi5icy5kcm9wZG93bi5kYXRhLWFwaSIsIi5kcm9wZG93bi1tZW51IixnLnByb3RvdHlwZS5rZXlkb3duKX0oalF1ZXJ5KSwrZnVuY3Rpb24oYSl7InVzZSBzdHJpY3QiO2Z1bmN0aW9uIGIoYixkKXtyZXR1cm4gdGhpcy5lYWNoKGZ1bmN0aW9uKCl7dmFyIGU9YSh0aGlzKSxmPWUuZGF0YSgiYnMubW9kYWwiKSxnPWEuZXh0ZW5kKHt9LGMuREVGQVVMVFMsZS5kYXRhKCksIm9iamVjdCI9PXR5cGVvZiBiJiZiKTtmfHxlLmRhdGEoImJzLm1vZGFsIixmPW5ldyBjKHRoaXMsZykpLCJzdHJpbmciPT10eXBlb2YgYj9mW2JdKGQpOmcuc2hvdyYmZi5zaG93KGQpfSl9dmFyIGM9ZnVuY3Rpb24oYixjKXt0aGlzLm9wdGlvbnM9Yyx0aGlzLiRib2R5PWEoZG9jdW1lbnQuYm9keSksdGhpcy4kZWxlbWVudD1hKGIpLHRoaXMuJGRpYWxvZz10aGlzLiRlbGVtZW50LmZpbmQoIi5tb2RhbC1kaWFsb2ciKSx0aGlzLiRiYWNrZHJvcD1udWxsLHRoaXMuaXNTaG93bj1udWxsLHRoaXMub3JpZ2luYWxCb2R5UGFkPW51bGwsdGhpcy5zY3JvbGxiYXJXaWR0aD0wLHRoaXMuaWdub3JlQmFja2Ryb3BDbGljaz0hMSx0aGlzLm9wdGlvbnMucmVtb3RlJiZ0aGlzLiRlbGVtZW50LmZpbmQoIi5tb2RhbC1jb250ZW50IikubG9hZCh0aGlzLm9wdGlvbnMucmVtb3RlLGEucHJveHkoZnVuY3Rpb24oKXt0aGlzLiRlbGVtZW50LnRyaWdnZXIoImxvYWRlZC5icy5tb2RhbCIpfSx0aGlzKSl9O2MuVkVSU0lPTj0iMy4zLjUiLGMuVFJBTlNJVElPTl9EVVJBVElPTj0zMDAsYy5CQUNLRFJPUF9UUkFOU0lUSU9OX0RVUkFUSU9OPTE1MCxjLkRFRkFVTFRTPXtiYWNrZHJvcDohMCxrZXlib2FyZDohMCxzaG93OiEwfSxjLnByb3RvdHlwZS50b2dnbGU9ZnVuY3Rpb24oYSl7cmV0dXJuIHRoaXMuaXNTaG93bj90aGlzLmhpZGUoKTp0aGlzLnNob3coYSl9LGMucHJvdG90eXBlLnNob3c9ZnVuY3Rpb24oYil7dmFyIGQ9dGhpcyxlPWEuRXZlbnQoInNob3cuYnMubW9kYWwiLHtyZWxhdGVkVGFyZ2V0OmJ9KTt0aGlzLiRlbGVtZW50LnRyaWdnZXIoZSksdGhpcy5pc1Nob3dufHxlLmlzRGVmYXVsdFByZXZlbnRlZCgpfHwodGhpcy5pc1Nob3duPSEwLHRoaXMuY2hlY2tTY3JvbGxiYXIoKSx0aGlzLnNldFNjcm9sbGJhcigpLHRoaXMuJGJvZHkuYWRkQ2xhc3MoIm1vZGFsLW9wZW4iKSx0aGlzLmVzY2FwZSgpLHRoaXMucmVzaXplKCksdGhpcy4kZWxlbWVudC5vbigiY2xpY2suZGlzbWlzcy5icy5tb2RhbCIsJ1tkYXRhLWRpc21pc3M9Im1vZGFsIl0nLGEucHJveHkodGhpcy5oaWRlLHRoaXMpKSx0aGlzLiRkaWFsb2cub24oIm1vdXNlZG93bi5kaXNtaXNzLmJzLm1vZGFsIixmdW5jdGlvbigpe2QuJGVsZW1lbnQub25lKCJtb3VzZXVwLmRpc21pc3MuYnMubW9kYWwiLGZ1bmN0aW9uKGIpe2EoYi50YXJnZXQpLmlzKGQuJGVsZW1lbnQpJiYoZC5pZ25vcmVCYWNrZHJvcENsaWNrPSEwKX0pfSksdGhpcy5iYWNrZHJvcChmdW5jdGlvbigpe3ZhciBlPWEuc3VwcG9ydC50cmFuc2l0aW9uJiZkLiRlbGVtZW50Lmhhc0NsYXNzKCJmYWRlIik7ZC4kZWxlbWVudC5wYXJlbnQoKS5sZW5ndGh8fGQuJGVsZW1lbnQuYXBwZW5kVG8oZC4kYm9keSksZC4kZWxlbWVudC5zaG93KCkuc2Nyb2xsVG9wKDApLGQuYWRqdXN0RGlhbG9nKCksZSYmZC4kZWxlbWVudFswXS5vZmZzZXRXaWR0aCxkLiRlbGVtZW50LmFkZENsYXNzKCJpbiIpLGQuZW5mb3JjZUZvY3VzKCk7dmFyIGY9YS5FdmVudCgic2hvd24uYnMubW9kYWwiLHtyZWxhdGVkVGFyZ2V0OmJ9KTtlP2QuJGRpYWxvZy5vbmUoImJzVHJhbnNpdGlvbkVuZCIsZnVuY3Rpb24oKXtkLiRlbGVtZW50LnRyaWdnZXIoImZvY3VzIikudHJpZ2dlcihmKX0pLmVtdWxhdGVUcmFuc2l0aW9uRW5kKGMuVFJBTlNJVElPTl9EVVJBVElPTik6ZC4kZWxlbWVudC50cmlnZ2VyKCJmb2N1cyIpLnRyaWdnZXIoZil9KSl9LGMucHJvdG90eXBlLmhpZGU9ZnVuY3Rpb24oYil7YiYmYi5wcmV2ZW50RGVmYXVsdCgpLGI9YS5FdmVudCgiaGlkZS5icy5tb2RhbCIpLHRoaXMuJGVsZW1lbnQudHJpZ2dlcihiKSx0aGlzLmlzU2hvd24mJiFiLmlzRGVmYXVsdFByZXZlbnRlZCgpJiYodGhpcy5pc1Nob3duPSExLHRoaXMuZXNjYXBlKCksdGhpcy5yZXNpemUoKSxhKGRvY3VtZW50KS5vZmYoImZvY3VzaW4uYnMubW9kYWwiKSx0aGlzLiRlbGVtZW50LnJlbW92ZUNsYXNzKCJpbiIpLm9mZigiY2xpY2suZGlzbWlzcy5icy5tb2RhbCIpLm9mZigibW91c2V1cC5kaXNtaXNzLmJzLm1vZGFsIiksdGhpcy4kZGlhbG9nLm9mZigibW91c2Vkb3duLmRpc21pc3MuYnMubW9kYWwiKSxhLnN1cHBvcnQudHJhbnNpdGlvbiYmdGhpcy4kZWxlbWVudC5oYXNDbGFzcygiZmFkZSIpP3RoaXMuJGVsZW1lbnQub25lKCJic1RyYW5zaXRpb25FbmQiLGEucHJveHkodGhpcy5oaWRlTW9kYWwsdGhpcykpLmVtdWxhdGVUcmFuc2l0aW9uRW5kKGMuVFJBTlNJVElPTl9EVVJBVElPTik6dGhpcy5oaWRlTW9kYWwoKSl9LGMucHJvdG90eXBlLmVuZm9yY2VGb2N1cz1mdW5jdGlvbigpe2EoZG9jdW1lbnQpLm9mZigiZm9jdXNpbi5icy5tb2RhbCIpLm9uKCJmb2N1c2luLmJzLm1vZGFsIixhLnByb3h5KGZ1bmN0aW9uKGEpe3RoaXMuJGVsZW1lbnRbMF09PT1hLnRhcmdldHx8dGhpcy4kZWxlbWVudC5oYXMoYS50YXJnZXQpLmxlbmd0aHx8dGhpcy4kZWxlbWVudC50cmlnZ2VyKCJmb2N1cyIpfSx0aGlzKSl9LGMucHJvdG90eXBlLmVzY2FwZT1mdW5jdGlvbigpe3RoaXMuaXNTaG93biYmdGhpcy5vcHRpb25zLmtleWJvYXJkP3RoaXMuJGVsZW1lbnQub24oImtleWRvd24uZGlzbWlzcy5icy5tb2RhbCIsYS5wcm94eShmdW5jdGlvbihhKXsyNz09YS53aGljaCYmdGhpcy5oaWRlKCl9LHRoaXMpKTp0aGlzLmlzU2hvd258fHRoaXMuJGVsZW1lbnQub2ZmKCJrZXlkb3duLmRpc21pc3MuYnMubW9kYWwiKX0sYy5wcm90b3R5cGUucmVzaXplPWZ1bmN0aW9uKCl7dGhpcy5pc1Nob3duP2Eod2luZG93KS5vbigicmVzaXplLmJzLm1vZGFsIixhLnByb3h5KHRoaXMuaGFuZGxlVXBkYXRlLHRoaXMpKTphKHdpbmRvdykub2ZmKCJyZXNpemUuYnMubW9kYWwiKX0sYy5wcm90b3R5cGUuaGlkZU1vZGFsPWZ1bmN0aW9uKCl7dmFyIGE9dGhpczt0aGlzLiRlbGVtZW50LmhpZGUoKSx0aGlzLmJhY2tkcm9wKGZ1bmN0aW9uKCl7YS4kYm9keS5yZW1vdmVDbGFzcygibW9kYWwtb3BlbiIpLGEucmVzZXRBZGp1c3RtZW50cygpLGEucmVzZXRTY3JvbGxiYXIoKSxhLiRlbGVtZW50LnRyaWdnZXIoImhpZGRlbi5icy5tb2RhbCIpfSl9LGMucHJvdG90eXBlLnJlbW92ZUJhY2tkcm9wPWZ1bmN0aW9uKCl7dGhpcy4kYmFja2Ryb3AmJnRoaXMuJGJhY2tkcm9wLnJlbW92ZSgpLHRoaXMuJGJhY2tkcm9wPW51bGx9LGMucHJvdG90eXBlLmJhY2tkcm9wPWZ1bmN0aW9uKGIpe3ZhciBkPXRoaXMsZT10aGlzLiRlbGVtZW50Lmhhc0NsYXNzKCJmYWRlIik/ImZhZGUiOiIiO2lmKHRoaXMuaXNTaG93biYmdGhpcy5vcHRpb25zLmJhY2tkcm9wKXt2YXIgZj1hLnN1cHBvcnQudHJhbnNpdGlvbiYmZTtpZih0aGlzLiRiYWNrZHJvcD1hKGRvY3VtZW50LmNyZWF0ZUVsZW1lbnQoImRpdiIpKS5hZGRDbGFzcygibW9kYWwtYmFja2Ryb3AgIitlKS5hcHBlbmRUbyh0aGlzLiRib2R5KSx0aGlzLiRlbGVtZW50Lm9uKCJjbGljay5kaXNtaXNzLmJzLm1vZGFsIixhLnByb3h5KGZ1bmN0aW9uKGEpe3JldHVybiB0aGlzLmlnbm9yZUJhY2tkcm9wQ2xpY2s/dm9pZCh0aGlzLmlnbm9yZUJhY2tkcm9wQ2xpY2s9ITEpOnZvaWQoYS50YXJnZXQ9PT1hLmN1cnJlbnRUYXJnZXQmJigic3RhdGljIj09dGhpcy5vcHRpb25zLmJhY2tkcm9wP3RoaXMuJGVsZW1lbnRbMF0uZm9jdXMoKTp0aGlzLmhpZGUoKSkpfSx0aGlzKSksZiYmdGhpcy4kYmFja2Ryb3BbMF0ub2Zmc2V0V2lkdGgsdGhpcy4kYmFja2Ryb3AuYWRkQ2xhc3MoImluIiksIWIpcmV0dXJuO2Y/dGhpcy4kYmFja2Ryb3Aub25lKCJic1RyYW5zaXRpb25FbmQiLGIpLmVtdWxhdGVUcmFuc2l0aW9uRW5kKGMuQkFDS0RST1BfVFJBTlNJVElPTl9EVVJBVElPTik6YigpfWVsc2UgaWYoIXRoaXMuaXNTaG93biYmdGhpcy4kYmFja2Ryb3Ape3RoaXMuJGJhY2tkcm9wLnJlbW92ZUNsYXNzKCJpbiIpO3ZhciBnPWZ1bmN0aW9uKCl7ZC5yZW1vdmVCYWNrZHJvcCgpLGImJmIoKX07YS5zdXBwb3J0LnRyYW5zaXRpb24mJnRoaXMuJGVsZW1lbnQuaGFzQ2xhc3MoImZhZGUiKT90aGlzLiRiYWNrZHJvcC5vbmUoImJzVHJhbnNpdGlvbkVuZCIsZykuZW11bGF0ZVRyYW5zaXRpb25FbmQoYy5CQUNLRFJPUF9UUkFOU0lUSU9OX0RVUkFUSU9OKTpnKCl9ZWxzZSBiJiZiKCl9LGMucHJvdG90eXBlLmhhbmRsZVVwZGF0ZT1mdW5jdGlvbigpe3RoaXMuYWRqdXN0RGlhbG9nKCl9LGMucHJvdG90eXBlLmFkanVzdERpYWxvZz1mdW5jdGlvbigpe3ZhciBhPXRoaXMuJGVsZW1lbnRbMF0uc2Nyb2xsSGVpZ2h0PmRvY3VtZW50LmRvY3VtZW50RWxlbWVudC5jbGllbnRIZWlnaHQ7dGhpcy4kZWxlbWVudC5jc3Moe3BhZGRpbmdMZWZ0OiF0aGlzLmJvZHlJc092ZXJmbG93aW5nJiZhP3RoaXMuc2Nyb2xsYmFyV2lkdGg6IiIscGFkZGluZ1JpZ2h0OnRoaXMuYm9keUlzT3ZlcmZsb3dpbmcmJiFhP3RoaXMuc2Nyb2xsYmFyV2lkdGg6IiJ9KX0sYy5wcm90b3R5cGUucmVzZXRBZGp1c3RtZW50cz1mdW5jdGlvbigpe3RoaXMuJGVsZW1lbnQuY3NzKHtwYWRkaW5nTGVmdDoiIixwYWRkaW5nUmlnaHQ6IiJ9KX0sYy5wcm90b3R5cGUuY2hlY2tTY3JvbGxiYXI9ZnVuY3Rpb24oKXt2YXIgYT13aW5kb3cuaW5uZXJXaWR0aDtpZighYSl7dmFyIGI9ZG9jdW1lbnQuZG9jdW1lbnRFbGVtZW50LmdldEJvdW5kaW5nQ2xpZW50UmVjdCgpO2E9Yi5yaWdodC1NYXRoLmFicyhiLmxlZnQpfXRoaXMuYm9keUlzT3ZlcmZsb3dpbmc9ZG9jdW1lbnQuYm9keS5jbGllbnRXaWR0aDxhLHRoaXMuc2Nyb2xsYmFyV2lkdGg9dGhpcy5tZWFzdXJlU2Nyb2xsYmFyKCl9LGMucHJvdG90eXBlLnNldFNjcm9sbGJhcj1mdW5jdGlvbigpe3ZhciBhPXBhcnNlSW50KHRoaXMuJGJvZHkuY3NzKCJwYWRkaW5nLXJpZ2h0Iil8fDAsMTApO3RoaXMub3JpZ2luYWxCb2R5UGFkPWRvY3VtZW50LmJvZHkuc3R5bGUucGFkZGluZ1JpZ2h0fHwiIix0aGlzLmJvZHlJc092ZXJmbG93aW5nJiZ0aGlzLiRib2R5LmNzcygicGFkZGluZy1yaWdodCIsYSt0aGlzLnNjcm9sbGJhcldpZHRoKX0sYy5wcm90b3R5cGUucmVzZXRTY3JvbGxiYXI9ZnVuY3Rpb24oKXt0aGlzLiRib2R5LmNzcygicGFkZGluZy1yaWdodCIsdGhpcy5vcmlnaW5hbEJvZHlQYWQpfSxjLnByb3RvdHlwZS5tZWFzdXJlU2Nyb2xsYmFyPWZ1bmN0aW9uKCl7dmFyIGE9ZG9jdW1lbnQuY3JlYXRlRWxlbWVudCgiZGl2Iik7YS5jbGFzc05hbWU9Im1vZGFsLXNjcm9sbGJhci1tZWFzdXJlIix0aGlzLiRib2R5LmFwcGVuZChhKTt2YXIgYj1hLm9mZnNldFdpZHRoLWEuY2xpZW50V2lkdGg7cmV0dXJuIHRoaXMuJGJvZHlbMF0ucmVtb3ZlQ2hpbGQoYSksYn07dmFyIGQ9YS5mbi5tb2RhbDthLmZuLm1vZGFsPWIsYS5mbi5tb2RhbC5Db25zdHJ1Y3Rvcj1jLGEuZm4ubW9kYWwubm9Db25mbGljdD1mdW5jdGlvbigpe3JldHVybiBhLmZuLm1vZGFsPWQsdGhpc30sYShkb2N1bWVudCkub24oImNsaWNrLmJzLm1vZGFsLmRhdGEtYXBpIiwnW2RhdGEtdG9nZ2xlPSJtb2RhbCJdJyxmdW5jdGlvbihjKXt2YXIgZD1hKHRoaXMpLGU9ZC5hdHRyKCJocmVmIiksZj1hKGQuYXR0cigiZGF0YS10YXJnZXQiKXx8ZSYmZS5yZXBsYWNlKC8uKig/PSNbXlxzXSskKS8sIiIpKSxnPWYuZGF0YSgiYnMubW9kYWwiKT8idG9nZ2xlIjphLmV4dGVuZCh7cmVtb3RlOiEvIy8udGVzdChlKSYmZX0sZi5kYXRhKCksZC5kYXRhKCkpO2QuaXMoImEiKSYmYy5wcmV2ZW50RGVmYXVsdCgpLGYub25lKCJzaG93LmJzLm1vZGFsIixmdW5jdGlvbihhKXthLmlzRGVmYXVsdFByZXZlbnRlZCgpfHxmLm9uZSgiaGlkZGVuLmJzLm1vZGFsIixmdW5jdGlvbigpe2QuaXMoIjp2aXNpYmxlIikmJmQudHJpZ2dlcigiZm9jdXMiKX0pfSksYi5jYWxsKGYsZyx0aGlzKX0pfShqUXVlcnkpLCtmdW5jdGlvbihhKXsidXNlIHN0cmljdCI7ZnVuY3Rpb24gYihiKXtyZXR1cm4gdGhpcy5lYWNoKGZ1bmN0aW9uKCl7dmFyIGQ9YSh0aGlzKSxlPWQuZGF0YSgiYnMudG9vbHRpcCIpLGY9Im9iamVjdCI9PXR5cGVvZiBiJiZiOyhlfHwhL2Rlc3Ryb3l8aGlkZS8udGVzdChiKSkmJihlfHxkLmRhdGEoImJzLnRvb2x0aXAiLGU9bmV3IGModGhpcyxmKSksInN0cmluZyI9PXR5cGVvZiBiJiZlW2JdKCkpfSl9dmFyIGM9ZnVuY3Rpb24oYSxiKXt0aGlzLnR5cGU9bnVsbCx0aGlzLm9wdGlvbnM9bnVsbCx0aGlzLmVuYWJsZWQ9bnVsbCx0aGlzLnRpbWVvdXQ9bnVsbCx0aGlzLmhvdmVyU3RhdGU9bnVsbCx0aGlzLiRlbGVtZW50PW51bGwsdGhpcy5pblN0YXRlPW51bGwsdGhpcy5pbml0KCJ0b29sdGlwIixhLGIpfTtjLlZFUlNJT049IjMuMy41IixjLlRSQU5TSVRJT05fRFVSQVRJT049MTUwLGMuREVGQVVMVFM9e2FuaW1hdGlvbjohMCxwbGFjZW1lbnQ6InRvcCIsc2VsZWN0b3I6ITEsdGVtcGxhdGU6JzxkaXYgY2xhc3M9InRvb2x0aXAiIHJvbGU9InRvb2x0aXAiPjxkaXYgY2xhc3M9InRvb2x0aXAtYXJyb3ciPjwvZGl2PjxkaXYgY2xhc3M9InRvb2x0aXAtaW5uZXIiPjwvZGl2PjwvZGl2PicsdHJpZ2dlcjoiaG92ZXIgZm9jdXMiLHRpdGxlOiIiLGRlbGF5OjAsaHRtbDohMSxjb250YWluZXI6ITEsdmlld3BvcnQ6e3NlbGVjdG9yOiJib2R5IixwYWRkaW5nOjB9fSxjLnByb3RvdHlwZS5pbml0PWZ1bmN0aW9uKGIsYyxkKXtpZih0aGlzLmVuYWJsZWQ9ITAsdGhpcy50eXBlPWIsdGhpcy4kZWxlbWVudD1hKGMpLHRoaXMub3B0aW9ucz10aGlzLmdldE9wdGlvbnMoZCksdGhpcy4kdmlld3BvcnQ9dGhpcy5vcHRpb25zLnZpZXdwb3J0JiZhKGEuaXNGdW5jdGlvbih0aGlzLm9wdGlvbnMudmlld3BvcnQpP3RoaXMub3B0aW9ucy52aWV3cG9ydC5jYWxsKHRoaXMsdGhpcy4kZWxlbWVudCk6dGhpcy5vcHRpb25zLnZpZXdwb3J0LnNlbGVjdG9yfHx0aGlzLm9wdGlvbnMudmlld3BvcnQpLHRoaXMuaW5TdGF0ZT17Y2xpY2s6ITEsaG92ZXI6ITEsZm9jdXM6ITF9LHRoaXMuJGVsZW1lbnRbMF1pbnN0YW5jZW9mIGRvY3VtZW50LmNvbnN0cnVjdG9yJiYhdGhpcy5vcHRpb25zLnNlbGVjdG9yKXRocm93IG5ldyBFcnJvcigiYHNlbGVjdG9yYCBvcHRpb24gbXVzdCBiZSBzcGVjaWZpZWQgd2hlbiBpbml0aWFsaXppbmcgIit0aGlzLnR5cGUrIiBvbiB0aGUgd2luZG93LmRvY3VtZW50IG9iamVjdCEiKTtmb3IodmFyIGU9dGhpcy5vcHRpb25zLnRyaWdnZXIuc3BsaXQoIiAiKSxmPWUubGVuZ3RoO2YtLTspe3ZhciBnPWVbZl07aWYoImNsaWNrIj09Zyl0aGlzLiRlbGVtZW50Lm9uKCJjbGljay4iK3RoaXMudHlwZSx0aGlzLm9wdGlvbnMuc2VsZWN0b3IsYS5wcm94eSh0aGlzLnRvZ2dsZSx0aGlzKSk7ZWxzZSBpZigibWFudWFsIiE9Zyl7dmFyIGg9ImhvdmVyIj09Zz8ibW91c2VlbnRlciI6ImZvY3VzaW4iLGk9ImhvdmVyIj09Zz8ibW91c2VsZWF2ZSI6ImZvY3Vzb3V0Ijt0aGlzLiRlbGVtZW50Lm9uKGgrIi4iK3RoaXMudHlwZSx0aGlzLm9wdGlvbnMuc2VsZWN0b3IsYS5wcm94eSh0aGlzLmVudGVyLHRoaXMpKSx0aGlzLiRlbGVtZW50Lm9uKGkrIi4iK3RoaXMudHlwZSx0aGlzLm9wdGlvbnMuc2VsZWN0b3IsYS5wcm94eSh0aGlzLmxlYXZlLHRoaXMpKX19dGhpcy5vcHRpb25zLnNlbGVjdG9yP3RoaXMuX29wdGlvbnM9YS5leHRlbmQoe30sdGhpcy5vcHRpb25zLHt0cmlnZ2VyOiJtYW51YWwiLHNlbGVjdG9yOiIifSk6dGhpcy5maXhUaXRsZSgpfSxjLnByb3RvdHlwZS5nZXREZWZhdWx0cz1mdW5jdGlvbigpe3JldHVybiBjLkRFRkFVTFRTfSxjLnByb3RvdHlwZS5nZXRPcHRpb25zPWZ1bmN0aW9uKGIpe3JldHVybiBiPWEuZXh0ZW5kKHt9LHRoaXMuZ2V0RGVmYXVsdHMoKSx0aGlzLiRlbGVtZW50LmRhdGEoKSxiKSxiLmRlbGF5JiYibnVtYmVyIj09dHlwZW9mIGIuZGVsYXkmJihiLmRlbGF5PXtzaG93OmIuZGVsYXksaGlkZTpiLmRlbGF5fSksYn0sYy5wcm90b3R5cGUuZ2V0RGVsZWdhdGVPcHRpb25zPWZ1bmN0aW9uKCl7dmFyIGI9e30sYz10aGlzLmdldERlZmF1bHRzKCk7cmV0dXJuIHRoaXMuX29wdGlvbnMmJmEuZWFjaCh0aGlzLl9vcHRpb25zLGZ1bmN0aW9uKGEsZCl7Y1thXSE9ZCYmKGJbYV09ZCl9KSxifSxjLnByb3RvdHlwZS5lbnRlcj1mdW5jdGlvbihiKXt2YXIgYz1iIGluc3RhbmNlb2YgdGhpcy5jb25zdHJ1Y3Rvcj9iOmEoYi5jdXJyZW50VGFyZ2V0KS5kYXRhKCJicy4iK3RoaXMudHlwZSk7cmV0dXJuIGN8fChjPW5ldyB0aGlzLmNvbnN0cnVjdG9yKGIuY3VycmVudFRhcmdldCx0aGlzLmdldERlbGVnYXRlT3B0aW9ucygpKSxhKGIuY3VycmVudFRhcmdldCkuZGF0YSgiYnMuIit0aGlzLnR5cGUsYykpLGIgaW5zdGFuY2VvZiBhLkV2ZW50JiYoYy5pblN0YXRlWyJmb2N1c2luIj09Yi50eXBlPyJmb2N1cyI6ImhvdmVyIl09ITApLGMudGlwKCkuaGFzQ2xhc3MoImluIil8fCJpbiI9PWMuaG92ZXJTdGF0ZT92b2lkKGMuaG92ZXJTdGF0ZT0iaW4iKTooY2xlYXJUaW1lb3V0KGMudGltZW91dCksYy5ob3ZlclN0YXRlPSJpbiIsYy5vcHRpb25zLmRlbGF5JiZjLm9wdGlvbnMuZGVsYXkuc2hvdz92b2lkKGMudGltZW91dD1zZXRUaW1lb3V0KGZ1bmN0aW9uKCl7ImluIj09Yy5ob3ZlclN0YXRlJiZjLnNob3coKX0sYy5vcHRpb25zLmRlbGF5LnNob3cpKTpjLnNob3coKSl9LGMucHJvdG90eXBlLmlzSW5TdGF0ZVRydWU9ZnVuY3Rpb24oKXtmb3IodmFyIGEgaW4gdGhpcy5pblN0YXRlKWlmKHRoaXMuaW5TdGF0ZVthXSlyZXR1cm4hMDtyZXR1cm4hMX0sYy5wcm90b3R5cGUubGVhdmU9ZnVuY3Rpb24oYil7dmFyIGM9YiBpbnN0YW5jZW9mIHRoaXMuY29uc3RydWN0b3I/YjphKGIuY3VycmVudFRhcmdldCkuZGF0YSgiYnMuIit0aGlzLnR5cGUpO3JldHVybiBjfHwoYz1uZXcgdGhpcy5jb25zdHJ1Y3RvcihiLmN1cnJlbnRUYXJnZXQsdGhpcy5nZXREZWxlZ2F0ZU9wdGlvbnMoKSksYShiLmN1cnJlbnRUYXJnZXQpLmRhdGEoImJzLiIrdGhpcy50eXBlLGMpKSxiIGluc3RhbmNlb2YgYS5FdmVudCYmKGMuaW5TdGF0ZVsiZm9jdXNvdXQiPT1iLnR5cGU/ImZvY3VzIjoiaG92ZXIiXT0hMSksYy5pc0luU3RhdGVUcnVlKCk/dm9pZCAwOihjbGVhclRpbWVvdXQoYy50aW1lb3V0KSxjLmhvdmVyU3RhdGU9Im91dCIsYy5vcHRpb25zLmRlbGF5JiZjLm9wdGlvbnMuZGVsYXkuaGlkZT92b2lkKGMudGltZW91dD1zZXRUaW1lb3V0KGZ1bmN0aW9uKCl7Im91dCI9PWMuaG92ZXJTdGF0ZSYmYy5oaWRlKCl9LGMub3B0aW9ucy5kZWxheS5oaWRlKSk6Yy5oaWRlKCkpfSxjLnByb3RvdHlwZS5zaG93PWZ1bmN0aW9uKCl7dmFyIGI9YS5FdmVudCgic2hvdy5icy4iK3RoaXMudHlwZSk7aWYodGhpcy5oYXNDb250ZW50KCkmJnRoaXMuZW5hYmxlZCl7dGhpcy4kZWxlbWVudC50cmlnZ2VyKGIpO3ZhciBkPWEuY29udGFpbnModGhpcy4kZWxlbWVudFswXS5vd25lckRvY3VtZW50LmRvY3VtZW50RWxlbWVudCx0aGlzLiRlbGVtZW50WzBdKTtpZihiLmlzRGVmYXVsdFByZXZlbnRlZCgpfHwhZClyZXR1cm47dmFyIGU9dGhpcyxmPXRoaXMudGlwKCksZz10aGlzLmdldFVJRCh0aGlzLnR5cGUpO3RoaXMuc2V0Q29udGVudCgpLGYuYXR0cigiaWQiLGcpLHRoaXMuJGVsZW1lbnQuYXR0cigiYXJpYS1kZXNjcmliZWRieSIsZyksdGhpcy5vcHRpb25zLmFuaW1hdGlvbiYmZi5hZGRDbGFzcygiZmFkZSIpO3ZhciBoPSJmdW5jdGlvbiI9PXR5cGVvZiB0aGlzLm9wdGlvbnMucGxhY2VtZW50P3RoaXMub3B0aW9ucy5wbGFjZW1lbnQuY2FsbCh0aGlzLGZbMF0sdGhpcy4kZWxlbWVudFswXSk6dGhpcy5vcHRpb25zLnBsYWNlbWVudCxpPS9ccz9hdXRvP1xzPy9pLGo9aS50ZXN0KGgpO2omJihoPWgucmVwbGFjZShpLCIiKXx8InRvcCIpLGYuZGV0YWNoKCkuY3NzKHt0b3A6MCxsZWZ0OjAsZGlzcGxheToiYmxvY2sifSkuYWRkQ2xhc3MoaCkuZGF0YSgiYnMuIit0aGlzLnR5cGUsdGhpcyksdGhpcy5vcHRpb25zLmNvbnRhaW5lcj9mLmFwcGVuZFRvKHRoaXMub3B0aW9ucy5jb250YWluZXIpOmYuaW5zZXJ0QWZ0ZXIodGhpcy4kZWxlbWVudCksdGhpcy4kZWxlbWVudC50cmlnZ2VyKCJpbnNlcnRlZC5icy4iK3RoaXMudHlwZSk7dmFyIGs9dGhpcy5nZXRQb3NpdGlvbigpLGw9ZlswXS5vZmZzZXRXaWR0aCxtPWZbMF0ub2Zmc2V0SGVpZ2h0O2lmKGope3ZhciBuPWgsbz10aGlzLmdldFBvc2l0aW9uKHRoaXMuJHZpZXdwb3J0KTtoPSJib3R0b20iPT1oJiZrLmJvdHRvbSttPm8uYm90dG9tPyJ0b3AiOiJ0b3AiPT1oJiZrLnRvcC1tPG8udG9wPyJib3R0b20iOiJyaWdodCI9PWgmJmsucmlnaHQrbD5vLndpZHRoPyJsZWZ0IjoibGVmdCI9PWgmJmsubGVmdC1sPG8ubGVmdD8icmlnaHQiOmgsZi5yZW1vdmVDbGFzcyhuKS5hZGRDbGFzcyhoKX12YXIgcD10aGlzLmdldENhbGN1bGF0ZWRPZmZzZXQoaCxrLGwsbSk7dGhpcy5hcHBseVBsYWNlbWVudChwLGgpO3ZhciBxPWZ1bmN0aW9uKCl7dmFyIGE9ZS5ob3ZlclN0YXRlO2UuJGVsZW1lbnQudHJpZ2dlcigic2hvd24uYnMuIitlLnR5cGUpLGUuaG92ZXJTdGF0ZT1udWxsLCJvdXQiPT1hJiZlLmxlYXZlKGUpfTthLnN1cHBvcnQudHJhbnNpdGlvbiYmdGhpcy4kdGlwLmhhc0NsYXNzKCJmYWRlIik/Zi5vbmUoImJzVHJhbnNpdGlvbkVuZCIscSkuZW11bGF0ZVRyYW5zaXRpb25FbmQoYy5UUkFOU0lUSU9OX0RVUkFUSU9OKTpxKCl9fSxjLnByb3RvdHlwZS5hcHBseVBsYWNlbWVudD1mdW5jdGlvbihiLGMpe3ZhciBkPXRoaXMudGlwKCksZT1kWzBdLm9mZnNldFdpZHRoLGY9ZFswXS5vZmZzZXRIZWlnaHQsZz1wYXJzZUludChkLmNzcygibWFyZ2luLXRvcCIpLDEwKSxoPXBhcnNlSW50KGQuY3NzKCJtYXJnaW4tbGVmdCIpLDEwKTtpc05hTihnKSYmKGc9MCksaXNOYU4oaCkmJihoPTApLGIudG9wKz1nLGIubGVmdCs9aCxhLm9mZnNldC5zZXRPZmZzZXQoZFswXSxhLmV4dGVuZCh7dXNpbmc6ZnVuY3Rpb24oYSl7ZC5jc3Moe3RvcDpNYXRoLnJvdW5kKGEudG9wKSxsZWZ0Ok1hdGgucm91bmQoYS5sZWZ0KX0pfX0sYiksMCksZC5hZGRDbGFzcygiaW4iKTt2YXIgaT1kWzBdLm9mZnNldFdpZHRoLGo9ZFswXS5vZmZzZXRIZWlnaHQ7InRvcCI9PWMmJmohPWYmJihiLnRvcD1iLnRvcCtmLWopO3ZhciBrPXRoaXMuZ2V0Vmlld3BvcnRBZGp1c3RlZERlbHRhKGMsYixpLGopO2subGVmdD9iLmxlZnQrPWsubGVmdDpiLnRvcCs9ay50b3A7dmFyIGw9L3RvcHxib3R0b20vLnRlc3QoYyksbT1sPzIqay5sZWZ0LWUraToyKmsudG9wLWYraixuPWw/Im9mZnNldFdpZHRoIjoib2Zmc2V0SGVpZ2h0IjtkLm9mZnNldChiKSx0aGlzLnJlcGxhY2VBcnJvdyhtLGRbMF1bbl0sbCl9LGMucHJvdG90eXBlLnJlcGxhY2VBcnJvdz1mdW5jdGlvbihhLGIsYyl7dGhpcy5hcnJvdygpLmNzcyhjPyJsZWZ0IjoidG9wIiw1MCooMS1hL2IpKyIlIikuY3NzKGM/InRvcCI6ImxlZnQiLCIiKX0sYy5wcm90b3R5cGUuc2V0Q29udGVudD1mdW5jdGlvbigpe3ZhciBhPXRoaXMudGlwKCksYj10aGlzLmdldFRpdGxlKCk7YS5maW5kKCIudG9vbHRpcC1pbm5lciIpW3RoaXMub3B0aW9ucy5odG1sPyJodG1sIjoidGV4dCJdKGIpLGEucmVtb3ZlQ2xhc3MoImZhZGUgaW4gdG9wIGJvdHRvbSBsZWZ0IHJpZ2h0Iil9LGMucHJvdG90eXBlLmhpZGU9ZnVuY3Rpb24oYil7ZnVuY3Rpb24gZCgpeyJpbiIhPWUuaG92ZXJTdGF0ZSYmZi5kZXRhY2goKSxlLiRlbGVtZW50LnJlbW92ZUF0dHIoImFyaWEtZGVzY3JpYmVkYnkiKS50cmlnZ2VyKCJoaWRkZW4uYnMuIitlLnR5cGUpLGImJmIoKX12YXIgZT10aGlzLGY9YSh0aGlzLiR0aXApLGc9YS5FdmVudCgiaGlkZS5icy4iK3RoaXMudHlwZSk7cmV0dXJuIHRoaXMuJGVsZW1lbnQudHJpZ2dlcihnKSxnLmlzRGVmYXVsdFByZXZlbnRlZCgpP3ZvaWQgMDooZi5yZW1vdmVDbGFzcygiaW4iKSxhLnN1cHBvcnQudHJhbnNpdGlvbiYmZi5oYXNDbGFzcygiZmFkZSIpP2Yub25lKCJic1RyYW5zaXRpb25FbmQiLGQpLmVtdWxhdGVUcmFuc2l0aW9uRW5kKGMuVFJBTlNJVElPTl9EVVJBVElPTik6ZCgpLHRoaXMuaG92ZXJTdGF0ZT1udWxsLHRoaXMpfSxjLnByb3RvdHlwZS5maXhUaXRsZT1mdW5jdGlvbigpe3ZhciBhPXRoaXMuJGVsZW1lbnQ7KGEuYXR0cigidGl0bGUiKXx8InN0cmluZyIhPXR5cGVvZiBhLmF0dHIoImRhdGEtb3JpZ2luYWwtdGl0bGUiKSkmJmEuYXR0cigiZGF0YS1vcmlnaW5hbC10aXRsZSIsYS5hdHRyKCJ0aXRsZSIpfHwiIikuYXR0cigidGl0bGUiLCIiKX0sYy5wcm90b3R5cGUuaGFzQ29udGVudD1mdW5jdGlvbigpe3JldHVybiB0aGlzLmdldFRpdGxlKCl9LGMucHJvdG90eXBlLmdldFBvc2l0aW9uPWZ1bmN0aW9uKGIpe2I9Ynx8dGhpcy4kZWxlbWVudDt2YXIgYz1iWzBdLGQ9IkJPRFkiPT1jLnRhZ05hbWUsZT1jLmdldEJvdW5kaW5nQ2xpZW50UmVjdCgpO251bGw9PWUud2lkdGgmJihlPWEuZXh0ZW5kKHt9LGUse3dpZHRoOmUucmlnaHQtZS5sZWZ0LGhlaWdodDplLmJvdHRvbS1lLnRvcH0pKTt2YXIgZj1kP3t0b3A6MCxsZWZ0OjB9OmIub2Zmc2V0KCksZz17c2Nyb2xsOmQ/ZG9jdW1lbnQuZG9jdW1lbnRFbGVtZW50LnNjcm9sbFRvcHx8ZG9jdW1lbnQuYm9keS5zY3JvbGxUb3A6Yi5zY3JvbGxUb3AoKX0saD1kP3t3aWR0aDphKHdpbmRvdykud2lkdGgoKSxoZWlnaHQ6YSh3aW5kb3cpLmhlaWdodCgpfTpudWxsO3JldHVybiBhLmV4dGVuZCh7fSxlLGcsaCxmKX0sYy5wcm90b3R5cGUuZ2V0Q2FsY3VsYXRlZE9mZnNldD1mdW5jdGlvbihhLGIsYyxkKXtyZXR1cm4iYm90dG9tIj09YT97dG9wOmIudG9wK2IuaGVpZ2h0LGxlZnQ6Yi5sZWZ0K2Iud2lkdGgvMi1jLzJ9OiJ0b3AiPT1hP3t0b3A6Yi50b3AtZCxsZWZ0OmIubGVmdCtiLndpZHRoLzItYy8yfToibGVmdCI9PWE/e3RvcDpiLnRvcCtiLmhlaWdodC8yLWQvMixsZWZ0OmIubGVmdC1jfTp7dG9wOmIudG9wK2IuaGVpZ2h0LzItZC8yLGxlZnQ6Yi5sZWZ0K2Iud2lkdGh9fSxjLnByb3RvdHlwZS5nZXRWaWV3cG9ydEFkanVzdGVkRGVsdGE9ZnVuY3Rpb24oYSxiLGMsZCl7dmFyIGU9e3RvcDowLGxlZnQ6MH07aWYoIXRoaXMuJHZpZXdwb3J0KXJldHVybiBlO3ZhciBmPXRoaXMub3B0aW9ucy52aWV3cG9ydCYmdGhpcy5vcHRpb25zLnZpZXdwb3J0LnBhZGRpbmd8fDAsZz10aGlzLmdldFBvc2l0aW9uKHRoaXMuJHZpZXdwb3J0KTtpZigvcmlnaHR8bGVmdC8udGVzdChhKSl7dmFyIGg9Yi50b3AtZi1nLnNjcm9sbCxpPWIudG9wK2YtZy5zY3JvbGwrZDtoPGcudG9wP2UudG9wPWcudG9wLWg6aT5nLnRvcCtnLmhlaWdodCYmKGUudG9wPWcudG9wK2cuaGVpZ2h0LWkpfWVsc2V7dmFyIGo9Yi5sZWZ0LWYsaz1iLmxlZnQrZitjO2o8Zy5sZWZ0P2UubGVmdD1nLmxlZnQtajprPmcucmlnaHQmJihlLmxlZnQ9Zy5sZWZ0K2cud2lkdGgtayl9cmV0dXJuIGV9LGMucHJvdG90eXBlLmdldFRpdGxlPWZ1bmN0aW9uKCl7dmFyIGEsYj10aGlzLiRlbGVtZW50LGM9dGhpcy5vcHRpb25zO3JldHVybiBhPWIuYXR0cigiZGF0YS1vcmlnaW5hbC10aXRsZSIpfHwoImZ1bmN0aW9uIj09dHlwZW9mIGMudGl0bGU/Yy50aXRsZS5jYWxsKGJbMF0pOmMudGl0bGUpfSxjLnByb3RvdHlwZS5nZXRVSUQ9ZnVuY3Rpb24oYSl7ZG8gYSs9fn4oMWU2Kk1hdGgucmFuZG9tKCkpO3doaWxlKGRvY3VtZW50LmdldEVsZW1lbnRCeUlkKGEpKTtyZXR1cm4gYX0sYy5wcm90b3R5cGUudGlwPWZ1bmN0aW9uKCl7aWYoIXRoaXMuJHRpcCYmKHRoaXMuJHRpcD1hKHRoaXMub3B0aW9ucy50ZW1wbGF0ZSksMSE9dGhpcy4kdGlwLmxlbmd0aCkpdGhyb3cgbmV3IEVycm9yKHRoaXMudHlwZSsiIGB0ZW1wbGF0ZWAgb3B0aW9uIG11c3QgY29uc2lzdCBvZiBleGFjdGx5IDEgdG9wLWxldmVsIGVsZW1lbnQhIik7cmV0dXJuIHRoaXMuJHRpcH0sYy5wcm90b3R5cGUuYXJyb3c9ZnVuY3Rpb24oKXtyZXR1cm4gdGhpcy4kYXJyb3c9dGhpcy4kYXJyb3d8fHRoaXMudGlwKCkuZmluZCgiLnRvb2x0aXAtYXJyb3ciKX0sYy5wcm90b3R5cGUuZW5hYmxlPWZ1bmN0aW9uKCl7dGhpcy5lbmFibGVkPSEwfSxjLnByb3RvdHlwZS5kaXNhYmxlPWZ1bmN0aW9uKCl7dGhpcy5lbmFibGVkPSExfSxjLnByb3RvdHlwZS50b2dnbGVFbmFibGVkPWZ1bmN0aW9uKCl7dGhpcy5lbmFibGVkPSF0aGlzLmVuYWJsZWR9LGMucHJvdG90eXBlLnRvZ2dsZT1mdW5jdGlvbihiKXt2YXIgYz10aGlzO2ImJihjPWEoYi5jdXJyZW50VGFyZ2V0KS5kYXRhKCJicy4iK3RoaXMudHlwZSksY3x8KGM9bmV3IHRoaXMuY29uc3RydWN0b3IoYi5jdXJyZW50VGFyZ2V0LHRoaXMuZ2V0RGVsZWdhdGVPcHRpb25zKCkpLGEoYi5jdXJyZW50VGFyZ2V0KS5kYXRhKCJicy4iK3RoaXMudHlwZSxjKSkpLGI/KGMuaW5TdGF0ZS5jbGljaz0hYy5pblN0YXRlLmNsaWNrLGMuaXNJblN0YXRlVHJ1ZSgpP2MuZW50ZXIoYyk6Yy5sZWF2ZShjKSk6Yy50aXAoKS5oYXNDbGFzcygiaW4iKT9jLmxlYXZlKGMpOmMuZW50ZXIoYyl9LGMucHJvdG90eXBlLmRlc3Ryb3k9ZnVuY3Rpb24oKXt2YXIgYT10aGlzO2NsZWFyVGltZW91dCh0aGlzLnRpbWVvdXQpLHRoaXMuaGlkZShmdW5jdGlvbigpe2EuJGVsZW1lbnQub2ZmKCIuIithLnR5cGUpLnJlbW92ZURhdGEoImJzLiIrYS50eXBlKSxhLiR0aXAmJmEuJHRpcC5kZXRhY2goKSxhLiR0aXA9bnVsbCxhLiRhcnJvdz1udWxsLGEuJHZpZXdwb3J0PW51bGx9KX07dmFyIGQ9YS5mbi50b29sdGlwO2EuZm4udG9vbHRpcD1iLGEuZm4udG9vbHRpcC5Db25zdHJ1Y3Rvcj1jLGEuZm4udG9vbHRpcC5ub0NvbmZsaWN0PWZ1bmN0aW9uKCl7cmV0dXJuIGEuZm4udG9vbHRpcD1kLHRoaXN9fShqUXVlcnkpLCtmdW5jdGlvbihhKXsidXNlIHN0cmljdCI7ZnVuY3Rpb24gYihiKXtyZXR1cm4gdGhpcy5lYWNoKGZ1bmN0aW9uKCl7dmFyIGQ9YSh0aGlzKSxlPWQuZGF0YSgiYnMucG9wb3ZlciIpLGY9Im9iamVjdCI9PXR5cGVvZiBiJiZiOyhlfHwhL2Rlc3Ryb3l8aGlkZS8udGVzdChiKSkmJihlfHxkLmRhdGEoImJzLnBvcG92ZXIiLGU9bmV3IGModGhpcyxmKSksInN0cmluZyI9PXR5cGVvZiBiJiZlW2JdKCkpfSl9dmFyIGM9ZnVuY3Rpb24oYSxiKXt0aGlzLmluaXQoInBvcG92ZXIiLGEsYil9O2lmKCFhLmZuLnRvb2x0aXApdGhyb3cgbmV3IEVycm9yKCJQb3BvdmVyIHJlcXVpcmVzIHRvb2x0aXAuanMiKTtjLlZFUlNJT049IjMuMy41IixjLkRFRkFVTFRTPWEuZXh0ZW5kKHt9LGEuZm4udG9vbHRpcC5Db25zdHJ1Y3Rvci5ERUZBVUxUUyx7cGxhY2VtZW50OiJyaWdodCIsdHJpZ2dlcjoiY2xpY2siLGNvbnRlbnQ6IiIsdGVtcGxhdGU6JzxkaXYgY2xhc3M9InBvcG92ZXIiIHJvbGU9InRvb2x0aXAiPjxkaXYgY2xhc3M9ImFycm93Ij48L2Rpdj48aDMgY2xhc3M9InBvcG92ZXItdGl0bGUiPjwvaDM+PGRpdiBjbGFzcz0icG9wb3Zlci1jb250ZW50Ij48L2Rpdj48L2Rpdj4nfSksYy5wcm90b3R5cGU9YS5leHRlbmQoe30sYS5mbi50b29sdGlwLkNvbnN0cnVjdG9yLnByb3RvdHlwZSksYy5wcm90b3R5cGUuY29uc3RydWN0b3I9YyxjLnByb3RvdHlwZS5nZXREZWZhdWx0cz1mdW5jdGlvbigpe3JldHVybiBjLkRFRkFVTFRTfSxjLnByb3RvdHlwZS5zZXRDb250ZW50PWZ1bmN0aW9uKCl7dmFyIGE9dGhpcy50aXAoKSxiPXRoaXMuZ2V0VGl0bGUoKSxjPXRoaXMuZ2V0Q29udGVudCgpO2EuZmluZCgiLnBvcG92ZXItdGl0bGUiKVt0aGlzLm9wdGlvbnMuaHRtbD8iaHRtbCI6InRleHQiXShiKSxhLmZpbmQoIi5wb3BvdmVyLWNvbnRlbnQiKS5jaGlsZHJlbigpLmRldGFjaCgpLmVuZCgpW3RoaXMub3B0aW9ucy5odG1sPyJzdHJpbmciPT10eXBlb2YgYz8iaHRtbCI6ImFwcGVuZCI6InRleHQiXShjKSxhLnJlbW92ZUNsYXNzKCJmYWRlIHRvcCBib3R0b20gbGVmdCByaWdodCBpbiIpLGEuZmluZCgiLnBvcG92ZXItdGl0bGUiKS5odG1sKCl8fGEuZmluZCgiLnBvcG92ZXItdGl0bGUiKS5oaWRlKCl9LGMucHJvdG90eXBlLmhhc0NvbnRlbnQ9ZnVuY3Rpb24oKXtyZXR1cm4gdGhpcy5nZXRUaXRsZSgpfHx0aGlzLmdldENvbnRlbnQoKX0sYy5wcm90b3R5cGUuZ2V0Q29udGVudD1mdW5jdGlvbigpe3ZhciBhPXRoaXMuJGVsZW1lbnQsYj10aGlzLm9wdGlvbnM7cmV0dXJuIGEuYXR0cigiZGF0YS1jb250ZW50Iil8fCgiZnVuY3Rpb24iPT10eXBlb2YgYi5jb250ZW50P2IuY29udGVudC5jYWxsKGFbMF0pOmIuY29udGVudCl9LGMucHJvdG90eXBlLmFycm93PWZ1bmN0aW9uKCl7cmV0dXJuIHRoaXMuJGFycm93PXRoaXMuJGFycm93fHx0aGlzLnRpcCgpLmZpbmQoIi5hcnJvdyIpfTt2YXIgZD1hLmZuLnBvcG92ZXI7YS5mbi5wb3BvdmVyPWIsYS5mbi5wb3BvdmVyLkNvbnN0cnVjdG9yPWMsYS5mbi5wb3BvdmVyLm5vQ29uZmxpY3Q9ZnVuY3Rpb24oKXtyZXR1cm4gYS5mbi5wb3BvdmVyPWQsdGhpc319KGpRdWVyeSksK2Z1bmN0aW9uKGEpeyJ1c2Ugc3RyaWN0IjtmdW5jdGlvbiBiKGMsZCl7dGhpcy4kYm9keT1hKGRvY3VtZW50LmJvZHkpLHRoaXMuJHNjcm9sbEVsZW1lbnQ9YShhKGMpLmlzKGRvY3VtZW50LmJvZHkpP3dpbmRvdzpjKSx0aGlzLm9wdGlvbnM9YS5leHRlbmQoe30sYi5ERUZBVUxUUyxkKSx0aGlzLnNlbGVjdG9yPSh0aGlzLm9wdGlvbnMudGFyZ2V0fHwiIikrIiAubmF2IGxpID4gYSIsdGhpcy5vZmZzZXRzPVtdLHRoaXMudGFyZ2V0cz1bXSx0aGlzLmFjdGl2ZVRhcmdldD1udWxsLHRoaXMuc2Nyb2xsSGVpZ2h0PTAsdGhpcy4kc2Nyb2xsRWxlbWVudC5vbigic2Nyb2xsLmJzLnNjcm9sbHNweSIsYS5wcm94eSh0aGlzLnByb2Nlc3MsdGhpcykpLHRoaXMucmVmcmVzaCgpLHRoaXMucHJvY2VzcygpfWZ1bmN0aW9uIGMoYyl7cmV0dXJuIHRoaXMuZWFjaChmdW5jdGlvbigpe3ZhciBkPWEodGhpcyksZT1kLmRhdGEoImJzLnNjcm9sbHNweSIpLGY9Im9iamVjdCI9PXR5cGVvZiBjJiZjO2V8fGQuZGF0YSgiYnMuc2Nyb2xsc3B5IixlPW5ldyBiKHRoaXMsZikpLCJzdHJpbmciPT10eXBlb2YgYyYmZVtjXSgpfSl9Yi5WRVJTSU9OPSIzLjMuNSIsYi5ERUZBVUxUUz17b2Zmc2V0OjEwfSxiLnByb3RvdHlwZS5nZXRTY3JvbGxIZWlnaHQ9ZnVuY3Rpb24oKXtyZXR1cm4gdGhpcy4kc2Nyb2xsRWxlbWVudFswXS5zY3JvbGxIZWlnaHR8fE1hdGgubWF4KHRoaXMuJGJvZHlbMF0uc2Nyb2xsSGVpZ2h0LGRvY3VtZW50LmRvY3VtZW50RWxlbWVudC5zY3JvbGxIZWlnaHQpfSxiLnByb3RvdHlwZS5yZWZyZXNoPWZ1bmN0aW9uKCl7dmFyIGI9dGhpcyxjPSJvZmZzZXQiLGQ9MDt0aGlzLm9mZnNldHM9W10sdGhpcy50YXJnZXRzPVtdLHRoaXMuc2Nyb2xsSGVpZ2h0PXRoaXMuZ2V0U2Nyb2xsSGVpZ2h0KCksYS5pc1dpbmRvdyh0aGlzLiRzY3JvbGxFbGVtZW50WzBdKXx8KGM9InBvc2l0aW9uIixkPXRoaXMuJHNjcm9sbEVsZW1lbnQuc2Nyb2xsVG9wKCkpLHRoaXMuJGJvZHkuZmluZCh0aGlzLnNlbGVjdG9yKS5tYXAoZnVuY3Rpb24oKXt2YXIgYj1hKHRoaXMpLGU9Yi5kYXRhKCJ0YXJnZXQiKXx8Yi5hdHRyKCJocmVmIiksZj0vXiMuLy50ZXN0KGUpJiZhKGUpO3JldHVybiBmJiZmLmxlbmd0aCYmZi5pcygiOnZpc2libGUiKSYmW1tmW2NdKCkudG9wK2QsZV1dfHxudWxsfSkuc29ydChmdW5jdGlvbihhLGIpe3JldHVybiBhWzBdLWJbMF19KS5lYWNoKGZ1bmN0aW9uKCl7Yi5vZmZzZXRzLnB1c2godGhpc1swXSksYi50YXJnZXRzLnB1c2godGhpc1sxXSl9KX0sYi5wcm90b3R5cGUucHJvY2Vzcz1mdW5jdGlvbigpe3ZhciBhLGI9dGhpcy4kc2Nyb2xsRWxlbWVudC5zY3JvbGxUb3AoKSt0aGlzLm9wdGlvbnMub2Zmc2V0LGM9dGhpcy5nZXRTY3JvbGxIZWlnaHQoKSxkPXRoaXMub3B0aW9ucy5vZmZzZXQrYy10aGlzLiRzY3JvbGxFbGVtZW50LmhlaWdodCgpLGU9dGhpcy5vZmZzZXRzLGY9dGhpcy50YXJnZXRzLGc9dGhpcy5hY3RpdmVUYXJnZXQ7aWYodGhpcy5zY3JvbGxIZWlnaHQhPWMmJnRoaXMucmVmcmVzaCgpLGI+PWQpcmV0dXJuIGchPShhPWZbZi5sZW5ndGgtMV0pJiZ0aGlzLmFjdGl2YXRlKGEpO2lmKGcmJmI8ZVswXSlyZXR1cm4gdGhpcy5hY3RpdmVUYXJnZXQ9bnVsbCx0aGlzLmNsZWFyKCk7Zm9yKGE9ZS5sZW5ndGg7YS0tOylnIT1mW2FdJiZiPj1lW2FdJiYodm9pZCAwPT09ZVthKzFdfHxiPGVbYSsxXSkmJnRoaXMuYWN0aXZhdGUoZlthXSl9LGIucHJvdG90eXBlLmFjdGl2YXRlPWZ1bmN0aW9uKGIpe3RoaXMuYWN0aXZlVGFyZ2V0PWIsdGhpcy5jbGVhcigpO3ZhciBjPXRoaXMuc2VsZWN0b3IrJ1tkYXRhLXRhcmdldD0iJytiKyciXSwnK3RoaXMuc2VsZWN0b3IrJ1tocmVmPSInK2IrJyJdJyxkPWEoYykucGFyZW50cygibGkiKS5hZGRDbGFzcygiYWN0aXZlIik7ZC5wYXJlbnQoIi5kcm9wZG93bi1tZW51IikubGVuZ3RoJiYoZD1kLmNsb3Nlc3QoImxpLmRyb3Bkb3duIikuYWRkQ2xhc3MoImFjdGl2ZSIpKSwKZC50cmlnZ2VyKCJhY3RpdmF0ZS5icy5zY3JvbGxzcHkiKX0sYi5wcm90b3R5cGUuY2xlYXI9ZnVuY3Rpb24oKXthKHRoaXMuc2VsZWN0b3IpLnBhcmVudHNVbnRpbCh0aGlzLm9wdGlvbnMudGFyZ2V0LCIuYWN0aXZlIikucmVtb3ZlQ2xhc3MoImFjdGl2ZSIpfTt2YXIgZD1hLmZuLnNjcm9sbHNweTthLmZuLnNjcm9sbHNweT1jLGEuZm4uc2Nyb2xsc3B5LkNvbnN0cnVjdG9yPWIsYS5mbi5zY3JvbGxzcHkubm9Db25mbGljdD1mdW5jdGlvbigpe3JldHVybiBhLmZuLnNjcm9sbHNweT1kLHRoaXN9LGEod2luZG93KS5vbigibG9hZC5icy5zY3JvbGxzcHkuZGF0YS1hcGkiLGZ1bmN0aW9uKCl7YSgnW2RhdGEtc3B5PSJzY3JvbGwiXScpLmVhY2goZnVuY3Rpb24oKXt2YXIgYj1hKHRoaXMpO2MuY2FsbChiLGIuZGF0YSgpKX0pfSl9KGpRdWVyeSksK2Z1bmN0aW9uKGEpeyJ1c2Ugc3RyaWN0IjtmdW5jdGlvbiBiKGIpe3JldHVybiB0aGlzLmVhY2goZnVuY3Rpb24oKXt2YXIgZD1hKHRoaXMpLGU9ZC5kYXRhKCJicy50YWIiKTtlfHxkLmRhdGEoImJzLnRhYiIsZT1uZXcgYyh0aGlzKSksInN0cmluZyI9PXR5cGVvZiBiJiZlW2JdKCl9KX12YXIgYz1mdW5jdGlvbihiKXt0aGlzLmVsZW1lbnQ9YShiKX07Yy5WRVJTSU9OPSIzLjMuNSIsYy5UUkFOU0lUSU9OX0RVUkFUSU9OPTE1MCxjLnByb3RvdHlwZS5zaG93PWZ1bmN0aW9uKCl7dmFyIGI9dGhpcy5lbGVtZW50LGM9Yi5jbG9zZXN0KCJ1bDpub3QoLmRyb3Bkb3duLW1lbnUpIiksZD1iLmRhdGEoInRhcmdldCIpO2lmKGR8fChkPWIuYXR0cigiaHJlZiIpLGQ9ZCYmZC5yZXBsYWNlKC8uKig/PSNbXlxzXSokKS8sIiIpKSwhYi5wYXJlbnQoImxpIikuaGFzQ2xhc3MoImFjdGl2ZSIpKXt2YXIgZT1jLmZpbmQoIi5hY3RpdmU6bGFzdCBhIiksZj1hLkV2ZW50KCJoaWRlLmJzLnRhYiIse3JlbGF0ZWRUYXJnZXQ6YlswXX0pLGc9YS5FdmVudCgic2hvdy5icy50YWIiLHtyZWxhdGVkVGFyZ2V0OmVbMF19KTtpZihlLnRyaWdnZXIoZiksYi50cmlnZ2VyKGcpLCFnLmlzRGVmYXVsdFByZXZlbnRlZCgpJiYhZi5pc0RlZmF1bHRQcmV2ZW50ZWQoKSl7dmFyIGg9YShkKTt0aGlzLmFjdGl2YXRlKGIuY2xvc2VzdCgibGkiKSxjKSx0aGlzLmFjdGl2YXRlKGgsaC5wYXJlbnQoKSxmdW5jdGlvbigpe2UudHJpZ2dlcih7dHlwZToiaGlkZGVuLmJzLnRhYiIscmVsYXRlZFRhcmdldDpiWzBdfSksYi50cmlnZ2VyKHt0eXBlOiJzaG93bi5icy50YWIiLHJlbGF0ZWRUYXJnZXQ6ZVswXX0pfSl9fX0sYy5wcm90b3R5cGUuYWN0aXZhdGU9ZnVuY3Rpb24oYixkLGUpe2Z1bmN0aW9uIGYoKXtnLnJlbW92ZUNsYXNzKCJhY3RpdmUiKS5maW5kKCI+IC5kcm9wZG93bi1tZW51ID4gLmFjdGl2ZSIpLnJlbW92ZUNsYXNzKCJhY3RpdmUiKS5lbmQoKS5maW5kKCdbZGF0YS10b2dnbGU9InRhYiJdJykuYXR0cigiYXJpYS1leHBhbmRlZCIsITEpLGIuYWRkQ2xhc3MoImFjdGl2ZSIpLmZpbmQoJ1tkYXRhLXRvZ2dsZT0idGFiIl0nKS5hdHRyKCJhcmlhLWV4cGFuZGVkIiwhMCksaD8oYlswXS5vZmZzZXRXaWR0aCxiLmFkZENsYXNzKCJpbiIpKTpiLnJlbW92ZUNsYXNzKCJmYWRlIiksYi5wYXJlbnQoIi5kcm9wZG93bi1tZW51IikubGVuZ3RoJiZiLmNsb3Nlc3QoImxpLmRyb3Bkb3duIikuYWRkQ2xhc3MoImFjdGl2ZSIpLmVuZCgpLmZpbmQoJ1tkYXRhLXRvZ2dsZT0idGFiIl0nKS5hdHRyKCJhcmlhLWV4cGFuZGVkIiwhMCksZSYmZSgpfXZhciBnPWQuZmluZCgiPiAuYWN0aXZlIiksaD1lJiZhLnN1cHBvcnQudHJhbnNpdGlvbiYmKGcubGVuZ3RoJiZnLmhhc0NsYXNzKCJmYWRlIil8fCEhZC5maW5kKCI+IC5mYWRlIikubGVuZ3RoKTtnLmxlbmd0aCYmaD9nLm9uZSgiYnNUcmFuc2l0aW9uRW5kIixmKS5lbXVsYXRlVHJhbnNpdGlvbkVuZChjLlRSQU5TSVRJT05fRFVSQVRJT04pOmYoKSxnLnJlbW92ZUNsYXNzKCJpbiIpfTt2YXIgZD1hLmZuLnRhYjthLmZuLnRhYj1iLGEuZm4udGFiLkNvbnN0cnVjdG9yPWMsYS5mbi50YWIubm9Db25mbGljdD1mdW5jdGlvbigpe3JldHVybiBhLmZuLnRhYj1kLHRoaXN9O3ZhciBlPWZ1bmN0aW9uKGMpe2MucHJldmVudERlZmF1bHQoKSxiLmNhbGwoYSh0aGlzKSwic2hvdyIpfTthKGRvY3VtZW50KS5vbigiY2xpY2suYnMudGFiLmRhdGEtYXBpIiwnW2RhdGEtdG9nZ2xlPSJ0YWIiXScsZSkub24oImNsaWNrLmJzLnRhYi5kYXRhLWFwaSIsJ1tkYXRhLXRvZ2dsZT0icGlsbCJdJyxlKX0oalF1ZXJ5KSwrZnVuY3Rpb24oYSl7InVzZSBzdHJpY3QiO2Z1bmN0aW9uIGIoYil7cmV0dXJuIHRoaXMuZWFjaChmdW5jdGlvbigpe3ZhciBkPWEodGhpcyksZT1kLmRhdGEoImJzLmFmZml4IiksZj0ib2JqZWN0Ij09dHlwZW9mIGImJmI7ZXx8ZC5kYXRhKCJicy5hZmZpeCIsZT1uZXcgYyh0aGlzLGYpKSwic3RyaW5nIj09dHlwZW9mIGImJmVbYl0oKX0pfXZhciBjPWZ1bmN0aW9uKGIsZCl7dGhpcy5vcHRpb25zPWEuZXh0ZW5kKHt9LGMuREVGQVVMVFMsZCksdGhpcy4kdGFyZ2V0PWEodGhpcy5vcHRpb25zLnRhcmdldCkub24oInNjcm9sbC5icy5hZmZpeC5kYXRhLWFwaSIsYS5wcm94eSh0aGlzLmNoZWNrUG9zaXRpb24sdGhpcykpLm9uKCJjbGljay5icy5hZmZpeC5kYXRhLWFwaSIsYS5wcm94eSh0aGlzLmNoZWNrUG9zaXRpb25XaXRoRXZlbnRMb29wLHRoaXMpKSx0aGlzLiRlbGVtZW50PWEoYiksdGhpcy5hZmZpeGVkPW51bGwsdGhpcy51bnBpbj1udWxsLHRoaXMucGlubmVkT2Zmc2V0PW51bGwsdGhpcy5jaGVja1Bvc2l0aW9uKCl9O2MuVkVSU0lPTj0iMy4zLjUiLGMuUkVTRVQ9ImFmZml4IGFmZml4LXRvcCBhZmZpeC1ib3R0b20iLGMuREVGQVVMVFM9e29mZnNldDowLHRhcmdldDp3aW5kb3d9LGMucHJvdG90eXBlLmdldFN0YXRlPWZ1bmN0aW9uKGEsYixjLGQpe3ZhciBlPXRoaXMuJHRhcmdldC5zY3JvbGxUb3AoKSxmPXRoaXMuJGVsZW1lbnQub2Zmc2V0KCksZz10aGlzLiR0YXJnZXQuaGVpZ2h0KCk7aWYobnVsbCE9YyYmInRvcCI9PXRoaXMuYWZmaXhlZClyZXR1cm4gYz5lPyJ0b3AiOiExO2lmKCJib3R0b20iPT10aGlzLmFmZml4ZWQpcmV0dXJuIG51bGwhPWM/ZSt0aGlzLnVucGluPD1mLnRvcD8hMToiYm90dG9tIjphLWQ+PWUrZz8hMToiYm90dG9tIjt2YXIgaD1udWxsPT10aGlzLmFmZml4ZWQsaT1oP2U6Zi50b3Asaj1oP2c6YjtyZXR1cm4gbnVsbCE9YyYmYz49ZT8idG9wIjpudWxsIT1kJiZpK2o+PWEtZD8iYm90dG9tIjohMX0sYy5wcm90b3R5cGUuZ2V0UGlubmVkT2Zmc2V0PWZ1bmN0aW9uKCl7aWYodGhpcy5waW5uZWRPZmZzZXQpcmV0dXJuIHRoaXMucGlubmVkT2Zmc2V0O3RoaXMuJGVsZW1lbnQucmVtb3ZlQ2xhc3MoYy5SRVNFVCkuYWRkQ2xhc3MoImFmZml4Iik7dmFyIGE9dGhpcy4kdGFyZ2V0LnNjcm9sbFRvcCgpLGI9dGhpcy4kZWxlbWVudC5vZmZzZXQoKTtyZXR1cm4gdGhpcy5waW5uZWRPZmZzZXQ9Yi50b3AtYX0sYy5wcm90b3R5cGUuY2hlY2tQb3NpdGlvbldpdGhFdmVudExvb3A9ZnVuY3Rpb24oKXtzZXRUaW1lb3V0KGEucHJveHkodGhpcy5jaGVja1Bvc2l0aW9uLHRoaXMpLDEpfSxjLnByb3RvdHlwZS5jaGVja1Bvc2l0aW9uPWZ1bmN0aW9uKCl7aWYodGhpcy4kZWxlbWVudC5pcygiOnZpc2libGUiKSl7dmFyIGI9dGhpcy4kZWxlbWVudC5oZWlnaHQoKSxkPXRoaXMub3B0aW9ucy5vZmZzZXQsZT1kLnRvcCxmPWQuYm90dG9tLGc9TWF0aC5tYXgoYShkb2N1bWVudCkuaGVpZ2h0KCksYShkb2N1bWVudC5ib2R5KS5oZWlnaHQoKSk7Im9iamVjdCIhPXR5cGVvZiBkJiYoZj1lPWQpLCJmdW5jdGlvbiI9PXR5cGVvZiBlJiYoZT1kLnRvcCh0aGlzLiRlbGVtZW50KSksImZ1bmN0aW9uIj09dHlwZW9mIGYmJihmPWQuYm90dG9tKHRoaXMuJGVsZW1lbnQpKTt2YXIgaD10aGlzLmdldFN0YXRlKGcsYixlLGYpO2lmKHRoaXMuYWZmaXhlZCE9aCl7bnVsbCE9dGhpcy51bnBpbiYmdGhpcy4kZWxlbWVudC5jc3MoInRvcCIsIiIpO3ZhciBpPSJhZmZpeCIrKGg/Ii0iK2g6IiIpLGo9YS5FdmVudChpKyIuYnMuYWZmaXgiKTtpZih0aGlzLiRlbGVtZW50LnRyaWdnZXIoaiksai5pc0RlZmF1bHRQcmV2ZW50ZWQoKSlyZXR1cm47dGhpcy5hZmZpeGVkPWgsdGhpcy51bnBpbj0iYm90dG9tIj09aD90aGlzLmdldFBpbm5lZE9mZnNldCgpOm51bGwsdGhpcy4kZWxlbWVudC5yZW1vdmVDbGFzcyhjLlJFU0VUKS5hZGRDbGFzcyhpKS50cmlnZ2VyKGkucmVwbGFjZSgiYWZmaXgiLCJhZmZpeGVkIikrIi5icy5hZmZpeCIpfSJib3R0b20iPT1oJiZ0aGlzLiRlbGVtZW50Lm9mZnNldCh7dG9wOmctYi1mfSl9fTt2YXIgZD1hLmZuLmFmZml4O2EuZm4uYWZmaXg9YixhLmZuLmFmZml4LkNvbnN0cnVjdG9yPWMsYS5mbi5hZmZpeC5ub0NvbmZsaWN0PWZ1bmN0aW9uKCl7cmV0dXJuIGEuZm4uYWZmaXg9ZCx0aGlzfSxhKHdpbmRvdykub24oImxvYWQiLGZ1bmN0aW9uKCl7YSgnW2RhdGEtc3B5PSJhZmZpeCJdJykuZWFjaChmdW5jdGlvbigpe3ZhciBjPWEodGhpcyksZD1jLmRhdGEoKTtkLm9mZnNldD1kLm9mZnNldHx8e30sbnVsbCE9ZC5vZmZzZXRCb3R0b20mJihkLm9mZnNldC5ib3R0b209ZC5vZmZzZXRCb3R0b20pLG51bGwhPWQub2Zmc2V0VG9wJiYoZC5vZmZzZXQudG9wPWQub2Zmc2V0VG9wKSxiLmNhbGwoYyxkKX0pfSl9KGpRdWVyeSk7"></script>
<script src="data:application/javascript;base64,LyoqCiogQHByZXNlcnZlIEhUTUw1IFNoaXYgMy43LjIgfCBAYWZhcmthcyBAamRhbHRvbiBAam9uX25lYWwgQHJlbSB8IE1JVC9HUEwyIExpY2Vuc2VkCiovCi8vIE9ubHkgcnVuIHRoaXMgY29kZSBpbiBJRSA4CmlmICghIXdpbmRvdy5uYXZpZ2F0b3IudXNlckFnZW50Lm1hdGNoKCJNU0lFIDgiKSkgewohZnVuY3Rpb24oYSxiKXtmdW5jdGlvbiBjKGEsYil7dmFyIGM9YS5jcmVhdGVFbGVtZW50KCJwIiksZD1hLmdldEVsZW1lbnRzQnlUYWdOYW1lKCJoZWFkIilbMF18fGEuZG9jdW1lbnRFbGVtZW50O3JldHVybiBjLmlubmVySFRNTD0ieDxzdHlsZT4iK2IrIjwvc3R5bGU+IixkLmluc2VydEJlZm9yZShjLmxhc3RDaGlsZCxkLmZpcnN0Q2hpbGQpfWZ1bmN0aW9uIGQoKXt2YXIgYT10LmVsZW1lbnRzO3JldHVybiJzdHJpbmciPT10eXBlb2YgYT9hLnNwbGl0KCIgIik6YX1mdW5jdGlvbiBlKGEsYil7dmFyIGM9dC5lbGVtZW50czsic3RyaW5nIiE9dHlwZW9mIGMmJihjPWMuam9pbigiICIpKSwic3RyaW5nIiE9dHlwZW9mIGEmJihhPWEuam9pbigiICIpKSx0LmVsZW1lbnRzPWMrIiAiK2EsaihiKX1mdW5jdGlvbiBmKGEpe3ZhciBiPXNbYVtxXV07cmV0dXJuIGJ8fChiPXt9LHIrKyxhW3FdPXIsc1tyXT1iKSxifWZ1bmN0aW9uIGcoYSxjLGQpe2lmKGN8fChjPWIpLGwpcmV0dXJuIGMuY3JlYXRlRWxlbWVudChhKTtkfHwoZD1mKGMpKTt2YXIgZTtyZXR1cm4gZT1kLmNhY2hlW2FdP2QuY2FjaGVbYV0uY2xvbmVOb2RlKCk6cC50ZXN0KGEpPyhkLmNhY2hlW2FdPWQuY3JlYXRlRWxlbShhKSkuY2xvbmVOb2RlKCk6ZC5jcmVhdGVFbGVtKGEpLCFlLmNhbkhhdmVDaGlsZHJlbnx8by50ZXN0KGEpfHxlLnRhZ1Vybj9lOmQuZnJhZy5hcHBlbmRDaGlsZChlKX1mdW5jdGlvbiBoKGEsYyl7aWYoYXx8KGE9YiksbClyZXR1cm4gYS5jcmVhdGVEb2N1bWVudEZyYWdtZW50KCk7Yz1jfHxmKGEpO2Zvcih2YXIgZT1jLmZyYWcuY2xvbmVOb2RlKCksZz0wLGg9ZCgpLGk9aC5sZW5ndGg7aT5nO2crKyllLmNyZWF0ZUVsZW1lbnQoaFtnXSk7cmV0dXJuIGV9ZnVuY3Rpb24gaShhLGIpe2IuY2FjaGV8fChiLmNhY2hlPXt9LGIuY3JlYXRlRWxlbT1hLmNyZWF0ZUVsZW1lbnQsYi5jcmVhdGVGcmFnPWEuY3JlYXRlRG9jdW1lbnRGcmFnbWVudCxiLmZyYWc9Yi5jcmVhdGVGcmFnKCkpLGEuY3JlYXRlRWxlbWVudD1mdW5jdGlvbihjKXtyZXR1cm4gdC5zaGl2TWV0aG9kcz9nKGMsYSxiKTpiLmNyZWF0ZUVsZW0oYyl9LGEuY3JlYXRlRG9jdW1lbnRGcmFnbWVudD1GdW5jdGlvbigiaCxmIiwicmV0dXJuIGZ1bmN0aW9uKCl7dmFyIG49Zi5jbG9uZU5vZGUoKSxjPW4uY3JlYXRlRWxlbWVudDtoLnNoaXZNZXRob2RzJiYoIitkKCkuam9pbigpLnJlcGxhY2UoL1tcd1wtOl0rL2csZnVuY3Rpb24oYSl7cmV0dXJuIGIuY3JlYXRlRWxlbShhKSxiLmZyYWcuY3JlYXRlRWxlbWVudChhKSwnYygiJythKyciKSd9KSsiKTtyZXR1cm4gbn0iKSh0LGIuZnJhZyl9ZnVuY3Rpb24gaihhKXthfHwoYT1iKTt2YXIgZD1mKGEpO3JldHVybiF0LnNoaXZDU1N8fGt8fGQuaGFzQ1NTfHwoZC5oYXNDU1M9ISFjKGEsImFydGljbGUsYXNpZGUsZGlhbG9nLGZpZ2NhcHRpb24sZmlndXJlLGZvb3RlcixoZWFkZXIsaGdyb3VwLG1haW4sbmF2LHNlY3Rpb257ZGlzcGxheTpibG9ja31tYXJre2JhY2tncm91bmQ6I0ZGMDtjb2xvcjojMDAwfXRlbXBsYXRle2Rpc3BsYXk6bm9uZX0iKSksbHx8aShhLGQpLGF9dmFyIGssbCxtPSIzLjcuMiIsbj1hLmh0bWw1fHx7fSxvPS9ePHxeKD86YnV0dG9ufG1hcHxzZWxlY3R8dGV4dGFyZWF8b2JqZWN0fGlmcmFtZXxvcHRpb258b3B0Z3JvdXApJC9pLHA9L14oPzphfGJ8Y29kZXxkaXZ8ZmllbGRzZXR8aDF8aDJ8aDN8aDR8aDV8aDZ8aXxsYWJlbHxsaXxvbHxwfHF8c3BhbnxzdHJvbmd8c3R5bGV8dGFibGV8dGJvZHl8dGR8dGh8dHJ8dWwpJC9pLHE9Il9odG1sNXNoaXYiLHI9MCxzPXt9OyFmdW5jdGlvbigpe3RyeXt2YXIgYT1iLmNyZWF0ZUVsZW1lbnQoImEiKTthLmlubmVySFRNTD0iPHh5ej48L3h5ej4iLGs9ImhpZGRlbiJpbiBhLGw9MT09YS5jaGlsZE5vZGVzLmxlbmd0aHx8ZnVuY3Rpb24oKXtiLmNyZWF0ZUVsZW1lbnQoImEiKTt2YXIgYT1iLmNyZWF0ZURvY3VtZW50RnJhZ21lbnQoKTtyZXR1cm4idW5kZWZpbmVkIj09dHlwZW9mIGEuY2xvbmVOb2RlfHwidW5kZWZpbmVkIj09dHlwZW9mIGEuY3JlYXRlRG9jdW1lbnRGcmFnbWVudHx8InVuZGVmaW5lZCI9PXR5cGVvZiBhLmNyZWF0ZUVsZW1lbnR9KCl9Y2F0Y2goYyl7az0hMCxsPSEwfX0oKTt2YXIgdD17ZWxlbWVudHM6bi5lbGVtZW50c3x8ImFiYnIgYXJ0aWNsZSBhc2lkZSBhdWRpbyBiZGkgY2FudmFzIGRhdGEgZGF0YWxpc3QgZGV0YWlscyBkaWFsb2cgZmlnY2FwdGlvbiBmaWd1cmUgZm9vdGVyIGhlYWRlciBoZ3JvdXAgbWFpbiBtYXJrIG1ldGVyIG5hdiBvdXRwdXQgcGljdHVyZSBwcm9ncmVzcyBzZWN0aW9uIHN1bW1hcnkgdGVtcGxhdGUgdGltZSB2aWRlbyIsdmVyc2lvbjptLHNoaXZDU1M6bi5zaGl2Q1NTIT09ITEsc3VwcG9ydHNVbmtub3duRWxlbWVudHM6bCxzaGl2TWV0aG9kczpuLnNoaXZNZXRob2RzIT09ITEsdHlwZToiZGVmYXVsdCIsc2hpdkRvY3VtZW50OmosY3JlYXRlRWxlbWVudDpnLGNyZWF0ZURvY3VtZW50RnJhZ21lbnQ6aCxhZGRFbGVtZW50czplfTthLmh0bWw1PXQsaihiKX0odGhpcyxkb2N1bWVudCk7Cn07Cg=="></script>
<script src="data:application/javascript;base64,LyohIFJlc3BvbmQuanMgdjEuNC4yOiBtaW4vbWF4LXdpZHRoIG1lZGlhIHF1ZXJ5IHBvbHlmaWxsICogQ29weXJpZ2h0IDIwMTMgU2NvdHQgSmVobAogKiBMaWNlbnNlZCB1bmRlciBodHRwczovL2dpdGh1Yi5jb20vc2NvdHRqZWhsL1Jlc3BvbmQvYmxvYi9tYXN0ZXIvTElDRU5TRS1NSVQKICogICovCgovLyBPbmx5IHJ1biB0aGlzIGNvZGUgaW4gSUUgOAppZiAoISF3aW5kb3cubmF2aWdhdG9yLnVzZXJBZ2VudC5tYXRjaCgiTVNJRSA4IikpIHsKIWZ1bmN0aW9uKGEpeyJ1c2Ugc3RyaWN0IjthLm1hdGNoTWVkaWE9YS5tYXRjaE1lZGlhfHxmdW5jdGlvbihhKXt2YXIgYixjPWEuZG9jdW1lbnRFbGVtZW50LGQ9Yy5maXJzdEVsZW1lbnRDaGlsZHx8Yy5maXJzdENoaWxkLGU9YS5jcmVhdGVFbGVtZW50KCJib2R5IiksZj1hLmNyZWF0ZUVsZW1lbnQoImRpdiIpO3JldHVybiBmLmlkPSJtcS10ZXN0LTEiLGYuc3R5bGUuY3NzVGV4dD0icG9zaXRpb246YWJzb2x1dGU7dG9wOi0xMDBlbSIsZS5zdHlsZS5iYWNrZ3JvdW5kPSJub25lIixlLmFwcGVuZENoaWxkKGYpLGZ1bmN0aW9uKGEpe3JldHVybiBmLmlubmVySFRNTD0nJnNoeTs8c3R5bGUgbWVkaWE9IicrYSsnIj4gI21xLXRlc3QtMSB7IHdpZHRoOiA0MnB4OyB9PC9zdHlsZT4nLGMuaW5zZXJ0QmVmb3JlKGUsZCksYj00Mj09PWYub2Zmc2V0V2lkdGgsYy5yZW1vdmVDaGlsZChlKSx7bWF0Y2hlczpiLG1lZGlhOmF9fX0oYS5kb2N1bWVudCl9KHRoaXMpLGZ1bmN0aW9uKGEpeyJ1c2Ugc3RyaWN0IjtmdW5jdGlvbiBiKCl7dSghMCl9dmFyIGM9e307YS5yZXNwb25kPWMsYy51cGRhdGU9ZnVuY3Rpb24oKXt9O3ZhciBkPVtdLGU9ZnVuY3Rpb24oKXt2YXIgYj0hMTt0cnl7Yj1uZXcgYS5YTUxIdHRwUmVxdWVzdH1jYXRjaChjKXtiPW5ldyBhLkFjdGl2ZVhPYmplY3QoIk1pY3Jvc29mdC5YTUxIVFRQIil9cmV0dXJuIGZ1bmN0aW9uKCl7cmV0dXJuIGJ9fSgpLGY9ZnVuY3Rpb24oYSxiKXt2YXIgYz1lKCk7YyYmKGMub3BlbigiR0VUIixhLCEwKSxjLm9ucmVhZHlzdGF0ZWNoYW5nZT1mdW5jdGlvbigpezQhPT1jLnJlYWR5U3RhdGV8fDIwMCE9PWMuc3RhdHVzJiYzMDQhPT1jLnN0YXR1c3x8YihjLnJlc3BvbnNlVGV4dCl9LDQhPT1jLnJlYWR5U3RhdGUmJmMuc2VuZChudWxsKSl9O2lmKGMuYWpheD1mLGMucXVldWU9ZCxjLnJlZ2V4PXttZWRpYTovQG1lZGlhW15ce10rXHsoW15ce1x9XSpce1teXH1ce10qXH0pKy9naSxrZXlmcmFtZXM6L0AoPzpcLSg/Om98bW96fHdlYmtpdClcLSk/a2V5ZnJhbWVzW15ce10rXHsoPzpbXlx7XH1dKlx7W15cfVx7XSpcfSkrW15cfV0qXH0vZ2ksdXJsczovKHVybFwoKVsnIl0/KFteXC9cKSciXVteOlwpJyJdKylbJyJdPyhcKSkvZyxmaW5kU3R5bGVzOi9AbWVkaWEgKihbXlx7XSspXHsoW1xTXHNdKz8pJC8sb25seTovKG9ubHlccyspPyhbYS16QS1aXSspXHM/LyxtaW53Oi9cKFtcc10qbWluXC13aWR0aFxzKjpbXHNdKihbXHNdKlswLTlcLl0rKShweHxlbSlbXHNdKlwpLyxtYXh3Oi9cKFtcc10qbWF4XC13aWR0aFxzKjpbXHNdKihbXHNdKlswLTlcLl0rKShweHxlbSlbXHNdKlwpL30sYy5tZWRpYVF1ZXJpZXNTdXBwb3J0ZWQ9YS5tYXRjaE1lZGlhJiZudWxsIT09YS5tYXRjaE1lZGlhKCJvbmx5IGFsbCIpJiZhLm1hdGNoTWVkaWEoIm9ubHkgYWxsIikubWF0Y2hlcywhYy5tZWRpYVF1ZXJpZXNTdXBwb3J0ZWQpe3ZhciBnLGgsaSxqPWEuZG9jdW1lbnQsaz1qLmRvY3VtZW50RWxlbWVudCxsPVtdLG09W10sbj1bXSxvPXt9LHA9MzAscT1qLmdldEVsZW1lbnRzQnlUYWdOYW1lKCJoZWFkIilbMF18fGsscj1qLmdldEVsZW1lbnRzQnlUYWdOYW1lKCJiYXNlIilbMF0scz1xLmdldEVsZW1lbnRzQnlUYWdOYW1lKCJsaW5rIiksdD1mdW5jdGlvbigpe3ZhciBhLGI9ai5jcmVhdGVFbGVtZW50KCJkaXYiKSxjPWouYm9keSxkPWsuc3R5bGUuZm9udFNpemUsZT1jJiZjLnN0eWxlLmZvbnRTaXplLGY9ITE7cmV0dXJuIGIuc3R5bGUuY3NzVGV4dD0icG9zaXRpb246YWJzb2x1dGU7Zm9udC1zaXplOjFlbTt3aWR0aDoxZW0iLGN8fChjPWY9ai5jcmVhdGVFbGVtZW50KCJib2R5IiksYy5zdHlsZS5iYWNrZ3JvdW5kPSJub25lIiksay5zdHlsZS5mb250U2l6ZT0iMTAwJSIsYy5zdHlsZS5mb250U2l6ZT0iMTAwJSIsYy5hcHBlbmRDaGlsZChiKSxmJiZrLmluc2VydEJlZm9yZShjLGsuZmlyc3RDaGlsZCksYT1iLm9mZnNldFdpZHRoLGY/ay5yZW1vdmVDaGlsZChjKTpjLnJlbW92ZUNoaWxkKGIpLGsuc3R5bGUuZm9udFNpemU9ZCxlJiYoYy5zdHlsZS5mb250U2l6ZT1lKSxhPWk9cGFyc2VGbG9hdChhKX0sdT1mdW5jdGlvbihiKXt2YXIgYz0iY2xpZW50V2lkdGgiLGQ9a1tjXSxlPSJDU1MxQ29tcGF0Ij09PWouY29tcGF0TW9kZSYmZHx8ai5ib2R5W2NdfHxkLGY9e30sbz1zW3MubGVuZ3RoLTFdLHI9KG5ldyBEYXRlKS5nZXRUaW1lKCk7aWYoYiYmZyYmcD5yLWcpcmV0dXJuIGEuY2xlYXJUaW1lb3V0KGgpLGg9YS5zZXRUaW1lb3V0KHUscCksdm9pZCAwO2c9cjtmb3IodmFyIHYgaW4gbClpZihsLmhhc093blByb3BlcnR5KHYpKXt2YXIgdz1sW3ZdLHg9dy5taW53LHk9dy5tYXh3LHo9bnVsbD09PXgsQT1udWxsPT09eSxCPSJlbSI7eCYmKHg9cGFyc2VGbG9hdCh4KSooeC5pbmRleE9mKEIpPi0xP2l8fHQoKToxKSkseSYmKHk9cGFyc2VGbG9hdCh5KSooeS5pbmRleE9mKEIpPi0xP2l8fHQoKToxKSksdy5oYXNxdWVyeSYmKHomJkF8fCEoenx8ZT49eCl8fCEoQXx8eT49ZSkpfHwoZlt3Lm1lZGlhXXx8KGZbdy5tZWRpYV09W10pLGZbdy5tZWRpYV0ucHVzaChtW3cucnVsZXNdKSl9Zm9yKHZhciBDIGluIG4pbi5oYXNPd25Qcm9wZXJ0eShDKSYmbltDXSYmbltDXS5wYXJlbnROb2RlPT09cSYmcS5yZW1vdmVDaGlsZChuW0NdKTtuLmxlbmd0aD0wO2Zvcih2YXIgRCBpbiBmKWlmKGYuaGFzT3duUHJvcGVydHkoRCkpe3ZhciBFPWouY3JlYXRlRWxlbWVudCgic3R5bGUiKSxGPWZbRF0uam9pbigiXG4iKTtFLnR5cGU9InRleHQvY3NzIixFLm1lZGlhPUQscS5pbnNlcnRCZWZvcmUoRSxvLm5leHRTaWJsaW5nKSxFLnN0eWxlU2hlZXQ/RS5zdHlsZVNoZWV0LmNzc1RleHQ9RjpFLmFwcGVuZENoaWxkKGouY3JlYXRlVGV4dE5vZGUoRikpLG4ucHVzaChFKX19LHY9ZnVuY3Rpb24oYSxiLGQpe3ZhciBlPWEucmVwbGFjZShjLnJlZ2V4LmtleWZyYW1lcywiIikubWF0Y2goYy5yZWdleC5tZWRpYSksZj1lJiZlLmxlbmd0aHx8MDtiPWIuc3Vic3RyaW5nKDAsYi5sYXN0SW5kZXhPZigiLyIpKTt2YXIgZz1mdW5jdGlvbihhKXtyZXR1cm4gYS5yZXBsYWNlKGMucmVnZXgudXJscywiJDEiK2IrIiQyJDMiKX0saD0hZiYmZDtiLmxlbmd0aCYmKGIrPSIvIiksaCYmKGY9MSk7Zm9yKHZhciBpPTA7Zj5pO2krKyl7dmFyIGosayxuLG87aD8oaj1kLG0ucHVzaChnKGEpKSk6KGo9ZVtpXS5tYXRjaChjLnJlZ2V4LmZpbmRTdHlsZXMpJiZSZWdFeHAuJDEsbS5wdXNoKFJlZ0V4cC4kMiYmZyhSZWdFeHAuJDIpKSksbj1qLnNwbGl0KCIsIiksbz1uLmxlbmd0aDtmb3IodmFyIHA9MDtvPnA7cCsrKWs9bltwXSxsLnB1c2goe21lZGlhOmsuc3BsaXQoIigiKVswXS5tYXRjaChjLnJlZ2V4Lm9ubHkpJiZSZWdFeHAuJDJ8fCJhbGwiLHJ1bGVzOm0ubGVuZ3RoLTEsaGFzcXVlcnk6ay5pbmRleE9mKCIoIik+LTEsbWludzprLm1hdGNoKGMucmVnZXgubWludykmJnBhcnNlRmxvYXQoUmVnRXhwLiQxKSsoUmVnRXhwLiQyfHwiIiksbWF4dzprLm1hdGNoKGMucmVnZXgubWF4dykmJnBhcnNlRmxvYXQoUmVnRXhwLiQxKSsoUmVnRXhwLiQyfHwiIil9KX11KCl9LHc9ZnVuY3Rpb24oKXtpZihkLmxlbmd0aCl7dmFyIGI9ZC5zaGlmdCgpO2YoYi5ocmVmLGZ1bmN0aW9uKGMpe3YoYyxiLmhyZWYsYi5tZWRpYSksb1tiLmhyZWZdPSEwLGEuc2V0VGltZW91dChmdW5jdGlvbigpe3coKX0sMCl9KX19LHg9ZnVuY3Rpb24oKXtmb3IodmFyIGI9MDtiPHMubGVuZ3RoO2IrKyl7dmFyIGM9c1tiXSxlPWMuaHJlZixmPWMubWVkaWEsZz1jLnJlbCYmInN0eWxlc2hlZXQiPT09Yy5yZWwudG9Mb3dlckNhc2UoKTtlJiZnJiYhb1tlXSYmKGMuc3R5bGVTaGVldCYmYy5zdHlsZVNoZWV0LnJhd0Nzc1RleHQ/KHYoYy5zdHlsZVNoZWV0LnJhd0Nzc1RleHQsZSxmKSxvW2VdPSEwKTooIS9eKFthLXpBLVo6XSpcL1wvKS8udGVzdChlKSYmIXJ8fGUucmVwbGFjZShSZWdFeHAuJDEsIiIpLnNwbGl0KCIvIilbMF09PT1hLmxvY2F0aW9uLmhvc3QpJiYoIi8vIj09PWUuc3Vic3RyaW5nKDAsMikmJihlPWEubG9jYXRpb24ucHJvdG9jb2wrZSksZC5wdXNoKHtocmVmOmUsbWVkaWE6Zn0pKSl9dygpfTt4KCksYy51cGRhdGU9eCxjLmdldEVtVmFsdWU9dCxhLmFkZEV2ZW50TGlzdGVuZXI/YS5hZGRFdmVudExpc3RlbmVyKCJyZXNpemUiLGIsITEpOmEuYXR0YWNoRXZlbnQmJmEuYXR0YWNoRXZlbnQoIm9ucmVzaXplIixiKX19KHRoaXMpOwp9Owo="></script>
<style>h1 {font-size: 34px;}
h1.title {font-size: 38px;}
h2 {font-size: 30px;}
h3 {font-size: 24px;}
h4 {font-size: 18px;}
h5 {font-size: 16px;}
h6 {font-size: 12px;}
code {color: inherit; background-color: rgba(0, 0, 0, 0.04);}
pre:not([class]) { background-color: white }</style>
<script src="data:application/javascript;base64,CgovKioKICogalF1ZXJ5IFBsdWdpbjogU3RpY2t5IFRhYnMKICoKICogQGF1dGhvciBBaWRhbiBMaXN0ZXIgPGFpZGFuQHBocC5uZXQ+CiAqIGFkYXB0ZWQgYnkgUnViZW4gQXJzbGFuIHRvIGFjdGl2YXRlIHBhcmVudCB0YWJzIHRvbwogKiBodHRwOi8vd3d3LmFpZGFubGlzdGVyLmNvbS8yMDE0LzAzL3BlcnNpc3RpbmctdGhlLXRhYi1zdGF0ZS1pbi1ib290c3RyYXAvCiAqLwooZnVuY3Rpb24oJCkgewogICJ1c2Ugc3RyaWN0IjsKICAkLmZuLnJtYXJrZG93blN0aWNreVRhYnMgPSBmdW5jdGlvbigpIHsKICAgIHZhciBjb250ZXh0ID0gdGhpczsKICAgIC8vIFNob3cgdGhlIHRhYiBjb3JyZXNwb25kaW5nIHdpdGggdGhlIGhhc2ggaW4gdGhlIFVSTCwgb3IgdGhlIGZpcnN0IHRhYgogICAgdmFyIHNob3dTdHVmZkZyb21IYXNoID0gZnVuY3Rpb24oKSB7CiAgICAgIHZhciBoYXNoID0gd2luZG93LmxvY2F0aW9uLmhhc2g7CiAgICAgIHZhciBzZWxlY3RvciA9IGhhc2ggPyAnYVtocmVmPSInICsgaGFzaCArICciXScgOiAnbGkuYWN0aXZlID4gYSc7CiAgICAgIHZhciAkc2VsZWN0b3IgPSAkKHNlbGVjdG9yLCBjb250ZXh0KTsKICAgICAgaWYoJHNlbGVjdG9yLmRhdGEoJ3RvZ2dsZScpID09PSAidGFiIikgewogICAgICAgICRzZWxlY3Rvci50YWIoJ3Nob3cnKTsKICAgICAgICAvLyB3YWxrIHVwIHRoZSBhbmNlc3RvcnMgb2YgdGhpcyBlbGVtZW50LCBzaG93IGFueSBoaWRkZW4gdGFicwogICAgICAgICRzZWxlY3Rvci5wYXJlbnRzKCcuc2VjdGlvbi50YWJzZXQnKS5lYWNoKGZ1bmN0aW9uKGksIGVsbSkgewogICAgICAgICAgdmFyIGxpbmsgPSAkKCdhW2hyZWY9IiMnICsgJChlbG0pLmF0dHIoJ2lkJykgKyAnIl0nKTsKICAgICAgICAgIGlmKGxpbmsuZGF0YSgndG9nZ2xlJykgPT09ICJ0YWIiKSB7CiAgICAgICAgICAgIGxpbmsudGFiKCJzaG93Iik7CiAgICAgICAgICB9CiAgICAgICAgfSk7CiAgICAgIH0KICAgIH07CgoKICAgIC8vIFNldCB0aGUgY29ycmVjdCB0YWIgd2hlbiB0aGUgcGFnZSBsb2FkcwogICAgc2hvd1N0dWZmRnJvbUhhc2goY29udGV4dCk7CgogICAgLy8gU2V0IHRoZSBjb3JyZWN0IHRhYiB3aGVuIGEgdXNlciB1c2VzIHRoZWlyIGJhY2svZm9yd2FyZCBidXR0b24KICAgICQod2luZG93KS5vbignaGFzaGNoYW5nZScsIGZ1bmN0aW9uKCkgewogICAgICBzaG93U3R1ZmZGcm9tSGFzaChjb250ZXh0KTsKICAgIH0pOwoKICAgIC8vIENoYW5nZSB0aGUgVVJMIHdoZW4gdGFicyBhcmUgY2xpY2tlZAogICAgJCgnYScsIGNvbnRleHQpLm9uKCdjbGljaycsIGZ1bmN0aW9uKGUpIHsKICAgICAgaGlzdG9yeS5wdXNoU3RhdGUobnVsbCwgbnVsbCwgdGhpcy5ocmVmKTsKICAgICAgc2hvd1N0dWZmRnJvbUhhc2goY29udGV4dCk7CiAgICB9KTsKCiAgICByZXR1cm4gdGhpczsKICB9Owp9KGpRdWVyeSkpOwoKd2luZG93LmJ1aWxkVGFic2V0cyA9IGZ1bmN0aW9uKHRvY0lEKSB7CgogIC8vIGJ1aWxkIGEgdGFic2V0IGZyb20gYSBzZWN0aW9uIGRpdiB3aXRoIHRoZSAudGFic2V0IGNsYXNzCiAgZnVuY3Rpb24gYnVpbGRUYWJzZXQodGFic2V0KSB7CgogICAgLy8gY2hlY2sgZm9yIGZhZGUgYW5kIHBpbGxzIG9wdGlvbnMKICAgIHZhciBmYWRlID0gdGFic2V0Lmhhc0NsYXNzKCJ0YWJzZXQtZmFkZSIpOwogICAgdmFyIHBpbGxzID0gdGFic2V0Lmhhc0NsYXNzKCJ0YWJzZXQtcGlsbHMiKTsKICAgIHZhciBuYXZDbGFzcyA9IHBpbGxzID8gIm5hdi1waWxscyIgOiAibmF2LXRhYnMiOwoKICAgIC8vIGRldGVybWluZSB0aGUgaGVhZGluZyBsZXZlbCBvZiB0aGUgdGFic2V0IGFuZCB0YWJzCiAgICB2YXIgbWF0Y2ggPSB0YWJzZXQuYXR0cignY2xhc3MnKS5tYXRjaCgvbGV2ZWwoXGQpIC8pOwogICAgaWYgKG1hdGNoID09PSBudWxsKQogICAgICByZXR1cm47CiAgICB2YXIgdGFic2V0TGV2ZWwgPSBOdW1iZXIobWF0Y2hbMV0pOwogICAgdmFyIHRhYkxldmVsID0gdGFic2V0TGV2ZWwgKyAxOwoKICAgIC8vIGZpbmQgYWxsIHN1YmhlYWRpbmdzIGltbWVkaWF0ZWx5IGJlbG93CiAgICB2YXIgdGFicyA9IHRhYnNldC5maW5kKCJkaXYuc2VjdGlvbi5sZXZlbCIgKyB0YWJMZXZlbCk7CiAgICBpZiAoIXRhYnMubGVuZ3RoKQogICAgICByZXR1cm47CgogICAgLy8gY3JlYXRlIHRhYmxpc3QgYW5kIHRhYi1jb250ZW50IGVsZW1lbnRzCiAgICB2YXIgdGFiTGlzdCA9ICQoJzx1bCBjbGFzcz0ibmF2ICcgKyBuYXZDbGFzcyArICciIHJvbGU9InRhYmxpc3QiPjwvdWw+Jyk7CiAgICAkKHRhYnNbMF0pLmJlZm9yZSh0YWJMaXN0KTsKICAgIHZhciB0YWJDb250ZW50ID0gJCgnPGRpdiBjbGFzcz0idGFiLWNvbnRlbnQiPjwvZGl2PicpOwogICAgJCh0YWJzWzBdKS5iZWZvcmUodGFiQ29udGVudCk7CgogICAgLy8gYnVpbGQgdGhlIHRhYnNldAogICAgdmFyIGFjdGl2ZVRhYiA9IDA7CiAgICB0YWJzLmVhY2goZnVuY3Rpb24oaSkgewoKICAgICAgLy8gZ2V0IHRoZSB0YWIgZGl2CiAgICAgIHZhciB0YWIgPSAkKHRhYnNbaV0pOwoKICAgICAgLy8gZ2V0IHRoZSBpZCB0aGVuIHNhbml0aXplIGl0IGZvciB1c2Ugd2l0aCBib290c3RyYXAgdGFicwogICAgICB2YXIgaWQgPSB0YWIuYXR0cignaWQnKTsKCiAgICAgIC8vIHNlZSBpZiB0aGlzIGlzIG1hcmtlZCBhcyB0aGUgYWN0aXZlIHRhYgogICAgICBpZiAodGFiLmhhc0NsYXNzKCdhY3RpdmUnKSkKICAgICAgICBhY3RpdmVUYWIgPSBpOwoKICAgICAgLy8gcmVtb3ZlIGFueSB0YWJsZSBvZiBjb250ZW50cyBlbnRyaWVzIGFzc29jaWF0ZWQgd2l0aAogICAgICAvLyB0aGlzIElEIChzaW5jZSB3ZSdsbCBiZSByZW1vdmluZyB0aGUgaGVhZGluZyBlbGVtZW50KQogICAgICAkKCJkaXYjIiArIHRvY0lEICsgIiBsaSBhW2hyZWY9JyMiICsgaWQgKyAiJ10iKS5wYXJlbnQoKS5yZW1vdmUoKTsKCiAgICAgIC8vIHNhbml0aXplIHRoZSBpZCBmb3IgdXNlIHdpdGggYm9vdHN0cmFwIHRhYnMKICAgICAgaWQgPSBpZC5yZXBsYWNlKC9bLlwvPyYhIzw+XS9nLCAnJykucmVwbGFjZSgvXHMvZywgJ18nKTsKICAgICAgdGFiLmF0dHIoJ2lkJywgaWQpOwoKICAgICAgLy8gZ2V0IHRoZSBoZWFkaW5nIGVsZW1lbnQgd2l0aGluIGl0LCBncmFiIGl0J3MgdGV4dCwgdGhlbiByZW1vdmUgaXQKICAgICAgdmFyIGhlYWRpbmcgPSB0YWIuZmluZCgnaCcgKyB0YWJMZXZlbCArICc6Zmlyc3QnKTsKICAgICAgdmFyIGhlYWRpbmdUZXh0ID0gaGVhZGluZy5odG1sKCk7CiAgICAgIGhlYWRpbmcucmVtb3ZlKCk7CgogICAgICAvLyBidWlsZCBhbmQgYXBwZW5kIHRoZSB0YWIgbGlzdCBpdGVtCiAgICAgIHZhciBhID0gJCgnPGEgcm9sZT0idGFiIiBkYXRhLXRvZ2dsZT0idGFiIj4nICsgaGVhZGluZ1RleHQgKyAnPC9hPicpOwogICAgICBhLmF0dHIoJ2hyZWYnLCAnIycgKyBpZCk7CiAgICAgIGEuYXR0cignYXJpYS1jb250cm9scycsIGlkKTsKICAgICAgdmFyIGxpID0gJCgnPGxpIHJvbGU9InByZXNlbnRhdGlvbiI+PC9saT4nKTsKICAgICAgbGkuYXBwZW5kKGEpOwogICAgICB0YWJMaXN0LmFwcGVuZChsaSk7CgogICAgICAvLyBzZXQgaXQncyBhdHRyaWJ1dGVzCiAgICAgIHRhYi5hdHRyKCdyb2xlJywgJ3RhYnBhbmVsJyk7CiAgICAgIHRhYi5hZGRDbGFzcygndGFiLXBhbmUnKTsKICAgICAgdGFiLmFkZENsYXNzKCd0YWJiZWQtcGFuZScpOwogICAgICBpZiAoZmFkZSkKICAgICAgICB0YWIuYWRkQ2xhc3MoJ2ZhZGUnKTsKCiAgICAgIC8vIG1vdmUgaXQgaW50byB0aGUgdGFiIGNvbnRlbnQgZGl2CiAgICAgIHRhYi5kZXRhY2goKS5hcHBlbmRUbyh0YWJDb250ZW50KTsKICAgIH0pOwoKICAgIC8vIHNldCBhY3RpdmUgdGFiCiAgICAkKHRhYkxpc3QuY2hpbGRyZW4oJ2xpJylbYWN0aXZlVGFiXSkuYWRkQ2xhc3MoJ2FjdGl2ZScpOwogICAgdmFyIGFjdGl2ZSA9ICQodGFiQ29udGVudC5jaGlsZHJlbignZGl2LnNlY3Rpb24nKVthY3RpdmVUYWJdKTsKICAgIGFjdGl2ZS5hZGRDbGFzcygnYWN0aXZlJyk7CiAgICBpZiAoZmFkZSkKICAgICAgYWN0aXZlLmFkZENsYXNzKCdpbicpOwoKICAgIGlmICh0YWJzZXQuaGFzQ2xhc3MoInRhYnNldC1zdGlja3kiKSkKICAgICAgdGFic2V0LnJtYXJrZG93blN0aWNreVRhYnMoKTsKICB9CgogIC8vIGNvbnZlcnQgc2VjdGlvbiBkaXZzIHdpdGggdGhlIC50YWJzZXQgY2xhc3MgdG8gdGFic2V0cwogIHZhciB0YWJzZXRzID0gJCgiZGl2LnNlY3Rpb24udGFic2V0Iik7CiAgdGFic2V0cy5lYWNoKGZ1bmN0aW9uKGkpIHsKICAgIGJ1aWxkVGFic2V0KCQodGFic2V0c1tpXSkpOwogIH0pOwp9OwoK"></script>
<link href="data:text/css,%2Ehljs%2Dliteral%20%7B%0Acolor%3A%20%23990073%3B%0A%7D%0A%2Ehljs%2Dnumber%20%7B%0Acolor%3A%20%23099%3B%0A%7D%0A%2Ehljs%2Dcomment%20%7B%0Acolor%3A%20%23998%3B%0Afont%2Dstyle%3A%20italic%3B%0A%7D%0A%2Ehljs%2Dkeyword%20%7B%0Acolor%3A%20%23900%3B%0Afont%2Dweight%3A%20bold%3B%0A%7D%0A%2Ehljs%2Dstring%20%7B%0Acolor%3A%20%23d14%3B%0A%7D%0A" rel="stylesheet" />
<script src="data:application/javascript;base64,LyohIGhpZ2hsaWdodC5qcyB2OS4xMi4wIHwgQlNEMyBMaWNlbnNlIHwgZ2l0LmlvL2hsanNsaWNlbnNlICovCiFmdW5jdGlvbihlKXt2YXIgbj0ib2JqZWN0Ij09dHlwZW9mIHdpbmRvdyYmd2luZG93fHwib2JqZWN0Ij09dHlwZW9mIHNlbGYmJnNlbGY7InVuZGVmaW5lZCIhPXR5cGVvZiBleHBvcnRzP2UoZXhwb3J0cyk6biYmKG4uaGxqcz1lKHt9KSwiZnVuY3Rpb24iPT10eXBlb2YgZGVmaW5lJiZkZWZpbmUuYW1kJiZkZWZpbmUoW10sZnVuY3Rpb24oKXtyZXR1cm4gbi5obGpzfSkpfShmdW5jdGlvbihlKXtmdW5jdGlvbiBuKGUpe3JldHVybiBlLnJlcGxhY2UoLyYvZywiJmFtcDsiKS5yZXBsYWNlKC88L2csIiZsdDsiKS5yZXBsYWNlKC8+L2csIiZndDsiKX1mdW5jdGlvbiB0KGUpe3JldHVybiBlLm5vZGVOYW1lLnRvTG93ZXJDYXNlKCl9ZnVuY3Rpb24gcihlLG4pe3ZhciB0PWUmJmUuZXhlYyhuKTtyZXR1cm4gdCYmMD09PXQuaW5kZXh9ZnVuY3Rpb24gYShlKXtyZXR1cm4gay50ZXN0KGUpfWZ1bmN0aW9uIGkoZSl7dmFyIG4sdCxyLGksbz1lLmNsYXNzTmFtZSsiICI7aWYobys9ZS5wYXJlbnROb2RlP2UucGFyZW50Tm9kZS5jbGFzc05hbWU6IiIsdD1CLmV4ZWMobykpcmV0dXJuIHcodFsxXSk/dFsxXToibm8taGlnaGxpZ2h0Ijtmb3Iobz1vLnNwbGl0KC9ccysvKSxuPTAscj1vLmxlbmd0aDtyPm47bisrKWlmKGk9b1tuXSxhKGkpfHx3KGkpKXJldHVybiBpfWZ1bmN0aW9uIG8oZSl7dmFyIG4sdD17fSxyPUFycmF5LnByb3RvdHlwZS5zbGljZS5jYWxsKGFyZ3VtZW50cywxKTtmb3IobiBpbiBlKXRbbl09ZVtuXTtyZXR1cm4gci5mb3JFYWNoKGZ1bmN0aW9uKGUpe2ZvcihuIGluIGUpdFtuXT1lW25dfSksdH1mdW5jdGlvbiB1KGUpe3ZhciBuPVtdO3JldHVybiBmdW5jdGlvbiByKGUsYSl7Zm9yKHZhciBpPWUuZmlyc3RDaGlsZDtpO2k9aS5uZXh0U2libGluZykzPT09aS5ub2RlVHlwZT9hKz1pLm5vZGVWYWx1ZS5sZW5ndGg6MT09PWkubm9kZVR5cGUmJihuLnB1c2goe2V2ZW50OiJzdGFydCIsb2Zmc2V0OmEsbm9kZTppfSksYT1yKGksYSksdChpKS5tYXRjaCgvYnJ8aHJ8aW1nfGlucHV0Lyl8fG4ucHVzaCh7ZXZlbnQ6InN0b3AiLG9mZnNldDphLG5vZGU6aX0pKTtyZXR1cm4gYX0oZSwwKSxufWZ1bmN0aW9uIGMoZSxyLGEpe2Z1bmN0aW9uIGkoKXtyZXR1cm4gZS5sZW5ndGgmJnIubGVuZ3RoP2VbMF0ub2Zmc2V0IT09clswXS5vZmZzZXQ/ZVswXS5vZmZzZXQ8clswXS5vZmZzZXQ/ZTpyOiJzdGFydCI9PT1yWzBdLmV2ZW50P2U6cjplLmxlbmd0aD9lOnJ9ZnVuY3Rpb24gbyhlKXtmdW5jdGlvbiByKGUpe3JldHVybiIgIitlLm5vZGVOYW1lKyc9IicrbihlLnZhbHVlKS5yZXBsYWNlKCciJywiJnF1b3Q7IikrJyInfXMrPSI8Iit0KGUpK0UubWFwLmNhbGwoZS5hdHRyaWJ1dGVzLHIpLmpvaW4oIiIpKyI+In1mdW5jdGlvbiB1KGUpe3MrPSI8LyIrdChlKSsiPiJ9ZnVuY3Rpb24gYyhlKXsoInN0YXJ0Ij09PWUuZXZlbnQ/bzp1KShlLm5vZGUpfWZvcih2YXIgbD0wLHM9IiIsZj1bXTtlLmxlbmd0aHx8ci5sZW5ndGg7KXt2YXIgZz1pKCk7aWYocys9bihhLnN1YnN0cmluZyhsLGdbMF0ub2Zmc2V0KSksbD1nWzBdLm9mZnNldCxnPT09ZSl7Zi5yZXZlcnNlKCkuZm9yRWFjaCh1KTtkbyBjKGcuc3BsaWNlKDAsMSlbMF0pLGc9aSgpO3doaWxlKGc9PT1lJiZnLmxlbmd0aCYmZ1swXS5vZmZzZXQ9PT1sKTtmLnJldmVyc2UoKS5mb3JFYWNoKG8pfWVsc2Uic3RhcnQiPT09Z1swXS5ldmVudD9mLnB1c2goZ1swXS5ub2RlKTpmLnBvcCgpLGMoZy5zcGxpY2UoMCwxKVswXSl9cmV0dXJuIHMrbihhLnN1YnN0cihsKSl9ZnVuY3Rpb24gbChlKXtyZXR1cm4gZS52JiYhZS5jYWNoZWRfdmFyaWFudHMmJihlLmNhY2hlZF92YXJpYW50cz1lLnYubWFwKGZ1bmN0aW9uKG4pe3JldHVybiBvKGUse3Y6bnVsbH0sbil9KSksZS5jYWNoZWRfdmFyaWFudHN8fGUuZVcmJltvKGUpXXx8W2VdfWZ1bmN0aW9uIHMoZSl7ZnVuY3Rpb24gbihlKXtyZXR1cm4gZSYmZS5zb3VyY2V8fGV9ZnVuY3Rpb24gdCh0LHIpe3JldHVybiBuZXcgUmVnRXhwKG4odCksIm0iKyhlLmNJPyJpIjoiIikrKHI/ImciOiIiKSl9ZnVuY3Rpb24gcihhLGkpe2lmKCFhLmNvbXBpbGVkKXtpZihhLmNvbXBpbGVkPSEwLGEuaz1hLmt8fGEuYkssYS5rKXt2YXIgbz17fSx1PWZ1bmN0aW9uKG4sdCl7ZS5jSSYmKHQ9dC50b0xvd2VyQ2FzZSgpKSx0LnNwbGl0KCIgIikuZm9yRWFjaChmdW5jdGlvbihlKXt2YXIgdD1lLnNwbGl0KCJ8Iik7b1t0WzBdXT1bbix0WzFdP051bWJlcih0WzFdKToxXX0pfTsic3RyaW5nIj09dHlwZW9mIGEuaz91KCJrZXl3b3JkIixhLmspOngoYS5rKS5mb3JFYWNoKGZ1bmN0aW9uKGUpe3UoZSxhLmtbZV0pfSksYS5rPW99YS5sUj10KGEubHx8L1x3Ky8sITApLGkmJihhLmJLJiYoYS5iPSJcXGIoIithLmJLLnNwbGl0KCIgIikuam9pbigifCIpKyIpXFxiIiksYS5ifHwoYS5iPS9cQnxcYi8pLGEuYlI9dChhLmIpLGEuZXx8YS5lV3x8KGEuZT0vXEJ8XGIvKSxhLmUmJihhLmVSPXQoYS5lKSksYS50RT1uKGEuZSl8fCIiLGEuZVcmJmkudEUmJihhLnRFKz0oYS5lPyJ8IjoiIikraS50RSkpLGEuaSYmKGEuaVI9dChhLmkpKSxudWxsPT1hLnImJihhLnI9MSksYS5jfHwoYS5jPVtdKSxhLmM9QXJyYXkucHJvdG90eXBlLmNvbmNhdC5hcHBseShbXSxhLmMubWFwKGZ1bmN0aW9uKGUpe3JldHVybiBsKCJzZWxmIj09PWU/YTplKX0pKSxhLmMuZm9yRWFjaChmdW5jdGlvbihlKXtyKGUsYSl9KSxhLnN0YXJ0cyYmcihhLnN0YXJ0cyxpKTt2YXIgYz1hLmMubWFwKGZ1bmN0aW9uKGUpe3JldHVybiBlLmJLPyJcXC4/KCIrZS5iKyIpXFwuPyI6ZS5ifSkuY29uY2F0KFthLnRFLGEuaV0pLm1hcChuKS5maWx0ZXIoQm9vbGVhbik7YS50PWMubGVuZ3RoP3QoYy5qb2luKCJ8IiksITApOntleGVjOmZ1bmN0aW9uKCl7cmV0dXJuIG51bGx9fX19cihlKX1mdW5jdGlvbiBmKGUsdCxhLGkpe2Z1bmN0aW9uIG8oZSxuKXt2YXIgdCxhO2Zvcih0PTAsYT1uLmMubGVuZ3RoO2E+dDt0KyspaWYocihuLmNbdF0uYlIsZSkpcmV0dXJuIG4uY1t0XX1mdW5jdGlvbiB1KGUsbil7aWYocihlLmVSLG4pKXtmb3IoO2UuZW5kc1BhcmVudCYmZS5wYXJlbnQ7KWU9ZS5wYXJlbnQ7cmV0dXJuIGV9cmV0dXJuIGUuZVc/dShlLnBhcmVudCxuKTp2b2lkIDB9ZnVuY3Rpb24gYyhlLG4pe3JldHVybiFhJiZyKG4uaVIsZSl9ZnVuY3Rpb24gbChlLG4pe3ZhciB0PU4uY0k/blswXS50b0xvd2VyQ2FzZSgpOm5bMF07cmV0dXJuIGUuay5oYXNPd25Qcm9wZXJ0eSh0KSYmZS5rW3RdfWZ1bmN0aW9uIHAoZSxuLHQscil7dmFyIGE9cj8iIjpJLmNsYXNzUHJlZml4LGk9JzxzcGFuIGNsYXNzPSInK2Esbz10PyIiOkM7cmV0dXJuIGkrPWUrJyI+JyxpK24rb31mdW5jdGlvbiBoKCl7dmFyIGUsdCxyLGE7aWYoIUUuaylyZXR1cm4gbihrKTtmb3IoYT0iIix0PTAsRS5sUi5sYXN0SW5kZXg9MCxyPUUubFIuZXhlYyhrKTtyOylhKz1uKGsuc3Vic3RyaW5nKHQsci5pbmRleCkpLGU9bChFLHIpLGU/KEIrPWVbMV0sYSs9cChlWzBdLG4oclswXSkpKTphKz1uKHJbMF0pLHQ9RS5sUi5sYXN0SW5kZXgscj1FLmxSLmV4ZWMoayk7cmV0dXJuIGErbihrLnN1YnN0cih0KSl9ZnVuY3Rpb24gZCgpe3ZhciBlPSJzdHJpbmciPT10eXBlb2YgRS5zTDtpZihlJiYheVtFLnNMXSlyZXR1cm4gbihrKTt2YXIgdD1lP2YoRS5zTCxrLCEwLHhbRS5zTF0pOmcoayxFLnNMLmxlbmd0aD9FLnNMOnZvaWQgMCk7cmV0dXJuIEUucj4wJiYoQis9dC5yKSxlJiYoeFtFLnNMXT10LnRvcCkscCh0Lmxhbmd1YWdlLHQudmFsdWUsITEsITApfWZ1bmN0aW9uIGIoKXtMKz1udWxsIT1FLnNMP2QoKTpoKCksaz0iIn1mdW5jdGlvbiB2KGUpe0wrPWUuY04/cChlLmNOLCIiLCEwKToiIixFPU9iamVjdC5jcmVhdGUoZSx7cGFyZW50Ont2YWx1ZTpFfX0pfWZ1bmN0aW9uIG0oZSxuKXtpZihrKz1lLG51bGw9PW4pcmV0dXJuIGIoKSwwO3ZhciB0PW8obixFKTtpZih0KXJldHVybiB0LnNraXA/ays9bjoodC5lQiYmKGsrPW4pLGIoKSx0LnJCfHx0LmVCfHwoaz1uKSksdih0LG4pLHQuckI/MDpuLmxlbmd0aDt2YXIgcj11KEUsbik7aWYocil7dmFyIGE9RTthLnNraXA/ays9bjooYS5yRXx8YS5lRXx8KGsrPW4pLGIoKSxhLmVFJiYoaz1uKSk7ZG8gRS5jTiYmKEwrPUMpLEUuc2tpcHx8KEIrPUUuciksRT1FLnBhcmVudDt3aGlsZShFIT09ci5wYXJlbnQpO3JldHVybiByLnN0YXJ0cyYmdihyLnN0YXJ0cywiIiksYS5yRT8wOm4ubGVuZ3RofWlmKGMobixFKSl0aHJvdyBuZXcgRXJyb3IoJ0lsbGVnYWwgbGV4ZW1lICInK24rJyIgZm9yIG1vZGUgIicrKEUuY058fCI8dW5uYW1lZD4iKSsnIicpO3JldHVybiBrKz1uLG4ubGVuZ3RofHwxfXZhciBOPXcoZSk7aWYoIU4pdGhyb3cgbmV3IEVycm9yKCdVbmtub3duIGxhbmd1YWdlOiAiJytlKyciJyk7cyhOKTt2YXIgUixFPWl8fE4seD17fSxMPSIiO2ZvcihSPUU7UiE9PU47Uj1SLnBhcmVudClSLmNOJiYoTD1wKFIuY04sIiIsITApK0wpO3ZhciBrPSIiLEI9MDt0cnl7Zm9yKHZhciBNLGosTz0wOzspe2lmKEUudC5sYXN0SW5kZXg9TyxNPUUudC5leGVjKHQpLCFNKWJyZWFrO2o9bSh0LnN1YnN0cmluZyhPLE0uaW5kZXgpLE1bMF0pLE89TS5pbmRleCtqfWZvcihtKHQuc3Vic3RyKE8pKSxSPUU7Ui5wYXJlbnQ7Uj1SLnBhcmVudClSLmNOJiYoTCs9Qyk7cmV0dXJue3I6Qix2YWx1ZTpMLGxhbmd1YWdlOmUsdG9wOkV9fWNhdGNoKFQpe2lmKFQubWVzc2FnZSYmLTEhPT1ULm1lc3NhZ2UuaW5kZXhPZigiSWxsZWdhbCIpKXJldHVybntyOjAsdmFsdWU6bih0KX07dGhyb3cgVH19ZnVuY3Rpb24gZyhlLHQpe3Q9dHx8SS5sYW5ndWFnZXN8fHgoeSk7dmFyIHI9e3I6MCx2YWx1ZTpuKGUpfSxhPXI7cmV0dXJuIHQuZmlsdGVyKHcpLmZvckVhY2goZnVuY3Rpb24obil7dmFyIHQ9ZihuLGUsITEpO3QubGFuZ3VhZ2U9bix0LnI+YS5yJiYoYT10KSx0LnI+ci5yJiYoYT1yLHI9dCl9KSxhLmxhbmd1YWdlJiYoci5zZWNvbmRfYmVzdD1hKSxyfWZ1bmN0aW9uIHAoZSl7cmV0dXJuIEkudGFiUmVwbGFjZXx8SS51c2VCUj9lLnJlcGxhY2UoTSxmdW5jdGlvbihlLG4pe3JldHVybiBJLnVzZUJSJiYiXG4iPT09ZT8iPGJyPiI6SS50YWJSZXBsYWNlP24ucmVwbGFjZSgvXHQvZyxJLnRhYlJlcGxhY2UpOiIifSk6ZX1mdW5jdGlvbiBoKGUsbix0KXt2YXIgcj1uP0xbbl06dCxhPVtlLnRyaW0oKV07cmV0dXJuIGUubWF0Y2goL1xiaGxqc1xiLyl8fGEucHVzaCgiaGxqcyIpLC0xPT09ZS5pbmRleE9mKHIpJiZhLnB1c2gociksYS5qb2luKCIgIikudHJpbSgpfWZ1bmN0aW9uIGQoZSl7dmFyIG4sdCxyLG8sbCxzPWkoZSk7YShzKXx8KEkudXNlQlI/KG49ZG9jdW1lbnQuY3JlYXRlRWxlbWVudE5TKCJodHRwOi8vd3d3LnczLm9yZy8xOTk5L3hodG1sIiwiZGl2Iiksbi5pbm5lckhUTUw9ZS5pbm5lckhUTUwucmVwbGFjZSgvXG4vZywiIikucmVwbGFjZSgvPGJyWyBcL10qPi9nLCJcbiIpKTpuPWUsbD1uLnRleHRDb250ZW50LHI9cz9mKHMsbCwhMCk6ZyhsKSx0PXUobiksdC5sZW5ndGgmJihvPWRvY3VtZW50LmNyZWF0ZUVsZW1lbnROUygiaHR0cDovL3d3dy53My5vcmcvMTk5OS94aHRtbCIsImRpdiIpLG8uaW5uZXJIVE1MPXIudmFsdWUsci52YWx1ZT1jKHQsdShvKSxsKSksci52YWx1ZT1wKHIudmFsdWUpLGUuaW5uZXJIVE1MPXIudmFsdWUsZS5jbGFzc05hbWU9aChlLmNsYXNzTmFtZSxzLHIubGFuZ3VhZ2UpLGUucmVzdWx0PXtsYW5ndWFnZTpyLmxhbmd1YWdlLHJlOnIucn0sci5zZWNvbmRfYmVzdCYmKGUuc2Vjb25kX2Jlc3Q9e2xhbmd1YWdlOnIuc2Vjb25kX2Jlc3QubGFuZ3VhZ2UscmU6ci5zZWNvbmRfYmVzdC5yfSkpfWZ1bmN0aW9uIGIoZSl7ST1vKEksZSl9ZnVuY3Rpb24gdigpe2lmKCF2LmNhbGxlZCl7di5jYWxsZWQ9ITA7dmFyIGU9ZG9jdW1lbnQucXVlcnlTZWxlY3RvckFsbCgicHJlIGNvZGUiKTtFLmZvckVhY2guY2FsbChlLGQpfX1mdW5jdGlvbiBtKCl7YWRkRXZlbnRMaXN0ZW5lcigiRE9NQ29udGVudExvYWRlZCIsdiwhMSksYWRkRXZlbnRMaXN0ZW5lcigibG9hZCIsdiwhMSl9ZnVuY3Rpb24gTihuLHQpe3ZhciByPXlbbl09dChlKTtyLmFsaWFzZXMmJnIuYWxpYXNlcy5mb3JFYWNoKGZ1bmN0aW9uKGUpe0xbZV09bn0pfWZ1bmN0aW9uIFIoKXtyZXR1cm4geCh5KX1mdW5jdGlvbiB3KGUpe3JldHVybiBlPShlfHwiIikudG9Mb3dlckNhc2UoKSx5W2VdfHx5W0xbZV1dfXZhciBFPVtdLHg9T2JqZWN0LmtleXMseT17fSxMPXt9LGs9L14obm8tP2hpZ2hsaWdodHxwbGFpbnx0ZXh0KSQvaSxCPS9cYmxhbmcoPzp1YWdlKT8tKFtcdy1dKylcYi9pLE09LygoXig8W14+XSs+fFx0fCkrfCg/OlxuKSkpL2dtLEM9Ijwvc3Bhbj4iLEk9e2NsYXNzUHJlZml4OiJobGpzLSIsdGFiUmVwbGFjZTpudWxsLHVzZUJSOiExLGxhbmd1YWdlczp2b2lkIDB9O3JldHVybiBlLmhpZ2hsaWdodD1mLGUuaGlnaGxpZ2h0QXV0bz1nLGUuZml4TWFya3VwPXAsZS5oaWdobGlnaHRCbG9jaz1kLGUuY29uZmlndXJlPWIsZS5pbml0SGlnaGxpZ2h0aW5nPXYsZS5pbml0SGlnaGxpZ2h0aW5nT25Mb2FkPW0sZS5yZWdpc3Rlckxhbmd1YWdlPU4sZS5saXN0TGFuZ3VhZ2VzPVIsZS5nZXRMYW5ndWFnZT13LGUuaW5oZXJpdD1vLGUuSVI9IlthLXpBLVpdXFx3KiIsZS5VSVI9IlthLXpBLVpfXVxcdyoiLGUuTlI9IlxcYlxcZCsoXFwuXFxkKyk/IixlLkNOUj0iKC0/KShcXGIwW3hYXVthLWZBLUYwLTldK3woXFxiXFxkKyhcXC5cXGQqKT98XFwuXFxkKykoW2VFXVstK10/XFxkKyk/KSIsZS5CTlI9IlxcYigwYlswMV0rKSIsZS5SU1I9IiF8IT18IT09fCV8JT18JnwmJnwmPXxcXCp8XFwqPXxcXCt8XFwrPXwsfC18LT18Lz18L3w6fDt8PDx8PDw9fDw9fDx8PT09fD09fD18Pj4+PXw+Pj18Pj18Pj4+fD4+fD58XFw/fFxcW3xcXHt8XFwofFxcXnxcXF49fFxcfHxcXHw9fFxcfFxcfHx+IixlLkJFPXtiOiJcXFxcW1xcc1xcU10iLHI6MH0sZS5BU009e2NOOiJzdHJpbmciLGI6IiciLGU6IiciLGk6IlxcbiIsYzpbZS5CRV19LGUuUVNNPXtjTjoic3RyaW5nIixiOiciJyxlOiciJyxpOiJcXG4iLGM6W2UuQkVdfSxlLlBXTT17YjovXGIoYXxhbnx0aGV8YXJlfEknbXxpc24ndHxkb24ndHxkb2Vzbid0fHdvbid0fGJ1dHxqdXN0fHNob3VsZHxwcmV0dHl8c2ltcGx5fGVub3VnaHxnb25uYXxnb2luZ3x3dGZ8c298c3VjaHx3aWxsfHlvdXx5b3VyfHRoZXl8bGlrZXxtb3JlKVxiL30sZS5DPWZ1bmN0aW9uKG4sdCxyKXt2YXIgYT1lLmluaGVyaXQoe2NOOiJjb21tZW50IixiOm4sZTp0LGM6W119LHJ8fHt9KTtyZXR1cm4gYS5jLnB1c2goZS5QV00pLGEuYy5wdXNoKHtjTjoiZG9jdGFnIixiOiIoPzpUT0RPfEZJWE1FfE5PVEV8QlVHfFhYWCk6IixyOjB9KSxhfSxlLkNMQ009ZS5DKCIvLyIsIiQiKSxlLkNCQ009ZS5DKCIvXFwqIiwiXFwqLyIpLGUuSENNPWUuQygiIyIsIiQiKSxlLk5NPXtjTjoibnVtYmVyIixiOmUuTlIscjowfSxlLkNOTT17Y046Im51bWJlciIsYjplLkNOUixyOjB9LGUuQk5NPXtjTjoibnVtYmVyIixiOmUuQk5SLHI6MH0sZS5DU1NOTT17Y046Im51bWJlciIsYjplLk5SKyIoJXxlbXxleHxjaHxyZW18dnd8dmh8dm1pbnx2bWF4fGNtfG1tfGlufHB0fHBjfHB4fGRlZ3xncmFkfHJhZHx0dXJufHN8bXN8SHp8a0h6fGRwaXxkcGNtfGRwcHgpPyIscjowfSxlLlJNPXtjTjoicmVnZXhwIixiOi9cLy8sZTovXC9bZ2ltdXldKi8saTovXG4vLGM6W2UuQkUse2I6L1xbLyxlOi9cXS8scjowLGM6W2UuQkVdfV19LGUuVE09e2NOOiJ0aXRsZSIsYjplLklSLHI6MH0sZS5VVE09e2NOOiJ0aXRsZSIsYjplLlVJUixyOjB9LGUuTUVUSE9EX0dVQVJEPXtiOiJcXC5cXHMqIitlLlVJUixyOjB9LGV9KTtobGpzLnJlZ2lzdGVyTGFuZ3VhZ2UoInNxbCIsZnVuY3Rpb24oZSl7dmFyIHQ9ZS5DKCItLSIsIiQiKTtyZXR1cm57Y0k6ITAsaTovWzw+e30qI10vLGM6W3tiSzoiYmVnaW4gZW5kIHN0YXJ0IGNvbW1pdCByb2xsYmFjayBzYXZlcG9pbnQgbG9jayBhbHRlciBjcmVhdGUgZHJvcCByZW5hbWUgY2FsbCBkZWxldGUgZG8gaGFuZGxlciBpbnNlcnQgbG9hZCByZXBsYWNlIHNlbGVjdCB0cnVuY2F0ZSB1cGRhdGUgc2V0IHNob3cgcHJhZ21hIGdyYW50IG1lcmdlIGRlc2NyaWJlIHVzZSBleHBsYWluIGhlbHAgZGVjbGFyZSBwcmVwYXJlIGV4ZWN1dGUgZGVhbGxvY2F0ZSByZWxlYXNlIHVubG9jayBwdXJnZSByZXNldCBjaGFuZ2Ugc3RvcCBhbmFseXplIGNhY2hlIGZsdXNoIG9wdGltaXplIHJlcGFpciBraWxsIGluc3RhbGwgdW5pbnN0YWxsIGNoZWNrc3VtIHJlc3RvcmUgY2hlY2sgYmFja3VwIHJldm9rZSBjb21tZW50IixlOi87LyxlVzohMCxsOi9bXHdcLl0rLyxrOntrZXl3b3JkOiJhYm9ydCBhYnMgYWJzb2x1dGUgYWNjIGFjY2UgYWNjZXAgYWNjZXB0IGFjY2VzcyBhY2Nlc3NlZCBhY2Nlc3NpYmxlIGFjY291bnQgYWNvcyBhY3Rpb24gYWN0aXZhdGUgYWRkIGFkZHRpbWUgYWRtaW4gYWRtaW5pc3RlciBhZHZhbmNlZCBhZHZpc2UgYWVzX2RlY3J5cHQgYWVzX2VuY3J5cHQgYWZ0ZXIgYWdlbnQgYWdncmVnYXRlIGFsaSBhbGlhIGFsaWFzIGFsbG9jYXRlIGFsbG93IGFsdGVyIGFsd2F5cyBhbmFseXplIGFuY2lsbGFyeSBhbmQgYW55IGFueWRhdGEgYW55ZGF0YXNldCBhbnlzY2hlbWEgYW55dHlwZSBhcHBseSBhcmNoaXZlIGFyY2hpdmVkIGFyY2hpdmVsb2cgYXJlIGFzIGFzYyBhc2NpaSBhc2luIGFzc2VtYmx5IGFzc2VydGlvbiBhc3NvY2lhdGUgYXN5bmNocm9ub3VzIGF0IGF0YW4gYXRuMiBhdHRyIGF0dHJpIGF0dHJpYiBhdHRyaWJ1IGF0dHJpYnV0IGF0dHJpYnV0ZSBhdHRyaWJ1dGVzIGF1ZGl0IGF1dGhlbnRpY2F0ZWQgYXV0aGVudGljYXRpb24gYXV0aGlkIGF1dGhvcnMgYXV0byBhdXRvYWxsb2NhdGUgYXV0b2RibGluayBhdXRvZXh0ZW5kIGF1dG9tYXRpYyBhdmFpbGFiaWxpdHkgYXZnIGJhY2t1cCBiYWRmaWxlIGJhc2ljZmlsZSBiZWZvcmUgYmVnaW4gYmVnaW5uaW5nIGJlbmNobWFyayBiZXR3ZWVuIGJmaWxlIGJmaWxlX2Jhc2UgYmlnIGJpZ2ZpbGUgYmluIGJpbmFyeV9kb3VibGUgYmluYXJ5X2Zsb2F0IGJpbmxvZyBiaXRfYW5kIGJpdF9jb3VudCBiaXRfbGVuZ3RoIGJpdF9vciBiaXRfeG9yIGJpdG1hcCBibG9iX2Jhc2UgYmxvY2sgYmxvY2tzaXplIGJvZHkgYm90aCBib3VuZCBidWZmZXJfY2FjaGUgYnVmZmVyX3Bvb2wgYnVpbGQgYnVsayBieSBieXRlIGJ5dGVvcmRlcm1hcmsgYnl0ZXMgY2FjaGUgY2FjaGluZyBjYWxsIGNhbGxpbmcgY2FuY2VsIGNhcGFjaXR5IGNhc2NhZGUgY2FzY2FkZWQgY2FzZSBjYXN0IGNhdGFsb2cgY2F0ZWdvcnkgY2VpbCBjZWlsaW5nIGNoYWluIGNoYW5nZSBjaGFuZ2VkIGNoYXJfYmFzZSBjaGFyX2xlbmd0aCBjaGFyYWN0ZXJfbGVuZ3RoIGNoYXJhY3RlcnMgY2hhcmFjdGVyc2V0IGNoYXJpbmRleCBjaGFyc2V0IGNoYXJzZXRmb3JtIGNoYXJzZXRpZCBjaGVjayBjaGVja3N1bSBjaGVja3N1bV9hZ2cgY2hpbGQgY2hvb3NlIGNociBjaHVuayBjbGFzcyBjbGVhbnVwIGNsZWFyIGNsaWVudCBjbG9iIGNsb2JfYmFzZSBjbG9uZSBjbG9zZSBjbHVzdGVyX2lkIGNsdXN0ZXJfcHJvYmFiaWxpdHkgY2x1c3Rlcl9zZXQgY2x1c3RlcmluZyBjb2FsZXNjZSBjb2VyY2liaWxpdHkgY29sIGNvbGxhdGUgY29sbGF0aW9uIGNvbGxlY3QgY29sdSBjb2x1bSBjb2x1bW4gY29sdW1uX3ZhbHVlIGNvbHVtbnMgY29sdW1uc191cGRhdGVkIGNvbW1lbnQgY29tbWl0IGNvbXBhY3QgY29tcGF0aWJpbGl0eSBjb21waWxlZCBjb21wbGV0ZSBjb21wb3NpdGVfbGltaXQgY29tcG91bmQgY29tcHJlc3MgY29tcHV0ZSBjb25jYXQgY29uY2F0X3dzIGNvbmN1cnJlbnQgY29uZmlybSBjb25uIGNvbm5lYyBjb25uZWN0IGNvbm5lY3RfYnlfaXNjeWNsZSBjb25uZWN0X2J5X2lzbGVhZiBjb25uZWN0X2J5X3Jvb3QgY29ubmVjdF90aW1lIGNvbm5lY3Rpb24gY29uc2lkZXIgY29uc2lzdGVudCBjb25zdGFudCBjb25zdHJhaW50IGNvbnN0cmFpbnRzIGNvbnN0cnVjdG9yIGNvbnRhaW5lciBjb250ZW50IGNvbnRlbnRzIGNvbnRleHQgY29udHJpYnV0b3JzIGNvbnRyb2xmaWxlIGNvbnYgY29udmVydCBjb252ZXJ0X3R6IGNvcnIgY29ycl9rIGNvcnJfcyBjb3JyZXNwb25kaW5nIGNvcnJ1cHRpb24gY29zIGNvc3QgY291bnQgY291bnRfYmlnIGNvdW50ZWQgY292YXJfcG9wIGNvdmFyX3NhbXAgY3B1X3Blcl9jYWxsIGNwdV9wZXJfc2Vzc2lvbiBjcmMzMiBjcmVhdGUgY3JlYXRpb24gY3JpdGljYWwgY3Jvc3MgY3ViZSBjdW1lX2Rpc3QgY3VyZGF0ZSBjdXJyZW50IGN1cnJlbnRfZGF0ZSBjdXJyZW50X3RpbWUgY3VycmVudF90aW1lc3RhbXAgY3VycmVudF91c2VyIGN1cnNvciBjdXJ0aW1lIGN1c3RvbWRhdHVtIGN5Y2xlIGRhdGEgZGF0YWJhc2UgZGF0YWJhc2VzIGRhdGFmaWxlIGRhdGFmaWxlcyBkYXRhbGVuZ3RoIGRhdGVfYWRkIGRhdGVfY2FjaGUgZGF0ZV9mb3JtYXQgZGF0ZV9zdWIgZGF0ZWFkZCBkYXRlZGlmZiBkYXRlZnJvbXBhcnRzIGRhdGVuYW1lIGRhdGVwYXJ0IGRhdGV0aW1lMmZyb21wYXJ0cyBkYXkgZGF5X3RvX3NlY29uZCBkYXluYW1lIGRheW9mbW9udGggZGF5b2Z3ZWVrIGRheW9meWVhciBkYXlzIGRiX3JvbGVfY2hhbmdlIGRidGltZXpvbmUgZGRsIGRlYWxsb2NhdGUgZGVjbGFyZSBkZWNvZGUgZGVjb21wb3NlIGRlY3JlbWVudCBkZWNyeXB0IGRlZHVwbGljYXRlIGRlZiBkZWZhIGRlZmF1IGRlZmF1bCBkZWZhdWx0IGRlZmF1bHRzIGRlZmVycmVkIGRlZmkgZGVmaW4gZGVmaW5lIGRlZ3JlZXMgZGVsYXllZCBkZWxlZ2F0ZSBkZWxldGUgZGVsZXRlX2FsbCBkZWxpbWl0ZWQgZGVtYW5kIGRlbnNlX3JhbmsgZGVwdGggZGVxdWV1ZSBkZXNfZGVjcnlwdCBkZXNfZW5jcnlwdCBkZXNfa2V5X2ZpbGUgZGVzYyBkZXNjciBkZXNjcmkgZGVzY3JpYiBkZXNjcmliZSBkZXNjcmlwdG9yIGRldGVybWluaXN0aWMgZGlhZ25vc3RpY3MgZGlmZmVyZW5jZSBkaW1lbnNpb24gZGlyZWN0X2xvYWQgZGlyZWN0b3J5IGRpc2FibGUgZGlzYWJsZV9hbGwgZGlzYWxsb3cgZGlzYXNzb2NpYXRlIGRpc2NhcmRmaWxlIGRpc2Nvbm5lY3QgZGlza2dyb3VwIGRpc3RpbmN0IGRpc3RpbmN0cm93IGRpc3RyaWJ1dGUgZGlzdHJpYnV0ZWQgZGl2IGRvIGRvY3VtZW50IGRvbWFpbiBkb3RuZXQgZG91YmxlIGRvd25ncmFkZSBkcm9wIGR1bXBmaWxlIGR1cGxpY2F0ZSBkdXJhdGlvbiBlYWNoIGVkaXRpb24gZWRpdGlvbmFibGUgZWRpdGlvbnMgZWxlbWVudCBlbGxpcHNpcyBlbHNlIGVsc2lmIGVsdCBlbXB0eSBlbmFibGUgZW5hYmxlX2FsbCBlbmNsb3NlZCBlbmNvZGUgZW5jb2RpbmcgZW5jcnlwdCBlbmQgZW5kLWV4ZWMgZW5kaWFuIGVuZm9yY2VkIGVuZ2luZSBlbmdpbmVzIGVucXVldWUgZW50ZXJwcmlzZSBlbnRpdHllc2NhcGluZyBlb21vbnRoIGVycm9yIGVycm9ycyBlc2NhcGVkIGV2YWxuYW1lIGV2YWx1YXRlIGV2ZW50IGV2ZW50ZGF0YSBldmVudHMgZXhjZXB0IGV4Y2VwdGlvbiBleGNlcHRpb25zIGV4Y2hhbmdlIGV4Y2x1ZGUgZXhjbHVkaW5nIGV4ZWN1IGV4ZWN1dCBleGVjdXRlIGV4ZW1wdCBleGlzdHMgZXhpdCBleHAgZXhwaXJlIGV4cGxhaW4gZXhwb3J0IGV4cG9ydF9zZXQgZXh0ZW5kZWQgZXh0ZW50IGV4dGVybmFsIGV4dGVybmFsXzEgZXh0ZXJuYWxfMiBleHRlcm5hbGx5IGV4dHJhY3QgZmFpbGVkIGZhaWxlZF9sb2dpbl9hdHRlbXB0cyBmYWlsb3ZlciBmYWlsdXJlIGZhciBmYXN0IGZlYXR1cmVfc2V0IGZlYXR1cmVfdmFsdWUgZmV0Y2ggZmllbGQgZmllbGRzIGZpbGUgZmlsZV9uYW1lX2NvbnZlcnQgZmlsZXN5c3RlbV9saWtlX2xvZ2dpbmcgZmluYWwgZmluaXNoIGZpcnN0IGZpcnN0X3ZhbHVlIGZpeGVkIGZsYXNoX2NhY2hlIGZsYXNoYmFjayBmbG9vciBmbHVzaCBmb2xsb3dpbmcgZm9sbG93cyBmb3IgZm9yYWxsIGZvcmNlIGZvcm0gZm9ybWEgZm9ybWF0IGZvdW5kIGZvdW5kX3Jvd3MgZnJlZWxpc3QgZnJlZWxpc3RzIGZyZWVwb29scyBmcmVzaCBmcm9tIGZyb21fYmFzZTY0IGZyb21fZGF5cyBmdHAgZnVsbCBmdW5jdGlvbiBnZW5lcmFsIGdlbmVyYXRlZCBnZXQgZ2V0X2Zvcm1hdCBnZXRfbG9jayBnZXRkYXRlIGdldHV0Y2RhdGUgZ2xvYmFsIGdsb2JhbF9uYW1lIGdsb2JhbGx5IGdvIGdvdG8gZ3JhbnQgZ3JhbnRzIGdyZWF0ZXN0IGdyb3VwIGdyb3VwX2NvbmNhdCBncm91cF9pZCBncm91cGluZyBncm91cGluZ19pZCBncm91cHMgZ3RpZF9zdWJ0cmFjdCBndWFyYW50ZWUgZ3VhcmQgaGFuZGxlciBoYXNoIGhhc2hrZXlzIGhhdmluZyBoZWEgaGVhZCBoZWFkaSBoZWFkaW4gaGVhZGluZyBoZWFwIGhlbHAgaGV4IGhpZXJhcmNoeSBoaWdoIGhpZ2hfcHJpb3JpdHkgaG9zdHMgaG91ciBodHRwIGlkIGlkZW50X2N1cnJlbnQgaWRlbnRfaW5jciBpZGVudF9zZWVkIGlkZW50aWZpZWQgaWRlbnRpdHkgaWRsZV90aW1lIGlmIGlmbnVsbCBpZ25vcmUgaWlmIGlsaWtlIGlsbSBpbW1lZGlhdGUgaW1wb3J0IGluIGluY2x1ZGUgaW5jbHVkaW5nIGluY3JlbWVudCBpbmRleCBpbmRleGVzIGluZGV4aW5nIGluZGV4dHlwZSBpbmRpY2F0b3IgaW5kaWNlcyBpbmV0Nl9hdG9uIGluZXQ2X250b2EgaW5ldF9hdG9uIGluZXRfbnRvYSBpbmZpbGUgaW5pdGlhbCBpbml0aWFsaXplZCBpbml0aWFsbHkgaW5pdHJhbnMgaW5tZW1vcnkgaW5uZXIgaW5ub2RiIGlucHV0IGluc2VydCBpbnN0YWxsIGluc3RhbmNlIGluc3RhbnRpYWJsZSBpbnN0ciBpbnRlcmZhY2UgaW50ZXJsZWF2ZWQgaW50ZXJzZWN0IGludG8gaW52YWxpZGF0ZSBpbnZpc2libGUgaXMgaXNfZnJlZV9sb2NrIGlzX2lwdjQgaXNfaXB2NF9jb21wYXQgaXNfbm90IGlzX25vdF9udWxsIGlzX3VzZWRfbG9jayBpc2RhdGUgaXNudWxsIGlzb2xhdGlvbiBpdGVyYXRlIGphdmEgam9pbiBqc29uIGpzb25fZXhpc3RzIGtlZXAga2VlcF9kdXBsaWNhdGVzIGtleSBrZXlzIGtpbGwgbGFuZ3VhZ2UgbGFyZ2UgbGFzdCBsYXN0X2RheSBsYXN0X2luc2VydF9pZCBsYXN0X3ZhbHVlIGxheCBsY2FzZSBsZWFkIGxlYWRpbmcgbGVhc3QgbGVhdmVzIGxlZnQgbGVuIGxlbmdodCBsZW5ndGggbGVzcyBsZXZlbCBsZXZlbHMgbGlicmFyeSBsaWtlIGxpa2UyIGxpa2U0IGxpa2VjIGxpbWl0IGxpbmVzIGxpbmsgbGlzdCBsaXN0YWdnIGxpdHRsZSBsbiBsb2FkIGxvYWRfZmlsZSBsb2IgbG9icyBsb2NhbCBsb2NhbHRpbWUgbG9jYWx0aW1lc3RhbXAgbG9jYXRlIGxvY2F0b3IgbG9jayBsb2NrZWQgbG9nIGxvZzEwIGxvZzIgbG9nZmlsZSBsb2dmaWxlcyBsb2dnaW5nIGxvZ2ljYWwgbG9naWNhbF9yZWFkc19wZXJfY2FsbCBsb2dvZmYgbG9nb24gbG9ncyBsb25nIGxvb3AgbG93IGxvd19wcmlvcml0eSBsb3dlciBscGFkIGxydHJpbSBsdHJpbSBtYWluIG1ha2Vfc2V0IG1ha2VkYXRlIG1ha2V0aW1lIG1hbmFnZWQgbWFuYWdlbWVudCBtYW51YWwgbWFwIG1hcHBpbmcgbWFzayBtYXN0ZXIgbWFzdGVyX3Bvc193YWl0IG1hdGNoIG1hdGNoZWQgbWF0ZXJpYWxpemVkIG1heCBtYXhleHRlbnRzIG1heGltaXplIG1heGluc3RhbmNlcyBtYXhsZW4gbWF4bG9nZmlsZXMgbWF4bG9naGlzdG9yeSBtYXhsb2dtZW1iZXJzIG1heHNpemUgbWF4dHJhbnMgbWQ1IG1lYXN1cmVzIG1lZGlhbiBtZWRpdW0gbWVtYmVyIG1lbWNvbXByZXNzIG1lbW9yeSBtZXJnZSBtaWNyb3NlY29uZCBtaWQgbWlncmF0aW9uIG1pbiBtaW5leHRlbnRzIG1pbmltdW0gbWluaW5nIG1pbnVzIG1pbnV0ZSBtaW52YWx1ZSBtaXNzaW5nIG1vZCBtb2RlIG1vZGVsIG1vZGlmaWNhdGlvbiBtb2RpZnkgbW9kdWxlIG1vbml0b3JpbmcgbW9udGggbW9udGhzIG1vdW50IG1vdmUgbW92ZW1lbnQgbXVsdGlzZXQgbXV0ZXggbmFtZSBuYW1lX2NvbnN0IG5hbWVzIG5hbiBuYXRpb25hbCBuYXRpdmUgbmF0dXJhbCBuYXYgbmNoYXIgbmNsb2IgbmVzdGVkIG5ldmVyIG5ldyBuZXdsaW5lIG5leHQgbmV4dHZhbCBubyBub193cml0ZV90b19iaW5sb2cgbm9hcmNoaXZlbG9nIG5vYXVkaXQgbm9iYWRmaWxlIG5vY2hlY2sgbm9jb21wcmVzcyBub2NvcHkgbm9jeWNsZSBub2RlbGF5IG5vZGlzY2FyZGZpbGUgbm9lbnRpdHllc2NhcGluZyBub2d1YXJhbnRlZSBub2tlZXAgbm9sb2dmaWxlIG5vbWFwcGluZyBub21heHZhbHVlIG5vbWluaW1pemUgbm9taW52YWx1ZSBub21vbml0b3Jpbmcgbm9uZSBub25lZGl0aW9uYWJsZSBub25zY2hlbWEgbm9vcmRlciBub3ByIG5vcHJvIG5vcHJvbSBub3Byb21wIG5vcHJvbXB0IG5vcmVseSBub3Jlc2V0bG9ncyBub3JldmVyc2Ugbm9ybWFsIG5vcm93ZGVwZW5kZW5jaWVzIG5vc2NoZW1hY2hlY2sgbm9zd2l0Y2ggbm90IG5vdGhpbmcgbm90aWNlIG5vdHJpbSBub3ZhbGlkYXRlIG5vdyBub3dhaXQgbnRoX3ZhbHVlIG51bGxpZiBudWxscyBudW0gbnVtYiBudW1iZSBudmFyY2hhciBudmFyY2hhcjIgb2JqZWN0IG9jaWNvbGwgb2NpZGF0ZSBvY2lkYXRldGltZSBvY2lkdXJhdGlvbiBvY2lpbnRlcnZhbCBvY2lsb2Jsb2NhdG9yIG9jaW51bWJlciBvY2lyZWYgb2NpcmVmY3Vyc29yIG9jaXJvd2lkIG9jaXN0cmluZyBvY2l0eXBlIG9jdCBvY3RldF9sZW5ndGggb2Ygb2ZmIG9mZmxpbmUgb2Zmc2V0IG9pZCBvaWRpbmRleCBvbGQgb24gb25saW5lIG9ubHkgb3BhcXVlIG9wZW4gb3BlcmF0aW9ucyBvcGVyYXRvciBvcHRpbWFsIG9wdGltaXplIG9wdGlvbiBvcHRpb25hbGx5IG9yIG9yYWNsZSBvcmFjbGVfZGF0ZSBvcmFkYXRhIG9yZCBvcmRhdWRpbyBvcmRkaWNvbSBvcmRkb2Mgb3JkZXIgb3JkaW1hZ2Ugb3JkaW5hbGl0eSBvcmR2aWRlbyBvcmdhbml6YXRpb24gb3JsYW55IG9ybHZhcnkgb3V0IG91dGVyIG91dGZpbGUgb3V0bGluZSBvdXRwdXQgb3ZlciBvdmVyZmxvdyBvdmVycmlkaW5nIHBhY2thZ2UgcGFkIHBhcmFsbGVsIHBhcmFsbGVsX2VuYWJsZSBwYXJhbWV0ZXJzIHBhcmVudCBwYXJzZSBwYXJ0aWFsIHBhcnRpdGlvbiBwYXJ0aXRpb25zIHBhc2NhbCBwYXNzaW5nIHBhc3N3b3JkIHBhc3N3b3JkX2dyYWNlX3RpbWUgcGFzc3dvcmRfbG9ja190aW1lIHBhc3N3b3JkX3JldXNlX21heCBwYXNzd29yZF9yZXVzZV90aW1lIHBhc3N3b3JkX3ZlcmlmeV9mdW5jdGlvbiBwYXRjaCBwYXRoIHBhdGluZGV4IHBjdGluY3JlYXNlIHBjdHRocmVzaG9sZCBwY3R1c2VkIHBjdHZlcnNpb24gcGVyY2VudCBwZXJjZW50X3JhbmsgcGVyY2VudGlsZV9jb250IHBlcmNlbnRpbGVfZGlzYyBwZXJmb3JtYW5jZSBwZXJpb2QgcGVyaW9kX2FkZCBwZXJpb2RfZGlmZiBwZXJtYW5lbnQgcGh5c2ljYWwgcGkgcGlwZSBwaXBlbGluZWQgcGl2b3QgcGx1Z2dhYmxlIHBsdWdpbiBwb2xpY3kgcG9zaXRpb24gcG9zdF90cmFuc2FjdGlvbiBwb3cgcG93ZXIgcHJhZ21hIHByZWJ1aWx0IHByZWNlZGVzIHByZWNlZGluZyBwcmVjaXNpb24gcHJlZGljdGlvbiBwcmVkaWN0aW9uX2Nvc3QgcHJlZGljdGlvbl9kZXRhaWxzIHByZWRpY3Rpb25fcHJvYmFiaWxpdHkgcHJlZGljdGlvbl9zZXQgcHJlcGFyZSBwcmVzZW50IHByZXNlcnZlIHByaW9yIHByaW9yaXR5IHByaXZhdGUgcHJpdmF0ZV9zZ2EgcHJpdmlsZWdlcyBwcm9jZWR1cmFsIHByb2NlZHVyZSBwcm9jZWR1cmVfYW5hbHl6ZSBwcm9jZXNzbGlzdCBwcm9maWxlcyBwcm9qZWN0IHByb21wdCBwcm90ZWN0aW9uIHB1YmxpYyBwdWJsaXNoaW5nc2VydmVybmFtZSBwdXJnZSBxdWFydGVyIHF1ZXJ5IHF1aWNrIHF1aWVzY2UgcXVvdGEgcXVvdGVuYW1lIHJhZGlhbnMgcmFpc2UgcmFuZCByYW5nZSByYW5rIHJhdyByZWFkIHJlYWRzIHJlYWRzaXplIHJlYnVpbGQgcmVjb3JkIHJlY29yZHMgcmVjb3ZlciByZWNvdmVyeSByZWN1cnNpdmUgcmVjeWNsZSByZWRvIHJlZHVjZWQgcmVmIHJlZmVyZW5jZSByZWZlcmVuY2VkIHJlZmVyZW5jZXMgcmVmZXJlbmNpbmcgcmVmcmVzaCByZWdleHBfbGlrZSByZWdpc3RlciByZWdyX2F2Z3ggcmVncl9hdmd5IHJlZ3JfY291bnQgcmVncl9pbnRlcmNlcHQgcmVncl9yMiByZWdyX3Nsb3BlIHJlZ3Jfc3h4IHJlZ3Jfc3h5IHJlamVjdCByZWtleSByZWxhdGlvbmFsIHJlbGF0aXZlIHJlbGF5bG9nIHJlbGVhc2UgcmVsZWFzZV9sb2NrIHJlbGllc19vbiByZWxvY2F0ZSByZWx5IHJlbSByZW1haW5kZXIgcmVuYW1lIHJlcGFpciByZXBlYXQgcmVwbGFjZSByZXBsaWNhdGUgcmVwbGljYXRpb24gcmVxdWlyZWQgcmVzZXQgcmVzZXRsb2dzIHJlc2l6ZSByZXNvdXJjZSByZXNwZWN0IHJlc3RvcmUgcmVzdHJpY3RlZCByZXN1bHQgcmVzdWx0X2NhY2hlIHJlc3VtYWJsZSByZXN1bWUgcmV0ZW50aW9uIHJldHVybiByZXR1cm5pbmcgcmV0dXJucyByZXVzZSByZXZlcnNlIHJldm9rZSByaWdodCBybGlrZSByb2xlIHJvbGVzIHJvbGxiYWNrIHJvbGxpbmcgcm9sbHVwIHJvdW5kIHJvdyByb3dfY291bnQgcm93ZGVwZW5kZW5jaWVzIHJvd2lkIHJvd251bSByb3dzIHJ0cmltIHJ1bGVzIHNhZmUgc2FsdCBzYW1wbGUgc2F2ZSBzYXZlcG9pbnQgc2IxIHNiMiBzYjQgc2NhbiBzY2hlbWEgc2NoZW1hY2hlY2sgc2NuIHNjb3BlIHNjcm9sbCBzZG9fZ2VvcmFzdGVyIHNkb190b3BvX2dlb21ldHJ5IHNlYXJjaCBzZWNfdG9fdGltZSBzZWNvbmQgc2VjdGlvbiBzZWN1cmVmaWxlIHNlY3VyaXR5IHNlZWQgc2VnbWVudCBzZWxlY3Qgc2VsZiBzZXF1ZW5jZSBzZXF1ZW50aWFsIHNlcmlhbGl6YWJsZSBzZXJ2ZXIgc2VydmVyZXJyb3Igc2Vzc2lvbiBzZXNzaW9uX3VzZXIgc2Vzc2lvbnNfcGVyX3VzZXIgc2V0IHNldHMgc2V0dGluZ3Mgc2hhIHNoYTEgc2hhMiBzaGFyZSBzaGFyZWQgc2hhcmVkX3Bvb2wgc2hvcnQgc2hvdyBzaHJpbmsgc2h1dGRvd24gc2lfYXZlcmFnZWNvbG9yIHNpX2NvbG9yaGlzdG9ncmFtIHNpX2ZlYXR1cmVsaXN0IHNpX3Bvc2l0aW9uYWxjb2xvciBzaV9zdGlsbGltYWdlIHNpX3RleHR1cmUgc2libGluZ3Mgc2lkIHNpZ24gc2luIHNpemUgc2l6ZV90IHNpemVzIHNraXAgc2xhdmUgc2xlZXAgc21hbGxkYXRldGltZWZyb21wYXJ0cyBzbWFsbGZpbGUgc25hcHNob3Qgc29tZSBzb25hbWUgc29ydCBzb3VuZGV4IHNvdXJjZSBzcGFjZSBzcGFyc2Ugc3BmaWxlIHNwbGl0IHNxbCBzcWxfYmlnX3Jlc3VsdCBzcWxfYnVmZmVyX3Jlc3VsdCBzcWxfY2FjaGUgc3FsX2NhbGNfZm91bmRfcm93cyBzcWxfc21hbGxfcmVzdWx0IHNxbF92YXJpYW50X3Byb3BlcnR5IHNxbGNvZGUgc3FsZGF0YSBzcWxlcnJvciBzcWxuYW1lIHNxbHN0YXRlIHNxcnQgc3F1YXJlIHN0YW5kYWxvbmUgc3RhbmRieSBzdGFydCBzdGFydGluZyBzdGFydHVwIHN0YXRlbWVudCBzdGF0aWMgc3RhdGlzdGljcyBzdGF0c19iaW5vbWlhbF90ZXN0IHN0YXRzX2Nyb3NzdGFiIHN0YXRzX2tzX3Rlc3Qgc3RhdHNfbW9kZSBzdGF0c19td190ZXN0IHN0YXRzX29uZV93YXlfYW5vdmEgc3RhdHNfdF90ZXN0XyBzdGF0c190X3Rlc3RfaW5kZXAgc3RhdHNfdF90ZXN0X29uZSBzdGF0c190X3Rlc3RfcGFpcmVkIHN0YXRzX3dzcl90ZXN0IHN0YXR1cyBzdGQgc3RkZGV2IHN0ZGRldl9wb3Agc3RkZGV2X3NhbXAgc3RkZXYgc3RvcCBzdG9yYWdlIHN0b3JlIHN0b3JlZCBzdHIgc3RyX3RvX2RhdGUgc3RyYWlnaHRfam9pbiBzdHJjbXAgc3RyaWN0IHN0cmluZyBzdHJ1Y3Qgc3R1ZmYgc3R5bGUgc3ViZGF0ZSBzdWJwYXJ0aXRpb24gc3VicGFydGl0aW9ucyBzdWJzdGl0dXRhYmxlIHN1YnN0ciBzdWJzdHJpbmcgc3VidGltZSBzdWJ0cmluZ19pbmRleCBzdWJ0eXBlIHN1Y2Nlc3Mgc3VtIHN1c3BlbmQgc3dpdGNoIHN3aXRjaG9mZnNldCBzd2l0Y2hvdmVyIHN5bmMgc3luY2hyb25vdXMgc3lub255bSBzeXMgc3lzX3htbGFnZyBzeXNhc20gc3lzYXV4IHN5c2RhdGUgc3lzZGF0ZXRpbWVvZmZzZXQgc3lzZGJhIHN5c29wZXIgc3lzdGVtIHN5c3RlbV91c2VyIHN5c3V0Y2RhdGV0aW1lIHRhYmxlIHRhYmxlcyB0YWJsZXNwYWNlIHRhbiB0ZG8gdGVtcGxhdGUgdGVtcG9yYXJ5IHRlcm1pbmF0ZWQgdGVydGlhcnlfd2VpZ2h0cyB0ZXN0IHRoYW4gdGhlbiB0aHJlYWQgdGhyb3VnaCB0aWVyIHRpZXMgdGltZSB0aW1lX2Zvcm1hdCB0aW1lX3pvbmUgdGltZWRpZmYgdGltZWZyb21wYXJ0cyB0aW1lb3V0IHRpbWVzdGFtcCB0aW1lc3RhbXBhZGQgdGltZXN0YW1wZGlmZiB0aW1lem9uZV9hYmJyIHRpbWV6b25lX21pbnV0ZSB0aW1lem9uZV9yZWdpb24gdG8gdG9fYmFzZTY0IHRvX2RhdGUgdG9fZGF5cyB0b19zZWNvbmRzIHRvZGF0ZXRpbWVvZmZzZXQgdHJhY2UgdHJhY2tpbmcgdHJhbnNhY3Rpb24gdHJhbnNhY3Rpb25hbCB0cmFuc2xhdGUgdHJhbnNsYXRpb24gdHJlYXQgdHJpZ2dlciB0cmlnZ2VyX25lc3RsZXZlbCB0cmlnZ2VycyB0cmltIHRydW5jYXRlIHRyeV9jYXN0IHRyeV9jb252ZXJ0IHRyeV9wYXJzZSB0eXBlIHViMSB1YjIgdWI0IHVjYXNlIHVuYXJjaGl2ZWQgdW5ib3VuZGVkIHVuY29tcHJlc3MgdW5kZXIgdW5kbyB1bmhleCB1bmljb2RlIHVuaWZvcm0gdW5pbnN0YWxsIHVuaW9uIHVuaXF1ZSB1bml4X3RpbWVzdGFtcCB1bmtub3duIHVubGltaXRlZCB1bmxvY2sgdW5waXZvdCB1bnJlY292ZXJhYmxlIHVuc2FmZSB1bnNpZ25lZCB1bnRpbCB1bnRydXN0ZWQgdW51c2FibGUgdW51c2VkIHVwZGF0ZSB1cGRhdGVkIHVwZ3JhZGUgdXBwZWQgdXBwZXIgdXBzZXJ0IHVybCB1cm93aWQgdXNhYmxlIHVzYWdlIHVzZSB1c2Vfc3RvcmVkX291dGxpbmVzIHVzZXIgdXNlcl9kYXRhIHVzZXJfcmVzb3VyY2VzIHVzZXJzIHVzaW5nIHV0Y19kYXRlIHV0Y190aW1lc3RhbXAgdXVpZCB1dWlkX3Nob3J0IHZhbGlkYXRlIHZhbGlkYXRlX3Bhc3N3b3JkX3N0cmVuZ3RoIHZhbGlkYXRpb24gdmFsaXN0IHZhbHVlIHZhbHVlcyB2YXIgdmFyX3NhbXAgdmFyY2hhcmMgdmFyaSB2YXJpYSB2YXJpYWIgdmFyaWFibCB2YXJpYWJsZSB2YXJpYWJsZXMgdmFyaWFuY2UgdmFycCB2YXJyYXcgdmFycmF3YyB2YXJyYXkgdmVyaWZ5IHZlcnNpb24gdmVyc2lvbnMgdmlldyB2aXJ0dWFsIHZpc2libGUgdm9pZCB3YWl0IHdhbGxldCB3YXJuaW5nIHdhcm5pbmdzIHdlZWsgd2Vla2RheSB3ZWVrb2Z5ZWFyIHdlbGxmb3JtZWQgd2hlbiB3aGVuZSB3aGVuZXYgd2hlbmV2ZSB3aGVuZXZlciB3aGVyZSB3aGlsZSB3aGl0ZXNwYWNlIHdpdGggd2l0aGluIHdpdGhvdXQgd29yayB3cmFwcGVkIHhkYiB4bWwgeG1sYWdnIHhtbGF0dHJpYnV0ZXMgeG1sY2FzdCB4bWxjb2xhdHR2YWwgeG1sZWxlbWVudCB4bWxleGlzdHMgeG1sZm9yZXN0IHhtbGluZGV4IHhtbG5hbWVzcGFjZXMgeG1scGkgeG1scXVlcnkgeG1scm9vdCB4bWxzY2hlbWEgeG1sc2VyaWFsaXplIHhtbHRhYmxlIHhtbHR5cGUgeG9yIHllYXIgeWVhcl90b19tb250aCB5ZWFycyB5ZWFyd2VlayIsbGl0ZXJhbDoidHJ1ZSBmYWxzZSBudWxsIixidWlsdF9pbjoiYXJyYXkgYmlnaW50IGJpbmFyeSBiaXQgYmxvYiBib29sZWFuIGNoYXIgY2hhcmFjdGVyIGRhdGUgZGVjIGRlY2ltYWwgZmxvYXQgaW50IGludDggaW50ZWdlciBpbnRlcnZhbCBudW1iZXIgbnVtZXJpYyByZWFsIHJlY29yZCBzZXJpYWwgc2VyaWFsOCBzbWFsbGludCB0ZXh0IHZhcmNoYXIgdmFyeWluZyB2b2lkIn0sYzpbe2NOOiJzdHJpbmciLGI6IiciLGU6IiciLGM6W2UuQkUse2I6IicnIn1dfSx7Y046InN0cmluZyIsYjonIicsZTonIicsYzpbZS5CRSx7YjonIiInfV19LHtjTjoic3RyaW5nIixiOiJgIixlOiJgIixjOltlLkJFXX0sZS5DTk0sZS5DQkNNLHRdfSxlLkNCQ00sdF19fSk7aGxqcy5yZWdpc3Rlckxhbmd1YWdlKCJyIixmdW5jdGlvbihlKXt2YXIgcj0iKFthLXpBLVpdfFxcLlthLXpBLVouXSlbYS16QS1aMC05Ll9dKiI7cmV0dXJue2M6W2UuSENNLHtiOnIsbDpyLGs6e2tleXdvcmQ6ImZ1bmN0aW9uIGlmIGluIGJyZWFrIG5leHQgcmVwZWF0IGVsc2UgZm9yIHJldHVybiBzd2l0Y2ggd2hpbGUgdHJ5IHRyeUNhdGNoIHN0b3Agd2FybmluZyByZXF1aXJlIGxpYnJhcnkgYXR0YWNoIGRldGFjaCBzb3VyY2Ugc2V0TWV0aG9kIHNldEdlbmVyaWMgc2V0R3JvdXBHZW5lcmljIHNldENsYXNzIC4uLiIsbGl0ZXJhbDoiTlVMTCBOQSBUUlVFIEZBTFNFIFQgRiBJbmYgTmFOIE5BX2ludGVnZXJffDEwIE5BX3JlYWxffDEwIE5BX2NoYXJhY3Rlcl98MTAgTkFfY29tcGxleF98MTAifSxyOjB9LHtjTjoibnVtYmVyIixiOiIwW3hYXVswLTlhLWZBLUZdK1tMaV0/XFxiIixyOjB9LHtjTjoibnVtYmVyIixiOiJcXGQrKD86W2VFXVsrXFwtXT9cXGQqKT9MXFxiIixyOjB9LHtjTjoibnVtYmVyIixiOiJcXGQrXFwuKD8hXFxkKSg/OmlcXGIpPyIscjowfSx7Y046Im51bWJlciIsYjoiXFxkKyg/OlxcLlxcZCopPyg/OltlRV1bK1xcLV0/XFxkKik/aT9cXGIiLHI6MH0se2NOOiJudW1iZXIiLGI6IlxcLlxcZCsoPzpbZUVdWytcXC1dP1xcZCopP2k/XFxiIixyOjB9LHtiOiJgIixlOiJgIixyOjB9LHtjTjoic3RyaW5nIixjOltlLkJFXSx2Olt7YjonIicsZTonIid9LHtiOiInIixlOiInIn1dfV19fSk7aGxqcy5yZWdpc3Rlckxhbmd1YWdlKCJwZXJsIixmdW5jdGlvbihlKXt2YXIgdD0iZ2V0cHdlbnQgZ2V0c2VydmVudCBxdW90ZW1ldGEgbXNncmN2IHNjYWxhciBraWxsIGRibWNsb3NlIHVuZGVmIGxjIG1hIHN5c3dyaXRlIHRyIHNlbmQgdW1hc2sgc3lzb3BlbiBzaG13cml0ZSB2ZWMgcXggdXRpbWUgbG9jYWwgb2N0IHNlbWN0bCBsb2NhbHRpbWUgcmVhZHBpcGUgZG8gcmV0dXJuIGZvcm1hdCByZWFkIHNwcmludGYgZGJtb3BlbiBwb3AgZ2V0cGdycCBub3QgZ2V0cHduYW0gcmV3aW5kZGlyIHFxZmlsZW5vIHF3IGVuZHByb3RvZW50IHdhaXQgc2V0aG9zdGVudCBibGVzcyBzfDAgb3BlbmRpciBjb250aW51ZSBlYWNoIHNsZWVwIGVuZGdyZW50IHNodXRkb3duIGR1bXAgY2hvbXAgY29ubmVjdCBnZXRzb2NrbmFtZSBkaWUgc29ja2V0cGFpciBjbG9zZSBmbG9jayBleGlzdHMgaW5kZXggc2htZ2V0c3ViIGZvciBlbmRwd2VudCByZWRvIGxzdGF0IG1zZ2N0bCBzZXRwZ3JwIGFicyBleGl0IHNlbGVjdCBwcmludCByZWYgZ2V0aG9zdGJ5YWRkciB1bnNoaWZ0IGZjbnRsIHN5c2NhbGwgZ290byBnZXRuZXRieWFkZHIgam9pbiBnbXRpbWUgc3ltbGluayBzZW1nZXQgc3BsaWNlIHh8MCBnZXRwZWVybmFtZSByZWN2IGxvZyBzZXRzb2Nrb3B0IGNvcyBsYXN0IHJldmVyc2UgZ2V0aG9zdGJ5bmFtZSBnZXRncm5hbSBzdHVkeSBmb3JtbGluZSBlbmRob3N0ZW50IHRpbWVzIGNob3AgbGVuZ3RoIGdldGhvc3RlbnQgZ2V0bmV0ZW50IHBhY2sgZ2V0cHJvdG9lbnQgZ2V0c2VydmJ5bmFtZSByYW5kIG1rZGlyIHBvcyBjaG1vZCB5fDAgc3Vic3RyIGVuZG5ldGVudCBwcmludGYgbmV4dCBvcGVuIG1zZ3NuZCByZWFkZGlyIHVzZSB1bmxpbmsgZ2V0c29ja29wdCBnZXRwcmlvcml0eSByaW5kZXggd2FudGFycmF5IGhleCBzeXN0ZW0gZ2V0c2VydmJ5cG9ydCBlbmRzZXJ2ZW50IGludCBjaHIgdW50aWUgcm1kaXIgcHJvdG90eXBlIHRlbGwgbGlzdGVuIGZvcmsgc2htcmVhZCB1Y2ZpcnN0IHNldHByb3RvZW50IGVsc2Ugc3lzc2VlayBsaW5rIGdldGdyZ2lkIHNobWN0bCB3YWl0cGlkIHVucGFjayBnZXRuZXRieW5hbWUgcmVzZXQgY2hkaXIgZ3JlcCBzcGxpdCByZXF1aXJlIGNhbGxlciBsY2ZpcnN0IHVudGlsIHdhcm4gd2hpbGUgdmFsdWVzIHNoaWZ0IHRlbGxkaXIgZ2V0cHd1aWQgbXkgZ2V0cHJvdG9ieW51bWJlciBkZWxldGUgYW5kIHNvcnQgdWMgZGVmaW5lZCBzcmFuZCBhY2NlcHQgcGFja2FnZSBzZWVrZGlyIGdldHByb3RvYnluYW1lIHNlbW9wIG91ciByZW5hbWUgc2VlayBpZiBxfDAgY2hyb290IHN5c3JlYWQgc2V0cHdlbnQgbm8gY3J5cHQgZ2V0YyBjaG93biBzcXJ0IHdyaXRlIHNldG5ldGVudCBzZXRwcmlvcml0eSBmb3JlYWNoIHRpZSBzaW4gbXNnZ2V0IG1hcCBzdGF0IGdldGxvZ2luIHVubGVzcyBlbHNpZiB0cnVuY2F0ZSBleGVjIGtleXMgZ2xvYiB0aWVkIGNsb3NlZGlyaW9jdGwgc29ja2V0IHJlYWRsaW5rIGV2YWwgeG9yIHJlYWRsaW5lIGJpbm1vZGUgc2V0c2VydmVudCBlb2Ygb3JkIGJpbmQgYWxhcm0gcGlwZSBhdGFuMiBnZXRncmVudCBleHAgdGltZSBwdXNoIHNldGdyZW50IGd0IGx0IG9yIG5lIG18MCBicmVhayBnaXZlbiBzYXkgc3RhdGUgd2hlbiIscj17Y046InN1YnN0IixiOiJbJEBdXFx7IixlOiJcXH0iLGs6dH0scz17YjoiLT57IixlOiJ9In0sbj17djpbe2I6L1wkXGQvfSx7YjovW1wkJUBdKFxeXHdcYnwjXHcrKDo6XHcrKSp8e1x3K318XHcrKDo6XHcqKSopL30se2I6L1tcJCVAXVteXHNcd3tdLyxyOjB9XX0saT1bZS5CRSxyLG5dLG89W24sZS5IQ00sZS5DKCJeXFw9XFx3IiwiXFw9Y3V0Iix7ZVc6ITB9KSxzLHtjTjoic3RyaW5nIixjOmksdjpbe2I6InFbcXd4cl0/XFxzKlxcKCIsZToiXFwpIixyOjV9LHtiOiJxW3F3eHJdP1xccypcXFsiLGU6IlxcXSIscjo1fSx7YjoicVtxd3hyXT9cXHMqXFx7IixlOiJcXH0iLHI6NX0se2I6InFbcXd4cl0/XFxzKlxcfCIsZToiXFx8IixyOjV9LHtiOiJxW3F3eHJdP1xccypcXDwiLGU6IlxcPiIscjo1fSx7YjoicXdcXHMrcSIsZToicSIscjo1fSx7YjoiJyIsZToiJyIsYzpbZS5CRV19LHtiOiciJyxlOiciJ30se2I6ImAiLGU6ImAiLGM6W2UuQkVdfSx7Yjoie1xcdyt9IixjOltdLHI6MH0se2I6Ii0/XFx3K1xccypcXD1cXD4iLGM6W10scjowfV19LHtjTjoibnVtYmVyIixiOiIoXFxiMFswLTdfXSspfChcXGIweFswLTlhLWZBLUZfXSspfChcXGJbMS05XVswLTlfXSooXFwuWzAtOV9dKyk/KXxbMF9dXFxiIixyOjB9LHtiOiIoXFwvXFwvfCIrZS5SU1IrInxcXGIoc3BsaXR8cmV0dXJufHByaW50fHJldmVyc2V8Z3JlcClcXGIpXFxzKiIsazoic3BsaXQgcmV0dXJuIHByaW50IHJldmVyc2UgZ3JlcCIscjowLGM6W2UuSENNLHtjTjoicmVnZXhwIixiOiIoc3x0cnx5KS8oXFxcXC58W14vXSkqLyhcXFxcLnxbXi9dKSovW2Etel0qIixyOjEwfSx7Y046InJlZ2V4cCIsYjoiKG18cXIpPy8iLGU6Ii9bYS16XSoiLGM6W2UuQkVdLHI6MH1dfSx7Y046ImZ1bmN0aW9uIixiSzoic3ViIixlOiIoXFxzKlxcKC4qP1xcKSk/Wzt7XSIsZUU6ITAscjo1LGM6W2UuVE1dfSx7YjoiLVxcd1xcYiIscjowfSx7YjoiXl9fREFUQV9fJCIsZToiXl9fRU5EX18kIixzTDoibW9qb2xpY2lvdXMiLGM6W3tiOiJeQEAuKiIsZToiJCIsY046ImNvbW1lbnQifV19XTtyZXR1cm4gci5jPW8scy5jPW8se2FsaWFzZXM6WyJwbCIsInBtIl0sbDovW1x3XC5dKy8sazp0LGM6b319KTtobGpzLnJlZ2lzdGVyTGFuZ3VhZ2UoImluaSIsZnVuY3Rpb24oZSl7dmFyIGI9e2NOOiJzdHJpbmciLGM6W2UuQkVdLHY6W3tiOiInJyciLGU6IicnJyIscjoxMH0se2I6JyIiIicsZTonIiIiJyxyOjEwfSx7YjonIicsZTonIid9LHtiOiInIixlOiInIn1dfTtyZXR1cm57YWxpYXNlczpbInRvbWwiXSxjSTohMCxpOi9cUy8sYzpbZS5DKCI7IiwiJCIpLGUuSENNLHtjTjoic2VjdGlvbiIsYjovXlxzKlxbKy8sZTovXF0rL30se2I6L15bYS16MC05XFtcXV8tXStccyo9XHMqLyxlOiIkIixyQjohMCxjOlt7Y046ImF0dHIiLGI6L1thLXowLTlcW1xdXy1dKy99LHtiOi89LyxlVzohMCxyOjAsYzpbe2NOOiJsaXRlcmFsIixiOi9cYm9ufG9mZnx0cnVlfGZhbHNlfHllc3xub1xiL30se2NOOiJ2YXJpYWJsZSIsdjpbe2I6L1wkW1x3XGQiXVtcd1xkX10qL30se2I6L1wkXHsoLio/KX0vfV19LGIse2NOOiJudW1iZXIiLGI6LyhbXCtcLV0rKT9bXGRdK19bXGRfXSsvfSxlLk5NXX1dfV19fSk7aGxqcy5yZWdpc3Rlckxhbmd1YWdlKCJkaWZmIixmdW5jdGlvbihlKXtyZXR1cm57YWxpYXNlczpbInBhdGNoIl0sYzpbe2NOOiJtZXRhIixyOjEwLHY6W3tiOi9eQEAgK1wtXGQrLFxkKyArXCtcZCssXGQrICtAQCQvfSx7YjovXlwqXCpcKiArXGQrLFxkKyArXCpcKlwqXCokL30se2I6L15cLVwtXC0gK1xkKyxcZCsgK1wtXC1cLVwtJC99XX0se2NOOiJjb21tZW50Iix2Olt7YjovSW5kZXg6IC8sZTovJC99LHtiOi89ezMsfS8sZTovJC99LHtiOi9eXC17M30vLGU6LyQvfSx7YjovXlwqezN9IC8sZTovJC99LHtiOi9eXCt7M30vLGU6LyQvfSx7YjovXCp7NX0vLGU6L1wqezV9JC99XX0se2NOOiJhZGRpdGlvbiIsYjoiXlxcKyIsZToiJCJ9LHtjTjoiZGVsZXRpb24iLGI6Il5cXC0iLGU6IiQifSx7Y046ImFkZGl0aW9uIixiOiJeXFwhIixlOiIkIn1dfX0pO2hsanMucmVnaXN0ZXJMYW5ndWFnZSgiZ28iLGZ1bmN0aW9uKGUpe3ZhciB0PXtrZXl3b3JkOiJicmVhayBkZWZhdWx0IGZ1bmMgaW50ZXJmYWNlIHNlbGVjdCBjYXNlIG1hcCBzdHJ1Y3QgY2hhbiBlbHNlIGdvdG8gcGFja2FnZSBzd2l0Y2ggY29uc3QgZmFsbHRocm91Z2ggaWYgcmFuZ2UgdHlwZSBjb250aW51ZSBmb3IgaW1wb3J0IHJldHVybiB2YXIgZ28gZGVmZXIgYm9vbCBieXRlIGNvbXBsZXg2NCBjb21wbGV4MTI4IGZsb2F0MzIgZmxvYXQ2NCBpbnQ4IGludDE2IGludDMyIGludDY0IHN0cmluZyB1aW50OCB1aW50MTYgdWludDMyIHVpbnQ2NCBpbnQgdWludCB1aW50cHRyIHJ1bmUiLGxpdGVyYWw6InRydWUgZmFsc2UgaW90YSBuaWwiLGJ1aWx0X2luOiJhcHBlbmQgY2FwIGNsb3NlIGNvbXBsZXggY29weSBpbWFnIGxlbiBtYWtlIG5ldyBwYW5pYyBwcmludCBwcmludGxuIHJlYWwgcmVjb3ZlciBkZWxldGUifTtyZXR1cm57YWxpYXNlczpbImdvbGFuZyJdLGs6dCxpOiI8LyIsYzpbZS5DTENNLGUuQ0JDTSx7Y046InN0cmluZyIsdjpbZS5RU00se2I6IiciLGU6IlteXFxcXF0nIn0se2I6ImAiLGU6ImAifV19LHtjTjoibnVtYmVyIix2Olt7YjplLkNOUisiW2RmbHNpXSIscjoxfSxlLkNOTV19LHtiOi86PS99LHtjTjoiZnVuY3Rpb24iLGJLOiJmdW5jIixlOi9ccypcey8sZUU6ITAsYzpbZS5UTSx7Y046InBhcmFtcyIsYjovXCgvLGU6L1wpLyxrOnQsaTovWyInXS99XX1dfX0pO2hsanMucmVnaXN0ZXJMYW5ndWFnZSgiYmFzaCIsZnVuY3Rpb24oZSl7dmFyIHQ9e2NOOiJ2YXJpYWJsZSIsdjpbe2I6L1wkW1x3XGQjQF1bXHdcZF9dKi99LHtiOi9cJFx7KC4qPyl9L31dfSxzPXtjTjoic3RyaW5nIixiOi8iLyxlOi8iLyxjOltlLkJFLHQse2NOOiJ2YXJpYWJsZSIsYjovXCRcKC8sZTovXCkvLGM6W2UuQkVdfV19LGE9e2NOOiJzdHJpbmciLGI6LycvLGU6LycvfTtyZXR1cm57YWxpYXNlczpbInNoIiwienNoIl0sbDovXGItP1thLXpcLl9dK1xiLyxrOntrZXl3b3JkOiJpZiB0aGVuIGVsc2UgZWxpZiBmaSBmb3Igd2hpbGUgaW4gZG8gZG9uZSBjYXNlIGVzYWMgZnVuY3Rpb24iLGxpdGVyYWw6InRydWUgZmFsc2UiLGJ1aWx0X2luOiJicmVhayBjZCBjb250aW51ZSBldmFsIGV4ZWMgZXhpdCBleHBvcnQgZ2V0b3B0cyBoYXNoIHB3ZCByZWFkb25seSByZXR1cm4gc2hpZnQgdGVzdCB0aW1lcyB0cmFwIHVtYXNrIHVuc2V0IGFsaWFzIGJpbmQgYnVpbHRpbiBjYWxsZXIgY29tbWFuZCBkZWNsYXJlIGVjaG8gZW5hYmxlIGhlbHAgbGV0IGxvY2FsIGxvZ291dCBtYXBmaWxlIHByaW50ZiByZWFkIHJlYWRhcnJheSBzb3VyY2UgdHlwZSB0eXBlc2V0IHVsaW1pdCB1bmFsaWFzIHNldCBzaG9wdCBhdXRvbG9hZCBiZyBiaW5ka2V5IGJ5ZSBjYXAgY2hkaXIgY2xvbmUgY29tcGFyZ3VtZW50cyBjb21wY2FsbCBjb21wY3RsIGNvbXBkZXNjcmliZSBjb21wZmlsZXMgY29tcGdyb3VwcyBjb21wcXVvdGUgY29tcHRhZ3MgY29tcHRyeSBjb21wdmFsdWVzIGRpcnMgZGlzYWJsZSBkaXNvd24gZWNob3RjIGVjaG90aSBlbXVsYXRlIGZjIGZnIGZsb2F0IGZ1bmN0aW9ucyBnZXRjYXAgZ2V0bG4gaGlzdG9yeSBpbnRlZ2VyIGpvYnMga2lsbCBsaW1pdCBsb2cgbm9nbG9iIHBvcGQgcHJpbnQgcHVzaGQgcHVzaGxuIHJlaGFzaCBzY2hlZCBzZXRjYXAgc2V0b3B0IHN0YXQgc3VzcGVuZCB0dHljdGwgdW5mdW5jdGlvbiB1bmhhc2ggdW5saW1pdCB1bnNldG9wdCB2YXJlZCB3YWl0IHdoZW5jZSB3aGVyZSB3aGljaCB6Y29tcGlsZSB6Zm9ybWF0IHpmdHAgemxlIHptb2Rsb2FkIHpwYXJzZW9wdHMgenByb2YgenB0eSB6cmVnZXhwYXJzZSB6c29ja2V0IHpzdHlsZSB6dGNwIixfOiItbmUgLWVxIC1sdCAtZ3QgLWYgLWQgLWUgLXMgLWwgLWEifSxjOlt7Y046Im1ldGEiLGI6L14jIVteXG5dK3NoXHMqJC8scjoxMH0se2NOOiJmdW5jdGlvbiIsYjovXHdbXHdcZF9dKlxzKlwoXHMqXClccypcey8sckI6ITAsYzpbZS5pbmhlcml0KGUuVE0se2I6L1x3W1x3XGRfXSovfSldLHI6MH0sZS5IQ00scyxhLHRdfX0pO2hsanMucmVnaXN0ZXJMYW5ndWFnZSgicHl0aG9uIixmdW5jdGlvbihlKXt2YXIgcj17a2V5d29yZDoiYW5kIGVsaWYgaXMgZ2xvYmFsIGFzIGluIGlmIGZyb20gcmFpc2UgZm9yIGV4Y2VwdCBmaW5hbGx5IHByaW50IGltcG9ydCBwYXNzIHJldHVybiBleGVjIGVsc2UgYnJlYWsgbm90IHdpdGggY2xhc3MgYXNzZXJ0IHlpZWxkIHRyeSB3aGlsZSBjb250aW51ZSBkZWwgb3IgZGVmIGxhbWJkYSBhc3luYyBhd2FpdCBub25sb2NhbHwxMCBOb25lIFRydWUgRmFsc2UiLGJ1aWx0X2luOiJFbGxpcHNpcyBOb3RJbXBsZW1lbnRlZCJ9LGI9e2NOOiJtZXRhIixiOi9eKD4+PnxcLlwuXC4pIC99LGM9e2NOOiJzdWJzdCIsYjovXHsvLGU6L1x9LyxrOnIsaTovIy99LGE9e2NOOiJzdHJpbmciLGM6W2UuQkVdLHY6W3tiOi8odXxiKT9yPycnJy8sZTovJycnLyxjOltiXSxyOjEwfSx7YjovKHV8Yik/cj8iIiIvLGU6LyIiIi8sYzpbYl0scjoxMH0se2I6LyhmcnxyZnxmKScnJy8sZTovJycnLyxjOltiLGNdfSx7YjovKGZyfHJmfGYpIiIiLyxlOi8iIiIvLGM6W2IsY119LHtiOi8odXxyfHVyKScvLGU6LycvLHI6MTB9LHtiOi8odXxyfHVyKSIvLGU6LyIvLHI6MTB9LHtiOi8oYnxiciknLyxlOi8nL30se2I6LyhifGJyKSIvLGU6LyIvfSx7YjovKGZyfHJmfGYpJy8sZTovJy8sYzpbY119LHtiOi8oZnJ8cmZ8ZikiLyxlOi8iLyxjOltjXX0sZS5BU00sZS5RU01dfSxzPXtjTjoibnVtYmVyIixyOjAsdjpbe2I6ZS5CTlIrIltsTGpKXT8ifSx7YjoiXFxiKDBvWzAtN10rKVtsTGpKXT8ifSx7YjplLkNOUisiW2xMakpdPyJ9XX0saT17Y046InBhcmFtcyIsYjovXCgvLGU6L1wpLyxjOlsic2VsZiIsYixzLGFdfTtyZXR1cm4gYy5jPVthLHMsYl0se2FsaWFzZXM6WyJweSIsImd5cCJdLGs6cixpOi8oPFwvfC0+fFw/KXw9Pi8sYzpbYixzLGEsZS5IQ00se3Y6W3tjTjoiZnVuY3Rpb24iLGJLOiJkZWYifSx7Y046ImNsYXNzIixiSzoiY2xhc3MifV0sZTovOi8saTovWyR7PTtcbixdLyxjOltlLlVUTSxpLHtiOi8tPi8sZVc6ITAsazoiTm9uZSJ9XX0se2NOOiJtZXRhIixiOi9eW1x0IF0qQC8sZTovJC99LHtiOi9cYihwcmludHxleGVjKVwoL31dfX0pO2hsanMucmVnaXN0ZXJMYW5ndWFnZSgianVsaWEiLGZ1bmN0aW9uKGUpe3ZhciByPXtrZXl3b3JkOiJpbiBpc2Egd2hlcmUgYmFyZW1vZHVsZSBiZWdpbiBicmVhayBjYXRjaCBjY2FsbCBjb25zdCBjb250aW51ZSBkbyBlbHNlIGVsc2VpZiBlbmQgZXhwb3J0IGZhbHNlIGZpbmFsbHkgZm9yIGZ1bmN0aW9uIGdsb2JhbCBpZiBpbXBvcnQgaW1wb3J0YWxsIGxldCBsb2NhbCBtYWNybyBtb2R1bGUgcXVvdGUgcmV0dXJuIHRydWUgdHJ5IHVzaW5nIHdoaWxlIHR5cGUgaW1tdXRhYmxlIGFic3RyYWN0IGJpdHN0eXBlIHR5cGVhbGlhcyAiLGxpdGVyYWw6InRydWUgZmFsc2UgQVJHUyBDX05VTEwgRGV2TnVsbCBFTkRJQU5fQk9NIEVOViBJIEluZiBJbmYxNiBJbmYzMiBJbmY2NCBJbnNlcnRpb25Tb3J0IEpVTElBX0hPTUUgTE9BRF9QQVRIIE1lcmdlU29ydCBOYU4gTmFOMTYgTmFOMzIgTmFONjQgUFJPR1JBTV9GSUxFIFF1aWNrU29ydCBSb3VuZERvd24gUm91bmRGcm9tWmVybyBSb3VuZE5lYXJlc3QgUm91bmROZWFyZXN0VGllc0F3YXkgUm91bmROZWFyZXN0VGllc1VwIFJvdW5kVG9aZXJvIFJvdW5kVXAgU1RERVJSIFNURElOIFNURE9VVCBWRVJTSU9OIGNhdGFsYW4gZXwwIGV1fDAgZXVsZXJnYW1tYSBnb2xkZW4gaW0gbm90aGluZyBwaSDOsyDPgCDPhiAiLGJ1aWx0X2luOiJBTlkgQWJzdHJhY3RBcnJheSBBYnN0cmFjdENoYW5uZWwgQWJzdHJhY3RGbG9hdCBBYnN0cmFjdE1hdHJpeCBBYnN0cmFjdFJORyBBYnN0cmFjdFNlcmlhbGl6ZXIgQWJzdHJhY3RTZXQgQWJzdHJhY3RTcGFyc2VBcnJheSBBYnN0cmFjdFNwYXJzZU1hdHJpeCBBYnN0cmFjdFNwYXJzZVZlY3RvciBBYnN0cmFjdFN0cmluZyBBYnN0cmFjdFVuaXRSYW5nZSBBYnN0cmFjdFZlY09yTWF0IEFic3RyYWN0VmVjdG9yIEFueSBBcmd1bWVudEVycm9yIEFycmF5IEFzc2VydGlvbkVycm9yIEFzc29jaWF0aXZlIEJhc2U2NERlY29kZVBpcGUgQmFzZTY0RW5jb2RlUGlwZSBCaWRpYWdvbmFsIEJpZ0Zsb2F0IEJpZ0ludCBCaXRBcnJheSBCaXRNYXRyaXggQml0VmVjdG9yIEJvb2wgQm91bmRzRXJyb3IgQnVmZmVyU3RyZWFtIENhY2hpbmdQb29sIENhcHR1cmVkRXhjZXB0aW9uIENhcnRlc2lhbkluZGV4IENhcnRlc2lhblJhbmdlIENjaGFyIENkb3VibGUgQ2Zsb2F0IENoYW5uZWwgQ2hhciBDaW50IENpbnRtYXhfdCBDbG9uZyBDbG9uZ2xvbmcgQ2x1c3Rlck1hbmFnZXIgQ21kIENvZGVJbmZvIENvbG9uIENvbXBsZXggQ29tcGxleDEyOCBDb21wbGV4MzIgQ29tcGxleDY0IENvbXBvc2l0ZUV4Y2VwdGlvbiBDb25kaXRpb24gQ29uakFycmF5IENvbmpNYXRyaXggQ29ualZlY3RvciBDcHRyZGlmZl90IENzaG9ydCBDc2l6ZV90IENzc2l6ZV90IENzdHJpbmcgQ3VjaGFyIEN1aW50IEN1aW50bWF4X3QgQ3Vsb25nIEN1bG9uZ2xvbmcgQ3VzaG9ydCBDd2NoYXJfdCBDd3N0cmluZyBEYXRhVHlwZSBEYXRlIERhdGVGb3JtYXQgRGF0ZVRpbWUgRGVuc2VBcnJheSBEZW5zZU1hdHJpeCBEZW5zZVZlY09yTWF0IERlbnNlVmVjdG9yIERpYWdvbmFsIERpY3QgRGltZW5zaW9uTWlzbWF0Y2ggRGltcyBEaXJlY3RJbmRleFN0cmluZyBEaXNwbGF5IERpdmlkZUVycm9yIERvbWFpbkVycm9yIEVPRkVycm9yIEVhY2hMaW5lIEVudW0gRW51bWVyYXRlIEVycm9yRXhjZXB0aW9uIEV4Y2VwdGlvbiBFeHBvbmVudGlhbEJhY2tPZmYgRXhwciBGYWN0b3JpemF0aW9uIEZpbGVNb25pdG9yIEZsb2F0MTYgRmxvYXQzMiBGbG9hdDY0IEZ1bmN0aW9uIEZ1dHVyZSBHbG9iYWxSZWYgR290b05vZGUgSFRNTCBIZXJtaXRpYW4gSU8gSU9CdWZmZXIgSU9Db250ZXh0IElPU3RyZWFtIElQQWRkciBJUHY0IElQdjYgSW5kZXhDYXJ0ZXNpYW4gSW5kZXhMaW5lYXIgSW5kZXhTdHlsZSBJbmV4YWN0RXJyb3IgSW5pdEVycm9yIEludCBJbnQxMjggSW50MTYgSW50MzIgSW50NjQgSW50OCBJbnRTZXQgSW50ZWdlciBJbnRlcnJ1cHRFeGNlcHRpb24gSW52YWxpZFN0YXRlRXhjZXB0aW9uIElycmF0aW9uYWwgS2V5RXJyb3IgTGFiZWxOb2RlIExpblNwYWNlIExpbmVOdW1iZXJOb2RlIExvYWRFcnJvciBMb3dlclRyaWFuZ3VsYXIgTUlNRSBNYXRyaXggTWVyc2VubmVUd2lzdGVyIE1ldGhvZCBNZXRob2RFcnJvciBNZXRob2RUYWJsZSBNb2R1bGUgTlR1cGxlIE5ld3Zhck5vZGUgTnVsbEV4Y2VwdGlvbiBOdWxsYWJsZSBOdW1iZXIgT2JqZWN0SWREaWN0IE9yZGluYWxSYW5nZSBPdXRPZk1lbW9yeUVycm9yIE92ZXJmbG93RXJyb3IgUGFpciBQYXJzZUVycm9yIFBhcnRpYWxRdWlja1NvcnQgUGVybXV0ZWREaW1zQXJyYXkgUGlwZSBQb2xsaW5nRmlsZVdhdGNoZXIgUHJvY2Vzc0V4aXRlZEV4Y2VwdGlvbiBQdHIgUXVvdGVOb2RlIFJhbmRvbURldmljZSBSYW5nZSBSYW5nZUluZGV4IFJhdGlvbmFsIFJhd0ZEIFJlYWRPbmx5TWVtb3J5RXJyb3IgUmVhbCBSZWVudHJhbnRMb2NrIFJlZiBSZWdleCBSZWdleE1hdGNoIFJlbW90ZUNoYW5uZWwgUmVtb3RlRXhjZXB0aW9uIFJldlN0cmluZyBSb3VuZGluZ01vZGUgUm93VmVjdG9yIFNTQVZhbHVlIFNlZ21lbnRhdGlvbkZhdWx0IFNlcmlhbGl6YXRpb25TdGF0ZSBTZXQgU2hhcmVkQXJyYXkgU2hhcmVkTWF0cml4IFNoYXJlZFZlY3RvciBTaWduZWQgU2ltcGxlVmVjdG9yIFNsb3QgU2xvdE51bWJlciBTcGFyc2VNYXRyaXhDU0MgU3BhcnNlVmVjdG9yIFN0YWNrRnJhbWUgU3RhY2tPdmVyZmxvd0Vycm9yIFN0YWNrVHJhY2UgU3RlcFJhbmdlIFN0ZXBSYW5nZUxlbiBTdHJpZGVkQXJyYXkgU3RyaWRlZE1hdHJpeCBTdHJpZGVkVmVjT3JNYXQgU3RyaWRlZFZlY3RvciBTdHJpbmcgU3ViQXJyYXkgU3ViU3RyaW5nIFN5bVRyaWRpYWdvbmFsIFN5bWJvbCBTeW1tZXRyaWMgU3lzdGVtRXJyb3IgVENQU29ja2V0IFRhc2sgVGV4dCBUZXh0RGlzcGxheSBUaW1lciBUcmlkaWFnb25hbCBUdXBsZSBUeXBlIFR5cGVFcnJvciBUeXBlTWFwRW50cnkgVHlwZU1hcExldmVsIFR5cGVOYW1lIFR5cGVWYXIgVHlwZWRTbG90IFVEUFNvY2tldCBVSW50IFVJbnQxMjggVUludDE2IFVJbnQzMiBVSW50NjQgVUludDggVW5kZWZSZWZFcnJvciBVbmRlZlZhckVycm9yIFVuaWNvZGVFcnJvciBVbmlmb3JtU2NhbGluZyBVbmlvbiBVbmlvbkFsbCBVbml0UmFuZ2UgVW5zaWduZWQgVXBwZXJUcmlhbmd1bGFyIFZhbCBWYXJhcmcgVmVjRWxlbWVudCBWZWNPck1hdCBWZWN0b3IgVmVyc2lvbk51bWJlciBWb2lkIFdlYWtLZXlEaWN0IFdlYWtSZWYgV29ya2VyQ29uZmlnIFdvcmtlclBvb2wgIn0sdD0iW0EtWmEtel9cXHUwMEExLVxcdUZGRkZdW0EtWmEtel8wLTlcXHUwMEExLVxcdUZGRkZdKiIsYT17bDp0LGs6cixpOi88XC8vfSxuPXtjTjoibnVtYmVyIixiOi8oXGIweFtcZF9dKihcLltcZF9dKik/fDB4XC5cZFtcZF9dKilwWy0rXT9cZCt8XGIwW2JveF1bYS1mQS1GMC05XVthLWZBLUYwLTlfXSp8KFxiXGRbXGRfXSooXC5bXGRfXSopP3xcLlxkW1xkX10qKShbZUVmRl1bLStdP1xkKyk/LyxyOjB9LG89e2NOOiJzdHJpbmciLGI6LycoLnxcXFt4WHVVXVthLXpBLVowLTldKyknL30saT17Y046InN1YnN0IixiOi9cJFwoLyxlOi9cKS8sazpyfSxsPXtjTjoidmFyaWFibGUiLGI6IlxcJCIrdH0sYz17Y046InN0cmluZyIsYzpbZS5CRSxpLGxdLHY6W3tiOi9cdyoiIiIvLGU6LyIiIlx3Ki8scjoxMH0se2I6L1x3KiIvLGU6LyJcdyovfV19LHM9e2NOOiJzdHJpbmciLGM6W2UuQkUsaSxsXSxiOiJgIixlOiJgIn0sZD17Y046Im1ldGEiLGI6IkAiK3R9LHU9e2NOOiJjb21tZW50Iix2Olt7YjoiIz0iLGU6Ij0jIixyOjEwfSx7YjoiIyIsZToiJCJ9XX07cmV0dXJuIGEuYz1bbixvLGMscyxkLHUsZS5IQ00se2NOOiJrZXl3b3JkIixiOiJcXGIoKChhYnN0cmFjdHxwcmltaXRpdmUpXFxzKyl0eXBlfChtdXRhYmxlXFxzKyk/c3RydWN0KVxcYiJ9LHtiOi88Oi99XSxpLmM9YS5jLGF9KTtobGpzLnJlZ2lzdGVyTGFuZ3VhZ2UoImNvZmZlZXNjcmlwdCIsZnVuY3Rpb24oZSl7dmFyIGM9e2tleXdvcmQ6ImluIGlmIGZvciB3aGlsZSBmaW5hbGx5IG5ldyBkbyByZXR1cm4gZWxzZSBicmVhayBjYXRjaCBpbnN0YW5jZW9mIHRocm93IHRyeSB0aGlzIHN3aXRjaCBjb250aW51ZSB0eXBlb2YgZGVsZXRlIGRlYnVnZ2VyIHN1cGVyIHlpZWxkIGltcG9ydCBleHBvcnQgZnJvbSBhcyBkZWZhdWx0IGF3YWl0IHRoZW4gdW5sZXNzIHVudGlsIGxvb3Agb2YgYnkgd2hlbiBhbmQgb3IgaXMgaXNudCBub3QiLGxpdGVyYWw6InRydWUgZmFsc2UgbnVsbCB1bmRlZmluZWQgeWVzIG5vIG9uIG9mZiIsYnVpbHRfaW46Im5wbSByZXF1aXJlIGNvbnNvbGUgcHJpbnQgbW9kdWxlIGdsb2JhbCB3aW5kb3cgZG9jdW1lbnQifSxuPSJbQS1aYS16JF9dWzAtOUEtWmEteiRfXSoiLHI9e2NOOiJzdWJzdCIsYjovI1x7LyxlOi99LyxrOmN9LGk9W2UuQk5NLGUuaW5oZXJpdChlLkNOTSx7c3RhcnRzOntlOiIoXFxzKi8pPyIscjowfX0pLHtjTjoic3RyaW5nIix2Olt7YjovJycnLyxlOi8nJycvLGM6W2UuQkVdfSx7YjovJy8sZTovJy8sYzpbZS5CRV19LHtiOi8iIiIvLGU6LyIiIi8sYzpbZS5CRSxyXX0se2I6LyIvLGU6LyIvLGM6W2UuQkUscl19XX0se2NOOiJyZWdleHAiLHY6W3tiOiIvLy8iLGU6Ii8vLyIsYzpbcixlLkhDTV19LHtiOiIvL1tnaW1dKiIscjowfSx7YjovXC8oPyFbICpdKShcXFwvfC4pKj9cL1tnaW1dKig/PVxXfCQpL31dfSx7YjoiQCIrbn0se3NMOiJqYXZhc2NyaXB0IixlQjohMCxlRTohMCx2Olt7YjoiYGBgIixlOiJgYGAifSx7YjoiYCIsZToiYCJ9XX1dO3IuYz1pO3ZhciBzPWUuaW5oZXJpdChlLlRNLHtiOm59KSx0PSIoXFwoLipcXCkpP1xccypcXEJbLT1dPiIsbz17Y046InBhcmFtcyIsYjoiXFwoW15cXChdIixyQjohMCxjOlt7YjovXCgvLGU6L1wpLyxrOmMsYzpbInNlbGYiXS5jb25jYXQoaSl9XX07cmV0dXJue2FsaWFzZXM6WyJjb2ZmZWUiLCJjc29uIiwiaWNlZCJdLGs6YyxpOi9cL1wqLyxjOmkuY29uY2F0KFtlLkMoIiMjIyIsIiMjIyIpLGUuSENNLHtjTjoiZnVuY3Rpb24iLGI6Il5cXHMqIituKyJcXHMqPVxccyoiK3QsZToiWy09XT4iLHJCOiEwLGM6W3Msb119LHtiOi9bOlwoLD1dXHMqLyxyOjAsYzpbe2NOOiJmdW5jdGlvbiIsYjp0LGU6IlstPV0+IixyQjohMCxjOltvXX1dfSx7Y046ImNsYXNzIixiSzoiY2xhc3MiLGU6IiQiLGk6L1s6PSJcW1xdXS8sYzpbe2JLOiJleHRlbmRzIixlVzohMCxpOi9bOj0iXFtcXV0vLGM6W3NdfSxzXX0se2I6bisiOiIsZToiOiIsckI6ITAsckU6ITAscjowfV0pfX0pO2hsanMucmVnaXN0ZXJMYW5ndWFnZSgiY3BwIixmdW5jdGlvbih0KXt2YXIgZT17Y046ImtleXdvcmQiLGI6IlxcYlthLXpcXGRfXSpfdFxcYiJ9LHI9e2NOOiJzdHJpbmciLHY6W3tiOicodTg/fFUpP0w/IicsZTonIicsaToiXFxuIixjOlt0LkJFXX0se2I6Jyh1OD98VSk/UiInLGU6JyInLGM6W3QuQkVdfSx7YjoiJ1xcXFw/LiIsZToiJyIsaToiLiJ9XX0scz17Y046Im51bWJlciIsdjpbe2I6IlxcYigwYlswMSddKykifSx7YjoiKC0/KVxcYihbXFxkJ10rKFxcLltcXGQnXSopP3xcXC5bXFxkJ10rKSh1fFV8bHxMfHVsfFVMfGZ8RnxifEIpIn0se2I6IigtPykoXFxiMFt4WF1bYS1mQS1GMC05J10rfChcXGJbXFxkJ10rKFxcLltcXGQnXSopP3xcXC5bXFxkJ10rKShbZUVdWy0rXT9bXFxkJ10rKT8pIn1dLHI6MH0saT17Y046Im1ldGEiLGI6LyNccypbYS16XStcYi8sZTovJC8sazp7Im1ldGEta2V5d29yZCI6ImlmIGVsc2UgZWxpZiBlbmRpZiBkZWZpbmUgdW5kZWYgd2FybmluZyBlcnJvciBsaW5lIHByYWdtYSBpZmRlZiBpZm5kZWYgaW5jbHVkZSJ9LGM6W3tiOi9cXFxuLyxyOjB9LHQuaW5oZXJpdChyLHtjTjoibWV0YS1zdHJpbmcifSkse2NOOiJtZXRhLXN0cmluZyIsYjovPFteXG4+XSo+LyxlOi8kLyxpOiJcXG4ifSx0LkNMQ00sdC5DQkNNXX0sYT10LklSKyJcXHMqXFwoIixjPXtrZXl3b3JkOiJpbnQgZmxvYXQgd2hpbGUgcHJpdmF0ZSBjaGFyIGNhdGNoIGltcG9ydCBtb2R1bGUgZXhwb3J0IHZpcnR1YWwgb3BlcmF0b3Igc2l6ZW9mIGR5bmFtaWNfY2FzdHwxMCB0eXBlZGVmIGNvbnN0X2Nhc3R8MTAgY29uc3QgZm9yIHN0YXRpY19jYXN0fDEwIHVuaW9uIG5hbWVzcGFjZSB1bnNpZ25lZCBsb25nIHZvbGF0aWxlIHN0YXRpYyBwcm90ZWN0ZWQgYm9vbCB0ZW1wbGF0ZSBtdXRhYmxlIGlmIHB1YmxpYyBmcmllbmQgZG8gZ290byBhdXRvIHZvaWQgZW51bSBlbHNlIGJyZWFrIGV4dGVybiB1c2luZyBhc20gY2FzZSB0eXBlaWQgc2hvcnQgcmVpbnRlcnByZXRfY2FzdHwxMCBkZWZhdWx0IGRvdWJsZSByZWdpc3RlciBleHBsaWNpdCBzaWduZWQgdHlwZW5hbWUgdHJ5IHRoaXMgc3dpdGNoIGNvbnRpbnVlIGlubGluZSBkZWxldGUgYWxpZ25vZiBjb25zdGV4cHIgZGVjbHR5cGUgbm9leGNlcHQgc3RhdGljX2Fzc2VydCB0aHJlYWRfbG9jYWwgcmVzdHJpY3QgX0Jvb2wgY29tcGxleCBfQ29tcGxleCBfSW1hZ2luYXJ5IGF0b21pY19ib29sIGF0b21pY19jaGFyIGF0b21pY19zY2hhciBhdG9taWNfdWNoYXIgYXRvbWljX3Nob3J0IGF0b21pY191c2hvcnQgYXRvbWljX2ludCBhdG9taWNfdWludCBhdG9taWNfbG9uZyBhdG9taWNfdWxvbmcgYXRvbWljX2xsb25nIGF0b21pY191bGxvbmcgbmV3IHRocm93IHJldHVybiBhbmQgb3Igbm90IixidWlsdF9pbjoic3RkIHN0cmluZyBjaW4gY291dCBjZXJyIGNsb2cgc3RkaW4gc3Rkb3V0IHN0ZGVyciBzdHJpbmdzdHJlYW0gaXN0cmluZ3N0cmVhbSBvc3RyaW5nc3RyZWFtIGF1dG9fcHRyIGRlcXVlIGxpc3QgcXVldWUgc3RhY2sgdmVjdG9yIG1hcCBzZXQgYml0c2V0IG11bHRpc2V0IG11bHRpbWFwIHVub3JkZXJlZF9zZXQgdW5vcmRlcmVkX21hcCB1bm9yZGVyZWRfbXVsdGlzZXQgdW5vcmRlcmVkX211bHRpbWFwIGFycmF5IHNoYXJlZF9wdHIgYWJvcnQgYWJzIGFjb3MgYXNpbiBhdGFuMiBhdGFuIGNhbGxvYyBjZWlsIGNvc2ggY29zIGV4aXQgZXhwIGZhYnMgZmxvb3IgZm1vZCBmcHJpbnRmIGZwdXRzIGZyZWUgZnJleHAgZnNjYW5mIGlzYWxudW0gaXNhbHBoYSBpc2NudHJsIGlzZGlnaXQgaXNncmFwaCBpc2xvd2VyIGlzcHJpbnQgaXNwdW5jdCBpc3NwYWNlIGlzdXBwZXIgaXN4ZGlnaXQgdG9sb3dlciB0b3VwcGVyIGxhYnMgbGRleHAgbG9nMTAgbG9nIG1hbGxvYyByZWFsbG9jIG1lbWNociBtZW1jbXAgbWVtY3B5IG1lbXNldCBtb2RmIHBvdyBwcmludGYgcHV0Y2hhciBwdXRzIHNjYW5mIHNpbmggc2luIHNucHJpbnRmIHNwcmludGYgc3FydCBzc2NhbmYgc3RyY2F0IHN0cmNociBzdHJjbXAgc3RyY3B5IHN0cmNzcG4gc3RybGVuIHN0cm5jYXQgc3RybmNtcCBzdHJuY3B5IHN0cnBicmsgc3RycmNociBzdHJzcG4gc3Ryc3RyIHRhbmggdGFuIHZmcHJpbnRmIHZwcmludGYgdnNwcmludGYgZW5kbCBpbml0aWFsaXplcl9saXN0IHVuaXF1ZV9wdHIiLGxpdGVyYWw6InRydWUgZmFsc2UgbnVsbHB0ciBOVUxMIn0sbj1bZSx0LkNMQ00sdC5DQkNNLHMscl07cmV0dXJue2FsaWFzZXM6WyJjIiwiY2MiLCJoIiwiYysrIiwiaCsrIiwiaHBwIl0sazpjLGk6IjwvIixjOm4uY29uY2F0KFtpLHtiOiJcXGIoZGVxdWV8bGlzdHxxdWV1ZXxzdGFja3x2ZWN0b3J8bWFwfHNldHxiaXRzZXR8bXVsdGlzZXR8bXVsdGltYXB8dW5vcmRlcmVkX21hcHx1bm9yZGVyZWRfc2V0fHVub3JkZXJlZF9tdWx0aXNldHx1bm9yZGVyZWRfbXVsdGltYXB8YXJyYXkpXFxzKjwiLGU6Ij4iLGs6YyxjOlsic2VsZiIsZV19LHtiOnQuSVIrIjo6IixrOmN9LHt2Olt7YjovPS8sZTovOy99LHtiOi9cKC8sZTovXCkvfSx7Yks6Im5ldyB0aHJvdyByZXR1cm4gZWxzZSIsZTovOy99XSxrOmMsYzpuLmNvbmNhdChbe2I6L1woLyxlOi9cKS8sazpjLGM6bi5jb25jYXQoWyJzZWxmIl0pLHI6MH1dKSxyOjB9LHtjTjoiZnVuY3Rpb24iLGI6IigiK3QuSVIrIltcXComXFxzXSspKyIrYSxyQjohMCxlOi9bezs9XS8sZUU6ITAsazpjLGk6L1teXHdcc1wqJl0vLGM6W3tiOmEsckI6ITAsYzpbdC5UTV0scjowfSx7Y046InBhcmFtcyIsYjovXCgvLGU6L1wpLyxrOmMscjowLGM6W3QuQ0xDTSx0LkNCQ00scixzLGVdfSx0LkNMQ00sdC5DQkNNLGldfSx7Y046ImNsYXNzIixiSzoiY2xhc3Mgc3RydWN0IixlOi9bezs6XS8sYzpbe2I6LzwvLGU6Lz4vLGM6WyJzZWxmIl19LHQuVE1dfV0pLGV4cG9ydHM6e3ByZXByb2Nlc3NvcjppLHN0cmluZ3M6cixrOmN9fX0pO2hsanMucmVnaXN0ZXJMYW5ndWFnZSgicnVieSIsZnVuY3Rpb24oZSl7dmFyIGI9IlthLXpBLVpfXVxcdypbIT89XT98Wy0rfl1cXEB8PDx8Pj58PX58PT09P3w8PT58Wzw+XT0/fFxcKlxcKnxbLS8rJV4mKn5gfF18XFxbXFxdPT8iLHI9e2tleXdvcmQ6ImFuZCB0aGVuIGRlZmluZWQgbW9kdWxlIGluIHJldHVybiByZWRvIGlmIEJFR0lOIHJldHJ5IGVuZCBmb3Igc2VsZiB3aGVuIG5leHQgdW50aWwgZG8gYmVnaW4gdW5sZXNzIEVORCByZXNjdWUgZWxzZSBicmVhayB1bmRlZiBub3Qgc3VwZXIgY2xhc3MgY2FzZSByZXF1aXJlIHlpZWxkIGFsaWFzIHdoaWxlIGVuc3VyZSBlbHNpZiBvciBpbmNsdWRlIGF0dHJfcmVhZGVyIGF0dHJfd3JpdGVyIGF0dHJfYWNjZXNzb3IiLGxpdGVyYWw6InRydWUgZmFsc2UgbmlsIn0sYz17Y046ImRvY3RhZyIsYjoiQFtBLVphLXpdKyJ9LGE9e2I6IiM8IixlOiI+In0scz1bZS5DKCIjIiwiJCIse2M6W2NdfSksZS5DKCJeXFw9YmVnaW4iLCJeXFw9ZW5kIix7YzpbY10scjoxMH0pLGUuQygiXl9fRU5EX18iLCJcXG4kIildLG49e2NOOiJzdWJzdCIsYjoiI1xceyIsZToifSIsazpyfSx0PXtjTjoic3RyaW5nIixjOltlLkJFLG5dLHY6W3tiOi8nLyxlOi8nL30se2I6LyIvLGU6LyIvfSx7YjovYC8sZTovYC99LHtiOiIlW3FRd1d4XT9cXCgiLGU6IlxcKSJ9LHtiOiIlW3FRd1d4XT9cXFsiLGU6IlxcXSJ9LHtiOiIlW3FRd1d4XT97IixlOiJ9In0se2I6IiVbcVF3V3hdPzwiLGU6Ij4ifSx7YjoiJVtxUXdXeF0/LyIsZToiLyJ9LHtiOiIlW3FRd1d4XT8lIixlOiIlIn0se2I6IiVbcVF3V3hdPy0iLGU6Ii0ifSx7YjoiJVtxUXdXeF0/XFx8IixlOiJcXHwifSx7YjovXEJcPyhcXFxkezEsM318XFx4W0EtRmEtZjAtOV17MSwyfXxcXHVbQS1GYS1mMC05XXs0fXxcXD9cUylcYi99LHtiOi88PCgtPylcdyskLyxlOi9eXHMqXHcrJC99XX0saT17Y046InBhcmFtcyIsYjoiXFwoIixlOiJcXCkiLGVuZHNQYXJlbnQ6ITAsazpyfSxkPVt0LGEse2NOOiJjbGFzcyIsYks6ImNsYXNzIG1vZHVsZSIsZToiJHw7IixpOi89LyxjOltlLmluaGVyaXQoZS5UTSx7YjoiW0EtWmEtel9dXFx3Kig6OlxcdyspKihcXD98XFwhKT8ifSkse2I6IjxcXHMqIixjOlt7YjoiKCIrZS5JUisiOjopPyIrZS5JUn1dfV0uY29uY2F0KHMpfSx7Y046ImZ1bmN0aW9uIixiSzoiZGVmIixlOiIkfDsiLGM6W2UuaW5oZXJpdChlLlRNLHtiOmJ9KSxpXS5jb25jYXQocyl9LHtiOmUuSVIrIjo6In0se2NOOiJzeW1ib2wiLGI6ZS5VSVIrIihcXCF8XFw/KT86IixyOjB9LHtjTjoic3ltYm9sIixiOiI6KD8hXFxzKSIsYzpbdCx7YjpifV0scjowfSx7Y046Im51bWJlciIsYjoiKFxcYjBbMC03X10rKXwoXFxiMHhbMC05YS1mQS1GX10rKXwoXFxiWzEtOV1bMC05X10qKFxcLlswLTlfXSspPyl8WzBfXVxcYiIscjowfSx7YjoiKFxcJFxcVyl8KChcXCR8XFxAXFxAPykoXFx3KykpIn0se2NOOiJwYXJhbXMiLGI6L1x8LyxlOi9cfC8sazpyfSx7YjoiKCIrZS5SU1IrInx1bmxlc3MpXFxzKiIsazoidW5sZXNzIixjOlthLHtjTjoicmVnZXhwIixjOltlLkJFLG5dLGk6L1xuLyx2Olt7YjoiLyIsZToiL1thLXpdKiJ9LHtiOiIlcnsiLGU6In1bYS16XSoifSx7YjoiJXJcXCgiLGU6IlxcKVthLXpdKiJ9LHtiOiIlciEiLGU6IiFbYS16XSoifSx7YjoiJXJcXFsiLGU6IlxcXVthLXpdKiJ9XX1dLmNvbmNhdChzKSxyOjB9XS5jb25jYXQocyk7bi5jPWQsaS5jPWQ7dmFyIGw9Ils+P10+IixvPSJbXFx3I10rXFwoXFx3K1xcKTpcXGQrOlxcZCs+Iix1PSIoXFx3Ky0pP1xcZCtcXC5cXGQrXFwuXFxkKHBcXGQrKT9bXj5dKz4iLHc9W3tiOi9eXHMqPT4vLHN0YXJ0czp7ZToiJCIsYzpkfX0se2NOOiJtZXRhIixiOiJeKCIrbCsifCIrbysifCIrdSsiKSIsc3RhcnRzOntlOiIkIixjOmR9fV07cmV0dXJue2FsaWFzZXM6WyJyYiIsImdlbXNwZWMiLCJwb2RzcGVjIiwidGhvciIsImlyYiJdLGs6cixpOi9cL1wqLyxjOnMuY29uY2F0KHcpLmNvbmNhdChkKX19KTtobGpzLnJlZ2lzdGVyTGFuZ3VhZ2UoInlhbWwiLGZ1bmN0aW9uKGUpe3ZhciBiPSJ0cnVlIGZhbHNlIHllcyBubyBudWxsIixhPSJeWyBcXC1dKiIscj0iW2EtekEtWl9dW1xcd1xcLV0qIix0PXtjTjoiYXR0ciIsdjpbe2I6YStyKyI6In0se2I6YSsnIicrcisnIjonfSx7YjphKyInIityKyInOiJ9XX0sYz17Y046InRlbXBsYXRlLXZhcmlhYmxlIix2Olt7Yjoie3siLGU6In19In0se2I6IiV7IixlOiJ9In1dfSxsPXtjTjoic3RyaW5nIixyOjAsdjpbe2I6LycvLGU6LycvfSx7YjovIi8sZTovIi99LHtiOi9cUysvfV0sYzpbZS5CRSxjXX07cmV0dXJue2NJOiEwLGFsaWFzZXM6WyJ5bWwiLCJZQU1MIiwieWFtbCJdLGM6W3Qse2NOOiJtZXRhIixiOiJeLS0tcyokIixyOjEwfSx7Y046InN0cmluZyIsYjoiW1xcfD5dICokIixyRTohMCxjOmwuYyxlOnQudlswXS5ifSx7YjoiPCVbJT0tXT8iLGU6IlslLV0/JT4iLHNMOiJydWJ5IixlQjohMCxlRTohMCxyOjB9LHtjTjoidHlwZSIsYjoiISEiK2UuVUlSfSx7Y046Im1ldGEiLGI6IiYiK2UuVUlSKyIkIn0se2NOOiJtZXRhIixiOiJcXCoiK2UuVUlSKyIkIn0se2NOOiJidWxsZXQiLGI6Il4gKi0iLHI6MH0sZS5IQ00se2JLOmIsazp7bGl0ZXJhbDpifX0sZS5DTk0sbF19fSk7aGxqcy5yZWdpc3Rlckxhbmd1YWdlKCJjc3MiLGZ1bmN0aW9uKGUpe3ZhciBjPSJbYS16QS1aLV1bYS16QS1aMC05Xy1dKiIsdD17YjovW0EtWlxfXC5cLV0rXHMqOi8sckI6ITAsZToiOyIsZVc6ITAsYzpbe2NOOiJhdHRyaWJ1dGUiLGI6L1xTLyxlOiI6IixlRTohMCxzdGFydHM6e2VXOiEwLGVFOiEwLGM6W3tiOi9bXHctXStcKC8sckI6ITAsYzpbe2NOOiJidWlsdF9pbiIsYjovW1x3LV0rL30se2I6L1woLyxlOi9cKS8sYzpbZS5BU00sZS5RU01dfV19LGUuQ1NTTk0sZS5RU00sZS5BU00sZS5DQkNNLHtjTjoibnVtYmVyIixiOiIjWzAtOUEtRmEtZl0rIn0se2NOOiJtZXRhIixiOiIhaW1wb3J0YW50In1dfX1dfTtyZXR1cm57Y0k6ITAsaTovWz1cL3wnXCRdLyxjOltlLkNCQ00se2NOOiJzZWxlY3Rvci1pZCIsYjovI1tBLVphLXowLTlfLV0rL30se2NOOiJzZWxlY3Rvci1jbGFzcyIsYjovXC5bQS1aYS16MC05Xy1dKy99LHtjTjoic2VsZWN0b3ItYXR0ciIsYjovXFsvLGU6L1xdLyxpOiIkIn0se2NOOiJzZWxlY3Rvci1wc2V1ZG8iLGI6LzooOik/W2EtekEtWjAtOVxfXC1cK1woXCkiJy5dKy99LHtiOiJAKGZvbnQtZmFjZXxwYWdlKSIsbDoiW2Etei1dKyIsazoiZm9udC1mYWNlIHBhZ2UifSx7YjoiQCIsZToiW3s7XSIsaTovOi8sYzpbe2NOOiJrZXl3b3JkIixiOi9cdysvfSx7YjovXHMvLGVXOiEwLGVFOiEwLHI6MCxjOltlLkFTTSxlLlFTTSxlLkNTU05NXX1dfSx7Y046InNlbGVjdG9yLXRhZyIsYjpjLHI6MH0se2I6InsiLGU6In0iLGk6L1xTLyxjOltlLkNCQ00sdF19XX19KTtobGpzLnJlZ2lzdGVyTGFuZ3VhZ2UoImZvcnRyYW4iLGZ1bmN0aW9uKGUpe3ZhciB0PXtjTjoicGFyYW1zIixiOiJcXCgiLGU6IlxcKSJ9LG49e2xpdGVyYWw6Ii5GYWxzZS4gLlRydWUuIixrZXl3b3JkOiJraW5kIGRvIHdoaWxlIHByaXZhdGUgY2FsbCBpbnRyaW5zaWMgd2hlcmUgZWxzZXdoZXJlIHR5cGUgZW5kdHlwZSBlbmRtb2R1bGUgZW5kc2VsZWN0IGVuZGludGVyZmFjZSBlbmQgZW5kZG8gZW5kaWYgaWYgZm9yYWxsIGVuZGZvcmFsbCBvbmx5IGNvbnRhaW5zIGRlZmF1bHQgcmV0dXJuIHN0b3AgdGhlbiBwdWJsaWMgc3Vicm91dGluZXwxMCBmdW5jdGlvbiBwcm9ncmFtIC5hbmQuIC5vci4gLm5vdC4gLmxlLiAuZXEuIC5nZS4gLmd0LiAubHQuIGdvdG8gc2F2ZSBlbHNlIHVzZSBtb2R1bGUgc2VsZWN0IGNhc2UgYWNjZXNzIGJsYW5rIGRpcmVjdCBleGlzdCBmaWxlIGZtdCBmb3JtIGZvcm1hdHRlZCBpb3N0YXQgbmFtZSBuYW1lZCBuZXh0cmVjIG51bWJlciBvcGVuZWQgcmVjIHJlY2wgc2VxdWVudGlhbCBzdGF0dXMgdW5mb3JtYXR0ZWQgdW5pdCBjb250aW51ZSBmb3JtYXQgcGF1c2UgY3ljbGUgZXhpdCBjX251bGxfY2hhciBjX2FsZXJ0IGNfYmFja3NwYWNlIGNfZm9ybV9mZWVkIGZsdXNoIHdhaXQgZGVjaW1hbCByb3VuZCBpb21zZyBzeW5jaHJvbm91cyBub3Bhc3Mgbm9uX292ZXJyaWRhYmxlIHBhc3MgcHJvdGVjdGVkIHZvbGF0aWxlIGFic3RyYWN0IGV4dGVuZHMgaW1wb3J0IG5vbl9pbnRyaW5zaWMgdmFsdWUgZGVmZXJyZWQgZ2VuZXJpYyBmaW5hbCBlbnVtZXJhdG9yIGNsYXNzIGFzc29jaWF0ZSBiaW5kIGVudW0gY19pbnQgY19zaG9ydCBjX2xvbmcgY19sb25nX2xvbmcgY19zaWduZWRfY2hhciBjX3NpemVfdCBjX2ludDhfdCBjX2ludDE2X3QgY19pbnQzMl90IGNfaW50NjRfdCBjX2ludF9sZWFzdDhfdCBjX2ludF9sZWFzdDE2X3QgY19pbnRfbGVhc3QzMl90IGNfaW50X2xlYXN0NjRfdCBjX2ludF9mYXN0OF90IGNfaW50X2Zhc3QxNl90IGNfaW50X2Zhc3QzMl90IGNfaW50X2Zhc3Q2NF90IGNfaW50bWF4X3QgQ19pbnRwdHJfdCBjX2Zsb2F0IGNfZG91YmxlIGNfbG9uZ19kb3VibGUgY19mbG9hdF9jb21wbGV4IGNfZG91YmxlX2NvbXBsZXggY19sb25nX2RvdWJsZV9jb21wbGV4IGNfYm9vbCBjX2NoYXIgY19udWxsX3B0ciBjX251bGxfZnVucHRyIGNfbmV3X2xpbmUgY19jYXJyaWFnZV9yZXR1cm4gY19ob3Jpem9udGFsX3RhYiBjX3ZlcnRpY2FsX3RhYiBpc29fY19iaW5kaW5nIGNfbG9jIGNfZnVubG9jIGNfYXNzb2NpYXRlZCAgY19mX3BvaW50ZXIgY19wdHIgY19mdW5wdHIgaXNvX2ZvcnRyYW5fZW52IGNoYXJhY3Rlcl9zdG9yYWdlX3NpemUgZXJyb3JfdW5pdCBmaWxlX3N0b3JhZ2Vfc2l6ZSBpbnB1dF91bml0IGlvc3RhdF9lbmQgaW9zdGF0X2VvciBudW1lcmljX3N0b3JhZ2Vfc2l6ZSBvdXRwdXRfdW5pdCBjX2ZfcHJvY3BvaW50ZXIgaWVlZV9hcml0aG1ldGljIGllZWVfc3VwcG9ydF91bmRlcmZsb3dfY29udHJvbCBpZWVlX2dldF91bmRlcmZsb3dfbW9kZSBpZWVlX3NldF91bmRlcmZsb3dfbW9kZSBuZXd1bml0IGNvbnRpZ3VvdXMgcmVjdXJzaXZlIHBhZCBwb3NpdGlvbiBhY3Rpb24gZGVsaW0gcmVhZHdyaXRlIGVvciBhZHZhbmNlIG5tbCBpbnRlcmZhY2UgcHJvY2VkdXJlIG5hbWVsaXN0IGluY2x1ZGUgc2VxdWVuY2UgZWxlbWVudGFsIHB1cmUgaW50ZWdlciByZWFsIGNoYXJhY3RlciBjb21wbGV4IGxvZ2ljYWwgZGltZW5zaW9uIGFsbG9jYXRhYmxlfDEwIHBhcmFtZXRlciBleHRlcm5hbCBpbXBsaWNpdHwxMCBub25lIGRvdWJsZSBwcmVjaXNpb24gYXNzaWduIGludGVudCBvcHRpb25hbCBwb2ludGVyIHRhcmdldCBpbiBvdXQgY29tbW9uIGVxdWl2YWxlbmNlIGRhdGEiLGJ1aWx0X2luOiJhbG9nIGFsb2cxMCBhbWF4MCBhbWF4MSBhbWluMCBhbWluMSBhbW9kIGNhYnMgY2NvcyBjZXhwIGNsb2cgY3NpbiBjc3FydCBkYWJzIGRhY29zIGRhc2luIGRhdGFuIGRhdGFuMiBkY29zIGRjb3NoIGRkaW0gZGV4cCBkaW50IGRsb2cgZGxvZzEwIGRtYXgxIGRtaW4xIGRtb2QgZG5pbnQgZHNpZ24gZHNpbiBkc2luaCBkc3FydCBkdGFuIGR0YW5oIGZsb2F0IGlhYnMgaWRpbSBpZGludCBpZG5pbnQgaWZpeCBpc2lnbiBtYXgwIG1heDEgbWluMCBtaW4xIHNuZ2wgYWxnYW1hIGNkYWJzIGNkY29zIGNkZXhwIGNkbG9nIGNkc2luIGNkc3FydCBjcWFicyBjcWNvcyBjcWV4cCBjcWxvZyBjcXNpbiBjcXNxcnQgZGNtcGx4IGRjb25qZyBkZXJmIGRlcmZjIGRmbG9hdCBkZ2FtbWEgZGltYWcgZGxnYW1hIGlxaW50IHFhYnMgcWFjb3MgcWFzaW4gcWF0YW4gcWF0YW4yIHFjbXBseCBxY29uamcgcWNvcyBxY29zaCBxZGltIHFlcmYgcWVyZmMgcWV4cCBxZ2FtbWEgcWltYWcgcWxnYW1hIHFsb2cgcWxvZzEwIHFtYXgxIHFtaW4xIHFtb2QgcW5pbnQgcXNpZ24gcXNpbiBxc2luaCBxc3FydCBxdGFuIHF0YW5oIGFicyBhY29zIGFpbWFnIGFpbnQgYW5pbnQgYXNpbiBhdGFuIGF0YW4yIGNoYXIgY21wbHggY29uamcgY29zIGNvc2ggZXhwIGljaGFyIGluZGV4IGludCBsb2cgbG9nMTAgbWF4IG1pbiBuaW50IHNpZ24gc2luIHNpbmggc3FydCB0YW4gdGFuaCBwcmludCB3cml0ZSBkaW0gbGdlIGxndCBsbGUgbGx0IG1vZCBudWxsaWZ5IGFsbG9jYXRlIGRlYWxsb2NhdGUgYWRqdXN0bCBhZGp1c3RyIGFsbCBhbGxvY2F0ZWQgYW55IGFzc29jaWF0ZWQgYml0X3NpemUgYnRlc3QgY2VpbGluZyBjb3VudCBjc2hpZnQgZGF0ZV9hbmRfdGltZSBkaWdpdHMgZG90X3Byb2R1Y3QgZW9zaGlmdCBlcHNpbG9uIGV4cG9uZW50IGZsb29yIGZyYWN0aW9uIGh1Z2UgaWFuZCBpYmNsciBpYml0cyBpYnNldCBpZW9yIGlvciBpc2hmdCBpc2hmdGMgbGJvdW5kIGxlbl90cmltIG1hdG11bCBtYXhleHBvbmVudCBtYXhsb2MgbWF4dmFsIG1lcmdlIG1pbmV4cG9uZW50IG1pbmxvYyBtaW52YWwgbW9kdWxvIG12Yml0cyBuZWFyZXN0IHBhY2sgcHJlc2VudCBwcm9kdWN0IHJhZGl4IHJhbmRvbV9udW1iZXIgcmFuZG9tX3NlZWQgcmFuZ2UgcmVwZWF0IHJlc2hhcGUgcnJzcGFjaW5nIHNjYWxlIHNjYW4gc2VsZWN0ZWRfaW50X2tpbmQgc2VsZWN0ZWRfcmVhbF9raW5kIHNldF9leHBvbmVudCBzaGFwZSBzaXplIHNwYWNpbmcgc3ByZWFkIHN1bSBzeXN0ZW1fY2xvY2sgdGlueSB0cmFuc3Bvc2UgdHJpbSB1Ym91bmQgdW5wYWNrIHZlcmlmeSBhY2hhciBpYWNoYXIgdHJhbnNmZXIgZGJsZSBlbnRyeSBkcHJvZCBjcHVfdGltZSBjb21tYW5kX2FyZ3VtZW50X2NvdW50IGdldF9jb21tYW5kIGdldF9jb21tYW5kX2FyZ3VtZW50IGdldF9lbnZpcm9ubWVudF92YXJpYWJsZSBpc19pb3N0YXRfZW5kIGllZWVfYXJpdGhtZXRpYyBpZWVlX3N1cHBvcnRfdW5kZXJmbG93X2NvbnRyb2wgaWVlZV9nZXRfdW5kZXJmbG93X21vZGUgaWVlZV9zZXRfdW5kZXJmbG93X21vZGUgaXNfaW9zdGF0X2VvciBtb3ZlX2FsbG9jIG5ld19saW5lIHNlbGVjdGVkX2NoYXJfa2luZCBzYW1lX3R5cGVfYXMgZXh0ZW5kc190eXBlX29mYWNvc2ggYXNpbmggYXRhbmggYmVzc2VsX2owIGJlc3NlbF9qMSBiZXNzZWxfam4gYmVzc2VsX3kwIGJlc3NlbF95MSBiZXNzZWxfeW4gZXJmIGVyZmMgZXJmY19zY2FsZWQgZ2FtbWEgbG9nX2dhbW1hIGh5cG90IG5vcm0yIGF0b21pY19kZWZpbmUgYXRvbWljX3JlZiBleGVjdXRlX2NvbW1hbmRfbGluZSBsZWFkeiB0cmFpbHogc3RvcmFnZV9zaXplIG1lcmdlX2JpdHMgYmdlIGJndCBibGUgYmx0IGRzaGlmdGwgZHNoaWZ0ciBmaW5kbG9jIGlhbGwgaWFueSBpcGFyaXR5IGltYWdlX2luZGV4IGxjb2JvdW5kIHVjb2JvdW5kIG1hc2tsIG1hc2tyIG51bV9pbWFnZXMgcGFyaXR5IHBvcGNudCBwb3BwYXIgc2hpZnRhIHNoaWZ0bCBzaGlmdHIgdGhpc19pbWFnZSJ9O3JldHVybntjSTohMCxhbGlhc2VzOlsiZjkwIiwiZjk1Il0sazpuLGk6L1wvXCovLGM6W2UuaW5oZXJpdChlLkFTTSx7Y046InN0cmluZyIscjowfSksZS5pbmhlcml0KGUuUVNNLHtjTjoic3RyaW5nIixyOjB9KSx7Y046ImZ1bmN0aW9uIixiSzoic3Vicm91dGluZSBmdW5jdGlvbiBwcm9ncmFtIixpOiJbJHs9XFxuXSIsYzpbZS5VVE0sdF19LGUuQygiISIsIiQiLHtyOjB9KSx7Y046Im51bWJlciIsYjoiKD89XFxifFxcK3xcXC18XFwuKSg/PVxcLlxcZHxcXGQpKD86XFxkKyk/KD86XFwuP1xcZCopKD86W2RlXVsrLV0/XFxkKyk/XFxiXFwuPyIscjowfV19fSk7aGxqcy5yZWdpc3Rlckxhbmd1YWdlKCJhd2siLGZ1bmN0aW9uKGUpe3ZhciByPXtjTjoidmFyaWFibGUiLHY6W3tiOi9cJFtcd1xkI0BdW1x3XGRfXSovfSx7YjovXCRceyguKj8pfS99XX0sYj0iQkVHSU4gRU5EIGlmIGVsc2Ugd2hpbGUgZG8gZm9yIGluIGJyZWFrIGNvbnRpbnVlIGRlbGV0ZSBuZXh0IG5leHRmaWxlIGZ1bmN0aW9uIGZ1bmMgZXhpdHwxMCIsbj17Y046InN0cmluZyIsYzpbZS5CRV0sdjpbe2I6Lyh1fGIpP3I/JycnLyxlOi8nJycvLHI6MTB9LHtiOi8odXxiKT9yPyIiIi8sZTovIiIiLyxyOjEwfSx7YjovKHV8cnx1ciknLyxlOi8nLyxyOjEwfSx7YjovKHV8cnx1cikiLyxlOi8iLyxyOjEwfSx7YjovKGJ8YnIpJy8sZTovJy99LHtiOi8oYnxicikiLyxlOi8iL30sZS5BU00sZS5RU01dfTtyZXR1cm57azp7a2V5d29yZDpifSxjOltyLG4sZS5STSxlLkhDTSxlLk5NXX19KTtobGpzLnJlZ2lzdGVyTGFuZ3VhZ2UoIm1ha2VmaWxlIixmdW5jdGlvbihlKXt2YXIgaT17Y046InZhcmlhYmxlIix2Olt7YjoiXFwkXFwoIitlLlVJUisiXFwpIixjOltlLkJFXX0se2I6L1wkW0AlPD9cXlwrXCpdL31dfSxyPXtjTjoic3RyaW5nIixiOi8iLyxlOi8iLyxjOltlLkJFLGldfSxhPXtjTjoidmFyaWFibGUiLGI6L1wkXChbXHctXStccy8sZTovXCkvLGs6e2J1aWx0X2luOiJzdWJzdCBwYXRzdWJzdCBzdHJpcCBmaW5kc3RyaW5nIGZpbHRlciBmaWx0ZXItb3V0IHNvcnQgd29yZCB3b3JkbGlzdCBmaXJzdHdvcmQgbGFzdHdvcmQgZGlyIG5vdGRpciBzdWZmaXggYmFzZW5hbWUgYWRkc3VmZml4IGFkZHByZWZpeCBqb2luIHdpbGRjYXJkIHJlYWxwYXRoIGFic3BhdGggZXJyb3Igd2FybmluZyBzaGVsbCBvcmlnaW4gZmxhdm9yIGZvcmVhY2ggaWYgb3IgYW5kIGNhbGwgZXZhbCBmaWxlIHZhbHVlIn0sYzpbaV19LG49e2I6Il4iK2UuVUlSKyJcXHMqWzorP10/PSIsaToiXFxuIixyQjohMCxjOlt7YjoiXiIrZS5VSVIsZToiWzorP10/PSIsZUU6ITB9XX0sdD17Y046Im1ldGEiLGI6L15cLlBIT05ZOi8sZTovJC8sazp7Im1ldGEta2V5d29yZCI6Ii5QSE9OWSJ9LGw6L1tcLlx3XSsvfSxsPXtjTjoic2VjdGlvbiIsYjovXlteXHNdKzovLGU6LyQvLGM6W2ldfTtyZXR1cm57YWxpYXNlczpbIm1rIiwibWFrIl0sazoiZGVmaW5lIGVuZGVmIHVuZGVmaW5lIGlmZGVmIGlmbmRlZiBpZmVxIGlmbmVxIGVsc2UgZW5kaWYgaW5jbHVkZSAtaW5jbHVkZSBzaW5jbHVkZSBvdmVycmlkZSBleHBvcnQgdW5leHBvcnQgcHJpdmF0ZSB2cGF0aCIsbDovW1x3LV0rLyxjOltlLkhDTSxpLHIsYSxuLHQsbF19fSk7aGxqcy5yZWdpc3Rlckxhbmd1YWdlKCJqYXZhIixmdW5jdGlvbihlKXt2YXIgYT0iW8OALcq4YS16QS1aXyRdW8OALcq4YS16QS1aXyQwLTldKiIsdD1hKyIoPCIrYSsiKFxccyosXFxzKiIrYSsiKSo+KT8iLHI9ImZhbHNlIHN5bmNocm9uaXplZCBpbnQgYWJzdHJhY3QgZmxvYXQgcHJpdmF0ZSBjaGFyIGJvb2xlYW4gc3RhdGljIG51bGwgaWYgY29uc3QgZm9yIHRydWUgd2hpbGUgbG9uZyBzdHJpY3RmcCBmaW5hbGx5IHByb3RlY3RlZCBpbXBvcnQgbmF0aXZlIGZpbmFsIHZvaWQgZW51bSBlbHNlIGJyZWFrIHRyYW5zaWVudCBjYXRjaCBpbnN0YW5jZW9mIGJ5dGUgc3VwZXIgdm9sYXRpbGUgY2FzZSBhc3NlcnQgc2hvcnQgcGFja2FnZSBkZWZhdWx0IGRvdWJsZSBwdWJsaWMgdHJ5IHRoaXMgc3dpdGNoIGNvbnRpbnVlIHRocm93cyBwcm90ZWN0ZWQgcHVibGljIHByaXZhdGUgbW9kdWxlIHJlcXVpcmVzIGV4cG9ydHMgZG8iLHM9IlxcYigwW2JCXShbMDFdK1swMV9dK1swMV0rfFswMV0rKXwwW3hYXShbYS1mQS1GMC05XStbYS1mQS1GMC05X10rW2EtZkEtRjAtOV0rfFthLWZBLUYwLTldKyl8KChbXFxkXStbXFxkX10rW1xcZF0rfFtcXGRdKykoXFwuKFtcXGRdK1tcXGRfXStbXFxkXSt8W1xcZF0rKSk/fFxcLihbXFxkXStbXFxkX10rW1xcZF0rfFtcXGRdKykpKFtlRV1bLStdP1xcZCspPylbbExmRl0/IixjPXtjTjoibnVtYmVyIixiOnMscjowfTtyZXR1cm57YWxpYXNlczpbImpzcCJdLGs6cixpOi88XC98Iy8sYzpbZS5DKCIvXFwqXFwqIiwiXFwqLyIse3I6MCxjOlt7YjovXHcrQC8scjowfSx7Y046ImRvY3RhZyIsYjoiQFtBLVphLXpdKyJ9XX0pLGUuQ0xDTSxlLkNCQ00sZS5BU00sZS5RU00se2NOOiJjbGFzcyIsYks6ImNsYXNzIGludGVyZmFjZSIsZTovW3s7PV0vLGVFOiEwLGs6ImNsYXNzIGludGVyZmFjZSIsaTovWzoiXFtcXV0vLGM6W3tiSzoiZXh0ZW5kcyBpbXBsZW1lbnRzIn0sZS5VVE1dfSx7Yks6Im5ldyB0aHJvdyByZXR1cm4gZWxzZSIscjowfSx7Y046ImZ1bmN0aW9uIixiOiIoIit0KyJcXHMrKSsiK2UuVUlSKyJcXHMqXFwoIixyQjohMCxlOi9bezs9XS8sZUU6ITAsazpyLGM6W3tiOmUuVUlSKyJcXHMqXFwoIixyQjohMCxyOjAsYzpbZS5VVE1dfSx7Y046InBhcmFtcyIsYjovXCgvLGU6L1wpLyxrOnIscjowLGM6W2UuQVNNLGUuUVNNLGUuQ05NLGUuQ0JDTV19LGUuQ0xDTSxlLkNCQ01dfSxjLHtjTjoibWV0YSIsYjoiQFtBLVphLXpdKyJ9XX19KTtobGpzLnJlZ2lzdGVyTGFuZ3VhZ2UoInN0YW4iLGZ1bmN0aW9uKGUpe3JldHVybntjOltlLkhDTSxlLkNMQ00sZS5DQkNNLHtiOmUuVUlSLGw6ZS5VSVIsazp7bmFtZToiZm9yIGluIHdoaWxlIHJlcGVhdCB1bnRpbCBpZiB0aGVuIGVsc2UiLHN5bWJvbDoiYmVybm91bGxpIGJlcm5vdWxsaV9sb2dpdCBiaW5vbWlhbCBiaW5vbWlhbF9sb2dpdCBiZXRhX2Jpbm9taWFsIGh5cGVyZ2VvbWV0cmljIGNhdGVnb3JpY2FsIGNhdGVnb3JpY2FsX2xvZ2l0IG9yZGVyZWRfbG9naXN0aWMgbmVnX2Jpbm9taWFsIG5lZ19iaW5vbWlhbF8yIG5lZ19iaW5vbWlhbF8yX2xvZyBwb2lzc29uIHBvaXNzb25fbG9nIG11bHRpbm9taWFsIG5vcm1hbCBleHBfbW9kX25vcm1hbCBza2V3X25vcm1hbCBzdHVkZW50X3QgY2F1Y2h5IGRvdWJsZV9leHBvbmVudGlhbCBsb2dpc3RpYyBndW1iZWwgbG9nbm9ybWFsIGNoaV9zcXVhcmUgaW52X2NoaV9zcXVhcmUgc2NhbGVkX2ludl9jaGlfc3F1YXJlIGV4cG9uZW50aWFsIGludl9nYW1tYSB3ZWlidWxsIGZyZWNoZXQgcmF5bGVpZ2ggd2llbmVyIHBhcmV0byBwYXJldG9fdHlwZV8yIHZvbl9taXNlcyB1bmlmb3JtIG11bHRpX25vcm1hbCBtdWx0aV9ub3JtYWxfcHJlYyBtdWx0aV9ub3JtYWxfY2hvbGVza3kgbXVsdGlfZ3AgbXVsdGlfZ3BfY2hvbGVza3kgbXVsdGlfc3R1ZGVudF90IGdhdXNzaWFuX2RsbV9vYnMgZGlyaWNobGV0IGxral9jb3JyIGxral9jb3JyX2Nob2xlc2t5IHdpc2hhcnQgaW52X3dpc2hhcnQiLCJzZWxlY3Rvci10YWciOiJpbnQgcmVhbCB2ZWN0b3Igc2ltcGxleCB1bml0X3ZlY3RvciBvcmRlcmVkIHBvc2l0aXZlX29yZGVyZWQgcm93X3ZlY3RvciBtYXRyaXggY2hvbGVza3lfZmFjdG9yX2NvcnIgY2hvbGVza3lfZmFjdG9yX2NvdiBjb3JyX21hdHJpeCBjb3ZfbWF0cml4Iix0aXRsZToiZnVuY3Rpb25zIG1vZGVsIGRhdGEgcGFyYW1ldGVycyBxdWFudGl0aWVzIHRyYW5zZm9ybWVkIGdlbmVyYXRlZCIsbGl0ZXJhbDoidHJ1ZSBmYWxzZSJ9LHI6MH0se2NOOiJudW1iZXIiLGI6IjBbeFhdWzAtOWEtZkEtRl0rW0xpXT9cXGIiLHI6MH0se2NOOiJudW1iZXIiLGI6IjBbeFhdWzAtOWEtZkEtRl0rW0xpXT9cXGIiLHI6MH0se2NOOiJudW1iZXIiLGI6IlxcZCsoPzpbZUVdWytcXC1dP1xcZCopP0xcXGIiLHI6MH0se2NOOiJudW1iZXIiLGI6IlxcZCtcXC4oPyFcXGQpKD86aVxcYik/IixyOjB9LHtjTjoibnVtYmVyIixiOiJcXGQrKD86XFwuXFxkKik/KD86W2VFXVsrXFwtXT9cXGQqKT9pP1xcYiIscjowfSx7Y046Im51bWJlciIsYjoiXFwuXFxkKyg/OltlRV1bK1xcLV0/XFxkKik/aT9cXGIiLHI6MH1dfX0pO2hsanMucmVnaXN0ZXJMYW5ndWFnZSgiamF2YXNjcmlwdCIsZnVuY3Rpb24oZSl7dmFyIHI9IltBLVphLXokX11bMC05QS1aYS16JF9dKiIsdD17a2V5d29yZDoiaW4gb2YgaWYgZm9yIHdoaWxlIGZpbmFsbHkgdmFyIG5ldyBmdW5jdGlvbiBkbyByZXR1cm4gdm9pZCBlbHNlIGJyZWFrIGNhdGNoIGluc3RhbmNlb2Ygd2l0aCB0aHJvdyBjYXNlIGRlZmF1bHQgdHJ5IHRoaXMgc3dpdGNoIGNvbnRpbnVlIHR5cGVvZiBkZWxldGUgbGV0IHlpZWxkIGNvbnN0IGV4cG9ydCBzdXBlciBkZWJ1Z2dlciBhcyBhc3luYyBhd2FpdCBzdGF0aWMgaW1wb3J0IGZyb20gYXMiLGxpdGVyYWw6InRydWUgZmFsc2UgbnVsbCB1bmRlZmluZWQgTmFOIEluZmluaXR5IixidWlsdF9pbjoiZXZhbCBpc0Zpbml0ZSBpc05hTiBwYXJzZUZsb2F0IHBhcnNlSW50IGRlY29kZVVSSSBkZWNvZGVVUklDb21wb25lbnQgZW5jb2RlVVJJIGVuY29kZVVSSUNvbXBvbmVudCBlc2NhcGUgdW5lc2NhcGUgT2JqZWN0IEZ1bmN0aW9uIEJvb2xlYW4gRXJyb3IgRXZhbEVycm9yIEludGVybmFsRXJyb3IgUmFuZ2VFcnJvciBSZWZlcmVuY2VFcnJvciBTdG9wSXRlcmF0aW9uIFN5bnRheEVycm9yIFR5cGVFcnJvciBVUklFcnJvciBOdW1iZXIgTWF0aCBEYXRlIFN0cmluZyBSZWdFeHAgQXJyYXkgRmxvYXQzMkFycmF5IEZsb2F0NjRBcnJheSBJbnQxNkFycmF5IEludDMyQXJyYXkgSW50OEFycmF5IFVpbnQxNkFycmF5IFVpbnQzMkFycmF5IFVpbnQ4QXJyYXkgVWludDhDbGFtcGVkQXJyYXkgQXJyYXlCdWZmZXIgRGF0YVZpZXcgSlNPTiBJbnRsIGFyZ3VtZW50cyByZXF1aXJlIG1vZHVsZSBjb25zb2xlIHdpbmRvdyBkb2N1bWVudCBTeW1ib2wgU2V0IE1hcCBXZWFrU2V0IFdlYWtNYXAgUHJveHkgUmVmbGVjdCBQcm9taXNlIn0sYT17Y046Im51bWJlciIsdjpbe2I6IlxcYigwW2JCXVswMV0rKSJ9LHtiOiJcXGIoMFtvT11bMC03XSspIn0se2I6ZS5DTlJ9XSxyOjB9LG49e2NOOiJzdWJzdCIsYjoiXFwkXFx7IixlOiJcXH0iLGs6dCxjOltdfSxjPXtjTjoic3RyaW5nIixiOiJgIixlOiJgIixjOltlLkJFLG5dfTtuLmM9W2UuQVNNLGUuUVNNLGMsYSxlLlJNXTt2YXIgcz1uLmMuY29uY2F0KFtlLkNCQ00sZS5DTENNXSk7cmV0dXJue2FsaWFzZXM6WyJqcyIsImpzeCJdLGs6dCxjOlt7Y046Im1ldGEiLHI6MTAsYjovXlxzKlsnIl11c2UgKHN0cmljdHxhc20pWyciXS99LHtjTjoibWV0YSIsYjovXiMhLyxlOi8kL30sZS5BU00sZS5RU00sYyxlLkNMQ00sZS5DQkNNLGEse2I6L1t7LF1ccyovLHI6MCxjOlt7YjpyKyJcXHMqOiIsckI6ITAscjowLGM6W3tjTjoiYXR0ciIsYjpyLHI6MH1dfV19LHtiOiIoIitlLlJTUisifFxcYihjYXNlfHJldHVybnx0aHJvdylcXGIpXFxzKiIsazoicmV0dXJuIHRocm93IGNhc2UiLGM6W2UuQ0xDTSxlLkNCQ00sZS5STSx7Y046ImZ1bmN0aW9uIixiOiIoXFwoLio/XFwpfCIrcisiKVxccyo9PiIsckI6ITAsZToiXFxzKj0+IixjOlt7Y046InBhcmFtcyIsdjpbe2I6cn0se2I6L1woXHMqXCkvfSx7YjovXCgvLGU6L1wpLyxlQjohMCxlRTohMCxrOnQsYzpzfV19XX0se2I6LzwvLGU6LyhcL1x3K3xcdytcLyk+LyxzTDoieG1sIixjOlt7YjovPFx3K1xzKlwvPi8sc2tpcDohMH0se2I6LzxcdysvLGU6LyhcL1x3K3xcdytcLyk+Lyxza2lwOiEwLGM6W3tiOi88XHcrXHMqXC8+Lyxza2lwOiEwfSwic2VsZiJdfV19XSxyOjB9LHtjTjoiZnVuY3Rpb24iLGJLOiJmdW5jdGlvbiIsZTovXHsvLGVFOiEwLGM6W2UuaW5oZXJpdChlLlRNLHtiOnJ9KSx7Y046InBhcmFtcyIsYjovXCgvLGU6L1wpLyxlQjohMCxlRTohMCxjOnN9XSxpOi9cW3wlL30se2I6L1wkWyguXS99LGUuTUVUSE9EX0dVQVJELHtjTjoiY2xhc3MiLGJLOiJjbGFzcyIsZTovW3s7PV0vLGVFOiEwLGk6L1s6IlxbXF1dLyxjOlt7Yks6ImV4dGVuZHMifSxlLlVUTV19LHtiSzoiY29uc3RydWN0b3IiLGU6L1x7LyxlRTohMH1dLGk6LyMoPyEhKS99fSk7aGxqcy5yZWdpc3Rlckxhbmd1YWdlKCJ0ZXgiLGZ1bmN0aW9uKGMpe3ZhciBlPXtjTjoidGFnIixiOi9cXC8scjowLGM6W3tjTjoibmFtZSIsdjpbe2I6L1thLXpBLVrQsC3Rj9CQLdGPXStbKl0/L30se2I6L1teYS16QS1a0LAt0Y/QkC3RjzAtOV0vfV0sc3RhcnRzOntlVzohMCxyOjAsYzpbe2NOOiJzdHJpbmciLHY6W3tiOi9cWy8sZTovXF0vfSx7YjovXHsvLGU6L1x9L31dfSx7YjovXHMqPVxzKi8sZVc6ITAscjowLGM6W3tjTjoibnVtYmVyIixiOi8tP1xkKlwuP1xkKyhwdHxwY3xtbXxjbXxpbnxkZHxjY3xleHxlbSk/L31dfV19fV19O3JldHVybntjOltlLHtjTjoiZm9ybXVsYSIsYzpbZV0scjowLHY6W3tiOi9cJFwkLyxlOi9cJFwkL30se2I6L1wkLyxlOi9cJC99XX0sYy5DKCIlIiwiJCIse3I6MH0pXX19KTtobGpzLnJlZ2lzdGVyTGFuZ3VhZ2UoInhtbCIsZnVuY3Rpb24ocyl7dmFyIGU9IltBLVphLXowLTlcXC5fOi1dKyIsdD17ZVc6ITAsaTovPC8scjowLGM6W3tjTjoiYXR0ciIsYjplLHI6MH0se2I6Lz1ccyovLHI6MCxjOlt7Y046InN0cmluZyIsZW5kc1BhcmVudDohMCx2Olt7YjovIi8sZTovIi99LHtiOi8nLyxlOi8nL30se2I6L1teXHMiJz08PmBdKy99XX1dfV19O3JldHVybnthbGlhc2VzOlsiaHRtbCIsInhodG1sIiwicnNzIiwiYXRvbSIsInhqYiIsInhzZCIsInhzbCIsInBsaXN0Il0sY0k6ITAsYzpbe2NOOiJtZXRhIixiOiI8IURPQ1RZUEUiLGU6Ij4iLHI6MTAsYzpbe2I6IlxcWyIsZToiXFxdIn1dfSxzLkMoIjwhLS0iLCItLT4iLHtyOjEwfSkse2I6IjxcXCFcXFtDREFUQVxcWyIsZToiXFxdXFxdPiIscjoxMH0se2I6LzxcPyhwaHApPy8sZTovXD8+LyxzTDoicGhwIixjOlt7YjoiL1xcKiIsZToiXFwqLyIsc2tpcDohMH1dfSx7Y046InRhZyIsYjoiPHN0eWxlKD89XFxzfD58JCkiLGU6Ij4iLGs6e25hbWU6InN0eWxlIn0sYzpbdF0sc3RhcnRzOntlOiI8L3N0eWxlPiIsckU6ITAsc0w6WyJjc3MiLCJ4bWwiXX19LHtjTjoidGFnIixiOiI8c2NyaXB0KD89XFxzfD58JCkiLGU6Ij4iLGs6e25hbWU6InNjcmlwdCJ9LGM6W3RdLHN0YXJ0czp7ZToiPC9zY3JpcHQ+IixyRTohMCxzTDpbImFjdGlvbnNjcmlwdCIsImphdmFzY3JpcHQiLCJoYW5kbGViYXJzIiwieG1sIl19fSx7Y046Im1ldGEiLHY6W3tiOi88XD94bWwvLGU6L1w/Pi8scjoxMH0se2I6LzxcP1x3Ky8sZTovXD8+L31dfSx7Y046InRhZyIsYjoiPC8/IixlOiIvPz4iLGM6W3tjTjoibmFtZSIsYjovW15cLz48XHNdKy8scjowfSx0XX1dfX0pO2hsanMucmVnaXN0ZXJMYW5ndWFnZSgibWFya2Rvd24iLGZ1bmN0aW9uKGUpe3JldHVybnthbGlhc2VzOlsibWQiLCJta2Rvd24iLCJta2QiXSxjOlt7Y046InNlY3Rpb24iLHY6W3tiOiJeI3sxLDZ9IixlOiIkIn0se2I6Il4uKz9cXG5bPS1dezIsfSQifV19LHtiOiI8IixlOiI+IixzTDoieG1sIixyOjB9LHtjTjoiYnVsbGV0IixiOiJeKFsqKy1dfChcXGQrXFwuKSlcXHMrIn0se2NOOiJzdHJvbmciLGI6IlsqX117Mn0uKz9bKl9dezJ9In0se2NOOiJlbXBoYXNpcyIsdjpbe2I6IlxcKi4rP1xcKiJ9LHtiOiJfLis/XyIscjowfV19LHtjTjoicXVvdGUiLGI6Il4+XFxzKyIsZToiJCJ9LHtjTjoiY29kZSIsdjpbe2I6Il5gYGB3KnMqJCIsZToiXmBgYHMqJCJ9LHtiOiJgLis/YCJ9LHtiOiJeKCB7NH18CSkiLGU6IiQiLHI6MH1dfSx7YjoiXlstXFwqXXszLH0iLGU6IiQifSx7YjoiXFxbLis/XFxdW1xcKFxcW10uKj9bXFwpXFxdXSIsckI6ITAsYzpbe2NOOiJzdHJpbmciLGI6IlxcWyIsZToiXFxdIixlQjohMCxyRTohMCxyOjB9LHtjTjoibGluayIsYjoiXFxdXFwoIixlOiJcXCkiLGVCOiEwLGVFOiEwfSx7Y046InN5bWJvbCIsYjoiXFxdXFxbIixlOiJcXF0iLGVCOiEwLGVFOiEwfV0scjoxMH0se2I6L15cW1teXG5dK1xdOi8sckI6ITAsYzpbe2NOOiJzeW1ib2wiLGI6L1xbLyxlOi9cXS8sZUI6ITAsZUU6ITB9LHtjTjoibGluayIsYjovOlxzKi8sZTovJC8sZUI6ITB9XX1dfX0pO2hsanMucmVnaXN0ZXJMYW5ndWFnZSgianNvbiIsZnVuY3Rpb24oZSl7dmFyIGk9e2xpdGVyYWw6InRydWUgZmFsc2UgbnVsbCJ9LG49W2UuUVNNLGUuQ05NXSxyPXtlOiIsIixlVzohMCxlRTohMCxjOm4sazppfSx0PXtiOiJ7IixlOiJ9IixjOlt7Y046ImF0dHIiLGI6LyIvLGU6LyIvLGM6W2UuQkVdLGk6IlxcbiJ9LGUuaW5oZXJpdChyLHtiOi86L30pXSxpOiJcXFMifSxjPXtiOiJcXFsiLGU6IlxcXSIsYzpbZS5pbmhlcml0KHIpXSxpOiJcXFMifTtyZXR1cm4gbi5zcGxpY2Uobi5sZW5ndGgsMCx0LGMpLHtjOm4sazppLGk6IlxcUyJ9fSk7"></script>
<style type="text/css">
code{white-space: pre-wrap;}
span.smallcaps{font-variant: small-caps;}
span.underline{text-decoration: underline;}
div.column{display: inline-block; vertical-align: top; width: 50%;}
div.hanging-indent{margin-left: 1.5em; text-indent: -1.5em;}
ul.task-list{list-style: none;}
</style>
<style type="text/css">code{white-space: pre;}</style>
<script type="text/javascript">
if (window.hljs) {
hljs.configure({languages: []});
hljs.initHighlightingOnLoad();
if (document.readyState && document.readyState === "complete") {
window.setTimeout(function() { hljs.initHighlighting(); }, 0);
}
}
</script>
<style type="text/css">
.main-container {
max-width: 940px;
margin-left: auto;
margin-right: auto;
}
img {
max-width:100%;
}
.tabbed-pane {
padding-top: 12px;
}
.html-widget {
margin-bottom: 20px;
}
button.code-folding-btn:focus {
outline: none;
}
summary {
display: list-item;
}
pre code {
padding: 0;
}
</style>
<!-- tabsets -->
<style type="text/css">
.tabset-dropdown > .nav-tabs {
display: inline-table;
max-height: 500px;
min-height: 44px;
overflow-y: auto;
border: 1px solid #ddd;
border-radius: 4px;
}
.tabset-dropdown > .nav-tabs > li.active:before {
content: "";
font-family: 'Glyphicons Halflings';
display: inline-block;
padding: 10px;
border-right: 1px solid #ddd;
}
.tabset-dropdown > .nav-tabs.nav-tabs-open > li.active:before {
content: "";
border: none;
}
.tabset-dropdown > .nav-tabs.nav-tabs-open:before {
content: "";
font-family: 'Glyphicons Halflings';
display: inline-block;
padding: 10px;
border-right: 1px solid #ddd;
}
.tabset-dropdown > .nav-tabs > li.active {
display: block;
}
.tabset-dropdown > .nav-tabs > li > a,
.tabset-dropdown > .nav-tabs > li > a:focus,
.tabset-dropdown > .nav-tabs > li > a:hover {
border: none;
display: inline-block;
border-radius: 4px;
background-color: transparent;
}
.tabset-dropdown > .nav-tabs.nav-tabs-open > li {
display: block;
float: none;
}
.tabset-dropdown > .nav-tabs > li {
display: none;
}
</style>
<!-- code folding -->
</head>
<body>
<div class="container-fluid main-container">
<div id="header">
</div>
<div id="mathematics" class="section level1">
<h1>Mathematics</h1>
;The text below is not a rigorous approach to the mathematical theory, nor is it a wholly systematic or comprehensive description of the topics covered. It is a selection of topics recommended by core instructors. These include mathematical concepts and procedures that will be encountered in your core courses, and instructors expect you to be familiar with them prior to the beginning of a course, i.e, they will not cover them in detail. Instead, use the content below as a reference as these topics arise and as a platform for more in-depth study. Please contact <a href="mailto:jonathan.emery@northwestern.edu" class="email">jonathan.emery@northwestern.edu</a> with suggestions for additional material to be included in this section.
;
;For those who have never seen the mathematics below or who are not comfortable with the material, further preparation may be necessary. Options for those students include: either a.) enroll in ES-APPM-311-1 and ES-APPM-311-2: Methods of Applied Mathematics and/or b.) utilizing the suggested resources for supplemental study.
;
<div id="linear-algebra" class="section level2">
<h2>Linear Algebra</h2>
;Linear algebra is a branch of mathematics that is central to physical description in Materials Science as it concerns the description of vectors spaces and is used in solving systems of equations. Materials Science graduate students will encounter application of linear algebra in all core courses. The sections below outline basic linear algebra concepts.
;
<div id="linear-systems" class="section level3">
<h3>Linear Systems</h3>
</div>
<div id="gauss-elimination-release-tbd" class="section level3">
<h3>Gauss Elimination (Release TBD)</h3>
<div id="matrix-algebra-and-operations-release-tbd" class="section level4">
<h4>MATrix Algebra and Operations (Release TBD)</h4>
</div>
</div>
<div id="linear-transformations-release-tbd" class="section level3">
<h3>Linear Transformations (Release TBD)</h3>
</div>
<div id="determinants-release-tbd" class="section level3">
<h3>Determinants (Release TBD)</h3>
</div>
<div id="eigenvalues-and-eigenvectors-release-tbd" class="section level3">
<h3>Eigenvalues and Eigenvectors (Release TBD)</h3>
</div>
<div id="linear-differential-equations-release-tbd" class="section level3">
<h3>Linear Differential Equations (Release TBD)</h3>
<ol style="list-style-type: decimal">
<li>;Linear Differential Operators
;</li>
<li>;Linear Differential Equations
;</li>
</ol>
</div>
</div>
<div id="subsec:Tensors" class="section level2">
<h2>Tensors (Release 1/2017)</h2>
;Tensors are mathematical objects that define relationships between scalars, vectors, matrices, and other tensors=. Tensors are represented as <em>arrays</em> of various dimensionality (defined by rank or order). The moniker “tensor” in general suggests a higher-rank array (most often <span class="math inline">\(\geq\)</span><!-- -->3 dimensions), but scalars, vectors, and matrices are also tensors.
;
;In the MSE graduate core, students will encounter tensors of various rank. In physical science, tensors characterize the properties of a physical system. Tensors are the <em>de facto</em> tool used to describe, for example, diffusion, nucleation and growth, states of stress and strain, Hamiltonians in quantum mechanics, and many, many, more physical phenomenon. Physical processes of interest to Materials Scientists take place in Euclidean 3-space (<span class="math inline">\({\rm I\!R}^3\)</span>) are are well-described by tensor representations.
;
;We build up our description of the handling of tensors starting by separately describing rank-0, rank-1, rank-2, and rank-3 tensors. Tensors of lower ranks should be familiar — students will have encountered them previously as scalars (rank-0), vectors (rank-1), and matrices (rank-2). The term <em>tensors</em> typically denotes arrays of higher dimensionality (rank <span class="math inline">\(\geq3\)</span>). Physical examples include the rank-2 <a href="https://en.wikipedia.org/wiki/Cauchy_stress_tensor">Cauchy stress tensor</a> which describes the stress state of a at a point within a material), the rank-3 piezoelectric tensor (which relates the dielectric polarization of a material to a stress state), and the rank-4 stiffness tensor (which relates strain state and stress state in a system that obeying Hooke’s law).
;
;Classifications of tensors by rank allows us to quickly identify the number of tensor components we will work with: a tensor of order <span class="math inline">\(p\)</span> has <span class="math inline">\(N^p\)</span> components, where <span class="math inline">\(N\)</span> is the dimensionality of space in which we are operating. In general, you will be operating in Eucledian 3-space, so the number of components of a tensor is defined as <span class="math inline">\(3^p\)</span>.
;
;<strong>Scalars</strong> are considered tensors with <em>order</em> or <em>rank</em> of 0. Scalars represent physical quantities (often accompanied by a unit of measurement) that possess only a magnitude: e.g., temperature, mass, charge, and distance. Scalars are typically represented by Latin or Greek symbols and have <span class="math inline">\(3^{0} = 1\)</span> component.
;
;<strong>Vectors</strong> are tensors with a <em>rank</em> of 1. In symbolic notation, vectors are typically represented using lowercase bold or bold-italic symbols such as <span class="math inline">\(\mathbf{u}\)</span> or <span class="math inline">\(\pmb{a}\)</span>. Bold typeface is not always amenable to handwriting, however, and so the a right arrow accent is employed: <span class="math inline">\(\vec{u}\)</span> or <span class="math inline">\(\vec{a}\)</span>. Students are likely to encounter various conventions depending on their field of study.
;
;In <span class="math inline">\({\rm I\!R}^3\)</span> a vector is defined by <span class="math inline">\(3^{1} = 3\)</span> components. In <em>xyz</em> Cartesian coordinates we utilize the Cartesian basis with 3 orthogonal unit vectors <span class="math inline">\(\{\mathbf{e}_{\mathbf{x}}\text{, } \mathbf{e}_{\mathbf{y}}\text{, } \mathbf{e}_{\mathbf{z}}\}\)</span>. We define 3D vector <span class="math inline">\(\mathbf{u}\)</span> in this basis with the components (<span class="math inline">\(u_x\)</span>, <span class="math inline">\(u_y\)</span>, <span class="math inline">\(u_z\)</span>), or equivalently (<span class="math inline">\(u_1\)</span>, <span class="math inline">\(u_2\)</span>, <span class="math inline">\(u_3\)</span>). Often, we represent the vector <span class="math inline">\(\mathbf{u}\)</span> using the shorthand <span class="math inline">\(u_i\)</span>, where the <span class="math inline">\(i\)</span> subscript denotes an index that ranges over the dimensionality of the system (1,2,3 for <span class="math inline">\({\rm I\!R}^3\)</span>, 1,2 for <span class="math inline">\({\rm I\!R}^2\)</span>).
;
;Vectors are often encountered in a bracketed vertical list to facilitate matrix operations. Using some of the notation defined above:
;
;<span class="math display">\[\mathbf{u} = u_i =
\begin{bmatrix}
u_x \\
u_y \\
u_z
\end{bmatrix} =
\begin{bmatrix}
u_1 \\
u_2 \\
u_3
\end{bmatrix}
\label{eq:Vector}\]</span>
;
;<strong>Matrices</strong> are tensors with a <em>rank</em> of 2. In <span class="math inline">\({\rm I\!R}^2\)</span> a matrix has <span class="math inline">\(2^{2} = 4\)</span> components and in <span class="math inline">\({\rm I\!R}^3\)</span> a matrix has <span class="math inline">\(3^{2} = 9\)</span> components. As with vectors, we will use the range convention when denoting a matrix, which now possesses two subscripts, <span class="math inline">\(i\)</span> and <span class="math inline">\(j\)</span>. We use the example of the true stress, or <a href="https://en.wikipedia.org/wiki/Cauchy_stress_tensor">Cauchy stress tensor</a>, <span class="math inline">\(\sigma_{ij}\)</span>:
;
;<span class="math display">\[\sigma_{ij} =
\begin{bmatrix}
\sigma_{xx} & \sigma_{xy} & \sigma_{xz}\\
\sigma_{yx} & \sigma_{yy} & \sigma_{yz}\\
\sigma_{zx} & \sigma_{zy} & \sigma_{zz}\\
\end{bmatrix}\]</span>
;
;Where the diagonal represents the normal components of stress and the off-diagonal represents the shear components of the stress. In this notation the first index denotes the row while the second denotes the column (<span class="math inline">\(x = 1\)</span>, <span class="math inline">\(y = 2\)</span>, <span class="math inline">\(z = 3\)</span>).
;
;<strong>Tensors</strong> A rank-3 tensor in <span class="math inline">\({\rm I\!R}^3\)</span> has <span class="math inline">\(3^{3} = 27\)</span> components and is represented in range notation using subscripts <span class="math inline">\(i\)</span>, <span class="math inline">\(j\)</span>, and <span class="math inline">\(k\)</span>, e.g., <span class="math inline">\(T_{ijk}\)</span> . At rank-3 (and it is even worse in rank-4, requiring an array of rank-3 tensors) it begins to become difficult to represent clearly on paper. An example of a simple tensor — <a href="https://en.wikipedia.org/wiki/Levi-Civita_symbol#Three_dimensions_2">the rank-3 permutation tensor</a> — is shown in Fig. <a href="#fig:PermutationTensor" reference-type="ref" reference="fig:PermutationTensor">1</a>. You can also watch <a href="https://www.youtube.com/watch?v=f5liqUk0ZTw">this video</a> which helps with the visualization.
;
<div class="figure">
<img src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAfQAAAD6CAYAAABXq7VOAAAABmJLR0QA/wD/AP+gvaeTAACeD0lEQVR42uydB1hU57b3zz23nXvvd597bk40uefc7zt2BQRBeu91BhQR6b33NkyfYRAUBRFFrAiCNKUYe0uMPfbeGLtRoiaKRhNj1Mj3vuDAu4e9YRiQvYe863nWk2SY2cze0f3bq/3XH/6ADRs2bNiwYcOGDRs2bNiwYcOGDRu234FZ1800wVcB20gz2w2exvgqYMOG7Xdh5o2+/2a1kbXGvJl1y6yR5WXWxJqFHbumu+VGdrxlI+tLi2b2A/PGGbr4bzo2bNhGtDmsd3ew3cA6A25+v4Eb310MAuya7qYb3Pxt6lhrbTaw7lk2stssmj2fmbew7lrv9B2F/8Zjw4ZtxBl7HXuiy3r3Woc6j1u2GzzegkjmvVkzax0GAnZNdoda93zHGvcrDnWsNpsN7DbLJtZli2ZWjXkzuwNkoM6NWRf+J/y3Hxs2bCPCfEF6nVXhnuK+zu2yc437dft6j9fWGz3gza4FAwG7prpdvUec2zq3r1yr3Nucatzb7Gs97ltt8Kgzb/YIgD8HQD/aCfUmdhO+C2DDhk3jzXuli4PXGpcDrLVucgB0ObjxPbJqZEGYnzJt9vDBYMCuaW4B0useFW5rPde43GNVurVBoNvXuB8038hOIqThm1nBZk3sR51Qb/FMx3cDbNiwaaT5l7iNmb3cpWLWKmf5jDWucgD0K861Ho0WTez3AOZPzTe4h2I4YNc0BxF5zqxVLpdnrnZt8yp3bXOvdL9qV+e+oI/P8Mya2b+ZN7F+sfqCZYjvDNiwYdOc9Ppi838LKnFK8S91vuy73FneBXSXatgIByKVH2G0YtbCWoDhgF2T3LHaLc53hdOXfmXObbNXuLTNXOV6373StTu93peDP/NbP9TT71hu8fpPfJfAhg0b4y2iyMEhbLHj/uASR7l/qZMcAP2wz2qXmYanDf8Z3MwufbipHcGAwK5J6XXfZc5rwZ/pewGlzm0Q6DNWuxy0q/VIUvUYJp3Q/5B6b2Z/ge8U2LBhY6zFF9iNiVlgXxFZ5CAPLXaUBy1xvBKwzEkUUuTyH/DnFpvYxR9uZi9AXTESgwK7JvjMlS45YUUOl8IXObYFlzi1+S1zvsaqdF5gunHgvR/gQVYK/vy/76qns6LwXQMbNmyMsowM839LzrNNiZ9ndwkAXf4B6DWBS50nKt5jucXDCDQE/dqZam/0XIFBgZ3xdfK1bnFRhQ57YxY4tEUWOraFLXK471PmVGfV4BE4mOOCvwcHu7reWU9N670+w3cQbNiwMcLSxTYOaTLb/UlzbeVx8+zlMQvsDkctdJxJeJOv7z8qUu1g3vyORSN7NgYGdsaqvDW4+4UVOa5NzLe7mzDfvg0CPaTY8ZBrtWvykPyOZvcYIKT0uitb5bkN30WwYcNGq4lEFn/niKzWZkht5KkyGzkA+lUQoYsSZXb/R/m9AOZFH1LtHabNnrkYGtiZ6nOWOuWkyWwupcps25Lm2rfFFti1+qxwUiu93mdNvpndrPg7Af5+ROI7CjZs2GhJrwuzrVP4fKtLHJG1/APQa1PzbCaSvd9iA2uqItUOZ84xNLAz0b3KXWIBxPdyxDZtmVKbttRcuweRhQ6NNnXuQR/nd7KDANSfwb8XQE3ue8PVTv+F7y7YsGEbNpOlWzhIsiz3C7lWcgB0OUdsfSRdbAfT6/9A9RmgjnXgA8yBvKtnKoYHdia5Ta27X2Ku3Voh3/IuT2DdBoGekmd7bMZKl4yP/bvB34nV3VF6C2sVvsNgw4bto1t+ksXf81MtynMzLOTSLEu5MNvqKgA6aXqdEJ2DNGVPWpF9FAMEO5M8vMguR5JtdVHCsWoDD6ltXKH1jfBFDqUWw6RcaNno7gdq6E86e0uaPN9YbWJPw3cbbNiwfRRb7Gv+b4UJZikFyeaXANDlEOgSjmWdQGA1qb/Pds2ce97+APP3pk0sDoYIdkaMoa12ihVlW+/JS7Nok2Vatok5Vg9SpTabnapch121EGSwKrofekE2C991sGHDNuRWEm3isDjW9OuiBFN5QZKZPC/V/Gheunmf6XXUQDd7PpJOPIFBgp0J6XWuwGptQZL53fkpFm0Q6CDbdHzOso+fXqf0zigdSCB/+Lti0cTyx3cfbNiwDYmVBRr8fVm48Zql0SZyAHR5UbzZtYIk00JZut2fVT2GeaPrJ1A8RnGTMtsIdKwxULDT6DEF9oIFieZnF8WbtS1MNG/LT7O4kZRnO2zp9X6i9GqkNHXjD7I//BHfibBhw6a2rQu3+9OaIMOUVaHGF8vCjeUfgN6yONZcd6DHAjelMuQG1YqBgp0uB1v+IvNTzDeXRpm2lcSYtUGgCzmWm10rXBmzFMiixSOkZy4d1tM9ovEdCRs2bGpZpe90h8qA6fvWBBvJAdDlAOgnS6NNQmVqRArWjb6jwE3qp550u2cJBgvDdMmBsI9pk2fiSBb4sd3A8hVmW5YuDzW5vTzcuA0CHaTaj4cststi4vcFf1f2ICWqO1CMCd+ZsGHDprKt9zT8fzU+01dX+xnKKwIM5WuCjK6tCjUpXBFo9d/qHtOihV2OCGY8h528tIGrmZVg1uJRCer5R8D3uQzdrNnjCHyt82e/R6BvYgeZtbDPgDRvG/jvXSPxHJNybQUrw4zOlgcZta0MBTCPML6ZLbQutWjoeoABDZr+nWJHTew98FqYNnnALNJp4FvAfLgMiB8NfxoejHR2a7x31dIT8R0KGzZs/afX7cb8qWmmQcoGb4OLNT4G8i6gT9+0KthgUGMzBg1efwU3o1c9XbusRroajcBq1gYA8vsQXGQOfwbe20DnAwc99VqP6u7r0Mx6MJLODeisR5ZEmWyu8jNsqwwwbAMPqG3zEs03s8vR9DpbBv55herPxYcHnePgwS91+B9AOx86FaWq+3BSBN+tsGHDRmmb3PUcWjyn7WucoS9v8NaXA6CfrPEzUiu9rmxmzew1SHT+3rSFFTv8N3Y2VPY63NcNW+nmffjDZ34HMHcHYGPfVjp/zU+v17F85yWbldb6GNyunT29DQJ9RZjxiegCpfR6C6sUPsSo9ueCfduskSUa3ii9exthVy292SMe37GwYcPWy/a4TP2/2110V2320JO3sKfJAdBb6731C9f66nwyFMe33OL1n2hnO4jOLw4/sFi+wPcrReJ3YSr1Q6NeWWdaFbym9J6vR/rCGFPYzd3M2kHyQKPR55UlsuHX+Uw/s3GGQVuDt0Fb9ZzpN6WZFqXWDe6ziefPLuidpWEfA9Bea97ssQRmLgBALxB/7nHHbOMwRuqd2SL2T8hceiu+c2HDhq3b9oP0+h6HqSk7nXQvbnfVk38A+qbGmfr6Q/l7LJrYOcTogr1s2IHewq7udcMGHcO93+sZrRzFd9baRzLQoYAJeYZCM5eolDpFrvU33LyZNa2txVO/bQMAemm40Wav1S5hvR9m2EnoQ9yHf59P1ixo3gjkWBvRa8S6CGvuw/dnmPUl4e9Rk7s7vothw4btD/tsplp8baeza6+DjhwAXQ4i9FOb3fVCG33/MLQdtKAjt7Ne3XMj+tW0mRU8rDf5jR4ZaM0cRF7nTZu9KL+DSbNHAAQ+Arb7Js3uySOyCa6JtbGPkoPGpddLYkxKt7ro3d7qOq0NAr3W1+Bk4lwbDlVHP0izH+0+ZwjrFtbcvlPfrGXoNQINlDXDOMImRoEOfv8+fCfDhu13bCeNdT4/ZK5VeMBaW77PVkcOIvTWHU5TCzc5TvnLx/h9cP0jMaqAdelhF+c4gMJZpaYmmE4lNs7tGRnpdRiRsptNG1kHlcsLmgx0oLfO2+qmd2aPo27bTme9ts0e+jcXJJmB9Dp1uQSk0uej5wseNOtVK094HCH8eerK6gxPaaSJ/QjJdP0GNxbiuxo2bL8zO21o+M8nTLRCvzHVOnfYQksOgQ4i9M1fOmkbfMzfC246Z4hA91wwvOlkFkcJUg2qNyJ5bECjt2GtmX68h5sT5J397GsghXxO04DuX+IU2eilv/lrG522L+112yDQa3ynb5+13CG8fziyTiOpdrl5o2egig9FaYSMD/hzMoznvAn9+2TRwlqH727YsP2O7KLBFPMz06fsOmE8RX7MVEt+xELr1EEbnaFPryuZcb2nDuxo7775AMWrznT28DbDtRCgTFo3p6wtRxBu3CA9rfFROlJKQEb0NoF0bjj4f7RbU4DuANLra0IMSw9Y6dw+ZKndBoG+zUXvHJ9rLVApfd3knqXU5LZuYNEyazcy4ndruGrpYKkRn5B2B3vTJ5RO+Fd8l8OGbYTbFR2dzy9NnVh40djg9iVb2/un7UxunHa3X3FTKJv6pHrb3z62z2kKrmE3+XUo3Ls56EzChtjo4fL4DfFxXo1+97wa/R9Bn9nof3Kgx5jVHHhQ8fkZjf534TGH8xyG2sMbIoWzmoJ2zW4M3OnXFFwZsTGK032ujYEHFOcKnannsCKbNe+wjd6Fk6Y6T46a6zzeb619Z02g0VoI+QFkX+qI6XZQihjYCKRM6fMFw5V2V6xVRdTjovDdDhu2EWoddnb/dFNrfOgV7YnnLunp3Lxp4/NK7hPcele2gPN43ZZZw+EP1m3yzW5I/TFzQ0qHwhfWCXZU1xQUDpeX1UqruA1pTxW+sJ6/faDHWFwvbkKPAY85nOcwnJ5TzzmHnivTvt/GEkHZsRmOJ86b6LWfNdNrP22m9+KshdVzztyBl0IAGE8h3eqn1BmD7EzTdx/Do2UYpWB3KwH9CL7rYcM2Au2qlpZZ6+RJO+VTJsiv6k6R37Txfnbbyu9ZG2dh9nDBHHpl3bwlKMwzNiS/X1OTv2w4ATC/TrAbBdTK2rw1Az1GRV3+UvQYCxqEOzHQh9fXV81b9GWU746LxtMeX5qu2w6BfsLe5M5X8cE7W+0C2k/NDD3tsMHLdwDRdRAqIgPKEHVqgnUnOjkxfCUHjzyltPs7m62eY/HdDxu2EWLHx0797NxkrcLLkyfLr02eJIdAv2U768Id64CH92YmbRxOmEOXNGRdRoEuaEi/P9wgkKKAqk9/XF2zoEid4/DBd1ccR9aQfQYDffj8C35CzXFri1vnDKa1XzLQbb9kMu3x/tAZX62vnLcI/vxYSMxRCPWj/mFfDaBRUjIk6XK4mwDtz2hmhQ0H0KEkMbqBrbM/ZRO7GN8FsWHTcNsP0usnJumFnpqkfQ4AXd4F9Im77zr5FwGYt91xCj/5aHmD33DC/HJVTWjWxtS3KNDnNnCPDDcMUBCLGzKvqnscSV3mRcVx+PXD/2DyewR63VJh2VdstxPHDQyfnjYwaIdAP+Fme76xmLeC8L6K/OJLnmHXIdQ3J4RVDhjEEOhgu5xa9exGVi5hWmAjSzKMQklniFG65218N8SGTYPt64l6pkcm6e04NklXfmqytvzs5CnnL02ZkvLtrBjjOzaBd+7YBN1pkyxLHO7ovKw+txKFOfQldZK6YYVCbUEhtyH1SU9kzTmp7rFyG7jHekCX+gQeGwP943hN9fyirVGBOw4YmT06om/cftxgevtxS/M727Oj66k+01IsXnXVKeiR3CHg+8K5fnwV6t+NKIjVnbxQ7pSHW9qGr47OqlJKu3dYbvEwwndFbNg0zPaM1xv95cTphV9P0pcfnjRN/gHoq05raf1Pq1fkf96zDz0Bo/O7IbzFww3zrnR75lUU5lkbUn+tqi1YNJxgUK59z63nHlL3WHn1vIPosWB/AAb6R2h64yfX7LSyv7VP36z9oL5J+xFD08d7g7y/qqmYW9zfZ79OT90Mo/QrbsG3g9b6hPWzVW6nkp6/esptG1iJRKB7rBzG7WuZykAHry3Fd0ds2DQovb5tkknorolGZ7+cZCiHQD80cdqeI5N0rBTvueMaWd2ZaneJOvi44guf4YY5Wbpd1JB5c7jhsKpm7moUTvMbePvUbq6r5+9DjwWPjYE+dF67VFy2iT3jxA59y6d79M3bIdD3ujqf31AsWDGQ45zxibjY2SQ3K+yExUYPnz5myA+igjJqg3WDZzRdMrBwfA0A/JkS0G/huyQ2bBpgjZPMTTZPMt0OgC7fNclI/tWk6ef3TTRIgQpwivfcY8fHdMLcOvDud7IV8XRE58vrctcqp9vn1fO+Hm44wY52FE559dzDQxWhq9Mtj4FO4lXzizZEhO7YZGT3aKu+VTsAevtuC7s7m7Lj6tU5XstS6YpWx8DHEOpbYsKq+wDiYURQ5tuhitDNGj3qhllg57BylG7d4jkd3y2xYWOorR9vMbp+omVh4wQL+ReTTOUQ6HsmGq3aO9ngr+j7bvon/t9btkE3INDvBWatpAPmZN3t0JfW5tQMN5zKa/NKUTjl1GefUr+Gnn0MPVb5+rxSDPRBjqKJ0tfXW7nfbJxm175J36Z9m6H195sC/b6qViG93pcfTEreAYEOwS5YOIdqPn3XR6mhg21swwt00NynBHRQW1+M75rYsDEwvV413j50/QTrsw0TrOQQ6Jsmmu7dNsnUiuz9d13Cmzujc8fQC9+v3uRLB8zvVLb4wXo5cf485V11zfzi4QfUgiLQwNYNJ1F91hW1x9/qUNClPlV3/A0DvaCwqlSyrIrte2L9NKen9dPs2yHQm13Z5+sGmF6ndNBUd4kVehNC/ZxnyCVbsvl0sJxGScc+Xr20N0tKjNDZxcO+p0AZ6C3sy/juiQ0bg2zlJAeTNRPtt6+bYCsHQJc3TLQ63zTRIqVRR+dfSGHuGRvdlWoPaGuLz82hKzqvrptfpByd8xvS2ugCFPjd3yngxGtIfajuccAM/Z3usTUaz0ejgQ7S62sjonaUG3k8qprm3F4zzam93tz1bl1WQsNQn8dOKbe2M0oHvjUmfD2J7Os6QmTd38pUKm9krSBq37Nlw7ynwBdE5L8oRejv7XbO+l98F8WGjWYrneA+qnS8U+GKiY6taybYyyHQaybarGqYbPlXqs/c98342x2bYHl3IxxNMIee18A/oAx02SBS3YN1cUPWJRRQq2vy1IgC5xej42+S+syLGOgD8zWCjPVlVt43V01zay+f5tpeNd3l+5rAYJBez/9omZszPpEXqFPvQGmN0J3OrlBPWAZsPiMAfXjWqCrNo1/unXZnp+G7KTZsNFnjH3z/sXC8e+ji8a5nlo13kq+Y4Cgvn2i3t2qijU1/n73rElXTOaJmE/DgfvaiNDqBDsGnDPTCOuFWugA1r473FQqokjrphgHrwdfLKtFjwGNioKvmlaU5y0pZQSeW6rGflul5tEOgV7j6nK8qFK782OeyqUi8ptU+8AmE+hnv0NOEVPVGViQBxC2svWpGyMeRbvmrNG2e26QMdPBgsRffVbFho8FkY9km88Z7bC8a7yYHQJeXjXe6sGKiUwqI1vtdiXhnZrLdbevAzlT7XVbcdjph/uX6FenKMIe+qo6+ES8oZoMCKr+et3/gI2tEPfilddJaDPR+6uQgvb40OnHrQkPvR4v0PNsB0NvLTGbcr0hJbBrO8zkVEHNckXpflxlarCTMcglpZrtp2uzpM6CGuBaPEFQPHsB9Oy1Ab/FYSBKhvzQ83TP9gg0bto9sggm+o6TjvQrzxnu2zh/vIYdALxnvsgrUz/+malR/xyH8AIQ5hDrd0fkSEP0qwxw2yNGpqlZZV7CYW9+TLldnHl5Un9Haowef+gQeEwO9j3FBCW/dfJsA+Ty9me0L9Wa0F+t7/bDCJ+xQ1Zq8Yb9uUEFOEaVfcgu67VbpGdAj2+rxBWGGvImVNcA58EKl3fGldAAdzL4nkAC9w6TRi4XvstiwDUN6nTfeO1Q4buYZAHT53PFsOQD6l0UT3OwGcpw7rPgERSPcHfeY3XTCvHNcrT7rojLQQTPZA7ohJa3POk9YfwpS6Kp+dkXd3HL0syN5MctggV5RJls63zvmUM40n6dz9XzaIdCLHfwvrZ0voHVm/5R/9ElFlL4rPKwRibDFhDp6E7tpQDBt9jiCpNvvg+OF0wH0zv3oLeyfSaC+BN9tsWH7iJY2zs84c5zPNu44bzkAuhwA/QKI0FVKr6N2MTDhv+/YhlxVAP1B9qIMuoHO2ZD6UhnoEBB0Q0p5n7m0Ieu8qp+FAEc/u6ReXI+B3ju9XhiX/oXAMPA7oe6cdqne7PZ5Jr73l8Ulf8GEc4K1dLmD/1MI9GugQS55sU/niJpFI3s2SJlfRgVmwLKVWBWjYpFSdL6Lpvq5Yo1rK8n42gl8x8WG7SNY7KSATxPG+hWmjfNtBUCXdwHde5Vo/Iz/q87xbnvE5Clgftc16mu6Yb6jpjSbrH6+oF6wl/6b+oIiYUPGbUIdvL5/oZuyWmkV+hlxQ8b1kbqURV2gL5UJKnnWEa1ZugHtPF3/dgD0J4U+0YfWrZ5bwqTzOu0XfUYRpR8JCNvbA0KPJUpg3tJ/ROwJImLWCeIcu2cGzUDf3QvoTaxfJpRO+Fd898WGbYjMF6TXI8cHh8aNCzydOM5PnjrOVw6AfpA7fuZMdY/5wFvwF4UiHN1z5z31c7BglATow75hTcUoHcJ5XZ9iN/OLQe38OvqZxXWShpEM84EAvXx5/lKhd/KhZL2gp2m6Qe0Q6FL78Msr5wnLmXheO3J4NQqgg5r6D5wiv2TFXnGwqOUisi3tAXid1w9AS4m71Fm76YT5hwa/1WR1dPD9HPFdGBu2ITD/cSFGYWNDtkaOC5THjguQJ4zzu5I61lck+6vnvw/muPc8Yhd2187tQy4/LG+ZTTfQc0BqmgzoTJJIJaq9ddXDK2t6N7hB0Oc0cAipdlk95/RIAndV7cJFcGOcsqN73xVb5VCvWJ+/NCcha0vc9Mjv4nVD25N0g9uzjEPuw5Q708/5omeXehz0w35hXyPiMMT0OVjWYgrmuMlnvjsFaO4jCnO3TVpYUXQDvfMcSIBu1uK5AN+JsWEbhHlOiv3Ud2x4YeDY0NbQsSHyTqCPDahKmBQ4brDHfhyQ9hnYc35LAfRvAzkr6IY5dEFd2vPSgtiOhozIjs1xYR1NKeEd64TRb5qW5Cxnyg0dPlyA1PtdFFhQAW5hvWBHWa2sCqbYF9bztyun58F77oLOdtXXpYKa8i5Rdv034fEHT/tHnz4VGH3yaHTSV5sWMiN6hbr63Pr0x+g5quLpJSnPI9jRv4Yahb+LNAh9BYD+ROydeKhiVX6Jqtflm4iE/Wd9o87B7vPhPu/9qalbFUCXg853wfyAdEScpVoJ6nClagMEJYQ7qK3ngkh+u3kjqtsOpV5Z+bTDvEuCNpIM6GD72iF8R8aGTS2T/dFzTNRM77GRJ+aMDZcHjA2Vgwj9UNT4gJlD9RvuusUUd0fncKNayboQOkEONeOvBac2XrP167ht5tvbzX3fn58ZcaV5qWwFE2AGu9Z59WltqkIMvhd+RtXjf52evllu5/+c9FoAv+wefHdbgbCCzmuQ18A9PBCQc9altkdGJ7zyM456F2QU+Q4CPdYr8vXSfNGAHlC+iU7Yp7gOl1hhw75Ot25t3uKrTkEPFVD/Zk7owe4mN9ggB4FN7Hrvxz1WMQHmSB2drNP9Gb4vY8M2QHMaF6vrMTa22WtstBwAXT5nTPiVgLEhoti/xv77UP0O2Nl+1za4u3Z+zzNuK50w/6F0Y8Adx7CzVPBC/YaN/0/b8/hVTID6qtq5K4Ek7PX+QCYGNXT4XlWOWQPHowJjTqpyLW6Zz3m3Ly1tC20ReqfYTs9sPpVn16c9jRUmv/Sxins72yjmnZ9R1LsQm+i3ycKEl7I6zoDG9+pX55fctPb7WXENrjoHPaLj3I8Hxx1Bo/TM4jlJxGY3djUcQesL5DDNDmfQmQTzrs579i2yKN3uC7cx+A6NDZsKZjcm/c8Of08UuYyJuwaALodAnzk2cr3v+KgJQ/277rJiRT3ROUi3J+ZJ6IL5w5XNc0D9/ooyrC45+Xcc8QnsOMUO6Lhl5vueAHUrv182LxQxpGlqQVFhnWizaEPWFSLcUp/ArWxArnZzde1C1XXDfaN6PdjA873mEvLgmkvww5sWfm+IP5/z25eczGa6zn91be4qqHhH5eJ8wTZf+5S7XrqJP3pPi/9xjn7c82S/lPPFa8UbYHlioNvmjofFHUHPny6gb8/lV3U3xwHfHxK2jSTSTe7SaGfdIMKcdRmMq9VYNNIzb65CY9wR0rR7o2cIvlNjw9ZPet18TPJM6zFJJxzGJMqdx8TJWWNjD8OU+8f4bR0y2T/dtQ290D2qZhfS+v3qJl+6gH7HI2YveoM+zQroKF4UR2iIW7Eie89Zn4iL6PtaHQKe1q3JW8K0BjG4tAU6/PeBfv5IXPIe9BxhJLo/NW3b+sqC7mPVr8ldcjw8/tBtiznvut9nNec1cx5wPqi8rZy3JHwm/5Dr1NQnHjpJ7V46ie1hNilXivNz1P6euwVZG+EDDBOADh2sVr2tAPpVp8BHfuXeodTiMawwkFqPA1vUgpgIcaKuPLuJtNO9mb0M36+xYaMwo/GcqUZ/T22yGJMiB0CXO/w94YrL3+NFLp+F/MfH+p13ZsRFEKLzWal1dMH8QVxOHnpzPjYz8B1vfVKvDvfSupxqeAM9ERL7DQH+YCZ4pHSLtyySrL5pOac7+pbb+L+EQiZU79+Xmf4Fmrm44hZ8HzaLMeFc0mLFXzgZZLY56KS1u+qktM8wSH7Ai+UNqnt9pyS7DmYqlLMXdAL9cFzSXjRK3xZLsl5VM72UHOgs3BiHDZuy6X3G+Q/dMdkF08dktBqPSZV/AHqV0/9LGPexf/dth5BDKNC/4xan05JqB1kB8PsfdteDLee8lpb3hnnnyFrtvFJFffkSO+QW2ii3NZ+/biQA/YJn2HUUVHt5mY39feZEcOxR9DMHE1N20nkO+XPnljtb8uRWOlnttjoZ7Y5T059Ez8w+tApE6+ocDzZA7hFyGs74Rp5XjsyZAPTGpdIVCuU46Jddg+7YbvDy1XSgmzaxJOSd7qzv8d0bGzYlmzSJn6g9nvto2tjMuwZjM84ZTEjPnKCVPX2CNt/gY3qeZUbUbvPw7xW+wyrq5vLkVZyVKauzhts3enI27jUO7lB49eykc1FL0jp6eUnabyJZXpVI2uXzOdLG3aYhbxWfa3GNuaP4maZ6USJ/K3otmp2j76nyObE4d/12q/Dnis/tsAr/USKZW03HOUhz8yo9PcQnpmtzX0Cgz7DJvrowX1Y+mHQ2aSMgg4AO/fyM8FY0Si/PCi7UdKCD5TKJFCn3DotN3qPxHRwbtg82UUeoP36K4N6kidwftCdk142bwgscN0Uwazh8kXnKl5Um0U8VvtQu81BWwJJCOnytaeyj9YYRHdDXGUX9HJ0hPOafk9Gh7IGSzJcxibmbUV/kmnxD8dlqw4j3aZGi3crv0SRf7JR4FzmfjoxQwZeqfjbXO/O04rPQRb7Zx+g6D2cn0cXJ2vw3/j7iQ4OB5MYyWRkZzEFJ4lfY1c8koB+KT9qNAv3E7LBvNB3onap3zez3pEBv8nTBd3Fs2ID9XUv4PxO0RGfHawvuT5gkkA4XyKFP1+UGVZjEPUSBnseS1dAB8xyv/AoUQsut086EcnmtZEAPFnG+VwZHephwbzXy+QJ2+mVNhXlCgmzrOuPIN4pzWWUV+3RAn4/L2VZlHPVW8fml9gkP6DoXPz/p1/rGoh/0jURPChbOU393PegFaHUKfIz2E4BNZ6c2lsrK4M+ZBPTOtaoI0OGK1dils6M1HeqgXv6cDOimLV5Z+E6O7Xdvhoayfx+vLdo3XkvYBgBbPJwwhy40z1iNwnytadzDbL/Fi+gAeol91n4U6HkeOXVBAs5jMqCHCLK/JYPHasuYZ+pCkEkunpP9DXot8j0zLg70GEsc4u8rPl9lHPEuIU62la7z8fbNOaytL3ppaC76rgzotKst3rIuvxjqDbSAOnWN0s+YBPSu8kDILRTqW6PDajQ+7U4xi27Rwi7Hd3Nsv3sbP0W4CsIcROjbhhvm0FeYJ1xCgV5mk3aSrnT7aouEm90AMor8hQNeC5Bm/kIG9FAeT04GjiLXlOvdIDSKeJ8cJdmpkel256TbKNDTw0V7B3oM2aysk4S0ux/3KJ3nZOssuQKhbusgbv0YAGUa0I8C5ToU6Bc8gq9rfIQOt8CRd7ofxHdzbL9vmGsJQzsjcy3huXFT+AHDDfM5RvwMFObQF7gIN9EBcwjvKsOo1wr4rDaPv5MWWrSMDOadQM8WXFAFYtLZWSc0EehrzGN+VJxDJUi9x6lxDFiCQK9FkVuKnNbzSpBtMbYQP4BQnx0k2T/Sgb4tjygyA71QFijUcKjvIl3S0sz+Ft/Rsf1+m+CmirUAzG8CfwCa4Th0ROcFFqnNykAX+hSW0QH0XM/cKhQ+y+zSj8fH5zVSAT08S3iSFGIgkiVADETsGlc/j8nZBpv6FOewwib+sTrHgQ8BlUgdXt3jDKUHheXs0Z0ueq49Tfgimze3biQDvbp6fhGq7Q59X0j4Vo2O0JtYGyk63d8Znjb8Z3xnx/a7szF2sj8BkB/oTLVPEdTSAXPoq83ib6AwX22ecJuudPtCZ952AoiduTujU6V7qYAemS4+TAWxaqPwbhgus09o0zSgc4IFhF4CmH5X91iwj0BxnAqz6FdMOD9ntuQsjNL1TUTfL102r3TEAv2DZC8KdDiTbrHRw0dzoc4upxpds6zxmozv7th+h6l2/hII8/FTRBfBP/3pgHmwESdbOTpfYpdxhC6gg1G5wyjEFrgJW8KzRCcogZ4m2UcFjAozJHVvFfNM04AuBSNm6LUo9Ei9pu6xymwTHqKjfHEf4fvyA3iHZT5ZJ1V18azMU1Ymgqd6eoJfWJa8tq/T07YofA8QzqkZQUA/kJy2TTntvmCuH19zge65iAroJo1eLHx3x/a7sgkTBLbjtYX3IdDHThEI6YrOC8xTNykDvcBN0kgX0Mts004ROtzZslqqkTXoUcmynarUn9eaR7/UNKDnemcRZsjzvdIvqnusJY4J99BjJcZItw/ldy1gpV1Bj6+ql0yP7jDT5naYaPM6Vk+PIMyVwx3vIwXovcbXgH8VHv6FBo+tSamADva3J+M7PLbfjf0VjKiBBrgTXdG5YBddMO9Kt8fdRGFeYRLzVDC7sJQuoC+3ST2H3vDndY6sZbeRAl2a/r4vyKw1j3nZk2aOfKVpQJ87M/Msei0KPNUHOpw/R4+VEiXeNZTfdaV13A/qAB16rF4yADq3w0Ynu+OkaUDPgh37gKcjBejQL7uG3EOBfsk9+KbGRugbPTIogd7MKsJ3eWy/GxunLSr+APP74ybz4+mCeYAxN0s5Oodd5XTBnCxCL3AVNQeKs56TAT1AkvG6L8iggizlGhmhE1XeFrDUT7nDRjhChB47tBG6dDbneDWYcVcH6OXTIztsdTidUI/QS+1e+3ooMWXXSAL6Gf+oU8pReu68gCyN1HNvZkVSAR10um/Ad3lsvwubNIlnBUHe2QinLaijMzqfa5lWpwz0ZTbpx+kEunINvQg0yYEZ9DdkQA8SZ76gAkwsGI2C8+eIuEy7povKLHJJvqnusVChnWqjyN/i4of++8KHBDgip457uQouT50m/Bl6SrBo34YVuaUjqSkOOlyOowz07dGh9Rra5e5LqefezMZb17D9LuyP47UE+zujczCqNnayMJhOoJeZJZxXBnqhC38rnUAvcubvINRYHTIoG+JA5E6pAJcVItiHHodOyVN1XfkcyuziHqk1tgbgXW0c+ZbR/QTgAczAVPwYdr1PMxY/Xb6yYMlIAzrZPPrZmSHnNbeOzv6VFOpN7Bv4Vo9txNt4bXHcB5hDL6cT5iZ6vFBQL/9BGeg5M+aV0wn0XHbueoKOu23CXSqgQzlYanU0DiF1v8A9tVUTddxhND3YcTO4zIX4YBD/kInnO2OW9BsIdOjuXjmnRhrQ6yryi+UOAT+gQJcDbfeQNTPDNVT+9Rn5ghb2D/huj21E2xh92Z9BdH7lQ+381rjJoiA6gc4xzSxRhnkF2HDG8S8pohPoUD++2jDyHVL7ftEH0ClnywnSrzRvGRuMw3E7dNOaOt3pUiXVvIUeaVeZer6GpuKHEOg6+qIX0tz8ypEE9M699uxQuXKUXpsaUqqZa1Q920gj9BbPX/EdH9uItgla/MWK6HzCFFElnTCHvtgieZ8y0FdaJl+hE+YKX2Mefw+FWDg3nRToIXzuHZVACARmkod4TGsoPDYpt98lKegqWHUlbBc7J95Bj8H35x1mxvnLtihfA7a39JgiSrewFd8caUA/GRx7VBnoR+eEHjBthiIz7CANG127SVVHt/ti5p/xXR/bCG2EE0wZryW62xWdC++M1eKF0g30tWbxd5WBTuf+8762rfHCEsl13PlcUjlXuP8cXZ+6AoxUMQ3modn8i4GgqS9YyPmuL7ALAXzRawHnyQdaP0cFdmDnP2wYpOu8I9Ml+8BCndYgIecJOP+X0ANEWc+DBdn3oIAQrKXrm4oed0Fd+DIuXrZ5JAF9f0rK9p5VqgHPLjv7/3zCK+gX0GR2H9Se28yaWXdBl/gxsyaPleaNnoEMb4y7SNnpvslbC9/5sY3M2rmWsBqpnTfQDfOZ07nJyjDvWsjC38wEoEtmzlu9HtEwX+waQw50Lo80dQwFWIgrR9MvMAnm0ak5XwaKM14qgBaVIT7UV7d+hQkCZJPIXwei8sYP5B8kNAc6Jt2lKxqHIEfPm8yDhFmPPGaLLyqidLhmtRLsPx8pQN8h46/vlH51CvjpnKv/O4UHrp71GAKd4M0erWYt7BzmAt3zOGWn+yZPB3znxzbibJyuRFcxpta5UW2yIIFuoAss01eRAT3Ha24FE4AOvdwM2eFtFNERk5naC+hhIMol03BfbRHzHB3RYtrq1BAe9yYKsfAM8ZE+0+5gXI2Qdgc1cVV/V4lj4l30s0Ia0u0wAwH31vcFctQDBFnPppmIflRAPTwmd/tIAXr9mrwlF50DXqEwh56f6/+8F9C7Ivb7AJ6LmAl09n5qcRnPAHz3xzbyovMpgvru6FxbtI9umFPVzytMop9w/YqLmQJ0sL51M2EendU7Sg/jCM71p38OgcYkmEdkig8rR6n9AT0jTPQlunUNPrCoEqXDjXNol7yqnxvyBxg+9xYR2lnPQrJ5VyMyRUfhcp1wjuAMLD2g77H35b7SMRD+DIFuYCp6VFFZsGgkAH1+nWDvN96Bb1GYX3IO+GVvSOhls0aWCKqsmTd67OsF9WaWiIFja7upgc5Ow3d/bCOrEU6bb0CIzqcIc5gAdCj3usYkpn2Jceyz1eCfnQpxFgk3mQJzxV500HX/uCfSjuhISElRWp0qOE0Y84rL2QZnrNHoHEKt3xQ4rGlH5u6EkeDHTbVL9waKsp4pR6T9AZ1Mi72/MgIENxxPU6ehLjRSthP6UJwzhDV6rsECzsPoZOlusu8bzhWcV7zPl5P1k46x4K0iSoffR9OBvrQ2p4bbkPp0V0TYawjy867+b685BPzYmYJ3CfyWAMsW1lxYT0egfh14GMNS7tsoa+hNbDEmALYRVjsXbOypnQsuj50smE0nyKGQzbSpgg2Oupw3xjq8dwq3nsp96zOd8zDMs7CcSVDPY8lqIMgVQFpjEdURmZ1Gugsd1prhilRVZ8+j4mRbXdnSM0bm4jYFNKDrGoieW9hIbnn7Sg8NbTMYjMyznpKlmFUBOiwbVIL6eXcZwjDyN6Efl/JzCz1SrxJmz8G2tb6Oz/bOOWZqJb6rY9CT6tbRF74wsZLcY82UnohWQ1kOgjsAyPZ218dFnCcxyX0/KIBmwUuK95uzuG+0pwted0Xp4sdrK+YXay7Q5xcLGtLvcBvSnjZmRP0Mga6AucKzC/1SlORVcwmRehNrC8Oi9E2UQG/xXIAJgG3E2OTJ4smE6FxLWEFvZC7MAd/jura28BkKc4XrT+W/0p4qeuJoOfdrJkE91zfhFQqmteaRHZzIpI5ACQB6pqhztpwHGr/AcpAn6Pug1GscgDYZNHwDcvbrG4t/QEFO5hDskXGyberVjedugRkE0Ah2FUalfdWMVQF6l1561gm0ex9mICC4k6MlO9D0/BLHxG/RawGb6tIiJbtJ0+GRObuMLcQP+rsWhhbitpDw3N0D6uTncq+j5xnRR/Mf2jwXJMp6DN/PTuC8AlH6O8V3iIySddfSW0rEq46HxR05FRRzXNlRoF+38f+J7D3HIuIP1K/JXTJcQF9Yz98OYQ59rTTmJWyKUx5f25gYvIoEmru6od4IG+XYyQzqct/YR8q9DFMA28hJt08RliGd7TQ3w/HnKx4u9HQEL8mArjdV+FJbV/wUupWZ7EQGQ4AeJMr8sYgV22uhR5UxjNijX6MLWNDNalQAg5E3jML7A5jCjQDI1EnFw/o+ZSf3B2ANFOhdkXfaVeXzhfX1CtPoV2g3fM91inwHO93JjhUYJtujyoONwvWNRE/AZ/aqGp3DsbyeVDv3tsp9Bp3ZDDjOlvlS34r/ThGlm1iIHigAec0l5AEKbnX8tF/kmeEB+oIifn36fQXQlxXFP1SGOfRDQeG7eoGz2T2GmHpnb2WOUpxnDWWXewu7ElMA24iwSZOyPgW7zm8iQP+GLpiPnyzMBr//W8V3MdDmvZ6tl/GaPz3x5TzDhB/FhgkvwvTTX03TEz1VAB26o9Xc/UwAeoA481WgNKOjYEasSpu71gBlufRI0R4qgOkaip4RgA1S7u5e0lOz/aUHIOyd3KQX9AC40PeYgVT0QFPOIdn8KyQg/yESwPvDDLpaQIe+gJ12uVqFa7HOOOoNlYhMZIxsG2w2IwDbWPS9s4f4nM+cnIPweriyxWcMld4DU9+qPOCEZvXUw6GDksPBgZyjIqthN5v7WhGlA/W4l+lZczdCSLY6BX4/WKCfnxlxZVhq53WSOgXMoZeu4BwgA/o5z5BLpJvNmlibe4Du8a15k3soQ5riKqiAbtnk2YhJgG1E2EQtoQSNzoEvoQXoUF5WW3gN+R7f8o1SfiAbWYvzLFhnYCC90wN1yVNf1wV1tANdktG9aS0jJrljpU0UKbxAJPq2yC1FDhvjSCNGAGSYNkbhBOFN2sgFgAXryeh7nT0k5wdaP4ZKdkAw5X4oj3s9IkP4DUwnI6IyagNdMV8OygpPya4FVMYrtU+8nxYhokyRWzuI5Oj5WdpJbkbFkgjcgN4EW2fJVeVShKpA7nRR1tO4gWc4zsLPeqdxftY2EvwGOt5fwd9t7SiRQ0juknJrL7uH3IM1cnX8Eiv09pYForXDAfTchuxjKNBXVc1d2eoQ+EMvqDsGPnbY4OVLAk8ecT6dtZghKfdV1CtUWTswCbBpfqp9Qsq/jtMSXOyGKEh1j9US0qQMJ2xCHyzMpgrLyWC+1jTuIYRn9MyiFVP1JA8VUJ9mIP42dfbixXQC3V+a/l55XC0uI7Wzjj5vRupNKCIj8uMehYtM+gIEiMJPo1CydhT3uawlKla2FY1OdaaLfgxQMd2sokrcoICOjqblemedng+i9vme6RdhnT0JqamTOYy+0WthDFLZMf2ox1nYiG6hn5nhIz1K+f5k2XZ0NI9KAKhPB81zimMYOvDfKtLuwF/I8vLWMmkUrT9XNMNBFzVkXoOvwQcKsig9j2Q/OpSFBfC8zLS0O/guZX3U0PdjGmDTeBunwwskRueCA7Sk2qcI4tCmvAlaooOZ5pwSMqCvskySKwDqbpu/A029u9rl76QV6BSLWaBHpkn2qQIH2NGOptH1jMRPVUkbz/bP2U+ITO0lN5gGdHXcxEJ8v6eTXfTCP0j2lSqjbGi5AqTrH1OVIRQ18J5mOOE36nxPRa+BY0D2ax1DwZueTWzS05oC8zU1+cvQ6Dy/nrcfvn7GJ/ICGdAbU8JWkAIUQBwZYbvKkDp6KWUNvYl9GNMAm+ZH6FrCzQSgTxGW0hSdN6NZgnFaosQCy7RNZEAvs0k7owBo+pySIsPp0usKoOvpSx5kgA1odMA8M7C4uC+gR6VJv1IFDO6e0lMomOEYlqpQsXYQX0fhFxQu263JQPfxyzmIXguYTlf1s+5sYpaDKkpHR8+gR6dI1bpmwR8EaXwyOD+h3e664IFs9Zp5izUB6CUNkkYU6IvrxU1US1qgHwgK20lerwba7ugI2wbPaPqb4jyWUAId6NFjGmDTaAOjamPRqPgDTGOGPTrX4vuB393TlKct2AJfX2qRfIwM6EvsMw+iIPV2XtCERumzXRY00AH09KCSkr6ADjXRVQEDOmsOo/PogUSJYTl7wDx2N8Qc3cQXNBnoFqBWjkJ5IA8oUfGyLSDT8bS7WdBGfJscxNl3kfr5M/Wvk+CC4jjT7XgA6MKfFL87GmRdNAHo8xt4+1Cgr67NXQVfB52KX5IB/fTMkLMUjXESAtAZoPEO5F0X9wH0k5gI2DTagHDLXMKompbwBC3pdi2l7zFFwO9SiEu4QQb0Rc48QlodRuS603pq6XCMjRaghywq7Rvo0n5r2hBYKMDsXSSXB5yithR/i6SaH2kq0GFfAOwFUJwLPK+BHgNE9Fd6rqfwBeiW71W6QGVc4bIVtWVyOcJTPVKwIO1uIPoZbeLTBKDnNnAJDXHrarrEcb7KSN9MBnRlxbielLtnBgHojexi+lPunouoleI8z2IiYNNg8/1HsCL1rBLQK2gC+hdIhuAWkKD11Z4qnFNhEkPa4V7gJmpUhqmlWe7J7ua4adL7dAA9NWRRWZ9AT+4f6FANrhtABoLXs5K5j4IEnO8G4k6B3Gc6RoK3nW4sfOuXmQWP0UamJc9koCun2z0GUHro7isIIDbUefvm9BqLQ1ejBoEuf7VlYzOFxxTHmZHE+Vlnelenu2KELX9+3hqmA11azzmHAP2x4vVdYm4tGdCh+5V7h5LU0OMJne6NrNUM2IdeRN3lzr6AmYBNY238ZL6b0qgahCmHlvq5lrC1pxlOeBC+NttIkE4Gc+gyz7nrlGHqYT9vO5p2j5yxaOVwAz0trHBFn0BXoTZrat01fgajOz1z/rtAkWobv1CfkZzdOTqlcI/o7FcDUT9jCtBhuQCFMZzLH3CUD1LdMDLvyXiIe2U8gHbAj92CMiD9rnaEniE62rMzPfOlnonwpVIN/wjTgS5uyLyqADq/Ie07xetfLJKspgJ6kTSg9yIWUDMnRugedbRH6C0eCym73FvYlzEVsGmsgXnvVcQ0t/A2jIyHv7udH4t+jwnawjr4eoZZ1iIqoIt8Fi5Thmkga8E6FOiejvOGfVd6Snjhqn4i9H6BrmsobFcA3diZ/3agMIfuL8x8qWPSA3SbWbxfewRTJAc0BejobD1Uy1NHnx26oZn4Yc/Im/hBb6Aj+u0gk6Hu9w3LFJ5Ar5O5k+AhQY4WfA+mA120IetKT4Se+qS6tuv1urV5i6mATtbpbtrMTlLSda+hG+jgOxVQAr2J3YqpgE0zzXD1P4NI+Aox3S7aQ1N3u0ypy34RfD3PIrOeAuhPOP4lRb3S3b4lxSjQbcxzj2oa0IPDZbtQANi4i+/DiBGIvdwbqE+34b8CKfc30I3s+a/Aa3dhjVeTUu66SEMbFNlR9zhWDpKezn+wzCW697jZDz1NcZnfq51yB1r46HVy9xFdVZajlebmVzIZ6DkNnDNoDb2yZl63fvw1p8DHZED/KjR0c6+O8iZWFhHoHisx0LFh+xjRuRaP1TvdTtO4mpagTClT0Lmytdgi5SsyoJebxbdRARVtjDMxzrmkaSl35Zqxg5vkovrRraQnugXz2JrWFAejcTh2pzgHWIpQ91gwzU7slCcubQF187buVDlIv6u7gz2MS7xOgTHSw8pAn+GTc5TRTXH13KMo0FfUzS1X/OyKe/BdMqCfmB36TS94NhI3r8H6NU65Y8P2EWyslmCNMtCBOlwSPQ1x/GqlxjwefH2ZedIZMqD3tQcdlYLVny69pWlNcZ6zpN8oybeeVRdilkrjXqQyqQwGemi0bAdR6lV8U91juYLriB4LCvAQdOyB5C1hDl2F5kVSPXw+7xZ6HKgeB/XmCVr8DE+7z6vjfYUCfVGduEXxswteoa2kmu7skF7CMbAJDgU6HGPDTXHYsA2x6ejI/mWCtuiqEtCvgw1nPvQAXVSvlCnI6hpZi79JBvQVVkmXqYA6HRGYoaPTfbBja7CLG735w2Uj6kLM2kFC0D6HymmaBHQoW0uQvgWCOeoey90z51Rfne7o/HjX+QmPDUYprnuXepfQT2vvtPt8xqbdF9dLGghKcQ38/YqfnfWJPE8GdKA1/6AvpTjoFo0e4bRH6M3sYjy2hm1EGViT6qocnYOoeC9d29VgE5xSpkA0UUfkU2Ea+5hUJc427RQVUKcZSL5Fdd01TViGpQT0gS5YQd0ciKigx1JnpSqdQIcd7QNdsELlcKlNX0CHm9XQ8wvl8gc8+x+blLsVXb8awsu+SfaQpvj9TAV6ZV3BEhTokvrMy4qfnQqIOU7VGOe5bkYgMb3NPoNsXLvAjG1rWFgG2wiz8VNERb3q51qiNbQBfYqoUun75Dsb8qOpOtyX2qUfpgIqWNTyWAF0EK3fHH7p15JBSb9CadLBisqQ6Z93ptzj+15mwjSgQwEY9PubWEnuqXssOycxoTnNN4CYcleGMRCaeTDg7wuuCeEaZQrOkGUaOs/FWnyPyWl3YUPGLeIs+oIi+Po3EQkHqIAumB+Q3tN8xookpNsbPb5gxj50LP2KbaQBXUt0tFf9fIpASBfQQVNciXJzXpgZV0QF9BLH7L1kME32WbwE7XI3M5GdH3agg+77wSxnmR1AXK5iZad+mhmt3UL5U01UioMd6UOheKe8eS00MrdX+QGOqyHn+ALWvwd0jcDKWUIdPr0nG6O80x42+xUtnrecqUCf25B9BI3Sl4D96PD1Q/FJu6mAvoobNL8nOgdLUFCgN3sUMmI5SwtezoJtJKXbJ2SP7x2dg5Q73ENOE9Bhil2py72JY5lZQgX0hc687aRbztwW1KBAt7fIO8iU9akI0L8eSCOYobn4O/Wi21xidAuidU0Eur6x+AdUtlXdLIOBqfhxd8f/dNFz0pEzjuAMeo4DUtVLzt2OzrLD3epU8/TdJZDY3O1MBXpZrbQKBTocZYOvH0hL20IF9KbE0DWK1angn6eRdPsd80bPQMavT21iH8CEwKZRNnaKOIUE6Gdoi867gB6q9H0OyyyzqqiAvsBFuIkMpO628wlrVL2dCxrpAHqANPMNJdBVEHVBIQbho46YivL+cDC2dUkTgW5hKyFE1gGhqi23UVaKQ5fVQLhS7zPvUYwDS1raYxJl29W5Psrz/nD8UBno9i7SS4wWmKnPvIkIzDwtq5VVfMnJbKYC+q6wsKYPtfMcwrhak0cLQ1anwi731dRd7qwdmBDYNMpA9NvSC+gfNpvR6SDNfgFVrJtnkfYFFdDnu4s3kIEU1XLX1pU8TZhVXEoL0CWZv1DW0FWQXVXeLhYQMnCIObOJY1ozSfTLNQHoLqiu/QDXyFLN9sMGOeq0Oe8aoTkOrFXt94EhJWdXgKgnOgcPAk9jE2WEEcEZvtIjykCHioAVlQWLmAr04jpRs1Jz3MXdoux6KqAfCgrfZd7k5UtshmPdh5ruTAE6+D7r+ojQmzAhsGmOGcb+MxxPI+lwX0k70JVG11JMsk5SAT2XnbteGaJw2xpoiHtI5wy6woPEWS+ogB6RKTraHyA8hqDTHW2I0+ncMKZ+hzudQJ8TKPua0OluO/BOd+WGOJi9oIQzjNLB+lRUZKavvgcoQANV+Qip+szeanwhShv0FM4X5tUwN0pfUCSqz7iOQn39gqx9VEA/7ht6GIizrCdE5y2sRsbAvCt7UEsJ9GbPKgwJbJrTDDdFZEFWPx+vJRDTDXQwAy9Av9Os6ZxvqYAu9cpbqwxRP7eFtWi63dYi9zBdQA8UcdqpgB6eJTyuiqCKDrJMZKCSp12f71FYI9Mu1xSgRys1lEE994EK5KDNgbCEAVPw/eixnyKovYGIOypNvL/XmBqIwkO5xEa44D42tSk3xikEbpicdi+rl1VAPXcF0OeXJT+96hjwggzoB/yCviVIvTazr5ltYgcxCejmTaxGaqCzyzAlsGlOQ5yOkEfaEKfNj6Qb6GMnC2aD79ItdmM2lffTGpOYdjKgi2ctWKEMURvzud+gQA9yX1hFW4Qu4jwmpNk5aR2ioISOQlZsx3Lb2JdldnGPFjsn3RL4cY/Exfe9cU2dLWPuntJT6ojTwNEtuDpUnWUwXZ4BZq+5faq5JUdJduZ5ZZxfap/wYKV13JMV1vHflzgm3pXOzjqRkEAOWhsnyTX0fDy9pcdUj/Bz9qkjTgOU424ond8LOFcOHshOhmeKjkEhmmAR53viewD4Qfqd6pjGFqIHSp3uLz0s+d+dmxVx6YpHyL0rbsH3L8yMuHo4Pnl34zLZMqZAfWG9YIcC6HPLk5+dc/V/d9HF//Vlx4Cfrjj6v7zsFPAT+O9f9/kF/UpItTexeIyKzjvV69hfUAEd6LwXYkpg06D6uaCJBOg36I/Ou+vo6xTfa7oO702KQcpPZEDn+y5aggI0flbxMh098fc98+c5tKXbO4EOdMEhyEOE6R35s+I6qo0iOtYbkvtqq5hn2UH8XtHfDCUJWAt7yQ1V9c/1TUWEjm4Ysau2y1t0TH2YI+NaqbJeanixCbItCz1Sr1YZR76juhblZlE/i3yze8Ea9hCg1wKOr6naKAjlYlVNtytH33ApjsrnLcp8RhbFE5T7HHsU4/R0+a+NdLjvbaZmd9ww8+24reQ3Lef8eiQq8evqqvlFTIB6Xj3vIAS6uCqlHQKdzI/NCHz7YasagLnHQqbBvBPoLaztlBF6o6cUUwKbhpjsjxOQCFh59zgTfKwWLxSo2N2G38tQh//Wair37SqT2F5RejaolxOiczPZMTQ6n+k0v4VOoENd8HB+esdy+2hKkKNeZRj5G4xQlcFsCMCF1MFf+gfn7BtodA7rxyqnt4GKHQDTi0EBHdSfY5Jk29DjJsTlbINZCVWuRTXwAlbald5z5MRudw8VmuNgdI52t8MIeSCpelgfh4px/V0TOL+uiva7Qn5WX1fwq4k2t0PhX5oE9QK6wmHEvp4hjXNF9cKtgvq0h1RAP+vm/85qI+sigLqAiTDvcs+91F3unhmYE9g0wibqCPXJ6+fCRqYAvas5TlgO/DsjHd47Y+DB+umvlFenovD0cSnYgMLcEGi5p8/pvVp1OD0qnXt9pW0UEdogSl/iHN1R5B73bJldwsNKk8hfCSAzivyN788jdKLPmJ1DUI2DtfS+6r9QkYxQbwZd1GED1G+HYiiwhqyOw3R0TIpkjzIUyWC+2iLm+RKH+Pul9gltMDJX/nm+Z/oFJRnYvajIDBTKIROH6c42gCZAAyRTAcGurA6n8jUBsA7N5l0G6nHfwUgcNsrBdauwvBCR0X+TY49okPSAgS7/DQpz6EWm8T+fnxHees47/EorWE+qDPWzPhEXmZJ+L6/NK73kHPDyAkixn3fxfwtBDv950dn/9RXHgJf+a70jmQtzOCPveZBSWKbRMwSTAptmpNu1RImk9XMt4XImAX2CNt93orbojPEHoEOP0E97tdYkphPoUN9dAU44Zz5Vt0fqVVtP8kMYa+FaOmHOAV7qGPcjCqdit5iOCG5aZz09lMtr7QQdADOMREFE+l7xvkrjqNepkeJdfemxm9lIbpNpsoNu8H1EEZbOEa/jw9G41pcXuaXI0Wux1iLmR26w4IAy9GU+YKrBOPJNzwNO+Ht+AJ8w4ufoJibosRuCrWVkvQUhkTm74MMP+l5bZ9UzFR/LOV6ccyjIYcpdV0/wi72z9AoKzZ1Sbm2rfUA7CnXwpPclU6B+zSnoMVWne+KS2XFMBjqYQz9FGaG3sJwwKbBpBtC1hatIgf5h9ziT3MJAyLOcmv0Ohbr91Ow30fqpr9Kmpzxzs8nfbWKYcwWNzKF7OMzbSifMoRc7cXehACsCjXAB0vTuBrkQHo/QNJbnnXkGfX+pXfx3ypGmMqhh5A0bxWAK1xXMaXeJr/R0xX9o/mqlG2DZgfwD6APLGvOYH5OjJZT1fF4g/yBaY19jHv0yAclIRHc2lhH16XWmi36E/QXwOsDrAc8b9g2g74Fd/v11tn9sh82AFSZRry11sjthbgxgPnWa4FVnCt5E9EgZmk1LcpZft/N/rgD6LYs5v7YskqxmAtDBZrXvVNFzZ2jK/QplhL6BNRWTAptGGBhNO0AeoYsSmQZ0HyN+8lzDhB/NlaAOHdbWlUEO3ck6/yu6Yc6dU1QCgPSqOxo1j+xsjEM73oOF2b1UyhY7Jd5FoQ6739Gf+wfLvgIp5idkc8xkDuvNdAMM+iqr2KdIbfx9drCg35Q37IBHr0UBO/2y8kgekMNtU/VaGJqKHw5mbexQebFL8k14Pu5TMzuBPk1X8Br5ni9Kls4rUwYnjNRvm835rbuePiP8GhOAfsUt5FsqoBfO9eMzGujNnrepm+JcP8GkwMZ4GzMm/E8A3ndIgP5gvBbfj2lADzbhZ3dqthvFP3fRzXpDBDrvDQpyvWmSNrqb4BS+xDFrPwqj7IjEXnPoAOi9ZsoTY6Tb1yE1dTDO9QOZMAmZHrhytOoIJEbVkYodaocPJei1AGN6t1VtREMfBGBUm6D0cAIfVmAkjja8kTkcUQMb27bRfS1So8S7FJmHAN20DqOpvHeE/2/ThC8zOHkNZPA84xt1tjv1bu77fssC0Vrage4eeocK6MuEgXOZnXJnP6YA+ts/dPzhHzAtsDHeJunITCga4i4xDebQY835EkUT3FrgAsPEF/7TMn9x1uW8sZjKfa1vIL1tZiy76GE/bzvcsMYEmMPaeaVx9DMFiFZZR4FUe29hGTi7THbTL2ClXkUBmBUi2EclYwrHn2DkCRvDYDoeqsI5AjW5kPDc3XTDS+Gw2Q2NzlOixLtU/azIj3sUvRa53pmnSZsAwTgb0Ki/DOvl+iCDAR3+O1w5q8pEwHD5AnbaZcW5JOgld+h9SLUT1rlSCMzA1PttiznvFFA/4x91im6gX2KF3qQC+trskIUMB/oLCqA/waTApiENcbwECoW4A0wEepIldz6VStwqyyQ5EwCu7HlsWS0KoRy/eFKluM6xLooaK1pvhs1kTAHSQB1mHKqNI7pr4cut4x4PdFxsrVnUT4rPr7CJf6yp1wI66OjvbpLMnp70hiybYO8qvkwF0IugA14B9Bs2/j/VVNM7m37BK0xOBfT61JBShgP9HcUu9FuYFNg0wsBsdxlFhP4FE4GeacUtpgS6RdI1JgK91D6DkGKOzkglXaEaKMn8ierGD1PtSEPYC00FWM6szFPECDvjzECPscg1+Qba8Q4fEjTxWsB0OyHzYpNKWv83NJM8pALo/tS0bWjH+05Jdh29QA+/RgX05qSw1UyFuUmzRwBlQ1wz+xgmBTYNaYgT7iQD+oQpokomAp1nkbWECugrrJKuMhHo5eYJ3Y1t4Hu+BOD+mQzocLUqZWrWPbUVvfmnh4v2aCLEljgm3EPPQ3kUTxUXz8k+hh5DWXhHU1w2K+skeh5pXtnnSPsfwJTCylXzlpABtHmpbAUK9JNBMcdoBfrMsKtUQG9JCFvL3IY4djzlyFqTZ8uw3pT/829/+8tfPvvM9C+jR88CHvrJp59FfzJq1OxPP/3c7vPPPx+FsYWNOuUuuEQ+ssZfzESg8y0zl1EBfaVl8hWmwRwq1wFhmDc9oikJN8GClu+pFrQor9ZUuNSXCDEZiHQ1EWJourzCNPKXoYhsYcSuidcCNgOi55EYJtpLDnTRS1FO/joqiF639f9JAfTLoMucTqCfnwkEcCiAvjkhrJKxQG9hc/uI0Jd+7PvwP3366aesv4z6rOKTUaNv/WXU6I4+ffToe3/5dPQKCHjwWdyth63T/vd/Mz7p6mYnTblLmAh0oVXW8j4i9MuMq5+zZDXoTXuJbcZRoCJ2mwro0SlS0ua1tEjRboIgDRh10jSAJcP6OXIOZXbxD9U9VoVZ1OvuOjpY5KKJQF8DFPG6H27A+VBtXYMOf0bdiBZ2s1vn3cLv1xo6ge4dcZkK6FtiwqqZCnSLZlY+tewrO/Mj3YJ1/gVE3+mdgO4P4hQOHgDO//eoUe4YZ9jG6YisKGDeNnaKKJmRQLfMXEUZoVulXGQa0IucuTsJ0aQTb3soV3Cecid6OvUSD7SZbDAwpFNMhnAtBvFQgo6vrTWN+kXTrgXcpIcK5az88FACFe7IgO7tKz1EBdHTfpFn0LR709Kc5TQC/RIV0LdGh9UwN0JnlVIB3RL8fMhvvqNGjbIBQL6hLsiVIvZQjDNs46cIYiiBriUIYSLQRRZZ5VRAX26dzDigw4icIIbiKmqOyBQfpgR6JrX+d6VZ9CtU71zTIAZr3ei1gBvW1D0W1LzvPpZRxPvYeNkWTboWaZESQsYFng983cxGdIcM6I4uUkrN9uOhsYdRoO/I4dXQBXSoLU8F9B3RYfUMln2tolydusVLb0hvvCC1LgYgfkcB6B+BVwFIh/zlL/+j9aFm/kdYVwdpeaO/jBqVBH6+G/jbDzA/MTLS7jr/As7nDFNcMyN04QIKoH8Laug+TAS6xCqrgjrlnnKeaUAvs0kndHXDFHxMomw7FdDDswSnVRlxgrVojWsCAx3tfS1ZGUxzXVIfsrFMdKglgH7/pY5JnSqBUBSHDOjGlmLK2jjUckeBvlfA2Ugb0GdHXqAC+q7IsI0MHlvbRAH093aNvv9nqO65f/xk9Og1FCD/+ZNPR0v+DEyVAwG4/xW8vwgcz3wkRJdjxoz505BkK4bINbPDXdBAAfSrTIQ5dKlVViUl0K2ZB/TlNqnn0Bv3PHdJQ1JUwToqoIdm8y9TN5RF9zSUmUW+0jSgz52ZeRa9FvOBqMpQiNNAH4g4DROcA6RuCTr99vH34esOQM2PDOi608XPKin2nx+LiD+AAv0rbkYTbUD3jTxPCfSwsCbGRugt7H2kQG9hPx6q++0/fDpqVDlFyvzKJ59/rvP7ThjjCH0IgL6fYsvaCaYCXeMidNs0QoRe4CLalBWweFGALOMdGdDh2k0qCICa61t0OYnmjWkRZ9AXuqWqvSRmpU3PXH6nylpMzjZNuhYZYaIv1xMaBOMewdfhIhmq0bVFS/JJa+OnAqJPoEDfLc6upwvoZ3z6iNDDwxoZLCpzgaLD/eSQ3Gw//XR0FkU0ePG//uu//htXgLEN1iZoiS6TRuhTBPuYCnSRpWbV0EscMg8RGsGceTvh64HirOdkQCfTc4eekCDbinaIw6YwTQO6smyrqhru/ZUfYHNZnAYq5q0n+f/J9pYeoxxdk+ZXkUH03KyISyjQN+cLKukDOnUNfWdUWANjgd7EbiOfQWc3DPpG++fRo6d117yVxs9Ac9znGEXYBmuGhrJ/H68tvE+Rct/MVKCDsbXVlF3uDAT6QmfedmLzU/px+HqIIPtbcvlXTjtph7hSinapfeJ9TQN6ZpjwK/QcllvHfq/OcWITZFuqDCN/0+RsBXR06c46sO8dvga72amAnpA6t5l0B7lL8EMU6HVr8pbQ1+UeSQn07dHhtQxuivuFAuiyIWiCG/0NWXQOZ88xirANhU2cKtai6nCfMEVQy1igW2atpIzQGTiHLvOcuw6FGBSWga9Tja4BtbhfVKk/F7DSrmgawDpBjIzeKWav1Wgo+5pYf05o00SgQx17ZdU8uA6XakNcIFg4owxQqN0OZs/fKGB+3T7wGZ3CMue8wynn0LfGhK9nZnTuHkq5NrWJ5TuoGy1oWnMlT7WP2oYxhG2o7O9aAg/KkTVt4WqmAp1nlVWmSUpxHP+SomrDHqU48D2fw9cj0yRfkzbGSdPfxyb1HsEqdk661ddedE1xOG+NngdcPDPYbvn5SnvRNcXhQxl6HrAkAfezUwGd7Z3TS9Z1W4GwAo3Oz9O8F/1cH0pxW2JDq5gpKsPOpAK61QbvSYOMzkdtJQM6FoPBNpQ2TlsUTwV0IAdbwlSgZ1tkl1ILyyRdYaKW+2qLxBuEbWsz8svjY/MaKNXikqV7+1IVg1Gu8h5wTfEFrNRrg5WwLXFMvIseA3aMa+K14AfyDypL2MJ97lRAt3eW9Nq6djguaS8K9EOJKbvo1XKPoNRy/yI+tIKRQG9hzaPocP95UHvQYbMbgPcbEqA/BD/+R4whbEPWEDdFLKME+hThfKYCnWPJKekD6IxczrLIiUsQEVnimLU/M7Ck2F+a8RuFWtzhXiIkRj3rUxUiJIxIoyflboWuslpcMF+pF2Bg6XKosAZH9tDxvTgNhHnntQNiONXI5IJCW0BnuuhHMqCb20ju9JJ99Qy90Q10c9/3dKrE9bttLT50DTMXs7DWkkforHODi84/+2wGabr909FfYARhG0obP0VYSg10gZSpQE+35BRRp9wTW5kIdMHswlIA5O7acblZfFtXpzvnKRnQwziCc+iNH85rE6NaDq2LWaIyxIfgeB3c3x4oznzZ6eDfQ3jZNyPAz/r7fDloYuvJNkS9HUi2QejPOzwSFrP0zNPH3yesUAX9AbpGoqfka1TFhDWqjctky25bzHnHlMUsXUAPbe0EuH3As1aHgOed//wA9I2pocsZmnLfQbFlrWaw6fY88vr5Z8s+++yzcYN1KC4zkqAEz4cprnkRuqCWCujjJwuzmQr0eAtuPvU+9MTrTAQ6Wdo91zO3KpTLvU4qLsPjXkcbyVBBGTiLnhBHz8x1dFLOjhA+9043xCkcvicmRbZd1bR73oz0cyoD0C7+O6al26PSxPvDsvkX4f9P+KATwuVdDc8UHotJkvX7/0mktEUPjvIZmIofkwFdz1DU3pfkK93p9rLanHVHZ4c8O+fq/w718y7+by85BbxaxQlZw1BRmTPkKXfP9MEBatSoDR9TzQwsZjk0UmCOleIGGaFrCbdr2mIW6NFmXBEV0NeYJ9xmKtDzWdJ65W53mFonn0XnfKe44efPyCAozRW5plynBVopObuCBFmP+4O5wuF74WdIt66BRjh0MQl8YFElSu9c7oKUHtQdexsqh4t04P8r6uuQ9SycIzwT108JAYzdvVCcE1zAY2oqekwlLrOqfH6JIjq/Ye33qru7HaxQrVk7bzE9MF9QNLeee4jbkPr0sG/wG2WgKzyt2OcxAOhiBo6sPSTVcN/gbja4CH306H0Y6Bjow5RyP0I5tqYljGYq0ANMuVm9QG4S077IKO651DjpURi7sDzZZ/ESJkK93DzhLjF1zj1KOosuzvxRUTuvRGaVYXTen8RpNABEYJhsz+yAnP1zAnP2wa7poaiTB4k4DwmwEmU9Dc3mXQ7PFB2DDv8dvoa+B8KOqr4OU+UDeVCBwjqrrWKedYMPOB+k3wdyHvBawGsyFDCH5xwoynyhysMNLEWQTS4oPEdJQY9lwPmFYhb9xcJF+SvJxGSORifsowvmsvqs09yGtKfQv5kVRAn02FKfJ10CLh4rmTOyxvIF8H5HEp3/qtOo8y+DTLmTz58DEJ/7dNRnjYP20aNzR1DG/Z+gzj1TXOO63LUEFykj9MnCYKYCfYaxKFEB8kIA8Tl6Ga/NdbLfGevw3hnq8N9q64qfAn9ibJhzxcelYAOTgA6726uQWnqVUeSbhJSU971m0XMyfkuOydkB1MPaVV1mEhqZu9PGSXKNrP5qaCp+6OYlPRWtJrxgCaBXSj2RLKUu2x7M595C3xvK48lJAR0r3Q6awH5GAU2VeofNY0sciLVm2Ok+kHOADzg6Bl3NZvYukkGNuYVnCI/1Ajd4mAkGe+7htSKL2tEySn8z6f666R0Guvw3ZFCX5OSv+yYiYT8K86vOQY/WV81bRAfQ8+t5BxUwh35iRtCby07+P19zCPix1cH/+TXHgB9Buv0XCPSQ1T7fdwK9kd1m1sjKZwLQTZvZSRQja1cHfZMF8N5DUUMX4jYubENnsj+CCP0OZYSuzfdlKtDtjYSREObJ+qk/mehwO0GucCPgH4De7eYmsrOpcxYvZgrUix25e1EwVYMUsmxOfEdMZmpHoARsW+OldWRHJoHGuZ5VqYr95zA9SwYDTzCfrGsgek417oSCPSRctntAaWXQ5EZMpXPaYhOp0+MwvRwsyL6LfiYyXXKAdGwLRNjVRj2KbwoFPDjOBYEPU/OS2Zzjyg82UBkOSqcO5DyMLcQPuq+Dufg7dWEO9AP2BYAMiuLc4L+HcwRnYpPmblF639fKJQr4Psp1qhGi3RUmUa/h+YXqpXaYaHM7DKfy3ulNE7yaqi/8CSrFwX9f7xT3LQrzm5Zzft0CZtHpgHlxnXgDCnNBQ8a3V50CfyDrcIdg962c8W0n0IEDBbbbZhs8oxkg+TqfXFCGXT14oI8eXUcaoYMtaRhC2IbK9PSK/oOyIQ7IwTIV5tD19EQBMfqpP6Mg7wvo0I0MZa1MgrryStX+HO4+T4wlB5i7p/RUfyAnNFYZiZ4EheeqDHU02gwA+vMxKdL+Pwveg0IPAJ5SpjbPO/MMiM7fq3otKgH0skJFXw4Ewt6+OYcJDzZqAj1O6XrAlLvyiCGh7yBZtjNYlPk9Cn8yjQGF8wJ5B2FZJeoD0Hu5Drej1iiiG+a3zOe8o2uzWmVdwWJ+ffp9BOiPV9TLyuUOAT9Qja3NKZ8F5r1ZDxRQN21k7aZ/ZI1dR1o/38SOGHzX9ujRxRRjazUYQ9iGynR0ZJ9TAh1E7kwG+iQt4QIjBOLmU7nv4vRTfobp9+XGMc8ivQpXu9vm75g2TXIfhbqlae5pJqXfl9plHlIFZGU28Y+pYA7TyNqgUQqFlbWDRA5fDwP14pDInF1w2QcEmHKkHqVCExqEFSFtDDq5VU7Tg/cSovQ08UGq90pnZ52A42v9XQs47ga3lA20bq4PHmKGAugRHOEpwvXIEpwfaETfVa7oe61qhEHqG1KgA187PbIrMrfy+2W3IIu2vefz6wW70ei8sE64tQqsd6WCOXS3dV7+Zo0edQqgd0bqjexMmhvijpLtQDff5vu3Qd9oPxk1ypei6eoGxhC2obLJk7mTKYGuJbzOVJhP0OKDZj3hbUMd3hsIc6up3LcQ5GiDHM+3sLMhDjbGGRlJr6JQ97Sft5lpOu8rrRJuVpoQwQXS8CDFHvNGNivrJGX0F5u7Vd9Y9D3aAT3DV0ouBwtG36wdxK0o1EC9/Wq/0TmxHv4CRpwqAzA5d7sSyPqcF4c65nBkC11Y0t0FD0AOZVJhY9yAOvPBQ4uJhfh+r9KDGkCHKXXQGPhDd+lBlPVYVUGbMOWHm3RJn415js6SK/q6gl+NdLjvlYFeYhz762n/6NMbQJc7XTCvql24iF+f1qaAuagh8yZsjoNLYahgDlLxj7pq1l7BAKK3uqP0ZnqjdADvByTp9ntDcqMFs+KjAbzfUyxm+StGEbYhAfpUkVEfQL/CVKCD7MFu+B2n6/B/hUDPNUz4UbnjXTBr/goFMFPmlJRMM5B8qwC67jTJw8TZxUuZ1v0eKsh6FpOR2pGclNKRkJraESpI7wgSZ73o66bv4Ca5iELK2UN6rr/udxMr8T3kAeAljOT76mwPRNPm/Oy7A4Vgp/gMkm5WRVEOQpITItgnBFr1sMaeHi7aq0407eOXcxAKsZD2EqgB9IhM0VEUymGZQtXFfcA8OixXdEf23L4b5BzdxBcU3xXUz3+GtfPOWvo04c+zA6QH6BaPWVwr2YhG5wvr+dvh61Cljgrol9yCbiOd5Y3dEXoz675pEzuCloa4JpY/SLn/1ktQptmzechutgDexyiWs/CG86b/6aefBYBmvAV//p//+TvVe4C+vBX4Xkv+e/RoS8qsw+ef64CSwULwQGKEUcoM+7sO36GPTWvnGQl0LWGa4jsaaPNe+0/L/IVsFj1nxrxyFJbezgWNaJTuaJ23j3FAz+ZfJV3SQtF8Fhkj265rKHqmuOlDIRJVUuhwnA2VFTWzEt+lThWLDyoB7MSAG8jS/3975wHX5Ln2/75n/c95z/ue0TrO6XuGMhK2g43KlL1BZO8R9gqETAgCigi4966iLY5qq9Zarat1VK0LlThRjJvaPT3t/74DCffz8DyBREiewH19PtenNYs8Ue5vrvW7RMcHmnYfDA8Iqzxt7yK6b2Mn7lLbHKgF0BMEvNto7RxmIDSbFKhoR3sR1H258Q4Qn6d776GR0o/0DXTp1rJPeoFe+GxNS60iW7CzQbSaDujngxPbVDAFaXZC2n1H4CJ9AN2hNaCcsiGuNaBoMEEaQ5N2fwRnr3UD87+5Ix32Z6kfM+rv4P5vex73Bcgu/BGp0v5OUT4YNeYDZcbh1dFjozFKmWHGLEGYmgj9DCOjc0QIB4ynfb3IPus5FdBnBc3aSAamk730khLoVjaSh4UzmNMgBz0zX7qHah6drjscRuPoIR8Gmr4GChYPH/Fl9LlwXSflaBZY74rCOGMgzXAUkammNWethW+y4FITYj+B0mHaHf0CpCnQYdYAjbD7q4PTyeUSOt5LxLTb8nyDxOfogB4YWnla30AXbCm+pwS6ZCtXtTDm3Rr+BjqgnwlPPk3ST7/QC/WAfXpJubcGL6Oqn7u+H/rPwTxvfwNA2EGZdh8zZpYuDnwwV+2N/NxLNEB/HXTl/9DzmO9Gjx79P6rnjxojgXK14PZnvbP0GOhMMbBpLV4N0E8yD+jCOPC+OpTvMXRS+U06tbg6f3DEkIAZ7TdnMxqlh02fs51JQC+Onz8/trLkRR8J2HIB5dy5raPokfKAn2gvfqpRpJgh3YtG6XQz2TDFjuq0awvaBFHZk5dJ22tSL7eeTBzdAx39Xf7BVWdguQFtjNMU6LCxjQBjruCsxjV4kG2BfQi9afeKdrrH+odVfkIHdO9A8Xl9wnzl5rolaLq9toWvErTZLyrfQgf0j6OTPySlu3epgL49oF1PojIHyUB32REkG4p0dwhNlP4fuC9dJ1H6mDFlsLsepNNt1IA/UqFuN2ZMOHX5YHQtBjrzzIQtSKfvchd9zMB0ez36HvMdSg7RAb3eT7iDCpoTJlSqut6dHaXnmJZ2h+NQZKDH8/uOe8UmVn2AHvBeoJauKVycXEV3+vtCAGRLVapviYKye1oDvQJNVXO7hjLlDuvm07zE7bC/AI6qoUI6LwP0lFLBOWLpQPKhNu8PVdsDX3Qeqisd0AHd06fvClXdzp6LtqNAn99S+abyvgNghI4O6IcSU94hNaMtQdPuIErn6KHDvbNv/Txo+dBEyaNHb6WB+jcAoBEv8dK/1VXqHrzPXAx0Rkbo2fRAF3zEvHS7YC/ahS+awt1AB/RGH/67VMB0dao+qQS6zQSJnGlATy0RnugjASsp/apvul1yAT3gYV1cU7DAqBV9jUTSXDpHAXQkmuxH5ayf2rEM7ZTXl+76ywAdbe6D9XN1wjoD/yxKvqKroweGVZ6iA7ob6IDXJ9DrtlR8iAJ95aaaZcr7DhUV7aYD+p6MpC3EDWeBIhTooNu9WrcKcYGw2/5nivq535Acut270UdfpYvU4cz6n/70j1c1ATkAbBKQkb0FI2edpO5Hj07DQGeeweUralLux5gFdFEkeE83e4VvRIe4TtxGOqBDJTYqYAZ5zt6Npt2TgxtWMwnoeRmzN/RtjCv5mTwq5jBFfE95uMO6sDZggXrmhLosiAgJHfH5VXsJUq/l/CvaghQ+F30tdVvYmAp0kD253xtZl2q9ECapjNiXkF5UeZBO+Y8W6EDeV59Ar95afhIF+sZNs5uU9x3LyXuPDugt+QmLiRvOAosJEfp23S5tAT+vmqJ+/pXtWdvfDtnB+9e/vv4vAEOZmqUgnwOwN8OaN1XUDb8UAKj6gXr2QvDYJ8jzvhszZoyxbjrlMdAZ1xRnISqk3YVuLjzKrHS7KJf0HjcmOfAr6IAOBVsoO8mDGtaiQA/wqNvDtCgdHvJkqEPdcHT0DK0TO0yV3NUKLmAu3Qqpo08FYjREoFceIAnKXNYWYsk84gx2RmHlAUMDOirhGi8ol2utAc8VfkJI3dM0xgUDMSA6oE/zkrTrE+hVW8rO9wK9+DF6H9CYP0IH9PniOAmxfh3AIXS6bwtareOU+1aK/ecHhvzwhVE4gOGeAWz8gt3kj0EUfgUA/Jri/2lm2nvU55YP9XuHEMdAZ2DK3UxUSh+hCw4zrLu9lrA4xpzf4DGpW8+dype4FZ2hgmVJdHMjXNqiBDpMwTMN6FCApE9jHDKzHJ9c9b6m4jB0jqrHwXltAtALiUBPVNPA1X+EXnGVAPR8wwM6bAocjMY+8iw7APwpqseFRlSeoAW6p/i6PoEORGSuKYHO31r0AL3vk3jOSTqg5zdHZhOBGpxBSrlv0bGgzMU+DXHbgzJ1dgh3w1EB6pdd9dkJIucs2E2v7ueBrnVTOD/+6qixxf2UBQph+l9ToL/66qv/AJ3ytmQHP3ciRu4QR+jmAh69lrvoEMMa4pYRMghmwipTS1HkWsesR1RAXzo1r40OmLB2rgS6A9jGxjSgZ2fVbO1TR0c6zCNnVh0lNEhp0RCnaowDM+iq1D1Y7ELUYpfuIa//1DrNzCNuatN0fpsRQEcEduLV6NIPIEI/RZztF1HO9odGVn5MB/Qp7uKb+gQ6HFNDZ9A3bp6ruu/TqPTzlED3iHvq9mZIFGEGfLt/PiHlviNoo+7G1fyjAcB/IAH9W/fWqP/R9Vn8q54U+loA0nsDhfio0WNujxo9es1rY8d6gdf4Nf3L950fB897k2JkzRak+VeC+7/u+RmXNQX6X8aMmQCu4V3kfV4Gf+aDDEMYRu4Qd7lbiAVqaugHGRahbyRlEHjw9pVOOTeogL7SJecmHTAnTq68pQT6xEmVt5m4Mx10l39FFphR1tHJqVifoMpz2sJlirvoBvpaZGEatCkO1pC17nLnEzavGWRTHLrnPUFA353eL9DLiN3yaDmFAHQg4UsHdBdXyS29isogu8+hr2upW6C870JoSjsV0Nt84zsoRV0Imu6By3QG9B1BVX3lXgPf0/vBDGfBgQiMBwBh8qhRY7hQTQ46iJizYf0aCsT8BZgGXelhUPkNfAG42PtlgAj0P48dOx7AfAV47G4Uxtqk3GH9H9z3ArwWD35ZwajVVYTOF9HX0AUfMAzoW0ld+GXw9sXOeeeogL7aKZu2g912suSmEuhwjI2JQKdKu6dwuyM58jiT70sAHS5xQV8LLjGhg5hiy5qWPwdoniP652XPDBHoEOKDMXpH7ieAq2mpHhdG2g6HupOr5I4+gT5ra/lHKNCXbJGqVre2+Sd0UAH909Cki33BGlBDSLm3BjToCuggtb6dDHSHnUFJw/bAB18U3OiAjthvFCN0WgIdpPIzoDANyAjMwIjVcYRuKeKrGVtjVMrdxELQQorQxfD25ikFH9DU0Z/RwRLdwDZxYmUHE4FOlXZXKpORx5mm+1Ve1Drl7iq5jb5WSiYxFZ6ISp0qutM1V4rr0YNXvQacSTfIsTVB+T3CZwEU8F56Jl/xmUre1zRCd3IV39Yn0Ge3CA6QtqztUt53dXr8I0pRmZlJR/qmvQPXkCJ0kc7q5zuCrhOb4QK/dj4R9Ydhe+BDMZkBAB3qzj/SBugwowDlYmH5AOMV19D7qaGvJX3hqIO3z5pS1ELXGCeInLeYCpZWNuInSqBPnlx5nYlAV6TdJcRud/DnbxQH/QxibZVO5W0gDjXP0UUtGeRoskxwnhBNgoYujZvAisWHCTVj8JoGCXRerw67oju9UDthGeJudO7ndNvayH/PhJS7m35T7gtaJC0o0Gdt4R2Dt29aU9fc7hHbRQX099KS3+q7hzxwrwrorbApLiRBN+pw/kkUC1neHtYHPojQWQMCeq9E7YCB3l0WGPPla6+N9cRoxV3uA/Am0ljdMnh7iZpZdLiWtE/kG9G0GB1bc3aQfspUoMO923103YE62cw46SFyg5S2gLNBAEelFkeGMexW17ghjrQ2NL1IfNgQgd63mU3zRTVkXfsENc11apviPCQ39An0dS1zmmEznBLo4q2lV+HtOxolK+k63N8oSpzfF+gBF5GNa+d0Vj/fHrSwT/38rUDfYX3ggw70fw4wQm8fKNC7l86MXqD4c3dzHjZ9Rehq5tBNmDaHbiYglwfehrfPsBMU0wF9tp+olQzJKN+GFsLWtamzDjMV6AUpDStgMxxhfK2CfxWmxQlbw4Cmu1ad50DPHX0dx6mSjr7pculudCGJNoIq8ULuI1VEKoIbxqS7DRHoYNRuP2Euv0LzMT7yyBr8skP32GA1Y2tT9Ty2Bl28lXtdFaVvKXoKxWX2VfI20wG9smYml1DD3hGYRZR9DdqmQ6CfHJLd5wwH+j8GBnSVkl3/QB895iNVEx1oqAN3/xdGq35svHlFnpou9+OMAjqbDxfJ3Eea9k7B2y2shDPXOmQ+pQL6PG/+XjIk/Vxr96NAn+FTv5WpQFdou4MIjqDrLu4eX4OrUnsPeOGX6dmaQ5I8/kanBw9q9zcIqebiga8/JUf4UPZUXzB/WaD36LA/623u4z592fE9dXrwQeqU4oBWvb6BXrul4iiadm/aLGk9WFr8NhXMZR5xz/w3B0WTVNpWknTcZ+sC5lO6x9W+JWq3B9ZioGsBdIUM7KgxbQjUeRitekq5G56W+1nkPd41MuPHdo+ucSi3ri3wKD1KBiRcyIICPT+yeQGTgQ5Wqu4jp92hKAsUFkEP+BmxVRqnscl68HCpCfU+c+JO9HhBmXzgneHlnYOx0IQpQO9TR9dgt7tCG19U+nygXwjUS7+Krukb6EtbqtegQJe0lF46zsk7QAX0y34JtwjReWvQDDTdDuB+E86F66a7PbCWlG7/yfndoP/DQNcK6GOje2rzX/Tc9hMQkXHFeNVDl7uBbVvrO4suqoG3L3TOO0WpFjet6CwKx8Ko+U1W1pLHhtAQp/L45sbYytLvUKDDkTZyOhbsN2/TQiVOrmqImyT6Au4SHyiYB9Icl1pCTC/Hv8S2NqYAHdb/te3YTykVniTU4Hl8tYJAgWq2rXn46nfbmkoxbktJOwr1I2kZFyn3oEcQ96A7bg+aozeFuB3BBwhA3xG0f0Qc+EMFdMVzxo4NRSRpHwHI/x0jVtcROj9ejZb7KcYB3UzIJXbiC3bD2+c4F+6kAvryKbntKBwjfOa8Sayf1xxmPNCBp5QJzxFV48o+S8uU7kH3mcMUvEad1inS91BAwGUv6neBk6J0GF2qW7AC7kNnz+FWMX1H54MB9G5N9zK5plkHTvdO+Ie93e2lX5AX7vRZnxpKD3QvMKrIBKA3b5FsRYH+QUrKc8q1qcnJO5Ed6DEgIr/cq98e2AklYHVTOw+YCSD+5YhqhtMF0BVd9EAqFkm9H3qlHxlabIPcFMcShKmpoZ9j3D50M34kgPpFpCxwC0jAxoGta82U4jKOWQ/UpduTg5i1aY3OC5Mbl8RKSl4Q0u7FVR+4uIpuoYc87H7XNt0O4TGAtZ+EdDNUjqOCErwN3UzWowN/Vd8wHyygQyEY4pebsof9rVIlj/8NZFqAvN6WICYUXHmOCUDfuBlG6dwrSqAfi4r/sc0r9msy0DcQO9x36kvuFQrXENPtgZdGzIFP7HIf+5a2QEe3rQElu3jkrt+ANa5HkUUxyzBmdRmhC73U1NAvMQ/oFJru5sLloZPL8+g63flRjQt6t6xJVDC3s628xlSAw3G7ZVPz2xa6lXxcFjN/nuL9A5gSu90r2slNbRDwAwESjO7hytXe9avCz9I4/YukQIEYAOoHKJigxjyENRzpgq5YwoLUiXtS7Q+03R3ORKD32Y3esyueo+4LgKhXQrdbKa//9bFQ0pcO6CGh0pOMADrwFZtmrQQwfwI63bvOBsS+OO8b8+KKV+xXKNCLm2bmddfNg1oIQjKgjg4jdp2JyWwLPkUCetqIOfDROfSejnTtgA4kaFUR+qgxpaSf8Xdw+1e98rGjCzFqdWMsS5EDbcrdQniNkUAHjXDg/V1Ho3QQtaesdsyUq5tFd3KQXkCj85m+c7cwEeblYBvcOofM52/Ypv4Cvd5HuEuxJz1zznp0hA2kbL9V1MFdeuvg6hrbUIfLXLRVmksvqHoPXSPan8ORNfgcTYGZkyN9h5so+FAYzfuYH1NxvChVsp9JQIe74oklhe4eAXTGPr1Aug+unEX18OH/00m9UmVRrCYKv55gLfje1rrihZ1lxX+gw/8v8Crt2DlPvIopUJ+3RbRz1ur85xDmSr/kE/tD2/SYby74xj132RH0BtBJbyPCPLDD6a2AQp3B/E0oJhP8IwL0+69ERf16BAF9bBai0/5g7Nixf9QC6P9FWL4yasymPpmA7gUvyp/zAqTlizBuh95MrcTmalLuN5kJdEUtvZEkgnOETtMdAHFngHvdOyjMnRyqLzA1Om/y4h1Qwhx603TefroRNtB9fhx2t0OFN1QcBs6X00FiRkzlEXQH+kR70RPyQpZ+HWxKS+DzbvUHc/gY0KWv0Va1kmTRBws8szs32Kf/hH4O0Fe6ZH5RE1JygcMAoHf3FUgOoTP6iH9Bc/tXsB9ioB3xM6eUPbS34P3sYMH7hezNkzN/ue0c9Z8zsRmnN62tbWIC1DfUFZ1Ega70Pcnx35HmzWFkfgdE5hJdrkp12Ra0iij1GiQeEQd99wa0MRvgmlaQEr+ldHDbSRBhN6gBOqEeAR4rAfcdRl+j53V2KtexQg138OdzFI/ZAZ5bgLE7hF3uNtJ/0ANd1MFUoCtq6UCaFn2/nta8u4vss56jMF/lkPlZjEOFDN1/bmUjeZgZ1riUiTAXzGhYtM4u4ys6oGdn17QSZtJ7xsfgPnQ04p7kKHock1B1iKJr+pT1ZNHnvVKvoi8HEtGrmzFPAmNcMGKHAIMO/x+OdmmjBgdhvcE27T9kkJN9xdSsroJ0sdqoPymtel98SvV+sgNlvC7kc3pE9Rjygpr+oI7OptM6SLkDZbkzA9K+B5oC8EsNx6bgFyqYQ19mm/7LbacohbcFJN3ZsrJ2vr6Bfriw8J2rnrFfXvCJ+QkF+srSuK+IMA86CYBeqEuYd6fbg+4iW9W69LEm1SAMAfoJ/GkYjv3rX/y/qonQ5RCcTIX6eHNBItogZ2EhfO5gyXsRalP6fcLE4m9n2pR8P82K99MkS/73qujcSvQs2re+hYkwLwO+0jnnNhleKNChgz3ccnSlKlQvgxG2HSn1Dt3eRXx/KtimNtVdfB1G4uT7QUr3UybUtaHXBxW19Qdy1Nc4pX9dSAN174DK83S154G6f3DlGU3kXLtT672b6VCQw9G2jELpgYG+XvP03A54jekI0GGafZI1/0fotta8F+vsUn9WAh36peDkGxs3zJ6nT6CfTM0+oqyZwxr6Ze/Y7y75xPwgrou+B2rVHzu1BmyHUbnj9uBIXcMc/lw0OgfRehUmAC3QldKvo9/Fn4YBmbv0N1CgRQ3UY5gbpcPUOz8LvMfLPVK1j+wtK16Q3day4kcFzG0kT8O967cxEea86Kam5VPzr1CBiwz07MzZm9FaOpCCvaboogZRJUwhDxRYnjSqcPrwqgju6Y3INW+0S/m50Sf/Jqyh54AvK/npkn2SGWWnQGT+GSlS/yyHolwAvsh0vizQ4TYzTa+D0x2xfwhn9GGDYHetXLOSA8xSKK8vxabwFztL3s/WEwTfkt9fWapo/1Wf+Aco1E8lZR3XJ9A/jUy7QDWylr0gMlPXAKeIzk8gc+ePh/VWtUEA+p0eoNfhT8PA0u7mojY1ne7JTAa6wi34aSBS3w/fL4Q3JdQnVd6O9a/fyCSICyMbltT5S7bO9+AeBuWBz+kiUTLQe2rpd1XNcUB0RqmNngY03oGCXDtMpdOBysZO3AVT70yBeWGa+L319mk/Kq8X1s55sTzKprGsHJCK9sq5i34+8/wKZJrMbw84Qg+TfKLrz6IIQHqDfZqqdyB2QvEL0BT3DdX74/JqtmxdPmthu2fcUxXUXWa+2FUrWKcvoF/xS7zXRyHOP+GmvmEOZ9wByF/01s6DK/DJrx7o3etTX/ubA/40DMsACE+qATqH8UDv9dLISWU3w6xLv/e15v4YbM39IR6k3kW2uV+Kg2vXMQnmNYHSTRtt015QQtwu9UV/QM/JqNuERukppQJCo1VssvSAF+iQdnIV3YFRO1yRCjeyBQDlsTTSvnN9+yKP7E70eisjuJ/0V1+GNXRVNG+b+nNZoqBPvwDMWFDVxwfi6poKh9Lne3Wn2pXu6cB/QgVz+IVNWlu7FkIUAvyWS9RPSqhfDkrUy1rVLauqF1CtTf0oNvkD/UfngbuQ6Fxue9b2t/jk7+16B+n1sbPBHxXt/q+//vp/g9u+7RGGwWZoQDcTvEevFicoNiCgRwhdildSdrr7do9+McXne5Yeo4L5SpecmzBi7w/oirl0fsV1lXIcqNUyCdIDdZBSPwS+wPysvNZlrtmPB9oJjzbPLfTIuW+I1496cYrofVhqUF7T0mlZT2APBDXQhV82LqhdqoTpJ/Gck0qg3wK+dxZ/o66B/q6U9wZVur01L3mZXoG+PTAZ1O+/622GC+DgU783Ev8UGS/bD2bIJ4ORs0aYcociNPgTMsgIfauapjiBIQE9fBKvkAro891LjjEwQlekmTfYpX2/ckqebLa/WFHfhwAfCNALUxqWA/W4H1VROlf4iaFBDI1IYQ2dKtKmc1hjR7IaPxenid43ZKA3BBReQ//e4ew97MKnAjocO1yzdrZqVO2tZdWLbrpE/6iE+tmo9PO6BvqRwsJ3qYAOBWX0XDvf1rtRLejiK7/g7Z5ohA4V354jUP8W+EawXOVv+NMxTCMrrxF2opsJqg0J6NBXOXHukoG+bGpeGxMb4Sp6VOwIc+gDBLpC471EdLJXaIb7uSEBDDazofXi5dM4zzSKaJOFB9Dofk5g0VVDBvpq595xxbWOGd9ySDPzqE+wF3WRgXo+PLVNCfSbU6O/0/Vs+snEzI/JML/im9Ch33R7UDzwr3tg/h/7bYEu+MTvY5a/AwA3fe2118zGjRv3e/x5GHrKXVRHB/Tx5vwGQwN6k0vBQTLQ1zhyHhqCZrumQIeb2KCICRKlnzIUgImiyk+i11kbXHxR09dAa+mrXDI/N9h0O8guEBr9fAuuw9tRzQDyOCIZqAdLinehHe/7Bdy3dAn0SyEp7WSgH49JPqBXoO8IehOJzlvwaY9tBEToomL6pjjhIkMDeqlj6XyqtLs4tHbVsAM6cE5e9S60lq7seGe6w+509DoL+xGKofK5AYVX0ZQ97BI3RKBXh3PPop+FeGb5iYzs6l10HfiwwZEM1DcXSxejQD8Tl/mJrmAOswGw254M9PWlSU16S7XvCExX1s6B3OvnLjvDx+DTHtuwt/GWghlqVqiuNTSgO9hUJK11yHxKIQG7azgCXTHGBiRWVXPp5YKLhgAxkGJ/iqaYtXkNCD70s5KGl5wzRKDPn55H6G6Hc/cpYBqBdnVqAPXq1OtusV8ogX7VJ+G+zhriagQb+tTPPeKeRq2JSNRj7fyQqhGuNSgfn/TYRoSxLPn2aoRlWg0N6NCXOOeeJwN9kVvRyeEK9KKkeYvhspaeufQfNNVP17XD0TNQP1eN5y32yJFr8zoQfITPyjvvliECfZVzxpeqLzdO3V9uYhOlB+iAHh5Z+RF12jtZpqqju8z8SVfKcUfz8veSgX42NPFT/XW2B5fAmnmPItxxfMpjGzH2uq10lBqg7zNEoM+aUtRCBjoYCbs1XIEOPSNfulcVpfN515kMMDh2hl7jXL/Cdm1fa61D+veqsTcQ9RsazGHz20a73hG85T3XAJfoUANd+FVSevU+KrCei0k/g6bddyysXKYLoJ+JyfyEDPQ9GSmb9Radg2727pnz4C9dW4PH41Me2wgy6a+MLYQ3aIB+3BCBPtOOX6JuN/pwBDr0REHFTaXGO1ycwlSIVcTxj75sQ5zS4QY25eusdkr/xtCADuv+6GehzFaEhleeoJxBnyD6qqB41jYqsJ5IyT6GAn1fJW+zThTi/JPukIEumh1bqp9GuMBFiGY73tqJbeQZ2Fx2kmZs7YIhAh36cqfs62Sgzw4QvzmcgV6Y2LhEmXqPF3OfM7VBDuqyE2rf/ajDqa3Fu/bW4uEYnKEBHc7eo5/FQq+8Dng7XA5Dk3L/UlRVu54KrMczcz9Agf5+RWnrUMN828KqpWSYXwxIkOkD5o7bglIBxL/shnngMXyyYxuRZmIm3G1oO9H789opRa1koC90Lz02nIGuXLEaW1Xyn+4GOX4bEyFWE156brCAvmxa9hNUBtbggJ4gICgDKlXvvPzEF+lU4uYvrFtCE6EfRYF+kFeybchXphYX7yID/f2U5Fb9pNoDP1LUzbcHPrHdEfF3fLJjG5lANxcupRWXseBHGSLQw237qsZBadXhDnSF4AyYR1c0yElKXqQXVR5kGsSkkdxPCCl3sGHsJVLunyMR+guDm0GHAjnIZ7HEnfMI3u5G2nGvWq5jL+5aR9PsBkfVUKC/JyrfMvT184wzjEi37wiY25NmB0tYQn3xqY5txNp4Mz6XFujmwgxDjdJXOOdeQ4EOxtm6BJHzFg93oHfX08vv9cymf5GVV/0OkyAmBLKm6DXOCSzUWuUNjrypOsRBg5yhAT2HU/Uuujp25ZTM5/B2F1fRLcq1rtOEd+ngeiGiVy0O+u65ojVDOn8OHI7HEdLtQYntOk+17wjMUqXadwbNwSc6thFtpmbiINpOd7aw3FCBXuNSspViUcuOkQB0WE+Pk3C/hlBPFPBuM7lu3Oyde0db+ViYZkf3oxvi2Npax7Tv0PWxsPPdzlksp55Bl1ygA+y16fGPVUB3jvp505q65qEE+u45wrXk6Pw9HafbwSa1KADy9u5Ue9AxrNWODTfFWfJN6Be0CGcbKtCDbXm5AOLPiPPohadHAtCh52bWbVQucEktE55hCsDyMiR70ah0uZbjZuVx/CPE+nNupyECfbF7zkP0OopSJfttaHTco+OkH9KptcF96EqgA+W2Z0Odbj/GyX+fKCYT21XeEF2g4wh9Z/eIWmCH7Rb3Ufg0x4btlahfg9G1WzRqccsMFegKkRmX3DNkXfeymPnzRgLQoWflVr8Dx9gSRGUPGbaM5MuXTZXXhBafRz+r2cHFlwwR6HPA+0avQxTFOwl3nlPsQf8qO796JxVc99TwN6Dp9vMRqZd1rd9+NkzXYjJB8QDknwGgf+GyJ9AKn+PYsCmjdDPhRzRR+lZDBnq5c3kzOe0+C6wvHQlALwZp97RS0ekEYdkDpgF9Pkizo9cJ9oEf0PQ1mqfnEiRTy+P5hw0R6OWkTvdZnoV3KTvcJwu/lNCMrJ1KyjqOAv0wWGc6lDB/a5F0CYzIUaBvLkhcopOa+faAyKnbAutdtgWAVHtgl9OOkBB8gmPDhhgYXWuhWdCy35CBbgG69Fc5ZnWiQF/gUXp0eAO9uZGTW7U3qYL7OFHE7UouE56HjXElCc3NJfFNC5ngDX4V7xNlW7lHNX2NdY69ojLrHdK/Lo1vXMSU69PE4fteb5emUryrs83+1sJG/JzslhPFz44sWJ95dX1LItlveyTcVsL8jvPMF+3NK7KpHjdYfiO9fNlt19iHKneLuzV3cdrr7m+H/WUo3Wuzn71HS8AOt7eCbri0Bt5w2RlSik9vbNjIEbo5X0STcj9tyECHPmdK0W4U6KucszuGK9DzM+pa0svKbydXcLuShNyuREHZQ05ODeMaAYUR9cvQhjawx75Tk+dXB1W/gX5OS10LzxvKilwqXz4tX5V2F0/M/sXKSvSFhbW4C3Vb20rZ4/W7I8j+YNayLADyn5VA75ieco7qcYPpHf4Zh+5Mi5UrvcM/c/FQnk8ha0P+13+Dv2j6G/5XPVsCZK5vBspctgWutW2N+jM+vbFhIxkAdyBNU9xtQwd6JMVMelVI7drhBPTixIYlnALB6TReSVdqRWkXBHpaifA0XNzCVIitds7pQEVhNFlxu2xawQX0c6oJqGoxZKDX+Uu2Kq+lYELeL7aWFT+SgT59Wu0HVHC9E5xN2IV+L7GieShh/mD++sQ7rnH3CECPKJ48ZDBf4+sXuM73Y78N/jIAdJnn5oBj7m8Fh+FTGxs2ugjdRjoGAPw+Tdo9xdChvtA57xQK9PkepUeGBdCjmxvzOFV7M0tLH6eXl3RBoKdxeTdApL6R6RBr8BXsfoPQ7V5waSDPE4XPWb7RtndbG9AXeFJmwDBXOmzYhNeTZFP4i4MFjxil24i7UoMbVveBa/XyzDvO0d+pgO4a9+jhym1RQwn0u0kVCwgwn566dyjOpKjFPuMjVviuD13lKwtc6yfzW+9/BQBd5POGzx/xiY0NW79RuuC8oc6ij2cLZoAsQwX48rEIlA82gv9fDt73LCMzfiy8n+NYXk3odgcpXiZ2u2sC9KLUmk3ZRWU3M7klXRnA08u4D7NB7ZzJXfyoQwhDsZ/e6035uQZEqv09b8WUvGvoZ9TgzX+nv+cUzJw/P9a/fmO49+zWGT71W5ODGlYz7fOY7S/eBq8nxKpUAXRbS/5PFtaiz3qA/qwubbmEANe1b0d2TE8mbFjrTOAtHvJ0u0/qxyjQ74XkDGpTWlRz1B9iF08vmLHUpy18ha8MAj1ore8bvmt8TfApjQ3bgOvowlaaTvcG5sJcFKl4fxbCazTvvcPYXPQGBPsy59w2FOo1gdLN+jq854LodAlIGy8j+Wqn7E4UVvDP5McscctvmxVReCu7pLiLU1LSBYGeXcg/W5LQN70e41e/yc5O2u7iWH22cOaCZgZC7M03kFo6+Hv5CtbX6R4/z5u/l/T5yNVF5xDczg5V5y1sJE/JKewJEyo7fVxrDxRGzW9iyucBv6y4WZYpgA59siX/B/BeP7OaIH5yuK4lpRfm70TeDcnZjcL8jlfyJQj5IU23Vy/l3J4Wp4L5bY+kU7+8MnhiLonzPD3jFk4/ErN4uixqqbcMAP142EofnF7Hhk1TA53uVdRQBBEvA2EOdeaNzQV71exzJ2yOy3IsX4sCfbFr8Sl9HNowZQyjURRM2nhZesEXnKKy24VptZRfTCDAbSZI5EqAhXjV7WR6Q1hPCr1rVtAsQsmAF93UBKcTQKr9P71197Qfq0JraSNtP7fa98B1PyODnOwTJ1XeSQttXM6IzyN07nJ7y4oXSqBDh3+eMlH4pLO8sUgunF9wP1XYeMcj8RoK89tTo5/fl67MGuro/N7MonVodH4nOIszGGdP9hz3cWnzPNclNXnJANBlIEK/ErXUR5SI0+vYsGkZobOE/jRA3MfIyByM1FG81yuKPe7mQqryQXuTQ85dlba7Y9bjCj3sSJeE1a1Eo1JtXRRbdgaOqNECzbV2PwquAPe6d5gIdAhrGGmTrw/WlJdNzW9b4ZJ7HYx1fUu8P+Xnub7Ct+leEzSQHaSCt6WN+ImFtaTP7TYTJfczwuYt0/dnkRAwd521tehzOwvezyjUcybk/0IAOBqZu8z85kHRbP5Qw/zJ6h0zwBeJKyqYuyVcueMu/f3LnDklzc5/4NR5FmTUe7YBoMsg0OMXem+KW+htik9kbNhewtjsuf8L0tMdhrAXHWYNSON152ENnfAYMwEH+Hvo4xys+B0rHTI/U0IdpnD1VStfPiWvvX/PvbHYg9O10DvzB+gLgC/y4jxv9io5oe71cyKaFqHROZOBDl0wo2ERHF0b0JcZu9QXc70r9tC9Vrh3/TYU2lbWksfeILWuBHYJaCSE9XQne+klwljY5Mrr+k6/h4IsSvd7Fj+3QyL1RZMzqYE+Nfbxfe5c7lDDHPr9jMpaQjNcIKfsZc6bfKmrZ16t+2HObA8ZALosrcHzo4RGL5hex3rs2LANSpRuIfyQIrKF3e8xjIG5maCM2JEvOGvE5sfTw1+4FbmWB0mTSp6qVqo6Z99hZMMYaGwrTZXsLeEUPSrOKeoqyi/qKswpuVOSOqvf8SwIJXvbqivkKJTJQFdG6gvdSj7eaJf2Ex3MQdT+AM6g0+6Dj2habGUjeai8ZusJkofJwfQNcO4us46hn5HX1JrD+vwMPFxqjvS+H9FnE6wE34CU+48H7BN+JkTlbvEddyMLNz1a8maMLmCuGI/zTT+mgrl7YtujxDKt0uF8qfu4Yonr2gKpmyyv1k2WXed+NWOupyhX6v4/+ATGhm1w6+jNNAIzJQxqgjuDzskbm/Gz+nuOibnoqPI5VhaCzxrtOJ8roV7HsBnmsoSajWWZxTe5nMKukmzgOUWPSzJEB9Wl11Gg2dlVXqVKNzMd6Gi0Ps+bt3eJa9E52CQG0+4LAOhBE+Om/sbTpjhVf4Jec6TPnDfVPb4EOCFStxI902cHPDlroIjWJ4gf3GzYlCQXL8x7IFhQ+Lhpc4KuIK70h+Bno9H53UBOgcbp9RLnP1QIpxWUiVwvl1S6yrqB7r6Z0+CK0+vYsA0J0C1EUdSz6IJ5zEi1i2pIM/KLBhjVc8Dj7ymfFzmBq2qOWza14AIjQB43b3F5Gu90eWZBVxmnoEsB9KyyC6UJ9Wpru4mB9WsDPOr2uDpVnwTR6WO65i9DAbq2nhIybxV6vU4O1QP6e80Kb1qCfm5wIkBf1wBq+XLy35ub46wTugZ4n1G1sJztqujcM/HTX6KifqfJuSIuc/EUVUw9XCGYJisTTZMBoH+UL3XH6XVs2IbSbKDAjIWws08d3ULYwgygC48jqfY22Ok+8OcK3lI+18JC0LXYPuu5ojkOdFWr65bWRXqdlyTay08veMjLKOiCQOdmFt8pTeo/vR7tN3czVZOXIrIjwX24A93VSXoSvd7UkIaVA32u19RZh9Hn6qNBLmdG46K+f4+irgT/ho36hPmjujVpd1zj76qAHpyVMdDzpJbr8m9pyZQ1ldwpMmHFVBmPP+1qmdgVp9exYdNZHZ0tPNY3Shcc0X/tnJ9FKANYCFZo9Brmolz0+emTSzqUUfoSt6Iz+oBQeVztekFKsUyYlt9VkV7QVZFR8Lg8RTig9DoymkWEAEgbu7lUHw/3ntM6UoBeFL2gEa2dg9n7q5o8PzOscSk64gab6HR9DVAzoM/fpY346Zys5SJ9Av1eeP4W1dy5V/LxVrBuub8zpBmk1+vznQpqC10uA6DLeoDeIhBMZeETFhs2XabdzYX1VJruCjU2fUId7GYnlQE4Gr+GhfAT5fNtrARnQXSubJB7BsfJdBeVNy0UJvKOiVPyu0Sp+V0KoKdyL5TG1WsUGWaENiyfOEnSASE+caKkAzRVHU0NnbcC3gcV0UYK0KN8G1qI11q7R9PXQHsPbCdLbur6Gqi+nMFJBdniHdH6gvnDOetT7kyL61BE5q6x92+H5Ln2d37My3DwbMhxOjwn30kGgC6Tlrh8LOY64/Q6Nmz6sH+zxZ5UdfTx5sI8vQrJmAuPIjC/pGXKHh1366h3LtivS6EZ2NQljK/cKUnMf1CZnNclhjBPKbpTnjhr0BvzRhLQySlzWBfX9DVgVK7PtLuzo/QcGeieU2uO6LV2HlGwWdUM55u2Tt25sSR90r8XZjisbspylM3NdZIBoF+tK3QR8XhT/hefqtiw6csspb+DIiwUS1oa9acKJ5wJ3sNdpASwV0ug16LXZGstqET2pT8bylp6RWztOml8Ubs0Ma+rKimvS5Kc/7giSTDg9DoGupro2rbqmkrSdZL4njavEe1bT4jygz3qdunyGqAULRnoORHzF+mzdt7hGn9HEZ1PS7h5P573D6rjYn2K+++XpTgULE5zuAyALoNABxH69vp8Z2t8mGLDxoQ6urlgC0Xafbse0+0lxPcjWjVYdXiRS+mqoex4r4htXFAZW35sVlxeVzWAOQS6OKH0QllM/ZBGgCMF6FDiFpYclNc5xbFaq36I/MjmBWiDoatz9ce6ugZOZNOSvk2N4ifb+W9k6wvod4NydveKyGRxqc6J1bGTPVfF2364LNleBoAuW5jheLqJ45Aklb7yK3yKYsPGFKCTwKcScNEf0OtJXy5ma/da/Eg00geR/zum4LYlLnlnVEtbBmkuHabXK2MkO2tjch/UxuZ01QCgS+MK7vBjq7foAhIjBehxgfXr0et8mYY2NErWtLHuZZzcwNjz89v1BfP7ZfNKlUtYOjxTDh2WSn+Dng9vRNn+a2OM7ao1sXayVQl2suXJ9tcWpTk0zE+Z+Bd8emLDxjAbZyn9GzHF3a0YZ8QWxetp/nwVaWGM5CVG364ir3UC3hYwiZe92jHroUI9ziXn5suuIBXG1K6tm1nYPjsmu6sOeE1s7hNJHEivRw9Nen0kAz1s+uwdg3Wdk4H8K7qNTXc9ADWHSd3tXTO857bqrXbum3ZcEZ27xt25G8qxUKXX3cf9fkvEpILNUZMvbYi2lUGgr4y327EsydEGn5rYsDHYgGrcOxS67tV6itA3kTrcy14C6GeodOpFLtzVyii90Yf/rrbp9dKQ8jPxHsXfxHgUfxsNPNyjXO7jKj0BG7e0caBN/hYGOr37u9XuRa8zbHrddm1fy8G+6jI6x6+zHgC7KhlxiYzk6fzc5Tx9wLwzTVxPpdfeGmzj+VbIpEMA6LJNUZNk66Mnf7I2zg6n17FhMwQzshBlU3S7b9WToMxWkhRtxUu81jnkta4qb0dT72AT2yNhZMMSTdLr1VGinXXhuQ+cJvF+mjyx4sXECfwfrWyEX/a3vnMgDuGMgU7tPq417xOBPkdroBOlVyVdunj/3bV74prXybaSm51g57nOx9SaNiTddkuUKYDumXQIzpzv8rH659v+E1buCJogeyt0omxLxORrm6ImN7TEWf8Vn5LYsBmIsVjcUXC0q89WMwZE6KAWXqU90AUyuk1yitS7E+c+hPpS18LzA9pvPqN2bUN4XntTRFaXNCTn+eQJFS9sbITfgIP5s8GAOXQYhWKgU7uve+0+9DqDPGfv1va1bJGUOxR10U39vP4tcrp9pt/srXpJtQdy9kCY33KLv3EjONlyn49Vwbt+NpfeDpgg6wH6zk3hkybg0xEbNgM0AL+3+86jC9J1DfTxFsKVpC8W9drvURd0IqN4H5Mfk+tUVgtH2CDUZ/uLt9Gn1xsWzAkvPTY/jPOsOTyrCwJ9TlTxhUB36WGoyQ2VywbDnR2knxbObG7GQKf2EDBeRvzyU7dP29eaOKnyLirqoov3D1X9COn2CeKnywtWcnWeas+RVirU4EAzXJvfjJr9ntYH93lbywDQZTsDJnyyM8gGp9exYTPoOrq5MINCYKZB713u5sK1Wq5e5RCux0Kwm+pxc6YU7YRAX+2ULRdG1i8hp9drI0Q7F4ZkyxeGZnUtCMvqagzP7ZDMlGxlEuhGCtBj/BoIkqnuAJBajb+B9a3o+BuYbZfp4v1PnFx5i9Ddblspe7D2bZ2m2+/PWZty2z3xGtiv/uiad+SZg26WMgB02T4f63YA9IZWX8tX8WmIDZuhA91E+iewrOUGCer79D+Hrt17ADr1swaiB29iKZix1CX3Uwj15VPyryi73iUgvb4wOO/a4qDMrkXBAOYhWU/qIssPlgEYMA10IwXo2RHNi9HrhLvgtXmdhIC569DXmeIoHXJ9f6hGR16uE+8/b4MuYf4A1Oo7/DI/vD0t+rnMM/Kro65W1yHQ3/e03rnX23IiPgWxYRtGRk53A78DPEYPSnH36GrfGnwxWDvQbnn/yfys1Y6cexDqC7y4HzaFlBxbFpj1bFlgZhcEemNY4QX+zDnLmQq6kaQUB1Lld5TXaQ32h2vzGrD2Tkjdu2ufute2Q98SiMnsEG/k6BLotyOyd9+aGvX9ddeoH0642t067Gp55kMPy6TWqFd+jU8/bNiGWx3dTOTSVzVO+6a0QdFy17KWT1y/KrzT3/rVZPsyAQD65xvtU39a5Z3x+fIAEJkHcTphyp3pkBtJQIe74AmrU4MbVr7sa8QFNKwf6vftYF/ZRioXHNMVyOVNq9JuxqUfvDk16qdb06J+POs25e6xKZYN+51xeh0btmFtRkQQ6kcG1ly4hPTFYoGGsq8pxF3vgsPqHh9qkVE419L/oxX2Mz7b6JD6YqVX+hfzQkuPlc9sbDYEyI0koId41e1Er9XXtXb/yzbElehiXA2p2Vtai54JExfWDjXIn6zZGXU3n7voRnTMbVlozDMI9MtuPudOOFtMwicdNmwjA+glpKa0dl2vUwXp8UxSuvyQZs8XNpIa4hZTPW4yuzi+yiy0ZbmFV+cSy+nyRdbT5UsdE2/XTS/bwQlrFGdHNFUZggd71q03A8BQ+vRptdsN5b1r6glB8xrMrcRPldcK4NymyfMjfOqXoZ8VmCw4NtTvGaxL3YL+TDAZcfPG0rd9Hq17x3OovLNElH8rNOL09aDQzuvBwfdk/hGd16dHbcfpdWzYRpCZmQleA9HtTVLaXaAHgZnjCNA7gRRttgZfCD7qhTmI1M2EKej9UFgmhx1Xv4jt076S7SVfZu4ln2/pc5VjGaMYkXO1ESTrdR+8xp8VX0LKqjQb0vvX+HothB+SZIqzNfh3tZO0t4Cng3/L+3r/LYvusyxEwqH6/b083mrsZTa7oZ1tIms3M5FdsWK1X7YxbbjlHWmKTzds2EZkLV2wkJTy3qkHoNeS3sOeAS5lERAkbMFSFvT+YDNOwRx24PHFbG/5UvZ0+XK2Z2eVRWiLjRk31mABN8KADmWJtfr3CcBPLMUIz8AlPkP6fsFOBOKSINEtYyvRPwf7d/awu/tvPmVZJl1gmX/axmbLFEA3N9l1xcIEp9exYRvRQLfkm6Cd5gAQt3Xd7a4QhgFb30jp/6L+O+SR54DDG8zS5ynT6+XsyJZmtm/nQraPHAK9ge1/OJCVmWvwEesIA3rPJr0zhCjdTFA6gC+Je0ireWt08F6bVTA3F0CBo0WD/ft60tTG8RTLeu9ZtoXsAttcBoB+RsYyTmp9BafXsWHD9opCOW4rqY5dp3tQCXikhTEXQMd7Iv0XAOEuwuOBjCxMr6ewE+rr2AHt89h+8vlsX/k8tu9VmHIfNinoEQd01b+N+0jqvI1cWiEoEJrzG0ip9sNDHp2Tyz/mgrvjLSsGTU71fWObMUdMJzZ8xLKRAaDLzrIt28+zzRvOslij8AmGDRs2lRmxKqaSouMDekmvWghaSOnVy90rVUW9hzFbkAMb58g73d3YeYUCdsSHs9mB8rlsf3kDy6+zwiyiZZIBp9cx0AkZmT7/Nvou8+HHGpkL1pBS7TfBJETW0MOcn0V4f2zBm4OVXt/Psks6aDr50yOsiTIF0E2td581N5+MTy5s2LBRR+kWwv1o+hrKw+pc2x0oucFoimIb3HVweJ8CUdlFitWvt+LYKW9KWSH3athBcgh0CTvkiB+LY9DpdYXwD2wIIzn4HE6TUsmfUj0OgH8j4YuQgTvdvw2YyQHNZ+DfruBIT7lITirDiHRT6xetQ372PaBe6PGyv5Nvs5wd9rDs9rzHspMdZE2SHWZNOnuCZZP0S1QUTq9jw4aN3sabV3qTot4NelqpGgOirA8ooN7Hzc0q7uaw4m5UskPk1cCl7OCrMOVu8FE4WZteS3+ZdbTMzE7AfxvCAwO8ftgXUqsrxUM48ol87nvAr9R/afu72GoybfR2U+eGt1mO7XtY9jIA9HYQoTccZtni9Do2bNgGGKWb89FGouvgz9H6i8aEC9CVqKibmvPlXmZ5t8tYkQ/FrDC5hBXaWciOMejuddJsfQphe5z2QC8abql3+G8DXNdy8BndUXPtJ3V67cQlQ3dB1sBNK5CDPeUtxq5JW01czm03cZEBoMv2mNrvf9/M3gWfTtiwYdMsSmcJpg3OOtNBOrzZisO7AnYLw5Qm26Jiha9ZzntFrKjOClaEXABgXsqKPOrFyskbfnVjoQBmSWDqXCsHC2uGdV0djIj1NL+1GpmL3u/uagfXrdDx122pAfzsE0gJYLc20fkalqfDBlPXPZtMpsm2mkyRbTd1ufC2qVPBWVvb3+KTCRs2bFqZESLGAVLfp5hygAewsqryTGPaSllR8jLWDDmXFXkthpVSb6qD7mXs2Ae0MdBCEZ07a/L7tsjEf/QKU6+G1aYe7RtMXGUQ6G+aTlmxw3za3/FphA0btpcDupXUDu0S1lVTEZ07sQuzU1kJh/JZ0fJC1kx5CWtGZzo7vsXarCwOAwU7A+r6+1Rz5+YD72yH6fUFxr5Ji42nn1th4ilbbeIhW2/iun+z8bQp+BTChg3b4KXezZDVqmbCj/RxUJqbV8REstLWZJnG3M01jZFDoGexYo+6s/LyMEiwMyM6F+Uq5+NNzEW3jcwk1gP5/Zpj5GffYOL77nxjXxkAumy5qeeFVaaeBStxeh0bNmyDbcbG0jEA5DJ9dUt7snKrkk0T2zJM4+RZprFyjmnstXBWOk6vY2fWbLy56F2lep2ppbC2v98rKSt4VI1xUEO9MRA+MvaTQaAvMfZesRKn17FhwzakUbqFkIvUBj/UxQFpZ1bKiWKlHkoxTZCnmcbLAdA7Y9gpOL2OnZmjhb2lqYv/sJS+qi69LjEOTZIah5ydZRwom2McIGsw8Xu/0Wj6VHzSYMOGTQeW9dvxSPfuUNbSYXo9gMVZE2eSfDfBNEkOgR7PSj42hVWQj+GBndHRORgvBPXzRLrfIq5xlG2FUcQ7IuNQWZVxiKzGJPBCvXFggdQy6nf4jMGGDZvOzMhcPB3R0D4zFLvSp7LyqyJMUtuiTVPkcabJwJPa/VmceiOcXsfOXJ2AnuyVQG5kIdr3SlRrH+W24nEpfykcHyXiGkVeqzAKl0GgS42DV0jZIa/jkwUbNmx6MSABuwRZ2jJvsA7FCSC9HmCa9UG4abo8yjRVPtM0tTPUNKPFgs2Lx9DAzvDtb8eVssPgv1bo74v0Femvsoxjw/KMZp4uNIqSAaDLeEbhB0RG4Ti9jg0bNj0D3aTgTyZQLxw2x1kIrykWYLzEgcgC6nPuJrlrgk0y74YCmEOgh5mmH3dgleD0OnZDqJ3XqfYdgDWu6O9KonGiVZpR/LYsoxhZnlG0DAD9Atd4Bk6vY8OGjUGpd4tKL9V4jplgs7aHoYNJYZWPcfblQJMsebBppjzEJP26JytvkekwWiKCfVhH57GK1a09GwktLaUKUEcZZf05fnyiKGl8/LV0ozhZD9BX5LNjcHodGzZsjEy9L1VGJuBwK9XkILQ042W5meYd8DbJkfuZZMsDTLLu+5hk77Ji8RIxJLAb2gpX8N9b49lCG5hejxyXHhY9PvVU3PgkWdL4BBkA+gHO+Jmu+MTAhg0bY83GpuyPUGRG2SBnYsGPGsDu7mgHk6I17sZ5HV4muXIIdOAn7VjcEgwI7AbmpYoxNdDVDgRlikHJyDJsfGZrxPg0WfT4FBkA+kUQoRdE4fQ6NmzYDCJKt5BYGluIbvbs4V6l7gC0MSmtcjYuujTNJF/uZpIn9zDJveFiWojT69gNdcPbabB3/T6Izrd7/ztLEjg+81ro+AyZAuhGqSuSWEn/h08IbNiwGZQpVnv2zN92b7YiHn5mZvwsW5PiA07GhXIXkwL5VJO8++C/u8xZ5UkYDtgNdExtfffaXuFNt3G553zHcWQB4zNlAOgfhI9LdcOnAjZs2AwY6qIerXdB23ggqqFMr1uZlK2ZbFzSYW9cJIdAdzIpPGXNKi3FUMBuwNvUKsC/9UcsM/7XjsbF9zzH5ch8x2VfBBF6gb9Jwf/DpwE2bNgM2mxtpf9tbCE41BOpv8cy4VVZG3MvTTIuldsaF8sdjItvTDItXWSE0+vYDdhN2fxsEzPhE1Nz/o8TTLiPXcflyTzGZa/w/7+Mf+BTABs2bMPGxllK/9Y9ny74xtyk/KmNMVc+ybjkPjj43mKzKxIwELAbNMxNeSJTFv9zUzPBT5Ys3mfO/y74YNq4HJxex4YN2/A0lqVkgilb8IOZKe+ZtUnZKTMWj4thgH04OMukYg2Izn9gswRf2BoVluL0OjZs2Ia9mRuVX2eb8FabAwlMY+zYh4GbWonN2eN5DSw2v8PCgj8J/5Zjw4ZtRNjEccV/AVpZv8afBLbhZNb/yvkrmy3FSm/YsGHDhg0bNmzYsGHDhg0bNmzYsGHDhg0bNmzYsGHDhg0bNmw99v8B5IX8cEEJgR0AAAAASUVORK5CYII=" id="fig:PermutationTensor" alt />
<p class="caption">The rank-3 permutation tensor, by Arian Kriesch. corrections made by Xmaster1123 and Luxo (Own work) [GFDL (<a href="http://www.gnu.org/copyleft/fdl.html" class="uri">http://www.gnu.org/copyleft/fdl.html</a>), CC-BY-SA-3.0 (<a href="http://creativecommons.org/licenses/by-sa/3.0/" class="uri">http://creativecommons.org/licenses/by-sa/3.0/</a>);
</div>
;One can write the <span class="math inline">\(i = 1,2,3\)</span> matrices that stack to form this tensor as:
;
;<span class="math display">\[\epsilon_{1jk}=
\begin{bmatrix}
0 & 0 & 0\\
0 & 0 & 1\\
0 & -1 & 0
\end{bmatrix}\]</span>
;
;<span class="math display">\[\epsilon_{2jk}=
\begin{bmatrix}
0 & 0 & -1\\
0 & 0 & 0\\
1 & 0 & 0
\end{bmatrix}\]</span>
;
;<span class="math display">\[\epsilon_{3jk}=
\begin{bmatrix}
0 & 1 & 0\\
-1 & 0 & 0\\
0 & 0 & 0
\end{bmatrix}\]</span>
;
</div>
<div id="sec:SummationNotation" class="section level2">
<h2>Summation Notation</h2>
;Often, it is useful to simplify notation when manipulating tensor equations. To do this, we utilize Einstein summation notation, or simply <em>summation notation</em>. This notation says that <em>if an index is repeated twice (and only twice) in a single term we assume summation over the range of the repeated subscript</em>. The simplest example of this is the representation of the trace of a matrix:
;
;<span class="math display">\[tr(\sigma) = \underbrace{\sigma_{kk}}_{\substack{\text{summation} \\ \text{notation}}} = \sum_{k}^{3}\sigma_{kk} = \sigma_{11}+\sigma_{22}+\sigma_{33}\]</span>
;
;In <span class="math inline">\(\sigma_{kk}\)</span> the index <span class="math inline">\(k\)</span> is repeated, and this means that we assume summation of the index over the range of the subscript (in this case, 1-3 as we are working with the stress tensor).
;
<div class="displayquote">
;<strong>Example 1:</strong>This comes in very useful when representing matrix multiplication. Let’s say we have an (<span class="math inline">\(M \times N\)</span>) matrix, <span class="math inline">\(\mathbf{A} = a_{ij}\)</span> and an <span class="math inline">\(R \times P\)</span> matrix <span class="math inline">\(\mathbf{B} = b_{ij}\)</span>. We know from linear algebra that the matrix product <span class="math inline">\(\mathbf{AB}\)</span> is defined only when <span class="math inline">\(R = N\)</span>, and the result is a (<span class="math inline">\(M \times P\)</span>) matrix, <span class="math inline">\(\mathbf{C} = c_{ij}\)</span>. Here’s an example with a (<span class="math inline">\(2 \times 3\)</span>) matrix times a (<span class="math inline">\(3 \times 2\)</span>) in conventional representation:
;
;<span class="math display">\[\begin{aligned}
\mathbf{AB} =
\begin{bmatrix}
a_{11} & a_{12} & a_{13}\\
a_{21} & a_{22} & a_{23}\\
\end{bmatrix}
&\begin{bmatrix}
b_{11} & b_{12}\\
b_{21} & b_{22}\\
b_{31} & b_{32}\\
\end{bmatrix}
= \\
&\begin{bmatrix}
a_{11}b_{11} + a_{12}b_{21} + a_{13}b_{31} & a_{11}b_{12} + a_{12}b_{22} + a_{13}b_{32}\\
a_{21}b_{11} + a_{22}b_{21} + a_{23}b_{31} & a_{21}b_{12} + a_{22}b_{22} + a_{23}b_{32}\\
\end{bmatrix}
=c_{ij}\end{aligned}\]</span>
;
;Here, we can use summation notation to greatly simply the expression. The components of the matrix <span class="math inline">\(c_{ij}\)</span> are <span class="math inline">\(c_{11}\)</span>, <span class="math inline">\(c_{12}\)</span>, <span class="math inline">\(c_{21}\)</span>, and <span class="math inline">\(c_{22}\)</span> and are defined:
;
;<span class="math display">\[\begin{aligned}
c_{11} = a_{11}b_{11} + a_{12}b_{21} + a_{13}b_{31}\\
c_{12} = a_{11}b_{12} + a_{12}b_{22} + a_{13}b_{32}\\
c_{21} = a_{21}b_{11} + a_{22}b_{21} + a_{23}b_{31}\\
c_{22} = a_{21}b_{12} + a_{22}b_{22} + a_{23}b_{32}\\\end{aligned}\]</span>
;
;These terms can all be represented using the following expression:
;
;<span class="math display">\[c_{ij} = \sum_{k=1}^{3} a_{ik}b_{kj} = a_{i1}b_{1j} + a_{i2}b_{2j} + a_{i3}b_{3j}\]</span>
;
;So, in general for any matrix product:
;
;<span class="math display">\[c_{ij} = \sum_{k=1}^{N} a_{ik}b_{kj} = a_{i1}b_{1j} + a_{i2}b_{2j} + \cdots + a_{iN}b_{Nj}
\label{eq:MatrixMultiply}\]</span>
;
;Or, by dropping the summation symbol and fully utilizing the summation convention:
;
;<span class="math display">\[c_{ij} = a_{ik}b_{ki}\]</span>
;
;Note that the term <span class="math inline">\(c_{ij}\)</span> <em>has no repeated subscript - there is no summation implied here. It is simply a matrix</em>. Summation <em>is</em> implied in the <span class="math inline">\(a_{ik}b_{kj}\)</span> term because of the repeated index <span class="math inline">\(k\)</span>, often called the dummy index.
;
</div>
<div class="displayquote">
;<strong>Example 2:</strong> Another example is a <span class="math inline">\(3 \times 3\)</span> matrix multiplied by a (3 ) column vector:
;
;<span class="math display">\[\begin{bmatrix}
a_{11} & a_{12} & a_{13}\\
a_{21} & a_{22} & a_{23}\\
a_{31} & a_{32} & a_{33}\\
\end{bmatrix}
\begin{bmatrix}
b_1\\
b_2\\
b_3\\
\end{bmatrix}
=
\begin{bmatrix}
a_{11}b_{1} + a_{12}b_{2} + a_{13}b_{3} \\
a_{21}b_{1} + a_{22}b_{2} + a_{23}b_{3}\\
a_{31}b_{1} + a_{32}b_{2} + a_{33}b_{3}\\
\end{bmatrix}
= a_{ij}b_{j}\]</span>
;
</div>
<table>
<caption>Uses of summation notation that students may encounter in the graduate core. Bracketed symbols indicate <span class="math inline">\(3 \times 3\)</span> matrices (tab:SummationIdentities)</caption>
<colgroup>
<col width="33%" />
<col width="40%" />
<col width="25%" />
</colgroup>
<thead>
<tr class="header">
<th>Summation convention</th>
<th>Non-summation Convention</th>
<th>Full expression</th>
</tr>
</thead>
<tbody>
<tr class="odd">
<td><span class="math inline">\(\lambda = a_ib_i\)</span></td>
<td><span class="math inline">\(\lambda = \sum\limits_{i=1}^{3}a_ib_i\)</span></td>
<td><span class="math inline">\(\lambda = a_1b_1 + a_2b_2 + a_3b_3\)</span></td>
</tr>
<tr class="even">
<td><span class="math inline">\(c_i = S_{ik}x_k\)</span></td>
<td><span class="math inline">\(c_i = \sum\limits_{i=1}^{3}S_{ik}x_k\)</span></td>
<td><span class="math inline">\(c_i = \begin{cases} c_1 = S_{11}x_1 + S_{12}x_2 + S_{13}x_3\\ c_2 = S_{21}x_1 + S_{22}x_2 + S_{23}x_3\\ c_3 = S_{31}x_1 + S_{32}x_2 + S_{33}x_3\\ \end{cases}\)</span></td>
</tr>
<tr class="odd">
<td><span class="math inline">\(\lambda = S_{ij}S_{ij}\)</span></td>
<td><span class="math inline">\(\lambda = \sum\limits_{j=1}^{3}\sum\limits_{i=1}^{3}S_{ij}S_{ij}\)</span></td>
<td><span class="math inline">\(\lambda = S_{11}S_{11} + S_{12}S_{12} + \cdots + S_{32}S_{32}+S_{33}S_{33}\)</span></td>
</tr>
<tr class="even">
<td><span class="math inline">\(C_{ij} = A_{ik}B_{kj}\)</span></td>
<td><span class="math inline">\(\lambda = \sum\limits_{k=1}^{3}A_{ik}B_{kj}\)</span></td>
<td><span class="math inline">\(\big[C\big]=\big[A\big]\big[B\big]\)</span></td>
</tr>
<tr class="odd">
<td><span class="math inline">\(C_{ij} = A_{ki}B_{kj}\)</span></td>
<td><span class="math inline">\(\lambda = \sum\limits_{k=1}^{3}A_{ki}B_{kj}\)</span></td>
<td><span class="math inline">\(\big[C\big]=\big[A\big]^{T}\big[B\big]\)</span></td>
</tr>
</tbody>
</table>
;It will be important to learn how to read such summation notation, so if you see a repeated dummy index (often represented with <span class="math inline">\(k\)</span> or <span class="math inline">\(l\)</span>, see Cai and Nix, 2.1.3), that you can recognize the notation.
;
;Some useful representations of summation notation are shown in Table <a href="#tab:SummationIdentities" reference-type="ref" reference="tab:SummationIdentities">1</a>:
;
;In future releases I will add summation notation for the Kronecker delta, <span class="math inline">\(\delta_{ij}\)</span>, the LeviCivita <span class="math inline">\(\epsilon\)</span>, the dot product, and the cross product, determinants, the <code>del</code> operator (<span class="math inline">\(\nabla\)</span>), and others as references.
;
</div>
<div id="coordinate-transformations-release-12017" class="section level2">
<h2>Coordinate Transformations (Release 1/2017)</h2>
;Cartesian coordinates are not the only coordinate system that MSE graduate students will encounter in the core. Cylindrical coordinates and spherical coordinates are both useful in, for example, describing stress and strain fields around dislocations and vacancies.
;
;<strong>Cartesian</strong> coordinates, as mentioned in Sec. <a href="#subsec:Tensors" reference-type="ref" reference="subsec:Tensors">1.2</a> utilize an orthogonal basis set and are often the easiest to use when describing and visualizing vector operations and physical laws. The rank-2 stress tensor (introduced in Sec. <a href="#subsec:Tensors" reference-type="ref" reference="subsec:Tensors">1.2</a>) is represented using the following <span class="math inline">\(3 \times 3 \times 3\)</span> matrix and is shown in Fig. <a href="#fig:StressTensors" reference-type="ref" reference="fig:StressTensors">2</a>:
;
<div class="figure">
<img src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAABd0AAAGxCAMAAACgDO//AAAC7lBMVEUAAAD///////////////////////8AAAABAQECAgIEBAQFBQUHBwcICAgJCQkKCgoLCwsMDAwNDQ0ODg4PDw8QEBARERESEhITExMUFBQWFhYaGhobGxscHBwdHR0eHh4fHx8gICAhISEiIiIkJCQlJSUnJycpKSkqKiosLCwtLS0uLi4vLy8wMDAxMTEyMjIzMzM0NDQ1NTU3Nzc6Ojo7Ozs8PDw9PT0+Pj4/Pz9AQEBBQUFCQkJDQ0NERERFRUVGRkZHR0dISEhJSUlKSkpLS0tMTExNTU1OTk5PT09QUFBRUVFSUlJTU1NUVFRVVVVWVlZXV1dYWFhZWVlaWlpbW1tcXFxdXV1eXl5fX19gYGBhYWFiYmJjY2NkZGRlZWVmZmZnZ2doaGhpaWlqampra2tsbGxtbW1ubm5vb29wcHBxcXFycnJzc3N0dHR1dXV2dnZ3d3d4eHh5eXl6enp7e3t8fHx9fX1+fn5/f3+AgICBgYGCgoKDg4OEhISFhYWGhoaHh4eIiIiJiYmKioqLi4uMjIyNjY2Ojo6Pj4+QkJCRkZGSkpKTk5OUlJSVlZWWlpaXl5eYmJiZmZmampqbm5ucnJydnZ2enp6fn5+goKChoaGioqKjo6OkpKSlpaWmpqanp6eoqKipqamqqqqrq6usrKytra2urq6vr6+wsLCxsbGysrKzs7O0tLS1tbW2tra3t7e4uLi5ubm6urq7u7u8vLy9vb2+vr6/v7/AwMDBwcHCwsLDw8PExMTFxcXGxsbHx8fIyMjJycnKysrLy8vMzMzNzc3Ozs7Pz8/Q0NDR0dHS0tLT09PU1NTV1dXW1tbX19fY2NjZ2dna2trb29vc3Nzd3d3e3t7f39/g4ODh4eHi4uLj4+Pk5OTl5eXm5ubn5+fo6Ojp6enq6urr6+vs7Ozt7e3u7u7v7+/w8PDx8fHy8vLz8/P09PT19fX29vb39/f4+Pj5+fn6+vr7+/v8/Pz9/f3+/v7///9vIwMtAAAAB3RSTlMABxslN3G7gw7y2QAAAAFiS0dE+UxkV/AAAJKkSURBVHja7L13WBvPm+C599zdo9/s3uzuzO3dbJi5292bC7u3Mzt3u1dC5JwxGZtgMDjngCP+YsA5YJyzkRM4YxvbgI1lbOMcsAEnEAZMzjlI/d9VdSt0Sy2pWwFaqN4/QB2qulRd/VH1W2/4RwQWLFgcS/77f4TFIQQPdSxYMN2xYLpjwYIF0x0LpjsWLFgw3bFgumPBgkX4dP9v/jssdiKY7liwYLrzkP8W95+9CKY7FiyY7pjumO5YsGDBdMeC6Y4FCxZMdyyY7liwYMF0x4LpjgULFkx3LJjuWLBgwXTHdMeCBQumO6Y7pjsWLFgw3bFgumPBggXTHQumOxYsWDDdsWC6Y8GCBdMdi5l0nycSXTR6grtI9BT3qUOJdkykikT/gAcFpjsXVOAxITi6v/oz0T8ojZ7x9k+i/zSJO9WBhDYmDNEdDwrHo7spVOAxITi6/1eR6J6JU8JEouO4Ux1IaGPCEN3xoHA8uptEBR4TAqP7bZHoP5k657VI9DejuFcdRuhjwiDd8aBwNLqbRgUeEwKj+38Wic6ZPMlJJMrDveowQh8TBumOB4Wj0Z0DKvCYEBTdH4lE/9OwybOkItHfKnC3OogwxoRhuuNB4Vh054IKPCYERfcgkWg+fVtZc+3Atr3nPjIXT0b/R5HoDu5WBxHGmFDRffDOkZyzVXhQODDddVEB5eul3G37rn3HY0KYdO/4JyJRmfbeFEb8KxEl/zprkH5ejEg0C3erYwhzTJB0H1r0F+So+LuneFA4Kt2ZwwLK8M5/q4LF/7q2HY8JAdI9D75taW2YHoto8n830M4rFIn+hz7crw4hzDGB6N72H9SD4s8O4kHhoHRnDguCePe/0GBRhMeEAOnuLRIFEHS6/6X3hrzTe+L+Et6xvx+j/XD/SSS6ivvVIYQ5JiDd/95DJPI4cPmgLxwEf7qEB4Vj0p05LAjZP4eI+Ku43adzF/09je54TAiH7qN/LhLtpNH97y+rlk16Y0WMI8T/JRIl4351BNEZE5DufxL901vk5/vwif6rdjwoHJHuOsOi/d9AQCztpza+pj3EY0J4dK+Et+iBdnNE+1HpJxL9W9rqN9Sn/Qfcr44gOmMiFb14q93Pr8HPy6dgUPReuiTHd0JQdNcZFjAmgSiT7TwMCsHQ/TC8R83shz7BQ5+1mzlQ5zqEO9YBRGdMILoDzRaMJPIvR20zKMbqPyL5hT7LPT3L8J0QFN2Zw6INzuT/K2tQAgwKwdB9uUj0TwyZp/5rkeiMdusCvLlVuGMdQHTGBKL7Wc3WFbj1yDaDovWPQCT70ed6AB7iOyEoujOHxQl452+ynodBIRi6w7gQf2Po2H8SibZpt5A5DTZkdQTRGROpjDlbD9zaYZtBMd5al+8BQBamuyDpzhwWc0SiPx9nPQ+DQjB0dxOJ/k/mnucrXf/mL/+ksnNapd0PI0iILgj9axelMqQIDwQzRGdMQLr/z7TNvxGJEm02KGqOq+jelRWK6S4sujOHxf8jEv0X9vPsAhSOQXcY9O3v6dsf/gvd4l20SHvkC9w8IeSvLIOS7cMQKR4IZojOmIB0/z9om9D6LdiGg0JF9+FbCZjuwqI7c1j8e/owYIjgQeE4dJeIRP+RtvmM9Ej8d5LgqNjY2L8SiRZqD71nqF8FKD76gulujuiMCUj3v6PjVyRyt+GgUNG9ISjyGb4TgqI7c1hAl/Y49vMEDwrHobsvDPqj3RqBv8j/fHebauvvGHR/Dm9aoZB1MpjuVhLmmDA6d7f+oFDr3WcV9uA7ISi6M4fFvzM4dxc4KByJ7kki0b/Qbl2GN6aUfgNpdL8Fj1UIVy1D6mSyoaSpP0CR4YFghjDHBKL7X9E2GXp36w8KAMJOtxOly2Lf4BshLLozh8U/GNS7CxsUDkX3THgrtNHCUuiqtcF/zKC7Ect4wahl0Cep+gMWM4U5JnRsZnrh1nYrDYrGJ2x0B8vklZu8DvzEN0JYdGcOi3iDNjPCBoVD0f0GvBXv6S9fUZqNuyIG3Zcxp3ACVMscIqOe9TbAj9haxgJhjgkde/cCET1QoGWDosCZle5L5VGei/FtEBrdmcPilEF7dyGDwsHo3gRv0nntDJgeJ8iTSXdXkcjL2q2UW0d1olLLyGjzeKyUMV+YY4Kku5g+Kmi+qhYNir6z7HRf8GHeiQ58G4RGd+aw6PinItH/x+qragtQYDGL7sTf0s0e4YP8L9TRO8+IGHRX/AuRKMfarZRaR4WiVcuwbWLhK4wxQcWZuazauMmIM2PZoLiUzE73wLU3v+ObIDi66wyL+QbizNgEFFjMo/tiesyf6/COzSIjiSmP/mPRn9Hp/gYe+mhNXQqSKB/tpp4uhbt2RauWwXS3hjDGBBUj8p9R3ocP/4IRI9KyQbEasNMdgF/4HgiQ7sxh0fnX8OYvU8WI/LHgoY1AgcUSuj+Bz26TemMSRu8U/fvNly5s/Y8iUch/ptM9SyT6363YPhkyaYEMlslVk3h9XQp3e0Yd40dMdwuFMSbU8d09c6/k+enEd7dsUKwGko/dLHT3mdeG74EA6c4cFkQF8o35q9l7zhxc+v/S4rtbGRRYLKG7Epq4a9Pt1PwrjZuqU/8/0OkOzZz/sHYjtVRmM3TBdJ8uYY4JndxMubQTLRsUqwGIeMJC98W1OO2yEOnOHBYE8fav2XIz2QIUWMykO5ENI3lqt34FUyFm/nq7gqDTvVYk+seNtqM7NHQ51KB7NCqVo5IH093KwhgTVF7VhSx5VS0cFJDugY/06C7Z1DaO74AQ6a6DCmgz/ce/UbH9bzd32RIUpAzfzFXJa0x3rtL1zxhh3Immizt3nHumO3taIRJFW72RdCrrztTlMq6ElvpgultZdMcE+SgXHc45/cmag4KV7k5rsLWTUOnOMiw+nN+z7cDNehuDgpR7SWJKFj3GdOcsMG7zfFPnDP1L0Z/eTynduTslYbpbX7iMCQsHRf/rJH26/y7f+hr3vlDpzmFY2AYU1FsdJZLIWqyZ4X5q+1+I/tzUMtZ+kSjC+o3UUhlqV8ymO+m+pEt3PT0PFj7CZUxYOCi+r3QGwPdip3q7+1v9YNuFkN4x3PuCpbvpYWEdUChaBvV+Nuols+bMmRMmXlA5genO49ytItEa42eM/I3on3y1Id2hO1K2TMkQku7kJ37vAJRKh82ZSWlA+LbaWvUIWkyPCUsHxdc0NBELu6HevhO/8v35UDFGtIDpbnJYWAkUQzkvdR+nt/G+xb9//77t0TqK7zMfuo/8b6I/N25hvFMkWmuDRmqoTE7TrUR3g5N+THerjglLBwVJdwBOae4bcE0IWfYUP7pCprupYWElUHSveqL7OA03NY0QV6JC3JT4NvOiO/F8y5YnRk84sCVj0KZ0R4oUy+iuNrCBHlIMuhepkzQhhykl+RlVCv9juls0JiwdFPp091iceRNPzARNd1PDwkqgyAl7wvo4HQdzrmC686T7dAmK1isldSlSgpXusnpO1KSi/spIocL/ao9RMWik5JxeqsyCZ2YhHZD6pwPTfbpeDh4lMOleNHv5e9wtQqf71AgAq9lyt1xLjq/A1rL2QneSuOq/bHT3yedGTSkjZwf7GwJJd80rAab7NEuNvzOT7kPtXXjijumuojvQz9039jE+TqrAj5l90R3qUuS9utSkFCxc6U6ZzVCiZy3TcIike68c0b1HTnFdnofpPq3ySWXgdgp3BaY7C92P6+2snBeDgh3VDuD7bDd0z5b5pGbrU1OF6nyu1MzWiMzAGwKhRHRXz9plWZjugqD7vLtDuDMw3ekyVMdC98GfAdGvRuC/2Hf4PtsN3bXmLhbR3bT+h0l3rJkRCN2dtnThzsB0p8vHRBa6v5nt+wC6QryKDXiF77Md0Z1Uy9iY7tCipihV3kOje54c010IdAcbMd0x3RnyOgAFCt1Gf6AmKoPFTsFRUVFB4qYRfJ/thu6p2azUtCbdSbMZeC1Nzci0RmoFe3eZnuCBx1HGXmG6Y7oboTtYSn8wK1aohwvAsyj7spmxNd0pbyka3Ul1kBXo7qMneOBxlOcZmO6Y7pzpXn1NI5ju9k53Kqgv6aNkLbpDIxyqbmgtg9RBPZbSHfpD6bIdB7fhLEc0c7GkiziaO6Y7TXpOeunRHStA7Y/uZHgZtjtIs1+3Ft190rL0vGAtoHu9TH/izj3dCBYt3SWek7g7MN218oEaF0sxx+2b7kxVho3pLlVak+75Ppju1qE7ADjmH6a7Pt1TmvCvvh3THapfGKoM29K9oZdWudZgxky6U85WciT16FMe/NDQ0IvHHVdpq6mpWQAjAEvhfzxJw3TXp7vLlj58Q+2R7nIZTJbNVMvYnO7a+qX0JVWz6E6pZdSqHvQZxa7Bg46nsOZmwoLpTsnyHnxD7ZHu5GKqnoWJ/dA9n2F1Y8V2YrpjwXTHdLd3ukel6lmY6AWZsSLdaRGGUVibHivQXVMJZYSD6Y7pjuluBXmxDtPd3unOkj6J3Y5cVm8FRRB5LXXlGuMZc+kOY9Qw1mXzMd0x3THdrSTn1IvtCUX4htot3VnmxKxeQvlWuBy9fqZaxhy6q18qMN0x3THdbUZ37JZqn3TvbYAyNXRHyZikDar6yTxNTLUMpjumO6Y7pjumu43FJnSnqYDI9VRdtQymO6Y7pjumO6a7ndJdW7+utQymO6Y7prvA6N7f1NQEyb4H/sM3dCbSHTkJkYYo9fCDZSvnNBUQSsykp5axAt0pCx9Md0x3THcrCWtuJiz2THemSIUbclEnHCTp2ZSN475jumO6Y7pjus88uutn/cZ0x3THdMd0x3S3A7pDYxvNZ5SGW9M2Klgxne6kZQ4ZIjiN+kuelobHJKY7pjumO6a7xXS3bpoklMuJ3hiybTBUDqHK++RD95ZS+TqRsWg0BeFpMhz8HdMd0x3THdPdUrpbd96vm3eJluybdogZdiafkbAJxwfGdMd0x3THdBcY3akcTAz3q145lTeKeUhj8FNPpYLSxAdWKXMw3THdMd0x3THdBUN3OVKtZGdn6+zOpol6H9NenxYfGOlkpJjumO6Y7pjumO4CojuPZjDpTo8PLMV0x3THdMd0x3QXEN2h9UuUD1tIHB50R25ZJN1x5iZMd0x3THdMdyHQHSaQymbRyfClO1pelSKbGTwmMd0x3THdMd2FQHfeDTBGd8F6ZmG6Y7pjumO62xHdSQ+jKdTJcKD7IWztjumO6Y7pjuluKd1p3kbmCfJRSsvmWUiN83pZViqiO3RlUtE9W4aXVDHdMd0x3THdrUR3S4BqVnHtZJ2crytVcSTzfbArE6Y7pjumO6a7AOiOfJQONfA3cSGjAacilQ4iOkwLnidHu3qQ6xM2mMF0x3THdMd0n166U+5L5kSpofkxkbFmsmSqGJH8lTyY7lgcm+6LH+O7ieludbqbf13GeiotvQeB1TKY7pju/Oj+BAfOxnS3Ot35m8ow6I5Cy/SoPmgCAmO6Y7pjumO6Y7pbg+5UVF5zmArVMuZrUdhzd0AlTbYMj0dMd0x3THdMd8vprgq8KzXroubPs9npjv2YMN0x3THdMd2nl+6UB5P5xi16YCeTNPnkYT8mTHdMd0x3THdr0p2nQsQsDyajdCct3bOwWgbTHdMd0x3T3ap051ncYp8jdrrjrNmY7pjumO6Y7tNI9yLzPJiM0r1HTlrO4MGI6Y7pjunu2HRnolHqozYZ512Phu5KTqJSy3BW5BirBwumO6Y7pjumu5Dozmeij+mO6Y7pjumO6W4fdCfVMpjumO6Y7pjumO7CpntWFhnmJSuLI935qGUw3THdMd0x3THdp4vuzDAvpuludg4mTHdMd0x3THdM96mkO5mbiSvc+allMN0x3THdbU/33bdIacVPFaa7Tj1S7kp3M+LAYLpjumO621C6nwO1HC3XyrMufIMx3fnRnb9VPaY7pjumu+1k8HqYhu5unloJuVqlFkcP7jEz6J5qnkTxKGvszCJMd0x3TPcplo/OgF0kLmrJcPCHzd7pTmY3mm7JlpknGDOY7pjuZs7cpYEA+DnfPOEFgMeV6rqWkkh/mniRnHefheRCd3d37zimu/3R3ceeBWMG0x3T3Ty5EAvp/TD5ScNpOFlPXfeQ6HpOnzgdc9PO5WPXrVuX8xPT3d7oThq9YLpjumNxLLqPng8GIP7u4JonytcA3J8LYk4zlTCdz54gOeqiIrzrgvT09AsTmO72Q3eVWiY1i5RsnpKVleZDeTOZkDSU4Zpf/amY7pjumO42k4J4AIKuDCK6y1e7Xju8Kznuxg0WJfu3/bugLFUhPvHqjRu9jnSf7ZruKkjmK21rMyOlMlzzqVuK6Y7pjuluI+muQPqWk0oC0Z34nuN+pOPRAgBknQbO/7hp48aNPhThLzyC4iiLrXZMd41axsZ0h6Y1ZIZrPnX3wpTackOC6Y7pjuluvpCmkDGFIwRF98khsdvlxrdpacEFn1pZC0wMQclKS4sRw4VWZDT56dMIprug6U6pZZDaxGy6k1WYYHs9TJCdZXakA/YKMd0x3THdzZYqJzgHL1UQKrojl1WnU8qJCbGT5IzhUpMTE6VqLbxE4hiLrPZLd1V4R6kFdOcSZ0allrEe3fOxZgbTHdPdbBm4AE0hZxWTk28V3X+udznYTxA/1gUEZ3QZ8VQdaW1packNCAiASvuwsO2dXV2TmO5CpDullsmT25ruarWM1ehOuVA1HMJ0t1e6Twz0amVQgek+tXIxBk6+X1AqdhXdJ6pToqAWfvzLs4yA1atNPKj1z549IyfwwatXr27HdBcg3VVqGZnS1nSnnWANulNqGZh0W4rpbpd0Vw71vFw6SyvbWjDdp1LGzyFTyPuqh1FFd4Ko3up/cgj+/3USgIyvJmuBgE8nCb9o9eqLmO5Co7s264Z90Z1Sy0gJTHd7pfvDnWt8aF7vK5sw3adSLifAwVAwQOjQnTgNVvah/z/37vXYc7XadEXle1dQdzD56v0ZG3bMLumuUcvYmu7wQtRVrER3lVqmF9PdPuleX3B+nobrR5DcsUv7aXule7dMZQqpR/fyRQm3VR/XB4JNHzg8rZ8ytmzxRHcy8GzJL0x3odBdq5axMd3hhVRXsQrdNWoZAtPdPun+KNRd4rcASjIA+78ODg8Pj2K9+9TJ0PVZAEQXaK0ZtXQffxfvXUXO3on2/fMjl9eZXi9FdpKb50cAIHbzOPxxRoaTtEe6M5Kh2pLuzKMW012jlsF0t1O6l/gCsK4HSg0MXbV/1G571E7pXg3t1cED2oOopTuhfO7jV6l67hTHwdpBbs+oopB6ExNnYroLQehqGbuiO6WWkfdguk833ZWTWuE+91YqLgQ7iU+QZhbjlfOBV7Shyg3XqZicNOvamO7QFPIiNIUMuzdMsNKdeBPj81AdCHLgXnBowlNOYSGHWlsDAwPdgHvYgredM83HScB0Z7c5odQy2jRJsuxsmfn1G6O71o/JGnHZ5TKGjTum+zTSvfG6VCNV3PUCTxbBOd51auMXWpNjPa3jnvSdwTreSekybS8kdkn3S8gUspKxAkqne89r57m16o2uU27OyT84VvzixYu1KFxw2soKTPfppLvUin5Apuiu9WOyBt11Wo7pPl10n/haccJPa/RynnPBNmREZ4rudRUXI8H6itfsZhivNjLSTKzAdOd+25Ap5JwHzKeQTnfksjr3gfpz9+uSxJQSzrXXV+ahGxK34hKm+7TRnVJu8MxebYLuqUUm/ZisQHfdlmO6Tw/d+35WbfbzFJtN9zmlRulev9svKHp2uF98Jdulf8aiqONhQcApdDaSnZjunGUM/jAGFA4QRui+Mwycor1qXQte/Zz7Q1u9PxO6sIKUa5ju00N3dYSWbJnV6ieXOQ0o3RlqGcvoLtdrOab79NC9PDXJlzF/5kn3L11G6b4oEMy+92UvCH2qf+xxSgqZK+7CQeBz/guSabPTsEO630kGcad0n0Em3YcuBq1/Q9s+NyflLY+I7h0nM6MBcC4uHp0xT4490V1q3fAspugutV4+VP2WY7pPC90vzIF4TX9aUYFIfboCSiM/uqs3DNDdAyR+GCAusNB99Aq6dCa8YmchcNGqEDDducjAF3en6EI97DLprhxd6ryBtj16bc7Sl5/7uV5DMTosDYfqd3fZ+9+Y7lNNd5VyI6/BivUbpDu0zLEe3VkUSpju00D3wXfz4eQspRjezGK4Qnr8G6/bSqf7cGECC93bK1zBcljjBeB7WHeUDm2DBVY/QVd8sQGADVXTOUO0N7or34UCcE//VjHpThArxasm6TseOYGg13we3ItOKP4kOKaYGU+O3dBdrZbJklmzfq1XlDE/JsvoLmdTKGG6Tz3dx18iR9MEalr9Dn7M5VWcpHszZUfdDD96zFIdGGtuHh5sbhkmyoOAL7KbvgCP6oYv+bke7mxTzRLhxw30VBNDUxytxs7oPvw+wAl4PzJN9+4TwVvobqcj98Od/F8O8fj9b/0VFCQGnrs7umdClj67obtauaFUWrN+QzYzbPutp5bBdJ8WutcHovjebSMsdB/vbm9v7xpT0boLbnTrWUt35HjAJdFC6BDZ3V4FgPdOlVJn8HVo6IPC0PiKoaIAsP9be/vYBeDke0OndLA7cAnoYKP7ZG/7nbj29j5Md0PyOBWGZD/eQZikO9F4xm8JfU83zLqaUsrnWpMvX8I4QsHLdzTNgCfHXuiuVsvI7Y7uqtgyDQ2Y7tNM9+/kMqpqg0l3+ZGMjIzc79TGj1y4cViuW3zkwxpYZm4BQRzJgPbRO76onN1LoQp+wVzgVyZb4AqSYNF6qJnJ0y2O3hrUPvRMuvdcyEh1zsiYSmMNO6P7JdhfrDamenQnYHBf5p5Xr2Ijz/N7dt+vRtbv85Y9x3SfErpr1TLKqaC7rh+TBXSX02LLYLpPP93nnWOj+8+t/nuXA+/NX9BG9Wafw4uB/1b99D1vt0CLxpgjR6DpnG/2dw0M9pC/Gn5l51VmOBmLWVZV4f5VzQQL3Yd3R67Jh0X/wHQ3IC/XguDt7IoUPbrXpbtc11FzFSQnPuWnZnmUuxzdx01V9v7k2AfdtWqZKaG7lHWp1QK1jJTAdBcG3bcPs9C94UxA6o9784HzbUje+sOBaS23UsQuT/QqmKhMXxLsFLRo2dKlmZ80Yarkl6EZ/NKl698hukctXbo0QMKD7r+feCeVjo5iuhsSxTuYEHtBK0e6E8+9/V7qwnpR0k2eT++HrHSon1l39yGmu83pTlPLTAXd9fyYVHRPLTJXLdOL6S4Quu+aZKH7Aef5NYrJXwBAZfnITsmyn8qJLwA81q9hcmxkJ1hQMzo6Oqa1qjgJrdghn8cmEd0vwGMLAQ+6X3IJLZ9EhzHd2WUiUwI89nVxpfvn1V4XdYwgx58neFT187vocF2WBDi7B9UMY7rblO4MtYwe3eUymdzKdDegjCeg1QsllqplMN2nne7SEABcDlOfo7yclkE1TCuk++RopKfTWrhc+o2V7nDQdP9qG2PuOgaiH5JmGZDu3/oJxRica0Y9Z6H7inpy7I7fiQJgdwfVkC1+IPo5oaL72AisenzE9rGs7InuwxuBU7KBKR0L3QnCRfxad5fMK/gVbyPHIBdoHTmndsyOrSPtgO4MtYwe3aVseg8b0Z1vtmtDahlM92mnOworkvVKDd644m6K7l9Pw3XTh32G6c4ix0D8B0JFd0j5tuthwK3wFwvdI/eQ5pQPkCPUcdXu+apzSboXHIdLto+PH8d01867O0PcvA8ZSp7ESvfvC0t1w/+OtoeEvBrieen2tlPeQBIQcn3Qbp8c4dOdqZaxPt1T9YR1J7WfEtW2KUWNquWY7gKhe+uaALC0mPxYtgr4rqBiCLY8AmA9eRjS/a47VM2jDe50f7KWSffPcwFgubOboRskKKwj+l7C4y4LqO/T8zwa+Kng/0dXRTCIGXw930DsScek+88MAPIM+hOz0r1neeJ9vZ2l8cmlvC/efBAtrsY+sNsnR+h011XLWJXu6srNFOOKGrVahj0qDqb71NN9smo+cPGpRRLm6rHlE2VIUR4JwBK077mK7uloo4Qz3ee4um3+qqX7YHEsCFjMMhM8At0tvQ7VPlro7J+05AnlqVq9WAK8yQZBun/LdgezKnfNS0rCdNfwNdEVgCIlL7pPfE+adUJ399i3mIhFJ8d5Xr7jXRH8UQ6328CRQqe7rlrGqnSX+lhFeKtlMN2nhe5E3WIU5RWJE0huVoUCKIXhgD3RvigV3b3RRgRnuoeC2U0jWrp/CncF2SwrQYr2E/DiAXERbmBrXYPqZb8qCQAnskGQ7sONEcBlWWldXR2mu2bqDmMurzWcA5uV7gSxFKzX312QAuac522S0XEJesDNu3DPLtPnCp3uemoZa9JdVbllouumxEUtg+k+PXQf+b5EZZJe8V5jrl5KC/ZO0l0tnOk+V/UJ0n3+QhgrrKCZHRTv3/uD2Pfv32sVDYjuXnDPcQ9S7x4Lwmr6p6JH7YXuP+EyyE7DcDdE90uJiS/1p+mPoC1TSSfvNuyDgSNB6JlJe3xyBE13SnOSmsUM+WIluqs0J1lcJY2plVGLOWoZTPfpoTtB3FDdNZqdG6T7PLQriaK703y0Ec+J7nfufILrs9mnVZvPsrMlIDg727AN18HsM4xtSPc5++D/+97itFuI7jFT06P2QverUC8zPMmb7mNHnDbqL4WOP50tjv7Ef0pwfnE0ELtWdtrhkyNoulPKjXyjXkVm012lOVFyFSkHbQxHtQym+3TRnUUg3ckgAOeAS8Tl065ud5AKZztwjXxtsig0wdHZk5awm8+1Id1Jq8z73pKbxJA8HNOdyeMLEKvGlCkG6E6cdlnVxXLgiXfIqxEzooPdgT8y4KYdhhUTMt1Vyg2r070ImbtQldf38KN7g1qMX8GgE5PldC9i2vEUETNfpoTuHXlg1oO93oCke4oHiCk3HaJXn+6dHbwUtCq69132hHT/uEjivRTTXfv89+7zkqyqJsyg++Bt12CWAyPtoSEhUv7h2oa/Q/djn3N9dvfkCJfucn1rGSvRXYrMXSidj5K7yAzrYQy03OTk3ow+kWUz1f5SYubLlNA9NwZEVu4CFN1nQTeW96aL6tOdp6jofjtRAun+JhZkvMV014jiTBAI/zpqDt2Jct1gYiopiwcRF/h7u4/fhiMi/DKmu9WExVrGenT3YX0rMC6867c+3fWNfDDdrUT3ucDnQev7P5wh3etPeYKQ0o6poXviob4bUMt/sw7R/dQU9ahd0H0SmrrPNv7UGaR7b7772hqW/WPfo0DASf4rpMO10HQmcD2mu5VEpTmRy61Od42pDA+1DB+6c0rtbQbdoU4mCtPdFnTf/fz586iIbROKydvuLgeenwsDUXsmODigW4PuYt97aeLgZeMKTHcdOZ8A5l4hzKM78dQz4BXrAWgYuckcDfoJaAzlddfODCMFQHclewxepDnhoAkxTXf2HE+2WtQ0aS3Dm+7adFFITwWFcppNI40/ZMTMF9vSvSyQtH+UnEQb97ypDW65tIHTHsuu/TlFAmOZOEm2DcCNt/GSM5ju9N9OcIAwl+4/cj33s799lS9OumpOJMLiRGgYefJ6gz09OQKlu5TzxJQv3aU+tqU7x5bzp7tWT5XvMLP2qaD70G8vJBVozWy07Ru58ZGb1bmbtMeya4+1NZ3wirnb1K0gL940Vet2dkD3AZj+Kua62XSfHBW7fGA9MiFLcPs0wL9B4zeWzBe7uB1rxXS3kO6UCkLO5T3IArrbwuDEtLWMeXQvStV6dfXUY7pbU64gIQNVlR04QG5wjBvlftfyi9dcudM85T0qfLorXsF1zBum5tiG6U4QXpLnY+xHyn3DXprlnNTuIQbg3Kj9PDlCpDt3tQyJSVPaCd102Gq220CtYSTkr4V0z2eYDyHlTJYjKGWmhO5aKVkiuXaNu92KNeg+LSJ8ujf6OwHf+5bQ/dsCv0L2IyPtYSFvzQn8OPkaBnf22t9hN/dZiHRXOTFx1YTwql87c8+3wVfhpVDiT3ft18h3JGeoqaP76KPFnp6bqqrGbEf34Z9VvzHdTc+TYICZkybdQ43RvWsZOGfoWNnspDJzWjVUIwEgaDOmu/l0VzsxcSvd28Cj/iJtFN/6Hut/E65qGf50p2rGdLe1DMMwwB5hYW22o3vdhrCTmO6mpCwBgCrTT6gxuk/UJ4YeN3B07GfELKlZSd4+r4Txm3PsRfcuOLprY8vYoH610h0anlgvgx9/tQx/uuua/mO620o+r0MhvW/biu4/o92vtGO6m5ICYMAdiTvdCWIh2GTwaEFKyhOzCPAoBYCQXKV9PDmCo7s2towN6W7V/Kz81TKY7rak+/CLQijfzbzY+EMUR3J14UOTDK6/zp/un/L8NvyY/h4VOt3fbwCBmRbTvWBu4jODpu3QMLLQLASUw1CTwE6y8QmN7rTwL9av3zbZt/mrZcyjOz0MMqa7QVGQjx/Y99Pcyz2bg4JGhReYUgzccTVK966PLDuPgISPAuhRodM9VwJS6jmcZ5zu44edNhlMej1x1cnVHMNIYuJRGgCvXtuFckZYdK+nh3+xdv268YSnTy1jHt2lupY/mO4s0v/dz8UvOhp4bGgZM+9yoxVL4dqZxOemiVhxxug+0d5wNbJBDx5NO1zTazHdTb59bQdOK7isPRunO3HWY1WbweN3PUDEZ7Oa99sLuqAVYrqbpznJV9qE7rrxhKdPLWMx3W3ojWXvdH8MZ+7Zb9+Kgd++JjOv1/eZdF+dvXix2XTvPrY4TrK0Qnf3prCY6gEB9KjA6b7XHUT2cLFIN0H3wZuuQQaPD98LD3tiVlRf0jDylD0EJRAU3ZlRea1cv17I3+lTy1iF7nl25RM9VXSXJgHv/VApA91O5n83+4qzVOmZMjJKzaL7cHowLO10k7n32wG3zZUGq/uYoZGcD45N962AY6B7E3QnyoytzfZUuc5pMat9Q1/FYJY9RIwUEN3VEWCsTV8aERkhf6dPLcON7rIGJt01vkxUR2FfVX0ZeD9X7JT1Cd7a9HBL6L5j3WKS7k5OG2SyCb50/yi7L0alxbuYYQqfR4Lz7Mtxrc9kslwnjXjfd2i6J/uCzdxWTUzRve+S68oaI0/YnNkl5jUR3t8AO4gYKSC664b8tQHd85U2obuUf+AXDnRXV6hnM4PjzBiQiTfJMEA79XkfSHlnQTadb9r8qs2jvOg+0Z9GFnPxBSB9gKZfGC0J8ylgn+pf9wJ08Sx2aLrDHtjP7UxTdCdk7kFGXI/7bvmuqjSLAydhxEjfO4JP5yEcuuslyLZq/dCPKU8u77EJ3XmrZTjQHaZdotNdnkcFxqEF4dGYdBSpkzQVqf+SmzMncxNnun8JcgFuYeTH7u3AJeib+df86eOsZm3obR50H+p+u9IFlfLI/AGA+5ZfmlE4eD0kgFXpPjlwxE8MPP39/VG8SG/4P6LMxj3qMHT/cTjYaGCJ8wkLXpjVxvvQ3SrsOKY7N/rW62di4qoVkck51C81leNpKtUypuguk8loMYTp8X9l6BCZ7Fvbfpg0Ko2cysO8TbCMenPmzO850/095MJSirg74uDnL+Zfs/dUtGYqfYkH3Uu3r/UjC218Owb/Lq5THxgrSpuTz2qf11s4G1I98/bt20Hwix6E/+81OjDdBz9yCA7Jle6KMb8LxpaxxwrjVrwyp5UThTCVtssrgafSFgrdWTIxccaklFP95udasrpaxhTdmRXqRchRrbCydIKqTqkD010164OK0ZCcNgsu2nU7RgX3gx8N0f2UnnXjxTT1T8JFaNyeCCL2d6sn9ZlgFWswyJFDMWD2weMof2gs5NrrqehRIdO9OgqAq1x/CdaYdDj1c64yeryQk1Msi9yGmjfxTWEHjBQI3dkyMVmV7j1yG9HdHLWMUbojncyhBlqFquZSyhlKeSXvMUB3KiEU3IxKRbm97SyVjIV0by5Ec+b3pEC6p362xKNQMXoskuJ054Qhug/rHOn57CcBnolQie4SB41tBnOAk5t6ebByRdBhtuCCrRVuTmBLO1lVZhgIu9zl2HSfeDIL+HNdd+BA969pj40G67/nD1rNcowY/hIkAd6XBP2ICYLu9Rptg9JWdLckT6rV1TKG6c7UyTDbL8tSib43FpkHnNAsxEpnljU8V7qf9oQsdvUlBVhkEUnNti+Sli/AUKzYO666e54hddDcN/MBCH4AJ3WTO+GmuhE+LtmDbL82hT7wpD8oAA0cBk6epY5N97Y4V3Ca6y8cB7p3LI67Z/Qd7QzYUGdWS0eLQgCYdQXT3QR9pT469tx2Q3epueYrBgDMVhuH9qtrc2y6H0Y2jBIkTsAKdCf65WRVUUWsjjWK20y69xyICZY4SRY8WeUGvBqH0I3rvAQjGiCnRkVZvKeUHVlS2NKjHSrun4IbxVPQowKmeyPsggdcT+ZEd2A82mzfV5do81R4w3UckgM6PN1V1jJ2SHcz1TIGAIx0Miy1cWh/bwOqrShVS/dDM8jXiQ/dNx9Fku5mDboTBKxqgydYxWoU/XyDhLF9HBrJgbyjJ3ZDRyb1nS2Bu1C832frJacMRCBAdNfM/zDdv+wF4DTnOGsc6D5UHLLksfGT9gfvM3P9/dQcMO+qgJ+c6ae7XJ3GmjQI4S3ZSClhkcinXC1DAVinIFkbzINt3q8TorsmTZVaUeOAdKd8Qcv8YZEjVsmS8TlbAuLfs6hutwOg3ah++hRePHD5KPES/o/cqtr9Ic0DbIbrpNn0cw3T/c0WS+j++SklHKYtwqX7VWC4q8yiO5w0gQzjJ/UUeqW/NWuyp8iAXk0PBwT75Ew/3aU+0yxSy1ouNbeslJOuhhfdTVXlSHRfNTBpjYuP983zkyz/apTuo03pftAO0n93g7LjJlTGnFW7uYzJYoBb8lhzus9sLnRPcwMu4RV8W9jzg5LVfkgiFnBYSxYs3eW7gdcCK9P9QLgJuivHwyWbzIrLrMgPBSC+WLBPDqY7NC8xU8xWy+jTvQjV1sAelJAr3WENqsmKtAHTHayz1uVrt4KUaqN0b9yBlkZBVuM4cRmayd/QRod9C9dZI1v2+K37yIXu0CJy1jXe46kkmRLK33XpS3ueux8AIPkXH7rfGTJ91pH0PhN9kuoOMs1r8BFPXi8bmO72JGlm5HhSRxPQiehrnoaHRndVDVDDQxq7ww+OSvf7Sc5gpzq+yPXVq9NfWXT9+rPeLDp8Dd2LVy9EcH/2DKr4NoTDT++0J/W+mwXcF/nt/6EwTffvuz342bu3HVuNJE4bwsDn6LPacQ4lBUx3SToPhdrgGp8jTR2m3tEuhuWYMEvvPuSb3mxWgwcK4Oy9eRjTfSbSXaq0Ct0t9zzS1qB2ZeKQT3ym0v04oMXfLkqROO8qhVJndgN+LPU58d0Q3SvSEVcjqVTKkM8+yxgXikdH7xgZ/vDwti8QyS0noIGdZy6lIfgF2yvvLaUJS9jI+iWAKU47Oa4OCpjuIfVjfOgOgubu7TdxVvu59aacjlpzfVPNM7PognEo573CdDdG9waz5ZCPvMH6omrSIQvoXpTKke7IVAY5KFlKd6QjojQ8vQxFjaPRfbJzDwARWmVo+RyKfQeampqGzGvB9/WuOc1sdB9saoLhA5yDI06hXcO/3YCbTmY9U3S/haINr/va1HQJzb2Xq/beC5SAQ4/gHi/4MuATAC08V5uke1BEHNfvI1S6H/MDkXzOH1xzZS/wiE17b/y0h16zTaG75xxYa97P/1hxMAgtx3Q3QndLituiUSrbFRizRStZOmKC7gYbxqQ76clFOihZSndVZ5L6GRhqhs38xhHorvyW6ekW1KLl+Eh7SAhSnXiFhITcbWvrGOHfgvHudSGxnaO6dFf2FYaEOAHnRc/a0Pxx8EGiGCzsHudF96Efga7ALRg20SUg5KQ6bsnQvRCyvSG5TQBsvxwXErJNr+TE2zQa2539y9o4p+MWKt0zAV+6PzmLwnFulht9eh5yiDbw47RvjnnGL1XwB3h1Jaa7/dDdIJWVOuoUi+meb50s3vQIM1PbLUKj+/i6EDDvFqM3S0p2qhiYumVLjlmJTd/+4bynRpfuYzfmokrDK6n3Ltl8mJB1uU5BU3Qnxq4mUW2bfalEG9X8GZzSR5WUlNSOwwMH75WU6E9P21cF0OgefqaD+7cRKN0vJIKkizzpTlqRgm35pUaen2/rJVdN5kGd3BF4xKysiC0XkKMDprtt6D5VcW55091Awxh0h/oTudziLN5FqSr3pV51bJleB/RmercLgE2HD0LCynTn5z+2+6kx6LLmMJT3fBtxCXisf8eg+9yzuUjnc1Sq9nQ/D7fWlPGlOzHwWEpKCd1aBtJ9JZnDA9J9mYxl1e7i4Rwa21dK77Xz+DICpbubGOwe51MA0n2yOhnGapY4z6sxHM1fUeYabvKGK38kOd9g2f/6hVoMaG4U4ysCwfpPmO42oftURULkTXcDDaPRHapltNF1LOrDmeS9ZC7dJ2pSvJxd3Zctuzeu25mTVdvcNDoMVyi7a3g24tFi4MwIBbx92WMXJ+A7v3WUAtL4D+iztLiUSae+qvBwqD/JqzdihK4cHyVlXMGk+9lxFd2P63wdRf2rV68iXV20cF/4YHSMT8g0gdIdRuU6wasAae/+kvrhXvS9zeDaaWV0YJnJn42mNU5ndRZoh1tbWz01vbzL4MDbDEBc16TwnhxM9+mkO8NyxqI+JGawcI4ArPg8D+ZmGhubZJtgRTDNS5bxbMRkNwAXGHQXo/weyzUa396tcO2zT+fS7xLAsXo4tdzFNwwhpDs1eiDdT+kcG9/t4uLC+DZtPMkiSLqPtTiBM4P86f4hhXon84++32jAWWCsy8nHZCqXyd75obmMYEB9lwMDA8Wm6T653xNI1rYJ78mxe7r3TlmcW2vTPQrZt8gtzuKN/KqkMzqDNve8qmNtjY1NBo79PuBK4+Hhdr6tUHxcHbhPpdueaIiKgnM634uN7Rp9QLgHjPero0J5Fuxc0YviYm03ZZKnHB8eHl4RFZ1O2TQWB0mqSIfX4kjgck57FjypLCES+S25us9pbGw8IwEu7ivfM+A+TMo4zFwxPKa0I7rXr6NF3OFB98Gf6l/siIQbhs4EoNp0dXWb/RnvDjdCGb+hBumu/A2tYue3CO/JsXu6T53wozsKgGOc7rpBj81slo/PjFbL8KK7UXm/j/akXuRffvDRgrhc1ZR8D1nJhe8MfoDYIzqv/yUoAjAnuk8+OXYM2gP63aR8eWCkesp8pgB4bNGaug/Bk9ZS0/YD527CHTclLhvPlTFtPY4fQ1JJ9BUfezRmP3RX1kSbR3cYemyR+rb6xe5in/2/TQ7nsDy3B2zTPobzY6HKJ0ZWvwFWW1cPxUgipo5DwC3SmqmaMd0FTXfDDkr0zNdKq9CdmNliJboTrWs1RiabnptTQekCl/voLenZRtKBKYN2qKEYhXYvZKzsKT/vCVjbSnStCwKLjKBl+G1xcfHdxbD82szDqn00ugdovvqL4qtk48WpmZmZ1FvE26ydest5pCphZdnIpXiQOWQ/dO/P8gUbq/mVUdG9f7X2Zzsil/VBalvE1KuxS+XKOSc1G5DtyeeLuonni4F7YbeJkshb4fhPTHdMd1UuKitl8TYQnQbTXX9+/C3bR8WAcrNeo0dv+/gW9dXUzCV1PFtpJohNJ71hI2P8PtIpUJ0ZkvNtklBULwLO3obuXk3N85XeUFyAZ9y3fvXEs9BrTq+K7svJ2AStNTU1872RSsYnYd6D/v5+ahF1rL9fb7UweS5MKvXq99s0X7uie6sZ8TFVdB8tjqK9lrE+SINFQRzoTnxYK7lJ/ax234bL8NuplyEAEk15On2EBrLOj4T25GC6TwvdzY9n74BiLbrDdbtVKgJE3zGrghJf8fXK2FhKN0IPXrIvEO7YUegfQ+dTrPeqFqQaaVhmONLU1tjYSA+qTfMqtHqUwkWvKV16geQXSfxzsbGxlNXP2mq5cdf7+vprAHy+nfZyoaPQXTlxUoN3/2WsD5JyYm42h3j/iiIQTy2/1kFXhigqnEXxHBBxw8S6taIarp0fFdrCKqY7prvD0B2CNk9lAjFrrznFe76AiGjS6780RUP3W2lpcJoMvE63lAcxFMcAbKEuapDuP7PV9nZOhz79pBnpd6ijrXTAnM9F8AJB5Fm+nz59+mXSPuYKjDU5JyxorN7guQKk++BHeFOemEd3KKdV/eiWbcjqJpmuUzcoj2dFVqBOU1TGao2VYFRnYMrDuR5mWQV3Md0dh+5Rqez1FKViuk8P3Ym329Wzd1k3/9LND8iy6TlHfq2g6N5WVqRS+u6vJr4elGzWuKQ33gdpN8lPnZfgzLK4kaW+qiT1lHPHO4OzyaK11KR0XU5OLqdWkqvH8QeNnCFAut+Dau62UZ6FtHS/Gkz9/G3rN2T3v8EnvcP0MzbaEhn0Ga5SD8H852q6957hQPeJVwsAyO8R1pOD6W5DuhvIxgHj/WalYrpPC90JIgkJNE2PvVfL+0W6xJdkCHx3J+leW1t7NQQEJcV6qCfnHmBeA8WB9rOeyY/V5aCfkweL1mHwbqwqcm886+VGGmprv1BnhCRlcV5eQXSPLiTsi+7XYaMneE/4NXTvukF20+7fBh+jxizvgxwcYRWymFg42AZRbadovxwmoxMNy+Fduozp7uh0R4Fl8jHdp4nuHUgSvIDELyiXZ26+vgJvGt031gcFBfk4heb/vhcPPMPJM2Z7uSx9Ts5AT4eEa+OVsdK9uflh8Cy4PisJDN/FkrGipbm5cnlQEFToe4eHhxd09HJmH6J7xaB90V15Dcx+zvsRoOVmGr7lBcTAb5fhOg6DDVzeDeqTwA1oRC/W0F15DE4FKtSvBEqFUqlQKKjLKKgN1RYskqcQ1JOD6T7VdIdqmbx6ZDOD6T4tdCfl5Xoy8tZGfqXuJjrT6B66kty429gIs3esfkae8WId8F5AhgDOW1SqLchK9/WrU2KuwNQb/ieffWUh9x+rVy+gTHwynj17xie3BKL7Z8K+6P58GZjL3/aLnnnvhY9bTjRYbfgxerc5OpfDQ9Z7z2M5jEV3MEhN90epdJuZ0kNPeg8dOkTFGzt0qOoj3DhCrdfmzwHJBZju1qT71GUg4kN3dSpw/SPQywnG+8V69+mlO/H5IOKm5NA37kX6r5MRwebmBW/YsWNzCKUxiTs3JEO/FHtUJx1AkcQeE33X4rfSLFveZUokix8yaLZjh9OmW7Kep+s9HrJYZ77ZsYOykFly69YtnpELd84GkSe67Izuh4CldG+UXmhcAaIeGJ6f3+MQCBjJpbkLZMRPeLMXPUWbMFqbx01Kod5x9WT8ilP70dLLZ6L35Emw4dQKNIyo0HHj0A0i6O6ggJ4cHAHYJnRXJ5xindNjm5npp/vk11Wr4DpewIlGriUmiufDV+9VYfNv/OHj7CyhbG/CjrcqT8D1t6TrNLpLjkzcS4u7SLNGnLzpApz2aUfS8+dZoStXl09MKCfKtkzovM23vnj+fLczekvwTF11fWJigufbvosYpNUo7Yvu3zcA1wO8g0Mw6K6EvXkiWrzWsLno67liTg/ZxA7xdqJlnzMQr4JvTc+Wg9A/JsmCowWzJIlndkq8FgOnq79vSSRr3u4Re6S5OR0m4wtP5MOf/CXtAnpyMN2nlO4oVK8c03366U7WC9dWwZkJjh3fj7xEnRV7wKIfCWpLFwm0qxyHYeUlmhfIPIh6cLATSJjra7ehfn23Gh5jo0Dispndr105MXadUv84u7ikfDbna4mBeLEJ027B0T0LgFAzitHpTkph0KJaw/fzkUszJ6ucE74bYLSiFLW1qu9x1f426KD8JBdI1v8Wg8JC5DjVudV7JcrecZs64bAfSPmA6e4odJfJddUyFNQx3QVA984zcJHUZxe3pdWx3zBy1+avijz3+Z+oVH7O3kFXeiYG07xBTKkmeljvPZQFKizoFjP2S3Ggiu6T/f3ZsUkRN5vZAsYO9vd/3RKOAtq6eHtXNze3j/H/UuMDYrC0fdxB6T78wMXfGN0TOf1eDh5xjYDODXnRlFxQKVv63yGjzVwQ1jcpBsePA9dwxS63Hb00ug+eBM5+mO6OQncdhyYN1DHdBUB34ivKqhO1g9O5b2FqkLWVo8q3WcFbqYDi8y5eryfqz0BryHjafO0leSz0KbN03TUV3Vv2749YWHDrF+s1zu/fn0mFJVxYUDBi3nf6Bi081po6acbSnXhmTLf+yCWU28z6LPCEfzvqKFEbsZdCt4VxIheEo/ejwEAQX6nIAAcIGt2JC4a9kjHdZzbdSSemhl5Md6HQnRjLieD4OJanAzK+O6Q7NGLZvw2ApQ+RocsLWEGAlBZ1WL7JH57pvUN3KRSGiH06cKfgoN/G/Y9ZryAvKAikFmr37jdwChcp87dDukMD1S2NZpTTp/vQTc/U94YepcEG57B6LvX2nndeU6dXCzKpH1ccEEcpJ8lVl3lNigzxQUh3p8tqZX8vzHSe8ArT3f7oriuGYw3Q6U7Ddz4V8tdUWSxTRnfl7zzoqVLVZfrMNS7AOfoBQXzKgBr063XfXWPLRuGd7LocDEK3DdO0LJNvEpGC3u1g46QO3Z2XlofPXvpH1aC+7renuqrqrKcnZIZrXOqZvsHBMbO/0ptVqamH7I3utFUJC+lOPPd222D4hwKAr5wq/nnOL3OYle4lSWlFrflATfcNbyHdJdp0izXwFpZjujsm3dVzfUx3QdCdmOzZC3UCHIJXLYFtuA31r6HILTXwYnP4ffLhv+8vAYeZPw6fyUzawHv/gA5XgGuQ05HWTjZwl88ODaXcYCNLWvsseosbaW9tNekPP4Pp3ngRgNcGCxya9ZVjzQD0sNI9Exq/VkeDjamI7sfirhPdWd7ntS8EHTmekg3fhPLkYLpPGd3VmZgw3YVDdzj7vuANgg6YmsptcQeeDYOXZs8WH/95NwpmOv2F7B1Hj6PgXucINroDur07UY4Cyiyo/MnG3Y69s0OcyCJPf/78NTwVPSosug+8dQaxN6xEd+XkCv+zvwwVaJ5/pYnbj+QizwctBug+cil4zZubsyHdncTXm6/7LZ3U2qwq3wQDp4eY7jOa7sg4BulhoOOSSrQJsjHdhUR3ohSukcY/Npq9sfVgGEg8UFCwNHrHgY9EY77fchQMsP7aBZTRM/sl8+SWi6Sj04JizbJo/5OCLchQchWLw+mjgoJTs5EqZ8n+/fs7p6pHhUX3r7GAS2oNFqle/ET/RadnOThr8E4u4JqVC3oz3SI/NGh+pUtjw52/rwMZL10jIc4fRMZXAnDiqEtGO7NJAEi7BfLkYLrbhO408ximWgbTXWh0f4tcTeNvG3ExbESWEJueusxZco46KwGEj3x7c4gK896qdz7MA+cSr1HF/n5zLwkELWah+683b97MJusIXLj82VT26Eyhu78zC937trvvMxQfruMPF450/5XudBq+aY01RzxQ7xrt/rjC3xUEz09HNvUjtfHzocVV8sp+xgLLeA/0QjvwWxhPDqb71NCdliAb011QdB/rifEGzj4yg8rqX/ugWXxo0oIFj7sHqFfwdL+Q12sCPIEYmsWBt3rT/syYKP/zFF9GmuVHAwIjYg626tJ9sFG+JyAgQAKcYmJi9jV1j05lj84UugPAQvfJtlTfvQbWLiZaYznSfey3d8BVaMm0RlxE3wnfwbY2tJDuBOMNDTAUTcNv/UYBn02Y7o5Dd61aBtNdaHSHUWCQtWOSwcynq5Cm5fK7d1Ua/tfkuKagAF+uh3MBSH2gW+Dbu6cus6kYYl+zFs0CoRffNSh06f5+/SIqVI3Xu3fv6iemtkcFRffuWc7gfJ9ZRWvYNDMEsVycPmloaTrR/zjHVevGjX7HusPdvzBWx51pi+jfl4kvscQ9+LYcLrhiujsO3RnxfjHdBUZ3ohaFFIvdY+AodEiPOMewizlMOqsuuv+4+Yb+qiqpHABIvau4vXmxF1hf+hwVvrdQS3fF5s2b08jcrOB06ZNp6FFB0b0DmJ3UiGVVFcnj5ZG3Db0LJYIcrjZJO8DsnUGHmTZOzkAbYuJzhLiEpdjoekz3GUH3hl5OdKepZTDdBUh3RdUCiPBZrMc6K2GwxuTPWiK0P3mCXKBAYuGoQlmZ6g626qdVGloRmPXkSfnK0PXp6Q+p8N+DmSDpBkTOwHt4QAwFZsdLT0+vU0xHRPAZTneY5zrSULDfOwviH8IuL/houvYXS4F7kc4CKQe6T5QngODbgggVae90h8Yp00h3UzN7rVerjk8qpruQ6A4f1MUSENzDEp1l+B40enReqbGSVg7eovKgelMKGeSrOle/WCvKlhcQsJMG/Ey4p22o63UKWd4d6txvTVuPCo3ua95Yl+4PkoGTAbpP5oItUA+WsN10Du2vm4GfroZnw1ptxPGGnevYAhsoFVuhJ3MHprvldJ/GzB+Y7jOH7mMdc4DTfJlubBfFwAV/J+CxplPF/bGezoPQgNI3wDe0kNLCv0lxAgm9ej8L7Zlwxt/S0qND928nw4JcSO4faWlpmb7pnZDo3vcGAHOXlA3RnSgHoH6IvUwe2ATpPgfsNKWgqd8AfdJ+mdO0o4Eg+Y0Qnhx7p3tDA7eY/0WpVm42GTSGE91RMiY5prug6U4Q0AfJc4WujmX4FnJN2vRCvf1lfzbKhHqqKN9zBTVta3vkC/xO6nnPDL9aoRO/hqT75njK06moqHZae1RIdL/nawO6vw4Vx75nL3MhaCWctq/z3dRmAu8xrv5xsfMqJs1o1gng7IvpbjnduV9liputoTvKkS1TYroLnO43kEW6rsNkbwbcefiT6pktO7MJJUwK29lJNGvDAsKgjgE5cpYpIgvd0bR924kTJ6e7R4VE95vABnQfvukRYCCYV895jwgl0ZrtdcDEiocf2NdY7RJqzhtWvkBCRWK625ruTLUMprtA6T56Zx5Mu9HAnKk9XQof007KXHHi8VJ3qFWJXLS3TkGn+6ZQIHZ9qlff9RgJY/vFCjKT66Ls6uHh4enuUYHR3dncoGkG6U4883MKqTbw1k0GCc4Fm4z9pijr1rqe6yV6nUG3GcvefaUwVORrTPepo3tq0XTQXVctg+kuULoTYz8BcNvD1Lx7oTRJqsnbgCeKJgAtnIfgLwCN7oPInFI/LODoLW/9qsBJsvS0i7DoHnLc3D4xTPdmuPj93jjdo/YYUc2MZvjlw0zZo0eDdlSZ0bDPcN1cNv332XHobmWacqR7Pnscd0x3wdGdaIW5Ur2itFlMJ+9DHbt4xXsFoRgfh/6n0FBm7WdV1JGJl/Nvqs0pUF7VMn0+PfCORR5NE+Pjv7KgOyoKJfO6oVcYPSogur9YBhLrzS28L4JJ91t5RUoiLy8PKWUM0v3HH+Jzv4m3cM30fIuhiqv3BR4kp/bf5wBzZoUduzwl675P+33GdMd0x3SnJue7kR37Bc0zWY6sGlMfQFfF3+fOkSbuS0o1U/tfK9KfqRxMX2VD7/SXLHR3ugn/3T53LjeS1Lgn3esTSo8KiO7HxRbQ3YkRiUAmS3JKfiJzcnLa+oUgVvqfZTe4UJZIIqoIBXREizKUh69hn8u+JrLm3/slexv4N0z5OgiIH037fcZ0tyndmX5MmO5TSffeN+V1vAp0noE51NzuqDfh5M45+T5BVJSfIjNkr19Pcyv9tQLkqPW2MGMD0Hd0ff+HeGd5eXkYcF+/PgxVsFs4PSoguh8FFtCdHmdm8Af0KU6IoNaulzRNdi1j8yJGUiYJ/0Tq+0OK2RX+bXt852s2vA1HnDQib6GbRBmm+0ymexY9vAym+9TSffBhyrzbvEpMDh4PEbuepuJ/jTYtg8nyykYG60N9USyC+LTeXtoyXMsuHw3d66LcwRa91/CuD8DdNyw1MX5lLzK9EYecw3RnpbtkY7O5heM8NXQfKgp3Cntedx6AGJhgxXnrEKT7vlbWUpUJwffHEN2dvFmzOMmz3TK0KrRUn33t/Fv2BZpgXeqa7vuM6W5DurMkT8V0nyq6v4t2K+b7WLaechWHnSE/Nu6AkSG/9xHvVpKZNW7WMhPujDWma+g+UpoI/JN063oBAwGDuY9qa38SBNTduJ1uxXRnpXtA+7i5hX8s1dD9faDY++5IQQAANQtgx68dhHT3YQ8VOfxbEtRAWmICVqVLiifIpv2Ob/I5xr9lozAoqP/F6b7PDkJ3qCGZFrrrqWUw3aeK7jIAvvAudNcdgO3oQ9N8FARyMH9FIoz2lVhZqb8cuj1kmfrj9wU69s1DK1asiIeLrYuqkcNk21EYDfJVu4B6VDh0P+oDgswv3b1aTfdrMD9u8EviFFhUAyMAI7pPtiWDTUpDGp0fxG1kxDRLP+micjxAso+eR2WXU445FpsuYnBsuu+zg9AdXSNbNpXNpuiuVGK6Tw/daw/6rWjifal32wBY/A4i+Rupvr2dhv4msOpUtmuB3noK4vuJZm7+puQ2LLRly+aI1LdwTXbo8hyBOLcIkO45wBK6b5+lpvtp2MV3WiHdV0GjpqWI7gSx0Cjd63LQvS3QO9Z53i2DMS14uzLusBltuxKP6T6FdLfuVTDdBU33hj88tsjNuRhKmvdyokcGVOIREX2HMEF3goBBX/3IRbRuGBojBThFR0M7usmdYDFc121EQdyjMN1tQPf82Sq634bTdWjFfmMene6PlkUVsSt9Tsz64x1RIkZhnMt1fgDGM/1P/2DuOg4CzWjb8DqQXIjpbhF3U1M5BZCZHrrr+jFhuk8R3UfaQ0O2dpuVEiPYHXgl1J4IINEu9g3Z+rWNPRzVIR9dug+2tbXlhYQnRYbEtaFCk0d8Id0HP8BcPbubBNWjQqL7rBzzSw+ovZmQ8Sqk+woQeHZYQ3flUZDO7hbclCa+QtEdrGZ6tLaUeC3p0wH+w0TvN/zjEUC6gwXCpzuTTfUyrbBPjqD/xsTkpEKpZNSgUAwPDAwODY2Oj9M7b2zkrA4mJycnR4aHB/q16Qq1UGSFqHDpLjXYn2wLrtz63/T5mO5EVQ7I/mTexe4vBgmFWbGqifv+R59GDJxYs9tZh+5PNm3aFAUi8x89onSAytoDkO6PVkJjyJpJQfWoYOheuxbstKC4xld1DXw9SkR0X422lwLvgwjrx8A6dro3p8Ew7S+pWMwZDLXMSfEm/ZXWmyCxjnfbEN3n2xvdpT5aYafXxNjY+MSEDt0VCsVgX1//wMDI2Bg9cMPosB7dJyaGBwf7ensnMN0x3c2je5k/MPeleKLy4rnDXuRzn3bxmjHlzh1X7een6cB1DVxbPXfx4gOaHZy8rPcSUt3fEViPCobu4S4W0b1qkZbuS6F1I0n3yeYUsHoQ7S8MW8y+sN6e6XqZGOsl7/Iqmi1r+7HQ5H79H+JHsWbQfXS/F0hsnpjW+8yD7kWpSKIw3aeZ7ql6gunOlMbjXsvMXUJXTjSdnUU+9vFXRsYmjdL9jSpFw1D1813Q3Slq2bJ+OPZpw3tyXDFXAtySKjHd2QV6ElhC9xBXLd1X9qno3rvVBawndw9cdwthfawmu2JQiiXyNruFak857r2xjW0aXmsG3ZU9a4DLlm67oDtUyGT56Ao7vRSkWkbJBPb4+PikAokOxlQvA5PooJL+W6AWE5NUTsyWy2YM3aE+TPcupGVjujPlpBMYNz+h3R0nSi1TqjD+enTH1ese9enHIgnS4R6ZmNAvASO6R1cqBNajAqK7ZJ8Fxd2ctHR3j1CMLQOrJ0cj3FzyVD+7ZWTAMDaZ43dCSagWzlWnKMYWem3vZD270yXMjCDFm+ALRadd0F3qwyLG6E7o0J05ZdfF5MTEpEL3YbIe3dWNnwF053wXHJbuyt+7AtKrLdBbDd6Bc/fYxsYhU78Cru53J2A4X2nkLB93d2gonzemd9XPK51BWMuI0HpUQHRP/2BB8YJ4Ld0BGCoMAat/HAAgV50bxQjdUW4mJt07z3uAQ+xndwJgxj20G7prFDLyPPS3Xg6lwUDEO0x3m9GdTAiF6W5UxvdFL3tiEU9fwnCQCRzm+JDuX44ePZoGAneePw9d4NMe6FlWvI2DEeGF16MCoXv7eWdw3pIKdoWr6F6xClJ6OwznM2uNi8cejXalcYfz8V+sJR8uVtF9YeFV1ZMnnws2GViKHzkcuIu/a9yLNSAkZ1rvMye616u0AVlZWUpSQSOr576qB2E/Njo6NKQNbA3VNH1dSIaR/YyUsguHvwDQWoZe6VBfH7SxGaO97sKL6pzDj+4yufU6bjroTinHskihdDJIZMQMF350HwFmhX0yh+4uOTDh0qasrBOIIJAU63VTJTcfDgYJh4XXowKhOwyvaxndxeooYsqyDRs2kBPxwLXZX7XAeOIe/Jb9ocpd/kUJy0Su+qxWzBRErKo08BAqv8aBu7xbpzw33V5snOiupqNWOZDPi+6jIyNDg4Nauo+NdbcjGUITei3dJ5h6y4GeHrgKS7egVJKnmU93a05zp4PuunfBQSzmedG966MkwsI8LZ/XO4PoOuOKmbFfNSddnOIWzp3b0N9PDm19uitbLno4gUODwutRodB9toV0B4wIwMneICT1IOO+ydyD2OkOs3dsQcqE/WqLyJ4PbnMMR/36lSHmT3fCnuiu9s1Bn6NSMd2nmu6UWoZ5FzDddaU4yr/QwhwZw83BwGVNtdFzWnKiA8Vu+dAzdUJDGl26K04GoXRMAuzRmUL3OV6M+O4p4HDvoJJJd7/b7Fq6iyEMundf8F1TZXjxe3LA7Qx/8xe7oLtKIaBO/ZyVRvGY4xUmx8ehhWN/X19Ha2tHZ2fL7981nz5VPH78RCarrqvrGz1H6d0HenvbWlqaGhubmppayDNbW1o6urqGRkYUTCWPwkHpns+8C6lTElvT3uieO8ulxvIESHBZdc57w4czU1MTYQRJ8IX+wL9Yqkv3ecjh9X6rAHt0ptC9YRmd7kEu4JTOCTJ3J79a1qIDUgbdb/k4dxkNVenmfW1m0l03ZIqUF90n1HRvJbHd2NDw8fXr0uLihyUlH79+7aF8VaEmvrv7d2NjfV1dfX19I3nm7+bm9s7OQUx3Ot21p+djuutJb8XsOGskyTiSAIIP/WY/1nz7dijw3BQMorIY+3s2gcSLE0y9AQja0CbEHhUG3ZWf48B5i/JVMfOqQq8x3dqGmwAwkBf1pkckLNtzAv0bORG0udH4pfwkZ3hHiuwrAWB4Or2UBUL3eTcdmu6kT1KacbpTZkuY7kZkqHhO9CWrXPI4JPNjll+Pr9XV0DhmdvLK8nmzzo7p0h0a5dHOrYXbi+sE2aPCoPtgujewbIlEl+4sXmOG6U6ZQhaif0dil783cal78+cW827fR5i065sd0J2eY4gn3R//GC6pgXR/L5NVPHv25PHjm4WFp48dO3v+fElFxY+mIyR3TzbJ5dVVVW9fv3758uXr16/fvX9fr6L7tyeW0l2WnQ21SalWNS/hQnf267HQXWXSQ0kDO911f2Mx3fXks5/zQ+usYV6GIX2v9TCGuAKqDG/GBAV5u4a876zxd7k0oDRK93KYKNtj6y9Md4PSDTtMCHTvyvcEuSZxlgV2mUN3j6d2QHep0my6+5wf9jkD6f66tPTR48clDx4UXLhwLC/vxOnTxeXltQ2HSGqd+FVX9/nDh5cvXjx/9uz5ixcvX72qU9H9rI+ldCemLTcTL7obeMHAdOdK9/esz7c58usazNlxjTHShleuXJmAMj7MuT5INMPY7zpFdOn+AGrmF34ZEmSPzhS6F8+l033jRpZ58hr/c+x20C/nqen+KwUk3DOJs2sxDkF3tYqAK91/dlhE93mRVqD71Odmor5XqgGhLF4YmxpR7U9joTs9pDCmu648XhN2xFpqbpS9Yw9tpF3aDk3bN9yGaTnmPusjnm0OOKD7ijX6Jp1O90eLXcR/vBFoj84UujMtIlmlYzHIZz9SIq6GL3qPo0FJ7NzHHC52ZF013/b9mO1sb3QnqZXFyyIys2xwcPD7p09VVVXv376tKC9/UFxcVl7++fv3rsEzqL7MR/29ve1tbVDXDgUq3ds7oL1MV19//+i2bVk0zulYTRLQm4dLI6xvHW6K7rJsHwtFraWhdbtU17MJ010rrzb57/9prYguzQt9wOoK6nP9s2fPkiRuq1eXTUwAsHFS+WGb5/Zq3SspJ89CXb1qKXa0eqMTcLo2KdAeFQzd4y3TlVpI96Qa6LhwCwTE/eSyYHrEZTbf9k088Xe/MmB3dDfHm6muurqmpqbq48fKZ88el5VVPH/+VS7vU9vMDA0M9HR1dbRDrHd0dXf39vX1cLF35yhTT3cfq4jUIN2tH1vBvuk+OerrvNyKF/2xiDRnmxgZGdkPxK5ubiiF0OQIcP5DMRoviWMrAtdbwRXqYytKJ+FRJNQeFQzdG0ctqsFCukd8hv8egvAXnH6Fj4AQ3g18HQi8nwuf7sh9ieZTY290R3qSqaQ71UuHoLOLHP5XaZ94CSpLRfJRMp3IaJuHGjDd1fJmgfhwh7Xp3td3OTw8cZbPggr4QgmDHJQk+krbXi933tNqnO7KnyuBs3fzoFB7VBB0L4VeBRb2EAe6d65yOsX+EzLUGInoXuYR8Y7TG1/v6eARvq+GkO6gXNh0V7svaZdUSZ8atQpCnaQJ/oexdmWyJzAUDDNzE3RogvryMVIg5iHFOzs7e6HWZXxcoV6jRRHDJrUCt5DvKvmB0RjzslYgPckU0p1Sy1AmM0h3JMumiSZKTJZG6OF8VSKjf2Wt+5ImQ5a+SY72LhAo6DH115qhdQRN94owYNUbTNJ9716Yr/Pi1auPKB912XLXaz++rvcFxwnjdB/ZFg7mXhBujwqC7rfAVNB9pDIy6YaBk0i6N9/1XM3NDfWG2ym+8wc7oLsawHSDGS1lNUoPRDt1sHamJoQeI5Iyf4einpQbxCSnGJHC1MwYVZsYtZmRsp+v683EtqSqvQtk81SNnAGxaLjQ/et2n51WXcMk6e668sCBA2qd7FDFkuidZFTZrc+N070WOSlu7cd0FwDdoUUFyDBwktfaTqoWbllvb4AkvnMlu6E7NONA6ZmiNJYbNKUHDHhC6iIo5s277bh0R5mS1GoZHnTPIyMqN7AGVWbQPbVIqb4LDTrX1d4F8oTUIhtYCgmU7pO/8oLnto1b7Yq1nz7dT4Tw8bkDB6pq/E0+XRF1tF3ZfNYz4Rv7IlxxtDNF9wIPGIr21JBwexTTXVW8gQfdv+fwp/vPXcKnuzotEzPgDEMNIZNmq1QQUI2zrRwaumQxdAsKdeTeCVJLM04GdIefR6jMe8PDo2S+PqiKGSdPgImzFUy82QPdySRQdLUMR7rTNV0G6a7uffV/xkmw86lLa+9CtgzpeWZAfGDTdB/c57XsixUTIM0LDvZHpu2+JbRrBLoe71MojvmkvjGQLHOoKICi+wVY9ESfQrg9KhC6e6RYmNfEQrqnenKk+/hbKBkARN1T8G/i6WZh053pbqMfF4XBTlU2Dv28qlq6j41RCvVxpIYnLSIHB0egYn4c8R3uRKuwQ0N2SHdaBivT/WluBGD1XTCqDpLOoMQepuke47Wt1WB+YtncOK2cMf14Po6LcwYx9fXLGXS/B11PoSY91mfFb4Pmc+VBIGA7QWwLAIHXeoXcowKh++xPFr6XW0j3r8kquj81onj/Vltb+xo9TK4AOHmO82+i+zmh011OE0x303Q3Zs1iPt2Zd4HtO2quS7akQdCIsSLdYbI1A0cGnlzOcAFa2WXc+K3u6uXLmwHIyb1IEHeXAPc/PqqPXAIea9803ABL7hkuDekOlnc+jAQg9Kmge1QgdI//aWEVFtK9aZ6K7r5GbFcj/f39fTXjxwy6G1iDFwjdObFTqwGQUkFpTLBK81lBqpNJ/TpH2gmX7loPJumUt4flLsyUbNqm6N7+WjL7BuuR36+KkwFDjNB99NWrV3muTnHLli2jTGSuw1TYR+D/X/DAq52SLZ+IEl/xdcIE3T/PBUCSUYXpbkKu+E8J3QcH67M9IpDcYqF7KPqtfhMPruphCi0NXkDF4CBw9iDHDvrXO+GIdGdgjxe3pFPhlTM1dOee69RGdDf/Ltgx3dulQckPWJcwfx/393UOjIGC0mj4oQ+nDWlmfsvf+fvHp8Qm3O3u7p7U0H172wRxCs7e/EOTe8e6L3nHlZige1rpbOCT0jsm6B4VAt1PgCmhe2Zm5mzqh/0CC91BAfr1TtGn+ygslxmvmhIsvkr+W1IALaE+YrpPHd2RjYpA6E5PaT1NdE8tojVvxmRuMkH305Ggil1vugP6y4DcD1COwA856EOjIRpsX5ACQN6HD5+06dcQ3UOOdRN56NHeDGfjN2IkHzpM0N07wQNsqRJ4jzoQ3TVvbSf0Lzb4LJCN7rnQMmGrqlTomTt31kRvQR83VLXBv8W8m2jfdKcMReQ07QQvQw3L6M6x7FTQnbakarIDbER3ndUPR6B72+nQpezzafkhHwACjpL2EHfgQ3bG4AWKNm3a5AP8ysqYthNNj2Cp9LZt0ejZjs7qvRCTdsdoQxHdkRwSeo86It1ZQ4BFZ9Yoic4THmq61z+A4qUqkbJ169ajrcSXdPLXfetTom+lJ9jF0ygSpnmxa7ozzTN4xz+ZiXSfhvY4Kt3rl4Id7GqQj8hiPfw5+fi/mQ9n1K+1x2AgO5qsEovhNN3v8eNypjxGj/htd+pZ97g9D2zp4UL3BcVC71Fh0N1552/b0x1GgzNGd7APVRCxt0GpeA1XV7arTg6Ciy/LkM/a0OdXK6HGfdkycozVQsOpy/yaOLQWbK21X7pDlxk5GcUFqQWgduJQA+VQIyi6T0GcGSowMsfwL9ane1Eq/TumSnneBXul+8T7+d6H2Fe6PkK1qdM8lQPrKzgBj6f1P+Ar7jBJquduI/6niv6OIpRI1dmvSvA9KgC6t2wHfoOWxtDkQHf5Ai50d8up+ewNBVo9usbOnTv3eD+UcaKnpizR2xn4LevvV5pPd9e1dkp3GNUE5jxCqIO+M9ky5E0jIyi3GkHR3ebZO0j1lCpQjIxTs63YHhTVJ9uH+o5Ufif4gXIdnuF0H64KDbrVqzRI98D2UVa6xwRAcSan5AFGRAt3GOdA7H22x9CabH9XV0NOmJ8TPDOhYkzwPSoAuu93Bf4WV8ItRiQHugMXH2/VedHv+vr6hqnDxT6e6JZuUwfxNY/uYImd0l1FKaZSgp9yZmbQnWfqVuvSXdXh5HfUNMMh6C5LDzpsyBUQ0V0Ts1WH7iV3oZC2FBvuGhEt3Q+fzfDZZ1hNfDUra8ss6sx5NcLvUQHQHepApoTukx2JRuhet8ULWT1K4CsXmrrnw+QSqoAWk0P9eRF+0H/J+3KzRh831iYBvqccie7yXhXbkH6GVErwC04rtSiSrbDofqiBowOR9ekO+7C3AdrJUNGGYTOQCY10RoQINkz3q4v8rhr086bT/WumL4PuxKvTp09HzDt58uQHY1c+RBnThZ88eWqF6yX29bQrsKbTsaofgaMnT97qEH6POhDdkTeTYbofjFb/fC94CIWWBbftSEYE3B0mfchYaofve3schu6q1EgydZAZdcxbHlYzlnGXI91tHQHYVGwZ29Jd0+GaaMO874J90j1eEjOq4EL3YhcxmJWjPtJb9fYPt4AFSwtgag6j3iltKFcqiDjQ9SElYvWonpZ4Ug7Dj4S5QYHv74uR9I6MjCqE36OY7qRsy/RERwJO+YMVDDv2p5mZa9HSzKLiCp2VFoeiu3UwaXu629pmhq+l0MwJAjOtdI8CsYaL0emOLCKPaTyeXsR5uYDENwMmEwP1ZqCn/9xw7RKnvSzhDEd2e3l5iVWTvwEkSvvoUYei++nZ7HT/fZ/cPyvzUFMEWEmj+6PiDZSOLVM/QEFWBKa7g9HdRMhfTHeb0F3xfqX7gd/G6R48gWbSQ0dhmG3JOUIJgxyNR0dHB0s+/PjROIK2kBiuIhLN7Wr7FJ+SJYdpu2HBxmxYT5QXEEucnZ1nP4Sxm+2pRwVB95DNU0N34ggb3eWVR9DvcmxsBmJ2GMhUv49VVpIGVR5pK16wVZYJ1rzn08SRUwGY7jamO4qIazO6I7UMz1i7mO6W0/17lt+et4RxuntebYSfTiahPEvviJ7iM2fOUPrxM2dutz84Q4kxepAxyJt3Bv9RSdt968yZA5HUjD1i74kTJ6612FmPCoLu2yxPTGg+3X/meLsBl9jku9KtcGvwbDK1VtpZ/cHbG/k+JG+qHRhnp7tLAp8mKofXYLrbmO42XVU1A9WY7pbSXVG713+50QVM+UHkq3rs8WPklBSworPu8ZU4EL5+bSgIWrUhyu/Qr+VRGzZsiAlZY6iCpscU3X+c9FmiNpdRfoX1qaxjACx+tssee1QQdN9heSXm0z0VmcPOej0wXojoTowOUJHmC7xITTzYOjBkwBY/Ey6y82vkekx3O6c731i7mO6W0n38gPvCz0a9YSYGNifEiT19fX0TEkKTimsPBC+cm3Cip2mD/275+03zByaW7+7tqs1I/2Wg/O8zfrOREfSnXcGbP8HF14nf3759+5oN64NrqC7hCQkJvb29gwp77NHpp3uSx9TRva+AQfexvr6IcGdo4e7TCj0TCj3CVQFr+/rSwuF8AD6ZF5sN+yR354BZ/G76euC6rQ/T3V7prjIcwnSfSrqP7QBLTYX8aPhaSc7Evn495RmXGBj19evXVmV/RmbT+KKARQSxPJfoORiw2dCTfCgUvF0BS8f7pzSgmV3XwUQofqroUtdgZXbbo9NPd4jRKaM78ZBB9zebN6PtZaWlqGwhAKrEE5s3u8HdLqWlpUZTNeUC96O8jF7Xw7DQPZju9kp385qN6W4R3ZeFLKsZNll07OXLl3muy5dDs4k7Lz9RT/GPhs9bJdvhw17bMLooIOu7oVXVDWsqJ37kIBAsbdi3fPnyhf4U2OfchJV+tOvEKA5G95ZcZw3dj25JQTdRWlJNlfy1l6T78y0k8teUlJmqLBeAZF5L6JjumO5Y+ND9d5k45SaXskNvH+xycULR/rQK8vqDvhufoQ/yO64LDK+FF9yFj30+euZnn4lQO73Ais622n2POhjdiXJXFd3v3AlDdzE7u402sVcSj+6QMX43ZZeZrgvTferozlUrguk+k+jeJfWYw+FB/C2Xv1oIvKLjHzN2X/SIpAKHXBYvfGWiinxNLAIxSv4RMzN61NHoXrUB0b2tooJUqq1Zo2SobZ5WBKL7u2YNJwYXzRYC3X9UfEf/vlP/Zirdp+0qmO7TSPfjPuJ2E2qZ/tbW1mXBYclRoTsbGecqeqUZXxX9cCrffSG6Y3Sgx8gSmaKXsrdwDggNjWtHguluj3SfGATg7uezXjBy+5x5pwYGxuo+a+Q0QB5pgfPmDwxwWiwdvQhiH/HxWrM+3Ud/fM7w2os+7fPaUoPpzu8qRalIijDdhUr3vQCYKnQHmiv6AF9ov1jNtKwZLjj+aYQoPkkQZ45BtczDy0bMroeuUH6OkfmPHz+dQT3qaHRHZ7p5kNnTPw2NKYmWpR4aoXKq7x0a5nrRa0Dsxsdoxvp0l6d5SAAZV2M7kIRhulMxinnNy1FAY1Iw3QVG977bCXPPGy3x7URuIgjPu3xZP1MysSdmbm5u7txFbQVhSfBDymYjT95uGPEVnL98+WHnzOpRIdD9gBWIx4HuvZRoFGzB4VBCXJjB+9/95mGyeA0WsCXdlWv+//bO8ytq7evjaz0vfn/SGdoAMkjvgoiKUkRUELBhuSrIxYINLl5RLCNWrgV7F1HBhgVUUGkqSO+dGd49O8n0xkRmQpLZ37XuJSaZnMw5OZ852WefvUND/+6GezYbKGOio3UrQ/cDUuKNdGcHY52AxmY/hXSfK7qP30qMPm0+jcYUeLQc9clISznQND5uwh/GVeLk6uoalf/j8Nq0NM+4tFOD5q7UXgWxx3ySBuAyCnHVKB/oXmyDq1hB98xNtCynZvnJplC70x1CFgduhHt+ZuGkXIbuX7Yg3dUwjrdSEXp0Z/Yh3flC9y4Juagw36lHnZycJGRyasrMOUx/PqNQKqamBv0fTZm/1GUI+03WtynFV6OipvvQic06olt72R0tyXc80Nd+PtKd1mK4/X0t5ugeSkXGubJwdTnSnYnQOxtRNpompPuc0330YuiCG6aH2+PDw8M7omI8PAp+/DCP5B+0mLG/otWCtXXsnIS45XVNibBG55ru/Y/dbUv3qmtaQbwJSm5rczQqnaAQz2xXGlzjLlu6vwbP+Ks/bEb3tpujz7uVP6k779GnOyWfQvo7maA78ZyeMZ6Dg9BdZhPJke5zTvfSlR5XzHTGFwUFBaGJcrncNolNb68h0m1vRVmjc033bxDgzTZ0/+cJrWUMCxM2aJX11eCN7Yzpa1RvIOTyLzal/oKL3WZF98U3n5hVodv1RaefHKJfKJk9YcamI2r3NyO6K1+sifzP4emujtBrUtZgXXVqH9J9zukeR/xMnfO9rKxsLfHO2HXPRoX2P48lxPueOGtULHRfLpN6BsEy4pQVjPn09ZBW+mHAlnqaozvlLelxhU2prOg+1bQSkrd7eJqVlHg4uXtK6czszB4nY7r7JKSkXjGme1hk6Zij091y4qRsYyXItCmws7NNL5hCus8F3Ycbov3WGp/x6VOBl1fyimXbPs6ckcM6jT5IAqv7miqkO5/p3gOPRvKYVubN4T9XmKM7Pa6/ZDe6D2+SkNkr7N3Y2KQx3X3+s5hazCHozjZxklUpsJHuc0H3L+vd/jbxFh0RAcG9altafo/ZqszGYDfKHjuMdOcv3Sf6gqWe7m4hIdFPemfyVm9fSYqG54LuralEuraVlaI1UHedD5LDro5xg8v2HSYetSn1Mzyfc053ykHFbpyjfF3YJ04CcpswxSDd557u76OkZe0GXW3PsmVgdd1W+2nSlmXWU+Hba8Rao+Kg+9cssLv/BQ3lHL/+7sx0X3hROQd0T/cjm9+z+lo6s6orHoMvh8lZJuVJ4rxqXs80z+k+S86ZXW2kvjjbfNaMKcfK8T3SnVO6f9jnu0l/5P7lyrFIEpWTm/vQtkV+/hfMMnf54gv569aVK1fKYagxCn/fTCDdGb3ylRZ2Nh0j5NHj2MiNGzcqLdOd7DRzQmkEWXyDRVuPyP3JsudWngyM/pfd12Lo/pjSJ7N3BXQnQWfHRU53y4idYUXSLA1KSHeO6b6fJOjEVO+FICE5bsvj4k5P2rrE+mzoX494UwGv18b5kUW3hjufU/7as09YJw66dx3w3A9+MY1pbjfaLuWmEXLlSvsf0b0FYgIfZPNL/mkBIRetOrMDMnOnlLP7XsoTuaCZToKx+/H2mS4lZrozNhm2ZhmkO1/p/nOn++YGZtfwrx8/Lvr5LV+8uqura9DGY+zRtiXuxCWgkjcVMNbTlUNcvJ8c9w8PDz9sg7kAMdC9qdg3nW74+iz3wkcN9Zs2Zfj9++jR+wnb0b3xyyzp3lcEyb0e2+ORUJ4M2T7zWSKmu3YFkz04inTnnO7pwctrVAPXVxtTUxcRUlb53g7lfdkFM6ohZ3iVMZVaURm3QFZZWfnNBsureED3sOuzu0Rznt9eJln51HBcgOfJqaGhjrzVCz1XVX0yFaWiZ687a7r/3LP5g5F62ND9o5Q4RdplycTP4uNW/MqLmO6mVyEh3QVK988HJVuZaOy9F3YluTjvBA/3QXsU9y4VMicHPeYicNjP4l2UXs58Zk0e4H3tXRuVywO6X55l6J6tTism1UTuTSNF1Hh2auIokTj7m6pO5WQsa7rvdpK4GOk2G7q/B1f6J3aJUbTniDU/8kh3pLsg6N5cOD+9HJ7o9xUVZXHOwWs3vpicnLTLtOd1WE2yIG+KiynVmuXOlHIrQJaztCrKCUm8bquoCDyg+7XZGc9ypNJ1mhZS9GwKCN5KBQcYbGtr818UEbyz28idZBnZYsaE9yvView2MZvRBxd7Ge+jr6hl0cF+sBRCFqxSco+xVP6ZpZAVJJQy8FUviX4MuwdtAfpRuFB37MUBa84VLd2byjVwzy63w30j3bmlO7hGTE5PjYyA96O7u3vOkL0KU45DlCjpGW6+2cel2gUrW0YojZoD+DNCXk3YqlzB0314Pcn8oMPq2r+IT6rq3xUVMcRPP/8SQ/dAM9PvI+/8SNg50wUNva0wVK7+QiOPDGPdZD4Mfi3kBWXgq5rvvBx2H7PBU6t8QhXgetWqk0VLd7nMjg4zSHeO6e5zo4CQ7r7yiMX+3hG/Wlt77fG6qxiCoNod+2FhVMXPPk5UGaOlhDsVeDw0+QV9YMQU3f1t9sQInu5pfgVNejuaj8OaB/Uk6MeKQkiAnZHxQJ/uJNOcByFEdtlhddmtQHgJ+VuH9+UrDJaWhjOQp7ID0BtxLkw8gVTYnmVwC2UJdaWbbQ5Nd00U36bmZrvcN9KdS7pLU6Fz7t6bHvpPaekNe5XTW7p3797cKMrrcC832uRjuOTcax194KEpupN/kO60Om44r60zGJs3Zri679XkM6/fuzc7kGSUPp+0Pd0pSfTs7ooyo5Zd724uqEB6aWnp9T9PvK58SV3eygkncdJdY5aJz7bXfSPduaS7WiGHztlPRyIJP+SS+sSwDt6e3OKDdFf9Cv/rlWWcTbQ+h5DC79p/D57cupDE3rx3r9cudN/5xeIJDXsyAwiZv5VWsmEDexbea+Ci54iT7nJ7zqci3eeO7k5SD/vJ3YkbePsnqrXIaIQnjYbda54YYujD9g2vYoDu4w2dIqD71K2w2dC9VkqGjC3oU8OJif67G7WD3NHhS4krUz08rr1vNqZ73XvdBf6b/UnqB3Z0d823/BVHyuMJiR+m9Uy3hYOphl+TepeLniNuujf1Id1FRXdRaFenWhWLDI+FP4DdXaOGVRDsnv5hCdD99/YyEdB9AMImzoLuHwkx6fwyNZUiWad7BLJvTREicfpLaUT3xU57dM5U7IVsH2ycpOAL5M18CklkNl/rtvCxKVqcRLkQJd1VsWWys+1430h3jqRUAt0lllWzTpL8qnHWaoCsO24nGu0trSe92meG+g7r6GM/jeZT+w5GRUVJCn8D3b2jwj0u2qJO55ruZBZ0HzwTlG7OKtLzr/9Wg6xJbW1rfENjgmNf1G9X0328uy7D2SNfl6/7wBxmU7pP9BIyr0C1IO69r2/4nTaVBjnsO6Kkux1dZZDuXKvnXhRxOmRZY3cPlfXPHjqP4WVaep3D76aiezL1Hcy9qndnwhkH3k1/oIJLeW545+h0PxMZVWM2elbLMZ8UQ0p/eP78Xxe3uLQwNd3frUv2Ijnf7Ur3r9thElztz9H3/HlVz1z0HRHS/Q9C/iLdeauB/xaS4DQuShq7AdmYyDouE3YA3UMgs9ATixVwIsx35SQ1Twdn7qi1SbnCpfvECf/MjxY43HPcfavxyL678hZlA/OjXOKvpS0hvmeft+qdYGu6Ny13JeTBnHceEdJdTrnK2GUFE9Kd+5H7A5kz+buXi6I6ZC5kXmTvGIffrj4zqhiWHo5aOkcxeGZ3M5Bnsh/O7LPNgibh0n1sIymweEJDgcceE7ETBy7kUe9JFy9eXEXC9x4zzADDju7dEPnRMt1rIOh8eh3S3S505wCcSHdOdJla77Ofk6J+Q0lpLzn9dkP171utuLGmCRuXK1y6X1+WeH+GUzL9C7+Z2p+vnri+ZLwU7uZSFnQfLvabge4NsLJ615e57z1Cp3uz0WIlWMdkR1cZDukeH5/A7qJlTOrgeM22COj+D/SjI1+5KOnRWigqe2TaESRUug/Wei6qmOmnrmO/n45jpEZ126hUdjErAlNfvvtkGBJg/DRx/mxlaOXOB1KJZbo350ES7JGpuW9nAdJdaVlZWVn6O2x1p/pXpelu8frmbtDab00llmLUZN0NlqvyfU+rvYaEj6FnG4jXys9ceI+9plK4LSkdn3YECZTuyjcB7tZES19NNigUug+NUqFQLKOdzd9NHwY0h7xXGDxT5wiJ/GzVPSguUU5OFum+nTqDD+0sPrqbpKlA6c56TZb6jYILryH7a6zbB9ZtfuagpIkesAA5ed+edgwJlO71vk6/R604r+dIQFCQpl/2dnbeCw8K8qdWjkH26YHf1wODFoeehXUFf0D3rt1BMuLs07rBPN2V/ZuIS4YJu8x4p1bcjCKQ7gKgewRtcLFmHQtDd/Aaym9ubm4WOINGHsY5kdguLjpCbYoLcVp2f3jaMSRQun8ys4zJSC1Hdc48kJq6BMbaFynPUnpnV1VlZUhkamqqkj3dMyC+AIkoU243T/eJYn8S+cnEU/slVStuZlyFTvdyYzWaP6pj4rBwCMLUmDpEX7FRvTOLunG6LL1PsaB7drllyQyUbYWVhrbIwP/s7jLEhV6u8iAkgZOi3sHQ3ftJh4PAXZh0L0mJgySlKa+tAXz3cekWCqAf16WkzIOHqKKqajCf6CD/Q9V+6mIaZ1Tr6P5jl4Tyma0Znf623izdV/tCGi3j3UUpOuGeySukuxV0lxnrtPmjclMjY2Prh9zkIe2QXeeQDt0N51lnovufyboRvwgINP4oFXrBmhtclNW405ckXZh2GAmM7l/OU1rGcPHOTHQfewIn57h57IE/uyD07pYDB8qosDQU3c+f16wq+nDgQJYf2Xj+hdV0/3b+EIA76RH9jzyzdIdiYs8b7jx/Plov4gTSfUa6g7lCdrjJUL3aE+h/NzfnU3GA4f+zp7smsLDGZmJA93gdae+jLN5Af073CB3HGHP1md8sAgI9S4eemXiLC7tMy0lXCSkYm3YYCYnuirc3t+py0TLd22/evKTlaMhOkDo0wf1EalexTnDGnuKdUST+5mNYTlG5Yka6f9lJfT5RlUzdHN27HxKywnAdU+d9Onrczp1bwbATQN0UJyEihU13+GhWuRV29/Jsxmqha6/INlC5nn3D1CGVQ45KtHcK7Z9j5lPZOq475Vk6ypbNXgnZtqtPnsoD0puRHxNcFHUIsmSTfx0H7oKi++u17rDKDIwyJDCJ0kuzdK8Glbi7S7WhPlfUDo2MqL3bJ8oXgl3FbX91o/oKirGRs0mr0iKuVlc3XSNBVy2NJN5XZ7kSj2VJT1XRKfM2fTJ12nBpMCRzN3xqX8HO6KQDIyPta8AeROXg4sZdUuh0F+Ksqg3oLrdhffJSU+Pgw7Lmjb07Qc++0vHxBV5E4vKkd9pxJBy6Kycp70LnZGqp2SELeXQVkGXXMN6mk4SsG9D9yCN6xEAyx/Sv4wJ799+AA78t3IaU+uRy7axXHokwdRs1VLmGIYOUzyHf11Nqqz9DQtZyEx9S4HQvo8wywqO7OgzOTGoyzXXmg31ip/uXE9CX7gzYu5jOjauPH6f8oHc7zIyqsOj+GQK7eeW3t3dIZFLP1F7Tv/aKvo7ioKAgQ7o/PCJzC9T1PRxt/5wW4EGkgR0duvHh29uXBURCAg/yycxatpGON0kQwS1gcdfkDHS/Aob50FuGXpsf5ksk3nT8IkXPSuK2k7MwkcKlO3itWGGW4R3dGWcba3xajK0xhhYk8dK99m/nmSNoz16Tl5mpusBjbdOOJOHQ/UMIIYdbpr9vcz66hngeMv2CNfLv6jATcfSrf4Bj5OZ63TPHPr+iHCNXr9YPNPPh1asCyqb+1PRNPFu9HJzlc17pxuc0TfczcJU3RuEgIb67xwnVrYOrQNoAV+0sXLpbZ5bhHd2t92lh6y0jHrqP/9zqTiTB9v8aI15MOuP0oalpR9Lc073cuhxTrUthSqRM+WOp65semNRcqX3DOp68X9PzkrxPvjGhgemeN29clxhMYP44TNtYks/pd9xb1N4Fyclrje6hJHkBHHr+Rn8AYJLu8nASYyIyJNDd69k00t1qypoyyxg6ppTxj+5sohNrsK4y1VgTPIe5foTAI8y05soIcT9pf2PJsGqUt3HasTT3dLcyGv93MLpnfJqupzzVdeleUrKIhD6gDSltJSUQH+i9uSvsDtpnEDW59jDN9/hnSkO65x5OIi4lJbr2mZ6bJcvhiE+W4URp+Sojuk89jSW+/w0i3WdH98ZyY7OMieU/p3lHd8YsY/0onHG+sf4WqXVMmlAzTYKFT9Nq6FBvu+xezqOVKrr7rF4tBidSUdLd+cH0tyK/rbp077wLxpWcjKiz0PfqDkHG6yCS8cJMPxws8d34xvBYTg4MH5Zfvd+jT/ff05U5WYScvXatWv0WeYxamxqZU2z8qnHRiO6XIT9ArKl70NJ9vDKaBF0Y5aqdBUl3LVmtWdbEI7qztbH8QWVqQ80I1j4zdGYhCd/GQUHndIy0n6cdSMKie1Pe/L2tioYU4nmANl4PXgh0iq4cqXKSKqe/57rKErrzvZ3Xm+mHyvHd4WnfDWL+jo7uDIQM7GGX37br031ytH/lyrRw9/VvP0FUita3T90kZMFK+eiYYka6D9aAK2ZgrmW6VyQ5kdRx9JmxRNneJgOzjOn1QXyje5nqJputC1DMLlAMvWCKsvmoQ8009wkUPT0V1EsyB47urQUatkvDG6YdSIKi++2dTsuV0+MwG7qM6WuQNXt+BUSPoMw1G8ByAw96Bkk138+PuqzvNzpa4EZPuZxVe1ne0vGI3OfmTBbWjo39S53hama1tAHdFa/BZ8f5iMlT34LD/mP69wGu57xe9YExWhPqv/ZAvkDt7npmmUaVTUZ3kRGlcn7RXWWWSbBPLm+52hVHHWpGqOTpLAKvMu9CDui+bZ4G7uuqJ6YdSEKiO/F2z4Xs0z/TiUc63deGywlpH6PpPtWXShJ7FYq+NZboPng9MNAoKONA+/UgPxfidbCdGb4/CtDSfaD9coCzb2CgJ5EEBjaacZO8GNqjMxU//MbHiXhfMe3rOH7HWzL/XjsIfpeOq5xnqhcHLQsPDNxdnRxIKcceS6XFECNSHThAH7q885lhHc6XPd21VSrcUDP7o6jUCHUK+5eUohm6x1UPTjuSBEV3WMYEWyt9yBbGenZvKRMNDOg+cmQ+Wa2cHi70tkT36e5i183GGWC639yBRy0wOVkVOFJ3NVPnM+bBmPfmzaSZi16U7tUxxj8E11rnY+amiqpgNdOiZBAhcnUyrt6T0sfwTTJ7q5mJfXsY48VDd8ZW00stAlJ7y/CJ7mqzTJOd1kTKta44jJuNMLnTcgrmu3z3cjAj/PtcsIrtFy48m3YsCYbuI6V+NN2/gV2mUOWjLoc9VEgCCOs5mAEW7aSkBHhmLNF9uve9a4yJR2qsnl4Bta2R+seEDt1vJSUwj4YzlGPm4bhI4n5qex/lb//ObNce+Pg8nnHBr9Z88XfRTmuvV1c3vgcvmv+qqxvsMZwRAd0Zi4fGVmMQJpIndFebZbKUdppS0Ymiw8rNhmd6C33WfdcnDkbuX1ZI6A7nt2p8fBLpzk+606uZSJJ8t5fTenU+DLl2Kpyiu0qplvvVHiPHSFpnCsA9a/4++Rea7oVM1PVSOf1Wl1cAyvIhmfLKGeiueAoj98Ddlsofu0FdTTfhN9iXiluovxDm+qOd2lkEdNeaZXhMdxMRg1Em9BpeliM5KelzHIOFLb2OV8uCoXt/vncuo32aZEdyErADdlBu6OdjyFLYzA4mSy9a7lcDZ32MHSMpvVlNPwRXXgPdSSksX75yxRO2XHJz6VQu7cW5uUtXXLlyZdIs3bvv/geukN4l/ewqAejO/PWQZvxEuluiu44LjTowL5/orjXLIN0t1fDY/QAXkvebi7KmqmOp+FRuhd1TjlfRc0v3zqdW073BjYyMMlI3U0MOWfkL/n2cyBLdnMg/sHl/GSmcIVK0cjw3POObiVfCyeer4j2JizQd7O5k/+vXL6QQLyxkVfroKN1RFeOjo1dS1kilL163maF7TRS4QgblsPVz1NLd74W9XlVFQvfTZofyfKC7jlkG6W6JuI/SoYsd56Ssnzv8oSzPHTWOWNFzS/cyYi3dJ2qd3A37C2Q3XwXTmWNFZHW3KnAz/Cma+WJH3Tb0Dpv6Kf+Z7OmiG5/Gw7PY4IxuTxjPHx8aGtHB8GV3mu4TQ1R4X7cjbCth/J6zBwWJyXvuEdX2amekOwd01zHLIN0t6PIKKj5rBSdlvaUnzfLrHLKiBUL3/jOB6UarzFR0z/V03darobvP2ZmvNng1KGC5KeP7VE/HQS8V2d0h1uTXjiGDMxQdHRFB0YsCVr/7rfGPHHlH0b2/JMDHKSjoMmufqzPea6h5XuUzb4n9MgcLiO7qzNGmfFH4THc9swzS3az6vsxzIZ6LvnKSLv73ZWpCNWlo0iGrWiB0PxsWWjduhu6ZJObrhIbup1utuFz3cZegd6YP/dirnpyFDCAmlz68r64+RGXv0M6wtlB0PxdGe8Kwj5rxL8mgfkOUD1UGGseme1O56cC5clMJU+OzLYz1bUN9ubU+5eXZ9lzEJCKVL6ZiO1Vxs6zoNGWXyf7loFUtCLorjvltrjPupS17gO6j/3iTFcrpl4lA99o0jzP9VvXmvo+uixLumTzU+YF6mTv04YeFj3d9uB5MIhISMjV0h1uEpEsP/6QSkO7W0NQk3eXT/KG7fRcxiUh3YOno2maOsptSYQIv/XbUqhYE3U/GkAMmex4JKzwWtaHwqnJ6KIOsOpXtftzq5RF7g8ja56Z7/lSuH+UzY1Ed5woLlxPZqVNKhu5wi2T+5f4/qYSXhUzK4O+FhUh3Kl21ycC5fc16V2DMIPyhuyYTU980yqI+ZLtJkq5zVNiNNf67dzc6bF0Lgu4QEvKRSS7upUSP6scu09vWd+X+c/NJQqVpF5Wm2BnpTunx3u0wMCgtfdcScgy+SMwJHrezMOhuzixjfAW5Yeajco0albrb3NCdMctYk4nJwTXeuBkmOa9y9tSF7HPk2hYA3Qc/kOjHJmdFJumoW7Tzi3KC3ra+aOX438FOKVWzofvkWOvq1ekhbptvSlxhbcbFcR63szDobhGlxnQ3YRihZ171w0dyQXdhh3zhTlPvN4KbcdR9rsqLPd/vyNXNf7orqkK8H9nlux/1cieDU39Od0a5rtQcrJdXGa/bWRB0N2uW0VyByUYEUXCNzpxLuqu9ZZDeM2lgBcRZIq/auSrvTZtDVzfv6T5U7ePUYZ8kF4Mdt8JiKyZmR/e2egh84xrQ0TGCdJ8d3S2aZUBMNiLK3mLKDCKLp4IBU4FoTpdrt8u5oDt6y1itHspd5jLWA9Kd0cMlTBxIu6j3o9uin7Oje2IC+FwtfMD3dhYA3WfkqFwvZ4fh9eXqFNtylVv8TH7qNqM7estYq5+3wbGsZAgrAunO6AJZ9MSOC0PKY6LvzoLujZsos0xQwzjf25n/dLdslqHU19ycryJpk1Hk2+Y+dYrt3iZqPZE23bad6c4yE5Mja6SYSNz/w3pAuqv0Is37qj0nRgau+Rg7RvZenmcV3T8X53rDsqejF/jfzvynu1U+J+XZ5hNMK3VTbOts25fuaJaxVpODG2QkoAxH7kh3lapWLD5p5xo4vSTBOM92kBV0f3khkxq4p1QLoZ0FQffZlaA0iA/Mjb87mmWs1a9TsOAv+BlWBNJdBdDUhXb3Mxy/FG3sGGkF3V+lQc5Vz4Q1LwQRWZT/dJ91miGlNj6w1ixjZ7qjWcZ6uO+DjJbSU41YE0h3RrBYiIM6uOlJ+ifZ0V3R20sFk3Ra81Mg7SzAGJEsBS43p43NMvalO5plrFeVVEIC0kemsCaQ7vSoup3Mv8VBHYzcClv2bJIF3ftbawPAU0YWktAjlIdV/HSXayNI2jJ25IwLrNAsY52eQ1/f14v1gHRn1JhJjnVzUQl9NW7RbSzo/l/cEsrivr+mXjDtLHq6g8tNY6+a7jopnOxIdzTLWC/FKUhcfKeHi6KUCoUS/sM65zXd2yNdP3O1jvjpooVLz+hwICjIgh/MMV+K7TVfugXUziKnO70SSkXzxnJdu4z96I5mGRY6lwhd5j0nRb0/c/13xZkzWOd8pnttXkAeZ9WwP5CQ5Y906E7yzZzZVXoM4lN7HjsmLAOiyOku18nkIZdxY5lBs4zV6noNs1ReiQ12L6j9+fPn20iwPMme0bSR7rOm+5sNZFkLq4vVnD17lnVXHrx3lhKdr2OJ9uPm6P717EFq4B5TLLR25i3d420Rn4daCQW5PMqUVF4nnW070h3NMtar9/ICyGK5+YO9EyQpO0t8fHykxMnLVbYQq53HdD/sLM3rsP5KU3VVu1xdXauqrJ+3+VgFurXYlZJ0eUpKpMT13aBFujdUHXSFQUh0yvkJobUzT+kOFhVbjH2pBU4JVFiZrAQZFWKG3rZrJAI0y7DQ9QXQa+K/2z0S08SpMHVG5A3vsdr5S/eBHPd4NldqSSEe/jIJIRXW9ObRTlC0TnrsuC9wM14k9PmUWbpP9nZuoxLwzve/L8B25ind5bazbDAGGblMY5yxK93RLMNCxdBvdn20fzlju1Y9AZ2H1Gr1mNaWv3T/lRWUz2KCfazNz9X3eGc5uLJcs2Yi9oE/yFnDdvfQbhiMj9wMdZqvGr0b032qKtFfSjxDUz92jgqwnflJd8qKYitA9jU1HZbBBSmg9zbZl+5olmGh8ZotMJZ+xgFuJ/4rhfZuOOuZ9B6TlvOY7vHeB9lEZv6USsiZ9unBOkIirlhx/k2ip5Ra+lno+wQW9Qdm6D4QLaVe+D41jAmynflI95lC/rIUtYoJxEylZmVptm1PdzTLsGmWunToONz1ms79Lqs/YrXzl+4N6wk5z+IyX8JgHE5HkoTrFbGme2abmgAV0SSgRGmC7pcX03acve1CbWc+0l1u24wX3OVVRbOM9RppD5ASN1+ugqiO9yQErOgcx3rnL90/LyCballc5h3kz/iryWq6Xz66Toft+4q1MSL7y4rj4h4Z0f300STqzCPF7wTbzjyk+8whf/lJdzTLsNFLarJqWSlX/sPfD3tswkBlfKb7UJ7P4S8srvJxNzigV9CbM9K95axcHqjD9nl/dRm8da9aCqN3HbpPyOXucKK0oGBMwO3MD7rrMLex3Da5k+xgStCT3NB+r8oMlY1mGat0CfpO8iPOEpe9XHDgHVY6j+n++/b8pFE2C4nlYJfZWDMj3cc/VVZWHvNwdU1IBanovvOrAV2mHix2fzeopntDZeVjV0icGp66eXxCyBM1vKO73EaznpzTHVOostG3POISfZWzrtNZlvmT8qpvaMZZVV7SffAkiWX3vn4SrvK7nZY5ug/Csc8JcNQtIDDwq+p3gLgHBpp4CB4Fhj0LoOg+2d2+nf4J8A88J/R25hvdKbOMTXIncUx3TJDNTptdiM8d7laH3Er7Ro8Ld+7HWJS8pPsJT+cNv9hcpOsQXMWPEZDYOEDMjx8/8uGYf2h4eHh2W1cXvWQu1I14H+jqMnG9sfawAKf58qEfr5L8wE9GEh7e1DWMdLcl3bVmGYHRHc0ybKT4ugWMmkGPuSpv8B/fVd/GxsYa/rrWjWN3XtI9n/g1s5rzzvfXdYC5YAzspUuWUOED5l+tq6v7pTb5vFhCDraZfgSUjxeSfzoqlkRJ6QF+XZ0IxgH8orteKBgh0R0H7mzUnguBISUlDVyVd2QJCdtXVFS0J+QeVj4v6X7Eeyu78DLTdP67hkbQNS/9tar9OQspUcF64WiL3tTOZGujWZ+HiV/+fgsDqMsea2xsEkU7847utsqdxCXdGbOMLf18xK0a6EERf3FVWutD7RgP6c5LuhfFpFbqoB40o+M70D2skN6qmq+l+2v46IFQuH7k0ZMnT7KJOlEPn/SkHhGfvSfrxNLO/KI7LDuyVe4kDumuMsuUIzWsU+ctQkKPcxXEe7oqfYlGlVj7c0/3z4f06d511TmdSUJdcYoSxdhIK+i+mg613prt7rqZdnsfu39qFeXFuLWwsPAWu6UNVacymcgzhYXnO8XTzrzzmVEKj+5olmGnCxDT6yJ3fWig4ZtGg1j7c093RY8+3etiyLWGF5RSXCixo/trZzKvnLar92UkZqxdu3ZL7cTExCQLfEDBG1ycKA/dtVfZfRLpLk66a3170CzDUpnBJPwiptpzXLpPD+jRfepZOCnJ1Y8BQ8K6dMJCD7XqqUupQ/fBO5AhgFmnNrCzmvWt9MP1mJhiISEhHWJrZ6T7n9Fdc9uQiRvNMizU8RgmwRZ/wIpAujMa/OjtROa5G9DdadXbFo2K/fSUrkv38zJClr5l3gkGWLrYwqX30Q6VIRER+7q7u0XnLYt0nyXd0SzDSn3/gVeCNLMeawLpzuhhFDElaWSMRv76h+J16X4Cdnwf+rP7WBwTM5++4rOvX3+LsZ2R7rOiO5plWOoGDNS80nomsCaQ7nSnOu/nQ/s1FklAWoKHUju3SiRLXzUaqZX6YPsB4h6hUOzzIYkfWHdkhUJxOiqK+lmRSDLgimJ9HHlBd71k1kKiO5pl2IoKL7O9GusB6a4auccTf3qjTg5aqqE7PataJZffMTsPTkUiyC+IIOEP2ObV+FpYUFAQSxdzWC6vEHE784LuesmshUR3NMuw0/htCKp64jNWBNJdtbmLxJZoDzwuKsrTobtFvSvaAcb6LUU32YHiyvHjmcw7QjSsbxN5OFek+5/TPYI2yxxGs4zVepzqNH9lF4Z6Qbqr6F65JvKijnPM1OTk73RQiBV0V0x+/is9/f2k9U9T+zNQhLMz5fyYlJ5+emJyUuRxKXhC93K2moOVwkZ0lzFWJYSFtRWogG6V9gsrAunO0H28zcP3sqkTjkek2vT7jvygXG/kzGuBZ3hERIRjDMl4QnfWmoP8R6bpjok6rdXYLZjGcslsw5pAutN0n3oeT86bjPA/1G0zk0kzpWtBviAINOActGDBQfB97J5Euttf6sC5rBURP7dS3Qa1oAlhYZ3upcArceJjXC6KdGfo3h/uSsrs/VUXRYOC1N44fje/f+9wnB47t3RXpZkWrHiZQ4qvyoKhUzKG8UK6q+iu7CKST3b5rVdMgXqyo6IYr0dYG0Upv6mp6ceoQ7Xz3NJdJnDxcvaXp3aZpnQq1d4Y1gTSnaF7zR7/w/ZxNL9yGLQnWONeuaSEUq3jtTMf6N5kWs1/qHyu2M7THFL81K8dHoS0DmNFIN0Zur9Od7/SY+PvdesorRCt2/zRYtBjR+2jc0n3JioTkywhS6m06VrV8mz7KMtQPM0hxUu1LaSCZ2M9IN1VdP+6LeSvKZv1ndoKWrHOtGiwZ1AqHp4EOawL7lzSXS4zH4aA9xGA+XuffNSnIuhvUbuxIpDuKrrnkL9n/z0U7ar3/GTdAGRBkZSwX84h3cviqSC6MllzH9Jd9KrLobIxncboMkh3Fd1rMucXzea1n9HnDT6MXHSwHveshxK2Mqd0N5H9gjbLYCOIXis9iEvgjSFsaqS7iu4R8/K6ZnGFKJrjkREeurEjva7SyG8ZwQbmB93lOPZ1BEUTEijvxHpAuqvpTo51TbLSaF6kjlQ8Z8zszo1NiHVe0Z0xyzT1It3Fr8ZCL+L3BOGOdNeh+5qD7JQXYSII/DlG2KC8onujrrcMNoK41X4SPNQiprCdke6MqKzZs1DSSY3wmeIj3fW8ZbARxCzl6DXokW6xWBNId0Yt+53Y4XzxOj3dmNIIW5KHdNcxyyDdRa6uQ5DcTPZPB9YE0p1WJ0Rwdw2PZqHHiAjh0L3RYBETNoKYlUNF+ijChB1Id5UOuRNJek0PC2H0CgHR3XAREzaCmAVsD9rVjfWAdFcpFyKst41jG4iT7vpmGaS7qNXzkRCffQ0KrAmkO82AyYR5ZNMPbAFx0r3ROLYMNoJ49Qj82DYO4OwX0p1Rl1xKyC5sAJHS3URsGWwEkUqpOOXvRCTbsSaQ7owmsn0IWfUCG0BcdC+LZ+huZJZBuotXQ49WECJJwYQdSHeVhiFH0uLbaKcTF90hB1N5k0mzDNJdvPq9DqZU1z3HikC6M+qHWZiFj7D6RUZ3lTXGdMhfbARxauplMpkX1Yv+bEh3Rr0lsPShEZ8HMdI9It6UWQbpLloNLfEiKS+xHpDuKl0GozvByLwiozuTg0kmM5OJCRtBlHqSCt4RXyaxIpDujCZPgF3mKfpPiYzucp1cpHLMfuEYerudiuGHrYt0V+t+PHG914uVLy66MwYZVYLsXqS7I2i8cznkyvG5hjWBdFepOIYQD6x6sdFdZ+QuK29EujuC6tJdiWTp3WGsCaQ7reE3MKMavA2rXsx0R8uMY6gmlhD38nasCKQ7o0Z4IPyOY82LjO5l8Xp0j4hHuotfLTv8yIrzWA9Id5UU5QtJwCl8lRMb3eUyA5mke3kTNoUYNPHtJwX3ElcJOYiOzUh3tcb9XciJAax4x6S7TI5NIQb17iiC/xe4gr9MPtYG0p3R1INwyNhxFetdbHTXdZihfGaamrQZmnSEdBeHwjxku9sWeREJ+r4h3TWCRcuEnG7AehcX3XXXMVFLmbJ1D+oeyS7HphCDoBdHHnAmJHB3G1YG0l2lEkJ8D6PRXWx0NzDL6A/QdY9gQ4hBzbdVeY79j/3S7m29rRFWkSPSvX4nkeT90PGemHwMgpm2wVfwtw6bQwR0z29u7tM5BL40sAeUTx3ChhCDrslUdI/9NKTep/xdgj/ijkr37tqaryP1mYS46e0ejotzIn//mrwTBs9KLjaHMOkOgX/N2l7Ks5k9cA6aZUSiUhXcicc2jZF1qjiQaIRV5Fh0v+rtvfhBtBvxWqa3W9nXl+gtPdjrFxUTE3MCm0OYdLfG9oIjOhHSnXgu+ap+C99Nltysrq6+E0vSX2EVORbdLxLi7ONESGaH4ZHObeTvnqhX7e3t6CcpSLrrrGMCA4yFc7AVxKE327WjdFKt2qm4mSWHvj10emHidQwY6Vh0nyhhnoVd3cbHcsi82LYJbAqh0l1tdM/OzrZ0TkI2toI4tFHLdmnEF71D3U9dQ59iDTkY3e/FM0/D4WlTdCc+2BDCp/sM56Cnuzg00ZmqZrt3SPprvWFZR1FAUvko1pGD0T1P9Tws3pOHdBcX3VXrmCz6w8TL9R1pUMJVa6G/mu67nr7Tt6bmRQa8xqQ8jkb3F2s173JuSHdx0Z1ZvmTJHwbWOuHAXTT6ukLdlS981T/SUixLu4sV5HB0D9fA3SfZ8FgtZFT3qsfXOSHT3TK80SwjIg2WRjM92W/VsELvSKc8POkmTKh++6bAanIcuo+3BGngXtBvRP5wXyJJavxW342tITy6084wlq0uYLphTogvw3YQvD6rerIks1Nvv1Jxmzh9p/7u3DWO1eQ4dG9Nd1LTfbex16Os5CAhMd8j/C9iawiO7tQapWyLzjBglmG8ZdA+IwaNvaX78bx5B7v18yL3FfjGPuwZHPy6zXcf0t2B6P4jjvm1l3qc0A8oN3F7SX2a580TriS61vNUP7aG4Og+sxe7xiyD9hkx6Nk2ui+fO/fe4MD+GBK44+DBg1nBW19OYT05HN19j143yN1QkeiyQXappS6LyDa44Gu7AOludvmSjlkG8jRRikC6i0BHqJ68aK/h7pZrWh/4G1hLjkT3rT50q9838pWq20ECjsJr3FUSWHQVI0wJkO4zSD8yMMaZEbzqdkJHjjg1ZLj/9aY4jZ5hNTkS3Wm2B281ceTNlsNUfOhXW/J/Y1OIkO76kYGxFQSv+HnQlS8bT6KP/G7VCAN8OxDde+h5mAAMEeaAdO9r1hW2guAFcSAX3BjEekC6q/SICgYdWDyCde14dEeJSm23vOL3nfqJFYF0V+suNXQ/ha9rSHeUwPUiLP4O1gLSXaPxMlirJH2DL3NId5TQVb3mO76CI911Ru7gDelbNIQVjXRHCV19H3GdEtJdRwfI8rKHGDYO6Y5CocRG94hLSqxlpDsKhRIb3f+7gHWMdEehUOKj+yiG9kW6o1AoEdIdhXRHoVBIdxTSHYVCId1RSHcUCoV0R7qjUCikO9Id6Y5CoZDuKKQ7CoVCuqOQ7igUCumOQrqjUCjO6f5//0MJREh3FArpjhKl8FFHoZDuKKQ7CoVCuqOQ7igUCumOQrqjUCikOwrpjkKhkO4opDsKhUK6I91RKBTSHYV0R6FQSHcU0h2FQiHdUUh3FAqFdEch3VEoFNIdhXRHoZDuKKQ7CoVCuqOQ7igUCumOmnP9P3nrefQQ8h4OAAAAAElFTkSuQmCC" id="fig:StressTensors" alt />
<p class="caption">Stress tensors for (a.) Cartesian, (b.) cylindrical, and (c.) spherical coordinate systems. From Nix and Cai.;
</div>
;<span class="math display">\[\sigma_{ij}
\begin{bmatrix}
\sigma_{xx} & \sigma_{xy} & \sigma_{xz}\\
\sigma_{yx} & \sigma_{yy} & \sigma_{yz}\\
\sigma_{zx} & \sigma_{zy} & \sigma_{zz}\\
\end{bmatrix}
\label{eq:CartesianStressTensor}\]</span>
;
;<strong>Cylindrical</strong> coordinates are also an orthogonal coordinate system defined in Fig. <a href="#fig:StressTensors" reference-type="ref" reference="fig:StressTensors">2</a>(b). The stress tensor in this coordinate system is defined by the cylinderical components <span class="math inline">\(r\)</span>, <span class="math inline">\(\theta\)</span>, and <span class="math inline">\(z\)</span>. Here, <span class="math inline">\(r\)</span> is the distance from the <span class="math inline">\(z\)</span>-axis to the point. <span class="math inline">\(\theta\)</span> is the angle between the reference direction (we use the <span class="math inline">\(x\)</span>-direction) and the vector that points from the origin to the coordinates projected onto the <span class="math inline">\(xy\)</span> plane. <span class="math inline">\(z\)</span> is the distance from the point’s coordinates projected onto <span class="math inline">\(xy\)</span> plane and the point itself. The stress tensor is represented as
;
;<span class="math display">\[\sigma_{ij}=
\begin{bmatrix}
\sigma_{rr} & \sigma_{r \theta} & \sigma_{r z}\\
\sigma_{\theta r} & \sigma_{\theta\theta} & \sigma_{\theta z}\\
\sigma_{z r} & \sigma_{z \theta} & \sigma_{zz}\\
\end{bmatrix}
\label{eq:CylindricalStressTensor}\]</span>
;
;<strong>Spherical</strong> coordinates are defined by <span class="math inline">\(r\)</span>, <span class="math inline">\(\theta\)</span> and <span class="math inline">\(\phi\)</span>. Here <span class="math inline">\(r\)</span> is the radial distance from the origin to the point. <span class="math inline">\(\theta\)</span> is the polar angle, or the angle between the <span class="math inline">\(x\)</span>-axis and the point, projected onto the <span class="math inline">\(xy\)</span> plane. <span class="math inline">\(\phi\)</span> is the azimuthal angle, or the angle between the <span class="math inline">\(z\)</span>-axis and the vector pointing from the origin to the point. The stress tensor is
;
;<span class="math display">\[\sigma_{ij}=
\begin{bmatrix}
\sigma_{rr} & \sigma_{r \theta} & \sigma_{r \phi}\\
\sigma_{\theta r} & \sigma_{\theta\theta} & \sigma_{\theta \phi}\\
\sigma_{\phi r} & \sigma_{\phi \theta} & \sigma_{\phi\phi}\\
\end{bmatrix}
\label{eq:SphericalStressTensor}\]</span>
;
;We will often want to transform tensor values from one coordinate system to another in <span class="math inline">\({\rm I\!R}^3\)</span>. As an example, we will convert the stress state from a cylinderical coordinate system to a Cartesian coordinate system. This transformation from stress state in the original coordinate system (<span class="math inline">\(\sigma_{kl } = \sigma_{kl}^{r \theta z}\)</span>) to the new coordinate system (<span class="math inline">\(\sigma_{ij }^{'} = \sigma_{ij}^{xyz}\)</span>) is performed using the following relationship:
;
;<span class="math display">\[\sigma_{ij}' = Q_{ik}Q_{jk}\sigma_{kl}
\label{eq:GeneralTransform}\]</span>
;
;Where the summation notation (Sec. <a href="#sec:SummationNotation" reference-type="ref" reference="sec:SummationNotation">1.3</a>) is implicit. In our example the indices <span class="math inline">\(kl\)</span> indicate the original cylindrical coordinate system (<span class="math inline">\(r\)</span>, <span class="math inline">\(\theta\)</span>, <span class="math inline">\(z\)</span>) and the indices <span class="math inline">\(ij\)</span> indicate the new coordinate system (<span class="math inline">\(x\)</span>, <span class="math inline">\(y\)</span>, <span class="math inline">\(z\)</span>).
;
;Note that Eq. <a href="#eq:GeneralTransform" reference-type="ref" reference="eq:GeneralTransform"><span class="math display">\[eq:GeneralTransform\]</span></a> can be written in matrix form as:
;
;<span class="math display">\[\sigma = Q \cdot \sigma \cdot Q^{T}\]</span>
;
;The <span class="math inline">\(Q\)</span> matrix is defined the dot products between the unit vectors in the coordinate systems of interest. In simplified 2D transformation from polar to Cartesian, there is no <span class="math inline">\(z\)</span> component in either coordinate system and terms with those indices can be dropped.
;
;<span class="math display">\[Q_{ik} \equiv (\hat{e}_{i}^{xy} \cdot \hat{e}_k^{r \theta}) =
\begin{bmatrix}
(\hat{e}_{x} \cdot \hat{e}_{r}) & (\hat{e}_{x} \cdot \hat{e}_{\theta})\\
(\hat{e}_{y} \cdot \hat{e}_{r}) & (\hat{e}_{y} \cdot \hat{e}_{\theta})\\
\end{bmatrix}\\
%Q_{jl} \equiv (\hat{e}_{j}^{xyz} \cdot \hat{e}_l^{r \theta z}) \\\]</span>
;
;where <span class="math inline">\(\hat{e}_{r}\)</span> and <span class="math inline">\(\hat{e}_{\theta}\)</span> is related geometrically to <span class="math inline">\(\hat{e}_{x}\)</span> and <span class="math inline">\(\hat{e}_{y}\)</span>:
;
;<span class="math display">\[\begin{bmatrix}
\hat{e}_{r} = \hat{e}_{x} \cos(\theta) + \hat{e}_{y} \sin(\theta)\\
\hat{e}_{\theta} = -\hat{e}_{x} \sin(\theta) + \hat{e}_{y} \cos(\theta)\\
\end{bmatrix}\\
%Q_{jl} \equiv (\hat{e}_{j}^{xyz} \cdot \hat{e}_l^{r \theta z}) \\\]</span>
;
;And therefore:
;
;<span class="math display">\[\begin{aligned}
Q_{ik} &\equiv (\hat{e}_{i}^{xy} \cdot \hat{e}_k^{r \theta}) =
\begin{bmatrix}
(\hat{e}_{x} \cdot \hat{e}_{r}) & (\hat{e}_{x} \cdot \hat{e}_{\theta})\\
(\hat{e}_{y} \cdot \hat{e}_{r}) & (\hat{e}_{y} \cdot \hat{e}_{\theta})\\
\end{bmatrix}
=
\begin{bmatrix}
Q_{xr} & Q_{x\theta}\\
Q_{yr} & Q_{y\theta}\\
\end{bmatrix} \\
&=
\begin{bmatrix}
\left(\hat{e}_{x} \cdot \left[\hat{e}_{x} \cos(\theta) + \hat{e}_{y} \sin(\theta)\right]\right) & \left(\hat{e}_{x} \cdot \left[-\hat{e}_{x} \sin(\theta) + \hat{e}_{y} \cos(\theta)\right]\right)\\
\left(\hat{e}_{y} \cdot \left[\hat{e}_{x} \cos(\theta) + \hat{e}_{y} \sin(\theta)\right]\right) & \left(\hat{e}_{y} \cdot \left[-\hat{e}_{x} \sin(\theta) + \hat{e}_{y} \cos(\theta)\right]\right)
\end{bmatrix}\\
&=
\begin{bmatrix}
\cos(\theta) & -\sin(\theta)\\
\sin(\theta) & \cos(\theta)
\end{bmatrix}\end{aligned}\]</span>
;
;So, to convert the stress tensor in polar coordinates (<span class="math inline">\(\sigma_{kl}^{r\theta}\)</span>) to Cartesian (<span class="math inline">\(\sigma_{ij}^{xy}\)</span>), we take the triple dot-product:
;
;<span class="math display">\[\begin{aligned}
\sigma' &= Q \cdot \sigma \cdot Q^{T} =
\begin{bmatrix}
\sigma_{xx} & \sigma_{xy}\\
\sigma_{yx} & \sigma_{yy}
\end{bmatrix}=
\begin{bmatrix}
\cos(\theta) & -\sin(\theta)\\
\sin(\theta) & con(\theta)
\end{bmatrix}\cdot
\begin{bmatrix}
\sigma_{rr} & \sigma_{r\theta}\\
\sigma_{\theta r} & \sigma_{\theta \theta}
\end{bmatrix}
\cdot
\begin{bmatrix}
\cos(\theta) & \sin(\theta)\\
-\sin(\theta) & con(\theta)
\end{bmatrix}
\end{aligned}\]</span>
;
;Completing the math yields:
;
;<span class="math display">\[\begin{aligned}
\sigma_{xx} &= \cos(\theta) \left[\sigma_{rr} \cos(\theta) - \sigma_{\theta r} \sin(
\theta)\right] - \sin(\theta)\left[\sigma_{r\theta}\cos(\theta) - \sigma_{\theta\theta}\sin(\theta)\right]\\
\sigma_{xy} &= \sin(\theta) \left[\sigma_{rr} \cos(\theta) - \sigma_{\theta r} \sin(
\theta)\right] + \cos(\theta)\left[\sigma_{r\theta}\cos(\theta) - \sigma_{\theta\theta}\sin(\theta)\right]\\
\sigma_{yx} &= \cos(\theta) \left[\sigma_{\theta r} \cos(\theta) + \sigma_{rr} \sin(
\theta)\right] - \sin(\theta)\left[\sigma_{\theta \theta}\cos(\theta) + \sigma_{r\theta}\sin(\theta)\right]\\
\sigma_{yy} &= \sin(\theta) \left[\sigma_{\theta r} \cos(\theta) + \sigma_{rr} \sin(
\theta)\right] + \cos(\theta)\left[\sigma_{\theta \theta}\cos(\theta) + \sigma_{r\theta}\sin(\theta)\right]\end{aligned}\]</span>
;
;In as system with only one or two stress components these coordinate transformations simplify greatly. Remember, though, in <span class="math inline">\({\rm I\!R}^3\)</span> there will be <span class="math inline">\(N = 3^2\)</span> components due to increased dimentionality.
;
</div>
<div id="calculus" class="section level2">
<h2>Calculus</h2>
;We assume that incoming graduate students have completed coursework in calculus including the basic calculation of derivatives, antiderivatives, definite integrals, series/sequences, and multivariate calculus. Below are outlined some more advanced calculus concepts that have specific physical relevance to concepts covered in the MSE core.
;
;Any college-level calculus text is suitable for supplemental study. The sections below on Total Differentials (Sec. <a href="#subsec:totdiff" reference-type="ref" reference="subsec:totdiff">1.5.1</a>) and Exact/Inexact Differentials (Sec. <a href="#subsec:eidiff" reference-type="ref" reference="subsec:eidiff">1.5.2</a>) were adapted from the course materials of Richard Fitzpatrick at UT-Austin (available <a href="http://farside.ph.utexas.edu/teaching/sm1/Thermal.pdf">here</a>).
;
<div id="subsec:totdiff" class="section level3">
<h3>Total Differentials: (Release 11/2016)</h3>
;<strong><em>Encountered in: MAT<code>_</code>SCI 401</em></strong>
;
;When there exists an explicit function of several variables such as <span class="math inline">\(f = f(x,y,t)\)</span>, which has <span class="math inline">\(f\)</span> has a <em>total</em> differential of form:
;
;<span class="math display">\[\begin{aligned}
\Diff{}{f} = \Big(\Partial{}{f}{t}\Big)_{x,y}\Diff{}{t} + \Big(\Partial{}{f}{x}\Big)_{t,y} \Diff{}{x} + \Big(\Partial{}{f}{y}\Big)_{t,x} \Diff{}{y}
\end{aligned}\]</span>
;
;Here, we do not assume that <span class="math inline">\(f\)</span> is constant with respect any of the arguments <span class="math inline">\((x\text{,}\, y\text{, or } t)\)</span>. This equation defines the differential change in the function <span class="math inline">\(\Diff{}{f}\)</span> and accounts for all interdependencies between <span class="math inline">\(x\)</span>, <span class="math inline">\(y\)</span>, and <span class="math inline">\(t\)</span>. In general, the total differential can be defined as:
;
;<span class="math display">\[\begin{aligned}
\label{eq:TotDiff}
\Diff{}{f} = \sum\limits_{i=1}^n \Big(\Partial{}{f}{x_i}\Big)_{x_{j\neq i}}\Diff{}{x_i}\end{aligned}\]</span>
;
;total differential is important when working with thermodynamic systems which is described by thermodynamic parameters (e.g. <span class="math inline">\(P\)</span>, <span class="math inline">\(T\)</span>, <span class="math inline">\(V\)</span>) which are not necessary independent. For example, the internal energy <span class="math inline">\(U\)</span> for some homogeneous system can be defined in terms of entropy <span class="math inline">\(S\)</span> and volume <span class="math inline">\(V\)</span>; <span class="math inline">\(U = U(S,V)\)</span>. According to Eq. <a href="#eq:TotDiff" reference-type="ref" reference="eq:TotDiff"><span class="math display">\[eq:TotDiff\]</span></a>, the infinitesimal change in internal entropy is therefore: <span class="math display">\[\begin{aligned}
\Diff{}{U} = \Big(\Partial{}{U}{S}\Big)_{V}\Diff{}{S} + \Big(\Partial{}{U}{V}\Big)_{S} \Diff{}{V}\end{aligned}\]</span>
;
</div>
<div id="subsec:eidiff" class="section level3">
<h3>Exact and Inexact Differentials (Release 11/2016)</h3>
;<strong><em>Encountered in: MAT<code>_</code>SCI 401</em></strong>
;
;Suppose we are assessing the infinitesimal change of some value: <span class="math inline">\(\Diff{}{f}\)</span>, in which <span class="math inline">\(\Diff{}{f}\)</span> is a linear differential of the form: <span class="math display">\[\begin{aligned}
\Diff{}{f} = \sum\limits_{i=1}^m M_i(x_1,x_2,...x_m)\Diff{}{x_i}.\end{aligned}\]</span> In thermodynamics we are often concerned with linear differentials of two independent variables such that <span class="math display">\[\begin{aligned}
\label{eq:LinearDiff}
\Diff{}{f} = M(x,y) \Diff{}{x} + N(x,y) \Diff{}{y}.\end{aligned}\]</span> An exact differential is one in which <span class="math inline">\(\int{\Diff{}{z}}\)</span> is path-independent. It can be shown (e.g. <a href="http://mathworld.wolfram.com/ExactDifferential.html">Wolfram Exact Differential</a>) that this means:
;
;<span class="math display">\[\begin{aligned}
\label{eq:ExactDiff}
\Diff{}{f} = \Big(\Partial{}{f}{x}\Big)_{y} \Diff{}{x} + \Big(\Partial{}{f}{y}\Big)_{x} \Diff{}{y}.
\end{aligned}\]</span>
;
;Which means that
;
;<span class="math display">\[\begin{aligned}
\label{eq:ExactDiff2}
\Big(\Partial{}{M}{y}\Big)_{x} = \Big(\Partial{}{N}{x}\Big)_{y}.
\end{aligned}\]</span>
;
;An inexact differential is one in which the equality defined in Eq. <a href="#eq:ExactDiff" reference-type="ref" reference="eq:ExactDiff"><span class="math display">\[eq:ExactDiff\]</span></a> (and therefore Eq. <a href="#eq:ExactDiff2" reference-type="ref" reference="eq:ExactDiff2"><span class="math display">\[eq:ExactDiff2\]</span></a>) is not necessary true. An inexact differential is typically denoted using <em>bar</em> notation to define the infinitesimal value: <span class="math display">\[\begin{aligned}
\text{\dj} f = \Big(\Partial{}{f}{x}\Big)_{y} \Diff{}{x} + \Big(\Partial{}{f}{y}\Big)_{x} \Diff{}{y}.\end{aligned}\]</span> Two physical examples make this more clear:
;
<div class="displayquote">
;<strong>Example 1:</strong> Imagine you are speaking with a classmate who recently traveled from from Chicago to Minneapolis. You know he is now in Minneapolis. Is it possible for you to know how much money he spent gas (<span class="math inline">\(G\)</span>)? No, you can’t. <span class="math inline">\(G\)</span> is dependent on <em>how</em> your friend traveled to Minneapolis: his gas mileage, the cost of gas, and, of course, the route he took. <span class="math inline">\(G\)</span> cannot be known without understanding the details of the path, and is therefore not path independent. The differenitial of <span class="math inline">\(G\)</span> is therefore <em>inexact</em>: <span class="math inline">\(G\)</span>.
;
;Now, what do we know about your friend’s distance, <span class="math inline">\(D\)</span>, to Chicago? This value does not dependent on how he traveled, the only information you need to know is his location, now, in Minneapolis. His distance to Chicago, therefore is a state variable and <span class="math inline">\(\Diff{}{D}\)</span> is an <em>exact</em> differential.
;
</div>
<div class="displayquote">
;<strong>Example 2:</strong> Let’s reconsider a situation like that of Example 1 this within the purview of thermodynamics. Consider the internal energy <span class="math inline">\(U\)</span> of a closed system. To achieve an infinitesimal change in energy <span class="math inline">\(\Diff{}{U}\)</span>, we provided a bit of work <span class="math inline">\(\text{\dj}W\)</span> or heat <span class="math inline">\(\text{\dj}Q\)</span>: <span class="math inline">\(\Diff{}{U} = \text{\dj}W + \text{\dj}Q\)</span> <a href="#fn1" class="footnote-ref" id="fnref1"><sup>1</sup></a>. The work performed and heat exchanged on the system is path-dependent — the total work done depends on <em>how</em> the work was performed or heat exchanged, and so <span class="math inline">\(\text{\dj}W\)</span> and <span class="math inline">\(\text{\dj}Q\)</span> are inexact.
;
</div>
;It is sometimes useful to ask yourself about the nature of a variable to ascertain whether the differential is exact or inexact. That is, it makes sense to ask yourself: “what is the energy of the system?” or “what is the pressure of the system”? This often helps in the identification of a state variable. However, it does not make sense to ask yourself “what is the work of the system” or “what is the heat” of the system — these values depend on the process. Instead, you have to ask yourself: “what is the work done on the system along this path?” or “what is the heat exchanged during this process?”.
;
;Finally, there are different properties we encounter during the evaluation exact differential (such as the linear differential in Eq. <a href="#eq:LinearDiff" reference-type="ref" reference="eq:LinearDiff"><span class="math display">\[eq:LinearDiff\]</span></a>), and inexact differentials (written as <span class="math inline">\(\text{\dj}f = M'(x,y) \Diff{}{x} + N'(x,y) \Diff{}{y}\)</span>). The integral of an exact differential over a closed path is necessary zero: <span class="math display">\[\begin{aligned}
\oint\Diff{}{f} \equiv 0,\end{aligned}\]</span> while the integral of an inexact differential over a closed path is not <em>necessarily</em> zero: <span class="math display">\[\begin{aligned}
\oint\text{\dj}f\underset{n}{\neq} 0.\end{aligned}\]</span> where <span class="math inline">\(\Big(\underset{n}{\neq}\Big)\)</span> symbolizes “not necessarily equal to”. Indeed, when evaluating the inexact differential, it is important to consider the path. For example, the work performed a system going from a macrostate <span class="math inline">\(s_i\)</span> to a macrostate <span class="math inline">\(s_2\)</span> is defined by path <span class="math inline">\(L_{1}\)</span>, then the total work performed is defined: <span class="math display">\[\begin{aligned}
W_{L_{1}} = \int\limits_{L_{1}} \text{\dj}W\end{aligned}\]</span> If we took a different path, <span class="math inline">\(L_{2}\)</span>, the total work performed by be different and <span class="math display">\[\begin{aligned}
W_{L_{1}} \underset{n}{\neq} W_{L_{2}}\end{aligned}\]</span> A good illustration of a line integral over a scalar field is shown in the multimedia Fig. <a href="#fig:LineIntegral" reference-type="ref" reference="fig:LineIntegral"><span class="math display">\[fig:LineIntegral\]</span></a>. It is clear that, depending on the path, the evaluated integral will have different values.
;
</div>
<div id="vector-calculus-release-tbd" class="section level3">
<h3>Vector Calculus (Release TBD)</h3>
;<strong><em>Encountered in: MAT<code>_</code>SCI 406, 408</em></strong>
;
</div>
</div>
<div id="sec:DiffEQ" class="section level2">
<h2>Differential Equations</h2>
;Differential equations — equations that relate functions with their derivatives — are central to the description of natural phenomena in physics, chemistry, biology and engineering. In the sections below, we will outline basic classification of differential equations and describe methods and techniques used in solving equations that are encountered in the MSE graduate core.
;
;The information provide below is distilled and specific to the MSE core, but is by <em>no means</em> a equivalent to a thorough 1- or 2-quarter course in ODEs and PDEs. For students who are completely unfamiliar with the material below; i.e., those who have not taken a course in differential equations, we highly recommend enrollment in Applied Math 311-1 and 311-2 <a href="#fn2" class="footnote-ref" id="fnref2"><sup>2</sup></a>.
;
<div id="classification-of-differential-equations-release-112016" class="section level3">
<h3>Classification of Differential Equations (Release: 11/2016)</h3>
;<strong><em>Encountered in: MAT<code>_</code>SCI 405, 406, 408</em></strong>
;
;Classification of differential equations provide intuition about the physical process that the equation describes, as well as providing context we use as we go about solving the equation. A differential equation can be classified as either ordinary or partial, linear or non-linear, and by its homogeneity and equation order. These are described briefly below, with examples.
;
<div id="ordinary-and-partial-differential-equations" class="section level4">
<h4>Ordinary and Partial Differential Equations —</h4>
;The primary classification we use to organize types of differential equations is whether they are <em>ordinary</em> or <em>partial</em> differential equations. <em>Ordinary differential equations</em> (ODEs) involve functions of a single variable. All derivatives present in the ODE are relative to that one variable. Partial differential equations are functions of more than one variable and the partial derivatives of these functions are taken with respect to those variables.
;
;An example of an ODE is shown in Eq. <a href="#eq:RLC" reference-type="ref" reference="eq:RLC"><span class="math display">\[eq:RLC\]</span></a>. This equation has two functions <span class="math inline">\(q(t)\)</span> (charge) and <span class="math inline">\(V(t)\)</span> (voltage), the values of which depend on time <span class="math inline">\(t\)</span>. All of the derivatives are with respect the independent variable <span class="math inline">\(t\)</span>. <span class="math inline">\(L\)</span>, <span class="math inline">\(R\)</span>, and <span class="math inline">\(C\)</span> are constants. <span class="math display">\[\begin{aligned}
L \FullDiff{2}{q(t)}{t} + R \FullDiff{}{q(t)}{t} + \frac{1}{C} q(t) = V(t) \label{eq:RLC}\end{aligned}\]</span> This general example describes the flow of charge as a function of time in a <a href="https://en.wikipedia.org/wiki/RLC_circuit">RLC circuit</a> with an applied voltage that changes with time. Other examples of ODEs you may encounter in the MSE core include ODEs for grain growth as a function of time and the equations of motion.
;
;<em>Partial differential equations</em> (PDEs) contain multivariable functions and their partial derivatives i.e., a derivative with respect to one variable with others held constant. As physical phenomenon often vary in both space and time, PDEs — and methods of solving them — will be encountered in many of the core MSE courses. These phenomena include wave behavior, diffusion, the Schödinger equation, heat conduction, the Cahn-Hilliard equation, and many others. A typical example of a PDEs you will encounter is Fick’s Second Law. In 1D, this is: <span class="math display">\[\begin{aligned}
\Partial{}{\varphi(x,t)}{t} = D\Partial{2}{\varphi(x,t)}{x} \label{eq:Ficks2}\end{aligned}\]</span> where <span class="math inline">\(\varphi\)</span> is the concentration as a function of position <span class="math inline">\(x\)</span> and time <span class="math inline">\(t\)</span>. This expression equates the change in the concentration over time to the shape (concavity) of the concentration profile. Partial differential equations are, by nature, often more difficult to solve than ODEs, but, as with ODEs, there exist simple, analytic, and systematic methods for solving many of these equations.
;
</div>
<div id="equation-order" class="section level4">
<h4>Equation Order —</h4>
;The <em>order</em> of a differential equation is simply the order of the highest derivative that is present in the equation. In the preceding section, Eq. <a href="#eq:RLC" reference-type="ref" reference="eq:RLC"><span class="math display">\[eq:RLC\]</span></a> is a second-order equation. Eq. <a href="#eq:Ficks2" reference-type="ref" reference="eq:Ficks2"><span class="math display">\[eq:Ficks2\]</span></a> is also a second-order equation. Students in the MSE core will encounter 4<sup>th</sup>-order equations such as the Cahn-Hilliard equation, which describes phase separation and is discussed in detail in MAT<code>_</code>SCI 408. One note concerning notation — when writing higher-order differential equations it is common to abandon Leibniz’s notation (where an <span class="math inline">\(n^{\text{th}}\)</span>-order derivative is denoted as <span class="math inline">\(\FullDiff{n}{f}{x}\)</span>) in favor of Lagrange’s notation in which the following representations are equivalent: <span class="math display">\[\begin{aligned}
\text{Leibniz}:& F\big[x,f(x),\FullDiff{}{f(t)}{x},\FullDiff{2}{f(t)}{x}...\FullDiff{n}{f(t)}{x}\big] = 0 \rightarrow\\
\text{Lagrange}:& F\big[x,f,f\prime,f\prime\prime...f^{(n)}\big] = 0 \label{eq:LagrangeNote}\end{aligned}\]</span> An example would be be the 3<sup>rd</sup>-order differential equation: <span class="math display">\[\begin{aligned}
f\prime\prime\prime + 3f\prime + f\exp{x} = x\end{aligned}\]</span>
;
</div>
<div id="linearity" class="section level4">
<h4>Linearity —</h4>
;While considering how to solve a differential equation, it is crucial to consider whether an equation is linear or non-linear. For example, an ODE like that represented in Eq. <a href="#eq:LagrangeNote" reference-type="ref" reference="eq:LagrangeNote"><span class="math display">\[eq:LagrangeNote\]</span></a> is linear if the <span class="math inline">\(F\)</span> is a linear function of the variables <span class="math inline">\(f, f', f\prime\prime...f^{(n)}\)</span>. This definition also applies to PDEs. The expression for the general linear ODE of order <span class="math inline">\(n\)</span> is: <span class="math display">\[\begin{aligned}
a_0(x)f^{(n)}+a_1(x)f^{(n-1)} + ... + a_n(x)f = g(t) \label{eq:LinearODE}\end{aligned}\]</span> Any expression that is not of this form is considered <em>nonlinear</em>. The presence of a product such as <span class="math inline">\(f\cdot f\prime\)</span>, a power such as <span class="math inline">\((f\prime)^2\)</span>, or a sinusoidal function of <span class="math inline">\(f\)</span> would make the equation nonlinear.
;
;The methods of solving linear differential equations are well-developed. Nonlinear differential equations, on the other hand, often require more complex analysis. As you will see, methods of <em>linearization</em> (small-angle approximations, stability theory) as well as numerical techniques are powerful ways to approach these problems.
;
</div>
<div id="homogeneity" class="section level4">
<h4>Homogeneity —</h4>
;Homogeneity of a linear differential equation, such as that shown in Eq. <a href="#eq:LinearODE" reference-type="ref" reference="eq:LinearODE"><span class="math display">\[eq:LinearODE\]</span></a> is satisfied if <span class="math inline">\(g(x) = 0\)</span>. This property of a differential equation is often connected to the <em>driving force</em> in a system. For example, the motion of a damped harmonic oscillator in 1D (derived from Newton’s laws of motion, <a href="https://en.wikipedia.org/wiki/Harmonic_oscillator">here</a>) is described by a homogeneous linear, 2<sup>nd</sup>-order ODE: <span class="math display">\[\begin{aligned}
x\prime\prime+2\zeta \omega_0 x\prime \omega_0^2 x = 0\end{aligned}\]</span> where <span class="math inline">\(x = x(t)\)</span> is position as a function of time (<span class="math inline">\(t\)</span>) , <span class="math inline">\(\omega_0\)</span> is the undamped angular frequency of the oscillator, and <span class="math inline">\(\zeta\)</span> is the damping ratio. If we add a sinusoidal driving force, however, the equation becomes inhomogeneous: <span class="math display">\[\begin{aligned}
x\prime\prime+2\zeta \omega_0 x\prime + \omega_0^2 x = \frac{1}{m} F_0 \sin{(\omega t)} \label{eq:DDSOscillator}\end{aligned}\]</span> One may notice that the form for Eq. <a href="#eq:DDSOscillator" reference-type="ref" reference="eq:DDSOscillator"><span class="math display">\[eq:DDSOscillator\]</span></a> is exactly that of the first equation shown in this section (Eq. <a href="#eq:RLC" reference-type="ref" reference="eq:RLC"><span class="math display">\[eq:RLC\]</span></a>) — the ODE for a damped, driven harmonic oscillator is exactly the same form as that of the RLC circuit operating under a alternating driving voltage.
;
</div>
<div id="boundary-conditions" class="section level4">
<h4>Boundary Conditions —</h4>
;Differential equations, when combined with a set of well-posed constraints, or boundary conditions, define a <em>boundary value problem</em>. Well-posed boundary value problems have unique solutions from the imposed physical constraints on the system of interest. This analysis allows for the extraction of relevant physical information investigating a physical system — the elemental composition at some position at time within a diffusion couple, the equilibrium displacement in a mechanically deformed body, or the energy eigenstate of a quantum system. While boundary conditions are not used not classify a differential equation itself, boundary conditions are used to classify the entire boundary value problem — which is defined by both the differential equation and the boundary value conditions.
;
;Boundary value problems are at the heart of physical description in science and engineering. Solving these types of problems allow for the extraction of information (concentration, deformation, stress state, quantum state, etc.) from a system. There are a few types of boundary conditions that you may encounter in the MSE core:
;
<ol style="list-style-type: decimal">
<li>;A <em>Dirichlet</em> (or first-type) boundary condition is one in which specific values are fixed on the boundary of a domain. An example of this is a system in which we have diffusion of carbon (in, for example, a carbourizing atmosphere) into iron (possessing a volume defined as domain <span class="math inline">\(\Omega\)</span>) where the carbon concentration <span class="math inline">\(C(\mathbf{r},t)\)</span> at the interface is known for all time <span class="math inline">\(t > 0\)</span>. Here, <span class="math inline">\(\mathbf{r}\)</span> is position vector and the domain boundary is denoted as <span class="math inline">\(\partial \Omega\)</span>). If this concentration is a known function, <span class="math inline">\(f(\textbf{r},t)\)</span>, then the Dirichlet condition is described as: <span class="math display">\[C(\textbf{r},t) = f(\textbf{r},t), \quad \forall\textbf{r} \in \partial \Omega\]</span>
;</li>
<li>;A <em>Neumann</em> (or second-type) boundary condition is the values of the normal derivative (a directional derivative with respect to the normal of a surface or boundary represented by the vector <span class="math inline">\(\mathbf{n}\)</span>) of the solution are known at the domain boundary. Continuing with our example above, this would mean we know the diffusion flux normal to the the boundary at <span class="math inline">\(r\)</span> at all times <span class="math inline">\(t\)</span>: <span class="math display">\[\Partial{}{C(\textbf{r},t)}{\mathbf{n}} = g(\textbf{r},t), \quad \forall\textbf{r} \in \partial \Omega\]</span> where <span class="math inline">\(g(\textbf{r},t)\)</span> is a known function, and the bold typesetting denotes a vector.
;</li>
<li>;Two other types of boundary conditions you may encounter are Cauchy and Robin. Cauchy boundary conditions specifies both the solution value and its normal derivative at the boundary — i.e., it provides both Dirichlet and Neumann conditions. The Robin condition provides a <em>linear combination</em> of the solution and its normal derivative and is common in convection-diffusion equations.
;</li>
<li>;Periodic boundary conditions are applied in periodic media or large, ordered systems. Previously described boundary conditions can therefore combined into periodic sets using infinite sums of sine and cosine functions to create <em>Fourier series</em>. This will be discussed in more detail in Sec. <a href="#sec:FourierMethods" reference-type="ref" reference="sec:FourierMethods">1.6.2.4</a>.
;</li>
</ol>
</div>
</div>
<div id="solving-differential-equations-release-112016" class="section level3">
<h3>Solving Differential Equations (Release: 11/2016)</h3>
;There are many ways to solve differential equations, including analytical and computational techniques. Below, we outline a number of methods that are used in the MSE core to solve relevant differential equations.
;
<div id="separation-of-variables" class="section level4">
<h4>Separation of Variables</h4>
;, also known as the <em>Fourier Method</em>, is a general method used in both ODEs and PDEs to reconstruct a differential equation so that the two variables are separated to opposite sides of the equation and then solved using techniques covered in an ODE class. <span id="sec:SepVar" label="sec:SepVar"><span class="math display">\[sec:SepVar\]</span></span>
;
;This method will be used in the solving of many simpler differential equations such as the heat and diffusion equations. These equations must be linear and homogeneous for separation of variables to work. The main goal is to take some sort of differential equation, for example an ordinary differential equation: <span class="math display">\[\begin{aligned}
\FullDiff{}{y}{x} &= g(x)h(y)\\
\intertext{which we can rearrange as:}
\frac{1}{h(y)}\mathop{dy} &= g(x)dx\\
\intertext{We now integrate both sides of the equation to find the solution:}
\int{\frac{1}{h(y)}\mathop{dy}} &= \int{g(x)\mathop{dx}}\end{aligned}\]</span> Clearly, we have separated our two variables, <span class="math inline">\(x\)</span> and <span class="math inline">\(y\)</span>, to opposite sides of the equation. If the functions are integrable and the resulting integration can be solved for <span class="math inline">\(y\)</span>, then a solution can be obtained.
;
;Note here that we have treated the <span class="math inline">\(\mathop{dy}/\mathop{dx}\)</span> derivative as a fraction which we have separated.
;
<div class="displayquote">
;<strong>Example 1:</strong> Exponential growth behavior can be represented by the equation: <span class="math display">\[\begin{aligned}
\FullDiff{}{y(t)}{t} &= k y(t)\\
\intertext{or}
\FullDiff{}{y}{t} &= k y\\
\intertext{This expression simply states that the growth rate of some quantity $y$ at time, $t$, is proportional to the value of $y$ itself at that time. This is a seperable equation:}
\frac{1}{y}dy &= k dt\\
\intertext{We can integrated both sides to get:}
\int{\frac{1}{y}dy} &= k \int{dt}\\
\text{ln}(y)+C_1 &= k t + C_2\\
\intertext{where $C_1$ and $C_2$ are the constants of integration. These can be combined:}
\text{ln}(y) &= kt+\tilde{C}\\
y &= e^{(kt+\tilde{C})}\\
y &= Ce^{kt}
\end{aligned}\]</span> This is clear exponential growth behavior as a function of time. Separation of variables is extremely useful in solving various ODEs and PDEs — it is employed in the solving of the diffusion equation in .
;
</div>
</div>
<div id="sec:Sturm-Liouville" class="section level4">
<h4>Sturm-Liouville Boundary Value Problems</h4>
;In this section, we use Sturm-Liouville theory in solving a separable, linear, second-order homogeneous partial differential equation. Sturm-Liouville theory can be used on differential equations (here, in 1D) of the form: <span class="math display">\[\begin{aligned}
\FullDiff{}{}{x}\Big[p(x)\FullDiff{}{y}{x}\Big]-q(x)y+\lambda r(x)y = 0 \label{eq:SturmLiouville}
\intertext{or}
\big[p(x)y\prime]\prime-q(x)y+\lambda r(x)y = 0 \label{eq:SturmLiouville-2}\end{aligned}\]</span> This type of problem requires knowledge of many use of many concepts and techniques in solving ODEs, including , Fundamental Solutions of Linear First- and Second-Order Homogeneous Equations, Fourier Series, and Orthogonal Solution Functions. It is important to note that the approach described below (adapted from JJ Hoyt’s <em>Phase Transformations</em>), which employs separation of variables and Fourier transforms, works only on linear equations. A different approach must be taken for non-linear equations (such as Cahn-Hilliard).
;
;We will use the example of a solid slab of material of length <span class="math inline">\(L\)</span> that has a constant concentration of some elemental species at time zero <span class="math inline">\(\varphi(x,0) = \varphi_0\)</span> for all <span class="math inline">\(x\)</span> within the slab. On either end of the slab we have homogeneous boundary conditions defining the surface concentrations fixed at <span class="math inline">\(\varphi(0,t) = \varphi(L,t) = 0\)</span> for all <span class="math inline">\(t\)</span>. The changing concentration profile, <span class="math inline">\(\varphi(x,t)\)</span> is dictated by Fick’s second law, as described earlier in Eq. <a href="#eq:Ficks2" reference-type="ref" reference="eq:Ficks2"><span class="math display">\[eq:Ficks2\]</span></a>:
;
;<span class="math display">\[\Partial{}{\varphi(x,t)}{t} = D\Partial{2}{\varphi(x,t)}{x} \label{eq:Ficks2-1}\]</span>
;
;To use separation of variables, we define the concentration <span class="math inline">\(\varphi(x,t)\)</span>, which is dependent on both position and time, to be a product of two functions, <span class="math inline">\(T(t)\)</span> and <span class="math inline">\(X(x)\)</span>:
;
;<span class="math display">\[\begin{aligned}
\varphi(x,t) &= T(t)X(x) \label{eq:SepVar-1}
\intertext{or, in shorthand,}
\varphi &= TX\end{aligned}\]</span>
;
;It isn’t clear why we do this at this point, but stay tuned. Combining Eqs. <a href="#eq:Ficks2-1" reference-type="ref" reference="eq:Ficks2-1"><span class="math display">\[eq:Ficks2-1\]</span></a> and <a href="#eq:SepVar-1" reference-type="ref" reference="eq:SepVar-1"><span class="math display">\[eq:SepVar-1\]</span></a> yields:
;
;<span class="math display">\[XT\prime = DTX\prime\prime\]</span>
;
;Where the primed Lagrange notation denotes total derivatives. <span class="math inline">\(T\)</span> and <span class="math inline">\(X\)</span> are functions only of <span class="math inline">\(t\)</span> and <span class="math inline">\(x\)</span>, respectively. Now, we separate the variables completely to acquire:
;
;<span class="math display">\[\frac{1}{DT}T\prime = \frac{1}{X}X\prime\prime\]</span>
;
;This representation conveys something critical: each side of the equation must be equal to <em>the same</em> constant. This is because the two sides of the equation are equal to each other and the only way a collection of time-dependent quantities can be equivilent to a selection of position-dependent quantities is for them to be constant with respect to both time and position. We select this constant — for reasons that become clear of the convience of this selection later in the analysis — as <span class="math inline">\(-\lambda^2\)</span>:
;
<div class="subequations">
;<span class="math display">\[\begin{aligned}
\frac{1}{DT}T\prime &= -\lambda^2 \label{eq:SepT}\\
\frac{1}{X}X\prime\prime &= -\lambda^2 \label{eq:SepX}
\end{aligned}\]</span>
;
</div>
;Integration of Eq. <a href="#eq:SepT" reference-type="ref" reference="eq:SepT"><span class="math display">\[eq:SepT\]</span></a> yields, from : <span class="math display">\[\begin{aligned}
\frac{1}{DT}T\prime &= -\lambda^2 \nonumber\\
\frac{1}{T}\FullDiff{}{T}{t} &= -\lambda^2 D \nonumber\\
\int \frac{1}{T}\Diff{}{T} &= -\int \lambda^2 D \Diff{}{t} \nonumber\\
\ln{T} &= -\lambda^2 D t + T_0 \nonumber\\
\intertext{where $T_0$ is the combined constant of integration:}
T = T(t) &= \exp{(-\lambda^2 D t + T_0)} \nonumber\\
T(t) &= T_0 \exp{(-\lambda^2 D t)} \label{eq:Tt}\end{aligned}\]</span> Eq. <a href="#eq:SepX" reference-type="ref" reference="eq:SepX"><span class="math display">\[eq:SepX\]</span></a>, on the other hand, is a linear, homogeneous, second-order ODE with constant coefficients that describes simple harmonic behavior. We can solve this by assessing its <a href="https://en.wikipedia.org/wiki/Characteristic_equation_(calculus)">characteristic equation</a>: <span class="math display">\[\begin{aligned}
r^2+\lambda^2 = 0\\
\intertext{which has roots:}
r = \pm \lambda i\end{aligned}\]</span> When the roots of the characteristic equation are of the form <span class="math inline">\(r = \alpha \pm \beta i\)</span>, the <a href="http://www.stewartcalculus.com/data/CALCULUS%20Concepts%20and%20Contexts/upfiles/3c3-2ndOrderLinearEqns_Stu.pdf">solution of the differential equation (Pg. 5)</a> is: <span class="math display">\[y = e^{\alpha x}(c_1 \cos{\beta x} + c_2 \sin{\beta x})\]</span>
;
;In this instance, <span class="math inline">\(\alpha = 0\)</span> and <span class="math inline">\(\beta = \lambda\)</span>, so our solution is:
;
;<span class="math display">\[X = X(x) = \tilde{A} \cos{\lambda x} + \tilde{B} \sin{\lambda x} \label{eq:Xx}\]</span>
;
;<span class="math inline">\(\tilde{A}\)</span> and <span class="math inline">\(\tilde{B}\)</span> are constants that will be further simplified later. Recalling Eq. <a href="#eq:SepVar-1" reference-type="ref" reference="eq:SepVar-1"><span class="math display">\[eq:SepVar-1\]</span></a> and utilizing our results from Eqs. <a href="#eq:Tt" reference-type="ref" reference="eq:Tt"><span class="math display">\[eq:Tt\]</span></a> and <a href="#eq:Xx" reference-type="ref" reference="eq:Xx"><span class="math display">\[eq:Xx\]</span></a>, we find: <span class="math display">\[\begin{aligned}
\varphi(x,y) &= X(x)T(x) = T_0 \big[\tilde{A} \cos{\lambda x} + \tilde{B} \cos{\lambda x}\big]\exp{(-\lambda^2 D t)}\\
\intertext{where we now define $T_0 \tilde{A} = A$ and $T_0 \tilde{B} = B$ to get:}
\varphi(x,y) &= X(x)T(x) = \big[A\cos{\lambda x} + B\sin{\lambda x}\big]\exp{(-\lambda^2 D t)} \label{eq:DiffSol}\end{aligned}\]</span> Physially, this solution begins to make sense. At <span class="math inline">\(t=0\)</span> we have a constant concentration, but concentration begins to decay esponentially with time as <span class="math inline">\(D\)</span>, <span class="math inline">\(t\)</span>, and <span class="math inline">\(\lambda\)</span> are all positive, real constants. The concentration profile is a linear combination of sine and cosine functions, which does not yet yield any physical intuition for this system as we have yet to utilize boundary conditions.
;
;Recall at this point that we have not specified any value for the constant <span class="math inline">\(\lambda\)</span>, as is typical when solving this type of Sturm-Liouville problem. This suggests that there are possible solutions for all values of <span class="math inline">\(\lambda_n\)</span>. The Principle of Superposition dictates, then, that if Eq. <a href="#eq:DiffSol" reference-type="ref" reference="eq:DiffSol"><span class="math display">\[eq:DiffSol\]</span></a> is a solution, the complete solution to the problem is a summation of all possible solutions:
;
;<span class="math display">\[\begin{aligned}
\Aboxed{\varphi(x,y) = \sum_{n=1}^\infty \big[A_n\cos{\lambda_n x} + B_n\sin{\lambda_n x}\big]\exp{(-\lambda_n^2 D t)}} \label{eq:DiffSolFull}\end{aligned}\]</span>
;
;As the value of <span class="math inline">\(\lambda\)</span> influences the values of <span class="math inline">\(A\)</span> and <span class="math inline">\(B\)</span>, these values must also be calculated for each <span class="math inline">\(\lambda_n\)</span>.
;
;Now, to completely solve our well-posed boundary value problem, we utilize our boundary conditions:
;
<div class="subequations">
;<span class="math display">\[\begin{aligned}
\varphi(0,t) &= 0\, \quad t \geq 0 \label{eq:Boundx0}\\
\varphi(L,t) &= 0\, \quad t \geq 0 \label{eq:BoundxL}\\
\varphi(x,0) &= \varphi_0\, \quad 0<x<L \label{eq:Time0}
\end{aligned}\]</span>
;
</div>
;At <span class="math inline">\(x = 0\)</span>, the sine term in Eq. <a href="#eq:DiffSolFull" reference-type="ref" reference="eq:DiffSolFull"><span class="math display">\[eq:DiffSolFull\]</span></a> is zero, and therefore the boundary condition in Eq. <a href="#eq:Boundx0" reference-type="ref" reference="eq:Boundx0"><span class="math display">\[eq:Boundx0\]</span></a> can only be satisfied at all t if <span class="math inline">\(A_n = 0\)</span>. At <span class="math inline">\(x = L\)</span>, <span class="math inline">\(\sin{\lambda_n x}\)</span> must be zero for all values of <span class="math inline">\(\lambda_n\)</span>, therefore <span class="math inline">\(\lambda_n = n\pi/L\)</span>. We need only solve now for <span class="math inline">\(B_n\)</span> using the intial condition, Eq. <a href="#eq:Time0" reference-type="ref" reference="eq:Time0"><span class="math display">\[eq:Time0\]</span></a>.
;
;Using our values of <span class="math inline">\(A_n\)</span> and <span class="math inline">\(\lambda_n\)</span> and assessing Eq. <a href="#eq:DiffSolFull" reference-type="ref" reference="eq:DiffSolFull"><span class="math display">\[eq:DiffSolFull\]</span></a> at time <span class="math inline">\(t=0\)</span> yields
;
;<span class="math display">\[\varphi_0 = \sum_{n=1}^\infty B_n \sin{\frac{n \pi x}{L}} \label{eq:Time0-1}\]</span>
;
;Here, we must recognized the orthogonal property of the sine function, which states that
;
;<span class="math display">\[\int_0^L \sin{\frac{n \pi x}{L}} \sin{\frac{m \pi x}{L}}
\begin{cases}
= 0, & \text{if}\ n\neq m \\
\neq 0, & \text{if}\ n = m
\end{cases}\]</span>
;
;You can test this graphically using a plotting program if you like — the integrated value of this product is only non-zero when <span class="math inline">\(n=m\)</span> — or you can follow the proof <a href="http://www.math.umd.edu/~psg/401/ortho.pdf">here</a>. We can multiply both sides of the Eq. <a href="#eq:Time0-1" reference-type="ref" reference="eq:Time0-1"><span class="math display">\[eq:Time0-1\]</span></a> by <span class="math inline">\(\sin{n \pi x/L}\)</span>, then, and integrate both sides from 0 to <span class="math inline">\(L\)</span>:
;
<div class="subequations">
;<span class="math display">\[\begin{aligned}
\varphi_0 \int_0^L\sin{\frac{m \pi x}{L}} &= \int_0^L \sum_{n=1}^\infty \big[B_n \sin{\frac{n \pi x}{L}} \sin{\frac{m \pi x}{L}}\big] \nonumber
\intertext{After integration, the only term that survives on the right-hand side is the $m=n$ term, and therefore:}
\varphi_0 \int_0^L\sin{\frac{n \pi x}{L}} &= B_n\int_0^L \sin{\frac{n \pi x}{L}}^2 \nonumber\\
\varphi_0 \int_0^L\sin{\frac{n \pi x}{L}} &= \frac{B_n L}{4} \big[2- \frac{\sin{2 n \pi}}{n \pi} \big] \nonumber\\
\intertext{the $\sin{2 n \pi}$ term is always zero:}
\varphi_0 \int_0^L\sin{\frac{n \pi x}{L}} &= \frac{B_n L}{2} \nonumber\\
2 \frac{\varphi_0}{L} \int_0^L\sin{{n \pi x}{L}} &= B_n \nonumber\\
B_n &= 2 \frac{\varphi_0}{L} \big[\frac{L}{n \pi}(1-\cos{n \pi})\big] \nonumber\\
\Aboxed{B_n &= 2 \frac{\varphi_0}{n \pi} (1-\cos{n \pi})}
\end{aligned}\]</span>
;
</div>
;For even values of <span class="math inline">\(n\)</span>, the <span class="math inline">\(B_n\)</span> constant is zero. For odd values of <span class="math inline">\(n\)</span>, <span class="math inline">\(B_n = \frac{4 \varphi_0}{n \pi}\)</span>. We utilize the values we acquired for <span class="math inline">\(A_n\)</span>, <span class="math inline">\(B_n\)</span>, and <span class="math inline">\(\lambda\)</span> and plug them into Eq. <a href="#eq:DiffSolFull" reference-type="ref" reference="eq:DiffSolFull"><span class="math display">\[eq:DiffSolFull\]</span></a>. A change in summation index to account for the <span class="math inline">\(B_n\)</span> values yields:
;
;<span class="math display">\[\begin{aligned}
\Aboxed{\varphi(x,t) = \frac{4 c_0}{\pi} \sum_{k=0}^\infty \frac{1}{2k+1} \sin{\frac{(2k+1)\pi x}{L}}\exp{\Big[-\big(\frac{(2k+1)\pi}{L}\big)^2 Dt\Big]}}\end{aligned}\]</span>
;
;This summation converges quickly. We now have the ability to calculate the function <span class="math inline">\(\varphi(x,t)\)</span> at any position <span class="math inline">\(0 < x < L\)</span> and time <span class="math inline">\(t > 0\)</span>!
;
</div>
<div id="method-of-integrating-factors" class="section level4">
<h4>Method of Integrating Factors</h4>
;is a technique that is commonly used in the solving of first-order linear ordinary differential equations (but is not restricted to equations of that type). In thermodynamics, it is used to convert a differential equation that is not exact (i.e., path-dependent, See Sec. <a href="#subsec:eidiff" reference-type="ref" reference="subsec:eidiff">1.5.2</a>) to an exact equation, such as in the derivation of entropy as an exact differential (Release TBD).
;
</div>
<div id="sec:FourierMethods" class="section level4">
<h4>Fourier Integral Transforms</h4>
;This section will introduce an extremely powerful technique in solving differential equations: the Fourier transform. This technique is useful because it allows us to transform a complicated problem — a boundary value problem — into a simpler problem which can often be approached with ODE techniques or even algebraically.
;
;There are many excellet sources provided for this section, listed below.
;
<ol style="list-style-type: decimal">
<li>;José Figueroa-O’Farrill’s wonderful <em>Integral Transforms</em> from <em>Mathematical Techniques III</em> at the University of Edinborough.
;</li>
<li>;W.E Olmstead and V.A. Volpert’s <em>Differential Equations in Applied Mathematics</em> at Northwestern University.
;</li>
<li>;J.J. Hoyt’s chapter on the <em>Mathematics of Diffusion</em> in his <em>Phase Transformations</em> text.
;</li>
<li>;Paul Shewman’s <em>Diffusion in Solids</em>.
;</li>
<li>;J.W. Brown and R.V. Churchill’s <em>Fourier Series and Boundary Values Problems</em>, 6<sup>th</sup> Edition.
;</li>
</ol>
;The primary goal behind the Fourier transform is to solve a differential equation with some unknown function <span class="math inline">\(f\)</span>. We apply the transform (<span class="math inline">\(\mathscr{F}\)</span>) to convert the function into something that can be solved more easily: <span class="math inline">\(f \xrightarrow{\mathscr{F}} F\)</span>. The transformed function is often also represented using a <span class="math inline">\(\hat{f}\)</span>. We solve for <span class="math inline">\(F\)</span> and then perform an inverse Fourier transform (<span class="math inline">\(\mathscr{F}^{-1}\)</span>) to recover the solution for <span class="math inline">\(f\)</span>.
;
;We find that Fourier <em>series</em> — which are used to when working with periodic functions — can be generalized to Fourier integral transforms (or Fourier transforms) when the period of the function becomes infinitely long. Let’s begin with the Fourier series an build on our results from our discussion above where we found that a continuous function <span class="math inline">\(f(x)\)</span> defined on some finite interval <span class="math inline">\(x \in[0,L]\)</span> and vanishing at the boundaries, <span class="math inline">\(f(0) = f(L) = 0\)</span> can be expanded as shown in <a href="#eq:DiffSolFull" reference-type="ref" reference="eq:DiffSolFull"><span class="math display">\[eq:DiffSolFull\]</span></a>.
;
;The following derivation is adapted from Olmstead and Volpert. In general, we can attempt to represent <em>any</em> function that is periodic over period <span class="math inline">\([0,L]\)</span> with a Fourier series of form:
;
;<span class="math display">\[f(x) = a_0 + \sum_{n=1}^\infty\left[a_n \cos{\frac{2 \pi n x}{L}} + b_n \sin{\frac{2 \pi n x}{L}}\right]
\label{eq:GenSol}\]</span>
;
;However, we need to know how to find the coefficients <span class="math inline">\(a_0\)</span>, <span class="math inline">\(a_n\)</span>, and <span class="math inline">\(b_n\)</span> for this representation of <span class="math inline">\(f(x)\)</span>. For this analysis we must utilize the following integral identities:
;
;<span class="math display">\[\int_0^L{\sin{\frac{2 \pi n x}{L}}\cos{\frac{2 \pi n x}{L}}}dx= 0 \quad n,m = 1,2,3,...,\]</span>
;
;<span class="math display">\[\int_0^L{\cos{\frac{2 \pi n x}{L}}\cos{\frac{2 \pi m x}{L}}} dx=
\begin{cases}
0, \text{\,if} \quad n,m = 1,2,3,..., n\neq m\\
L/2, \text{\,if} \quad n = m = 1,2,3,...,\\
\end{cases}\]</span>
;
;<span class="math display">\[\int_0^L{\sin{\frac{2 \pi n x}{L}}\sin{\frac{2 \pi m x}{L}}} dx =
\begin{cases}
0, \text{\,if} \quad n,m = 1,2,3,..., n\neq m\\
L/2, \text{\,if} \quad n = m = 1,2,3,...,\\
\end{cases}\]</span>
;
;<span class="math display">\[\int_0^L{\cos{\frac{2 \pi n x}{L}}} dx =
\begin{cases}
0, \text{\,if} \quad n,m = 1,2,3,...,\\
L, \text{\,if} \quad n = 0\\
\end{cases}\]</span>
;
;<span class="math display">\[\int_0^L{\sin{\frac{2 \pi n x}{L}}} dx =
0, \text{\,if} \quad n,m = 0,1,2,3,...,\\\]</span>
;
;These identities state the orthogonal properties of sines and cosines that will be used to derive the coefficients <span class="math inline">\(a_0\)</span>, <span class="math inline">\(a_n\)</span>, and <span class="math inline">\(b_n\)</span>. Recall that two functions are orthogonal on an interval if
;
;<span class="math display">\[\int_a^b f(x)g(x)dx = 0\]</span>
;
;We can therefore multiply Eq. <a href="#eq:GenSol" reference-type="ref" reference="eq:GenSol"><span class="math display">\[eq:GenSol\]</span></a> by <span class="math inline">\(\cos{\frac{2 \pi x}{L}}\)</span> (note <span class="math inline">\(n = 1\)</span>) and integrate over <span class="math inline">\([0,L]\)</span>:
;
;<span class="math display">\[\begin{aligned}
\int_0^L f(x)\cos{\frac{2 \pi x}{L}} dx &= a_0 \int_0^L \cos{\frac{2 \pi x}{L}} dx +\\
&a_1 \int_0^L \cos{\frac{2 \pi x}{L}} \cos{\frac{2 \pi x}{L}} dx +b_1 \int_0^L \sin{\frac{2 \pi x}{L}} cos{\frac{2 \pi x}{L}} dx +\\
&a_2 \int_0^L \cos{\frac{4 \pi x}{L}} \cos{\frac{2 \pi x}{L}} dx +b_2 \int_0^L \sin{\frac{4 \pi x}{L}} cos{\frac{2 \pi x}{L}} dx + ...\\\end{aligned}\]</span>
;
;Applying the orthogonal properties of the integral products finds that all terms on the right-hand side of this equation are zero apart from the <span class="math inline">\(a_1\)</span> term. The equation therefore reduces to:
;
;<span class="math display">\[\int_0^L f(x)\cos{\frac{2 \pi x}{L}} dx = a_1 \int_0^L \cos{\frac{2 \pi x}{L}} cos{\frac{2 \pi x}{L}} dx= a_1\frac{L}{2}\]</span>
;
;and
;
;<span class="math display">\[a_1 = \frac{2}{L} \int_0^L f(x)\cos{\frac{2 \pi x}{L}} dx\]</span>.
;
;The other Fourier coefficients can be solved for in a similar manner, which yields the general solutions:
;
;<span class="math display">\[\begin{aligned}
a_0 &= \frac{1}{L} \int_0^L f(x)\\
a_n &= \frac{2}{L} \int_0^L f(x)\cos{\frac{2 n \pi x}{L}}dx \quad (n = 1,2,3...)\\
b_n &= \frac{2}{L} \int_0^L f(x)\sin{\frac{2 n \pi x}{L}}dx\quad (n = 1,2,3...)\end{aligned}\]</span>
;
;To this point we’ve solved, generally, for the coefficients of a Fourier series over a finite interval. This is useful, but we my want to use the full complex form of the Fourier series in later discussion of the Fourier transform. We know that <a href="https://en.wikipedia.org/wiki/Euler's_formula#Relationship_to_trigonometry">Euler’s formula</a> can be used to express trigonometric functions with the complex exponential function:
;
;<span class="math display">\[\begin{aligned}
\sin{\frac{2 \pi n x}{L}} &= \frac{1}{2i}\left(e^{i\frac{n \pi x}{L}}+e^{-i\frac{n \pi x}{L}}\right) \nonumber \\
\cos{\frac{2 \pi n x}{L}} &= \frac{1}{2}\left(e^{i\frac{n \pi x}{L}}+e^{-i\frac{n \pi x}{L}}\right) \label{eq:Euler}\end{aligned}\]</span>
;
;and we define the wavenumbers to be:
;
;<span class="math display">\[k_n = 2 \pi n/L \quad n=0,1,2,...,
\label{eq:Wavenumber}\]</span>
;
;and therefore Eq. <a href="#eq:Euler" reference-type="ref" reference="eq:Euler"><span class="math display">\[eq:Euler\]</span></a> is written as:
;
;<span class="math display">\[\begin{aligned}
\sin{k_n x} &= \frac{1}{2i}\left(e^{i k_n x}+e^{-i k_n x}\right) \nonumber \\
\cos{k_n x} &= \frac{1}{2}\left(e^{i k_n x}+e^{-i\ k_n x}\right) \label{eq:Euler}\end{aligned}\]</span>
;
;This allows us to write the complete Fourier series (Substitute Eq. <a href="#eq:Euler" reference-type="ref" reference="eq:Euler"><span class="math display">\[eq:Euler\]</span></a> into <a href="#eq:GenSol" reference-type="ref" reference="eq:GenSol"><span class="math display">\[eq:GenSol\]</span></a>):
;
;<span class="math display">\[f_{L}(x) \sim \sum_{n=-\infty}^{\infty} c_n e^{i k_n x}
\label{eq:ComplexFourierSeries}\]</span>
;
;For convenience, we’ll define the integral to be <span class="math inline">\([-\frac{L}{2},\frac{L}{2}]\)</span>. The <span class="math inline">\(\sim\)</span> notation indicates that the series representation is an approximation, and the <span class="math inline">\(L\)</span> represents the period over which the series is applied. The orthogonality condition holds for these complex exponential and its complex conjugate over this interval:
;
;<span class="math display">\[\int_{-\frac{L}{2}}^{\frac{L}{2}} e^{i k_n x} e^{-i k_m x} dx =
\begin{cases}
0, \text{\,if} \quad n \neq m\\
L, \text{\,if} \quad n = m\\
\end{cases}\]</span>
;
;Therefore, if we multiply Eq. <a href="#eq:ComplexFourierSeries" reference-type="ref" reference="eq:ComplexFourierSeries"><span class="math display">\[eq:ComplexFourierSeries\]</span></a> by <span class="math inline">\(e^{-i k_m x}\)</span> and solve we find the only term that survives is when <span class="math inline">\(n=m\)</span>:
;
;<span class="math display">\[\int_{-\frac{L}{2}}^{\frac{L}{2}} f_L(x) e^{-i k_m x} dx = L c_m.\]</span>
;
;We can revert the place-keeping subscript <span class="math inline">\(m\)</span> to <span class="math inline">\(n\)</span> and solve for the Fourier coefficients to find:
;
;<span class="math display">\[c_n = \frac{1}{L}\int_{-\frac{L}{2}}^{\frac{L}{2}} f_L(x) e^{-i k_n x} dx \quad \text{for\,} n = 0, \pm1, \pm2,...
\label{eq:FourierComps}\]</span>
;
;Alright, we’ve defined an interval <span class="math inline">\([-L/2, L/2]\)</span>, but we want to investigate this interval as <span class="math inline">\(L \rightarrow \infty\)</span> in an attempt to eliminate the periodicity of the Fourier series. If <span class="math inline">\(L \rightarrow \infty\)</span>, we know that our function <span class="math inline">\(f_L(x)\)</span> will be non-zero over only a very small range — say an interval of <span class="math inline">\([-a/2, a/2]\)</span> where <span class="math inline">\(a << L\)</span>. This means that
;
;<span class="math display">\[f_L{x} =
\begin{cases}
1 \quad \text{for} |x|<a/2\\
0 \quad \text{for} a/2 < |x| < L/2
\end{cases}
\label{eq:Linfty}\]</span>
;
;This function is zero except for a small bump at the origin of height 1 and width <span class="math inline">\(a\)</span>. Let’s assess our function over the non-zero interval:
;
;<span class="math display">\[\int_{-\frac{a}{2}}^{\frac{a}{2}} e^{-i k_n x} dx = \frac{\sin k_n a/2}{k_n L/2} = \frac{\sin n \pi a/L}{n \pi}.
\label{eq:Thing}\]</span>
;
;But how does this allow us to consider a continuous Fourier integral transform? Well, we need to consider the function <span class="math inline">\(f_L(x)\)</span> as <span class="math inline">\(L \rightarrow \infty\)</span>. By doing so, we drive all the harmonics of the Fourier function — apart from the central one — out beyond infinity. <span class="math inline">\(f(x)\)</span> then has a single bump of width <span class="math inline">\(L\)</span> centered at the origin. That is, the separation between the <span class="math inline">\(n\)</span> harmonics goes to zero, and the representation contains all harmonics. Further, as <span class="math inline">\(L \rightarrow \infty\)</span> we no longer have a periodic function and we can i.e., the fundamental period becomes so large that we no longer have non-periodic function at all.
;
;This allows us to transition from a discrete description to a continuum and our Fourier sum can now be described as a Fourier integral. Recall the Fourier series (Eq/ <a href="#eq:ComplexFourierSeries" reference-type="ref" reference="eq:ComplexFourierSeries"><span class="math display">\[eq:ComplexFourierSeries\]</span></a>):
;
;<span class="math display">\[f_{L}(x) \sim \sum_{n=-\infty}^{\infty} c_n e^{i k_n x}\]</span>
;
;Which we now write as:
;
;<span class="math display">\[f_{L}(x) \sim \sum_{n=-\infty}^{\infty} \frac{\Delta k}{2\pi/L} c_n e^{i k_n x} = \sum_{n=-\infty}^{\infty} \frac{\Delta k}{2\pi} L c_n e^{i k_n x}
\label{eq:Thing2}\]</span>
;
;where <span class="math inline">\(\Delta k = 2\pi/L\)</span> is the difference between successive values of <span class="math inline">\(k_n\)</span>. We now define a function <span class="math inline">\(F(k)\)</span> as
;
;<span class="math display">\[F(k) \equiv \Lim{L \rightarrow \infty} L c_n = \Lim{L \rightarrow \infty} L c_{kL/2 \pi}
\label{eq:DefFourierTransform}\]</span>
;
;Combining this definition with Eq. <a href="#eq:Thing" reference-type="ref" reference="eq:Thing"><span class="math display">\[eq:Thing\]</span></a> gives:
;
;<span class="math display">\[F(k) = \frac{\sin{(ka/2)}}{k/2}\]</span>
;
;and as <span class="math inline">\(L \rightarrow \infty\)</span>, Eq. <a href="#eq:Thing2" reference-type="ref" reference="eq:Thing2"><span class="math display">\[eq:Thing2\]</span></a> goes as
;
;<span class="math display">\[\begin{aligned}
f(x) &= \Lim{L \rightarrow \infty} \sum_{n=-\infty}^{\infty} \frac{\Delta k}{2\pi} L c_n e^{i k_n x} \\
\Aboxed{f(x) &= \frac{1}{2\pi}\int_{-\infty}^{\infty}F(k) e^{ikx} dk}
\label{eq:FourierInversion}\end{aligned}\]</span>
;
;The function <span class="math inline">\(F(x)\)</span> is the Fourier transform of <span class="math inline">\(f(x)\)</span> and Eq. <a href="#eq:FourierInversion" reference-type="ref" reference="eq:FourierInversion"><span class="math display">\[eq:FourierInversion\]</span></a> as a continuous superposition of Fourier component, with each component now represented by a <em>continuous</em> function <span class="math inline">\(f(x)\)</span>. Similarly, from Eq. <a href="#eq:DefFourierTransform" reference-type="ref" reference="eq:DefFourierTransform"><span class="math display">\[eq:DefFourierTransform\]</span></a> and Eq. <a href="#eq:FourierComps" reference-type="ref" reference="eq:FourierComps"><span class="math display">\[eq:FourierComps\]</span></a>:
;
;<span class="math display">\[\begin{aligned}
\Aboxed{F(k) &= \int_{\infty}^{\infty} f(x) e^{-i k x} dx}
\label{eq:FourierTransform}\end{aligned}\]</span>
;
;Eq. <a href="#eq:FourierTransform" reference-type="ref" reference="eq:FourierTransform"><span class="math display">\[eq:FourierTransform\]</span></a> is non-periodic analog to the expression for deriving the Fourier coefficients <span class="math inline">\(c_n\)</span> in the periodic case. We call this function the <em>Fourier (Integral) Transform</em> of the function <span class="math inline">\(f(x)\)</span> and it is often written as
;
;<span class="math display">\[F(k) \equiv \mathscr{F}\big[f(t)\big]
\label{eq:InversionFormula}\]</span>
;
;Similarly, Eq. <a href="#eq:InversionFormula" reference-type="ref" reference="eq:InversionFormula"><span class="math display">\[eq:InversionFormula\]</span></a> is known as the <em>Inversion Formula</em> or <em>Inverse Fourier (Integral) Transform</em> and is used to return the Fourier-transformed function from frequency space. It is often represented as:
;
;<span class="math display">\[f(x) \equiv \mathscr{F}^{-1}\big[F(k)\big]\]</span>
;
<div class="displayquote">
;<strong>Example:</strong> Let’s do a simple Fourier transform of a <a href="https://en.wikipedia.org/wiki/Square-integrable_function">square-integrable function</a> (this condition establishes that the function has a Fourier transform). We’ll try a square pulse over the interval <span class="math display">\[-, \]</span>:
;
;<span class="math display">\[f(x) =
\begin{cases}
1, \text{\,if\,} |x| < \pi\\
0, \text{\,otherwise}\\
\end{cases}\]</span>
;
;We take the Fourier integral transform over the non-zero interval:
;
;<span class="math display">\[\begin{aligned}
F(x) &= \frac{1}{2 \pi}\int_{-\infty}^{\infty} f(x) e^{-i k x} dx\\
&= \frac{1}{2 \pi}\int_{-\pi}^{\pi} e^{-i k x} dx\\
&= -\frac{1}{2i \pi k} e^{-i k x}\Big|_{-\pi}^{\pi}\\
&= -\frac{1}{2i \pi k} (e^{-i k \pi}-e^{i k \pi})\\
&= \frac{\sin{\pi k }}{\pi k}
\end{aligned}\]</span>
;
</div>
;Integral transforms will prove massively useful in solving boundary value problems in the MAT<code>_</code>SCI core.
;
<div class="displayquote">
;<strong>Example</strong> One example is diffusion in the thin film problem. Imagine that there is thin region of finite width with high concentration of some species <strong>B</strong> situated between two “infinite” (thick) plate of pure <strong>A</strong> (after Hoyt, 1-6). Diffusion from the thin film is allowed to proceed over time into the adjacent plates. The thin film is centered at <span class="math inline">\(x = 0\)</span>, so the concentration profile will be an even function <span class="math inline">\([\varphi(x,t) = \varphi(-x,t)]\)</span> How do we solve for the evolution of the concentration profile over time?
;
;This is an example in which we want to interpret this geometry as one with infinite period. When doing so we should consider using a Fourier integral transform.
;
;From the section above, we understand that the concentration profile <span class="math inline">\(c(x,t)\)</span> can be obtained from the inverse transform of the Fourier space function <span class="math inline">\(\Phi(k,t)\)</span>. Above, we derived the full Fourier integral transform, but here we know that the function is even, and so we can perform a Fourier Cosine integral transform, which simplifies the mathematics and allows us to perform the transform from <span class="math inline">\([0,\infty]\)</span>. The following derivation is after Hoyt, Ch. 1-8.
;
;<span class="math display">\[\begin{aligned}
f(x) = \frac{1}{\pi} \int_{-\infty}^{\infty} F(x) \cos{(kx)} dk\\
F(x) = \frac{1}{\pi} \int_0^{\infty} f(x) \cos{(kx)} dx\end{aligned}\]</span>
;
;In our case, we have:
;
;<span class="math display">\[\begin{aligned}
\varphi(x,t) = \frac{1}{\pi} \int_{-\infty}^{\infty} \Phi(k,t) \cos{(kx)} dk\\
\Phi(k,t) = \frac{1}{\pi} \int_0^{\infty} \varphi(x,t) \cos{(kx)} dx
\label{eq:OddSol1}\end{aligned}\]</span>
;
;The utility of utilizing the Fourier intergral transform is that the PDEs in space and time can be converted to ODEs in the time domain alone, which are often much easier to solve. The ability for us to do this hinges on a key property of a Fourier transform that relates the Fourier transform of the <span class="math inline">\(n\)</span><sup>th</sup> derivative of a function to the Fourier transform of the function itself.
;
;<span class="math display">\[\mathscr{F}\big[f^{(n)}(x)\big](k) = (ik)^{n}\mathscr{F}\big[f(x)\big](k)
\label{eq:}\]</span>
;
;This, as you will see, allows us to convert a PDE in <span class="math inline">\(t\)</span> and <span class="math inline">\(x\)</span> to a ODE in <span class="math inline">\(t\)</span> alone. Let’s apply this property to the 1D diffusion equation. First, we know we are performing a Fourier transform in <span class="math inline">\(x\)</span>, so the time derivative can be pulled from the integral on the left-hand side of the equation.
;
;<span class="math display">\[\begin{aligned}
\mathscr{F}[\Partial{}{\varphi(x,t)}{t}] &= \frac{1}{\pi}\int_{0}^{\infty} \Partial{}{\varphi(x,t)}{t} \cos{(-ikx)} dx\\
&= \frac{1}{\pi}\Partial{}{}{t}\left[\int_{0}^{\infty}\varphi(x,t)\cos{(-ikx)} dx\right]\\
&= \frac{1}{\pi}\Partial{}{}{t}\left[\Phi(k,t)\right]\end{aligned}\]</span>
;
;and the right-hand side of the equation is:
;
;<span class="math display">\[\begin{aligned}
\mathscr{F}\big[D\Partial{2}{}{x}\varphi(x,t)\big] &= (ik)^2D\mathscr{F}\big[\varphi(x,t)\big]\\
&= -D\frac{k^2}{\pi}\int_0^{\infty}\varphi(x,t)\cos{(-ikx)} dx\\
&= -D\frac{k^2}{\pi} \Phi(k,t)\end{aligned}\]</span>
;
;and therefore:
;
;<span class="math display">\[\begin{aligned}
\frac{1}{\cancel{\pi}}\Partial{}{}{t}\left[\Phi(k,t)\right] &= -D\frac{k^2}{\cancel{\pi}} \Phi(k,t)\\
\Aboxed{\Partial{}{}{t}\left[\Phi(k,t)\right] &= -Dk^2 \Phi(k,t)}\end{aligned}\]</span>
;
;This differential equation can be solved by inspection<a href="#fn3" class="footnote-ref" id="fnref3"><sup>3</sup></a> to be:
;
;<span class="math display">\[\Phi(k,t) = A^{0}(k) e^{-k^2Dt}
\label{eq:Sol1}\]</span>
;
;Where <span class="math inline">\(A^0(k)\)</span> is a constant that that defines the Fourier space function <span class="math inline">\(\Phi\)</span> at <span class="math inline">\(t=0\)</span>. To fully solve this problem and derive <span class="math inline">\(\varphi(x,t)\)</span> we must next solve this value <span class="math inline">\(A^0(k)\)</span> and apply the inverse Fourier transform.
;
;Let us consider our initial condition. Our concentration profile can be modeled as a <span class="math inline">\(delta\)</span>-function concentration profile, <span class="math inline">\(\varphi(x,0) = \alpha \delta(x)\)</span>) fixed between two infinite plates, where the integrated concentration is <span class="math inline">\(\alpha\)</span>:
;
;<span class="math display">\[\int_{\infty}^{\infty} \varphi(x,0)dx = \int_{\infty}^{\infty} \alpha \delta(x) dx = \alpha\]</span>
;
;The constant <span class="math inline">\(A^0(k)\)</span> is, at <span class="math inline">\(t = 0\)</span>, defined by Eq. <a href="#eq:Sol1" reference-type="ref" reference="eq:Sol1"><span class="math display">\[eq:Sol1\]</span></a> and Eq. <a href="#eq:OddSol1" reference-type="ref" reference="eq:OddSol1"><span class="math display">\[eq:OddSol1\]</span></a> to be:
;
;<span class="math display">\[\begin{aligned}
\Phi(k,t) &= A^{0}(k)e^{0}\\
&= \frac{1}{2\pi}\int_{0}^{\infty}\varphi(x,t) \cos{(kx)} dx\end{aligned}\]</span>
;
;Inserting the delta function for (x,t) yields:
;
;<span class="math display">\[A^{0}(k) = \frac{\alpha}{\pi}\int_{0}^{\infty} \delta(x) \cos{(kx)} dx\]</span>
;
;We’ll take advantage of the evenness of this function and instead integrate over <span class="math inline">\([\infty, \infty]\)</span>. This allows us to avoid the messiness at <span class="math inline">\(x=0\)</span> as well circumvent using the Heaviside step function.
;
;<span class="math display">\[\begin{aligned}
A^{0}(k) &= \frac{\alpha}{2\pi}\int_{-\infty}^{\infty} \delta(x) \cos{(kx)} dx\\
A^{0}(k) &= \frac{\alpha}{2\pi} \cos{(0)} dx\\ %Deltafunction fundamental property
\Aboxed{A^{0}(k) &= \frac{\alpha}{2\pi}}\end{aligned}\]</span>
;
;Finally, now that we have <span class="math inline">\(A^{0}\)</span>, we must perform the inverse transformation to find the expression for <span class="math inline">\(\varphi(x,t)\)</span>.
;
;<span class="math display">\[\begin{aligned}
\varphi(x,t) &= \frac{\alpha}{2\pi}\int_{-\infty}^{\infty} e^{-k^2Dt} \cos{(kx)} dk\\
\intertext{This can be completed through integration by parts, trigonometric identities, and completing the square... for explicit step-by-step analysis use Wolfram$|$Alpha or \href{http://www.integral-calculator.com/}{Scherfgen's Integral Calculator}. Let's state the result:}
\varphi(x,t) &= \frac{\alpha}{2\sqrt{\pi D t}} e^{-x^2/4Dt}\end{aligned}\]</span>
;
;This is a Gaussian distribution centered at <span class="math inline">\(x = 0\)</span> and which increases in width with time. This is good — it certainly makes sense intuitively.
;
</div>
</div>
<div id="bessel-functions" class="section level4">
<h4>Bessel Functions</h4>
</div>
<div id="legendre-polynomials" class="section level4">
<h4>Legendre Polynomials</h4>
</div>
<div id="eulers-method" class="section level4">
<h4>Euler’s Method</h4>
</div>
</div>
<div id="solving-second-order-linear-odes-release-tbd" class="section level3">
<h3>Solving Second-order Linear ODEs (Release TBD)</h3>
<ol style="list-style-type: decimal">
<li>;Principle of Superposition
;</li>
<li>;Series Solutions
;</li>
</ol>
</div>
<div id="laplace-transforms-release-tbd" class="section level3">
<h3>Laplace Transforms (Release TBD)</h3>
</div>
<div id="stability-theory-release-tbd" class="section level3">
<h3>Stability Theory (Release TBD)</h3>
</div>
</div>
</div>
<div class="footnotes">
<hr />
<ol>
<li id="fn1">;sometimes, an inexact differential will be denoted as <span class="math inline">\(\delta f\)</span><a href="#fnref1" class="footnote-back">↩︎</a>
;</li>
<li id="fn2">;these may be combined to a 1-quarter class in the future<a href="#fnref2" class="footnote-back">↩︎</a>
;</li>
<li id="fn3">;If you don’t see this, that’s fine, review <em>Separation of Variables</em> — this equation is separable<a href="#fnref3" class="footnote-back">↩︎</a>
;</li>
</ol>
</div>
</div>
<script>
// add bootstrap table styles to pandoc tables
function bootstrapStylePandocTables() {
$('tr.odd').parent('tbody').parent('table').addClass('table table-condensed');
}
$(document).ready(function () {
bootstrapStylePandocTables();
});
</script>
<!-- tabsets -->
<script>
$(document).ready(function () {
window.buildTabsets("TOC");
});
$(document).ready(function () {
$('.tabset-dropdown > .nav-tabs > li').click(function () {
$(this).parent().toggleClass('nav-tabs-open');
});
});
</script>
<!-- code folding -->
<!-- dynamically load mathjax for compatibility with self-contained -->
<script>
(function () {
var script = document.createElement("script");
script.type = "text/javascript";
script.src = "https://mathjax.rstudio.com/latest/MathJax.js?config=TeX-AMS-MML_HTMLorMML";
document.getElementsByTagName("head")[0].appendChild(script);
})();
</script>
</body>
</html>
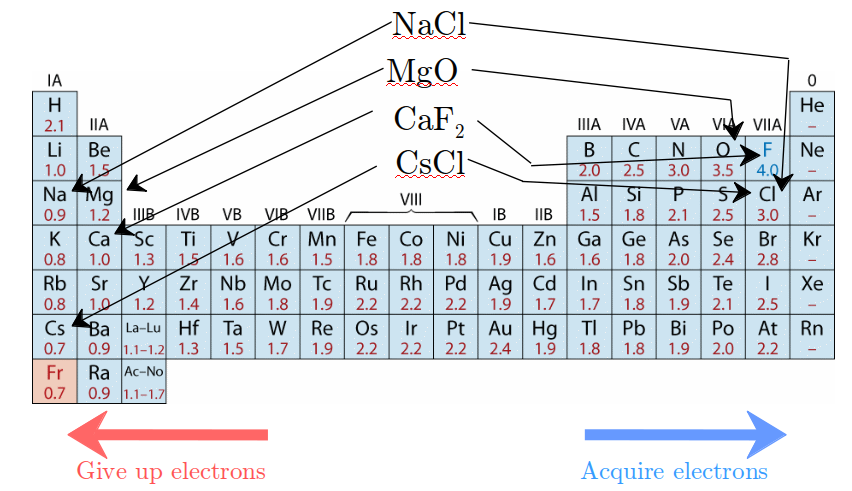
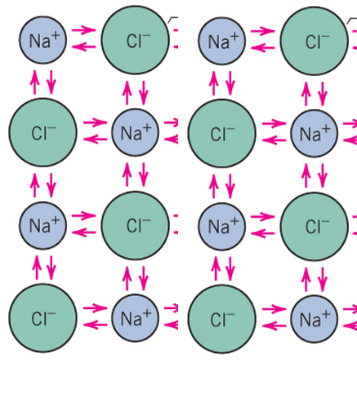
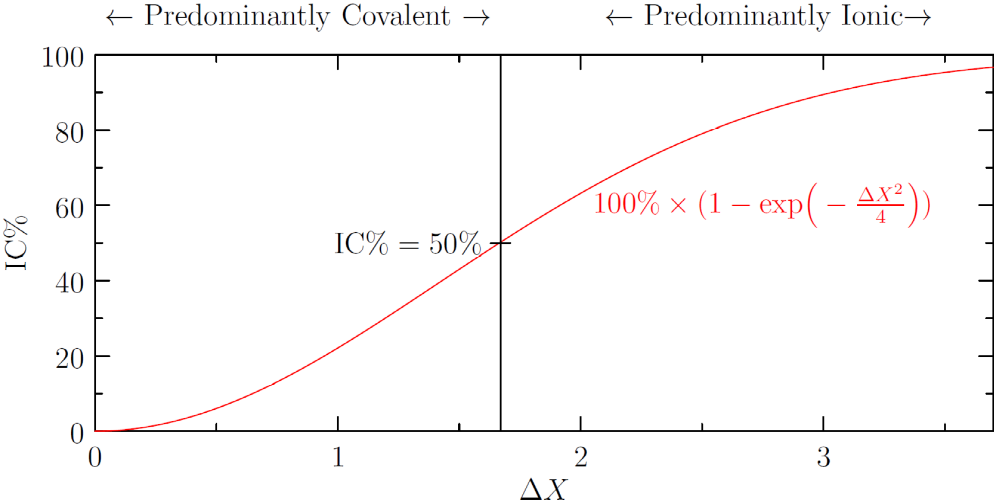
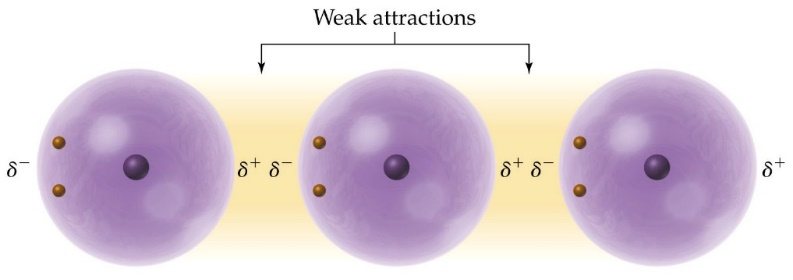
;;
;
|
Metal
|
Structure
|
(psi)
|
(Pa)
|
(psi)
|
(Pa)
|
|
Al
|
fcc
|
3.9x10
|
27x10
|
148
|
1.0x10
|
|
Cu
|
fcc
|
7.0x10
|
48x10
|
92
|
0.64x10
|
|
Mg
|
hcp
|
2.4x10
|
17x10
|
63
|
0.44x10
|
|
Zn
|
hcp
|
5.6x10
|
38x10
|
26
|
0.18x10
|
|
-Fe
|
bcc
|
9x10
|
27x10
|
4000
|
28x10
|
|
Exercise: How high above the earths surface must a single oxygen molecule be lifted in order for its gravitational potential energy to be increased by ?
Solution: The gravitational potential energy is , where is the mass of the object, is the gravitational acceleration (9.8 m/s ) and is height. The mass of a single molecule is obtained by dividing the molecular weight in g/mole by Avogadro's number:
The conversion to kg illustrates the first point that we want to make with this simple calculation: Don't mix units and convert everything to SI units (m-kg-s) to keep yourself sane and avoid unit errors. Boltmann's constant, needs to be in SI units as well:
Now we just need to equate to , using something reasonable for the absolute temperature, . I'll use =300 K to get the following:
|
 Figure 12.3: Schematic representation of a polymer
Figure 12.3: Schematic representation of a polymer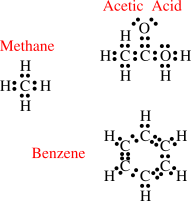 Figure 12.8: Examples of Lewis Diagrams
Figure 12.8: Examples of Lewis Diagrams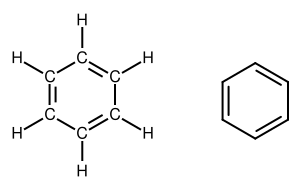 Figure 12.9: Examples of Shorthand Notation when drawing chemical structures
Figure 12.9: Examples of Shorthand Notation when drawing chemical structures Figure 13.1: Polymers produced by step growth polymerization. The red and green circles correspond to 'A' and 'B' monomers that react with one another to form the polymer.
Figure 13.1: Polymers produced by step growth polymerization. The red and green circles correspond to 'A' and 'B' monomers that react with one another to form the polymer.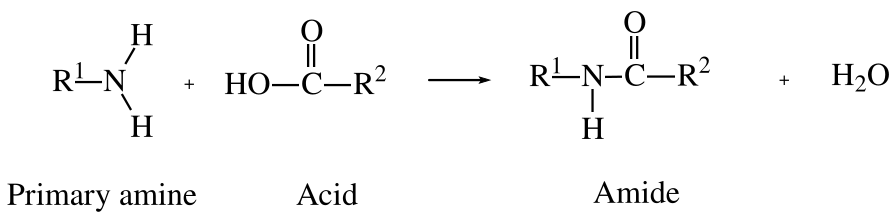 Figure 13.2: Formation of an amide from an amine and a carboxylic acid
Figure 13.2: Formation of an amide from an amine and a carboxylic acid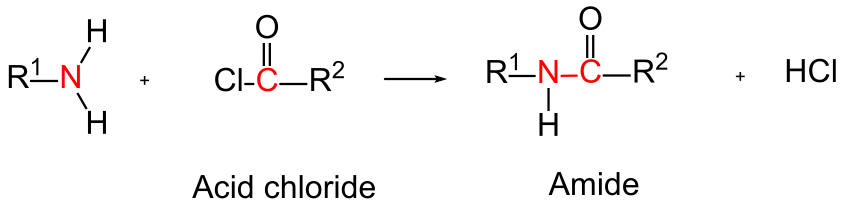 Figure 13.3: Formation of an amide from a primary amine and an acid chloride
Figure 13.3: Formation of an amide from a primary amine and an acid chloride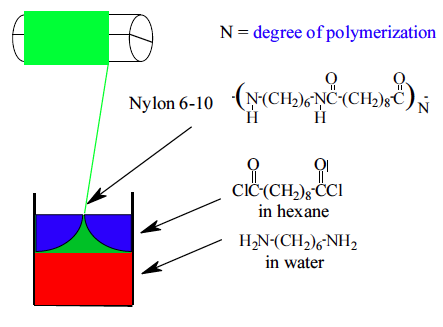 Figure 13.4: Schematic representation of the interfacial polymerization off nylon.
Figure 13.4: Schematic representation of the interfacial polymerization off nylon. Figure 13.5: Formation of an ester from an alcohol and a carboxylic acid.
Figure 13.5: Formation of an ester from an alcohol and a carboxylic acid. Figure 13.6: Ester hydrolysis: The reverse of the esterification reaction.
Figure 13.6: Ester hydrolysis: The reverse of the esterification reaction.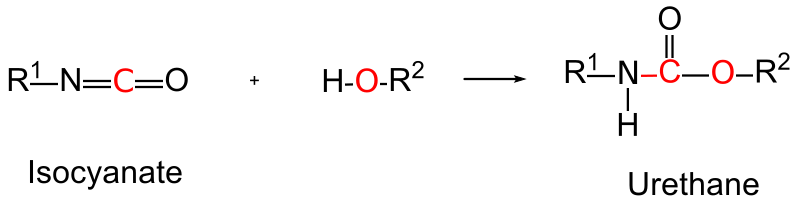 Figure 13.7: Urethane Formation
Figure 13.7: Urethane Formation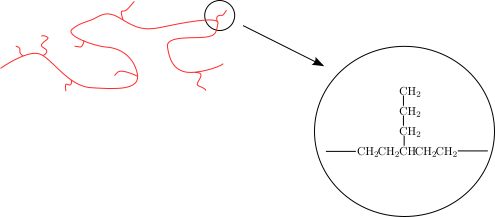
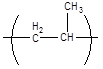
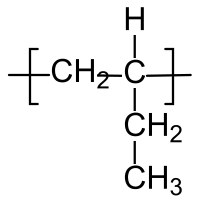

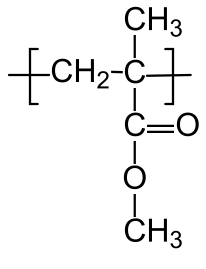


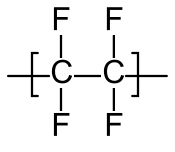

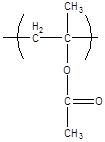
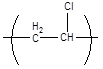 Figure 14.12: Structure of poly(vinyl chloride)
Figure 14.12: Structure of poly(vinyl chloride)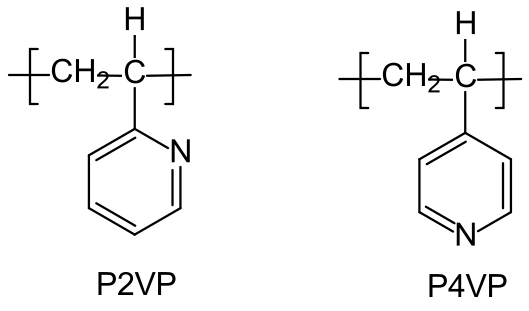
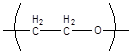
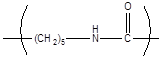
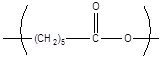

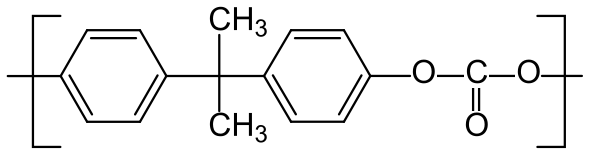
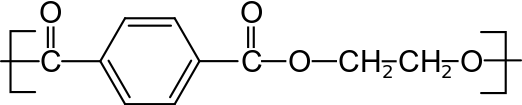




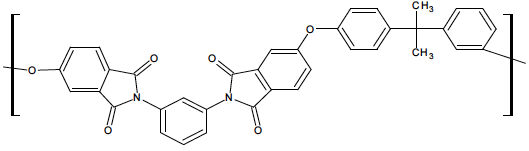

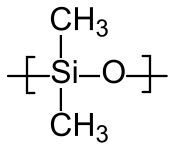
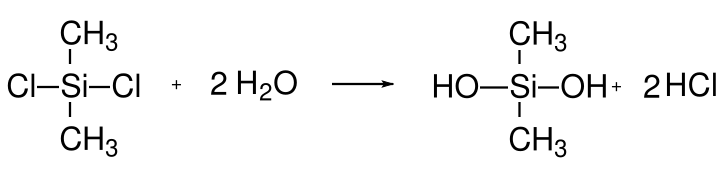


|
Element
|
Bonding Energy (kJ/mol)
|
Melting Temperature (C)
|
|
Hg
|
62
|
-39
|
|
Al
|
330
|
660
|
|
Ag
|
282
|
962
|
|
W
|
850
|
3414
|
|
Element
|
Atomic Radius (nm)
|
Crystal Structure
|
Electronegativity
|
Valence
|
|
Ni
|
0.1246
|
FCC
|
1.8
|
+2
|
|
C
|
0.0710
|
|||
|
H
|
0.0460
|
|||
|
O
|
0.0600
|
|||
|
Ag
|
0.1445
|
FCC
|
1.9
|
+1
|
|
Al
|
0.1431
|
FCC
|
1.5
|
+3
|
|
Co
|
0.1253
|
HCP
|
1.8
|
+2
|
|
Cr
|
0.1249
|
BCC
|
1.6
|
+3
|
|
Fe
|
0.1241
|
BCC
|
1.8
|
+2
|
|
Pt
|
0.1387
|
FCC
|
2.2
|
+2
|
|
Zn
|
0.1332
|
HCP
|
1.6
|
+2
|
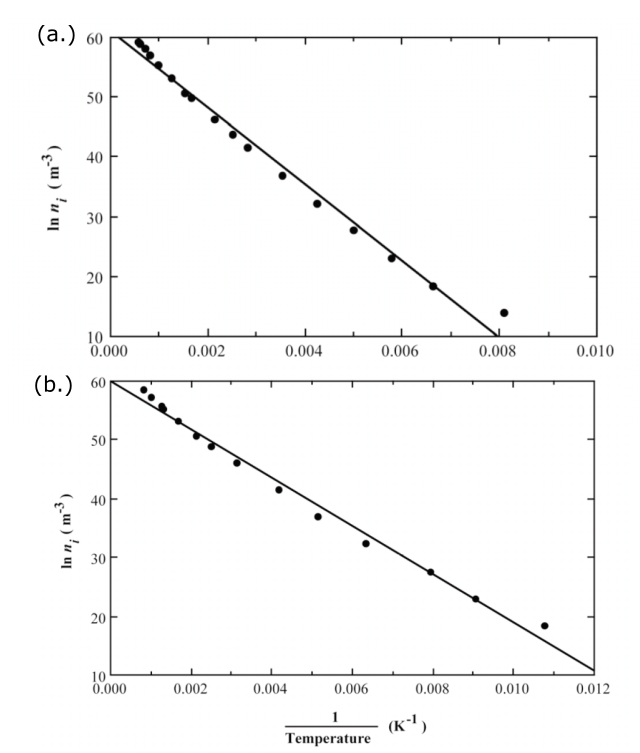 Figure 15.4: An Arrhenius plot relating and for (a.) Si and (b.) Ge.
Figure 15.4: An Arrhenius plot relating and for (a.) Si and (b.) Ge.|
Impurity
|
Semiconductor
|
|
N
|
Si
|
|
B
|
Ge
|
|
S
|
InSb
|
|
In
|
CdS
|
|
As
|
ZnTe
|
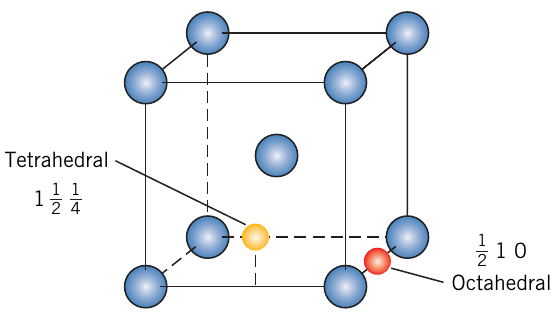
|
|
|
|
1473
|
|
|
1673
|
|
|
|
|
600
|
|
|
700
|
|
Fraction Transformed
|
Times ()
|
|
0.2
|
280
|
|
0.6
|
425
|
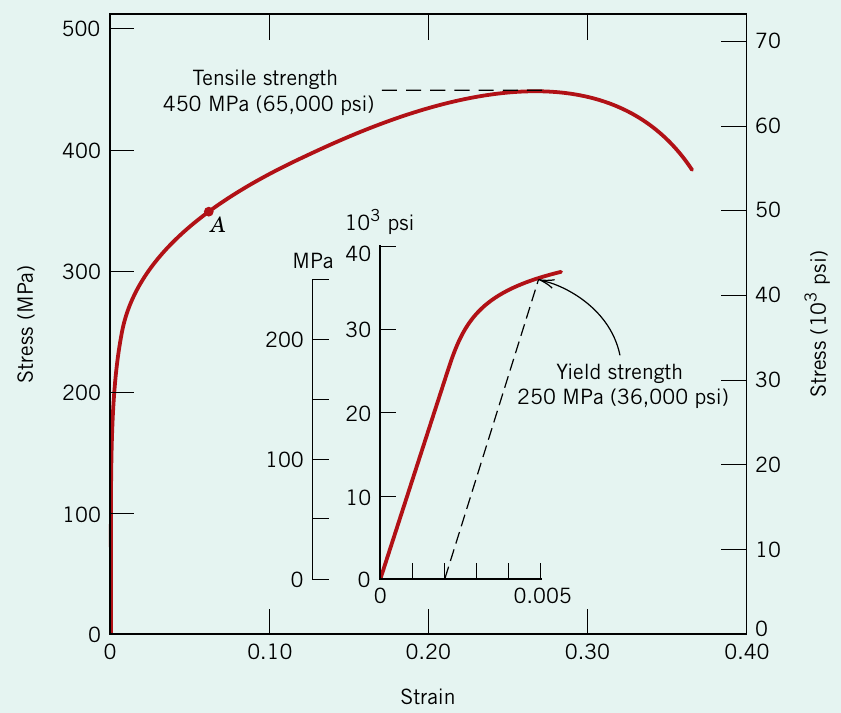
|
Material
|
Yield Strength (GPa)
|
Young's Modulus (GPa)
|
|
Steel alloy
|
0.830
|
207
|
|
Brass alloy
|
0.380
|
97
|
|
Aluminum alloy
|
0.275
|
69
|
|
Titanium alloy
|
0.690
|
107
|