315: Phase Equilibria and Diffusion in Materials
Professor Thomas O. Mason
1 Catalog Description
MAT_SCI 315 covers, broadly, two topics: phase equilibra and diffusion in materials.
In the first half of this course, we concentrate on foundational thermodynamics. Namely, the application of thermodynamics to the prediction and interpretation of phase diagrams. The level of presentation assumes that students have a background in the laws of thermodynamics - especially in the area of solution thermodynamics (MAT_SCI 314). We'll build from these foundations so that students can apply thermodymics to Type I, II, and III phase diagrams.
In the second half of the course we'll concentrate on the foundations of diffusion in solids. We'll introduce the atomistic descriptions of diffusion and introduce the physical laws (Fick's laws) that govern how atoms are transported in solids. We'll apply these behaviors in engineering scenarios.
Prerequisite: MAT_SCI 314-0 or equivalent.
2 Course Outcomes
3 315: Phase Equilibria and Diffusion in Materials
At the conclusion of the course students will be able to:
- Classify, interpret, and analyze Type I, II, and III phase diagrams.
- Construct schematic phase diagrams from elementary thermodynamics.
- Navigate binary and ternary phase diagrams to assess phase equilibrium of mixtures.
- Utilize ternary phase diagrams to follow crystallization paths and predict microstructure evolution. Utilize an understanding of the role of point defects in diffusion and atomistic behavior of solids.
- Describe the equilibrium thermodynamics of point defects in both crystalline solids.
- Use thermodynamics and computational tools to predict and interpret phase equilibria in simple unary and binary systems. Examine the role of phase equilibria and diffusion in the context of relevant applications --- alloys, batteries, fuel cells, etc.
- Prepare alloy specimens for microstructural observation and measurement of hardness profile. Assess experimental results within the context of phase equilibria/diagrams and diffusion.
4 Introduction
“Thermodynamics” and “kinetics” are fundamental skill sets/tool boxes required of all materials scientists/engineers.
Thermodynamics tells us which phase - or assemblage of phases - has the absolute lowest free energy, and therefore represents the equilibrium state. (Note: there may be other metastable states at higher energies.)
Kinetics tells us much more: how fast those phases will form, and the paths they will take along the way. Together, thermodynamics and kinetics determine the phase assemblages/microstructures that can be obtained, and how to obtain them. In the materials science and engineering paradigm of Fig.
4.1, thermodynamics and kinetics come primarily into play in the first “chain link” between “Processing” and “Structure.”
The interplay between thermodynamics and kinetics can be illustrated with two case studies. The first involves the Fe-C phase diagram, which is introduced in virtually all introductory Materials Science and Engineering courses. A schematic of the Fe-rich end (small concentrations of carbon:
2%) of this diagram is given in Fig.
4.2.
If we solutionize the eutectoid composition austenite (
-phase) at the point indicated in Fig.
4.2, and then cool it (follow the arrow) below the eutectoid temperature
(thermodynamics), various microstructures can result, depending upon the rate of cooling (kinetics). For example, slow cooling can result in discrete coarse-grained phases (
-phase ferrite and cementite, or
). This assemblage of phases is not very strong or hard. On the other hand, by cooling more rapidly, we can produce a layered structure of ferrite and cementite, referred to as pearlite for its “mother of pearl” appearance under the microscope. This microstructure is found to be quite strong and hard. This is a prime example of how the processing-structure “chain link” can influence the resulting structure
properties “chain-link” in the Materials Science and Engineering paradigm (Fig.
4.1).
The second example involves the oxidation of silicon to silicon dioxide through the reaction of equation
4.1.
Later in this course we will learn about Richardson-Ellingham diagrams (for simplicity, these will be referred to as Ellingham diagrams). An Ellingham diagram is just a superposition of lines representing the free energy of oxidation for a large number of metals. A schematic of the Ellingham diagram for silicon alone is given in Fig.
4.3 (later graphs, like Fig.
6.2 show much more data).
The top left of the diagram is at zero
and at
. (Note that the letter “
” and “
” refer to the melting points of the metal (Si) and oxide (
), respectively.) As we will see, the free energies of formation of most oxides, including silica, are strongly
negative. This means that reactions like that in Eq.
4.1 have a strong tendency to go to the right, that is, to produce their oxide at the expense of the corresponding metal. For example, if we throw an iron bar out in the “elements”, we know that it rusts (forms the oxide) quite readily. However, an aluminum object, in spite of having an even
larger negative free energy of oxidation than either iron or silicon, will hardly corrode under the same conditions. That is due to the formation of a coherent “passive” oxide film on the surface, through which diffusion is extremely slow.
The same phenomenon takes place on silicon, as illustrated in Fig.
4.4.
The passive
film that forms is extremely important to the microelectronics at work in many computers. (Note: silica has been largely replaced [ca. 2007] by oxides with larger dielectric constants [such as hafnia], to ensure that the miniaturization necessary to keep extending Moore's Law, i.e., the observation that the number of transistors on a processor chip doubles every 18 months, can continue.) On the right side of Fig.
4.4 part of the film has been intentionally removed (in a process known as photolithography) so that dopants can be introduced to induce a local change in the semiconductor's electronic properties. Doping may be achevied by ion implantation or by diffusion from a gaseous source. Again, this is a good illustration of the interplay of thermodynamics and kinetics in both processing
structure and structure
properties links in Fig.
4.1.
In the first half of this text, we concentrate on the thermodynamics, namely, the application of thermodynamics to the prediction and interpretation of phase diagrams. The level of presentation assumes two things:
- You have had an introductory course in materials science and engineering, one that introduced simple phase diagrams, the phase rule, and the lever rule.
- You have a background in the laws of thermodynamics, and especially in the area of solution thermodynamics. If you know the difference between Raoultian and Henrian solution behavior and have been introduced to the Regular Solution Model, you will be in a good position to follow along. If not, it is suggested that you spend some time reading about basic solution thermodynamics in DeHoff or Gaskell.
5 A Most Useful Equation: The Generalized Gibbs-Duhem Equation
From our knowledge of thermodynamics, most of us are familiar with the standard form of the
Gibbs-Duhem equation
5.1 at constant temperature and pressure. This expression arises for binary solutions and relates the total moles
and infinitessimal increase in chemical potential
, for chemical species
.
which is used extensively to describe the behavior of solutions, namely, it plays a big role in “solution thermodynamics.” This equation only holds true for binary systems at fixed temperature and pressure, the X terms represent mole fractions, and the
terms represent chemical potentials. A more general form of the Gibbs-Duhem equation can be derived as follows. Let's start with a binary system. The total internal energy (U) is given by equation
5.2.
where
is absolute temperature,
is pressure, the n terms represent the number of moles of each component, and the
terms are chemical potentials, as in equation
5.1. However, from the
First law of thermodynamics
(equation
5.3) we know that the change of internal energy is a balance between heat
in (
) and work done
by (or out of) our system (
). For now and for the sake of simplicity,
will be limited to
-work only (at constant pressure
becomes
).
The second law of thermodynamics (equation
5.4) tells us that the change of the entropy (
) of the system is always greater than the actual heat in (
) divided by absolute temperature.
In fact, the entropy change is equal to the reversible heat in (
) divided by absolute temperature, as expressed in equation
5.5.
If we now combine the first law (equation
5.3) and the second law (equation
5.4) for a closed system (no matter in or out, i.e., no
terms), we obtain equation
5.6.
or at equilibrium, using
, and equation
5.5 instead of equation
5.4, we get equation
5.7.
Now let's consider an open system that can exchange matter with the environment. We will keep it a binary system for now (and for the sake of simplicity). With the
terms added, the combined first and second law equation
5.7 becomes equation
5.8.
On the other hand, the total differential of total internal energy, equation
5.2, gives us equation
5.9.
If we now subtract equation
5.8 from equation
5.9, we obtain a more complete form of the Gibbs-Duhem equation, at least for binary systems, given in equation
5.10.
Although we will “generalize” this equation still further, this equation is powerful! The author refers to this equation as the “Swiss army knife” for understanding degrees of freedom and the phase rule, and also for classifying and interpreting phase diagrams of all kinds.
5.1 The Gibbs-Duhem Eq. and Degrees of Freedom
For example, as we look at equation
5.10, how many total variables do we have? The answer is “four,” including
(temperature),
(pressure), and two chemical potentials (
,
). But if we ask (for the case of a single phase) how many variables we need to control to establish thermodynamic equilibrium, the answer is “three.” For example, if we fix temperature (
), pressure (
), and the chemical potential of component 1 (
), then according to equation
5.10 the other chemical potential must also be fixed (
). In other words, there are three
degrees of freedom
, which we refer to by the variable
. Later we will understand degrees of freedom to be the number of thermodynamic variables that need to be fixed to establish equilibrium, or alternatively, the number of thermodynamic variables that can be independently varied without a change in the number of phases present in our system. We should also note in passing that we get a hint of the (
) term in the familiar
Gibbs phase rule
, equation
5.11.
In the (
) term,
stands for the number of components (
) and the 2 represents the contributions due to temperature (
) and pressure (
). In other words, (
) is the total number of thermodynamic variables. Note that we have employed a different symbol to represent the number of phases (
) to differentiate this from pressure (
). If we add another component (component 3), then we would have to add a
term to equation
5.10. Now let's see what happens when we have more than one phase, which means adding a second Gibbs-Duhem equation.
5.2 Using the Gibbs-Duhem Eq. to Derive the Phase Rule
Let keep it simple by limiting ourselves to a single-component system (
). The relevant version of the Gibbs-Duhem equation in equation
5.10 would become equation
5.12,
where we have dropped the subscripts for component 1, i.e.,
. But now let's imagine that we have two phases,
and
, in equilibrium along the phase boundary in Fig.
5.1.
Since the moles are distributed between the two phases, it is not necessarily true that
, where the superscripts refer to the two phases. The same can be said of entropy or volume. Imagine ice floating in water. The two phases (solid, liquid) are in equilibrium, which we know by the fact that the temperature remains constant as long as there is any significant amount (moles, volume) of ice. But once all the ice melts, the water is free to rise in temperature. So what we need to do is to write two Gibbs-Duhem equations, one for the alpha phase (equation
5.13) and one for the beta phase (equation
5.14).
Now let's combine these two equations to eliminate one thermodynamic variable, e.g., the chemical potential (d
), to arrive at equation
5.15:
Reorganizing, equation
5.15 becomes equation
5.16:
Think for a minute about what equation
5.16 means. For a single-phase in a single-component system, equation
5.12 tells us that two thermodynamic potentials must be fixed in order to establish the equilibrium state. As pointed out above, in order to fix the chemical potential (
), we have to fix both temperature (
) and pressure (
). But now that we have two phases in equilibrium (
), we only need fix one variable. In equation
5.16 if pressure is fixed (
), then temperature must also be fixed (
), or vice versa; so we have decreased the “degrees of freedom” by one by adding the second Gibbs-Duhem equation (the second phase in equilibrium with the first). (Note: It is assumed that the molar volumes and molar entropies of the two phases are constant.) In other words, the coexistence of two phases in thermodynamic equilibrium requires the writing of two Gibbs-Duhem equations--one for each phase (equations
5.13 and
5.14). This clearly demonstrates that “
degrees of freedom
” (
) equals the total number of thermodynamic variables, which equals the number of components plus 2 (for temperature and pressure) or (
) minus the number of Gibbs-Duhem equations, which is equal to the number of phases in equilibrium (
). We have thereby derived the Gibbs Phase Rule in equation
5.11. Note that if we have three phases in thermodynamic equilibrium in a single-component system (
), we would have to add an additional Gibbs-Duhem equation
5.17:
From this equation and equations
5.13 and
5.14 we could write equations like equation
5.16 for each of the three phase boundaries meeting at what is known as a “triple point,” as in the P-T diagram for water in Fig.
5.2. We could then eliminate one of the two remaining thermodynamic variables, e.g., temperature (
), giving us equation
5.18:
Assuming that all molar volumes and molar entropies are constants and non-zero, there is only one possible solution to equation
5.18, namely that
must be zero. By adding the third Gibbs-Duhem equation for the third phase (
), we end up with zero degrees of freedom. In fact, the “triple point” of water is something you can look up in a handbook, 273.16K (0.01
C) and 0.00604 atm, and can only be changed by increasing the number of components (for example, by doping water with salt, as is done to lower its freezing point at constant pressure, which we describe later).
You probably saw equation
5.16 in prior courses (e.g., chemical or materials thermodynamics), but in a slightly different form, as in equation
5.19:
If we let
stand for molar entropy and
stand for molar volume, this equation becomes the well-known Clausius-Claypeyron equation
5.20:
since in equilibrium the free energy difference is zero, , which means that . As you already know, this is a powerful equation for - diagrams. Given the molar volume difference between alpha and beta phases, from the slope of their - equilibrium phase boundary at a chosen we can calculate the enthalpy (and entropy) of the phase transformation, or vice versa.
Before moving on, we must make one clarification regarding the number of components. It would seem that the number of components should be 2 for the system, one each for hydrogen and oxygen. However, if the ratio of hydrogen-to-oxygen remains constant for all phases in the system, namely H:O remains 2:1, then we can consider this as a one-component system.
5.3 Using the Generalized Gibbs-Duhem Equation to Classify All Phase Diagrams
In Section 2.1 we spoke of the Gibbs-Duhem equation as the “Swiss army knife” of phase equilibrium thermodynamics. We have used it thus far to determine the degrees of freedom in a single-phase, one-component system. We have added second and then third phases in equilibrium (and therefore second and third Gibbs-Duhem equations) to derive Gibbs' Phase Rule. And we have used it to derive the Clausius-Clapeyron equation. Now we will use it to derive an overarching classification scheme for
all phase diagrams. We acknowledge Professor Arthur Pelton of École Polytechnique Montreal as the originator of this powerful classification scheme [
9].
First of all, let's generalize the Gibbs-Duhem equation to equation
5.21:
in which
stands for the various thermodynamic “potentials” and
stands for the corresponding “conjugate extensive variables.” In Table
1 the thermodynamic potentials, whether thermal (
), mechanical (
) or chemical (
), are “intensive,” meaning that they do not depend upon the size of the “system” under consideration. For example, take copper at standard temperature and pressure (STP). A cube of copper 1 cm on a side has the same temperature, pressure and chemical potential as a cube of copper 1 m on a side. On the other hand, the conjugate variables are definitely “extensive,” meaning that they clearly depend upon the size of the system. On going from the 1 cm cube of copper to the 1 m cube of copper all of these variables increase: volume, number of moles, and entropy (although the last is not as obvious).
|
(intensive thermodynamic potential)
|
(conjugate, extensive variable)
|
|
(thermal)
|
(entropy)
|
|
(mechanical)
|
(volume)
|
|
(chemical)
|
(moles)
|
Table 1: Thermodynamic “potentials” vs. “conjugate extensive variables.”
We are now in a position to understand Pelton's classification scheme for all phase diagrams. Schematic representations of the three types are given in Fig.
5.3. Type I diagrams are plots of one thermodynamic potential vs. another, in other words
vs.
. Type II diagrams are plots of a thermodynamic potential (
) vs. a ratio of conjugate extensive variables (
). (Later we will prove that fixing a ratio of conjugate extensive variables is tantamount to fixing their thermodynamic potentials.) Type III diagrams are plots of one ratio of thermodynamic potentials vs. another, in other words
. vs
.
Schematic representations of “real” phase diagrams for each case are given in the second row of diagrams. For example, a conventional P-T diagram like that of water is a good example of a Type I diagram. However, you may have noticed a couple of anomalies in the other “representative” diagrams. For example, the schematic (and easy to recognize) Type II binary eutectic diagram does not have
as its x-axis. There is a good reason for this. Think of what happens if we let
go to zero. This would result in an infinite value of
. Instead, we use mole fraction (
), which is zero for
and unity for
. Note in Fig.
5.3 that mole fraction can be easily related to the ratio of
, which is just the inverse of
. The other anomaly is that we seldom, if ever, see Type III ternary diagrams in rectilinear form, namely
vs.
. The reason is pretty obvious. Pure “end-member” A, using phase diagram terminology to be discussed later (
), is at the origin of this plot, but pure end-members B and C are at infinity on the
- and
-axes, respectively. We can thank J. Willard Gibbs for introducing the now universally employed “Gibbs phase triangle” diagram, where the mole fraction of each component goes to unity in its respective corner. The Gibbs triangle diagram at the bottom right of Fig.
5.3 is a representative isothermal section of a “real” ternary phase diagram in the “subsolidus,” meaning well below temperatures that would result in the formation of any liquid. Furthermore, this system exhibits negligible solid solubility, so the “end-member” and intermediate compounds (
) are the vertices of “tie-triangles.” Such triangles are the hallmark of ternary phase diagrams, which we discuss in detail later.
6 Type I (Single Component) Phase Diagrams
Given the well-known phase diagram of water (see Fig.
5.2), Type I phase diagrams are mistakenly thought of as “unary” or single-component phase diagrams, but this is incorrect. Type I diagrams can be unary, binary or even higher. But they all have in common the plotting of one thermodynamic potential vs. another. They are also interpreted in the same way, as we will show. In fact, this is true for each category of diagrams; the rules of interpretation are identical within each type.
Fig.
6.1 shows schematics of four different Type I diagrams. The first (a) is a repeat of the single-component
phase diagram. The second (b) is a
diagram of the two-component
system. The third diagram (c) is a slighty different version of the
binary system.
This is actually a
diagram in disguise, as we later show. The top lines on this diagram are actually taken from a very special Type I diagram, known as the Richardson-Ellingham diagram (shown later). We will refer to this as the “Ellingham” diagram, and will spend quite a bit of time with it shortly. The final Type I phase diagram (d) is a
diagram for the
ternary system. Such diagrams are referred to as “stability area” diagrams or “predominance area” diagrams. The descriptor, “stability area,” is quite informative. It speaks to the fact that interpretation is identical for all Type I phase diagrams: areas represent single-phase regimes (or the “area”/range of thermodynamic potentials over which a given phase is solely “stable”); lines represent the combination of the thermodynamic potentials required for co-equilibrium of two phases; “triple points” (where three lines meet) indicate the thermodynamic conditions (potentials) where co-equilibrium of three phases occurs. Note that in going from a one-component system (
) to a two component system (
), one of the thermodynamic potentials, in this case pressure (
1 atm), must be held constant to arrive at a Type I diagram (equilibrium being determined by the two potentials on the axes). And in going further to a three-component system (
) two thermodynamic potentials, in this case pressure (
1 atm) and temperature (
1000 K), must be held constant to arrive at a Type I diagram (equilibrium being determined by the two potentials on the axes.
6.1 The Ellingham-Richardson Diagram
In 1944, it was observed (by Ellingham) that plots of standard free energy of oxidation of metals to oxides had essentially the same slope (
) as long as the reaction was written per mole of oxygen gas
as in equation
6.1:
where M in this equation represents a metal. For example, if we are dealing with the oxide
(
), equation
6.1 simplifies to equation
6.2:
But we might be dealing with a different metal, N, which forms the
(
), for which equation
6.1 becomes equation
6.3:
Note that if we subtract equation
6.3 from equation
6.2, the oxygen term cancels out and we obtain equation
6.4:
This is a powerful capability to determine whether, thermodynamically speaking, a given metal will reduce another's oxide or vice versa, as we show later. There is a simple rationale for all oxidation reactions having nearly the same slope on an
Ellingham diagram
. Let's consider the reaction of calcium to calcium oxide as in equation
6.5:
The overall standard free energy of reaction can be determined by equation
6.6:
What we are interested in is the Ellingham slope (
) in equation
6.6, which amounts to the change in standard entropy as given by equation
6.7:
If we consult thermodynamic data for the three terms on the right side of equation, we obtain equation
6.8:
It can be seen that the first two terms, the standard entropy terms of the two solids (calcium oxide, calcium), roughly cancel and that the overall value is dominated by the standard entropy of the oxygen gas (the third term). Hence, the slopes of all oxidation reactions on Ellingham diagrams involving solid metals and oxides will be very similar, owing to the fact that
in equation
6.6. An actual Ellingham diagram is shown in Fig.
6.2.
At first, this may seem like a complicated diagram. However, the following discussion and “case studies” should help to simplify it and demonstrate its usefulness. As can be seen there are three different nomographic scales on the sides of the diagram. These were added by Richardson; hence, the diagram is often referred to as the Richardson-Ellingham diagram. We will highlight each of these scales as we come to them. First let's consider three ways to arrive at a specific
coordinate on the diagram. Consider the reaction of Ti with
to yield
at
. From the line and the diagram legend we know that both the metal and the oxide are solids at this temperature, because we do not encounter an “
” symbol (where the metal melts) until a much higher temperature (
), and there is no boxed “
” symbol, which stands for the melting point of the oxide. This means that the oxide melts at a temperature above the melting point of the metal, however no thermodynamic data are provided for higher temperatures. Note: a “
” symbol is fairly rare and corresponds to the boiling point of the metal, as in the case of
and
, the bottommost lines on the diagram. The large increase in slope at such a “B” point is due to the fact that both reactants on the left side of the Ellingham equation
6.1 are in gaseous form (oxygen gas plus metal vapor) and therefore contribute to the entropy or slope of the line.
The three ways to reach a specific coordinate are illustrated in Fig.
6.3. The first way or path (1) to reach the coordinates in question is by what I call “direct read.” The topmost horizontal line of the Ellingham diagram, directly below the
nomographic scales, is the line of zero
. At
we draw an arrow down from this line until we hit the line representing the
equilibrium at a value of
. The second path (2) to reach the same coordinates is to use the Ellingham relation in equation
6.6. It is important to realize where the coordinates
occur on the diagram. On the very left of the Ellingham diagram in Fig.
6.2 is a vertical line with “
” indicated. Since the x-axis is in degrees C, the absolute zero in degrees Kelvin is to the left another
. So the actual
point of the Ellingham diagram is at the top left corner where the line which passes through the “
” and “
” points makes an angle with the horizontal line of zero
. This is a very important point on the Ellingham diagram, which I tend to call the “
” point (O for oxygen) and later the O-fulcrum. Starting at the O-point, we can draw the
line from the origin as shown in Fig.
6.3. One can crudely think of this in terms of
for the
equilibrium.
By the way, there is a perfectly good thermodynamic reason why Ellingham did not extend the lines on the diagram below . You may recall from your basic thermodynamics background that the heat capacity of a solid begins to vary dramatically below its “Debye” temperature approaching absolute zero. This would make for large deviations from linearity of the lines on the Ellingham diagram below approaching ; hence, the lines terminate at .
The third way or path to reach the same coordinates of
at
requires some explanation. As found in basic chemistry textbooks we know from equation
6.9:
that the
of a reaction is related to the standard free energy of that reaction plus a second term that depends upon the so-called “activity quotient” or
. In the case of
this becomes equation
6.10:
where the activities of the solid phases can be assumed to be unity (assuming pure metal and oxide) and the activity of oxygen is given by its partial pressure. However, if the metal and oxide are in equilibrium we know that
, yielding the following equation
6.11:
where
is the oxygen partial pressure where
and
are in equilibrium. In effect, path (3) is a line with zero intercept and a slope of
vs. temperature, as shown in Fig.
6.3. We can solve mathematically for
by plugging
for
and
or rather
into equation
6.11 to arrive at a value of
, for which the
(base 10) is
. This is where the nomographic scale comes in handy. If we draw a line from the origin or “O-point” through the coordinates in question (the
line at
) to the
nomographic scale, we get approximately the same value. Keep in mind that this is really a log scale, so we must interpolate the “logs,” for example one quarter of the way from
to
is
and definitely not
or
. So we have a short cut or “easy button” for finding the
value for any set of coordinates on the Ellingham diagram. Simply take a ruler and connect it from the O-point through the coordinates in question and read the
value off the nomographic scale. Since all lines radiate from the “O-point,” I tend to refer to this point as the “O-fulcrum”. You will note on the Ellingham diagram that all the “tick” marks on the O-nomographic scale point back to the O-fulcrum.
Of course, achieving such a low oxygen partial pressure is impossible with even the best available vacuum systems. That is where the outer two nomographic scales come in. These involve so-called “buffer gas systems.” Consider the reaction of equation
6.12:
Let's flow an arbitrary mixture of
and
through a furnace at 1 atm total pressure. The equilibrium constant would be given by equation
6.13:
where partial pressures are now expressed in terms of mole fractions and total pressure. If we let the total pressure be 1 atm and assume that the amount of oxygen produced is negligible compared to the moles of
and
and let
we arrive at a simplified equation
6.14:
Let's go back to the situation we considered above, namely the
equilibrium at
with an equilibrium
of
. Given the
for reaction
6.12 is
and plugging this into equations
6.13 and
6.14, we can solve for an
value of
. On a base 10 log scale this corresponds to 7.1. Now let's use the second nomographic scale and its corresponding C-fulcrum (this is the letter “C” on the line to the left side of the Ellingham diagram
6.2) to solve the same problem. Note that all the tick marks on the
radiate from the C-fulcrum. As illustrated in Fig.
6.4, using a ruler to draw a line from the C-fulcrum through the
line where it crosses
all the way to the second nomographic scale obtains
, in excellent agreement with the calculations. Even though the
would be quite small (on the order of
atm) this is still way larger than the value of
, so our assumption that the amount of oxygen can be neglected is mathematically justified. In reality, however, just as with aqueous buffers, there are limits to buffer reliability. For example, buffer gases become unreliable if the R value is too large or too small, owing to the potential for oxygen “leaks” in the lines feeding gases into a commercial furnace. Therefore, buffer gases are usually limited to values of
. Nevertheless, we have a valuable short cut to obtain the
value for any coordinates on the Ellingham diagram.
You will notice that there is still another nomographic scale on the Ellingham diagram of Fig.
6.2. This nomographic scale involves a different buffer gas system of reaction
6.15:
Here we are mixing hydrogen gas and water vapor, whose ratios are given along the outermost nomographic scale. Again, note that all tick marks radiate to the H-point or H-fulcrum on the line to the very left of the diagram. If we want to know a mixture of hydrogen gas and water vapor that would correspond to a set of coordinates on the Ellingham diagram, we would use a ruler to draw a line between the H-fulcrum through those coordinates to the nomographic scale, once again being careful to interpolate the log values.
Another use of the Ellingham diagram is to find a driving force for a given reaction. Consider the reaction of Mn metal with oxygen to form
by the reaction
6.16:
If we subject a mixture of Mn/MnO to an “applied” oxygen pressure of
atm (for example, by using a buffer gas mixture) at
, what is the driving force for the reaction to take place? There are several ways to solve for this. They each derive from equation
6.9. In this case, assuming
and
to be pure solids (activity=1) we would obtain equation
6.17:
From the Ellingham diagram of Fig.
6.2 we can find that the
of the reaction is approximately
at
. Plugging
and
into equation
6.17, we obtain
. But we also know from equation
6.11 that
. Plugging this into equation
6.17 we obtain equation
6.18:
Using the O-nomographic scale on the Ellingham diagram of Fig.
6.2 we can find the
to be very close to
atm at
. Plugging this into equation
6.18 we obtain
. The third method is what I refer to as “direct read.” This is illustrated on Fig.
6.5. We always draw the arrow at constant temperature from the
applied condition to the
equilibrium condition, which falls on the
line for the reaction in question. What we obtain is approximately
. All three values are in agreement with one another, with a relatively small error determined by our ability to accurately extract values from the Ellingham diagram.
To summarize, Ellingham diagrams are characterized by the following features:
- Curves in Ellingham diagrams for the formation of metallic oxides are basically straight lines with a positive slope. The slope is proportional to , which is fairly constant with temperature.
- The lower position of a metal's line in the Ellingham diagram, the greater the stability of its oxide. For example, the line for (oxidation of aluminum) is found to be below that for (formation of ).
- Stability of metallic oxides decreases with increasing temperature. Highly unstable oxides like and easily undergo thermal decomposition.
- A reduced substance (such as a metal), whose Gibbs free energy of formation is lower on the diagram at a given temperature, will reduce an oxide whose free energy of formation is higher on the diagram. For example, metallic aluminum can reduce iron oxide to metallic iron, with the aluminum itself being oxidized to aluminum oxide.
- The greater the gap between any two lines, the greater the effectiveness of the reducing agent corresponding to the lower line.
6.2 Two More Type I Phase Diagrams
So regardless of the method used to obtain the driving force, it is obvious that that driving force is negative; reaction
6.16 will proceed to the right and
metal will be oxidized to its oxide. This also allows us to see that we can make a Type I phase diagram out of each "line" (or metal/oxide pair) on the Ellingham diagram. If we consider the
/
"line" in Fig.
6.6, it follows that a “direct read” arrow from any set of coordinates above the line (corresponding oxygen pressures larger than
) to the equilibrium
/
line will be negative, i.e., the
will be negative so the oxide will be favored. On the other hand, a “direct read” arrow from any set of coordinates below the line (corresponding to oxygen pressures smaller than
) to the equilibrium
/
line will be positive, i.e.,
will be positive so the reaction of does not proceed; the metal will be stable. Therefore manganese oxide exists everywhere above the "line" and manganese metal exists everywhere below the "line." But there are two different forms of manganese metal and therefore two Type I phase boundaries: one between the solid oxide and the solid metal, below
, and another between the solid oxide and the liquid metal, above
. So at
we get a Type I triple point. The vertical phase boundary at
corresponds to the melting of
; solid
is stable to the left and liquid
is stable to the right. This vertical line intersects the other two at the triple point, where both solid and liquid
exist in equilibrium with solid
.
A more useful Type I phase diagram for the laboratory, however, is a plot of
vs.
. For example, we can convert the Ellingham-type phase diagram of Fig.
6.6 into such a diagram for the
system by either 1) using the O-nomographic scale over and over to estimate the values of
for
/
equilibrium each temperature, or 2) solving
for each temperature, given the thermodynamic data for reaction
6.16. A schematic of this diagram is shown in Fig.
6.7. There are many applications of such diagrams. For example, in
metal heat treating, we want to keep the
below the pressure of the phase boundary with MnO. For ceramists dealing with MnO the opposite would hold true: we would want to maintain the
above that of the oxygen partial pressure of the phase boundary with either solid or liquid Mn.
We can apply Gibbs' phase rule to both kinds of phase diagrams. We know that
, however, the overall pressure is understood to be 1 atm for both diagrams, so the phase rule reduces to
. As opposed to the water
phase diagram where the
ratio was everywhere 2 on the diagram, here the
ratio differs from phase field to phase field (e.g., it is 1:1 for
but 0:1 for
); hence,
(for
and
). This yields a phase rule of
, which means that in both the Ellingham-like Type I phase diagram of Fig.
6.6 and in the T vs.
phase diagram of Fig.
6.7, we have the same features as we had for the
diagram: single-phase areas have 2 degrees of freedom, i.e., both
and
must be specified, two-phase situations are phase boundaries/lines of
, i.e., if we fix one variable (say
), we immediately know the other (
) or vice versa, and three-phase situations have zero degrees of freedom at three-line junctions or “triple points.” As with the triple point of water, we have no control over the
/
/
triple point (unless we increase or decrease the total pressure from
).
7 Type II (Binary) Phase Diagrams
As illustrated in Fig.
5.3 Type II phase diagrams are really quite different from Type I phase diagrams. Instead of two thermodynamic potential axes, one of the axes is a ratio of conjugate extensive variables. Later, when dealing with free energy vs. composition diagrams, we will return to answering the question of how a potential axis can be replaced by a “ratio” axis to establish thermodynamic equilibrium. For now, suffice it to say that if we eliminate the -VdP term in the Gibbs-Duhem equation (by holding pressure fixed) we obtain for a two-component system:
One can chose to fix T and one of the chemical potentials (
), which is relatively difficult to do, or one can chose to fix T and the ratio of the moles of B to the moles of A. Fixing
is inconvenient, however, since at one extreme (
) the ratio goes to infinity. Instead, as you well know, we fix the mole fraction of B, as seen in the x-axis of the common binary eutectic phase diagram sketched schematically in Fig.
7.1. The following sections deal with how we can estimate each type of phase boundary (liquidus, solidus, solvus) in Type II phase diagrams from the simple solution thermodynamic models you already know (Raoultian, Henrian, Regular), as long as we make some simplifying assumptions. More complicated situations are better handled by software dedicated to predicting phase diagrams, taking into account more sophisticated models and behavior of individual solutions. Such software programs are discussed briefly at the end of this text. But for now, the following sections will build confidence in linking phase diagrams with their underlying solution thermodynamic origins, and will hopefully cause you to think about and question the specific models that lie behind the "black boxes" of modern phase diagram algorithms.
7.1 Estimating Liquidus Lines on a Binary Eutectic with Negligible Solid Solution
To simplify our prediction of liquidus behavior, let's assume there to be negligible solid solubility and that the liquid is ideal or Raoultian. The former assumption is reflected in Fig.
7.2 by the notations, “A” and “B,” denoting nearly pure solid A and B, and
denoting a liquid solution. Of course, we know from solution thermodynamics that there is no such thing as a perfectly pure solid. The assumption of liquid ideality just means that the activity of each component in the liquid is approximately equal to its mole fraction (
). Given these two assumptions, it is fairly straightforward to estimate the liquidus line for a "negligible solid solubility" system. Consider the situation in Fig.
7.2:
Thermodynamically, the equilibrium of essentially pure solid A and the ideal liquid solution at the temperature shown in Fig.
7.2 can be expressed by the equality of their chemical potentials, as shown in equation
7.2:
where
is the standard state chemical potential of pure solid A. From solution thermodynamics we know that the chemical potential in a solution (in this case, the liquid solution) is related to the chemical potential in the pure state by equation
7.3:
We also know that the activity of the liquid can be replaced by its mole fraction (ideal solution). This leads to equation
7.4:
Rearranging, we obtain equation :
But the right side of equation
7.5 is simply the
of melting of component A per mole, which we know to be
. At the melting point (
) we know that
, such that
or
. However, the temperature of equilibrium in Fig.
7.2 is not the melting temperature. Modern software packages can account for changes in enthalpy and entropy for pure liquid and solid A at different temperatures. But we can at least make an estimate of what might happen by employing a further simplification, and assume that the enthalpy of melting is approximately constant and does not change significantly with temperature. This is often referred to as the “
” approximation, namely that the difference in heat capacities between pure solid A and pure liquid A is negligible such that the enthalpy of melting is approximately temperature-independent. This gives the following equation
7.6:
By plugging this into equation
7.5 we arrive at equation
7.7:
which is a rough estimate of the point on the liquidus curve in Fig.
7.2. In fact, we can solve the same equation for any temperature, starting with the melting temperature
, for which the right side of equation
7.7 is zero. This requires that the mole fraction of A in the liquid be unity, i.e.,
or pure A, corresponding to the top of the liquidus in diagram
7.2. As we decrease the input temperature, the right side of the equation becomes increasingly positive, corresponding to smaller and smaller fractional values of
decreasing from unity to go along with the steady reduction in the liquidus temperature, as shown schematically in Fig.
7.2. By writing the corresponding equation for the B-liquidus at the other side of the phase diagram, again assuming negligible solid solution and ideal liquid behavior, we obtain equation
7.8:
Both liquidus lines (actually curves) are captured schematically in Fig.
7.3. They fall away from the pure end-members, A and B, and can be extended far beyond the horizontal line shown on the figure. The horizontal line is where the two liquidus curves intersect. At this point, the same liquid solution is in equilibrium with both solids A and B, and equations
7.7 and
7.8 are simultaneously satisfied. According to the phase rule, there are three phases in equilibrium and there are no degrees of freedom. We have arrived at an “invariant point,” which you know well as a binary eutectic.
Let's pause for a moment to consider a couple of things about the behavior we have just described. First of all, the falling liquidus lines are examples of “freezing point lowering.” This important phenomenon is used to advantage on icy streets by applying salt, which lowers the freezing point of ice. Of course, this requires that the ice melt and the liquid dissolve some salt as component “B” in Fig.
7.2. Upon refreezing, however, the liquidus (first occurrence of solid water) is not reached until a significantly lower temperature. Furthermore, when we drop the temperature still lower, we enter a two-phase region where ice is in equilibrium with liquid salt solution, a mixture we commonly refer to as “slush.”
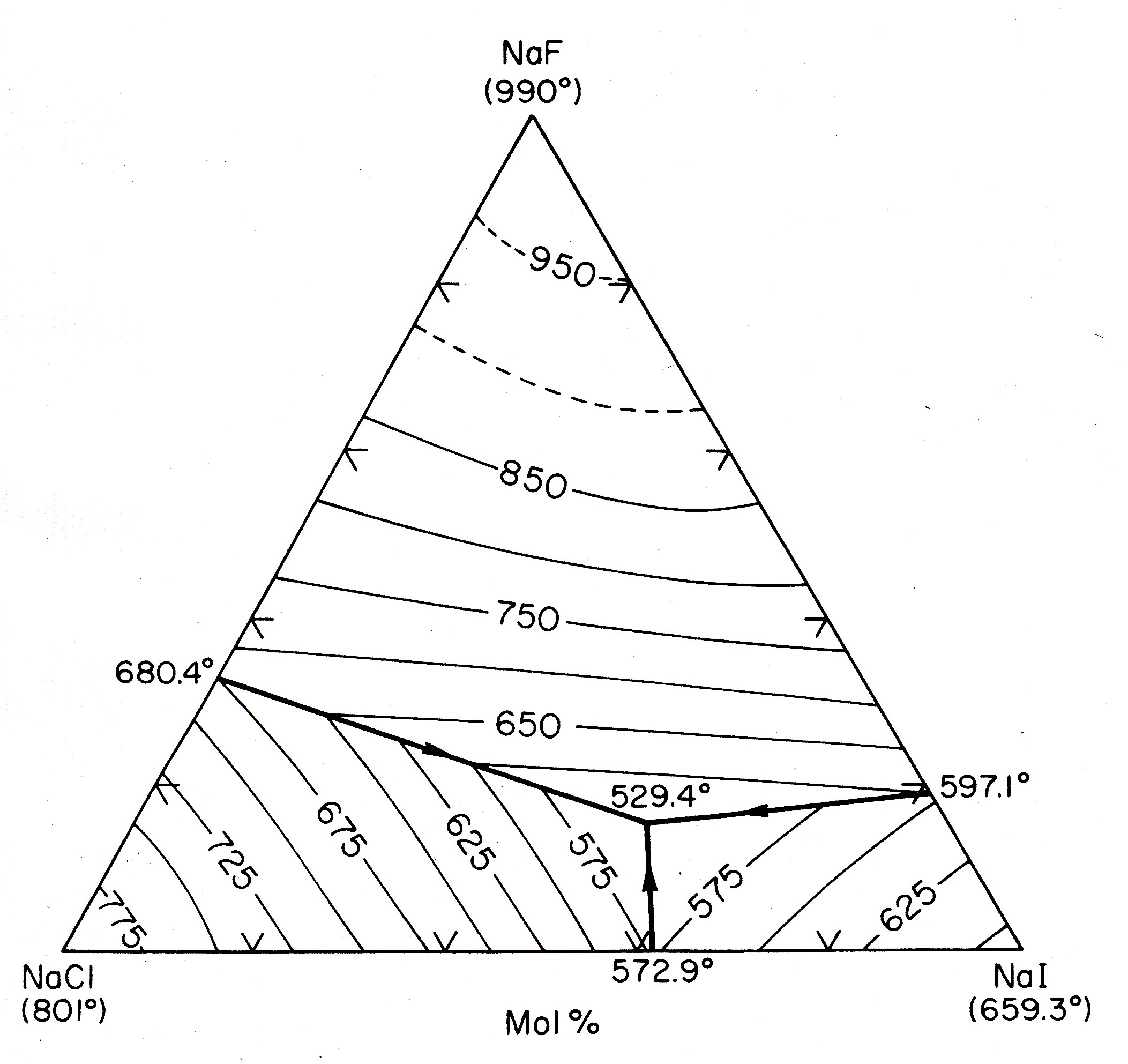
Another good example of “freezing point lowering” is in the manufacture of Portland cement by the process of “klinkering.” There are two compounds produced by this process, or “” in “cement speak” and or “”. These compounds, when pulverized to powders and mixed with water, react to form the so-called gel (“” for or ), the “glue” that upon “hardening” holds everything together in mortar (Portland cement plus sand) and concrete (Portland cement plus sand plus “aggregate”/crushed rock).
What does this have to do with “freezing point lowering”? Well, with a rare exception in the dessicated regions of Israel, and do not occur in nature. If they did, they would spontaneously react with any water to form gel. By the way, if you ever have a concrete sidewalk or driveway poured, don't let it “dry,” which is a common (and disastrous!) misconception. Cement “hydration”/hardening actually consumes water, so once initial “set” has taken place, gently hose is down (or cover it with plastic) to keep it from drying out, which can lead to ruinous surface cracking.
The point here is that
and
are man-made compounds, and their manufacture depends upon “freezing point lowering.” Both compounds have melting points in excess of
, higher than just about any low-cost “refractories” (the high-melting ceramics used to line furnaces and kilns). But with certain “fluxing agents,” for example,
and
, the liquidus drops dramatically to the
to
range. Since this is now at least a ternary system (
), we will come back to the phase diagram when considering Type III phase diagrams. For now it is enough to know that in enormous, gradually-sloped rotary kilns (pronounced “kills”) the length of football fields,
and
“balls” (referred to by the German word, “klinker”) tumble in their quasi-equilibrium liquid. Imagine an overall composition midway between “A” (
) and the eutectic composition in Fig.
7.2, but at the temperature indicated by the horizontal dashed line (a roughly 50:50 combination of solid and liquid would result). The klinker “balls” that emerge from the lower end of a cement kiln (both in terms of height and temperature), when cooled, pulverized, and ground to the consistency of fine flour become what we refer to as “Portland cement.” This process is only possible owing to “freezing point lowering.” By the way, Portland cement is a very important man-made material. Every year, approximately one ton of concrete is poured per capita in the developed and developing countries of the world!
One last point can be made regarding the the origin of the name “eutectic,” whose Greek origins refer to “easy melting.” In the binary eutectic diagram of Fig.
7.3, the liquidus lines fall away from the A and B end-members to the eutectic point, which is therefore the lowest-melting composition in the entire A-B system. We refer to the composition as the “eutectic” or easy-melting composition.
7.2 Estimating Liquidus and Solidus Lines for a Binary Isomorphous System
In the previous example we were dealing with a continuous liquid solution, but negligible solid solution. But what happens if both liquid and solid solutions are continuous across the A-B phase diagram? An example of such a phase diagram is shown schematically in Fig.
7.4, where the upper line is the liquidus and the lower line is the solidus. This is a very unique situation that only happens if the end-member solids obey certain requirements, as put forth in the well-known Hume-Rothery rules: 1) the two solids must have the same crystal structure, 2) the two species should have similar electronegativities, and 3) their atomic radii must not differ by more than 15 percent. Thermodynamically speaking, the enthalpies of mixing should be nearly the same for the liquid solution as for the solid solution, or
. For our estimation of liquidus and solidus lines we will assume both enthalpies of solution to be zero, or that both solutions are ideal or Raoultian.
Let's start with the two-phase equilibrium between liquid solution and solid solution as shown in Fig.
7.4 and as expressed by equation
7.9:
However, as per equation
7.3 we can replace each side of equation
7.9 with the appropriate
term, giving us equation :
Rearranging this equation and substituting mole fractions in place of activities (we are assuming both solutions to be ideal), we obtain equation
7.11:
The right side of this equation is the free energy of melting per mole of pure A, which we previously approximated by equation
7.6. Making the same simplifying approximation and rearranging, we obtain equation
7.12:
This equation only gives us the ratio of mole fractions of component A at a given equilibrium temperature. Fortunately, an analogous equation can be derived for component B:
For each given temperature, we can solve for each ratio in equations
7.12 and
7.13. If we let the two ratios be
and
, and remind ourselves of the fact that the mole fractions must sum to unity for each solution (
, we can show that:
from which the mole fraction of A on the liquidus can be obtained, namely . The mole fraction of A on the solidus can then be obtained from the ratio . Of course, to plot rather in terms of the mole fraction of B, one need only employ the relations for each solution.
This example shows how the binary isomorphous diagram can be estimated for an A-B system, given only the two melting points and the enthalpies of melting. The process above need only be repeated systematically between the melting points of the two end-members to arrive at a diagram like the schematic in Fig.
7.4.
Before the development of chemical vapor deposition, currently employed to purify silicon to transistor-grade levels (impurities at parts per billion!), a method called "zone-refining" was used to clean up crystalline ingots of silicon. The idea can be understood from the binary isomorphous diagram of Fig.
7.4. Let component "B" be silicon. If we melt silicon with an impurity content at the left end of the equilibrium line in the figure, it can be seen that the solid crystallizing from the melt is significantly cleaner. Suppose we could isolate this cleaner solid. If we could repeat the process with this solid, melting it and crystallizing it, the composition of the solid would move progressively to the right, toward higher purity silicon. In fact, this was accomplished by repeated passes of a localized heater along the length of a cylindrical silicon crystal held at nearly its melting point. The "molten zone" was held in place by surface tension and it concentrated impurities and took them along for the ride. This happened to impurities with a positive "distribution coefficient," or
as in Fig.
7.4. Impurities with a negative distribution coefficient went the opposite direction and were left behind. Either way, with each pass of the "molten zone" the central portion of the crystalline ingot became more and more pure, as the impurities were dragged/left behind at the ends, which were cut off and discarded.
7.3 Estimating Solvus Lines
It is rare when a system satisfies the conditions for a continuous solid solution. Instead, we see phase separation into two solids at low temperatures as on the schematic binary eutectic diagram of Fig.
7.1. These can be entirely different crystal structures as in Fig.
7.1, described as phase
and phase
. Or they can be the same crystal structure, but phase-separation into phases
and
occurs at low temperature. The latter behavior can be described by the
regular solution model
you learned about in solution thermodynamics. In the following development, let's assume that the entropy of mixing is solely “configurational,” namely that it consists of only the ideal entropy of mixing in equation
7.15:
Now, for the excess free energy of mixing, let's assume the symmetrical enthalpy of mixing for a Regular solution as in equation
7.16:
where
is known as the “interaction parameter.” It describes how A and B interact upon dissolving in one another. For example, the type of phase separation we will describe requires significantly large positive values of
, which raises the free energy of mixing, especially in the middle of the solution (
). The overall free energy of mixing is the sum of equation
7.15 and
7.16:
Let's take the first derivative of this equation with respect to :
Remember that
when differentiating. It turns out that this is the equation describing the phase boundaries of the dome-shaped solvus at any temperature in Fig.
7.5. We can find additional useful information by taking the second and third derivatives of equation
7.17. The second derivative is:
This equation also has special significance, namely the second derivative marks the inflection points in the
vs composition curve of Fig.
7.5. Outside of each inflection point, marked with a square, the second derivative is positive (the curve is concave up) whereas in the middle the second derivative is negative (the curve is concave down). You will discuss in later materials science and engineering coursework the importance of these "spinodes," especially with respect to a process known as “spinodal decomposition.”
To arrive at useful forms of both derivative functions, we need to take yet another derivative. It turns out that at the very top of the solvus in Fig.
7.5 all three derivatives are zero. The third derivative of equation
7.17 is:
Now we can begin to put all the derivatives to good use. For the third derivative to be zero requires that
. This tells us that the top of the solvus is at the equimolar composition as shown in Fig.
7.5. But the second derivative is also zero at the top of the solvus. For equation
7.19 to be zero requires that
or
. We refer to this as the "critical" temperature,
, such that
. This is an important relationship. Given the critical temperature or top of the solvus in Fig.
7.5, we can estimate the interaction parameter. Or given the interaction parameter, we can estimate the top of the solvus. Now let's plug these results into the first derivative equation
7.18, also setting it equal to zero:
or more simply:
There are two solutions (phase boundaries) to this equation. For example, if we chose a temperature 80% of the critical temperature or
the two solutions are at
and
, the latter being the symmetrical solution (
). In the lower diagram of Fig.
7.5 the lowest free energy situation between the two phase boundaries is to strike out along the dashed line, meaning an assemblage of two separate phases rather than a continuous solid solution, which is at higher free energies. It is actually easier to isolate T in equation
7.22 and solve for it by plugging in a composition. To obtain the following equation, remember that
such that
.
Again, don't forget the two solutions at each temperature; the second
solution is the value of
for the first solution. To find the "spinodes," we need to set the second derivative equal to zero. The quantity
on the right side of equation
7.19 can be replaced by
, which is simply
. For the second derivative to be zero requires that
or:
Inverting both sides of this equation yields:
This turns out to be a simple quadratic function, which can be readily solved for composition:
Again, there are two solutions at every temperature. For example, at the two solutions are 0.276 and 0.724. There is much more to spinodes and spinodal decomposition than these very simplified equations, as you will discover in higher level materials coursework.
7.4 Activity vs. Composition Plots
Although computer programs are able to do a far better job predicting the liquidus, solidus and solvus lines on Type II or “binary” phase diagrams, the previous three sections illustrate how far we can get with some very simple models and assumptions. In that same vein, we now turn to how thermodynamic activity varies with composition in the very phase diagrams considered thus far.
7.4.1 Binary Isomorphous Systems
Consider the binary isomorphous phase diagram in Fig.
7.6. As above, we will consider both liquid and solid solutions to behave “ideally,” meaning that they each follow Raoult's Law (
). At the melting point of B,
, the activity vs. composition plot is very simple, as shown to the right. The line follows Raoult's Law, hence the “RL” label. Since pure liquid B and pure solid B are in equilibrium at
, the plot will be the same regardless of which we chose to be the “standard state” at that temperature.
However, consider a temperature midway between the two melting temperatures (T*), as depicted in Fig.
7.6. It makes sense to choose pure solid B as the standard state, since we are well below the melting point of B. The plot immediately below the phase diagram shows how the activity changes with composition. We always start with the phase that is in the same state as the standard state. In this case we begin at the
point (top right) and begin working backwards down the dashed Raoult's Law line until we reach the two-phase equilibrium between liquid solution and solid solution. In a two-component system at fixed temperature and pressure the degrees of freedom are 2-
, or zero in the two-phase region. This requires that both chemical potential and thermodynamic activity be constant in this region, marked “EQ” for equilibrium. The leftmost regime is seemingly straightforward, since we know that thermodynamic activity must go to zero at zero composition. But this region is also labeled “RL,” yet the line drawn is far from the dashed line for Raoult's Law. The reason is that we are now dealing with a liquid solution on a plot for which the standard state is pure B solid. In fact, if we extrapolate Raoult's Law in the liquid solution all the way to the right side of the activity plot, we obtain the activity of pure liquid B (if it could be obtained at this temperature) with respect to (“WRT”) pure solid B being the standard state and having unit activity.
In the bottommost activity plot, we have chosen pure liquid B to be the standard state, having unit activity. But here we must start our activity plot in the regime where liquid exists, which is on the left side of the phase diagram in Fig.
7.6. We know that the activity must be zero at
so (0,0) is our starting point. Since we have assumed a Raoultian liquid, the activity follows Raoult's Law (“RL”) until the two-phase equilibrium (“EQ”) between liquid and solid solutions, where the activity is constant. The rightmost region is also labeled “RL” for Raoult's Law, but is again far from the dashed Raoult's Law line. Again, the reason is that we are now dealing with a solid solution on a plot for which the standard state is pure B liquid (if it could be obtained at this temperature). By fitting a line from the (0,0) point through the rightmost circled point of the two-phase equilibrium and continuing it to the right side of the diagram, we obtain the activity of pure solid B with respect to (“WRT”) pure liquid B being the standard state at T*. It can be shown that the ratio of
(s) is the same for the two diagrams. Furthermore, it is determined by the free energy of melting or fusion of component B, as we will now show.
At the two-phase equilibrium between liquid solution and solid solution, we can write the following relationships between chemical potential and activity. For the solid we get equation
7.27:
and for the liquid we get equation
7.28:
Until now, we have always assumed the standard state activity to be unity, namely
such that
. However, now we can make a choice as to which standard state we set equal to unity. If we consider the two-phase equilibrium in Fig.
7.6, where
and
, we can subtract equation
7.28 from equation
7.27 to obtain equation
7.29:
Recognizing that
is the free energy of melting per mole of pure B or
, we can use the same approximation as in Eq.
7.6, namely that
or
is not a function of temperature to obtain equation
7.30:
This provides the explanation for how the activity vs. composition plots behave in Fig.
7.6. At
the right side of equation
7.30 is zero; the two standard state activities are the same (
. However, at other temperatures, we have the choice of which standard state activity we set equal to unity, hence the two diagrams for the temperature T*. If we divide both sides of equation
7.30 by
and exponentiate, we find that at a fixed temperature less than
(e.g., T*) the activity ratio
is a constant and is greater than unity, given that the right side of equation
7.30 is now positive. If we set
, it follows that the projected activity of pure liquid B (if it could exist at T*) would have an activity greater than unity. On the other hand, if we set
it follows that the projected activity of pure solid B will have a value less than unity, as on the lower diagram of Fig.
7.6. It should be stressed, however, that Raoult's Law is really
. When dealing with the same “phase” (liquid or solid solution) as the standard state, it is understood that
and the “RL” line will fall on the dashed line in Fig.
7.6. However, when dealing with the opposite “phase” (liquid or solid solution) from the standard state, Raoult's Law will still be a line, but its slope will be governed by the activity ratio
. In the lower two activity plots of Fig.
7.6, we draw a line from the origin to or through the point at which we know the activity relative to the opposing standard state scale. In the bottom diagram, this linear projection ends at the activity of pure B solid with respect to pure B liquid having unit activity.
7.4.2 Binary Eutectic Systems with Dilute Solid Solutions
We can also draw schematic activity vs. composition diagrams for many binary eutectic systems by making the simplifying assumption that the solid solutions are "dilute" solutions. A dilute solution is one for which the solute (the minor component) behaves in a Henry's Law fashion and the solvent (the majority or "host" component) behaves in a Raoult's Law fashion. In fact, it can be proven that if the solute is Henrian, the solvent must be Raoultian. In a dilute solution, the solute (B) atoms are only surrounded by A atoms. It makes sense that the
activity coefficient
(
) in the general equation
7.31:
will not vary with composition over the "dilute" regime until it begins to encounter other B atoms in its surroundings, giving us
Henry's Law
(equation
7.32):
Let's find out what this requires of the solvent, component A. Since
is a constant, it follows that
. But consider a version of the Gibbs-Duhem equation
7.33:
Dividing out the "RT" term and rearranging gives us equation
7.34, where we employ our knowledge of the solute behavior (
) to replace
on the right by
:
But, of course,
,
and
such that equation
7.34 becomes equation
7.35:
If we integrate both sides of this equation, we obtain equation
7.36:
However, by definition, the activity of A must be unity when , requiring that the integration constant be unity, or , which is Raoult's Law. This means that over the composition range that the solute behaves in a Henrian fashion, the solvent behaves in a Raoultian fashion. This will greatly aid us in sketching activity vs. composition plots. For the sake of simplicity, we will also make the simplifying assumption that the liquid is an ideal solution.
Fig.
7.7 is a binary eutectic system with limited solid solubility; we will assume "dilute" behavior. As with the binary isomorphous phase diagram, at the melting point of B it follows that both standard state activities are unity so the activity-composition plot on the right is quite straightforward. The activity of B follows Raoult's Law across the diagram. Similarly, at the temperature
the behavior is quite similar to what we saw with the binary isomorphous phase diagram. We have the choice of B two standard states: solid and liquid. In each diagram we have a two-phase equilibrium ("EQ") separating two Raoult's Law lines (one for the liquid and one for the solvent of the "dilute" solution on the right) and the ratio of
is a constant. If we assume further that the enthalpy of melting of pure B is roughly temperature-independent, we can invoke equation
7.30 to estimate the ratio, given the melting temperature and melting enthalpy of B.
At temperature
the situation is a bit more complicated, as depicted in Fig.
7.8. If we chose solid B as the standard state, we would begin on the right of the diagram and follow the dashed line for Raoult's Law (B being the ideal solvent) down to the phase boundary of the two-phase regime, where the activity would be constant owing to equilibrium "EQ" between liquid solution and the
solid solution. The third line is marked "RL" for Raoult's Law, since we have assumed that the liquid solution behaves this way. The reason that this "RL" line lies above the dashed line is that this is Raoult's Law in the liquid solution with respect to pure solid B having unit activity. To obtain this line, simply draw a line from the origin through the leftmost point of the previous "EQ" situation. The extrapolation of this line to the right side of the diagram would give the activity of pure liquid B (if it could be obtained at this temperature) with respect to pure solid B. Continuing to the left on the plot, we have yet another two-phase equilibrium (between liquid solution and the
solid solution) and a horizontal "EQ" situation. The final regime is strictly in the
phase, for which the B-component is the dilute solute, hence Henry's Law ("HL") is obeyed.
But we have another choice of standard state that can be made, namely pure B liquid, shown in the bottom diagram of Fig.
7.8. As before, we must begin where the phase in question is in the same state as the standard state (liquid). So we start in the very middle of the diagram where liquid solution exists by itself. The activity of B must fall on the standard Raoult's law
dashed line as shown. At each end of this “RL” line segment we encounter two-phase equilibria between liquid solution and
solid solution on the left, and between liquid solution and
solid solution on the right. These are the two horizontal segments marked “EQ” on the plot. The final segment on the left brings the activity to zero at the origin of the plot. This segment is marked “HL” for Henry's Law, since B is the “dilute” solute in the
solid solution. For the final segment on the right, we know that B is the solvent in the
solid solution, and should behave according to Raoult's Law as marked on the diagram. However, this is Raoult's law in the solid solution with respect to pure liquid B being the standard state. Therefore the segment falls on a lower line extrapolated from the origin through the activity at the rightmost point of the two-phase liquid solution-
equilibrium (“EQ”). Where it strikes the right axis of the plot corresponds to the activity of pure solid B with respect to pure liquid B having unit activity. As with the binary isomorphous example, the ratio of
in the two lower plots must be the same. Again, if we assume that the enthalpy of melting of pure B is roughly temperature-independent, we can invoke equation
7.30 to estimate the ratio, given the melting temperature and melting enthalpy of component B.
Below the eutectic temperature we are only dealing with solid solutions, so the situation is quite straightforward. The
plot to the right of the phase diagram in Fig.
7.8 shows how the activity of B varies with composition. We start by defining pure solid B as the standard state. Since B is the solvent in the
solid solution, the plot follows Raoult's Law until the two-phase equilibrium between the
and
solutions, the long horizontal segment marked “EQ” in the diagram. The third and final segment takes the activity of B to zero at the origin. Since B is the “dilute” solute in the
phase, this segment is marked “HL” for Henry's Law.
7.5 Schematic Free Energy vs. Composition Diagrams
In order to compare the free energies of two or more phases in Type II phase diagrams, we need to plot absolute free energies rather than the free energy change upon mixing (
) as in Fig.
7.5. Before working with such diagrams, however, we need to have two more thermodynamic “tools” in our toolbox. The first deals with determining the chemical potentials at a given composition from free energy vs. composition curves, and the second has to do with how free energy curves approach the y-axes (G-axes) at either end of such diagrams.
7.5.1 Method of Tangential Intercepts
In Fig.
7.9 is a schematic diagram of absolute free energy vs. composition of a continuous solution in the A-B system. This could be a liquid solution or a solid solution. The total free energy is given by equation
7.37:
If we divide both sides by (
) we arrive at the free energy per mole of solution or equation
7.38:
Taking the total differential, we obtain equation
7.39:
However, from the Gibbs-Duhem equation (per mole of solution) at constant temperature and pressure in equation
7.33 we have equation
7.40:
Now let's subtract equation
7.40 from equation
7.39 to obtain equation
7.41:
since
. If we multiply both sides of equation
7.41 by
we obtain equation
7.42:
Now let's add equations
7.38 and
7.42 to obtain equation
7.43:
By analogy, we can derive a similar equation for the chemical potential of B as equation
7.44:
These are very important equations. For example, equation
7.44 tells us that if we take the slope of the G vs.
curve at any point (e.g.,
in Fig.
7.9) and place the corresponding line on the diagram, the right intercept will be the chemical potential of B at that particular composition (
at
). This follows from the left side of equation
7.44. The sum of the absolute value of G at that composition plus the product of the mole fraction of A (marked as "run" on the diagram) and the slope
(marked "rise/run" on the diagram) yields
at that composition. Similarly, at the left end of this tangent line will be the chemical potential of component A at that same composition.
This procedure is often referred to as the “method of tangential intercepts.” It is important for several reasons: 1) It conclusively proves that we can fix two chemical potentials by fixing the ratio of two conjugate extensive variables, in this case the ratio of or rather the mole fraction, 2) Given a specific G vs. curve, we can determine the chemical potentials at any composition. 3) Since we know the chemical potential of the pure end-members A () and B (), namely the extreme ends of each G vs. curve, we can also know the activity at any composition using the relationship. 4) Finally, if we have two phases in equilibrium, they must share the same common tangent and intercepts so that the chemical potentials and activities are the same in both phases. We will illustrate this when we draw schematic free energy vs. composition curves for actual phase diagrams (below).
7.5.2 Terminal Slopes on Free Energy vs. Composition Plots
It can be shown that the terminal slopes on a free energy vs. composition plot should be infinitely negative as
and infinitely positive as
. Let's begin with the regular solution model of equation
7.17:
The first derivative of this equation with respect to
gives us equation
7.46:
In the limit that ( ) the derivative becomes negative infinity and in the opposite limit where ( ) the derivative becomes positive infinity. These hold true regardless of the size of the interaction parameter . What this means is that in any free energy vs. composition plots we sketch, the terminal slopes must be at the left and at the right.
7.5.3 Schematic Free Energy vs. Composition Curves for a Binary Isomorphous System
Given these tools, we can sketch schematic free energy vs. composition curves for specific phase diagrams. In Fig.
7.10 are three such plots for three different temperatures in the A-B binary isomorphous system. Temperature
is above the melting point of component B and the liquid solution has the lowest free energy at all compositions compared to the solid solution. The situation at the melting point of B would be essentially the same, with the curve for the liquid solution being everywhere below that of the solid solution with the exception of the composition,
, where the two curves would meet. The situation is reversed at temperature
This temperature is below the melting point of component A and the solid solution now has the lowest free energy at all compositions compared to the liquid solution. The situation at the melting point of A would be essentially the same, with the curve for the solid solution being everywhere below that of the liquid solution with the exception of the composition,
, where the two curves would meet.
At temperature
, however, the two curves overlap in such a way that the liquid solution has the lowest free energy on the left side of the phase diagram and the solid solution has the lowest free energy on the right side of the phase diagram. Between the two phase boundaries, however, the lowest free energy situation can be found on the “common tangent” or dashed line between the two curves. In other words, the equilibrium situation is an assemblage of the two solutions, liquid and solid. In fact, any combination of composition and temperature inside the “lens” of the phase diagram will have a microstructure consisting of a combination of liquid solution and solid solution, whose compositions are determined by the ends of the horizontal “
tie line
” for the temperature in question, as shown for
in the phase diagram.
7.5.4 Schematic Free Energy vs. Composition Plots for Binary Eutectic Diagrams
When dealing with a binary eutectic phase diagram, we have to consider the thermodynamic interaction of three phases: the liquid solution (ls) and two solid solutions. When the
solid solution on the A side of the diagram and the
solid solution on the B side of the diagram have different crystal structures, as in Fig.
7.11, there will be three distinct free energy vs. composition curves at each temperature.
The temperature is above the eutectic temperature. In the middle of the phase diagram the liquid solution (ls) has the lowest free energy. But beyond the liquidus curves to left and right we have two-phase equilibria between liquid solution and one of the solid solutions: solid solution on the left and solid solution on the right. The lowest free energy situation in each case is along the respective line of common tangency, as shown. In these two-phase regions, the chemical potentials can be found at the extremes of the associated common tangent line. Beyond the solidus lines to the left and right, we have either solid solution by itself () or solid solution by itself (). In each case, the lowest free energy situation is the curve for that phase by itself ( or ).
On the other hand, the temperature is below the eutectic temperature. The free energy vs. compostion curve for the liquid solution lies everywhere above those of the two solid solutions. The lowest free energy situation is either a single solid solution by itself, namely solid solution or solid solution on the left and right ends of the phase diagram, respectively, or a microstructure incorporating both and solid solutions in the middle of the phase diagram. Their equilibrium is reflected in the common tangent line between their free energy vs. composition curves in the diagram to the right of the phase diagram.
At the eutectic temperature all three phases (ls, , ) are in equilibrium. This is reflected in the free energy vs. composition curves for all three phases sharing the same common tangent line at , hence the chemical potentials and thermodynamic activities are the same in all three phases. Only at the left and right extremes of the phase diagram do we have solid solution by itself () or solid solution by itself (). The solidus and solvus lines intersect the horizontal eutectic line at the maximum solubilities (of B in and of A in ), at least for this phase diagram. Any composition between these points will exhibit a three-phase microstructure involving differing amounts of solid solution, liquid solution, and solid solution, depending upon overall composition.
There is another way, however, to realize a binary eutectic phase diagram similar to that in Fig.
7.11. Such a diagram and its associated free energy vs. composition curves are shown in Fig.
7.12.
In this case, the solid solution on either side of the phase diagram is essentially the same solid solution with the same crystal structure. However, owing to interaction between the A and B atoms, the solid solution is prone to phase-separation. We described this previously, making use of the Regular solution model with a positive interaction parameter . Temperature is below the eutectic temperature. As shown in the diagram to the right, the free energy vs. composition curve for the liquid solution lies everywhere above that of the solid solution. However, the free energy vs. composition curve for the solid solution is consistent with phase separation into two solid solutions, and At the eutectic temperature, all three "phases" share the same common tangent line. The solidus and solvus lines intersect the horizontal eutectic line at the maximum solubilities (of B in and of A in ). Any composition between these points will exhibit a three-phase microstructure involving differing amounts of solid soution, liquid solution, and solid solution, depending upon overall composition. The temperature lies above the eutectic temperature. In the middle of the phase diagram the liquid solution (ls) has the lowest free energy. But beyond the liquidus curves to left and right we have two-phase equilibria between liquid solution and either or . The lowest free energy situation in each case is along the respective line of common tangency, as shown. In these two-phase regions, the chemical potentials can be found at the extremes of the associated common tangent line. Beyond the solidus lines to the left and right, the lowest energy situation is the curve for solid solution by itself, either on the left or on the right.
7.6 Regular Solution Predictions
Pelton and Thompson showed what could be done by just employing the Regular solution model for both liquid and solid solutions [
9]. The resulting set of diagrams is given in Fig.
7.13.
The phase diagram toward the middle of Fig.
7.13 (row 3, column 3) can be easily recognized as corresponding to a binary isomorphous system, for which the interaction parameters for both solutions (liquid, solid) are equal. In this case, it is assumed that the interaction parameters are both zero,
. In other words, both solutions are taken to be ideal or Raoultian. Note what happens as we stay in the same column (
but moving upward, the value of the interaction parameter for the solid solution is made progressively more and more positive. We obtain the conventional binary eutectic phase diagram, first with limited solid solubility (
kJ
mol
) and then with negligible solid solubility (
30 kJ
mol
). The behavior at the top-right of Fig.
7.13 is particularly distinctive. This is referred to as “monotectic” behavior. If we dramatically increase the interaction parameter of the liquid solution (to +20 or +30 kJ
mole
), we can produce phase-separation in the liquid, i.e., the coexistence of two liquid solutions. Such behavior is employed in the manufacture of a low-cost, high-silica glass called Vycor (by the Corning Company). Glass bodies are made out of borosilicate glass, which then phase-separates into two interconnected phases. The one with lower silica content is leached out by acid at room temperature, leaving the silica-rich phase, which is then densified at elevated temperature into an essentially dense silica body.
7.7 Another Category of Type II Phase Diagrams: Oxygen Partial Pressure vs. Composition
Just as we saw with Type I phase diagrams, there is more than one kind of phase diagram within the Type II category. In the case of Type I diagrams we became aware of several kinds, namely P vs. T, chemical potential vs. T (both Ellingham-type and log
vs. T), and chemical potential vs. chemical potential (stability or predominance area diagrams). For Type II diagrams we have thus far only treated T vs. mole fraction diagrams, but there are definitely other kinds. Fig.
7.14 shows a schematic log
vs. mole fraction diagram. Note that both the total pressure (1 atm) and temperature (1000 K) had to be fixed (C+2 becomes C+0 in the phase rule) in order to result in a 2-dimensional phase diagram for this three-component A-B-O system, namely, F=C+0-
or F=3-
.
At first glance, this would seem to be a T vs. mole fraction phase diagram for a binary isomorphous system as in Fig.
7.4, which it closely resembles. However, this is not the case. In a T-X binary isomorphous phase diagram the two phases in equilibrium at the “lens” are liquid solution (prevails at higher temperature) and solid solution (prevails at lower temperature). In Fig.
7.14 the two phases in equilibrium are an oxide AO-BO solid solution (prevails at higher
) and an alloy A-B solid solution (prevails at lower
). The x-axis is the mole fraction of B in either phase, namely
, which translates into
in the oxide solid solution (see the dual x-axis in Fig.
7.14). Both solutions are 1) solid and 2) continuous. So this is an oxidation phase diagram. The
values at either end of the “lens” correspond the point of oxidation of pure metal to pure oxide, either A to AO (on the left) or B to BO (on the right). Since the interpretation of all phase diagrams within a given Type is the same, the “lens” corresponds to two-phase equilibrium between an oxide solid solution (ceramists never refer to solid solutions as “alloys!”) and an alloy solid solution, as at the ends of the tie-line at the selected
in the phase diagram.
In fact, we can actually simulate the phase diagram in Fig.
7.14. Of course, this is an extremely unique situation, involving continuous solid solutions of both phases. This would mean that Hume-Rothery rules would need to be satisfied for both solid solutions. For our simulation, we will assume that both solid solutions behave ideally, i.e., they behave according to Raoult's law such that
and
in the alloy and
and
in the oxide solid solution. We begin by writing the oxidation reaction for component A as equation
7.47:
We can write the equilibrium relationship for this reaction as follows in equation
7.48:
We can evaluate the equilibrium constant
in one of two ways. First, we can find the value of
at 1000 K from the Ellingham diagram in Fig.
6.2. Second, we can use the
nomographic scale on the Ellingham diagram to solve the following equilibrium equation :
We are dealing here exclusively with the point at the leftmost end of the “lens” in Fig.
7.14, where essentially pure A metal is in equilibrium with pure AO oxide. The value of
can be established by drawing a line from the O-fulcrum through the
intersection of the A/AO line to the O-nomographic scale on the Ellingham diagram of Fig.
6.2. A similar process can be carried out at the right side of the “lens” in Fig.
7.14 involving the oxidation reaction for component B as per equation
7.50:
yielding an analogous equilibrium relationship as described by equation
7.51:
As for the A/AO equilibrium, we can establish the value of
from either the
value at 1000K from the Ellingham diagram, or alternatively the value of
by drawing a line from the O-fulcrum through the 1000 K intersection of the B/BO line to the O-nomographic scale on the Ellingham diagram of Fig.
6.2.
This gives us the two endpoints of the “lens,” but how can we establish the phase boundaries of the “lens” for, say, a given
value as illustrated by the tie line in Fig.
7.14? This can be accomplished by recognizing that both equilibrium relationships of equations
7.49 and
7.51 must also hold for every
value between the extrema (
and
). Furthermore, the situation is simplified by our assumption of Raoultian behavior for each solid solution. We can therefore write two equilibrium expressions
7.52 and
7.53:
Taking into account that
and
we can divide equation
7.53 by equation
7.52 to eliminate the unknown
to arrive at equation
7.54:
Taking the square root of both sides and rearranging, we obtain equation
7.55:
Since at each temperature, including 1000 K, the ratio
is a constant, we can solve equation
7.55 for a unique value of
for each inputted value of
. We can then plug the values of
and
into equation
7.52 to solve for the corresponding value of
. By varying the value of
, we can solve for individual tie-lines (
). Once again,
and
. Intrepreting the phase diagram in Fig.
7.14 is straightforward. In each of the single-phase regions there are two degrees of freedom, i.e., to establish thermodynamic equilibrium (in addition to fixing overall pressure (1 atm) and temperature (1000 K), one would have to fix the overall composition (B/A ratio) and the oxygen partial pressure). Inside the "lens" however, there is a single degree of freedom. If we fix the oxygen partial pressure, both phases' compositions are fixed. Alternatively, we need only fix one composition of the two phases in equilibrium, say
, and the composition of the other phase,
, plus the oxygen partial pressure are thereby also fixed.
8 Type III (Ternary) Phase Diagrams
As we begin to introduce Type III phase diagrams, it is useful to compare and contrast their appearance with that of Type I and Type II phase diagrams as schematically represented in Fig.
8.1.
Type I diagrams are distinctive in their absence of tie-lines. Areas are always single-phase regions, and lines are always phase boundaries between two adjacent phases. Type II diagrams are distinctive because of their having tie-lines perpendicular to the “thermodynamic potential” (
) axis. The dashed lines are usually not drawn as in the Type II diagram of Fig.
8.1; but they are understood. In fact, since we can always draw another tie-line between any adjacent pair of tie-lines, there is an infinite array of tie-lines within the three two-phase regions on the diagram. However, when these tie-lines converge to unique three-phase (F=O) invariancies, these are represented as solid lines perpendicular to the
-axis. For example, we are quite familiar with the horizontal invariant lines in T vs. mole fraction eutectic (as in Fig.
7.1) or eutectoid diagrams (see Fig.
4.2). So there are two different “areas” in Type II diagrams: single-phase regions (
,
,
) and two-phase regions consisting of an infinite array of parallel tie-lines perpendicular to the
-axis (
). Type III diagrams are distinctive owing to the presence of tie-triangles involving three phases in equilibrium (
in Fig.
8.1). They are also distinctive in that tie-lines need neither be parallel nor perpendicular to any axis, as shown in Fig.
8.1. In contrast with Type II diagrams, tie-lines for two-phase equilibria are typically drawn. However, once again since we can always find another tie-line between any adjacent pair of tie-lines, there is an infinite array of tie-lines within the two-phase regions on the diagram. Furthermore, as these converge to the sides of unique three-phase equilibrium triangles, these solid lines become very important, representing the terminal compositions of the two phases in equilibrium with that of the third. So lines are either phase boundaries of single-phase regions (can be curved) or the straight line sides of tie-triangles. As can be seen, open “areas” can either be single-phase regions (
,
,
) or tie-triangles. These tie-triangles are usually referred to as “compatibility” triangles, meaning that the terminal compositions of the three phases are “compatible” and do not react with one another.
Various axis schemes have been employed for Type III phase diagrams, as illustrated in Fig.
8.2.
The strictly
vs.
scheme at the top-left finds limited use in the literature, but can be useful for representing phase equilibria in dilute solutions. The reason that this representation is not practicable for full-scale diagrams has to do with the loci of the end-members B and C on the diagram. Component A lies at the origin, however pure B and pure C exist at
and
values of inifinity on their respective axes. The mole fraction C vs. mole fraction B diagram at the top-right corrects this problem. Solutions to the overall mole fraction equation,
, exist only within the dashed region. Again, this axis scheme has found limited use in the literature. The near-universal axis scheme used by materials scientists and engineers involves collapsing the diagram at the upper right of Fig.
8.2 into an equilateral triangle as shown in the bottom diagram of the Fig.. Since this axis scheme was developed by J. Willard Gibbs of Gibbs free energy fame, it is usually referred to as a Gibbs phase triangle. The mole fraction of a given component is read from equally-spaced lines drawn parallel to the opposing side of the diagram, as shown for component C in Fig.
8.2. Comparable lines can be drawn parallel to the other two sides of the diagram, to establish the mole fractions of components A and B for a specific composition.
8.1 The Ternary Lever Rule
The Gibbs phase triangle axis scheme actually is a specific case of the ternary lever rule. This is represented for a more general three-phase (
) equilibrium in Fig.
8.3.
The ternary lever rule is applicable to all tie-triangles, and not just equilateral ones. The best approach is to employ a ruler to measure the length of line segments in the specific triangle. For example, take the composition marked by the “X” in Fig.
8.3. The fraction of the
phase,
is the length of the line segment marked AX divided by the entire length of the line drawn from the
side of the tie triangle through the overall composition “X” to the
vertex. Similarly, the fractions of the
and
phases can be determined from their relative line lengths, so we have:
The three fractions sum to unity. It can be readily seen that when this scheme is applied to an equilateral triangle, we obtain the axis scheme associated with Gibbs' phase triangle. We will employ the ternary lever rule quite frequently when dealing with so-called “horizontal sections” and crystallization sequences in so-called “liquidus projection” diagrams.
8.2 Dealing with an Additional Degree of Freedom
It can be easily demonstrated that we need 3-dimensions to do justice to Type III or “ternary” phase diagrams. Fig.
8.4 shows such a schematic three-dimensional phase diagram for the system A-B-C with negligible solid solubility.
Since there are three components (C=3), even if pressure is fixed at 1 atm such that (C+2) becomes (C+1), the phase rule will be F=4-
. This means that we need three axes to fully represent the phase equilibria: temperature (T), and two of the three mole fractions in the equation,
, e.g., the mole fraction of component A (
) plus the mole fraction of B (
), hence the 3-D diagram in Fig.
8.4 with temperature (T) as the vertical axis.
The major features of this diagram are the three “mountain peaks” known as “primary phase fields” in phase diagram parlance, which meet at three “valleys” or liquidus phase boundaries that descend from the “passes” (think of “Donner Pass”) at the binary eutectics on the bounding binary eutectic phase diagrams into the interior of the ternary diagram until all three valleys converge at the ternary eutectic (think of “Jackson Hole”).
8.3 Liquidus Projection Diagrams
This is all very visual, but we tend to be “flat-landers,” preferring 2-dimensional representations. One way to achieve 3-D perspective on a 2-D diagram is by projection, as in the bottom of Fig.
8.4. This is referred to as a "liquidus projection diagram." To capture all the 3-D information, however, the projection needs to include liquidus "isotherms" or lines of constant liquidus temperature, as shown in Fig.
8.5 for the NaCl-NaF-NaI system. One can think of such diagrams as being like topographic maps, which contain "contour lines" of constant altitude. We will return to the “mountain/valley/hole” analogy and use these isotherms to advantage when we discuss "isothermal sections" (below). Note that C=3 (NaCl, NaF, NaI) rather than C=4, owing to the fact that, as with the
Type I phase diagram (C=1), the ratios of Na:Cl, NaF, and Na:I remain fixed.
We can actually produce a schematic liquidus projection diagram based upon some thermodynamic data (melting points and enthalpies of melting for the end members) and some simple assumptions, namely that there is negligible solid solubility and that the liquid solution behaves in a Raoultian fashion. These assumptions are not far from reality for many ceramic systems, for which fulfillment of the Hume Rothery rules (same crystal structure, same cation valence, similar electronegativities, similar cation radii) is fairly rare. We previously found an equation for the liquidus line in a binary system with negligible solid solubility and an ideal liquid (equation
7.7). We employed two such equations to establish the two liquidus curves and their intersection (the binary eutectic) in Fig.
7.3. By combining each of the three possible pairs of equations, we can produce the bounding binary eutectic phase diagrams in Fig.
8.4. However, if we assume the ternary liquid solution to be Raoultian, namely
for each component, there is no reason that the same procedure cannot be extended into the ternary diagram. First, we write the three equations for each of the three components:
The procedure for predicting the liquidus projection diagram using these three equations is outlined in Fig.
8.6.
Solutions for each equation are lines parallel to the opposite boundary of the phase diagram, i.e., at constant mole fraction of that particular component. For example, at 900K the solution to equation
8.4 is a constant mole fraction of C as shown (
). Similarly, at 800K the solution to equation
8.2 is a constant mole fraction of A as shown (
). Note that if we keep ramping down the temperature the two solutions meet at the temperature of 700K, the binary eutectic temperature for the A-C system. But the solutions can extend to smaller mole fractions as well. This is the genesis of the solid line extending into the interior of the phase diagram from the binary eutectic (see solutions for 650K and 600K). This would require smaller value of
and
than at the binary eutectic, where
. However, this is not a problem since we are now dealing with ternary compositions, such that
. We are now following the A plus C plus liquid phase boundary (“valley”) descending from the “pass” of the A-C binary eutectic into the interior of the phase diagram as in Fig.
8.6. If we do the same procedure for the A plus B plus liquid phase boundary and the B plus C plus liquid phase boundary, the three valleys will meet at the ternary eutectic point (“E” in Fig.
8.4).
The resulting “liquidus projection diagram” should look something like the bottom diagram in Fig.
8.6. There are obvious differences between our predicted phase diagram (Fig.
8.6) and an actual liquidus projection diagram (see Fig.
8.5). The main difference is that predicted isotherms are straight and parallel to one another and parallel to the opposing side of the triangle. This is an automatic result of the ideal liquid solution assumption underlyling equations
8.2 through
8.4. In the real phase diagram, although the isotherms are approximately parallel, they are curved and deviate substantially from being parallel to the opposing side of the triangle. This simply makes us challenge our assumptions underlying our predictions. First, the liquid solution may be far from Raoultian and second, there may actually be appreciable solid solubility.
8.4 Hummel's Rules for Ternary Systems with Negligible Solid Solubility
We can relax the Raoultian liquid specification in our considerations, but if a given ternary phase diagram involves negligible solid solubility it can be shown that very specific rules hold for the interpretation of liquidus projection diagrams. Once we have laid the foundation for interpretation of such Type III phase diagrams, we can turn to more sophisticated simulation engines/algorithms to help us interpret ternary diagrams with appreciable solid solubility. For examples, many metal alloy ternaries fall into the latter category.
In order to introduce Hummel's Rules (adapted from F. A. Hummel's class notes and his textbook,
Phase Equilibria in Ceramic Systems, Marcel Dekker, 1984), we need to develop a binary analogy. We need to think carefully about how to generate both eutectic and peritectic behavior in the absence of solid solubility. Conventional binary eutectic and peritectic phase diagrams are displayed in Fig.
8.7. We have already described the “easy melting” character of eutectic systems, but the melting/heating reactions are quite different between eutectic and peritectic diagrams. We can describe them as follows in equations
8.5 and
8.6:
In these reactions, the forward arrow stands for heating and the reverse arrow stands for cooling. From the Greek, “peritectic” means “covered melting.” This can be seen in that the “primary phase field” of (the two-phase area where only is in equilibrium with liquid) overhangs or covers the phase. Another way to describe peritectic melting is that the phase melts to a liquid of a different composition and another solid (). This is referred to as “incongruent melting,” as described below.
But now let's imagine what happens on both diagrams as the solid solubilities, namely the solubility of B in
and the solubility of A in
, go to zero. This works for the eutectic system (as in Fig.
7.3), where the quotation marks around “A” and “B” remind us that thermodynamically speaking, there is no such thing as an absolutely “pure” solid. In contrast, note that it is impossible to preserve peritectic behavior when solid solubilities go to zero in a simple binary peritectic diagram of Fig.
8.7. However, we can introduce peritectic behavior in a negligible solid solubility system by introducing an intermediate compound (AB), as shown in Fig.
8.8. The diagram on the left has an intermediate compound (AB), which melts “congruently,” namely it melts to a liquid of identical composition, AB. In fact, we can recognize that this diagram can be thought of as consisting of two side-by-side eutectic diagrams: A-AB and AB-B. However, this cannot be said of the diagram on the right. It similarly has an intermediate compound (AB), however in this case the compound (AB) melts “incongruently” to a liquid of a quite different composition (the “peritectic” composition at
) and a different solid (“B”). It obeys the peritectic melting behavior described by equation
8.6. The apparatus beneath the two phase diagrams will be discussed shortly.
As we introduce each of Hummel's Rules we will, 1) make reference to the binary analogues in Fig.
8.8, and 2) try to place each rule on a firm solution thermodynamic footing. Before we proceed, however, we need to introduce and define common phase diagram terminology. The first term is “primary phase,” referring to the first phase to crystallize from the melt on cooling, thus the major or “primary” solid phase in the developing microstructure. For example, in the dual-eutectic diagram on the left side of Fig.
8.8 between the pure A end-member and the binary eutectic,
A is the “primary phase.” The second term is closely related. A “primary phase field” is the area in a liquidus projection diagram where a single (primary) phase is in equilibrium with liquid. For example, in the dual-eutectic diagram on the left side of Fig.
8.8 between the two eutectic points,
and
, exists a quite large “primary phase field” for compound AB. In contrast, the primary phase field of AB is significantly compressed in the eutectic-peritectic diagram on the right side of Fig.
8.8, existing only between the eutectic
) and peritectic (
) points. The third term, “subsolidus compatibility,” requires additional explanation. First of all, we need to understand what “subsolidus” means. On the left side of Fig.
8.9 we see a conventional binary eutectic phase diagram with limited solid solubility. The “solidus” lines are circled on the left and right and correspond to the first appearance of liquid upon heating, or the last occurrence of liquid upon cooling; hence “subsolidus,” meaning “below the solidus.” However, you will see that the horizontal eutectic line is also circled. For all compositions between the ends of this line (the extrema of solid solubility) the first liquid appears on heating upon crossing this line. Conversely, upon cooling the last liquid disappears upon cooling through this line. Therefore, the horizontal eutectic line can be thought of as part of the “solidus.” If we shrink the solid solubilities to essentially zero, we obtain the phase diagram on the right side of Fig.
8.9. Here, “subsolidus” applies to all compositions when below the eutectic temperature. We can now introduce two additional terms that are valid for negligible solid solubility systems: “subsolidus compatibility join” and “subsolidus compatibility triangle.” A “subsolidus compatibility join” is any line connecting two phases that are compatible, meaning that they do not react to form other phases in the subsolidus. In Type III ternary phase diagrams we have both “subsolidus compatibility joins” and “subsolidus compatibility triangles,” the latter referring to composition triangles connecting three compatible solid phases in equilibrium in the subsolidus. As mentioned previously with regard to the distinctive characteristics of the various phase diagram Types in Fig.
8.1, compatibility triangles are the hallmark of Type III diagrams.
We can now put the analogues and the apparatus at the bottom of Fig.
8.8 to good use. Hummel's first rule states that “liquidus surfaces always fall away (in temperature) from the corresponding primary phase.” Thermodynamically, we can understand this from the familiar equation
8.7, developed for situations where the “primary phase” exhibits negligible solid solubility and the liquid solution behaves in a Raoultian fashion.
where “i” stands for the Raoultian liquid host (A, B, AB). Starting with the melting temperature (
), for which the right side of equation
8.7 is zero, requiring the mole fraction of component “i” in the liquid to be 100%, we can see that as the temperature decreases the right side of this equation becomes increasingly positive, requiring increasingly fractional mole fractions of “i.” In other words, the liquidus falls away (in temperature and in composition) from the corresponding primary phase. This can be readily seen in Fig.
8.8; in both diagrams the liquidus in a given primary phase field always falls away from the corresponding primary phase. This holds true even for the incongruently melting intermediate compound, AB, in the eutectic-peritectic diagram of Fig.
8.8. Even though the primary phase field is at some distance from the AB composition, it can be seen that the liquidus still falls away from the primary phase (AB).
Hummel's second rule state that “there are as many primary phase fields as there are primary phases that melt.” To understand this rule, let's take an imaginary helicopter trip up above “mount A,” “mount B” and “mount AB” in each of the diagrams in Fig.
8.8. Looking down on each diagram, it is easy to identify three “mountains” or primary phase fields, one for A, one for B, and one for AB. It is true that we only see a “shoulder” of mount AB in the eutectic-peritectic diagram on the right of Fig.
8.8. Nevertheless, the primary phase field is visible for the AB primary phase. In each diagram, there are three primary phase fields (PPFs) and three primary phases (A, AB, B). This may seem overly obvious on these binary diagrams, but this rule will be a big help when dealing with ternary liquidus projection diagrams, where primary phase fields are areas rather than lines. The rule refers to “primary phases that melt” for good reason. Fig.
8.10 shows an intermediate compound with “an upper temperature limit of stability,” namely the compound AB decomposes into solid A and solid B well before it has the chance to melt. Above the decomposition temperature, it is as if the system is a straightforward A-B eutectic system. Believe it or not, it is possible for the compound AB to have a primary phase field in a ternary A-B-C system, but this complication is beyond the scope of the present treatment; hence the disclaimer referring to “primary phases that melt.”
Hummel's third rule states that “there is a one-to-one correspondence between liquidus invariant points and the corresponding subsolidus compatibilities.” If we go down in temperature into the subsolidus, there are two subsolidus compatibilities in each diagram of Fig.
8.8, namely A-AB and AB-B. In other words, for any composition between A and the intermediate compound, AB, in the subsolidus there will be two phases in equilibrium: A and AB. Similarly, for any composition between AB and B in the subsolidus, there will be two solid phases in equilibrium: AB and B. Since there are precisely two subsolidus compatibilities in each diagram, from Hummel's third rule we can anticipate two invariant points. On the dual-eutectic diagram on the left side of Fig.
8.8, there is an invariant point where the primary phase fields of A and AB meet (
) and one where the primary phase fields of AB and B meet (
). On the eutectic-peritectic diagram to the right side of Fig.
8.8, there is an invariant point where the primary phase fields of A and AB meet (
) and one where the primary phase fields of AB and B meet (
). This rule may seem simplistic when dealing with the uncomplicated binary diagrams in Fig.
8.8, but will be quite powerful when dealing with a complicated ternary liquidus projection diagram. If there are 10 subsolidus compatibility triangles, there will be precisely 10 ternary invariant points, with a one-to-one correspondence between them.
Hummel's fourth rule states that “invariant points inside their respective subsolidus compatibilities are eutectics, whereas those outside their respective subsolidus compatibilities are peritectics.” Looking in 2-D at the two phase diagrams in Fig.
8.8, it is quite obvious which points are eutectics and which are peritectics. But now imagine that we are back in the helicopter hovering above the 1-D phase diagrams (see the lines labeled “1-D view” in the apparatus beneath each diagram). It is clear on the left diagram that the point where the primary phase fields of A and AB (PPFs) come together lies within the corresponding A-AB subsolidus compatibility (see “compats” in the apparatus). This is therefore a eutectic. The same is true for the eutectic-peritectic diagram on the right side of Fig.
8.8. In the case of the invariant point involving AB and B, the situation is different between the two phase diagrams. From the helicopter, we can see in the apparatus for the diagram on the left side of Fig.
8.8 that the point where the primary phase fields of AB and B come together lies within the corresponding AB-B subsolidus compatibility; hence, this is a eutectic. In contrast, the point where the primary phase fields of AB and B come together in the diagram on the right side of Fig.
8.8 lies outside the corresponding AB-B subsolidus compatibility; hence, this is a peritectic. Again, these relationships may seem quite simplistic when dealing with binary phase diagrams, but rule no. 4 will be quite powerful when dealing with complex liquidus projection diagrams. Ternary invariant points inside their corresponding subsolidus compatibility triangles will be eutectics; those falling outside their subsolidus compatibility triangles with be peritectics.
Let's begin to illustrate the first four Hummel's rules with regard to the liquidus projection diagram in Fig.
8.11.
It may seem that this diagram is useless in the absence of primary phase field labels and liquidus projection isotherms, but application of Hummel's rules will show this not to be the case. First, let's apply rules no. 2 and 3: “there are as many primary phase fields as there are primary phases that melt” and “there is a one-to-one correspondence between liquidus invariant points and the corresponding subsolidus compatibilities.” If we go around the diagram we can count four “primary phases that melt,” namely the end-members A, B, C, and the binary compound AB. In ternary phase space, primary phase fields are areas. We can identify four primary phase fields in ternary space. We can make assignments beginning from the vertices (end-members) and then dealing with any binary and ternary compounds. This is done in Fig.
8.12.
Using the third rule (“there is a one-to-one correspondence between liquidus invariant points and the corresponding subsolidus compatibilities”) we can now sketch in the subsolidus compatibilities. There are two ternary invariant points (intersections of three phase boundaries or “valleys” as well as intersections of three primary phase fields or “mountains,” namely where the primary phase fields of A, C, and AB come together and where the primary phase fields of AB, C, and B come together). The one-to-one correspondence of Hummel's third rule requires that there be two subsolidus compatibility triangles: A-C-AB and AB-C-B, as shown in Fig.
8.13.
Furthermore, Hummel's rule no. 4 allows us to identify the nature of the ternary invariant points: “invariant points inside their respective subsolidus compatibilities are eutectics, whereas those outside their respective subsolidus compatibilities are peritectics.” In this case, both invariant points are inside their respective subsolidus compatibility triangles; hence, they are both ternary eutectics, as labeled in Fig.
8.13. In other words, the point where the primary phase fields of A, C, and AB converge is inside the corresponding A-C-AB compatibility triangle, and similarly for the PPFs of AB, C, and B.
However, there is much more that can be done with a schematic liquidus projection diagram, as captured in Hummel's fifth and sixth rules. The fifth rule, in combination with rule no. 1, allows us to draw in “directions of falling temperature” on all the liquidus phase boundaries or “valleys.” It states, “the direction of falling temperature on a liquid-solid(1)-solid(2) phase boundary is always away from the corresponding solid(1)-solid(2) join.” This follows from what we did in predicting liquidus phase boundaries (“valleys”) in the simple ternary eutectic phase diagram of Fig.
8.6 (assuming ideal liquid solution and negligible solid solubility). By the governing equations for two of the components, e.g., A and C:
we found the phase boundary or “valley” descending from the “pass” or binary eutectic on the A-C binary into the interior of the ternary diagram and headed for the ternary eutectic. Fig.
8.14 shows most of the directions of falling temperature (DFTs) for the current ternary phase diagram. For example, beginning at the A-C binary eutectic (
) the liquid-solid(A)-solid(C) phase boundary “falls away” from the A-C join, which happens to be the bounding binary. The same argument goes for all the “valleys” descending into the interior of the phase diagram from the bounding binaries. In the middle of the diagram we find a special case, but rule 5 still holds: the liquid-solid(C)-solid(AB) phase boundary falls to the left of the AB-C join toward one ternary eutectic (
), just as the liquid-solid(C)-solid(AB) phase boundary falls to the right of the AB-C join toward the other ternary eutectic (
).
We are nearly finished with the phase diagram but we need to introduce the final Hummel's rule: No. 6. This may seem complicated at first, but it is nicely illustrated in Fig.
8.15. Rule no. 6, also referred to as “the
Alkemade Theorem
” (pronounced “awl-keh-mah-deh”) states that “a compatibility join solid(1)-solid(2) intersected solely by its own liquid-solid(1)-solid(2) boundary is a true binary eutectic in its own right; temperature falls to this point (a true binary eutectic) along this join, but falls away to either side in the ternary diagram.” Hence, the crossing point labeled as
in the diagram is a “saddle point,” with DFTs descending to it from the end points (pure A, pure AB) but descending into the ternary on either side (also fulfilling rule no. 5).
You will note that directions of falling temperature on all the bounding binaries have also been drawn in. This is in accordance with Hummel rule no. 1, “liquidus surfaces always fall away (in temperature) from the corresponding primary phase.” This completes the ternary liquidus projection diagram, but we can also sketch all the binary phase diagrams, at least schematically. As long as we are provided no isotherms or melting temperatures of the end members (A,B,C) or the intermediate compound (AB), only schematic diagrams can be sketched. So if you sketch a diagram with the melting point of C lower that that of AB, I cannot argue with you. The resulting schematics are shown in Fig.
8.16. Note that the AB-C eutectic diagram, determined by the Alkemade Theorem, is also represented in schematic fashion.
Since we are dealing with schematic phase diagrams, just as with the choice of relative melting temperatures for the end-members (and compounds) the choice of relative eutectic temperatures is also arbitrary. For example, in Fig.
8.16 the A-AB eutectic temperature is shown as being higher than for the AB-B eutectic. Were you to sketch it in the reverse fashion I could not argue with you, given the absence of more precise input information. However, there is one situation that is forbidden. This is shown in Fig.
8.17, where both A-AB and AB-B eutectics seem to have the same temperature. This is a violation of Gibbs phase rule. For any 2-D phase diagram, Gibbs phase rule is F=3-
. In Fig.
8.17 there are actually five phases in equilibrium: three solid phases (A,AB,B) and two liquid solutions (the A-AB eutectic liquid and the AB-B eutectic liquid). Therefore, such a representation is to be avoided.
A slightly more complicated liquidus projection diagram is given in Fig.
8.18, which involves an incongruently melting binary compound,
. You are more than welcome to take a crack at the diagram, using Hummel's rules to 1) label all primary phase fields, 2) determine the four subsolidus compatibility triangles (there are four ternary invariant points), 3) label all invariant points, both ternary and binary, 4) label directions of falling temperature on all ternary liquid-solid(1)-solid(2) boundaries and on the bounding binaries, and 5) sketch schematics of the bounding binary phase diagrams and any other true binary diagrams (satisfying the Alkemade Theorem) within the ternary. There are some “quirks” to this phase diagram, whose solution is given in Fig.
8.19.
The AC-AB binary is a clear solution to Hummel's rule no. 6 (the Alkemade Theorem). Only the liquid-solid(AC)-solid(AB) liquidus boundary crosses the AC-AB join. Hence, the intersection point is a true binary eutectic (), which is a saddle-point in the liquidus; temperature falls to this point along the AC-AB binary (see the figure in the upper right), but falls to either side toward the ternary eutectics (). But what about the seemingly corresponding point on the join? According to Hummel's rule no. 1, temperature falls away from the end members on this join, as shown. Furthermore, according to Hummel's rule no. 5, temperature on the liquid-solid(AB)-solid() phase phase boundary falls away from the AB- join, as shown. However, the AB- join is NOT a true binary eutectic, owing to the fact that the primary phase field of C overlaps the AB- join at the upper right. There is no way on an AB- binary eutectic to combine AB and and arrive at pure C. So the AB- join is NOT a true binary eutectic phase diagram.
All this results from the peritectic behavior in the C-B binary. As shown in the C-B phase diagram, the primary phase field of solid C overhangs the
composition, requiring that
melt incongruently to a different solid (C) and a liquid of a different composition (
). This behavior persists into the ternary, with the primary phase field of C overhanging the liquid-solid(C)-solid(
) phase boundary. The two circled arrows in Fig.
8.20 showing temperature descending from the C-B binary peritectic (
) to the ternary peritectic (
) follow from Hummel's rule no. 5: “the direction of falling temperature on a liquid-solid(1)-solid(2) phase boundary is always away from the corresponding solid(1)-solid(2) join.” In this case we have to extend the C-
subsolidus compatibility join, as shown by the dotted line in Fig.
8.20, away from which the liquid-solid(C)-solid(
) boundary descends from the binary peritectic to the ternary peritectic. A final clarification has to do with the single arrow along the liquid-solid(AC)-solid(
) liquidus phase boundary, between the ternary peritectic (
) and the ternary eutectic (
). This satisfies Hummel's fifth rule, with the direction of falling temperature being away from the corresponding AC-
join, which is well above it on the diagram.
8.5 Isothermal Sections
Believe it or not, the ternary phase diagrams considered thus far are actually NOT valid Type III phase diagrams. This is owing to their 3-D character, or at least the projection of 3-D character onto liquidus projection diagrams. We now turn to so-called “isothermal sections,” which are true Type III phase diagrams. In Fig.
8.21 we have reproduced the limited solid solubility liquidus projection diagram for the NaCl-NaF-NaI system.
We will now derive a series of isothermal sections from this phase diagram. It should be emphasized that 1) these are NOT schematic, but rather real phase diagrams which, 2) are true Type III phase diagrams. The first diagram at 991
C is particularly straightforward in Fig.
8.22, being one degree C above the melting point of the most refractory end-member (refractory is from the French, meaning “high-melting;” NaF melts at 990
C). The entire isothermal section consists of a continuous liquid solution. We can return to the “mountain/valley/hole” analogies and the great Noahic flood; water is above the tops of all the mountains.
But now let's begin to drain the water from “Jackson Hole,” bringing its level down to 850 meters, or rather the temperature to 850
C as in Fig.
8.23. In doing such isothermal sections, it is helpful to overlay tracing or other “see-through” paper to trace the boundaries of the ternary and the specific “contours” (isotherms). At 850 meters the water is still above the tops of “mount NaCl” and “mount NaI.” But the top of “mount NaF is exposed. Actually, for the diagram in Fig.
8.23 a “strip mining” analogy is probably more appropriate. Imagine removing the top of the mountain down to the 850 meter (or 850
C) level (plus one centimeter as a “levee” to keep the water out). Water would be everywhere to the south on the diagram; to the north would be the flattened top of mount NaF. In the diagram you see dashed tie lines connecting various liquidus compositions around the perimeter back to the NaF vertex. This is a result of negligible solid solubility, namely that little NaCl or NaI tends to dissolve in solid NaF. All tie-lines radiate from the vertex. Imagine a friend standing and holding a rope at the composition of “pure” NaF, with you holding the opposite end and walking the “perimeter” or the shoreline of the water (the 850
C isotherm) all the while keeping the rope taut. I refer to these constructions as “waffle cone” features. But we still don't see the tie-triangles characteristic of Type III diagrams. This happens at lower temperatures, however.
For example, at 650
C in Fig.
8.24 we are well below the melting points of NaF and NaCl, and even the very top of “mount” NaI (melts at 659.3
C) is exposed. More importantly, the dropping water has exposed the NaCl-NaF-liquid “valley” descending from the NaCl-NaF eutectic at 680.4
C. The remaining liquid solution portion is significantly smaller. There are now three “waffle cone” features, involving each of the primary phases in equilibrium with a range of liquid solutions. Again, tie-lines radiate from the “pure” end-members. Remember, we can always draw an intermediate tie-line between any two adjacent tie-lines; the “waffle cone” regions consist of an infinite array of tie-lines connecting primary phases and liquidus. More significantly, we see our first “tie-triangle” involving solid NaCl, solid NaF, and liquid solution. As pointed out previously, such tie-triangles are the hallmark of Type III phase diagrams.
Let's go further down in altitude (or rather temperature). There are no contour lines at 550 meters (550
C), but we can certainly envision/approximate them as being roughly midway between 575 meters and the 529.4 meter altitude of “Jackson Hole” (529.4
C). The resulting phase diagram in Fig.
8.25 has a greatly shrunken liquid solution region. There are now three “waffle cone,” or rather “ice cream cone,” constructions involving each of the primary phases and different small ranges of liquid solution. Dominating the diagram, around the perimeter are three tie-triangles involving two solid phases and three unique compositions of liquid solution. Clockwise, these are solid NaCl plus solid NaF plus liquid solution(1), solid NaF plus solid NaI plus liquid solution(2), and finally solid NaCl plus solid NaI plus liquid solution(3).
Let's pause and consider the nature of these isothermal sections. Later we return to the question of microstructure, however these series of diagrams give a good representation of isothermal sections which, once again, are true Type III phase diagrams. The phase rule for a C=3 system at fixed overall pressure and temperature, where C+2 becomes C+0, is given as F=3-
. Applying this to Fig.
8.25, we would find that F=2 in the small liquid solution region (
=1); we would have to specify two of the three mole fractions to establish equilibrium. In the “ice cream cone” features
=2, so we would have one degree of freedom. Specifying overall composition determines which tie line we are on, and the particular liquid solution in equilibrium with the associated solid phase. Or given the liquid solution composition, we would know on which tie-line the overall composition falls. Finally, in each of the tie-triangles
=3 making F=0; all of the compositions are fixed, including that of the associated liquid solution.
The situation is a bit different at the ternary eutectic temperature. As we continue to go down in temperature it is apparent that the liquid solution region in Fig.
8.25 is shrinking and approaching the “drain” (“Jackson Hole” in our mountain/valley/hole analogy). What happens at precisely the point where the altitude of the “hole” is reached is displayed in Fig.
8.26. At first, this would seem to be a violation of the phase rule (F=3-
), with four phases in equilibrium: solid(NaCl), solid(NaF), solid(NaI), and ternary eutectic liquid. However, we do not have the luxury of selecting the temperature, in the same way that we have no control over the altitude of Jackson Hole. The eutectic temperature is fixed for us, meaning that we can only look it up in a handbook (or on the published phase diagram of Fig.
8.21). We have no ability to change it. So (C+2) does not reduce to (C+0) as for the other isothermal sections, for which both temperature and pressure is fixed. Instead, temperature remains a free variable such that (C+2) becomes (C+1), the “1” standing for temperature, and the phase rule becomes F=4-
. So under the unique conditions of a ternary invariant point, we can have four phases in equilibrium.
Let's complete our isothermal section “journey” by reducing the temperature to below the “hole” or the ternary invariant point. We are now in the subsolidus, and the entire phase triangle becomes one big tie-triangle involving the three “pure” end-members in equilibrium. The temperature of 529
C is 4/10ths of a degree below the ternary eutectic temperature. There is no remaining liquid solution; everything has solidified. So the resulting isothermal section in Fig.
8.27 is nearly as straightforward as the one with which we started.
8.6 Crystallization Paths and Microstructure Evolution
Just as with binary phase diagrams, crystallization sequences/paths that take place during cooling in Type III (ternary) liquidus-projection diagrams play a major role in establishing the the ultimate microstructures obtained. This is a prime example of the processing
microstructure chain link in the materials science and engineering paradigm in Fig
4.1. It must be stressed that we will be considering so-called “equilibrium” cooling sequences/liquidus paths. In reality, microstructural evolution also depends upon cooling rates, for example, the occurrence of dendrites (dendritic growth) treated in later materials science and engineering coursework. Let's begin by considering some crystallization sequences in the simple binary eutectic of Fig.
8.28. This will be a quick review of what you should have already learned in your “Intro to Materials Science and Engineering” coursework.
The sequence is particularly simple for the eutectic composition (
). Above the liquidus/eutectic we have 100% liquid solution of eutectic composition which, by binary lever rule is 46% B and 54% A. Upon cooling through the eutectic reaction, all the eutectic liquid is converted to the lamellar eutectic microstructural constituent indicated by the banded regions in the bottom diagram on the left of Fig.
8.28. This layered microstructural constituent results from the growth of layers being the most efficient way to separate A and B (by diffusion at the growth front) from a solution into separate phases, as shown schematically in Fig.
8.29.
In contrast, the crystallization sequence and liquidus “path” for the composition
is quite different. Above the liquidus, we have 100% liquid of the composition
. As we cool below the liquidus the “primary phase” to crystallize from solution is B. As B is removed from the liquid solution, the liquid becomes progressively richer in A, following the liquidus line as shown, until it reaches the eutectic point. Since the composition (
) is approximately half way between the end-member B and the eutectic composition, at just above the eutectic temperature we would have a microstructure with 50% primary B grains and 50% liquid of eutectic composition. Now, if we somehow sieved out the primary crystals, what would remain would be a liquid of eutectic composition, which would go through the same crystallization to lamellar eutectic microstructural constituent as happened for
The ultimate microstructure would consist of 50% primary B grains suspended in 50% lamellar eutectic microstructural constituent, as shown on the bottom-right of Fig.
8.28.
Before considering crystallization sequences/liquidus paths in ternary liquidus-projection diagrams, we need to learn a framework for their interpretation. I refer to these as the “Crystallization Path Dicta” or “CPD,” as spelled out in Fig.
8.31. Note the reversal of “CPD” to “DPC” in the diagram. The C stands for “compatibility” and gives us the “D” or “destination,” namely the ending point of the liquidus path: the ternary invariant point where the final liquid disappears in the crystallization sequence. Since there is a one-to-one correspondence of subsolidus compatibilities and ternary invariant points, the “destination” will always be the ternary eutectic or peritectic corresponding to the subsolidus compatibility in which the overall composition lies. In the simple ternary eutectic phase diagram of Fig.
8.30, there is only one subsolidus compatibility and therefore only one invariant point. “All paths lead to Rome,” they say. In this system, for all compositions within the A-B-C compatibility triangle, all paths end up the the ternary eutectic. The path taken to get there will differ according to the overall composition.
The second letter in CPD, “P” stands for “primary phase field” and tells us the initial “P” for “path.” If we return to the “mountain/valley/hole” analogy, our helicopter has just dropped a skier or snowboarder on the liquidus surface at the point marked “X.” Since essentially pure C is crystallizing from the liquid solution, our skier's/snowboarder's “path” (or rather the “path” of the liquid) is directly down the mountainside away from the peak, namely directly away from “mount C.” The composition “X” was chosen so that its crystallization path would intersect the ternary eutectic. If we pause just at/above the ternary eutectic, what would be the microstructure? We would employ the binary lever rule, since there are only two phases. On the line from C through the original composition “X” to the eutectic point, the length marked “” divided by the entire length of the line would give us the fraction of primary C grains in the microstructure (~50%), with the remainder being eutectic liquid. Once again, if we somehow sieved out the primary crystals, what would remain would be a liquid of eutectic composition, which would go through crystallization to ~50% lamellar eutectic microstructural constituent, this time consisting of three layers: A plus B plus C. If we wanted to know the fractions of phases in the lamellar eutectic, we could do the triangular lever rule at the eutectic composition, using the entire Gibbs triangle for the calculation.
Now let's consider the composition marked X' on the ternary liquidus-projection diagram of Fig.
8.30. Again, “C” for “compatibility” tells us that we have to end up somehow at the ternary eutectic (“D”=destination). “P” for “primary phase field” gives us the initial “P” or path, namely directly away from “mount C” as shown in the diagram. Again, our skier/snowboarder is headed full-tilt down the mountain directly away from its peak. This time, however, his/her path intersects the solid(C)-solid(A)-liquid phase boundary or “valley.” Just at this point, labeled “
” in the second microstructure on the right side of Fig.
8.30, we can use the binary lever rule to establish the microstructure. The point X' is roughly half way between end-member C and the solid(C)-solid(A)-liquid boundary. This means we have ~50% primary C grains and ~50% liquid of the composition at the boundary. Here we employ the final dictum of our “CPD” dicta. The letter “D” stands for “directions of falling temperature” and informs us of “changes in path” or the “C” in DPC. Quite naturally, the skier/snowboarder carves to the left to follow the valley down to the hole. What this actually means is that both C and A are crystallizing simultaneously from the liquid, the latter as a secondary crystallization product; its grains will end up smaller in size than primary phase C grains, owing to the fact that they have had less time to nucleate and grow. Now let's analyze the situation at a temperature just above the ternary eutectic. Since we now have three phases in equilibrium, we need to employ the ternary lever rule of Fig.
8.3. The analysis is shown in Fig.
8.32. A dashed triangle is drawn from end-member C to end-member A and to the eutectic composition, on which we carry out the ternary lever rule to establish phase fractions. Lines from each vertex of this triangle are drawn through the overall composition X'. The relative line lengths (divided by the total line lengths) give us the fractions of primary C (~65%), secondary A(~16.5%), and eutectic liquid (~18.5%). As before, if we somehow sieved out both primary and secondary crystals, what would remain would be a liquid of eutectic composition, which would go through crystallization to lamellar eutectic microstructural constituent. The resulting microstructure (~65% primary C, ~16.5% secondary A, ~18.5% lamellar eutectic) is shown at the bottom right of Fig.
8.30.
8.7 Isothermal Sections of “Real” A-B-C Systems
Of course, very few actual Type III/ternary systems satisfy the assumptions we have made thus far (for simplification), namely that the liquid solution is everywhere ideal and that there are essentially no solid solutions. It should be strongly emphasized that Hummel's rules strictly apply only to such narrowly-constrained systems. “All bets are off!” when dealing with “real” ternary systems, in which non-ideality of the liquid solution and significant, even substantial, solid solutions can be present. However, as we will see, all of the same characteristic features of Type III diagrams will be present, namely 1) the presence of tie-triangles, 2) the occurrence of tie-lines that are neither parallel nor perpendicular to any axis, and 3) open areas that can either be tie-triangles or single-phase solutions. There are, however, important differences. In “real” Type III isothermal sections, open areas that are not tie-triangles can also be solid solution regions in addition to liquid solution regions, as we will show. More importantly, “waffle cone” and “ice cream cone” regions, in which solid-liquid tie-lines radiate from a point (pure solid), will morph into quite a variety of quadrilateral constructions, with tie-lines connecting compositions on one side (solid solution) to compatible compositions on the other side (liquid solutions).
As you can imagine, experimental determination of even one isothermal section can be highly time-consuming. This has led to the development of and usage of powerful phase diagram calculation programs. Two of these are FactSage (C.R.C.T., Ecole Polytechnique de Montreal) and Thermo-Calc (Thermo-Calc Software, McMurray, PA; Thermo-Calc Software AB, Stockholm, Sweden), but there are many more. We will employ Thermo-Calc to calculate both the liquidus and one isotherm for the Sn-Pb-Bi phase diagram. But the user should be aware that there is a lot that does not “meet the eye” when using such high-powered “black box” programs. Behind the scenes, each such program employs a massive database of thermodynamic parameters, including solution thermodynamic parameters which, in certain cases (not all!) can be far more sophisticated than the dilute solution and regular solution models employed in this text. Truly inquisitive scientists and engineers are encouraged to check what is “under the hood” rather than just “kick the tires.”
The liquidus-projection phase diagram calculated by Thermo-Calc for the Sn-Pb-Bi system is shown in Fig.
8.33. On the “surface” (no pun intended!) this would look like just any other liquidus-projection diagram for an A-B-C Type III system involving ideal liquid solution and negligible solid solution. But there are
big problems, which may have already occurred to you. First of all, there are four primary phase fields, but only three end-members. Second, there are two ternary invariant points, but seemingly only one compatibility triangle (involving the three end-members) in the subsolidus!
Things get even more interesting if we do an isothermal section. In Fig.
8.34 we see the isothermal section predicted by Thermo-Calc at 423.15K (150
C). Note that the low temperature has to do with the relatively low melting points (for metals) of Sn (231.9
C), Pb (327.5
C), and Bi (271.4
C). Again, at first glance, things seem to be familiar. There is a “waffle cone” structure at the Bi-vertex, where liquid solutions of a wide range of compositions are compatible with/have tie-lines connecting with essentially “pure” Bi. (But the “ice cream” seems to have melted, i.e., the liquidus boundary is convex.) Also, there is one tie-triangle involving Sn-solid solution, Pb-solid solution, and liquid solution (ls). But elsewhere this isothermal section is quite different from what we have seen thus far. There are significant solubilities in both solid Sn (Bi is much more soluble than Pb) and in solid Pb (both Sn and Bi are quite soluble, with Bi being roughly twice as soluble as Sn). We also see a small solid solubility range for an intermediate compound in the Pb-Bi system. If we look at the Pb-Bi phase diagram (not shown) we find out that the intermediate compound is called “
-Pb.” It is apparent in the isothermal section of Fig.
8.34 that
-Pb dissolves a considerable amount of Sn, but to determine the amount of excess Bi or Pb it dissolves, we would have to consult the binary diagram to ascertain the 150
C values in comparison with its nominal Bi/Pb stoichiometry. Anyway, this explains the four primary phase fields and the two ternary invariant points in the liquidus diagram of Fig.
8.33. However, the biggest differences in the isothermal section of Fig.
8.34 are the regions of tie-lines connecting various phases in equilibrium. These turn out to be strangely-shaped quadrilateral constructions bearing no resemblance to the “waffle cone” and “ice cream cone” constructions with which we are familiar.
The most important distinction between “real” Type III systems (non-ideal liquid solution, non-negligible solid solutions) and the constrained Type III systems (ideal liquid solution, negligible solid solutions) we have studied thus far has to do with crystallization sequences/liquidus paths and microstructure evolution. For example, in a two-phase equilibrium region, the compositions of the solutions at the end of tie-lines through a fixed overall composition change with temperature. Think of the overall composition as “anchoring” all the tie-lines, but the end-points (solution compositions) change progressively and in opposite directions as temperature is lowered. A schematic representation of this phenomenon is given in Fig.
8.35. From above, the resulting two paths, e.g., of liquid solution and of solid solution, would trace out a “butterfly-shaped” or “hour glass-shaped' construction, as in the diagram on the right. The important “take away” point is that crystallization becomes much more complicated. For example, liquidus paths are seldom straight lines in “real” Type III/ternary systems, but are rather curved trajectories.
Micro structurally speaking, since the solid solution ranges change with temperature, the likelihood of a process called “coring” increases. A very simplified perspective on coring can be taken from the simple binary eutectic in Fig.
8.36. This A-B-system shows significant solid solution at both ends of the diagram. The diagram on the right shows a blow-up of the liquidus and
-solidus. When a liquid of composition “X” is cooled to the liquidus, the first solid
to precipitate from solution has a fairly high A-content, as shown. However, at a much lower temperature, the equilibrium solid
phase will have a significantly smaller A-content, if equilibrium were maintained. The problem is that alloys are seldom cooled at rates slow enough to maintain equilibrium. That is because, once precipitated out, a solid phase “locks up” its constituents, since diffusion in solids is so much slower than in liquids. So what happens is that the new
precipitating out will do so at a more B-rich composition. In the schematic microstructure beneath the two phase diagrams this is represented as a distinct layer of
around a core of
. In reality, there will be a gradual shift in composition from the center outward and, in fact, this will occur by dendritic growth. You will learn about dendrites and dendritic growth in later materials science and engineering coursework. For now, we need only point out that the “average” solid composition (averaging the composition of
,
,
, etc.) deviates from the solidus line. Since less A is being removed from the liquid, the liquidus trajectory must also therefore deviate from the equilibrium liquidus, as shown. All this is beyond the scope of the present text, but gives you a good idea of what you can look forward to in upcoming microstructure-evolution coursework. The conclusion of this discussion is that crystallization sequences/liquidus paths in “real” Type III/ternary systems can be quite complicated, along with microstructure evolution, which will also be cooling rate-dependent. This is a good place to close the present text, by pointing out once again the synergistic influences of both thermodynamics and kinetics in the processing
microstructure “chain link” of the materials science and engineering processing
microstructure
properties
performance paradigm. Students interested in pursuing further the topic of the interpretation of “real” Type III/ternary diagrams are directed to old treatises like Georg Masing's
Ternary Systems: Introduction to the Theory of Three Component Systems [
7].
8.8 Some Technologically Important Type III Phase Diagrams
We mentioned “freezing point lowering” when discussing binary (Type II) phase diagrams. There we mentioned the klinkering of cement as one example of major technological importance. A portion of the
liquidus projection diagram is reproduced in Fig.
8.37. On the
binary diagram to the left, the incongruent melting point of
is given as
and the congruent melting point of
is given as
, which are way too high for economical manufacturing. The dashed circle shows the composition ranges over which so-called “Portland cement” is made by klinkering. I will leave it to you to apply your ternary phase diagram prowess and decipher the lower lying ternary invariant points involving the
and
phases.
Another technologically important application is that of “solders.” A solder is a fusible alloy of two or more metals used to join metal parts together and having a melting point lower than those of the constituents or of the parts being joined. Solders are commonly used in plumbing, sheet metal joining, and electronics. The application in electronics is of particular importance, since solder is employed for making permanent mechanical and electrical connection of parts to the printed circuit boards on which they are mounted. Eutectic compositions are of special interest owing to the low melting points and absence of any primary phase that could disrupt electrical contact, for example if the joint solidifies in the so-called “pasty” (eutectic liquid plus primary phase) state. For decades, the alloy of choice for electrical soldering was 60/40 Sn/Pb. This is because the eutectic composition in the Sn-Pb system is 63% Sn and 37% Pb, which melts at the lowest possible (eutectic) temperature of . On the other hand, the Sn/Pb ratio is closer to 50/50 in plumbing solder, so chosen because this alloy solidifies more slowly and manageably.
In recent years, however, environmental safety concerns have motivated a steady move away from Pb-based solders owing to the recognized toxicity of Pb in both manufacturing and recycling. In the European Union, directives issued in 2006 prohibited the inclusion of significant Pb contents in consumer electronics. In the U.S., there are also tax incentives for the reduction of Pb content in consumer electronics. There are many binary and ternary (largely eutectic) systems that have been investigated and employed as Pb-free solders. One of the most commercially successful solders to date comes from the Sn-Ag-Cu ternary system shown in Fig.
8.38. Unfortunately, the eutectic in question is where the primary phase fields of
,
and
come together, which is very near the Sn-vertex and therefore extremely difficult to see on the full ternary. Fig.
8.39 is a blow-up of the Sn-corner showing the low-melting eutectic composition of approximately 4 mass% silver and 1 mass% copper (~95 mass% Sn) at
. It seems appropriate to conclude our discussion of ternary phase diagrams with a true Type III or
vs.
phase diagram, in this case the mass fraction of Ag/Sn plotted vs. the mass fraction of Cu/Sn plotted in proper Type III rectilinear fashion.
9 Fick's Laws of Diffusion
Just as there are fundamental laws governing the thermodynamics of materials, so there are basic laws governing diffusion, or how atoms/ions move around in materials. Consider the two adjacent planes in an isotropic solid as shown in Fig.
9.1a:
By isotropic, we mean that the diffusion rate of an impurity atom is independent of direction. The planes are separated by the distance,
which we will refer to as the jump distance. Each plane has a different areal density of impurity atoms (# per
),
on plane 1 and
on plane 2. Things are simplified by assuming an isotropic solid, since we can consider jumps from plane 1 to plane 2 (along the +
axis) to be only one of six possible jump directions (
). Therefore, the number of atoms jumping from plane 1 to plane 2 during a time period
will be equation
9.1:
where
is the jump frequency of an atom (#/s). Similarly, the counter jumps from plane 2 to plane 1 during the same time period is equation
9.2:
The net flow to the right through an imaginary plane midway between the two planes, as in Fig.
9.1b, is given by subtracting equation
9.2 from equation
9.1 for equation
9.3:
If we define the net flux
as the number of atoms passing through a unit
area per unit time (
), we arrive at equation
9.4:
such that (see Fig.
9.1b) the flux can be written as equation
9.5:
Two immediate observations can be made from Eq.
9.5. The units of flux are
. Furthermore, if the area concentration of the impurity is the same on the two planes, the net flux will be zero. However, this does not indicate a static situation; it only means that the flux to the right (
) is the same as the flux to the left (
). In fact, each of these fluxes can be enormous. Net zero flux only requires that their magnitudes be the same, namely
.
9.1 Fick's First Law
Until now we have only considered area concentrations of impurities (
); however, Fick's Laws are given in terms of volume concentrations (
). We can convert to volume concentrations in Fig.
9.1 by shifting the frame of reference by one-half a jump distance to the right, as shown in Fig.
9.2:
If we consider the jump distance in centimeters, it follows that the area inside the dashed box will be
. The volume concentration in this block (
) is the area concentration of impurities, (
), divided by the jump distance,
, or
. The net flux from plane 1 to plane 2 can therefore be written as equation
9.6:
Of course, concentration is seldom treated as a perfectly atomistic, plane-by-plane level. Rather it is treated as continuous, as displayed schematically by the dashed line in Fig.
9.3.
If we do a Taylor series expansion about
and ignore higher order terms, we obtain equation
9.7:
However, since the “gradient” between planes 1 and 2 is given by equation
9.8:
the concentration difference between the two planes can be expressed as equation
9.9:
Substituting for (
) in equation
9.6, we find that equation
9.10 holds:
This important equation tells us that the flux is proportional to the negative of the concentration gradient at time t, or
, and the proportionality coefficient is given by equation
9.11:
where D is the isotropic diffusion coefficient. Since the jump frequency (
) has units of
and the jump distance (
) has units of
, it follows that the diffusion coefficient will have units of
. Many times we will see diffusion coefficients in other units, such as
. Regardless, we can rewrite equation
9.10 as equation
9.12, which is the most common form of Fick's first law of diffusion:
It should be stressed that the diffusion coefficient of equation
9.11 holds strictly true only for isotropic solids. These include amorphous solids (glasses) and cubic crystal structures, such as face-centered cubic (fcc), body-centered cubic (bcc), sodium chloride (NaCl), fluorite (
), etc. More complex equations describe diffusion in non-cubic systems, e.g., hexagonal close-packed (hcp), which are beyond the scope of the present treatment.
9.2 Random Walk Diffusion
Above we mentioned that lots of jumps are taking place in both directions between planes 1 and 2 in Fig.
9.1, even under a condition of zero net-flux. Consider the diffusion coefficient of interstitial carbon in fcc
, which has been found experimentally to be
at
. Fig.
9.4 shows the nearest-neighbor jump distance of an interstitial on a (100) plane in the fcc structure.
The lattice parameter of
(
) is known to be 0.37 nm, such that the face-diagonal is
. The jump distance shown is half of that distance, or
, which would be 0.26 nm. Rearranging equation
9.11 to yield the jump frequency, we obtain equation
9.13:
Wow! An average interstitial carbon atom makes approximately 2.2 billion jumps in just one second at this temperature! Yet the lattice vibrational frequency (recall the Debye frequency from your thermodynamics background, ) is on the order of . We can look at this frequency as the “attempt” frequency, or how many times per second the interstitial is attempting to jump from the original position to the new one. So only approximately 2 out of 10,000 attempts is successful at this temperature.
It is also of interest to compare how far an average interstitial atom moves from its initial position in one second vs. the total distance of back-and-forth motions it makes in that same second. Consider the sketch in Fig.
9.5, where the sphere represents the initial carbon atom position, and arrows represent individual jumps in each of the
,
, and
directions. The circle with the dot represents a jump out of the plane of the diagram and then back.
It can be seen that many of the jumps are ineffective for long-range diffusion, since they are simply reversed. Nevertheless, the interstitial atom makes steady progress away from its initial position, and the dashed line connects the initial position with the final position after all the jumps are considered. This is referred to as the “random walk distance” (
). Computer simulations can keep track of both the random walk distance and the “total” distance traveled by the impurity, taking into account the sum of all back-and-forth motions. The “total” distance traveled is given by equation
9.14:
On the other hand, the random walk distance is given by equation
9.15:
This reinforces the facts 1) that lots of jumps are taking place each second, and 2) that lots of the jumps are ineffective insofar as long-distance diffusion is concerned. An average interstitial finds itself 12 micrometers away from its starting point, but having traveled a staggering half a meter plus to get there!
You may see another form of the random walk equation
9.15. Plugging
for
(from equation
9.11) into equation
9.15, we obtain equation
9.16:
in agreement with what we obtained previously.
9.3 Steady State Diffusion
A “steady state” situation is one in which the local concentration of impurities does not change with time, such that
at each value of
. A good example involves the gradual diffusion of hydrogen through the steel wall of a pressurized gas tank, as represented schematically in Fig.
9.6.
It has been found that hydrogen dissolves to some extent in steel, maintaining a constant surface composition on the inner surface of the tank that depends upon the tank pressure. Since air surrounds the tank and the hydrogen content in air at ground level is less than 1 part per million, we can assume the hydrogen content on the outside of the tank to be zero. Let the equilibrium hydrogen content on the inner surface be
and the wall thickness be
. A steady state situation means that the hydrogen content decreases linearly with distance from
at the inner wall to zero at the outer wall (
). This can be expressed mathematically as equation
9.17:
Plugging this into Fick's First Law of equation
9.12, we obtain equation
9.18:
The product
is often called the “gas permeability,” since to be permeable through the solid wall the gas has to be both soluble (
) and mobile (
). Gas permeability is given in units of
or
, which reflects the product of the diffusion coefficient (
or
) and the appropriate mass concentration (
or
). Fortunately, the gas permeability of hydrogen through steel is relatively small at room temperature. Nevertheless, given sufficient time and sufficient diffusion the internal gas pressure (and
) will gradually decline to yet another steady state situation. A compelling demonstration of this effect is the loss of helium from mylar balloons. Helium rapidly diffuses through typical rubber balloons. However, mylar balloons have a thin aluminum metal coating that helps to slow down helium diffusion. Nevertheless, helium eventually escapes causing the balloon to slowly lose buoyancy. The situation at any point can be well described by equation
9.18.
9.4 Fick's Second Law
The steady state example just described is an exception rather than the rule. In virtually all other instances of diffusion, the impurity concentration at a given point is changing with time. For such situations we will need another diffusion law, referred to as Fick's Second Law of diffusion. Consider the two concentration profiles in Fig.
9.7 and what is happening at imaginary planes 1 and 2, in each case separated by the distance,
.
Fick's First Law in equation
9.12 tells us that the flux is proportional to the negative of the concentration gradient at each point. Based upon the gradient (slope) at each plane, it can be seen that the flux across plane 1 is greater than the flux across plane 2 in the concave-up
vs.
profile on the left, and the opposite is true in the concave-down
vs.
profile on the right. We might therefore expect the local concentration between the planes to increase with time in the first situation, but decrease with time in the second. To simplify our discussion, let's assume that the flux is a linear function of distance, as shown in Fig.
9.8.
This might correspond to the first situation in Fig.
9.7. As can be seen, the flux into the volume between the planes is greater than the flux out, so we would expect the impurity concentration in that volume to increase with time. If we specify an identical area,
, on each plane, we can calculate the number of impurity atoms that are added to the volume between the two planes during an increment of time,
, with the following equation
9.19:
Since the units of flux are
, when we multiply
by the product of area (
in
) and time increment (
in
), we arrive at the number of impurity atoms that are added to the volume between the planes. Since the volume in question is just the product of
and
, this amounts to an increment in the impurity concentration (
in
). We can use equation
9.19 to help us derive Fick's Second Law. Let's begin by doing a Taylor series expansion of flux around
in equation
9.20:
again ignoring higher order terms. Rearranging equation
9.20 we obtain equation
9.21:
Inserting the right side of this equation in place of
in equation
9.19 and canceling the
and
terms on both sides of the resulting equation yields equation :
In the limit that the increments (
,
) go to zero, it follows that equation
9.22 can be expressed as equation
9.23:
However, we know from Fick's First Law that
. Substituting
for
in equation
9.23, we obtain equation
9.24:
This is the most general form of Fick's Second Law, which holds for all situations, including those in which the diffusion coefficient is a function of composition (and therefore position). Fortunately, in many situations the diffusion coefficient does not vary significantly over the concentration range involved and therefore does not change significantly with position. This simplifies things considerably. Fick's Second Law of diffusion becomes equation
9.25:
This equation tells us that the rate of change of concentration at a given point is proportional (by the diffusion coefficient) to the second derivative of concentration with respect to distance at that point. We can use this equation to 1) ascertain whether the concentration of an impurity is increasing or decreasing with time at a chosen point, given a specific concentration profile, and 2) to test whether specific diffusion equations are valid, namely that all such equations must obey Fick's Second Law as expressed in equation
9.25 (see the following section). As an illustration of the first application, consider the three concentration profiles in Fig.
9.9:
The concave-up concentration profile on the left has a second derivative of concentration with respect to distance that is everywhere positive. This means that must be positive; concentration is increasing with time as shown by the vertical double-arrow. The linear concentration profile in the middle plot has a second derivative with respect to distance that is zero. This means that is zero; local concentration is not changing with time. This is the “steady-state” situation discussed in the previous section. The concave-down concentration profile on the right has a second derivative of concentration with respect to distance that is everywhere negative. This means the is everywhere negative; concentration is decreasing with time as shown by the vertical double-arrow.
10 Applications of Fick's Laws
10.1 Homogenization and Point Defect Relaxation
Imagine a sinusoidal concentration profile as shown in Fig.
10.1. Using Fick's Second Law, it follows that in the concave-down portions of the profile where the local concentration is greater than the average composition,
, the concentration will be decreasing with time. At the same time, in the concave-up portions of the profile where the local concentration is less than the average composition, the concentration will be increasing with time.
At time zero we can express the concentration profile as equation
10.1:
where
is the amplitude of the sine wave at time zero. If we allow diffusion to proceed, the concentration profile will relax as shown in Fig.
10.1. It turns out that the solution to Fick's Second Law for these boundary conditions is given by equation :
You can prove to yourself that this equation is a solution to Fick's Second Law by taking the first derivative with respect to time
and comparing the result with the second derivative with respect to distance
. The two derivatives should be identical. Let's test this equation by setting
. This simply reverts to the time zero function in equation
10.1. Now let's consider the variation of composition at the point,
. Since the sine of
or
is unity, equation
10.2 becomes equation
10.3:
The parameter, , is referred to as the “relaxation time,” and is given by equation :
When time is equal to the relaxation time
the amplitude above the average composition at the point,
, according to equation
10.3 will be
or 0.368
This will, in fact, be true of every point along the profile; each composition will be 36.8% of its value at time equal to zero, as shown in Fig.
10.2.
One very important application of the sine function concentration profile of equation
10.2 has to do with point defect relaxation. In metals and in some oxides, we can quench in a high vacancy population by quenching from high temperature. If we then take the specimen to an intermediate temperature, excess vacancies can be annihilated, but only by migrating to a surface. In polycrystalline materials, grain boundaries can act as internal “surfaces.” In either single crystal or polycrystalline materials, dislocation cores can also act as internal “surfaces.” Fig.
10.3 shows schematic diagrams of how grain boundaries and dislocations can act as “sinks” for excess vacancies.
In the case of grain boundaries we can equate the grain size to the value of
in the relaxation time equation
10.4. If instead dislocations dominate, we can equate the average dislocation spacing to the value of
in equation
10.4. In both cases, the diffusivity of interest will be the vacancy diffusion coefficient at the temperature of interest. Polishing and etching can be employed to determine the dislocation density (etch pits) or
. Inverting the value obtained gives an area per dislocation or
per dislocation, as shown in Fig.
10.4. If we take the square root of this value, we obtain the average separation distance of dislocations to use as
in the relaxation time equation
10.4.
10.2 Non-Infinite Systems
“Non-infinite systems” are those where concentration profiles span the entire specimen, from one end to the other. If diffusion is taking place from both sides of a plate or slab, the two concentration profiles overlap in the middle of the specimen. A classic example is diffusion out of a slab. For example, in Fig.
10.5 a slab of thickness,
, with initial impurity concentration,
, is held in an environment that takes the surface concentration,
, to zero.
At short times the diffusion profiles do not overlap. They are described by “semi-infinite” solutions to Fick's Second Law, as will be described in the following section. At longer times, however, the diffusion profiles do overlap. The solution to Fick's Second Law for this situation is complicated, as shown in equation
10.5.
Fortunately, the first term dominates, giving us equation
10.6:
This equation would be used if one wanted to estimate a composition at a specific point and time. More often, however, we are interested in the average composition in the overall slab, as shown in the diagram on the right side of Fig.
10.5. This is found by integrating equation
10.5 to obtain equation
10.7:
Again, fortunately, the first term dominates, and for average compositions less than 80% of the initial composition (
) the first term is an excellent approximation to the solution. The results in equation
10.8:
where is called the relaxation time.
Eq.
10.8 is very useful for describing the degassing of metals, including decarburization of steels. In this case the diffusion coefficient in the relaxation time would be that of the particular gas species or of carbon in the particular metal. Another application involves the relaxation of vacancies in a supersaturated metal, for example a metal quenched from high temperature has a large vacancy population. If the metal is taken to an intermediate temperature where the equilibrium vacancy concentration is small (effectively zero compared to the quenched-in concentration,
) and vacancies are sufficiently mobile that they can annihilate at sinks such as dislocation cores or grain boundaries, relaxation will occur. The situation involving dislocation cores is represented schematically in Fig.
10.6, where the concentration of vacancies is shown during relaxation from the initial, quenched-in concentration,
, to a point where the average vacancy concentration is
. In this case,
would be the average dislocation spacing and the diffusion coefficient would be that of vacancies in the metal of interest.
10.3 Semi-Infinite Systems
By “semi-infinite” systems we are referring to situations where the specimen can be treated as essentially “infinite” in size compared to the extent of the impurity concentration profile at the surface. Another way of describing this is that the concentration profile resulting from diffusion never reaches the other end of the specimen. The specimen, although not infinite in extent, is effectively “infinite” insofar as diffusion is concerned. In terms of diffusion it is “semi-infinite.”
10.3.1 Thin Film Tracer Diffusion
Thin film “tracer” diffusion is of special importance to materials science and engineering. It is how diffusion coefficients are often measured. Imagine a thin film containing an area concentration (
) of a “tracer” that is deposited on a highly polished, flat surface of a single crystal (crystal #1 in Fig.
10.7). To prevent any loss of “tracer” (for example by evaporation) and also to provide a second crystal in which to study diffusion, the highly polished, flat surface of crystal #2 in Fig.
10.7 is butted up against crystal #1, sandwiching the tracer thin film between them. For self-diffusion studies, the tracer is the same chemical species as constitutes both crystals, however with a different atomic mass (namely, another isotope than that of the host atoms making up the two crystals). In many instances, a radioactive tracer is employed at low concentrations (and low radioactive emission levels to protect lab workers). In this case, the relative concentration of tracer at a specific diffusion depth is determined by the number of radioactive “counts” registered at that depth, usually by “serial sectioning” (see below). In other cases, the amount of a non-radioactive tracer diffused to a given depth can be established by the use of a mass spectrometer that can differentiate and quantify the relative amounts of tracer species vs. naturally occurring (host crystal) species.
For impurity diffusion studies, the tracer is a different chemical species from the host. Again, either radioactive or non-radioactive tracers can be employed, with mass spectrometry being used in the latter case to quantify the amount of a diffused species found at a given depth from the surface by serial sectioning, as described below.
The unique aspect of thin film tracer diffusion is that the overall amount of tracer remains constant, once applied to the surface and sandwiched between the two crystals. On the right side of Fig.
10.7 are the concentration profiles at early, intermediate, and long times of diffusion at a specified temperature. Assuming no loss of tracer, the area under each curve (the total amount of tracer) must remain the same at all times.
The actual diffusion process is carried out by heating the pair of crystals to a predetermined temperature as rapidly as possible, holding for a set time, and “quenching” to room temperature as quickly as possible. For ceramic samples, heating and cooling rates are limited by what the crystals can sustain without fracture caused by thermal shock. Once a diffusion heat treatment is completed, the two crystals are cleaved at the thin film interface and each crystal is subjected to the process called “serial sectioning,” as represented in Fig.
10.8. Roughly equivalent “sections” are carefully removed, beginning with the surface to which tracer was applied, and being careful to maintain a flat/planar surface throughout the process.
Sectioning is typically accomplished using the same grinding media (abrasive cloths, powders) used for metallographic sample preparation. It is very important, however, to quantify both the “depth” removed (each
in Fig.
10.8) and the tracer concentration (
in Fig.
10.8) for each section. Alternatively, the count rate (counts/time) can be measured by a radiation detector. The count rate will be directly proportional to the concentration in each section. The increment of depth can be measured directly by a high precision micro-caliper. Alternatively, it can be indirectly calculated from the mass removed, which can be measured quite accurately. In the case of non-radioactive tracers, mass spectrometry is employed to calculate the tracer content in a given section. With a radioactive tracer, the abrasive cloth holding the powder of the “section” removed can be placed in a radiation detector and counted for a predetermined time period. The solution to Fick's Second Law that reflects the boundary conditions for thin film tracer diffusion is given in equation
10.9:
where
is either the tracer concentration or the tracer's radioactive count rate, and
is the area concentration of tracer deposited on the surface of crystal #1 in Fig.
10.7. Taking the natural logarithm of both sides of equation
10.9 gives equation
10.10:
The slope of a plot of the natural logarithm of
vs.
yields
, as depicted on the right side of Fig.
10.8. Since the diffusion time is known, the diffusion coefficient can be calculated. This process is repeated at other temperatures in order to establish the pre-exponential factor (
) and activation energy (
) of the tracer diffusion coefficient (
) as in equation
10.11:
where is called the “pre-exponential factor” and is the activation energy of diffusion. We discuss the origin(s) of this characteristic of diffusion vs. temperature behavior (so-called Arrhenius behavior) in a later section.
10.3.2 Constant Surface Composition Situations
As opposed to thin film tracer diffusion, where the “surface” composition diminishes with time, there are a number of situations in materials science and engineering where the “surface” composition is maintained constant with time. These include “doping” situations, where a solid is held in an atmosphere that keeps the composition of an impurity at a constant level on the exposed surface. Similarly, the carburization of iron or steel can be controlled by holding the surface in an atmosphere with a fixed ratio of carbon monoxide and carbon dioxide. The amount of carbon in solution at the surface is thereby fixed according to equation
10.12:
As carbon diffuses into the interior of the solid, the above reaction guarantees that additional carbon is added to the surface to maintain the surface carbon composition. The overall impurity (or carbon) content of the solid is given by equation
10.13:
where A is the area of the surface into which solute is diffusing. This means, of course, that as opposed to thin film tracer diffusion, the overall solute content steadily increases with time. This is shown schematically on the left side of Fig.
10.9, where
is the initial carbon content and
is the surface composition. The concentration profile moves progressively to the right with time, as the interior of the solid is progressively enriched with solute. We later consider how thick the sample must be to be “semi-infinite” compared to the diffusion profile, but from Fig.
10.9 it follows that the sample dimension should be large relative to the diffusion profile at the longest time applied.
Before we introduce the solution to Fick's Second Law that meets the boundary conditions of Fig.
10.9, we will make the simplifying assumption that the diffusion coefficient does not vary with impurity content, and therefore distance from the surface (
). This is valid for the doping of semiconductors from gas phase precursors, where relatively small dopant levels are involved. However, in the case of carburization, relatively large changes in solute (carbon) content occur and the diffusion coefficient is known to vary somewhat with carbon composition (and therefore position) along the diffusion profile. Fortunately, relatively good predictions of carbon diffusion profiles can be obtained by employing an “average” carbon diffusion coefficient (discussed later) that can be assumed invariant with carbon content (and position).
The solution to Fick's Second Law corresponding to the boundary conditions in Fig.
10.9 is given by equation
10.14:
which is usually written as equation
10.15:
where
is the distance from the surface,
is the diffusion coefficient (a constant diffusion temperature is assumed), and
is the time period over which diffusion takes place. You should have encountered the “error function” (erf) in prior math courses. It is an indefinite integral of the form in equation
10.16:
where
is known as a “dummy variable.” In our case,
. In days past, with no closed-form solution to equation
10.16, one resorted to tables of the error function. Fortunately, many modern calculators now include the error function. Alternatively, there have been many mathematical approximations. The most straightforward amongst the collection in the Handbook of Mathematical Functions [
1], having a reported accuracy of
, is equation
10.17:
where
,
,
, and
. This approximation can be used in a either a computer program or in a mathematical spreadsheet to estimate
. In equation
10.17 we have also introduced the “complementary error function,” denoted as
. The simple relationship between the two functions in equation
10.18:
is illustrated in Fig.
10.10. On the right side of Fig.
10.9 we see these two functions as applied to the above mentioned instance of doping/carburization of a sample with an initial dopant concentration. An abbreviated table of error function values is given in Table 1.
Table 2: Examples of Error Function Values
|
z
|
erf(z)
|
z
|
erf(z)
|
z
|
erf(z)
|
|
0
|
0
|
0.8
|
0.742
|
1.6
|
0.976
|
|
0.2
|
0.223
|
1.0
|
0.842
|
1.8
|
0.989
|
|
0.4
|
0.428
|
1.2
|
0.910
|
2.0
|
0.995
|
|
0.6
|
0.604
|
1.4
|
0.952
|
2.2
|
0.998
|
We can generate a useful “metric” to describe diffusion in cases of constant surface composition (error function solutions to Fick's Second Law). In the case just described, consider the diffusion profile in Fig.
10.11.
You will see one special composition highlighted, labeled
. This corresponds to the point where the composition is half way between the surface composition (
) and the original sample composition (
), which modifies equation
10.15 to equation
10.19:
It turns out that erf
=0.5 for a value of
that is very close to 0.5 (see the error function Table or Fig.
10.10), or more precisely
. If we let
, it follows that
. This distance of “root Dt” is commonly referred to as the “diffusion depth.” It is a useful “metric” for diffusion in situations involving constant surface composition. For example, one might ask, “How much longer must I diffuse at the same temperature to double the diffusion depth?” The answer follows from the definition of
in equation
10.20:
or four times the length of time. We can also establish the thickness of sample required to be “semi-infinite” with respect to a given combination of diffusion coefficient and time. From the previous Table of error function values, we can observe that at the diffusion profile has diminished by 99.5% toward the original composition. In other words, very little (0.5%) impurity has been delivered at this point in the diffusion profile. For diffusion from one side, a specimen must therefore be greater than or twice the “diffusion depth.” For diffusion from both sides of a plate we might define “semi-infinite” as being or roughly four times the “diffusion depth.” Of course, this is arbitrary and more stringent definitions of “semi-infinite” can be made (e.g., , for which ). For diffusion from both sides of a plate, this would amount to 0.08% added impurity at the middle of the specimen.
Of course, we should not forget our non-infinite solutions to Fick's Second Law, which are required in place of error function (semi-infinite) solutions when there is significant overlap of diffusion profiles from the two sides of a plate. Eq.s
10.5 and
10.6 would be used to determine the concentration at a given position, whereas equations
10.7 and
10.8 would be employed to determine the average composition (above the initial composition) for the plate. We revisit such overlap when we consider decarburization (below).
All the solutions that follow are simply permutations of equation
10.15. For instance, let's consider carburization or doping of an initially “pure” host. Of course, from thermodynamics we know that there is no such thing as complete purity. Impurities, including the one we are interested in, are always present to some degree. However, their level can be considered so inconsequential as to be effectively zero, namely
can be taken to be zero in equation
10.15. By making this assumption and rearranging, we obtain equation
10.21:
A representative diffusion profile is displayed in Fig.
10.12, showing how the complementary error function comes into the picture.
Now let's consider decarburizing, which is the opposite of carburizing (adding carbon to iron or steel). On the left side of Fig. C, we are holding the surface carbon content at a lower value than the initial carbon content of the specimen. This can be accomplished by employing appropriate carbon monoxide/carbon dioxide gas ratios, as per equation
10.12. As time proceeds, carbon is removed by diffusion from progressively larger depths. Keep in mind, however, that the specimen is “semi-infinite,” namely that its width is at least 2 diffusion depths (or 4 diffusion depths if decarburized from both sides). The solution to Fick's Second Law satisfying the boundary conditions in Fig. C is given in equation
10.22:
In the event that complete decarburization is desired, the surface carbon content is taken to zero, simplifying equation
10.22 to equation
10.23:
A schematic illustrating this situation is given on the right side of Fig.
10.13, where it can be seen that the straightforward error function is the simple solution for the boundary conditions applied. It should once again be stressed that the sample must be “semi-infinite,” namely if being decarburized from both sides it should be several (>4) “diffusion lengths” in width, such that there is no overlap of error function solutions at the middle of the sample. If there is considerable overlap, we once again turn to our non-infinite solutions. These take into account both the carbon contents vs. position (equation
10.6) and the average carbon content of the slab (for values below 80% of the original, equation
10.8). It might be a good time to refer back to Fig.
10.5 for a schematic of decarburization in the “non-infinite” case.
Before considering the special case of interdiffusion, let's introduce some practical uses for all the error function solutions considered thus far. For many years, the n-type and p-type regions of microelectronic circuits were made by exposing “semiconductor-grade” (ultra-high purity) silicon wafers to gases containing n-type dopants or p-type dopants through removable masks in a process called “photolithography.” Although diffusion is sometimes still used, for instance to set the background impurity level of a silicon layer, nowadays doping is usually accomplished by ion-implantation of dopants owing to improved controllability and speed.
Carburization and decarburization are fundamental to the processing of steels and for the preparation of their surfaces. For example, carburization is well known to increase the hardness of steels. In the case of a machine gear, for instance, the materials engineer may be interested in maintaining different properties of the gear core (high strength with toughness) and the gear surface (high strength with hardness). This calls for a different carbon content in the core vs. on its surface. In particular, carburization is employed to boost the carbon content at the surface, making it hard and wear-resistant. This can be done by a process of “pack carburization,” namely packing the gear in a high temperature bed of charcoal, often referred to as “case hardening.” However, carburization is more often accomplished by exposing steel surfaces to carbon-containing gases (see equation
10.12) or to carbon-containing plasmas.
The final instance of constant surface composition that we consider involves the interdiffusion of solute across an interface, as depicted in Fig.
10.14.
Here a solid with impurity concentration,
, is butted up against a solid having a lower impurity concentration,
. It should be stressed that for the error function solution to be employed, the differences in solute content should be small and/or the diffusion coefficient must not vary much with solute content (and therefore distance in the diffusion “couple”). With these qualifications, the mid-point of the diffusion profile, both in terms of composition and in terms of distance, remains stationary with time as shown in Fig.
10.14. It can be seen that the composition at this point remains the average of the two initial solute contents, or
. Looking to the right from the interface (
), the situation looks identical to the carburization situation in Fig.
10.9, and we can insert
in place of
in equation
10.15 as is done in equation
10.24:
The denominator of the left side of equation can be simplified to
, and the resulting solution to Fick's Second Law for interdiffusion with a constant diffusion coefficient is equation
10.25:
This equation also holds for the left side of the interdiffusion couple in Fig. , since
as shown in Fig.
10.15.
Some textbooks have equation
10.25 as equation
10.26:
This arises from reversing the sense of “
” (and therefore “
”), namely that the solid with the higher solute concentration is now on the right, so be careful to use the solution that matches your boundary conditions. Note how the overall error function in Fig.
10.15 actually looks like an interdiffusion profile with the more highly doped specimen on the right.
Before moving on, it should be stressed that interdiffusion with an essentially composition-independent and therefore position-independent diffusion coefficient is rather the exception than the rule. Most interdiffusion problems involve “interdiffusion” coefficients that are clearly functions of concentration and therefore of position. In an A:B couple, where A and B are different metals, the usual case is for A to diffuse faster into B or vice versa. In fact, the point of average composition, , moves with diffusion time. Fortunately, procedures exist to solve interdiffusion profiles for composition-dependent diffusion coefficients at each point. You will learn about these methods in lab projects and in upper level materials science and engineering coursework.
11 Atomistics of Diffusion
We now turn to the “basics” of diffusion, namely the “nuts and bolts” of how diffusion takes place in solids. We want to “unpack” all the contributions, the so-called “atomistics” that contribute to the pre-exponential factor (
) and the activation energy (
) of the general equation for diffusion in solids, as per equation
11.1:
It turns out that we can do a pretty good job estimating ranges of values for the pre-exponential factor for each of the primary diffusion mechanisms. In what follows, we take a modular “plug-in” approach to the problem, as outlined in Fig.
11.1.
We begin with our basic diffusion equation
9.11 repeated and reorganized here as equation
11.2:
To review,
is the atomic jump distance (determined by the crystal structure) and
is the atomic jump frequency. This equation (
11.2) is found in Box A of Fig.
11.1 and will be the “jumping off point” for each of the diffusion mechanisms we consider. The first “plug-in” is equation
11.3:
Here the atomistic jump frequency is related to the product of a “defect” jump frequency (
) and a defect availability factor (
). The availability factor will be further described as we consider each of the individual diffusion mechanisms. The rest of Fig.
11.1 may seem quite daunting, however not every diffusion mechanism involves all of the “plug-ins” or boxes in the figure. We will proceed from simplest (interstitial diffusion) to most complex (vacancy and interstitialcy diffusion). Along the way, the “plug-ins”/boxes should come into focus, so be patient. The object is to develop for each mechanism an atomistic-based description of the diffusion coefficient. Right now Box E in Fig.
11.1 seems quite complicated; however, this massive equation can be reduced to the standard equation
11.1 in Box F or to the even simpler equation
11.4:
in Box G, which tells us that three groupings of factors govern each individual diffusion mechanism: a geometric factor (), and entropic factor (), and a thermally-activated term (). Let's get started by considering the most straightforward of diffusion mechanisms, interstitial diffusion.
11.1 Interstitial Diffusion
Although self-diffusion by interstitials is possible in certain ceramic materials, we will restrict our consideration to impurity diffusion where the impurity spends all of its time in the interstices of the crystal lattice. A good example is carbon diffusion in iron. This type of impurity diffusion has special requirements, namely that 1) the atomic radius of the impurity is significantly less than that of the host (e.g., ), and 2) the atomic radius of the impurity is comparable to that of the interstices. It should be stressed that self-diffusion in close-packed metals never takes place by interstitial diffusion. The radius of a host atom is far too great for it to squeeze into the much smaller interstices in between host atoms. To place a host atom into such an interstice would be highly unfavorable energetically; self-interstitials are therefore highly unlikely.
Let's begin to analyze interstitial diffusion using the modular plug-in chart in Fig.
11.1. Since the interstitial is always an interstitial, there is no thermal activation process associated with its formation as in Box D. Furthermore, the availability factor for interstitial jumps can be assumed to be essentially unity (
), namely adjacent interstitial sites into which the interstitial can jump can be assumed to be empty. Of course, at the highest carbon contents there is a finite possibility that an adjacent interstitial is occupied. We could express the availability factor as (
), where
is the site fraction of carbon interstitials. But for simplicity we will assume that
and assume an availability factor (
) of unity.
It is time to add important functions to our diffusion “toolkit.” These have to do with the defect jump frequency in Box C of Fig.
11.1. In moving from one interstitial site to another, a certain amount of lattice dilation must occur, as illustrated in Fig.
11.2.
In other words, adjacent atoms must move apart to enable the interstitial to pass. Energetically, this amounts to surpassing an energy barrier that separates the two sites. Fig.
11.2 illustrates the special configuration with the interstitial at the so-called “
saddle-point
”. The energy landscape is shaped like a saddle. Alternately, you can think about a mountain pass. You go up and over the pass, but when you are at the top of the pass you find the land rising to either side. From statistical mechanics, the probability that an interstitial has sufficient energy to reach the saddle point is small. It is governed by the height of the pass (
) and the temperature. Higher temperature means more energy being available to the interstitials, and an increasing fraction of them having the probability to make it to/past the saddle point. The relationship is given by equation
11.5:
We refer to
as the free energy of motion which, in turn, can be separated into enthalpy of motion (
) and entropy of motion (
) components as in equation
11.6:
It should be apparent that an interstitial at the saddle point has a different entropy. Certainly, its vibrational frequency, and thus its vibrational entropy, should be different at the dilated/congested saddle than in either interstice, i.e., the energy wells on either side of the energy barrier in Fig.
11.2. We can use the information in equation
11.6 to arrive at the equation in Box C of Fig.
11.1, or equation
11.7:
Here we have replaced with ( for interstitial), and and for and , respectively. The other constants are , the attempt frequency, and , the coordination number of how many empty interstitial sites surround an occupied interstitial site. The attempt frequency can be assumed to be the lattice vibrational frequency, on the order of per second. You probably encountered the “Debye frequency” in your prior materials thermodynamics work.
Plugging
from equation for
in Boxes C and B and
for
in Boxes D and B of Fig.
11.1, we obtain the following equation :
If we consider A to be the host lattice and B to be the species moving via interstices, we can simplify equation
11.8 to equation
11.9:
where
is the pre-exponential factor for impurity diffusion of species B by interstitial mechanism, which includes all the entities within the brackets of equation
11.8, and
is the activation energy for interstitial motion. Since there is no defect formation energy,
is the same as the enthalpy of motion or
. Before we take a try at predicting pre-exponential factors for interstitial diffusion, let's rearrange equation
11.9 to separate out geometric (
) and entropic (
) factors, as in equation
11.10:
Let's first unpack the underlying parameters in the geometric factor (
). We already know that the attempt frequency (
) is on the order of
. But the jump distance (
) and coordination number (
) depend upon not only the crystal structure, but upon the actual element/metal under consideration. Let's focus our concentration on iron in both fcc (austenite) and bcc (ferrite) forms, and consider the case of the interstitial diffusion of carbon. The two crystal structures are displayed in Fig.
11.3. More importantly, the interstitial positions are marked with “X's.” In addition, a typical jump distance is shown by an arrow for each structure.
Let's first consider carbon diffusion in fcc-Fe (austenite), whose structure is shown on the left side of Fig.
11.3. It is obvious that the two sets of lattice positions (host atoms, interstices) form interpenetrating fcc lattices. In fact, we will encounter interpenetrating lattices when we consider the “rocksalt” structure of sodium chloride or table salt (NaCl), where the electropositive
“cations” sit on one set of sites and the electronegative
“anions” sit on the other. In austenite, most of the second interpenetrating (interstitial) lattice is empty. However, the fact that it (the interstitial lattice) is also fcc is quite important. It means that the coordination number of empty interstitials sites around any given occupied interstitial site will be the same as the coordination number of neighboring iron atoms around any given iron host atom. This gives us the value we need for the coordination number in
of equation
11.10, namely 12.
On the other hand, the jump distance (or the arrow length in Fig.
11.3) is the same as the distance between close-packed atoms (see the lower diagram in Fig.
11.3), or one-half of the face-diagonal
. Since the lattice parameter (
) of fcc iron is
0.37 nm, the jump distance would be
nm. Diffusion coefficients are rarely given in terms of
, however. So let's convert 0.26 nm to centimeters, or
. This yields the following for the geometric factor for diffusion:
There have been several estimates of the entropic term (
) in equation
11.10. One of the most straightforward calculations took into account the elastic strain associated with the saddle point (C. Zener in Imperfections in Nearly Perfect Crystals, 1952, p.289) and also the change in vibrational entropy associated with the saddle point [
4], arriving at the result that the entropy of interstitial motion was
, such that the entropic term (
) was approximately 2.7. The product of the geometric factor (
) and the entropic factor (S) in equation
11.10 is the pre-exponential coefficient of equation
11.9. Based upon our “back of the envelope” calculations, we predict a value for
of
.
Before we make a comparison with experimental values, it must be stressed that owing to the larger interstice size in fcc iron vs. bcc iron, the former (austenite) can incorporate a much larger carbon content than the latter (ferrite). We mentioned previously that the diffusion of carbon in fcc iron was not a constant, but rather varied measurably with carbon content. Fortunately, the variation is not extreme and a practicable composition-independent approximation appears in most diffusion textbooks. This approximation is given by the following equation
11.12:
Given our rather simplistic assumptions and the fact that the experimental equation is itself an approximation, the agreement of pre-exponential values (estimated: vs. experimental: ) is remarkable.
Let's see how we do estimating the geometric factor and pre-exponent for carbon diffusion in the bcc (ferrite) form of iron. Interestingly, the interstices in bcc iron exist only on the faces of the unit cell as shown on the right side of Fig.
11.3. These interstices are found along the edges and at the face centers of the unit cell. As a result, the jump distance is half of the cube edge or lattice parameter, such that
. Since there are no bcc interstices within the unit cell, the coordination number can be determined by looking at the face-centered interstice on any face in Fig.
11.3. If occupied, it is surrounded by 4 empty interstices at the 4 cube edge positions, so
. Assuming once again an attempt frequency of
, we arrive at a geometric factor of
.
Once again, there have been several estimates of the entropic term (
) in equation
11.10. If we assume, as with the fcc structure, that the entropy of interstitial motion is
such that the entropic term of
is approximately 2.7, we arrive at a “back of the envelope” estimate for
of
. The experimental equation for carbon diffusion in bcc iron is [
11]:
This time there is only agreement of pre-exponent within an order of magnitude, however this can be considered quite good considering all the approximations we have made. As additional support for our atomistic approach, the corresponding
values are
for nitrogen [
12] and
for hydrogen [
6], in quite satisfactory agreement with our prediction. The corresponding enthalpies of motion (
) are
and
for N [
12] and H [
6], respectively.
11.2 Vacancy Diffusion
Self-diffusion or impurity-diffusion by vacancy mechanism can be likened to the “tile” puzzles we have handled physically or solved as a computer game. Consider the tile puzzle in Fig.
11.4. The configuration on the top left is insoluble owing to the absence of a vacancy, whereas the configuration on the top right is soluble by virtue of the vacancy's presence. The analogy to solids is that without such defects, there can be no diffusion and thus no reactivity. This is further illustrated in the bottom diagrams of Fig.
11.4, each illustrating a close-packed plane in either hcp or fcc solids. With the addition of the vacancy in the bottom-right configuration, it is obvious that self diffusion of the atom to the left of the vacancy takes place by exchange with the vacancy. By moving the vacancy all around the lattice, each atom will eventually have its turn to exchange with the vacancy. From the outset, we might guess that the vacancy diffusivity will be much larger than that of the host or “self” atoms; the self-diffusion coefficient will be much smaller than the vacancy diffusion coefficient.
Substitutional impurities, namely those that sit on host atom sites rather than in its interstices, also depend upon vacancy motion for diffusion to take place. The shaded atom in the bottom-right configuration in Fig.
11.4 represents such a substitutional impurity. It is obvious that for this to take place, the atomic radius of the impurity must be comparable to that of the host. Impurity atoms will similarly bide their time waiting to exchange with a host vacancy that comes their way. They may exchange more readily or less so than the host atoms, but both diffuse by so-called “vacancy mechanism.”
Let's consider vacancy diffusion within the rubric of the modular “plug-in” diagram of Fig.
11.1. Box B of Fig.
11.1 will become equation
11.14:
where
is the vacancy jump frequency and
is the “availability” factor or site fraction of vacancies. The latter amounts to the probability that each adjacent site is unoccupied. The first of these two terms can be derived by analogy to equation
11.7 for interstitial motion, or equation
11.15:
where is the coordination number, is the attempt frequency, and and are the entropy and enthalpy of vacancy motion, respectively.
We will address each of these parameters later, but for now let's concentrate on the site fraction of vacancies or
. If temperature is sufficiently high, the vacancy concentration will be in thermodynamic equilibrium. We can approach this problem as was done for the regular solution model in your prior thermodynamics coursework. Expressions were written for both the enthalpy of mixing in equation
11.16:
and the entropy of mixing in equation
11.17:
where
is the “interaction parameter” and
and
represent the mole fractions of the two components. The phase boundaries of the regular solution solvus were found by plugging these two equations into the overall expression for the free energy of mixing, equation
11.18:
taking the derivative with respect to composition (), and setting the result equal to zero.
In the case of the formation of vacancies in a solid metal, the corresponding enthalpy term is given by equation
11.19:
where
represents the enthalpy increase per mole of vacancies. Similarly, the entropy of forming a mole of vacancies is given by equation
11.20:
where the non-configurational entropy, incorporating the thermal/vibrational entropy per mole of vacancies (
), is given by equation
11.21:
and the configurational entropy looks a lot like the entropy of mixing (in equation
11.17) or equation
11.22:
If we begin with the standard free energy of the “perfect” crystal (
), and insert all the enthalpic and entropic terms for vacancy formation, the Gibbs free energy of the defective crystal compared to that of the perfect crystal is given by equation
11.23:
Fig.
11.5 shows how the enthalpic and entropic factors contribute to the overall free energy of vacancy formation.
At first,
decreases with increasing vacancy concentration, being dominated by the entropy terms. Eventually, however, the enthalpy term turns things around, dominating at higher vacancy concentrations. A minimum in the free energy of vacancy formation occurs at the so-called equilibrium value (
). This value can be derived by taking the first derivative of equation
11.23 and setting it equation to zero as in equation
11.24:
Rearranging equation
11.24, exponentiating, and making the assumption that
, we obtain equation
11.25, which relates the equilibrium vacancy concentration (site fraction of vacancies) to temperature:
For now, let's leave the testing of our assumption (
) for later, and plug this equation (
11.25) into Box D of Fig.
11.1. We previously derived equation
11.15, which is Box C of Fig.
11.1. Plugging these equations into the jump frequency expression of Box B, we obtain an overall equation for self-diffusion (Box A) by vacancy mechanism, or equation
11.26:
which can be simplified to the basic equation
11.27:
where
, the activation energy of self-diffusion, is the sum of formation (
) and motion (
) enthalpies, and
is the pre-exponential factor that incorporates all the factors within the first bracket of equation
11.26. As with interstitial diffusion, we can reorganize equation
11.26 into geometric (
), entropic (
), and activation energy (
) factors, as in equation
11.28:
Before we examine the factors in the pre-exponent and estimate its value, it is useful to calculate the diffusion coefficient of the vacancies themselves. Plugging equation
11.15 into Box C of Fig.
11.1 and inserting this for the
term in Box A, we obtain equation
11.29:
As we said above, the vacancies are moving around much more frequently than individual host atoms. In the following section, we mention that the vacancy concentration in fcc metals can be as high as at just below their melting points. Simple math shows us that the ratio of jump frequencies () or diffusivities (), that is of vacancies vs. host atoms, will therefore be 1000x! Actually, you can prove this to yourself by solving a “tile” puzzle and counting the number of jumps made by each numbered tile compared to the number of jumps the “vacancy” makes to solve the puzzle.
Now let's estimate a range of pre-exponential factors for self-diffusion in fcc metals based upon our best guess of atomistic factors. We will assume a representative value for the jump distance in equation
11.26 of approximately
or
. For example, recall that we obtained
for fcc iron. We also established that the coordination number (
) of adjacent sites around any given host atom, on which a vacancy might sit, is 12. Again, we will assume the familiar value for the attempt frequency (
) of
. Theorists find values for both the entropy of formation and motion to be on the order of R, or
, however a range of values is found in the literature. We will employ a range of values of
and
. Plugging all these values into equation
11.26, we obtain a range of pre-exponent values of
.
So how did we do? The pre-exponential factors for self diffusion are
,
, and
for fcc aluminum, nickel, and copper, respectively [
3]. Given all the assumptions we made, the agreement is quite good.
What about self-diffusion in bcc metals? Again, let's assume a representative value for the jump distance in equation of approximately
or
. As opposed to fcc metals, the jump distance is different for site-to-site jumps vs. interstitial-to-interstitial jumps. This is demonstrated in the bcc structure of Fig.
11.6, where the near-neighbor jump is one-half the body diagonal, or
. In bcc iron, this jump distance would be
or
. From the same Fig.
11.6, the coordination number is obviously 8 as opposed to 12 for fcc metals. Again, assuming a typical attempt frequency (
) of
and a range of entropic factors, such that
and
, and inserting these values into the first bracket of equation
11.26, we obtain as an estimate,
.
Again, how did we do? The pre-exponential factors for self-diffusion are
,
, and
for bcc iron, molybdenum, and chromium, respectively[
3]. Again, the experimental values are in good agreement with our simple-minded predictions.
11.3 Interstitialcy Diffusion
Of the three diffusion mechanisms we have thus far considered, interstitialcy diffusion is certainly the most unusual. The German word for this mechanism is “zwischengitterstossmechanismus,” which does a far better job conveying the concept. The words that make up this moniker will help us understand its meaning. The word “gitter” refers to the normal lattice sites. The word “zwischen” means “between.” And the word “stoss” means “shove.” This mechanism is exclusive to compounds with more than one sublattice. This is because the interstice size in metals is never big enough to accommodate a self-interstitial. However, in certain ceramic materials one species, for example the electropositive cations, can be much smaller than the electronegative anions. And in this case the cation interstices can be large enough to accommodate cation self-interstitials. The classic example is AgBr, which readily forms Ag self-interstitials. But rather than moving around by interstitial mechanism, as carbon does in iron, a coordinated two-cation motion mechanism takes place, in which an interstitial cation bumps another cation off its normal site and takes its place. That's where the “shove” part of zwischengitterstossmechanismus comes in. The normal cation now becomes an interstitial cation, and the process continues. A schematic of the first step of such a process in AgBr is shown in Fig.
11.7 in terms of “before” and “after” positions of ions. Only the
species are shown, since all the action involves silver cations.
I like to think of one of two analogies for interstitialcy mechanism. The first involves “sending” an opponent's ball in croquet. Once I touch your ball with mine, I have the option of positioning my ball under my foot right next to yours and then clobbering my ball, the transferred momentum sending your ball way off course. The other analogy involves shuffleboard (or curling, if you have ever seen it), where the momentum of my puck/stone is transferred to your puck, which (hopefully) is removed from the scoring area while mine takes its place. Two points need to be made about the interstitialcy event. As shown in Fig.
11.7, the process is “collinear,” meaning that the pushed atom moves along the same line as the pushing atom. This need not be the case, as we well know from the shuffleboard/curling analogy. Non-collinear interstitialcy mechanisms are definitely known to occur. Second, note that the interstitial has moved twice as far as the host atom that got pushed. This may not seem significant, but it is actually one way to confirm that the collinear interstitialcy mechanism is occurring. Later we will find out how to use electrical conductivity to establish the diffusivity by charged ions, so-called ionic diffusivity/conductivity. It turns out that when we measure the diffusivity of silver ions by tracer methods in AgBr, we get an answer that is approximately half the diffusivity of silver ions measured by electrical conductivity. Why is this? Look again at Fig.
11.7. The charge (the interstitial) is moving twice as far as the shaded host ion (which could be a tracer ion).
Given the complexity of the interstitialcy mechanism and the relative dearth of representative pre-exponential factors, we will not subject this mechanism to the intense atomistic scrutiny as we did for interstitial and vacancy mechanisms. However, we can make some remarks about “jump frequency” and “defect availability” in Box B of Fig.
11.1. It makes sense that the interstitialcy defects are jumping with a frequency,
(
for interstitialcy). But if I am a silver cation on a host site, instead of waiting for “pullers” to come along (vacancies), I am now biding my time awaiting the arrival of a “pusher” to come along (interstitialcy defects) and knock me on my way. Hence the defect availability factor will be the fraction of occupied interstices, or
. By analogy with the vacancy mechanism, the corresponding Box E interstitialcy diffusion coefficient (with direct analogy to equation
11.26) is equation
11.32:
As with the vacancy mechanism, this equation has geometric (
), entropic (
), and thermally-activated components (
), as in equation
11.33:
The motion-related components are relatively straightforward to understand, however the formation components () and () will have to wait until we have considered point defects in ionic solids, including the introduction of a special shorthand representation for ionic defects called “Kröger-Vink” notation.
11.4 The Arrhenius Behavior of Diffusion
We have shown that for all diffusion mechanisms considered thus far, Arrhenius behavior results, namely that the diffusion coefficient is thermally activated as per the equation in Box F of Fig.
11.1. We already saw this behavior for tracer diffusion in equation
10.7 and for general diffusion in equation
11.1, which is repeated here:
As materials scientists and engineers, we need to be confident in using and manipulating diffusion data that behave in this Arrhenius, thermally-activated fashion. Here are some things we need to be able to do: 1) Plot experimental data for diffusion on a
vs inverse temperature (T
) plot to extract pre-exponent and activation energy; 2) Given the pre-exponent and activation energy for diffusion, calculate the diffusion coefficient for a specified temperature, or make the corresponding Arrhenius plot of
vs.
; 3) Given the diffusion coefficient at one temperature and the activation energy, predict the diffusion coefficient at another temperature; 4) Given diffusion coefficients at two temperatures, be able to extract the pre-exponential factor and activation energy, plus predict the diffusion coefficient at an intermediate temperature. All of these tasks are quite straightforward once we recognize that taking the logarithm of both sides of equation
11.34 results in the formula of a line, as in equation
11.35:
where the axes are
and
the slope is
and the intercept is
. Alternatively, the slope is given by equation
11.36:
These relationships are represented schematically in Fig. A. It should be noted that diffusion data are more commonly plotted on base-10
vs.
plots, but it is easy enough to modify equation
11.35 to equation
11.37:
Be certain not to make the mistake of plotting temperature in ! All diffusion plots employ temperature in degrees Kelvin.
12 How We Know That Point Defects Exist and Move, Plus Some Useful Relationships
We are going to “turn back the hands of time” to answer these questions. Of course, we can now image individual atoms on very sharp tips in machines called (what else?) atom probes. But long before the existence of such atom probes or high resolution electron microscopes, we knew about atoms and their absence (vacancies) and that such defects moved around. At the times in question (the 1950s and 1960s) the following methods were “de rigueur.” Along the way we have learned quite a bit about diffusion in crystalline solids (metals, ceramics) and distilled some important relationships concerning their transport behavior.
12.1 The Classic Simmons-Balluffi Experiment
You can read about the original experiment for yourself in the reference [
10], but this classic experiment employed simultaneous measurement of macroscopic expansion (using a high-accuracy dilatometer) and sub-microscopic/lattice spacing changes (using in situ X-ray diffraction) on a single crystal specimen of an fcc metal during controlled heating. This may seem like a circular argument, but we already anticipate that the vacancy concentration will increase with temperature (see equation
11.25) and should be highest near the melting point. So the procedure involved intrepid experimenters willing to go to high temperatures, even approaching the melting temperature. The general concept is given schematically in Fig.
12.1.
First we see a vacancy added to one of the close-packed planes in the fcc structure. We anticipate that the average lattice spacing would change (possibly decreasing), but in the end this influence ends up being factored out. The second effect has to do with the fact that vacancies can only be added at surfaces, as shown. Given enough vacancies, however, this will amount to extra planes being added to the crystal. This should be reflected in the dilatometer measurements, if we are able to measure very small strains. So whereas the change in lattice parameter,
, will be reflected in both X-ray diffraction or XRD (see the schematic of X-rays diffracting from the planes in Fig.
12.1) and in dilatometry, the increase in the number of planes owing to vacancy formation (
) will only be reflected in dilatometry. What we need to do is relate a uniaxial (1D) length change to the overall volume change (3D). Turning to Fig.
12.2, if the volume of a cube of material at room temperature is given by
, its volume once expanded (and at temperature) will be given by
.
Doing the math for
and dropping all terms involving
or
, since
itself is quite small, we find equation
12.1:
where the first term on the right reflects the addition of planes owing to vacancy formation, and the second term takes into account the lattice contraction and/or expansion in proportion to the site fraction of vacancies being formed. But we can also argue equation
12.2:
The contraction and/or expansion of lattice planes by X-ray diffraction is in proportion to the site fraction of vacancies. Subtracting equation
12.2 from equation
12.1 eliminates the
term (so we needn't concern ourselves with the value of
) and yields the desired equation
12.3:
This equation may seem simple enough, but careful examination reveals just how difficult (how de rigueur) this experiment was at the time. Simmons and Balluffi had to measure extremely small differences between two very small quantities as they changed with temperature. You can pull up the original references to examine the original data and plots, but a schematic representation is given in Fig.
12.3.
A first observation is that both quantities (
) and (
) increase significantly with temperature, much more than can be explained by the addition of vacancies, and that both are concave upward with temperature. In fact, both quantities are reflecting the fact that thermal expansion is occurring with increasing temperature. This might seem to be a “deal-breaker” at first, until you realize that thermal expansion should be reflected identically in both quantities (dilatometry, XRD). Therefore, as per equation
12.3, any thermal expansion-induced changes will cancel out. A second observation is that up to an onset temperature (
) there is no apparent difference in the two quantities. Actually, there should be a difference at every temperature (as long as the vacancy concentration is in thermal equilibrium); however, below
the vacancy concentration is simply too small to be registered, meaning that any difference will be undetectable within the experimental limits of the two measurement methods. Above
, however, there is a noticeable difference between (
) and (
), whose value is precisely one-third the vacancy concentration. It is obvious that the vacancy concentration increases monotonically with temperature up to the melting point.
Taking the natural logarithm of both sides of equation
11.25 we obtain equation
12.4:
This tells us that by plotting the Simmons-Balluffi-derived
vs. temperature data on an Arrhenius plot of
vs. inverse temperature, as shown schematically in Fig.
12.4, we can extract both the entropy of vacancy formation (from the y-axis intercept) and the enthalpy of formation (from the slope).
In the original work on aluminum, the values obtained for and were and (or 0.75 eV), respectively.
12.2 Some Important Numbers and a Useful Relationship Regarding Vacancy Formation in fcc Metals
Now that we have the ability to establish equilibrium vacancy concentrations in metals, we can derive useful relationships, for example between the enthalpies of vacancy formation and the melting points of fcc metals. It turns out experimentally that the equilibrium vacancy concentrations at the melting points of fcc metals are almost always in the range,
. Let's plug this range of values into equation
11.25 and assume that
or
This yields equation
12.5:
from which it follows that
, or approximately equation
12.6:
This rough estimate can come in quite handy, for example when you know the melting point of an fcc metal, but lack a readily available measured value for the enthalpy of vacancy formation. In addition, knowing that vacancy concentrations of fcc metals are on the order of to at their melting points is also good to put to memory.
12.3 The Classic Bauerle and Kohler Experiment
So far we have good evidence for the existence of point defects like vacancies, but is there evidence for their motion? We can certainly argue “yes” on the basis of tracer diffusion experiments. However, this question was answered in another way by Bauerle and Kohler [
2]. This experiment is a bit more difficult to describe, but following the development will pay dividends. Since the experiment involved the use of electrical resistivity measurements, we need to introduce what is referred to as Matthiessen's rule, given by equation
12.7:
where the total resistivity of a metal is shown to be governed by several electron-scattering mechanisms, including thermal vibrations (
), scattering by vacancies (
), and scattering by other defects like dislocations (
). Since the resistivity of metals tends to be quite low, Bauerle and Kohler employed wires to enhance the measurable resistance, given by
, where
is wire length and
is cross-sectional area. The experimental campaign is represented schematically in Fig.
12.5.
A wire of fcc metal was heated to what we will refer to as a “quench temperature” () in order to set the equilibrium vacancy concentration for that temperature. In two separate experiments, the wire was heated and held at and then quenched to room temperature, freezing in the equilibrium vacancy concentration of the quench temperature, or . After electrical measurement at room temperature, the same wire was heated and held at and then slow-cooled to room temperature. This second process allows for vacancy annihilation to take place, such that the resulting vacancy concentration is negligibly small. By subtracting the wire's resistivity slow-cooled () from that quenched (), we find equation :
We are assuming that there are no changes in the other defects (including dislocations) during quenching vs. slow cooling, and that the thermal contribution to resistivity will be the same, since both measurements are made at room temperature. The thermal and other defect contributions therefore cancel, leaving only the vacancy scattering contribution, which we can set equal to a constant (
) times the vacancy concentration frozen-in from the quench temperature [
], as in equation
12.8. This gives us something proportional to the equilibrium vacancy concentration at only one quench temperature, so Bauerle and Kohler repeated the procedure in Fig. at several other quench temperatures. They then plotted the natural logarithm of
vs. the inverse of quench temperature in Arrhenius fashion, as shown schematically in Fig.
12.6. Since
is a constant that does not change with quench temperature, the slope of the plot should reflect only the activation energy for vacancy formation,
, as shown in the Fig..
The result obtained for fcc gold by Bauerle and Kohler was or 0.98 eV, in excellent agreement with later work of Simmons and Balluffi by dilatometry/XRD ( or 0.94 eV). We should stress that since the quench-resistivity method only yields a quantity that is proportional to the vacancy concentration as opposed to the vacancy concentration itself (as in the dilatometry/XRD work), it is impossible to extract information regarding the pre-exponential factor and underlying entropic term by quench-resistivity method.
The real advantage of the Bauerle-Kohler method, however, is that in addition to the enthalpy of vacancy formation, the enthalpy of vacancy motion can also be determined. To appreciate how this is done, we have to resurrect an old equation for the relaxation of vacancies, namely equation
10.8 repeated here:
You will recall this as the “diffusion out of a slab” equation that we also employed to describe vacancy relaxation to sinks such as dislocations or grain boundaries. It is valid when the average composition relaxes to below 80% of the initial composition. In the present situation (quench-resistivity measurements) we can modify this equation to equation
12.10:
where
is the average vacancy concentration and
is the quenched-in starting vacancy concentration. This, in turn, can be related to the quench-resistivity measurements by equation
12.11:
having inserted the relationship from equation
12.8, namely that
.
Here is where the process of obtaining the motion enthalpy of vacancies gets a little complicated, so stay with me. Fig.
12.7 shows a schematic of the temperature-time history of the series of experiments.
Bauerle and Kohler began by setting a high initial concentration of quenched-in vacancies, by quenching from
to room temperature, where the initial value of
was measured. Remember that
is always the as-quenched resistivity minus the slow-cooled resistivity. They then proceeded to take the wire to a relatively low intermediate temperature,
, high enough to facilitate vacancy relaxation to sinks, but not so high that a significant fraction of the residual vacancies are lost. This involved a series of sub-experiments: 1) heat at
for a set time, 2) quench to room temperature, and 3) measure
, and then repeat. As shown in Fig.
12.7, the measured
is for the cumulative time, e.g.,
, at the relaxation temperature. They then went to a higher relaxation temperature,
, and repeated the same series of heat-quench-measure procedures. By taking the natural logarithm of both sides of equation
12.11, noting that
,
, and
are all constants, we obtain equation
12.12:
We can normalize each
by the initial
, and plot the natural logarithm of
vs. cumulative relaxation time, as shown schematically in Fig.
12.8.
The plot starts at time zero, where
and
vs. time follows a straight line of slope,
, up to the point where the change was made to relax at the higher temperature,
, after which the slope increases, becoming
. You might be asking, “Are we there yet?” And the answer is, “Almost!” Remember the definition of the relaxation time in equation
10.4, repeated here in terms of vacancies:
where
is the spacing between sinks, which we assume is not changing throughout thermal history, and
is the vacancy diffusivity. Using our knowledge of vacancy diffusivity, we can write the following equation
12.14:
Since
and
are constants, we can relate the relaxation times at the two temperatures in Fig.
12.8 to the corresponding vacancy diffusivities, and the enthalpy of motion in equation
12.15:
Using this procedure Bauerle and Kohler found the enthalpy of vacancy motion in solid gold to be 79.1 kJ/mole or 0.82 eV. Adding this to their enthalpy of vacancy formation (94.6 kJ/mole or 0.98 eV), we obtain a value of 173.7 kJ/mole or 1.80 eV. This happens to be virtually identical to the activation energy for gold self-diffusion (by tracer method), which is a nice double-check.
12.4 Some Useful Relationships Regarding Self-Diffusion and Vacancy Motion in fcc Metals
Another highly useful relationship has been found for fcc metals, as expressed in equation
12.16:
where the activation energy for self-diffusion (typically measured by tracer diffusion) is approximately 18 times the product of
and the melting point (in degrees Kelvin). Since
, subtracting equation
12.6 from equation
12.16 gives the approximation of equation
12.17:
For example, the melting point of gold is or , for which we would predict a vacancy motion enthalpy of 82.1 kJ/mole or 0.85 eV, in good agreement with the Bauerle and Kohler value (79.1 kJ/mole or 0.82 eV).
It turns out that the normalized self-diffusion activation energy, , is roughly constant for each type of crystal structure (including ceramics in addition to metals), however there is a different normalization factor for each structure type. It would pay to do a literature search for the appropriate relationship when exploring a solid with a crystal structure new to you.
This is also a good chance to introduce the concept of “homologous temperature,” which is defined as the fraction of an element's melting temperature on an absolute temperature scale. You will encounter this a lot when dealing with kinetic phenomena in materials. For example, the two “intermediate” temperatures employed for vacancy relaxation in quenched gold, represented schematically as
and
in Figs.
12.7 and
12.8 were
and
or
and
on the absolute temperature scale. These temperatures are 25.4% and 27.0% of the melting temperature of gold. Were we to make similar measurements on a different fcc metal, a good guess for relaxation temperatures would be to start with the same homologous temperatures of
.
One last useful number to keep in mind is the melting point diffusivity of solid fcc metals. From the fact we were just given, namely that
, we can exponentiate as in equation
12.18:
You may recall that we employed a range of pre-exponential values for fcc metals, namely . If we arbitrarily choose a value of , this means that the melting point diffusivity of fcc metals should be on the order of , which is in fact quite common experimentally. This number, , is therefore a good one to put to memory.
13 Point Defects and Transport in Ionic Solids (Ceramics)
Many properties/functions of ionic solids/ceramics are governed by their point defect structures, including ionic diffusivity and ionic charge transport/conductivity. However, in order to understand defect-related structure-property relationships we need first to master the notation now near universally employed to describe point defects, their formation reactions, and their point defect equilibria–otherwise known as “point defect chemistry.” The particular notation employed is referred to as “Kröger-Vink” notation, which we introduce in the following section.
13.1 Kröger-Vink Notation
A helpful shorthand scheme for Kröger-Vink (K-V) notation is given in Fig.
13.1. An easy way to recall this shorthand scheme is by remembering it as the M, S and C in “Materials SCience.” The “M” stands for matter, or the lack thereof (for example a vacancy). The “S” stands for the site on which the defect sits. And the “C” stands for charge. However, in K-V notation the “C” is not real charge (as on the individual ions), but rather effective charge, namely the charge of a defect species relative to the perfect crystal. How these all work can best be illustrated by considering a number of examples.
Let's begin by considering host species and fully-charged point defects in zirconia, . Before we start, it is useful to consider the real charges on the ions with which we are dealing. We can write the formula unit of as . Hence, we can write the host cation species as , where the superscript “” represents a neutral species insofar as effective charge is concerned. That is, the perfect (non-defective) crystal is charge-neutral. What we have written is that a cation on a host site has an effective charge of zero (represented by the superscript “” in K-V notation. Similarly, we can write the host anion species as , representing an host anion on an site, with neutral effective charge. For a while we will continue to write host and defect species with real charge inside the parentheses, however this practice not part of the K-V system, but only a temporary “crutch” to help get us comfortable with the notation scheme. In K-V notation, the host species we have thus far considered would be, and .
But what about point defects? Let's first consider oxygen defects, both vacancies and interstitials. Oxygen vacancies could be written as, , representing a vacancy with zero real charge on an oxygen 2- site. The effective charge is thus +2, represented by the two dots. Another way to think about this is to begin with a charge-neutral occupied oxygen site and remove from it (and the perfect crystal) an species. Since the crystal began electrically neutral, what remains must be doubly-charged positive. How about oxygen interstitials? Remember that, as opposed to close-packed metals where self-interstitials are energetically unfavorable, self-interstitials of cations or anions in ionic crystals are quite possible so long as the ionic radius of the interstitial species is close to that of the interstice on which it resides. We can write an oxygen anion interstitial as, , which represents a doubly-charged oxygen anion on an originally uncharged interstice. The effective charge is doubly-negative, as represented by the two strike marks. Another way to think about this is to insert a doubly-charged negative ion in an empty interstice in an otherwise neutral crystal. The effective charge should be doubly-negative. In K-V notation, these two species would be represented as and for vacancy and interstitial, respectively. Are you beginning to get the overall idea?
Let's test out our understanding by considering cation defects. A cation vacancy would be or in K-V notation. Again, you can think of this as removing a a cation from an otherwise neutral crystal. What is left behind must have a quadruply-charged positive effective charge. Note that instead of a superscript of (4'), K-V writes the effective charge in terms of quadruple-strike marks. Similarly, a cation interstitial would be or in K-V-notation. Again, you can think of this as inserting a cation in an empty interstice in an otherwise neutral crystal.
Now let's consider donor and acceptor doping. For example, let's put a 5-valent tungsten cation on a site. We could represent this as or in K-V notation. The fact that this is a donor is obvious from its positive effective charge. If we compensated for this doping by electronic species, we would have to choose electrons over electron holes. We will consider their K-V representation shortly. Now, consider putting a 2-valent calcium ion on a site. We could represent this as or in K-V notation. The fact that this is an acceptor is obvious from its negative effective charge. If we compensated by electronic species, we would have to chose electron holes over electrons.
Finally, how do we represent those electronic species–electrons and holes. Electrons have the following notation in K-V: . And electron holes have the following notation in K-V: . Note that in neither symbol is there a subscript. This is because electrons and holes do not belong to specific sites, but rather to the crystal at large.
So we are now equipped to begin writing balanced point defect reaction equations and mass-action relationships. But there is one caveat that must be made. In most cases the concentration of a specific species is indicated by putting a set of brackets around the particular species. For example, the concentration of oxygen vacancies and zirconium cation interstitials would be represented as and , respectively. However, there is a special practice for the electronic species, namely that the concentrations of electrons and holes are represented as and , respectively, rather than and . But this is easy to remember, since you are probably aware of n-type vs. p-type behavior in donor-doped vs. acceptor-doped semiconductors.
13.2 Rules for Balancing Point Defect Reactions
The Kröger-Vink rules for writing balanced point defect reactions can also be made to play off the M, S and C in “Materials SCience, as shown in Fig. KV2. Here “M” refers to mass-balance, namely that the mass on the left of a reaction must equal the mass on the right. The “C” stands for charge-balance, meaning that the charge on the left side of a reaction must equal the charge on the right. It should be stressed that the charge need not be zero for this to hold; both sides may have net effective charge, as long as that charge is the same both before and after the reaction proceeds. Finally, the “S” stands for site ratio and not site-balance. What this means is that sites need not be balanced. In fact, we can create sites with our reaction, as long as we preserve the site ratio of the host. For example, if we create two cation sites in a reaction involving as the host, as long as we simultaneously create three oxygen sites, preserving the 2:3 ratio of cation:anion sites, we will satisfy this rule. It is best to learn and apply these rules by writing some actual balanced point defect reactions, which we do in the following sections.
13.2.1 Stoichiometric Point Defect Reactions
In what follows three important distinctions must be made: 1) between “intrinsic” and “extrinsic” defects, 2) between stoichiometric and non-stoichiometric point defect reactions, and 3) between homogeneous and inhomogeneous point defect reactions. By “intrinsic” we mean that the reactions involve only species that are part of the undoped host crystal. You can think of the defects as being generated from “within.” On the other hand, “extrinsic” defects come from “without,” for example dopant species. The following two sections on stoichiometric and non-stoichiometric point defect reactions involve “intrinsic” point defects exclusively. In the third section, we consider doping and are therefore dealing with “extrinsic” point defects. Stoichiometric point defect reactions preserve the stoichiometry of the host, namely the O:M ratio in an oxide, , will be preserved at fixed y/x throughout the reaction. In non-stoichiometric point defect reactions (dealt with in the following section), the O:M ratio will be shifted from y/x(stoichiometric). The third distinction involves homogeneous vs. inhomogeneous point defect reactions. Homogeneous point defect reactions can take place anywhere throughout the crystal, and do not require surfaces to act as a source/sink for defects. No point defect gradients are generated between surface and bulk. On the other hand, inhomogeneous point defect reactions require a surface to act as a source/sink. Furthermore, as they occur a gradient of point defects is generated between the surface and the bulk. They also tend to be relatively slow vis-a-vis homogeneous reactions, which can take place at any point in the crystal, and no migration to/from a surface source/sink is required. This may seem confusing right now, but the distinction will be made clear as we consider specific cases.
The first stoichiometric reaction involves the formation of vacancy/interstitial pairs in what are known as Frenkel point defect reactions. These can be either cation Frenkel or anion Frenkel pairs. For sake of simplicity, we will consider all the point defect reactions of the present section as taking place in the M-monoxide host, MO or
. I strongly suggest putting the host above the double arrows representing the reaction equilibrium in every case to remind yourself of the host you are dealing with. The first reaction involves cation Frenkel pair formation, as per equation
13.1:
The species within the parentheses stands for an unoccupied interstitial site. Since the interstitial population is usually quite small in ionic solids, the site fraction of unoccupied interstices is usually considered to be unity, and this part of the equation is usually not written, since it is understood to exist as in the revised equation
13.2:
This is the form of the reaction that you will see in textbooks. Let's do two things with this reaction:
- Confirm that it satisfies all the requirements for a balanced K-V reaction as per the rules in Fig. 13.2:
- Mass Balance: As we consider reaction 13.2, we can see one M species on each side of the equation; this makes it mass-balanced.
- Charge Balance: The left side of the reaction has zero effective charge and the right side has two positive effective charges and two negative effective charges, which sum to zero; the equation is therefore charge-balanced.
- Site Ratio: Since there is one cation site on the left and one cation site on the right, there is no change in site ratio; the reaction satisfies the site-ratio rule. You might question the appearance of the interstice on the right, whereas there is no interstice on the left. However, site ratio pertains strictly to the normal host sites, and the availability of unoccupied interstices (as expressed in the equation ) is understood. So this is a balanced K-V point defect reaction.
- Consider whether it is homogeneous or non-homogeneous.
As shown in Fig.
13.3, the reaction simply involves a metal cation jumping from a normal host site into an ever-present empty interstice. This can occur everywhere homogeneously throughout the crystal, as shown, and does not require the presence of a surface to serve as source/sink. As a result, there will be no gradient of defect population between the surface and bulk of the crystal.
The corresponding oxygen interstitial reaction can be written as equation
13.3:
Once again, we can test this equation against the
rules. There is one oxygen species on either side, so mass-balance is obeyed. There is zero effective charge on either side, so charge-balance in achieved. Finally, there is one anion site on either side, so site-balance is maintained. This is once again a balanced K-V point defect reaction. Of course, the empty interstitial on the left side of the reaction is understood. As with the cation Frenkel reaction, the anion Frenkel reaction can occur homogeneously throughout the crystal, as represented schematically in Fig.
13.3. So oxygen Frenkel pair formation is a homogeneous point defect reaction. One final very important point should be made. Whereas the cation Frenkel reaction will vary with host crystal stoichiometry, namely the aluminum interstitial in
will be trivalent (
) as will the vacancy left behind (
), the anion Frenkel reaction is universal to all oxides. In other words, the identical reaction as in equation
13.3 can be written for any oxide, including
.
The second stoichiometric point defect reaction is the formation of Schottky defects. This will provide an important example of an inhomogeneous point defect reaction. The balanced point defect reaction is given by equation
13.4:
At first glance this seems like an incomplete reaction. There is no mass present, and what the heck is “null?” Well, believe it or not this is, in fact, a balanced K-V point defect reaction. There is no mass on either side, so mass balance is maintained. Both sides are charge-neutral (the 2+ and 2- on the right side cancel), so charge balance is preserved. But what about the fact that there are no sites on the left, whereas there are two on the right? The site-ratio rule does not prohibit the formation or annihilation of sites, but rather specifies that if formed or annihilated, this must be done in the stoichiometric ratio of the host. In this case we create anion and cation sites in the requisite 1:1 ratio of the host MO crystal (O:M=1). The “null” simply represents the perfect, non-defective crystal prior to the formation of the Schottky pair.
But now let's consider what makes this an inhomogeneous point defect reaction. Consider the schematic of a surface of MO crystal in Fig.
13.4, where the subscript “S” represents a surface species.
Let's move a bulk oxygen species to the surface, as shown, making it a surface anion and turning the underlying M surface species into a bulk cation. Next move a bulk metal species to the surface, as shown, making it a surface cation and turning the underlying O surface species into a bulk O species. By these two sub-steps, two vacancies are formed, one cationic and one anionic. The net point defect reaction can be written as equation :
It can be seen that all species involving mass (an M cation or an O anion) cancel, leaving the much simpler equation
13.4. However, the exercise has been an important one, since pairs of vacancies cannot arbitrarily form in the bulk of a crystal. Instead, Schottky pairs must be formed at surfaces and then migrate into the interior of the crystal, as shown in Fig.
13.5, thereby creating a point defect concentration gradient, hence the inhomogeneous nature of Schottky defect formation.
Two additional caveats must be made, however. Grain boundaries and dislocation cores can also serve as internal surfaces in ionic solids, where Schottky reactions can take place in either forward direction (they act as sources) or reverse direction (they act as sinks). The second caveat is to be careful to refer to “Schottky pairs” only when the O:M ratio is 1:1, as in MO. In
, for example, the Schottky formation reaction would produce five point defects, as in equation
13.6:
I will leave it to you to check and see whether or not this equation satisfies the rules.
In addition to Frenkel and Schottky defect reactions, there are two additional “stoichiometric” point defect reactions. The first involves site-exchange. For example, in the spinel
there are two different coordination environments for cations. The Mg cations reside on tetrahedral sites, meaning that they are bonded to four oxygen anions. The Al cations reside on octahedral sites, meaning that they are bonded to six oxygen anions. However, at elevated temperature the two cations can switch sites, as represented by the following equation
13.7:
As with Frenkel reactions, this exchange need not take place only at surfaces, since the two cations are only changing places. Hence, such cation exchange reactions are homogeneous in nature. Once again, we can test whether or not this equation is balanced in terms of the rules. There is one Mg species and one Al species on each side, so the equation is mass-balanced. There is one tetrahedral site and one octahedral site on each side, so the equation preserves site balance. In this case, the site ratio is O:Al:Mg equal to 4:2:1. Finally, both sides are charge-neutral. This is a balanced K-V reaction.
The final homogeneous point defect reaction involves electrons and electron holes. Fig.
13.6 shows a schematic representation of the top of the filled valence band (VBM or valence band maximum) and bottom of the unfilled conduction band (CBM or conduction band minimum) of a semiconducting ceramic, and the thermal promotion of an electron from the top of the VBM to the bottom of the CBM.
This process in Kröger-Vink notation is given in the intrinsic electronic reaction of equation
13.8:
So we have considered four different cases of stoichiometric point defect reactions, namely those that result in no change of the overall stoichiometry of the host. The ratio of O:M is maintained by each such reaction.
13.2.2 Non-stoichiometric Point Defect Reactions
We can divide non-stoichiometric point defect reactions into two categories, namely 1) those that decrease the O:M ratio, otherwise known as reduction reactions, and 2) those that increase the O:M ratio, otherwise known as oxidation reactions. As we will show, the former always produces electrons for charge-compensation and are n-type in nature, whereas the latter always produces electron holes for charge-compensation and are p-type in nature. Let's first consider reduction/n-type point defect reactions. Since oxygen gas either is produced (reduction reactions) or consumed (oxidation reactions) and this can only take place at surfaces, all non-stoichiometric point defect reactions are inhomogeneous.
We can decrease the O:M ratio by either decreasing the oxygen content or by increasing the cation content. Both are accomplished by the removal of oxygen, resulting in oxygen gas being released, plus the simultaneous production of electrons. The oxygen-decreasing reaction, otherwise referred to as an “oxygen deficit” reaction, results in the formation of oxygen vacancies, as per equation
13.9:
This is probably unnecessary at this point, but to keep you in the practice of checking off the rules, it can be seen that 1) there is one oxygen species on each side of the equation, 2) both sides are charge-neutral, and 3) we started with one anion site and end up with one anion site such that site-ratio is preserved. This is a balanced K-V reaction.
We can also decrease the O:M ratio by increasing the cation content. The cation-increasing reaction, otherwise referred to as a “metal-excess” reaction results in the formation of metal interstitials, as per equation
13.10:
I will leave it to you to check and see whether or not this equation satisfies the rules.
We can increase the O:M ratio by either increasing the oxygen content or by decreasing the cation content. Both are accomplished by the addition of oxygen and the simultaneous production of electron holes. The oxygen-increasing reaction, otherwise referred to as an “oxygen excess” reaction, results in the formation of oxygen interstitials, as per equation
13.11:
It should be stressed that this equation is universal in oxides, meaning that the O:M ratio of the host (above the arrow in the equation) does not matter; the same reaction is as true in
as it is in
. The cation-decreasing reaction, known otherwise as a “cation deficit” reaction, results in the formation of cation vacancies, as per equation
13.12:
We must be careful, however, since this reaction is not universal but rather depends upon the O:M ratio of the host. For example, the corresponding cation deficit reaction for
would be given by equation
13.13:
Note that we are producing both anion sites and cation sites, but in the requisite 3:2 ratio for .
13.2.3 Aliovalent Doping Reactions
We now consider how the oxide, MO, might be aliovalently-doped. Isovalent doping would be doping MO with oxide NO, where the valence state of the species N is 2+, as it is in the MO host. Aliovalent doping means doping with oxides having cations of different prevailing valence states than the host. We can write reactions for donor-doping, where the doping cation has a higher valence state than
and for acceptor-doping, where the doping cation has a lower valence state than
. In each case we can charge-compensate with ionic point defects or with electronic defects. For example, let's consider donor-doping of MO with the trivalent cation N, or
. The ionic compensation reaction involves the formation of cation vacancies, as per equation
13.14:
This is a good reaction on which to test your K-V balancing skills. The reaction is obviously mass-balanced and charge-balanced, but what about site-ratio? Well, the reaction yields 3 anion sites and 3 cation sites, which are created in precisely the O:M ratio of the host (3:3 equals 1:1).
The alternative to ionic compensation is electronic compensation. Note that in so doing, we need to release some of the oxygen as gas to maintain the M:O ratio of the host. The resulting reaction is given by equation
13.15:
Now let's consider acceptor-doping of MO with the monovalent cation N, or
for which the valence states are
. The ionic compensation reaction involves the formation of oxygen vacancies, as per equation
13.16:
The electronic compensation reaction requires the addition of some oxygen on the left side of the equation
13.17:
An obvious question to ask is which compensation mechanism (ionic, electronic) will take place in a certain dopant oxide/host oxide combination? The answer is that it depends upon the defect formation energetics, which we consider in the following section. You may also have missed a critical changeover from the previous two sections on stoichiometric and non-stoichiometric reactions to the present one on aliovalent doping reactions. You will notice forward and reverse arrows in the reactions of the prior two sections, but only a forward arrow in the reactions of the present section. This is owing to the fact that the first two sections dealt with equilibrium point defect reactions, meaning that the forward and reverse arrows were balanced. With aliovalent doping of ceramics, this is not the case, unless one has excess dopant oxide present at high temperature, namely a two-phase mixture. Instead, ceramics are donor-doped and acceptor-doped by incorporating a fixed amount of aliovalent dopant in the initial processing of the doped host ceramic. It is expected that the forward reaction goes to completion during processing at elevated temperature. Therefore, there is only a forward arrow. In other words, in equation
13.14 for example, we can set the vacancy concentration equal to one-half the trivalent donor concentration, or
It should be quite clear that all doping reactions, whether isovalent or aliovalent are “extrinsic” reactions, since the dopant species comes from “outside” the host crystal. It should also be clear that all doping reactions are inhomogeneous, reflecting the fact that dopants react with the surfaces of host oxide crystals/particles and undergo what is referred to as “solid state reaction” (and long range diffusion) to achieve doping uniformity throughout the doped ceramic.
13.3 Point Defect Thermodynamics in Ionic Solids/Ceramics
We can approach the thermodynamics of point defect reactions in ionic solids/ceramics in the same way we dealt with vacancy formation in metals. For example, for the formation of Schottky pairs in the oxide MO the reaction is repeated in equation
13.18:
The only difference is that we cannot consider the formation of individual cation vacancies or oxygen vacancies. Given their charge, their formation would be highly unfavorable energetically. Instead, we form pairs consisting of a cation vacancy and an anion vacancy to maintain electroneutrality of the crystal, as per equation
13.18. The enthalpy of this reaction can be written as equation
13.19:
where
is the site fraction of Schottky pairs, namely the site fraction of each kind of vacancy on its sublattice, and
is the enthalpy per mole of Schottky pairs. The entropy of Schottky pair formation can be written as in equation
13.20:
where
represents the non-configurational entropy of Schottky pair formation (per mole of Schottky pairs) and the term inside the brackets represents the configurational entropy. If we plot the two functions in equations
13.19 and
13.20 vs. the site fraction of Schottky pairs,
, and recall that
, we obtain the curves in Fig.
13.7.
The behavior closely resembles the same plot for vacancies in metals seen in Fig.
11.5. Initially, the entropy term dominates, but with increasing Schottky pair production the enthalpy term begins to dominate. The result is a minimum in the free energy vs.
curve corresponding to the equilibrium Schottky pair concentration (
). We can write a mass-action expression (an equilibrium constant expression) for the Schottky pair formation, as in equation
13.21:
where
and
represent the individual defect activities. We have assumed dilute solution behavior so the two
factors are Henry's Law constants. These have to be the same for both cation and anion vacancies, such that they are formed in equal populations. By dividing both sides of equation by
we arrive at equation
13.22:
Similarly, we can write an equilibrium expression for oxygen Frenkel formation, repeated as equation
13.23:
for which the equilibrium expression is given by equation
13.24:
In this expression, the site fraction of oxygen on oxygen sites is assumed to be unity, since the site fraction of oxygen vacancies is negligibly small. Hence, their activity can be assumed to be unity. We will employ these reactions and equilibrium expressions when generating and interpreting so-called Brouwer diagrams in the following sections.
Similarly, we can write point defect equilibrium expressions for each of the reduction and oxidation reactions introduced previously. For the oxygen-deficit reaction, repeated in equation
13.25:
the equilibrium expression would be equation
13.26:
For the metal-excess reaction, repeated in equation
13.27:
the equilibrium expression would be equation
13.28:
It should be pointed out that both the oxygen-deficit reaction (equation
13.25) and the metal-excess reaction (equation
13.27) have point defect concentrations decreasing as the oxygen partial pressure increases (at constant temperature). This can be seen by applying Le Chatelier's principle, namely increasing oxygen partial pressure causes a response in the direction (arrow) opposite to the side on which the
term occurs. It also follows from the point defect equilibrium expressions of equations
13.26 and
13.28, namely that to maintain the equilibrium constant, increasing
must be accompanied by a decrease in point defect concentration.
Similarly, we can now consider oxidation reactions. For the oxygen-excess reaction, repeated in equation
13.29:
the equilibrium expression would be equation
13.30:
And for the metal-deficit reaction, repeated in equation
13.31:
the equilibrium expression would be equation
13.32:
It should be pointed out that both the oxygen-excess reaction (equation
13.29) and the metal-excess reaction (equation
13.31) have point defect concentrations increasing as the oxygen partial pressure increases (at constant temperature). Again, this can be seen by applying Le Chatelier's principle, namely increasing oxygen partial pressure causes a response in the direction (arrow) opposite to the side on which the
term occurs. It also follows from the point defect equilibrium expressions of equations
13.30 and
13.32, namely that to maintain the equilibrium constant, increasing
must be accompanied by an increase in point defect concentration. The reactions and equilibria of the present section will form the foundation upon which schematic Brouwer diagrams can be constructed and interpreted.
We must consider one last equilibrium expression, namely that between electrons and electron holes as described by equation
13.8. The equilibrium expression for this reaction is :
where
is the “band gap,” corresponding to the difference in energy between the conduction band minimum and the valence band minimum as shown in Fig.
13.6.
13.4 Brouwer Diagrams
In 1954, G. Brouwer introduced what are now referred to as “Brouwer diagrams” (Phillips Res. Rep., 9, 366). Brouwer diagrams are logarithmic plots of defect populations 1) vs. temperature (or rather inverse temperature), 2) vs. oxygen partial pressure, or 3) vs. dopant concentration, again on a logarithmic scale. We consider schematic versions for each of these in the following sections.
13.4.1 Brouwer Diagrams of Defect Concentration vs. Inverse Temperature
This type of diagram is useful for determining the energetics of point defect formation and motion in ionic solids/ceramics. For example, consider the extrinsic doping of NaCl by
, where Ca is divalent (
), as given by equation
13.34:
Note the use of the forward arrow only, implying that this reaction goes to completion during the initial processing of the Ca-doped NaCl ceramic. Now consider the Schottky pair formation in NaCl, according to equation
13.35:
for which the equilibrium expression is given by equation
13.36:
The next step is to write what is commonly called the “electroneutrality condition,” which we will henceforth refer to as the “ENC.” This condition is required to maintain the overall electroneutrality of the host crystal. The ENC is a straightforward expression setting the sum of all the negatively-charged point defects equal to the sum of all the positively-charged point defects, as per equation
13.37:
The next step is to make so-called “Brouwer approximations.” These are regimes in which two species–one positively charged and one negatively charged–predominate. As we consider equation
13.37, it is clear that there should be two such regimes: 1) one where the Na-vacancy concentration is set by the Ca-donor doping, or
, and 2) one where the Na-vacancy concentration is determined by the Schottky equilibrium with Cl-vacancies, or
. But which regime will be on the left and which will be on the right on a log [defect] vs. inverse temperature plot? Since temperature increases from right to left on plot with an inverse temperature (1/T) x-axis, it makes sense that the extrinsic, donor-doped regime would dominate at low temperatures, or to the right, whereas intrinsic, Schottky pair defects would dominate at high temperatures, or to the left. The resulting schematic Brouwer diagram is given in Fig. T, with the two Brouwer approximations/regimes clearly marked.
The slope of the Na-vacancy concentration (important for later) is marked as
. This follows from inserting the ENC for that regime, namely
, into the equilibrium expression of equation
13.36 such that
. This means that
and that the activation energy for this regime will be
. However, the diagram isn't complete until we show a line for each species in both regimes. The donor-dopant, , is easy. It is just a horizontal line extending from the extrinsic regime into the intrinsic regime as shown. The Ca-dopant is a minority species in this regime. So we have lines for each of the three species in the ENC of equation
13.37 in the intrinsic regime. But what about the behavior of
in the extrinsic regime? Well, we know its concentration at the dashed line demarking the transition between electroneutrality regimes. In the extrinsic regime, the concentration of Na-vacancies is fixed by the aliovalent dopant concentration, namely
constant (not a function of temperature). This means from the equilibrium expression of equation that Cl-vacancy concentration will be directly proportional to the Schottky formation constant, or
. Therefore, the slope on the Cl-vacancy concentration in the extrinsic regime will be
, as shown.
This Brouwer diagram is especially helpful in determining the formation and motion enthalpies of Na-vacancies in NaCl. A schematic representation of the tracer-diffusion data for Na in NaCl is shown in Fig.
13.9.
Based upon the Brouwer diagram of Fig.
13.8, we know that there is no energy of formation of Na-vacancies in the extrinsic regime; the slope is attributable solely to the enthalpy of motion, or
. However, in the intrinsic regime there are contributions from both the enthalpy of motion and the enthalpy of formation. From the Brouwer diagram of Fig.
13.8, we know that the contribution from formation is
, so the combined slope is
. Since we know the enthalpy of motion from the slope of the diffusion plot in the extrinsic regime, this means that we can now calculate the enthalpy of Schottky pair formation from the slope of the diffusion plot in the intrinsic regime. This demonstrates the power of Brouwer diagrams for the study of point defect formation and motion in ionic solids/ceramics.
13.4.2 Brouwer Diagrams of Defect Concentration vs. Oxygen Partial Pressure
The second type of Brouwer diagram plots the defect concentrations vs. the oxygen partial pressure on a log-log plot made at constant temperature. The most commonly portrayed diagrams of this type are often referred to as “butterfly” diagrams, owing to their appearance. Although we will not construct such diagrams, we will display a couple of examples and discuss their construction and interpretation. For example, let's consider an oxide MO that has prevailing Schottky disorder. We have already written the stoichiometric point defect reactions that can occur in such a material, repeated here in equations
13.38 and
13.39:
for which the equilibrium expressions are equations
13.40 and
13.41:
respectively. In addition, we write the appropriate reduction and oxidation reactions, repeated here in equations
13.42 and
13.43:
respectively. The equilibrium expressions for these reactions are repeated here as equations
13.44 and
13.45:
respectively. Now let's write the ENC for this system, as in equation :
At first glance it would seem like the factors of “2” are in front of the wrong species, until we consider that according to the reduction reaction of equation
13.42, two electrons are formed for each oxygen vacancy formed. Hence, the electron population should be twice the concentration of oxygen vacancies. Were these the prevailing species, the Brouwer approximation would be
.
Based upon the overall ENC, it would seem that there should be four Brouwer approximations, namely
,
,
, and
, however this is not the case. Instead, the oxide in question will either have ionic species dominating at stoichiometry, such that the electrons and electron holes are minority species, or electronic species dominating at stoichiometry, such that cation vacancies and anion vacancies are minority species. This makes for two slightly different “butterfly” diagrams, as shown in Fig.
13.10. We can understand and interpret such diagrams by considering their point defect equilibria.
The diagram on the top is for ionic species dominating at stoichiometry, such that
. With increasing oxygen partial pressure, the oxidation reaction takes over, such that the electroneutrality condition transitions to
. Inserting this Brouwer approximation into the equilibrium expression of equation
13.43, we obtain equation
13.47:
Taking the logarithm of this expression and rearranging a bit, we obtain equation
13.48:
Dividing both sides by 3, it follows that
will be +1/6 in this regime, which appears on the right side of the upper diagram in Fig.
13.10. Note that the electron hole line lies above the cation vacancy line, owing to the factor of 2 in the Brouwer approximation,
. The shift upwards of the electron hole line vs. the cation vacancy line will be precisely the logarithm of 2, as shown.
Now let's consider what happens under reduction, when the reduction reaction takes over, such that the electroneutrality condition transitions to
. Inserting this Brouwer approximation into the equilibrium expression of equation
13.42, we obtain equation
13.49:
Again, taking the logarithm of this expression and rearranging a bit, we obtain equation
13.50:
Dividing both sides by 3, it follows that
will be -1/6 in this regime, which appears on the left side of upper diagram in Fig.
13.10. The slopes of the electrons and electron holes in the central regime follows from consideration of oxidation and reduction reactions. For example, reorganizing the reduction reaction of equation
13.49 we obtain equation
13.51:
Taking the logarithm of this expression and rearranging a bit, we obtain equation :
from which it follows that, since
is constant in the middle regime,
will be -1/4. Hence the -1/4 slope in the middle regime. For all other species, one can play off the corresponding majority defect to establish individual slopes. For example, from the intrinsic electronic disorder reaction of equation
13.39, for
to remain constant in a regime where the electron population is found to vary with
to the -1/6 power, the electron hole population must vary with
to the +1/6 power. Similarly, from the Schottky pair formation reaction of
13.38, for
to remain constant in a regime where the metal vacancy population is found to vary with
to the +1/6 power, the oxygen vacancy population must vary with
to the -1/6 power.
The second diagram in Fig.
13.10 is for the situation where electronic disorder predominates in the stoichiometric (middle) regime, such that
. It can be seen that in this regime the ionic defects (cation vacancies and anion vacancies) are minority species. Note, however, that the Brouwer approximations for the oxidation and reduction regimes are the same as for the upper diagram in Fig.
13.10.
There are six such Brouwer diagrams like the two represented in Fig.
13.10. This is communicated by Fig.
13.11, where the six situations are delineated. There are two each for the three main types of stoichiometric disorder: Schottky, Cation Frenkel, and Anion Frenkel. In each case there will be a diagram where ionic disorder predominates (
, where
stands for either the Schottky or Frenkel equilibrium constant and
stands for the intrinsic electronic disorder equilibrium constant) and a diagram where electronic disorder predominates (
).
The power of Brouwer diagrams like those in Fig.
13.10 can be demonstrated by their predictive capability. For example, if the MO oxide were a Schottky pair-former, with
as in the top diagram of Fig.
13.10, with cation motion governed by vacancy mechanism, this could be confirmed by tracer diffusion studies of M-cations vs. oxygen partial pressure. According to the top diagram of Fig.
13.10, we would predict +1/6 slopes vs. oxygen partial pressure at extreme reducing and extreme oxidizing conditions, with a plateau where the diffusion coefficient should not vary with
in the middle regime. Similar predictions could be made concerning the O-anion diffusivity.
One must be careful in drawing “butterfly” diagrams in oxides for which the O:M stoichiometry is other than 1:1. For example, the oxidation reaction for the oxide
(assumed to be a Schottky former) would be given by equation
13.53:
whereas the reduction reaction would be equation
13.54:
I'll give you a moment to establish the slopes of the majority species on either side of this “butterfly” plot. They will prove NOT to be the same, which tells us that asymmetrical “butterfly” Brouwer diagrams (warped butterflies) can be anticipated for oxides with stoichiometries other than O:M of 1:1. (Spoiler alert! I am about to tell you the slopes in the “wings” of the butterfly diagram. If you want to test your Kröger-Vink/Brouwer prowess, look away and see if you can solve for the slopes.)
The slopes on the
butterfly would be -1/6 on the left (this is essentially unchanged from the
butterfly situation), and +1/8 on the right. This latter slope can be obtained if we write the equilibrium reaction for equation
13.53 as equation
13.55:
Reminding ourselves that the Brouwer approximation for the ENC in the right “wing” will be
, and taking the logarithm of equation
13.55 and rearranging, we obtain equation
13.56:
It follows that will be +1/8.
We end this section by pointing out that “butterfly” Brouwer diagrams have limited practical application, owing to two facts. First, few oxides are amphoteric, meaning that they exhibit both n-type and p-type behavior. Most go in one direction (oxidation or reduction, p-type or n-type), but seldom both. Second, few oxides are employed in an undoped intrinsic state. We will discuss additional log[defect] vs. log diagrams as we consider two-regime extrinsic/intrinsic Brouwer diagrams in the following section.
13.4.3 Brouwer Diagrams of Defect Concentration vs. Dopant Concentration
A very useful type of Brouwer diagram involves plots of defect populations vs. dopant concentration (at fixed T and ) on a log-log plot. As with the log[defect] vs. inverse temperature plots already discussed, these have two Brouwer approximations, namely two ENC regimes: one intrinsic and one extrinsic. The procedures for creating such Brouwer diagrams are as follows:
- Write the appropriate intrinsic point defect reaction and the corresponding mass-action (equilibrium constant) equation.
- Write the extrinsic doping reaction.
- Write the overall electroneutrality condition, from which the two Brouwer approximations will be made clear.
- Decide which regime goes where, for example on which side the extrinsic regime should fall.
- Solve the mass-action (equilibrium constant) equation for all point defect species in each Brouwer regime.
Let's start by considering cation-deficit oxide MO, which is known to be a p-type semiconductor under oxidizing conditions. It is known that it can be acceptor-doped by the oxide,
, where the dopant is monovalent, namely
, resulting in electronic compensation by electron holes. The intrinsic point defect reaction is the oxidation reaction to form cation vacancies, as in equation
13.57:
for which the mass-action (or equilibrium constant) equation is equation
13.58:
Next let's write the acceptor-doping reaction, repeated as equation
13.59:
As we discussed previously, the forward arrow (with no reverse arrow) indicates that the reaction goes to completion during the processing of N-doped MO. The overall electroneutrality condition will be equation
13.60:
The next task is to decide on which side of the Brouwer diagram to place the extrinsic regime. This is pretty straightforward in the present case, owing to the fact that with increasing donor-doping, extrinsic behavior should “win out” over intrinsic behavior. We can begin by drawing a dashed line of slope +1 on the Brouwer plot, representing the concentration of acceptor species, or
, as shown in Fig.
13.12.
The vertical dashed line represents the transition between intrinsic behavior (at low doping levels,
) and extrinsic behavior (at high doping levels,
). In the intrinsic regime, the Brouwer approximation is given by
. Rearranging equation
13.58 we obtain equation
13.61:
However, since temperature (and therefore
) and
are both constants, the metal vacancy concentration and hole content will also be fixed (
) and independent of doping level. It can be seen that all three defect species (
) are represented in the intrinsic regime, but it remains to be established how the metal vacancy concentration varies with doping level in the extrinsic regime. Rearranging equation
13.61 and substituting
for
we obtain equation :
Since temperature (and
and
are constants, it follows that
] will be proportional to the dopant concentration to the -2 power, as shown in Fig.
13.12.
We can also create a log[defect] vs. log
diagram (at fixed temperature and fixed acceptor dopant level) for this system. Again, we need to decide where the extrinsic regime belongs, on the left or on the right. This is not as straightforward as with the log[defect] vs. log[dopant] diagram. However, examination of the intrinsic defect reaction of equation
13.57 indicates that as the oxygen partial pressure increases, the metal vacancy concentration will increase. This suggests that the intrinsic regime should be on the right with the extrinsic regime on the left. (Hint: if you try doing it the other way around, the resulting diagram will not make sense.) We begin by drawing a horizontal dashed line in Fig.
13.13 indicating the fixed acceptor dopant level.
Again, the vertical dashed line indicates the transition between the two Brouwer approximations or ENC regimes. The intrinsic regime is solved the same way as for the butterfly diagrams of the previous section. Inserting the ENC, namely that
, and rearranging equation
13.58 we obtain equation
13.63:
If we take the logarithm of both sides and rearrange, we obtain equation :
from which it follows that
will be +1/6, as shown in Fig.
13.13. All three species (
) are represented in the intrinsic regime, but we need to decide how the metal vacancy concentration behaves in the extrinsic regime. Once again we can employ equation
13.58, which rearranged gives us equation
13.65:
Since both
(fixed by temperature) and
are constants, it follows that the metal vacancy concentration will vary with
to the +1/2 power, as shown in Fig.
13.13.
Now let's consider a cation-excess oxide MO that becomes an n-type semiconductor under reducing conditions. It can also be donor-doped with
additions during initial processing, again with electronic compensation. As with the prior example, we will generate dual-regime isothermal Brouwer diagrams vs.
and also vs. dopant concentration. We begin by writing the metal-excess (metal interstitial) equilibrium, reproduced in equation
13.66:
for which the mass-action/equilibrium relationship is given by equation
13.67:
The
donor-doping reaction is given by equation
13.68:
Note that the one-way arrow indicates that this reaction goes to completion during the firing of
-doped MO. The overall ENC can be written as equation
13.69:
This time, let's begin with the log[defect] vs.
Brouwer diagram (at fixed dopant level). But will the intrinsic regime be on the left or on the right? One way of resolving this issue is to examine the intrinsic defect reaction of equation
13.66 and the corresponding mass-action/equilibrium relationship of equation
13.67. It can be seen that the metal interstitial population will increase (and overwhelm the extrinsic dopant level) as the oxygen partial pressure is reduced. This tells us to expect the intrinsic regime on the left (low
). In Fig.
13.14 we begin by drawing a horizontal dashed line to represent the constant
or
level.
The vertical dashed line represents that transition from intrinsic behavior on the left to extrinsic behavior on the right. Assuming the Brouwer approximation in the intrinsic regime to be
and rearranging equation
13.67, we obtain equation
13.70:
Rearranging once again and taking the logarithm of both sides, we obtain equation
13.71:
from which it follows that
will be -1/6, as shown in Fig.
13.14. We have lines for each of the three species in the ENC for the intrinsic regime, but how does the metal interstitial concentration behave in the extrinsic regime? Rearranging equation
13.67 and substituting
, we obtain equation
13.72:
from which it follows that
will be -1/2, as shown in Fig.
13.14.
Now let's consider the corresponding log[defect] vs. log[dopant] Brouwer diagram (at constant
). The increasing donor-dopant level is represented by the dashed line of slope +1 in Fig.
13.15.
The vertical dashed line represents the transition from intrinsic behavior to extrinsic behavior, the latter of which must fall on the right side of the diagram (high dopant level). In the intrinsic regime, since temperature (and therefore
) and
are both constant, if we rearrange equation
13.67 and insert the ENC (
), we obtain equation
13.73:
from which it follows that
, as shown in Fig.
13.15. We have lines for all three species in the overall ENC in the intrinsic regime, but how does the metal interstitial population behave in the extrinsic regime? Again, rearranging equation and inserting the ENC (
) we obtain equation :
Again, since
is a constant (because T is constant) and
is also constant, the metal interstitial population will vary with the dopant concentration to the -2 power, as shown in Fig.
13.15. We will revisit this diagram when we consider electrical conductivity in the following section.
As a transition to our consideration of ionic conductivity, we will construct one last log[defect] vs.
Brouwer diagram. Calcia-doped zirconia is an oxygen vacancy ionic conductor except at very reducing oxygen partial pressures, where electrons can begin to contribute electronic conductivity. The intrinsic equilibrium between oxygen vacancies and electrons is given by equation
13.75:
for which the mass-action/equilibrium relationship is given by equation
13.76:
The calcia (CaO) doping reaction is given by equation
13.77:
Note here that the dopant cations are divalent (
) whereas the host cations are tetravalent (
). Note also the forward arrow, which indicates that this reaction goes to completion during the processing of CaO-doped
. The overall electroneutrality condition is given by equation
13.78:
This time we will focus exclusively on the log[defect] vs.
Brouwer diagram, which is presented in Fig.
13.16.
You should be able to rationalize: 1) that the intrinsic regime belongs on the left, and 2) that the slope in the intrinsic regime should be -1/6. It may not be obvious why the electrons have a -1/4 slope in the extrinsic regime. Isolating the electron population in equation
13.76, we obtain equation
13.79:
Taking the logarithm of both sides, and remembering that
is constant (because temperature is constant) and
is also constant, it follows from equation
13.80:
that will be -1/4. We will return to this Brouwer diagram (Fig. ) in the following section.
14 Electrical Conductivity
The usefulness and predictive power of schematic Brouwer diagrams can best be illustrated by considering electrical conductivity, which is controlled by the point defect species with the highest product of concentration and mobility. It turns out that there can be contributions from electronic species (electrons and electron holes), and from mobile ionic species. The former determines the electronic conductivity of a solid and the second determines the ionic conductivity of that solid. Together, these two contributions determine the overall electrical conductivity.
14.1 Electronic Conductivity
From introductory materials science and engineering courses, you should be familiar with the following equation for the electronic conductivity:
where
is the unit of electron charge,
and
are the mobilities of electrons and holes, respectively, and
and
are their concentrations, as previously defined. Usually, however, one species will dominate (as a majority species) whereas the other will have negligible concentration (a minority species). For example, electrons are majority species in the n-type semiconducting oxide MO, as reflected in the Brouwer diagram of Fig.
13.14. In this case, the electronic conductivity reduces to equation :
It is useful to do a unit analysis on the parameters in this equation to understand common usage in the materials community. The basic unit of conductivity is a Sieman per centimeter, or S/cm. The Sieman is the same as a reciprocal ohm (
), and according to Ohm's law an ohm is voltage/current (V/I) or a Joule per coulomb (J/C) divided by a coulomb per second (C/s), such that an ohm is given by
. Placing these values into equation
14.2, we obtain equation
14.3:
It follows that the basic units for mobility are per Vs (). This may make more sense written as a centimeter per second (carrier velocity) per volt per centimeter (driving force), or .
Here is where the predictive power of schematic Brouwer diagrams comes in handy. If the electronic mobility is independent of carrier concentration, then the conductivity in equation
14.2 will depend solely upon the carrier concentration,
. Let's consider the case of M-excess semiconductor MO, whose Brouwer diagram is represented in Fig.
13.14. The corresponding predicted behavior of conductivity vs. oxygen partial pressure is given in Fig.
14.1. Note that if the donor-dopant level is reduced to a minimum, the intrinsic regime (
) can be preserved to high
values, as reflected by the “undoped” behavior in the Fig..
In the 1970s, the Ford Motor company developed a resistance-based oxygen sensor based upon such a
vs.
behavior as shown in Fig.
14.1. Employing a highly pure titanium metal filament, which was subsequently oxidized to
, they achieved a reproducible conductance (the inverse of resistance, or G=1/R) vs.
behavior that could be employed to monitor the oxygen content in the exhaust gases of the internal combustion engine. This enabled engineers to control the air-to-fuel ratio, otherwise known at the lambda-ratio. Hence, automotive oxygen sensors are typically referred to as lambda-sensors. It should be noted that given the different cation valence (4+ in
vs. 2+ for MO), and therefore the different charge on an interstitial cation, the slope on a log-log plot of G vs.
was not the -1/6 for titania. Nevertheless, the invention of a resistance-based oxygen sensor was an important development. However, resistance-based oxygen sensors lost out to electrochemical sensors as described in the following section.
14.2 Ionic Conductivity
It makes sense that
Ionic conductivity
will likewise be determined by the product of ion concentration, ion charge, and ion mobility. A development of the so-called “Nernst-Einstein” relationship is beyond the scope of the present text, but one form of it describes the ionic mobility of a charged species, as given in equation
14.4:
where
is the diffusivity of an ionic species of charge
,
is absolute temperature and
is Boltzmann's constant. Since the product
is in units of Joules, the product of
and C divided by Joules yields the appropriate units for mobility of
per
. The carrier concentration will be the concentration of mobile ions or
in units of
. The charge of the mobile species is given by
, which in turn is equal to the product of
(the number of charges on a mobile ion, e.g., -2 in the case of oxygen ions) and
, the unit of electron charge, or
. Putting all this together, the product of carrier content, carrier charge, and carrier mobility is given by equation
14.5:
which is yet another version of the Nernst-Einstein relationship. Let's apply this equation to the situation of calcia-doped zirconia, whose doping reaction is repeated here as equation
14.6:
As always, the forward arrow indicates a reaction that goes to completion during the firing of calcia-doped zirconia. The resulting electroneutrality condition is
, as shown on the right side of Fig.
13.16. The formula unit for CaO-doped
can be written as in equation
14.7:
where the box represents oxygen vacancies. In fact, we can write the ionic conductivity in terms of either oxygen diffusivity or oxygen vacancy diffusivity, as in equation
14.8:
where the
subscript refers to oxygen vacancies. Since
, we can cancel these terms and also the
product from both sides to obtain equation
14.9:
If we divide both sides by the concentration of overall oxygen sites (
), and replace
and
by the respective site fractions,
and
, respectively, we obtain equation
14.10:
This may not look familiar, but we have previously dealt with a version of this equation when dealing with self diffusion by vacancy mechanism in metals. You can find it back in equation
11.31, which can be rewritten as
. In reality, this expression should be
. In the case of metals, however, the site fraction of vacancies is negligibly small such that
. However, in the case of CaO-doped
the sizable vacancy content cannot be ignored.
Let's consider zirconia doped by 15 mole percent of calcia. The formula unit can be written as in equation
14.11:
such that the site fractions will be
and
. Note that the ratio of site fractions (
) is 12.33. From equation
14.10 it follows that the vacancy diffusivity at every temperature will be 12.33 times the oxygen ion diffusivity.
What we need to be able to do is to go back and forth between ionic conductivity and either of the diffusivities (oxygen, vacancy). If we know the concentration of overall oxygen sites, we can calculate the concentration of either occupied oxygen sites (
) or of oxygen vacancies (
). The concentration of overall oxygen sites can be calculated in a couple of ways. The cubic fluorite structure of
is given in Fig.
14.2.
There are 4 formula units or 8 oxygen sites per unit cell. If given the lattice parameter (
), the concentration of oxygen sites will be
. Alternatively, we might be given the density of the the 15 mole percent-doped zirconia in
. The mass per formula unit (f.u.) in equation
14.11 can be calculated as in equation
14.12:
Where
stands for atomic weight. The density (
) divided by the mass per f.u. (
) gives the number of formula units per
. The number of oxygen sites per
(
) is just twice this value, since there are 2 oxygen sites per formula unit. Either way, we can now go back and forth between diffusivity (oxygen ion or oxygen vacancy) and ionic conductivity using the Nernst-Einstein relationship of equation
14.8 as illustrated in Fig.
14.3.
Given that the oxygen vacancy concentration is fixed by the CaO doping, it follows that the oxygen diffusivity will be given by equation
14.13:
Incorporating this expression into equation
14.8 we obtain equation :
Except for temperature, all the other parameters within the brackets are constant or nearly so. This allows us to rearrange equation
14.14 into equation
14.15:
By plotting the natural logarithm of the product of ionic conductivity and temperature (
) vs. inverse temperature, we can determine the enthalpy of oxygen/vacancy motion, as shown in Fig.
14.3. This figure shows how to calculate individual diffusivities from the ionic conductivity, and vice versa. It should be pointed out that once one diffusivity is determined, the other diffusivity can be readily calculated from the
relationship.
The oxygen sensors in the internal combustion engines of gas-powered automobiles are zirconia-based. However, instead of registering conductance (resistance) vs. oxygen partial pressure, the zirconia sensor serves as a solid electrolyte membrane between two environments. One side is exposed to air () as a reference, while the other is exposed to the hot combustion gases coming from the engine. High temperature is required to keep the ionic conductivity high enough for the zirconia sensor to function. An electrochemical voltage is produced between the two sides of the zirconia electrolyte that is proportional to the difference in between the two sides. When the air-to-fuel ratio is high, excess oxygen decreases the difference (and the voltage). But when the air-to-fuel ratio is low, the reducing products of combustion increase the difference (and the voltage). A micro-processor uses the output of the oxygen sensor to adjust the air-to-fuel ratio by controlling the fuel injectors in the engine. You might suppose that the purpose of the oxygen sensor would be to keep the engine operating at optimal efficiency, but this is not the case. The purpose of the oxygen sensor is to maintain the air-to-fuel ratio in a narrow range where all three catalysts in the catalytic converter function optimally to react unwanted pollutants (reduction of , oxidation of CO, and oxidation of unburnt hydrocarbons).
15 315 Problems
Use the Ellingham Diagram (reproduced here as Figure
15.1) to answer the following.
- Find the temperature and partial pressure of where Ni(s), Ni(l), and NiO(s) are in equilibrium.
- Can the same equilibrium be achieved with and instead of oxygen? If so, what is the ratio of
- At , , and with a ratio of partial pressures of 10:1 is flowed through a tube furnace containing a crucible filled with MnO powder. Determine the driving force for the reaction
- Can you safely melt aluminum in a magnesia (MgO) container? Why or why not? What is the resulting reaction and its driving force?
- Establish the T-log phase diagram between and fort he Mn-O system at 1 atm total pressure.
In the days before the industrial revolution the
in the earth's atmosphere was 275 ppm. Use the data in Figure
15.2 to calculate how high one would need to heat
to decompose it at a
for the preindustrial concentration of 275 ppm and for present day
(You will have to look this up, please give your source). Also calculate how high one would need to heat
to decompose it if the
level in the atmosphere reaches 500 ppm.
Based on Raoultian liquid solution behavior, calculate the Sn-Bi eutectic phase diagram (using Excel, Mathematica, MATLAB, etc). Assume that there is negligible solid solubility of both Sn and Bi in the other component, and that for both end members. Use the following melting points and enthalpies of fusion:
|
Material
|
Tm(K)
|
|
|
Sn
|
505.12
|
7030
|
|
Bi
|
544.59
|
11300
|
Use MATLAB or a spreadsheet to calculate liquidus and solidus lines for a “lens-type” T-X diagram for the A-B system, using the data below. You may assume both the liquid and solid solutions behave ideally.
|
Type
|
Tm()
|
Hm(J/mol)
|
|
A
|
910
|
34700
|
|
B
|
1300
|
49800
|
- Plot the T vs. X phase diagram. Label each region on the diagram with the phases present and the degrees of freedom.
- For the temperatures , , and , draw plots of the activity of component A vs. composition. Include two plots for each: One with respect to liquid as the reference state and one with respect to solid as the reference state.
Based upon the temperature at the top of the miscibility gap in the Cr-W system (see Figure
15.3), do the following:
- Predict the miscibility gap (solvus) and spinodals based upon the regular solution model. Use the spreadsheet and plot the results.
- Compare your miscibility gap with the experimental one in the attached figure. Speculate about why there might be differences.
Consider the Pb-Sn phase diagram (see Figure
15.4).
- Label each region on the diagram with the degrees of freedom.
- Sketch free energy vs. composition curves for all phases at , , , and the eutectic temperature.
- For each temperature from part (b), draw plots of the activity of Sn vs. composition. Include two plots for each: One with respect to liquid as the reference state and one with respect to solid as the reference state. You may assume the liquid solution to be Raoultia. At , only plot activity of Sn vs. composition with respect to the solid reference state. At , only plot activity of Sn vs. composition with respect to the liquid reference state.
Calculate and plot the liquidus projection of the ternary phase diagram for the NaF-NaCl-NaI system. The melting temperatures and heats of fusion are as follows: NaF (
, 29,300 J/mol), NaCl (
, 30,200 J/mol) and NaI (
, 22,300 J/mol). Assume and ideal liquid solution and negligible solid solubility. Compare your result with the experimental diagram shown in Figure
15.5. Why might they be different?
On the liquidus projection diagram for the hypothetical system A-B-C shown in Figure
15.6), complete the following:
- Label primary phase fields
- Draw the subsolidus compatibility joins.
- Label all the binary and ternary invariant points.
- Indicate the directions of falling temperature (binaries and ternary).
- Sketch all the binary phase diagrams (including those formed by subsolidus compatibility joins).
Using the attached liquidus projection diagram for the hypothetical system A-B-C shown in Figure
15.7, complete the following:
- Determine the equilibrium crystallization path for the composition marked with the star.
- Determine the microstructural constituents:
- Just prior tot he liquid striking the phase boundary (liquid + solid 1 + solid 2).
- At the eutectic but just prior to eutectic crystallization.
- After crystallization is complete.
On the
phase diagram shown in Figure
15.8, draw isothermal sections at the following temperatures: (note- Ternary eutectic
is at
and ternary eutectic
is at
)
- Also determine the precise (not schematic!) phase diagram.
(Bonus question - 10% of problem set value) Starting with the regular solution model, prove that regardless of how positive the interaction parameter (or heat of mixing) might be, the inital slope on any free energy vs. composition curve must be infinitely negative on the left side () and infinitely positive on the right side ().
A steel tank contains hydrogen at 15 atm pressure. If the solubility of hydrogen in steel is 1x g/ under 15 atm pressure, the diffusion coefficient is 8x at room temperature and the tank is placed in a vacuum, calculate the flux of hydrogen through a 3.5 mm thick wall.
Austenite (Fe) with .85 wt% carbon has a diffusion coefficient of 1.9x/s at 900.
- Determine the jump distance in terms of the lattice parameter and the coordination number for carbon diffusion in this structure.
- How many jumps does a carbon interstitial make each second? Assuming a lattice vibration frequency of , what fraction of jumps is successful?
- Calculate and compare the random walk distance with the total distance (back and forth) traveled by an interstitial carbon atom in one second.
Ferrite (Fe) (BCC structure) dissolves carbon to a lesser extent than austenite (FCC structure).
- Determine the jump distance in terms of the lattice parameter and the coordination number for carbon diffusion in this structure.
- Given the data in Table 2.1 of Porter, Easterling & Sherif, make an Arrhenius plot of diffusion coefficients of carbon and nitrogen from room temperature to .
- A different interstitial solute diffuses at a rate of 4.1x/s at 300 and 7.3x/s at 600. Determine its activation energy and pre-exponential factor.
Write a MATLAB code to evaluate the composition as a function of distance for the draining plate problem.
- For = 0.05 how many terms in the series is necessary to obtain a composition that is converged to within 1% of the exact answer. The percent error is the maximum value of x100. To determine the exact answer evaluate the summation to . L=100um, at. %
- Plot the converged solution as a function of for = 0.05, 0.5, 1.0, 2.0.
- For what approximate value of does a single term in the summation with provide an approximation to the exact solution within 10%?
(After Shewmon 2-13) We wish to consider the rate at which the vacancy concentration increases in a specimen after an increase in temperature. We assume that the vacancy concentration in the lattice near the free surface, grain boundaries and edge dislocations will rise to the new equilibrium value of the new temperature as soon as the temperature is raised. The vacancy concentration far from these vacancy sources rises only as fast as vacancies can diffuse to the region from the source.
- Assume that vacancies come only from grain boundaries, and the grain diameter is approximately 1 mm. Calculate the relaxation time in two regimes, at high temperatures where the diffusion coefficient is /s.
- Calculate the relaxation time () given a dislocation line length (dislocation density) of cm/ (Hint: First, calculate the distance between dislocations, i.e, the vacancy sources.)
The diffusion coefficient of carbon in austenite can be approximated as:
- How long does it take for the composition during carburization to penetrate .45 mm at ? How long for 5 mm?
- What annealing temperature is required to double the penetration in a given time?
Consider two blocks initially one pure and the other pure that are welded together and annealed at Plot the diffusion profile as a function of distance after half an hour. Assume that the diffusion coefficient of both specie is and that is not a function of concentration.
Calculate the enthalpy and entropy of vacancy formation () for a system given the equilibrium concentration of vacancies () is at 440 K and at 650 K.
Given that , consider the diffusion of vacancies in an FCC lattice:
- Let and . Calculate the pre-exponential factor for vacancies (assume nm.)
- If kJ/mol, calculate for vacancies at 750
Below are the linear thermal expansion () and X-ray lattice parameter () results at different temperatures for aluminum. Calculate and plot ln from this data versus and determine the enthalpy and entropy of vacancy formation in aluminum. Show all equations used.
Below is a table of linear thermal expansion (L/L) and lattice parameter expansion (a/a) vs. temperature for aluminum. Calculate and plot ln form this data versus 1/T and determine the enthalpy and entropy of vacancy formation in this material. Show all equations used.
A gold specimen is quenched from to room temperature (). An identical specimen is air cooled from to room temperature. The difference in their resistances is . The quenched specimen is annealed at for 120 hours and then annealed at . Resistivity measurements were taken periodically by quenching the sample to room temperature. From the two slopes shown in attached Figure 2-16, find .
Write balanced Kröger-Vink reactions for the following reactions, assuming full ionic charge for all ionic species.
- Schottky defect formation in
- Anion Frenkel defect formation in
- Oxidation of CdO to yield Cd/O < 1/1 (write both possible reactions)
- Doping with ZnO to produce oxygen vacancies.
Pure ZnO is an n-type semiconductor dominated by oxygen vacancies, but it can be further donor-doped by substituting for sites.
- Draw a schematic Brouwer diagram as a function of at fixed Al content.
- Draw a schematic Brouwer diagram at fixed as a function of Al content.Include all relevant point defect reactions and mass-action relationships.
Given the following oxygen ion diffusivities for calcia-stabilized zirconia (CSZ) of composition ()(CaO) and density 5.5 g/, calculate a) the ionic conductivity at each temperature, and b) the enthalpy of motion. Assume oxygen vacancies are the dominant defect.
16 315 Labs
[PDFPages: 136_home_ken_Mydocs_MSEcore_315_nonlyxinputs_315_lab_schedule.pdf]
[PDFPages: 137_home_ken_Mydocs_MSEcore_315_nonlyxinputs_Metlab_Safety.pdf]
[PDFPages: 138_home_ken_Mydocs_MSEcore_315_nonlyxinputs_315_lab_worksheet_1.pdf]
[PDFPages: 139_home_ken_Mydocs_MSEcore_315_nonlyxinputs_315_lab_worksheet_2.pdf]
[PDFPages: 140_home_ken_Mydocs_MSEcore_315_nonlyxinputs_315_Lab1_BiSn_17.pdf]
[PDFPages: 141_home_ken_Mydocs_MSEcore_315_nonlyxinputs_315_lab_worksheet_3_Bi_Sn_Pb_ternary.pdf]
[PDFPages: 142_home_ken_Mydocs_MSEcore_315_nonlyxinputs_315_Lab2_BiSn_sample_prep_and_microscopy.pdf]
[PDFPages: 143_home_ken_Mydocs_MSEcore_315_nonlyxinputs_315_lab_worksheet_4_Pack-Carb_pre-lab.pdf]
[PDFPages: 144_home_ken_Mydocs_MSEcore_315_nonlyxinputs_315_lab_worksheet_5_Dictra_plots.pdf]
[PDFPages: 145_home_ken_Mydocs_MSEcore_315_nonlyxinputs_315_Lab3_Pack-Carb.pdf]
16.1 Laboratory 1: Phase diagram generation from free energy curves in Thermocalc
16.1.1 Laboratory Notebook
You should purchase a lab notebook, which can be used for 315, 316-1, 316-2 and 351-2 labs. A spiral notebook will do; it does not need to be the type containing carbon pages, or graph paper. I also recommend a notebook (three-ring or a folder) in which you can keep lab handouts. You will need to refer to these notes when writing your lab reports.
16.1.2 Part 1: Use of Thermocalc to Obtain Calculated Bi-Sn Phase Diagram
Thermocalc (TCW2) is found on the computers in Bodeen (Tech C115). To generate free energy plots to obtain the Bi-Sn phase diagram, follow these procedures:
- Open Thermo-Calc for Windows (TCW5)
- Click on the icon for a binary phase diagram (center of the top tab) – this opens the 'TCW Binary Phase Diagram' window.
- Within the new window, select Bi and Sn
- Choose Phase Diagram. This will display the binary phase diagram – note that you may redefine the axes. Choose weight percent Bi to be consistent with the experimental plot you will generate.
NOW – the question is – how was was this phase diagram generated, and how does it relate to the free energy curves? To understand this, follow the following steps:
- Click on G-curves
- Enter a temperature (in Kelvin); begin at a temperature above 573K
- Click on Apply. This will generate a series of free energy curves at that temperature. Note: you can normalize to 1 mole or 1 gram; to find wt% choose the latter.
Generate enough free energy curves to map out the BiSn phase diagram on the blank sheet. You are also provided with some hardcopies. Show your work on these - draw in how your determined compositions corresponding to transitions at any given temperature.
Write-up:
Include in your report the phase diagram generated from Thermocalc and free energy curves, marked and labeled appropriately to show how you used the free energy curves to determine the phase diagram.
16.1.3 Part 2: Experimental Determination of Bi-Sn Phase Diagram from Cooling Curves
Calibration:
We will be using type K thermocouples and data-logging devices to measure temperature as a function of time for Bi, Sn and a series of binary alloys of BiSn. The change in the rate of change in temperature as a function of time indicates changes in phases, as described by the Gibbs Phase Rule (also see http://www.doitpoms.ac.uk/tlplib/phase-diagrams/cooling.php) How accurate and precise is your measurement device? Think about how you might check this and anticipate that you will discuss this in your report.
Pure Components:
Start by measuring a cooling curve of either Bi or Sn. Plan to pool group data.
- Heat the crucible on a hotplate until the endpoint metal has melted. (This might not be obvious if there is an oxide on the surface. You can remove surface oxides by skimming the melt with a stirring rod.)
- Insert a (calibrated, but dry) thermocouple into the melt. Make sure the thermocouple is not shorted anywhere along its length.
- Turn off the power to the hotplate, and record temperature every 15 seconds as the melt cools and solidifies, down to 100°C or lower. Re-heat your sample, again measuring temperature vs. time to remove your thermocouple.
- Plot your data using Excel.
- Determine the solidification temperature and record this on the pooled data sheet.
- Save your Excel files with a logically formatted name as follows: metal_daytime_initials, i.e. Sn_Mon9_KS or 40Bi_Tues10_KS
Alloys:
Repeat the procedure, above, for an alloy. These are designated by wt% Bi. Determine the inflection points or changes in slope that correspond to phase transitions. Record these on the pooled data sheets.
Write-up:
1) Write a short paragraph describing the theory behind cooling curve measurements.
2) Write a second short paragraph describing what was measured and how and include some mention of measurement uncertainty.
3) Using a plotting program (Excel or Matlab…or other) plot your endpoint (Bi or Sn) and alloy cooling curves. Indicate what phases are present in what temperature ranges by labeling the two curves with phase and temperature information.
4) Use the tabulated data, as well as the posted raw data, to determine all phase transition temperatures that can be determined for alloys in the Bi-Sn system. Again, using a plotting program, plot these transition temperatures as a function of wt% Bismuth, to determine the phase diagram. You will need to decide which points form a set corresponding to the same phase transition, i.e. a given liquidus line, for instance. Add appropriate fit(s), label phases, label axes, etc.....in order to generate a neat, complete, self-explanatory phase diagram.
5) Write a paragraph discussing the results. Also discuss what assumptions were made and how your plot does/doesn't agree with theory and other experimentally-determined Bi-Sn phase diagrams. (Be especially aware of what assumptions you make in compositional ranges where no measurements were made.) You will find a calculated Bi-Sn plot at http://www.metallurgy.nist.gov/phase/solder/bisn.html. Note that the temperature and composition that correspond to the invariant reaction (that is the eutectic temperature and composition) are listed in a table below this figure.
Notes on graphing:
Please keep the following points in mind as you prepare your report:
- You are gathering discrete data points, hence plot the data as such. (In Excel, choose a scatter-plot, without additional lines.) When you fit the data (i.e. by adding a trendline) use a line. Always consider your options: which points should you include or not include when fitting a given line? Should you let the program find the best regressive fit? Or should you fix the slope? Is the fit linear? Non-linear? Can you use data to determine all the liquidus, solidus and solvus lines in the system? Are there any you cannot determine? (You could indicate an approximation as dashed lines.) The details should be discussed in paragraph II of your text.
- Represent data with the appropriate number of significant figures. If you are averaging 321 °C, 323 °C, 324 °C the average value is 323 °C. (Do not add false significance when computing an average value.) If there is uncertainty in determination of a transition temperature, it is OK to indicate this as a range. Likewise, if you have several data points for a single value, i.e. the melting temperatures of the endpoints, then you could plot all the points, or plot the average but indicate the range which was measured. Assuming a normal (Gaussian) distribution of these values, you can find the uncertainty of the mean to within a 95% confidence level by determining 2X the standard error of the mean: 2x the standard deviation (STDEV in Exel) divided by the square root of the number of points measured. Indicate these values on your plots by adding error bars: left click the data set and choose Format data series > Y error bars.
- Label axes appropriately AND label all phases present in different regimes.
16.1.4 Appendix: Metlab Safety Guidelines
THINK FIRST!
Be alert. Act cautiously. Don’t rush. Ask.
Use Proper Equipment
- Safety glasses or goggles are mandatory.
- Hoods should be used when handling chemicals. Use them properly. Use the sash for shielding; keep the sash open only the minimal amount.
- Gloves must be used when handling chemicals.
- Latex– OK for sample preparation, light etching (nital, methanol or ethanol). NOT OK for strong acids or anything containing HF.
- Nitrile gloves – more chemically resistant than latex. But thin gloves offer limited protection.
- Silver Shield gloves – recommended for HF.
- Heat resistant gloves should be used when handling hot samples or working with furnaces (room 2028).
- Tools – Use the right one for the job.
- Clothing – open-toed shoes and shorts do not provide adequate protection against spills. Dress appropriately (pants, closed-toe shoes) for lab.
Use Common Sense
- Do not eat in the laboratory.
- Use caution: hot items might not look hot; be careful what you touch; use PPE.
- Use proper techniques: properly mounted samples, wheels and pads will avoid finger/ hand injuries during grinding or polishing.
- Sharp blades should be moved in a direction away from body parts.
- Ask - check with the lab instructor or manager if you have questions.
Be Considerate
- Clean up incidental spills immediately to avoid further contamination. Dispose of cleaning materials properly – not in the general waste.
- Notify lab manager (or Research Safety) immediately about large spills.
- Dispose of chemicals properly. There are separate solvent, acid, base waste containers. There are also separate waste containers for HF based solns. & nital.
- Dispose of sharps properly. There are separate containers provided for broken glass and metal sharps.
- Do NOT dispose of chemicals down the drain.
- Do NOT leave unlabelled chemicals in the hood or elsewhere in the lab. Label containers with chemical names, quantities, date, your name.
- Do NOT track chemicals from etching hood to microscope (or elsewhere). Remove gloves before using scopes or other equipment outside the etching area.
- Do NOT add other solvents to the nital container (see below).
Metlab particulars
- Consult MSDS sheets, available on the reference table in 2008.
- DO NOT bring chemicals into the lab without discussing particulars with lab manager. You must provide an MSDS sheet with your proposed use.
- Nitric acid. Strong oxidizer. Do NOT mix with organics or solvents. The only exception to this is nital: 2% nitric acid in methanol. Do not exceed this concentration. Do not use another solvent. Dispose of separately from acid or solvent waste.
- HF consult lab manager prior to use. Latex gloves are not sufficient. Do not store in glass. Make sure calcium gluconate is available before use.
- Please notify the lab manager of any accidents, spills, equipment malfunctions.
Be aware of the following hazards, and use appropriate equipment and steps to avoid problems:
|
Activity
|
Location
|
Safety issues
|
Safety equipment provided
|
|---|
|
Heat treatment
|
2028
|
Burns (carelessness). Dust from refractory materials. Proper use of gas tanks on tube furnaces (see below).
|
Heat-resistant gloves, tongs, refractory bricks. Face shields.
|
|
Gas Cylinders (with furnaces)
|
2028
|
High pressure venting.
|
Dual stage regulators to be used on each tank when in use. Tank caps must in place for any transport. Tank belts must be used to secure tanks in lab.
|
|
Swaging
|
2028
|
Noise
|
Ear muffs
|
|
Sawing
|
2086
|
Disposal of residual scarf and cutting fluids/ coolants.
|
All saws in the lab are enclosed. Disposal containers are provided.
|
|
Mounting
|
2086
|
Noxious smell, acrylic irritant.
|
Use of hood for acrylic or epoxy mounting
|
|
Grinding/ polishing
|
2086
|
Spinning wheels. Clogged drains and overflow sometimes leads to wet floor. Concern about materials in drain. Eye protection for samples and debris off wheels.
|
Safety glasses. Mop Proper sample/wheel/pad mounting. Caution when using spinning/motorized equipment: keep hands free of wheels.
|
|
Polishing
|
2084
|
Same as grinding
|
Same as grinding
|
|
Chemical Etching
|
2084
|
Improper mixing of chemicals and solvents.
Spills.
Transport of chemicals outside of hood. (Remove gloves before using other equipment (microscopes, etc.) and before exiting lab.
|
Goggles and safety glasses, face shields. Rubber aprons. Gloves (rubber, latex, nitrile and silver shield). Labeled waste containers are provided in hood. Undergraduate students should ask for help mixing etchants. Calcium gluconate is provided. Cautions against mixing particular chemicals are highlighted. Additional reference material is provided in 2008. Spill trays are provided. Spill kits are supplied in lab.
|
16.2 Laboratory 2: Metallographic preparation and microstructural examination of Bi-Sn Alloys
Recall that we determined the phase diagram of Bi-Sn using cooling curves. In this lab we will examine microstructures of the alloys. Part of the learning objective is to become familiar with metallographic preparation procedures and use of the optical microscope, as well as correlating microstructure to the phase diagram. Read through all steps before starting.
16.2.1 Laboratory Procedure
- Put on safety glasses.
- Choose a sectioned sample of Bi-Sn; make sure each group (every subgroup of 2-3) in the lab section selects a different composition. Record the composition. Each of these samples contains saw-cut damage. Your objective is to reveal the true microstructure of the sample by removing this damage, as well as sequentially removing damage from the initial grinding steps.
- Gloves are located in the two drawers to the left of the hood in 2084. Set the side of the sample to be examined face down in a Sampl Kup (blue) mold. Measure two parts acrylic powder into a small paper cup. Add one part acrylic resin. Mix (or more appropriately, “fold” – to avoid mixing in too many air bubbles) the powder and liquid (it should have a consistency of honey or syrup), then pour the mixture over the sample in a Sampl Kup. Add a label to the back of your mount before the acrylic solidifies. A small piece of paper stuck just under the surface will suffice. Make sure you label your sample appropriately. Include the wt% Bi and your initials for later identification. The acrylic will harden in about 15 minutes.
- Round the sharp edge of the sample by rotating the edge on a piece of grit paper. This helps keep the samples from “grabbing” the paper or cloths on the autopolisher. Use the autopolisher to sequentially grind with SiC grit (~ 1-2 minutes for each size) , then polish diamond suspension. (Note that this is slightly modified from the recommended “universal” autopolishing sequence; the diamond suspensions tend to become embedded in the soft metals you are polishing, and the surfaces become gummy and discolored when using the normally-recommended 0.05 micron alumina final step. Also you can use lower force – 4 or 5 lbs – and shorter times than are recommended for harder materials.) It is critical that you wash and ultrasonically clean the samples between each polishing step (but not each grinding step) to avoid contaminating the polishing pad with larger sized grit or sample debris.
- Before looking at samples on the light microscope, make sure they are clean and DRY. Use ethanol as a final rinse, and then dry the samples under the hand dryer. Please be careful. Moisture or solvents will ruin the objective lenses. Set the samples face down on a piece of paper to make sure water does not seep from between the sample and mount. Microscope instructions are attached.
- Since this is your first chance to polish, you should record images at each step. Be prepared to document this process in your report, and include representative images.
- Etch (using the assigned etchant) to reveal microstructure. The etchant for this lab is 5% HCl in methanol, by volume – prepared by your TA or lab instructor. Make sure you are wearing your safety glasses and add gloves – rubber gloves or latex gloves are OK – before working with the etchant. The etchant should remain in the hood. (You should remain entirely outside the hood.) You are etching until you rinse the sample. Use tongs to dip the sample in the etchant for ~ 5 seconds; rinse; examine the surface by eye. It will become slightly cloudy as etching occurs.
- Record images that are representative of your sample, to be included in your lab report. Be sure to mark each micrograph with a micron bar.
- Share images of all the final polished, etched samples between all members of your lab group.
- Analyze the volume fraction of the different phases present using a point grid. Note: you could measure the relative amount of each phase or the relative amount of primary phase vs. eutectic (remember, the eutectic is a two-phase micro-constituent). Make a careful note of what you measured and why.
Write-up:
This (short memo-style) report will be a truncated version of a formal lab report. The intent is to document your sample preparation and relate the final microstructures to the phase diagram. Your report should include the following elements.
- Title, author
- Methods and Materials: Describe your samples and how you prepared them. Include images that show the progression of grinding, polishing, etching steps. Include details about grit size, diamond suspension size, loads, etchant and etching times. Label images as figure 1, etc. and include captions. Note that figure captions are placed below a figure. (The convention for tables is that the title is above the table.)
- Results & Discussion: (Begin this section with text.) Discuss the alloys that were prepared by your group. Show corresponding images. Include figure numbers and captions and label the phases present. Include a discussion of the volume fraction analysis and conversion to weight percent and how it agrees (or doesn’t) with the known composition of your alloy.
16.2.2 Appendix 1: Instructions for the Nikon Epiphot-TME Inverted Light Microscope
- Turning the microscope on and adjusting filters
- Light – the light is turned on using the thumbwheel knob marked On/Off on the lower-left side of the scope. Adjust the intensity so the light meter (on the lower right side of the scope) reads in the green range (~9). Check the lamp housing at the rear of the scope to make sure the light is on.
- Filters – The diffuser lever, just in front of the lamp housing, on the left side of the scope, should be up (the “in” position). If the incident light intensity is too bright, it may be decreased by rotating a neutral density filter into place. These are located on the first turnwheel in front of the lamp housing. If there is reason to use a known source wavelength (468nm) the green filter (GIF) on the second turnwheel may be rotated into place.
- Diaphragms/ Apertures – There are two aperture controls located on the left side of the scope. The aperture diaphragm, located closer to the lamp housing, should be positioned between 10 and 11 o’clock. If this diaphragm is too far closed, the light is coming through a pinhole, and resolution of the image will be limited. Conversely, if it is too open (lever at 6 o’clock) there will be too much stray light, and sample contrast will be decreased. The field diaphragm focuses on the sample surface, should be adjusted so the outline of this aperture is just outside the field of view.
- Polarizer and analyzer – These are located on the right hand side of the scope, just below the nosepiece containing the objective lenses. They may be pulled out, to the right, or in place the polarizer may be rotated. This will affect light intensity.
- Beam-splitters – The knob just above the Analyzer should always be pushed in (B for Brightfield); there is no dark-field attachment for this scope. The beam-splitters below the polarizer should be out, so the image is also focused on the digital camera.
- Putting a sample in place and obtaining an image
- Rotate the objective nosepiece to start with the lowest power magnification. This is the 5X objective. (Note this is not the overall magnification. For viewing from the eyepieces, the magnification would be (5 x 15) X, etc.)
- Place the sample face-down over the objective. Use glass slides for support, if necessary. You can check where the light is hitting the sample by looking up from below. Move the sample using the x-y controls on the stage.
- Focus the image by rotating the concentric coarse and/or fine focus knobs, either on the right or left of the scope.
- Increase the magnification by rotating the objective nosepiece counter-clockwise:5x (red), 10X (yellow), 20X (green), 40X (blue), 100X (white). Be careful to avoid bumping the sample. Note that the working distance for the 40X and 100X objectives is less that the thickness of a microscope slide (1mm) so any slides supporting the sample must be farther apart than the width of these objective housings.
- Capturing a digital image
- Turn on the camera power supply. (Red button.)
- Open the Spot Advanced program on the computer (MSE profile; see the underside of the keyboard for the password.)
- Open LiveImage to see a “realtime” image (usually in grayscale) that can be used for focusing.
- Click the camera icon on the right-hand menu bar to capture a digital image.
- Add a micron bar to the image using “Add calibration” from the Edit pulldown menu. Make sure the correct objective lens is selected in this window. Click on the image to see the micron bar. You may edit size, font, color, position, etc. Stamp to write it into the image. (Be careful here; this process will re-write the existing pixels.)
- You may create a temporary folder on the Nikon: (D:) users drive, and save images there.
16.2.3 Appendix 2: Using Stereology to Measure Volume Fraction
(for more details, see ASTM E562-83)
Often, when viewing cross-section of metallography (or ceramic, etc) samples under a microscope, it is desirable to make quantitative measurements of such values as the grain size and volume fractions, , of particular phases. Volume fractions are easily obtained using point-counting techniques. In this case, a test grid is superimposed upon the image of the sample and the number of points, , falling within the microstructural constituent of interest is counted. This, divided by the total number of points in the grid, , provide an estimate of the volume fraction of the constituent of interest. The volume fraction of phase alpha is given by:
Size of grid/ Number of Measurements:
The size of the test grid is typically 4x4 or 5x5 points. In order to lower the uncertainty in the measurements, one should count approximately 100 points on the constituent of interest. In other words, we want to be at least 100. This is achieved by overlaying the grid many times, on different areas of the sample. Often, an eyepiece reticle is used to facilitate this counting.
Magnification:
The magnification should be high enough to avoid adjacent grid points falling on the same microconstituent feature. Choose a magnification giving an average constituent size of half the grid spacing.
Counting:
Count and record the number of points on the microconstituent in each application of the grid. Count points falling on a boundary between constituents as ½.
Measurement Uncertainty:
You can easily determine the standard deviation, standard error of the mean and confidence levels by tabulating all the values measured. In theory, the value of the coefficient of variation (the standard deviation / mean) is:
Comparison to mass fraction:
Note that the volume fraction and mass fraction are not equivalent, but one may convert from one to the other using the densities of the respective phases (see Callister, chapter 9). For a two phase system consisting of and phases, the weight fraction of alpha () is given related to the volume fractions ( and ) and densities ( and ) by the following expression:
16.3 Laboratory 3: Diffusion of Carbon in to 1018 Steel Using Pack-Carburization
16.3.1 Introduction
Samples of 1018 steel were packed in a mixture of 85wt% activated charcoal and 15wt% calcium carbonate in steel bags. Samples were subsequently pack-carburized for three times at three temperatures (915°C, 940°C and 960°C). Each lab group will examine three samples from a single carburization temperature.
16.3.2 Laboratory Procedure
Part I:
Mount the samples in thermo-setting resin and label. Grind (320, 400, 600, 800 girt SiC) then polish with 3µ and 1µ diamond suspension on a microcloth pad. Briefly (1-3 seconds) etch with nital (2% nitric acid in methanol). You might swab the etchant on the surface with a cotton-tipped swab. Rinse with water, then with solvent; dry. Examine the microstructure across the sample. Gather images that you can relate to the change in composition from center-to-edge of the samples.
Part II:
Measure a hardness profile from edge toward the center of the sample. (Note that this might work best on an unetched sample. If you have already etched, return to the 1 micron diamond wheel to remove the etched layer from the surface.) Use the Struers semi-automated microhardness tester to measure Vickers hardness from the carburized surface toward the center of the specimen in increments of ~50-100 microns for the first ~2 mm, then ~200 microns until the values clearly plateau. Use the 10X objective to focus; use the 40X objective to measure the indent. Rotating between objectives and indenter is best done using the automated program (Duramin5). To avoid interference between indentations, spacing should be about 3x the indent size – but zig-zagging is allowed. You want to obtain 10-20 points to define your hardness profile. In addition, you should measure ~ 10 points near the center (undiffused region of the sample) to determine what uncertainty is associated with the measurement on these samples, independent of the change in hardness.
16.3.3 Write-Up
Your results will include micrographs with appropriate captions that describe the effect of carburization on the steel microstructure. You will need images from both the center and the edge of your sample(s). Label phases/ microconstituents, add micron bars, etc. on these. Estimate the carbon content at the surface, and explain your rationale.
Your results will also include experimental hardness profiles along with a fit from which you estimate the diffusivity of carbon in steel. The experimental data should be represented as points; the fit should be represented as a smooth curve. (Note that this curve will NOT be a polynomial; you know the functionality based on the solutions to planar diffusion -see in-lab handout from week 1 of this lab. USE THESE, NOT a polynomial, which will give a very poor fit. ERF and ERFC functions are available in Excel and Matlab.
Use the DICTRA solutions (in-lab handout week 2 of this lab) as a starting point to determine D and also for comparison. Also include values of D based on other sources (Porter & Easterling, Callister, etc.). Show the comparison graphically.
Include answers to these questions:
- What equations (solutions to the diffusion equations) describe diffusion from a plane source, i.e. carburization?
- Re-write these equations to describe the change in hardness. What assumptions are made in our experiment?
- Briefly describe the following hardness measurements:
- Rockwell
- Vickers
- Knoop
- What are the units for Vickers and Knoop testing? Assuming a ductile material, hardness 3 x yield strength. What units will you use for the comparison between hardness and yield strength? Explain the conversion.
- In the lab write-up you will compare your experimental results (data POINTS) to the Dictra prediction (FIT; represented by a line – but based on your answers above, not a linear fit). You should also compare to other sources from the literature – e.g. see Porter and Easterling Chapter 2. Here, write down comparisons.
16.3.4 Appendix: Instructions for the Microhardness Measurements
- Turn on microhardness tester (rear) and restart computer.
- Insert specimen into holder.
VERY IMPORTANT: THE SAMPLE MUST BE FLUSH WITH THE TOP OF THE HOLDER. Note that the tip clearance is very small. IF the sample is at all recessed, when you focus you will be below the tip clearance level. If the tip runs into the sample holder this is a VERY COSTLY and TIME-CONSUMING repair. (The equipment must be shipped back to Struers for repair.)
- Inspect with 10X objective to focus and find the test area. Also, focus the eyepeice. Set the load to 300gm. (Note on load selection – you want a large enough indent to measure accurately; but use a load that does not cause excessive damage to your sample, such as deformation or cracking at the indent tips.)
- Vickers is chosen, and the processor load is set to 300gm; objective to 40X.
- Select “indent.” Do NOT move the indentor with the start button illuminated. Note that for a Vickers test the indent should be an equiaxed pyramid.
- Change to the 40X objective.
- You may use (or over-ride as necessary) the Automeasure feature.
- Make sure you record both hardness and distance from the edge of the sample.
NOTE: Use the Struers semi-automated microhardness tester to measure Vickers hardness from the carburized surface toward the center of the specimen in increments of 50-100 microns for the first 2 mm, then 200 microns until the values clearly plateau. Use the 10X objective to focus; use the 40X objective to measure the indent. Rotating between objectives and indenter is best done using the automated program (Duramin5). To avoid interference between indentations, spacing should be about 3x the indent size – but zig-zagging is allowed. You want to obtain 10-20 points to define your hardness profile. In addition, you should measure ~ 10 points near the center (undiffused region of the sample) to determine what uncertainty is associated with the measurement on these samples, independent of the change in hardness.
Appendix: Determining Diffusivities from DICTRA curves
The DICTRA program has been used to generate three diffusion curves for each of three temperatures, assuming a surface carbon concentration of 1wt%C. Your job is to back-calculate the diffusivity expression, D(T), used to determine the diffusivity. You will then be able to compare that to your experimental data.
- Write the expression for the diffusion profile in this case – e.g. .
- Choose a ) value at which you can (easily) solve the equation above.
- Determine the x values for each time (in seconds) for that value of . You will have three sets of values for each temperature. Solve for at that temperature, graphically. (Figure out what to plot so you might fit a linear trendline to the appropriate data in order to determine .)
- Now you have one value of for each of three temperatures. Solve graphically using an appropriate expression to obtain a general expression of at any temperature.
References
1Abramowitz, Milton and Stegun, Irene A., eds., Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables 0009-Revised edition (New York: Dover Publications, 1965).
2Bauerle, James Edward and Koehler, J. S., "Quenched-in Lattice Defects in Gold", Physical Review 107, 6 (1957), pp. 1493.
3Brown, A. M. and Ashby, M. F., "Correlations for Diffusion Constants", Acta Metallurgica 28, 8 (1980), pp. 1085--1101.
4Huntington, H. B., Shirn, G. A., and Wajda, E. S., "Calculation of the Entropies of Lattice Defects", Phys. Rev. 99, 4 (1955), pp. 1085--1091.
5Johnson, Carl E. and Hathaway, Ellen J., "Solid-Liquid Phase Equilibria for the Ternary Systems Li(F,Cl,I) and Na(F,Cl,I)", J. Electrochem. Soc. 118, 4 (1971), pp. 631--634.
6Johnson, E.W. and Hill, M.L., "The Diffusivity of Hydrogen in Alpha Iron", Trans. AIME 218, 6 (1960), pp. 1104--1112.
7Masing, G. and Rogers, Bruce A., Ternary Systems; Introduction to the Theory of Three Component Systems (New York: Reinhold publishing corporation, 1944).
8Metallos, "Ellingham Diagram Giving the Free Energy of Formation of Metal Oxides and the Corresponding Oxygen Partial Pressure at Equilibrium. Labels in Greek." (2007).
9Pelton, A. D. and Thompson, W. T., "Phase Diagrams", Progress in Solid State Chemistry 10, Part 3 (1975), pp. 119--155.
10Simmons, R. O. and Balluffi, R. W., "Measurements of Equilibrium Vacancy Concentrations in Aluminum", Phys. Rev. 117, 1 (1960), pp. 52--61.
11Wert, C. A., "Diffusion Coefficient of C in $\alpha$-Iron", Physical Review 79, 4 (1950), pp. 601.
12Wert, C. A., "Measurements on the Diffusion of Interstitial Atoms in B.C.C. Lattices", Journal of Applied Physics 21, 11 (1950), pp. 1196.
Index
- Activity coefficient: 1
- Alkemade Theorem: 1
- degrees of freedom: 1, 2
- Ellingham diagram: 1
- First law of thermodynamics: 1
- Gibbs phase rule: 1
- Gibbs-Duhem equation: 1
- Henry's Law: 1
- ionic conductivity: 1
- regular solution model: 1
- Saddle-point: 1
- Steady state diffusion: 1
- Ternary Lever Rule: 1
- Ternary Phase Diagrams!Isothermal Sections: 1
- tie line