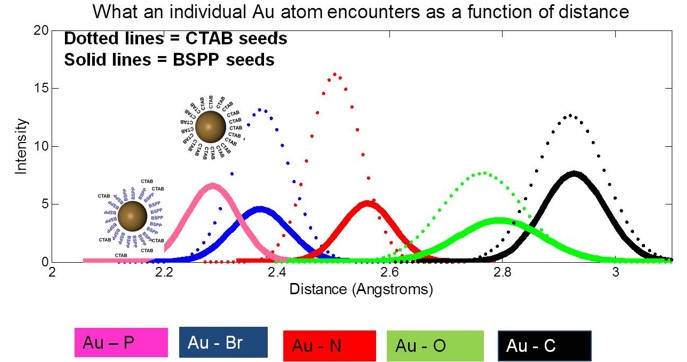
361: Crystallography and Diffraction
Michael BedzykDepartment of Materials Science and EngineeringNorthwestern University
1 Catalog Description
Elementary crystallography. Basic diffraction theory; reciprocal space. Applications to structure analysis, preferred orientation. Point and 2D Detector techniques. Lectures, laboratory. Prerequisites: GEN ENG 205 4; PHYSICS 135 2,3. Mathematics including Calculus 1-3 and Linear Algebra will be required.
2 Course Outcomes
3 361: Crystallography and Diffraction
At the conclusion of the course students will be able to:
- Identify different types of crystal structures and symmetry elements such as space groups, point symmetry and glide planes that occur in metals, ceramics, and polymers.
- Perform standard x-ray diffraction measurements on metals, ceramics and polymers and quantitatively determine lattice constants, grain size, texture, and strain in bulk crystals and epitaxial films.
- Describe the basic particle and wave physical processes underlying x-ray emission, elastic and inelastic scattering, absorption, and interference of coherent waves.
- Identify symmetry elements in (point, translation) in 2D and 3D patterns and crystals.
- Describe basic principles underlying synchrotron x-ray sources, x-ray fluorescence spectroscopy, and electron and neutron diffraction.
- Use reciprocal space graphical constructions and vector algebra to interpret diffraction from 3D and 2D single crystals, and random and textured polycrystalline samples.
4 Symmetry of Crystals
A
crystal
can be defined as a solid which is composed of an atomic array that is periodic in three dimensions. Crystal systems may exhibit various kinds of
symmetry
, or types of repetitiveness. The specific type of symmetry is determined by a number of operations, which when performed on the crystal, bring it into self-coincidence. In other words, a crystal will be symmetric with regard to a certain operation, if it is impossible to distinguish the crystal before or after said operation.
4.1 Types of Symmetry
Symmetry elements can be of the following types:
- Rotational axis
- Mirror plane
- Inversion center
- Translation symmetry
(or a combination of these):
- Rotoinversion axis
- Glide plane
- Screw axis
4.1.1 Mirror Planes and Chirality
Probably the most familar form of symmetry from daily life is reflection symmetry. We refer to some object as being symmetric with respect to reflection if putting a mirror crossing through the object would result in no apparrent change to the object (we call this lack of change self coincidence). The lines (or planes in 3D) on which these hypothetical mirrors could be placed are appropriately called mirror planes. Observe Figure
4.1, noticing that the image could be replicated by holding half of it up to an appropriately placed mirror. In a sense, symmetry thus allows us to define structures or patterns in terms of unique, fundamental units. Mirror planes will typically be denoted in figures by bolded lines. It is also worth noting that the two shapes in Figure
4.1 have an opposite handedness, or chirality. The points of the two objects proceed outward in either a clockwise or counterclockwise manner; as a result, the object on the right can be identified as distinct from the one on the left. Thus, we see that a reflection changes the chirality of an object. We encounter this phenomenon in daily life; it is possible to tell a person's right hand from their left because of the arrangement of their fingers, but an image of a left hand reflected from a mirror will have the same arrangement as that of a right hand (similar conclusions follow for the reflection of the right hand).
4.1.2 Proper Rotation Axes
A rotational axis refers to some line which can be utilized as the center of some specific rotation that will leave the system (such as a pattern or crystal) seemingly unchanged (invariant). Rotational axes can occur in both three dimensions, or two dimensions, with the “line” being represented as a point in the latter case, indicating lines perpendicular to the plane of view. The plane object pictured in Figure
4.2 demonstrates rotational symmetry, as a 120
turn about its center brings it into self coincidence. In addition, the object has three mirror planes, and the object's reflection across these planes also brings it into self coincidence.
Figure
4.3 shows the types of proper rotation axes that we're concerned with, as well as the symbols which will be used to represent each type. Referring back to Figure
4.2, the object pictured has 3-fold rotational symmetry about an axis directed out of the page, as a
or
rotation allows for self coincidence. In other words, an object has
-fold symmetry about an axis if a
rotation about that axis brings it into self coincidence. All objects exhibit 1-fold symmetry, or are brought into self coincidence by a full
turn. This case is trivial (hence why there is no associated symbol) but important nonetheless.
You may notice that other types of rotational axes (i.e. 5, 7 or greater) are not provided; This is due to the fact that such rotational axes are incompatable with translation symmetry (which will be discussed in Section
4.3). In brief, this simply refers to the fact that objects with, for example, 5-fold symmetry cannot be translated in a way that fills all of space. For instance, Figure
4.4 demonstrates that pentagons cannot be used to fill space without gaps (this also known as tiling).
4.1.3 Inversion Centers
An object is said to contain an inversion center if there is some point (the center) in which identical elements would be encountered when preceding forward or backwards (with the point as the origin) along any line passing through the point. An example of inversion center symmetry is pictured in Figure
4.5. When a line is drawn through the center of this plane object, corresponding points of the object are equidistant from the center line. It will come into coincidence with itself if all points on the object are inverted through the inversion center which is also on this center line. You will note that this object also exhibits rotational symmetry, as a 180
turn about its center brings it into self coincidence. The nature of the inversion operation depends on dimensionality of the system. In 2D, inversion is identical to 2-fold rotation, and preserves the chirality of objects, while in 3D, inversion is distinct from other symmetries and inverts the chirality of objects. Open circles are commonly used to denote an inversion center in figures.
4.1.4 Improper Rotation Axes
An
improper rotation axis
, also known as a rotoinversion axis, is an example of a compound symmetry operation, with it being a combination of a rotational axis and an inversion center. Note that for a system containing such hybrid operations, it is not necessarily the case that the two component symmetries are present individually; rather, it is the seqential application of both of them that results in self-coincidence. This operation is only well-defined in 3D, due to the redundancy of inversion with rotation in 2D. Since this operation is a combination of one that inverts chirality of objects (inversion) and one that preserves chirality (rotation), this operation will invert the chirality of components.
Figure
4.3 shows the symbols utilized to denote rotoinversion axes in images. Note that the 1-fold rotoinversion operation (
) is denoted by an open circle, as it is exactly equivalent to the inversion operation (given that 1-fold rotation is equivalent to not changing the structure at all). In order to help visualize these operations, observe Figure
4.6, which is adapted from Vainhstein's
Modern Crystallography Vol I. The arrangements depicted consist of perfectly asymmetrical, three dimensional, chiral objects related by both proper and improper rotational axes. Note the nature of the 3D inversion operation demonstrated by the
example, and that the
operation is equivalent to a mirror plane perpendicular to the axis of rotoinversion.
4.2 Projections of Symmetry Elements and Point Groups
There are simpler ways of representing symmetry operations, namely through a system of
stereographic projections. The top half of Figure
4.7 depicts a view of a body with its symmetry axis pointing out of the page and the circle representing its perimeter. The symbol in the center indicates the 2-fold rotation symmetry operation, and the two solid circles depict the
rotation of the body. The darkened circle in the
symmetry operation projection represents a mirror plane.
4.2.1 Arrangement of symmetry equivalent objects as an effect of a rotoinversion axis
The following steps breakdown the
operations used to generate the object in Figure
4.9:
- Start at
- Rotate 120º
- Invert to arrive at
- Rotate 120º
- Invert to arrive at ,
- Continue until you return to
- 's and 's mark all symmetry-equivalent positions (see Fig. 4.6).
Certain symmetry elements can be combined to form new patterns, such as the product of a 2-fold and inversion center shown in
4.10. This produces a 2-fold rotation axis which is perpendicular to a mirror plane as indicated by the darkened circle around the object.
Just like an algebraic operation, if A is one symmetry operation and B is another, they may be grouped through some operator to produce a third symmetry element, or C.
For the
symmetry operation shown in
4.11, the mirror plane lies parallel to the rotation axis. There is also a third mirror plane that arises from this combination, as shown by the second line drawn through the center of the dashed circle.
Figure
4.12 illustrates an object with symmetry that combines two rotation axes, or a 3-fold rotation axis perpendicular to a 2-fold rotation axis. Note that it does not matter whether the 3-fold or 2-fold operation is performed first, but the 3 2 point group symmetry is not equivalent to the 2 3 symmetry.
4.2.2 Quartz Crystal
Note the point symmetry of a quartz crystal, as pictured in the figure below.
The perfect shape (or habit) is brought into self coincidence by (or is invariant to) the following symmetry operations:
Note that successive symmetry operations also bring the object into self coincidence.
Note that and are the inverse of each other and that , and are their own inverse operation. For instance, if you perform the operation followed by the operation, the object is at its starting position.
This is the 3 2 or D point symmetry group.
4.2.3 Group Theory Axioms
- A group G consists of an operator “multiplication” and a set of elements , such that the group is closed under “multiplication.”
- Multiplication is associative:
- There exists an identity element such that
- For any there is an inverse such that
The completion of the following table is left as an exercise for the reader.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Table 1: Multiplication of symmetry elements within the 3 2 point group
The following demonstrates the multiplication for the 3 2 point symmetry group:
Note that the Cyclic group under modulo-3 addition is directly analogous to the 3-fold rotation axes point group.
There are only 32 point groups that can be generated by combinations of the 1,2,3,4,6,
,m,
symmetry operators, whose stereographic projections are shown in Figure
4.14. Furthermore, every crystal has a set of symmetry elements that is one of these 32 point groups or
Crystal Classes. A crystal's highest degree of symmetry is used to describe its structure. Crystal classes are further separated into
Crystal Systems based on minimal symmetry requirements. (See Hammond Table 3.1, Azaroff Table 1-2)
|
Crystal system
|
Minimal symmetry†
|
Crystal classes
|
|
Triclinic
|
1(or )
|
|
|
Monoclinic
|
One 2 (or )
|
|
|
Orthorhombic
|
Three 2's (or )
|
|
|
Tetragonal
|
One 4 (or )
|
|
|
Cubic(isometric)
|
Four 3's (or )
|
|
|
Hexagonal
|
One 3 or 6 (or or )
|
|
† The symmetry elements shown in this column are the least symmetry that a crystal can have and still belong to the corresponding crystal system. In this sense, this column shows the diagnostic symmetry elements of each system.
Table 2: Azaroff Table 1-2; Crystal systems and crystal classes
Note that different crystal habits can have the same symmetry, as shown in Figure
4.16.
4.2.4 The 5 Point Groups belonging to a Cubic Crystal System
Note that a cubic crystal does not necessarily have 4-fold axes. (See Vainshtein “Modern Cryst.” Vol 1 Fig 2.45-2.47)
Note the symmetry of the octahedron in Figure
4.19 with vertices at midpoints of square faces of cube.
A regular octahedron has
point group symmetry, also known as
. Figure
4.20 shows the projection of the octahedron on the [111] plane, with a
improper rotation axis.
4.3 Translational Symmetry
The object in Figure
4.22 demonstrates translation center symmetry or a repetitiveness in space. This figure may be interpreted as a flat representation of a diatomic molecule, which is being translated in equal steps both to the right and to the left.
5 Crystal Lattices
5.1 Indexing within a crystal lattice
The unit cell of a crystal may be described by the following three parameters:
Crystal axes: a, b, c
Length: a, b, c
Angles:
Crystal axes, illustrated in Figure
5.1, share an origin at one corner of the unit cell. The angle between these axes, or
and
, are based on the symmetry of the crystal. For instance, only the cubic crystal system has
The c-axis usually points to the highest symmetry element. Finally, the lengths of the axes are determined by the natural repeat lengths of the unit cell and based on the crystal habit.
The crystal axes may be used to specify planes within the crystal lattice structure using
Miller indices. The following procedure is used to determine the Miller indices of a plane.
- Determine the plane's intercepts with the crystal axes
- Take reciprocals of the intercepts
- Remove common factors
- Put in ( ), no commas
All parallel planes have the same (hkl) Miller Indices. If a plane crosses through the origin, as shown in the left axes in Figure
5.2, it can be translated to determine its intercepts. By convention, a bar over the number is used to indicate a negative index.
a, b ,c Intercepts: ,
Reciprocals: 0, -4, 5
Miller Indices: (0 5)
Determine the hkl indices of the plane shown in the figure below:
Note: Faces of cube are of the same ((hkl)) form ((100))
5.1.1 Hexagonal Prism
Indices of hexagonal prism faces are not of the same (hkl) form. Instead, a new index
is introduced to identify planes, in which
or
. Thus, there are only three independent indices. The four-index (
)
Bravais-Miller
system more easily defines planes within a hexagonally structured crystal. Figure
5.4 shows indexing within a hexagonal structure using the three Miller indices, whereas Figure
5.5 uses the
axes in the Bravais-Miller scheme.
By using the Bravais-Miller scheme, the symmetry equivalent faces are all of the same form (1100).
5.1.2 Form
Planes (or faces) of a
form are related by crystal symmetry and generally have the same spacing but different indices. For instance, the six square faces of a cube (100), (010), (001),(
and
, are of the form ((100)) or
These planes are all related by the 4-fold rotation axes perpendicular to the cube faces. Note that a form is indicated by the indices of one plane enclosed in braces, or {hkl}.
Example: Octahedron
Faces are of the {111} plane form
What Crystal System?
5.1.3 Direction Indices
Direction indices define a direction with respect to the unit cell axes - a, b and c.
5.8 demonstrates direction indices with respect to unit cell axes.
5.1.4 Zone
Planes of a
zone intersect at a line [uvw] known as a
zone axis, to which they are all parallel. All (hkl) planes that contain this line belong to the same zone.
For instance:
- Let be the normal vector for the plane (hkl).
- Then if hkl plane belongs to [uvw] zone
- For cubic unit cell
- [010] is the zone axis for (001), (100), (102), (10) planes
5.2 Lattices
A
crystal lattice is a periodic array of objects, i.e. 7's, atoms, molecules ions. Each object has identical surroundings. Periodicity is generated by translation symmetry operators
.
The entire infinite array of objects can be described by giving the structure within the unit cell and by giving .
|
1-D
|
|
|
|
2-D
|
|
|
|
3-D
|
|
|
Table 3: Translation symmetry operations
Lattice points are an imaginary set of periodic points which make up the vertices of a unit cell and are translated to make an array pertaining to crystal's structure. Each lattice point has identical surroundings.
2-D Plane Lattice
3-D Space Lattice
There are five possible plane lattices, or ways to arrange points in two dimensions such that each has identical surroundings. The five plane lattices, shown in Figure
5.11, include the oblique
p-lattice, rectangular
p-lattice, rectangular
c-lattice, square
p-lattice, and hexagonal
p-lattice.
|
Azaroff
|
International Tables
|
|
Parallelogram
|
Oblique p
|
|
Rectangular
|
Rectangular P
|
|
Diamond
|
Rectangular C
|
|
Triangular
|
Hexagonal P
|
|
Square
|
Square P
|
Table 4: Two-dimensional lattices
The five types of plane lattices are grouped into
four axial systems.
|
Axial System
|
Min. Sym.
|
|
|
|
Oblique
|
1
|
|
|
|
Rectangular
|
m
|
|
|
|
Hexagonal
|
3
|
|
|
|
Square
|
4
|
|
|
Table 5: Four axial systems for 2D lattices along with their minimal symmetry requirements and lattice vector conditions.
Note: Only 1,2,3,4,6 are consistent with translation symmetry.
5.2.1 Unit cell
A
unit cell is defined as a small region of space chosen to represent a lattice. For 2D lattices, it is defined by cell edges
a, b. Translation of cell by
a, b generates lattice.
A
primitive unit cell has one lattice point per cell and uses the smallest possible area to represent the lattice. A
non-primitive unit cell, such as the rectangular-c unit cell in two dimensions, contains more than one lattice points within the unit cell and is conventionally and conveniently chosen to emphasize the symmetry of the lattice.
5.2.2 Plane Groups
Two dimensional point symmetry is combined with two dimensional translation symmetry to create a
plane group, as shown in Figure
5.14.
There are 17 such
plane groups from which any two dimensional periodic pattern may be classified. The shorthand names of these plane groups, as shown in Figure
5.15 below, are generated by the following scheme: the “1” represents 1-fold symmetry, the integers indicate the type of rotational symmetry, the
” indicates the presence of a mirror plane, and the “g” stands for glide symmetry.
Glide symmetry is a hybrid symmetry, resulting from the combination of a mirror reflection and a translation along the mirror line direction. The first image in Figure
5.16 demonstrates a familiar mirror plane symmetry, with R's reflected across the solid lines, while the second image shows reflection with one R translated half a lattice spacing down. The dashed lines in the second image indicate a special type of symmetry known as a reflection glide or a glide line of symmetry. The glide lines give this pattern a translational form of symmetry along the lattice rather than a simple reflection. In crystal structures, this shift in glide symmetry would only be observable in an electron microscope which allowing for sight of distances of the order of 0.5–2 Å (50–200 pm). Lastly, note that 3-fold symmetry axes do not exist in oblique, rectangular or square lattices.
5.2.3 Space Lattices or Bravais Lattices
Points in 3-D space can be arranged such that each has identical surroundings in 14 ways. These are divided into
7 Crystal Systems.
|
Crystal System
|
Lattice Types
|
|
|
|
Triclinic
|
P
|
|
|
|
Monoclinic
|
P,C
|
|
|
|
Orthorhombic
|
P,I,F,C
|
|
|
|
Tetragonal
|
P,I
|
|
|
|
Trigonal
|
P,R
|
|
|
|
Hexagonal
|
P
|
|
|
|
Cubic
|
P,I,F
|
|
|
P: Primitive (1/cell) I:Body Centered (2/cell) C: Base Centered (2/cell)
F: Face Centered (4/cell) Rhombohedral pattern in Hex. Cell (3/cell)
Table 6: 7 Crystal Systems
5.2.4 Positions Within the Unit Cell
The origin of a unit cell is arbitrary. By convention, it is chosen to be at the highest symmetry point. The position of any point in the cell is given by fractional translations along
, written with no parentheses. Table
7 notes the positions of lattice points using this scheme.
Translation to an identical point is achieved by the following: , where n is an integer.
|
Body Centered
|
I
|
000;
|
|
C-Centered
|
C
|
000;
|
|
Face Centered 000+fct
|
F
|
000; ;; 0
|
Table 7: Lattice Point locations for non-primitive unit cells
5.2.5 Hexagonal Close Packed Structure HCP
Note that he HCP structure for Zn has two atoms per hexagonal-P unit cell ( or two atoms per lattice point). The 000 and points do not have equivalent surroundings and therefore do not qualify as lattice points.
5.2.6 Rhombohedral (Hexagonal)
For a Rhombohedral Primitive Cell:
- 1 lattice point per unit cell at 000
For a Hexagonal R Non-Primitive Unit Cell:
- 3 lattice points per unit cell at 000, ,
Counting Lattice Points: 1 corner point per unit cell at 000, since 8 corners shared with 8 cells.
6 Stereographic Projections
Recall the regular octahedron illustrated in Figure
6.1 exhibiting various types of symmetry.
How did we position these Symmetry Rotation Axes and Mirror Planes in this 2D projection?
Stereographic projections are a two-dimensional form of representing three-dimensional crystal structure. Namely, these are graphic representation of the orientation of planes. Stereographic projections allow for an easy visualization of crystallographic features. Looking at Figure
6.3, the normal to the (hkl) plane of the unit cell at the center of the sphere, (
), intersects the reference sphere at the hkl pole.
Consider that all hkl planes pass through the center of the reference sphere.
A plane can be represented by a trace made by the plane through the reference sphere.
Traces for planes passing through the center of reference sphere are
Great Circles, or Longitudinal Lines (or Meridians).
Traces for planes perpendicular to diameter of reference sphere, but not passing through center are Small Circles or Latitudes (except those at the equator).
Rather than measuring angles between planes on the surface of the sphere, we employ an equi-angular stereographic projection.
Note: geographers use equal area projection.
Angle between two planes in Fig. 6.4 can be measured as being
=Angle between their traces along Great Circles (Angle-True)
=Angle between their Normal's
=Angle along Great Circle connecting their Poles
The plane of the crystal being described is located at the center of the reference sphere, labeled “C” in Figure
6.5. The following terms describe useful parameters to define in the stereographic projection method:
6.1
Projection plane
Placed normal to the end of any chosen diameter. See point “A” in Figure
6.5.
6.2
Point of projection
Other end of chosen diameter. “B”
Note the projections of the Great Circles.
6.2.1 Basic Circle
N' E' S' W' = Projection of Great Circle N E S W from plane N E S W with normal A B.
Steps for representing the angle for a plane C on a projection:
- Plane C Normal CP
- Normal CP Pole P
- Pole P Stereographic Projection P'
6.2.2 Wulff Net
A Wulff Net is used to make angle measurements between planes using their surface normals that produce poles on the reference sphere (
. Starting from the center of the Wulff Net and moving laterally outward, the angles increase from
to
Angles between poles are measured along great circles (longitude lines, basic circle, or equator). The horizontal arcs are
projections of
small circles.
To find the angle between two planes, rotate the projection around until both poles lie on the same great circles, as shown in Figure
6.6.
6.2.3 Standard Projections in a Cubic System
Figure
6.7 below illustrates
and
stereographic projections of cubic system poles for low indexed
planes..
As shown in figure above, the [uvw] zone has (hkl) planes whose normals are perpendicular to These normals lie in a plane whose intersection with the reference sphere forms a trace.
Note: See C&S Table 2-4 for listing of cubic inter-planar angles.
6.3 Representing Atomic Planes with Vectors
When representing a set of periodic planes within a crystal with a vector, its direction is perpendicular to the (hkl) plane. An example for a cubic system is shown in Figure
6.9. The magnitude of this vector is the interplanar spacing, or
d-spacing,
d-spacing (
, given by the following expression:
Examples for (110) and (220) planes are:
Define vector ,to represent cubic (hkl) planes:
planes
Direction:
Unfortunately, this scheme only works for cubic.
Try orthorhombic,
For the orthorhombic case, the [110] vector is not perpendicular to the (110) planes, therefore the above definition of vector
does not work in this case for defining the periodic
planes. We need a vector scheme that works for all axial systems, not just cubic. This can be achieved by using the
reciprocal lattice concept.
6.4 Concept of Reciprocal Lattice
Any (hkl) set of diffraction planes will be represented by a point whose coordinate is hkl, such that:
- The vector which starts at the origin and ends at hkl is normal to the planes.
- The distance from the origin to where is the inter-planar spacing
Consider a monoclinic crystal with and
Show reciprocal lattice points 000,100, and 010 in relation to direct space axes a and b.
Construct a hk0 reciprocal lattice corresponding to the (hkl) planes belonging to the [001] zone.
Note: plane
The
reciprocal lattice is a vector representation of direction of planes and their
inter-planar spacing. It is important for understanding the geometry of diffraction patterns.
Consider a primitive lattice in direct space, whose unit cell is defined by
.
The reciprocal axes,
, are illustrated in Figure
6.15.
The following equations define the reciprocal axes:
Note:
- plane plane plane
- = Volume of unit cell
- , , Reciprocal Relationship
Special Case:
For (i.e. all but triclinic or rhombohedral)
∥
For Cartesian axial system
(Cubic, tetragonal, orthorhombic)
∥ ∥ , ∥
And...
, ,
...hence “reciprocal.”
6.5 Reciprocal Lattice Vector
The reciprocal lattice vector extends in reciprocal space from origin 000 to the lattice point and is perpendicular to the corresponding planes. The set of all such points corresponds to the reciprocal lattice. These vectors have units of 1/length, so a larger vector indicates smaller spacing between planes.
Note: Hammond - Cullity[1] -
The following examples show applications of reciprocal lattice vectors in determining inter-planar relationships.
- Find inter-planar angle between planesand
i.e.find angle between reciprocal lattice vectors &
, where
Note: etc.
Example:
Find angle between (111) and (110) in cube?
- Find the zone axis for two intersecting planes
(and
Since plane, for any (hkl) belonging to zone
Solve simultaneous equations for u, v, w
2 equations and 3 unknowns uvw determined to within a scale factor
Example:
What is the zone axis (or edge formed by) for ) and (010)?
or
Equivalent to doing vector cross product:
- Find d-spacing
Use
distance between 2 ‖ planes with intercept differences =
For ,
Note:
For Orthorhombic -
For Cubic -
Monoclinic
(
since
Use
Likewise, .
Note: For monoclinic, since
- Cell axis transformations (primitive non-primitive)
e.g. Rhombohedral FCC
Let old rhombohedral unit cell axes be
The new FCC unit cell axes are related to the old by:
or:
Matrix of transformation
For rhombohedral to FCC example:
Transformation Matrix:
Modulus of Transformation:
Determinant ( The FCC unit cell has four times the volume of the rhombohedral unit cell)
For transforming
Since the inter-planar spacing and direction are the same, the planes have the same reciprocal lattice vector,
take dot product with
Same matrix of transformation used for axes and indices.
Old Rhombohedral New FCC example
Note that , or an even integer and , also an even integer.
Therefore,must all be even or all odd “unmixed.”
Transformation of the (110) plane in the rhombohedral structure to its (hkl) in the face-centered cubic structure.
In Figure
6.26 below, a non-primitive orthorhombic-c unit cell is illustrated, with the c axis pointing out of the page. The transformation of its lattice in real space to reciprocal space is shown in Figure
6.27. Notice that the
a and
b axes only reach halfway to the first lattice point in their respective directions. The reason for this is due to the organization of lattice planes in the
a and
b directions of the real space. For instance, going vertically in the
a direction of Figure
6.26, the first set of planes appears halfway between the lattice spacing. The planes that follow in this
a direction appear at the same spacing. Thus, this set of
planes within the Orthorhombic-c unit cell, can represent the fundamental period of planes in the
a direction. The same analysis can be done in the
b direction, yielding the
fundamental period of planes. From this, the first point in the reciprocal space appears at 200 in the
direction and 020 in the
direction. Note that in the
c direction, which is not shown, the first plane is found at
, due to the base-centered structure.
Note that the original, real lattice and the reciprocal lattice have a similar shape, with an inverted aspect ratio in the reciprocal lattice. Furthermore, they are both base-centered and have a similar primitive unit cell, which is monoclinic. The missing base-centered reciprocal lattice points (e.g. 010, 100, 210, etc.) are due to the use of a non-primitive unit cell in real space for the transformation. Had the primitive cell been used, all allowed reciprocal lattice points, corresponding to allowed Bragg diffraction planes, would be present. Anytime a nonprimative unit cell is used to describe the lattice, there will be missing reciprocal lattice points.
A two dimensional projection of the FCC unit cell on the
a and
b axes is illustrated in Figure
6.28 below. The solid circles represent the lattice points in the plane of the paper, and the circles with the
label represent lattice points half a lattice spacing above the plane. The dashed lines indicate the set of (110) planes within this unit cell. The transformation from the FCC to its reciprocal lattice generates a BCC structure as shown in Figure
6.29, and vice versa. Note that the (100) planes are missing, since the fundamental period of planes is (200) in the
a direction. This reasoning can be applied to other missing reciprocal space points, using the fundamental period of planes in the real FCC lattice.
7 Representative Crystal Structures
7.1 Crystal Structure Examples
The combination of the previously discussed point and translation symmetry elements with the fourteen Bravais lattices give rise to 230 possible three-dimensional space groups. For these three-dimensional crystal structures, an identical atom or a fixed arrangement of atoms (ions, molecules) is found at each Bravais lattice point.
The following examples show a one atom per lattice point structure. Another example which is not shown below is the simple cubic structure.
Ex.: BCC Metals Cr, Mo, V, etc.
Ex.: FCC Metals Fe, Cu, Pb, Ni, etc.
7.2 The hexagonal close packed structure, unlike the examples in Figures 7.1 and 7.2, has two atoms per lattice point. These two atoms are considered to be the motif, or repeating object within the HCP lattice.
Ex.: HCP (hexagonal close-packed)
Figure
7.3 shows four different representations of a hexagonal close-packed structure with two atoms per unit cell - one atom at 000, and one atom at
or
. The atoms in Figure
7.3(b) correspond to the nine atoms illustrated in Figure
7.3(a). The association of two atoms with a single lattice point is represent by the dashed lines connecting the pairs. Furthermore, (c) and (d) show more of a hexagonal representation of the HCP atomic structure with the stacking of atomic planes in a periodic arrangement. Some elements with this structure include zinc, magnesium, and beryllium.
The FCC crystal structure is as close-packed as the HCP structure. Though its relation to the HCP structure is not immediately apparent, Figure
7.4 demonstrates the stacking of FCC (111) planes in a hexagonal pattern, similar to the (0002) HCP planes stacking. One distinction between the two is that the HCP layer stacking occurs in an ABAB pattern in the
or [001] direction, and the layer stacking for FCC occurs in an ABCABC pattern in the [111] directions. This is illustrated in Figures
7.5 and
7.7 below.
The following are other examples of crystal structures with two atoms per lattice point. The first example, in Figure
7.8, is the diamond crystal structure that is seen in other atoms besides carbon, such as silicon and germanium. In the examples following Figure
7.8, compounds consisting of two unlike atoms follow unique characteristics of arrangement. For instance, if a compound's structure consists of atoms A and B, the structure of A atoms must possess the same symmetry elements of the crystal as a whole. Namely, a symmetry operation characteristic of the entire crystal, when performed on a given A atom, must bring it into coincidence with another A atom. Furthermore, body-centering, face-centering, and base-centering translations, if present, should begin and end on like atoms. An example of this is detailed above figure
7.11.
Diamond Structure
ex. C, Si, Ge
4C at 000 + face-center translations (fct)
4C at
Zinc Blend
The face-centered cubic zinc blend structure can be likened to the diamond structure in Figure
7.8 above, but the atoms at 000+fct (S) are now different from those at the second set of positions -
(Zn).
Ex. GaAs, ZnS
4S at 000+fct
4Zn at
The CsCl structure illustrated in Figure
7.10 below is common to compounds such as CsBr, NiAl, ordered
and ordered CuPd. Though it appears to be a body-centered cubic structure at first glance, the body centering translation of
connects two unlike atoms, rather than the required self-coincidence of a single atomic element. Therefore, the structure is simple cubic, and one may think of the Cs atom at 000 and the
atom at
as being related to the single lattice point at
In the NaCl or rock salt crystal structure of Figure
7.11 below, the sodium atoms are face-centered. When face centering translations are applied to the chlorine atom at
, all chlorine atom positions are mapped. In addition, a
rotation about the four fold rotation axis at [010] brings the chlorine atoms into self coincidence.
7.3 Voids in FCC
The FCC structure has two types of voids, namely octahedral and tetrahedral voids, which naturally arise from the arrangement of atoms in its crystal lattice.
Octahedral voids are located at
+fct in the FCC structure. There is one located at the center of the unit cell, and one at the center of each of the unit cell edges. Since there are twelve edges and each edge is shared with four other unit cells, this yields three edge octahedral voids per unit cell in addition to the one at the center. Thus, there are a total of four octahedral voids per unit cell. The space labeled “A” in Figure
7.12 is an octahedral hole in the structure, which is surrounded by eight sulfur atoms. In Figure
7.11, note that
is NaCl octahedrally surrounded by
.
The Zn atom at
marked “B” in Figure
7.12, is surrounded by four S atoms at the corners of a tetrahedron. This is known as a
tetrahedral void
in the structure, as the Zn atom is surrounded by a tetrahedral structure of sulfur atoms. In the zinc blend structure as well as other FCC structured crystals, there are a total of eight octahedral voids per unit cell. For the zinc blend structure, however,only half of these tetrahedral sites are occupied by Zn atoms, which is illustrated more clearly in Figure
7.9.
7.4 Atom Sizes and Coordination
When picturing atoms within a crystal structure, atoms in ionic or metallic crystals can be represented by a simplified hard sphere structure, with atomic spheres in direct contact with one another. This number is specific to a given crystal structure. The radius of a given atomic element is generally considered to be constant regardless of conditions such as phase or presence in a solution. The size of atom may also be deduced from its
coordination number (CN), or number of nearest neighbors specific to its crystal structure. The Cs and Cl atoms in the simple cubic structure, for instance, have a coordination number of 8 as shown below.
Ex.: CsCl
Structure - Cubic P (not BCC)
at 000 CN=8
at CN=8
Using the hard sphere model for atoms, the placement of atoms in the unit cell of a given structure, as well as known atomic radii, the lattice constant of a crystal structure may be determined.
The following procedure demonstrates the evaluation lattice constant “” in CsCl using known ionic radii:
Body diagonal of cube =
Note that the nearest neighbors experience an attractive force due to their opposite charges and that the second nearest neighbors experience a repulsive force due to their like charges. Therefore, if the two ionic sizes become more disparate than CsCl, then the packing changes to an NaCl structure.
NaCl structure:
4 at 000 + fct CN=6 (octahedral surroundings)
4 at + fct CN=6 (octahedral surroundings)
fct face-center translations
If the NaCl structure were like “CsCl” structure,
then
Therefore, the NaCl CN=8 structure would not bond since the -distance
In other words, for the CN=8 CsCl structure, the distance of the required lattice parameter would be greater than the available distance of two radii of the larger ions that make up the lattice parameter “a”. Thus, there is a critical or minimum radius ratio for which cation–anion contact is established in the CsCl structure.
where radius of larger ion & radius of smaller ion
Radius Ratio
This radius ratio rule is different for different crystal structures, as shown in Table
8 below. Deviation from the radius ratio rule indicates a shift from ionic to covalent bonding.
Ex. Zinc blend structure:
Table 8: Radius Ratio Rules
What about HCP, FCC close-packed structures? For the HCP structures, the coordination number is 12. An ionic crystal cannot have this coordination number because there would be an equal number of anions and cations surrounding each ion.
8 Introduction to Diffraction
The experimental technique of X-ray diffraction in crystals, since early applications at the start of the 20th century, has been an important method for mapping crystal structures. The following section introduces the basic, key concepts of X-ray diffraction such as the nature of X-rays and Bragg's Law.
8.1 X-ray
An
X-ray is an electromagnetic wave similar to light, but of a much shorter wavelength. As illustrated in Figure
8.1 below, a beam of X-rays of a single wavelength traveling in the same direction (i.e.
) has an electric field
) perpendicular to its propagation direction and a magnetic field
) perpendicular to its electric field. A plane-polarized wave is one in which the electric field is confined to the a plane, such as the x-y plane, as the wave travels along the x direction, labeled the Poynting vector in Figure
8.1. The magnetic field is not considered in the following applications.
The following equation models the oscillation of the electric field as a transverse plane wave traveling in the x-direction, with an amplitude of in the and a time varying in the y direction:
= wavelength,=velocity traveling in x-direction
Let
After a time, t, has elapsed the wave has been phase shifted to the right by .
8.2 Interference
Interference occurs when two or more
coherent, or same wavelength, waves are superimposed. If two interfering waves are in phase, then constructive interference occurs, as illustrated in Figure
8.2. Waves out of phase, as shown in Figure
8.3, may produce a resultant wave wit
(1800) Young's two-slit experiment
Young's two slit experiment, as illustrated in Figure
8.4 below, is a classic example of the interference of light waves and resulting diffraction patterns.
In Young's experiment, a plane light wave of wavelength traveling to the right with an “in-phase” wave front parallel to the grating produces two coherent circular waves emanating from the 2 slits at A and B. The two waves will add up in phase at point P on a screen, if the path length difference, , is a multiple of wavelength .
interference maxima at y
To produce interference fringe pattern, of dark destructive interference and bright constructive interference spots,
If impossible
If too small to separate n=1 max. from n=0 direct beam
8.3 X-ray Diffraction History
In 1912, Max von Laue, a young Assistant Professor in Munich, was inspired by PhD thesis work of Ewald who was working in Sommerfeld Lab at the University of Munich. Ewald's thesis concerned solving for a mathematical physics relationship of the scattering of waves from a periodic array of dipole oscillators. Laue realized that Ewald's discovery directly related to scattering of waves from a crystal's periodic structure, and collaborated with Friedrich and Rongten's (discoverer of X-rays) student Knipping to explore this idea. Their experiment demonstrated an X-ray diffraction pattern from a crystal, and proved that X-rays were waves with wavelength of the order of a d-spacing within a crystal.
Later in 1912, W.L. Bragg, excited by the Laue discovery, worked with his father to develop a simpler picture to explain X-ray diffraction.
8.4 How does X-ray diffraction work?
First, consider reflection from a plane of atoms, as represented by a horizontal line in Figure
8.5. Note that the atoms do not have to evenly spaced within the plane.
A plane-wave is represented by rays 1 & 2 in-phase at AC in Figure
8.5, and also reflecting in phase . The path length difference of rays 1-1' and rays 2-2' are equal when
, and by trigonometry, when the incident angle is equal to the outgoing angle.
Since path lengths will be equal for all rays under the specular reflection condition, the outgoing angle will equal the angle of incidence. This is known as the Law of Reflection.
Law of Reflection
Scattering from two planes
Second, consider the reflection from a set of equally spaced atom planes as illustrated in
8.6.
In this case, scattering occurs in both planes. Here, we would like to know when the scattering from both planes will result in constructive interference. If the path difference, =BCD of rays 1 and 2 is equal to the length equal to an integer multiple of the wavelength of the X-rays ( ,where n is an integer) then the scattered rays 1' & 2' are in-phase at yy.' If the angle of incidence were tilted down slightly, then the waves would no longer be in phase, and the conditions would no longer allow for constructive interference. Applying the geometric relationship below yield's Bragg's law. This states the essential condition necessary for diffraction to occur.
Bragg's Law:
- order of reflection, number of wavelengths in the path difference between rays scattered by adjacent planes
If
is slightly different from the Bragg condition, each successive ray 1',2',3',...will be slightly phase shifted with respect to previous ray as illustrated in Figure
8.7. The amplitudes of the waves would sum to zero since every plane will have another plane at some depth which will scatter out of phase by
What about the “n” in ?
The “n” value , or order of reflection, may take on any integral value as long as sin does not exceed one in the Bragg's law equation. For fixed values of d and , various n values (n=1,2,3...) correspond to different angles of incidence ( at which diffraction may occur.
For a first-order reflection (n=1) the path length and phase difference of the scattered X-rays 1' and 2' in Figure
8.6 would differ by one wavelength. For a second-order reflection (n=2) the path length and phase difference of the scattered rays would differ by two wavelengths. Thus, the rays scattered by all the planes of atoms are completely in phase, leading to constructive interference.
1st order n=1 between consecutive planes spaced by “d”
2nd order n = 2 between consecutive planes spaced by “d”
Another way of looking at the reflection order:
where hkl corresponds to the 1st order or fundamental reflection planes. Thus, the Bragg equation may be rearranged in the following form, in which the “n” term is dropped and the does not need to be the lowest set of indices for a given plane (i.e. =110,220,etc.):
or
If the diffracted intensity is plotted as a function of sin
, peaks corresponding to crystallographic planes would be visible as shown in Figure
8.8.
Now, consider diffraction from NaCl (111), for which a two-dimensional representation is shown in Figure
8.9 below.
The (111) diffraction condition ( allows for constructive interference from the 1' and 3' waves and the 2' and 4' waves , as their path length difference measures exactly one wavelength. Note that rays 1'&3' from are in phase with each other, but out of phase with rays 2'&4' from
If Na and Cl were equal in scattering strength, then this would lead to complete destructive interference and 0 intensity. Due to the number of electrons in the two atomic species, which are the primary source of scattering in atoms, the scattering strength is not equal and therefore a small diffraction intensity peak will be observed for
as shown in Figure
8.10.
For
the overall path length becomes longer and all rays 1',2',3',4' from all planes
and
are in phase. This leads to constructive interference and higher intensity peaks shown in Figure
8.10. Note that this is a simplified model, which solely accounts for the path length difference effect in scattering from different planes which are not identical to each other. Other effects will be discussed later in the text.
Observing the Bragg Angles tells us about unit cell dimensions, namely the d-spacing between planes which can be used to derive the lattice constant. Furthermore, observing relative intensities as shown in the NaCl structure for different tells us about the structure within the unit cell. Namely, that there were a pair of ions (and ) associated with an FCC lattice point.
On the other hand, in a simple FCC metal (111),(333), etc., would not have been weak.
Hint: Look for weak and absent reflections
8.5 Absent (or forbidden) Reflections
Figure below shows a two dimensional projection side view of (100) planes in a simple FCC metal. The white circles represent atoms that are half of a lattice spacing out of the plane.
The plane of atoms half way between the planes will scatter at out of phase, canceling out the waves reflecting at the 100 planes. Therefore, the Bragg diffraction condition leads to destructive interference, and the (100) reflection is absent or not allowed. For simple cubic, the atoms halfway between the planes would not be present.
However, all (200) planes scatter in phase and the (200) reflection would be observed. This reinforces the fact that in an FCC structure, the following conditions are true:
- etc. allowed.
- etc. forbidden
- hkl all even or hkl all odd (unmixed) for FCC
How would Bragg diffraction show that a crystal is cubic? i.e., not orthorhombic
Realize that for the cubic structure the following relationship between the d-spacing of the 110 and the 100 planes is true: .
By determining the reflection angle for the (100) and (110) planes and then taking the ratio of the sines, the cubic structure can be confirmed if it is equal to .
This same procedure may be used to determine if a crystal structure is FCC. Since (110) and (100) are forbidden for FCC, then (220) and (200) can be used instead.
9 Absorption/Emission
9.1 Spectrometers
The following three X-ray sources will be discussed in this text:
- X-ray tube e.g., Cu target
- Radioactive Source e.g.,
- Synchrotron e.g., storage ring
An X-ray tube must contain three vital components, namely a source of electrons, a high accelerating voltage to move these electrons, and a metal target on which these highly-accelerated electrons will collide. Figure
9.1(a) below illustrates the cross section of an
X-ray filament tube. This consists of an evacuated glass casing that insulates the anode at one end from the cathode at another. The cathode is a tungsten filament and the anode is a water-cooled block of copper which also contains the desired target metal at one end. A lead of the high-voltage transformer, detailed in Figure
9.1(b) is connected to the filament and the other is connected to ground. The target is grounded . In operation, the filament is heated with a current and emits electrons that are drawn to the target. Around the filament is a metal focusing cup which is kept at a high negative voltage close to that of the filament and tends to focus the electrons on a focal spot on the target. X-rays are emitted from this focal spot in all directions and escape through the window in the tube usually made from very thin beryllium. Approximately 99% of the X-ray tube power goes into producing unwanted heat. Unlike the fixed anode X-ray tube that typically operates at a power of 1 to 2kW, a rotating anode distributes the heat over a much larger area of a rotating, water-cooled, cylindrical anode; allowing it to run at 5 to 18 kW . In this case the power P = V i , where V is the negative voltage potential of the filament relative to the grounded anode and i is the electron current flowing from the filament to the anode. V is typically 20 to 60 kV.
Figure
9.2, below illustrates an X-ray radiation spectrum, plotting X-ray intensity as a function of energy.
9.2 Bremsstrahlung Radiation
Bremsstrahlung radiation is a continuous X-ray spectrum from X-ray tube, which is the smooth curve in the intensity plot in Figure
9.2. This occurs as a result of the deceleration, or braking of electrons in the target. The accelerating (or decelerating) of any charge q, an electron in this case, generates electromagnetic radiation.
Figure
9.3 illustrates a charge q, with acceleration in the
direction. If you look in the
direction relative to its acceleration vector, you will have electromagnetic radiation at point P whose distance from charged particle q is indicated by
The electric field
of this radiation is pointing in the transverse direction to the radius
. The following formula yields the magnitude of the electric field generated by the accelerated charge:
The following relationships for the electric field also hold true:
- (transverse wave)
In the case of X-ray tube Bremsstrahlung radiation, the electrons accelerate (negatively) from the tungsten filament cathode to the grounded anode. Electrons accelerating in the negative
direction as illustrated in Figure
9.4 create an azimuthally symmetric dipole radiation field. In Figure
9.4, the angle
is the complement of the angle
in Figure
9.3. Note that the magnitude of
does not change, and
is the factor that affects the intensity of the generated
field. Because the intensity is proportional to the magnitude of the electric field squared, it is also proportional to
or
This is consistent with what is observed in Figure
9.4 and the three-dimensional representation in Figure
9.5, since the intensity at a minimum when when
is
and at a maximum when
goes to
.
Max intensity
9.3 Synchrotron Radiation
Synchrotron radiation occurs when electrons are accelerated in a curved path. The electron experiences centripetal acceleration in the radial direction, producing the dipole radiation pattern is of the same toroid shape as illustrated in Figures
9.4 and
9.5. The minimum intensity is observed in the radial direction and maximized perpendicular. However, there is a high relativistic effect due to the electron's speed, such that the dipole radiation field is distorted in the lab frame of reference creating an extremely narrow cone of radiation in the forward direction of the electron's tangential velocity.
Recall that Bremsstrahlung radiation is white, or polychromatic, radiation resulting from the deceleration of electrons following inelastic collisions with target atoms. The kinetic energy analysis of this process is as follows:
The maximum energy loss is the kinetic energy (KE) of the electron at the vacuum target interface. This is the case in which the electron loses all of its energy from one inelastic collision.
The maximum energy of the photon, by the de Broglie relationship , is directly related to the wavelength of the radiation. Note that this is a maximum case, and the range of energies will be anywhere from this maximum value to zero.This maximum kinetic energy is therefore directly related to the set potential of the X-ray tube, as shown below.
KE [keV] = V [kV]
Typically, If X-ray tube high voltage, HV = 50kV Max photon energy = 50keV
The maximum photon energy in the continuous Bremsstrahlung spectrum will show 50keV at its maximum along with lower values.
de Broglie wavelength relationship: short wavelength limit
Therefore, in the Bremsstrahlung spectrum there will be a continuum of wavelengths showing an intensity pattern as well as a short wavelength limit (SWL) corresponding to the maximum available energy. This is due to the fact that the wavelength and energy are inversely proportional.
Figure
9.7 below shows a radiation spectrum from a copper X-ray tube, for various set potentials (25kV, 20kV, 15kV, etc.). The smooth curve indicates the continuous or Bremsstrahlung radiation curve, with the short wavelength limit (SWL) corresponding to the leftmost point on a given curve. The spikes are indicative of characteristic radiation, but
The integrated intensity, or area under the curves in Figure
9.7 is proportional to the voltage of the X-ray cubed multiplied by the the atomic number of the target and the current through the filament. Typically the the voltage will be increased rather than the current, as this increases the intensity by three orders of magnitude.
The following is a comparison of the spectra from different synchrotons on a log scale. Notice the Bremsstrahlung spectrum located near the bottom of the plot.
9.4 Characteristic Spectrum
Raising the voltage on an X-ray tube above a certain critical value for a given target metal yields sharp, narrow intensity peaks, or
fluorescent lines superimposed on the continuous radiation spectrum. The
characteristic spectrum is comprised of several of these fluorescent lines (i.e. K,L,M,etc.) that are specific to the target in use. In order for fluorescent lines from the target to occur, the electron beam must have enough kinetic energy to overcome the binding energy of an inner core electron and knock it out of the target. The transition of a higher energy electron to fill this hole leads to the production of an X-ray which is characteristic of the given target element. Figure
9.10 illustrates these fluorescent peaks on a continuous background radiation spectrum for a copper target sample at 30 kV.
For fluorescence: (or)
where is electron energy & is the binding energy of target electrons.
Typically, the K fluorescence lines comprised of
,
and
are useful in X-ray diffraction. The
and
lines, referred to as the
doublet
, often have very close wavelengths and are treated as a single line. In addition, the subscript in the
is usually dropped. The K indicates the principal quantum number of an electron which corresponds to its energy level in the electron cloud. A useful diagram of the electron energy states for copper is shown in Figure
9.10, with different principal energy levels (n=1=K and n=2=L) followed by an integer number that indicates the sub-shell within a given energy level (i.e. L1, L2, etc.). When an electron in the K shell is knocked out , the atom is left in a high-energy state. The excited target metal atom transitions to ground state when an electron in a higher energy state, such as one from the L shell or the M shell, drops down to fill the K electron-hole. Filling a K electron with an L-shell electron is more probable than filling it with M-shell electron, therefore yielding a higher
(corresponding to the L shell transition) intensity peak relative to the
(corresponding to the M shell transition) intensity peak. Note that the K radiation has a definite wavelength for a given target atom and that it is impossible to excite one K fluorescence line without also exciting the other.
In Figure
9.9 above, note that the intensity of the
peak is one hundred times stronger than the background radiation curve. Furthermore, the
doublet differ in intensity by a factor of two, and the
and
differ by approximately a factor of five.
The arrows in Figure
9.10 below demonstrate the
and
transitions, with their lengths representing the difference in the energies of the two states. This energy difference also equals the energy of the outgoing fluorescent photon. Note that an arrow does not go from the 1s to the 2s electron energy state. This is due to conservation of angular momentum (
) with electrons in an s-state having
=0 and p-state having
=1 and photons having
=1 . The 1s and 2s states do not differ in angular momentum by 1, thus the 2s
1s transition is extremely low in probability. Whereas, the 2p
1s has a
which balances out with the emitted fluorescent photon's angular momentum and obeys the so-called dipole transition rule in atomic physics.
Note that in Figure
9.10 there are twice the number of electrons in the L3 state than there are in the L2 state. Due to this, the
electron transition from the L3 energy level to K energy level is twice as likely to occur as the
transition from the L2 energy state to the K energy state. This is consistent with the double intensity of the
fluorescence peak relative to the
fluorescence peak shown above.
The following calculations determine the characteristic and fluorescence energies for a copper target and their corresponding wavelengths:
()
9.5 Auger Effect
The
Auger effect is a non-radiative process that competes with the radiative X-ray emission process to fill an inner electron hole. Rather than producing a photon, this process ejects an outer energy level electron known as the
Auger electron. An energy level diagram for Auger electron emission from a copper atom is illustrated in Figure
9.11. This process involves three discrete electron energy levels: the first is the K energy level of the electron hole, the second is the L1 or higher energy level from which an electron drops down to fill the K-hole, and the last is the L3 valence energy level from which the Auger electron is emitted. The energy released from the transition of the L1 level electron the lower energy level of the K-hole is transmitted to the L3 valence shell Auger electron, allowing for its ejection from the atom. The kinetic energy of the Auger electron, therefore, is equal to the difference between its binding energy and the energy difference between the L1 and K energy levels involved in the filling of the electron hole.
Note that the creation of the K hole leads an L1 electron to drop down and fill the hole as shown by the arrow indicating the movement of the hole from the K to L1 energy level. Following this, the energy is transmitted to the L3 valence electron which becomes the ejected Auger electron, as shown by its arrow pointing outside of the electron's energy levels. The energy of this ejected L3 electron is equal to the binding energy difference between the K and L1 energy levels and the binding energy of the L3 that must be overcome for its emission from the copper atom.
Example:
Copper K Auger electron emission follows creation of k-hole
- K-hole is created in copper atom via accelerated electron bombardment
- L1 electron drops down to fill K hole, creating useful energy
- Useful transition energy is transferred to L3 electron, overcomes the binding energy and ejects the L3 electron from the atom
Energy analysis, where is the energy of the Auger electron:
Recall that the Auger effect and radiative fluorescence are two process that compete to fill a K-electron hole. If the
fluorescence yield, or probability of filling a K-electron hole via X-ray emission, is
, then the probability of an filling an electron hole via the Auger effect is
This Auger emission probability is very high for a low atomic number. For germanium of atomic number 32, there is an equal probability of filling an electron hole by either the non-radiative or radiative processes. Elements with an atomic number lower than germanium (i.e. Z<32) will favor the Auger effect over a radiative process.
Fluorescence yield: = probability for K hole being filled by radiative process
K Auger Probability = 1-
The “K” line in Figure
9.12 below shows this relationship, in which a higher atomic number corresponds to a higher fluorescence yield probability for filling a K electron hole. The L-hole electron fluorescence probability is also shown in this diagram as the line labeled “L.”
Note that because electrons cannot transmit through air very easily like X-rays, the Auger spectrometer is located inside a vacuum chamber. Furthermore, Auger emission spectroscopy (AES) is much more surface sensitive than X-ray fluorescene (XRF) spectroscopy.
9.6 Radioactive Source
Moving from atomic physics to nuclear physics we find another form of X-ray emission due to radioactive decay of an unstable nucleus following electron capture. For example, the
isotope of iron exhibits a high probability of undergoing electron capture in which a proton in the nucleus combines with a 1s electron to creating a neutron and a neutrino. The atomic species is now a Mn+ ion with an electron hole in its K energy level. Following this, the Mn emits a
XRF photon in filling the K hole with an L3 level electron as shown in Figure
9.13. The observed spectrum will be characteristic of manganese.
(neutron + neutrino)
with K hole
with hole + fluorescence
Example:
Electron Capture
The isotope of cadmium undergoes a similar process, whereby the electron capture leads to its conversion into and characteristic fluorescence lines of Ag are observed in the XRF spectrum.
9.7 X-ray Absorption
When an X-ray impinges on a material, part of it is transmitted and part of it is absorbed. The attenuation of the incident X-ray beams intensity has been experimentally shown to be directly related to the traversed distance of the X-ray through the material. Referring to the diagram of Figure
9.14, if an X-ray of
incident intensity passes through the slab through a distance
, the
transmitted intensity will have a fractional intensity of the incident beam. This difference is equal to the
adsorbed intensity
,
, which is proportional to the distance traversed.
= incident intensity
= transmitted intensity
The constant of proportionality relating the absorbed intensity to the distance traversed is
, or the
linear absorption coefficient. The plot in Figure
9 below shows this exponential relationship, in which the incident intensity
decays at a rate of
times the distance
through the material.
Differential form: ,= linear absorption coefficient
Exponential Relationship:
The linear absorption coefficient is directly proportional to the density of the material, thus the quantity
, called the
mass absorption coefficient, is constant for a given material regardless of its state of matter. The
value for a given atom is normally listed in tables, rather than listing various
values for various compounds or elements and accounting for structure or density factors. Furthermore, the mass absorption coefficient is a function of the atomic number of the element as well as the energy of the X-ray. The energy dependence is due to the fact that there is a critical energy above which the X-rays are able to overcome the binding energy of the electrons in the atoms of the material and emit a photoelectron. Thus, there is a much higher probability of X-ray absorption above this critical energy leading to a higher
value. Furthermore, there is a certain distance at which the initial intensity
is divided by a factor of
This distance is equal to
, which is referred to as the
absorption length.
constant of material, independent of state (solid,liquid,gas)
mass absorption coefficient
= absorption length
For more complicated structures such as chemical compounds or mixtures, the mass absorption coefficient of the substance is the weighted average of the mass absorption coefficient of its constituent elements. A general formula for this is shown below. The mass absorption coefficient for the mixture of air is calculated in Table
9, using tabulated mass absorption coefficients of nitrogen, oxygen, and argon along with their respective weight percents in air.
=weight fraction
Mass absorption coefficient for variable composition
Example:
Air=76% +23% +1.3% Ar
|
i
|
|
|
|
|
|
0.76
|
7.14
|
5.53
|
|
|
0.23
|
11.0
|
2.53
|
|
Ar
|
0.013
|
120.0
|
1.56
|
|
|
|
(C&S Appendix 8)
|
9.52=
|
@ STP ,,
Table 9: X-ray absorption in Air at =8.05 keV (Cu )
From these calculations, it is determined that a copper (8.05 keV) X-ray beam is attenuated to after traveling through 81 cm of air.
Figures
9.16 and
9.17 below plot the linear absorption coefficients and X-ray transmission for beryllium as a function of the photon energy. Recall that a beryllium window is used in an X-ray tube.
9.8 X-ray Transmission Filters
As previously shown, the spectrum from an X-ray tube yields several fluorescent lines, such as the characteristic
and the
. Some applications require that an X-ray beam be monochromatic, such that the
fluorescence is significantly reduced in comparison to the
fluorescence. This more monochromatic spectrum may be achieved by using a metal foil filter that preferentially reduces the intensity of the
in the X-ray spectrum compared to the
. (Note that absorption filters cannot be used to remove the unwanted
component from the
radiation. This is done by inserting a Bragg diffracting single crystal in place of the Ni Foil.) Figure
9.18 below shows a basic setup of a nickel foil filter used in a copper X-ray tube.
Transmission filters make use of the X-ray absorption edge of a particular element. In the second plot of Figure
9.19 below, the absorption edge for nickel can be observed. This discontinuity corresponds to the energy required to eject an inner core electron from an atom of the foil material. At energies just below this edge the
mass absorption coefficient is significantly less than the mass absorption coefficient at energies slightly above the edge. This translates into higher transmission for x-rays with energies below the absorption edge line on the energy axis. By this process the initial x-ray spectrum, plotted as
at the top of the figure, undergoes significant reduction in the intensity of the
line as shown in the final plot of transmitted intensity,
. Note that the high energy background radiation is also significantly reduced in the final plot.
Recall the X-ray transmission intensity formula, .
For an 8 mil Ni Filter, (1mil=0.001”=25.4) the intensity of the fluorescence is five hundred times greater than the fluorescence. Recall that without a filter, the transmitted intensity was five times greater than the intensity; thus, the nickel filter only transmits of the original X-ray intensity.
8 mil (0.8 mils = ) Ni Filter:
In general, a filter with an atomic number that is one less than the target metal in the X-ray tube is used and the thickness X is chosen such that . This Z-1 relationship is utilized so that the absorption edge lies just above the desired and below the to be filtered. The mass-absorption law may used to calculate the thickness of the filter.
Generally, use a filter:
CuNi Filter
AgPd Filter
MoZr (Z-2)
A thicker filter will better suppress the component, but this will also result in unwanted suppression of the component. Thus, it is useful to follow the intensity ratio.
Figure
9.20 below illustrates a general absorption spectra for an atom, by plotting the log of the mass absorption coefficient against increasing energy. Note the presence of the absorption edge previously discussed, which is labeled as the the “K-edge.” In addition to the K-edge, other discontinuity spikes corresponding to the L electron shell binding energies are present. The location of the K-edge, and its associated K-branch, further to the right on the energy axis is due to the fact that this inner electron shell has the highest binding energy in a given atomic element.
The overall absorption, labeled
is equal to the addition of the absorption from the different electron energy level branches, i.e.
etc. Note that a single increase in the energy unit or in the atomic number have a cube effect on the mass absorption coefficient. For instance, if the X-ray energy is increased from 10keV to 20keV, the x-ray absorption will decrease by one eighth. Furthermore, if the atomic species is increased by two from, say, nickel to beryllium, then eight times the absorption occurs. Since the mass absorption coefficient
is inversely proportional to the cube of the energy, it follows that it the wavelength of the X-ray cubed is directly proportional to the mass absorption coefficient. These relationships are summarized in Figure
9.20 below.
9.9 Photoelectric effect
X-ray absorption is dominated by the
photoelectric effect, as initially discovered by Einstein. Photoelectric absorption of polarized x-rays occurs when an x-ray photon is absorbed and a core ( K, L ,..) electron from the atom's inner core is emitted. This process is illustrated in Figure
9.21 below for emission of a K photoelectron.
In order for photoelectric absorption to occur, the photon's energy must be greater than the binding energy of the K-shell electron. The kinetic energy of this emitted photoelectron is given by the difference of the incident photon's energy, and the binding energy overcome in the electrons emission. This is followed by XRF bor Auger emission, allowing for the atom to return to its ground state.
In addition to conservation of energy, the angular momentum in this process is conserved. That is, the incident photon's intrinsic angular momentum of =1 and the 1s electrons angular momentum of =0 are combined into a dipole angular distribution in the emitted photoelectron with =1 with p-state polarized along the polarization direction of the incident photon. That is, for polarization along the z-axis as shown below, there is a high probability that the emitted electron will be on along the z-axis perpendicular to the incident direction of the photon, and a minimal probability of its emission in the x and y direction.
Dipole selection rule for electronic transition:
9.10 X ray scattered by an electron
Classical Thomson scattering is a wave phenomena in which a polarized X-ray plane-wave interacts with an electron, causing an acceleration of the electron due to the X-ray's electric field. The effect of the X-ray beam's magnetic field on the electron's acceleration is negligible. This idea is illustrated in Figure
9.23 below.
The oscillating field of the incoming X-ray is given by the equation:
The force on this electron is given by its charge multiplied by the magnitude of the incident electric field.
Therefore, the acceleration of the electron is given by the following equation:
This oscillating electron emits electromagnetic radiation in all directions, or a scattered wave. The wavelength of this scattered wave is equal to the wavelength of the incident X-ray wave Therefore, this type of scattering is coherent, or elastic.
Oscillating E-field
Oscillating Charge Particle
E-M Radiation (oscillating fields)
9.11 Theory for Radiation Generating by Accelerated Charge
The electric field generated by an accelerated charge
at a given position
away from the charge is illustrated in Figure
9.24 below. The acceleration vector is indicated as
in the vertical direction, with the
position being at angle
relative to the charge
's acceleration vector.
- Direction of the electric field: and in-plane of and
- Magnitude of the electric field: Note that the electric field gets weaker as you increase the distance from the charged particle.
Classical radius
The classical Thomson scattering equation, as shown below, gives the intensity of the scattered x-rays from the electron as the square of the magnitude of the electric field generated by the oscillating electron. Note that the intensity is a maximum in the direction perpendicular to the acceleration
Intensity of scattered X-rays from at
Intensity of incident X-rays
Why ignore Thomson scattering from the (charged) nucleus?
Relative to the scattering of electrons, the scattering intensity from protons in the nucleus of an atom is negligible, as shown in the following ratio:
10 Scattering
10.1 X-ray Scattering & Polarization
Consider incident X-rays traveling in
direction and scattered from an electron
” at the origin “O” as shown in Figure
10.1 below. The scattered X-rays are observed at point P, where OP =
lies in the x-z plane with
scattering angle 2 relative to the incident direction
. The
scattering plane is defined as the plane containing the incident and scattered wave vectors, which in this case is the x-z plane. Since E-M waves are transverse, each incident X-ray photon has an electric field that is polarized in some direction in the y-z plane. We can therefore represent this electric field
of the incident X-ray as being subdivided into two orthogonal components - one in the y-direction
and one in the z-direction
.
Electric field of incident X-ray traveling in the direction.
We will seperately consider scattering of X-rays polarized perpendicular and then parallel to the scattering plane. Lastly, we will consider unpolarized X-rays from an X-ray tube.
1) For incident X-ray polarized perpendicular to the scattering plane, the scattered x-rays along vector are also polarized perpendicular to the scattering plane.
(
polarization
case,
scattering plane)
Here, , thus yielding maximum intensity as expected by the term in the classical Thomson scattering equation.
2) For incident X-ray polarized parallel to the scattering plane, the scattered x-rays along vector are also polarized parallel to the scattering plane.
(
polarization case,
scattering plane)
Here, , yielding an intensity which varies depending on the term.
Figure
10.2 below plots this
relationship with a varying
value that is present in the intensity function for the
polarization case.
3) For unpolarized incident x-rays traveling in the direction, the E-field polarization direction can be considered on average as evenly distributed in the direction and in the direction. Recall that the square of the electric field amplitude measures the intensity of the wave. It follows that the intensity polarized in the direction is equal to the intensity in the direction and half of the total intensity.
i.e.
To obtain the total scattered intensity for unpolarized e.g. characteristic radiation from an X-ray tube, at P, sum the intensities of the polarized and polarized cases.
polarization factor P
Note that the scattered intensity from an electron is independent of and dependent on .
At (forward scattering) and R=1cm
very weak, a small fraction of the incident beam's intensity
At
only polarization X-rays are scattered in direction.
10.1.1 Barkla
British Nobel Laureate Charles Barkla designed and performed a double scattering experiment in 1905 to prove that x-rays scattering at
produces a polarized beam. In this experiment, as shown in Figure
10.3 below, unpolarized x-rays traveling in the
direction scatter from a small particle at O. X-rays scattered at
for O in the -
direction are then rescattered from a second small particle at P. The rescattered x-ray intensity is measured at point Q in the in the x'y' plane, which is perpendicular to
, at an angle
relative to the
direction.
is parallel to
. Barkla found that the scattered intensity at Q varied as
as shown in Figure
10.4. This proved that an X-ray is polarized as a transverse wave and that unpolarized X-rays scattered at
produce polarized x-rays . Essentially, in this experiment we have an x-ray polarizer and an x-ray polarimeter.
10.2 Thomson Scattering by electrons
Recall the intensity of a scattered wave from a free electron:
unpolarized X-ray beam
Note: independence & dependence
As shown in Figure
10.5 below, we can define the following parameters:
incident direction unit vector
scattered direction unit vector
scattering angle
Now consider the scattering from 2 free electrons, one at origin and one at
, as shown in Figure
10.6 below.
The two scattered rays will have a phase difference
Where , and
Equivalently,
Note that in the forward scattering direction, as shown in Figure
10.7 below, the angle
is 0, so the scattered direction is equal to incident direction and there is no phase difference.
The scattered waves from each electron at a detector located a distance R in direction are represented by the following equations:
Note that the second electron's scattered wave has a phase shift added into its cosine function.
Since the detector is at a distance which is much greater than the distance between the two electrons, the amplitude of the electric fields scattered from both electrons are taken to be equal. Furthermore, the cosine factors of the equations may be condensed using Euler's formula.
use
At the detector, the total field is equal to the sum of the scattered field amplitudes from each electron. Note that Euler's formula is used in place of the cosine terms in the first line below. The intensity is determined by dotting the total field, labeled below, by its complex conjugate Recall that the scattered intensity from one electron was simply Now, this term includes a cosine term that accounts for the fact that the electrons are at two different positions and a certain angle that can lead to scattering waves at different phases. Notice that if or any even multiple of then, the scattered waves are in phase and four times the intensity is observed. On the other hand, if is an odd multiple of then the scattered waves are out of phase, and no intensity is detected. Of course, there are instances in between, such as , in which the intensity is in between the two extremes due to interference effects in the scattered waves.
for
for
for
10.2.1 Review of Thomson scattering from one and two electrons
Thomson scattering from one free electron
Thomson scattering from 2 free electrons separated by
, as shown in Figure
10.8 below.
The phase of scattered wave 2 is relative to scattered wave 1.
The total field is the sum of the field generated by each of the two electrons.
where
The phase difference of scattered wave 1 is zero:
Where R is the distance of the detector and r is the distance between the electrons,
In general, for N free electrons, the total scattered electric field amplitude generated is the sum of the scattered fields of all of the electrons. This is based on the superposition principle, in which the sum of the individual forces yields an equivalent total force. The detector “sees” the sum of all of these individual electric force fields, having equal amplitude but individual phase factors resulting from varying positions and angles. Recall that only in the forward direction will this phase difference equal zero.
Thus, the total intensity is equal to the square of this total electric field, where in the equation below, the first terms in front of the summation equal the scattering from one electron. This is abbreviated as as seen in the second line below.
If the scattered direction is zero, then the total intensity will be the intensity of one electron times , where N is the total number of electrons. The intensity of the scattered wave is times, rather than times, the intensity of an individual electron, because of the interference of coherently scattered waves (waves of equal wavelength). Furthermore, if the angle is not zero, then the intensity is less than .
Note if the scattered waves had slightly different wavelengths this is called modified or incoherent scattering. The waves will not interfere and the intensity will be affected by a factor of as opposed to in classical Thomson scattering.
10.2.2 X-ray Scattering from atom with Z electrons in spherically symmetrical distributions
According to quantum mechanics, the electrons involved in scattering are not at discrete points in space as described in the previous section, but have a probability distribution that describes their location around an atom. This probability of finding an electron in a given shell is given by a wave function and may be pictorially represented by an electron-cloud rather than set electron locations, as illustrated Figure
10.9 below. The electron density in a given atom, therefore, is the sum of the individual probability densities of its Z electrons. Thus the sum is equal to the sum of each electron's wave functions multiplied by the wave function's complex conjugate, as shown below.
H-like wave function
10.2.3 Defining Atomic Scattering Factor
In Figure
10.9 below, an incident x-ray beam, represented by the blue arrow pointing to the right and positioned to the left of the red electron cloud, is incident on some differential volume multiplied by the electron density to yield a differential charge value.
The
atomic scattering factor,
is defined as the ratio of the magnitude of the scattered field from an atom as compared to the scattered field from one single electron according to Thomson scattering.
The atomic scattering factor is calculated by the following integral which sums the scattering contributions from each differential volume while accounting for phase differences over the entire atomic volume.
Recall that for N electrons, the magnitude of the electric field scattered in the forward direction should equal N, since there is no phase shift between the scattered waves. This is consistent with the formula below, as the term, where is the phase shift, goes to one, and The atomic scattering factor, therefore, is dictated by the angle describing the phase shift between scattered waves different locations in the electron cloud.
Essentially, as waves scattered by the atom's electrons become more out of phase (2 increases), the atomic scattering factor decreases ( decreases) due to the partially destructive interference in scattered waves. In addition to the angle, the atomic scattering factor also depends on the wavelength. At a fixed value, for instance, a decrease in wavelength will make path differences larger relative to the wavelength, thus causing greater phase shift between interfering scattered waves.
10.2.4 Calculating the Atomic Scattering Factor
Figure
10.10 below illustrates an incident x-ray beam
, interacting with an atom O and scattering in the
direction. The following formula may be used to calculate the amplitude of the scattering for one electron:
Here, is the charge density for the electron at position relative to the nucleus, and the exponential factor accounts for the variation in the interference effect for scattering from different locations at different scattering directions
Note: Integration by parts.
Let
Let Azaroff
If (assuming spherical symmetric)
for spherically symmetrical charge distribution
Example: Lithium
Suppose that the individual electron densities for a neutral lithium atom, of atomic number 3 and electron configuration, are given by the following hydrogen-like expression:
Where for one K electron and for one L electron
The scattering factor for each electron may be calculated from the following equation:
Furthermore, the total scattering factor for lithium is obtained by summing the scattering factors of the two electrons in its K shell and the one electron in its L shell.
Note that the electron scattering factor for lithium is decreasing a function of
in Figure
10.13 below.
10.3 Compton Scattering
Compton scattering, also known as modified or incoherent scattering is the effect in which scattered waves have slightly different wavelengths than their incident x-ray wavelengths. This occurs when x-rays encounter loosely bound electrons, and may be explained by considering the incident beam to be comprised of a stream of photons of energy
, as illustrated in Figure
10.13 below. When one of these photons strikes a loosely bound electron that is initially at rest, energy and momentum are transferred from the photon to the electron. Due to this transfer of energy and momentum, the scattered x-ray photon has lower energy and therefore a larger wavelength. Note that another important characteristic of Compton scattering is that the phase of the scattered wave has no direct relationship to the phase of the incident beam, thus making this scattering incoherent and preventing interference effects.
The following equations combine the principles of conservation of energy and momentum in the photon-electron collision to yield a function of the change in wavelength of the x-ray beam with respect to the scattering angle, 2 Note that the theory of Compton scattering expresses the energy and momentum of the photons and electrons in relativistic values. These relativistic values are necessary because the photons scattered are massless and because the energy transferred to the electron is measured relative to its rest energy.
Conservation of energy:
assuming initial at rest
Conservation of momentum
x direction
y direction
Eliminate and
Note that the change in wavelength in the forward direction is 0 and the change in wavelength in the backward direction is about 0.05
at ( only elastic scattered photons in forward direction.)
at ( maximum energy loss to inelastic back scattered photon.)
The change in wavelength may be related to the change in energy by the following equations:
where (rest mass energy of electron)
In the experiment illustrated below, an undulator at the Advanced Photon Source (APS) has its 3rd harmonic tuned to generate an18.5 keV X-ray beam with a bandwidth of ~ 200 eV. This is monochromated further to a bandwidth of ~2 eV by downstream Si(111) single crystal optics. This x-ray beam then strikes a sample which is a Si single crystal with a monolaer of Sr atoms on its surface. An energy dispersive solid-state detector with a resolution of ~180 eV collects X-ray fluorescent photons from the sample. This detector also collects the elastic scattered and inelastic Compton x-rays with a scattering angle of ~90°.
Ex: If
Note that Compton scattering will not occur if the change in energy is less than the binding energy for the electron.
For hydrogen, a one electron atom, the total intensity according to the Thomson scattering equation is equal to the summed intensities of the modified (Compton) and unmodified (Bragg) scattered wave.
1= in electron units
The modified, or Compton scattering, and the unmodified, or Thomson scattering, vary in opposite ways with respect to
, as shown in Figure
10.16 below.
The scattering intensity for atoms with atomic numbers greater than one, such as lithium (Z=3), varies from the simple hydrogen model shown above. Again, the modified scattering intensity for each electron is given by . Recall that no interference effects can occur for incoherent scattering due to wavelength variations after collisions; thus, the total incoherent scattering intensity is simply given by the sum of the incoherent scattering intensities of the individual electrons.
Furthermore, the unmodified scattering intensity is equal to the square of the atomic scattering factor, since , and the intensity is the square of the magnitude of the electric field. Recall that for coherently scattered rays, the most efficient scattering is in the forward direction, where Since the unmodified intensity varies as its magnitude will be less than or equal to Furthermore, the modified scattering intensity will be less than or equal to the atomic number of a given element. For lighter elements and for a low wavelength, the modified scattering intensity will be significant relative to the total scattering intensity.
significant for low Z and low
Figure
10.17 below demonstrates the relationship between scattering intensities and
for atoms with
10.3.1 Anomalous Dispersion - dependence of
Anomalous dispersion is a phenomenon that occurs when the x-ray's photon energy is close to the energy of the absorption edge for a given element. In other words, the frequency of the incoming photon is close to the natural bound frequency for an electron within the atom, causing a resonance effect and a change in the scattering phase and photo-effect absorption. When this effect is considered, the following wavelength-dependent formula gives the atomic scattering factor:
Atomic form factor
which is the Fourier transform of atom's electron distribution,
The atomic form factor term is what was previously taken to be the atomic scattering factor, and the and correction terms account for the anomalous dispersion effect. The latter two terms are dependent on the element and the wavelength of the incident x-ray.
If the frequency of the incident x-ray beam is much greater than the natural resonance frequency of the electron (i.e. if the energy of the x-ray is much greater than the binding energy for a K shell electron) the scattered wave will be out of phase with respect to the incident wave, similar to the phase lag in Thomson scattering by free electrons. However, if the energy of the incident beam is close to the electron's binding energy, the scattered wave will deviate from this phase shift with respect to the incident wave. Therefore, the in-phase rays scattered from the K electrons destructively interfere with the out of phase x-rays scattered from outer electrons.
10.3.2 Hönl's Correction Factors
As shown in Figure
10.18 below, the
real component is
out of phase with the normally scattered radiation,
, and affects the amplitude of the wave. Furthermore, the
imaginary component is
out of phase with respect to
and affects the phase of the scattered wave.
Figure
10.19 below demonstrates the effect of increasing energy on the
and
correction factors. Note that the
imaginary component becomes highly positive slightly above the absorption edge. Conversely, the real
component becomes largely negative close to the absorption edge. This proximity to the absorption edge indicates that the frequency of the incident ray is close to the electron's natural frequency. Since the absorption edge is characteristic of a given element, the correction factors in
can give chemical sensitivity to the x-ray scattering process. These
terms are tabulated in the International Tables of Crystallography Vol. IV. They can also be found at the CXRO WebSite. (https://henke.lbl.gov/optical_constants/asf.html) In addition, since the intensity is proportional to
- the scattering factor times its complex conjugate - the scattered intensity may be manipulated by using a synchrotron radiation source with a tunable
or wavelength of the incident x-ray beam.
Evidently, if the incident x-ray is not close to the absorption edge for an element, i.e. , or etc., then the correction factors will be negligible with respect to . In 361, we will ignore anomalous dispersion effects unless specifically stated.
10.3.3 X-ray Scattering by Many Atoms
For one atom scattered E-field amplitude is
for -polarized case; for -polarized case
Elastic Coherent Scattering
For unpolarized
11 Kinematic Theory
Consider the scattering from a collection of N atoms, as shown in Figure
11.1 below. Note the incident direction
and scattering direction
If we consider the scattering from atoms “0” and “3,” their scattered wave vectors will be parallel and of the same wavelength, but the scattered waves will be out of phase with each other due to a separation between the two atoms, indicated by The difference between the incident wave vector and the scattered wave vector dotted with the distance between the two atoms yields this extra path length, as shown in the following expression:
Extra path length
The scattered wavevector minus the incident wavevector gives the scattering vector.
Scattering vector
Multiplying the scattering vector by and taking its dot product with yields the radian phase lag of the scattered wave from the atom at relative to the atom at the origin O. If this phase angle is an integer multiple of , then perfect constructive interference occurs. The following equation sums the total scattered E-field amplitude by N atoms, in which the exponential terms make up a phase factor that keeps track of the phase difference for all of the atoms in a sample:
Note that is the amplitude of scattering by an individual atom, which will be the same for all atoms of the same type and distinct for different atoms. The summed fields are normalized by the scattering amplitude that is expected from one electron according to classical Thomson scattering- .
If all atoms are same type, otherwise different
The scattered intensity in electron units, or the scattered intensity of N atoms as compared to the scattered intensity of a single electron is given by the following equation:
Here, the normalized total electric field equation is multiplied by its complex conjugate to yield the intensity as given by .
In the following step, the is subdivided into and allowing for a grouping into a double summation. Here the and factors account for possibilities of interference of scattered waves between two atoms.
In the following vector diagram for the term, the origin is conveniently chosen to be at the location of the green “0” atom. The difference of and gives the inter-atomic distance between atoms 3 and 4, labeled .
Scattered intensity for N atoms
Now, the inter-atomic spacing vector replaces the term previously used.
From this double summation, there are terms that are of the type
There are N terms of the type: m=0,1,2...N-1
These terms, where m = n , are like the scattered intensities from single isolated atoms, in which no interference effects occur. Here is 0, and the exponential term goes to 1.
There are of the type:
These are the cross terms, where
This is the general equation for kinematical scattering from any type of atomic collection - i.e. gas, solid, liquid, crystal, amorphous, etc. The following conditions are specific to to gases, liquids and crystals:
- gases & liquids require proper averaging of (angle averaging) by small angle x-ray scattering
- crystals are periodic can use symmetry to reduce terms
Consider an X-ray plane wave
incident on a small crystal with a detector for coherently scattered X-rays at R and direction
, as seen in Figure
11.3 below.
The scattering vector determination is illustrated in Figure
11.4 below.
The crystal contains unit cells, such that mark the crystal size in the 3 basis vector directions. Each unit cell contains N atoms, which may or may not be of different types. Therefore, there are MN total atoms in the small crystal.
Each atom in the unit cell is located by a vector
, as shown in Figure
11.5 below. The atom is illustrated as a black dot in the unit cell block.
Assuming the crystal is a parallelepiped, any unit cell's origin may be located by , where is an integer. This is given by translational symmetry of unit cells.
Therefore, any atom within the entire crystal is located by the following position vector:
u.c. locationatom location in u.c.
The first three indices locate the specific unit cell containing the atom, using a translational symmetry operator. The term indicates the atom's position within that specific unit cell.
Figure
11.6 below illustrates the use of these four indices to locate an atom within a crystal. Note that the location of the origin is selected and arbitrary.
11.0.1 The scattered electric field amplitude from the entire crystal relative to the scattered field from a single electron is given by the following summation:
The four indices yield four summations, where only the last summation term is related to the exponential phase factor.
The structure factor, given by the following summation, is the amplitude of the scattered electric field from a single unit cell:
This structure factor accounts for internal interference effects from the N atoms in the unit cell. Adding the structure factor to the calculation of the total scattered field yields the following triple summation:
Consider the following simplification:
Geometric series converges
In one dimension, the total scattering intensity for M unit cells relative to the scattering intensity from one electron is given by the following:
1D Interference Function
The scattering from a single unit cell is given by the structure factor modulus squared, and the second factor accounts for interference from M repeated unit cells.
In three dimensions, each M factor is multiplied by its complex conjugate
yielding the following three dimensional interference function. This is a rigorous theory for explaining x-ray scattering from a 3-D periodic lattice. Note that the three terms account for repeated unit cells along three axes.
3D Interference Function
Considering the 1D Interference Function
when
Both the numerator and denominator vary, with the numerator having M times more oscillations than the denominator. In addition, both have periodic zeros at the same integer values of , this causes the function to go to at these values. Physically, this condition is when
Recall that is extra length in units of for scattering by two atoms separated by This makes sense with previous considerations of Bragg's law, in which an integer multiple wavelength difference in paths yields a diffraction peak.
In Figure
11.7 below,
, and
are plotted against
. The green
curve represents the denominator, and the red curve represents the
numerator where M=5. Note that the red curve has five times the oscillations of the green curve and the two have three common zeros in this range of
In the one dimensional interference function, the red function in Figure
11.7 is divided by the green function to yield the plot in Figure
11.8.
11.0.2 Note that the one dimensional interference function is multiplied by a factor to yield the following normalized function that has a maximum of one:
Figure
11.8 illustrates the unity amplitude diffraction peaks that occur when the numerator and denominator have common zeros, at
with
, etc. There is a zeroth order peak that occurs when all waves are scattered in phase and in the forward direction. In addition, there are always
subsidiary peaks between any two diffraction peaks, with the other two peaks hidden at half of the width of the large diffraction peaks at either side. These subsidiary peaks are due to the fact that the numerator,
gives zero intensity when
. The width of these peaks is also due to the
periodicity of the numerator.
What is in terms of the angle ?
The quantity is the scattering vector multiplied by , and projected in the direction of the lattice constant, . If the lattice constant and the scattering vector are in the same direction , this simplifies to the following expression:
At
Here, represents the first appearing minimum of in the periodic intensity pattern.
For a very large M,
can be set equal to
and the following expression can be used to determine the full width, full max diffraction peak width as illustrated in Figure
11.10. Note that this is simply twice the value of
for h=0
Therefore by measuring the width of the entire diffraction peak, the value may be determined, which indicates the number of unit cells in the direction of . Multiplying by yields the thickness of the crystal in the direction of Notice that and are inversely proportional, therefore as the width of a crystal increases the , or width of the peak, gets smaller.
Note the following correlation with Bragg's Law:
, in this case
Furthermore, for all other peaks ()
For all peaks, therefore, the width is inversely proportional to the size of the crystal. Therefore, by looking at the width of the peak, one can see the size of the crystal along the direction.
- for M, the area under the intensity curve becomes :
As
approaches
the intensity as a function of
approaches a delta function as shown in Figure
11.11.
12 Diffraction
Recall the the following 3D interference function for crystal, where gives the number of unit cells:
, M = # of unit cells
12.1 Laue condition for diffraction
In three dimensions, the diffraction condition is satisfied and the intensity reaches a maximum when all three fractional factors after the in the interference function simultaneously go to zero, that is when the following three conditions are met:
, , where are integers
This is known as the Laue condition for diffraction. Note that the indices are the same indices used in describing the planes of a crystal in real space.
The three scalar quantities describing in the Laue condition are equivalent to the following vector equation, which also describes the reciprocal lattice vector that points perpendicular to the planes in real space with a length of
Consider the scalar of this equation . Recall that is equivalent to and that is equivalent to the inverse of the inter-planar spacing, which leads to Bragg's Law:
Bragg's Law:
Therefore, the diffraction peak maxima occurs at:
- Scattering vector, - Scattered wave vector,- Incident wave vector ,- Reciprocal lattice vector
This relationship is illustrated in Figure
12.1 below. The scattering vector may be seen as the instrument being used in the diffraction experiment, since the incident direction, the wavelength, the location of the crystal, and the orientation of the detector as indicated by
are selected by the instrument (diffractometer). The
describes the sample's discrete set of planes in reciprocal space. Therefore, as described by the Laue condition, when the instrument's continuosly variable scattering vector
coincides with an
vector belonging to a descrete set of
vectors , a diffraction max intensity occurs.
12.1.1 Vector Representation in Reciprocal Space
In order to picture a diffraction experiment in reciprocal space, recall that the crystal planes as referenced by Miller indices are transformed into reciprocal lattice points in reciprocal space.
Figure
12.2 illustrates the
reflection in the
layer of a cubic unit cell. In this example incident beam
is represented by the incident wave vector
, and has a fixed direction and wavelength. The beam interacts with the sample at point C, and the scattered wave vector
is in direction 2
. The possible scattered wave vector form a locus of points known as the
Ewald sphere. A cross section of the Ewald sphere with radius
is illustrated in Figure
12.2 .
Ex. 012 reflection, cubic h=0 layer
12.1.2 Ewald Sphere (Radius=
If incident direction ( is fixed and fixed ,
- Sphere does not move.
- always points from center (C) to 000.
- Rotating crystal, represented by rotating reciprocal lattice, about 000.
- points form C to any points on sphere.
- Diffraction occurs when an () reciprocal lattice point coincides with the surface of the Ewald sphere.
- For X-ray wavelengths multiple reflections are rare. This probability increases with higher energies and a larger Ewald sphere.
12.2 Single Crystal Diffractometer
Consider a silicon wafer
How would you use a diffractometer and a monochromatic beam to determine if its face is (111) or (001)?
- Rotate detector to
- Rotate sample to , i.e., surface to beam
In reciprocal space, move into diffractometer plane, i.e., rotate crystal axis
- Do coupled scan
Notice that at
and
the incident wave vector and the scattered wave vector coincide with each other.
and
will be rotated, so that
is always half of
. This rotation is continued until the condition in the third illustration of Figure
12.4b is reached. Note that the Ewald sphere is fixed, and the reciprocal lattice points are now angled indicating rotation of the crystal.
- Looking at the diffraction peaks, the silicon wafer face is found to be (111), since a (001) face would yield diffraction peaks of the order (00), with .
Note: The 222 is missing because for Si.
12.3 Diffraction Methods
10 summarizes the Laue method, rotating crystal method, and powder method based on the variability of
and
. The rotating crystal method, discussed in the previous section, uses a monochromatic beam of fixed wavelength and has a variable
for scanning diffraction peaks in series. The Laue method has a fixed
and a variable wavelength since the incident beam is continuous rather than monochromatic and allows for various diffraction peaks to appear at once. The powder method has a monochromatic beam of fixed wavelength and a variable
since the crystallites in the beam have random orientations.
|
Diffraction Methods
|
|
|
|
Laue Method
|
Variable
|
Fixed
|
|
Rotating Crystal Method
|
Fixed
|
Variable
|
|
Powder Method
|
Fixed
|
Variable
|
Table 10: Diffraction methods
12.3.1 Laue Method - white beam / single crystal
For the Laue method, there is an incident white beam consisting of a continuum of wavelengths which interacts with a crystal as shown in Figure
12.5 below.The crystal consists of sets of planes, indexed in reciprocal space by the
vector perpendicular to the planes in real space. Satisfying Bragg's law based on these crystal planes creates a Laue spot on the film located downstream from the sample. This film location is used in the transmission Laue experiment setup.
Transmission Laue
In the back reflection geometry, the beam comes through a hole in the film or 2D area detector and hits the crystal planes in the single crystal sample as illustrated in Figure
12.6. The crystal selects a particular wavelength that matches up to a particular reflection of planes and spacings such that the scattered monochromatic beam that satisfies Bragg's law. There are multiple wavelengths that are harmonics or integer multiples of each other that make up a Laue spot i.e. 220,440,880,etc. However, the diffraction intensity gets weaker for higher harmonics due to many different factors including the atomic scattering factor.
Back Reflection Laue
12.3.2 Reciprocal lattice treatment of Laue method
In reciprocal space, there is a continuum of Ewald spheres due to the continuum of wavelengths in the incident white beam. Recall that the Ewald sphere radius is equal to
All Ewald spheres touch the origin, as illustrated in Figure
12.7. Note that this illustration shows cross sections of the Ewald spheres , and a cut of the orthorhombic P reciprocal lattice.
The incident wave vector is in the direction of
, and its length is continuum over some range due to the continuum of wavelengths in the incident beam. In the case of Figure
12.8 , the crystal is oriented in a fixed direction such that the [100] direction is coincident with the incident beam. The wavelength range of this beam is from the short wavelength limit set by the accelerating voltage to a rough upper limit of
due to absorption effects.
Looking back at Figure
12.7, the smaller sphere corresponds to the upper wavelength limit of lower energy and the larger sphere corresponds to the short wavelength limit of higher energy. Note that the radius of the small sphere is
and the radius of the larger sphere is
The two radii correspond to the limits of the incident wave vector
ranging in length from
to
Consider the (
Bragg reflection whose vector diagram is illustrated in Figure
12.9. Note that the length of the normalized incident wave vector is equal to the length of the normalized scattering vector due to their equal wavelengths. This
reflection is allowed since its vector is between the minimum and maximum Ewald spheres AO and BO in Figure
12.7. Note that the two vectors form an isosceles triangle and that the scattering vector
is coincident with the reciprocal lattice vector
Since the
angle is less than
this is the transmission Laue condition.
Transmission Laue
Now consider the (
) reflection illustrated in Figure
12.10 , in which
is greater than
. This is a back reflection Laue condition. Note that the incident and scattered wave vector form two legs of an isosceles triangle with their vertex at some point between the smallest and largest Ewald spheres for the experiment.
Back Reflection Laue
In general, the reciprocal lattice points outside the smallest Ewald sphere of radius and inside the largest sphere of radius will produce Bragg diffracted beams.
12.4 Structure Factor Examples
Recall that at the Bragg peak, the intensity relative to the intensity of one electron scatterer is derived from the three dimensional interference function. The following equation yields this relative intensity:
Here, represents the number of unit cells that are diffracted, where in three dimensions and define the number of unit cells in the three distinct axes. The structure factor times its complex conjugate, , affects the relative intensity of the Bragg peak and is given by summation of the individual atomic scattering factors of the atoms in the unit cell and their respective phase factors.
Structure Factor for unit cell with N atoms per unit cell
Recall that the individual atomic scattering factor has a form factor and correction factors where in general. We simplify this by assuming that for atoms at positions
where .
At the Bragg peak the scattering vector coincides with a distinct vector within the crystal. . This may replace the scattering vector in the structure factor equation to yield the following simplified relationship for a structure factor at a Bragg peak:
Structure Factor at hkl Bragg Peak
12.4.1 Primitive Unit Cell (P)
The simplest structure factor example is a primitive unit cell with one atom per lattice point. This atom is placed at the origin for convenience. In this case, is the same for all reflections and does not depend on the .
1 atom/lattice point N=1
for all
12.4.2 Body-Centered (I) Bravais Lattice
For the body centered cubic, tetragonal, and orthorhombic Bravais lattices, there are a total of two atoms of the same kind with one atom per lattice point. A two dimensional projection is illustrated in Figure
12.11.
1 atom/lattice point N=1
The 2 identical atoms are located at positions and :
,
The following is the structure factor calculation for the body-centered Bravais lattice:
If h+k+l is an even integer, then the structure factor is equal to and the two atoms are scattering perfectly in phase.
for all (even sum)
If h+k+l is an odd integer, then the structure factor is zero, and the two atoms are scattering perfectly out of phase.
for all (odd sum)
Note:
12.4.3 Base Center (C) Bravais Lattice
The base centered lattices have two lattice points per unit cell.
1 atom per lattice point N=2
The atoms are located at the following positions:
,
Plugging these positions into the structure factor equation yields the following:
Again, there are two cases, one in which the two atoms are scattering perfectly in phase and one in which they are scattering perfectly out of phase.
The index has no effect on the body-centered structure factor - for instance, 111, 112, and 113 all have the same structure factor.
12.4.4 Face Center (F) Bravais Lattice
For the face centered lattice, if there were one atom per lattice point, there will be four atoms total in the non-primitive unit cell.
1 atom per lattice point N=4
The atoms are located at the following positions with the unit cell:
The face center lattice positions yield the following structure factor:
There are two distinct cases for the face center structure. That is, when the are unmixed (all even or all odd), then all four atoms scatter waves perfectly in phase and when the are mixed (even and odd) then the four atoms scatter waves that destructively interfere.
For instance, the 022 planes would yield perfectly constructive interference and the 011 planes would yield perfectly destructive interference.
,
12.4.5 Hexagonal Closed Pack (HCP)
For the hexagonal closed pack structure, there are two atoms of the same type per lattice point. Recall that the unit cell is hexagonal primitive, and there are two atoms in total. One atom is positioned at the origin 000 and the other atom is in the position.
Hexagonal-P Bravais Lattice
Ex. Zn, Ti, Mg
Using the hexagonal closed pack atom locations yields the following structure factor:
, where
The structure factor times its complex conjugate eliminates the imaginary terms and simplifies the expression into the following:
Because there are two atoms in the unit cell, we expect two extreme conditions - one in which the two scatter perfectly out of phase and one in which the two scatter perfectly out of phase. When the parameter is an integer, will equal , producing a very strong reflection due to constructive interference. If is equal to an odd integer, then will equal , yielding a total intensity of zero.
Squaring the structure factor yields the following expression:
- (even) AND
e.g., (002), (112), ... very strong (in-phase scattering)
AND
e.g., (102), (200), (100)...weak reflection
- (odd) AND
e.g., (001), (111), ... forbidden reflection
AND
e.g., (103), (013), (101)... strong reflection
Therefore, there are four types of diffraction peak intensities for this hexagonal closed pack structure, ranging from forbidden reflections to very strong reflections.
12.4.6 More than one atom type per unit cell
We will now analyze the case of more than one atom type per unit cell such as the rock-salt lithium fluoride structure.
LiF NaCl structure FCC
The following indices locate the lithium the lithium and fluorine atoms within the face centered cubic unit cell:
at 000 +
at
The structure factor is given by the following equation:
- for all even (200), (222), etc.
- for all odd (111), (311), etc.
- 0 for mixed (210), (001), etc.
Recall, in the lab that you saw: strong, weak, & forbidden FCC.
Kinematical scattering ignores multiple scattering due to low probabilities of re-scattering after a wave has scattered from one atom.
Note that the Laue method is useful for finding the symmetry of crystal orientations, but not useful for finding the lattice constant due to a variable wavelength. Furthermore, the Laue spot position is is independent of the length of and only dependent on direction.
12.5 Width of Diffraction Peaks (single crystal)
Reciprocal lattice points have dimensions which are inversely proportional to the size of a crystal in a given direction.
Recall the 3-D Interference Function whose component is given by the following:
The numerator in the function determines the oscillation and width of the diffraction pattern, whereas the denominator causes the Bragg peaks to occur. As
and
increase the diffraction peaks become narrower as 1/M and the peak heights increase as M
. Cosequentially, the area under the peak goes as M. The reciprocal lattice points which were previously thought of as infinitesimal points, now can be given a breadth related to the width of the Bragg peaks as shown in the two dimensional projection of Figure
12.16. Note that the size of the crystal may be different in the a and b directions.
For a scan along the direction, the diffraction peak width is proportional to the breadth of reciprocal lattice spot in direction or The full width half max length is estimated by Scherrer's Formula
Scherrer's Formula
where is the crystal size in the direction. (The measured peak width is also affected by the incident beam's X-ray coherence length.)
e.g.,
If crystallites, such as those in a powder sample, are on the order of a tenth of a micron, then the width of the peak will be one milliradian.
Therefore when measuring a diffraction pattern, you first locate the peaks which give information about the lattice constant and symmetry of the crystal. The shape of the peak is an indicator of the crystal size in different direction.
Each Bragg peak maximum is given by , where is affected by atomic positions in the unit cell.
Each Peak Width crystal size
In addition, crystal size may be determined from a transverse or longitudinal scan.
from scan (longitudinal scan) from scan (transverse scan)
What else can affect the height and width of the diffraction peaks?
- Angular divergence of incident beam - if an incident beam is very divergent
- Crystal defects - affects the width of the peak
To smooth over these two effects, we use angle integrated peak intensities to find relative values of (then compare to calculated from model).
12.6 Transverse scan rock crystal through peak with fixed
In a
transverse scan, the sample is always at the center of the Ewald sphere. This experiment setup is illustrated in Figure
12.17 below. The incident beam wave vector of length
enters the sample and always hits the origin (000) of the reciprocal lattice on the Ewald sphere. For the
fixed scan, in which the angle of the sample
is varied, the reciprocal lattice points rotate about 000, as illustrated by the black dashed lines on the left side of Figure
12.17. Since
is restricted to the width of the slit, the Ewald sphere intersection with lattice point at 010 will produce a line of points that does not capture the entire integrated intensity of the reciprocal lattice ellipsoid. Recall that this is a two dimensional projection, and that the line of points depicted by a horizontal red line across the blue ellipse in Figure
12.17, is actually a plane intersection of the 010 reciprocal lattice ellipsoid. If we remove the slit and do the same scan across
, the entire intensity is captured, as illustrated by the red ellipse in Figure
12.17. This is an angle integrated scan.
The integrated counts or the energy in a peak is given by the following equation:
angular velocity of crystal rotation, a step rotational scan is now used
step rotational scan, a faster scan yields fewer counts
unit cell volume
Effective volume of irradiated sample
Polarization Factor for unpolarized beam
Lorentz Factor for single crystal diffraction with constant , time taken to sweep Ewald sphere through a relative point (reciprocal lattice point)
Note that the tangential velocity of relative point through Ewald sphere is given by .
In Figure
12.18, notice that the 200 and 400 diffraction conditions are scanned at different speeds due to the geometry of the Ewald sphere . The intensity for the 200 lattice point will be greater because the Ewald sphere travels and scans more quickly through this point yielding a smaller intensity relative to the 400 lattice point.
This is another reason why for LiF
12.7 Polycrystalline Aggregate (Powder sample)
In the
powder method, the sample is reduced to a fine powder of thousands of randomly oriented small single crystalline grains to be placed in a beam of monochromatic x-rays. In reciprocal space, this random orientation results in concentric spherical shells with radii corresponding to the crystal's set of
values. The illustration in Figure
12.19 below illustrates reciprocal lattice vectors
and
being smeared out in angle to form two concentric spherical shells.
The surface density of relative points is equal to the number of crystallites divided by the surface area of the spherical shell.
- Surface density
We assume that since the powder sample is isotropic, each sphere has uniform surface density. If a texture sample is used, a preferred direction may exist and the density will be non-uniform.
12.7.1 Powder XRD Ewald construction for one with uniform density
The Ewald sphere for one
with uniform density is illustrated in Figure
12.20 below. This blue Ewald sphere has a definite center and radius, and the monochromatic incident beam
goes from its center to the origin of the sample's reciprocal lattice sphere at 000. The intersection of the Ewald sphere and the sample's sphere for one
, marked by the red dashed circle, represents the entire set of allowed scattered wave vectors
that will emanate from the center of the Ewald sphere. This circular locus of points will produce a diffraction cone of scattered wave vectors beginning from the origin of the Ewald sphere and ending at the circular intersection of the two spheres. In a small slit powder diffractometer, only a segment of the circle is captured as the slit scans around
Placing a film downstream from the sample would show the entire
Bragg ring
.
This satisfies the Laue condition in which the scattering vector is equal to a specific reciprocal lattice vector of the sample.
12.7.2 Calculated Diffracted Intensity (Power)
This is for entire Bragg Ring of circumference:
,
A horizontal diffractometer with detector slit at R and vertical slit height records a fraction of the Bragg ring .
12.7.3 Multiplicity Correction
The case of
multiplicity occurs when different combinations of hkl have the same same
length in reciprocal space. Since these all contribute to the same spherical shell, then the overall intensity of the diffraction condition will be greater.
E.g. Cubic:
Note: C&S
12.7.4 Powder Diffraction Intensity
Including the multiplicity correction factor, the measure of the power for a diffraction condition of a given hkl is given by the following:
Where effective sample volume and
Lorentz-Polarization factor for powder diffraction
Note:
Why do we use a symmetric reflection geometry for powder diffraction?
(i.e. or scan)
As proven in the following section, this geometry causes the effective sample volume to be constant over the entire scan range.
12.7.5 Absorption Effects
Recall that the linear absorption coefficient is represented by and that the absorption length of a material is given by . A low Z material like water or a hydrocarbon has a longer absorption length than a solid metal.
Consider a large planar sample with thickness t in reflection geometry as illustrated in Figure
12.22. The incident beam with area A across enters at an angle
, and scatters from a differential volume at some depth z. The
detector is lined up to pick up the scattered intensity at the angle
. In general,
and
do not have to be equal.
the beam area produces a projected area of the slab that is
Therefore the volume element is given by
The diffracted intensity at depth z is given by the following:
There is an absorption effect that attenuates the beam as it enters and exits sample, which is accounted for by the following two transmission factors:
- in transmission factor
- out transmission factor
To calculate the total intensity, we integrate over the total thickness:
Assuming the thickness is much greater than the attenuation length, or - for a typical oxide material this thickness is about 0.5 mm.
“t” drops out by assuming or
For symmetric reflection effective volume =
Note that the effective volume, , is constant and independent of for . As you increase the angle in this geometry, you are increasing the depth but decreasing the effective area. Therefore, it is convenient to use symmetric reflection geometry for a powder diffraction experiment, in order to be able to avoid varying absorption effects from a varying effective volume.
We could also do diffractometry in symmetric transmission mode as illustrated in Figure
12.23.
We want as much material in front of the beam to yield a high scattering intensity, but we also want a small enough thickness to avoid too much absorption. There is an optimal thickness in this transmission geometry, that yields the maximum scattering compromised correctly with the absorption. Recall that is the absorption length.
Effective Volume:
Here, depends on .
12.7.6 Summarize: Powder diffractometer in symmetric reflection geometry
The area under the diffraction peak is proportional to:
- structure factor and
- multiplicity
- Lorentz polarization factor,
- temperature dependent Debye-Waller factor accounting for atomic vibrations
Our objective is to measure the integrated intensities 's and use the structure factor 's to determine the crystal structure.
At extreme angles, the Lorentz polarization factor has a considerable effect, as shown in Figure
12.24.
12.7.7 Multiplicity Factor
: number of planes in the family for a given crystal system
Example:
0kk
|
022
|
|
|
202
|
|
|
220
|
|
|
|
|
|
|
|
|
|
0
|
Cubic , since all 12 's are equal
triclinic ,
triclinic
Since only
See Cullity and Stock Appendix 11
|
Cubic:
|
|
|
|
|
|
|
|
|
Hexagonal and Rhombohedral:
|
|
|
|
|
|
|
|
|
Tetragonal:
|
|
|
|
|
|
|
|
|
Orthorhombic:
|
|
|
|
|
|
|
|
|
Monoclinic:
|
|
|
|
|
|
|
|
|
Triclinic:
|
|
|
|
|
|
|
|
Table 11: Multiplicity factors for powder XRD
12.7.8 Indexing Powder Diffraction Patterns
We can determine lengths (not directions) from experimentally measured and the known value of using the following relationships:
First index the series of peaks (i.e. determine ), then determine the lattice constants of the Bravais lattice :
Initially check for cubic, the simplest case, where .
Cubic: subject to Bravais lattice conditions.
See Cullity and Stock, Appendix 9 - also shown below in Table
12.
|
|
|
P
|
F
|
I
|
Diamond
|
|
1
|
100
|
x
|
|
|
|
|
2
|
110
|
x
|
|
x
|
|
|
3
|
111
|
x
|
x
|
|
x
|
|
4
|
200
|
x
|
x
|
x
|
|
|
5
|
210
|
x
|
|
|
|
|
6
|
211
|
x
|
|
x
|
|
|
7
|
|
|
|
|
|
|
8
|
220
|
x
|
x
|
x
|
x
|
|
9
|
300,221
|
x,x
|
|
|
|
|
10
|
310
|
x
|
|
x
|
|
|
11
|
311
|
x
|
x
|
|
x
|
|
12
|
222
|
x
|
x
|
x
|
|
|
13
|
320
|
x
|
|
|
|
|
14
|
321
|
x
|
|
x
|
|
|
15
|
|
|
|
|
|
|
16
|
400
|
x
|
x
|
x
|
x
|
Table 12: Determining if unit cell is cubic from
Therefore, we can check for pattern in the sequence of measured
values, which are proportional to
, and relate these to the corresponding unit cells using Table
12.
If
Cubic-P
Cubic-F
Cubic-I
Diamond
Note that we need to measure for at least the first seven peaks to distinguish between Cubic-P and Cubic-I.
Tetragonal and hexagonal (“uniaxial”)
Tetragonal:
Hexagonal:
is unknown
is 1st peak ?:
100 or 001 (P)
110 or 002 (Tetragonal I)
100 or 002 (HCP)
12.7.9 Example 1
|
Line No.
|
|
|
|
|
|
|
1
|
0.0603
|
1
|
3/3
|
3
|
111
|
|
2
|
0.1610
|
2.67
|
8/3
|
8
|
220
|
|
3
|
0.221
|
3.67
|
11/3
|
11
|
311
|
|
4
|
0.322
|
5.34
|
16/3
|
16
|
400
|
|
5
|
0.383
|
6.35
|
19/3
|
19
|
331
|
|
6
|
0.484
|
8.03
|
24/3
|
24
|
422
|
|
7
|
0.545
|
9.04
|
27/3
|
27
|
333
|
|
8
|
0.645
|
10.7
|
32/3
|
32
|
440
|
Table 13: Indexing Powder Patterns, Example 1
Ratios Cubic
unmixed hkl: Cubic F
: diamond cubic
What is “a”?
Silicon a=
12.7.10 Example 2
|
Line No.
|
|
|
|
|
hkl
|
|
1
|
0.0806
|
1.00
|
A+C
|
0.0806
|
101
|
|
2
|
0.0975
|
1.21
|
4C
|
0.0976
|
002
|
|
3
|
0.1122
|
1.39
|
2A
|
0.1124
|
110
|
|
4
|
0.210
|
2.61
|
2A+4C
|
0.210
|
112
|
|
5
|
0.226
|
2.80
|
4A
|
0.225
|
200
|
|
6
|
0.274
|
3.40
|
A+9C
|
0.276
|
103
|
|
7
|
0.305
|
3.78
|
5A+C
|
0.306
|
211
|
|
8
|
0.321
|
3.98
|
4A+4C
|
0.323
|
202
|
Table 14: Indexing powder patterns, example 2
Ratios not cubic
Note Relations:
(4)=(2)+(3)
(5)=2(3)
(7)=(5)+(1)
(8)=4(1)
Assume Tetragonal:
Tetragonal P(1) = 100 or 001
No peak at 2(1) not P
2(1) =110, if (1) = 100
Tetragonal I: (1) =110,101, or 002
Try (1)=101
hk 00 10 11 20 21 22 30 31 32 ... 0 1 2 3 4 ...
0 14 5 8 9 10 13 ...0 1 4 9 16 ...
If *
Think about it
Try:
Note
Check to see if each for A = 0.0652 and C = 0.0244
Conclusion: Tetragonal I
Lattice constant: a=? c=?
Indium
Procedure for hexagonal similar to tetragonal except:
where
Indexing difficulty increases as crystal symmetry decreases: need computer
Note: When and are unresolved (at lower ), use avg
At higher and may be resolved, use correct and , not
12.7.11 Quantitative Analysis
Recall: , ignore
Consider a 2 phase powder with:
volume fraction of phase A, volume fraction of phase B
Phase A diffraction peaks
varies with
varies with
Phase B diffraction peaks
is the same
Hence,
To determine volume fraction for mixture of 2 powder crystalline phases A&B
The relative intensities of peaks for each phase should be checked to ensure an ideally random powder sample. Texture will cause errors in quantitative analysis.
In the analysis of the integrated area under the diffraction peaks, the Debye-Waller factor, , may be included if known. The two different phases are made up of atoms in two different lattices with different vibrational amplitudes. The vibrational amplitude is given by the following:
Here is the root-mean-square (rms) vibrational amplitude in the hkl direction. These vibrations are typically isotropic with a magnitude of 0.1. An increase in temperature increases the vibrational amplitude of atoms.
12.8 Rotating Crystal Method
In the
rotating crystal method, a single crystal is mounted with an axis that is normal to a monochromatic beam. A cylindrical film encloses the single crystal, which records a diffraction pattern as the crystal is rotated. This setup is illustrated in Figure
12.25. Whereas older films required chemical exposure to develop, x-ray sensitive image plates are used today and diffraction patterns are read out by a laser.
In this procedure, the crystal is rotated smoothly about a chosen axis that coincides with the axis of the film cylinder and different planes cause diffraction peaks at points in the rotation. Diffraction peaks occur when a set of lattice planes make the correct Bragg angle for reflection. In the setup illustrated in Figure
12.25, prior to inserting the crystal in the camera, the c-axis of the crystal's unit cell was determined and the crystal is then rotated about this axis. Due to this rotation about the c-axis, the spots appear in layers with heights according to constant
index values. All of the center spots are
.
The rotating crystal method helps determine the structure of a crystal in an organized manner, and is useful for methods where a single crystal can be attained as well as when the and axes of a crystal's unit cell coincide with each other.
12.8.1 Rotating Crystal Method
- Monochromatic X-ray beam diffraction from single crystal surrounded by film cylinder.
- The crystal continually rotated about the axis that coincides with film cylinder axis
- If rotation axis = unit cell axis (e.g., ) then reflection pattern (spots) on film form circles at heights corresponding to constant (e.g., )
- This is for unit cells where
Figure
12.26 below illustrates a developed rotating-crystal film of a quartz crystal. The extra streaks around the center of the pattern are due to Brems-strahlung radiation not removed by the filter.
12.8.2 Reciprocal Lattice Treatment of Rotating-Crystal Method
How do we picture the rotating-crystal method in reciprocal space? Visualizing the method in reciprocal space, the Ewald sphere is the instrument, and the reciprocal lattice structure is the crystal sample. An orthorhombic crystal crystal centered at the Ewald sphere may be rotated about the c-axis, as illustrated in Figure
12.27 Recall that the incident wave vector always points from the center of the Ewald sphere to the origin of the reciprocal lattice. If the crystal is rotating about the c-axis, then reciprocal lattice rotates about its
or
axis. A diffraction peak will appear when a reciprocal lattice point touches the Ewald sphere. In this camera, all diffracted beams will be detected and recorded except those that travel close to the cylinder's central axis and miss the film.
- The reciprocal lattice rotates about as the crystal rotates about
- Spots appear on the film when reciprocal lattice points coincide with the Ewald sphere.
- Recall the Laue condition, when
We will divide the scattering vector into horizontal and vertical components, and The and angles determine the in plane and out of plane components of
After the scattered diffracted beam places various spots on the film, the film is unrolled and the specific and coordinates of these characteristic spots are noted. Using these coordinates and the radius of the cylinder, and may be determined using the following equations:
Example: , , , and mm
12.8.3 Ewald Construction for Rotating Crystal Method
In the rotating crystal method, the diffraction spot positions (
coordinates) are experimentally determined and the film cylinder radius is known. The
coordinate gives the layer line, such as
etc. and the
coordinate indicates where this spot is located on the layer line. Using these values, we can determine the in-plane (
) and elevation (
) angles, as well as information about the scattering vector which is coincident with the reciprocal lattice vector for a diffraction spot. Geometric relationships using the Ewald sphere are pictured in Figure
12.20 below.
Define angles:
in-plane angle
elevation angle
Separate
Note:
Bragg's law below
A. For hexagonal ,tetragonal, cubic, orthorhombic, etc., where coincides with , measuring the coordinate allows us to calculate the elevation angle, and the vertical component of the scattering vector determined directly
By remounting the crystal to rotate about or , we can determine and .
B. Indexing a reflection in layer line
For a given layer line, is constant.
for constant layer line
12.8.4 Bernal Chart
The
Bernal chart is a graphical method that aids in the conversion the
and
coordinates of diffraction spots to
. This graphical aid can be superimposed on the film roll, as shown in Figure
12.31 below.
Graphical method for converting
Horizontal Lines constant for axis rotating
lines equally incremented from 0 to 2.0. The maximum is when
for
Start with layer
- Assume
- Assume
Once the lattice constants and orthorhombic unit cell have been determined, index and determine Lattice Type: P, I, C, F.
Measure X and Y from the film
R = 50 mm ,
For layer,
|
X [mm]
|
|
[]
|
|
hkl
|
|
22.4
|
0.488
|
25.67
|
0.288
|
110
|
|
23.3
|
0.466
|
26.70
|
0.299
|
020
|
|
39.6
|
0.792
|
45.38
|
0.500
|
200
|
|
40.8
|
0.816
|
46.75
|
0.515
|
130
|
|
46.6
|
0.932
|
53.40
|
0.583
|
220
|
|
48.1
|
0.962
|
55.12
|
0.600
|
040
|
|
63.1
|
1.262
|
72.31
|
0.765
|
310
|
|
64.6
|
1.292
|
74.03
|
0.781
|
240
|
|
65.5
|
1.31
|
75.06
|
0.790
|
150
|
|
74
|
1.48
|
84.80
|
0.875
|
330
|
|
76.7
|
1.534
|
87.89
|
0.900
|
060
|
|
88
|
1.76
|
100.84
|
1.000
|
400
|
defines radius of circle in the reciprocal space plane
Table 15: Conversion of X to hkl
Figure
12.33 below demonstrates the graphical solution for layer
Plot hk0 lattice: &
Plot circles with radii
, shown in Figure
12.33 below.
The blue squares represent the reciprocal lattice points corresponding to the planes that caused diffraction to occur.
Repeat this procedure for layer
13 Temperature Effects
The atoms in a crystal vibrate about equilibrium lattice positions, even at K and the vibrational amplitudes increase as temperature increases. With increasing atomic kinetic energies, the unit cell expands and the lattice constant becomes greater. This temperature effect, also known as the Debye-Waller effect, affects the area under diffraction peaks even at room temperature. It is important to account for this effect since the area under diffraction peaks gives information about the crystal structure via the structural factor.
Figure
13.1 illustrates a simple model of interatomic spacing in a crystal as a function of energy, in which the red dots indicate the average interatomic distance. Note that as temperature and energy increase, the width of the potential well widens to the right, towards a greater separation distance. An increase in temperature leads to a sampling of higher energies in the potential well and a lattice expansion as indicated by the red dots in the plot. The width bounded by the two walls of the potential also increases, allowing the atoms to take greater path lengths and have greater vibrational amplitudes.
13.1 Describe a crystal in terms of primitive unit crystal.
Considering a crystal of M primitive unit cells, the will replace the former lattice point position vector, which now includes an extra factor - a time dependent displacement vector for each atom.
- For simplicity sake we will assume one atom per lattice point at origin
- Let # of unit cells
- Let = unit crystal index
- Let lattice point position vector. Locates origin of the unit cell
- Let
Atoms can vibrate longitudinally or transversely, as shown in the figures below.
The summation of the coherently scattered wave intensities in electron units from atoms for a crystal with one atom per unit cell is given by the following:
Assuming all of the atoms are the same, the and terms may be taken out of the summation. Adding in the time dependent Debye-Waller factors yields the following:
Recall that is the scattering vector that is coincident with under the Bragg diffraction condition.
<table class='mathtable'><tr><td class='math'>\bar{Q}\cdot\bar{\Delta}_{m}=\frac{2sin\theta}{\underset{\hookrightarrow Q}{\lambda}}\Delta_{m}cos\phi_{m}</td><td>(13.3)</td></tr></table>
The vector is the projection of the instantaneous displacement vector along the scattering vector's direction:
Note that for longitudinal wave along diffraction plane.
Using , the intensity equation is the following:
Note that are instantaneous vibrations that occur in the phonon lifetime which is on the order of ~ seconds , and the intensity measurement time is > seconds. Therefore, a time average of these instantaneous intensities as affected by vibrational effects is used.
The function is integrated over a period of time that is long relative to the fluctuations and is normalized by dividing by
The time averaged intensity is indicated by bracket notation:
Simplifying, by Maclaurin series expansion:
Let
which accounts for the correlation of vibrational motion between the atoms, and may range from 0 to 1.
and
[3-D interference function]
With higher , the diffraction peak intensities decrease due to the damping term at the front.
The new term, B, is sensitive to the temperature and vibrational amplitudes. Using B, the intensity can be written as follows:
Since the correlation function is equal to unity at an atom (i.e. ) and only has a considerable effect at a small region around an atom, the diffraction peaks in the second summation are broadened. Recall that a smaller number of unit cells produces broader peaks than a relatively larger amount of unit cells.
Why time average?
Because measurement time for intensity (1 sec) phonon lifetime ( sec)
Why do odd powers of ?
We assume about = 0
The average time displacement for odd powers averages to zero, but for even powers, the area under the curve is . This explains why even powers are present in the time average and odd powers are not.
13.2 Debye Theory of Lattice Dynamics/heat capacity — Corrected by Waller
The quantity B, which describes the vibration of the atoms, is described by the following equation:
where the variables are defined as follows:
- atomic mass =
- Planck's constant =
- absolute temp
- Boltzmann's constant =
- Debye temperature (related to stiffness of crystal) e.g. ,
for declines rapidly for
Unvarying constants:
Therefore, the mean square vibrational amplitude (assume Q=1) is given by the following:
- For at R.T. (
- For at R.T. (
- For at R.T. (
Debye-Waller Factor
If we look at the Debye-Waller factor in terms of real components, and , we see a comparison between the vibrational displacement and the d-spacing within a crystal.
For silicon, the (220) peak intensity is diminished by as shown below. If we move to greater peaks, such as (880) with a smaller spacing, the attenuation significantly affects the peak intensity.
- For Si (220), at R.T.
- For Si (880), at R.T.
Note that the (880) d-spacing is of the (220) d-spacing. Since the is squared in the Debye Waller factor, this causes the peak intensity of the (880) to be of the (220) intensity.
Note : Original Debye Theory { 1, m=n; 0, otherwise
If we only account for the 3-D interference function and divided by
, then the intensity will always have an intensity of
, as shown by the dashed curves in Figure
13.8. However, the Debye-Waller factor attenuates the peaks in an exponential fashion with an increasing Q, as shown by the three peaks with amplitudes following the
curve. Finally, the TDS increases the background radiation and widens the peaks, but this effect is exaggerated in the figure below.
13.3 Symmetrical Reflection Powder Diffraction
The intensities are multiplied by the Debye-Waller factor - , therefore as increases, the peak intensities diminish.
M depends on:
- crystal type (Si, Ge, etc. )
- direction (anisotropic crystals) - network of “springs” different in different directions, such as graphite
- d-spacing ~ 1/
- Temp. T
- Crystal bonding (covalent, molecular, etc. )
“B” can be measured by comparing integrated intensity of hkl to 2h 2k 2l reflection, Measuring B is like measuring bonding properties and temperature effects.
13.3.1 For h k l
13.3.2 For 2h 2k 2l
13.3.3 Since
All of the above are known, except B
where, u is the vibrational amplitude around a given atom.
14 Thin Film X-ray Scattering
Recall the 1-D interference function:
of the scattering angle
An incident wave vector and a scattered wave vector, as well as the scattering vector are illustrated in Figure below.
14.1 1-D interference function
For a linearly periodic series of N identical scattering points with period d, the scattered intensity from these points is:
Note that the function peaks at
, as shown in Figure
14.2. The
indicates the scattering pattern by one scatterer. The Bragg peak half width full max is shown in the period of the fringes, which is numerically the period of the numerator, given by
.
- Peak intensity
- Denominator Bragg peaks
- Numerator Bragg peak width
- Crystal size (thickness) = =
- Bragg peak HWFM = Fringe period = period of the numerator =
- Bragg peak area
14.2 HRXRD of single crystal Ferro-Electric Ultra-Thin Film
In the following experiment, a film is grown on a (001) substrate, where the two lattices nearly line-up latterly at the interface and create a structure very similar to a single crystal,
At 001 Bragg peak:
cubic:
tetragonal:
,
The following figure shows the reflectivity from this thin film in a scan in reciprocal space along the (001) direction. The strontium titanate is like a semi-infinite crystal, therefore yielding a very narrow delta-function like peak. The broad peak is twice the width of the subsidiary peaks
paraelectric and ferroelectric
transition temperature
Tetragonal structure: c/a = 1.063
Metal organic chemical vapor deposition grown films on
Polarization of as-grown c-domain film?
The structures are comprised of anions and cations, and there is displacement of the positive anions relative to the negative cations. Overall, there is an electric dipole moment in a given unit cell. There are two energy equivalent states, “up” or “down,” as shown in Figure
14.6.
In determining the structure factor, the exact positions of the atoms must be known.
14.3 Friedel's Law
If X-ray Absorption is neglected, then
PbTiO3
3.9051 3.9051 4.156 90.0 90.0 90.0
400.
1.0 1.0 1.0
3 1 1 1
Atoms in basis # 1
Pb
82 1.000
1
0.00 0.00 0.1159
Atoms in basis # 2
Ti
22 1.000
1
0.500 0.500 0.5769
Atoms in basis # 3
O
08 1.000
3
0.50 0.00 0.5
0.50 0.5 0.00
0.0 0.50 0.50
14.4 Experimental Reflectivity along the (00L) Crystal Truncation Rod (CTR) for ferro-electric PZT thin-film capacitor heterostructure
In Figure
14.7, the experimentally measured X-ray reflectivity of the PZT capacitor structure is taken at
. The inset shows the layers within the heteroepitaxial structure, a
(001) substrate, a 136-nm-thick
bottom electrode, a 20-nm-thick PZT film and a 30-nm-thick Ag top electrode. The angle positions for the three distinct (001) Bragg peaks mark off the the three distinct
lattice constants of
, and PZT.
The two patterns of oscillation are due to the thickness of the and PZT films, where the smaller period oscillation belongs to the thicker film. The Ag top electrode has a polycrystalline structure and does not measurably contribute to the scattered intensity in this high-resolution scan.
As predicted by the numerator of the interference function, the widths of the peaks and their Laue fringes are inversely proportional to the film thickness.
What about diffraction from 2D crystals?
In one dimension, there is a set of periodic scatterers and in reciprocal space, there exists a set of parallel periodic planes with a
spacing. In two dimensions, there are two constants for the Laue condition, yielding a net of parallel rods in reciprocal space as shown in Figure
14.8.
|
Crystal D
|
Real-Space Basis
|
Laue Condition
|
Recip. Space Periodicity
|
|
1D
|
|
|
planes,
|
|
2D
|
|
|
rods, plane
|
|
3D
|
|
|
points
|
Table 16: Real Space Reciprocal Space
From 1D Laue Condition:
- diffraction peak at
2D crystal diffraction can be explained in reciprocal space by combining the
radius Ewald sphere with the set of rods depicted in Figure
14.8. The Ewald sphere center (C) connects to the k-space origin by the incident wave-vector
.
Figure
14.10 illustrates an example of low energy electron diffraction (LEED), where
is directly perpendicular to the 2D crystal
AC-plane. This is a cut in k-space showing only the (h0) rods with ~ 13
.
Diffracted wave vectors (or k) extend from C to the intersection point of the (hk) rod and the Ewald sphere. Note that each rod can produce a forward diffracted beam and a back reflected beam, due to two intersections with the Ewald sphere. This diagram also portrays diffraction from a 1D periodic grating, in which case the (h0) rods become (h) planes seen edge-on in k-space.
Low-Energy Electron Diffraction
For a low energy electron diffraction instrument, the accelerating voltage is controlled.
Recall the de Broglie relation for X-rays: , where
More generally, where momentum and for a photon since
- For non-relativistic massive particles,
- For electrons: for 150V (electron beam with a wavelength on one angstrom requires 150 V).
- For neutrons: , . Greater kinetic energy is required for neutron of greater mass relative to electrons.
- Thermal neutrons at RT.
- Neutron diffraction has a different sensitivity to elements than x-rays.
The filament is in vacuum, and a negative potential relative to sample at ground is applied to accelerate the the electrons toward the sample. The diffracted electrons hit a fluorescent screen placed below the sample reveals the diffraction spots.
Wavelength gives radius, spacing is for copper.
Why is electron diffraction surface sensitive, in comparison to x-ray diffraction?
Electron beam interacts very strongly with matter, showing scattering from top one or two layers whereas x-rays interact very weakly.
Universal mean free path for electrons based on inelastic scattering (plot vs KE)
To achieve surface sensitivity with x-rays we must use total external reflection which produces and evanescent wave with nanometer penetration depth.
4-Bromostyrene SAM on Si (111) surface.
R( calculated for 1/2 ML coverage.
A z-axis projection can be performed for the structure.
Substrate Reflectivity:
like 1D interference function. The period of the subsidiary peaks has gone to zero since N is so large.
Molecules per 1x1 u.c = 1/2
- LS: Vertical Line Source, at focus of parabola.
- Cu Anode (8.04 keV) used for XRR;
- Mo anode (17.44 keV) used for XRF and XSW
- MM: Parabolic multilayer-mirror
- S1-4: slits
- SS1&2: solar slit for vertical collimation
- PM: Si (111) post-monochromator to increase angle resolution
- Sample on stepping motor driven 2-circle, X-translation, and -tilt
- Nal: pulse counting X-ray detector for reflected intensity on arm
- SSD: Solid-state XRF detector with pulse-height analysis and multi-channel analyzer
14.4.1 Total External Reflection of X-rays from a Mirror Surface
Start with the zeroth order structure factor number of electrons in the unit cell
is related to the zeroth order Bragg diffraction peak
For x-rays, the index of refraction: , because x-rays are above the natural frequency of the electrons in the sample.
where , ,
= electron density
critical angle
Snell's law
therefore = for
Dynamical Theory for Total External Reflection of X-rays form a Mirror Surface
,
Fresnel Theory for reflectivity from ideal mirror
where and
Penetration Depth: For
For
This is a Dynamical Theory
X-ray Reflectivity (XRR) Analysis
XRR is very sensitive to surfaces
Example: SAM/Si (111)
Fresnel Theory:
for Si mirror TER
for . Fourier transform of a step function
At dip, the scattered plane-waves from the top and bottom interfaces have a path-length difference (or phase difference).
Modulation period film thickness Range: 1 to 100nm
Modulation amplitude relative electron density of film
Modulation damping roughness of interface(s) Range: < 2nm
14.4.2 X-ray Reflectivity of UDAME monolayer on Si (111) Substrate
First step in DNA covalent attachment
Sample: Reagan Kinser (Prof. Mark Hersam)
UDAME:
(111)
UDAME-Si (111)
|
|
Exper.
|
Theor.
|
|
|
0.28
|
0.30(liq)
|
|
|
12.5
|
15.0
|
|
|
1.8
|
|
|
|
3.8
|
|
ML
Table 17:
14.4.3 X-ray Reflectivity Analysis Fundamentals
Kinematical approach:
FT of gradient of density profile
For 1 slab model
density profile, , film thickness
|
b
|
t(
|
|
|
0.5,0
|
12.2
|
3.2
|
|
0.5,3
|
13.3
|
3.6
|
Table 18: 15 Order-Disorder
15.1 Order-disorder geometry
Consider Brass CuZn (Cubic Structure)
- Ordered from Cu at 000, Zn at , or CsCl structure
- Diffraction pattern would indicate Cubic P structure
- Disordered some Cu occupy Zn sites, some Zn occupy Cu sites. In a randomly disordered structure, each site has an equal likelihood of Zn or Cu occupation Cubic I.
- Diffraction pattern would indicate Cubic I structure
The is out of phase, and the zinc and copper do not scatter equally. The absent reflections for the randomly disordered phase are called superlattice reflections, and are sensitive to the order of the crystal.
Fundamental reflections are allowed by both P and I :
The intensity in the superlattice reflection indicates the degree of order present in the crystal. A high temperature form is generally disordered, while one that is cooling down has ordered domains meeting at domain walls. Zinc would like to have copper nearest neighbors and copper would like to have zinc nearest neighbors, therefore favoring an ordered structure at cooling.
15.2 Long-range order (W.L. Bragg and E.J. Williams)
Consider a binary compound (CuZn, , etc.) with 2 types of atoms - A and B - and two correct sites in the unit cell - and .
There are atoms of type A and sites and atoms of type B and sites . Therefore the total number of atoms in the crystal is given by the following:
The following are fractions that change with temperature:
- = fraction of rightly occupied sites
- = fraction of wrongly occupied sites
- = fraction of rightly occupied sites
- = fraction of wrongly occupied sites
The fraction of wrongly occupied sites and rightly occupied sites sum to one:
In the complete order case, , .
For complete or random disorder
In general
15.2.1 Long range order parameter
The unitless quantity S is the long range order parameter, ranging from 0 to 1. Complete order has a value of S=1 and random disorder has a value of S=0.
Consider in P cubic cell
- Cu
at (000) site
- Au
at {sites
-
15.2.2 Effective Atomic Scattering Factor
The ensemble average of the atomic scattering factor from the and sites is calculated by the following equations:
-
site scattering factor
-
site scattering factor
For hkl unmixed
-
- The beta site is at 000 and the alpha sites are face centered.
-
-
Simplifying with
- yields
for hkl unmixed (fundamental reflection) independent of S
For hkl mixed (superlattice reflections)
-
-
-
-
-
recall This is completely sensitive to the long range order parameter.
Therefore, for
-
for hkl unmixed and for hkl mixed
- Note
, ,
Powder diffraction pattern, as S goes from 1 to zero, there is a
15.2.3 Order-disorder phase transitions
Measured by comparing a superlattice XRD peak to a fundamental
Temperature is normalized by the critical temperature. Measure S by comparing a fundamental diffraction peak intensity to a superlattice diffraction peak intensity.
order phase transition: and both have a discontinuity at , for
order (continuous) phase transition
16 Special Topics in X-ray Physics: Extended X-ray Absorption Fine Structure (EXAFS)
EXAFS: Why Look at photoelectron scattering?
Unlike XRD, EXAFS does not require a crystalline or semi-crystalline material to determine a material's structure. The probability of dissociating a core photoelectron is related to ionization energy, which is different for every element. This allows for an element-specific structural probe.
16.1 X-ray Absorption of Fine Structure (XAFS): an overview
The incident x ray beam cases a dissociation of core photoelectron. The electron “feels” the surrounding atoms, which yields an absorption spectrum.
X-ray Absorption Spectroscopy proves the perfect tool for studying in-depth nanoparticle structure.
From the lower energy XANES region of the spectrum, we can determine the oxidation state, charge transfer, and chemical fingerprint of our element of interest.
From the extended EXAFS region, we obtain information about atomic coordination, inter-atomic spacing, as well as structural and thermal disorder. This ultimately enables us to answer the question: How many of what type of atom are at what distance from my element of interest?
16.2 Outgoing photoelectron: electrons as spherical waves
Relationships from classical physics:
, or
Due to electron delocalization, we can describe the dissociated core photoelectron as the spherical wave to describe its trajectory
16.3 XAFS spectra of mono and diatomic gases
How the photoelectron interacts with surrounding atoms
Here, is the wave incident on the second atom, is the scattered fraction, and is the new spherical wave centered on the second atom
simplification when :
16.3.1 How surrounding atoms affect the modulations
Nearby atoms can affect the probability of creating a core hole
Recall from earlier in the course:
16.3.2 How XAFS date is measured: transmission and fluorescence detection
Transmission and Fluorescence
16.3.3 Background subtraction: extracting the quasi-periodic modulations
16.3.4 E-Space to K-Space conversion
16.3.5 The EXAFS equation: Describing the k-space data mathematically
- Degeneracy; - Amplitude Reaction Factor
- Scattering Factor; - Wave number
- Interatomic distance; - Mean-squared disorder
- Phase shift
16.3.6 What affects the k-space data?
Reduction in CN reduction in amplitude of k-space oscillations
Change in interatomic spacing change in period of k-space oscillations
16.3.7 Fourier transform
(Fourier transform):
(inverse Fourier transform):
16.3.8 How do multiple coordination shells affect the spectrum?
In the figure below, the Au spectrum with only the first shell is shown in red, and the Au spectrum with the first four shells is shown in blue.
16.3.9 Recap: Extended X-ray Absorption Fine Structure (EXAFS)
The EXAFS method allows one to determine how many of what type of atom is at what distance from the absorbing atom.
16.3.10 The modeling process (crystallography)
Pathways generated from crystal structure
You can also generate own pathways based on pre-existing knowledge. Each pathway has its own set of variables which must be considered.
16.3.11 The EXAFS equation: how do we treat this in creating a model?
Recall:
- Parameters we can determine through theoretical modeling
- Parameters calculated using fitting program, a function of the material
- Parameters which are related to the measurement
16.3.12 Variables defined for each pathway
- N is related to the average coordination number
- R is defined in fitting as , or the deviation from the interatomic distance defined in the pathway creation
- is the mean squared disorder, a convolution of the Debye-Waller factor (thermal disorder) and the radial disorder
16.3.13 Evaluating best-fit model (Statistics)
; ;
A “good” model minimizes the factor and factor with physically reasonable parameters. There are many “well-fitting” models but only one “correct” model.
16.3.14 Some Examples: Materials Science problems solved by EXAFS
EXAFS is particularly useful in systems which involve amorphous phases or dopant atoms, such as amorphous thin films, heavy atoms in glass or polymeric materials, nanoparticles, phase-change materials, as well as systems where element-specific structural details are not available by other methods
- EXAFS discovers amorphous phases
Moreau, Ha et. al, 2013. Chem. Mater. 25 (12), 2394.
Moreau, Ha et. al. Nano Letters, 2012, 12, 4530
- EXAFS as a means to study nanoscale transformation
Ha, Moreau et. al. J. Mater. Chem, 2011, 21, 11498.
- EXAFS elucidates nanoparticle growth mechanisms
From EXAFS results (top) we can determine the coordination number of an average Au atom and Ag atom within the nanorods as a function of reaction time (still time course). We expect that the coordination number will be 12 when the atoms are in the bulk and less than 12 when atoms are on the surface. From the plot we see that although the CN for Au is approximately 12 in all cases, the CN for Ag increases over time until it reaches 12 by ~30 minutes. This reveals that Ag is initially on the nanoparticle surface and over time as deposition of Ag slows, very little to no Ag is on the nanoparticle surface.
Combining EXAFS, XRF and TEM results (bottom) we can relate the growth rate of the length and width of the nanorods (as determined from TEM) to the fraction of Ag vs. Au on the nanoparticle surface (determined from XRF and EXAFS data). We see that the length growth rate of the nanorods is directly correlated with surface Ag. Early on in the reaction (higher fraction Ag vs. Au on the surface), Ag on preferential facets causes the length growth rate to exceed the width and anisotropy is induced. As the reaction progresses and less Ag is on the surface, the length and width growth rates equilibrate and the aspect ratio of the nanorods is maintained.
- Probing nanoscale surface structure:
2nm particle structure cannot be determined with bulk pathways alone.
17 361 Appendix: Mathematics Primer
17.0.0.1 Contributing Authors:
Roger Reinertsen, Jonathan Emery, Michael Bedzyk
In MAT_SCI 361, students are expected to be familiar with algebra, trigonometry, and calculus (differential and integral). Additionally, students will need to work with vectors, matrices, and complex numbers. Fourier Transforms will be utilized in derivations and provide a very useful tool in interpeting the concept of reciprocal space. This primer reviews these basic mathematical concepts and should serve as a mathematical reference for the course.
1 Vector Algebra
1.1 Vector Basics
For our purposes in MAT_SCI 361, we're interested in Euclidean vectors, which are geometric objects in Euclidean Space (which is the space where familiar, conventional geometry holds). Euclidean vectors can be considered as objects that possess some length (or magnitude) and some directionality, thus allowing them to connect points in space. Hereafter, we'll just refer to Euclidean vectors as vectors.
Consider the Cartesian Coordinate system, which consists of a space defined in reference to three orthogonal axes, which are the familiar x, y and z axes. Geometrically, when two straight lines (or vectors) are orthogonal, it means they form a right angle. Conceptually, this indicates you could move some object in the direction of one axis, and not move it in the direction of the other, orthogonal axes. In order to represent vectors in this space, we define a unit vector along each of the axes, each with a length of 1 unit. Together, these vectors form an orthonormal basis set, and can be written as:
Note that the first number in parentheses refers to the length of the vector as measured along the x-axis, the second to the length as measured along the y-axis, and so on. Also, all unit vectors are of length 1.
Now, we can define an arbitrary vector, , as a sum of these three vectors, each multiplied by some appropriate constant (also called a component or coordinate):
You'll note that we just took advantage of the way vectors can be added or subtracted. This is done by considering the individual components of the vector:
Vectors can be multiplied by numbers (also refered to as scalars) by distributing the multiplication operation to each individual component:
You may often see vectors represented as column matrices simply containing the components :
This notation leaves the basis set unstated; more formally, you may write:
When writing a vector in the compact column matrix form, it is important to keep track of the basis set with which its components were defined.
1.2 Basis Sets
While the basis set defined by the Cartesian unit vectors introduced in the previous section is likely to be the most familar and intuitive choice, it is often useful in crystallography to define vectors with respect to basis sets which are not necessarily normalized or orthogonal.
Consider, for example, the vectors defining a tetragonal unit cell. You can picture a box, with its top and bottom faces being squares, and its height being twice its width or depth. In reference to the Cartesian unit vectors, we define basis vectors:
Where is the width and length of the box, and the height is given by . Now, some arbitrary vector can be represented by:
Where r,v, and w are used to denote the components. Writing a vector defined in reference to this basis in compact column notation yields:
Here, it is important to remember that if , the vector will be measured as longer along the Cartesian z-axis than along the x or y, because the lengths of the basis vectors are not equal.
1.3 Fractional Coordinates and Crystallographic Directions
In 361, we will utilize two types of vectors which are slightly modified in their definitions in order to describe crystals. The first of these are used to describe the relative positioning of atoms in unit cells, and they are typically represented as follows:
Where is a vector that denotes the position of an atom, in so-called fractional coordinates. By dividing the components by the corresponding basis vector lengths, an atom's position in the unit cell can be compactly written with just three numbers (, and ) which vary between 0 and 1. Occasionally, fractional coordinates may include a number greater than one or less than 0; if this is the case, translational symmetry permits the simple addition or subtraction of integers to that particular coordinate, to bring it within the range of interest (this will be discussed more thoroughly in the course).
The other type of vectors of interest are crystallographic directions. The definition of these vectors are not changed explicitly; rather the difference lies in that only the direction of the vector has physical significance. Crystallographic directions are commonly written as:
Again, this definition is the same as that of an arbitrary vector. The difference is probably best demonstrated with an example:
Here, we see that the vectors defining the [123] and [246] directions consist of the same relative combination of basis vectors, differing only by a factor in their total length. So, these vectors share the same direction, and we write:
One common convention to denote negative components to a direction is to place a bar over the corresponding numbers:
Note that changing the sign of a relative combination of vectors will result in a vector pointing in the opposite direction (, just as points in the opposite direction of .
Finally, the vector operations discussed in subsequent sections can be employed on vectors representing directions; this simply requires being consistent about how the total length and components of the vector are defined.
1.4 Dot Products, Vector Magnitudes, and Angles Between Vectors
The dot product, also known as the scalar product or the inner product, is an operation performed one two vectors which returns the length of one vector as measured along the other vector, times the length of that other vector. Following this definition, we write:
Where denotes the total length, or magnitude of the vector. To define the length of a vector, we consider the square root of the dot product of said vector with itself:
This makes sense, as using the dot product to operate on the same vector yields the product of the length of that vector, times the length of the vector measured along itself (which is the same, full length). Thus, the ouput will be the length squared.
As can be inferred from the above definitions, the dot product is commutative, and so the order that the vectors are entered does not matter:
We can now consider how to write the dot product can be written in terms of the components of two vectors (note the analogy to the distributive property of multiplication):
While this formula may at first look rather cumbersome, it simplifies drastically when we employ an orthogonal basis set. Letting:
We make the observation that:
Where , and denote the length of the basis vectors. And so, for vectors defined in terms of an orthogonal basis set, the dot product simplifies to:
If the basis set were orthonormal (that is, ), the result would simplify to the sum of the products of the corresponding vector components.
Finally, the formula for the dot product can be rewritten to allow for the determination of the angle between vectors:
1.5 Cross Products
The cross product, also refered to as the vector product or area product, is an operation performed on two vectors which returns a third vector pointing in a direction perpendicular to the two input vectors, with a magnitude given by the length of one vector as measured in a plane perpendicular to the other, times the length of the other.
2 Complex Numbers
2.1 Basics of Complex Numbers
All rational and irrational numbers are contained within the set of real numbers, which, most generally, consists of all numbers which can be used to measure distance.
Complex numbers are constructed from real numbers by including the imaginary unit , which is defined by . Any real number multiplied by the imaginary unit (for instance ) is refered to as an imaginary number. A complex number is defined as a number that can be written as , where and are real numbers. The set of complex numbers contains all real and imaginary numbers and every complex number has a real and imaginary component. Complex numbers have broad application in describing wave behavior and are central to the mathemical description of wave phenomenon such as diffraction, as we will see in MAT_SCI 361.
2.2 The Complex Plane
One effective way to visualize complex numbers is by plotting them on the so-called complex plane, sometimes refered to as the Argand plane. In this representation, a point's position in reference to the horizontal axis is determined by the value of the real (
) argument (
), and its position in reference to the vertical axis is determined by the value of the imaginary (
) argument (
). Fig.
17.1 shows the Argand diagram.
As can be seen by these plots, a single complex number can be used to represent a 2D vector. Continuing to explore how these numbers can be represented, we now represent the same number in polar coordinates (Fig.
17.2). This construction makes apparent that complex numbers can be characterized by a magnitude (or amplitude),
, and an angle (or phase),
which hints at their utility in describing wave phenomena. Employing basic trigonometry, the magnitude can calculated by
, and the angle by
. The x and y values can be calculated from these quantities via the equations
and
.
2.3 Euler's Formula
Since it is useful to write complex numbers in terms of their magnitudes and phases, we employ Euler's Formula ,
Though we will not prove this identity here (it is commonly proven using an argument based on Taylor expansions of these functions), we highlight the important implication that a purely complex input into the exponential function will result in a complex output with a magnitude of one (
). This allows us to write any complex number in the form
, where the quantities are related by
and
. Euler's Formula can be used to generate other relationships between complex exponentials and trigonometric functions, as can be seen below.
2.4 Operations on Complex Numbers
Addition and subtraction for complex numbers is conducted by adding and subtracting the real and imaginary components of each number separately. These operations are equivalent to translations in the complex plane. For example:
Multiplication and division are conducted in the same manner as for real numbers (the operation has the same properties). For example, mlutiplication is distributive:
However, multiplication and division of complex numbers can be are more intuitively and efficiently handled in terms of their magnitudes
and phases
(note that these quantities are calculated by the identities listed in Sec.
17.12):
This means that the products of complex numbers in exponential form are found by
multiplying the magnitudes, and
adding the phases. These operations are equivalent to a combination of rotation and scaling in the complex plane.
2.5 Complex Conjugates and Absolute Values
During previous calculations of complex number magnitudes, we relied upon the ability to separate the real and imaginary components (
). Unfortunately, this is not possible in all scenarios. Take, for example, the complex exponential function,
. While we can use Euler's Formula (Eq.
17.13), we'd like to be able to use a simpler operation to find the magnitude (sometimes called the complex modulus). So, we introduce the complex conjugate of a function:
In simple terms, the complex conjugate of a function is the same function, but with every instance of the imaginary unit
replaced with
:
This operation is of great importance in various mathematical and scientific disciplines, including quantum physics and X-ray diffraction. Furthermore, it is very useful for calculating the magnitudes of complex numbers through the identity:
We can use Eq.
17.14 to work through some example magnitude calculations:
As we see, we can recover that we recover the modulus of a complex number as computed in Sec.
17.12, as well as the result that the modulus of the exponential with a purely imaginary input is one (Sec.
17.12).
3 Fourier Transforms
18 361 Problems
Homework Policy: You may consult with other class members when preparing your homework answers; indicate clearly on your paper the names of the students with whom you worked. The solutions you submit should, nevertheless, be your own and in your own hand.
Reading Assignments: See the Syllabus, which is published on the NU Blackboard for this course.
18.0.0.1
By operating on a "7" in the plane of the paper, show that an inversion center is equivalent to a 2-fold rotation axis (perpendicular to the plane of the paper) in two dimensions.
Show that the inversion center and 2-fold rotation axis are not equivalent in three dimensions by doing the same type of operation on a 3D asymmetrical unit “
.”
18.0.0.2
Below are sketched a 2-fold axis parallel to a mirror and two perpendicular mirrors. Operate on the "7" with the indicated symmetry elements and show that a third symmetry element is present in each case and that the two cases are equivalent. Which point group does this pattern of 7's belong to ?
18.0.0.3
For the following 2D primitive rectangular unit cell:
- Fill in the pattern of 7's based on the indicated unit cell and symmetry elements.
- Draw in the additional symmetry elements that are present.
- Indicate which 2D space group this pattern belongs to.
18.0.0.4
From Azaroff 1-7
Examine the crystal on page 22 of Week 1 notes (Azaroff Fig. 1-29) and list all the symmetry elements that you find present. Determine the correct crystal class and system.
18.0.0.5
From Azaroff 1-8
Consider the tetragonal crystal shown on page 21 of Week 1 notes (Azaroff Fig. 1-24). Using the axis labeled a1, a2, and c in that figure, what are the indices of the four faces visible? What is the form?
18.0.0.6
C&S Prob. 2-6
18.0.0.7
Hammond Prob. 2-3
18.0.0.8
C&S Prob. 2-10
18.0.0.9
C&S Problem 2-13 (Use tracing paper on top of a Wulff net for this problem, in addition to the following two).
18.0.0.10
C&S Problem 2-14
18.0.0.11
C&S Problem 2-15
18.0.0.12
Prepare a drawing of the layer in the reciprocal lattice of a monoclinic crystal for which a = 2.5 Å, b = 3.0 Å, c = 5.12 Å, and γ=120°. Note that γ* = 180° - γ = 60°.
18.0.0.13
Using the figure from lecture notes Week 2 slide 11, draw two lines that represent the edge-on view of the (010), (110) and (210) hkl planes. Draw the corresponding reciprocal lattice vectors, noting that they are perpendicular to the hkl planes. This is already done below for the (210) plane. Using a ruler, measure the interplanar spacing, , and the length of the reciprocal lattice vector . Verify that the product is the same for each set of planes, thus demonstrating that reciprocal lattice vector lengths are inversely proportional to d-spacings in direct space.
18.0.0.14
Using the general definition of the reciprocal lattice vector (see Week 2 Lecture Notes), derive the relation for for the tetragonal, orthorhombic, and monoclinic systems in terms of the unit cell parameters a, b, c, and the Miller indices h, k, l. Check answer with C&S A3-1.
18.0.0.15
- Determine the lattice constant "a" in terms of R for a BCC (body centered cubic) structure with spheres of radius R at each lattice point packed as closely as possible.
- repeat part (a) for an FCC lattice.
18.0.0.16
GaAs is a zinc blende structure, which has Ga atoms at FCC positions and As atoms at FCC + (1/4, 1/4, 1/4) positions. Write out the 4 coordinates for Ga and the 4 coordinates for As for a unit cell. Make a sketch of this unit cell with the 8 atoms or use Crystal Maker.
18.0.0.17
Hammond Prob. 5.6. Plus use MatLab to perform the matrix transformations between cubic-I (HKL) and rhombohedral (hkl) for HKL = {100, 111, 110} and hkl = {100, 111, 110}.
18.0.0.18
C&S Problem 2-7
18.0.0.19
C&S Problem 2-8
18.0.0.20
Hammond Exercise 5.2
18.0.0.21
One formula weight of NiO equals 74.69 amu, and the density of a NiO crystal is 6.67 . (a) Calculate the length of the unit cell edge, a. (b) Using = 1.54 Å prepare a list of the first 6 allowed reflections (hkl) and the corresponding Bragg angles, . Refer to CS Appendix 9 which lists the allowed reflections for various Bravais direct-space lattices.
18.0.0.22
Prepare a 3-d drawing of the reciprocal lattice for a body-centered-cubic direct space lattice. Show and label all reciprocal lattice points for 0 h,k,l 2. Show and label the reciprocal space axes, a*, b*, and c*. Identify the Bravais lattice type for this reciprocal space lattice.
18.0.0.23
- What are the (hkl) Rhombohedral unit cell Miller indices for the three nonparallel faces of the Rhombohedral unit cell?
- Read Hammond Section 5.9, make sure you understand how the transformation matrices were generated for trigonal crystals with rhombohedral lattices. Using the transformation matrix derived in Sec. 5.9, what are the (HKL) Hexagonal unit cell Miller indices for the three nonparallel faces of the Rhombohedral unit cell?
- Now list these as (hkil) Miller- Bravais indices.
- What is the [uvw] direction in the Rhombohedral unit cell for the hexagonal c-axis direction [001]?
- EXTRA CREDIT: Hematite -Fe2O3 has a rhombohedral crystal structure with a=5.43Å and . What is the angle between the hexagonal c-axis and the rhombohedral c-axis? What is the angle between the hexagonal c-face and the rhombohedral c-face?
18.0.0.24
Find Azaroff Chapters 6 and 8 on BlackBoard, Read Azaroff Ch 6. pp 86-113, an Azaroff Ch. 8 pp. 155-165
18.0.0.25
[Azaroff 6-1]
18.0.0.26
Refer to Azaroff Fig. 6-2 on page 88. This experiment is with continuous radiation.
- The x ray beam from the x-ray tube is traveling along y. Is this x ray beam:
- preferentially polarized along x ?
- preferentially polarized along y ?
- preferentially polarized along z ?
- not preferentially polarized ? Explain your answer.
- Is radiation scattered by the block stronger in detector 1 (along x) or in detector 2 (along z)? Again explain your answer.
18.0.0.27
[Azaroff 6-2]
18.0.0.28
[Azaroff 6-3]
18.0.0.29
[Azaroff 8-1] Hint : According to the Bohr model, the radius rn of the nth orbit is proportional to , where Z is the atomic number. Plot the scattering-factor curves , and as functions of .
Note that there is a typo in the text book. “a missing factor of 8”.
18.0.0.30
[Azaroff 8-2] (see Cullity & Stock Appendix 10)
18.0.0.31
[Azaroff 8-9]
18.0.0.32
The one dimensional interference function is:
is the scattering vector. and are unit vectors in the scattered and incident directions where is one-half the phase angle difference (in radians) for rays scattered by planes separated by a. The crystal contains M planes separated by a.
- Use a computer with a suitable program or spreadsheet and plotting program (MSE Ugrads must use MatLab) to plot this function over the domain 0 ≤ β ≤ π . Note that this is a periodic function repeated every π radians. Make separate plots of the function for the cases of M = 2, 4, and 16. You will have to appropriately adjust the evaluation interval Δβ to accommodate the sharpness of the function that varies with M.
- For each M above, tabulate the height of the primary maxima, the height of the first subsidiary maxima, and the ratio of the height of the first subsidiary maxima to the height of the primary maxima. This demonstrates how the subsidiary maxima become less significant as M increases.
- By numerical integration determine the area under the β = 0 primary diffraction peak between the first intensity minima (nulls) for each M above. How does this vary with M?
- The integral breadth of a peak is the quotient of the area over the height. This represents the full width of a rectangle that has the same height and area as the peak in question. Calculate the integral breadth of the primary maximum for the three cases, and consider its relation to M.
18.0.0.33
Consider powder diffraction from CsCl (a = 4.11 Å) with Cu Kα radiation (λ = 1.542 Å). This is a simple cubic structure with at 0,0,0 and at 1/2,1/2,1/2. (Note: CsCl is not BCC.)
- What are the indices for the first 7 observed reflections from CsCl?
- For the first four of these calculate and tabulate sinθ/λ ,, , 2θ, and LP.
- Look up multiplicities (Cullity & Stock Appendix 11). Combine these with your results from part B to calculate the relative intensities of the four peaks in question. Assign the value of 100 to the most intense peak.
18.0.0.34
The relation of multiplicity factors to powder diffraction intensities can be appreciated with the reciprocal lattice.
- Sketch the hk0 plane of the reciprocal lattice for an HCP crystal, using solid dots (•) to indicate nonzero Cover the range from -2a* to +2a* and -2b* to +2b*.
- Show that there are 6 reciprocal lattice vectors of the same length . Give the indices for these six vectors. In a powder sample, these will all diffract at the same value of (scalar) Q (or in the same direction).
- The six planes responsible for this diffraction are of the form {100}, though this is seen more clearly in the 4 axis Bravais-Miller system hkil , where i = -(h+k). Write the indices hkil for these six planes.
18.0.0.35
Write the structure factor for a crystal with two atoms of the same type per unit cell at and . This conforms to a body centered (I) unit cell with an arbitrarily displaced origin at x,y,z.
Now evaluate the product for all possible values of h, k, and l. You should see that the result is independent of x,y,z. Therefore, the intensity (FF*) depends only on the separation between atoms; absolute positions are not relevant.
Make a perspective sketch of the reciprocal lattice for an orthorhombic I crystal, a = 3Å, b = 4 Å and c = 5 Å. Include 8 reciprocal lattice unit cells ( from origin to 2a*, 2b*, 2c*). Indicate nonzero values of FF* by dots (•).
You should notice two things: the "missing" reciprocal lattice points result from the choice of the nonprimitive unit cell; the pattern of nonzero points forms a face centered (F) array in reciprocal space. The same is true for cubic I and tetragonal I Bravais lattices, the reciprocal lattices of which are face centered.
18.0.0.36
(Cullity & Stock Prob. 4-4) Derive simplified expressions for F and for diamond, including the rules governing observed reflections. This crystal is FCC and contains 8 atoms per unit cell located at: FCC and FCC + 1/4 1/4 1/4 . Note, silicon and germanium are diamond structure.
18.0.0.37
Construct a diagram that illustrates the Bragg condition, showing , and an (hkl) reflecting plane such that the two unit vectors originate from the same point as shown below. Continue the diagram and show that the vector must be perpendicular to the hkl plane. From the construction derive Braggs’ Law recalling that Q must be the same as a reciprocal lattice vector.
18.0.0.38
Figure P2 is a c-axis-rotation photograph of an orthorhombic crystal which has a* = 0.25 , b* = 0.15 and c* = 0.36 . The radius of the cylindrical camera used for taking this photograph is 50 mm and the x-ray wavelength is 1.542 . Construct the appropriate reciprocal lattice nets (l=0 and l=1) to index all the reflections shown. What is the lattice type of this crystal?
18.0.0.39
Use the Scherrer equation to evaluate the FWHM peak width (in degrees) for crystallite sizes D = 25, 75, 125, 450, and 900 Å. Assume that = 1.542 Å and that the peak in this scan whose width we are considering occurs at .
The ability to measure small peak widths is hampered by instrumental broadening. Even if the incident and diffracted beams were perfectly collimated, the peaks would still be broadened by the splitting. Differentiate Braggs law to obtain an expression for as a function of , , and d. Using this expression, calculate d for the splitting of Cu radiation at .
.
From this you should appreciate that it is difficult to measure D values greater than about 500 . when using the Cu doublet as a radiation source. Note that the wavelength resolution can be improved by an order of magnitude by using a single crystal monochromator to select out the Cu , whose width is approximately 2 eV in comparison to the 20 eV energy separation between the and .
18.0.0.40
Identical powder diffraction scans are made of a diamond powder sample and a germanium powder sample with Cu radiation. Each has "diamond cubic" crystal structure with 8 atoms per unit cell. Other pertinent information for this problem is as follows:
|
Sample
|
Z
|
a[Å]
|
[]
|
ρ [g/
|
|
Carbon
|
6
|
3.5671
|
4.22
|
3.51
|
|
Germanium
|
32
|
5.6577
|
67.9
|
5.91
|
The scans were done in symmetric reflection. One might think that the ratio of observed intensities would be given by the ratio of the quantities
where x is C or Ge. However, the observed intensity of diamond, relative to that of germanium, was 25 times larger than that calculated from the ratio . Explain where this factor of 25 comes from.
19 361 Laboratories
19.1 Laboratory 1: Symmetry in Two Dimensions
19.1.1 Objectives
We will be working with 2-dimensional lattices. You will see the how the symmetry of the lattice and not its shape determines to which of the four axial systems it belongs. Parts A and B examine unit cells, translational symmetry, and Miller Planes. Parts C and D add rotational symmetry, mirror, and glide planes. In Part E, we will examine 2-D Si and Ga surface structures grown on a Si (100) substrate.
19.1.2 Laboratory Procedure
19.1.2.1 Part A1: Lattices and Unit Cells (see worksheet p.4)
A unit cell must be able to reproduce the lattice when translated along the axes directions. A primitive unit cell is the simplest case where there is only one lattice point per unit cell. Non-Primitive unit cells contain more than one lattice point per unit cell. All lattice points must have identical surroundings. NOTE: this lattice belongs to the Oblique axial system.
- You are to locate and outline two different primitive unit cells. Use as your lattice point the
- angle corner of the triangle. Note that any point would be equally valid as a lattice point but I chose that so everyone would use the same point.
- Now locate and outline a non-primitive unit cell.
- Label your unit cells 1,2, and 3. For all unit cells, locate a corner where the angle and mark it as the origin. Using a right-handed convention, (i) label the axes a,b and (ii) measure a,b, and In the worksheet margin, calculate the unit cell area:
Area =
You will note that non-primitive cells have an area that is an integer multiple of the area for a primitive cell.
19.1.2.2 Part A2: Miller Indices
- Draw a line parallel to MN and another to OP inside each of your cells; the lines must touch somewhere on the cell axes. Label them MN’ and OP’. For convenience, you may want to make these lines intersect a cell axis at: 1, 1/3, 1/10, 3/4 ... etc of the unit length.
- Using the table at the bottom of the worksheet, calculate the Miller Indices for each line (six total).
19.1.2.3 Part B: More Lattices
Select a printed fabric. Note: all fabrics belong to the Oblique axial system. Choose a feature in the pattern that “stands out to your eye” as a lattice point. Locate a primitive unit cell. Examine it for translational symmetry. Trace the primitive unit cell on 2 the tracing paper provided. Measure and label a, b, γ, and record the pattern number.
19.1.2.4 Part C: Symmetry, Plane Group, Plane Lattice, and Axial System (worksheets p.5, 6)
- See the example. Look for symmetry in the pattern #1 and draw the appropriate symbol at all the locations. (e.g. 3-fold ▲, mirror plane , glide plane —-)
- In the blank area to the right of hte pattern, make a sketch of the primitive unit cell.
- Draw the appropriate symbols for all the symmetry you found at the locations where you found them on your sketch. It should match up with a plane group in Hammond p.67. 4) On the work sheet state the: 1) plane group 2) axial system (Symmetry Notes) and 3) plane lattice (Hammond p.62). At home do the same for patterns #2 and #3. These are more difficult.
19.1.2.5 Part D: Motif (asymmetric)
For two Escher drawings:
- On tracing paper, repeat what you did in Part C.
- Trace the motif of the pattern.
19.1.2.6 Part E: Surface Reconstruction (worksheet p.7)
The lattice vectors for a surface structure will be different from those of the substrate. This change is known as a surface reconstruction. If we define the lattice vectors of the substrate as a and b; the lattice vectors for a given surface structure can then expressed in terms relative to the substrate. The unit length of the surface vectors will be
e.g. If and , then N=3, M=5. The surface is then called a 3x5(NxM).
Now consider the two surface structures on the Si (001) substrate Here, Ga-addimers have been adsorbed on a surface consisting of Si-dimers on top of a Si (001) bulk. Sketch the primitive lattice of: 1) Si bulk 2) Si-dimer 3) Ga ad-dimer layers with the NxM for each structure. Ignore the symmetry of the pattern. I am only interested in the primitive unit cells.
19.1.3 Deliverables
Please do everything asked for. Make everything neat and orderly so as to get full credit. Erase all unnecessary lines, marks etc.
19.1.4 Symmetry Notes
I. Periodic structures or patterns in two dimensions belong to one of four axial systems. These are named according to the shape of the unit cell: oblique (parallelogram), rectangular, square, hexagonal (triangular).
There are, however, a total of five two-dimensional plane lattices (Hammond p.62) in which all lattice points have equivalent surroundings; these are analogous to the 14 Bravais lattices in three dimensions. The two-dimensional plane lattices (or nets) are sketched below. Four are primitive and one is non-primitive (rectangular centered/diamond).
II. The preceding applies to arrays of featureless points, or, if you prefer, circles, which have "perfect" symmetry. A real pattern is made up of motifs (asymmetric objects, e.g."7"), which have certain spatial relations. Each lattice point has one or more motifs associated with it. Any pattern can be classified by the symmetry of the collection of motifs at each (or any) lattice point. There are only 17 different patterns in two dimensions; every periodic wallpaper, decorator fabric, etc. conforms to one of these. Such classification is beyond the scope of this course, but a few instructions or conventions are useful. (The summary of the 17 patterns plane groups Hammond p.67).
|
|
Cell 1
|
Cell 2
|
Cell 3
|
|
|
(MN)'
|
(OP)'
|
(MN)'
|
(OP)'
|
(MN)'
|
(OP)'
|
|
|
a
|
b
|
a
|
b
|
a
|
b
|
a
|
b
|
a
|
b
|
a
|
b
|
|
Intercept
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Reciprocal
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Miller Indice
|
|
|
|
|
|
|
|
|
|
|
|
|
Table 19: Part A2
19.2 Laboratory 2: Symmetry in Three Dimensions
Reading: Cullity and Stock sec 2.5, 2.6, 2.7, 2.9, 2.10, 2.11, Hammond Sec 12.1, 12.2, 12.3
19.2.1 Part A1: Crystal Shapes and Point Group Symmetry
Inspection of a crystal can provide significant information about its symmetry. One can observe the presence (or absence) of mirror planes, rotation axes, rotoinversion axes and inversion centers. These identify the crystal system and the orientation of the conventional unit cell. One can do even better: the presence of more than the minimum crystal symmetry (C&S table 2.3) specifies the point group symmetry within the crystal system. There are 32 of these: stereographic projections are from the International Tables of Crystallography vol. 1.
You have 5 crystal models; each is from a different crystal axial system (trigonal is combined with hexagonal and orthorhombic will be studied in Part 2). Inspect each for symmetry: mirror planes, rotation axes, roto-inversion axes, and inversion center. Make a stereographic projection of the collection symmetry you found using the symbols below. Next to this, make a perspective sketch of the model indicating which face is at the projection point (center) of your stereographic projection.
Consult the point group symmetry table only after you have thoroughly examined your models to help find any symmetry elements you may have missed. On your worksheet you should have: 1) the identifying number 2) the stereographic projection along with a simple sketch of the model 3) state the axial system 4) state whether the crystal has or does not have a inversion center. NOTE: Please do not draw on the models and be careful with them; they are very fragile.
Part A2: Wulff net (orthorhombic)
Use a right-handed coordinate system and make 1) a simple sketch the model, 2) label the axes a, b, c 3) record the axes ratio a:b:c, and include the model number.
Now select two faces (only one can be a {100} type) and label these faces “A” and “B” on your sketch. Approximate the angle of the plane-normal between the faces relative to the axes and plot these as poles on the provided stereographic (m) ( 2 ) (3) (3) (4) (4) (6) (6) 2 projection. Use the c axis as the projection point (center).
GRADUATE STUDENTS: (after class) From the three direction cosines for both poles and the axis ratio a:b:c , calculate and normalize the ratio of integers (C&S p. 82.) These are the Miller Indices of the crystal faces.
19.2.2 Part B: Crystal Models-Cubic
You are provided with open and space filling models of FCC and an open diamond cubic model.
- Inspect the FCC structure; this can be formed by stacking close packed planes (ABCABC...) which become {111} in the cubic representation. There are octahedral voids (CN=6) at 1/2, 1/2, 1/2 + fct and tetrahedral voids (CN=4) at 1/4, 1/4, 1/4, etc. (one in each corner).
a. After class, calculate the radius of the void(r) in terms of the lattice parameter(a) and radius of the atom(R). Do this for both the octahedral and tetrahedral voids.
b. GRADUATE STUDENTS (after class): Consider the primitive unit cell of the FCC structure. (Hammond section 5.8.) Write Miller indices for planes in the primitive cell (HKL) in terms of (hkl) in the FCC cell. You can consult Azaroff p. 53-54. The figure 3-19 is incorrect. Switch and (a b in the primitive cell) so the axis system is right handed.
2. Examine the Diamond Cubic structure. Tetrahedral coordination of each atom should be evident. Note the "diamond glide" planes. <110> 2 per face.
a. Give the coordinates of each atom in primitive unit cell.
b. Are all atoms equivalent? Briefly explain your answer with a simple sketch. _
c. Is the three-fold axis along <111> a 3 or 3? Briefly explain. _
d. Is the four-fold axis along < 100> a 4 or 4? Briefly explain.
e. Identify "diamond glide" planes (2 per face). Note both the plane orientation {hkl} and glide direction <uvw>. Briefly explain.
19.2.3 Part C: Crystal Models - Hexagonal
For the open HCP model, primitive hexagonal, locate the 2 atoms per unit cell. Observe the 6 roto-inversion axis that is present in this structure with 3 inversion centers at z=0, z=1/2. Identify the 4 tetrahedral voids per cell. The two "internal" ones are easy to see and the others are on vertical edges.
- Locate the octahedral interstices (voids) and give the coordinates; 2 per unit cell.
- All the octahedral sites could be occupied in a compound. Alumina, Al2O3, presents an interesting variation. The O-2 form an HCP structure however; the Al+3‘s occupy only 2/3 of the available octahedral sites. Note the pattern of occupation varies from layer to layer.
- How many layers are required for the structure to repeat? Hint: Start counting at the midpoint of the bottom most HCP structure.
- The crystal system is actually rhombohedral (trigonal), but the model and structure are most easily visualized in a hexagonal setting. To determine the proper symmetry, show the following:
- A 6 fold is not present along c.
- A 3 fold is present along c. _
- A 6 is not present along c (this is trickier; consider both O and Al atoms).
19.3 Laboratory 3: Laue Diffraction Patterns
Reading: Cullity sec. 16-1, 16-2, 2-13, Hammond sec 12.1, 12.2, 12.3
19.3.1 Lab Summary
You will use the Laue Back Scattering technique to determine the crystallographic orientation of a single crystal. Then you will re-orientate the crystal to a different plane.
19.3.2 Introduction
The Laue method records the x-ray diffraction pattern on a CCD camera, image plate or photographic film. The Back Reflection Laue technique is for high x-ray absorbing samples at diffraction angles between and . The Front Reflection Laue method is used for but is suitable only with low absorbing samples like polymers.
While Laue methods are used for several purposes, one of the most important is to determine the orientation of single crystals. Well-grown crystals have habits (shapes or facets) that indicate the symmetry possessed by the lattice on which the crystal was "constructed". But if a crystal is poorly formed or was made in such a way that facet development is prevented, xrays can be used to determine the presence and orientation of planes within a crystal using Bragg Diffraction. Bragg Diffraction or Bragg Scattering only occurs when:
i) the Bragg condition is satisfied,
ii) the normal to a plane(hkl), bisects the incident and diffracted x-rays. This is shown in the figure above.
Crystals have many planes of atoms with different values of . To ensure that the Bragg condition will be satisfied for many of these, a large range of ’s are supplied by the white or Bremsstrahlung radiation of the x-ray tube. Generally Mo or W anode x-ray tubes are used for Laue because of the greater white component to their spectrum at lower operating voltages but any target material (e.g. Cu, Cr, etc.) is suitable.
The incident x-rays are collimated into a beam, pass through a hole in the film holder and strike the sample. X-rays backscatter onto the film where the pattern is recorded. The sample is mounted on a goniostat, a device that permits the rotation of the sample about its horizontal and vertical axes (see figure page 3). The position of a diffraction spot enables us to determine the direction of , if we remember that bisects So the incident beam direction and S the scattered beam direction.
19.3.3 Experimental Procedure
With both goniostat axes set to 0.0°, record a back reflection Laue pattern of the MgO crystal. Your instructor will give you recommended voltage, current, and exposure times. Note the symmetry apparent in the diffraction pattern. Given that MgO has the sodium chloride crystal structure, which pole (plane normal) is nearly parallel to the x-ray beam?
With the assistance of your instructor, locate six zones and label them as 1,2,3 etc. Measure the position of each zone using the Greninger Chart. The Greninger Chart is a device that saves tedious trigonometric calculations, allowing you to read directly the latitude () and longitude () of individual poles. We will further simplify the work by measuring ã° for an entire zone of poles simply by rotating( the Greninger Chart) and aligning . Make a table of , its direction(CW/CCW), and . For accuracy, read all angles to the nearest 1/2°.
To Plot: Orientate the Wulff Net with NS axis horizontal to make tracing easier. You need to rotate the Wulff Net the same direction as the Greninger Chart to plot the zones. However, the Wulff Net will be remaining stationary and you will be rotating the tracing paper. Therefore, you need to rotate the tracing paper in the opposite direction that you rotated the Greninger Chart. Plot zones as great circles.
Now measure the interplaner angles between zones simply by placing two poles (intersecting zones) on the same great circle and measuring the angle between them. Index all intersecting zones with this technique referring to the table of inter-axial angles for cubic crystals provided in lab. Note: If you cannot match a pole, label it with a “?”. Bad guesses will be graded as incorrect. When you finish, you should find at least one pole to be a {111} or {110}. Reorientate the sample to one of these reflections by adjusting the goniostat arcs. Record the diffraction pattern and note the symmetry.
19.3.4 Report:
Provide the experimental conditions: x-ray tube anode material, voltage, current, exposure times, beam size, and sample to film distance. Attach both photographs, table of zones with , CW/CCW, and goniostat setting for the second photo. Lastly, your stereographic projection using a standard projection (Cullity fig 2-40.)
19.4 Laboratory 4: X-Ray Diffractometer Part I
19.4.1 Lab Summary
Labs IV and V examine the principle of operation of the X-ray Diffractometer system. The instrument you will be using is a Rigaku Dmax. Note that both labs will be combined into one report. This week you will investigate the details of: 1) the X-ray spectrum emitted from the X-ray tube, 2) absorption of X-rays by materials.
19.4.2 Experimental Procedure
The instrument is equipped with a Cu anode X-ray tube. The source is a line, 10mm high x 0.4mm wide at a “take-off angle”. The apparent source size therefore is 0.04mm or at a sample distance of 185mm, the “radius of the diffractometer.” With your instructors assistance and X-rays off
: 1) Inspect the X-ray generator and X-ray shutter operation to be certain how they work together with the indicator lights.
2) Note the X-ray collimating system with the incident beam slit “Divergence Slit” (DS), and the scattered beam slits, “Receiving Slit” (RS) and “Scatter Slit” (SS). These are used to define the incident and scattered beam directions and S.
3) Note the Specular Reflection geometry of the diffractometer with the sample axis and detector axis as they change simultaneously. The X-ray detector is a scintillation type and uses an electronic device called a Pulse Height Analyzer (PHA). We will need to re-adjust the PHA for this weekfs lab. Record the initial PHA settings: Baseline (BL) and Window (W) voltages. Adjust the BL to 0.5V and the W to 5.0V.
19.4.3 Part A: X-ray Tube Emission Spectrum
Energize the X-ray tube to -20kV and 2mA. X-rays will irradiate a LiF (100) single crystal that acts like a diffraction grating scattering X-rays. LiF has the FCC NaCl crystal structure. Scan from to , Appendix L4A1. Ignoring the absorption effects of: 1) the X-ray tube Be window, 2) the detector Be window, 3) air, and 4) the Al absorber foil, you have recorded the emission spectrum of the Cu anode X-ray tube.
Note that the most intense peak in the spectrum is from the Cu emission line, . You will now determine a more precise position for the line by scanning with a smaller step size, L4A2. Now having an accurate value for the Cu position, calculate the exact value for . For your report, using Bragg's Law and of LiF, calculate for all the notable lines and features present in the spectrum i.e. the Bremsstrahlung radiation, short wavelength limit (SWL), and all emission lines. Identify the element(s) responsible for each noted emission line, see Cullity app 7. (Hint: What impurity metal is present inside the X-ray tube?) Also include in your report, the comparison between your measured wavelength and the calculated value using the X-ray tube operating voltage (kV).
19.4.4 Part B: Scattering from LiF (400)
Calculate the position for the LiF (004) line. Scan from to (L4B) to determine the exact angles for and wavelengths. Compare measured and calculated positions.
19.4.5 Part C: Absorption of X-rays by Al
Move the detector to the Cu line. Use the Ratemeter to count the X-ray intensity for ten one-second measurements, average these values (), and record. CLOSE THE SHUTTER, insert two sheets of Al foil in front of the detector, open the shutter and average 10 more one-second measurements. Repeat, adding two foils at a time until I = 0.1 . For your report plot vs. t ( foil thickness in cm). If the detector response is linear, this will be a straight line. From the slope of this line you can calculate the absorption coefficient . Calculate the Al foil thickness given the density = 2.70 and the weight of 100 of foil = 0.439g. Compare your value of ƒÊ to that found in the International Tables for X-ray Crystallography (SEL).
19.4.6 Part D: Absorption of X-rays by Ni
Insert the Ni filter. Scan from to to include the Cu and Cu emission lines (L4D). Note the differences in the spectrum, especially the relative intensities of the and lines by comparing to L4A1. Re-plot the region between the and peaks to experimentally locate the K absorption edge of Ni. For your report, calculate the thickness of the Ni filter using the data from the Cu absorption. You will need to look up the and values for Ni. Calculate the wavelength of the Ni K absorption edge and compare this to the value in the International Tables. Close the shutter, turn off the X-rays, and return the PHA to the original settings.
19.4.7 APPENDIX
|
File Name
|
Start (
|
Stop (
|
Step Size (
|
Dwell (s)
|
Axis
|
|
L4A1
|
15
|
50
|
0.05
|
1
|
|
|
L4A2
|
44.5
|
45.5
|
0.02
|
1
|
|
|
L4B
|
99
|
101
|
0.02
|
1
|
|
|
L4D
|
39
|
46
|
0.05
|
1
|
|
19.5 Laboratory 5: X-Ray Diffractometer Part 2
Reading, Cullity and Stock: sec 6-7, 6-9, 6-11, and p.201-202
19.5.1 Lab Summary
This week you will study the details of the X-ray detector system. You will: 1) perform measurements to determine the energy resolution of the NaI scintillation detector 2) select filters and make adjustments to the PHA to produce a monochromatic X-ray beam from the polychromatic X-ray source suitable for Powder X-ray Diffraction (PXRD) experiments.
19.5.2 Part A: Energy resolution of the NaI detector
When a single X-ray photon enters a scintillation detector, it produces a voltage pulse whose amplitude (in volts) is linearly proportional to the X-ray energy. However, there is a limit (resolution) where a small change in λ produces no change in voltage.
19.5.2.1 Procedure
Adjust the PHA, slits, and the X-ray tube power to that used last week. Scan the LiF (200) crystal (L5) to locate the Cu emission line and move the detector to the position.
- Open the shutter so X-rays from the emission line enter the detector. (Note: Δλ/λ is ~ 0.1%)
- Adjust the PHA: Baseline = 0.4V, Window = 0.2V. Lock the Window setting, as it must remain constant throughout the entire measurement!
- Use the Ratemeter function and average ten one-second readings and record: i) Intensity (counts), ii)
- Increase the by 0.5V and repeat step 3.
- Keep repeating until the upper limit of is reached.
- Collect additional data around the maxima by stepping at 0.2V intervals. A plot of I vs. Vdetector is the differential voltage curve for the detector. Measuring the Full Width Half Maximum (FWHM) of the curve yields the resolution:
More useful plots are of I vs. and especially I vs. E (keV) as
To plot I vs. E:
To plot I vs. :
You have now calibarated the PHA for Energy (keV), Wavelength ( and Voltage (V).
19.5.3 Part B: Adjusting the PHA for a 90% Window
The PHA can be adjusted to prevent the scattering from unwanted wavelengths from being recorded in an X-ray pattern. That is desirable in kinematic scattering experiments like PXRD. Also, to keep the intensity high, you will set a “90% window” as it allows 90% of the intensity to pass to the counter and rejects 10%.
19.5.3.1 Procedure
Open the shutter to allow Cu radiation to enter the detector
- Set = 0.5V and = 5.0V.
- Start the Ratemeter and record I0 (average ten one-second readings.) Note this is the integrated intensity (100%) of the differential curve: I vs.
- Increase and reduce I0 by 5%, record 4) Without changing , decrease to reduce I by another 5%, record .
You have now set the PHA to pass 90% of the intensity. Consequently, x-rays whose energy is lower than or higher than will be rejected and not be counted.
For your report on each plot I vs. E, I vs. , and I vs. V, indicate the positions of:
1) Cu 2) Cu 3) 4)
For your report answer the following questions: With the PHA set to pass 90% of the Cu :
1) What range of wavelengths are: i) passed and ii) eliminated by the 90% window?
2) What energies are: i) passed and ii) eliminated?
3) Is Cu Kβ eliminated by the 90% window?
19.5.4 Part C: Powder X-ray Diffraction (PXRD)
With instructor's assistance, replace the LiF single crystal with a polycrystalline LiF sample. Scan the sample with the same conditions as L5, (L5C1). Note the difference. With your instructor's assistance, remove Al absorber, increase the tube power, and change slits to increase the diffracted intensity. Scan from to (L5C2).
For your report, 1) discuss why the intensity is lower (L5C1) 2) identify all the diffraction peaks present in L5C2
19.5.5 Part D: Determining the best condition for PXRD
For a PXRD experiment, you want to have monochromatic radiation in order to simplify interpretation of the diffraction pattern. You also would like high peak intensities and a low background. We will investigate various combinations of PHA settings and the Ni filter to determine the optimum conditions for recording a diffraction pattern. The best condition will result with a high-diffracted intensity () for only one wavelength and a low background level (). Note: Do not use the Jade peak finder.
- Set the PHA, BL = 0.5V, W= 5.0V, and scan the and peaks for LiF (200) (L5D1).
- Close the shutter, insert the Ni filter and scan the same region (L5D2).
- Set the PHA for a 90% window determined in Part B. Scan again (L5D3).
- Close the shutter, remove the Ni filter and scan again. (L5D4).
In your report, calculate () and for the peak for each of the four conditions. Also calculate for and the ratio in each case. This data should be presented in a table. The best condition is a large value of for , subject to a small σ for () and a relatively small peak. In other words, we want a large peak-to-background ratio and a high intensity for only one peak. (We cannot eliminate the radiation.) Your report should identify the best condition for obtaining the powder diffraction pattern.
19.5.6 APPENDIX
|
File Name
|
Start
|
Stop (
|
Step Size (
|
Dwell (s)
|
|
L5
|
44.5
|
45.5
|
0.02
|
1
|
|
L5C1
|
44.5
|
45.5
|
0.02
|
1
|
|
L5C2
|
35
|
70
|
0.1
|
0.5
|
|
L5D1
|
39
|
46
|
0.1
|
1
|
|
L5D2
|
39
|
46
|
0.1
|
1
|
|
L5D3
|
39
|
46
|
0.1
|
1
|
|
L5D4
|
39
|
46
|
0.1
|
1
|
19.6 Laboratory 6: Quantitative Analysis of a Mixture
Reading: Cullity and Stock. sec 6-1,2,3, 9-1,2,3,7, 10-1,2,3 Supplement for Lab VI at the end of this handout.
19.6.1 Lab Summary
You are supplied with a mixture of two unknown powdered materials. One has a cubic structure and the other is non-cubic. We will collect a powder diffraction pattern for the mixture and use Search/Match software to identify the unknowns. After class, you will get information online or from the SEL library and calculate the volume fraction for each phase in the mixture.
19.6.2 Experimental Procedure
Prepare a powder xrd sample holder with the unknowns as instructed in lab. Slit sizes to use are 1°DS/SS and 0.3mm RS , Ni filter. Adjust the x-ray tube power to 40kV and 20mA. Perform a scan from from to , 0.05 step size, and 1s count time (L6A). Note the peak splitting at the higher angles. Examine the data to see that for all peaks there are least three data points within the FWHM. Check that the receiving slit has an angular size that is smaller than the FWHM. Also, the peak height for the six most intense peaks should have adequate counts to better define the peak shape ( = .03~1000 counts.)
Identify the diffraction lines using Jade. With the instructor’s assistance, use the diffraction analysis software to identify peaks. Check the pattern carefully that Jade did not miss any peaks or incorrectly chooses a peak from or a tungsten L line. Use the peak editor tool to correct peak finder. Print the peak list, as you will need the info for the Volume % calculation you do at home.
Search Match using Jade. Per instructor’s assistance, perform a Search/Match for your unknowns. Overlay the many results of the search on your data to solve the unknowns.
GRADUATE STUDENTS: Texture can be a problem in this type of analysis. The theory assumes that each phase is randomly oriented, which may not be the case. You can check this assumption by comparing the calculated and observed intensity ratios for more than one pair of peaks. Check for random orientation by comparing the ratios for a second set of using different (’s). Do not try to correct your derived volume fraction for any texture effect you may have. Simple knowledge of how close your intensities are to those with random orientation is adequate for this laboratory.
19.6.3 Deliverables (non-formal report):
1) Experimental conditions: tube target and power, slit sizes, sample ID number, survey-scan, other scans and peak reports.
2) A table of: The unknowns, , , F*F(show work), multiplicity, LP factor, unit cell volume and measured integrated intensities. You will use one peak for each phase (undergraduates) or two peaks for each phase (graduates). The instructor will tell you which peaks you should use for this.
3) Calculation of volume fractions of phases from XRD. See Supplement for Lab IV
To calculate F, you will need to look up the atom positions for the given structure:
1) Use ICCD tables to determine structure space group number, lattice constants and z, the number of atoms per unit cell.
2) Online databases or the R.W.G. Wyckoff (SEL library ref. section)"Crystal Structures, 2nd., ed., Wiley (1963) to obtain .
19.6.4 Supplement for Lab IV
The following is to clarify the ideas and procedure of Laboratory IV from Azaroff Ch 19. We start with the result of the powder diffraction theorem (Azaroff eq.19-5):
Here C is a constant (involving λ, electron characteristics and diffractometer geometry), is the unit cell volume and is the effective diffracting volume of the sample (which depends on sample absorption coefficient μ). This is for one material. If you have a two-component mixture, with material A present with volume fraction , the intensity of a reflection from that material is given by:
The left hand side is from the experimental data. The first ratio on the right hand side is calculated. This gives you , or since . Azaroff is incorrect in omitting from the denominators in eqs: 19-5, 19-7 and 19-9 of the text.
To use this you must be able to evaluate for the two materials. An example will be worked here. Take the case of antimony (Sb). You must know its crystal structure. The JCPDS file says that the crystal system is "Rhombohedral (Hex)". That means that the primitive unit cell is rhombohedral, but that the pattern is indexed () with the larger (more convenient) hexagonal cell (). There are three lattice points in the hexagonal cell at 000; 2/3 1/3 1/3; 1/3 2/3 2/3 (Azaroff, pp. 49 ff; Cullity, Appendix 4). You must look up the crystal structure of Sb (it is not HCP!). A good reference is: R.W.G. Wyckoff, Crystal Structures, 2nd. edn., Wiley (1963). This multivolume set is in the reference section of SEL. There you find that there are two Sb per lattice point with displacements ±z = 0.233. This information locates the 6 Sb atoms per hexagonal unit cell. In writing down structure factors, it is convenient to factor the positions of lattice points and the atom displacements from the lattice points (you have done this with FCC structures such as diamond/silicon or NaCl):
Recalling that and that , straightforward algebra yields:
Remember that the arguments of the trigonometric functions are in radians. An easy check on is to see that it gives when ; here Z = 6 is the number of atoms per unit cell.
Multiplicity m is looked up or derived for each reflection, and LP factor and f depend on (or ). The remaining factor to be calculated is ( abc in hexagonal systems!). Do the same calculations for the other material and solve for .
19.7 Laboratory 7: Rotating Crystal Method (et al.)
Reading: Lecture notes: “Rotating Crystal Method”(bring to lab), Cullity pp. 111-113, sec 5-2, 5- 6, Hammond App. 6 Table A6.1, “Correction Term For Powder Diffractometry” (attached), and Digital Image Plates (Lab Documents Folder).
19.7.1 Lab Summary
Polyethylene -()- crystallizes into an orthorhombic unit cell. One sample has been heated and drawn causing it to have a strong c-axis orientation along the draw direction but random in the a-b plane. The other is an isotropic polycrystalline sheet.
A) This week you will perform a rotating crystal experiment using the Cylindrical Camera to determine lattice parameter and Miller Indices for an orientated polyethylene sample.
B) For isotropic polyethylene, you will perform PXRD to measure, 1) the average crystallite size, 2) the percent of the crystalline and amorphous phases, and 3) the 2θ peak shift due to sample displacement for the Bragg/Brentano diffractometer geometry.
19.7.2 Part A: Determine Lattice Parameter and Index Sample
With your instructor’s assistance, mount the sample in the cylindrical camera with the sample draw direction along the axis of the camera and insert the Image Plate (IP, a film like image recording media). Mount the camera to a point focus port of a Ni filtered Cu x-ray tube (monochromatic radiation, λ=1.5418). Record a diffraction pattern for 5min at 40 kV, 11 mA. Process the IP.
Use the image analysis program “Image Quant” to process your data. You will observe two “layer lines” corresponding to and . With the software, convert the image to an Intensity vs. Distance plot and with the peak finder function, locate peak positions. Print data.
After lab:
Use the data from the layer line and for each of the first two diffraction lines and solve for a* and b*. You will have two equations and four unknowns. Start by guessing values for h and k. (Hint: h and k are not (10) or (01)). Understand that h and k can only be integers and start with numerically low values. Once a* and b* are known, you can now index all other diffraction lines (use a spreadsheet program) for both the l=0 and l=1. Do this for six line pairs for each the and layer lines (12 total). Make a table of the measured and compare with calculated (using the a* and b* from above) to check accuracy.
19.7.3 Part B: Perform a PXRD scan
Cu , 40kV, 5mA, DS/SS=2/3°, RS=0.1°(0.6mm), Ni filter, 2θ from 10°-50°, step= 0.05°, dwell=1s (L7B).
1) Determine crystallite size. Measure the FWHM (convert to radians) for each of the first eight peaks. Use the Scherrer equation to average the results to calculate the apparent average crystallite size D.
2) Determine percent crystallinity. Some materials are not totally crystalline or totally amorphous like glass, but a mix of both. In the diffraction pattern, a distinct amorphous halo will be seen mixed with the crystalline diffraction peaks. The percentage of each is determined by the ratio of the integrated intensities after subtracting background i.e. . Use the peaks in the range of 2θ from 10° to 28°.
3) Peak shift due to sample displacement. To simulate the error produced by an off-center sample, the instructor will displace the sample holder with the spacer. Rescan 2θ from 20°-23° (L7B3). Note the peak shift and calculated the thickness of the spacer using the attached handout: “Correction term for Powder Diffractometry.” The radius(R) of the Rigaku Ultima diffractometer is 285mm.
19.7.4 Report
19.7.4.1 Part A
1) Make a table of the peaks #1-6 for both layer lines l=0, l=1 with: x, y, measured , hkl, a*, b*, c*, calculated , and Miller Indices. Include the multiple (ambiguous) indexing as appropriate.
2) Make another table with a, b, c, (unit cell volume).
3) Based on your unit cell parameters and a density of 1 , how many -- units are there per unit cell?
4) Look for the systematic absences of Miller Indices to determine the Bravais lattice (Hammond Table A6.1).
19.7.4.2 Part B
1) Calculate percent crystallinity, include calculations for background and integrated intensities and L7B plot.
2) The crystallite size calculation with a table of peak widths (degrees, radians) for the first six peaks, and the averaged grain size. Check that the angular size of the RS (0.6mm=0.1°) < FWHM in order to make a valid measurement.
3) For the displaced sample, include plot (L7B3) for the shifted 2θ peak. Referring to the attached handout, calculate (show work) the spacer thickness (δ) from the Δ2θ peak shifts. Explain how sample absorption (the depth that x-rays penetrate the sample) can cause shifting of peaks.
19.7.5 APPENDIX
19.7.5.1 Correction Term For Powder Diffractometry
If the sample is displaced from the center of the powder camera or diffractometer of radius R by a distance of ( may be due to misalignment and/or sample absorption), the following diagram applies:
Using
For small errors,
To determine effect on d, use
then
Complete Nelson-Riley function also corrects for vertical divergence of beam, leading to additional term of ; see Cullity, p. 356.
19.8 Laboratory 8: Single Crystal Epitaxial Thin Film
Reading: C.R.Wie, Introduction sec1,2,3, sec2.1, 3.1, 3.2
19.8.1 Lab Summary
The sample to be studied is a PTO () (001) single crystal thin film grown epitaxially by MOCVD on a STO () (001) single crystal substrate. Several things will be examined: 1) Measure the thickness of the PTO film. 2) Determine the quality (how single crystal it is) of the PTO single crystal film. 3) Generate a simulated data set to compare with raw data to better refine measured parameters.4) Determine the angular resolution limit of the x-ray diffraction system using the “perfect crystal” STO substrate as a standard.
Note you will be using an instrument that has been optimized for thin film diffraction studies. That is: 1) the radiation source is having removed by using a monochromator and slit, 2) the incident beam divergence is ~0.02°.
19.8.2 Introduction
Both materials have the perovskite crystal structures, with the STO substrate forming a cubic perovskite and the PTO forming a tetragonal perovskite structure at RT (room temperature.) The current interest in PTO thin films arises from its ferroelectric properties; under an applied electric field, the
anion sublattice can shift in position with respect to the
and
cation sub-lattices, resulting a net dipole moment along the
c axis. This shift is depicted in Figure
19.8 below, which shows an a axis projection of the PTO perovskite at its two different stable polarization states. Investigating this ferroelectric behavior in thin films requires very high crystalline perfection. Since the cubic a-axis lattice constant (a=3.905 Å at RT) of bulk STO matches closely with the a-axis lattice constant of bulk PTO (a=3.905 Å at RT), the PTO film grows in the c-axis direction (for film thicknesses less than a critical thickness of 600 Å). The bulk PTO at RT is tetragonal with a c/a ratio of 1.063 (c = 4.151 Å.)
19.8.3 Experimental Procedure
- Perform the “Half Beam Alignment” sample alignment procedure with the aid of lab instructor, to align the sample with the x-ray beam.
- Calculate for Bragg peaks of both the substrate and film (001) reflections, given that the xray source is Cu = 1.54056 and move the STO (001) peak. Located and maximize the scattering intensity by making small positional corrections to, and to better align the substrate scattering vector to the scatter plane. Perform a “ or Rocking Scan” of the STO (001) peak and record the peak width. Rocking scans measure the distribution of plane-normals of the domains within the sample. The smaller the angle, the more “single crystal” it is. Because the STO is a “perfect” crystal, the value will be the minimum angular divergence of the instrument.
- Perform a scan along a path in reciprocal space that passes through the (001) peaks for both the PTO film and STO substrate peaks. Thus you will be able to determine the c lattice constants for both the film and substrate from their respective peak positions. Compare these to the bulk values. Depending on the amount of perpendicular strain on the film due to any lattice mismatch, the peak separation can vary from the amount predicted by the bulk lattice constants of PTO. With the data plotted on a log scale, you will also note the kinematic thickness fringe peaks about the film peak maxima. From the scan it is possible to calculate the film thicknesses from the width of the diffraction peaks by understanding the one dimensional interference function,
where the scattering vector magnitude is and M= number of unit cells. Note that the film thickness is t = Mc. This interference function, which is based on simple kinematical diffraction theory, can describe the scan scattered intensity from a thin epitaxial film such as the PTO. This measured intensity I(s) will consist of the primary diffraction peaks from the film and the substrate. It will also show the thickness fringes from the film. From the numerator of the interference function it can be seen that the fringe periodicity (angular spacing) is directly related to the thickness of the film by: .
- Move to the PTO (001) and locate the peak position. Optimize and again. Perform a rocking scan of the PTO (001) peak and record the peak width. This angular width quantifies the film quality. You can then determine if the film is epitaxial as depicted in Fig. 1. For example, if the film were polycrystalline with no preferred growth direction an ω-scan of the PTO peak position would be rather flat and featureless. If on the other hand the ω-scan shows a sharp peak then there is a preferred growth direction.
19.8.3.1 Simulation of kinematical diffraction
Once c (PTO (001)) and the film thickness t are known, use a spreadsheet program and plot the diffraction pattern from the PTO (001) film using the one dimensional interference function described above plotting log I vs. q). Over-lay the simulation output on your data (convert to q(A-1) and re-scale the intensity if necessary. Refine the values of t (M(t)) and c so the simulation will best match your data.
19.8.4 Deliverables
For your report:
- Include the instrument parameter information: slits, target, scan parameters etc,
- Rocking scans plots for STO and PTO with width measured and discuss the significance of each plot.
- A log plot of the 2θ/θ scan over the film and substrate peaks show thickness fringes and calculation of the film thickness.
- A simulation plot with t and c refined for the best match to your raw data (overlaid.) Report the refined values you found for c(PTO (001) and t. (see example below).
Simulation example: A scan at l = 1.540 of t ~103 thick PTO (001) film grown by MOCVD on a (001) STO substrate. Note the thickness fringes about the broad PTO (001) peak. The solid line is a fit to the experimental data using the interference function corrected for absorption from the film and substrate. (From C. Thompson, C. Foster, J.A. Eastman, and G. B. Stephenson, Appl. Phys. Lett. 71, 3516 (1997).)
References
1B. D. Cullity and S. R. Stock, Elements of X-Ray Diffraction 3rd edition (Upper Saddle River, NJ: Pearson, 2001).
Index
- 7 Crystal Systems.: 1
- <math xmlns="http://www.w3.org/1998/Math/MathML">
<mrow><mi> π </mi>
</mrow></math> polarization case: 1
- \sigma polarization: 1
- absorption length: 1
- adsorbed intensity: 1
- Anomalous dispersion: 1
- atomic scattering factor: 1
- Auger effect: 1
- Auger electron: 1
- Bernal chart: 1
- Bragg ring: 1
- Bravais-Miller: 1
- Bremsstrahlung radiation: 1
- characteristic spectrum: 1
- Classical Thomson scattering: 1
- coherent: 1
- Compton scattering: 1
- coordination number: 1
- Crystal: 1
- Crystal axes: 1
- Crystal Classes: 1
- crystal lattice: 1
- Crystal Systems: 1
- d-spacing: 1
- Ewald sphere.: 1
- fluorescence yield: 1
- fluorescent lines: 1
- form: 1
- four axial systems: 1
- Glide symmetry: 1
- Great Circles: 1
- improper rotation axis: 1
- incident intensity: 1
- Interference: 1
- Inversion center: 1
- K\alpha doublet: 1
- Lattice points: 1
- linear absorption coefficient: 1
- mass absorption coefficient: 1
- Miller indices: 1
- Mirror plane: 1
- multiplicity: 1
- non-primitive unit cell: 1
- Octahedral voids: 1
- photoelectric effect: 1
- plane group: 1
- plane groups: 1
- Point of projection: 1
- powder method: 1
- primitive unit cell: 1
- Projection plane: 1
- reciprocal lattice: 1, 2
- rotating crystal method: 1
- Rotational axis: 1, 2, 3, 4
- small circles: 1
- stereographic projections: 1
- Stereographic projections: 1
- Symmetry: 1
- Synchrotron radiation: 1
- tetrahedral void: 1
- Translation symmetry: 1
- transmitted intensity: 1
- transverse scan: 1
- unit cell: 1
- X-ray: 1
- X-ray filament tube: 1
- zone: 1
- zone axis: 1
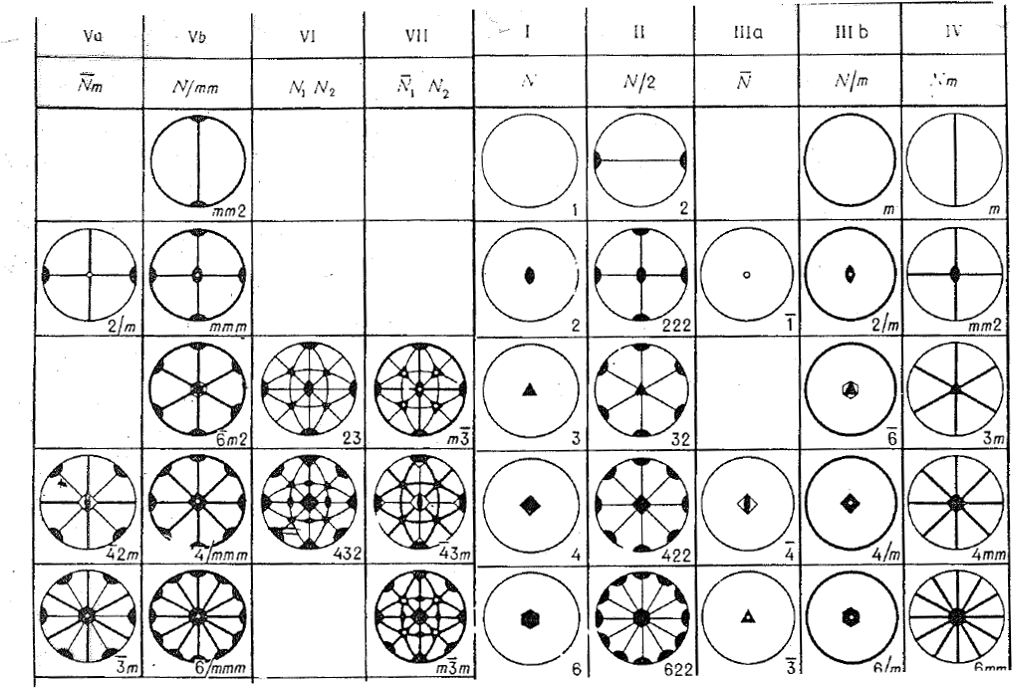
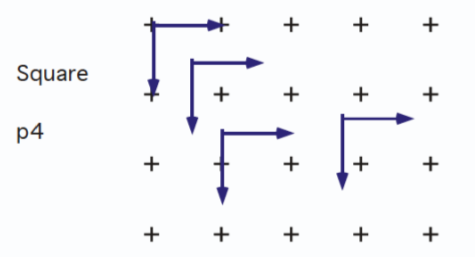
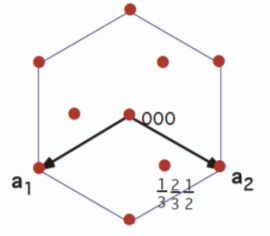
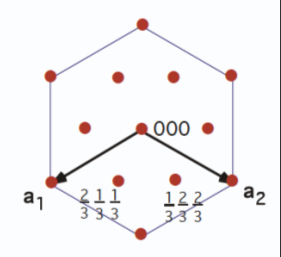
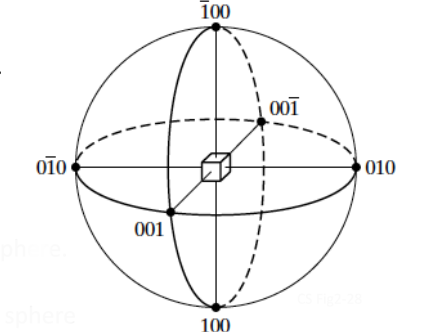
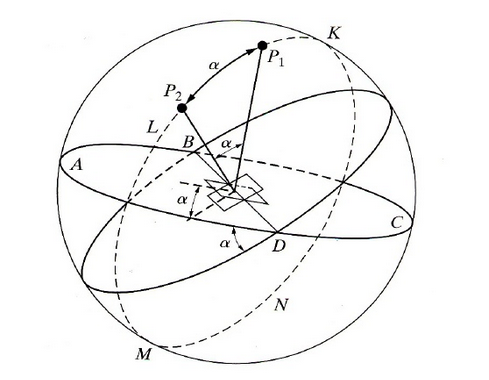
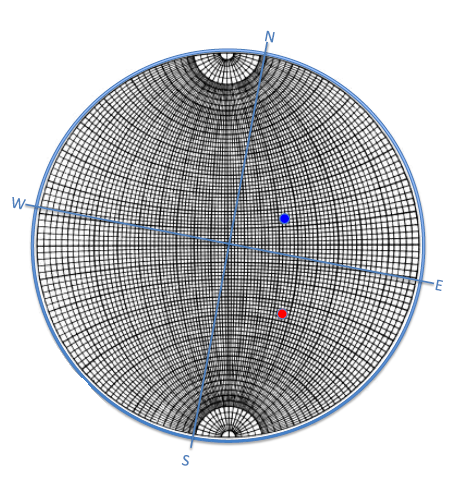
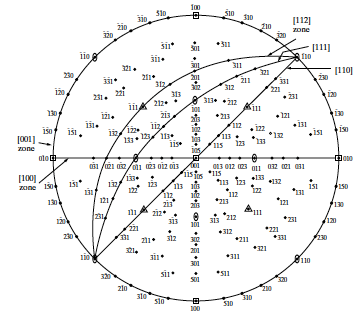
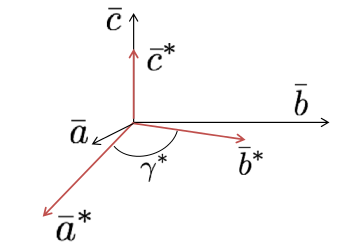
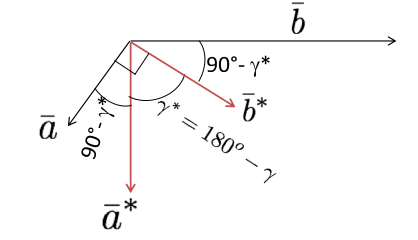
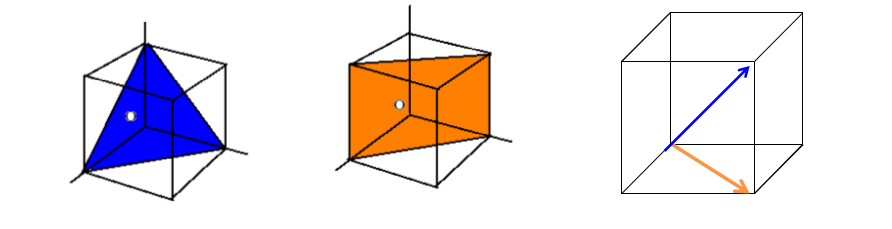
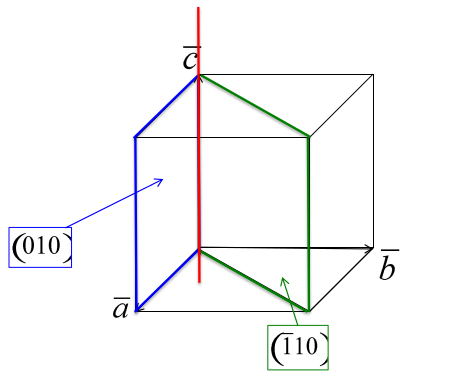
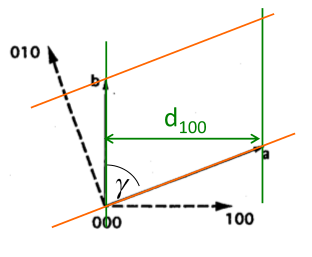
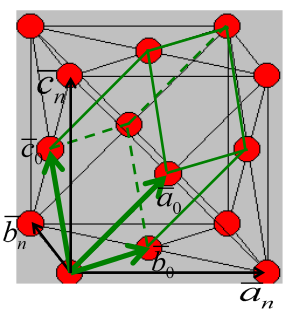
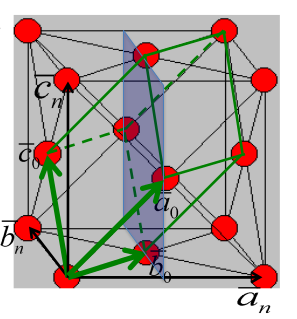
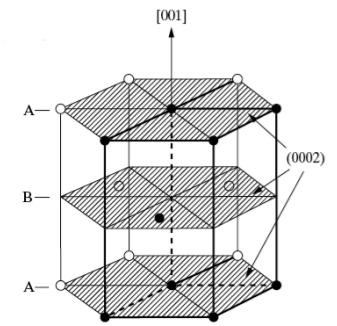

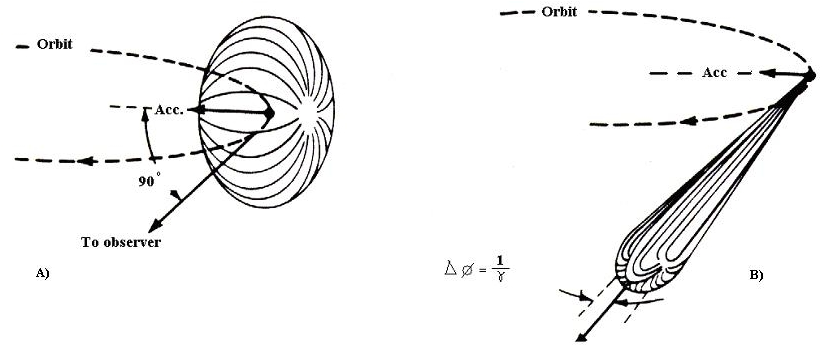
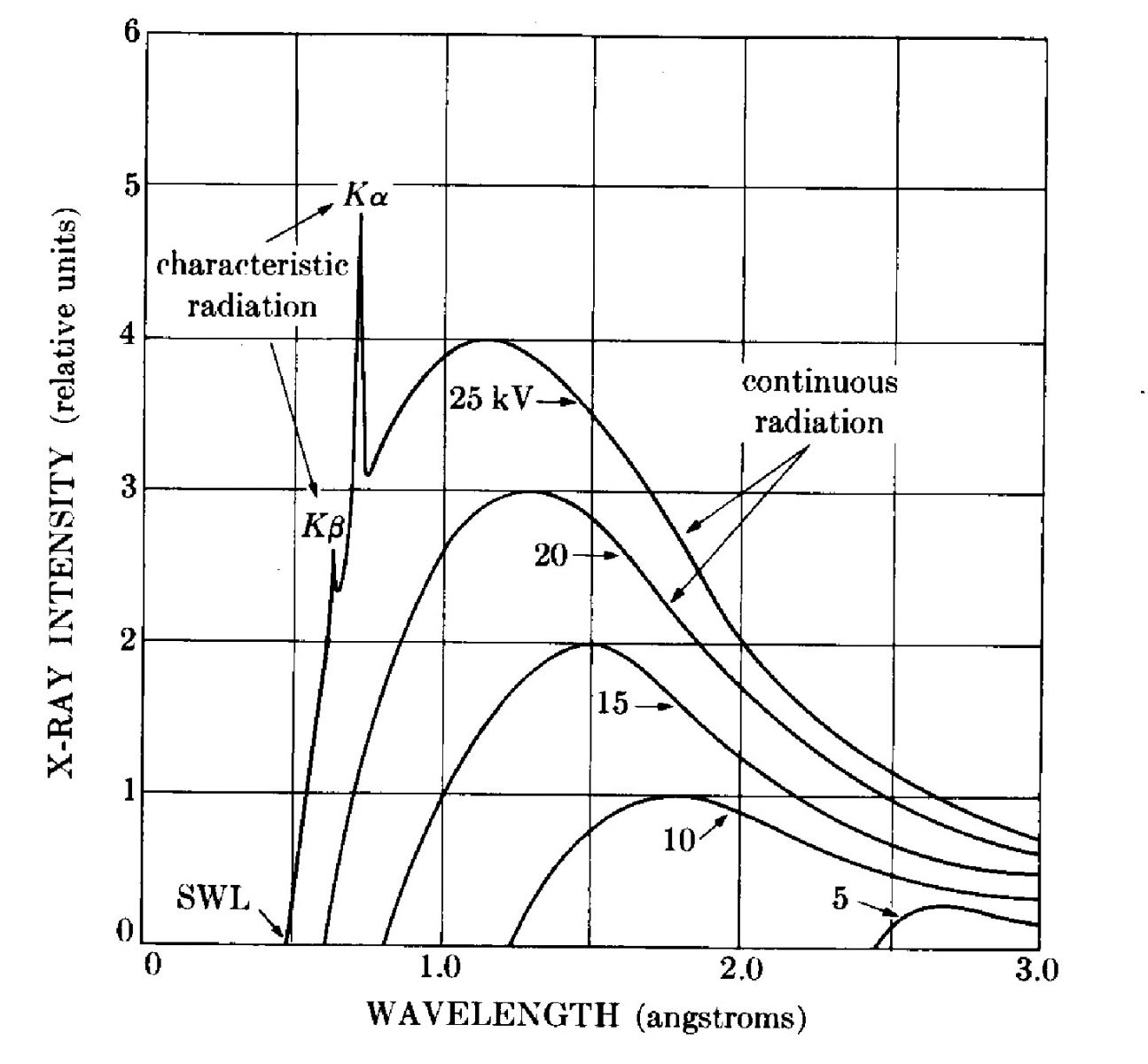
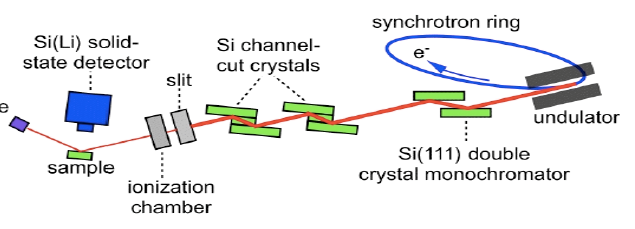
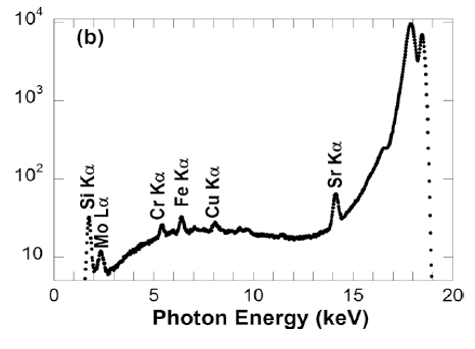
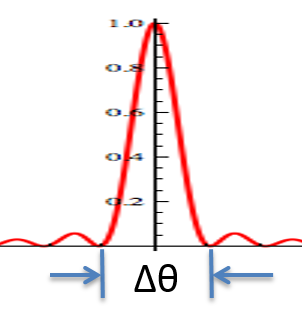
 Figure 12.3: Si wafer
Figure 12.3: Si wafer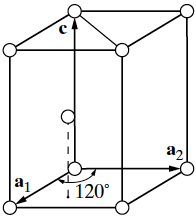
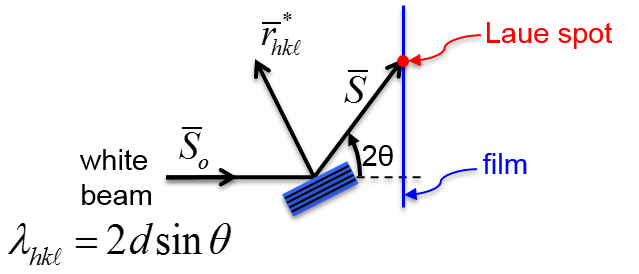 Figure 12.14: Laue spot position
Figure 12.14: Laue spot position
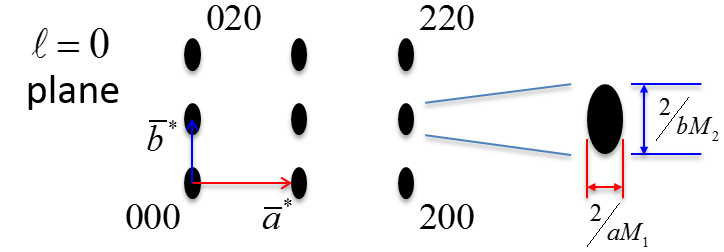

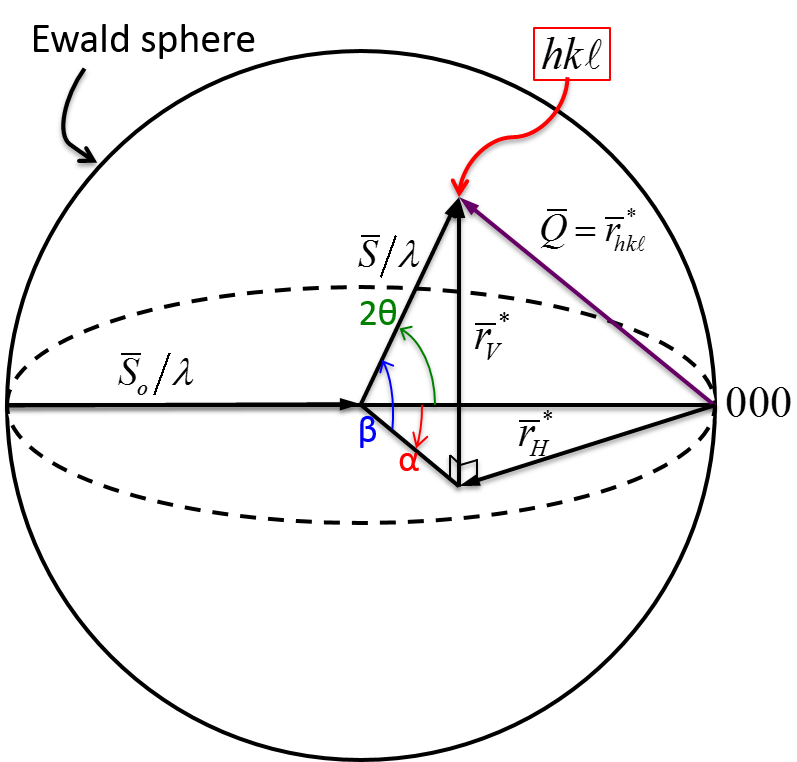


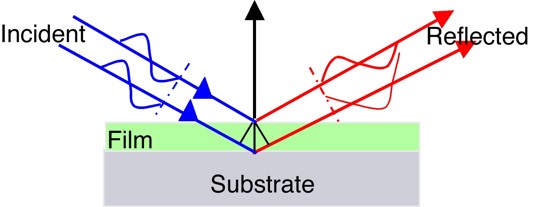
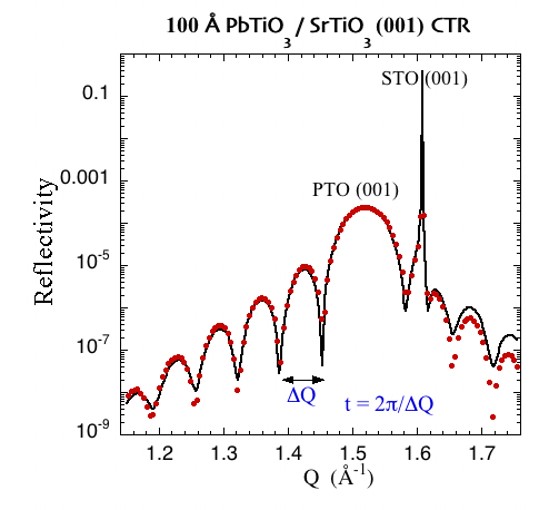
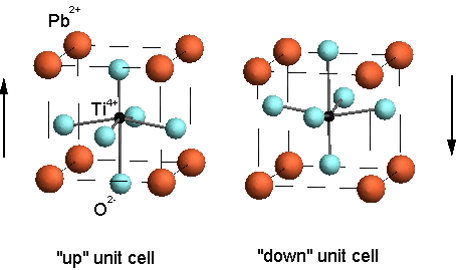
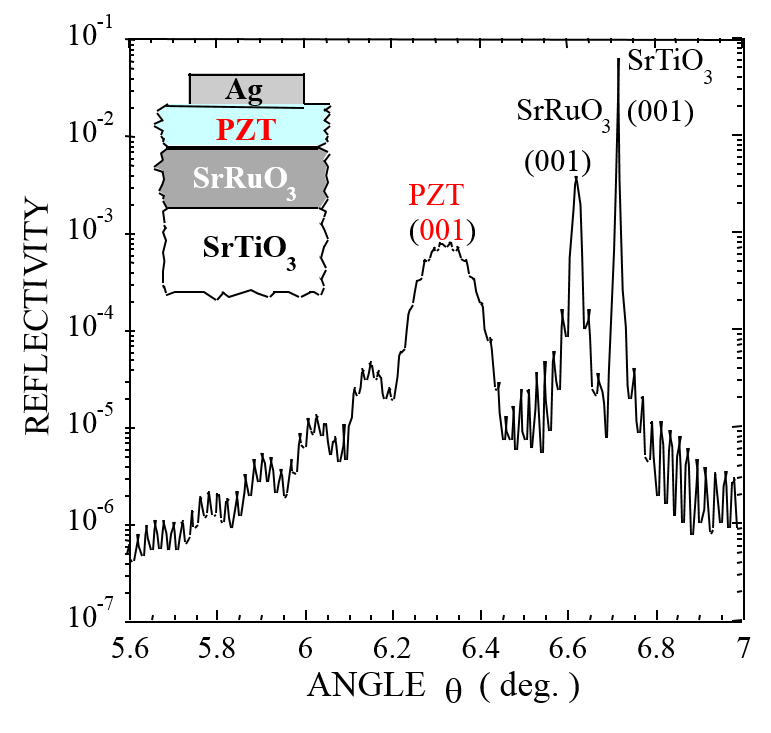
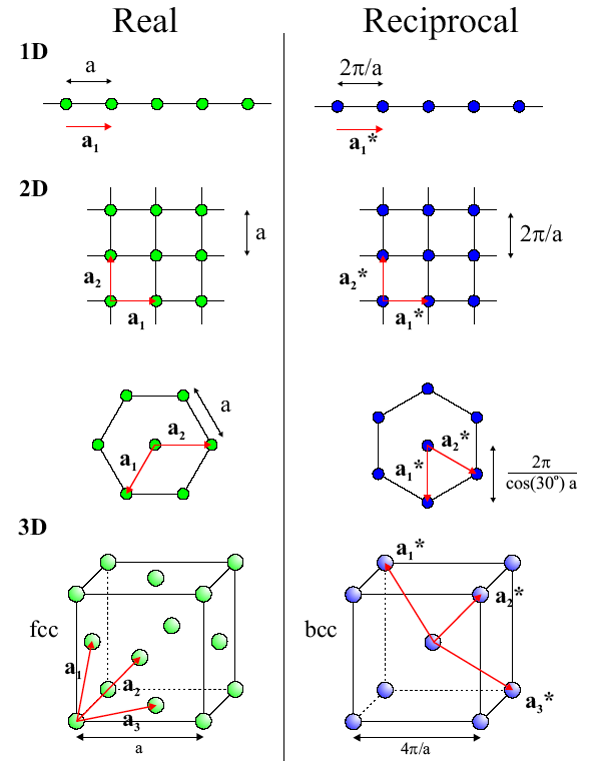
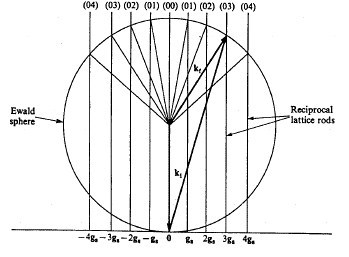
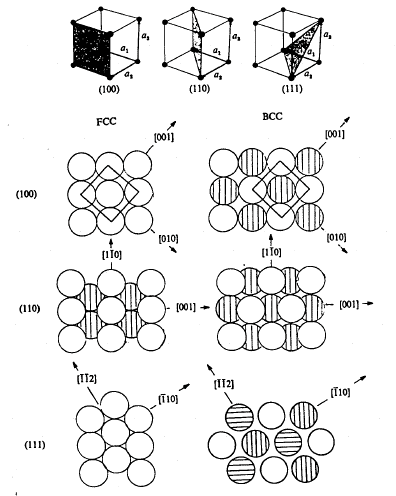 Figure 14.12: Low-index ideal surfaces of hard-sphere cubic-F & cubic-I crystals
Figure 14.12: Low-index ideal surfaces of hard-sphere cubic-F & cubic-I crystals Figure 14.13:
Figure 14.13: 
 Figure 14.15: Overhead schematic view of 18kW rotating anode setup in Nu X-ray Lab used for XRR, XRF and XSW measurements of SAM-Si (111) samples
Figure 14.15: Overhead schematic view of 18kW rotating anode setup in Nu X-ray Lab used for XRR, XRF and XSW measurements of SAM-Si (111) samples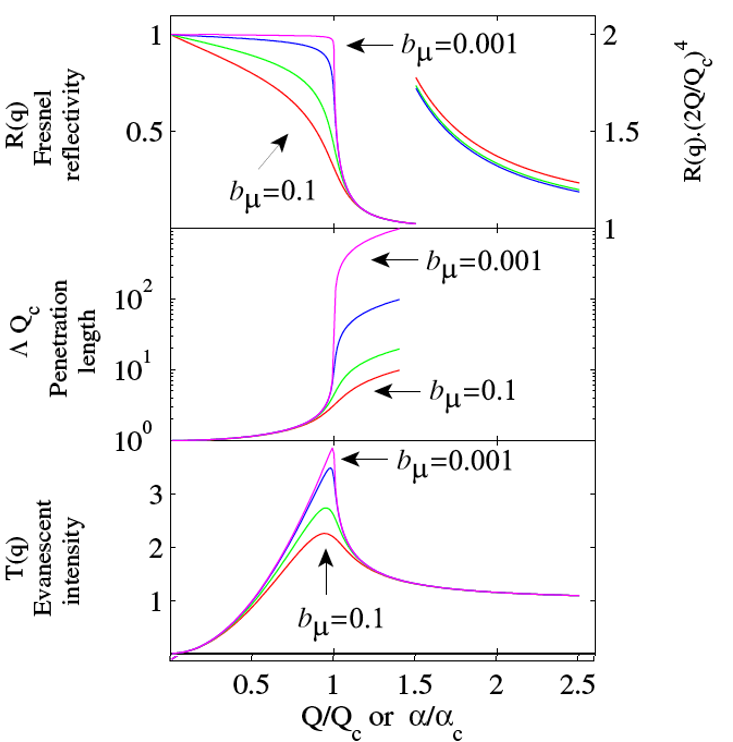 Figure 14.17:
Figure 14.17:  Figure 14.18: SAM/Si (111)
Figure 14.18: SAM/Si (111)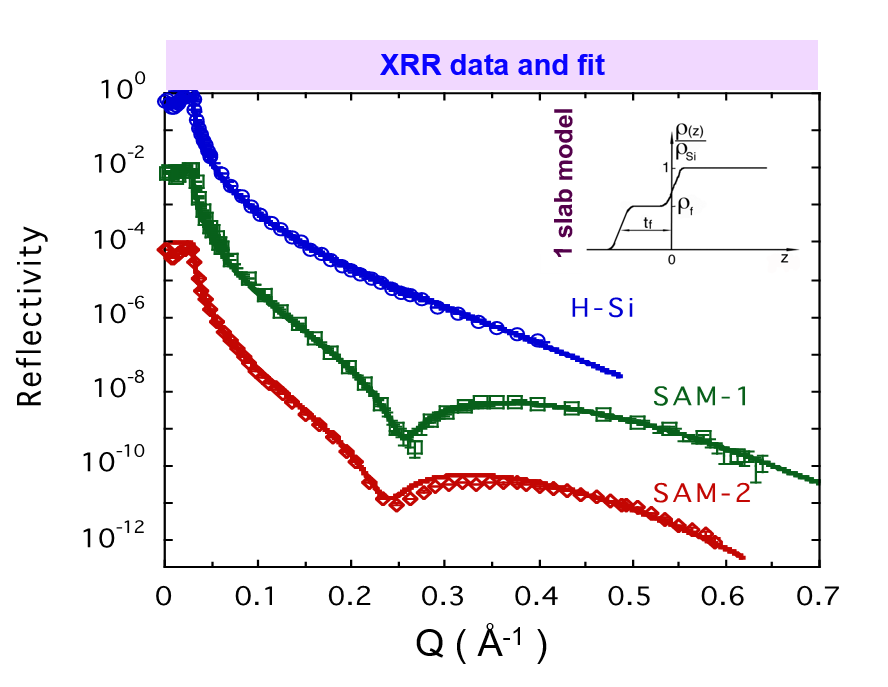
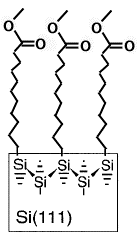
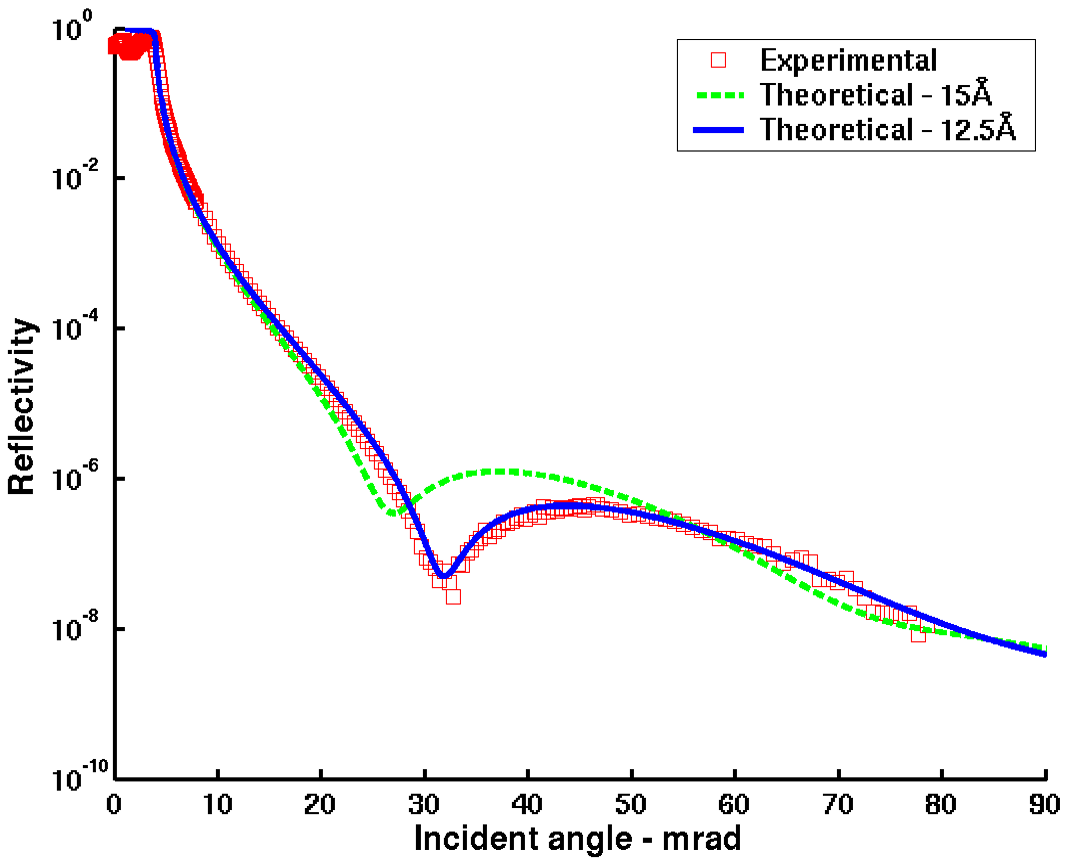 Figure 14.21: Tilt Angle = , 8.04keV @NWU X-ray Lab March 2003
Figure 14.21: Tilt Angle = , 8.04keV @NWU X-ray Lab March 2003 Figure 14.22:
Figure 14.22: 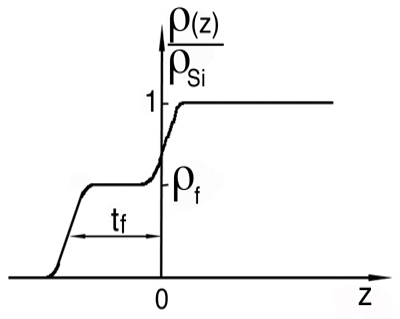 Figure 14.23:
Figure 14.23:  Figure 14.24:
Figure 14.24:  Figure 14.25: XRR Analysis of attached to Silica surface; Grown by the Mirkin Group at NU
Figure 14.25: XRR Analysis of attached to Silica surface; Grown by the Mirkin Group at NU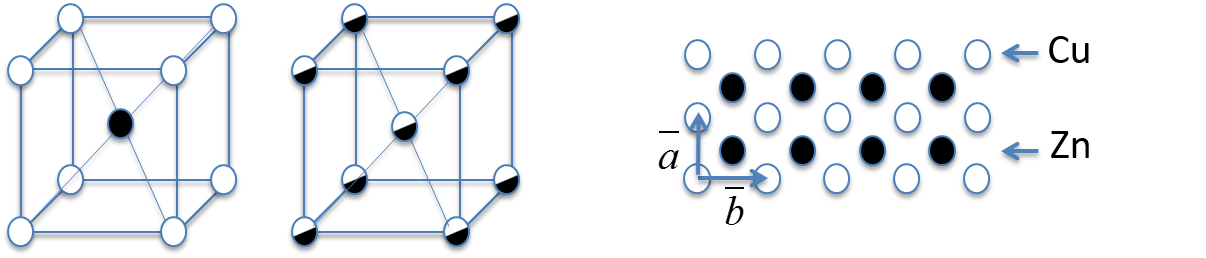
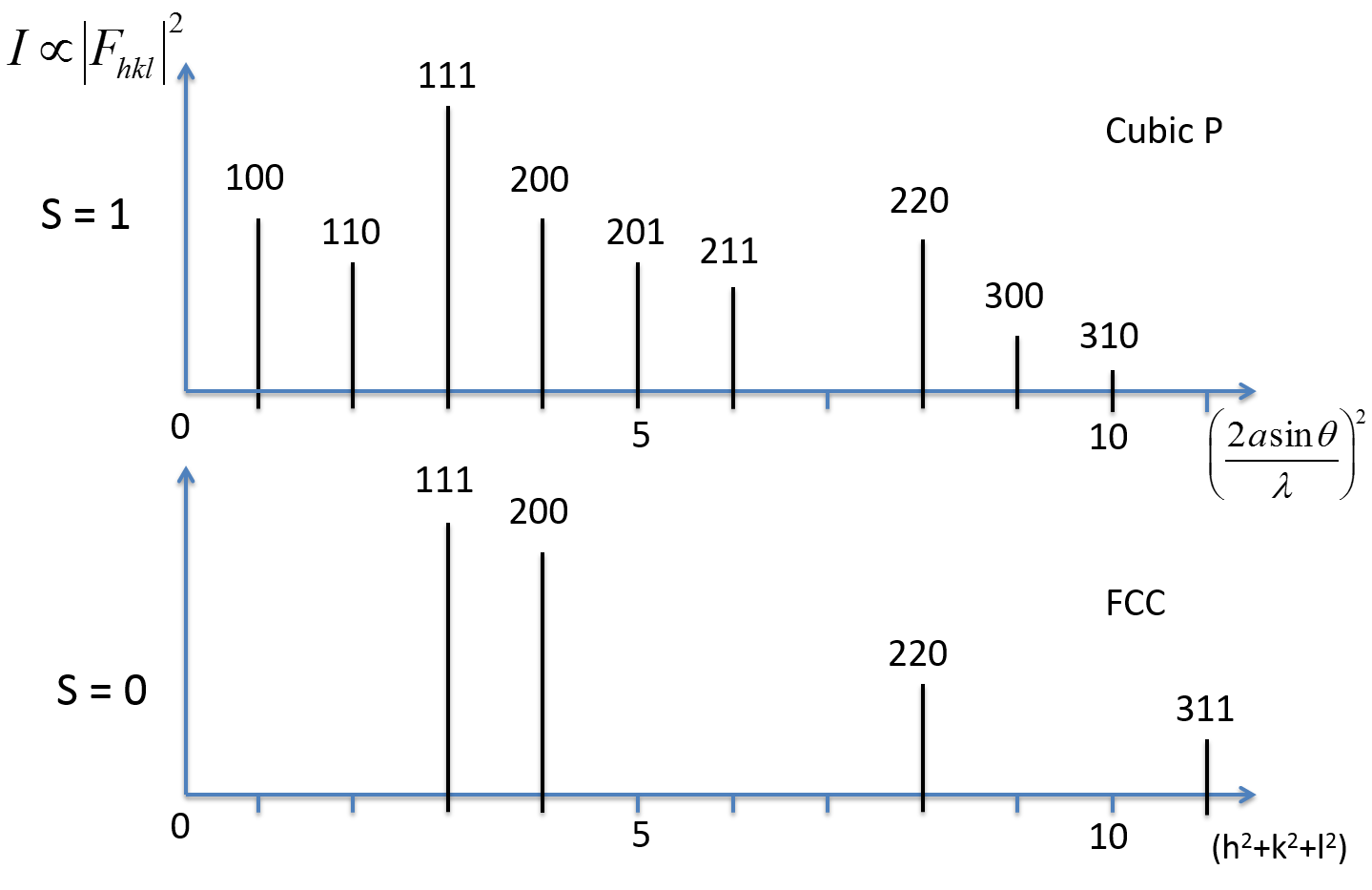 Figure 15.3: Powder XRD Patterns
Figure 15.3: Powder XRD Patterns
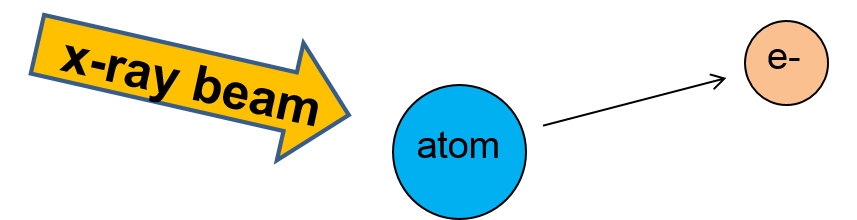
 Figure 16.1: XAFS overview
Figure 16.1: XAFS overview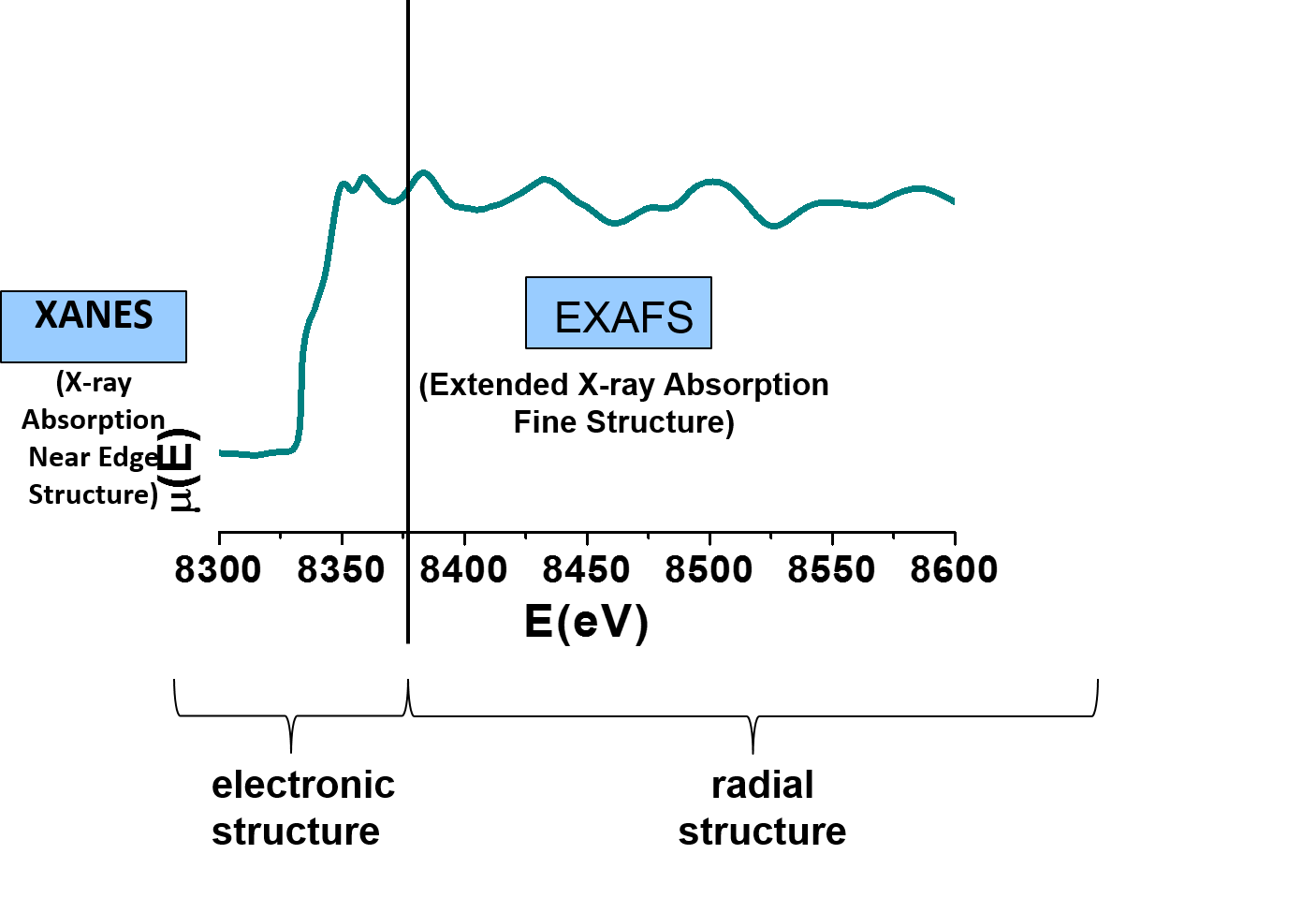 Figure 16.2:
Figure 16.2: 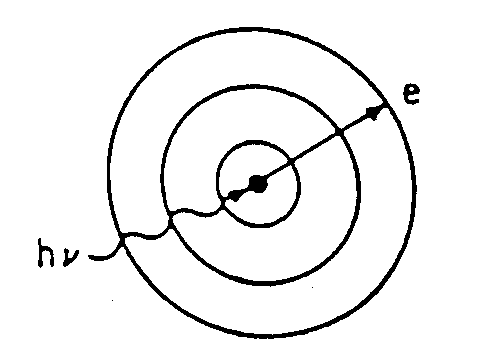 Figure 16.3: Outgoing photoelectron
Figure 16.3: Outgoing photoelectron
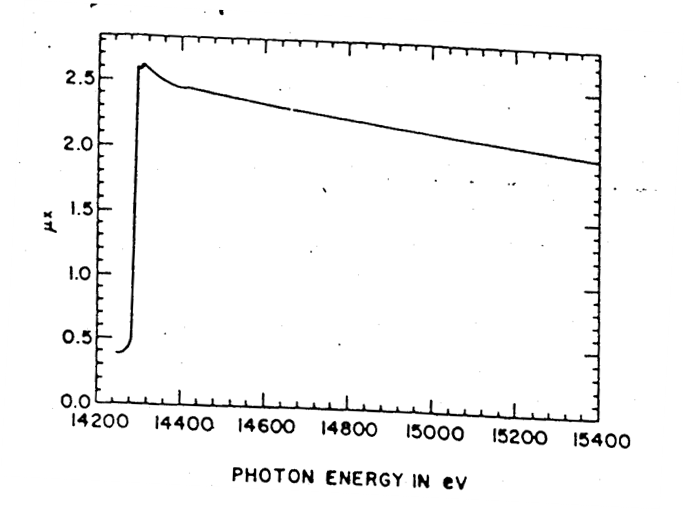
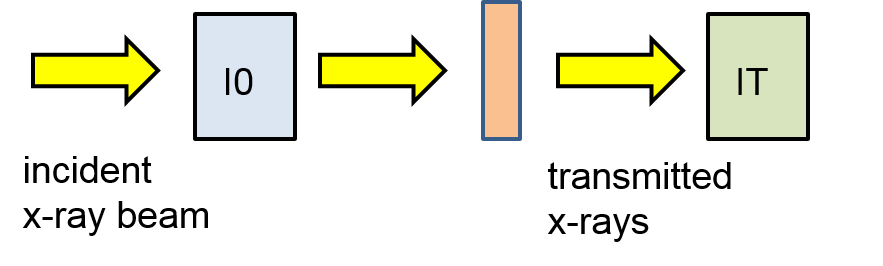
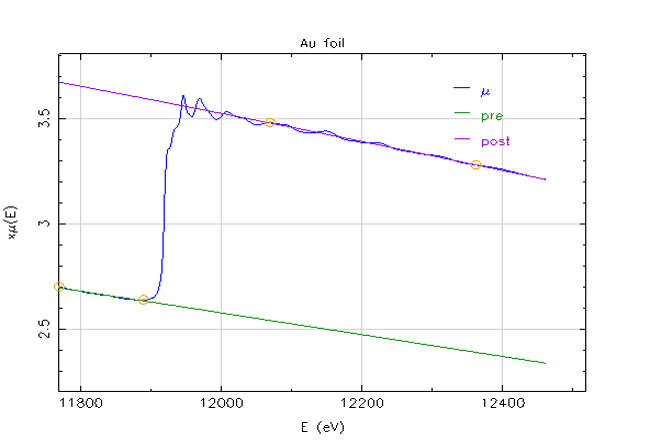
 Figure 16.10: Background subtracted data in k-space
Figure 16.10: Background subtracted data in k-space
 Figure 16.12: Reduction in CN
Figure 16.12: Reduction in CN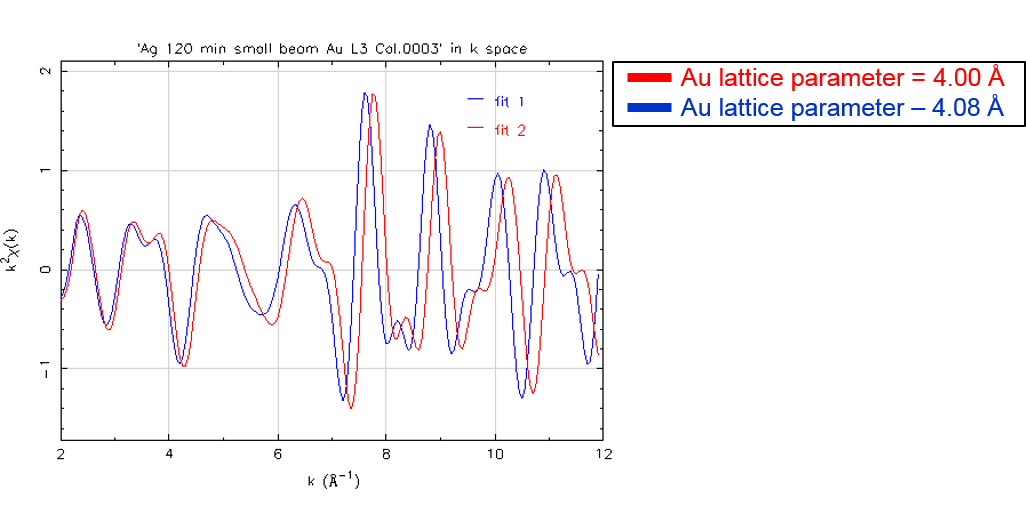 Figure 16.13: Change in interatomic spacing
Figure 16.13: Change in interatomic spacing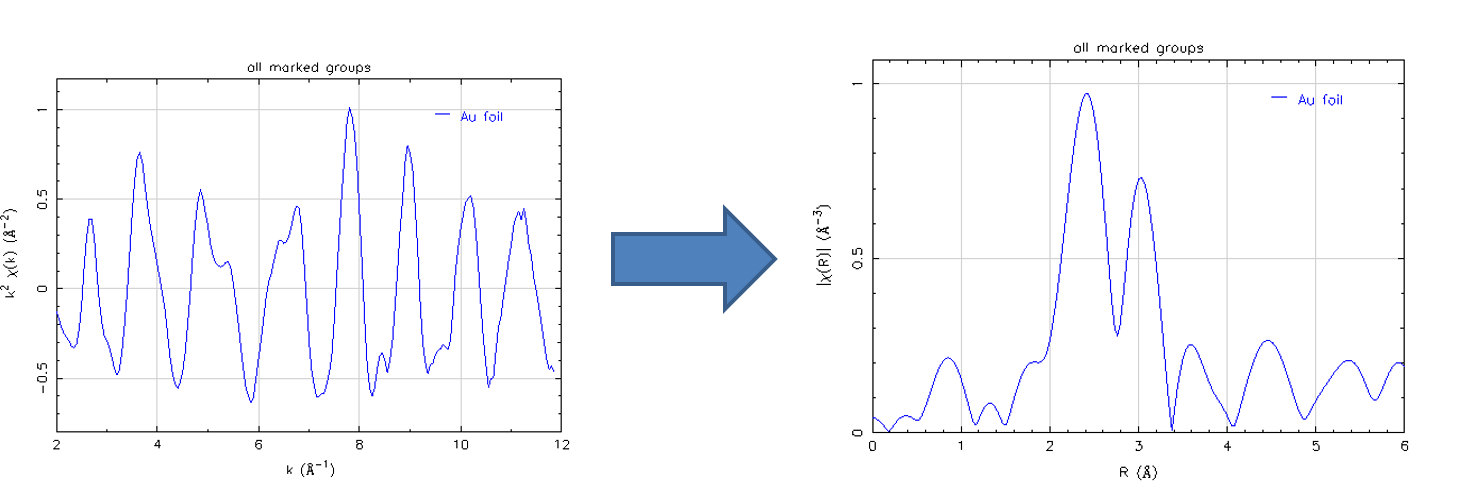
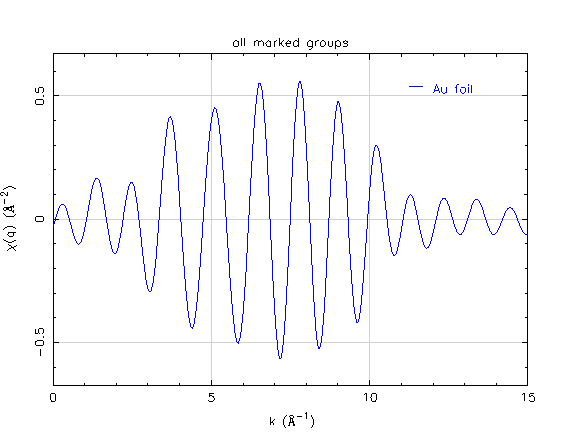
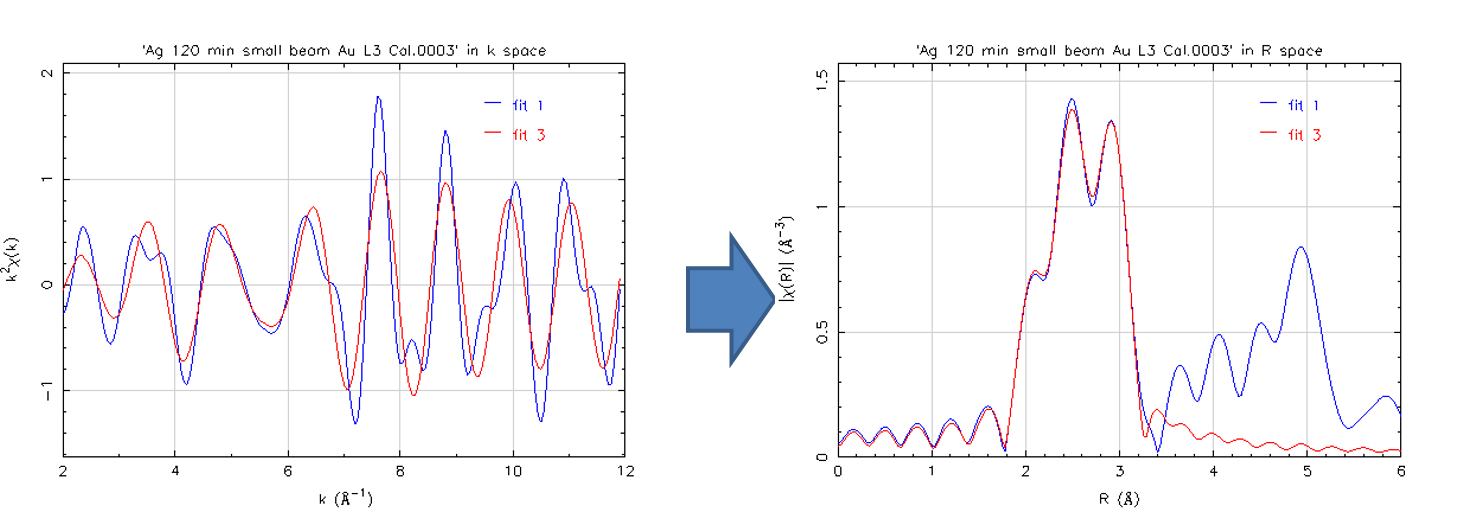 Figure 16.16: Single vs. multiple coordination shells
Figure 16.16: Single vs. multiple coordination shells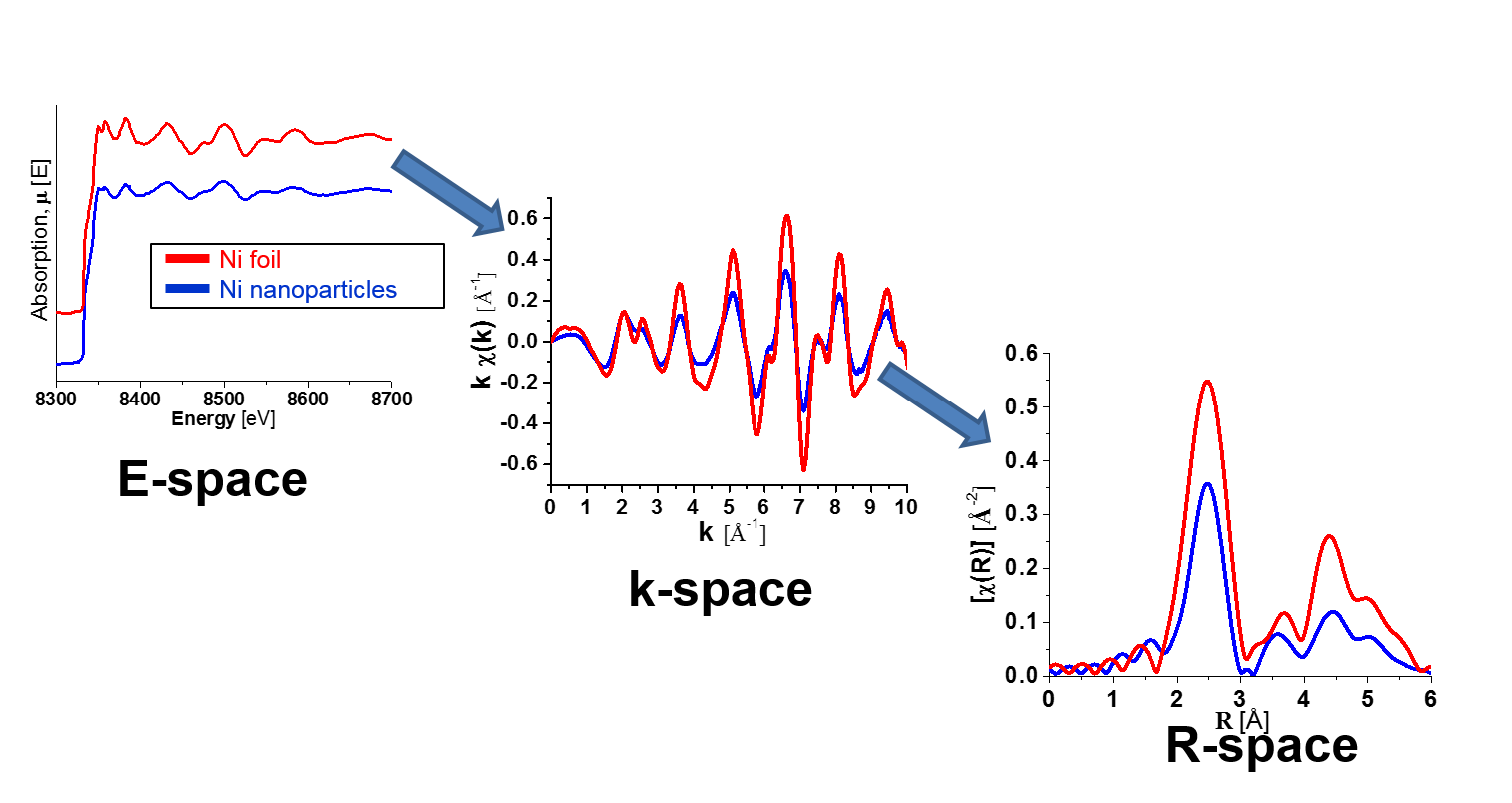 Figure 16.18:
Figure 16.18: 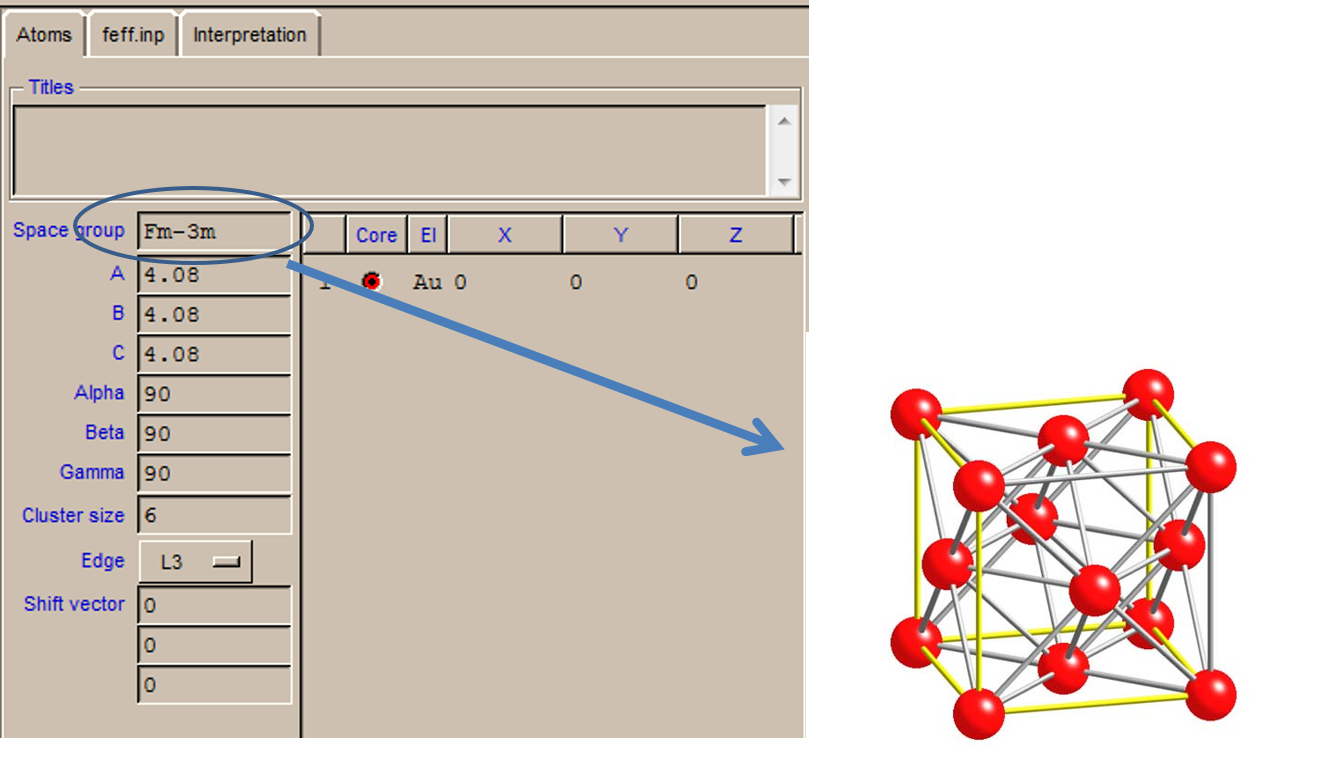 Figure 16.19: , space group
Figure 16.19: , space group 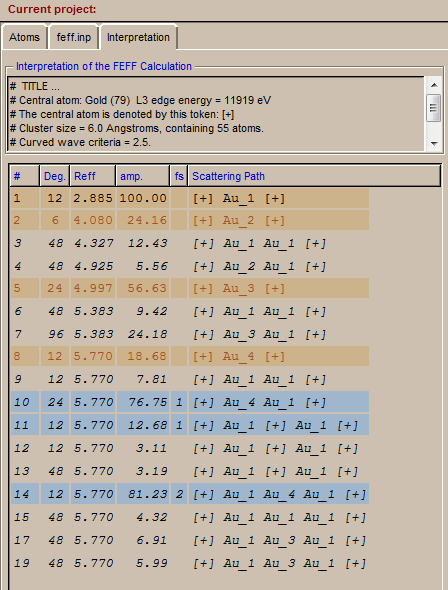
 Figure 16.20: Pathways
Figure 16.20: Pathways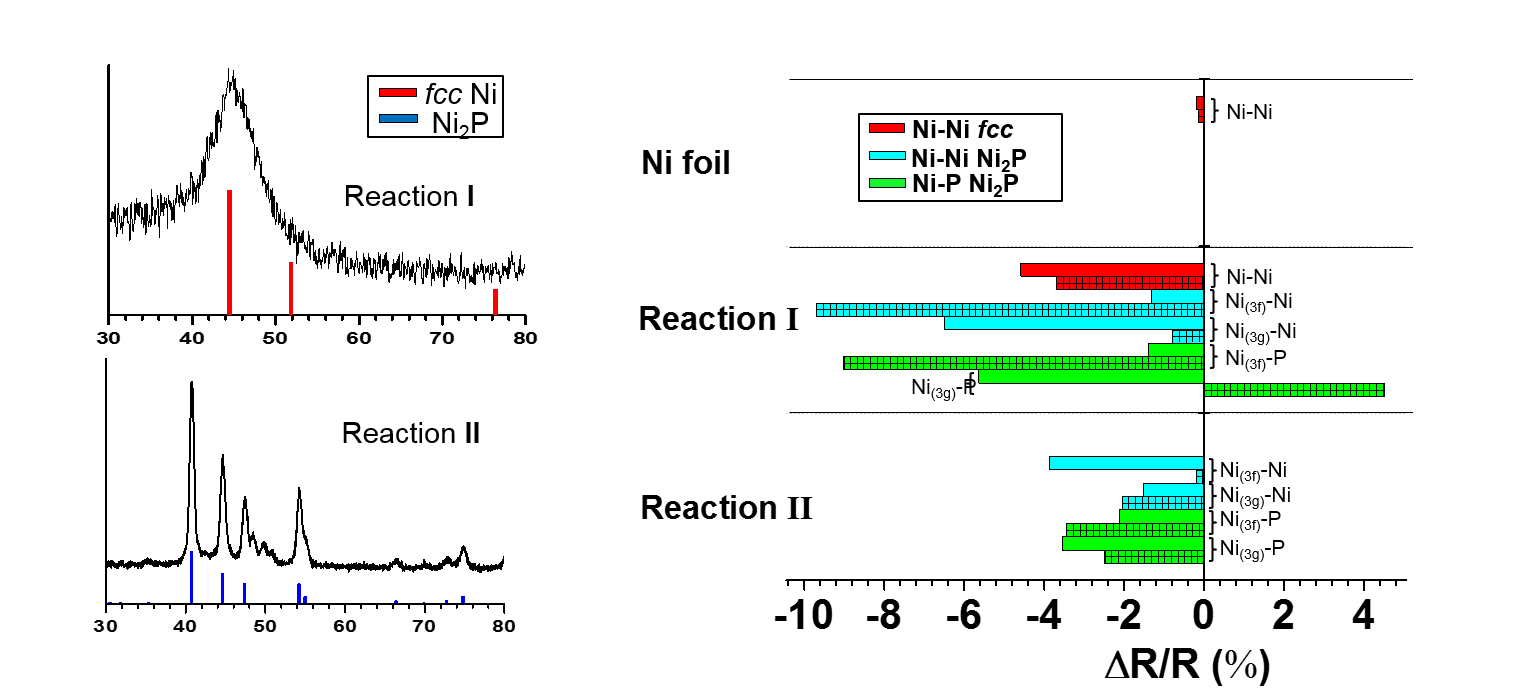
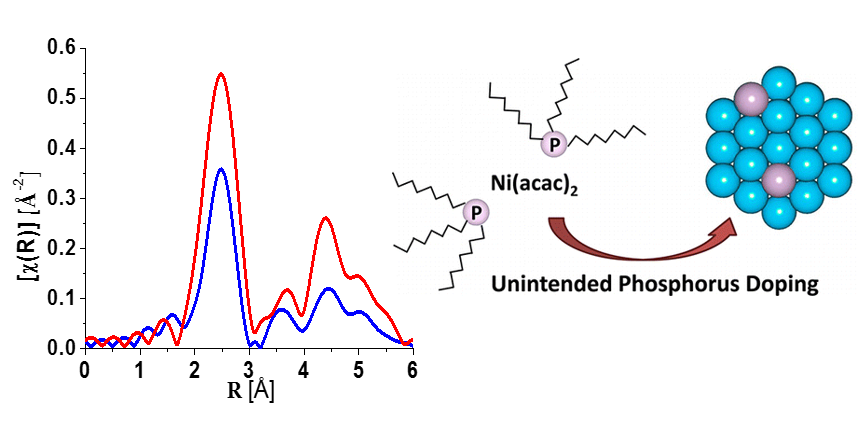
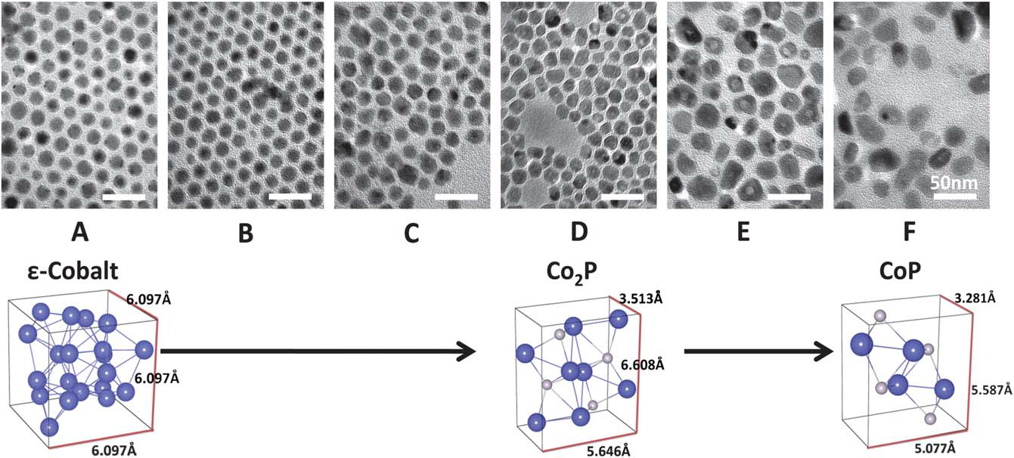
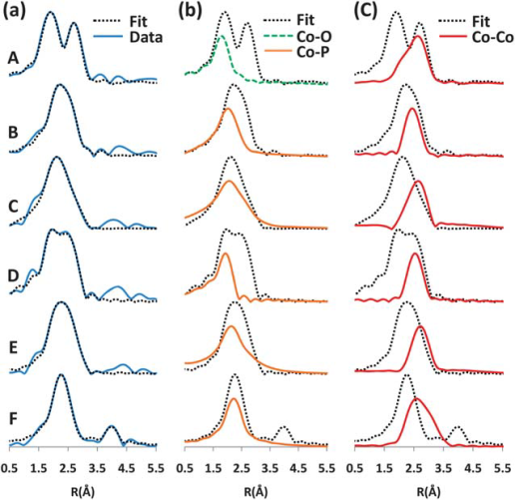
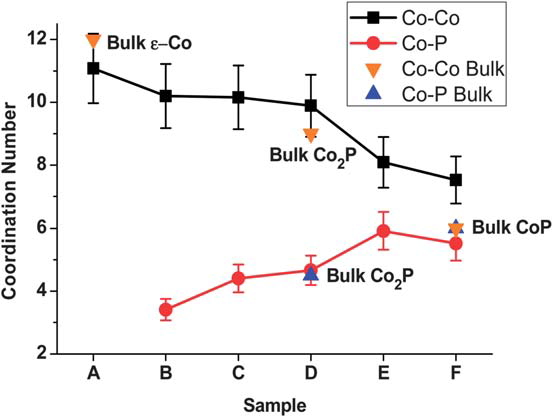

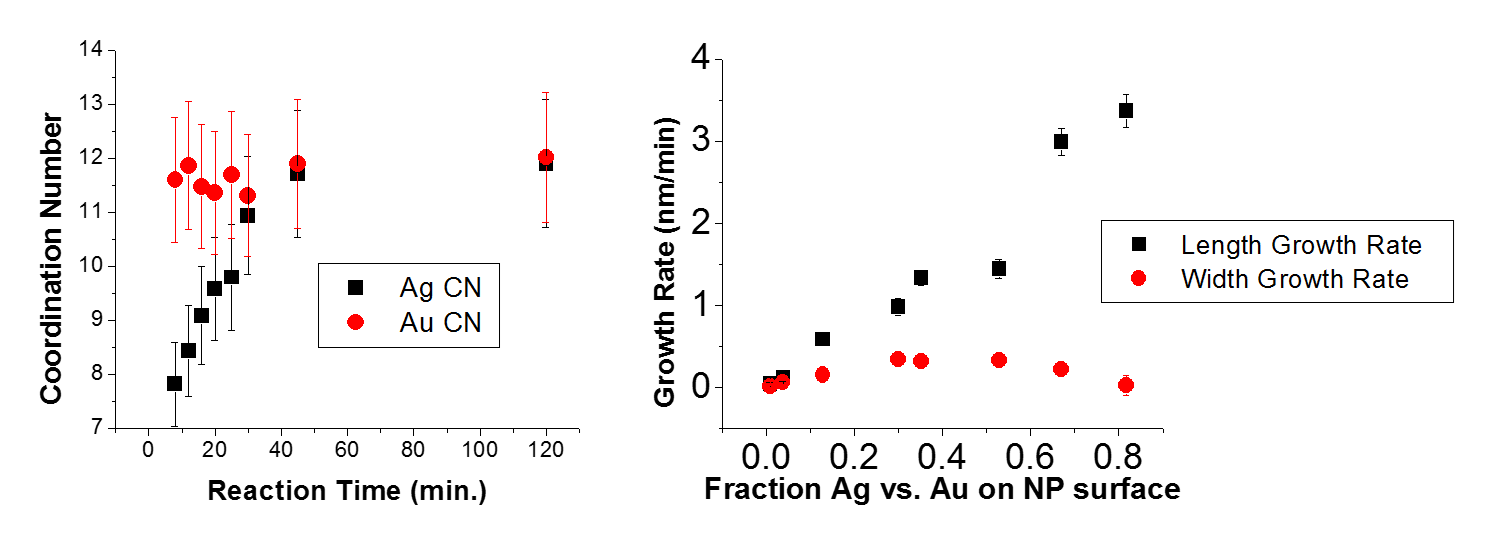
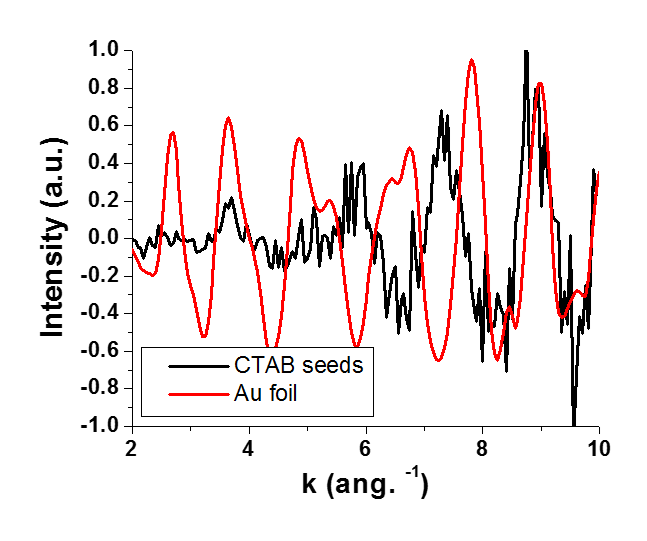
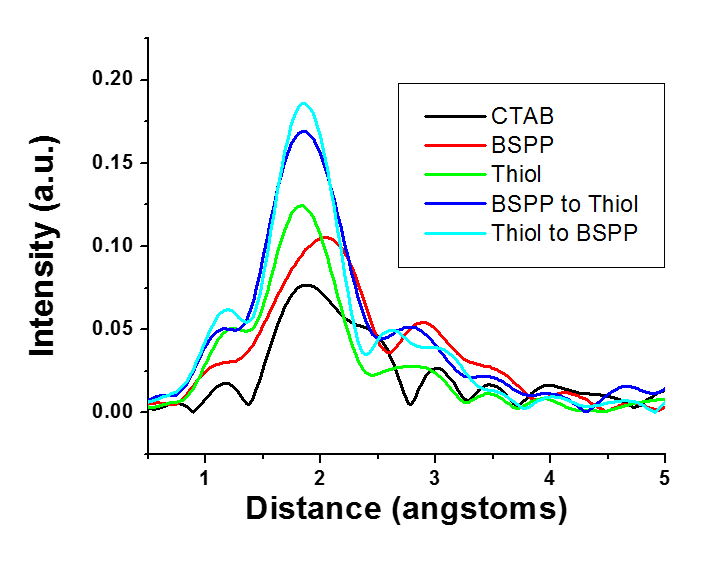 Figure 16.29:
Figure 16.29: